1-я Логика. Догматик. Особенность носителя первой логики — уверенность в своей правоте.
Если это человек умный, то подобная
уверенность, как правило, рождается не на
пустом месте: прежде чем сформировать
собственное мнение, он вначале собирает
информацию, а уж потом формирует свое
собственное. Вот почему попытки же оспорить его
мнение позволяют
посчитать спорщиков «людьми неумными»,
и искренне удивляться, как можно не
понимать очевидных вещей. Догматик
любит поговорить на интересующую его тему,
и послушать, что скажут другие умные люди,
чтобы в процессе обсуждения сформировать
свое мнение, и не любит спорить только для
того, чтобы доказать свою правоту. Он не любит длинных рассуждений, допущений и
прочих риторических приемов, целью которых
является подвести слушателей к принятию
его точки зрения. Так же ему неинтересны
чужие рассуждения, целью которых является
доказать ошибочность его собственных
суждений — он ведь уверен в их правильности,
поэтому попытки его переубедить кажутся
ему глупыми и смешными, а если оппоненты
ведут себя слишком активно, это может его раздражать. 2-я Физика. Труженик. Область материального мира — это та сфера,
где Труженик может проявить себя. Труженик — трезвый и практичный
человек, крепко стоящий на ногах. Всю свою
жизнь Труженик совершенствует свои навыки
в различных прикладных областях,
оттачивает различные технологии, повышает
квалификацию. Обладатель второй физики
способен помогать окружающим в их
взаимодействии с материальным миром ради
собственного удовольствия. Труженику
доставляет удовольствие разбирать все
детали, мелочи, из которых складывается
жизнь, давать советы, принимать активное
участие в материальной жизни близких ему людей. В тоже время он не
забывает и о своих собственных
потребностях, умея получать физическое
удовольствие и приспосабливаться к любым
условиям, обеспечивая и себе и окружающим
его людям физический комфорт. 3 Воля. Мещанин. Свои желания представителем третьей воли осознаются
плохо. Он может фантазировать на тему «чего
бы я хотел», но не сделает и шага в
выполнении хотя бы одного своего желания, а
если ему указать на это, упрекнув тем самым
в непоследовательности, он может обидеться.
При этом Мещанину свойственно
ощущение, что его собственные желания и его
права никем
не учитываются. А поскольку четкого
определения, что это за «права», и где
находятся их границы, Мещанин не имеет,
подобное противоречие
доставляет ему множество страданий. Когда у
него возникает чувство, что его в чем-то «ущемили»,
Мещанин способен возмущаться и «добиваться
справедливости». Или же он будет молча
страдать в сторонке, если не уверен, что
имеет право возмущаться, или будет копаться
в себе и убеждать себя, что это ему просто
показалось. По этой причине Мещанин нуждается в активном
диалоге окружающих в вопросах его
собственных прав и желаний. 4-я Эмоция. Зевака. Для Зеваки свои собственные эмоции
имеют очень мало значения. Он не уверен ни в
«правильности» своих эмоций, ни в самом
факте их существования. Однако
эмоциональные люди его привлекают. Зевака
способен заражаться чужими эмоциями:
улыбаться, когда вокруг все улыбаются, или
грустить, когда окружающие грустят. В то же время его могут раздражать попытки
«вникнуть в его эмоциональное состояние»
и подстроиться под него, для Зеваки это
может показаться неискренностью. Носитель
четвертой эмоции полностью зависим в
своих эмоциональных оценках от
мнения окружающих, особенно если эти оценки
хорошо сочетаются с его мнением по
вышестоящим функциям, со временем он
нарабатывает готовые шаблоны таких мнений
по вопросам человеческих отношений,
нравственности, характеристикам тех или
иных произведений искусства и т. |
Психософия (психейога, типология Афанасьева)
Психософия (Психе-йога, психейога, типология Афанасьева) — это типология, созданная А.Ю.Афанасьевым на базе соционики, которую он по-своему интерпретировал. В отличие от соционики, которая исследует структуру человеческой психики, психософия изучает сферу
Согласно психософии, всю сферу человеческого бытия можно условно разделить на 4 аспекта — Физика (материя), Логика (знания), Эмоция (эмоции, предчувствия), и Воля (цель).
Подробнее: Аспекты в психософии
По каждому аспекту у любого человека возможна одна из установок сознания (прим. — введено Василенко А.
Я+ Вы- «Мое мнение — единственно
верное, вашего мнения не существует.
Я+ Вы+ «Я оставляю за собой право
думать так как я считаю нужным, ваше мнение
я тоже учитываю»
Я- Вы- «Я не уверен в себе, но и ваше
мнение вызывает у меня сомнение»
Я- Вы+ «Я не разбираюсь в этом и
полностью принимаю ваше мнение».
Подробнее: Структура приоритетов. Функциональные установки в психософии
Комбинирование различных вариантов
установок по каждому аспекту бытия дает нам
24 варианта типов в психософии (ПС-типов),
обозначающиеся буквенными аббревиатурами (в
зависимости от порядка каждого аспекта в
его структуре) и псевдонимами.
Подробнее: Описание типов в психософии
Как и в соционике, в психософии изучается вопрос совместимости. Возможны различные варианты отношений между представителями различных ПС-типов, которые могут быть более, или менее комфортными, в зависимости от положения того или иного аспекта в структуре приоритетов каждого типа.
Подробнее: Интертипные отношения в психософии
Таблица интертипных отношений в психософии
Психософия: шкала приоритетов человека
Познакомившись с соционикой, люди часто задумываются о том, что соционический тип не описывает их целиком, а дуальные отношения не всегда такие идеальные, как об этом пишут. В этот момент стоит отметить важность такого знания, как психософия. Психософия позволяет определить характер человека порой лучше, чем соционика.
Психософия (психейога) — это типология людей
Психософский тип, в отличие от соционического, меняться может: для этого нужно пережить какое-то потрясение. Кроме этого, если соционический тип человек приобретает с рождения, то психософский тип формируем. Чаще всего он формируется из самого детства – детские обиды и недомолвки становятся третьей функцией в психософии (слабой и ранимой), а детская уверенность и похвала родителей формирует первую функцию (самую уверенную и сильную).Основатель психософии А.Ю. Афанасьев выделил 4 сферы жизни человека, которые для каждого имеют свой приоритет. Эти сферы называются:
Содержание статьи
Логика
Логика отвечает за мыслительный процесс человека, с помощью нее человек приходит к ответам на жизненно-важные вопросы, в зависимости от того, важен ли этот аспект человеку, он либо задается философскими вопросами и уделяет внимание мыслительной деятельности, либо же его это не беспокоит.
1 логика
Человек, обладающей первой логикой, постоянно мыслит. Этот человек думает перед сном, по дороге на работу, за обедом, в отпуске — всегда. Поэтому обладатель первой логики имеет установившиеся в своей голове истины, которые сложно поколебать. Представителя первой логики очень сложно переубедить в чем-либо. Этот человек уверен, что его точка зрения – правильная, поскольку он достаточно над ней подумал.
Человек с первой логикой не любит спорить, поскольку для него истина уже ясна и ему не нужно ее никому доказывать. Для того, чтобы чувствовать себя умным, ему не нужна отдача – он и так прекрасно знает, что его мысли правильные (даже если это далеко не так). Представитель первой логики не любит объяснять материал другим людям и делиться знаниями, он не видит в этом смысла.
2 логика
Человек, обладающей второй логикой, считает, что истина рождается в споре. Этому человеку нужно услышать не только себя, но и других, ему нравится процесс обмена мыслями и идеями, ведь только совместно можно достичь какой-то правильной мысли.
Представители второй логики обладают удивительным качеством строить долгие речи: именно среди них часты ораторы, способные говорить подряд по 5-10 часов. Люди со второй логикой любят задавать вопросы и отвечать на вопросы, они стараются объяснить максимально ясно любой непонятный момент. Из них получаются лучшие учителя, которым нравится процесс преподавания материала.
3 логика
Человек, обладающий третьей логикой, имеет прозвище «скептика». Третья функция в типе психософии является ранимой, одновременно сильной и слабой, жаждущей признания и боящейся выделиться. Именно третья логика позволяет обладателю ее долго молчать, слушать речи представителей высоких логик, а затем разнести в пух и прах все их теории, указав на явные несостыковки. При этом, третья логика редко высказывается сама – ей проще искать ошибки в мыслях других людей.
Представители третьей логики очень не любят категоричные суждения, и, даже зная ответы на вопросы, часто молчат, боясь ошибиться.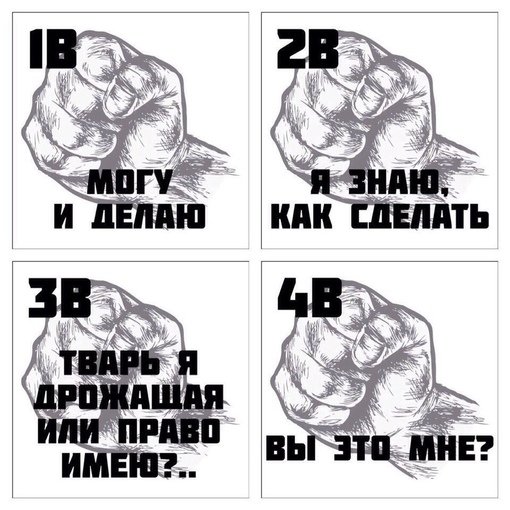
Особенно сильно третья логика страдает в школе, когда преподаватель спрашивает что-либо, а школьник с третьей логикой знает ответ, но боится его произнести, чтобы, в случае чего, не остаться осмеянным.
4 логика
Может сложится ложное впечатление, что представители четвертой логики не думают вообще. Это совсем не так: просто в своей шкале приоритетов эти люди отводят логике последнее, менее важное место. Представители четвертой логики очень просто усваивают любую информацию, не особо «переваривая» ее.
Их не задевает догматичность первой логики, они лишь могут уставать, когда от них требуется постоянный диалог: им просто это не интересно. Люди с четвертой логикой должны понимать, что не стоит выбирать профессию, связанную с постоянной интеллектуальной деятельностью – этим они испортят жизнь и себе, и другим.
Физика
Физика отвечает за ощущения человека в материальном мире. Физика – это материальный аспект, это ощущение себя частью физического мира, это важность осознания потребностей своего тела.
1 физика
Представителя первой физики видно издалека – этот человек занимает пространство. Не обязательно у него должен быть избыточный вес, хотя многие обладатели первой физики имеют крупную фигуру, скорее это просто ощущение себя в пространстве. Представители первой физики имеют «избыточную» красоту, про них говорят, что этих людей «много».
Для обладатели первой физики очень важно быть всегда сытым, выспавшимся, здоровым – эти люди могут плохо работать потому, что они поели меньше, чем нужно. Люди с первой физикой имеют свой стиль в одежде, умеют себя подать. Если их критиковать в плане внешности, то эти люди просто рассмеются – они уверены в своей неотразимости и знают лучше других, как нужно одеваться.
2 физика
Представители второй физики – это люди хозяйственные, сильные, способные долго и упорно работать. Обычно люди со второй физикой – лучшие врачи и массажисты: везде, где нужен контакт с человеком, где необходимо почувствовать, как больно, а как нет – эти люди эксперты.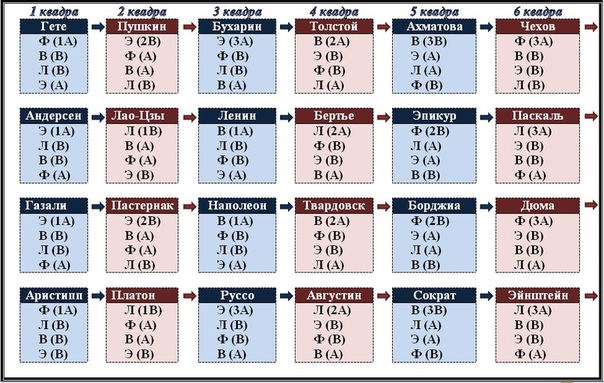
Они чувствуют других людей.
Представители второй физики стараются сделать комфортной жизнь своих близких — пытаются накормить детей и внуков, убрать квартиру и протереть везде пыль, при этом, у них остаются силы и на другую деятельность. Люди со второй физикой любят обсуждать кулинарию, домашнее хозяйство, болезни и другие аспекты, связанные с телом человека и его ощущениями.
3 физика
Люди с третьей физикой не уверены в себе в вопросах внешности и тела: часто такие люди комплексуют по поводу лишнего веса, садятся на диеты, долго не могут выбрать подходящую одежду, иногда делают пластические операции. Для них вопросы внешности являются очень важными, но при этом у них нет уверенности в своей неотразимости.
Любой прыщик может испортить настроение представителю третьей физики, а над прической такой человек может работать каждое утро по часу, и ему будет не лень – так ведь красиво! Большинство третьих физик отличается худобой, реже сутулостью. В вопросах физических отношений с противоположным полом третья физика часто имеет множество «тараканов».
4 физика
Представители четвертой физики отличаются некоторой ленью по отношению к вопросам тела. Обычно девушки с четвертой физикой не красятся вовсе, одеваются просто и не любят разговоров о косметике. Мужчинам с четвертой физике попроще — их обычно не мучают обсуждениями рецептов, болезней, одежды и красоты.
Люди с четвертой физикой имеют различное телосложение, при этом они всегда выглядят «воздушно». Эти люди не стремятся к материальной роскоши, им не нужны деликатесы и сложные сочетания вкусов: им достаточно удобной кровати и регулярного питания. Еще лучше, если о питании позаботится кто-то еще, а то самому можно и забыть о такой мелочи.
Эмоция
Эмоция отвечает за поддержание душевного фона в себе и в компании, за эмоции, за настроение и атмосферу.
1 эмоция
Для человека с первой эмоцией жизненная опора — это эмоции. Такой человек живет в своих переживаниях, при этом часто не замечая эмоций других. Представители первой эмоции очень вспыльчивы, эмоциональны, они могут сначала смеяться от вида красоты неба, а спустя минуту плакать, думая о том, как скоротечна жизнь.
Люди с первой эмоцией могут заразить любого человека своим настроением, перебить настроение толпы, испортить настроение кого-угодно. Со стороны первая эмоция порой выглядит неадекватной, но представитель этого часто не замечает — для него существуют лишь его эмоции.
2 эмоция
Человек со второй эмоцией – это лучшая «зажигалочка» в компании. Именно он поддерживает позитивный эмоциональный фон, старается улучшить настроение грустных друзей, всячески поддерживает шутки других. Представитель второй эмоции всегда проявляет свои эмоции уместно, в отличие от первой эмоции. Ему важно не его собственное состояние, а состояние людей вокруг — веселы они или нет, как можно их развеселить и сделать так, чтобы всем стало комфортно и хорошо.
В веселой компании представитель второй эмоции будет веселиться, на похоронах – грустить, и всегда это будет искренне и адекватно ситуации. Вторая эмоция прекрасно чувствует эмоции других людей и подстраивается под них.
3 эмоция
Представитель третьей эмоции — это человек, который внешне выглядит неприступной скалой, а внутри переживает ураган эмоций.
Он видит эмоции других людей, он чувствует, когда эмоция уместна, а когда нет, но сам не может выразить себя через эмоции — что-то мешает.
Нет ничего хуже для третьей эмоции, чем громкая истерика или неуправляемая эмоциональность. Человеку с третьей эмоцией физически становится плохо от криков людей, от чрезмерного смеха, от слез. Если при любой ссоре человек сразу просит: «Только без эмоций!», то, наверняка, это говорит его третья эмоция.
4 эмоция
Люди с четвертой эмоцией крайне редко проявляют свои эмоции. Обычно они настраиваются на волны других людей: к примеру, приходит четвертая эмоция в компанию, где все веселятся, и, волей-неволей, сама начинает улыбаться; вечер заканчивается, человек возвращается домой – эмоции куда-то делись. Представителям четвертой эмоции нравится, когда за них выставляют эмоциональный фон, а им остается лишь подстроиться – только так они чувствуют себя комфортно.
Воля
Воля отвечает за уверенность человека в способности изменить мир, обладать определенными желаниями и исполнять их.
От позиции воли зависит сила духа человека, пробивная способность.
1 воля
Человек с первой волей — это хозяин своей судьбы. Такой человек понимает, что от него зависит все, и готов идти к своим целям чего бы ему это не стоило. Он знает, что имеет право на любую цель и ее достижение. Представитель первой воли готов вести за собой людей — он прирожденный лидер. Ему не нужно советоваться с другими людьми по поводу своих действий: он идет и делает, пока другие переживают и думают, имеют ли они на это право. Представители первой воли готовы пожертвовать своими маленькими целями ради достижения чего-то грандиозного. Им нередко удается добиться всего, что они задумали.
2 воля
Представители второй воли — это те люди, которые, обладая большой силой духа, стараются не мешать другими жить своей жизнью. Люди со второй волей – это терпеливые, упорные и спокойные личности, которые способны заинтересовать других людей в том, чтобы вместе решить какую-то проблему.
Если первая воля двигается к цели в одиночку, то вторая воля предпочитает содружество и близость единомышленников. Среди начальников со второй волей много «демократов», людей, которые не ограничивают своих подчиненных, поощряя инициативу, и, при этом, не забывают о себе. Как правило, представители второй воли – это люди, имеющие внутри себя ощущение душевного комфорта.
3 воля
Представители третьей воли – это люди целеустремленные, активные, но при это очень неуверенные в себе и в том, что они имеют право на достижение поставленных целей. Именно третья воля часто знает больше всех, но боится идти на экзамен, ожидая провала. В любом, самом простом случае, третья воля задается вопросом: «А имею ли я право так делать?». В то время, пока первая воля бежит к цели, не обращая внимание на такие «глупости», третья воля стоит на месте, переживая и страдая.
Третьей воле не стоит брать на себя ответственность за всех и быть лидером — для нее это очень тяжело психологически.
При этом, представители третьей воли очень не любят, когда за них решают и им приказывают — поэтому людям с третьей волей оптимально работать либо на себя, либо в свободном демократичном коллективе.
4 воля
Люди с четвертой волей — совсем не безвольные существа, как могло бы показаться. Просто у представителей четвертой воли нет четких глобальных жизненных целей, они живут более маленькими отрезками. Люди с четвертой волей – милые, уступчивые и приятные в общении. Им нравится чужая инициатива, они легко соглашаются с решениями других людей.
Им не нравится уговаривать, придумывать, мотивировать, на это у них не хватает энергии – они просто хотят получить результат. Представители четвертой воли, чаще всего, являются ведомыми и в отношениях, и в карьере, и их это устраивает. Четвертой воле несложно отказаться от своих желаний и уступить, особенно, если они видят, как сильно другие хотят чего-либо.
Психософия: типы
Всего в психософии насчитывается 24 типа:
Психософия: отношения
В психософии выделяют три вида отношений: агапэ, эрос и филия.
Агапэ – это лучшие отношения, гармоничные и комфортные, по своей сути напоминают дуальные отношения в соционике. При них у партнеров меняются местами вторая и третья функции, а первая и четвертая остаются на одинаковых местах. Полное агапэ – это отношения, при которых меняются вторая и третья функции, а также первая и четвертая.
Филия – это отношения тождественных типов. С одной стороны, людям с одинаковыми типами несложно друг друга понять, а с другой – им невозможно прикрыть друг другу болевые точки.
Эрос – самые неблагоприятные отношения, в которых единица партнера попадает на вашу тройку, и наоборот. Полный эрос – это отношения, когда единица попадает на тройку, а двойка – на четверку. Эрос похож на конфликтные отношения в соционике.
Кроме этих видов взаимодействия, в психософии имеется множество несимметричных отношений, когда партнеры ощущают комфорт и дискомфорт неравноценно.
Смартфон Samsung Galaxy A40 64Gb черный характеристики
Обращаем Ваше внимание на то, что данный интернет-сайт и его содержимое носят исключительно информационный характер и ни при каких условиях не являются публичной офертой, определяемой положениями Статьи 437 Гражданского кодекса РФ.
Для получения подробной информации о наличии и стоимости указанных товаров Вы можете обращаться в официальные партнерские магазины Samsung.
Все изображения являются лишь иллюстрациями, все аксессуары продаются отдельно.
Все особенности и технические характеристики устройства актуальны на момент старта продаж, но в дальнейшем могут меняться без предварительного уведомления.
Доступный пользователю объем встроенной памяти меньше полной памяти устройства, поскольку часть памяти занята операционной системой и приложениями, обеспечивающими функционирование устройства. Реальный объем пользовательской памяти может зависеть от оператора связи и после обновления встроенного ПО.
Сеть: поддерживаемые диапазоны частот могут зависеть от региона и сетевого провайдера.
Экран измеряется по диагонали как полный прямоугольник без учета закругленных углов. Фактическая видимая область меньше из-за закругленных углов и выреза камеры.
Типичное значение, проверенное в сторонней лаборатории.
Стандартным значением является расчетное среднее значение с учетом различий в емкости среди образцов аккумуляторов, протестированных в соответствии со стандартом IEC 61960. Номинальная (минимальная) емкость составляет 3020 мА·ч. Фактический срок службы аккумулятора может варьироваться в зависимости от сетевой среды, способов использования и других факторов.
Используемый объем памяти меньше общего объема памяти из-за хранения операционной системы и программного обеспечения, необходимого для работы функций телефона. Фактический объем используемой памяти также может варьироваться в зависимости от оператора мобильной связи и может изменяться после выполнения обновлений программного обеспечения.
Пи закодировано в образцах жизни
— Автор: Santiago Schnell
Каждый год 14 марта -го математическим ученым, таким как я, поручают писать статьи о древнем и загадочном числе: Пи. Обозначается греческой буквой «π» и используется в математике для обозначения константы, приблизительно равной 3,14159.
Первоначально Pi был открыт как константа, равная отношению длины окружности к ее диаметру. Это число рассчитано с точностью до одного триллиона цифр после десятичной точки.Вычисления могут продолжаться бесконечно без повторений или шаблонов, потому что Pi — иррациональное число. Математики назвали это иррациональным, потому что Пи нельзя выразить как отношение целых чисел.
Как для детей, так и для взрослых, число Пи вызывает недоумение … константа с бесконечным числом цифр и без образца. Все мы узнаем о Пи на уроках геометрии в старшей школе. Однако Пи, похоже, не имеет практического применения за пределами мира геометрии. Так почему же Пи — геометрическая постоянная — заслуживает празднования? Если мы празднуем Пи, почему бы нам не отметить другое число? Ну, Пи отличается от всех остальных чисел.Это универсальная константа, закодированная в большинстве процессов, происходящих во Вселенной, в том числе в науках о жизни!
Теперь вам, вероятно, интересно, как Pi появляется в биологических процессах.
Ответ на этот вопрос лежит в междисциплинарной области биофизики: биология + физика. Биология изучает жизнь и живые организмы. Биологи изучают, как организмы растут, добывают пищу, общаются, ощущают окружающую среду и реагируют на нее, воспроизводятся и развиваются. С другой стороны, физика изучает природу и свойства материи и энергии.Физики ищут математические законы природы и Вселенной. Биофизики ищут закономерности в жизни и анализируют их с помощью математики, чтобы получить новое представление о том, как работают организмы.
Давайте теперь рассмотрим одну из закономерностей, наблюдаемых в науках о жизни. Внешний вид плана тела организма — процесс, называемый морфогенезом, — одна из самых ярких черт живых существ. У животных эмбрион вырастает из почти однородной группы клеток в узорчатую структуру с мозгом, позвоночником и конечностями.В 1952 году математик и отец информатики Алан Тьюринг предложил математическую модель, описывающую простые биофизические принципы формирования паттернов во время морфогенеза.
Он предположил, что эмбрион приобретает различные анатомические особенности с помощью химических веществ (названных Тьюрингом морфогенами), которые диффундируют через ткани. В простейшем случае формирование рисунка происходит в результате реакции двух морфогенов, активатора и ингибитора. Активатор усиливается самостоятельно и может распространяться только локально.Он также стимулирует рост ингибитора, который, в свою очередь, подавляет активатор и распространяется на большие расстояния. Математический анализ и компьютерное моделирование этой, казалось бы, простой системы показывают, что модель Тьюринга дает ошеломляющее множество узоров, включая пятна и полосы. Морфоген-активатор образует локальные пятна из пятен или полос, в то время как ингибитор предотвращает слишком близкое срастание пятен друг с другом. Модель Тьюринга подтверждается экспериментальными данными как один из возможных механизмов, управляющих формированием паттернов во время роста организмов.Фактически, это может объяснить образование полос и пятен на шубах животных, пигментных отметин на тканях, строение конечностей и развитие небольших пальцевидных выступов в кишечнике животных, которые значительно увеличивают площадь поверхности кишечника, используемую для поглощения пищи.
Как число Пи, не имеющее паттерна, играет роль в формировании паттерна ? Закройте глаза и представьте себе полосы зебры. Эти полосы имеют размер и интервал, которые кодируются константой: Pi! То же самое и с пятнами леопарда.Фактически, кажется, что Пи кодирует размер и интервал многих паттернов, не ограниченных областью биологии.
Компьютерное моделирование модели Тьюринга дает ошеломляющее множество паттернов, включая пятна и полосы. [/ caption] Пи также тесно связано с периодическими процессами. Это проявляется в управляющих биофизических законах времени деления клеток, ударов сердца, дыхательного цикла и циркадных ритмов, контролирующих циклы сна и бодрствования. Однако это еще одна интересная и захватывающая тема на стыке физики и биологии, которую нам нужно оставить на следующий год.Вам просто нужно подождать π x10 7 секунд!
Об авторе
Сантьяго Шнелл — профессор молекулярной и интегративной физиологии, вычислительной медицины и биоинформатики Медицинской школы Мичиганского университета.
Он является одним из ученых, которые обнаружили, что модель Тьюринга объясняет образование небольших пальцевидных выступов в кишечнике млекопитающих. Сантьяго Шнелл является членом Биофизического общества, членом Королевского химического общества и президентом Общества математической биологии.
Страница Pi-Search
Страница Pi-SearchРезультаты
Строка встречается в позиции. Эта строка встречается раз в первых 200 млн цифр числа Пи.
отсчет от первой цифры после десятичной точки. 3. Не в счет.
Строка и окружающие цифры:
(текстовая версия — бета!)
Извините, нам не удалось найти вашу строку в Pi! Но продолжайте поиски — Пи содержит много других интересных строк.
2013-05-19 Существенная переработка: поиск числа числа числа пи стал интерактивным. Он ищет по мере ввода. Могут быть ошибки — дайте нам знать.
11/7/2011 — Pi Searcher пытается присоединиться к современному миру.
Подпишитесь на нас в Google Plus, чтобы получать обновления каждые несколько недель, а также занимательные математические и мелкие вопросы о Пи.
Pi Searcher позволяет искать любую строку цифр (до 120 из них) в первых 200 миллионах цифр числа Пи . Ты можешь также показать любую подстроку Pi.
В 1996 году Артур Бебак из ныне несуществующей компании Netsurfer Дайджест в шутку подсказал эту идею. Я выложил сайт онлайн, связал из также ныне несуществующих страниц бесполезных веб-страниц. Исходное предложение должен был найти свой день рождения в Пи, но все вышло из-под контроля. В в оригинальном поисковике числа пи было 1,25 миллиона цифр. Он был обновлен в В 1998 г. до 50 млн, в 2001 г. до 100 млн, в 2005 г. до 200 миллион цифр, чтобы идти в ногу со временем. Pi Searcher доказал, что как исключительно бесполезные (см. комментарии ниже), так и иногда полезно на уроках математики и начальных естественных наук.
Как это работает
Pi Searcher использует комбинацию линейного поиска (поиск каждой цифры один за другим) для небольших строк поиска и предварительно вычисленный индекс для большие строки поиска.
В результате поисковик Pi чрезвычайно
быстро — для обработки большинства запросов требуется менее 1/50 секунды.
Для получения дополнительной информации посмотрите, как работает Pi Searcher.См. Нашу новую страницу с цифрами Пи еще больше цифр …
Меня часто спрашивают, где люди могут получить такой смехотворно большое количество пи.Имейте в виду, что 50 миллионов цифры пи занимает 50 мегабайт. Это может занять до 4 часа скачать с модемом 28,8к!
Я проверил цифры своих 200 миллионов по источникам, перечисленным выше, и считаю, что они верны. Однако, если есть ошибка, пожалуйста уведомить меня по электронной почте dga — at — pobox DOT com и я обновлюсь.
Вы можете найти исходный код поисковика pi здесь в формате tar.gz.
Почему я не могу найти свой номер в Пи? Если мы рассмотрим Пи как большую случайную строку чисел (что достаточно близко для наших целей), тогда мы можем вычислить шансы найти любой строка из первых 100 миллионов цифр числа Пи:
| Длина номера | Вероятность нахождения |
|---|---|
| 1-5 | 100% |
| 6 | Почти 100% |
| 7 | 99. 995% |
| 8 | 63% |
| 9 | 9,5% |
| 10 | 0,995 %% |
| 11 | 0,09995% |
К счастью, если вы добавите нули, дни рождения состоят из 8 цифр, поэтому у вас есть 63% шанс найти свой день рождения из первых 100 миллионов цифры пи. Теперь, когда мы достигли 200 миллионов, шансы до 86%, так что пройдет некоторое время, прежде чем каждый сможет найти свой день рождения в Пи.
Я также опубликовал более подробное объяснение вероятности нахождения строк в Pi для любопытных людей.
Информация о конфиденциальности запроса.
Дополнительная информация о Pi …
День из жизни Пи
Большинство людей слышали о математической константе Пи (π) и знают, что она примерно равна 3,14. Вдохновленный этими тремя цифрами, 14 марта (3/14 в формате даты в США) объявлен Международным днем Пи, впервые отмеченным американским физиком Ларри Шоу в 1988 году.
Этот год дает уникальную возможность продемонстрировать совершенно ненужное рвение, отметив День Пи с точностью до девяти знаков после запятой 14 марта 2015 года, в 9,26 утра 53 секунды, что соответствует 3,141592653, первым 10 цифрам числа Пи. Если вы слишком заняты в эти выходные, вы можете забронировать номер на 22 июля — еще один способ приблизительно обозначить Пи — это дробь 22/7.
Пи Пай в Делфтском университете.Пи рассчитывается как отношение длины окружности к ее диаметру.
Пи — это всегда одно и то же значение, независимо от размера круга, что делает его важной математической константой.
Древние вавилоняне вычислили Пи как три, взяв в три раза квадрат радиуса круга, а затем уточнили это значение до 3,125. Архимед Сиракузский (287–212 гг. До н.э.) аппроксимировал число Пи, вписывая многоугольники внутри и снаружи круга. Увеличивая количество сторон многоугольников, можно было бы вычислить Pi с более высокой точностью.
Даже сегодня вычисление числа Пи с постоянно возрастающей точностью продолжается — теперь его точность превышает 13 триллионов цифр. Нет причин подозревать, что эта запись останется навсегда, хотя для обеспечения астрономической точности достаточно всего 39 десятичных знаков. Для практических целей нет причин быть более точными, но это своего рода научный спорт — стремиться быть еще точнее.
Постоянно уменьшающееся число Пи. НемецкийНекоторые свойства Pi
Пи — иррациональное число, что означает, что его нельзя точно представить в виде дроби, a / b , где a и b — целые числа.Приблизительно это выражается как 22/7 (3,1428…), что неточно на 0,04025%. Более близкое приближение — 104348/33215, что имеет гораздо меньшую ошибку 0,00000001056%, но все же технически неверно.
Пи также является трансцендентным числом, которое в упрощенном виде представляет собой числа, которые не могут быть уменьшены алгебраически (точнее, число, которое не является корнем любого ненулевого полиномиального уравнения с рациональными коэффициентами).
Доказательство трансцендентности Пи было найдено в 1882 году, но было известно гораздо дольше, что если бы Пи было трансцендентным, то было бы невозможно возвести круг в квадрат — построить квадрат с такой же площадью, как у круга.
Numberphile: квадрат в круге.Использование Pi
Среди необычных применений Пи — его связь с природой извилистых рек. Путь реки описывается ее извилистостью, она имеет тенденцию изгибаться из стороны в сторону, пересекая равнину. Математически это описывается как длина извилистого пути, деленная на длину реки по прямой. Средняя река имеет извилистость около 3,14.
Альберт Эйнштейн на самом деле сделал несколько наблюдений о том, почему реки так изгибаются.Он заметил, что вода, которая быстрее течет по внешней стороне изгиба, быстрее размывает берег. Это создает больший изгиб.
Эти изгибы в конечном итоге встречаются, и река образует короткий путь через них. Ханс-Хенрик Столум использовал эти наблюдения и отметил связь с теорией хаоса, которая предполагает, что, несмотря на выпрямление рек, когда реки пересекают короткие пути, извилистость имеет тенденцию возвращаться к Пи.
Дополнительные примеры того, где Пи появляется в реальном мире, можно увидеть в материале BBC, написанном для Дня Пи 2008 года, и в этом материале New Scientist, написанном для Дня Пи 2010 года. Например, число Пи можно найти в измерениях Великой пирамиды в Гизе, угловых расстояниях звезд на небе и в песне Кейт Буш. В текст были включены первые сто цифр или около того числа Пи, но она немного ошиблась на цифре 50.
Пи Кейт Буш.
Как отметить день Пи?
Если вам нравятся развлечения на субботу, связанные с Пи, вы можете попробовать:
- Проверить, отображается ли дата вашего рождения в десятичных разрядах числа Пи — у меня есть, начиная с 200703, хотя, если вы хотите узнать мой возраст, вам нужно будет найти его.
Запоминание первых цифр числа Пи. Может помочь пифилология — система мнемоники, которая поможет вам запоминать цифры. Есть даже пьес (стихотворений Пи), которые помогут вам запомнить. Вы не сможете побить рекордсмена, который на данный момент составляет 67 000 мест.
Изучив первый миллион цифр числа Пи, вы можете увидеть закономерность, которой нет ни у кого.
Ищу Пи в повседневной жизни.Например, он был показан в «Разрушителях легенд».
Подпишитесь на # piday2015 в Twitter и узнайте, как другие отмечали этот день в прошлом.
… и наконец
Альберт Эйнштейн, один из величайших ученых, которых знал мир, некоторое время работал над Пи, связанным с реками.
Случайно ли, что Альберт Эйнштейн родился 14 марта 1879 года? Как он сам сказал бы, Бог не играет в кости.
Чтобы получить больше кусочков Пи, попробуйте здесь или здесь.
Что такое Пи? | Живая наука
Понять число Пи так же просто, как сосчитать до единицы, двух, 3,1415926535…
Хорошо, мы будем здесь на некоторое время, если будем продолжать в том же духе. Вот что важно: Пи (π) — это 16-я буква греческого алфавита, которая используется для обозначения наиболее широко известной математической константы.
По определению, пи — это отношение длины окружности к ее диаметру. Другими словами, pi равно длине окружности, деленной на диаметр (π = c / d).И наоборот, длина окружности равна pi, умноженному на диаметр (c = πd). Независимо от того, насколько большой или маленький круг, число Пи всегда будет одним и тем же. Это число равно приблизительно 3,14, но это немного сложнее. [10 удивительных фактов о пи]
Значение пи
Пи — иррациональное число, что означает, что это действительное число, которое не может быть выражено простой дробью.
Это потому, что математики называют «бесконечной десятичной дробью» — после десятичной точки цифры идут вечно.
Приступая к изучению математики, учащиеся знакомятся с числом пи как 3,14 или 3,14159. Хотя это иррациональное число, некоторые используют рациональные выражения для оценки числа Пи, например 22/7 из 333/106. (Эти рациональные выражения имеют точность только до пары десятичных знаков.)
Хотя нет точного значения числа Пи, многие математики и любители математики заинтересованы в вычислении числа Пи с точностью до как можно большего числа цифр. Мировой рекорд Гиннеса по количеству цифр числа Пи принадлежит Раджвиру Мине из Индии, который в 2015 году называл число Пи с точностью до 70000 знаков после запятой (с завязанными глазами).Между тем, некоторые компьютерные программисты вычислили значение числа Пи более чем с 22 триллионами цифр. Подобные расчеты часто проводятся в День числа Пи, псевдопраздник, который отмечается каждый год 14 марта (3/14).
Цифры Пи
Первые 100 цифр Пи:
3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 7067
На первом сайте piday.
org указан миллион цифр.
Жизнь пи
Пи была известна уже почти 4000 лет и была открыта древними вавилонянами.Табличка где-то между 1900-1680 годами до нашей эры. обнаружил, что пи равно 3,125. Древние египтяне делали аналогичные открытия, о чем свидетельствует папирус Райнда 1650 г. до н. Э. В этом документе египтяне вычислили площадь круга по формуле, которая дает пи примерно 3,1605. Есть даже библейский стих, где кажется, что число пи было приблизительно равным:
И сделал он расплавленное море в десять локтей от края до края; оно было кругом, и его высота была пять локтей; вокруг него было тридцать локтей. — 3 Царств 7:23 (версия короля Якова)
Первое вычисление числа пи было выполнено Архимедом Сиракузским (287-212 до н.э.). Один из величайших математиков мира Архимед использовал теорему Пифагора, чтобы найти площади двух многоугольников. Архимед аппроксимировал площадь круга на основе площади правильного многоугольника, вписанного в круг, и площади правильного многоугольника, внутри которого был описан круг.
Полигоны, как их отображал Архимед, давали верхнюю и нижнюю границы площади круга, и он аппроксимировал число пи между 3 1/7 и 3 10/71.
Пи начал обозначаться символом пи (π) в 1706 году британским математиком Уильямом Джонсом. Джонс использовал 3,14159 в качестве вычисления числа пи.
Pi r в квадрате
В основной математике число «пи» используется для определения площади и длины окружности. Пи используется для нахождения площади путем умножения квадрата радиуса на пи. Итак, пытаясь найти площадь круга радиусом 3 сантиметра, π3 2 = 28,27 см. Поскольку круги естественным образом встречаются в природе и часто используются в других математических уравнениях, число «Пи» присутствует повсюду и используется постоянно.
Пи даже проник в литературный мир. Пилиш — это диалект английского языка, в котором количество букв в последовательных словах следует за цифрами числа пи. Вот пример из «Not A Wake» Майка Кейта, первой книги, когда-либо написанной полностью на пилише.
Теперь я падаю, усталый житель пригорода в жидкости под деревьями, Дрейфую среди лесов, тлеющих красным в сумерках над Европой.
Теперь имеет 3 буквы, I имеет 1 букву, осень имеет 4 буквы, имеет 1 букву и т. Д. И т. Д.
Эта статья была обновлена 19 октября 2018 г. старшим писателем Live Science Брэндоном Спектором.
Pi My Life Up — 300+ DIY-проектов, руководств и руководств
Присоединяйтесь и наслаждайтесь нашим последним предложением обучающих программ и проектов, которые помогут вам узнать больше о технологиях, программировании, Raspberry Pi, Arduino и многом другом.
Последние руководства и проекты Raspberry Pi
Наши самые популярные типы проектов
Последние учебные пособия по Linux
Последние учебные пособия по программированию
С помощью этого простого руководства вы узнаете все о том, как обрабатываются строки в языке программирования Python.
Узнайте, как определять, форматировать и изменять строки. Изучение строк — важная часть любого языка программирования.
В этом руководстве по Python мы проведем вас через шаги по использованию массивов. В этом руководстве вы узнаете, как использовать модуль массива в Python для создания и управления массивами с ограничениями типа.
ПодробнееПоследние электронные учебные пособия
Узнайте, как рассчитать последовательное сопротивление в этом простом руководстве.Мы рассмотрим пример того, как быстро рассчитать общее сопротивление с помощью. Существует также калькулятор, с помощью которого вы можете с минимальными усилиями проверить свои собственные расчеты.
ПодробнееВ этом руководстве мы рассмотрим все основы делителей напряжения и все, что вам нужно о них знать. Это важная часть электронных схем, и я настоятельно рекомендую вам потратить время на ее изучение и понимание.
Подробнее Электронные учебные пособияПоследние проекты Arduino
В этом учебном пособии вы пройдете все шаги по подключению светодиодной ленты APA102 RGB к Arduino.
Мы также проведем вас через процесс написания некоторого кода для управления светодиодной лентой. Это отличный проект, если вы любите играть с огнями.
Узнайте, как настроить акселерометр ADXL345 с Arduino. Это отличный датчик, который пригодится во многих уроках, особенно в тех, где есть движение. Мы используем библиотеку Adafruit, которая значительно упрощает это руководство.
ПодробнееБесплотный, романтичный, таинственный и полностью запоминающийся; НАСТОЯЩАЯ жизнь Пи.| Элиза Сэм | GIVE Nation
История, объяснение и любовь к π
“ Вероятно, ни один символ в математике не вызывал столько тайн, романтизма, заблуждений и человеческого интереса, как число Pi ” ~ Уильям Л. Шааф, Nature and История Pi πЧто такое Pi, π, peeeeeeeeeee?
Pi взаимозаменяемо обозначается строчной греческой буквой π (правильно или традиционно произносится «горох» или «пииии») , — универсальная известная математическая константа.
π уникален, потому что связан с циклами. Пример из реальной жизни, с которым все знакомы, — это ритмические процессы, такие как пульсирующее сердце, планета, вращающаяся вокруг солнца, или волны океана.
π — это отношение длины окружности круга (расстояние вокруг круга, обозначенное буквой C) к его диаметру (расстояние диаметра круга в его самой широкой точке, представленное буквой D ). Это соотношение, равное примерно 3,14, также фигурирует в формуле для площади внутри круга. A = πr 2, где π — греческая буква «пи», а r — радиус окружности ( расстояние от центра до обода ).
Длина окружности всегда равна 3,14 диаметра. π — это только приближение, потому что десятичные дроби бесконечны и в конечном итоге неизвестны. Удивительно, но π всегда выражает математическую связь между диаметром и длиной окружности, независимо от того, насколько мал или велик круг.
Если греческое изображение не рисует вам мысленную картину,
Введите π в калькулятор и нажмите ENTER .
3.14159265 появляется, но не потому, что это точное значение π, а потому, что дисплей калькулятора часто ограничен таким количеством цифр.
История π
Вселенная содержит множество круглых и почти круглых объектов; нахождение точного значения π помогает внести ясность в проектирование, строительство, производство и понимание того, что мы знаем.
Исторически сложилось так, что в течение некоторого времени у нас была только приблизительная оценка π.Получение более точного значения π привело к большей точности и развитию важных концепций и методов; такие как ограничения и итерационные алгоритмы. Что стало фундаментальной базой для новых областей науки и математики.
Источник фото.1900–1600 гг. До н. Э.
Около 4000 лет назад «древние вавилоняне вычислили площадь круга, взяв в 3 раза квадрат его радиуса, что дало значение пи = 3. Одна вавилонская табличка (ок. 1900–1680 гг.) BC) указывает значение 3,125 для π, что является более близким приближением.
Источник
1600–1500 до н.э.
«Папирус Ринда (около 1650 г. до н.э.) дает нам представление о математике древнего Египта. Египтяне рассчитали площадь круга по формуле, которая дала приблизительное значение 3,1605 для π ». Источник
Архимед нарисовал многоугольник внутри круга и нарисовал второй многоугольник за пределами круга. Затем он непрерывно добавлял все новые и новые стороны обоих многоугольников, приближаясь к форме круга. Достигнув 96-сторонних многоугольников, он доказал, что 223/71200 г. до н.э.
π было впервые вычислено греческим математиком Архимедом Сиракузским (287–212 гг. До н.э.). Архимед аппроксимировал площадь круга, используя теорему Пифагора, чтобы найти площади двух правильных многоугольников: многоугольника, вписанного в круг, и многоугольника, внутри которого была описана круг.
Поскольку фактическая площадь круга лежит между областями вписанных и описанных многоугольников, площади многоугольников задают верхнюю и нижнюю границы площади круга.
Архимед обнаружил, что значение π приближенно находится в этих пределах. В своем эксперименте Архимед доказал, что π находится между 3 1/7 и 3 10/71 ». Источник.
400–500 н.э.
Незнакомый с Архимедом или его работами, китайский математик и астроном Цзу Чунчжи (429–501) использовал аналогичный подход для вычисления отношения длины окружности к диаметру, равному 355 /. 113. Чтобы вычислить эту точность для π, он начал с вписанного обычного 24,576-угольника и выполнил длительные вычисления с использованием сотен квадратных корней с точностью до 9 знаков после запятой.Источник.
1500 нашей эры
Развитие техник бесконечных серий в 16-17 веках значительно расширило способность людей более эффективно определять число Пи. Бесконечный ряд — это сумма (или, что реже, произведение) членов бесконечной последовательности, такой как ½, ¼, 1/8, 1/16,… 1 / (2n). Первое письменное описание бесконечного ряда, которое можно было использовать для вычисления числа пи, было изложено в стихах на санскрите индийским астрономом Нилакантхой Сомаяджи около 1500 г.
D., доказательство которого было представлено около 1530 г. н.э.
1600 г. н.э. и после
Затем, в середине 1600-х, английский математик и физик Исаак Ньютон использовал бесконечные ряды для вычисления π до 15 цифр. В 1699 году Ньютон и немецкий математик Готфрид Вильгельм Лейбниц вместе обнаружили, что π состоит из 71 цифры. Те нашли 100 цифр в 1706 году и вычислили 620 цифр в 1956 году, что было лучшим приближением, достигнутым вручную.
В 1761 году швейцарский математик Иоганн Генрих Ламберт впервые доказал, что π является иррациональным числом, имеет бесконечное количество цифр и никогда не повторяется.
Немецкий математик Фердинанд фон Линдеманн в 1882 году обнаружил, что π не может быть выражено рациональным алгебраическим уравнением (например, pi² = 10 или 9pi4–240pi2 + 1492 = 0)
В самых последних открытиях родился математик шотландского происхождения. Джонатан Майкл Борвейн, ведущий мировой эксперт по вычислению числа Пи.
Это было записано с точностью до 2,7 триллиона десятичных знаков. В 1984 году Джонатан Майкл Борвейн и его брат Питер Борвейн « » создали итерационный алгоритм, увеличивающий в четыре раза количество цифр на каждом шаге; а в 1987 году — тот, который увеличивает количество цифр в пять раз на каждом шаге . Источник.
и открытия продолжаются …
« У каждой крупной цивилизации были свои теории π и математики, которые пытались это объяснить. Древний Египет, Вавилон и Индия. Греческий Архимед, греко-римский Птолемей, древние китайцы и индийцы — все выяснили это соотношение, которое существует как на бумаге, так и, как если бы по некоему божественному плану, во всей природе. ”Источник
Источник фото.Романтика и тайна в магии №
« Красота числа π отчасти в том, что оно делает бесконечность доступной. Это понимают даже маленькие дети. Цифры π никогда не заканчиваются и никогда не показывают шаблон.
Они продолжаются вечно и кажутся случайными — за исключением того, что они не могут быть случайными, поскольку воплощают порядок, присущий идеальному кругу. Это противоречие между порядком и случайностью — один из самых заманчивых аспектов π . ”Dr.Говорит Стивен Строгац, удостоенный наград американский математик и профессор. Он продолжает: « Пи касается бесконечности другими способами. Например, есть удивительные формулы, в которых бесконечная последовательность все меньших и меньших чисел складывается в π . Один из первых таких бесконечных рядов, который был обнаружен, говорит, что π равно четырехкратной сумме 1–1⁄3 + 1⁄5–1⁄7 + 1⁄9–1⁄11 + ⋯. Одно лишь появление этой формулы — повод для радости.Он соединяет все нечетные числа с π , тем самым также связывая теорию чисел с кругами и геометрией. Таким образом, π соединяет две, казалось бы, отдельные математические вселенные, подобно космической червоточине.
»Источник.
Что-то особенное в этих числах
Для тех из нас, кто интересуется приложениями математики к реальному миру, необходимо π . Всякий раз, когда мы думаем о ритмах — процессах, которые периодически повторяются с фиксированным темпом, как сердцебиение, мы неизбежно сталкиваемся с π .
Формула называется рядом Фурье и выглядит так:
Эта серия представляет собой всеобъемлющее изображение любого «фиксированного темпа» x (t), повторяющегося каждые T единиц времени. Основа формулы — π, синус и косинус функции из тригонометрии.
Посредством ряда Фурье π появляется в математике, которая описывает тонкое дыхание младенца и мирные циркадные ритмы ночного отдыха, а также энергичное бодрствование, которое управляет нашим телом .
Доктор Джеймс Грайм утверждает, что мы можем вычислить размер Вселенной с удивительной точностью, используя число пи. Первые 39 цифр числа пи могут измерить окружность Вселенной с точностью до размера атомного ядра.Источник. π и пространство«Когда инженерам-строителям необходимо спроектировать здания, выдерживающие землетрясения, в их расчетах всегда отображается значение π .
π неизбежно, потому что циклы являются временными родственниками кругов; они относятся ко времени, как круги к пространству. π находится в сердце обоих ». Источник .π — бесконечное число, поэтому оно помогает в изучении нашей бесконечной Вселенной. π был разработан ранними астрономами для изучения вращения Земли и орбитальных моделей. π может быть использовано при вычислении плотности планеты, которая, в свою очередь, говорит нам об экосистеме планеты (если атмосфера i s твердое тело или газы ).
НАСА использует π для расчета траектории космического корабля (так называемый «перенос пи»), для измерения кратеров и изучения состава астероидов.
Совсем недавно , π также использовалось для расчета количества водорода, присутствующего в океане под поверхностью спутника Юпитера Европы. НАСА, ноябрь 2019 г. Источник.
π появляется как в формулировке принципа неопределенности Гейзенберга, так и в волновом уравнении Шредингера, которые фиксируют фундаментальное поведение атомов и субатомных частиц.
Дизайнеры Кристиан Илиес Василий и Мартин Кшивински превратили математические числа, теории и символы в подробные произведения искусства. Вероятности перехода для каждого 10-значного бина для первых 2000 цифр пи, фи и е показаны на этом изображении. Фото Источник .Как видите, π вплетено в наши описания самых сокровенных механизмов Вселенной.
π потенциально может содержать ключ к, казалось бы, неразрешимым вопросам о нашей Вселенной.
Несмотря на то, что законы физики гласят, что Вселенная возникла из хаоса, π остается, по-видимому, случайным по природе и может использоваться для создания стабильности, одновременно представляя состояние бесконечности.
π открывает окно в основу реальности и демонстрирует чарующие силы, используемые для формирования каждой частицы во Вселенной.
π Празднование
День числа Пи ( π) — это ежегодно отмечаемый день, чтобы прославить числовую константу. Первое заявленное празднование Дня Пи было организовано в 1988 году Ларри Шоу, физиком из Исследовательской лаборатории Сан-Франциско.Г-н Шоу и сотрудники публично маршировали вокруг одного из круговых пространств здания, поедая фрукты «пи-эс». (хе-хе) Эксплораториум продолжает проводить развлекательные мероприятия в честь Дня Пи.
π День наблюдается 14 марта в соответствии с порядком дат в формате североамериканского календаря. Март — третий месяц, поэтому 14.03 показывает первые три значащие цифры π.
Палата представителей Соединенных Штатов поддержала определение « день пи » и сделала его национальным праздником в 2009 году, приняв необязательную резолюцию (111 H.
Res. 224). Все было подписано 12 марта, а два дня спустя 14 марта 2009 года было признано первым официальным «Национальным днем числа Пи ».
В следующем году «День Пи 2010» принес массу удовольствия в «Математическую вечеринку», когда Google представил в честь праздника « Google Doodle » со словом Google, наложенным на изображения кругов и π символов; а в 2018 году к 30-летнему юбилею Google представил пирог Доминика Анселя с окружностью, разделенной на его диаметр, чтобы красиво сформулировать дудл Google, посвященный 30-летию
Pi, от Dominique Ansel Photo Source.π Fun Fact π
Фото. КАК СОБЛЮДАТЬВесь март 2014 года (3/14) наблюдался некоторыми как «π Месяц» .
В 2015 году 14 марта отмечалось как « Super π Day» .
Этот особый день числа Пи имел особое значение, потому что были представлены первые 10 цифр числа π.
14.03.15 в 9:26:53, дата, записанная в формате месяц / день / год после времени, оставила многих Pi-fectly Party с большим количеством Pi-e! #SorryNotSorry #punny
Празднование Национального Дня Пи включало:
- Есть пи-э ручной работы!
- Обсуждая значение числа π
- Изучите число Пи и Тау (π, умноженное на два)
- Найдите 3.14 предложения в Интернете или бесплатные предложения, связанные с π образование .
- Сделайте арт-проект в стиле π!
- Примите участие в конкурсе по поеданию пи-э!
- Посетите PiDay.org и играйте в арифметические игры, ориентированные на π!
- Посмотрите, сколько чисел π вы можете запомнить! Проверь своих друзей!
- Сделайте домашнее задание…. π — это греческое слово… Бесплатное шифрование для первого человека, который может отправить мне голосовое сообщение Telegram в чате GIVE Nation, произносящее π на правильном греческом языке!
- Проведите следующий π-эксперимент.
«Задача Бюффона об игле» была впервые поставлена Жоржем-Луи Леклерком, графом де Буффона, французским математиком восемнадцатого века. Он непреднамеренно изобрел способ вычисления π на основе вероятности.
Вопрос .«Предположим, у нас есть пол, сделанный из параллельных деревянных полос одинаковой ширины, и мы бросаем на пол иглу. Какова вероятность того, что игла окажется на линии между двумя полосами? »
Это решение было самой ранней проблемой геометрической вероятности, которая была задокументирована; просто используя интегральную геометрию.
Решение для искомой вероятности p в случае, когда длина иглы l не превышает ширину t полосок, есть;
Это можно использовать для разработки метода Монте-Карло для аппроксимации числа π, хотя это не было первоначальным желанием де Бюффона провести этот эксперимент.
Этот простой эксперимент используется для вычисления π
- Поместите лист линованной бумаги на ровную поверхность, затем опустите иглу на линованную бумагу, игла упадет либо в пустое пространство, либо будет касаться линий бумага.
- Опустите иглу на лист бумаги 100 раз, а затем вычислите, сколько раз она попадала на линию или в пустое пространство, используя следующую формулу:
Уравнение должно приблизительно привести к 3,14 при каждом испытании.
Математика ужина в Монте-Карло? π-rfect!
Думаешь, Olive Garden даст мне попробовать 200 хлебных палочек?
Будьте классным ребенком вместе с остальными фанатами STEM, используйте #NationalPiDay с #GIVENation и опубликуйте свою любовь к Пи в социальных сетях.
Увидимся 4 мая….
- π чаще всего сокращается до десятичной 3.14 или дробь 22/7.
- π также появляются вычисления, определяющие площадь эллипса, а также, в области нахождения радиуса, площади поверхности и объема сферы.
- Благодаря суперкомпьютерам в π теперь известно 10 триллионов цифр… и их количество продолжает расти.
- Австрийский астроном Кристоф Гринбергер смог определить 38 цифр в 1630 году, что задокументировано как наиболее точное приближение π , полученное вручную с помощью многоугольных алгоритмов.
- Истинная природа круга никогда не может быть вычислена, потому что π — иррациональное и неизвестное число. Кроме того, вместо того, чтобы думать о кругах как о безугловых, правильнее распознать их как формы с бесконечным количеством углов.
- «Великая пирамида в Гизе, построенная тысячи лет назад, имеет периметр, равный квадрату отношения π. Он был построен между 2550 и 2500 годами до нашей эры, имеет периметр 1760 локтей и высоту 280 локтей, что дает соотношение 1760/280, или примерно в 2 раза больше пи. (Один локоть составляет около 18 дюймов, хотя он измерялся длиной предплечья человека и, следовательно, варьировался от одного человека к другому.) Египтологи считают, что эти пропорции были выбраны по символическим причинам ». Источник.
- π часто называют магическим числом в вычислениях, а вычисление решения — это стресс-тест для компьютеров. Это не только помогает в вычислениях и числах, но также появляется во многих фундаментальных уравнениях, которые не имеют ничего общего с кругами.
- π имеет большое значение в статистике, а также широко используется для анализа вероятности или вероятности того, что что-то происходит или не происходит. π используется статистиками для отслеживания динамики населения и встречается в таблицах смертности.
Источник.- Поскольку π состоит из бесконечных цифр, каждое возможное число, которое мы можем придумать, спрятано где-то в π. Удивительно думать, что любое число, например наша дата рождения, номер телефона или даже номер банковского счета, можно найти в π.
- Математическое выражение колоколообразной кривой, известное как нормальное распределение, содержит π. Нормальное распределение важно в статистике.
- Все, что имеет диаметр и окружность, может иметь π. π встречается в радуге, луне, солнце, зрачке глаза и капле дождя. Мы также можем найти это магическое число в звуке пульсирующего сердца или планеты, вращающейся вокруг звезды. Когда люди хотят измерить рябь, исходящую от центральной точки, они используют π. π также отображается в цветах.
- π использовалось для измерения извилистости рек и изгибов реки. Если мы измерим общую длину любой реки в мире и разделим ее на прямой путь от истока до устья, в среднем получится π.
- Мы не можем увидеть π невооруженным глазом, но мы зависим от π.
- π — это числовое соотношение, которое определяет нашу жизнь и присутствует практически во всех аспектах жизни, какими мы ее знаем.
- π также использовалось при вычислении количества секунд в году, которое приблизительно равно π , умноженным на 10 миллионов секунд.
π встречается в радуге, луне, солнце, зрачке глаза и капле дождя. Мы также можем найти это магическое число в звуке пульсирующего сердца или планеты, вращающейся вокруг звезды. Когда люди хотят измерить рябь, исходящую от центральной точки, они используют π. π также отображается в цветах.- Библия размером π . « Взаимосвязь между диаметром круга — прямой, пересекающей его на две равные половины — и его окружностью — расстоянием по кругу — первоначально упоминалась в Еврейской Книге Царств в отношении ритуального пруда в Храме царя Соломона. .В соответствующем стихе (3 Царств 7:23) говорится, что диаметр пруда был десять локтей, а окружность — 30 локтей. Другими словами, Библия округляет число Пи до трех, как бы говоря, этого достаточно для подков и бассейнов. »Источник.
- “ Великий Маймонид вмешался в эту дискуссию с тем, что звучит почти как предупреждение не копаться слишком глубоко в тайне Пи. «Соотношение диаметра круга и его длины неизвестно и никогда не может быть обсуждено с точностью», — писал он в XII веке.«Это не недостаток знаний с нашей стороны, как думают идиоты, а скорее то, что по своей природе эта вещь неизвестна, и в силу своей реальности не может быть познана, и о ней невозможно говорить … его настоящая ценность не может быть воспринята ». Непостижимо. Непознаваемый. Неприступный. Вроде как Б-г. «Никто не видит моего лица и не живет», как ОН сказал Моисею. »Источник
- « Некоторые типы Массачусетского технологического института или математики в Принстонском университете, где преподавал Альберт Эйнштейн, радуются тому факту, что великий математик и еврейский мыслитель родился 14 марта. В городе Принстон, штат Нью-Джерси, в дополнение к поеданию пирогов и декламации числа Пи, где участники соревнуются, чтобы выяснить, кто сможет правильно написать Пи в наибольшей степени, проводится ежегодный конкурс двойников Эйнштейна. Массачусетский технологический институт часто отправлял письма с решениями по заявкам будущим студентам для доставки 14 марта года ». Источник
.В соответствующем стихе (3 Царств 7:23) говорится, что диаметр пруда был десять локтей, а окружность — 30 локтей. Другими словами, Библия округляет число Пи до трех, как бы говоря, этого достаточно для подков и бассейнов. »Источник.
В городе Принстон, штат Нью-Джерси, в дополнение к поеданию пирогов и декламации числа Пи, где участники соревнуются, чтобы выяснить, кто сможет правильно написать Пи в наибольшей степени, проводится ежегодный конкурс двойников Эйнштейна. Массачусетский технологический институт часто отправлял письма с решениями по заявкам будущим студентам для доставки 14 марта года ». ИсточникСпасибо за внимание!
Если вы нашли ценность, прокомментируйте или поставьте пару лайков и поделитесь!
Я хотел бы профессионально обсуждать, сотрудничать и общаться со всеми вами.Буду рад любым отзывам, положительным и отрицательным; поскольку я здесь только для того, чтобы совершенствоваться и обучать себя / других.
Как мы можем приносить друг другу пользу?
Пи (3,14159) — это метафора жизни и природы Вселенной, математика не требуется — Quartz
Вы, вероятно, впервые встретили пи — число, используемое для вычисления числа окружность круга — когда вы учились в школе.
Если вы не склонны к математике, вы, вероятно, не задумывались об этом с тех пор.Но пи имеет практическое применение для всех как реальный инструмент, позволяющий лучше понять Вселенную и саму жизнь. Не вдаваясь в математику.
В Visions of Infinity, математик Ян Стюарт объясняет, что потребовалось около 2000 лет великим умам, работавшим над проблемой пи — переход от евклидовой геометрии к алгебраическим вычислениям — чтобы понять его как иррациональное и трансцендентное число. С математической точки зрения это означает, что число пи не может быть представлено дробью или алгебраическим выражением.
В числовом выражении число Пи равно 3,14159 плюс несколько. Этот добавленный бит — плюс несколько — продолжается бесконечно, серия цифр, которые никогда не заканчиваются в числовой последовательности, которая никогда не повторяется. В этом бесконечном повторении заключается величайший урок пи.
На первый взгляд незнание кажется проблематичным
Компьютеры вычислили число Пи до триллионов цифр.
Но число Пи на самом деле не решено и, похоже, не решаемо. Это делает его фантастическим философским инструментом, напоминанием математически и мистически склонным обо всем, что не может быть окончательно понято, несмотря на большие усилия.
Пи замечательно именно потому, что его можно понять только теоретически, а не понять полностью. Отсутствие решения может быть освобождением, демонстрацией классической аксиомы: самые мудрые из нас знают только то, как мало мы знаем.
Величайшие математические умы веков добились успехов. Тем не менее, каждый шаг вперед в понимании и расчетах также обнаруживает ограниченность человеческих знаний. Пи показывает, что знание в целом невозможно.
Чем больше мы знаем, тем очевиднее, что нужно знать гораздо больше.Для каждого человека и для человечества в целом всегда есть этот дополнительный элемент, который просто невозможно понять, независимо от того, сколько информации или образования мы имеем.
Существование превосходит разум — его нельзя понять
Тайны остаются, всегда, и это может быть хорошо.