Циклоид это: Циклоида — Википедия – Циклоидный (циклотимный) тип личности: особенности поведения — inakhan.ru

Содержание

Циклоида — Википедия

Материал из Википедии — свободной энциклопедии

Катящаяся окружность рисует циклоиду

Цикло́ида (от греч. κυκλοειδής «круглый») — плоская трансцендентная кривая.

Циклоида определяется кинематически как траектория фиксированной точки производящей окружности (радиуса r{\displaystyle r}), катящейся без скольжения по прямой.

Примем горизонтальную ось координат в качестве прямой, по которой катится производящая окружность радиуса r{\displaystyle r}. Циклоида описывается:

Таутохронность циклоиды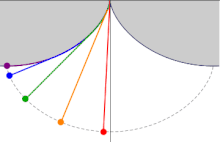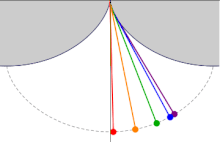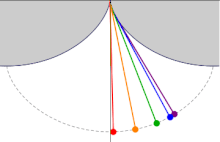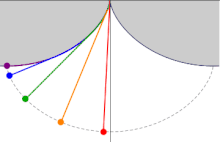

Колебания с циклоидным регулятором.

Циклоида — периодическая функция по оси абсцисс, с периодом 2πr{\displaystyle 2\pi r}. За границы периода удобно принять особые точки (точки возврата) вида t=2πk{\displaystyle t=2\pi k}, где k{\displaystyle k} — произвольное целое число.
Для проведения касательной к циклоиде в произвольной её точке A достаточно соединить эту точку с верхней точкой производящей окружности. Соединив A с нижней точкой производящей окружности, мы получим нормаль.
Длина арки циклоиды равна 8r{\displaystyle 8r}. Это свойство открыл Кристофер Рен (1658). Зависимость длины дуги циклоиды (s) от параметра t следующая^[1]: s(t)=4r(1−cos⁡t2){\displaystyle s(t)=4r(1-\cos {t \over 2})}.
Площадь под каждой аркой циклоиды втрое больше, чем площадь порождающего круга. Торричелли сообщил, что этот факт Галилей открыл экспериментально: сравнил вес пластинок с кругом и с аркой циклоиды.^[2] Математически этот факт первым доказал Роберваль около 1634 года с помощью метода неделимых.
Радиус кривизны у первой арки циклоиды равен 4rsin⁡t2{\displaystyle 4r\sin {\frac {t}{2}}}.
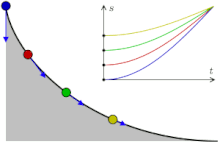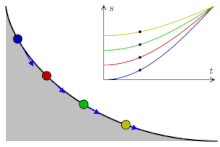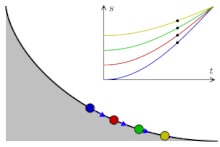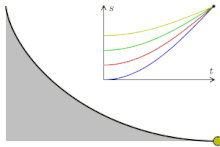
«Перевёрнутая» циклоида является кривой скорейшего спуска (брахистохроной). Более того, она имеет также свойство таутохронности: тяжёлое тело, помещённое в любую точку арки циклоиды, достигает горизонтали за одно и то же время.
Период колебаний материальной точки, скользящей по перевёрнутой циклоиде, не зависит от амплитуды. (Непосредственное следствие таутохронности).

Эволюта циклоиды является циклоидой, конгруэнтной исходной и параллельно сдвинутой от исходной так, что вершины переходят в «острия».
Детали машин, которые совершают одновременно равномерное вращательное и поступательное движение, описывают циклоидальные кривые: циклоида, эпициклоида, гипоциклоида, трохоида, астроида (ср. построение лемнискаты Бернулли).

Первыми из учёных обратили внимание на циклоиду Николай Кузанский в XV веке и Шарль де Бовель в труде 1501 года. Но серьёзное исследование этой кривой началось только в XVII веке.

Название циклоида придумал Галилей (во Франции эту кривую сначала называли

рулеттой). Содержательное исследование циклоиды провёл современник Галилея Мерсенн. Среди трансцендентных кривых, то есть кривых, уравнение которых не может быть записано в виде многочлена от x,y{\displaystyle x,y}, циклоида — первая из исследованных.

Паскаль писал о циклоиде^[3]^[4]:

Рулетта является линией столь обычной, что после прямой и окружности нет более часто встречающейся линии; она так часто вычерчивается перед глазами каждого, что надо удивляться тому, как не рассмотрели её древние… ибо это не что иное, как путь, описываемый в воздухе гвоздём колеса…
Оригинальный текст (фр.)

La Roulette est une ligne si commune, qu’apres la droitte, & la circulaire, il n’y en a point de si frequente; Et elle se décrit si fouuent aux yeux de tout le monde, qu’il y a lieu de s’estonner qu’elle n’ait point esté considerée par les anciens, dans lesquels on n’en trouue rien : Car ce n’est autre chose que le chemin que fait en l’air, le clou d’une rouë…

Новая кривая быстро завоевала популярность и подверглась глубокому анализу, в котором участвовали Декарт, Ферма, Ньютон, Лейбниц, братья Бернулли и другие корифеи науки XVII—XVIII веков. На циклоиде активно оттачивались методы появившегося в те годы математического анализа.

Тот факт, что аналитическое исследование циклоиды оказалось столь же успешным, как и анализ алгебраических кривых, произвёл большое впечатление и стал важным аргументом в пользу «уравнения в правах» алгебраических и трансцендентных кривых.

↑ Архипов Г.И., Садовничий В.А., Чубариков В.Н. Лекции по математическому анализу / Под ред. В. А. Садовничего. — 2-е изд. — М.: Высшая школа, 2000. — С. 261. — 695 с. — 8000 экз. — ISBN 5-06-003955-2.
↑ Александрова Н. В. История математических терминов, понятий, обозначений: Словарь-справочник, изд. 3-е. — СПб: ЛКИ, 2008. — С. 213. — 248 с. — ISBN 978-5-382-00839-4.
↑ Кляус Е. М., Погребысский И. Б., Франкфурт У. И. Паскаль. — М.: Наука, 1971. — С. 191. — (Научно-биографическая литература). — 10 000 экз.

↑ Pascal, Blaise. Histoire de la roulette, appellée autrement la trochoïde, ou la cycloïde, où l’on rapporte par quels degrez on est arrivé à la connoissance de la nature de cette ligne. 10 octobre 1658. P.1.

Берман Г. Н. Циклоида. М., Наука, 1980, 112 с.
Гиндикин С. Г. Рассказы о физиках и математиках. — издание третье, расширенное. — М.: МЦНМО, 2001. — С. 126-165. — ISBN 5-900916-83-9.
Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 5.
Маркушевич А. И. Замечательные кривые, Популярные лекции по математике, выпуск 4, Наука 1978 г., стр. 32.

Циклоида — это… Что такое Циклоида?

Катящаяся окружность рисует циклоиду

Цикло́ида (от греч. κυκλοειδής — круглый) — плоская трансцендентная кривая. Циклоида определяется кинематически как траектория фиксированной точки производящей окружности радиуса , катящейся без скольжения по прямой.

Уравнения

Примем горизонтальную ось координат в качестве прямой, по которой катится производящая окружность радиуса .

Циклоида описывается параметрически
,
.
Уравнение в декартовых координатах:
Циклоида может быть получена как решение дифференциального уравнения:

Свойства

$\left(\frac{dy}{dx}\right)^2 = \frac{2r-y}{y}.$ Таутохронность циклоиды

«Перевёрнутая» циклоида является кривой скорейшего спуска (брахистохроной). Более того, она имеет также свойство таутохронности: тяжёлое тело, помещённое в любую точку арки циклоиды, достигает горизонтали за одно и то же время.
Период колебаний материальной точки, скользящей по перевёрнутой циклоиде, не зависит от амплитуды, этот факт был использован Гюйгенсом для создания точных механических часов.
Эволюта циклоиды является циклоидой, конгруэнтной исходной, а именно — параллельно сдвинутой так, что вершины переходят в «острия».
Детали машин, которые совершают одновременно равномерное вращательное и поступательное движение, описывают циклоидальные кривые (циклоида, эпициклоида, гипоциклоида, трохоида, астроида) (ср. построение лемнискаты Бернулли).

Исторический очерк

Первыми из учёных обратили внимание на циклоиду Николай Кузанский в XV веке и Шарль де Бовель (фр. Charles de Bovelles, 1479—1566) в труде 1501 года. Но серьёзное исследование этой кривой началось только в XVII веке.

Название циклоида придумал Галилей (во Франции эту кривую сначала называли рулеттой). Содержательное исследование циклоиды провёл современник Галилея Мерсенн. Среди трансцендентных кривых, то есть кривых, уравнение которых не может быть записано в виде многочлена от , циклоида — первая из исследованных.

Паскаль писал о циклоиде:

Рулетта является линией столь обычной, что после прямой и окружности нет более часто встречающейся линии; она так часто вычерчивается перед глазами каждого, что надо удивляться тому, как не рассмотрели её древние… ибо это не что иное, как путь, описываемый в воздухе гвоздём колеса.

Литература

Берман Г. Н. Циклоида. М., Наука, 1980, 112 с.
Гиндикин С. Г. Рассказы о физиках и математиках. — издание третье, расширенное. — М.: МЦНМО, 2001. — С. 126-165. — ISBN 5-900916-83-9
Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 5.
Маркушевич А. И. Замечательные кривые, Популярные лекции по математике, выпуск 4, Наука 1978 г., стр. 32.

Ссылки

Примечания

↑ Александрова Н. В. История математических терминов, понятий, обозначений: Словарь-справочник, изд. 3-е. — СПб: ЛКИ, 2008. — С. 213. — 248 с. — ISBN 978-5-382-00839-4

См. также

ЦИКЛОИДА | Энциклопедия Кругосвет

ЦИКЛОИДА (в переводе с греч. кругообразный) – плоская трансцендентная кривая, которую описывает точка окружности радиуса r, катящейся по прямой без скольжения (трансцендентной кривой называется кривая, которая в прямоугольных координатах не может быть описана алгебраическим уравнением). Ее параметрическое уравнение

x = rt – r sin t,
y = r – r cos t

Точки пересечения циклоиды с прямой, по которой катится окружность (эта окружность называется производящей, а прямая, по которой она катится, – направляющей), называются точками возврата, а самые высокие точки на циклоиде, расположенные посредине между соседними точками возврата, называются вершинами циклоиды.

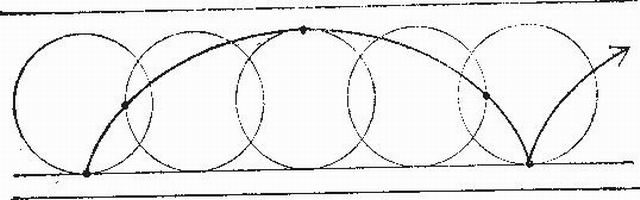
Первым изучать циклоиду начал Галилео Галилей. Длина одной арки циклоиды была определена в 1658 английским архитектором и математиком Кристофером Реном, автором проекта и строителем купола собора Святого Павла в Лондоне. Оказалось, что длина циклоиды равна 8-ми радиусам производящей окружности.
Одно из замечательных свойств циклоиды, давшее ей название – брахистохрона (от греческих слов «кратчайший» и «время) связано с решением задачи о наискорейшем спуске. Встал вопрос, какую форму надо придать хорошо отшлифованному (чтобы практически исключить трение) желобу, соединяющему две точки, чтобы шарик скатился вниз от одной точки к другой в кратчайшее время. Братья Бернулли доказали, что желоб должен иметь форму опрокинутой вниз циклоиды.

Родственные циклоиде кривые можно получить, рассматривая траектории точек, не находящихся на производящей окружности.

Пусть точка С₀ находится внутри окружности. Если провести через С₀ вспомогательную окружность с тем же центром, что и у производящей окружности, то при качении производящей окружности по прямой АВ маленькая окружность будет катиться по прямой A´В´, но ее качение будет сопровождаться скольжением, и точка С₀ описывает кривую, называемую укороченной циклоидой.

Аналогичным образом определяется удлиненная циклоида – это траектория точки, расположенной на продолжении радиуса производящей окружности, при этом качение сопровождается скольжением в противоположном направлении.

Циклоидальные кривые применяются при многих технических расчетах и свойства их используются, например, при построении профилей зубьев шестерен, в циклоидальных маятниках, в оптике и, таким образом, изучение этих кривых важно с прикладной точки зрения. Не менее важно и то, что, изучая эти кривые и их свойства, ученые 17 в. разрабатывали приемы, которые привели к созданию дифференциального и интегрального исчислений, а задача о брахистохроне явилась шагом к изобретению вариационного исчисления.

Елена Малишевская

Проверь себя!
Ответь на вопросы викторины «Математика»

Как звали математика, который в 19 лет решил задачу, не поддававшуюся усилиям лучших геометров со времен Евклида?

Циклоида — Математические этюды

Помните оранжевые пластмассовые катафоты — светоотражатели, прикрепляющиеся к спицам велосипедного колеса? Прикрепим катафот к самому ободу колеса и проследим за его траекторией. Полученные кривые принадлежат семейству циклоид.

Колесо при этом называется производящим кругом (или окружностью) циклоиды.

Но давайте вернёмся в наш век и пересядем на более современную технику. На пути байка попался камушек, который застрял в протекторе колеса. Провернувшись несколько кругов с колесом, куда полетит камень, когда выскочит из протектора? Против направления движения мотоцикла или по направлению?

Как известно, свободное движение тела начинается по касательной к той траектории, по которой оно двигалось. Касательная к циклоиде всегда направлена по направлению движения и проходит через верхнюю точку производящей окружности. По направлению движения полетит и наш камушек.

Помните, как Вы катались в детстве по лужам на велосипеде без заднего крыла? Мокрая полоска на вашей спине является житейским подтверждением только что полученного результата.

Век XVII — это век циклоиды. Лучшие учёные изучали её удивительные свойства.

Какая траектория приведёт тело, движущееся под действием силы тяжести, из одной точки в другую за кратчайшее время? Это была одна из первых задач той науки, которая сейчас носит название вариационное исчисление.

Минимизировать (или максимизировать) можно разные вещи — длину пути, скорость, время. В задаче о брахистохроне минимизируется именно время (что подчёркивается самим названием: греч. βράχιστος — наименьший, χρόνος — время).

Первое, что приходит на ум, — это прямолинейная траектория. Давайте также рассмотрим перевёрнутую циклоиду с точкой возврата в верхней из заданных точек. И, следуя за Галилео Галилеем, — четвертинку окружности, соединяющую наши точки.

Сделаем бобслейные трассы с рассмотренными профилями и проследим, какой из бобов приедет первым.

История бобслея берёт своё начало в Швейцарии. В 1924 году во французском городе Шамони проходят первые зимние Олимпийские игры. На них уже проводятся соревнования по бобслею для экипажей двоек и четвёрок. Единственный год, когда на Олимпийских играх экипаж боба состоял из пяти человек, был 1928. С тех пор в бобслее всегда соревнуются мужские экипажи двойки и четвёрки. В правилах бобслея много интересного. Конечно же, существует ограничения на вес боба и команды, но существуют даже ограничения на материалы, которые можно использовать в коньках боба (передняя пара их подвижна и связана с рулём, задняя закреплена жёстко). Например, радий не может использоваться при изготовлении коньков.

Дадим старт нашим четвёркам. Какой же боб первым приедет к финишу? Боб зелёного цвета, выступающий за команду Математических этюдов и катившийся по циклоидальной горке, приходит первым!

Почему же Галилео Галилей рассматривал четвертинку окружности и считал, что это наилучшая в смысле времени траектория спуска? Он вписывал в неё ломаные и заметил, что при увеличении числа звеньев время спуска уменьшается. Отсюда Галилей естественным образом перешёл к окружности, но сделал неверный вывод, что эта траектория наилучшая среди всех возможных. Как мы видели, наилучшей траекторией является циклоида.

Через две данные точки можно провести единственную циклоиду с условием, что в верхней точке находится точка возврата циклоиды. И даже когда циклоиде приходится подниматься, чтобы пройти через вторую точку, она всё равно будет кривой наискорейшего спуска!

Ещё одна красивая задача, связанная с циклоидой, — задача о таутохроне. В переводе с греческого ταύτίς означает «тот же самый», χρόνος, как мы уже знаем — «время».

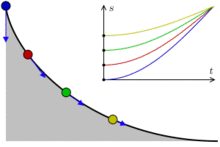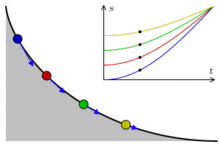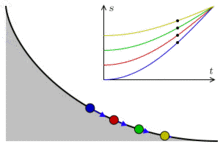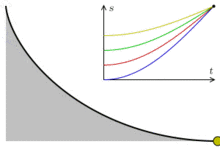
Сделаем три одинаковые горки с профилем в виде циклоиды, так, чтобы концы горок совпадали и располагались в вершине циклоиды. Поставим три боба на разные высоты и дадим отмашку. Удивительнейший факт — все бобы приедут вниз одновременно!

Зимой Вы можете построить во дворе горку изо льда и проверить это свойство вживую.

Задача о таутохроне состоит в нахождении такой кривой, что, начиная с любого начального положения, время спуска в заданную точку будет одинаковым.

Христиан Гюйгенс доказал, что единственной таутохроной является циклоида.

Конечно же, Гюйгенса не интересовал спуск по ледяным горкам. В то время учёные не имели такой роскоши заниматься науками из любви к искусству. Задачи, которые изучались, исходили из жизни и запросов техники того времени. В XVII веке совершаются уже дальние морские плавания. Широту моряки умели определять уже достаточно точно, но удивительно, что долготу не умели определять совсем. И один из предлагавшихся способов измерения широты был основан на наличии точных хронометров.

Первым, кто задумал делать маятниковые часы, которые были бы точны, был Галилео Галилей. Однако в тот момент, когда он начинает их реализовывать, он уже стар, он слеп, и за оставшийся год своей жизни учёный не успевает сделать часы. Он завещает это сыну, однако тот медлит и начинает заниматься маятником тоже лишь перед смертью и не успевает реализовать замысел. Следующей знаковой фигурой был Христиан Гюйгенс.

Он заметил, что период колебания обычного маятника, рассматривавшегося Галилеем, зависит от изначального положения, т.е. от амплитуды. Задумавшись о том, какова должна быть траектория движения груза, чтобы время качения по ней не зависело от амплитуды, он решает задачу о таутохроне. Но как заставить груз двигаться по циклоиде? Переводя теоретические исследования в практическую плоскость, Гюйгенс делает «щёчки», на которые наматывается веревка маятника, и решает ещё несколько математических задач. Он доказывает, что «щёчки» должны иметь профиль той же самой циклоиды, тем самым показывая, что эволютой циклоиды является циклоида с теми же параметрами.

Кроме того, предложенная Гюйгенсом конструкция циклоидального маятника позволяет посчитать длину циклоиды. Если синюю ниточку, длина которой равна четырём радиусам производящего круга, максимально отклонить, то её конец будет в точке пересечения «щёчки» и циклоиды-траектории, т.е. в вершине циклоиды-«щёчки». Так как это половина длины арки циклоиды, то полная длина равна восьми радиусам производящего круга.

Христиан Гюйгенс сделал циклоидальный маятник, и часы с ним проходили испытания в морских путешествиях, но не прижились. Впрочем, так же, как и часы с обычным маятником для этих целей.

Отчего же, однако, до сих пор существуют часовые механизмы с обыкновенным маятником? Если приглядеться, то при малых отклонениях, как у красного маятника, «щёчки» циклоидального маятника почти не оказывают влияния. Соответственно, движение по циклоиде и по окружности при малых отклонениях почти совпадают.

ЦИКЛОИДА — это… Что такое ЦИКЛОИДА?

ЦИКЛОИДА — (греч., от kyklos круг, и eidos вид). В геометрии, кривая, описываемая точкою круга, катящегося по прямой линии; кривообразная линия. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ЦИКЛОИДА греч., от kyklos, круг … Словарь иностранных слов русского языка

циклоида — ы, ж. cycloïde &LT;гр. kykloeides кругообразный. геом. Плоская кривая, описываемая точкой окружности, катящейся без скольжения по прямой. БАС 1. Поэтический полет определен циклоидой. В. Ф. Одоевский Импровизатор. Эллипс имеет не те качества,… … Исторический словарь галлицизмов русского языка

ЦИКЛОИДА — (от греч. kykloeides кругообразный) плоская кривая, описываемая точкой Р окружности, катящейся без скольжения по неподвижной прямой. Циклоида трансцендентная кривая. См. также Гипоциклоида, Эпициклоида … Большой Энциклопедический словарь

ЦИКЛОИДА — ЦИКЛОИДА, циклоиды, жен., (греч. kykloeidos кругообразный) (мат.). Кривая линия, описываемая точкой окружности, которая катится без скольжения по прямой линии. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова

циклоида — сущ., кол во синонимов: 2 • кривая (56) • линия (182) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов

циклоида — Траектория точки окружности круга, катящегося без скольжения по прямой линии. [http://sl3d.ru/o slovare.html] Тематики машиностроение в целом … Справочник технического переводчика

Циклоида — Катящаяся окружность рисует циклоиду Циклоида (от греч. κυκλοειδής круглый) пло … Википедия

циклоида — ы; ж. [греч. kykloeides кругообразный от kyklos круг и eidos вид] Матем. Плоская кривая, описываемая фиксированной точкой окружности, катящейся без скольжения по неподвижной прямой. * * * циклоида (от греч. kykloeidēs кругообразный), плоская… … Энциклопедический словарь

Циклоида — Гипоциклоида. ЦИКЛОИДА (от греческого kykloeides кругообразный), плоская кривая, описываемая точкой окружности, катящейся без скольжения по неподвижной прямой. Если кривая описывается точкой окружности, которая катится без скольжения по… … Иллюстрированный энциклопедический словарь

ЦИКЛОИДА — (от греч. kykloeides кругообразный, круглый) плоская траектория точки окружности, катящейся по прямой линии (см. рис.). Циклоида … Большой энциклопедический политехнический словарь

ЦИКЛОИДА — (от греч. kykloeides кругообразный), плоская трансцендентная кривая (рис.), описываемая точкой Р окружности, катящейся без скольжения по неподвижной прямой. См. также Гипоциклоида, Эпициклоида … Естествознание. Энциклопедический словарь

Эпициклоида — Википедия

Материал из Википедии — свободной энциклопедии

Эпицикло́ида (от др.-греч. ὲπί — на, над, при и κύκλος — круг, окружность) — плоская кривая, образуемая фиксированной точкой окружности, катящейся по внешней стороне другой окружности без скольжения.

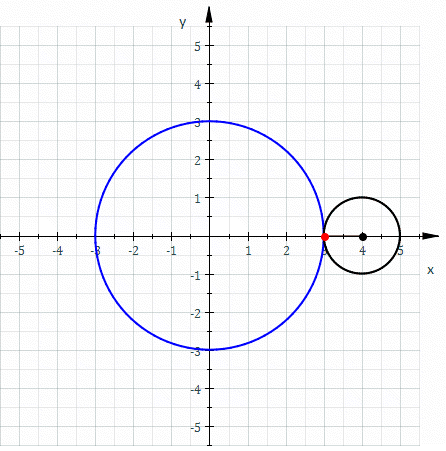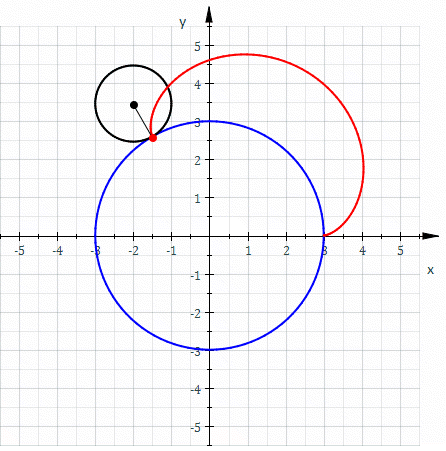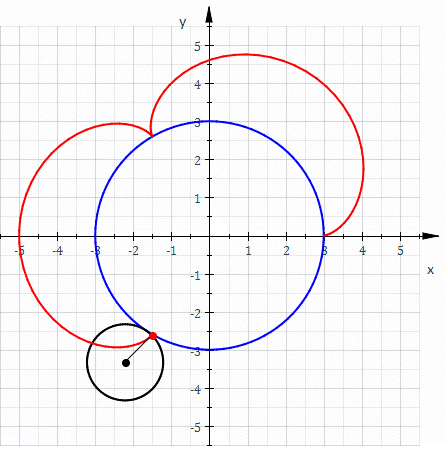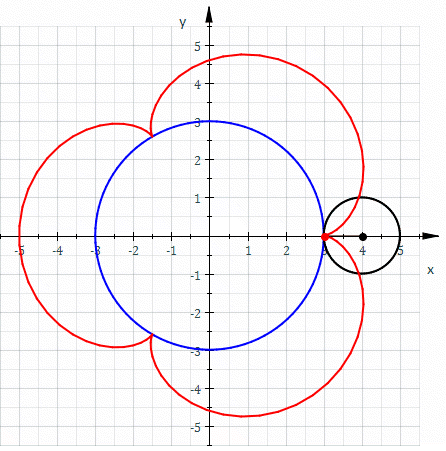
Если центр неподвижной окружности находится в начале координат, её радиус равен R{\displaystyle R}, радиус катящейся по ней окружности равен r{\displaystyle r}, то эпициклоида описывается параметрическими уравнениями относительно φ{\displaystyle \varphi }:

{x=(R+r)cos⁡φ−rcos⁡(α+R+rrφ)y=(R+r)sin⁡φ−rsin⁡(α+R+rrφ){\displaystyle {\begin{cases}x=(R+r)\cos \varphi -r\cos(\alpha +{\frac {R+r}{r}}\varphi )\\y=(R+r)\sin \varphi -r\sin(\alpha +{\frac {R+r}{r}}\varphi )\end{cases}}}

где α{\displaystyle \alpha } — угол поворота точки, описывающей эпициклоиду, относительно центра подвижной окружности в момент начала движения (против часовой стрелки от оси x), φ{\displaystyle \varphi } — параметр, но фактически это угол наклона отрезка между центрами к оси OX{\displaystyle OX}.

Можно ввести величину k=Rr{\displaystyle \textstyle k={\frac {R}{r}}}, тогда уравнения предстанут в виде

{x=r(k+1)(cos⁡φ−cos⁡((k+1)φ)k+1)y=r(k+1)(sin⁡φ−sin⁡((k+1)φ)k+1){\displaystyle {\begin{cases}x=r(k+1)\left(\cos \varphi -{\frac {\cos((k+1)\varphi )}{k+1}}\right)\\y=r(k+1)\left(\sin \varphi -{\frac {\sin((k+1)\varphi )}{k+1}}\right)\end{cases}}}

Величина k{\displaystyle k} определяет форму эпициклоиды. При k=1{\displaystyle k=1} эпициклоида образует кардиоиду, а при k=2{\displaystyle k=2} — нефроиду. Если k{\displaystyle k} — несократимая дробь вида mn{\displaystyle {\frac {m}{n}}} (m,n∈N{\displaystyle m,n\in \mathbb {N} }), то m{\displaystyle m} — это количество каспов данной эпициклоиды, а n{\displaystyle n} — количество полных вращений катящейся окружности. Если k{\displaystyle k} иррациональное число, то кривая является незамкнутой и имеет бесконечное множество несовпадающих каспов.

Гипоциклоида — Википедия

Пусть в начальный момент окружности касаются в точке A{\displaystyle A}, лежащей на оси OX{\displaystyle OX}, где точка O{\displaystyle O} — центр большой окружности. Координаты точки A{\displaystyle A} при этом — (kr,0){\displaystyle (kr,0)}, где k=Rr{\displaystyle k={\frac {R}{r}}}. Рассмотрим, как меняются координаты точки A{\displaystyle A}, привязанной к катящейся окружности (A{\displaystyle A} переходит в A′{\displaystyle A’}). Пусть маленькая окружность прокатилась так, что её центр перешел из точки C′{\displaystyle C’} в точку C′{\displaystyle C’} и повернулся относительно точки O{\displaystyle O} на угол t{\displaystyle t}. Во-первых, можно показать, что поворот маленькой окружности относительно своего центра при этом (т.е. угол между CA{\displaystyle CA} и C′A′{\displaystyle C’A’}) равен t−kt=−(k−1)t{\displaystyle t-kt=-(k-1)t}. Во-вторых, координаты точки C′{\displaystyle C’} будут такими: (cos(t)(k−1)r,sin(t)(k−1)r){\displaystyle (cos(t)(k-1)r,sin(t)(k-1)r)}. Тогда, зная, куда перейдет центр катящейся окружности, и на какой угол она повернулась относительно этого центра, можно записать координаты точки A′{\displaystyle A’}:

{x=cos(t)(k−1)r+cos((k−1)t)ry=sin(t)(k−1)r−sin((k−1)t)r{\displaystyle {\begin{cases}x=cos(t)(k-1)r+cos((k-1)t)r\\y=sin(t)(k-1)r-sin((k-1)t)r\end{cases}}}