Дедукция это в философии: Дедукция / Философский словарь

ДЕДУКЦИЯ — это… Что такое ДЕДУКЦИЯ?

ДЕДУКЦИЯ — (от лат. deductio выведение) переход от посылок к заключению, опирающийся на логический закон, в силу чего заключение с логической необходимостью следует из принятых посылок. Характерная особенность Д. заключается в том, что от истинных посылок… …   Философская энциклопедия

ДЕДУКЦИЯ — (лат. deductio, от deducere выводить). Вывод частных фактов из общих основных положений. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ДЕДУКЦИЯ [лат. deductio выведение] лог. способ рассуждения, при котором новое …   Словарь иностранных слов русского языка

дедукция — и, ж. déduction f., нем. Deduktion <лат. deductio выведение. 1. дипл. Изложение, изъяснение чего л. Сл. 18. Шведы против сего мира пространную дедукцию писменно Королю подали. ЖПВ 2 493. Министерство потом вручило ему письменную дедукцию своих …   Исторический словарь галлицизмов русского языка

Дедукция —  Дедукция  ♦ Déduction    Рассуждать методом дедукции значит выводить из истинных или предположительно истинных суждений (принципов или предпосылок) другие суждения, с необходимостью из них вытекающие. Под дедукцией, пишет Декарт, мы понимаем… …   Философский словарь Спонвиля

дедукция — (от лат. deductio выведение) движение знания от более общего к менее общему, частному, выведение следствия из посылок. Д. тесно связана с индукцией. Логика рассматривает Д. как вид умозаключения. Психология изучает развитие и нарушение… …   Большая психологическая энциклопедия

Дедукция — (лат. deductio шығару) бастапқы пайымдаулар (алғышарттар) жиынтығынан қажетті шығарылатын салдарларды алатын рационалды танымның әдісі. Дедукция процесінде пікірлердің тек логикалық қатал, әдепті (корректный) амалдары – логикалық формалары −… …   Философиялық терминдердің сөздігі

ДЕДУКЦИЯ — (от латинского deductio выведение), вывод по правилам логики; цепь умозаключений (рассуждение), звенья которой (высказывания) связаны отношением логического следования. Началом (посылками) дедукции являются аксиомы, постулаты или гипотезы,… …   Современная энциклопедия

ДЕДУКЦИЯ — (от лат.

deductio выведение) вывод по правилам логики; цепь умозаключений (рассуждение), звенья которой (высказывания) связаны отношением логического следования. Началом (посылками) дедукции являются аксиомы, постулаты или просто гипотезы,… …   Большой Энциклопедический словарь

Дедукция — Дедукция (лат. deductio  выведение)  метод мышления, при котором частное положение логическим путем выводится из общего, вывод по правилам логики; цепь умозаключений (рассуждение), звенья которой (высказывания) связаны отношением логического… …   Википедия

дедукция — выведение, вывод, умозаключение, заключение Словарь русских синонимов. дедукция сущ., кол во синонимов: 3 • вывод (31) • …   Словарь синонимов

дедукция —     спец. ДЕДУКЦИЯ, вывод, книжн. умозаключение     ВЫВОД, заключение, книжн. умозаключение     ВЫВОДИТЬ/ВЫВЕСТИ, заключать/заключить, книжн. умозаключать/умозаключить …   Словарь-тезаурус синонимов русской речи

Дедукция — что это такое

Обновлено 20 января 2021

1. Дедукция — это. ..
2. Где она применяется
3. Что такое индукция
4. История дедуктивного метода
5. Дедукция и индукция: как избежать ошибок
6. Как развивать дедуктивные способности

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Большинство людей слышали о дедукции из книг, фильмов и сериалов о Шерлоке Холмсе.

На самом деле, знаменитый сыщик применял целый арсенал логических методов, подкрепляя все это дьявольской наблюдательностью и профессиональным чутьем.

Сегодня я расскажу, что такое дедукция, чем она отличается от индукции, как правильно и неправильно строить умозаключения.

Дедукция — это метод логического мышления

Термин образован от латинского слова deductio – выведение.

Есть простое определение: дедукция – это метод мышления, который предполагает переход от общего к частному.

То, что верно для целого класса вещей, также истинно и для каждого объекта, относящегося к этому классу.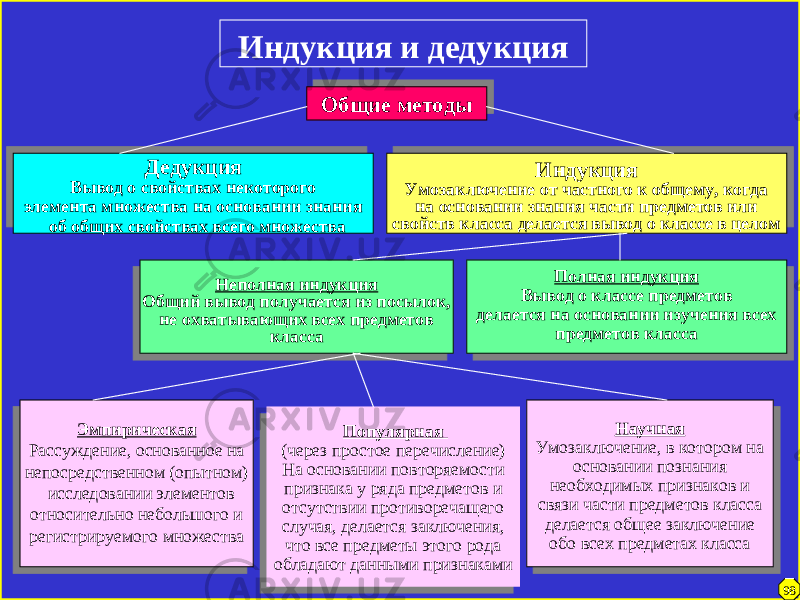

Дедуктивное рассуждение начинается с посылки – общего правила, которое считается истинным. Затем с помощью логических звеньев из посылки должно выводиться частное заключение.

Поясним на примере:

1. Посылка: у людей есть голова (класс объектов «человек» имеет общее свойство «наличие головы»).
2. Логическое звено: Петя – человек (он принадлежит к классу «человек»).
3. Заключение: у Пети есть голова.

Чтобы сделать такой вывод, вовсе не обязательно лично знать Петю.

Где применяется дедукция

Мы используем такое мышление ежедневно, даже не догадываясь об этом. Не замечаем, что в голове выстраиваются логические цепочки: теплая одежда защищает от холода, на улице холодно, куртка – теплая одежда, надену куртку. Все происходит автоматически за доли секунды.

Но метод дедуктивного мышления применяется осознанно во многих сферах:

1. Споры и дискуссии. Когда нужно убедить оппонента принять вашу точку зрения, достаточно найти очевидное утверждение, с которым он согласится. А потом логически связать предпосылку с нужным выводом. Менеджер в автосалоне убеждает клиента купить дорогой автомобиль: «Решайтесь, мы живем лишь раз. Зачем откладывать мечту?».
2. Математика. Доказательство теоремы основывается на аксиомах – утверждениях, которые по умолчанию истинны.
3. Криминалистика. Используя общую картину происшествия, эксперт устанавливает отдельные обстоятельства дела.
4. Наука. Дедукция – это основной логический способ доказательства. Ученый берет гипотезу (что это такое?), которую нужно подтвердить или опровергнуть, и выводит следствия. Если в ходе экспериментов удается обнаружить эти следствия, то гипотеза считается доказанной.
5. Философия. Это наука, где эксперименты – мысленные, а доказательства — логические. В той же физике можно подкинуть яблоко в небо, чтобы убедиться в существовании силы притяжения. Дедукция в философии – это способ логически обосновать гипотезу.

Индукция – что это?

Слово «индукция» (от лат. inductio – наведение) означает движение в противоположном направлении: от частного к общему.

На основании отдельных фактов выводится общее правило или закономерность.

Например:

1. Кеша умеет разговаривать.
2. Гоша умеет разговаривать.
3. Кеша и Гоша – попугаи.
4. Все попугаи умеют разговаривать.

К выводам, которые получены способом индуктивных рассуждений, не стоит относиться как к абсолютной истине. Это всего лишь гипотеза, которая может быть верной или ложной.

Чем больше фактов подтверждают вывод, тем он достовернее. В нашем случае, для получения на 100% верного предположения, нужно проверить всех попугаев на свете. Если хотя бы один не разговаривает, то вывод ложный.

Индукция имеет огромное значение для научного познания. Многие открытия совершены благодаря этому методу. Ученый наблюдает отдельные явления, выявляет связи и закономерности между ними, обобщает и выдвигает научную гипотезу.

Например, Аристотель обнаружил:

1. во время затмения Земля бросает на Луну круглую тень;
2. корабль скрывается за горизонтом по частям – сначала уходит корпус, а паруса еще видны;
3. звездное небо из разных точек планеты выглядит по-разному.

Из этих фактов методом индукции греческий мыслитель сделал вывод: Земля – шарообразной формы.

История метода дедукции

Теория дедукции создана древнегреческим мыслителем Аристотелем. Он сформулировал основные правила выведения умозаключений, в основе которых лежит связь между родом и единичной вещью. Такие умозаключения Аристотель называл категорическими силлогизмами.

Дедукцию постоянно пытались сравнивать с другими методами познания, стараясь выяснить, что лучше, а что хуже. Французский философ Рене Декарт противопоставлял дедукции интуицию. По его мнению, интуиция обеспечивает прямой доступ к подлинным знаниям, а дедукция лишь позволяет извлекать информацию путем рассуждения.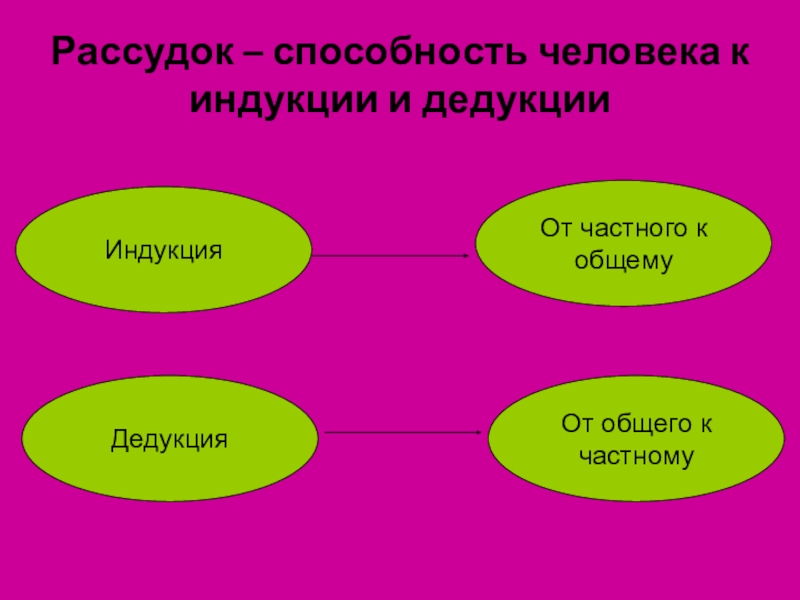

Фрэнсис Бэкон нещадно критиковал дедукцию. Дедуктивные рассуждения не дают новую информацию, а просто проливают свет на частный случай из общего правила. Правильным способом постижения новых истин Бэкон считал индукцию.

Готфрид Вильгельм Лейбниц, наоборот, называл дедуктивно-полученные знания «истинными во всех возможных мирах».

На самом деле, все методы познания работают в тесной связке друг с другом:

1. Интуиция помогает ученому понять, в каком направлении двигаться, что важно, а что нет.
2. С помощью индукции удается объединить набор разрозненных фактов в единое предположение.
3. Дедуктивная логика помогает проверить это предположение: если следствия верны, то и сама гипотеза – это истина.

Дедукция и индукция: как избежать ложных выводов

Когда плутаешь по логическим тропинкам, легко свернуть не туда. В дедукции, если общее утверждение ложно, то и выводы из него будут неправильными.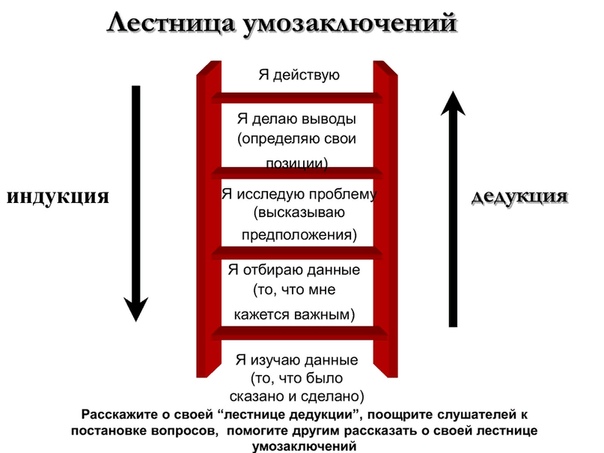 В индукции недостаточное количество фактов дает ошибочное предположение. Если одно яблоко червивое, это не значит, что все остальные такие же.

Опаснее всего ошибочные выводы, которые получены путем объединения индукции с дедукцией.

Представьте девушку, которая избегает отношений с противоположным полом из-за печального опыта. Она думает так:

1. Индуктивное получение недостоверного вывода.
   1. Саша мне изменял, Сережа – бил, Коля – пропивал все деньги;
   2. Саша, Сережа и Коля – мужчины;
   3. все мужики – козлы.
2. Дедуктивное получение ошибочного следствия из ложного умозаключения.
   1. все мужики – козлы;
   2. новый ухажер – мужчина;
   3. значит, он козел, а козлы мне не нужны.

Проблема в том, что умозаключение «все мужики – козлы» основано на неполной выборке. Саша, Сережа и Коля – не все мужчины в мире.

Пример неудачной дедукции:

Как развивать дедуктивные способности

Дедуктивное мышление – это не врожденный талант, а навык, который можно и нужно развивать. Как это сделать:

1. Расширить кругозор. Чтобы уметь быстро подбирать общее правило под конкретный случай, нужно хранить в голове настоящую библиотеку. Шерлок Холмс обладал глубокими познаниями в химии, медицине, анатомии, криминалистике, ботанике и геологии. А еще играл на скрипке и занимался боксом.
2. Тренировать мозги. Без нагрузки наши мысли замедляются, а разум «костенеет». Помогут логические задачи, головоломки, шахматы и шашки. Можно учить иностранные языки или осваивать новую профессию.
3. Развивать наблюдательность. В этом деле важно подмечать мелкие детали и особенности. Шерлок Холмс, просто взглянув на часы, рассказал доктору Ватсону историю жизни их предыдущего владельца.
4. Научиться контролировать свое внимание. Сложно мыслить логически, когда рой из несвязанных мыслей хаотично носится в голове. Есть простое упражнение: следите за секундной стрелкой часов, стараясь не отвлекаться. Это непросто: скоро вы обнаружите, что забыли про стрелку и размышляете о чем-то постороннем.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Индукция и дедукция. Какой тип умозаключений мы используем чаще?

Из этой статьи вы узнаете, что большинство управленческих решений принимается на основе индуктивных (вероятностных) суждений, а также о том, как грамотно использовать понимание этого в повседневной практике.

Холмс: Ватсон! Взгляните на эти звезды и расскажите мне, какой вывод, используя дедуктивный метод, вы можете сделать.

Ватсон: Я вижу на небе миллионы звезд. А раз они существуют, значит, среди них, возможно, есть и планеты. Из чего мы, в свою очередь, делаем вывод, что некоторые из них напоминают нашу Землю. Следовательно, на каких-то из них может существовать жизнь.

Холмс: Ватсон, вы – идиот. Это означает, что у нас украли палатку.

Определение понятий «индукция» и «дедукция»[1]

Возможно, вы удивились, встретив такой заголовок в блоге по менеджменту! Скоро вы поймете, какую огромную роль играет индукция в нашей жизни (не путайте понятие индукции в логике и магнитную индукцию :)).

Благодаря Артуру Конан Дойлу и его герою весь мир познакомился с дедуктивным методом. «Дедукция» из специального и известного только немногим термина превратилась в общеупотребительное и даже модное понятие.

Чего нельзя сказать об индукции. Вообще говоря, в логике существует два типа умозаключений: дедукция и индукция. В зависимости от того, существует ли между посылками, и заключением связь логического следования, можно выделить два вида умозаключений.

В дедуктивном умозаключении эта связь опирается на логический закон, в силу чего заключение с логической необходимостью вытекает из принятых посылок. Отличительная особенность такого умозаключения в том, что оно от истинных посылок всегда ведет к истинному заключению.

В индуктивном умозаключении связь посылок и заключения опирается не на закон логики, а на некоторые фактические или психологические основания, не имеющие чисто формального характера. В таком умозаключении заключение не следует логически из посылок и может содержать информацию, отсутствующую в них. Достоверность посылок, не означает поэтому, достоверности выведенного из них индуктивно утверждения. Индукция дает только вероятные, или правдоподобные, заключения, нуждающиеся в дальнейшей проверке.

Скачать заметку в формате Word

Прочитав эти строки, я в очередной раз убедился, как важны в нашей жизни определения. См. на эту тему, например, «Определение – ключ к овладению понятием» и «Использование методов менеджмента качества в работе оптовой торговой компании». До тех пор, пока я не познакомился с определением индукции (для лучшего понимания этого термина ниже я приведу несколько примеров), я «плавал», когда встречал упоминание о нем в литературе.

Примеры дедукции

Если идет дождь, земля мокрая

Все люди смертны. Все греки – люди. Следовательно, все греки – смертны.

Примеры индукции

Аргентина является республикой; Бразилия – республика; Венесуэла – республика; Эквадор – республика. Аргентина, Бразилия, Венесуэла, Эквадор – латиноамериканские государства. Все латиноамериканские государства являются республиками.

Италия – республика; Португалия – республика; Финляндия – республика; Франция – республика. Италия, Португалия, Финляндия, Франция – западноевропейские страны. Все западноевропейские страны являются республиками.

Индукция не дает полной гарантии получения новой истины из уже имеющихся [истин]. Максимум, о котором можно говорить, – это определенная степень вероятности выводимого утверждения. Так, посылки и первого и второго индуктивного умозаключения истинны, но заключение первого из них истинно, а второго – ложно. Действительно, все латиноамериканские государства – республики; но среди западноевропейских стран имеются не только республики, но и монархии, например Англия, Бельгия и Испания.

Почувствовали разницу? Ничего не вспомнили из вашей бизнес-практики на эту тему? Не делали ли вы ранее скоропалительных выводов на основе индукции?

Вот несколько примеров «работы» индукции: «Петров вчера не справился с производственным заданием. Петров сегодня не справился с заданием. Следовательно, Петров не способен выполнять производственные задания», «В марте объем продаж вырос. В апреле объем продаж вырос. Нас ждет дальнейший рост продаж», «Ранее мы всегда действовали

таким образом, и это приносило успех. Зачем же менять подходы?»

Углубим наше понимание индукции, ознакомившись с определениями из Википедии:

В экономике: индукция – вид обобщения, связанный с предвосхищением результатов наблюдений и экспериментов на основе данных опыта. В индукции данные опыта «наводят» на общее, поэтому индуктивные обобщения рассматриваются обычно как опытные истины или эмпирические законы. Изучая финансово-хозяйственную деятельность ряда типичных российских предприятий, мы можем делать, например, выводы о закономерностях развития совокупности предприятий.

В логике: полная индукция – метод доказательства, при котором утверждение доказывается для конечного числа частных случаев, исчерпывающих все возможности; неполная индукция – наблюдения за отдельными частными случаями наводит на гипотезу, которая нуждается в доказательстве.

Итак, позвольте дать собственное определение для целей управления:

индукция – обобщающее суждение, основанное на нескольких прецедентах; возможно, лучшее предположение на основе имеющихся данных

Индукция и ограничивающие ментальные модели[2]

В Википедии нет определения понятия «ментальные модели». Я бы сказал, что ментальные модели – это совокупность наших знаний служащая нам для восприятия действительности. Другими словами –  это то, как мы представляем себе некий предмет, явление, событие. Через ментальные модели мы истолковываем свой опыт. Они не представляют собой факты, хотя иногда мы именно так к ним относимся.

Ментальные модели мы создаем для упрощения картины мира. Строительство ментальных моделей основано на индукции. Наблюдая за событиями, мы их обобщаем, и храним в памяти единую картину. С одной стороны, это позволяет не запоминать всё многообразие. С другой стороны, мы теряем изменчивость присущую вещам и событиям. Сначала процесс познания работает на ментальную модель, потом ментальная модель подгоняет увиденное под себя. Именно в это время и теряется гибкость и восприимчивость к новому.

Глубоко укоренившиеся в нас ментальные модели определенным образом организуют наше восприятие мира. Мы используем их, чтобы проводить различия и выбирать, что имеет для нас значение, а что – нет. И можем принять свои представления за реальность, спутать карту с той территорией, которая на ней изображена.

По каким характерным признакам можно судить о наличии ограничивающих ментальных моделей?

• Если вы настаиваете на том, что ваши идеи полностью соответствуют реальности.
• Если у вас узкий круг интересов, который исключает приобретение опыта.
• Если вы не допускаете неопределенности и стараетесь как можно быстрее делать выводы.
• Не стесняетесь делать обобщения на основании единственного случая.
• Каждый раз, когда вас не устраивают поведение людей и ход событий, вы имеете наготове богатый запас объяснений.
• Вину за неудачи и проблемы возлагаете на людей (не забывая при этом и себя).
• Осмысляете происходящее в терминах прямолинейной логики «причина – следствие».
• Никогда не проявляете любознательности.
• Не пересматриваете своих убеждений на основе полученного опыта.

Как противостоять формированию ограничивающих ментальных моделей? Как не позволить индукции «закрыть» путь к развитию, изучению и осмыслению нового опыта, новых данных? Как сделать так, чтобы вслед за изменением мира, менялись наши ментальные модели?

1. Почаще перечитывайте признаки ограничивающих ментальных моделей, и… делайте всё наоборот.
2. Выделите и проанализируйте использование в речи оценочных суждений и обобщающих понятий. Все сказанное сказано кем-то. Нельзя ли поставить это под сомнение? Если вам говорят, что «у нас так принято»[3], уточните, когда и почему так было принято? Может быть, изменились условия внешней или внутренней среды, изменились исходные посылки, и выводы [сделанные на основе индукции] более не верны!?
3. Такие выражения, как «следует», «должен», «не следует», «не можете» известны в лингвистике как модальные операторы. Заведите «капканы» для «отлавливания» модальных операторов, потому что они устанавливают границы и зачастую маскируют ограничивающие ментальные модели.
4. Есть слова, называемые лингвистическими универсалиями, такие как: «все», «каждый», «никогда», «всегда» «никто», «любой»… Это обобщения, указывающие на отсутствие исключений, но исключения есть всегда. Вот несколько примеров: «Все делают так», «Никогда так не говори», «Мы всегда делали это так», «Никто еще никогда не возражал». Универсалии ограничивают нас, потому что, если принять их буквально, они лишают права выбора и поиска других возможностей. Услышав такое универсальное обобщение, сразу задайте вопрос о возможности исключений.
5. Используйте выражения типа: «как мне представляется», «я так вижу», «по имеющимся данным»… Когда коллеги говорят на таком языке, споры переходят в плоскость данных и предположений; становится удобным обсуждать, как и почему сделаны именно такие выводы. Все понимают, что есть посылки и взгляды, и относятся к ним не как к фактам, а как к преломлению фактов через ментальные модели конкретных людей… 🙂

Краткий вывод для менеджеров:

индукция подменяет многообразие реальной жизни однообразными представлениями о ней; понимание этого дает вам в руки оружие против ограничивающих ментальных моделей

Индукция и теории[4]

«Никакое количество наблюдений белых лебедей не может позволить сделать вывод, что все лебеди являются белыми, но достаточно наблюдения единственного черного лебедя, чтобы опровергнуть это заключение». Нассим Талеб «Одураченные случайностью»

Ричард Фейнман, физик, Нобелевский лауреат,[5] отзываясь о философе с особо большим самомнением, говорил: «Меня раздражает вовсе не философия как наука, а та помпезность, которая создана вокруг нее. Если бы только философы могли сами над собой посмеяться! Если бы только они могли сказать: «Я говорю, что это вот так, а Фон Лейпциг считает, что это по-другому,а ведь он тоже кое-что в этом смыслит». Если бы только они не забывали пояснить, чтоэто всего лишь их лучшее предположение»

Карл Поппер, на которого широко ссылается Нассим Талеб, вторит Фейнману. Решая проблему индукции, Поппер считает, что наука не должна восприниматься так серьезно, как это принято. Есть только два типа теорий:

1. Теории, о которых известно, что они являются неверными, поскольку они были проверены и, соответственно, отвергнуты (он называет их фальсифицированными).
2. Теории, о которых ещё не известно, что они неправильны, они ещё не фальсифицированы, но рискуют стать таковыми.

Теория, которая выпадает из этих двух категорий – не является теорией. Теория, которая не предоставляет набор условий, при которых она считалась бы неправильной, должна быть названа шарлатанством. Почему? Потому, что астролог всегда может найти причину приспособиться к прошлому событию, говоря, что Марс был, вероятно, на линии, но не слишком долго 🙂 В самом деле, различие между ньютоновской физикой, которая была фальсифицирована теорией относительности Эйнштейна, и астрологией заключается в следующей иронии. Ньютоновская физика научна потому, что позволяет нам фальсифицировать её, поскольку мы знаем, что она неправильна, в то время как астрология – нет, потому, что она не предлагает условия, при которых мы могли бы отвергнуть её. Астрология не может быть опровергнута, вследствие вспомогательных гипотез, которые входят в игру. Этот пункт находится в основе разграничения между наукой и ерундой.

Для Поппера вопрос знания не так много имеет дело с тем, что мы знаем, как с тем, что мы не знаем. Его знаменитая цитата: Они – люди со смелыми идеями, но высоко критичные к этим, их собственным идеям, они пытаются определить, являются ли их идеи правыми, пробуя сначала определить,  возможно ли, что они не неправильны. Они работают со смелыми догадками и серьезными попытками опровержения своих собственных догадок.

«Они» ­– это ученые. Но они могли быть кем угодно [для нас интересно, если – менеджерами].

Память людей является машиной по производству индуктивных выводов. Задумайтесь о воспоминаниях: что легче вспомнить – набор случайных фактов, слепленных вместе, или историю, некую последовательность логических связей? Причинно-следственные связи легче закрепляются в памяти. В этом случае нашему мозгу приходится проделать меньшую работу для сохранения информации. Ее объем меньше. Это очень удобно, так как общее занимает в памяти гораздо меньше места, чем набор частностей. Вот только в результате такого сжатия сокращается степень наблюдаемой случайности.

Краткий вывод для менеджеров

индукция формирует стереотипы, которыми имеет смысл пользоваться, пока не появился хотя бы один факт, опровергающий первоначальное предположение; когда же такой факт выявлен, вместо того, чтобы упорствовать, и «подгонять» факты под стереотипы, попытайтесь выдвинуть иную гипотезу, объясняющую  как прежние, так и новые факты

Индукция и методы менеджмента качества[6]

Типичные примеры индукции – сводки[7] данных или статистики на основе исходных данных: среднее значение (µ), медиана, стандартное отклонение (σ). Вместо того, чтобы изучать множество значений, мы ограничиваемся лишь небольшим набором статистик (например, µ ± σ). Преимущества очевидны: статистики неплохо описывают выборку значений. Недостатки не так заметны: за средними значениями могут прятаться значительные нежелательные «выбросы».

На индукции основано применение контрольных карт Шухарта: если управляемый процесс ранее был в неких рамках, то и в будущем мы считаем, что с определенной вероятностью он будет в таких же рамках (рис. 1а). С другой стороны, прогноз поведения неуправляемого процесса затруднен (рис. 1б).

Рис. 1. Динамика среднего значения и стандартного отклонения во времени в присутствии общих (а) или специальных (б) причин вариаций.

* * *

Возвращаясь к методу Шерлока Холмса с прискорбием должен сообщить, что [на мой взгляд / в соответствии с моими ментальными моделями :)] он использовал индукцию, а вовсе не дедукцию! Изучая факты, Холмс делал выводы, имеющие вероятностную природу. Виртуозно обнаруживая мельчайшие «зацепки», он выстраивал гипотезы (вряд ли, одну), затем проверял их, и лишь затем, являл миру свое объяснение фактов.

Практические выводы для менеджеров:

а) подавляющее большинство умозаключений [и решений, принимаемых на их основе] имеют индуктивную природу, то есть их истинность не абсолютна, а вероятностна;

б) необходимо отдавать себе отчет, что мир и наши представления о нем – не одно и то же; не сдавайтесь на милость жестким [ограничивающим] ментальным моделям, развивайте их, будьте любознательны;

в) «черный лебедь» [факт, не укладывающийся в господствующую систему] – повод пересмотреть стереотипы, и выдвинуть новые гипотезы, а не «латать» прежние.

---

[1] В этом разделе цитируется учебное пособие А.А.Ивина ЛОГИКА.

[2] В этом разделе используются идеи из Джозеф О’Коннор, Иан Макдермотт «Искусство системного мышления»

[3] На тему «у нас так принято» есть любопытная притча (цитируется с сокращениями по http://www.litvar.ru/a-potomu-chto-zdes-tak-prinyato-eksperiment/):

Возьмём металлическую клетку, к потолку подвесим банан, под бананом поставим стремянку, а в клетку запустим пять обезьян. Наступает момент, когда какой-нибудь обезьяне захочется кушать. Она лезет к банану, но мы с помощью пожарного брандспойта сбиваем её со стремянки ледяной водой, а заодно окатываем и всех остальных. Какое-то время они сидят ошалевшие, но наступает момент, когда томимая голодом обезьяна опять делает попытку добраться до банана. Повторяем процедуру… И так раза три-четыре. Кончается дело тем, что когда беспокойное животное опять пытается подойти к стремянке, остальные четверо его от неё оттаскивают и банально бьют.

Убираем из клетки беспокойную обезьяну и добавляем туда “свежую”. Проходит какое-то время, и она делает попытку добраться до банана. Четыре бдительные обезьяны, оставшиеся с прошлого раза, оттаскивают её и… бьют, хотя на этот раз никого не обливали. Разумеется, бедное животное не может понять за что, поэтому делает ещё одну попытку. Его опять бьют, но уже сильнее. В конечном итоге и эта обезьяна присоединяется к остальным в бездеятельном созерцании еды.

Убираем из клетки ещё одну находившуюся там с самого начала обезьяну и сажаем новую “свежую”. Результат предсказуем – она лезет за бананом, остальные вскакивают, оттаскивают и бьют. При этом с особым зверством бьёт та обезьяна, которую не обливали. Ситуация повторяется n-ное количество раз, где “n” зависит от сообразительности животного. Опять обезьяны просто сидят и смотрят на банан.

Опять вытаскиваем обезьяну из первого “эшелона” и снова добавляем “свежую”…  В итоге получаем ситуацию, когда в клетке сидят пять ни разу не облитых обезьян, но ни одна из них не делает попыток дотянуться до банана. Почему? А потому, что здесь так принято.

[4] А этот раздел написан по мотивам книги Нассима Талеба «Одураченные случайностью».

[5] Если вы имеете отношение к физике, то вполне могли слышать о «Фейнмановских лекциях по физике» – замечательном, очень хорошо написанном курсе.

[6] В этом разделе использованы идеи из книги Д. Уилер, Д. Чамберс «Статистическое управление процессами».

[7] Сводка – представление большого числа исходных данных одним числом.

Рационализм Декарта. Основные правила дедуктивного метода

Поможем написать любую работу на аналогичную тему

Получить выполненную работу или консультацию специалиста по вашему учебному проекту

Узнать стоимость

Иным, отличным от Бэкона путём в разработке проблем методологи и научного исследования пошёл великий французский мыслитель, учёный и философ Р. Декарт (1596 – 1650). Но поскольку Бэкон и Декарт были людьми одной эпохи, их философские системы имели и много общего. Главное, что сближало Бэкона и Декарта, – это разработка проблем методологии научного исследования.  Как и у Бэкона методология Декарта носила антисхоластическую направленность. Эта направленность проявлялась, прежде всего, в стремлении к достижению таких знаний, которые усиливали бы власть человека над природой, а не являлись бы самоцелью илт средством доказательства религиозных истин. Другой важной чертой декартовской методологии, также сближающей её с Бэконовский, является критика схоластической силлогистики. Схоластика, как известно, считала силлогизм главным орудием познавательных усилий человека. И Бэкон, и Декарт стремились доказать несостоятельность такого подхода. Оба они не отказывались от применения силлогизма как способа рассуждения, средства сообщения уже открытых истин. Но нового знания, по их мнению, силлогизм дать не может. Поэтому они стремились к разработке такого метода, который был бы эффективен в отыскании нового знания.

Однако путь, разработанный Декартом, весьма отличался от пути предложенного Бэконом. Как мы уже видели, бэконовская методология была эмпирической, опытно-индивидуальной. Метод же Декарта можно назвать Рационалистическим. Декарт отдавал должное опытно-экспериментальным исследованиям в естественных науках, но неоднократно подчёркивал значение опыта в научном познании. Но научные открытия, по мнению Декарта, совершаются не в следствии опытов, сколь искусными они не были, а в следствие деятельности ума, который направляет и сами опыты. Преимущественная ориентация на деятельность человеческого ума в процессе познания и делает методологию Декарта рационалистической.

Учение Декарта об интеллектуальной интуиции. Рационализм Декарта основывается на том, что он попытался применить ко всем наукам особенности математического метода познания.  Бэкон прошёл мимо такого эффективного и могучего способа осмысления опытных данных, каким в его эпоху становилась математика. Декарт же, будучи одним из великих математиков своего времени, выдвинул идею всеобщей математизации научного знания. Французский философ при этом истолковывал математику не просто как науку о порядке и мере, царящей во всей природе. В математике Декарт более всего ценил то, то что с её помощью можно прийти к твёрдым, точным, достоверным выводам. К таким выводам, по его мнению, не может привести опыт. Рационалистический метод Декарта и представляет собой, прежде всего философские осмысления и общение тех приёмов открытия истин, которыми оперировала математика.

Суть рационалистического метода Декарта сводиться к двум основным положениям. Во-первых, в познании следует отталкиваться от некоторых интуитивно ясных, фундаментальных истин, или, иначе говоря, в основе познания по Декарту, должна лежать интеллектуальная интуиция. Интеллектуальная интуиция, по Декарту, – это твёрдое и отчётливое представление, рождающееся в здоровом уме посредством самого ума , настолько простое и отчётливое, что оно не вызывает ни какого сомнения. Во-вторых, разум должен из этих интуитивных воззрений на основе дедукции вывести все необходимые следствия. Дедукция – это такое действие ума, посредством которого мы из определенных предпосылок делаем какие-то заключения, получаем определенные следствия. Дедукция, по Декарту  необходима потому, что вывод не всегда может представляться ясно и отчётливо. К нему можно прийти лишь через постепенное движение мысли при ясном и отчётливом осознании каждого шага. С помощью дедукции мы неизвестное делаем известным.

Декарт сформулировал следующие три основных правила дедуктивного метода:

1. Во всяком вопросе должно содержаться неизвестное.

2. Это неизвестное должно иметь какие-то характерные особенности, чтобы исследование было направлено на постижение именно этого неизвестного.

3. В вопросе также должно содержаться нечто известное.

Таким образом, дедукция – это определение неизвестного через ранее познанное и известное.

После определения основных положений метода перед Декартом встала задача сформировать такой исходный достоверный принцип, из которого, руководствуясь правилами дедукции, можно было бы логически вывести все остальные понятия философской системы, то есть Декарт должен был осуществить интеллектуальную интуицию. Интеллектуальная  интуиция у Декарта начинается с сомнения. Декарт подверг сомнению истинность всех знаний, которыми располагало человечество. Провозгласив сомнения в качестве исходного пункта всякого исследования, Декарт ставил цель – помочь человечеству избавиться от всех предрассудков (или идолов, как их называл Бэкон), от всех фантастических и ложных представлений , принятых на веру, и таким образом расчистить путь для подлинного научного познания, и вместе с тем, найти искомый, исходящий принцип, отчётливое ясное представление, которое уже нельзя подвергнуть сомнению. Поставив под сомнение достоверность всех наших представлений о мире, мы можем легко допустить, писал Декарт, «что нет ни бога, ни неба, ни земли что даже у нас самих нет тела. Но мы всё таки не можем предположить, что мы не существуем, в то время как сомневаемся в истинности всех этих вещей. Столь же нелепо полагать несуществующим то, что мыслит, в то время как оно мыслит, что, невзирая на самые крайние предположения, мы не можем не верить, что заключение «я мыслю, следовательно я существую»истинно и, что поэтому есть первое и вернейшее из всех заключений» (Декарт  Р. избр. произв. – М.,1950. – с. 428). Итак, положение «я мыслю, следовательно, я существую», то есть представление о том,  что мышление само по себе, независимо от его содержания и объектов, демонстрирует реальность мыслящего субъекта и является той первичной исходной интеллектуальной интуицией, из которой, по Декарту, выводятся все знания о мире.

 Следует отметить, что принцип сомнения применялся в философии и до Декарта в античном скептицизме, в учении Августина, в учении Ш. Монтеня и др. Уже  Августин на основе сомнения утверждал достоверность существования мыслящего существа. Следовательно, в этих вопросах Декарт не оригинален и находится в русле философской традиции. За пределы этой традиции его выводит крайне рационалистическое положение, что только мышление обладает абсолютной и непосредственной достоверностью. Оригинальность Декарта состоит в том, что он приписывает несомненный характер самому сомнению, мышлению и бытию субъекта мышления: обратившись к самому себе, сомнение, по Декарту, исчезает. Сомнению противостоит непосредственная  ясность самого факта мышления, мышления независящего от своего предмета, от предмета сомнения. Таким образом, «я мыслю» у Декарта есть как бы та абсолютно достоверная аксиома, из которой должно вырасти всё здание науки, подобно тому, как из небольшого числа аксиом и постулатов выводятся все положения Евклидовой геометрии.

Рационалистический постулат «Я мыслю» является основой единого научного метода. Этот метод, по мнению Декарта, должен превратить познание в организационную деятельность, освободив его от случайности, от таких субъективных факторов, как наблюдательность и острый ум, с одной стороны, удача  и счастливое обстоятельств с другой. Метод позволяет науке не ориентироваться на отдельные открытия, а планомерно и целенаправленно развивается, включая в свою орбиту все более широкие области неизвестного, иначе говоря, превратить науку в важнейшую сферу человеческой жизнедеятельности.

Декарт был сыном своего времени, и его философская система, как и Бэкона, не была лишена внутренних противоречий. Выдвигая на первый план проблемы познания, Бэкон и Декарт заложили основы для построения философских систем Нового времени. Если в средневековой философии центральное место отводилось учению о бытии – онтологии, то со времени Бэкона и Декарта на передний план в философских системах выходит учение о познании – гносеология.

Бэкон и Декарт положили начало раскола всей действительности на субъект и объект. Субъект – это носитель познавательного действия, объект – это то, на что направлено это действие. Субъектом в системе Декарта является мыслящая субстанция – мыслящее «Я». Однако Декарт сознавал, что «Я» как особой мыслящей субстанции надо найти выход к объективному миру. Иначе говоря, гносеология должна опираться на учение о бытии – онтологию. Декарт решает эту проблему на основе введения в свою метафизику идеи Бога. Бог является творцом объективного мира. Он же – создатель человека. Истинность исходного принципа как знания ясного и отчётливого гарантирована у Декарта существованием Бога – совершенного и всемогущего, вложившего в человека естественный свет разума. Таким образом, самосознание субъекта у Декарта не замкнуто на себе, а разомкнуто, открыто Богу, выступающему источником объективной значимости человеческого мышления. С признанием Бога в качестве источника и гаранта человеческого самосознания, разума связано учение Декарта о врожденных идеях. К ним Декарт относил идею Бога как существа всесовершенного, идеи чисел и фигур, а также некоторые наиболее общие понятия, как например, «из ничего ничего не происходит». В учении о врожденных идеях по-новому было развито платоновское положение об истинном знании как припоминании того, что запечатлелось в душе, когда она пребывала в мире идей.

Рационалистические мотивы в учении Декарта переплетаются с теологическим учением о свободе воли, дарованной человеку Богом в силу особого расположения благодати. Согласно Декарту, источником заблуждений не может быть разум сам по себе. Заблуждения есть продукт злоупотребления человеком присущей ему свободной воли. Заблуждения возникают тогда, когда бесконечно свободная воля переступает границы конечного человеческого разума, выносит суждения, лишенные разумного основания. Однако из этих идей Декарт не делает агностических выводов. Он верит в неограниченные возможности человеческого разума в деле познания всей окружающей его действительности.

Таким образом, Ф. Бэкон и Р. Декарт заложили основы новой методологии научного познания и дали этой методологии глубокое философское обоснование.

Внимание!

Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы.

Дедукция в философии и психологии

Дедукция — это метод мышления, следствием которого является логический вывод, где частное заключение выводится из общего.

«По одной лишь капле воды человек, умеющий мыслить логически, сможет вывести существование Атлантического океана или Ниагарского водопада, даже если он не видел ни того и ни другого» – так рассуждал самый знаменитый литературный сыщик.

Учитывая незаметные другим людям мелкие детали, он строил безупречные логические умозаключения, используя метод дедукции. Именно благодаря Шерлоку Холмсу весь мир узнал, что такое дедукция.

В своих рассуждениях великий сыщик всегда отталкивался от общего – всей картины преступления с предполагаемыми преступниками, и двигался к частным моментам – рассматривал каждого в отдельности, всех, кто мог совершить злодеяние, изучал мотивы, поведение, доказательства.

Этот удивительный герой Конан Дойля по частицам почвы на обуви мог угадать из какой части страны приехал человек. Также он различал сто сорок видов табачного пепла. Шерлок Холмс интересовался абсолютно всем, имел обширные знания во всех областях.

В чем суть дедуктивной логики

Дедуктивный метод начинается с гипотезы, которую человек считает априори верной, а затем он должен проверить ее с помощью наблюдений. Книги по философии и психологии определяют это понятие как умозаключение, построенное на принципе от общего к частному по законам логики.

В отличие от других типов логических рассуждений, дедукция выводит новую мысль из других, приводя к конкретному выводу, применимому в данной ситуации.

Дедуктивный метод позволяет нашему мышлению быть более конкретным и результативным.

Суть состоит в том, что дедукция строится на выведении частного на основе общих предпосылок. Другими словами, это рассуждения на основе подтвержденных, общепринятых и всем известных общих данных, которые и приводят к логичному фактическому выводу.

Дедуктивный метод с успехом применяется в математике, физике, научной философии и экономике. Врачам и юристам также приходится применять навыки дедуктивного мышления, но они будут полезны и для представителей любой профессии. Даже для писателей, работающих над книгами, немаловажным является умение разбираться в персонажах и делать выводы, основываясь на эмпирических знаниях.

Дедуктивная логика – это философское понятие, оно известно еще со времен Аристотеля, но интенсивно оно стало разрабатываться лишь в девятнадцатом веке, когда развивающаяся математическая логика дала толчок к развитию учения о дедуктивном методе.

Аристотель под дедуктивной логикой понимал доказательства с силлогизмами: рассуждение с двумя посылами и одним заключением. Высокую познавательную или когнитивную функцию дедукции подчеркивал и Рене Декарт. В своих работах ученый противопоставлял её интуиции.

По его мнению, интуиция непосредственно раскрывает истину, а дедукция эту истину постигает опосредованно, то есть, путём дополнительных рассуждений.

В повседневных рассуждениях дедукция крайне редко используется в форме силлогизма или двух посылов и одного вывода. Чаще всего указывается только один посыл, а второй посыл, как общеизвестный и всеми признанный, опускается. Вывод также не всегда формулируется в явной форме. Логическая связь между посылами и выводами выражается словами «вот», «следовательно», «значит», «поэтому».

Примеры использования метода

Первая часть: «Все российские офицеры бережно хранят боевые традиции». Вторая: «Все хранители боевых традиций – патриоты». Наконец, вывод: «Некоторые патриоты – российские офицеры».

Другой пример: «Платина – металл, все металлы проводят электрический ток, значит, платина электропроводна».

Цитата из анекдота про Шерлока Холмса: «Извозчик приветствует героя Конан Дойля, говоря, что рад видеть его после Константинополя и Милана. На удивление Холмса извозчик поясняет, что узнал эту информацию по биркам на багаже». И это пример использования дедуктивного метода.

Примеры дедуктивной логики в романе Конан Дойля и сериале МакГигана «Шерлок Холмс»

Что такое дедукция в художественной интерпретации Пола МакГигана становится понятно на следующих примерах. Цитата, олицетворяющая дедуктивный метод из сериала: «Выправка у этого человека, как у бывшего военного. Лицо загорелое, но это не его оттенок кожи, так как запястья у него не такие смуглые. Лицо уставшее, как после тяжелой болезни. Держит руку неподвижно, скорее всего, был когда-то ранен в нее». Здесь Бенедикт Камбэрбеч использует метод заключения от общего к частному.

Часто дедуктивные заключения бывают настолько урезанными, что о них можно только догадываться. Восстановить дедукцию в полной мере, с указанием двух посылов и вывода, а также логических связей между ними бывает затруднительно.

Цитата из детектива Конан Дойля: «Благодаря тому, что я так давно использую дедуктивную логику, умозаключения возникают в моей голове с такой скоростью, что я даже не замечаю промежуточных выводов или взаимосвязей между двумя положениями».

Что дает дедуктивная логика в жизни

В изучении какого-либо предмета подход дедуктивного мышления позволит рассматривать объект изучения тщательнее и со всех сторон, на работе – принимать верные решения и просчитывать эффективность; а в повседневной жизни – лучше ориентироваться в выстраивании отношений с другими людьми. Следовательно, дедукция может улучшить качество жизни при правильном использовании этого подхода.

Тот невероятный интерес, который показывают к дедуктивным умозаключениям в различных сферах научной деятельности, абсолютно объясним.

Ведь дедукция позволяет из уже имеющегося факта, события, эмпирического знания, получить новые законы и аксиомы, к тому же исключительно теоретическим путем, без применения его на опытах, исключительно благодаря наблюдениям.

Дедукция дает полную гарантию того, что факты, полученные в результате логического подхода, операции будут достоверны и истинны.

Говоря о важности логической дедуктивной операции, не стоит забывать об индуктивном методе мышления и обоснования новых фактов. Почти все общие явления и заключения, включая аксиомы, теоремы и научные законы, появляются в результате индукции, то есть движения научной мысли от частного к общему.

Таким образом, индуктивные соображения — основа наших знаний. Правда, сам по себе этот подход не гарантирует полноценности полученных знаний, но индуктивный метод вызывает новые предположения, связывает их со знанием, установленным опытным путем.

Опыт в данном случае является источником и основой всех наших научных представлений о мире.

Дедуктивная аргументация – мощное средство познания, используется для получения новых фактов и знаний. В совокупности с индукцией дедукция представляет собой инструментарий для познания мира.

Источник: https://HeadLife.ru/deduktsiya/

Что такое дедукция — достоинства и недостатки метода

Мышление является важным познавательным процессом для человека, благодаря которому он получает новые знания, развивается и становится лучше. Есть разные мыслительные методики, которые можно использовать в любое время и в разных ситуациях.

Что это дедукция?

Метод мышления, с помощью которого делаются логические выводы о конкретном предмете или ситуации на основе общей информации, называется дедукцией.

В переводе с латыни это слово означает «вывод или логическое умозаключение». Человек использует общеизвестную информацию и конкретные детали, анализирует, складывая факты в некую цепочку, и в завершении делает вывод.

Метод дедукции стал известным благодаря книгам и фильмам о детективе Шерлоке Холмсе.

Дедукция в философии

Использовать дедуктивное мышление для построения научных знаний начали еще в античные времена. Известные философы, например, Платон, Аристотель и Евклид, применяли его для того, чтобы сделать умозаключения на основе существующей информации.

Дедукция в философии – это понятие, которое разные умы толковали и понимали по-своему. Декарт считал этот тип мышления подобным интуиции, с помощью которой человек может получить знания посредством размышлений.

Свое мнение по поводу того, что такое дедукция, имели Лейбниц и Вольф, считая ее основой для получения истинных знаний.

Дедукция в психологии

Мышление используется в разных направлениях, но есть сферы, направленные на изучение самой дедукции. Основное предназначение психологии заключается в изучении развития и нарушения дедуктивных рассуждений у человека.

Связано это с тем, что поскольку этот тип мышления подразумевает движение от общей информации к конкретному анализу, то задействуются все психические процессы.

Теория дедукции изучается в процессе формирования понятий и решений разных задач.

Дедукция – достоинства и недостатки

Чтобы лучше понять возможности дедуктивного метода мышления, нужно разобраться в его преимуществах и недостатках.

1. Помогает экономить время и уменьшать объем излагаемого материала.
2. Можно использовать даже, когда нет предварительных знаний в конкретной области.
3. Дедуктивные умозаключения способствуют развитию логичного, доказательного мышления.
4. Дает общие знания, понятия и умения.
5. Помогает проводить проверку исследовательских гипотез, как правдоподобных объяснений.
6. Улучшает причинное мышление практикующих людей.

Минусы:

1. Человек в большинстве случаев получает знания в готовом виде, то есть не занимается изучением информации.
2. В некоторых случаях сложно конкретный случай подвести под общее правило.
3. Нельзя использовать для открытия новых явлений, законов и формулирования гипотез.

Дедукция и индукция

Если в значении первого термина уже разобрались, то, что касается индукции – это прием для построения общего вывода на основе частных посылок.

Он не использует логических законов, а опирается на некоторую психологическую и фактическую информацию, которая имеет чисто формальный характер.

Дедукция и индукция – это два важных принципа, которые дополняют друг друга. Для лучшего понимания, стоит рассмотреть пример:

1. Дедукция от общего к частному подразумевает получение из одной правдивой информации другую, и она будет истиной. Например, все поэты являются писателями, вывод: Пушкин – поэт и писатель.
2. Индукция является умозаключением, которое возникает от знания части предметов и ведущее к обобщению, поэтому говорят, что происходит переход от достоверной информации к вероятной. Например, Пушкин является поэтом, как Блок и Маяковский, значит, все люди поэты.

У каждого человека есть возможность развить в себе дедуктивное мышление, которое пригодится в разных жизненных ситуациях.

1. Игры. Для развития памяти можно использовать разные игры: шахматы, пазлы, судоку и даже карточные развлечения заставляют игроков продумывать свои ходы и запоминать карты.
2. Решение задач. Вот когда пригодится школьная программа по физике, математике и другим наукам. Во время решения задач происходит тренировка медленного мышления. Не стоит останавливаться на одном варианте решения и рекомендуется посмотреть на задачу с другой точки зрения, предложив альтернативу.
3. Расширение знаний. Развитие дедукции подразумевает, что человек должен постоянно работать над увеличением своего кругозора, «поглощая» много информации из разных областей. Это поможет в будущем строить свои умозаключения, опираясь на конкретные знания и опыт.
4. Проявляйте наблюдательность. Дедукция на практике невозможна, если человек не умеет замечать важные детали. Во время общения с людьми рекомендуется обращать внимание на жесты, мимику, тембр голоса и другие нюансы, что поможет понимать намерения собеседника, вычислять его искренность и так далее. Находясь в общественном транспорте, наблюдайте за людьми и делайте разные предположения, например, куда направляется человек, чем он занимается и многое другое.

Дедукция – упражнения

Чтобы развивать дедуктивное мышление, рекомендуется тренировать внимание, абстрактное мышление и оперативную память. Есть простые упражнение, как научиться дедукции, которые могут выполнять и взрослые, и дети:

1. Используйте любые картинки и лучше, если на них будет много мелких деталей. Смотрите на изображение в течение минуты, стараясь запомнить, как можно больше деталей, а затем запишите все, что отложилось в памяти, и проверьте. Постепенно сокращайте время просмотра.
2. Используйте похожие по смыслу слова и старайтесь найти в них максимальное количество отличий. Например: дуб/сосна, пейзаж/портрет, поэма/сказка и так далее. Еще специалисты рекомендуют учиться читать слова наоборот.
3. Запишите имена людей и даты конкретного события в их жизни. Хватит четырех позиций. Прочитайте их три раза, а затем, запишите все, что запомнили.

Дедуктивный метод мышления – книги

Одним из важных способов для развития дедуктивного мышления является чтение книг. Многие люди даже и не подозревают, сколько от этого пользы: происходит тренировка памяти, расширение кругозора и личностный рост. Чтобы применять дедуктивный метод, необходимо не просто читать литературу, а анализировать описанные ситуации, запоминать, сравнивать и проводить другие манипуляции.

1. Для тех, кому интересно, что такое дедукция, будет интересно почитать произведение автора этого метода мышления – Ренэ Декарта «Рассуждение о методе, чтоб верно направлять свой разум и отыскивать истину в науках».
2. К рекомендованной литературе относятся разные детективы, например, классика – А. К. Дойл «Приключения Шерлока Холмса» и многие стоящие авторы: А. Кристи, Д. Донцова, С. Шепард и другие. Читая подобную литературу необходимо применять дедуктивный метод мышления, чтобы предположить, кто же может быть преступником.

Источник: https://womanadvice.ru/chto-takoe-dedukciya-dostoinstva-i-nedostatki-metoda

Индукция в философии: дедукция, что это такое

Индукция — способ проверки гипотезы. Индукция в философии — это метод мышления, с помощью которого можно найти один общий признак и, таким образом, классифицировать предметы и явления. Для уточнения результатов индуктивного мышления в науке также применяется дедукция — противопоставляемый индукции метод мышления, для которого необходимо от общего заключения прийти к частному.

История появления термина

Впервые термин «индукция» упоминается в работах Сократа. Но он вкладывал в него иное значение. Сократ называл индукцией познание, заключавшееся в поиске общего определения для описания нескольких частных случаев. Аристотель описывает индукцию, как сравнительное умозаключение, при котором мыслительный процесс оценивает частные случаи и приводит их к общему знаменателю. Мыслитель противопоставлял индукцию силлогизму, направленному на поиск усредненного значения.

В эпоху Возрождения наследие Аристотеля переоценивается и критикуется. В научных кругах силлогизм, как метод исследования, отрицается, а индуктивный метод считается единственным способом получения достоверной информации. Создателем современного индуктивного метода считается Ф. Бэкон.

Он отказывается от использования силлогизма, но при этом его теория индукции вовсе не противоречит силлогизму. В основе индуктивного метода Бэкона, лежит принцип сравнения. Чтобы прийти к заключению, необходимо провести анализ всех случаев и вывести закономерность, т. е. сделать обобщение.

Следующей попыткой отказаться от силлогизма в пользу индукции было исследование Дж. Милля. Он полагал, что для получения силлогического заключения необходимо идти от частного к частному, не стремясь к общему. Индуктивное заключение видится ему анализом явлений одного порядка. Все умозаключения требуют применения четырех методов:

1. Метод согласия. Если у исследуемых явлений есть хотя бы один общий признак, вероятно, он является первопричиной.
2. Метод различия. Если у двух сравниваемых случаев имеется только одно различие, а в остальном они сходны, то это различие — причина явления.
3. Метод остатков. Для той части явления, которую невозможно объяснить очевидной причиной, необходимо искать обоснование среди оставшихся версий. На первый взгляд они часто кажутся невероятными, но одна в конечном итоге окажется достоверным объяснением.
4. Метод соответствующих изменений. Если несколько явлений изменяются под влиянием одного обстоятельства, вероятно, между ними есть причинная связь.

Примечательно, что методы, которые Бэкон представляет, как индуктивные, имеют дедуктивную составляющую. В частности, метод остатков работает по принципу исключения версий, продвигаясь от общего к частному.

Особенности индуктивного метода

В науке различают два вида индуктивного метода: полная индукция и неполная индукция.

Полная индукция

При полной индукции, мыслительному анализу поочередно подвергаются все предметы из группы. Они отождествляются с заданным признаком. Если каждый предмет будет соответствовать поставленному условию, можно с уверенностью предположить, что предметы имеют общую природу.

Неполная индукция

Главное отличие неполной индукции — отсутствие возможности сделать достоверное умозаключение. При неполной индукции сравнению подвергаются отдельные элементы предметов, и на основании результата делает предположение. Неполная индукция позволяет сделать только частное заключение, тогда как полная индукция стремится к общему.

Как правильно использовать дедуктивный и индуктивный подход

Использование индукции, как единственного метода поиска информации не дает объективной картины.

Индуктивный и дедуктивный методы рассуждения имеют противоположный способ движения мысли, но они не противоречат друг другу, а дополняют.

Для дедуктивного рассуждения нужно общее утверждение, а индуктивное собирает частные случаи, подводя их под одну теорию. Чтобы получить результат, приближенный к истине, необходимо использовать оба метода сразу.

Это позволяет проверить каждую теорию и отсеять неправдоподобные. А из оставшихся путем сравнения выбрать одну, которая будет отвечать все заданным требованиям.

Предполагается, что сам Декарт и другие представители научного сообщества, использовавшие метод индукции, на самом деле применяли комбинацию методов.

Использование одного метода повышает риск формулировки ложных выводов.

Если исследователь не может подвести все предметы к общему фактору, у него возникнет желание отбросить несоответствия и тем самым исказить условия эксперимента, и получить неправильный результат.

Роль методов мышления в психологии

Дедукция и индукция — методы мышления, которые нужно применять в комплексе. Изучение психических процессов, отвечающих за развитие, взаимосвязь и взаимодействие мыслительных процессов — одна из задач психологии. Форма проявления дедукции и индукции в психологии называется дедуктивным мышлением.

Люди, обращающиеся к психотерапевту, используют неполную индукцию и получают ошибочные выводы. Например, у изменившей мужу жены волосы рыжего цвета, значит все женщины с рыжими волосами — изменщицы.

Иногда, выводы, полученные в результате дедуктивного мышления, настолько оторваны от реальности, что несут угрозу жизни пациента. Если человек решит, что для него опасна вода, он полностью откажется от ее использования. Без лечения он погибнет. Вода для него — источник стресса, вызывающий паническую реакцию.

Самостоятельно справиться с такой нагрузкой на психику человек не может и в момент эмоционального всплеска он становится опасен для окружающих.

Такое неосознанное применение индуктивного мышления называется фиксацией. Способом избавления от фиксации станет правильное дедуктивное мышление, но его развитие, как и любой другой метод терапии, должен проходить под наблюдением психотерапевта.

Психологи рекомендуют людям, склонным к нервозности, развивать у себя дедуктивное мышление. Для этого используются простые способы:

1. Решение логических задач. Классический метод дедуктивного мышления — это математическое мышление. Чтобы решить задачу, человек использует логику, а это способствует развитию навыка отличать ложное суждение от правдоподобного.
2. Расширение кругозора. По сути, это пополнение багажа знаний любой информацией, которая интересна конкретному человеку. Для этого необязательно читать учебники. Новую информацию можно получить, просматривая фильмы или сайты, общаясь с другими людьми, путешествуя.
3. Развитие точности. Умение конкретизировать помогает подобрать правильный критерий, по которому оценивается явления.
4. Гибкость ума. Малый объем знаний способствует закостенелости ума. Имея ограниченный набор типовых ситуаций, человек выбирает не наиболее вероятную, а ту, которая вспомнится ему первой. А поскольку выбор у него невелик, она вряд ли будет подходящей.
5. Наблюдательность. Это инструмент, с помощью которого человек пополняет внутреннюю копилку личного опыта. Именно на его основе, делаются умозаключения.

Иногда, можно встретить термин «психологическая индукция», но у него нет конкретного определения. Часто, под индукцией подразумевают проявление некоторых психических заболеваний или аффективное состояние.

Минусы индуктивного подхода

Применение индуктивного метода имеет границы. Задача логики — обозначить их. Проведение аналогии не является доказательным методом, но дает возможность для поиска общих черт предметов и явлений. Для получения достоверного результата, необходимо иметь достаточное количество разнообразных примеров, чтобы представлять всю группу явлений.

Учитывая это, индуктивные заключения часто приводят к ошибочному выводу. Использование индукции предполагает работу со следствием, которое может быть вызвано разными причинами или их сочетанием. Поэтому достоверность полученной информации напрямую зависит от интеллектуальных способностей исследователя. Формируя умозаключения, он опирается только на свою логику и рационализм.

Неспособность отделить правдоподобные версии приводит к ошибочному выводу. А поскольку познавательные возможности человека ограничены, всегда существует риск анализа по ошибочному признаку и получения ложного результата.

В чем отличие дедукции от индукции?

Дедукция в философии — особый способ мышления, используя который человек делает логические выводы, основываясь на общей информации и выбирая из нее наиболее подходящий ситуации вариант развития событий.

Применение дедуктивного метода требует умения составлять логические цепочки, в которых из одного явления последовательно вытекает второе.

Этот способ обработки информации получил известность благодаря книгам о Шерлоке Холмсе, который использовал его для раскрытия преступлений.

О дедукции было известно еще мыслителям античного периода. Дедукция использовалась в философии для формирования умозаключений на основании уже имеющихся знаний. У каждого философа было свое представление о правильной дедукции.

Например, Декарт называл дедукцию интуитивным способом получения информации, который в результате продолжительных размышлений, обязательно приводит к единственной правильной версии.

Лейбниц полагал, что дедукция — единственный способ достичь истинного знания.

Дедукция превосходит большинство методов, поскольку выполняет такие функции:

• помогает быстрее найти верное решение;
• используется в тех областях, знания о которых поверхностны;
• способствует развитию логического мышления;
• помогает анализировать гипотезы, оценивая их правдоподобность;
• ускоряет мышление.

К минусам дедуктивного метода относятся:

• невозможность применять метод для изучения новых явлений;
• некоторые частные случаи очень сложно привести к общему знаменателю;
• полученные, благодаря дедукции, знания сложнее усвоить, поскольку человек получает готовый ответ, не утруждая себя сбором предварительной информации.

Использование дедукции в философии позволяет быстро и достоверно проверять информацию при условии правильного употребления законов логики.

Применение индукции в философии

Английский энциклопедист и философ У. Уэвелл был главным оппонентом Дж. Милля. Но и он признавал индукцию — необходимым и незаменимым методом познания в философии. В книге «Философия индуктивных наук» он пересмотрел саму суть научного знания, выведя науку из сферы туманного и закрытого в область доступного и необходимого. Благодаря его трудам научное сообщество получило возможность проводить исследования открыто. Уэвелл популяризовал само слово «наука», которое заменило натурфилоосфию. Переосмысление философом теории индукции, позволило ей стать одним из основных методов исследования.

Исследователь К. Поппер, в процессе проверки гипотез, отводит индукции ключевое значение. Индукция не может определить истинно ли утверждение, но помогает с точностью отобрать те версии, которые не выдерживают проверки экспериментом.

Если в результате проведения опытов часть теорий подтвердилась, а другая часть была опровергнута, предпочитаемыми будут те теории, которые дали положительный результат.

Но при этом следует помнить, что индукция не помогает найти универсальное подтверждение, которое подойдет всем выдвинутым версиям.

Источник: https://mystroimmir.ru/filosofiya/induktsiya.html

Дедукция

ДЕДУКЦИЯ
(лат. deductio
— выведение) — в широком смысле слова —
такая форма мышления, когда новая мысль
выводится чисто логическим путем (т.е.
по законам логики) из предшествующих
мыслей.

Такая последовательность мыслей
называется выводом, а каждый компонент
этого вывода является либо ранее
доказанной мыслью, либо аксиомой, либо
гипотезой. Последняя мысль данного
вывода называется заключением.

Процессы дедукции на
строгом уровне описываются в исчислениях
математической логики.

В узком смысле слова,
принятом в традиционной логике, под
термином “дедукция” понимают дедуктивное
умозаключение, т. е. такое умозаключение,
в результате которого получается новое
знание о предмете или группе предметов
на основании уже имеющегося некоторого
знания об исследуемых предметах и
применения к ним некоторого правила
логики.

Дедуктивное умозаключение,
являющееся предметом традиционной
логики, применяется нами всякий раз,
когда требуется рассмотреть какое —
либо явление на основании уже известного
нам общего положения и вывести в отношении
этого явления необходимое заключение.

Нам известен, например, следующий
конкретный факт — “данная плоскость
пересекает шар” и общее правило
относительно всех плоскостей, пересекающих
шар, -“всякое сечение шара плоскостью
есть круг”.

Применяя это общее правило
к конкретному факту, каждый правильно
мыслящий человек необходимо придет к
одному и тому же выводу: “значит данная
плоскость есть круг”.

Ход рассуждения при
этом будет таков: если данная плоскость
пересекает шар, а всякое сечение шара
плоскостью есть круг, то, следовательно,
и данная плоскость есть круг.

В итоге
данного умозаключения получено новое
знание о данной плоскости, которого не
содержится непосредственно ни в первой
мысли, ни во второй, взятых отдельно
друг от друга.

Вывод о том, что данная
плоскость есть круг”, получен в результате
сочетания этих мыслей в дедуктивном
умозаключении.

Структура дедуктивного
умозаключения и принудительный характер
его правил, заставляющих с необходимостью
принять заключение, логически вытекающее
из посылок, отобразили самое распространенные
отношения между предметами материального
мира: отношения рода, вида и особи, т. е.
общего, частного и единичного.

Сущность
этих отношений заключается в следующем:
то, что присуще всем видам данного рода,
то присуще и любому виду; то, что присуще
всем особям рода, то присуще и каждой
особи. Например,что присуще всем видам
данного рода, то присуще и любому виду;
то, что присуще всем особям рода, то
присуще и каждой особи.

Например, что
присуще всем нервным клеткам(например,
способность передавать информацию),то
присуще и каждой клетке, если она,
конечно, не отмерла. Но это именно и
отобразилось в дедуктивном умозаключении:
единичное и частное подводится под
общее.

Миллиарды раз наблюдая в процессе
практической деятельности отношения
между видом, родом и особью в объективной
действительности, человек выработал
соответствующую логическую фигуру,
приобретающую затем статус правила
дедуктивного умозаключения.

Дедукция играет большую
роль в нашем мышлении. Во всех случаях,
когда конкретный факт мы подводим под
общее правило и затем из общего правила
выводим какое-то заключение в отношении
этого конкретного факта, мы умозаключаем
в форме дедукции.

И если посылки истинны,
то правильность вывода будет зависеть
от того, насколько строго мы придерживались
правил дедукции, в которых отобразились
закономерности материального мира,
объективные связи и отношения всеобщего
и едентичного. Известную роль дедукция
играет во всех случаях, когда требуется
проверить правильность построения
наших рассуждений.

Так, чтобы удостовериться
в том, что заключение действительно
вытекает из посылок, которые иногда
даже не все высказываются, а только
подразумеваются, мы придаем дедуктивному
рассуждению форму силлогизма: находим
большую посылку, подводим под нее меньшую
посылку и затем выводим заключение.

При
этом обращаем внимание на то ,насколько
в умозаключении соблюдены правила
силлогизма. Применение дедукции на
основе формализации рассуждений
облегчает нахождение логических ошибок
и способствует более точному выражению
мысли.

Но особенно важно
использование правил дедуктивного
умозаключения на основе формализации
соответствующих рассуждений для
математиков, стремящихся дать точный
анализ этих рассуждений, например, с
целью доказательства их непротиворечивости.

Впервые теория дедукции
была обстоятельно разработана Аристотелем.

Он выяснил требования, которым должны
отвечать отдельные мысли, входящие в
состав дедуктивного умозаключения,
определил значение терминов и раскрыл
правила некоторых видов дедуктивных
умозаключений.

Положительной стороной
аристотелевского учения о дедукции
является то ,что в нем отобразились
реальные закономерности объективного
мира.

Переоценка дедукции
и ее роли в процессе познания особенно
характерна для Декарта. Он считал, что
к познанию вещей человек приходит двумя
путями: путем опыта и дедукции.

Но опыт
вводит часто нас в заблуждение, тогда
как дедукция, или, как Декарт говорил,
чистое умозаключение от одной вещи
через посредство другой, избавлено от,
этого недостатка.

При этом основным
недостатком декартовской теории дедукции
является то, что исходные положения для
дедукции, с его точки зрения, в конечном
счете дает будто бы интуиция, или
способность внутреннего созерцания,
благодаря которой человек познает
истину без участия логической деятельности
сознания. Это приводит Декарта в конце
концов к идеалистическому учению о том,
что исходные положения дедукции являются
очевидными истинами благодаря тому,
что составляющие их идеи изначала
“врождены” нашему разуму.

Философы и логики
эмпирического направления, выступившие
против учения рационалистов по
“врожденных” идеях, заодно принизили
значение дедукции. Так, ряд английских
буржуазных логиков пытался совершенно
отрицать какое — либо самостоятельное
значение дедукции в мыслительном
процессе.

Все логическое мышление они
сводили к одной только индукции. Так
английский философ Д. С. Милль утверждал,
что дедукции вообще не существует, что
дедукция — это только момент индукции.

По его мнению люди всегда заключают от
наблюдавшихся случаев к наблюдавшимся
случаям, а общая мысль, с которой
начинается дедуктивное умозаключение,
— это всего лишь словесный оборот,
обозначающий суммирование тех случаев,
которые находились в нашем наблюдении,
только запись об отдельных случаях,
сделанная для удобства. Единичные
случаи, по его мнению, представляют
собою единственное основание вывода.

Повод к недооценки
дедукции дал также и английский философ
Фр. Бэкон. Но Бэкон не относился
нигилистически к силлогизму.

Он выступал
лишь против того, что в “обычной логике”
почти все внимание сосредоточено на
силлогизме, в ущерб другому способу
рассуждения.

При этом совершенно ясно,
что Бэкон имеет в виду схоластический
силлогизм, оторванный от изучения
природы и покоящийся на посылках, взятых
из чистого умозрения.

В дальнейшем развитии
английской философии индукция все
больше превозносилась за счет дедукции.
Бэконовская логика выродилась в
одностороннюю индуктивную, эмпирическую
логику, главными представителями которой
были В. Уэвель и Д. С. Милль.

Они отбросили
слова Бэкона о том, что философ не должен
уподобляться эмпирику — муравью, но и
не походить на паука — рационалиста,
которой из собственного разума ткет
хитрую философскую паутину.

Они забыли,
что, по Бэкену, философ должен быть
подобен пчеле, которая собирает дань в
полях и лугах и затем вырабатывает из
нее мед.

В процессе изучения
индукции и дедукции можно рассматривать
их раздельно, но в действительности,
говорил русский логик Рудковский, все
наиболее важные и обширные научные
исследования пользуются одной из них
столько же, сколько и другой, ибо всякое
полное научное исследование состоит в
соединении индуктивных и дедуктивных
приемов мышления.

Метафизический взгляд
на дедукция и индукцию был резко осужден
Ф. Энгельсом. Он говорил, что вакханалия
с индукцией идет от англичан, которыми
выдумана противоположность индукции
и дедукции.

Логиков, которые неумеренно
раздували значение индукции, Энгельс
иронически называл “всеиндуктивистами”.

Индукция и дедукция только в метафизическом
представлении является взаимно
противопоставленными и исключающими
друг друга.

Метафизический разрыв
дедукции и индукции, абстрактное
противопоставление их друг другу,
извращение действительного соотношения
дедукции и индукции характерны и для
современной буржуазной науки. Некоторые
буржуазные философы теологического
толка исходят при этом из антинаучного
идеалистического решения философского
вопроса, согласно которому идея, понятие
даны извечно, от бога.

В противоположность
идеализму, марксистский философский
материализм учит, что всякая дедукция
является результатом предварительного
индуктивного изучения материала.

В свою
очередь индукция является подлинно
научной только тогда, когда изучение
отдельных частных явлений основано на
знании уже известных каких — то общих
законов развития этих явлений. При этом
процесс познания начинается и идет
одновременно дедуктивною и индуктивно.

Этот правильный взгляд на соотношение
индукции и дедукции был впервые доказан
марксистской философией. “Индукция и
дедукция связаны между собой столь же
необходимым образом, — пишет Ф. Энгельс,
— как синтез и анализ.

Вместо того чтобы
односторонне не превозносить одну из
них до небес за счет другой, надо стараться
применять каждую на своем месте, а этого
можно добиться только в том случае, если
не упускать из виду их связь между собою,
их взаимное дополнение друг друга.

В правильном мышлении,
таким образом, одинаково важны и индукция,
и дедукция. Они составляют две неразрывные
стороны единого процесса познания,
которые дополняют друг друга. Нельзя
себе представить себе такое мышление,
которое совершается только индуктивно
или только дедуктивною.

Индукция в
процессе реального опытного исследования
осуществляется в неразрывной связи с
дедукцией. Это именно и дает возможность
приходить к вполне достоверным выводам
в процессе такого исследования.

Значит,
в научном и повседневном мышлении по
любому вопросу дедукция и индукция
всегда тесно связаны друг другом,
неотъемлемы друг от друга, находятся в
неразрывном единстве.

Классическая
аристотелевская логика начала уже
формализовать дедуктивный вывод. Дальше
эту тенденцию продолжила математическая
логика, которая разрабатывает проблемы
формального вывода в дедуктивных
рассуждениях.

Под термином “дедукция”
в узком смысле слова понимают также
следующее:

1. Метод исследования, заключающийся в следующем: для того, чтобы

получить новое знание
о предмете или группе однородных
предметов, надо, во — первых найти
ближайший род, в который входят эти
предметы, и, во — вторых, применить к ним
соответствующий закон, присущий всему
данному роду предметов; переход от
знания более общих положений к знанию
менее общих положений. Дедуктивный
метод играет огромную роль в математике.
Известно, что все доказуемые предложения,
то есть теоремы выводятся логическим
путем с помощью дедукции из небольшого
конечного числа исходных начал, доказуемых
в рамках данной системы, называемых
аксиомами.

Классики марксизма —
ленинизма неоднократно указывали на
дедукцию, как на метод исследования.

Так, говоря о классификации в биологии,
Энгельс отмечал, что благодаря успехам
теории развития классификация организмов
сведена к “дедукции”, к учению о
происхождении, когда какой — нибуть вид
буквально дедуцируется из другого.

Энгельс относит дедукцию, наряду с
индукцией, анализом и синтезом, к методам
научного исследования. Но при этом он
указывает, что все эти средства научного
исследования являются элементарными.

Поэтому дедукция как самостоятельный
метод познания недостаточно для
всестороннего исследования действительности.
Связь единичного предмета с видом, вида
с родом, которая отображается в дедукции,
— это только одна из сторон бесконечно
многообразной связи предметов и явлений
объективного мира.

2) Форма изложения
материала в книге, лекции, докладе,
беседе, когда от общих положений, правил,
законов идут к менее общим положениям,
правилам, законам.

Миф

Что такое мифы? В обыденном понимании — это прежде всего
античные, библейские и другие старинные
«сказки» о сотворении мира и
человека, рассказы о деяниях древних
богов и героев — Зевсе, Аполлоне, Дионисе,
Геракле, аргонавтах, искавших «золотое
руно», Троянской войне и злоключениях
Одиссея.

Само
слово «миф» имеет древнегреческое происхождение и означает именно
«предание», «сказание».
Европейским народам вплоть до XVI-XVII
вв.

были известны лишь знаменитые и
поныне греческие и римские мифы, позже
им стало известно об арабских, индейских,
германских, славянских, индийских
сказаниях и их героях.

Со временем
сначала ученым, а потом и более широкой
публике оказались доступны мифы народов
Австралии, Океании, Африки. Выяснилось,
что в основе священных книг христиан,
мусульман, буддистов также лежат
различные, подвергшиеся переработке
мифологические предания.

Что удивительно: обнаружилось, что на определенной стадии
исторического развития более или менее
развитая мифология существовала практически у всех известных науке
народов, что некоторые сюжеты и рассказы
в той или иной мере повторяются в
мифологических циклах разных народов.

Так встал вопрос о
происхождении мифа. Сегодня большинство
ученых склоняются к тому мнению, что
секрет происхождения мифа следует искать в том, что мифологическое сознание
явилось древнейшей формой понимания и
осмысления мира, понимания природы,
общества и человека. Миф возник из
потребности древних людей в осознании
окружающей его природной и социальной
стихии, сущности человека.

Миф не есть выдумка,
или фикция, не есть фантастический
вымысел. Разумеется, мифология есть
выдумка, если применить к ней точку
зрения науки, да и то не всякой, но лишь
той, которая характерна для узкого круга
ученых новоевропейской истории последних
двух трех столетий.

Однако, мы условились
рассматривать миф исключительно лишь
с точки зрения самого же мифа, глазами мифа, мифическими глазами. А с точки
зрения самого мифического сознания ни
в каком случае нельзя сказать, что миф есть фикция, и игра фантазии.

Миф есть
наивысшая по своей конкретности,
максимально интенсивная и в величайшей
мере напряженная реальность. Это не
выдумка, но наиболее яркое и самая
подлинная действительность. Это –
совершенно необходимая категория мысли
и жизни, далекая от всякой случайности
и произвола.

Миф – необходимейшая, прямо
нужно сказать, трансцендентально-необходимая
категория мысли и жизни, и в нем нет
ровно ничего случайного, ненужного,
произвольного, выдуманного или
фантастического. Это – подлинное и
максимально конкретная реальность.

Ученые мифологи почти всегда находятся
во власти этого всеобщего предрассудка,
но нас интересует миф, а не та или иная
эпоха в развитии научного сознания. Миф
не выдумка, а содержит в себе строгую и
определенную структуру, а, следовательно,
является основной категорией сознания
и бытия вообще.

Источник: https://StudFiles.net/preview/1485452/page:5/

Пример дедукции и индукции из жизни

Дедукция это– способ рассуждения от общих положений к частным выводам.

Дедуктивное рассуждение только конкретизирует наше знание. В дедуктивном заключении содержится лишь та информация, которая есть в принятых посылках. Дедукция позволяет из уже имеющегося знания получать новые истины с помощью чистого рассуждения.

Дедукция даёт стопроцентную гарантию правильного заключения (при достоверных посылках). Дедукция из истины даёт истину.

• Пример 1.
• Все металлы пластичны (большая достоверная посылка или основной аргумент).
• Висмут – металл (достоверная посылка).
• Следовательно, висмут пластичен (правильное заключение).
• Дедуктивное рассуждение, обеспечивающее истинный вывод, называется силлогизмом.
• Пример 2.
• Все политики, допускающие противоречия – посмешище (большая достоверная посылка).

Ельцин Б. Н. допускал противоречия (достоверная посылка).

Следовательно, Е. Б. Н. – посмешище (правильный вывод).

1. Дедукция из лжи даёт ложь.
2. Пример.
3.  Помощь Международного Валютного Фонда всегда и всех ведёт к процветанию (ложная посылка).
4. России давно помогает МВФ (достоверная посылка).
5. Следовательно, Россия процветает (ложное заключение).
6. Индукция – способ рассуждения от частных положений к общим выводам.

В индуктивном заключении может содержаться информация, отсутствующая в принятых посылках. Достоверность посылок не означает достоверности индуктивного заключения. Посылки придают заключению большую или меньшую вероятность.

Индукция даёт не достоверное, а вероятностное знание, нуждающееся в проверке.

Пример 1.

 Г. М. С. – шут гороховый, Е. Б. Н. – шут гороховый, Ч. А. Б. – шут гороховый (достоверные посылки).

Г. М. С., Е. Б. Н., Ч. А. Б. – политики (достоверные посылки).

Следовательно, все политики – шуты гороховые (вероятностное заключение).

Обобщение правдоподобное. Однако, умеющие мыслить политики есть.

• Пример 2.
• В последние годы в районе 1, в районе 2 и в районе 3 проводились военные учения – повышалась боеспособность подразделений (достоверные посылки).
• В районе 1, в районе 2 и в районе 3 в учениях принимали участие подразделения Российской Армии (достоверные посылки).
• Следовательно, в последние годы во всех подразделениях Российской Армии повышалась боеспособность (индуктивное недостоверное  заключение).
• Из частных положений не следует логически общий вывод. Показные мероприятия не доказывают, что везде и всюду благополучие:
• На самом деле общая боеспособность Российской Армии катастрофически снижается.
• Вариант индукции – умозаключение по аналогии (на основе сходства двух объектов по одним параметрам делается вывод об их сходстве также и по другим параметрам).

Пример. Планеты Марс и Земля во многом похожи. На Земле есть жизнь. Поскольку Марс похож на Землю, на Марсе также имеется жизнь

Это заключение является, конечно, только вероятностным.

Любое индуктивное заключение нуждается в проверке.

Дмитрий Мезенцев    (координатор проекта «Русское Общество Добродействия»)        2011 г.

Источник: http://www.ob-dobr.ru/logika-zakony-pravilnogo-myshleniya/dedukciya-i-indukciya/

Философия: Энциклопедический словарь (А.А. Ивин). ДЕДУКЦИЯ

Приглашаем посетить сайт

ДЕДУКЦИЯ

ДЕДУКЦИЯ (от лат. deductio — выведение) — переход от посылок к заключению, опирающийся на логический закон, в силу чего заключение с логической необходимостью следует из принятых посылок. Характерная особенность Д. заключается в том, что от истинных посылок она всегда ведет только к истинному заключению.

Д. как умозаключению, опирающемуся на логический закон и с необходимостью дающему истинное заключение из истинных посылок, противопоставляется индукция — умозаключение, не опирающееся на закон логики и ведущее от истинных посылок к вероятному, или проблематичному, заключению.

• Дедуктивными являются, напр., умозаключения:
• Если лед нагревается, он тает.
• Лед нагревается.
• Лед тает.
• Черта, отделяющая посылки от заключения, стоит вместо слова «следовательно».
• Примерами индукции могут служить рассуждения:
• Бразилия — республика; Аргентина — республика.
• Бразилия и Аргентина — южноамериканские государства.
• Все южноамериканские государства являются республиками.
• Италия — республика; Португалия — республика; Финляндия — республика; Франция — республика.
• Италия, Португалия, Финляндия, Франция — западноевропейские страны.
• Все западноевропейские страны являются республиками.

Индуктивное умозаключение опирается на некоторые фактические или психологические основания. В таком умозаключении заключение может содержать информацию, отсутствующую в посылках. Достоверность посылок не означает поэтому достоверности выведенного из них индуктивного утверждения.

Заключение индукции проблематично и нуждается в дальнейшем исследовании. Так, посылки и первого, и второго приведенных индуктивных умозаключений истинны, но заключение первого из них истинно, а второго — ложно.

Действительно, все южноамериканские государства — республики; но среди западноевропейских стран имеются не только республики, но и монархии.

1. Особенно характерными Д. являются логические переходы от общего знания к частному типа:
2. Все люди смертны.
3. Все греки — люди.
4. Все греки смертны.

Во всех случаях, когда требуется рассмотреть какое-то явление на основании уже известного общего правила и вывести в отношении этого явления необходимое заключение, мы умозаключаем в форме Д.

Рассуждения, ведущие от знания о части предметов (частного знания) к знанию обо всех предметах определенного класса (общему знанию), — это типичные индукции.

Всегда остается вероятность того, что обобщение окажется поспешным и необоснованным («Сократ — умелый спорщик; Платон — умелый спорщик; значит, каждый человек — умелый спорщик»).

Нельзя вместе с тем отождествлять Д. с переходом от общего к частному, а индукцию — с переходом от частного к общему. В рассуждении «Шекспир писал сонеты; следовательно, неверно, что Шекспир не писал сонетов» есть Д., но нет перехода от общего к частному.

Рассуждение «Если алюминий пластичен или глина пластична, то алюминий пластичен» является, как принято думать, индуктивным, но в нем нет перехода от частного к общему. Д. — это выведение заключений, столь же достоверных, как и принятые посылки, индукция — выведение вероятных (правдоподобных) заключений.

К индуктивным умозаключениям относятся как переходы от частного к общему, так и аналогия, каноны индукции, целевое обоснование и т.д.

Дедуктивные умозаключения позволяют из уже имеющегося знания получать новые истины, и притом с помощью чистого рассуждения, без обращения к опыту, интуиции, здравому смыслу и т.п. Д. дает стопроцентную гарантию успеха. Отправляясь от истинных посылок и рассуждая дедуктивно, мы обязательно во всех случаях получим достоверное знание.

Не следует, однако, отрывать Д. от индукции и недооценивать последнюю. Почти все общие положения, включая и научные законы, являются результатами индуктивного обобщения. В этом смысле индукция — основа нашего знания.

Сама по себе она не гарантирует его истинности и обоснованности, но она порождает предположения, связывает их с опытом и тем самым сообщает им определенное правдоподобие, более или менее высокую степень вероятности. Опыт — источник и фундамент человеческого знания.

Индукция, отправляющаяся от того, что постигается в опыте, является необходимым средством его обобщения и систематизации.

В обычных рассуждениях Д. только в редких случаях предстает в полной и развернутой форме. Чаще всего указываются не все используемые посылки, а лишь некоторые. Общие утверждения, которые кажутся хорошо известными, опускаются.

Не всегда явно формулируются и заключения, вытекающие из принятых посылок. Сама логическая связь, существующая между исходными и выводимыми утверждениями, лишь иногда отмечается словами, подобными «следовательно» и «значит». Нередко Д.

является настолько сокращенной, что о ней можно только догадываться. Проводить дедуктивное рассуждение, ничего не опуская и не сокращая, обременительно.

Однако всякий раз, когда возникает сомнение в обоснованности сделанного вывода, необходимо возвращаться к началу рассуждения и воспроизводить его в возможно более полной форме. Без этого трудно или даже невозможно обнаружить допущенную ошибку.

Дедуктивная аргументация представляет собой выведение обосновываемого положения из иных, ранее принятых положений. Если выдвинутое положение удается логически (дедуктивно) вывести из уже установленных положений, это означает, что оно приемлемо в той же мере, что и сами эти положения. Обоснование одних утверждений путем ссылки на истинность или приемлемость др.

утверждений — не единственная функция, выполняемая Д. в процессах аргументации. Дедуктивное рассуждение служит также для верификации (косвенного подтверждения) утверждений: из проверяемого положения дедуктивно выводятся его эмпирические следствия; подтверждение этих следствий оценивается как индуктивный довод в пользу исходного положения.

Дедуктивное рассуждение используется также для фальсификации утверждений путем показа того, что вытекающие из них следствия являются ложными. Не достигшая успеха фальсификация представляет собой ослабленный вариант верификации: неудача в опровержении эмпирических следствий проверяемой гипотезы является аргументом, хотя и весьма слабым, в поддержку этой гипотезы.

И наконец, Д. используется для систематизации теории или системы знания, прослеживания логических связей входящих в нее утверждений, построения объяснений и пониманий, опирающихся на общие принципы, предлагаемые теорией.

Прояснение логической структуры теории, укрепление ее эмпирической базы и выявление ее общих предпосылок является вкладом в обоснование входящих в нее утверждений.

Дедуктивная аргументация является универсальной, применимой во всех областях рассуждения и в любой аудитории. «И если блаженство есть не что иное, как жизнь вечная, а жизнь вечная — это познание истины, то блаженство — это не что иное, как познание истины» — Иоанн Скот (Эриугена). Это теологическое рассуждение представляет собой дедуктивное рассуждение, а именно силлогизм.

Удельный вес дедуктивной аргументации в разных областях знания существенно различен. Очень широко она применяется в математике и математической физике и только эпизодически — в истории или эстетике. Имея в виду сферу приложения Д.

, Аристотель писал: «Не следует требовать от оратора научных доказательств, точно так же как от математика не следует требовать эмоционального убеждения». Дедуктивная аргументация является очень сильным средством, но, как и всякое такое средство, она должна использоваться узконаправленно. Попытка строить аргументацию в форме Д.

в тех областях или в той аудитории, которые для этого не годятся, приводит к поверхностным рассуждениям, способным создать только иллюзию убедительности.

В зависимости от того, насколько широко используется дедуктивная аргументация, все науки принято делить на деду кти вн ы е и индуктивные. В первых используется по преимуществу или даже единственно дедуктивная аргументация.

Во вторых такая аргументация играет лишь заведомо вспомогательную роль, а на первом месте стоит эмпирическая аргументация, имеющая индуктивный, вероятностный характер. Типично дедуктивной наукой считается математика, образцом индуктивных наук являются естественные науки. Однако деление наук на дедуктивные и индуктивные, широко распространенное еще в нач. 20 в.

, сейчас во многом утратило свое значение. Оно ориентировано на науку, рассматриваемую в статике, как систему надежно и окончательно установленных истин.

Понятие «Д.» является общеметодологическим понятием. В логике ему соответствует понятие доказательства.

Источник: http://philosophy.niv.ru/doc/dictionary/encyclopedic/articles/345/dedukciya.htm

ГИПОТЕТИКО-ДЕДУКТИВНЫЙ МЕТОД • Большая российская энциклопедия

• В книжной версии

  Том 7. Москва, 2007, стр. 168

• Скопировать библиографическую ссылку:

  ---

Авторы: Г. И. Рузавин

ГИПОТЕ́ТИКО-ДЕДУКТИ́ВНЫЙ МЕ́ТОД, ме­тод рас­су­ж­де­ния, ос­но­ван­ный на де­дук­ции, или вы­ве­де­нии, за­клю­че­ний из ги­по­тез. По­сколь­ку де­дук­ция пе­ре­но­сит ис­тин­но­ст­ное зна­че­ние ги­по­тез как ве­ро­ят­но­ст­ных су­ж­де­ний на за­клю­че­ние, то оно ока­зы­ва­ет­ся не дос­то­вер­но ис­тин­ным, а лишь ве­ро­ят­но­ст­ным или прав­до­по­доб­ным.

Ги­по­те­ти­ко-де­дук­тив­ные рас­су­ж­де­ния впер­вые ста­ли при­ме­нять­ся в ан­тич­ной фи­ло­со­фии в про­цес­се ве­де­ния по­ле­ми­ки, в хо­де ко­то­рой ста­ви­лась за­да­ча убе­дить про­тив­ни­ка ли­бо от­ка­зать­ся от сво­его те­зи­са, ли­бо уточ­нить его (по­сред­ст­вом вы­во­да из не­го след­ст­вий, про­ти­во­ре­ча­щих фак­там; Пла­тон на­зы­вал та­кой ме­тод со­кра­ти­че­ским). В на­уч. по­зна­нии Г.-д. м. стал ши­ро­ко ис­поль­зо­вать­ся с воз­ник­но­ве­ни­ем экс­пе­рим. ес­те­ст­во­зна­ния на­чи­ная с 17 в. Впер­вые он был при­ме­нён Г. Га­ли­ле­ем для от­кры­тия за­ко­на сво­бод­но­го па­де­ния тел, а И. Нью­тон ис­поль­зо­вал его для по­строе­ния за­кон­чен­ной сис­те­мы клас­сич. ме­ха­ни­ки. Г.-д. м. на­столь­ко глу­бо­ко про­ник в ме­то­до­ло­гию совр. ес­те­ст­во­зна­ния, что стал рас­смат­ри­вать­ся как мо­дель для эпи­сте­мо­ло­гич. ана­ли­за ес­теств.-на­уч. тео­рии. Раз­но­вид­но­стью Г.-д. м. яв­ля­ет­ся ма­те­ма­тич. ги­по­те­за, пред­став­ляю­щая со­бой сис­те­му ги­по­те­тич. урав­не­ний и слу­жа­щая эв­ри­стич. сред­ст­вом по­ис­ка но­вых тео­рий в ма­те­ма­тич. ес­те­ст­во­зна­нии.

С ло­гич. точ­ки зре­ния Г.-д. м. пред­став­ля­ет со­бой ие­рар­хию ги­по­тез, сте­пень аб­ст­ракт­но­сти и общ­но­сти ко­то­рых воз­рас­та­ет по ме­ре уда­ле­ния от эм­пи­рич. ба­зи­са. Ме­то­до­ло­ги­че­ски та­кая сис­те­ма да­ёт воз­мож­ность ис­сле­до­вать не толь­ко струк­ту­ру и взаи­мо­связь ме­ж­ду ги­по­те­за­ми раз­но­го уров­ня, но и ха­рак­тер их под­твер­жде­ния эм­пи­рич. дан­ны­ми: под­твер­жде­ние од­ной из них кос­вен­но сви­де­тель­ст­ву­ет о под­твер­жде­нии дру­гих, ло­ги­че­ски с ней свя­зан­ных ги­по­тез. Этим объ­яс­ня­ет­ся стрем­ле­ние к объ­е­ди­не­нию их в рам­ках ги­по­те­ти­ко-де­дук­тив­ных сис­тем.

анализ и синтез, индукция и дедукция, аналогия и моделирование.

Подробности

Категория: Вопросы и ответы по философии

Поможем написать любую работу на аналогичную тему

Получить выполненную работу или консультацию специалиста по вашему учебному проекту

Узнать стоимость

Методами обработки и систематизации знаний эмпирического уровня прежде всего являются синтез и анализ. Анализ- процесс мысленного, а нередко и реального расчленения предмета, явления на части(признаки, свойства, отношения). Процедурой, обратной анализу, является синтез. Синтез- это соединение выделенных в ходе анализа сторон предмета в единое целое.

Индукция- способ рассуждения или метод получения знаний, при котором общий вывод делается на основе обобщения частных посылок. Индукция может полной и неполной.

Дедукция –способ рассуждения или метод движения знания от частного, т. е. процесс логического перехода от общих посылок к заключениям о частных случаях.

Аналогия – прием познания, при котором наличие сходства, совпадение признаков нетождественных объектов позволяет предложить их сходство и в других признаках. Аналогия- незаменимое средство наглядности, изобразительности мышления.

Метод моделирования основан на принципе подобия. Его сущность состоит в том, что непосредственно исследуется не сам объект, а его аналог, его заместитель, его модель, а затем полученные при изучении модели результаты по особым правилам переносятся на объект. Моделирование используется в тех случаях, когда сам объект труднодоступен, либо его прямое изучение экономически невыгодно

Внимание!

Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы.

дедуктивных и индуктивных аргументов | Интернет-энциклопедия философии

При оценке качества аргумента мы спрашиваем, насколько хорошо его посылки подтверждают его вывод. Более конкретно, мы спрашиваем, является ли аргумент дедуктивно действительным или индуктивно сильным .

Дедуктивный аргумент — это аргумент, который предполагается, что аргумент является дедуктивно действительным, то есть обеспечивает гарантию истинности вывода при условии, что посылки аргумента верны.Эту точку зрения можно также выразить, сказав, что в дедуктивном аргументе посылки призваны обеспечить такую ​​сильную поддержку вывода, что, если посылки истинны, тогда невозможно, чтобы этот вывод был ложным. Аргумент, в котором посылки действительно позволяют гарантировать заключение, называется (дедуктивно) действительным аргументом . Если действительный аргумент имеет истинные посылки, то говорят, что аргумент также имеет звук . Все аргументы либо действительны, либо недействительны, либо верны, либо необоснованны; не существует компромисса, например, быть в некоторой степени обоснованным.

Вот допустимый дедуктивный аргумент:

В Сингапуре солнечно. Если в Сингапуре солнечно, то зонтика у него не будет. Значит, он не будет носить зонтик.

Заключение следует за словом «So». Две посылки этого аргумента, если они верны, гарантируют истинность вывода. Однако нам не предоставили никакой информации, которая позволила бы нам решить, верны ли обе эти посылки, поэтому мы не можем оценить, является ли этот аргумент дедуктивно обоснованным.Одно или другое, но мы не знаем, какой именно. Если выяснится, что аргумент имеет ложную предпосылку и, следовательно, необоснован, это не изменит того факта, что он действителен.

Вот довольно сильный индуктивный аргумент:

Каждый раз, когда я проходил мимо этой собаки, она не пыталась меня укусить. Итак, в следующий раз, когда я прохожу мимо этой собаки, она не будет пытаться меня укусить.

Индуктивный аргумент — это аргумент, который, по мнению аргумента, должен быть достаточно сильным, чтобы, если бы посылки были истинными, то маловероятно , что заключение было бы ложным.Итак, успех или сила индуктивного аргумента зависит от степени, в отличие от дедуктивного аргумента. Не существует стандартного термина для успешного индуктивного аргумента, но в этой статье используется термин «сильный». Слабые индуктивные аргументы называются слабыми; нет четкой границы между сильным и слабым. Аргумент о том, что собака кусает меня, был бы сильнее, если бы мы не могли придумать каких-либо соответствующих условий, объясняющих, почему следующий раз будет отличаться от предыдущего. Аргумент также будет тем сильнее, чем больше раз я гулял с собакой.Аргумент будет тем слабее, чем реже я выгуливаю собаку. Он будет слабее, если соответствующие условия о прошедшем времени будут другими в следующий раз, например, когда в прошлом собака находилась за закрытыми воротами, но в следующий раз ворота будут открыты.

На индуктивный аргумент может повлиять приобретение новых посылок (свидетельство), но на дедуктивный аргумент — нет. Например, это достаточно сильный индуктивный аргумент:

Сегодня Джон сказал, что ему нравится Ромона.
Итак, Джону сегодня нравится Ромона.

, но его сила радикально меняется, когда мы добавляем эту предпосылку:

Сегодня Джон сказал Фелипе, что ему не очень нравится Ромона.

Различие между дедуктивной и индуктивной аргументацией было впервые замечено Аристотелем (384-322 до н. Э.) В Древней Греции. Разница между дедуктивными и индуктивными аргументами заключается не в словах, используемых в аргументах, а в намерениях аргументации. Оно проистекает из отношения, которое, по мнению оппонента, существует между посылками и заключением.Если аргумент считает, что истинность посылки определенно устанавливает истинность заключения, то аргумент дедуктивный . Если аргумент считает, что истинность посылок дает только веские основания полагать, что вывод, вероятно, верен, то аргумент индуктивный . Если мы, оценивающие качество аргументации, не располагаем информацией о намерениях оппонента, мы проверяем и то, и другое. То есть мы оцениваем аргумент, чтобы увидеть, является ли он дедуктивно верным и индуктивно сильным.

Концепции дедуктивной достоверности можно дать альтернативные определения, чтобы помочь вам понять эту концепцию. Ниже приведены пять различных определений одного и того же понятия. Обычно слово , дедуктивно , отбрасывают из термина , дедуктивно действительный :

.

1. Аргумент действителен , если все посылки не могут быть истинными без истинного заключения.
2. Аргумент действителен , если истинность всех его предпосылок заставляет заключение быть истинным.
3. Аргумент является действительным , если он несовместим, чтобы все его посылки были истинными, а его вывод был бы ложным.
4. Аргумент действителен , если его вывод с уверенностью следует из его посылок.
5. Аргумент действителен , если у него нет контрпримера, то есть возможной ситуации, которая делает все предпосылки истинными, а вывод ложным.

Некоторые аналитики предпочитают отличать индуктивные аргументы от «кондуктивных» аргументов; последние представляют собой аргументы, дающие явные причины за и против заключения и требующие от лица, оценивающего аргумент, взвесить эти конкурирующие соображения, то есть рассмотреть все «за» и «против».В этой статье кондуктивные аргументы рассматриваются как своего рода индуктивные аргументы.

Существительное «дедукция» относится к процессу развития или обоснования дедуктивного аргумента или прохождения процесса рассуждения, который может быть реконструирован как дедуктивный аргумент. «Индукция» относится к процессу продвижения индуктивного аргумента или использования аргументации, которая может быть реконструирована как индуктивный аргумент.

Хотя индуктивная сила — это вопрос степени, дедуктивная достоверность и дедуктивная обоснованность — нет.В этом смысле дедуктивное рассуждение является гораздо более строгим, чем индуктивное рассуждение. Тем не менее, индуктивная сила — это не вопрос личных предпочтений; это вопрос того, должно ли посылка способствовать более высокой степени веры в заключение.

Поскольку дедуктивные аргументы — это те аргументы, в которых истинность вывода считается полностью гарантированной , а не только , сделанной вероятной истинностью посылок, если аргумент является здравым, то мы говорим, что вывод « содержащиеся внутри »помещения; то есть заключение не выходит за рамки того, что неявно требуют исходные посылки.Думайте о здравых дедуктивных аргументах как о выдавливании вывода из посылок, в которых он спрятан. По этой причине дедуктивные аргументы обычно решающим образом основываются на определениях и правилах математики и формальной логики.

Рассмотрим, как правила формальной логики применимы к этому дедуктивному аргументу:

Джон болен. Если Джон болен, он не сможет присутствовать на нашем сегодняшнем собрании. Следовательно, Джон не сможет присутствовать на нашем собрании сегодня.

Этот аргумент допустим в силу его формальной или логической структуры.Чтобы понять, почему, обратите внимание, что если бы слово «плохо» было заменено на «счастливый», аргумент все еще был бы действителен, потому что он сохранил бы свою особую логическую структуру (называемую логиками modus ponens ). Вот форма любого аргумента, имеющего структуру modus ponens:

-П

Если P, то Q

Итак, Q

Заглавные буквы следует рассматривать как переменные, которые можно заменить декларативными предложениями, утверждениями или предложениями, а именно элементами, которые являются истинными или ложными.Исследование логических форм, которые включают целые предложения, а не их подлежащие, глаголы и другие части, называется логикой высказываний.

Вопрос о том, являются ли все или только большинство допустимых дедуктивных аргументов действительными из-за их логической структуры, все еще остается спорным в области философии логики, но этот вопрос не будет исследоваться далее в этой статье.

Индуктивные аргументы могут принимать самые разнообразные формы. Некоторые из них имеют форму утверждения о совокупности или наборе, основанном только на информации из выборки этой совокупности, подмножества.Другие индуктивные аргументы делают выводы, апеллируя к свидетельствам, авторитету или причинно-следственным связям. Есть и другие формы.

Вот довольно сильный индуктивный аргумент, имеющий форму аргумента, основанного на авторитете:

Полиция сообщила, что убийство совершил Джон. Итак, Джон совершил убийство.

Вот индуктивный аргумент, основанный на доказательствах:

Свидетель сказал, что убийство совершил Джон. Итак, Джон совершил убийство.

Вот более сильный индуктивный аргумент, основанный на более убедительных доказательствах:

Два независимых свидетеля заявили, что убийство совершил Джон.Отпечатки пальцев Джона на орудии убийства. Джон признался в преступлении. Итак, Джон совершил убийство.

Этот последний аргумент, если известно, что его посылки верны, без сомнения, достаточно хорош, чтобы присяжные могли осудить Джона, но ни один из этих трех аргументов о совершении убийства Джоном не является достаточно сильным, чтобы его можно было назвать «действительным», по крайней мере, не в техническом смысле дедуктивно действительный. Тем не менее, некоторые юристы скажут присяжным, что это веские аргументы, поэтому мы, критически мыслящие люди, должны быть начеку в отношении того, как люди вокруг нас используют термин «достоверный».«Вы должны быть внимательны к тому, что они имеют в виду, а не к тому, что они говорят. По малейшим уликам английский детектив Шерлок Холмс ловко «вычислил», кто кого убил, но на самом деле он сделал только обоснованное предположение. Строго говоря, он привел индуктивный, а не дедуктивный аргумент. Чарльз Дарвин, открывший процесс эволюции, известен своим «выводом» о том, что круглые атоллы в океанах на самом деле являются коралловыми наростами на вершинах едва затопленных вулканов, но он действительно провел индукцию, а не дедукцию.

Стоит отметить, что некоторые словари и тексты определяют «дедукцию» как рассуждения от общего к частному и определяют «индукцию» как рассуждения от частного к общему . Однако есть много индуктивных аргументов, которые не имеют такой формы, например: «Я видел, как она его целовала, на самом деле целовала его, поэтому я уверен, что у нее роман».

Метод математического доказательства, называемый «математическая индукция», является дедуктивным, а не индуктивным.Доказательства, использующие математическую индукцию, обычно имеют следующую форму:

Свойство P истинно для натурального числа 0.
Для всех натуральных чисел n , если P имеет значение n , то P также имеет значение n + 1.
Следовательно, P истинно для всех натуральных чисел. числа.

Когда такое доказательство дает математик, и когда все посылки верны, то неизбежно следует вывод. Следовательно, такой индуктивный аргумент является дедуктивным.Это тоже дедуктивно звучит.

Поскольку различие между индуктивными и дедуктивными аргументами связано с силой доказательства, которую, по мнению автора , предпосылки обеспечивают заключение, индуктивные и дедуктивные аргументы различаются в отношении стандартов оценки, которые к ним применимы. Разница не связана с содержанием или предметом аргументации, а также с наличием или отсутствием какого-либо конкретного слова. В самом деле, одно и то же высказывание может использоваться для представления либо дедуктивного, либо индуктивного аргумента, в зависимости от того, во что верит человек, который его продвигает.Рассмотрим для примера:

Dom Perignon — шампанское, поэтому оно должно быть произведено во Франции.

Из контекста может быть ясно, что докладчик считает, что то, что было произведено в районе Шампани во Франции, является частью определяющего признака «шампанского», и поэтому вывод следует из предпосылки по определению. Если говорящий предполагает, что доказательства такого рода, то аргумент является дедуктивным. Однако может случиться так, что у говорящего нет такой мысли.Он или она может просто полагать, что почти все шампанское производится во Франции, и могут рассуждать вероятностно. Если это его намерение, то аргумент является индуктивным.

Как уже отмечалось, различие между дедуктивным и индуктивным связано с силой обоснования того, что аргумент имеет в виду , что посылки обеспечивают заключение. Еще одна сложность в нашем обсуждении дедукции и индукции состоит в том, что аргумент может иметь в виду, что посылки оправдывают вывод, в то время как на самом деле посылки не дают никакого оправдания.Вот пример:

Все нечетные числа целые.
Все четные числа являются целыми.
Следовательно, все нечетные числа являются четными числами.

Этот аргумент недействителен, поскольку исходные данные не подтверждают заключения. Однако, если бы этот аргумент был когда-либо серьезно выдвинут, мы должны предположить, что автор поверил бы , что истинность посылок гарантирует истинность заключения. Следовательно, этот аргумент остается дедуктивным.Это не индуктивно.

Учитывая то, как здесь определены термины «дедуктивный аргумент» и «индуктивный аргумент», аргумент всегда один или другой, а не оба сразу, но, решая, какой из двух он является, обычно спрашивают, соответствует ли он как дедуктивные стандарты, так и индуктивные стандарты. Учитывая набор предпосылок и предполагаемый вывод, мы, аналитики, спросим, ​​является ли оно дедуктивно обоснованным, и, если да, то также и дедуктивно обоснованным. Если это не дедуктивно, то мы можем продолжить оценку, является ли оно индуктивно сильным.

Мы очень вероятно воспользуемся информацией о том, что этот аргумент не является дедуктивно достоверным, чтобы спросить себя, какие предпосылки, если бы они были приняты, сделали бы этот аргумент достоверным. Тогда мы можем спросить, были ли эти посылки подразумеваемыми и предполагаемыми изначально. Точно так же мы можем спросить, какие посылки необходимы для усиления индуктивного аргумента, и мы можем спросить, были ли эти посылки предназначаемыми с самого начала. Если так, то мы передумаем, какой аргумент существовал в исходном отрывке.Итак, применение дедуктивных и индуктивных стандартов используется в процессе извлечения аргумента из отрывка, в который он встроен. Процесс идет следующим образом: извлеките аргумент из отрывка; оцените его с помощью дедуктивных и индуктивных стандартов; возможно, пересмотреть решение о том, какой аргумент существовал в исходном отрывке; затем пересмотрите этот новый аргумент, используя наши дедуктивные и индуктивные стандарты.

Неявные посылки и неявные особенности явных посылок могут играть важную роль в оценке аргументов.Предположим, мы хотим знать, действительно ли Юлий Цезарь завоевал Рим. В ответ какой-нибудь историк мог бы указать, что это можно сделать с уверенностью из этих двух частей информации:

Генерал римских легионов Галлии пересек реку Рубикон и завоевал Рим.

Цезарь в то время был генералом римских легионов в Галлии.

Это даст верный аргумент. Но теперь обратите внимание, что, если бы «в то время» отсутствовало во второй части информации, то аргумент был бы недействительным.Вот почему. Возможно, Цезарь когда-то был генералом, но Тиберий был генералом во время переправы через реку и завоевания Рима. Если фраза «в то время» отсутствовала, вы, аналитик, должны беспокоиться о том, насколько вероятно, что эта фраза была задумана. Итак, вы столкнулись с двумя аргументами, одним действительным и одним недопустимым, и вы не знаете, какой аргумент является предполагаемым.

См. Также статьи «Аргумент» и «Достоверность и обоснованность» в этой энциклопедии.

Информация об авторе

Персонал IEP
IEP активно ищет автора, который напишет более подробную статью, заменяющую ее.

Deduction — New World Encyclopedia

В традиционной логике Аристотеля дедукция или дедуктивное рассуждение — это умозаключение, в котором посылки, если они верны, призваны гарантировать истинность вывода, в отличие от абдуктивных и индуктивных рассуждений, где посылки предлагаются как некоторые доказательства для вывода, но не гарантирующие его истинность.

Дедуктивный вывод

Нам действительно нужно сказать, что в дедуктивном выводе посылки «призваны гарантировать заключение», потому что нам нужно создать место для тех выводов, которые претендуют на дедуктивный характер, но не могут на самом деле достичь этого статуса — i.е. это неверные дедуктивные выводы — потому что это ложные выводы. Примеры таких ложных или недействительных дедуктивных выводов — отрицание антецедента (если p, то q. Не p. Следовательно, не q.) И подтверждение консеквента (если p, то q. Q истинно. Следовательно, p истинно.). Эти конкретные недействительные выводы имитируют действительные выводы подтверждения антецедента (то есть Modus Ponens) и отрицания консеквента (то есть Modus Tollens).

Действительный аргумент — это аргумент, структура или форма которого невозможны для того, чтобы посылки были истинными, а вывод — ложным.

Вывод действительного дедуктивного вывода: обусловлено предпосылками. В индуктивных и абдуктивных выводах предпосылки могут быть истинными, в то время как заключение ложным — таким образом, со строгой логической точки зрения, все индуктивные и абдуктивные выводы, строго говоря, недействительны. Пример индуктивного вывода: «Все образцы серебра, которые мы исследовали, плавились при 961,78 ° C, таким образом, все образцы серебра во Вселенной будут плавиться при 961,78 ° C». Пример абдуктивного вывода: «Моя машина не заводилась после ливня.Если дождь вызвал короткое замыкание в моей машине, это могло бы объяснить, почему он не запустился после ливня. Поэтому ливень вызвал короткое замыкание в моей машине, из-за которого она не завелась ».

Другой способ, которым это иногда описывают, состоит в том, что дедукция — это умозаключение, в котором заключение не является более общим, чем посылки, в отличие от абдуктивных и индуктивное рассуждение, при котором вывод является более универсальным, чем посылки. Другие теории логики определяют дедуктивное рассуждение как вывод, в котором вывод является таким же определенным, как и посылки, в отличие от индуктивного рассуждения, где вывод может иметь меньшую достоверность, чем предположения. предпосылки.Каким бы способом это ни описывалось, вывод дедуктивного вывода обусловлен предпосылками — посылки не могут быть истинными, в то время как заключение ложно. Но в индуктивных и абдуктивных выводах предположения могут быть истинными, но заключение, тем не менее, ложным.

Примеры

Действителен:

Все люди смертны.

Сократ — мужчина.

Следовательно, Сократ смертен.

Картинка над столом.

Стол над полом.

Значит картинка находится над полом.

У всех птиц есть крылья.

Кардинал — птица.

Значит, у кардинала есть крылья.

Недействительный:

Каждый преступник выступает против правительства.

Все в оппозиционной партии выступают против правительства.

Следовательно, все в оппозиционной партии — преступники.

Это недействительно, поскольку посылки не позволяют установить общность между членством в оппозиционной партии и преступностью.Это известная ошибка нераспределенной середины.

Недействительно:

Если вы совершили мошенничество, вы будете осуждены.

Вы не совершали мошенничества.

Следовательно, вы не будете осуждены.

Это неверно, потому что это пример ошибки отрицания антецедента. В этом случае вас могут осудить за другое преступление, которое вы совершили, например, поджог, даже если вы не совершали мошенничества.

Неверно:

Если это Leica, то это камера.

Это камера.

Значит, это Leica.

Это неверно, потому что это пример ошибочного утверждения консеквента. В данном случае это камера, но на самом деле это может быть Contax или какая-то другая камера, отличная от Leica.

Основные формы аргументов исчисления
Имя	Sequent	Описание
Modus Ponens	[( p → q ) 902 p, затем q; п; поэтому q
Modus Tollens	[( p → q ) ∧ ¬ q ] ⊢ p	если p, то q; не q; следовательно, не p
Гипотетический силлогизм	[( p → q ) ∧ ( q → r )] ⊢ ( p → r)	если p, то q; если q, то r; следовательно, если p, то r
Дизъюнктивный силлогизм	[( p q ) ∧ ¬ p ] ⊢ q	Либо p, либо q; не р; следовательно, q
Конструктивная дилемма	[( p → q ) ∧ ( r → s ) ∧ ( p ∨ r )] ⊢ (902 902 q )	Если p, то q; а если r, то s; но либо p, либо r; следовательно, либо q, либо s
Деструктивная дилемма	[( p → q ) ∧ ( r → s ) ∧ (¬ q ∨ ¬ s )] ⊢ ( s )] ⊢ ∨ r )	Если p, то q; а если r, то s; но либо не q, либо не s; поэтому скорее не p или нет r
Упрощение	( p ∧ q ) ⊢ p , q	p и q истинны; следовательно, p истинно
Соединение	p , q ⊢ ( p ∧ q )	p и q истинны по отдельности; следовательно, они истинны вместе
Дополнение	p ⊢ ( p ∨ q )	p истинно; следовательно, дизъюнкция (p или q) истинна
Состав	[( p → q ) ∧ ( p → r )] ⊢ [ p → ( q ∧ r )]	Если p, то q; а если p, то r; следовательно, если p истинно, то q и r истинны
Теорема Де Моргана (1)	( p ∧ q ) ⊢ ( p ∨ q )	Отрицание (p и q) эквивалентно.к (не p или не q)
Теорема Де Моргана (2)	( p ∨ q ) ⊢ ( p ∧ q )	Отрицание (p или q) равно эквивалент к (не p и не q)
Коммутация (1)	( p ∨ q ) ⊢ ( q ∨ p )	(p или q) эквивалентно. к (q или p)
Коммутация (2)	( p ∧ q ) ⊢ ( q ∧ p )	(p и q) эквивалентно.к (q и p)
Association (1)	[ p ∨ ( q ∨ r )] ⊢ [( p ∨ q ) ∨ r ]	p или (q или r) эквивалентно. to (p или q) или r
Association (2)	[ p ∧ ( q ∧ r )] ⊢ [( p ∧ q ) ∧ r ]	p и (q и r) эквивалентны. to (p и q) и r
Распределение (1)	[ p ∧ ( q ∨ r )] ⊢ [( p ∧ q ) ∨ ( p ∧ r )]	p и (q или r) эквивалентны.к (p и q) или (p и r)
Распределение (2)	[ p ∨ ( q ∧ r )] ⊢ [( p ∨ q ) ∧ ( p ∨ r )]	p или (q и r) эквивалентны. to (p или q) и (p или r)
Двойное отрицание	p ⊢ p	p эквивалентно отрицанию not p
Транспонирование	( p → q ) ⊢ ( q → p )	Если p, то q эквивалентно.если не q, то не p
Значение материала	( p → q ) ⊢ ( p ∨ q )	Если p, то q эквивалентно. либо не p, либо q
Эквивалентность материалов (1)	( p ↔ q ) ⊢ [( p → q ) ∧ ( q → p )]	(p эквивалентно q) означает, (если p истинно, то q истинно) и (если q истинно, то p истинно)
Материальная эквивалентность (2)	( p ↔ q ) ⊢ [( p ∧ q ) ∨ (¬ q ∧ ¬ p )]	(p эквивалентно.к q) означает либо (p и q истинны), либо (оба p и q ложны)
Экспорт	[( p ∧ q ) → r ] ⊢ [ p → ( q → r )]	из (если p и q истинны, то r истинно) мы можем доказать (если q истинно, то r истинно, если p истинно)
Импорт	[ p → ( q → r )] ⊢ [( p ∧ q ) → r ]
Тавтология	p ⊢ ( p 902 )	п верно эквивалентно.to p истинно или p истинно

Аксиоматизация

Говоря более формальным языком, дедукция — это последовательность утверждений, так что каждое утверждение может быть выведено из предшествующих. Понятно, что это оставляет открытым вопрос о том, как мы доказываем первое предложение (поскольку оно не может следовать ни из чего). Аксиоматическая логика высказываний решает эту проблему, требуя выполнения следующих условий доказательства:

Доказательство α из ансамбля Σ правильно сформированных формул ( wff s) представляет собой конечную последовательность из wff s:

β1 ,…, βi, …, βn

, где

βn = α

и для каждого βi (1 ≤ i ≤ n),

или

или

• βi — результат Modus Ponens для двух предыдущих wffs, βi-g и βi-h.

Различные версии аксиоматической логики высказываний содержат несколько аксиом, обычно три или более трех, в дополнение к одному или нескольким правилам вывода. Например, аксиоматизация логики высказываний Готтлобом Фреге, которая также является первым примером такой попытки, включает шесть аксиом высказываний и два правила.Бертран Рассел и Альфред Норт Уайтхед также предложили систему с пятью аксиомами.

Например, версия аксиоматической логики высказываний Яна Лукасевича (1878-1956) имеет набор A аксиом, принятых следующим образом:

• [PL1] p → ( q → p )
• [PL2] ( p → ( q → r )) → (( p → q ) → ( p → r ))
• [PL3] ( ¬ p → ¬ q ) → ( q → p )

и он имеет набор правил вывода R с одним правилом в нем, Modu Ponendo Ponens, следующим образом:

• [MP] из α и α → β, вывести β.

Правило (а) вывода позволяет нам выводить утверждения, следуя аксиомам или заданным wff s ансамбля Σ.

Естественная дедуктивная логика

В одной из версий естественной дедуктивной логики, представленной E.J. Леммон, что мы должны называть ее системой L, у нас нет никакой аксиомы для начала. У нас есть всего девять примитивных правил, управляющих синтаксисом доказательства.

Девять основных правил системы L:

1. Правило допущения (A)
2. Modus Ponendo Ponens (MPP)
3. Правило двойного отрицания (DN)
4. Правило условного доказательства (CP)
5. Правило-введения (∧I)
6. Правило-исключения (E)
7. Правило-исключения (∨I)
8. Правило-исключения (∨E)
9. Reductio Ad Absurdum (RAA)

В системе L , доказательство имеет определение со следующими условиями:

1. имеет конечную последовательность wff s (правильно сформированная формула)
2. каждая строка обоснована правилом системы L
3. последняя строка доказательства — это то, что задумано (В.E.D, quod erat manifestrandum, это латинское выражение, означающее: «что должно было быть доказано»), и эта последняя строка доказательства использует единственную (ые) исходную (ые) посылку (я); или нет предпосылки, если ничего не указано.

Тогда, если посылка не указана, секвенция называется теоремой. Следовательно, определение теоремы в системе L:

• теорема — это секвенция, которую можно доказать в системе L, используя пустой набор предположений.

или другими словами:

• теорема — это секвенция, которая может быть доказана из пустого набора предположений в системе L

Пример доказательства секвенции (в данном случае Modus Tollendo Tollens):

9030 3 q ∧ ¬ q

p → q , ¬ q ¬ ¬ p [Modus Tollendo Tollens (MTT)]
Номер допущения	(номер строки	) Используемые линии и обоснование
1	(1)	( p → q )	A
2	(2)	¬18
3	(3)	p	A (для RAA)
1,3	(4)	q	1,3, MPP	1 , 2,3	(5)	2,4, ∧I
1,2	(6)	¬ p	3,5, RAA
Q.ED

Пример доказательства секвенции (в данном случае теорема):

(wff) 93 1 902 902

⊢ p ¬ ¬ p
Номер предположения	Номер строки	Используемые линии и обоснование
1	(1)	¬ ( p ∨ ¬ p )	A (для RAA)
2)	¬ p	A (для RAA)
2	(3)	( p ¬ ¬ p )	2, ∨I
(4)	( p ¬ p ) ∧ ¬ ( p ∨ ¬ p )	1, 2, ∧I
1		(5) 9029¬3 ¬ p	2, 4, RAA
1	(6)	p	5, DN
1	(7)	( p ¬ p )	6, ∨I
1	(8)	(8)	¬ p ) ∧ ¬ ( p ∨ ¬ p )	1, 7, ∧I
	(9)	¬¬ ( p ∨ ¬ 2 p ) 9029 , 8, RAA
	(10)	( p ∨ ¬ p )	9, DN
Q.E.D

Каждое правило системы L имеет свои собственные требования к типу входных данных или записей, которые оно может принять, и имеет свой собственный способ обработки и расчета допущений, используемых его входными данными.

См. Также

Ссылки

Все учебники по логике — а их сейчас сотни — посвящены дедукции и умозаключениям. Вот некоторые репрезентативные:

• Копи, Ирвинг М. и Карл Коэн. Введение в логику . Прентис Холл.(Многие издания; последнее, с 2004 года, является 12-м.)
• Херли, Патрик Дж. Краткое введение в логику . Бельмонт, Калифорния: Обучение Уодсворта / Томпсона. (Многие издания; последнее — девятое.)
• Jennings, RE Continuing Logic , учебник курса «Аксиоматическая логика» в Университете Саймона Фрейзера, Ванкувер, Канада
• Джонсон, Роберт М. Основы мышления: A Книга логики . Бельмонт, Калифорния: Уодсворт. (Последнее — 4-е издание.)
• Риз, Уильям Л.«Дедукция» в словаре по философии и религии , новое и расширенное издание. Атлантическое нагорье, Нью-Джерси: Humanities Press, 1996.
• Zarefsky, David. Аргументация: Исследование частей I и II эффективного мышления , The Teaching Company, 2002.

Внешние ссылки

Все ссылки получены 7 ноября 2017 года.

Источники общей философии

Кредиты

New World Encyclopedia писатели и редакторы переписали и дополнили статью Википедия в соответствии со стандартами New World Encyclopedia .Эта статья соответствует условиям лицензии Creative Commons CC-by-sa 3.0 (CC-by-sa), которая может использоваться и распространяться с указанием авторства. Кредит предоставляется в соответствии с условиями этой лицензии, которая может ссылаться как на участников New World Encyclopedia, и на самоотверженных добровольцев, вносящих вклад в Фонд Викимедиа. Чтобы процитировать эту статью, щелкните здесь, чтобы просмотреть список допустимых форматов цитирования. История более ранних вкладов википедистов доступна исследователям здесь:

История этой статьи с момента ее импорта в New World Encyclopedia :

Примечание. могут применяться ограничения на использование отдельных изображений, на которые распространяется отдельная лицензия.

Великий вывод Парменида: логическая реконструкция пути истины | Отзывы | Философские обзоры Нотр-Дама

В стимулирующей монографии Майкла В. Ведина содержится призыв к оружию в защиту статуса Парменида как «сурового арбитра философского дискурса» (1) и строгого мониста, который стоит отдельно от ионийской традиции натурфилософии и действительно отвергает ее. . Таким образом, он пытается противостоять все более популярному желанию реабилитировать значение Парменида как космолога, занимающегося эмпирическими научными исследованиями, и того вида квалифицированного монизма, которого требует такой подход.Ведину с самого начала ясно, что его прочтение предлагается как «логическая реконструкция» (2) аргументов Парменида и что эта озабоченность является «главным ограничением» его интерпретации. Его нетерпение к переводчикам, не подчиняющимся его критериям толкования, очевидно. Такой критический подход, наряду с приверженностью Wedin к последовательной аргументации без особого обозначения выводов или их анализа, затрудняет чтение. Тем не менее, книга будет полезна любому, кто серьезно интересуется поэмой Парменида, не в последнюю очередь из-за степени несогласия, которую она может вызвать.Я подозреваю, что немногие из приверженцев более щедрого прочтения проекта Парменида (и монизма) обнаружат, что защита Wedin от того, что может показаться немодными логическими ограничениями. Тем не менее, любой, кто стремится придерживаться альтернативной линии, захочет решить серьезные проблемы, которые Wedin ставит в своей критике недавних отчетов.

Том разделен на три раздела. В первом («Управляющий вывод и главный аргумент Парменида») Ведин пытается установить природу фундаментальных и сложных рассуждений Парменида, обнаруженных в том, что он называет «главным аргументом» фрагментов B2, B3 и B6.Согласно интерпретации Ведина, фрагменты B2 и B3 представляют «Управляющую дедукцию» Парменида, в которой исключена возможность исследования того, «чего нет». Он рассматривает несколько общих претензий к рассуждениям Парменида, например, что они основаны на несчастливом допущении эквивалентности между существованием и необходимым существованием.

Повсюду он недвусмысленно заявляет о своей готовности принять определенную логическую структуру для аргумента, даже если эта структура не обязательно очевидна в тексте.Так, например, он считает Закон Исключенного Середина (LEM) центральным по отношению к разграничению, установленному во фрагменте B2 между «тем, что есть и не может быть» и «тем, что не является и не может быть», и, таким образом, к Пути. Истины в целом. Как он отмечает, в B2 нет «явного лингвистического выражения» (14) LEM. Фактически, на первый взгляд кажется, что это модальное различие, которое не является примером LEM. Но Ведин указывает на наличие явного экземпляра LEM во фрагменте B8 (B8.15: «есть или нет»), который относится к B2 и, таким образом, утверждает он, объясняет природу (или, скорее, оправдывает его собственное мнение). характеристика) прежнего различия.Затем, установив центральную роль LEM, Ведин ставит перед собой задачу объяснить «удивительный» факт, что богиня «характеризует пути исследования не просто как примеры LEM» (15), а скорее в модальных терминах.

Те, кто считает, что то, что говорится во фрагментах, является лучшим доказательством рассуждений Парменида или, по крайней мере, лучшей отправной точкой, могут быть разочарованы таким подходом. В другом месте мы можем увидеть, как эта приверженность логической реконструкции влияет на интерпретацию Wedin.В заключительном разделе Части 1 он кратко обращается к спорному вопросу о соответствующем предмете « estin » Парменида, отмечая, что он может «обойти эту проблему, отдав предпочтение количественным формулам» (79). Таким образом, его интерпретация свободна от (или, по крайней мере, сводит к минимуму) ограничения любых забот о том, как работает сам греческий глагол (либо в стихах Парменида, либо в греческом языке в целом).

В Части II Wedin обращается к «Дедуктивным последствиям управляющего вычета», т. Е.е. описание и ограничения природы «того, что есть», как они изложены во фрагменте B8, где утверждается, что Парменид привержен «онтологическому монизму». Wedin предлагает реконструкцию аргументов B8, которая пытается исправить предыдущие попытки, подчеркивая, в частности, центральную аргументативную роль Управляющей дедукции на протяжении всей этой части стихотворения. Согласно Ведину, управляющий вывод — это не только «фундаментальный аргумент» Парменида Путь истины , «каждый другой аргумент в стихотворении подтверждается им» (4).Вэдин рассматривает каждую из характеристик «того, что есть», в свою очередь, и приходит к интригующему выводу о том, что самая значительная проблема для рассуждений Парменида заключается не в кажущемся парадоксе идентификации «того, чего нет» как незаконного объекта мысли. Скорее, наиболее важная проблема заключается в том, что аргументы Парменида, устанавливающие природу «того, что есть» в B8, и, следовательно, в самом Управляющем вычитании, по-видимому, влекут за собой нежелательные утверждения о том, «чего не является» (которые, конечно, должны ликвидировано).

В третьей части, «Критические размышления», Ведин представляет собранную критику некоторых конкретных направлений интерпретации Парменида наряду с оценкой того, как Платон воспринимает Парменида. В Части I Wedin защищает Большой вычет от обвинения в несостоятельности на том основании, что это запрет второго порядка утверждений первого порядка о том, «что не является». В Части III он находит время, чтобы подвергнуть дальнейшей критике некоторые альтернативные попытки защитить Парменида от того же обвинения, «хотя бы потому, что они расходятся с моим решением» (193).Он также предлагает некоторую явную критику интерпретаций фрагмента B3 как установления тождества между мышлением и бытием.

Затем Ведин возвращается к вопросу о связи Парменида с ионической традицией. В своем более раннем обсуждении аргумента Учителя Ведин отверг предположение, что фрагмент B6 предлагает какое-либо оправдание для приписывания Пармениду «открытости натурфилософии его ионийских предшественников» (229). Возвращаясь к проблеме в Части III, он сосредотачивает свое внимание на более широких аргументах Патрисии Курд и Джона Палмера.Он заключает, что ни один из них не дает удовлетворительного объяснения предполагаемого интереса Парменида к космологии, так что «я считаю, что нам рекомендуется отказаться от проекта гармонизации элеатских евангелий Парменида [ Путь Истины и Путь Мнения ]. ‘(248). Это отражает самопровозглашенное отсутствие интереса Вэдина к чему-либо, кроме аргументов Путь истины , но также подчеркивает слабость его рассказа. Если он хочет предположить, что невозможно примирить эти две части стихотворения Парменида, он также должен быть в состоянии объяснить, почему космология вообще является частью стихотворения.Одним из основных мотивов защиты интереса Парменида к космологии является тот факт, что его стихотворение включает космологию. Опять же, вопрос заключается в том, должна ли интерпретация соответствовать свидетельствам или свидетельства должны быть сформированы (и отредактированы), чтобы соответствовать интерпретации.

Wedin не претендует на полную трактовку поэмы Парменида. Фактически, он освежающе ясно говорит о пределах своего проекта, поскольку он интересуется исключительно (выборками) Путь истины и, в частности, логической формой его аргументов.Он демонстрирует замечательное понимание опасений, которые могут возникнуть у некоторых по поводу использования им логики предикатов первого порядка при реконструкции аргументов философа, работающего без такого инструментария.

Тем не менее, некоторые могут задаться вопросом, может ли такой исключительный фокус и узкий подход действительно претендовать на предложение реконструкции философии Парменида. Можно беспокоиться, что на самом деле нам предлагают аргумент, с которым отдельные части стихотворения можно сделать совместимыми.Такой проект, возможно, стоит сам по себе, но можно с натяжкой утверждать, что обоснованность должна быть не только основным, но, фактически, единственным критерием интерпретации. Так, например, Ведин заявляет во введении не только, что логические соображения должны способствовать реконструкции аргументов Парменида, но также и то, что «утверждения о влиянии эпической традиции не должны ограничивать, а, скорее, ограничиваться структурой [ Путь истины ] выводов »(5).Кажется, что Wedin хочет заявить, что рассуждения Парменида можно изолировать от культурного контекста. Это провокационное предложение, и было бы интересно прочитать более обстоятельную защиту. Конечно, Wedin прав, критикуя тех (немногих), кто отвергает ценность логики в реконструкции «мысли Парменида» «глобальным взмахом руки» (8). Однако можно беспокоиться, что Wedin просто заменяет один пренебрежительный жест другим, отказываясь интерпретировать значение культурного контекста, филологических проблем или, действительно, любого стихотворения за пределами фрагментов B2-8.

Deduction — The Decision Lab

Один из самых известных экспериментов в дедуктивном мышлении — это задача выбора Wason. Питер Уэйсон разработал логическую головоломку в 1966 году, чтобы определить, насколько хорошо люди решают задачи, требующие дедуктивного мышления. ⁸

Эксперимент был организован следующим образом:

«Вам показан набор из четырех карточек, размещенных на столе, каждая из которых имеет номер на одной стороне и цветное пятно на другой стороне. На лицевых сторонах карт изображены 3, 8, красный и коричневый.Какую карту (карты) вы должны перевернуть, чтобы проверить истинность утверждения о том, что если карта показывает четное число на одной стороне, то ее противоположная сторона красная? »

Правильное решение — перевернуть коричневую карточку, а карточку с цифрой 8. Разобрались?

Головоломка решается путем применения структуры аргументов «если P, то Q» и решения, какие карты вам нужно увидеть, чтобы убедиться в истинности предложения. Таким образом, в этом случае, если коричневая карта четная, это нарушает правило, а если карта с 8 не красная, это нарушает правило.На самом деле не имеет значения, какого цвета на обратной стороне карты 3, поскольку в предложении не говорится о нечетных числах. Мы также не озабочены тем, является ли красная карточка нечетной или четной, потому что, хотя нам говорят, что все четные числа красные, предложение не утверждает, что все красные карточки четные или нечетные в этом отношении.

Что делает этот эксперимент (и его повторение в 1993 году) действительно интересным, так это то, что, хотя большинство людей с треском не справляются с задачей, когда она представлена ​​в этой структуре (правильных ответов <10%), они работают намного лучше, когда та же головоломка применяется в более реалистичный контекст или сценарий, который легче представить.

Например, Cosmides and Tooby (1993) ^{показали, что люди способны решать аналогичные головоломки, когда они рассматривают их в соответствии с социальными правилами или нормами. В их задачу входило правило «Чтобы употреблять алкоголь, вы должны быть старше 25», , и вместо цифр и цветов они попросили участников представить группу людей в баре, где одни пили пиво, а другие пили кокаин. кола. На одной стороне карточки они написали возраст людей, а на другой — напиток, который они употребляли.Таким образом, карточка с цифрой 16 не могла показать, что слово «пьёт пиво» ​​было обратной стороной. В такой обстановке подавляющее большинство людей пришло к правильному решению, хотя основы задачи остались прежними. Это открытие поддерживает эволюционную школу психологии и аргумент о том, что на человеческое мышление влияют контекстуальные факторы и стимулы в нашей окружающей среде.}

Китайская логика и (не) истоки дедукции

Вчера я посетил интересную конференцию по истории логики в Китае, организованную Фенронгом Лю, Джереми Селигманом и Йоханом ван Бентемом, которая проходила в Амстердаме (к сожалению, сегодня мне пришлось пропустить второй день из-за семинара в Вене. , где я сейчас нахожусь).На конференции я встретил некоторых выдающихся исследователей в области древнекитайской логики, таких как Чад Хансен, Крис Фрейзер и Кристоф Харбсмайер. Я практически ничего не знал о древнекитайской логике, но, как историк так называемой «западной логики» (как обычно, ужасный ярлык), мне было очень интересно узнать больше о различиях и сходствах между двумя традициями.

Одна из причин, почему меня интересуют такие сравнения, заключается в том, что они должны предлагать привилегированную точку зрения на исторические источники аксиоматически-дедуктивного метода в древнегреческой философии и математике.Китайская и индийская традиции, возможно, представляют собой две древние традиции, достигшие такого же интеллектуального уровня сложности, что и греческая, но в этих традициях научные исследования развивались совершенно по-разному. В частности, аксиоматико-дедуктивный метод в своих конкретных деталях (изначально) уникален для древнегреческой философии и математики. Теперь, если мы сможем выделить конкретные элементы значительного несходства между греческой традицией и этими другими традициями, тогда мы сможем лучше понять некоторые из решающих факторов для развития дедуктивного метода.

Одна убедительная гипотеза, выдвинутая выдающимся ученым Г.Е.Р. Ллойда и Р. Нетца в его книге «Формирование дедукции » заключается в том, что социальный фон публичных дебатов в Древней Греции сыграл решающую роль в развитии аксиоматически-дедуктивного метода. Идея заключалась бы в том, что дедуктивный способ аргументации возник как альтернатива другим подходам к аргументации и дебатам, текущим в то время, в частности, подходам софистов.С этой точки зрения дедуктивное доказательство можно рассматривать как форму диалога, в котором один из участников пытается заставить других участников сделать какой-то вывод, если они предоставили какие-то предпосылки; каждый шаг дедуктивного доказательства был бы фактически диалогическим ходом, который, таким образом, должен быть убедительным и неуязвимым для контрпримеров. Действия других участников больше не являются явными в регламентированной формулировке доказательства, но, по-видимому, в каждом пункте они соглашаются с действиями, предложенными лицом, ведущим диалог (любое сходство с сократовскими диалогами — не совпадение!).

Ллойд утверждает, что, хотя общественные дебаты были широко распространены в Древней Греции, этого не было в древнем Китае, где Император представлял высшую, неоспоримую власть. Он утверждает, что это (по крайней мере частично) объясняет, почему аксиоматически-дедуктивный метод появился в Древней Греции, а не в Древнем Китае. Это очень привлекательная гипотеза, и я, например, несколько раз одобрительно ее упоминал. Но есть проблема, как я обнаружил вчера: это просто неправда, что в китайской традиции дебаты и диалогические ситуации не играли значительной роли.Вчера я узнал о моистской традиции, которая сложилась в Китае примерно за столетие до золотого века Древней Греции, и что она также глубоко отмечена исследованиями моделей правильной аргументации, причем явно на фоне диалогических ситуаций. Модель этого фона обеспечивается правовым контекстом (информация предоставлена ​​Крисом Фрейзером). На самом деле, слушая о моистской традиции, я часто ловил себя на мысли о темах и «Софистические опровержения » Аристотеля, а также о некоторых более поздних (средневековых) дискуссиях, сформулированных на фоне этих двух книг.

Я по-прежнему считаю, что диалогический компонент очень важен для понимания самой концепции дедукции, как я намерен показать в ближайшие годы (в следующем году я начну пятилетний исследовательский проект под названием «Корни дедукции»). Но вчера я узнал, что наличие или отсутствие сильной диалогической традиции само по себе не объясняет изолированного появления понятия дедукции в греческой математике и философии, как, кажется, предполагает Ллойд, учитывая, что подобная ситуация может быть нашел в китайском корпусе.Клири, нам нужно копать глубже, и для этого нужны долгосрочные исследовательские проекты.

Перейти к основному содержанию Поиск

Поиск

• Где угодно

Быстрый поиск где угодно

Поиск Поиск

Расширенный поиск

• Войти | регистр

Пропустить основную навигацию Закрыть меню ящика Открыть меню ящика Домой

• Подписка / продление
  • Учреждения
  • Индивидуальные подписки
  • Индивидуальное продление
• Библиотекари
• тарифы, полные платежи Пакет для Чикаго
• Полный цикл и охват содержимого
• Файлы KBART и RSS-каналы
• Разрешения и перепечатки
• Инициатива развивающихся стран Чикаго
• Даты отправки и претензии
• Часто задаваемые вопросы библиотекарей

Агенты

• Тарифы, заказы, и платежи
• Полный пакет Chicago
• Полный охват и содержание
• Даты отправки и претензии
• Часто задаваемые вопросы агента

Партнеры по издательству

• О нас
• Публикуйте у нас
• Недавно приобретенные журналы
• Издательская стоимость tners

Новости прессы

• Подпишитесь на уведомления eTOC
• Пресс-релизы
• СМИ

• Книги издательства Чикагского университета
• Распределительный центр в Чикаго
• Чикагский университет

• Положения и условия
• Заявление об издательской этике
• Уведомление о конфиденциальности
• Доступность Chicago Journals
• Доступность университета

• Следуйте за нами на facebook
• Следуйте за нами в Twitter

• Свяжитесь с нами
• Запросы СМИ и рекламы
• Открытый доступ в Чикаго

• Следуйте за нами на facebook
• Следуйте за нами в Twitter

Аристотель (384–322 до н. Э.) — Философская энциклопедия Рутледжа

DOI: 10.4324/9780415249126-A022-1
Версия: v1, опубликовано в Интернете: 1998
Источник по состоянию на 31 мая 2021 г., с https://www.rep.routledge.com/articles/biographic/aristotle-384-322-bc/v- 1

---

Аристотель из Стагиры — один из двух самых важных философов древнего мира и один из четырех или пяти самых важных философов любого времени и места. Он не был афинянином, но большую часть жизни провел в Афинах, будучи студентом и преподавателем философии. Двадцать лет он был членом Платоновской академии; позже он основал свою философскую школу — Лицей.Еще при жизни он публиковал философские диалоги, от которых сейчас сохранились лишь фрагменты. «Аристотелевский корпус» (1462 страницы греческого текста, включая некоторые ложные сочинения), вероятно, основан на лекциях, которые он читал в лицее.

Аристотель является основателем не только философии как дисциплины с отдельными областями или ветвями, но, в более общем плане, концепции интеллектуального исследования как относящегося к отдельным дисциплинам. Он настаивает, например, на том, что стандарты доказательства и свидетельства дедуктивной логики и математики не должны применяться к изучению природы, и что ни одна из этих дисциплин не должна использоваться в качестве надлежащей модели для морального и политического исследования.Он отличает философское размышление о дисциплине от практики самой дисциплины. Корпус содержит статьи по многим различным дисциплинам, а не только по философии.

Вот некоторые области исследований, в которые Аристотель вносит фундаментальный вклад:

(1) Логика. «Предыдущая аналитика» Аристотеля представляет собой первую попытку сформулировать систему дедуктивной формальной логики, основанную на теории «силлогизма». Posterior Analytics использует эту систему для составления отчета о строгих научных знаниях.«Логика», как ее понимает Аристотель, также включает изучение языка, значения и их отношения к неязыковой реальности; следовательно, он включает множество тем, которые теперь можно отнести к философии языка или философской логике (Категории, Интерпретация, Темы).

(2) Изучение природы. Около четверти корпуса (см. Особенно «Историю животных», «Части животных» и «Порождение животных»; также «Движение животных», «Развитие животных») составляют работы, связанные с биологией.Некоторые из них содержат сборники подробных наблюдений. («Метеорология» содержит аналогичный сборник о неодушевленной природе.) Другие пытаются объяснить эти наблюдения в свете пояснительной схемы, которую защищает Аристотель в своих более теоретических размышлениях об изучении природы. Эти размышления (особенно в «Физике» и в «Генерации и порче») развивают понимание природы, формы, материи, причин и изменений, которое выражает взгляды Аристотеля на понимание и объяснение естественных организмов и их поведения.Натурфилософия и космология объединены в «На небесах».

(3) Метафизика. В своих размышлениях об основах и предпосылках других дисциплин Аристотель описывает универсальную «науку о бытии как бытия» — предмет метафизики. Часть этой универсальной науки исследует основы исследования природы. Аристотель формулирует свое учение о субстанции, которое он объясняет через связанные контрасты между формой и материей, а также между потенциальностью и действительностью.Одна из его целей — описать отличительный и неповторимый характер живых организмов. Другая цель универсальной науки состоит в том, чтобы использовать его исследование субстанции, чтобы дать отчет о божественной субстанции, высшем принципе космического порядка.

(4) Философия разума. Доктрина формы и материи используется для объяснения отношения души и тела, а также различных типов души, обнаруживаемых у разных типов живых существ. По мнению Аристотеля, душа — это форма живого тела.Он исследует различные аспекты этой формы у растений, нерациональных животных и людей, описывая питание, восприятие, мысли и желания. Его обсуждение (в «О душе», а также в «Parva Naturalia») затрагивает темы философии разума, психологии, физиологии, эпистемологии и теории действия.

(5) Этика и политика (Никомахова этика, Евдемова этика, Magna Moralia). По мнению Аристотеля, понимание естественных и существенных целей человеческих агентов является правильной основой для понимания принципов, которыми руководствуются моральные и политические практики.Эти принципы выражены в его описании человеческого благополучия и различных добродетелей, которые составляют хорошего человека и способствуют благополучию. Описание общества, воплощающего эти добродетели в индивидуальной и социальной жизни, является задачей Политики, которая также исследует достоинства и пороки реальных государств и обществ, сравнивая их с принципами, вытекающими из этической теории.

(6) Литературоведение и риторическая теория (Поэтика, Риторика). Эти работы тесно связаны как с логикой Аристотеля, так и с его этической и политической теорией.

Цитирование этой статьи:
Irwin, T.H .. Aristotle (384–322 до н.э.), 1998, DOI: 10.4324 / 9780415249126-A022-1. Энциклопедия философии Рутледжа, Тейлор и Фрэнсис, https://www.rep.routledge.com/articles/biographic/aristotle-384-322-bc/v-1.