ФОРМАЛЬНАЯ ЛОГИКА — это… Что такое ФОРМАЛЬНАЯ ЛОГИКА?
наука о мышлении, предметом к-рой является исследование умозаключений и доказательств с т. зр. их формы (формы логической) и в отвлечении от их конкретного содержания. Ф. л. является базисной наукой – ее идеи и методы используются как в повседневной практике, напр. в качестве средства от логич. ошибок, так и в особенности в теории для логического анализа науч. знания и для дедуктивного (синтетического) построения на базе логических исчислений любых «нелогических» науч. дисциплин. Историч. основу Ф. л. образует т.н. т р а д и ц и о н н а я Ф. л., к к-рой относят обычно учение о понятии, учение о мышления законах, учение о суждении и теорию силлогистич. вывода – учение о силлогизме, или силлогистику, учения о непосредственных умозаключениях и несиллогистических умозаключениях, учение о логических ошибках и, наконец, традиц. логику индуктивную. Основоположником традиц. Ф. л. является Аристотель: обобщив опыт повседневного и отчасти науч. мышления тогда только формировавшейся науки, Аристотель создал учение о силлогизме и дал первые примеры анализа рассуждений с т. зр. их формы. Однако уже сам Аристотель сознавал, что в силлогистич. схемы нельзя уложить многие рассуждения, в особенности математические. Это побудило мегариков и ранних стоиков исследовать др. формы дедукции (см. Древнегреческая логика). Частично в том же направлении шло развитие логики и в средние века (см. раздел Схоластическая логика в ст. Схоластика), и в эпоху Возрождения (Галилей, Валла, Раме). Развитие опытного естествознания и математики, усилившееся в 17 в., поставило вопрос о прикладной роли Ф. л., о дальнейшем развитии несиллогистич. форм вывода, характерных для логики науки. (В этой области работали с большим или меньшим успехом Ф. Бэкон, Декарт, Паскаль, авторы Пор-Рояля логики, И. Юнг, Лейбниц и их последователи.) Одна из осн. «логистических» идей Лейбница состояла в том, чтобы свести к «вычислению» не только математические, но и любые умозаключения. Лишь ко 2-й пол. 19 в. относятся ощутимые шаги в реализации этой идеи, когда работами Буля, де Моргана, Джевонса, Шрёдера, Порецкого, Пирса, Фреге, Пеано и др. были заложены основы первых совр. логико-матем. исчислений. «Principia Mathematica» Б. Рассела и А. Уайтхеда открывает совр. этап в развитии Ф. л. С о в р е м е н н а я Ф. л. является историч. преемником традиц. Ф. л. и в ряде случаев ее прямым продолжением. Расширение и обогащение языка Ф. л., ее осн. понятий в известной мере служат указанием на то, в каком направлении шло развитие Ф. л. от традиционной к современной. В частности, в логич. словаре появились такие понятия, как исчисление и логическое исчисление, математическая индукция, формализация и формализованный язык, независимость, непротиворечивость и полнота, алгоритм и разрешения проблемы, область предметов и переменная, операция и функция и др. неизвестные традиц. Ф. л. понятия. С др. стороны, определ. связь с традицией сохранили такие понятия совр. Ф. л., как аксиома, посылка и постулат, вывод и правило вывода, квантор, следствие и следование (импликация), теорема о дедукции и др., хотя в совр. трактовке этих понятий не сразу узнаются их историч. прообразы. На протяжении более чем двухтысячелетней истории Ф. л. основную ее цель видели в том, чтобы исследовать, каким образом можно выводить одни высказывания из других. Для совр. Ф. л. характерно построение формальных теорий логич. вывода (см. Вывод в математической логике) в рамках тех или иных логич. «формализмов» (исчислений), а следовательно, и особое внимание к построению самих этих формализмов и применяемых при этом формально-дедуктивных методов. В зависимости от того, какие осн. понятия и методы используются для построения формальных теорий логич. вывода [в том числе и в зависимости от того, как интерпретируются осн. логич. константы: дизъюнкция, конъюнкция, импликация, отрицание (в логике), эквиваленция] различают: классическую (иначе двузначную) логику, интуиционистскую логику, конструктивную логику, модальную логику, многозначную логику и др. Каковы бы ни были различия в построении этих теорий, каждая теория состоит из двух осн. разделов: логики высказываний и логики предикатов. Классич. вариант последней непосредственно примыкает к традиц. силлогистике (логике «одноместных» предикатов), хотя в многочисленных и различных предикатов исчислениях (см. также ст. Натуральное исчисление, Секвенций исчисление) формализуется субъектно-предикатная структура предложений, понимаемая в более широком, чем в традиц. Ф. л., смысле: помимо свойств («одноместных» предикатов), в них формализуются и отношения («многоместные» предикаты), что делает излишней особую логику отношений в ее традиц. филос. истолковании. Каждая из указанных выше формальных теорий имеет определ. филос. смысл, являясь логической реализацие й тех или иных методологич. подходов в науке. Связь совр. Ф. л. и философии стимулируется прежде всего актуальной задачей обоснования математики – науч. направлением, имеющим как логический, так и филос. характер (см. ст. Алгоритм, Интуиционизм, Исчисление задач, Конструктивное направление, Логицизм, Математическая бесконечность, Математическая логика, Метод аксиоматический, Минимальная логика, Номинализм в философии математики, Положительная логика, Принцип исключенного третьего, Проверяемость, Теория множеств, формализм, Эффективизм). Примером обогащения и углубления логич. исследований, вызванных стимулирующим влиянием проблем обоснования математики, может служить возникновение металогики – в узком (гильбертовском) смысле как теории формальных систем, ограниченной рамками финитизма, и в широком смысле как метатеории Ф. л. вообще, включающей логический синтаксис (см. Синтаксис в логике, Метаязык), логическую семантику (см. такжеСемантика в логике и примыкающие к ней ст. Взаимозаменимости отношение, Знак, Значение, Имя, Интерпретация, Контрфактические предложения, Логическая истинность, Модель, Название, Описания операторы, Реализуемость, Синтетические и аналитические суждения, Тавтология, Тождественная истинность, Фактическая истинность, Экстенсиональные и неэкстенсиональные языки), теории определения и определимости и теорию тождества (см. А=А, Правило замены равного равным, Принцип замещения, Равенство в логике и математике). Дальнейшим расширением металогич. проблематики явилось выделение в особую дисциплину прагматики, развивавшейся первоначально в рамках логико-семантич. и психологич. анализа (см. Психологизм в логике), и, наконец, появление семиотики. Т.о., связь между мышлением и языком как «практической действительностью мысли» (К. Маркс) нашла отражение во взаимосвязи философии, психологии, лингвистики и логики. В развитии совр. Ф. л. особую роль играют вопросы ее приложений, особенно в вычислит. математике и технике, кибернетике и теории информации, лингвистике математической и пр. (см., напр., ст. Логические машины, Логические схемы автоматов). Связующим звеном между Ф. л. и вычислит. математикой исторически явилась логика классов, к-рая развилась в результате попыток свести силлогистич. методы решения логич. задач к алгебраич. методам их решения, образовав, т.о., первое алгебраич. направление в совр. Ф. л. – алгебру логики (см. также Теоретико-множественная логика). Дальнейшим развитием алгебраич. направления явилось объединение алгебры логики и логики предикатов в теории конечных автоматов, расширение алгебры логики в сторону «алгебраизации» логики предикатов – теория моделей и математич. теория структур. Другую – «арифметическую» – ветвь, связавшую Ф. л. и вычислит. математику, образуют теория рекурсивных функций и предикатов (см. также ст. Алгоритм, Массовая проблема, Разрешимое и перечислимое множества, Сводимость), исчисление λ-конверсии (см. Оператор абстракции, Функция), логика комбинаторная и др. Из общих науч. приложений Ф. л. следует отметить вопросы, связанные с задачами уточнения понятия науч. закона (см. Диспозициональный предикат, Каузальная импликация, Номологические высказывания, Связь), с попытками применения логики в биологии и физике (см. Логика квантовой механики), в этике и юриспруденции (см. Нормативная логика). Успехи, достигнутые в формальной теории дедукции, способствовали применению точных методов в разработке широкого комплекса проблем теории индукции и индуктивной логики (см. ст. Логика индуктивная, раздел Современная логика индуктивная, ст. Научная индукция, Неполная индукция, Популярная индукция), и вероятностной логики. Т.о., ответ на вопрос «Что такое Ф. л.?» можно дать, лишь опираясь на историч. анализ ведущих тенденций развития логики, а также принимая во внимание, что термин «Ф. л.» употребляется неоднозначно, что в рамках Ф. л. в широком смысле можно говорить о различных разделах и дисциплинах, к-рые также носят имя «Ф. л.». Такая дифференциация Ф. л., с др. стороны, дополняется интеграцией, появлением новых теорий и концепций, в к-рых Ф. л. рассматривается с к.-л. единой, общей т. зр.Философская Энциклопедия. В 5-х т. — М.: Советская энциклопедия. Под редакцией Ф. В. Константинова. 1960—1970.
Логика — Википедия
Грегор Рейш. «Логика представляет её центральные темы», Margarita Philosophica, 1503/08 (?). Две собаки veritas (с лат. — «истина») и falsitas (с лат. — «ложь») преследуют зайца problema (с лат. — «проблема»), логика, вооружённая мечом силлогизма, спешит позади. Слева внизу в гроте изображён Парменид, с которым логическая аргументация проложила себе путь в философию. Ло́гика (др.-греч. λογική — «наука о правильном мышлении», «способность к рассуждению» от др.-греч. λόγος — «логос», «рассуждение», «мысль», «разум», «смысл») — раздел философии, нормативная
В любой науке логика служит одним из основных инструментов[2]. Логика является подразделом не только философии, но и математики, а булева алгебра — одной из основ информатики.
Классическая логическая теория далеко не совершенна: основное её содержание формулируется на особом, созданном для своих целей языке, использует предметное мышление. В ней не предполагается использование контроля прагматических ошибок, погрешностей, нелинейностей используемых систем отсчёта, пограничных ошибок описания, релятивизма масштабирования (относительность предметов и их пространственных характеристик, к примеру: человек велик относительно муравья, но в то же время мал относительно слона) и т. п. Вследствие чего принято считать нормальным факт наличия в её языке парадоксов и априорных утверждений, кустовых эффектов словаря и т. п. Подобно тому как умение говорить существовало ещё до возникновения науки грамматики, так и искусство правильно мыслить существовало задолго до науки логики. Логические операции: определение, классификация, доказательство, опровержение и др. — нередко применяются каждым человеком в его мыслительной деятельности неосознанно и с погрешностями. Некоторые склонны считать собственное мышление естественным процессом, не требующим анализа и контроля больше, чем, скажем, дыхание или движение, но реальное мышление не сводится просто к логической последовательности. В процессе решения возникающих задач также существенны: интуиция, эмоции, образное видение мира и многое другое[3]. Однако нестрогость мышления ещё не значит, что оно не подчинено логике[4]. Основная цель (функция) логики всегда оставалась неизменной: исследование того, как из одних утверждений можно выводить другие. При этом предполагается, что вывод зависит только от способа связи входящих в него утверждений и их строения, а не от их конкретного содержания. Изучая, «что из чего следует», логика выявляет наиболее общие или, как говорят, формальные условия правильного мышления. Сфера конкретных интересов логики существенно менялась на протяжении её истории.
Значение слова[править | править код]
Слово «логика» используется также в значениях «внутренняя закономерность, присущая тем или иным явлениям» или «правильный, разумный ход рассуждений»[5]. В частности этим словом могут называться следующие вещи:
- процесс мышления — если говорится о логичном и нелогичном мышлении, когда последовательность утверждений соответствует изученным в логике схемам, в отличие от полностью бессвязных и рассуждений по аналогии с произвольными понравившимися автору образами или стереотипами.
- В электронике — вид схем, предназначенных для обработки информации и управления. В отличие от силовых схем трансформации и распределения энергии. И маломощных, но обрабатывающих атомарные сигналы — фильтрации, регистрации, генерации.
- В произвольных явлениях — приписываемое или обнаруженное в них определённое функционирование, повторяющиеся процессы, которые могут быть описаны в логических категориях — состояние, подчинение, отражение, зависимость и т. п.
Неформальная, формальная, символическая и диалектическая логика[править | править код]
Неформальная логика (термин принят прежде всего в англоязычной литературе) — исследование аргументации в естественном языке. Одной из главных задач её является исследование логических ошибок — см. Логическая семантика, философская логика, теория аргументации, логический анализ языка. Любой вывод, сделанный на естественном языке, обладает чисто формальным содержанием (смысл рассуждения может быть разделён на форму мысли и собственно содержание), если можно показать, что он является частным применением абстрактного универсального правила, которое отвлекается от всякого конкретного предмета, свойства или отношения. Именно этот вывод с чисто формальным содержанием называют логическим выводом и основным предметом логики. Анализ вывода, который раскрывает это чисто формальное содержание, называется формальной логикой. Символическая логика изучает символические абстракции, которые фиксируют формальную структуру логического вывода.
Диалектическая логика — наука о мышлении в марксизме. Здесь понятие мышления употребляется в смысле Логоса как предмета античной философии, а диалектическая логика — уже в смысле отдельной науки, как физика или формальная логика. Диалектическое рассуждение учитывает законы формальной логики. Вместе с тем, осуществляя анализ динамики перехода понятий в свою противоположность, оно допускает, что противоположности совпадают, ориентируется на законы диалектики.
В рамках формальной логики имеется группа логик, именуемых неклассическими (иногда также используется термин «альтернативные логики»). Эта группа логик существенно отличается от классических логик путём различных вариаций законов и правил (например, логики, отменяющие закон исключённого третьего, меняющие таблицы истинности и т. д.). Благодаря этим вариациям возможно построение различных моделей логических следствий и логической истины[6].
Отношение к другим наукам[править | править код]
Исторически логика изучалась как часть философии и риторики. Сейчас символическая логика также изучается как часть математики, информатики.
Метатеоретические проблемы логики[править | править код]
Концепции логики[править | править код]
Концепции логики различаются между собой прежде всего по способам решения метатеоретических проблем логики, связанных с основаниями математики:
Проблемы аксиоматизации теории множеств[править | править код]
Хотя многие культуры выработали сложные системы рассуждения, логика как эксплицитный анализ методов рассуждения получила основательное развитие изначально только в трёх традициях: в китайской, индийской и греческой. Хотя точные даты не слишком достоверны (особенно в случае Индии), скорее всего, логика возникла во всех трёх культурах в IV веке до н. э.[источник не указан 1932 дня]. Современная логика, разработанная формально изощрённо, происходит в конечном счёте из греческой традиции (аристотелевской логики), которая, однако, была воспринята не напрямую, а при посредничестве и комментаторской деятельности арабо-мусульманских философов и средневековых европейских логиков. Можно выделить следующие исторические и региональные формы логики (приведены также их наименования, исторически существовавшие и принятые в литературе по истории формальной логики):
- Древнекитайская логика
- Индийская логика
- Европейская и ближневосточная логика: традиционная логика (в широком смысле)
- Античная и раннесредневековая логика: диалектика
- Средневековая логика
- Арабская и еврейская средневековая логика
- Восточнохристианская средневековая логика
- Западноевропейская средневековая логика: схоластическая логика, диалектика
- Логика европейского Возрождения; диалектика
- Логика Нового времени: традиционная логика (в узком смысле), формальная логика
- Современная логика (общемировая, со второй половины XIX века): математическая логика, символическая логика, логистика (последнее — как правило, в западной литературе).
Логика в своём развитии прошла три порога:
- порог формализации рассуждений (во всех трёх традициях)
- введение условных (символических, буквенных и числовых) обозначений (только европейская традиционная логика)
- научная революция, с которой началась современная логика, — математизация (внесение в логику математических методов).
Логика в Древнем Китае[править | править код]
Логика в Китае появилась в период появления большого количества школ, конкуренции и дискуссий между ними. Современник Конфуция Мо-цзы («Учитель Мо», «Мудрец Мо»; V—IV вв. до н. э) был известен как основатель моизма (школы мо цзя), представители которой занимались поиском источников достоверного рассуждения и условий его правильности. В области аргументации они предпочитали разработку рассуждения по аналогии разработке дедукции. В процессе анализа семантики языка моисты разработали метод классификации имён по степени их общности и деления вещей по видам (метод «трёх правил», «трёх фа»).
Одно из ответвлений моизма, логики (мин цзя, школа имён, V—III вв. до н. э), приступило к исследованию собственно формальной логики (её представители подошли к открытию категорического силлогизма ранее или одновременно с её формулировкой Аристотелем).
Позднее, при династии Цинь, эта линия исследований исчезла в Китае, поскольку тогда философия легизма жестоко подавляла все остальные философские школы. Вновь логика в Китае появилась только с проникновением туда индийской логики буддистов и далее сильно отстала от развития европейской и ближневосточной логики.
Индийская логика[править | править код]
Истоки логики в Индии можно проследить в грамматических текстах V века до н. э.. Две из шести ортодоксально-индуистских (ведийских) школ индийской философии — ньяя и вайшешика — занимались методологией познания, из этого проблемного поля и выделилась логика.
Само название школы «ньяя» значит «логика». Главным её достижением и была разработка логики и методологии, ставших впоследствии общим достоянием (ср. аристотелевская логика в Европе). Основным текстом школы были Ньяя-сутры Акшапады Гаутамы (II век н. э.). Поскольку ньяики считали единственным путём освобождения от страданий достижение надёжного знания, они разрабатывали тонкие методы отличения надёжных источников знания от ложных мнений. Есть только четыре источника знания (четыре праманы): восприятие, умозаключение, сравнение и свидетельство. Строгая пятичленная схема умозаключения включала в себя: начальную посылку, основание, пример, приложение и вывод.
Буддийская философия (не входившая в число шести ортодоксальных школ) была главным оппонентом ньяиков в логике. Нагарджуна, основатель мадхьямики («срединного пути»), развил рассуждение, известное как «чатушкоти», или тетралемма. Этот четырёхсторонний аргумент систематически проверял и отклонял утверждение высказывания, его отрицание, соединение утверждения и отрицания и, наконец, отклонение и его утверждения, и его отрицания.
У Дигнаги и его последователя Дхармакирти буддийская логика достигла вершины. Центральным пунктом их анализа было установление (определение) необходимой логической присущности (включённости в определение), «вьяпти», также известное как «неизменное следование» или «убеждение». Для этой цели они развили учение об «апоха» или различении, о правилах включения признаков в определение или исключения их из него.
Школа навья-ньяя («новая ньяя», «новая логика») была основана в XIII веке Ганешей Упадхьяей из Митилы, автора «Таттвачинтамами» («Сокровище мысли о реальности»). Впрочем, и он опирался на работы своих предшественников X века.
Европейская и ближневосточная логика[править | править код]
В истории европейской логики можно выделить этапы:
- аристотелевский (традиционный) продолжался сотни лет, в течение которых логика развивалась очень медленно;
- схоластический этап развития, пик которого приходится на XIV век;
- нововременной этап.
Логика античности[править | править код]
Основателем логики в древнегреческой философии считается древнегреческий философ Аристотель, так как полагается, что он вывел первую логическую теорию. Предшественниками Аристотеля в развитии логической науки в Древней Греции были Парменид, Зенон Элейский, Сократ и Платон. Аристотель же впервые систематизировал доступные знания о логике, обосновал формы и правила логического мышления. Его цикл сочинений «Органон» состоит из шести работ, посвящённых логике: «Категории», «Об истолковании», «Топика», «Первая аналитика» и «Вторая аналитика», «Софистические опровержения».
После Аристотеля в Древней Греции логика также разрабатывалась представителями школы стоиков. Большой вклад в развитие этой науки внесли оратор Цицерон и древнеримский теоретик ораторского искусства Квинтилиан.
Логика в Средневековье[править | править код]
По мере приближения к Средним векам логика получала более широкое распространение. Её начали разрабатывать арабоязычные исследователи, например, Аль-Фараби (ок. 870—950 гг.). Средневековая логика называется схоластической, а её расцвет в XIV веке связывают с именами учёных Уильяма Оккама, Альберта Саксонского и Уолтера Берли.
Логика в эпоху Возрождения и в Новое время[править | править код]
Этот исторический период в логике отмечается появлением множества крайне значимых для науки публикаций.
Френсис Бэкон в 1620 году опубликовывает свой «Новый органон», содержащий основы индуктивных методов, усовершенствованных позднее Джоном Стюартом Миллем и получивших название методов установления причинных связей между явлениями Бэкона-Милля. Суть индукции (обобщения) — в восхождении (в процессе познания) от частных случаев к общим правилам. Также необходимо искать причины своих ошибок.
В 1662 году в Париже издан учебник «Логика Пор-Рояля», авторами которого являются П. Николь и А. Арно, создавшие логическое учение на основе методологических принципов Рене Декарта.
Современная логика[править | править код]
В конце XIX — начале XX веков были заложены основы т. н. математической, или символической, логики. Её суть заключается в том, что для обнаружения истинностного значения выражений естественного языка можно применять математические методы. Именно использование символической логики отличает современную логическую науку от традиционной.
Огромный вклад в развитие символической логики внесли такие учёные, как Дж. Буль, О. де Морган, Г. Фреге, Ч. Пирс и др. В XX веке математическая логика оформилась в качестве самостоятельной дисциплины в рамках логической науки.
Начало XX века ознаменовалось становлением идей неклассической логики, многие важные положения которой были предвосхищены и/или заложены Н. А. Васильевым и И. Е. Орловым.
В середине XX века развитие вычислительной техники привело к появлению логических элементов, логических блоков и устройств вычислительной техники, что было связано с дополнительной разработкой таких областей логики, как проблемы логического синтеза, логическое проектирование и проблемы логического моделирования логических устройств и средств вычислительной техники.
В 80-х годах XX века начались исследования в области искусственного интеллекта на базе языков и систем логического программирования. Началось и создание экспертных систем с использованием и развитием автоматического доказательства теорем, а также методов доказательного программирования для верификации алгоритмов и программ для ЭВМ.
В 80-е годы начались также изменения в образовании. Появление персональных компьютеров в средних школах привело к созданию учебников информатики с изучением элементов математической логики для объяснения логических принципов работы логических схем и устройств вычислительной техники, а также принципов логического программирования для компьютеров пятого поколения, и разработке учебников информатики с изучением языка исчисления предикатов для проектирования баз знаний.
Понятия логики, необходимые для понимания предмета:[7]
Дедуктивное и индуктивное рассуждение в традиционной логике[править | править код]
Силлогистика[править | править код]
Аппарат математической логики[править | править код]
Пропозициональная логика[править | править код]
Логика предикатов[править | править код]
Исчисления и логические методы[править | править код]
Логическая семантика[править | править код]
Законы логики[править | править код]
Теория моделей[править | править код]
Теория доказательств[править | править код]
Теории логического вывода[править | править код]
Логики с неклассическим пониманием следования[править | править код]
Логики, отменяющие закон исключённого третьего[править | править код]
Логики, меняющие таблицы истинности[править | править код]
Логики, расширяющие состав высказывания[править | править код]
Модальная логика[править | править код]
Недедуктивные логические теории[править | править код]
Другие неклассические логики[править | править код]
- Категориальная логика
- Комбинаторная логика — это логика, которая заменяет переменные функциями с целью прояснить такие интуитивные операции с переменными, как подстановка. Построенная на базе комбинаторной логики система арифметики содержит все частично рекурсивные функции и избегает гёделевской неполноты.
- Кондициональная логика (условная логика). Её предмет — истинность условных предложений (в частности, сослагательного наклонения). Логика контрафактических утверждений.
Прикладные проблемы логики (см. Прикладная логика) и логической семантики
- Приложения логики в методологии науки
- Приложения логики в философии
- Приложения логики в теологии
- Приложения логики в психологии
- Приложения логики в правовых науках
- Приложения логики в лингвистике
- Приложения логики в других дисциплинах
- Искусственный интеллект
Приложения логики в анализе познавательных процедур[править | править код]
Логический анализ форм и приёмов познания
Приложения логики в методологии науки[править | править код]
Приложения логики в философии[править | править код]
Приложения логики в психологии[править | править код]
Поскольку логика устанавливает законы и схемы мышления, существует проблема соотнесения логики с творчеством, которое опирается на интуицию. Творчество без ограничений является идеализацией: оно ограничено психологическими закономерностями восприятия или, например, законами композиции в изобразительном искусстве. Творчество предполагает не только способность выдвинуть интересную идею, но и умение убедительно обосновать её и претворить в жизнь по определённым правилам, следовательно, должно следовать каким-то правилам мышления.
Приложения логики в лингвистике[править | править код]
Приложения логики в компьютерных науках[править | править код]
ФОРМАЛЬНАЯ ЛОГИКА — что такое в Философской энциклопедии
наука о мышлении, предметом к-рой является исследование умозаключений и доказательств с т.зр. их формы (формы логической) и в отвлечении от их конкретного содержания. Ф. л. является базисной наукой – ее идеи и методы используются как в повседневной практике, напр. в качестве средства от логич. ошибок, так и в особенности в теории для логического анализа науч. знания и для дедуктивного (синтетического) построения на базе логических исчислений любых «нелогических» науч. дисциплин.
Историч. основу Ф. л. образует т.н. т р а д и ц и о н н а я Ф. л., к к-рой относят обычно учение о понятии, учение о мышления законах, учение о суждении и теорию силлогистич. вывода – учение о силлогизме, или силлогистику, учения о непосредственных умозаключениях и несиллогистических умозаключениях, учение о логических ошибках и, наконец, традиц. логику индуктивную. Основоположником традиц. Ф. л. является Аристотель: обобщив опыт повседневного и отчасти науч. мышления тогда только формировавшейся науки, Аристотель создал учение о силлогизме и дал первые примеры анализа рассуждений с т. зр. их формы. Однако уже сам Аристотель сознавал, что в силлогистич. схемы нельзя уложить многие рассуждения, в особенности математические. Это побудило мегариков и ранних стоиков исследовать др. формы дедукции (см. Древнегреческая логика). Частично в том же направлении шло развитие логики и в средние века (см. раздел Схоластическая логика в ст. Схоластика), и в эпоху Возрождения (Галилей, Валла, Раме). Развитие опытного естествознания и математики, усилившееся в 17 в., поставило вопрос о прикладной роли Ф. л., о дальнейшем развитии несиллогистич. форм вывода, характерных для логики науки. (В этой области работали с большим или меньшим успехом Ф. Бэкон, Декарт, Паскаль, авторы Пор-Рояля логики, И. Юнг, Лейбниц и их последователи.) Одна из осн. «логистических» идей Лейбница состояла в том, чтобы свести к «вычислению» не только математические, но и любые умозаключения. Лишь ко 2-й пол. 19 в. относятся ощутимые шаги в реализации этой идеи, когда работами Буля, де Моргана, Джевонса, Шрёдера, Порецкого, Пирса, Фреге, Пеано и др. были заложены основы первых совр. логико-матем. исчислений. «Principia Mathematica» Б. Рассела и А. Уайтхеда открывает совр. этап в развитии Ф. л.
С о в р е м е н н а я Ф. л. является историч. преемником традиц. Ф. л. и в ряде случаев ее прямым продолжением. Расширение и обогащение языка Ф. л., ее осн. понятий в известной мере служат указанием на то, в каком направлении шло развитие Ф. л. от традиционной к современной. В частности, в логич. словаре появились такие понятия, как исчисление и логическое исчисление, математическая индукция, формализация и формализованный язык, независимость, непротиворечивость и полнота, алгоритм и разрешения проблемы, область предметов и переменная, операция и функция и др. неизвестные традиц. Ф. л. понятия. С др. стороны, определ. связь с традицией сохранили такие понятия совр. Ф. л., как аксиома, посылка и постулат, вывод и правило вывода, квантор, следствие и следование (импликация), теорема о дедукции и др., хотя в совр. трактовке этих понятий не сразу узнаются их историч. прообразы.
На протяжении более чем двухтысячелетней истории Ф. л. основную ее цель видели в том, чтобы исследовать, каким образом можно выводить одни высказывания из других. Для совр. Ф. л. характерно построение формальных теорий логич. вывода (см. Вывод в математической логике) в рамках тех или иных логич. «формализмов» (исчислений), а следовательно, и особое внимание к построению самих этих формализмов и применяемых при этом формально-дедуктивных методов. В зависимости от того, какие осн. понятия и методы используются для построения формальных теорий логич. вывода [в том числе и в зависимости от того, как интерпретируются осн. логич. константы: дизъюнкция, конъюнкция, импликация, отрицание (в логике), эквиваленция] различают: классическую (иначе двузначную) логику, интуиционистскую логику, конструктивную логику, модальную логику, многозначную логику и др. Каковы бы ни были различия в построении этих теорий, каждая теория состоит из двух осн. разделов: логики высказываний и логики предикатов. Классич. вариант последней непосредственно примыкает к традиц. силлогистике (логике «одноместных» предикатов), хотя в многочисленных и различных предикатов исчислениях (см. также ст. Натуральное исчисление, Секвенций исчисление) формализуется субъектно-предикатная структура предложений, понимаемая в более широком, чем в традиц. Ф. л., смысле: помимо свойств («одноместных» предикатов), в них формализуются и отношения («многоместные» предикаты), что делает излишней особую логику отношений в ее традиц. филос. истолковании.
Каждая из указанных выше формальных теорий имеет определ. филос. смысл, являясь логической реализацие й тех или иных методологич. подходов в науке. Связь совр. Ф. л. и философии стимулируется прежде всего актуальной задачей обоснования математики – науч. направлением, имеющим как логический, так и филос. характер (см. ст. Алгоритм, Интуиционизм, Исчисление задач, Конструктивное направление, Логицизм, Математическая бесконечность, Математическая логика, Метод аксиоматический, Минимальная логика, Номинализм в философии математики, Положительная логика, Принцип исключенного третьего, Проверяемость, Теория множеств, формализм, Эффективизм). Примером обогащения и углубления логич. исследований, вызванных стимулирующим влиянием проблем обоснования математики, может служить возникновение металогики – в узком (гильбертовском) смысле как теории формальных систем, ограниченной рамками финитизма, и в широком смысле как метатеории Ф. л. вообще, включающей логический синтаксис (см. Синтаксис в логике, Метаязык), логическую семантику (см. такжеСемантика в логике и примыкающие к ней ст. Взаимозаменимости отношение, Знак, Значение, Имя, Интерпретация, Контрфактические предложения, Логическая истинность, Модель, Название, Описания операторы, Реализуемость, Синтетические и аналитические суждения, Тавтология, Тождественная истинность, Фактическая истинность, Экстенсиональные и неэкстенсиональные языки), теории определения и определимости и теорию тождества (см. А=А, Правило замены равного равным, Принцип замещения, Равенство в логике и математике). Дальнейшим расширением металогич. проблематики явилось выделение в особую дисциплину прагматики, развивавшейся первоначально в рамках логико-семантич. и психологич. анализа (см. Психологизм в логике), и, наконец, появление семиотики. Т.о., связь между мышлением и языком как «практической действительностью мысли» (К. Маркс) нашла отражение во взаимосвязи философии, психологии, лингвистики и логики.
В развитии совр. Ф. л. особую роль играют вопросы ее приложений, особенно в вычислит. математике и технике, кибернетике и теории информации, лингвистике математической и пр. (см., напр., ст. Логические машины, Логические схемы автоматов). Связующим звеном между Ф. л. и вычислит. математикой исторически явилась логика классов, к-рая развилась в результате попыток свести силлогистич. методы решения логич. задач к алгебраич. методам их решения, образовав, т.о., первое алгебраич. направление в совр. Ф. л. – алгебру логики (см. также Теоретико-множественная логика). Дальнейшим развитием алгебраич. направления явилось объединение алгебры логики и логики предикатов в теории конечных автоматов, расширение алгебры логики в сторону «алгебраизации» логики предикатов – теория моделей и математич. теория структур. Другую – «арифметическую» – ветвь, связавшую Ф. л. и вычислит. математику, образуют теория рекурсивных функций и предикатов (см. также ст. Алгоритм, Массовая проблема, Разрешимое и перечислимое множества, Сводимость), исчисление λ-конверсии (см. Оператор абстракции, Функция), логика комбинаторная и др. Из общих науч. приложений Ф. л. следует отметить вопросы, связанные с задачами уточнения понятия науч. закона (см. Диспозициональный предикат, Каузальная импликация, Номологические высказывания, Связь), с попытками применения логики в биологии и физике (см. Логика квантовой механики), в этике и юриспруденции (см. Нормативная логика). Успехи, достигнутые в формальной теории дедукции, способствовали применению точных методов в разработке широкого комплекса проблем теории индукции и индуктивной логики (см. ст. Логика индуктивная, раздел Современная логика индуктивная, ст. Научная индукция, Неполная индукция, Популярная индукция), и вероятностной логики.
Т.о., ответ на вопрос «Что такое Ф. л.?» можно дать, лишь опираясь на историч. анализ ведущих тенденций развития логики, а также принимая во внимание, что термин «Ф. л.» употребляется неоднозначно, что в рамках Ф. л. в широком смысле можно говорить о различных разделах и дисциплинах, к-рые также носят имя «Ф. л.». Такая дифференциация Ф. л., с др. стороны, дополняется интеграцией, появлением новых теорий и концепций, в к-рых Ф. л. рассматривается с к.-л. единой, общей т. зр.
М. Новосёлов, Г. Рузавин, П. Таванец. Москва.
Философская Энциклопедия. В 5-х т. — М.: Советская энциклопедия.Под редакцией Ф. В. Константинова.1960—1970.
Логика (философия) — это… Что такое Логика (философия)?
Ло́гика (др.-греч. λογική «наука о рассуждении», «искусство рассуждения» от λόγος — «речь», «рассуждение») — наука о формах, методах и законах интеллектуальной познавательной деятельности, формализуемых с помощью логического языка. Поскольку это знание получено разумом, логика также определяется как наука о правильном мышлении. Поскольку мышление оформляется в языке в виде рассуждения, частным случаем которого являются доказательство и опровержение, логика иногда определяется как наука о способах рассуждения или наука о способах доказательств и опровержений. Логика как наука изучает способы достижения истины в процессе познания опосредованным путём, не из чувственного опыта, а из знаний, полученных ранее, поэтому её также можно определить как науку о способах получения выводного знания.
Выводное знание, полученное с помощью применения законов логики и методов логического мышления, — цель любого логического действия, нацеленного на достижение истины и применение полученного знания для более глубокого познания явлений и событий окружающего мира.
Одна из главных задач логики — определить, как прийти к выводу из предпосылок (правильное рассуждение) и получить истинное знание о предмете размышления, чтобы глубже разобраться в нюансах изучаемого предмета мысли и его соотношениях с другими аспектами рассматриваемого явления.
Логика служит одним из инструментов почти любой науки.
Сущность логики
Классическая логическая теория далеко не совершенна: основное её содержание формулируется на особом, созданном специально для своих целей языке, использует абсолютное предметное мышление. В ней не предполагается использование контроля прагматических ошибок, погрешностей нелинейностей используемых систем отсчёта, пограничных ошибок описания, релятивизма масштабирования и т. п. Вследствие чего принято считать нормальным факт наличия в её языке парадоксов и априорных утверждений, кустовых эффектов словаря и т. п.
Подобно тому как умение говорить существовало ещё до возникновения науки грамматики, так и искусство правильно мыслить существовало задолго до науки логики. Логические операции: определение, классификация, доказательство, опровержение и др. нередко применяются каждым человеком в его мыслительной деятельности неосознанно и с погрешностями, некоторые склонны считать собственное мышление естественным процессом, не требующим анализа и контроля больше, чем, скажем, дыхание или движение.
Реальное мышление не сводится просто к логической последовательности. В процессе решения возникающих задач важным оказывается, как правило, всё: и последовательность, и интуиция, и эмоции, и образное видение мира, и многое другое.
Основная цель (функция) логики всегда оставалась неизменной: исследование того, как из одних утверждений можно выводить другие. При этом предполагается, что вывод зависит только от способа связи входящих в него утверждений и их строения, а не от их конкретного содержания. Изучая, «что из чего следует», логика выявляет наиболее общие или, как говорят, формальные условия правильного мышления. Сфера конкретных интересов логики существенно менялась на протяжении её истории.
Значение слова
Слово «логика» используется также в значениях «внутренняя закономерность, присущая тем или иным явлениям» или «правильный, разумный ход рассуждений»[1]. В частности этим словом могут называться следующие вещи:
- процесс мышления — если говорится о логичном и нелогичном мышлении, имеется в виду его логичность, понимаемая как свойство памяти помнить и использовать один и тот же язык.
- В электронике — электронные логические схемы
- В аспектонике и соционике — тип воспринимаемой человеком информации, обобщённое название для аспектов «белая логика» (информация об измеримых отношениях объектов) и «чёрная логика» (информация об измеримом движении объектов).
Используются выражения:
- логика событий — имеется в виду некоторая виртуальная модель реальных событий, созданная в языке описания, достаточном для прогнозирования будущего с достаточной точностью.
- логика характера — имеется в виду некоторая виртуальная модель характера личности, позволяющая более или менее точно прогнозировать события-поступки в будущем.
Пример: «Быть может, он безумец, — говорит один из героев рассказа английского писателя Г. К. Честертона, — но в его безумии есть логика. Почти всегда в безумии есть логика. Именно это и сводит человека с ума». Здесь «логика» означает, что наблюдатель имеет в своей памяти достаточно точное описание характера — «безумия», позволяющее ему зафиксировать в используемом языке причинно-следственные связи черт характера и поведения субъекта — «безумца», а также и вообще любых других людей, страдающих «безумием».
- Есть выражения «женская логика», «мужская логика».
Неформальная, формальная, символическая и диалектическая логика
Неформальная логика (термин принят прежде всего в англоязычной литературе) — исследование аргументации в естественном языке. Одной из главных задач её является исследование логических ошибок. См. Логическая семантика, философская логика, теория аргументации, логический анализ языка.
Любой вывод, сделанный на естественном языке, обладает чисто формальным содержанием (смысл рассуждения может быть разделён на форму мысли и собственно содержание), если можно показать, что он является частным применением абстрактного универсального правила, которое отвлекается от всякого конкретного предмета, свойства или отношения. Именно этот вывод с чисто формальным содержанием называют логическим выводом и основным предметом логики.
Анализ вывода, который раскрывает это чисто формальное содержание, называется формальной логикой.
Символическая логика изучает символические абстракции, которые фиксируют формальную структуру логического вывода.
Диалектическая логика — особый метод философского спекулятивного рассуждения и наука о таком методе, которая, как предполагается, даёт знание о способе рассуждения, расширяющем возможности формально-логического вывода. Здесь понятие логики употребляется как в собственном логическом, так и в метафорическом смысле. Диалектическое рассуждение учитывает законы формальной логики. Вместе с тем, осуществляет анализ динамики перехода понятий в свою противоположность, допускает, что противоположности совпадают, ориентируется на законы диалектики. Собственно Гегель, от которого идёт эта традиция, называл логику мышлением мышления и рассматривал как основу деятельности людей вообще и в частности, философии. Поэтому он предлагал единую логику, состоящую из трёх логических форм: абстрактной (рассудочной), диалектической (отрицательно-разумной) и спекулятивной (положительно-разумной, которая постигает единство определений в их противоположности, утверждение, содержащееся в их разрешении и в их взаимном переходе). В традиции диалектической логики формальная логика трактуется как низшая разновидность логики.
Отношение к другим наукам
Исторически логика изучалась как часть философии. Сейчас символическая логика также изучается как часть математики, информатики.
Металогика
Основная статья: Металогика
Метатеоретические проблемы логики
- Непротиворечивость формализованных теорий
- Полнота формализованных теорий
- Разрешимость формализованных теорий
- Независимость аксиом формализованных теорий
- Определимость
- Сравнительный анализ логических теорий
Концепции логики
Концепции логики различаются между собой прежде всего по способам решения метатеоретических проблем логики, связанных с основаниями математики
Проблемы аксиоматизации теории множеств
- Логические парадоксы
- Семантические парадоксы
История логики
Основная статья: История логики
Хотя многие культуры выработали сложные системы рассуждения, логика как эксплицитный анализ методов рассуждения получила основательное развитие изначально только в трёх традициях: в китайской, индийской и греческой. Хотя точные даты не слишком достоверны (особенно в случае Индии), скорее всего, логика возникла во всех трёх культурах в IV веке до н. э.. Современная логика, разработанная формально изощрённо, происходит в конечном счёте из греческой традиции (аристотелевской логики), которая, однако, была воспринята не напрямую, а при посредничестве и комментаторской деятельности арабо-мусульманских философов и средневековых европейских логиков. Можно выделить следующие исторические и региональные формы логики (приведены также их имена, исторически существовавшие и принятые в литературе по истории формальной логики):
- Древнекитайская логика:
- Индийская логика
- Европейская и ближневосточная логика: традиционная логика (в широком смысле)
- Античная и раннесредневековая логика: диалектика
- Средневековая логика
- Арабская и еврейская средневековая логика
- Восточнохристианская (византийская, грузинская, армянская) средневековая логика
- Западноевропейская средневековая логика: схоластическая логика, диалектика
- Логика европейского Возрождения; диалектика
- Логика Нового времени: традиционная логика (в узком смысле), формальная логика
- Современная логика (общемировая, со второй половины XIX века): математическая логика, символическая логика, логистика (последнее — как правило, в западной литературе).
Логика в своём развитии прошла три порога:
- порог формализации рассуждений (во всех трёх традициях)
- введение условных (символических, буквенных и числовых) обозначений (только европейская традиционная логика)
- научная революция, с которой началась современная логика, — математизация (внесение в логику математических методов).
Логика в Древнем Китае
Логика в Китае появилась в период появления большого количества школ, конкуренции и дискуссий между ними. Современник Конфуция Мо-цзы («Учитель Мо», «Мудрец Мо») был известен как основатель моизма (школы мо цзя), представители которой занимались поиском источников достоверного рассуждения и условий его правильности. В области аргументации они предпочитали разработку рассуждения по аналогии разработке дедукции. В процессе анализа семантики языка моисты разработали метод классификации имён по степени их общности и деления вещей по видам (метод «трёх правил», «трёх фа»).
Одно из ответвлений моизма, логики (мин цзя, школа имён), приступило к исследованию собственно формальной логики (её представители подошли к открытию категорического силлогизма).
К сожалению, позднее, при династии Цинь, эта линия исследований исчезла в Китае, поскольку тогда философия легизма жестоко подавляла все остальные философские школы. Вновь логика в Китае появилась только с проникновением туда индийской логики буддистов.
Индийская логика
Истоки логики в Индии можно проследить в грамматических текстах V века до н. э.. Две из шести ортодоксально-индуистских (ведийских) школ индийской философии — ньяя и вайшешика — занимались методологией познания, из этого проблемного поля и выделилась логика.
Само название школы «ньяя» значит «логика». Главным её достижением и была разработка логики и методологии, ставших впоследствии общим достоянием (ср. аристотелевская логика в Европе). Основным текстом школы были Ньяя-сутры Акшапады Гаутамы (II век н. э.). Поскольку ньяики считали единственным путём освобождения от страданий достижение надёжного знания, они разрабатывали тонкие методы отличения надёжных источников знания от ложных мнений. Есть только четыре источника знания (четыре праманы): восприятие, умозаключение, сравнение и свидетельство. Строгая пятичленная схема умозаключения включала в себя: начальную посылку, основание, пример, приложение и вывод.
Буддийская философия (не входившая в число шести ортодоксальных школ) была главным оппонентом ньяиков в логике. Нагарджуна, основатель мадхьямики («среднего пути»), развил рассуждение, известное как «катускоти», или тетралемма. Этот четырёхсторонний аргумент систематически проверял и отклонял утверждение высказывания, его отрицание, соединение утверждения и отрицания и, наконец, отклонение и его утверждения, и его отрицания.
у Дигнаги и его последователя Дхармакрити буддийская логика достигла вершины. Центральным пунктом их анализа было установление (определение) необходимой логической присущности (включённости в определение), «вьяпти», также известное как «неизменное следование» или «убеждение». Для этой цели они развили учение об «апоха» или различении, о правилах включения признаков в определение или исключения их из него.
Школа навья-ньяя («новая ньяя», «новая логика») была основана в XIII веке Ганешей Упадхьяей из Митилы, автора «Таттвачинтамами» («Сокровище мысли о реальности»). Впрочем, он и опирался на работы своих предшественников X века.
Европейская и ближневосточная логика
В истории европейской логики можно выделить этапы: аристотелевский, или традиционный — период доминирования формальной логики — продолжался сотни лет, в течение которых логика развивалась очень медленно; схоластический этап развития, пик которого приходится на XIV век; нововременной этап.
Логика античности
Основателем логики в древнегреческой философии считается древнегреческий философ Аристотель, так как полагается, что он вывел первую логическую теорию. Предшественниками Аристотеля в развитии логической науки в Древней Греции были Парменид, Зенон Элейский, Сократ и Платон. Аристотель же впервые систематизировал доступные знания о логике, обосновал формы и правила логического мышления. Его цикл сочинений «Органон» состоит из шести работ, посвящённых логике: «Категории», «Об истолковании», «Топика», «Первая аналитика» и «Вторая аналитика», «Софистические опровержения».
После Аристотеля в Древней Греции логика также разрабатывалась представителями школы стоиков. Большой вклад в развитие этой науки внесли оратор Цицерон и древнеримский теоретик ораторского искусства Квинтилиан.
Логика в Средневековье
По мере приближения к Средним векам логика получала более широкое распространение. Её начали разрабатывать арабоязычные исследователи, например, Аль-Фараби (ок. 870—950 гг.). Средневековая логика называется схоластической, а её расцвет в XIV веке связывают с именами учёных Уильяма Оккама, Альберта Саксонского и Уолтера Берли.
Логика в эпоху Возрождения и в Новое время
Этот исторический период в логике отмечается появлением множества крайне значимых для науки публикаций.
Френсис Бэкон в 1620 году опубликовывает свой «Новый органон», содержащий основы индуктивных методов, усовершенствованных позднее Джоном Стюартом Миллем и получивших название методов установления причинных связей между явлениями Бэкона-Милля.
В 1662 году в Париже издан учебник «Логика Пор-Рояля», авторами которого являются П. Николь и А. Арно, создавшие логическое учение на основе методологических принципов Рене Декарта.
Современная логика
Как охарактеризовал её известный русский логик П. С. Порецкий, она представляет собой современную теорию правильного рассуждения, «логику по предмету и математику по методу» и не является логическим исследованием исключительно математических доказательств.
В конце XIX — начале XX веков были заложены основы т. н. математической, или символической, логики. Её суть заключается в том, что для обнаружения истинностного значения выражений естественного языка можно применять математические методы. Именно использование символической логики отличает современную логическую науку от традиционной.
Огромный вклад в развитие символической логики внесли такие учёные, как Дж. Буль, О. де Морган, Г. Фреге, Ч. Пирс и др. В XX веке математическая логика оформилась в качестве самостоятельной дисциплины в рамках логической науки.
Начало XX века ознаменовалось становлением идей неклассической логики, многие важные положения которой были предвосхищены и/или заложены Н. А. Васильевым и И. Е. Орловым.
В середине ХХ века развитие вычислительной техники привело к появлению логических элементов, логических блоков и устройств вычислительной техники, что было связано с дополнительной разработкой таких областей логики, как проблемы логического синтеза, логическое проектирование и логического моделирования логических устройств и средств вычислительной техники.
В 80-х годах ХХ века начались исследования в области искусственного интеллекта на базе языков и систем логического программирования. Началось и создание экспертных систем с использованием и развитием автоматического доказательства теорем, а также методов доказательного программирования для верификации алгоритмов и программ для ЭВМ.
80-ые годы начались также изменения в образовании. Появление персональных компьютеров в средних школах привело к созданию учебников информатики с изучением элементов математической логики для объяснения логических принципов работы логических схем и устройств вычислительной техники, а также принципов логического программирования для компьютеров пятого поколения и разработка учебников информатики с изучением языка исчисления предикатов для проектирования баз знаний.
Основные понятия науки логики
Традиционная логика
Основная статья: Традиционная логика
Дедуктивное и индуктивное рассуждение в традиционной логике
Силлогистика
Классическая математическая логика
Аппарат математической логики
Пропозициональная логика
Логика предикатов
Исчисления и логические методы
Логическая семантика
Основная статья: Логическая семантика
- Алгебраические семантики
- Теоретико-множественные семантики
- Реляционные семантики возможных миров
- Проблема содержательности семантик логических систем
- Категорная семантика
- Теория семантических категорий
Законы логики
Теория моделей
Теория доказательств
Теории логического вывода
- Теории логического вывода (теория логического вывода)
- Теории следования (теория следования)
- Теории импликаций (теория импликаций)
- Материальная импликация
Неклассические логики
Основная статья: Неклассические логики
Логики с неклассическим пониманием следования
- Релевантная логика
- Паранепротиворечивая логика
- Немонотонные логики
- Динамическая логика
Логики, отменяющие закон исключённого третьего
Логики, меняющие таблицы истинности
Основная статья: Многозначные логики
Логики, расширяющие состав высказывания
Модальная логика
- Модальность
- Алетические модальности (алетическая модальность, алетическая модальная логика, алетические модальные логики)
- Деонтические модальности (деонтическая модальность, деонтическая модальная логика, деонтические модальные логики)
- Эпистемологические модальности (эпистемологическая модальность, эпистемологическая модальная логика, эпистемологические модальные логики)
- Временные модальности (временная модальность, временные модальные логики, временная модальная логика)
- Строгая импликация
- Материальная импликация
Недедуктивные логические теории
Другие неклассические логики
- Категориальная логика
- Комбинаторная логика — это логика, которая заменяет переменные функциями с целью прояснить такие интуитивные операции с переменными, как подстановка. Построенная на базе комбинаторной логики система арифметики содержит все частично рекурсивные функции и избегает гёделевской неполноты.
- Кондициональная логика (условная логика). Её предмет — истинность условных предложений (в частности, сослагательного наклонения). Логика контрафактических утверждений.
Приложения логики
Прикладные проблемы логики и логической семантики
- Приложения логики в методологии науки
- Приложения логики в философии
- Приложения логики в теологии
- Приложения логики в психологии
- Приложения логики в правовых науках
- Приложения логики в лингвистике
- Приложения логики в других дисциплинах
Приложения логики в анализе познавательных процедур
Логический анализ форм и приёмов познания
Приложения логики в методологии науки
Приложения логики в философии
Основная статья: Философская логика
Приложения логики в психологии
Поскольку логика устанавливает законы и схемы мышления, существует проблема соотнесения логики с творчеством, которое опирается на интуицию. Творчество без ограничений является идеализацией: оно ограничено психологическими закономерностями восприятия или, например, законами композиции в изобразительном искусстве. Творчество предполагает не только способность выдвинуть интересную идею, но и умение убедительно обосновать её и претворить в жизнь по определённым правилам, следовательно, должно следовать каким-то правилам мышления.
Приложения логики в лингвистике
Приложения логики в компьютерных науках
Источники
- ↑ Ефремова Т. Ф. Новый словарь русского языка. Толково-словообразовательный. — 2001—2002.
Литература
- Кондаков Н. И. Логический словарь-справочник. — М.: Наука, 1976. — 720 с.
- Ивлев Ю. В. Учебник логики: Семестровый курс: Учебник. — М.: Дело, 2003. — 208 с — ISBN 5-7749-0317-6
- Бочаров В. А., Маркин В. И. Основы логики: Учебник. — М.: ИНФРА-М, 2001. — 296 с — ISBN 5-16-000496-3
- Ивин А. А. Логика: Учебное пособие. — Изд. 2-е. — М.: Знание, 1998. — (На портале «Философия в России»; на сайте Славы Янко)
- Ивин А. А., Никифоров А. Л. Словарь по логике — М.: Туманит, ВЛАДОС, 1997. — 384 с — ISBN 5-691-00099-3.
- Горский Д. П. — Логика: Учебное пособие для педагогических училищ. — Изд. 3-е. — М.: Учпедгиз, 1961. — 160 с.
- Челпанов Г. И. Учебник логики. М., 1994.
Литература по истории логики
- Бажанов В. А. История логики в России и СССР. — М.: Канон+, 2007. — 336 с — ISBN 5-88373-032-9
- Маковельский А. О. История логики. — М., 1967. — 504 с.
- Попов П. С. История логики нового времени. — М., Издательство МГУ, 1960.
- Стяжкин Н. И. Формирование математической логики. — М., 1967.
- Scholtz H. Geschichte der Logik, 1931. (Concise History of Logic. — New York, 1961).
Литература по китайской логике
- Спирин B. C. О «третьих» и «пятых» понятиях в логике древнего Китая // Дальний Восток. Сборник статей по филологии, истории, философии. — М., 1961.
- Кроль Ю. Л. Спор как явление культуры древнего Китая. — // Народы Азии и Африки. — 1987. — № 2.
- Крушинский А. А. Имена и реалии в древнекитайской логике и методологии (Обзор) // Современные историко-научные исследования: наука в традиционном Китае. — М., 1987.
- Крушинский А. А. Древнекитайская логика: формальная реконструкция одной характерной системы вывода.// 22-я Научная конференция «Общество и государство в Китае». Ч.1. — М.,1991. — С. 26-35.
- Пань Шимо (КНР). Логика Древнего Китая (краткий очерк) // Философские науки. — 1991. — № 12.
- Чжоу Юньчжи. Основные вехи развития древнекитайской логики мин бянь, ее главные особенности и реальные достижения // Рационалистическая традиция и современность. Китай. 1993. №. — С. 152—178.
- Крушинский А. А. Логика «И цзина». Дедукция в древнем Китае. — М., 1999.
- Кварталова Н. П. Логические идеи трактата «Гунсунь Лун-цзы» // Человек и духовная культура Востока. Альманах. Вып. I. — М., 2003. — С. 167—172.
- Кобзев А. И. Школа имен (мин цзя): коллизия логики и диалектики // Китай в диалоге цивилизации: К 70-летию академика М. Л. Титаренко. — М. 2004. — С. 550—557
См. также
Ссылки
| Логика | |
|---|---|
| Формальная | Логические операции с понятиями Изменение содержания понятия: отрицание • ограничение • обобщение • деление |
| Математическая (теоретическая, символическая) | Логические связки (операции) над высказываниями Высказывание — построение над множеством {B, |
| Прочее | импликация ( ) ) |
Wikimedia Foundation. 2010.
ЛОГИКА или Формальная логика это что такое ЛОГИКА или Формальная логика: определение — Философия.НЭС
ФОРМАЛЬНАЯ ЛОГИКА, или: Логика
— наука, занимающаяся анализом структуры высказываний и доказательств, обращающая основное внимание на форму в отвлечении от содержания (см.: Содержание и форма). Определение «формальная» было введено И. Кантом (1724-1804) с намерением подчеркнуть ведущую особенность Ф. л. в подходе к изучаемым объектам и отграничить ее тем самым от других возможных логик.
Оцените определение:
Источник: Словарь по логике
ЛОГИКА или Формальная логика
— наука о законах и операциях правильного мышления. Согласно основному принципу Л., правильность рассуждения (вывода) определяется только его логической формой, или структурой, и не зависит от конкретного содержания входящих в него утверждений. Различие между формой и содержанием может быть сделано явным с помощью особого языка, или символики, оно относительно и зависит от выбора языка.
Отличительная особенность правильного вывода в том, что от истинных посылок он всегда ведет к истинному заключению. Такой вывод позволяет из имеющихся истин получать новые истины с помощью чистого рассуждения, без обращения к опыту, интуиции и т. п. Неправильные выводы могут от истинных посылок вести как к истинным, так и к ложным заключениям.
Л. занимается не только связями высказываний в правильных выводах, но и многими иными проблемами: смыслом и значением выражений языка, различными отношениями между терминами (понятиями), операциями определения и логического деления понятий, вероятностными и статистическими рассуждениями, парадоксами и логическими ошибками и т. д. Но главные темы логических исследований — анализ правильности рассуждения, формулировка законов и принципов, соблюдение которых является необходимым условием получения истинных заключений в процессе вывода.
Правильным является, напр., рассуждение, следующее схеме: «Если есть первое, то есть и второе; есть первое, значит, есть и второе» (см.: Модус поненс). По этой схеме из высказываний «Если сейчас день, то светло» и «Сейчас день» вытекает высказывание «Сейчас светло». Какие бы конкретные истинные высказывания ни подставлялись в указанную схему, заключение обязательно будет истинным.
В правильном рассуждении заключение вытекает из посылок с логической необходимостью, общая схема такого рассуждения выражает логический закон. Рассуждать логически правильно — значит рассуждать в соответствии с законами Л.
Л. не просто перечисляет некоторые схемы правильного рассуждения. Она выявляет различные типы таких схем, устанавливает общие критерии их правильности, выделяет исходные схемы, из которых по определенным правилам могут быть получены другие схемы данного типа, исследует проблему взаимной совместимости схем и т. д.
В современной Л. логические процессы изучаются путем их отображения в языках формализованных, или логических, исчислений. Построение исчисления отличается тщательностью, с которой формулируются его синтаксические и семантические правила, отсутствием исключений, характерных для естественного языка. Исследованием формального строения логических исчислений, правил образования и преобразования входящих в них выражений занимается логический синтаксис. Отношения между исчислениями и содержательными областями, служащими их интерпретациями или моделями, исследуются семантикой логической.
Современная Л. слагается из большого числа логических систем, описывающих отдельные фрагменты, или типы, содержательных рассуждений. Эти системы принято делить на Л. классическую, включающую классические Л. высказываний и Л. предикатов, и Л. неклассическую, в которую входят модальная Л., интуиционистская Л., многозначная Л., неклассические теории логического следования, паранепротиворечивая Л., Л. квантовой механики и др. Каждая из этих Л. также включает, как правило, соответствующие Л. высказываний и Л. предикатов. Таким образом, хотя Л. как наука едина, она слагается из множества более или менее частных систем, ни одна из которых не может претендовать на выявление логических характеристик мышления в целом. Единство Л. проявляется прежде всего в том, что входящие в нее «отдельные» Л. пользуются при описании логических процессов одними и теми же методами исследования. Все они отвлекаются от конкретного содержания высказываний и умозаключений и оперируют только их формальным, структурным содержанием. В каждой применяется язык символов и формул, строящийся в соответствии с общими для всех систем принципами. И наконец, «сконструированная» Л. вызывает ряд вопросов, характерных для любой системы: нет ли в ней противоречий, охватывает ли она все истины рассматриваемого рода и др. (см.: Непротиворечивость, Полнота, Разрешения проблема). Между разными логическими системами имеются определенные связи. Одни системы могут быть эквивалентны другим, или включаться в них, или быть их обобщением и т. д. Единство Л. проявляется также в том, что разные Л. не противоречат друг другу: законами одной из
|
Формальная логика — это широкая область логических исследований, изучающая идеализированные рассуждения и их системы посредством логических исчислений на основе метода формализации (см. Формализация). Метод формализации подразумевает, что логические рассуждения изучаются в отвлечении от их конкретного содержания; при этом сами логические рассуждения формулируются на некотором точном (формализованном) языке при помощи специального аппарата символов (см. Язык формализованный). Такие точные языки имеют две составляющие: синтаксис (см. Синтактика) и семантику (см. Семантика). Синтаксисом называется совокупность правил построения объектов языка (обычно называемых формулами). Семантикой называется совокупность соглашений, описывающих наше понимание формул (или некоторых из них) и позволяющих считать одни формулы верными, а другие — нет. Формализованный язык позволяет избежать двусмысленной и логической неясности естественного языка, которым пользовалась при описании рассуждений традиционная логика (см. Логика), развивавшаяся в рамках философии (см. Философия). Методы формализации дали логике такие преимущества, как высокая точность формулировок, возможность изучения более сложных, с точки зрения логической формы, объектов. Определение «формальная логика» было введено И. Кантом с намерением подчеркнуть её ведущую особенность в подходе к изучаемым объектам и отграничить её тем самым от других возможных логик. Способность человеческого мышления к конструктивной языковой деятельности порождает возможность оперировать следующими логическими формами: понятиями, суждениями, умозаключениями, которые представляют собой пространство логических исследований. В качестве наиболее сложного вида логических форм иногда выделяют и теории (см. Теория). Часто эту последовательность воспринимают как некую структурную иерархию. Понятие объявляется наиболее простой из форм мышления, суждение представляется как система понятий, умозаключение как система суждений, а теория как система умозаключений. Эта иерархия недостаточно ясна, и её обоснования порой легко подвергаются критике, однако она часто используется в качестве удобной схемы изложения предметной области формальной логики, что, собственно, подкрепляется многовековой традицией преподавания этой дисциплины. Эти логические формы и лежащие в основе операций с ними законы и принципы, то есть так называемый логический аппарат, составляют основную область исследований формальной логики, а выработка самих эффективных логических аппаратов — её основную цель. В связи с различием логических форм выделяют два основных направления формальной логики:
Кроме того, формальная логика затрагивает и такие вопросы, например, как формализация содержательных теорий, проблема смысла и значения, логические ошибки и парадоксы и многие другие. Самостоятельное выделение этих вопросов достаточно условно, все они погружаются в проблематику основных направлений и тесно переплетены друг с другом. Логика возникла в Древней Греции в рамках философии (см. Философия). История её развития насчитывает около двух с половиной тысячелетий и делится на два основных периода:
Античную и схоластическую логику сейчас объединяет общее название «традиционной логики». Она, кроме историко-философского, по-прежнему имеет важное пропедевтическое значение и, будучи своеобразным стержнем интеллектуальной культуры человека, признается неотъемлемым элементом широкого гуманитарного образования. Новый этап в развитии логики (со второй половины XIX века) был связан с её формализацией и последующей математизацией. В связи с этим новая логика получила название математической (или символической) логики (см. Логика символическая, Логика математическая). Современные логические системы в большинстве своём полностью опираются на формальные математические методы и являются логически интерпретированными исчислениями. Основные разделы математической логики — классические логика высказываний (см. Логика высказываний) и логика предикатов (см. Логика предикатов). Широкое распространение получили исследования модальной логики (см. Логика модальная). Системы логики, отрицающие те или иные фундаментальные законы логики, образовали спектр неклассических логик (см. Логики неклассические). Значительное число различных систем формальной логики обусловлено широкой сферой их приложения. Теоретическая математика, пожалуй, потеряла абсолютно лидирующее место в этом смысле, поскольку не менее интересные приложения осуществляются в областях теоретической физики (квантовая логика), прикладной математики (вычислительная математика и теория алгоритмов), информатики (компьютерные технологии, сети, программирование и исследования в области искусственного интеллекта), гуманитарного знания (лингвистика, юриспруденция, этика) и других. Важным разделом современной формальной логики является металогика (см. Металогика), в которой исследуются различные проблемы, относящиеся к логическим теориям. Основными здесь являются вопросы о тех свойствах, которыми обладают логические теории: о непротиворечивости, полноте, наличии разрешающих процедур, независимости исходных дедуктивных принципов, а также о различных отношениях между теориями и так далее. В этом смысле металогика является своего рода саморефлексией логики относительно своих построений. Все метатеоретические исследования проводятся на специальном метаязыке, в качестве которого используется естественный язык, обогащённый специальной терминологией и метатеоретическими дедуктивными средствами. |
Диалектическая логика — Википедия
Диалектическая логика — философский раздел марксизма, частная наука, предмет которой совпадает с предметом классической философии — теоретическим мышлением (или идеальным).
Систематическое изложение того, чем является научно-теоретическое мышление есть «диалектика как логика». Тем самым диалектическая логика является частной наукой, наследующей теории познания классической философии. Также диалектическая логика понималась как особая логическая дисциплина о формах правильных рассуждений.
Предмет диалектической логики — мышление. Диалектическая логика имела своей целью развернуть его изображение в необходимых его моментах и притом в независящей ни от воли, ни от сознания последовательности, а также утвердить свой статус как логической дисциплины.
С точки зрения Э. В. Ильенкова диалектическая логика имеет свои истоки в истории философии начиная с самого её начала, а современный вид приобретает уже начиная с работ Декарта и Спинозы.
Термин «логика» применительно к науке о мышлении впервые был введен стоиками, выделившими под этим названием лишь ту часть действительного учения Аристотеля, которая согласовывалась с их собственными представлениями о природе мышления. Само название «логика» производилось ими от греческого термина «логос» (который буквально означает «слово»), а указанная наука сближалась по предмету с грамматикой и риторикой. Средневековая схоластика, окончательно оформившая и узаконившая эту традицию, как раз и превратила логику в простой инструмент («органон») ведения словесных диспутов, в орудие истолкования текстов «священного писания», в чисто формальный аппарат. В результате оказалось дискредитированным не только [7] официальное толкование логики, но даже и самое название её. Выхолощенная «аристотелевская логика» поэтому и утратила кредит в глазах всех выдающихся естествоиспытателей и философов нового времени. По той же причине большинство философов XVI—XVIII веков вообще избегает употреблять термин «логика» в качестве названия науки о мышлении, об интеллекте, о разуме. Это название не фигурирует вообще в заглавиях выдающихся сочинений о мышлении. Достаточно напомнить «Рассуждение о методе», «Трактат об усовершенствовании интеллекта», «Разыскание истины», «Опыт о человеческом разуме», «Новые опыты о человеческом разуме» и т. д. и т. п.
На основе работ Гегеля Карл Маркс и Фридрих Энгельс сформулировали основные методологические принципы, которые потом В. И. Ленин назвал принципами диалектической логики. Значительное влияние на развитие диалектической логики оказала незаконченная книга Энгельса «Диалектика природы», впервые опубликованная в 1925 году в СССР (двуязычный текст на русском и немецком).
Диалектическая логика была наиболее распространена в социалистических странах, прежде всего СССР, по идеологическим и политическим причинам вырождаясь в догматизм и начётничество по мере ужесточения политического режима[когда?]. Полноценная дискуссия и критика «диалектической логики» стала невозможной.
Значительный вклад в развитие диалектической логики внесли Э. В. Ильенков, В. А. Вазюлин, З. М. Оруджев, И. С. Нарский.
В СССР подчёркивался классовый и партийный характер науки и в том же смысле диалектической логики[a][b][1][2][3], что привело к гонениям на традиционную («формальную», «устаревшую», «метафизическую») логику.[4] После войны эти гонения прекратились, и подчеркивалась совместимость диалектической логики с формальной[5]. В 1954 году во 2-м издании БСЭ в статье «Логика» разъяснялось:
За время своего существования Л. обслуживала потребности разных классов. В этом смысле Л. и её законы не являются классовыми, как не являются классовыми положения грамматики или арифметики. Классовым является то или иное теоретическое истолкование Л. и её законов, например кантианская концепция Л., отрицание Л. фашиствующими идеологами амер. империализма и т. п.
(…) Общечеловеческие законы Л. никем не могут быть нарушены, так как они объективны.
Появилась возможность относительно спокойного развития формальной логики, а также её применения в технических науках. Советские философы в своих работах неоднократно указывали на то, что диалектическая логика не отвергает законы формальной логики. В частности, М. М. Розенталь в 1960 году писал о «мнимом конфликте между диалектической и формальной логикой», обращая внимание на высказывание Энгельса в его работе «Анти-Дюринг»[5]:94—95:
из всей прежней философии самостоятельное значение сохраняет… учение о мышлении и его законах — формальная логика и диалектика.
По мысли М. М. Розенталя, главная задача формальной логики состоит в том, чтобы «быть учением о правильном, непротиворечивом, последовательном мышлении, о логической связи мыслей, о способах логически аргументированного, доказательного мышления». В рассуждениях и о простых, и о сложных предметах нужно следовать правилам формальной логики, «чтобы структура мысли была правильной, чтобы в ней была последовательность, ясность, определённость». В частности, высказывая мысли о каком-либо предмете, следует соблюдать закон тождества. Если же в процессе рассуждения этот закон будет нарушен, и один предмет будет заменён другим, то это лишит нас возможности сделать следующий шаг в познании и «проанализировать данный предмет глубже, с точки зрения его изменчивости, превращаемости, то есть проанализировать его диалектически». Диалектическая логика — это логика развития, изменения[5]:97, 102, 94.
В странах за пределами социалистического лагеря диалектической логикой интересовались только левые интеллектуалы. К. Поппер подверг диалектическую логику критике в своей работе «Что такое диалектика?»
В настоящий момент диалектического направления в логике придерживаются лишь немногие философы, как правило, квазимарксистского, марксистского и постмарксистского толка.
- Вазюлин В. А. Логика «Капитала» К. Маркса. — М., 1968—2002.
- Ильенков Э. В. Диалектическая логика. Очерки истории и теории. — 1984.
- Алексеев М. Н. Диалектическая логика. — М., 1968.
- Андреев И. Д. Диалектическая логика. — М., 1985. — 367 с.
- Астафьев В. К. Законы мышления в формальной и диалектической логике. — Львов, 1968.
- Горский Д. П., Нарский И. С. О функциях и структуре диалектической логики как науки. // Философские науки. 1976. № 1.
- Ведин Ю. П. О предмете диалектической логики. // Философские науки, 1977. № 3.
- Кумпф Ф., Оруджев З. Диалектическая логика. Основные принципы и проблемы. — М., 1979.
- Нарский И. С. Проблема противоречия в диалектической логике. — М., 1969.
- Науменко Л. К. Монизм как принцип диалектической логики. — Алма-Ата, 1968.
- Орлов И. Е. Логика формальная, естественно-научная и диалектическая // Под знаменем марксизма. 1924. № 6—7.
- Оруджев З. М. К. Маркс и диалектическая логика. — Баку, 1964.
- Розенталь М. М. Принципы диалектической логики. — М., 1960.
- Ситковский Е. П. Проблема возникновения новых категорий в диалектической логике. // Вопросы философии. 1975. № 10.
- Солопов Е. Ф. Введение в диалектическую логику. — Л., 1979.
- Шептулин А. П. Диалектическая логика как всеобщая методология познания. В кн.: Актуальные проблемы диалектической логики. — М., 1981.
- Lefebvre H. Logique formelle, logique dialectique. — P., 1969.
- a.^ «В противоположность буржуазной философской историографии, марксизм-ленинизм не рассматривает Логику как вне или надклассовую науку, открыто провозглашая принцип партийности Логики как науки. Борьба партий в философии, ярко выраженная в борьбе материализма с идеализмом, находит своё проявление и в борьбе Логики диалектической с логикой формальной, метафизической»… «Анализируя новый этап мирового развития империализма, научно освещая путь борьбы пролетариата за социалистическую революцию и диктатуру рабочего класса, создавая и развивая великое учение о построении социализма в одной стране, создавая стройную систему взглядов но вопросам стратегии и тактики большевизма, разрабатывая учение о партии пролетариата, подытоживая все научное развитие после Маркса и Энгельса, Ленин и Сталин всесторонне развили и обогатили Логику рабочего класса — диалектический материализм»… «Благодаря выполнению этого основного требования диалектической логики, стратегическая линия поведения рабочего класса и его партии указывает самый верный, наиболее прямой и единственно победоносный путь, ведущий к осуществлению поставленной цели»… «Дальнейшее развитие диалектической Логики, обогащение её новым опытом борьбы со всеми врагами рабочего класса, опытом современного научного развития, опытом международного рабочего движения и строительству социализма в СССР осуществляется т. Сталиным. Понимая диалектическую логику, как и марксизм в целом, творчески, т. Сталин с великим ленинским мастерством разрабатывает все её актуальнейшие проблемы. Весь сложнейший, неизведанный ещё историей до опыта СССР путь к коммунизму товарищ Сталин освещает революционной теорией, диалектической логикой, даст партии и всему народу „уверенность, силу ориентировки и понимание внутренней связи окружающих событий“»… «Развивая революционную диалектическую Логику и беспощадно уничтожая и разоблачая „логику“ современной реакции, т. Сталин учит подходить к каждому явлению всесторонне и конкретно.»[6]
- b.^ «Теоретическое мышление каждой эпохи, писал Энгельс, есть исторический продукт. Будучи таковым, оно неизбежно несет на себе печать классовых интересов и идеалов. Двум противоположным типам мышления соответствуют и две диаметрально противоположные философские теории мышления, две концепции логики. Одна — теория материалистической диалектики как высшей формы мышления, как логика и теория познания современного материализма, в которой Маркс видел логическую основу коммунистического мировоззрения. Другая — позитивистская, имеющая в своем фундаменте идеалистически и метафизически интерпретируемую формальную логику, отождествляемую адептами позитивизма с логикой вообще и аттестуемую как единственно возможная концепция логики XX века.»[7]
- ↑ Э. В. Ильенков. Диалектика абстрактного и конкретного в научно-теоретическом мышлении. М.: Институт философии АН СССР, 1960.
- ↑ 3. M. Оруджев, К. Маркс и диалектическая логика. Баку: АГИ, 1964.
- ↑ Копнин П. В. Диалектика как логика и теория познания. М.: Наука, 1973
- ↑ В. А. Бажанов. Партия и логика. К истории одного судьбоносного постановления ЦК ВКП(б) 1946 года // Логические исследования. Вып. 12. М.: Наука, 2004. С. 32—48.
- ↑ 1 2 3 Розенталь М. М. Принципы диалектической логики. М., Издательство социально-экономической литературы, 1960. — 477 с.
- ↑ Большая Советская Энциклопедия, Т. 37, С. 306, М: ОГИЗ, 1938.
- ↑ Г. Садовский. Логика революционного мышления и классовый подход к логике. // Коммунист, 1979, № 11, С. 63—75.
 ,
,  ,
, 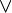 , 0, 1}
, 0, 1} ,унарная)
,унарная)