Функции задачи: «В чем разница между функциями и задачами?» – Яндекс.Кью – Чем отличаются задачи от функций

Чем отличаются задачи от функций

Давно подмечено, что успеха добивается лишь тот, кто знает, к чему стремится и что делает. Для реализации своих целей необходимо успешно выполнять поставленные задачи и знать заданные функции. Тождественны ли данные понятия или между ними есть какая-то разница? Почему так важно знать точное значение указанных категорий и чем грозит их подмена и путаница?

Определение

Задача – это проблема, требующая разрешения с помощью имеющихся средств, поручение, которое нуждается в исполнении к указанному сроку. В её качестве может выступать любой вопрос, стоящий перед человеком, будь то сложная научная проблема (лекарство против рака) или относительно небольшая трудность (строительство дороги). Исполнитель ограничен тем набором ресурсов, который имеется у него в распоряжении.

Функция – деятельность человека или механизма, направленная на достижение определённого результата, роль и предназначение объекта внутри отдельной системы. Каждая вещь обладает определённой функцией: орудия труда служат для производства и обработки продуктов, предметы искусства – для удовлетворения эстетических запросов, компьютеры – для сбора и хранения информации.

к содержанию ↑

Сравнение

В чем же разница между функцией и задачей? Итак, как задачи, так и функции ставятся человеку либо лидером, управленцем, либо самостоятельно. Однако категории различаются между собой по конечному результату, который должен достигнуть человек. Функция выполняется постоянно или периодически (доставка воды к жилым домам), и измерить результат можно лишь в определённую единицу времени. Задачи имеют совершенно другое качество: у каждой из них либо есть конкретное решение (одно или несколько), либо оно отсутствует (неразрешимая проблема).

Выполнять определённую функцию может как человек (ремонт теплотрассы, настройка доступа в интернет), так и механизм, программа (проверка целостности трубопровода, очистка воды). Задача всегда стоит перед существом, наделённым сознанием, для её решения необходимо использовать знания или опыт. Неодушевлённые предметы и механизмы выполняют рутинные задачи, только осуществляя свои функции.

Задача состоит из таких обязательных элементов, как спорная ситуация, проблема и решение. Если ответить на поставленный вызов не представляется возможным, он считается неразрешимым. Функция – это процесс, который включает в себя правила, алгоритм действий и ожидаемый результат. Нарушение заданной последовательности сделает реализацию невозможной. Задача может достигаться различными способами, в том числе и новыми путями.

При этом для реализации задач и выполнения функций требуются ресурсы (материальные, трудовые), которые могут быть достаточными, недостаточными или избыточными. Свобода действия исполнителя  ограничена определёнными правилами, нарушение которых влечёт негативные последствия. Задачи и функции необходимы для достижения глобальных целей, поставленных перед человеком, рабочей группой, обществом.

к содержанию ↑

Выводы TheDifference.ru

1. Результат. У задачи есть конкретное решение, в то время как у функции – нет, и она должна выполняться постоянно.
2. Соотношение. Понятие «задача» является предельно широким: для реализации одной цели может использоваться несколько функций.
3. Исполнитель. Решать задачу может только существо, наделённое разумом, выполнять функцию – любой механизм.
4. Иерархия. Функции служат для реализации задач, поставленных перед человеком и обществом.
5. Состав. Задача включает в себя фабулу (описание ситуации), проблему и решение. Функция – алгоритм действий и результат.

Задачи, функции

Задачи

ГКУ «ЦОА Москвы» создано для выполнения работ, оказания услуг в целях обеспечения реализации предусмотренных федеральными законами, законами города Москвы, нормативными правовыми актами Правительства Москвы, полномочий города Москвы в сфере архивного дела.

Цели

Основными целями деятельности ГКУ «ЦОА Москвы» являются:

1. Осуществление мероприятий по хранению, учету, комплектованию, созданию справочно-поисковых систем и использованию относящихся к собственности субъекта Российской Федерации — города Москвы архивных документов по личному составу, образовавшимися в процессе деятельности государственных образовательных учреждений города Москвы, государственных учреждений жилищно-коммунального хозяйства города Москвы.

2. Рассмотрение и согласование на Экспертно-проверочной комиссии Учреждения описей дел по личному составу государственных образовательных учреждений города Москвы, государственных учреждений жилищно-коммунального хозяйства города Москвы.

Основные функции ГКУ «ЦОА Москвы»

1. Комплектование Учреждения документами в соответствии с основными целями деятельности Учреждения.

2. Формирование и ведение списка организаций-источников комплектования Учреждения в соответствии с основными целями деятельности Учреждения.

3. Организация приема на хранение в Учреждение в упорядоченном состоянии документов от организаций-источников комплектования Учреждения.

4. Осуществление комплекса мероприятий по обеспечению сохранности архивных документов, в том числе соблюдение нормативных режимов хранения (противопожарного, охранного, температурно­влажностного, светового, санитарно-гигиенического) в зданиях и помещениях Учреждения, обеспечение оптимальной организации хранения.

5. Проведение в установленном порядке проверок наличия и состояния архивных документов.

6. Организация и ведение учета документов, хранящихся в Учреждении.

7. Оказание методической помощи организациям-источникам комплектования Учреждения по вопросам проведения экспертизы ценности документов, упорядочения и передачи на хранение документов.

8. Проведение научного описания архивных документов, поступивших в Учреждение в неупорядоченном виде.

9. Создание, совершенствование и пополнение научно-справочного аппарата к хранящимся в Учреждении документам.

10. Внедрение в практику работы Учреждения современных средств хранения, поиска, копирования и использования документов с применением средств электронно-вычислительной техники.

11. Предоставление государственной услуги «Исполнение социально-правовых запросов граждан, связанных с подготовкой и предоставлением архивной справки, архивной выписки, архивной копии и информационного письма по архивным документам, хранящимся в подведомственных Главному архивному управлению города Москвы архивных учреждениях» в соответствии с федеральным законодательством и правовыми актами города Москвы.

12. Исполнение в установленном порядке запросов органов государственной власти и местного самоуправления, относящихся к сфере их деятельности, путем подготовки архивных справок установленного образца, архивных копий, архивных выписок, информационных писем.

13. Исполнение в установленном порядке социально-правовых запросов граждан Российской Федерации (их законных представителей), связанных с социальной защитой граждан, предусматривающей их пенсионное обеспечение, а также получение льгот и компенсаций в соответствии с законодательством Российской Федерации, путем подготовки архивных справок установленного образца, архивных копий, архивных выписок, информационных писем.

14. Исполнение тематических запросов физических и юридических лиц.

15. Информационное обеспечение органов государственной власти, органов местного самоуправления, других заинтересованных организаций и физических лиц о составе и содержании документов, хранящихся в Учреждении. Выдача архивных документов в установленном порядке во временное пользование судебным, правоохранительным и иным уполномоченным органам, организациям и физическим лицам.

16. Участие в подготовке документальных выставок и публикаций документов, организуемых и проводимых Учредителем.

17. Участие в работе государственных информационных систем города Москвы.

Задачи, функции

Основные задачи и функции

ГБУ «ЦГА Москвы» в соответствии с его уставом

Задачи: комплектование, постоянное хранение и учет документов Архивного фонда Москвы, являющегося составной частью Архивного фонда Российской Федерации, создание справочно-поисковых средств и использование архивных документов.

В соответствии с указанными задачами архив в установленном порядке осуществляет следующие функции:

‑ постоянное хранение управленческих документов, документов личного происхождения, научно-технической документации, электронных и аудиовизуальных документов, включенных в состав Архивного фонда Москвы;

‑ учет документов, хранящихся в архиве;

‑ работу с организациями и гражданами – источниками комплектования архива, представление на утверждение и согласование ЦЭПК Главархива Москвы описей дел постоянного хранения и по личному составу организаций – источников комплектования архива, прием на хранение документов Архивного фонда Москвы;

‑ научное описание документов, принятых в архив в неупорядоченном виде;

‑ создание и совершенствование справочно-поисковых средств к архивным документам;

‑ предоставление государственной услуги «Исполнение социально-правовых запросов граждан, связанных с подготовкой и представлением архивной справки, архивной выписки, архивной копии и информационного письма по архивным документам, хранящимся в архиве»;

‑ исполнение запросов органов государственной власти и местного самоуправления, организаций и граждан;

‑ предоставление пользователям архивных документов и печатных изданий для изучения в читальном зале, обеспечение доступа к справочно-поисковым средствам архива;

‑ представление информации о деятельности архива для размещения в сети Интернет;

‑ работу по рассекречиванию архивных документов;

‑ научно-исследовательскую и методическую работу по профильной проблематике, подготовку публикаций архивных документов, путеводителей и других архивных справочников, научно-популярной и учебной литературы;

‑ подготовку выставок на основе архивных документов;

‑ другие виды деятельности по популяризации архивных документов.

Архив на платной основе оказывает услуги по исполнению тематических и генеалогических запросов, копированию документов, хранящихся в архиве, и др.

Функции задач в обучении математике

В данной работе нам хотелось бы рассмотреть вопрос о функциях задач, разделенных нами на три основных категории: обучающих, воспитывающих и развивающих.

Под обучающими функциями задач будем понимать такие функции, которые направлены на формирование системы математических знаний, умений, навыков у обучающихся (как предусмотренных программой, так и расширяющих и углубляющих ее содержание) на различных этапах ее усвоения. Обучающие функции задач можно подразделить на функции общего характера, специального и конкретного характера. Под общими обучающими функциями понимаются такие функции задач, которые имеют место не только в ходе обучения математике, но и всем предметам естественно-математического цикла. Под специальными функциями математических задач понимаются функции общего характера, соотнесенные только к обучению математике. Под конкретными функциями задач будем понимать частные виды специальных функций. Ограничимся одним примером. Формирование у учащихся некоторого понятия (на уровне представлений о нем) — общеобучающая функция; формирование представления о натуральном числе — специальная обучающая функция; формирование представления о числе нуль конкретная обучающая функция.

К числу общих обучающих функций задач относятся:

1)      Формирование у учащихся некоторого понятия (на уровне представлений о нем, на уровне его усвоения и на уровне закрепления).

2)      Установление различных связей между понятиями (от рода к виду, внутри предметные и межпредметные связи и т. д.).

3)      Формирование описания, определения понятия; подведение объекта под понятие.

4)      Формирование ведущих идей, законов, суждений.

5)      Установление различных связей между ведущими идеями,. законами, суждениями; структурных соотношений между ними, иерархии.

6)      Формирование основных видов умозаключений, способов и приемов их проведения.

7)      Формирование ведущих умений и навыков, характерных для данного учебного предмета.

8)      Формирование умений и навыков выражения мысли в речи и записи.

9)      Формирование умений и навыков моделирования учебного материала (чертежи, графики и т. п.).

10)  Формирование умений и навыков в обращении с приборами, инструментами, таблицами, с учебной и справочной литературой

В процессе обучения математике, наряду с образовательными целями, должны реализовываться и определенные воспитательные цели. Известно, что обучение воспитывает прежде всего своим содержанием — фактами и их истолкованием. Главное состоит в том, чтобы планомерно использовать изучаемый материал, сам процесс учения, и в частности процесс решения задач для воспитания у учащихся устойчивых взглядов и убеждений. Эта общая цель воспитания реализуется на уроках математики различными путями. Итак, под воспитывающими функциями задач будем понимать функции, которые направлены на формирование нравственных качеств учащихся. В отличие от обучающих функций задач их воспитывающие функции, на наш взгляд, можно подразделить лишь на функции общего и специального характера. К числу общих воспитывающих функций задач относятся:

1)        Формирование у школьников высокой степени сознательности, чувства ответственности перед обществом, социальной активности, оптимизма и гуманистической направленности.

2)        Воспитание у школьников чувства товарищества, взаимопомощи, творческой инициативы, дисциплинированности и организованности.

3)        Эстетическое воспитание учащихся (формирование чувства прекрасного, вкуса к прекрасному, потребности, желания и способности преобразовать окружающий мир и строить человеческие отношения по законам красоты, стремление пополнить свой запас художественных и эстетических знаний и т. д.).

4)        Воспитание положительного отношения школьника к учебной деятельности, развитие интереса к учебе, любознательности.

5)        Формирование умений рационализировать свою учебную работу и приемы ее оформления; воспитание способности доводить любое учебное задание до конца; формирование критичности в оценке результатов своей работы, наряду с чувством уверенности в правильности ее выполнения.

Наконец, под развивающими функциями задач будем понимать такие их функции, которые направлены на развитие мышления учащихся, на формирование качеств, присущих научному мышлению, на овладение приемами эффективной умственной деятельности. Такие функции делятся на общие и конкретные. К специальным развивающим функциям математических задач могут быть отнесены, например, следующие:

1)        Умение математизировать простейшие ситуации жизненного характера, усматривать математические закономерности в окружающем мире.

2)        Умение предсказать (предположить существование того или иного факта или свойства, относящегося к математическим объектам с достаточной степенью правдоподобия).

3)        Умение доказать или опровергнуть то или иное математическое положение дедуктивным путем.

4)        Умение планировать поиск решения задачи, исключить из условия ненужные данные, дополнять недостающие, отбирать методы, средства и операции, необходимые для ее решения, умение осуществить проверку правильности решения.

5)        Иметь четкое представление о логической структуре курса математики, о том, что абстрактный характер математики является основной причиной ее многочисленных приложений в других науках, в технике, в народном хозяйстве.

6)        Умение формулировать определения математических понятий и умение соотнести то или иное понятие с данным определением.

7)        Умение быстро и правильно проводить вычисления с привлечением простейших вычислительных средств для облегчения исчисления на соответствующем его этапе; умение создать на основе теоретических знаний удобную вычислительную ситуацию, осуществлять проверку и прикидку правильности вычислений.

8)        Умение распознавать то или иное математическое понятие в различных ситуациях.

9)        Умение проводить исследование в простейших учебных ситуациях.

В качестве примера общих специальных и конкретных развивающих функций задач рассмотрим следующую функцию. Развить способности учащихся к обобщению изученного — общая развивающая функция; развитие способности обобщить то или иное геометрическое понятие — специальная развивающая функция; формирование способности усмотреть обобщение понятий симметрии, вращения и параллельного переноса в понятии перемещения конкретная развивающая функция задач.

Литература:

1.        Буркина В. А., Титова Е. И. Методика работы с аномальными задачами// Молодой ученый. 2014. № 2 (61). С. 740–741.

2.        Ермолаева Е. И. Систематизация математических знаний у студентов строительных специальностей в рамках модульного обучения// Наука и школа. 2008. № 1. С. 33–37.

3.        Титова Е. И., Чапрасова А. В. Различные трактовки понятия «задача» и методика их решения// Молодой ученый. 2014. № 6 (65). С. 760–762.

Урок 13. Построение и преобразование графиков функций. Обзор графиков основных функций. Практика

Подготовка к ЕГЭ по математике 

Эксперимент 

Урок 13. Построение и преобразование графиков функций. Обзор графиков основных функций 

Практика

Конспект урока

Сначала разберем примеры на построение графиков основных функций.

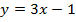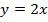Задача №1. Построить графики функций: а) ; б) ; в) ; г) .

Решение. Воспользуемся методом построения линейных функций «по точкам».

а)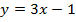

0	-1
1	2

Как видим, 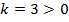 и угол наклона к оси  острый,  смещение по оси .

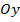б)

0	2
1	1

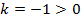 и 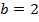 можно сделать аналогичные выводы, как и в первом пункте.

в)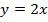

0	0
1	2

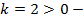 угол наклона к оси острый,  график проходит через начало координат.

г)

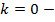 константная функция, прямая проходит через точку  и параллельно оси .

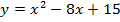Задача №2. Построить графики функций: а) ; б) ; в) .

Решение. Воспользуемся методом построения квадратичных функций «по вершине».

а)

 ветки параболы направлены вверх, .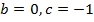

 

Если возникает вопрос, как точно строится парабола, т.е. с какой именно скоростью растут и убывают ее ветки, то можно запомнить следующий факт: если старший коэффициент  или , как это часто бывает, то при смещении от иксовой координаты вершины на единицу влево или вправо значение функции сначала изменяется на 1, потом на 3, затем на 5 и т.д., т.е. на нечетные числа.

Например, в нашем графике:

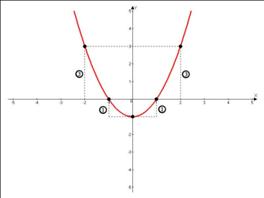
Для функций, у которых старший коэффициент 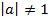, значения изменений функции умножаются на это «». Например, построение функции  выглядит так:

Но, как правило такая точность построения не важна, а нужен только эскиз графика, поэтому в дальнейшем мы не будем это учитывать.

б)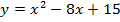

 ветки параболы направлены вверх, .

 

в)

 ветки параболы направлены вниз, .

 

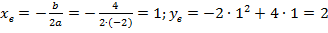
Кстати, график проходит через ноль, что легко проверить подстановкой в функцию точки 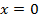 или обратив внимание на то, что .

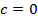Задача №3. Построить графики функций: а) ; б) ; в) .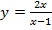

Решение. Воспользуемся нашим методом построения дробно-рациональных функций «по асимптотам».

а)

Вертикальная асимптота определяется решением уравнения, которое показывает, что знаменатель дроби равен нулю: .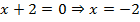

Горизонтальную асимптоту определим по тому быстрому способу, который мы указали в лекции. Она определяется отношением коэффициентов при иксах в числителе и знаменателе: .

Для определения расположения веток гиперболы подставим в функцию любую точку из области определения, т.е. кроме, например, 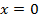: 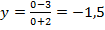, т.е. координаты этой точки  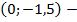через нее и проведем одну ветку гиперболы, вторая будет располагаться наискось.

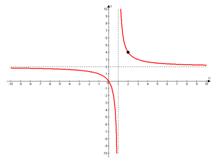
Теперь строим гиперболу, прижимая ее к асимптотам:

Остальные пункты строим аналогично.

б)

Вертикальная асимптота: .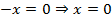

Горизонтальная асимптота: , т.е. асимптотами являются оси координат.

Проверочная точка: .

в)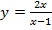

Вертикальная асимптота: .

Горизонтальная асимптота: .

Проверочная точка: .

Задача №4. Построить графики функций: а) , б) , в) .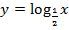

Решение. По сути дела, указаны функции, которые не имеют особых методов построения их графиков. Поэтому если необходимо изобразить их эскиз, то просто вспоминаем теорию, а если необходимо построить графики более точно, то следует подставить несколько контрольных точек, так и поступим.

а)

Подставим полные квадраты, чтобы вычислить из них целые значения корня.

0	0
1	1
4	2

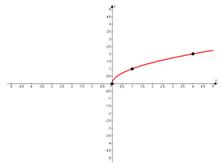
б)

Подставим несколько значений и учтем общий вид графика.

0	1
1	3
2	9

Т.к. основание степени , то функция растет.

в)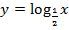

Подставим такие значения аргумента, при которых значения логарифма будут целыми. При построении учтем общий вид графика.

Т.к. основание логарифма , то функция убывает.

 

 

Теперь давайте попробуем научиться решать обратную задачу – по изображенному графику исследовать функцию.

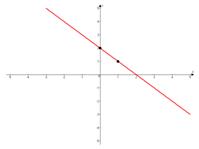
Задача №5. По виду графика определить знаки коэффициентов общего вида функции :

а)

б)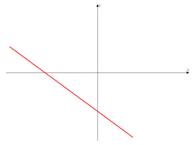

в)

г)

Решение. Для определения знаков коэффициентов  и  вспомним, как от них зависят формы графиков.

а) Острый угол наклона прямой к оси 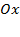 (функция возрастает) – это . Точка пересечения с осью 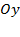 — это .

Далее аналогичные рассуждения.

б)

в)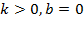

г) Константная функция, т.к. график параллелен оси 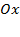, т.е. 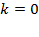, а .

Задача №6. По виду графика определить знаки коэффициентов общего вида функции :

а)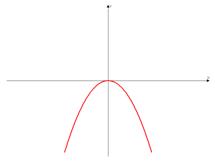

б)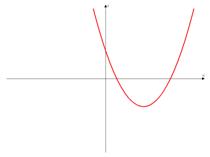

в)

Решение. Вспомним, как параметры  и  определяют положение параболы.

а) Ветви вниз, следовательно, .

Точка пересечения с осью .

Иксовая координата вершины .

б) Ветви вверх, следовательно, .

Точка пересечения с осью .

Иксовая координата вершины , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, .

в) Ветви вниз, следовательно, .

Точка пересечения с осью .

Иксовая координата вершины 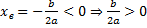, т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, .

И теперь переходим к рассмотрению примеров на преобразование графиков функций.

Задача №7. Построить графики функций: а) ; б) ; в) ; г) ; д) .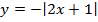

Решение. Когда сложная функция получена из простейшей путем нескольких преобразований, то преобразования графиков выполняются в порядке арифметических действий с аргументом, например, умножение идет до сложения и т.п.

а)

Преобразование в одно действие типа .

Сдвигаем график вверх на 1:

б)

Преобразование в одно действие типа .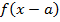

Сдвигаем график вправо на 1:

в)

В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках 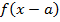, затем сложение .

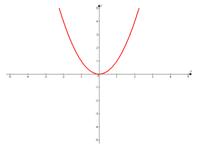
Сдвигаем график вправо на 1:

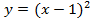
Сдвигаем график вверх на 2:

Конечно же, можно построить эту функцию как квадратичную после раскрывания скобок. Проверьте

В чем разница между функциями и задачами?

При движении к цели всегда важно определиться со стоящими на пути задачами и с функциями, которые при этом необходимо осуществлять. Это важно и в случае построения бизнес-стратегии, и при выполнении повседневной работы, и даже в обычной семейной жизни. Цель – это желаемый финальный результат. Но не все понимают, что такое задачи, а что такое функции. Для полноценного планирования целей и путей их достижения стоит разобраться с этими категориями.

Что такое функции?

В первую очередь, это набор возможных действий, которые будет выполнять человек (или предмет) при тех или иных обстоятельствах. То есть, упрощенно говоря, это его роль при движении к желаемому итогу.

Если рассматривать функции человека в привязке к его трудовой деятельности, то они могут быть включены в должностную инструкцию работника. То есть это те действия, которые он выполняет ежедневно и у которых есть заведомо прогнозируемый результат. Но перечень данных действий может измениться, если меняются текущие задачи.

В качестве примера функционала в повседневной жизни можно рассмотреть роль матери, которая ежедневно ухаживает за маленьким ребенком: она его кормит, водит на прогулку, одевает и т.п. Все это и есть функции.

При определении функции не ставится вопрос «для чего это делается», а определяется набор действий, которые должны быть выполнены. Ее элементами являются:

• Установленные правила.
• Разработанный алгоритм.
• Ожидаемый результат.

Это понятие относится не только к человеку, но и к любой вещи, ведь каждая из них функциональна. Ложка необходима, что бы есть пищу, картина нужна для эстетического удовольствия. Нет вещей, которые были бы абсолютно бесполезны и неприменимы.

Что такое задачи?

Для достижения цели обязательно они ставятся в обязательном порядке (одна или несколько). Это пути решения проблемных ситуаций, средство для достижения замысла. Они отвечают на вопрос «как это сделать». Если чтобы добиться цели необходимо выполнить только одну задачу, то эти понятия могут сливаться.

Задача может быть поставлена исключительно перед человеком, поскольку ее выполнение требует осмысленной деятельности, определенных знаний. Ставятся они либо руководящим лицом, либо исполнителем для себя самостоятельно. Могут быть текущими, оперативными или ключевыми.

Элементами рассматриваемого понятия являются:

• Спорная ситуация.
• Проблема.
• Решение проблемы.

В случае, когда решения найти не удается, задачи относят к категории неразрешимых.

Если рассмотреть задачи на примере организации бизнеса, то это могут быть: увеличение дохода (ключевая), увеличение клиентской базы (текущая), своевременное предоставление документов на запрос контролирующих органов (оперативная) и т.п.

В случае с воспитывающей ребенка матерью примерами являются: воспитание хорошего, доброго человека (глобальная), поддержание здоровья малыша (текущая), организация незапланированного праздника (оперативная).

Существует интересный и простой способ определения приоритетности задач – это матрица Эйзенхауэра. С ее помощью легко четко выделить, что на данный момент является важным и срочным, а что можно отложить на потом, а возможно и вовсе исключить из своего списка без ущерба.

Общее между задачами и функциями

1. Во-первых, выполнение и тех, и других необходимо для достижения цели.
2. Во-вторых, применительно к человеческой деятельности, они могут определяться в разных ситуациях либо руководителем, либо непосредственно выполняющим их человеком.
3. В-третьих, эти категории могут меняться в зависимости от внешних обстоятельств.
4. В-четвертых, для их реализации всегда необходимы ресурсы (например, материальные, трудовые, информационные), от достаточности которых будет зависеть конечный итог.

Основные различия

Рассматриваемые категории отличны по результату. У задачи всегда есть конкретное решение (за исключением неразрешимых), конечная точка, когда результат можно считать достигнутым или недостигнутым. Функция же выполняется постоянно. Разрешение первых, как правило, ограничено конкретными сроками, а вторые, в связи со своей постоянностью, временными рамками ограничены достаточно смутно.

Понятие «задача» шире понятия «функция». Для решения задачи всегда необходимо будет выполнить ряд функций. При выполнении первых допустим творческий подход, поиск новых путей, для вторых существует регламентированных алгоритм и всегда известно какой результат должен быть достигнут. Для первых существуют приоритеты, для вторых — нет.

Следующее различие в том, что задачу может выполнить только человек, а функции помимо человека присущи, в том числе, любой вещи.

Если человек, стремясь достичь цели, выполняет только определенные функции, которые присущи его обычной жизни, и не выделяет при этом четких задач, то желаемого итога он может и не добиться. Например, цель – получить повышение по работе. Если продолжать работать на прежней должности без какой-либо стратеги, то такое повышение вряд ли произойдет, если только в силу внешних обстоятельств. Если же поставить конкретные задачи (повысить квалификацию, провести беседу с руководителем, презентовать новый проект и т.п.), то желаемый финал уже будет не призрачным, а приобретет конкретные очертания.

Даже не зная рассмотренных различий, практически все современные люди вырабатывают в себе навыки планирования жизни. Но, имея представление о данной структуре, гораздо проще понять принципы построения пути у своей цели.

Задачи, функции и роль функций менеджмента

Понятие, состав и роль функций менеджмента

Содержание процесса управления можно рассматривать посредством его функций, под которыми понимается система общих задач менеджмента.

Определение 1

Функция управления (менеджмента) — обособленное, относительно однородное направление в сфере осуществления управленческой деятельности, которое составляет процесс менеджмента.

Функции менеджмента разделяются по двум направлениям:

• основные функции, осуществляемые в соответствии с содержанием процесса управления;
• специфические (конкретные) функции, которые осуществляются в соответствии с направлением воздействия в сторону объектов управления.

В управлении различают пять основных функций менеджмента:

1. Планирование, которое представляет собой прогноз и подготовку к будущему.
2. Организация, в процессе которой происходит обеспечение предприятия всем необходимым для эффективного функционирования (оборудованием, материалами, финансирование, персоналом).
3. Мотивация, заключающаяся в средствах выполнения организационной работы.
4. Координация в качестве гармонизации деятельности для достижения поставленных целей.
5. Контроль в виде проверки и надзора за всем происходящим на предприятии.

Цели и задачи функций управления

Процесс управления в соответствии с выполняемыми функциями берет свое начало с постановки системы целей и задач деятельности компании на соответствующий промежуток времени.

В процессе планирования определяется система целей функционирования и развития предприятия, а также пути и средства их достижения.

С помощью планирования решения принимаются своевременно, что дает возможность избежать поспешности в их реализации, установить четкие связи и способы их реализации, а также производить контроль ситуации.

Целью организации как функции является создание структуры компании, дающей возможность коллективу эффективно работать совместно для достижения ее целей.

В процессе осуществления функции организация, происходит решение следующих задач:

• Разделение компании на подразделения в соответствии с целями и стратегиями.
• Делегирование полномочий.

Важной задачей при обеспечении эффективной организации является организация потоков информации, которая должна быть достаточной, но не излишней.

Мотивация имеет своей задачей побудить себя и других к деятельности с целью достижения личных результатов или планов предприятия.

Координация действий работников может происходить при подготовке документов (плана, приказа, отчёта, предложения, которые направляются в другие организации, ответы на распоряжения и запросы властей).

В процессе координации решаются задачи по формулированию и донесению до всех сотрудников целей предприятия, а также до каждого его подразделения в связи с общими целями.

При осуществлении контроля происходит обеспечение достижения целей предприятии. Контроль нужен, что бы обнаружить или разрешить возникающие проблемы своевременно, пока они не станут чрезвычайно серьезными, ее можно использовать в качестве стимулирования успешной деятельности.

В процессе контроля происходит постановка стандартов, изменение фактических и достигнутых результатов и проведение корректировки в тех случаях, если достигнутый результат значительно отличается от установленного стандарта.

Замечание 1

Важной целью контроля, которую следует учитывать первостепенно, является то, что он должен быть всеобъемлющим.

Все менеджеры, независимо от уровня управления, должны производить контроль в качестве неотъемлемой части своих должностных обязанностей, даже если на это не было дано особого поручения.

Основными видами контроля являются предварительный, текущий и заключительный.