« Основные свойства функции. » – Яндекс.Кью
К основным свойствам функции относятся:
- Четность и нечетность функции
Функция называется четной, если
– область определения функции симметрична относительно нуля
– для любого х из области определения f(-x) = f(x)
!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image003.gif
График четной функции симметричен относительно оси 0y
Функция называется нечетной, если
– область определения функции симметрична относительно нуля
– для любого х из области определения f(-x) = –f(x)
!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image004.gif
График нечетной функции симметричен относительно начала координат.
2.Периодичность
Функция f(x) называется периодической с периодом !https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image005.gif, если для любого х из области определения f(x) = f(x+Т) = f(x-Т).
!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image006.gif
График периодической функции состоит из неограниченно повторяющихся одинаковых фрагментов.
- Монотонность (возрастание, убывание)
Функция f(x) возрастает на множестве Р , если для любых x1 и x2 из этого множества, таких, что x1 < x2 выполнено неравенство f(x1)< f(x2).
!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image011.gif
Функция f(x) убывает на множестве Р , если для любых x1 и x2 из этого множества, таких, что x1 < x2 выполнено неравенство f(x1) > f(x2).
!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image013.gif
- Экстремумы
Точка Хmax называется точкой максимума функции f(x) , если для всех х из некоторой окрестности Хmax , выполнено неравенство f(х)!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image014.gif f(Xmax).
Значение Ymax=f(Xmax) называется максимумом этой функции.
!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image015.gif
Хmax – точка максимума
Уmax – максимум
Точка Хmin называется точкой минимума функции f(x) , если для всех х из некоторой окрестности Хmin , выполнено неравенство f(х)!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image016.gif f(Xmin).
Значение Ymin=f(Xmin) называется минимумом этой функции.
!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image017.gif
Xmin – точка минимума
Ymin – минимум
Xmin, Хmax – точки экстремума
Ymin, Уmax – экстремумы.
- Нули функции
Нулем функции y = f(x) называется такое значение аргумента х , при котором функция обращается в нуль: f(x) = 0.
!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image018.gif
Х1,Х2,Х3 – нули функции y = f(x).
Функция (математика) — Википедия
У этого термина существуют и другие значения, см. функция.
График функцииf(x)=(4×3−6×2+1)x+13−x{\displaystyle {\begin{aligned}&\scriptstyle \\&\textstyle f(x)={\frac {(4x^{3}-6x^{2}+1){\sqrt {x+1}}}{3-x}}\end{aligned}}}.
Фу́нкция (отображе́ние, опера́тор, преобразова́ние) — в математике соответствие между элементами двух множеств, установленное по такому правилу, что каждому элементу первого множества соответствует один и только один элемент второго множества.
Математическое понятие функции выражает интуитивное представление о том, как одна величина полностью определяет значение другой величины. Так, значение переменной x{\displaystyle x} однозначно определяет значение выражения x2{\displaystyle x^{2}}, также значение месяца однозначно определяет значение следующего за ним месяца. Другой пример функции: каждому человеку можно однозначно поставить в соответствие его биологическую мать.
Аналогично, задуманный заранее алгоритм по значению входного данного выдаёт значение выходного данного.
Часто под термином «функция» понимается числовая функция, то есть функция, которая ставит одни числа в соответствие другим. Эти функции удобно представлять в виде графиков.
Термин «функция» (в некотором более узком смысле) был впервые использован Лейбницем (1692 год). В свою очередь, Иоганн Бернулли в письме к тому же Лейбницу употребил этот термин в смысле, более близком к современному[1][2].
Первоначально понятие функции было неотличимо от понятия аналитического представления. Впоследствии появилось определение функции, данное Эйлером (1751 год), затем — у Лакруа (1806 год), — уже практически в современном виде. Наконец, общее определение функции (в современной форме, но для числовых функций) было дано Лобачевским (1834 год) и Дирихле (1837 год)
К концу XIX века понятие функции переросло рамки числовых систем. Сначала понятие функции было распространено на векторные функции, вскоре Фреге ввёл логические функции (1879), а после появления теории множеств Дедекинд (1887) и Пеано (1911) сформулировали современное универсальное определение[2].
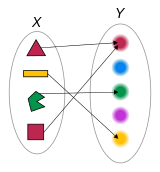Функция, сопоставляющая каждой из четырёх фигур её цвет.Наиболее строгим является теоретико-множественное определение функции (на основе понятия бинарного отношения). Часто вместо определения функции даётся понятие функции, то есть описание математического объекта с помощью понятий обычного языка, таких как «закон», «правило» или «соответствие».
Понятие функции[править | править код]
Говорят, что на множестве X{\displaystyle X} имеется функция (отображение, операция, оператор) f{\displaystyle f} со значениями из множества Y{\displaystyle Y}, если каждому элементу x{\displaystyle x} из множества X{\displaystyle X} по правилу f{\displaystyle f} поставлен в соответствие некоторый элемент y{\displaystyle y} из множества Y{\displaystyle Y}[1].
Говорят также, что функция f{\displaystyle f} отображает множество X{\displaystyle X} в множество Y{\displaystyle Y}. Функцию обозначают также записью y=f(x){\displaystyle y=f(x)}.
Если используется термин оператор, то говорят, что оператор f{\displaystyle f} действует из множества X{\displaystyle X} в множество Y{\displaystyle Y} и добавляют запись y=fx{\displaystyle y=fx}.
Если хотят подчеркнуть, что правило соответствия считается известным, то говорят, что на множестве X{\displaystyle X} задана функция f{\displaystyle f}, принимающая значения из Y{\displaystyle Y}. Если функция f{\displaystyle f} должна находиться в результате решения какого-нибудь уравнения, то говорят, что f{\displaystyle f} — неизвестная или неявно заданная функция. Но в любом случае, функция, по смыслу этого понятия, считается заданной, хотя и косвенно.
Заметим, что в формулировке понятия функции требование соответствия «по правилу» является повтором, поскольку оно содержится в понятии однозначного соответствия. Формулировка понятия функции без понятия правило и необходимости его обозначать:
Говорят, что на множестве X{\displaystyle X} задана функция f{\displaystyle f}, принимающая значения из Y{\displaystyle Y}, если каждому элементу x{\displaystyle x} из множества X{\displaystyle X} поставлен в соответствие некоторый элемент y{\displaystyle y} из множества Y{\displaystyle Y}
Например, функция, заданная на X{\displaystyle X} таблицей пар элементов x{\displaystyle x} и y{\displaystyle y}, содержит и правило соответствия для каждого элемента из X{\displaystyle X}, поскольку значения функции при переходе от элемента к элементу множества X{\displaystyle X} располагаются по вполне определенному правилу.
Для числовых функций, часто задаваемых формулами, понятие функции формулируется как соответствие между элементами множеств посредством правила. Правило не обозначается, чтобы избежать совпадения обозначений правила и функции:
Если каждому элементу x{\displaystyle x} из множества X{\displaystyle X} по какому-либо правилу ставится в соответствие некоторый элемент y{\displaystyle y} из множества Y{\displaystyle Y}, то указанное соответствие называется функцией y=f(x){\displaystyle y=f(x)}, заданной на множестве X{\displaystyle X} со значениями из Y{\displaystyle Y}[3][5].
Буква f{\displaystyle f} в этом обозначении — индивидуальный знак функции.
Итак, функция y=f(x){\displaystyle y=f(x)} (или кратко: функция f(x){\displaystyle f(x)} или f{\displaystyle f}) представляет собой
Обозначенный буквой x{\displaystyle x} каждый элемент множества X{\displaystyle X} называется независимой переменной или аргументом функции. Множество X{\displaystyle X} при этом называется областью изменения переменной x{\displaystyle x}.
Элемент y{\displaystyle y}, соответствующий фиксированному элементу x{\displaystyle x} называется частным значением функции в точке x{\displaystyle x}.
Совокупность всех частных значений y{\displaystyle y}, обозначаемая символом {y}{\displaystyle \{y\}}, называется множеством значений функции.
Теоретико-множественное определение[править | править код]
Понятие множества упорядоченных пар (отношения) позволяет исключить из формулировки понятия функции не только понятие правило, но и понятие соответствие, к которому сводится понятие функции в обычных формулировках предыдущего подраздела.
Таким образом, для функции можно сформулировать определение, использующее только начальные математические понятия:
- Функцией f{\displaystyle f} называется множество упорядоченных пар (x,y)∈X×Y{\displaystyle (x,y)\in X\times Y}, таких, что пары существуют для всех элементов множества X{\displaystyle X}, и, если первые элементы пар совпадают, то совпадают и вторые их элементы[1].
При этом:
Функции f{\displaystyle f} и g{\displaystyle g} называются равными, если их графики совпадают
Поскольку равенство функций (в любой формулировке понятия функции) включает в себя не только совпадение правил соответствия между элементами множеств, но и совпадение областей задания, то функции f1(x)=x:R→R{\displaystyle f_{1}(x)=x:\mathbb {R} \to \mathbb {R} } и f2(x)=x:R+→R{\displaystyle f_{2}(x)=x:\mathbb {R} ^{+}\to \mathbb {R} }, где R{\displaystyle \mathbb {R} } — множество вещественных чисел, а R+{\displaystyle \mathbb {R} ^{+}} — множество положительных вещественных чисел, являются разными функциями.
Более общим, включающим в себя не только однозначные функции, является следующее определение функции:
Функцией f{\displaystyle f} называется любое множество упорядоченных пар (x,y)∈X×Y{\displaystyle (x,y)\in X\times Y}[1][нет в источнике].
При этом:
- Множество X{\displaystyle X} называется областью отправления функции. Множество всех элементов x∈X{\displaystyle x\in X}, для которых существует пара (x,y)∈f{\displaystyle (x,y)\in f}, называется областью задания функции;
- множество Y{\displaystyle Y} называется областью прибытия функции. Множество всех элементов y∈Y{\displaystyle y\in Y}, для которых существует пара (x,y)∈f{\displaystyle (x,y)\in f}, называется множеством значений функции.
Если на множестве X{\displaystyle X} задана функция f{\displaystyle f}, принимающая значения из множества Y{\displaystyle Y}, то
- этот факт записывают в виде f:X→Y{\displaystyle f\colon X\to Y} или X⟶fY{\displaystyle X{\stackrel {f}{\longrightarrow }}Y};
- множество X{\displaystyle X} — область задания функции f{\displaystyle f} — обозначается символом D(f){\displaystyle D(f)} или domf;{\displaystyle \mathrm {dom} \,f;}
- множество Y{\displaystyle Y} — область значений[3] функции f{\displaystyle f};
- множество значений {y}{\displaystyle \{y\}} функции f{\displaystyle f} обозначается символом E(f){\displaystyle E(f)} или codf{\displaystyle \mathrm {cod} \,f} (ranf{\displaystyle \mathrm {ran} \,f}).
- Если область значений Y{\displaystyle Y} и множество значений E(f){\displaystyle E(f)} совпадают, то говорят, что f{\displaystyle f} отображает множество X{\displaystyle X} на Y{\displaystyle Y}.
- Функция, заданная на множестве X{\displaystyle X}, наиболее часто обозначается как соответствие между элементами x∈X{\displaystyle x\in X} и y∈Y{\displaystyle y\in Y}:
- y=f(x){\displaystyle y=f(x)}, или кратко:f(x){\displaystyle f(x)} или f{\displaystyle f};
- x↦y{\textstyle x\mapsto y} или x↦f(x){\displaystyle x\mapsto f(x)};
- для сокращения числа обозначений знак функции, заданной на множестве X{\displaystyle X}, может обозначаться той же буквой, что и каждое значение функции:
- y=y(x){\displaystyle y=y(x)}, z=z(x){\displaystyle z=z(x)};
- функция обозначается и как функция f{\displaystyle f}, которая отображает множество X{\displaystyle X} в Y{\displaystyle Y}с обозначением соответствия между элементами x∈X{\displaystyle x\in X} и y∈Y{\displaystyle y\in Y}:
- f:x↦y{\displaystyle f\colon x\mapsto y} или f:y=f(x){\displaystyle f\colon y=f(x)};
- реже используется обозначение функции как соответствие между элементами x∈X{\displaystyle x\in X} и y∈Y{\displaystyle y\in Y} без скобок: y=fx{\displaystyle y=fx}, y=f∘x{\displaystyle y=f\circ x} или y=xf{\displaystyle y=xf},
- а там, где необходимо подчеркнуть двойственность, используются обозначения со скобками: y=(f,x){\displaystyle y=(f,x)} или y=(x,f){\displaystyle y=(x,f)};
- также существует и операторное обозначение y=xf{\displaystyle y=x^{f}}, которое можно встретить в общей алгебре.
- В лямбда-исчислении Чёрча используется обозначение λx.y{\displaystyle \lambda x.y} .
Функции нескольких аргументов[править | править код]
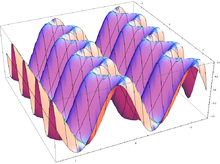График функции двух переменных f(x,y)=sin(x−sin(2y)){\displaystyle f(x,y)=\sin(x-\sin(2y))}Понятие функции легко обобщается на случай функции многих аргументов.
Если множество X{\displaystyle X} представляет собой декартово произведение множеств X1,X2,…,Xn{\displaystyle X_{1},\;X_{2},\;\ldots ,\;X_{n}}, тогда отображение f:X→Y{\displaystyle f\colon X\to Y}, где Y{\displaystyle Y} — множество вещественных чисел, оказывается n{\displaystyle n}-местным отображением, при этом элементы упорядоченного набора x=(x1,x2,…,xn){\displaystyle x=(x_{1},\;x_{2},\;\ldots ,\;x_{n})} называются аргументами (данной n{\displaystyle n}-местной функции), каждый из которых пробегает своё множество:
- xi∈Xi{\displaystyle x_{i}\in X_{i}} где i=1,n¯{\displaystyle i={\overline {1,n}}}.
В этом случае запись y=f(x){\displaystyle y=f(x)} означает, что y=f(x1,x2,…,xn){\displaystyle y=f(x_{1},\;x_{2},\;\ldots ,\;x_{n})}.
Аналитический способ[править | править код]
Функцию можно задать с помощью аналитического выражения (например, формулой). В этом случае её обозначают как соответствие в форме равенства записью y=f(x),{\displaystyle y=f(x),} где x{\displaystyle x} есть переменная, пробегающая область задания функции, а соответствующие значения переменной y{\displaystyle y} (или, что то же самое, значения выражения f(x){\displaystyle f(x)} ) принадлежат области значений функции. Например, равенство y=x2{\displaystyle y=x^{2}}
| Главная > Учебные материалы > Математика: Функция | ||||
|
|
||||
1.Понятие функции. 2.Свойства функций. 3.Основные элементарные функции.
|
||||
| 1 2 3 4 5 6 7 8 9 | ||||
1. Понятие функции Понятие «функция» является одним из основных понятий в математике. Под функцией понимают некий закон, по которому одна переменная величина зависит от другой. Согласно определению, если каждому значению переменной х множества Х ставится в соответствие одно определенное значение переменной у множества Y, то такое соответствие называется функцией. Исходя из этого, можно дать другую формулировку: однозначное соответствие двух переменных величин на множестве действительных чисел R называется функцией.
|
||||
2. Cвойства функций1.Четность и нечетность. Функция f(x) называется четной, если ее значения симметричны относительно оси OY, т.е. f(-x) = f(x). Функция f(x) называется нечетной, если ее значение изменяется на противоположное при изменении переменной х на -х , т.е. f(-x) = -f(x). В противном случае функция называется функцией общего вида. 2.Монотонность. Функция называется возрастающей (убывающей) на промежутке Х, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции, т.е. при x1< (>) x2, f(x1) < (>) f(x2). 3.Периодичность. Если значение функции f(x) повторяется через определенный период Т, то функция называется периодической с периодом Т ≠ 0 , т.е. f(x + T) = f(x). В противном случае непериодической. 4. Ограниченность. Функция f (x) называется ограниченной на промежутке Х, если существует такое положительное число М > 0 , что для любого x, принадлежащего промежутку Х, | f (x) | < M. В противном случае функция называется неограниченной.
|
||||
3. Основные элементарные функцииСтепенная функция у = х |
|
|||
| у = х² область определения (-∞,∞) |
|
|||
| у = х³ область определения (-∞,∞) |
|
|||
| у = 1/х область определения (-∞,0)U(0,∞) |
|
|||
| у = 1/х² область определения (-∞,0)U(0,∞) |
|
|||
|
область определения [0,∞) |
|
|||
|
область определения (-∞,∞) |
|
|||
Показательная функция у = а ͯ (a>0 a≠1) область определения (-∞,∞) |
|
|||
Логарифмическая функция у = log ₐ x (a>0 a≠1) область определения (0,∞) |
|
|||
Тригонометрические функции y = sin x область определения (-∞; ∞) |
|
|||
y = cos x область определения (-∞; ∞) |
|
|||
y = tg x область определения |
|
|||
y = ctg x область определения нечетная убывает на (πn, π + πn) nϵZ; период Т=π |
|
|||
y = arcsin x область определения [-1; 1] |
|
|||
y = arccos x область определения [-1; 1] функция центрально-симметрична относительно точки (0; π/2) убывает на [-1; 1] |
|
|||
y = arctg x область определения (-∞; ∞) |
|
|||
y = arcctg x область определения (-∞; ∞) ни четная, ни нечетная убывает на (-∞; ∞) |
||||
Пример 1.Найти область определения функции. |
||||
Пример 2Выяснить четность или нечетность функции. |
График функции y=x³+2sin x |
|||
Пример 3 |
||||
| 1 2 3 4 5 6 7 8 9 | ||||
« Основные свойства функции. » – Яндекс.Знатоки
К основным свойствам функции относятся:
- Четность и нечетность функции
Функция называется четной, если
– область определения функции симметрична относительно нуля
– для любого х из области определения f(-x) = f(x)
!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image003.gif
График четной функции симметричен относительно оси 0y
Функция называется нечетной, если
– область определения функции симметрична относительно нуля
– для любого х из области определения f(-x) = –f(x)
!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image004.gif
График нечетной функции симметричен относительно начала координат.
2.Периодичность
Функция f(x) называется периодической с периодом !https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image005.gif, если для любого х из области определения f(x) = f(x+Т) = f(x-Т).
!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image006.gif
График периодической функции состоит из неограниченно повторяющихся одинаковых фрагментов.
- Монотонность (возрастание, убывание)
Функция f(x) возрастает на множестве Р , если для любых x1 и x2 из этого множества, таких, что x1 < x2 выполнено неравенство f(x1)< f(x2).
!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image011.gif
Функция f(x) убывает на множестве Р , если для любых x1 и x2 из этого множества, таких, что x1 < x2 выполнено неравенство f(x1) > f(x2).
!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image013.gif
- Экстремумы
Точка Хmax называется точкой максимума функции f(x) , если для всех х из некоторой окрестности Хmax , выполнено неравенство f(х)!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image014.gif f(Xmax).
Значение Ymax=f(Xmax) называется максимумом этой функции.
!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image015.gif
Хmax – точка максимума
Уmax – максимум
Точка Хmin называется точкой минимума функции f(x) , если для всех х из некоторой окрестности Хmin , выполнено неравенство f(х)!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image016.gif f(Xmin).
Значение Ymin=f(Xmin) называется минимумом этой функции.
!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image017.gif
Xmin – точка минимума
Ymin – минимум
Xmin, Хmax – точки экстремума
Ymin, Уmax – экстремумы.
- Нули функции
Нулем функции y = f(x) называется такое значение аргумента х , при котором функция обращается в нуль: f(x) = 0.
!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image018.gif
Х1,Х2,Х3 – нули функции y = f(x).
Функции и графики — Математика — Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Координаты и базовые понятия о функциях
К оглавлению…
Длина отрезка на координатной оси находится по формуле:
Длина отрезка на координатной плоскости ищется по формуле:
Для нахождения длины отрезка в трёхмерной системе координат используется следующая формула:
Координаты середины отрезка (для координатной оси используется только первая формула, для координатной плоскости — первые две формулы, для трехмерной системы координат — все три формулы) вычисляются по формулам:
Функция – это соответствие вида y = f(x) между переменными величинами, в силу которого каждому рассматриваемому значению некоторой переменной величины x (аргумента или независимой переменной) соответствует определенное значение другой переменной величины, y (зависимой переменной, иногда это значение просто называют значением функции). Обратите внимание, что функция подразумевает, что одному значению аргумента х может соответствовать только одно значение зависимой переменной у. При этом одно и то же значение у может быть получено при различных х.
Область определения функции – это все значения независимой переменной (аргумента функции, обычно это х), при которых функция определена, т.е. ее значение существует. Обозначается область определения D(y). По большому счету Вы уже знакомы с этим понятием. Область определения функции по другому называется областью допустимых значений, или ОДЗ, которую Вы давно умеете находить.
Область значений функции – это все возможные значения зависимой переменной данной функции. Обозначается Е(у).
Функция возрастает на промежутке, на котором большему значению аргумента соответствует большее значение функции. Функция убывает на промежутке, на котором большему значению аргумента соответствует меньшее значение функции.
Промежутки знакопостоянства функции – это промежутки независимой переменной, на которых зависимая переменная сохраняет свой положительный или отрицательный знак.
Нули функции – это такие значения аргумента, при которых величина функции равна нулю. В этих точках график функции пересекает ось абсцисс (ось ОХ). Очень часто необходимость найти нули функции означает необходимость просто решить уравнение. Также часто необходимость найти промежутки знакопостоянства означает необходимость просто решить неравенство.
Функцию y = f(x) называют четной, если она определена на симметричном множестве и для любого х из области определения выполняется равенство:
Это означает, что для любых противоположных значений аргумента, значения четной функции равны. График чётной функции всегда симметричен относительно оси ординат ОУ.
Функцию y = f(x) называют нечетной, если она определена на симметричном множестве и для любого х из области определения выполняется равенство:
Это означает, что для любых противоположных значений аргумента, значения нечетной функции также противоположны. График нечётной функции всегда симметричен относительно начала координат.
Сумма корней чётной и нечетной функций (точек пересечения оси абсцисс ОХ) всегда равна нулю, т.к. на каждый положительный корень х приходится отрицательный корень –х.
Важно отметить: некоторая функция не обязательно должна быть четной либо нечетной. Существует множество функций не являющихся ни четными ни нечетными. Такие функции называются функциями общего вида, и для них не выполняется ни одно из равенств или свойств приведенных выше.
График линейной функции
К оглавлению…
Линейной функцией называют функцию, которую можно задать формулой:
График линейной функции представляет из себя прямую и в общем случае выглядит следующим образом (приведен пример для случая когда k > 0, в этом случае функция возрастающая; для случая k < 0 функция будет убывающей, т.е. прямая будет наклонена в другую сторону — слева направо):
График квадратичной функции (Парабола)
К оглавлению…
График параболы задается квадратичной функцией:
Квадратичная функция, как и любая другая функция, пересекает ось ОХ в точках являющихся её корнями: (x1; 0) и (x2; 0). Если корней нет, значит квадратичная функция ось ОХ не пересекает, если корень один, значит в этой точке (x0; 0) квадратичная функция только касается оси ОХ, но не пересекает её. Квадратичная функция всегда пересекает ось OY в точке с координатами: (0; c). График квадратичной функции (парабола) может выглядеть следующим образом (на рисунке примеры, которые далеко не исчерпывают все возможные виды парабол):
При этом:
- если коэффициент a > 0, в функции y = ax2 + bx + c, то ветви параболы направлены вверх;
- если же a < 0, то ветви параболы направлены вниз.
Координаты вершины параболы могут быть вычислены по следующим формулам. Икс вершины (p — на рисунках выше) параболы (или точка в которой квадратный трехчлен достигает своего наибольшего или наименьшего значения):
Игрек вершины (q — на рисунках выше) параболы или максимальное, если ветви параболы направлены вниз (a < 0), либо минимальное, если ветви параболы направлены вверх (a > 0), значение квадратного трехчлена:
Графики других функций
К оглавлению…
Степенной функцией называют функцию, заданную формулой:
Приведем несколько примеров графиков степенных функций:
Обратно пропорциональной зависимостью называют функцию, заданную формулой:
В зависимости от знака числа k график обратно пропорциональной зависимости может иметь два принципиальных варианта:
Асимптота — это линия, к которой линия графика функции бесконечно близко приближается, но не пересекает. Асимптотами для графиков обратной пропорциональности приведенных на рисунке выше являются оси координат, к которым график функции бесконечно близко приближается, но не пересекает их.
Показательной функцией с основанием а называют функцию, заданную формулой:
В зависимости от того больше или меньше единицы число a график показательной функции может иметь два принципиальных варианта (приведем также примеры, см. ниже):
Логарифмической функцией называют функцию, заданную формулой:
В зависимости от того больше или меньше единицы число a график логарифмической функции может иметь два принципиальных варианта:
График функции y = |x| выглядит следующим образом:
Графики периодических (тригонометрических) функций
К оглавлению…
Функция у = f(x) называется периодической, если существует такое, неравное нулю, число Т, что f(x + Т) = f(x), для любого х из области определения функции f(x). Если функция f(x) является периодической с периодом T, то функция:
где: A, k, b – постоянные числа, причем k не равно нулю, также периодическая с периодом T1, который определяется формулой:
Большинство примеров периодических функций — это тригонометрические функции. Приведем графики основных тригонометрических функций. На следующем рисунке изображена часть графика функции y = sinx (весь график неограниченно продолжается влево и вправо), график функции y = sinx называют синусоидой:
График функции y = cosx называется косинусоидой. Этот график изображен на следующем рисунке. Так как и график синуса он бесконечно продолжается вдоль оси ОХ влево и вправо:
График функции y = tgx называют тангенсоидой. Этот график изображен на следующем рисунке. Как и графики других периодических функций, данный график неограниченно далеко повторяется вдоль оси ОХ влево и вправо.
Ну и наконец, график функции y = ctgx называется котангенсоидой. Этот график изображен на следующем рисунке. Как и графики других периодических и тригонометрических функций, данный график неограниченно далеко повторяется вдоль оси ОХ влево и вправо.
Что такое функция — материалы для подготовки к ЕГЭ по Математике
Понятие функции – одно из основных в математике.
На уроках математики вы часто слышите это слово. Вы строите графики функций, занимаетесь исследованием функции, находите наибольшее или наименьшее значение функции. Но для понимания всех этих действий давайте определим, что такое функция.
Определение функции можно дать несколькими способами. Все они будут дополнять друг друга.
1. Функция – это зависимость одной переменной величины от другой. Другими словами, взаимосвязь между величинами.
Любой физический закон, любая формула отражает такую взаимосвязь величин. Например, формула – это зависимость давления жидкости от глубины .
Чем больше глубина, тем больше давление жидкости. Можно сказать, что давление жидкости является функцией от глубины, на которой его измеряют.
Знакомое вам обозначение как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины по определенному закону, или правилу, обозначаемому .
Другими словами: меняем (независимую переменную, или аргумент) – и по определенному правилу меняется .
Совсем необязательно обозначать переменные и . Например, – зависимость длины от температуры , то есть закон теплового расширения. Сама запись означает, что величина зависит от .
2. Можно дать и другое определение.
Функция – это определенное действие над переменной.
Это означает, что мы берем величину , делаем с ней определенное действие (например, возводим в квадрат или вычисляем ее логарифм) – и получаем величину .
В технической литературе встречается определение функции как устройства, на вход которого подается – а на выходе получается .
Итак, функция – это действие над переменной. В этом значении слово «функция» применяется и в областях, далеких от математики. Например, можно говорить о функциях мобильного телефона, о функциях головного мозга или функциях депутата. Во всех этих случаях речь идет именно о совершаемых действиях.
3. Дадим еще одно определение функции – то, что чаще всего встречается в учебниках.
Функция – это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один и только один элемент второго множества.
Например, функция каждому действительному числу ставит в соответствие число в два раза большее, чем .
Повторим еще раз: каждому элементу множества по определенному правилу мы ставим в соответствие элемент множества . Множество называется областью определения функции. Множество – областью значений.
Но зачем здесь такое длинное уточнение: «каждому элементу первого множества соответствует один и только один элемент второго»? Оказывается, что соответствия между множествами тоже бывают разные.
Рассмотрим в качестве примера соответствие между двумя множествами – гражданами России, у которых есть паспорта, и номерами их паспортов. Ясно, что это соответствие взаимно-однозначное – у каждого гражданина только один российский паспорт. И наоборот – по номеру паспорта можно найти человека.
В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция . Каждому значению соответствует одно и только одно значение . И наоборот – зная , можно однозначно найти .
Могут быть и другие типы соответствий между множествами. Возьмем для примера компанию друзей и месяцы, в которые они родились:
Каждый человек родился в какой-то определенный месяц. Но данное соответствие не является взаимно-однозначным. Например, в июне родились Сергей и Олег.
Пример такого соответствия в математике – функция . Один и тот же элемент второго множества соответствует двум разным элементам первого множества: и .
А каким должно быть соответствие между двумя множествами, чтобы оно не являлось функцией? Очень просто! Возьмем ту же компанию друзей и их хобби:
Мы видим, что в первом множестве есть элементы, которым соответствует два или три элемента из второго множества.
Очень сложно было бы описать такое соответствие математически, не правда ли?
Вот другой пример. На рисунках изображены кривые. Как вы думаете, какая из них является графиком функции, а какая – нет?
Ответ очевиден. Первая кривая – это график некоторой функции, а вторая – нет. Ведь на ней есть точки, где каждому значению соответствует не одно, а целых три значения .
Ты нашел то, что искал? Поделись с друзьями!
Перечислим способы задания функции.
1. С помощью формулы. Это удобный и привычный для нас способ. Например:
,
,
,
.
Это примеры функций, заданных формулами.
2. Графический способ. Он является самым наглядным. На графике сразу видно все – возрастание и убывание функции, наибольшие и наименьшие значения, точки максимума и минимума. В следующей статье будет рассказано об исследовании функции с помощью графика.
К тому же не всегда легко вывести точную формулу функции. Например, курс доллара (то есть зависимость стоимости доллара от времени) можно показать только на графике.
3. С помощью таблицы. С этого способа вы когда-то начинали изучение темы «Функция» — строили таблицу и только после этого – график. А при экспериментальном исследовании какой-либо новой закономерности, когда еще неизвестны ни формула, ни график, этот способ будет единственно возможным.
4. С помощью описания. Бывает, что на разных участках функция задается разными формулами. Известная вам функция задается описанием:
Читайте также: Чтение графика функции
Главная функция экономики — Энциклопедия по экономике
Главная функция экономики [c.6]Весь смысл хозяйственной деятельности связан прежде всего с основным предназначением. Главная функция экономики состоит в том, чтобы постоянно создавать такие блага, которые необходимы для жизнедеятельности людей. [c.6]
Чтобы выполнять главную функцию экономики, нужно создавать блага второго вида— средства производства (хлопок, нефть, металл, древесину, станки и т. п.). Без этих средств нельзя изготовить предметы потребления. Стало быть, для каждой страны важен и другой показатель хозяйственного развития — объем выпуска разных средств производства на душу населения. [c.9]
Главная функция экономики как области хозяйственной деятельности состоит в том, чтобы постоянно создавать такие блага, которые необходимы для жизнедеятельности людей. / [c.19]
Стало быть, более полное определение главной функции экономики таково она создает для людей предметы потребления и необходимые для этого средства производства. [c.19]
В чем причина неудачной постановки задачи Причина очевидна мы могли неограниченно увеличивать валовые выпуски отраслей, лишь бы вектор выпусков был сбалансирован соотношением (2.8) (или (2.3)) по производственному потреблению. В реальной экономической системе валовые выпуски отраслей ограничены не только из-за ограничений по сырью, топливу и энергии, но и по другим причинам, которые мы не рассмотрели. Для правильной постановки задачи хотя бы главные из этих причин необходимо учесть. Вспомним предыдущую главу в производственной функции экономики ресурсами считались основные фонды и трудовые ресурсы. В межотраслевой модели, рассматриваемой нами сейчас, каждая отрасль описывается функцией затрат (2.2), в которой учитывается лишь производственное потребление промежуточного продукта. Отсутствие учета основных фондов и трудовых ресурсов — одна из причин неправильной постановки задачи. Попробуем включить эти ресурсы в описание отрасли. Для этого обычно используется производственная функция с постоянными пропорциями [c.139]
Но здесь надо учитывать, что господство частного сектора в экономике неизбежно ведет к господству частного капитала в политике, а это несовместимо с главной функцией государства как гаранта социальной справедливости. В то же время наличие мощного государственного сектора создает в известной мере условия для сохранения бюрократии. Выход один государственные предприятия должны быть лишены монопольного положения по сравнению с другими формами собственности и поставлены в условия рыночной конкуренции. Этого можно достичь путем акционирования предприятий, причем государство должно быть основным держателем акций. Тогда представители государства будут не только находиться в правлении, но и играть немаловажную роль в принятии решений. При этом государство получает и налог с прибыли, и дивиденды по акциям. [c.138]
Главными функциями ФРС являются а) хранение вкладов, или резервов, коммерческих банков и других депозитарных учреждений б) обеспечение быстрой инкассации чеков в) деятельность в качестве фискального агента федерального правительства г) надзор за деятельностью банков-членов д) регулирование денежного предложения в интересах экономики в целом. [c.293]
ЭКОНОМИКА ЕЕ ГЛАВНАЯ ФУНКЦИЯ И СТРУКТУРА [c.8]
Значит, главная функция (назначение) экономики заключается в создании продуктов, необходимых для жизнедеятельности общества. При этом изготавливаются два вида экономических благ а) предметы потребления и б) средства производства (условия созидательной деятельности). [c.8]
По существу, банки уклонились от своей главной функции — аккумулировать свободные денежные средства и направлять их в отрасли, которые больше всего нуждаются в финансировании для своего развития. Отмеченные особенности банковской системы стали отрицательно влиять на всю экономику. Эти последствия проявились в нарушении механизмов инвестирования, в существенных сбоях товарно-денежного обращения (кризис оплаты) и задержках заработной платы (результат банковских спекуляций), а также в невозможности проведения эффективной банковской политики. Крайним проявлением этой тенденции стала криминализация банковского дела. [c.330]
В условиях рыночной экономики главная функция Ц. —информационная Ц. сообщает участникам обмена сведения, необходимые для принятия ими [c.387]
Однако в рамках современной комплексной экономики люди не всегда бывают легко заменимыми. Не взаимозаменяемы работники университетов или организаций в сложных многоступенчатых видах бизнеса, где они наделены высокими полномочиями, а прямое руководство сведено практически к нулю. Подобная структура жизнеспособна только в том случае, если персонал, наделенный всеми этими полномочиями и обязанностями, четко знает, что делать, обучен и подготовлен для выполнения этих задач, имеет четко разграниченные участки деятельности, ответственности и полную информацию о функционировании этих участков, может составлять эффективные команды, одной из главных функций которых является поддержка друг друга. Отсутствие руководящей структуры означает, что подобная организация может функционировать, только опираясь на доверие. [c.91]
Информационная функция. Одна из главных функций, которую выполняет бухгалтерский учет в системе управления в условиях формирования рыночной экономики, — информационная функция. На современном этапе роль и значение своевременно поступающей объективной экономической информации усиливаются. [c.13]
Биржа является инструментом вторичного рынка — сферы обращения ценных бумаг. Обращение необходимо, так как иначе рынок потеряет свою роль индикатора эффективности и соответствующего стимулятора перераспределения капиталов. Ценные бумаги, обращающиеся на фондовой бирже, обладают следующим свойством колебания цен на эти бумаги, как правило, должны быть постоянными и минимальными. Фондовая биржа способна обеспечить именно такую концентрацию спроса и предложения на ценные бумаги, которая позволяет установить цены на них, реально отражающие экономическую ситуацию. Таким образом, фондовая биржа являет собой частную модель рыночной экономики в целом. Главной функцией обоих институтов является сопоставление спроса и предложения и выявление справедливой цены. [c.425]
Главная функция (назначение) экономики — постоянно обеспечивать людей необходимыми для них благами. [c.11]
Главная функция банков — обеспечить передачу денежного капитала из тех сфер хозяйства и общества, где он накапливается, в те сферы, где он используется. Благодаря банкам действует механизм распределения капитала по сферам и отраслям производства и происходит выравнивание нормы прибыли. Банки играют важную роль в экономии общественных издержек обращения и рационализации всех процессов обращения товаров и капитала. Их функционирование тесно связано с денежным обращением. Банки остаются центрами хозяйственной жизни, активно участвуя в процессах централизации и концентрации капитала, в развитии мощной структуры экономики. Этому способствует и законодательство, согласно которому фирма, организация, предприятие обязаны держать свои денежные средства на своих счетах в банках. [c.31]
Биржа — классический институт рыночной экономики, формирующий оптовый рынок товаров путем организации и регулирования биржевой торговли. Основным содержанием деятельности биржи является создание наиболее благоприятных условий для заключения торговых сделок во время гласных публичных торгов, проводимых в определенном месте и в установленное время. Биржа как организация с правом юридического лица не выступает стороной в сделках купли-продажи, т.е. не осуществляет торгово-посредническую деятельность. Главная функция товарной биржи — организация постоянно действующего товарного рынка и оказание посреднических, информационных и других услуг участникам биржевых торгов. [c.36]
Распределительная функция — главная функция налогов, заключающаяся в перераспределении доходов государства, воздействии на те или иные отрасли экономики, социальной защите отдельных групп населения (инвалидов, малоимущих, и т. п.). Долгое время эта функция носила лишь фискальный (касающийся интересов государства) характер — наполнив казну, расходовать средства на содержание армии, государственного аппарата, впоследствии — и социальной сферы. Вмешательство государства в экономику придало этой функции налогов и регулирующий характер. Изменяя налоговые ставки и условия налогообложения, органы власти воз-действующ на деловую активность в различных сферах экономики, на перемещение капиталов из одних отраслей в другие. [c.193]
Совет трудового коллектива не является совещательным органом при дирекции предприятия. Его главная функция — реализовать самоуправление трудящихся на уровне первичного звена социалистической экономики. Вместе с тем возникает проблема обеспечения взаимодействия непосредственных производителей и их совета со специализированным аппаратом хозяйственного управления предприятием, с директором. [c.617]
Налог является одним из основных источников пополнения государственной казны. Регулирование экономики и перераспределение денежных средств — его главные функции. Государство воздействует на состояние хозяйственной конъюнктуры, стимулирует экономический рост, используя рычаги налоговой политики. [c.397]
Характеризуя социальную политику Республики Беларусь и систему государственного регулирования развития социальной сферы в целом, следует отметить, что с развитием рыночных отношений в стране будет происходить перераспределение функций социального партнерства в пользу негосударственных субъектов. Целесообразность такого перераспределения показывает опыт стран с рыночной экономикой, где система социального развития построена на многостороннем взаимодействии государства, общественных объединений, частных структур. Однако основная ответственность в области социального развития, главные функции управления — законодательная, регулирующая, контролирующая — останутся за государством, которое и впредь будет выступать как гарант всеобщего социального благополучия. [c.590]
Рыночный механизм сам по себе в «чистом виде» не позволяет своевременно выявлять преимущества стран в конкурентной борьбе, быстро концентрировать ресурсы для приоритетного развития соответствующих отраслей, ускоренной структурной перестройки промышленности. Это функция государственного регулирования экономики. Одна из главных функций государственного регулирования — активизация, интенсификация прежде всего инвестиционной, инновационной и предпринимательской деятельности, при обеспечении стабильности национальной валюты. Это достигается мерами финансовой, денежной и кредитной политики. [c.9]
Золото — анахронизм, который не играет никакой конструктивной роли в современной экономике. Вообще-то, поскольку курс золота имеет тенденцию к повышению, когда национальные валюты слабеют, от него лишь одна головная боль, потому что оно отвлекает правительство от выполнения главной функции — заботы о росте экономических по- [c.10]
Основной характеристикой фондовых рынков практически всех постсоветских стран является тот факт, что они не выполняют своей главной функции — финансирование инвестиций в реальный сектор экономики, привлечение средств для этой цели. Этот рынок существует в основном как бы сам для себя и не является органической частью финансовой системы, призванной обеспечить эффективное использование капитала в интересах экономики в целом. Его роль, как фактора роста экономики, пока не может проявиться из-за относительной экономической отсталости и неразвитости финансового рынка в целом и фондового рынка в частности. [c.29]
Как уже отмечалось выше, главной функцией фондового рынка является мобилизация капитала и его перераспределение в различные секторы экономики. Поэтому, на наш взгляд, действия государственной политики регулирования должны быть подчинены этой главной задаче. При этом, естественно, не должны принижаться другие важнейшие предназначения государственного регулирования. [c.84]
Любая компания выполняет главную экономическую функцию, заключающуюся в удовлетворении нужд потребителей посредством своих услуг или своих товаров. В условиях планируемой экономики критерии надлежащего выполнения этой функции должны быть найдены в увязке с планом. В условиях рыночной экономики деятельность компании определяется ценами на товары и предоставленные услуги, на факторы производства и на сырьевые материалы, — а также затратами на функционирование компании. Поэтому целью компании становится создание такой организационной структуры, при которой затраты на функционирование были бы как можно более низкими и в то же время настолько эффективными, насколько это требуется для выполнения главной функции. [c.36]
Одновременно с этим методом в нефтяной промышленности применим метод индексного анализа себестоимости, а также трансцендентная кинетическая производственная функция как экономико-математическая модель [28]. Одним из главных условий получения хороших результатов является правильный выбор исходных статистических показателей, от которых зависит в значительной степени точность расчетов. [c.23]
Маркетинг. Главная его задача — обеспечение рынка для сбыта продукции фирмы, формирование спроса. В развитой рыночной экономике наиболее сложной проблемой для предприятия является не производство, а продажа продукции, поэтому маркетинг представляет собой важнейшую функцию предприятия. В силу этого маркетинг является одной из наиболее обширных областей профессионального обеспечения предпринимательства. [c.81]
Основные задачи и цели деятельности ЕБРР. Главная задача ЕБРР — содействовать переходу европейских постсоциалистических стран к открытой, ориентированной на рынок экономике, а также развитию частной и предпринимательской инициативы. В целях реализации основной задачи Банка — способствовать переходу стран Центральной и Восточной Европы к рыночной экономике — Уставом ЕБРР предусмотрены следующие функции [c.472]
Данную функцию выполняют наличные деньги, главным образом при участии физических лиц, и безналичные деньги — преимущественно между юридическими лицами. Безналичные расчеты, когда наличные деньги заменяются кредитными, становятся преобладающей формой платежа в рыночной экономике. [c.19]
Современные функции денег и их роль в современной рыночной экономике. Современный капитализм, характеризующийся всеобщим характером товарно-денежных отношений и господством вместо действительных денег знаков стоимости — главным образом, кредитных денег, — обусловил модификацию функций денег. [c.21]
В управлении финансами, как правило, принимают участие различные органы исполнительной власти. В США к этим органам относятся Министерство финансов, Административно-бюджетное управление при Президенте. Кроме того, управление исполнением бюджета осуществляется наряду с Министерством финансов Таможенной службой. Бюро по алкогольным напиткам, табачным изделиям и огнестрельному оружию. В Великобритании главным исполнительным органом управления выступает Казначейство. Оно не только руководит разработкой и исполнением государственного бюджета, но и осуществляет контроль за расходованием средств государственными предприятиями. В исполнении бюджета участвует Управление таможенных пошлин и акцизов, которое осуществляет сбор таможенных пошлин и акцизов. В Германии главным органом управления финансами исполнительной власти выступает Министерство финансов. Оно составляет проект бюджета, осуществляет кассовое обслуживание бюджета, контроль за его исполнением, регулирует межбюджетные отношения и т. п. Во Франции управление финансами осуществляет Министерство экономики, финансов и бюджета. В его функции входит не только разработка государственного бюджета и контроль за его исполнением, но и сбор налогов и пошлин. [c.38]
Планирование представляет очень важную функцию в системе управления производством на предприятии. С его помощью определяются направление и содержание деятельности предприятия, его структурных подразделений и отдельных работников. Главной задачей планирования является обеспечение планомерности развития экономики предприятия и деятельности каждого его члена, определение путей достижения лучших конечных результатов производства. [c.17]
Экономика главная функция экономики производство распределение обмен потребление закон возвышения потребностей закон Эигсля факторы производства ограниченность ресурсов производственные возможности альтернативная стоимость стадии развития производства структура современного производства услуги экономическая система. [c.31]
Очевидно, что социалистическая экономика в СССР и странах Восточной Европы оказалась сравнительно малоэффективной не потому, что в них имелся государственный сектор, а потому, что она была практически полностью огосударствлена. Отсутствовало естественное противоречие между общими ичастными интересами, разрешение которых является главной функцией государства. Вместо различных форм и методов государственного влияния, целью которого должно было быть развитие частного сектора экономики, происходила абсолютизация общих, государственных экономических интересов. Это привело в конечном счете к умалению, даже игнорированию личного интереса граждан, превращая их постепенно из активных созидателей в пассивных потребителей созданных государством материальных и духовных благ. [c.460]
Дескриптивно-телеологические дефиниции. Авторы таких дефиниций, как видно из названия, пытаются сочетать характеристику целей менеджмента персонала с перечислением его важнейших функций. Экономика персонала (или управление персоналом), — пишут немецкие ученые Р. Марр и В. Вебер, — является сферой деятельности, характерной для всех организаций, и ее главная задача состоит в обеспечении организации персоналом и целенаправленном использовании персонала 12. [c.25]
См. работы Г. Беккера Экономический анализ и человеческое поведение. // THESIS. — 1993. -T.I. — Вып. 1. Выбор партнера на брачных рынках. // THESIS. — 1994. — Вып. 6 Теория распределения времени // США — ЭПИ — 1996. № 1,2. Отечественные авторы также склонны возлагать на нее эту функцию «Экономика со времен классиков, считавшаяся царицей социальных наук, является одной из главных ценностно-образующих (курсив мой — С.Б.) предметных областей в образовании и воспитании новых поколений». См. Экономическая наука, образование и практика в России в 90-е годы // Вопросы экономики. — 2001. — №1. — С. 89. [c.14]
Все-таки выполнение домашним хозяйством функции «экономики выживания» еще не делает его экономическим субъектом. Оно остается еще только субъектом хозяйствования, основная цель которого — удовлетворение потребностей путем производства необходимых для этого благ. И, главное — не в том, что в данном случае оно слабо связано с рынком, а в том, что рынок, цены и другие рыночные инструменты еще не выполняют здесь «большую часть функций (если не все ), которыми в социологических теориях наделяется «структура» (или субъектоподобная структура — С.Б.). Пока не работает еще механизм «вмененных цен» «нерыночного сектора», «альтернативных издержек» использования «редких ресурсов», то есть, пока хозяйствующий субъект не максимизирует поведение пока он не стремится к максимизации функции полезности, до тех пор еще нет экономического субъекта. Однако исторически для его появления недостаточно наличия рынка как сферы обмена. Для того, чтобы заработали те условия становления экономического субъекта о которых только что было сказано, необходимо превращение рыночных (товарных и денежных и вообще стоимостно-полезностных) отношений во всеобщую форму, а это возможно только при капиталистической форме общественного производства. Это означает, что экономический субъект, как достаточно массовое явление, впервые появляется на исторической арене в виде капиталистического предпринимателя, свободного крестьянина, («беглого крепостного»( ) — Маркс), а не торговца или цехового ремесленника. [c.86]
Регион как квазигосударство представляет собой относительно обособленную подсистему государства и национальной экономики. Во многих странах регионы аккумулируют все больше функций и финансовых ресурсов, ранее принадлежавших «центру» (процессы децентрализации и федерализации). Одна из главных функций региональной власти — регулирование экономики региона. Взаимодействие общегосударственных (федеральных) и региональных властей, а также разные формы межрегиональных экономических отношений (например, в рамках межрегиональных ассоциаций экономического взаимодействия) обеспечивают функционирование региональных экономик в системе национальной экономики. [c.5]
Вальрасовская модель общего экономического равновесия представляет упрощенную теоретическую конструкцию менового хозяйства (ex hange e onomy), где отсутствуют производство, процессы инвестирования и накопления капитала и т. д. Экономика в ней представлена набором товарных рынков, состояние которых характеризуется уравнениями спроса и предложения различных товаров. Все существенные связи регулируются здесь относительными ценами товаров, т.е. их обменными соотношениями, устанавливаемыми на каждом рынке через механизм спроса и предложения. Денежный сектор в определении меновых пропорций не участвует. Как отметил Самуэльсон, главная функция денег в указанном классе моделей- пришпилить (pin down) абсолютный уровень цен, для чего используется классическое уравнение количественной теории, где общий уровень цен является функцией объема платежных средств в обращении. [c.30]
Еще нагляднее результаты активизации экономических функций ливийского государства прослеживаются непосредственно в его инвестиционной деятельности. За 1964—1969 гг. из суммы валовых вложений в основной капитал на его долю пришлось лишь 38% против 62% на долю частного сектора, в рамках которого, так же как в масштабах всей экономики, центральное место занимал иностранный нефтяной бизнес — до 46%. Прочие инвестиции — около 16%—принадлежали главным, образом ливийским частным предпринимателям (рассчитано по [334, с. 20J). За бремя реализации трехлетнего плана развития удельный вес государственных капитальных расходов вырос почти в 2,2 раза, превысив 82% реального накопления [311, с. 17]. Эта тенденция продолжала действовать и в дальнейшем, так что в 1976—1979 гг. государство осуществило уже 88—89% всех внутренних капиталовложений (рассчитано по [94, с. 2 376, 1980, т. XXXIV, № 12, с. 194 1983, т. XXXVII,,№ 1, с. XXX]). [c.169]
Главное достоинство ЦФП (6.18) состоит в использовании объективной основы для оценки продукции, выходящей за пределы производственной сферы экономики страны. Одним из ее недостатков является наличие единственной рациональной структуры потребления, не зависящей от уровня потребления в стране. Такой недостаток не позволяет использовать ЦФП (6.18) в моделях, предназначенных для анализа проблем долгосрочного развития народного хозяйства. В этом случае излишнюю жесткость функции (6.18) чадто компенсируют на основе использования нескольких различных структур, связанных с различными уровнями потребления. [c.131]