Корреляционное исследование — это… Что такое Корреляционное исследование?
Корреля́ция — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом, изменения одной или нескольких из этих величин приводят к систематическому изменению другой или других величин. Математической мерой корреляции двух случайных величин служит коэффициент корреляции.
Корреляция может быть положительной и отрицательной (возможна также ситуация отсутствия статистической взаимосвязи — например, для независимых случайных величин). Отрицательная корреляция — корреляция, при которой увеличение одной переменной связано с уменьшением другой переменной, при этом коэффициент корреляции отрицателен. Положительная корреляция — корреляция, при которой увеличение одной переменной связано с увеличением другой переменной, при этом коэффициент корреляции положителен.
Автокорреляция — статистическая взаимосвязь между случайными величинами из одного ряда, но взятых со сдвигом, например, для случайного процесса — со сдвигом по времени.
Метод обработки статистических данных, заключающийся в изучении коэффициентов (корреляции) между переменными, называется корреляционным анализом.
Коэффициент корреляции
Коэффицие́нт корреля́ции или парный коэффицие́нт корреля́ции в теории вероятностей и статистике — это показатель характера изменения двух случайных величин. Коэффициент корреляции обозначается латинской буквой R и может принимать значения между -1 и +1. Если значение по модулю находится ближе к 1, то это означает наличие сильной связи (при коэффициенте корреляции равном единице говорят о функциональной связи), а если ближе к 0, то слабой.
Коэффициент корреляции Пирсона
Для метрических величин применяется коэффициент корреляции Пирсона, точная формула которого была введена Фрэнсисом Гальтоном:
Пусть X,Y — две случайные величины, определённые на одном вероятностном пространстве. Тогда их коэффициент корреляции задаётся формулой:
Тогда их коэффициент корреляции задаётся формулой:
- ,
где cov обозначает ковариацию, а D — дисперсию, или, что то же самое,
- ,
где символ обозначает математическое ожидание.
Для графического представления подобной связи можно использовать прямоугольную систему координат с осями, которые соответствуют обеим переменным. Каждая пара значений маркируется при помощи определенного символа. Такой график называется «диаграммой рассеяния».
Метод вычисления коэффициента корреляции зависит от вида шкалы, к которой относятся переменные. Так, для измерения переменных с интервальной и количественной шкалами необходимо использовать коэффициент корреляции Пирсона (корреляция моментов произведений). Если по меньшей мере одна из двух переменных имеет порядковую шкалу, либо не является нормально распределённой, необходимо использовать ранговую корреляцию Спирмена или τ (тау) Кендала. В случае, когда одна из двух переменных является дихотомической, используется точечная двухрядная корреляция, а если обе переменные являются дихотомическими: четырёхполевая корреляция.
Коэффициент корреляции Кенделла
Используется для измерения взаимной неупорядоченности.
Коэффициент корреляции Спирмена
Свойства коэффициента корреляции
- если принять в качестве скалярного произведения двух случайных величин ковариацию , то норма случайной величины будет равна , и следствием неравенства Коши — Буняковского будет:
- Коэффициент корреляции равен тогда и только тогда, когда X и Y линейно зависимы:
- ,
- где . Более того в этом случае знаки и k совпадают:
- .
- Если X,Y независимые случайные величины, то . Обратное в общем случае неверно.
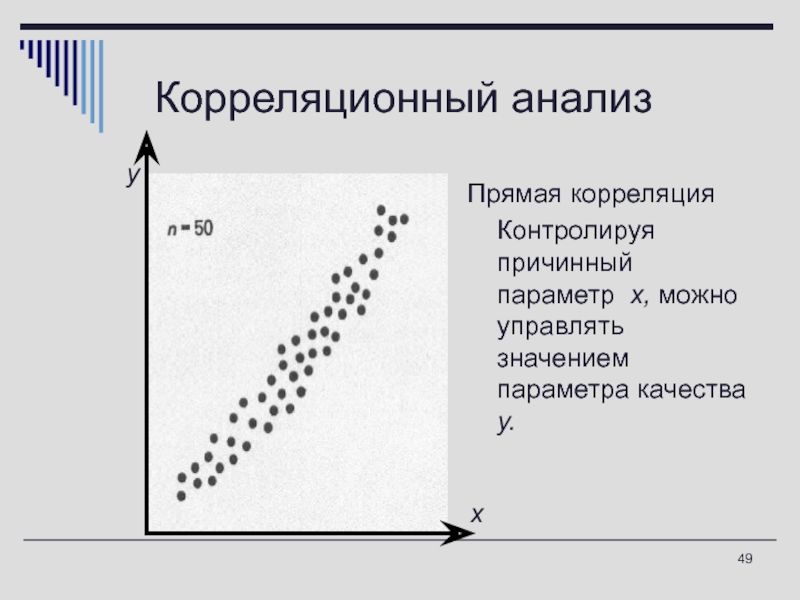
Корреляционный анализ
Корреляционный анализ — метод обработки статистических данных, заключающийся в изучении коэффициентов (корреляции) между переменными. При этом сравниваются коэффициенты корреляции между одной парой или множеством пар признаков для установления между ними статистических взаимосвязей.
При этом сравниваются коэффициенты корреляции между одной парой или множеством пар признаков для установления между ними статистических взаимосвязей.
Цель корреляционного анализа — обеспечить получение некоторой информации об одной переменной с помощью другой переменной. В случаях, когда возможно достижение цели, говорят, что переменные коррелируют. В самом общем виде принятие гипотезы о наличии корреляции означает что изменение значения переменной А, произойдет одновременно с пропорциональным изменением значения Б: если обе переменные растут то корреляция положительная, если одна переменная растёт, а вторая уменьшается, корреляция отрицательная.
Корреляция отражает лишь линейную зависимость величин, но не отражает их функциональной связности. Например, если вычислить коэффициент корреляции между величинами A = s
 Между тем, величины A и B очевидно связаны функционально по закону sin2(x) + cos2(x) = 1.
Между тем, величины A и B очевидно связаны функционально по закону sin2(x) + cos2(x) = 1.Ограничения корреляционного анализа
Графики распределений пар (x,y) с соответствующими коэффициентами корреляций x и y для каждого из них. Обратите внимание, что коэффициент корреляции отражает линейную зависимость (верхняя строка), но не описывает кривую зависимости (средняя строка), и совсем не подходит для описания сложных, нелинейных зависимостей (нижняя строка).
- Применение возможно в случае наличия достаточного количества случаев для изучения: для конкретного вида коэффициента корреляции составляет от 25 до 100 пар наблюдений.
- Второе ограничение вытекает из гипотезы корреляционного анализа, в которую заложена линейная зависимость переменных. Во многих случаях, когда достоверно известно, что зависимость существует, корреляционный анализ может не дать результатов просто ввиду того, что зависимость нелинейна (выражена, например, в виде параболы).

- Сам по себе факт корреляционной зависимости не даёт основания утверждать, какая из переменных предшествует или является причиной изменений, или что переменные вообще причинно связаны между собой, например, ввиду действия третьего фактора.
Область применения
Данный метод обработки статистических данных весьма популярен в экономике и социальных науках (в частности в психологии и социологии), хотя сфера применения коэффициентов корреляции обширна: контроль качества промышленной продукции, металловедение, агрохимия, гидробиология, биометрия и прочие.
Популярность метода обусловлена двумя моментами: коэффициенты корреляции относительно просты в подсчете, их применение не требует специальной математической подготовки. В сочетании с простотой интерпретации, простота применения коэффициента привела к его широкому распространению в сфере анализа статистических данных.
Ложная корреляция
Часто заманчивая простота корреляционного исследования подталкивает исследователя делать ложные интуитивные выводы о наличии причинно-следственной связи между парами признаков, в то время как коэффициенты корреляции устанавливают лишь статистические взаимосвязи.
В современной количественной методологии социальных наук, фактически, произошел отказ от попыток установить причинно-следственные связи между наблюдаемыми переменными эмпирическими методами. Поэтому, когда исследователи в социальных науках говорят об установлении взаимосвязей между изучаемыми переменными, подразумевается либо общетеоретическое допущение, либо статистическая зависимость.
См. также
Wikimedia Foundation. 2010.
Корреляционное исследование — это… Что такое Корреляционное исследование?
Корреля́ция — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом, изменения одной или нескольких из этих величин приводят к систематическому изменению другой или других величин. Математической мерой корреляции двух случайных величин служит коэффициент корреляции.
Корреляция может быть положительной и отрицательной (возможна также ситуация отсутствия статистической взаимосвязи — например, для независимых случайных величин).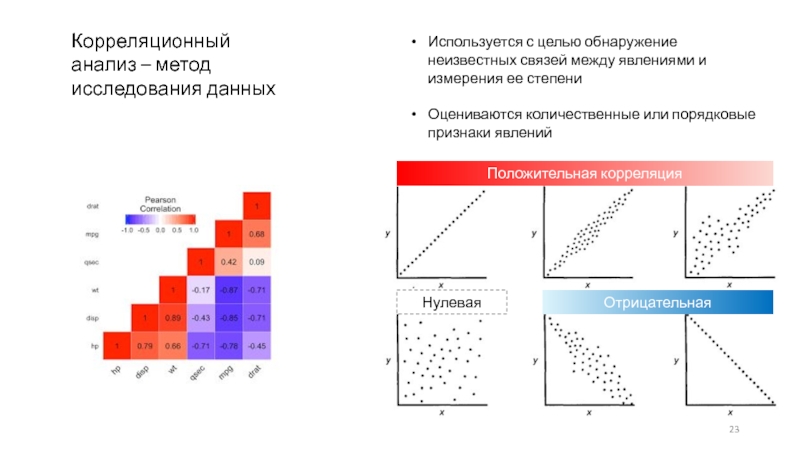
Автокорреляция — статистическая взаимосвязь между случайными величинами из одного ряда, но взятых со сдвигом, например, для случайного процесса — со сдвигом по времени.
Метод обработки статистических данных, заключающийся в изучении коэффициентов (корреляции) между переменными, называется корреляционным анализом.
Коэффициент корреляции
Коэффицие́нт корреля́ции или парный коэффицие́нт корреля́ции в теории вероятностей и статистике — это показатель характера изменения двух случайных величин. Коэффициент корреляции обозначается латинской буквой R и может принимать значения между -1 и +1. Если значение по модулю находится ближе к 1, то это означает наличие сильной связи (при коэффициенте корреляции равном единице говорят о функциональной связи), а если ближе к 0, то слабой.
Если значение по модулю находится ближе к 1, то это означает наличие сильной связи (при коэффициенте корреляции равном единице говорят о функциональной связи), а если ближе к 0, то слабой.
Коэффициент корреляции Пирсона
Для метрических величин применяется коэффициент корреляции Пирсона, точная формула которого была введена Фрэнсисом Гальтоном:
Пусть X,Y — две случайные величины, определённые на одном вероятностном пространстве. Тогда их коэффициент корреляции задаётся формулой:
- ,
где cov обозначает ковариацию, а D — дисперсию, или, что то же самое,
- ,
где символ обозначает математическое ожидание.
Для графического представления подобной связи можно использовать прямоугольную систему координат с осями, которые соответствуют обеим переменным. Каждая пара значений маркируется при помощи определенного символа. Такой график называется «диаграммой рассеяния».
Метод вычисления коэффициента корреляции зависит от вида шкалы, к которой относятся переменные. Так, для измерения переменных с интервальной и количественной шкалами необходимо использовать коэффициент корреляции Пирсона (корреляция моментов произведений). Если по меньшей мере одна из двух переменных имеет порядковую шкалу, либо не является нормально распределённой, необходимо использовать ранговую корреляцию Спирмена или τ (тау) Кендала. В случае, когда одна из двух переменных является дихотомической, используется точечная двухрядная корреляция, а если обе переменные являются дихотомическими: четырёхполевая корреляция. Расчёт коэффициента корреляции между двумя недихотомическими переменными не лишён смысла только тогда, кода связь между ними линейна (однонаправлена).
Так, для измерения переменных с интервальной и количественной шкалами необходимо использовать коэффициент корреляции Пирсона (корреляция моментов произведений). Если по меньшей мере одна из двух переменных имеет порядковую шкалу, либо не является нормально распределённой, необходимо использовать ранговую корреляцию Спирмена или τ (тау) Кендала. В случае, когда одна из двух переменных является дихотомической, используется точечная двухрядная корреляция, а если обе переменные являются дихотомическими: четырёхполевая корреляция. Расчёт коэффициента корреляции между двумя недихотомическими переменными не лишён смысла только тогда, кода связь между ними линейна (однонаправлена).
Коэффициент корреляции Кенделла
Используется для измерения взаимной неупорядоченности.
Коэффициент корреляции Спирмена
Свойства коэффициента корреляции
- если принять в качестве скалярного произведения двух случайных величин ковариацию , то норма случайной величины будет равна , и следствием неравенства Коши — Буняковского будет:
- .

- Коэффициент корреляции равен тогда и только тогда, когда X и Y линейно зависимы:
- ,
- где . Более того в этом случае знаки и k совпадают:
- .
- Если X,Y независимые случайные величины, то . Обратное в общем случае неверно.
Корреляционный анализ
Корреляционный анализ — метод обработки статистических данных, заключающийся в изучении коэффициентов (корреляции) между переменными. При этом сравниваются коэффициенты корреляции между одной парой или множеством пар признаков для установления между ними статистических взаимосвязей.
Цель корреляционного анализа — обеспечить получение некоторой информации об одной переменной с помощью другой переменной. В случаях, когда возможно достижение цели, говорят, что переменные коррелируют. В самом общем виде принятие гипотезы о наличии корреляции означает что изменение значения переменной А, произойдет одновременно с пропорциональным изменением значения Б: если обе переменные растут то корреляция положительная, если одна переменная растёт, а вторая уменьшается, корреляция отрицательная.
Корреляция отражает лишь линейную зависимость величин, но не отражает их функциональной связности. Например, если вычислить коэффициент корреляции между величинами A = sin(x) и B = cos(x), то он будет близок к нулю, т. е. зависимость между величинами отсутствует. Между тем, величины A и B очевидно связаны функционально по закону sin2(x) + cos2(x) = 1.
Ограничения корреляционного анализа
Графики распределений пар (x,y) с соответствующими коэффициентами корреляций x и y для каждого из них. Обратите внимание, что коэффициент корреляции отражает линейную зависимость (верхняя строка), но не описывает кривую зависимости (средняя строка), и совсем не подходит для описания сложных, нелинейных зависимостей (нижняя строка).
- Применение возможно в случае наличия достаточного количества случаев для изучения: для конкретного вида коэффициента корреляции составляет от 25 до 100 пар наблюдений.

- Второе ограничение вытекает из гипотезы корреляционного анализа, в которую заложена линейная зависимость переменных. Во многих случаях, когда достоверно известно, что зависимость существует, корреляционный анализ может не дать результатов просто ввиду того, что зависимость нелинейна (выражена, например, в виде параболы).
- Сам по себе факт корреляционной зависимости не даёт основания утверждать, какая из переменных предшествует или является причиной изменений, или что переменные вообще причинно связаны между собой, например, ввиду действия третьего фактора.
Область применения
Данный метод обработки статистических данных весьма популярен в экономике и социальных науках (в частности в психологии и социологии), хотя сфера применения коэффициентов корреляции обширна: контроль качества промышленной продукции, металловедение, агрохимия, гидробиология, биометрия и прочие.
Популярность метода обусловлена двумя моментами: коэффициенты корреляции относительно просты в подсчете, их применение не требует специальной математической подготовки.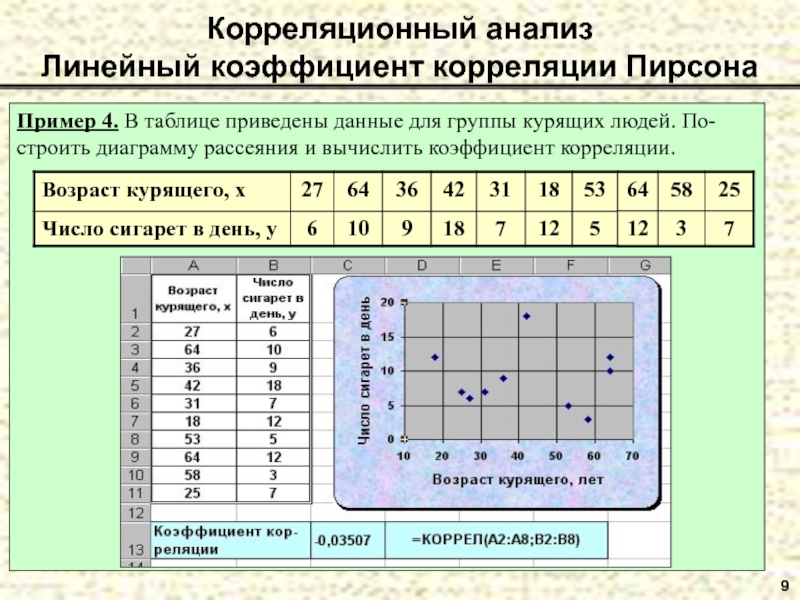 В сочетании с простотой интерпретации, простота применения коэффициента привела к его широкому распространению в сфере анализа статистических данных.
В сочетании с простотой интерпретации, простота применения коэффициента привела к его широкому распространению в сфере анализа статистических данных.
Ложная корреляция
Часто заманчивая простота корреляционного исследования подталкивает исследователя делать ложные интуитивные выводы о наличии причинно-следственной связи между парами признаков, в то время как коэффициенты корреляции устанавливают лишь статистические взаимосвязи.
В современной количественной методологии социальных наук, фактически, произошел отказ от попыток установить причинно-следственные связи между наблюдаемыми переменными эмпирическими методами. Поэтому, когда исследователи в социальных науках говорят об установлении взаимосвязей между изучаемыми переменными, подразумевается либо общетеоретическое допущение, либо статистическая зависимость.
См. также
Wikimedia Foundation. 2010.
Корреляционное исследование — это… Что такое Корреляционное исследование?
Корреля́ция — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом, изменения одной или нескольких из этих величин приводят к систематическому изменению другой или других величин. Математической мерой корреляции двух случайных величин служит коэффициент корреляции.
При этом, изменения одной или нескольких из этих величин приводят к систематическому изменению другой или других величин. Математической мерой корреляции двух случайных величин служит коэффициент корреляции.
Корреляция может быть положительной и отрицательной (возможна также ситуация отсутствия статистической взаимосвязи — например, для независимых случайных величин). Отрицательная корреляция — корреляция, при которой увеличение одной переменной связано с уменьшением другой переменной, при этом коэффициент корреляции отрицателен. Положительная корреляция — корреляция, при которой увеличение одной переменной связано с увеличением другой переменной, при этом коэффициент корреляции положителен.
Автокорреляция — статистическая взаимосвязь между случайными величинами из одного ряда, но взятых со сдвигом, например, для случайного процесса — со сдвигом по времени.
Метод обработки статистических данных, заключающийся в изучении коэффициентов (корреляции) между переменными, называется корреляционным анализом.
Коэффициент корреляции
Коэффицие́нт корреля́ции или парный коэффицие́нт корреля́ции в теории вероятностей и статистике — это показатель характера изменения двух случайных величин. Коэффициент корреляции обозначается латинской буквой R и может принимать значения между -1 и +1. Если значение по модулю находится ближе к 1, то это означает наличие сильной связи (при коэффициенте корреляции равном единице говорят о функциональной связи), а если ближе к 0, то слабой.
Коэффициент корреляции Пирсона
Для метрических величин применяется коэффициент корреляции Пирсона, точная формула которого была введена Фрэнсисом Гальтоном:
Пусть X,Y — две случайные величины, определённые на одном вероятностном пространстве. Тогда их коэффициент корреляции задаётся формулой:
- ,
где cov обозначает ковариацию, а D — дисперсию, или, что то же самое,
- ,
где символ обозначает математическое ожидание.
Для графического представления подобной связи можно использовать прямоугольную систему координат с осями, которые соответствуют обеим переменным. Каждая пара значений маркируется при помощи определенного символа. Такой график называется «диаграммой рассеяния».
Метод вычисления коэффициента корреляции зависит от вида шкалы, к которой относятся переменные. Так, для измерения переменных с интервальной и количественной шкалами необходимо использовать коэффициент корреляции Пирсона (корреляция моментов произведений). Если по меньшей мере одна из двух переменных имеет порядковую шкалу, либо не является нормально распределённой, необходимо использовать ранговую корреляцию Спирмена или τ (тау) Кендала. В случае, когда одна из двух переменных является дихотомической, используется точечная двухрядная корреляция, а если обе переменные являются дихотомическими: четырёхполевая корреляция. Расчёт коэффициента корреляции между двумя недихотомическими переменными не лишён смысла только тогда, кода связь между ними линейна (однонаправлена).
Коэффициент корреляции Кенделла
Используется для измерения взаимной неупорядоченности.
Коэффициент корреляции Спирмена
Свойства коэффициента корреляции
- если принять в качестве скалярного произведения двух случайных величин ковариацию , то норма случайной величины будет равна , и следствием неравенства Коши — Буняковского будет:
- .
- Коэффициент корреляции равен тогда и только тогда, когда X и Y линейно зависимы:
- ,
- где . Более того в этом случае знаки и k совпадают:
- .
- Если X,Y независимые случайные величины, то . Обратное в общем случае неверно.
Корреляционный анализ
Корреляционный анализ — метод обработки статистических данных, заключающийся в изучении коэффициентов (корреляции) между переменными. При этом сравниваются коэффициенты корреляции между одной парой или множеством пар признаков для установления между ними статистических взаимосвязей.
Цель корреляционного анализа — обеспечить получение некоторой информации об одной переменной с помощью другой переменной. В случаях, когда возможно достижение цели, говорят, что переменные коррелируют. В самом общем виде принятие гипотезы о наличии корреляции означает что изменение значения переменной А, произойдет одновременно с пропорциональным изменением значения Б: если обе переменные растут то корреляция положительная, если одна переменная растёт, а вторая уменьшается, корреляция отрицательная.
Корреляция отражает лишь линейную зависимость величин, но не отражает их функциональной связности. Например, если вычислить коэффициент корреляции между величинами A = sin(x) и B = cos(x), то он будет близок к нулю, т. е. зависимость между величинами отсутствует. Между тем, величины A и B очевидно связаны функционально по закону sin2(x) + cos2(x) = 1.
Ограничения корреляционного анализа
Графики распределений пар (x,y) с соответствующими коэффициентами корреляций x и y для каждого из них. Обратите внимание, что коэффициент корреляции отражает линейную зависимость (верхняя строка), но не описывает кривую зависимости (средняя строка), и совсем не подходит для описания сложных, нелинейных зависимостей (нижняя строка).
- Применение возможно в случае наличия достаточного количества случаев для изучения: для конкретного вида коэффициента корреляции составляет от 25 до 100 пар наблюдений.
- Второе ограничение вытекает из гипотезы корреляционного анализа, в которую заложена линейная зависимость переменных. Во многих случаях, когда достоверно известно, что зависимость существует, корреляционный анализ может не дать результатов просто ввиду того, что зависимость нелинейна (выражена, например, в виде параболы).
- Сам по себе факт корреляционной зависимости не даёт основания утверждать, какая из переменных предшествует или является причиной изменений, или что переменные вообще причинно связаны между собой, например, ввиду действия третьего фактора.

Область применения
Данный метод обработки статистических данных весьма популярен в экономике и социальных науках (в частности в психологии и социологии), хотя сфера применения коэффициентов корреляции обширна: контроль качества промышленной продукции, металловедение, агрохимия, гидробиология, биометрия и прочие.
Популярность метода обусловлена двумя моментами: коэффициенты корреляции относительно просты в подсчете, их применение не требует специальной математической подготовки. В сочетании с простотой интерпретации, простота применения коэффициента привела к его широкому распространению в сфере анализа статистических данных.
Ложная корреляция
Часто заманчивая простота корреляционного исследования подталкивает исследователя делать ложные интуитивные выводы о наличии причинно-следственной связи между парами признаков, в то время как коэффициенты корреляции устанавливают лишь статистические взаимосвязи.
В современной количественной методологии социальных наук, фактически, произошел отказ от попыток установить причинно-следственные связи между наблюдаемыми переменными эмпирическими методами. Поэтому, когда исследователи в социальных науках говорят об установлении взаимосвязей между изучаемыми переменными, подразумевается либо общетеоретическое допущение, либо статистическая зависимость.
Поэтому, когда исследователи в социальных науках говорят об установлении взаимосвязей между изучаемыми переменными, подразумевается либо общетеоретическое допущение, либо статистическая зависимость.
См. также
Wikimedia Foundation. 2010.
Корреляционное исследование — это… Что такое Корреляционное исследование?
Корреля́ция — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом, изменения одной или нескольких из этих величин приводят к систематическому изменению другой или других величин. Математической мерой корреляции двух случайных величин служит коэффициент корреляции.
Корреляция может быть положительной и отрицательной (возможна также ситуация отсутствия статистической взаимосвязи — например, для независимых случайных величин). Отрицательная корреляция — корреляция, при которой увеличение одной переменной связано с уменьшением другой переменной, при этом коэффициент корреляции отрицателен. Положительная корреляция — корреляция, при которой увеличение одной переменной связано с увеличением другой переменной, при этом коэффициент корреляции положителен.
Положительная корреляция — корреляция, при которой увеличение одной переменной связано с увеличением другой переменной, при этом коэффициент корреляции положителен.
Автокорреляция — статистическая взаимосвязь между случайными величинами из одного ряда, но взятых со сдвигом, например, для случайного процесса — со сдвигом по времени.
Метод обработки статистических данных, заключающийся в изучении коэффициентов (корреляции) между переменными, называется корреляционным анализом.
Коэффициент корреляции
Коэффицие́нт корреля́ции или парный коэффицие́нт корреля́ции в теории вероятностей и статистике — это показатель характера изменения двух случайных величин. Коэффициент корреляции обозначается латинской буквой R и может принимать значения между -1 и +1. Если значение по модулю находится ближе к 1, то это означает наличие сильной связи (при коэффициенте корреляции равном единице говорят о функциональной связи), а если ближе к 0, то слабой.
Коэффициент корреляции Пирсона
Для метрических величин применяется коэффициент корреляции Пирсона, точная формула которого была введена Фрэнсисом Гальтоном:
Пусть X,Y — две случайные величины, определённые на одном вероятностном пространстве. Тогда их коэффициент корреляции задаётся формулой:
- ,
где cov обозначает ковариацию, а D — дисперсию, или, что то же самое,
- ,
где символ обозначает математическое ожидание.
Для графического представления подобной связи можно использовать прямоугольную систему координат с осями, которые соответствуют обеим переменным. Каждая пара значений маркируется при помощи определенного символа. Такой график называется «диаграммой рассеяния».
Метод вычисления коэффициента корреляции зависит от вида шкалы, к которой относятся переменные. Так, для измерения переменных с интервальной и количественной шкалами необходимо использовать коэффициент корреляции Пирсона (корреляция моментов произведений). Если по меньшей мере одна из двух переменных имеет порядковую шкалу, либо не является нормально распределённой, необходимо использовать ранговую корреляцию Спирмена или τ (тау) Кендала. В случае, когда одна из двух переменных является дихотомической, используется точечная двухрядная корреляция, а если обе переменные являются дихотомическими: четырёхполевая корреляция. Расчёт коэффициента корреляции между двумя недихотомическими переменными не лишён смысла только тогда, кода связь между ними линейна (однонаправлена).
Если по меньшей мере одна из двух переменных имеет порядковую шкалу, либо не является нормально распределённой, необходимо использовать ранговую корреляцию Спирмена или τ (тау) Кендала. В случае, когда одна из двух переменных является дихотомической, используется точечная двухрядная корреляция, а если обе переменные являются дихотомическими: четырёхполевая корреляция. Расчёт коэффициента корреляции между двумя недихотомическими переменными не лишён смысла только тогда, кода связь между ними линейна (однонаправлена).
Коэффициент корреляции Кенделла
Используется для измерения взаимной неупорядоченности.
Коэффициент корреляции Спирмена
Свойства коэффициента корреляции
- если принять в качестве скалярного произведения двух случайных величин ковариацию , то норма случайной величины будет равна , и следствием неравенства Коши — Буняковского будет:
- .
- Коэффициент корреляции равен тогда и только тогда, когда X и Y линейно зависимы:
- ,
- где .
 Более того в этом случае знаки и k совпадают:
Более того в этом случае знаки и k совпадают: - .
- Если X,Y независимые случайные величины, то . Обратное в общем случае неверно.
Корреляционный анализ
Корреляционный анализ — метод обработки статистических данных, заключающийся в изучении коэффициентов (корреляции) между переменными. При этом сравниваются коэффициенты корреляции между одной парой или множеством пар признаков для установления между ними статистических взаимосвязей.
Цель корреляционного анализа — обеспечить получение некоторой информации об одной переменной с помощью другой переменной. В случаях, когда возможно достижение цели, говорят, что переменные коррелируют. В самом общем виде принятие гипотезы о наличии корреляции означает что изменение значения переменной А, произойдет одновременно с пропорциональным изменением значения Б: если обе переменные растут то корреляция положительная, если одна переменная растёт, а вторая уменьшается, корреляция отрицательная.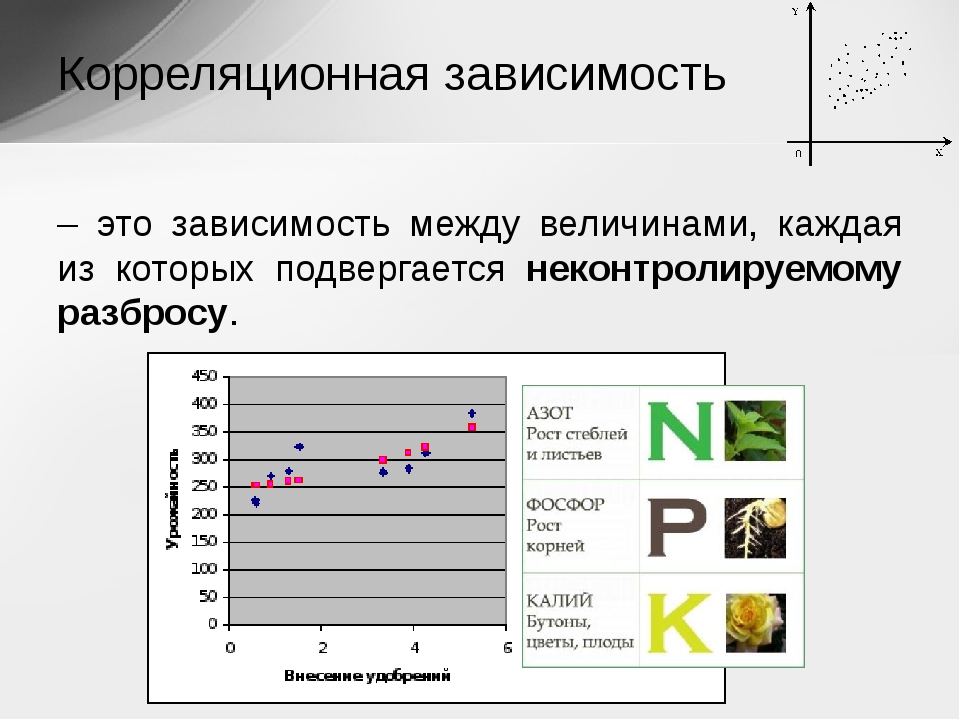
Корреляция отражает лишь линейную зависимость величин, но не отражает их функциональной связности. Например, если вычислить коэффициент корреляции между величинами A = sin(x) и B = cos(x), то он будет близок к нулю, т. е. зависимость между величинами отсутствует. Между тем, величины A и B очевидно связаны функционально по закону sin2(x) + cos2(x) = 1.
Ограничения корреляционного анализа
Графики распределений пар (x,y) с соответствующими коэффициентами корреляций x и y для каждого из них. Обратите внимание, что коэффициент корреляции отражает линейную зависимость (верхняя строка), но не описывает кривую зависимости (средняя строка), и совсем не подходит для описания сложных, нелинейных зависимостей (нижняя строка).
- Применение возможно в случае наличия достаточного количества случаев для изучения: для конкретного вида коэффициента корреляции составляет от 25 до 100 пар наблюдений.

- Второе ограничение вытекает из гипотезы корреляционного анализа, в которую заложена линейная зависимость переменных. Во многих случаях, когда достоверно известно, что зависимость существует, корреляционный анализ может не дать результатов просто ввиду того, что зависимость нелинейна (выражена, например, в виде параболы).
- Сам по себе факт корреляционной зависимости не даёт основания утверждать, какая из переменных предшествует или является причиной изменений, или что переменные вообще причинно связаны между собой, например, ввиду действия третьего фактора.
Область применения
Данный метод обработки статистических данных весьма популярен в экономике и социальных науках (в частности в психологии и социологии), хотя сфера применения коэффициентов корреляции обширна: контроль качества промышленной продукции, металловедение, агрохимия, гидробиология, биометрия и прочие.
Популярность метода обусловлена двумя моментами: коэффициенты корреляции относительно просты в подсчете, их применение не требует специальной математической подготовки. В сочетании с простотой интерпретации, простота применения коэффициента привела к его широкому распространению в сфере анализа статистических данных.
В сочетании с простотой интерпретации, простота применения коэффициента привела к его широкому распространению в сфере анализа статистических данных.
Ложная корреляция
Часто заманчивая простота корреляционного исследования подталкивает исследователя делать ложные интуитивные выводы о наличии причинно-следственной связи между парами признаков, в то время как коэффициенты корреляции устанавливают лишь статистические взаимосвязи.
В современной количественной методологии социальных наук, фактически, произошел отказ от попыток установить причинно-следственные связи между наблюдаемыми переменными эмпирическими методами. Поэтому, когда исследователи в социальных науках говорят об установлении взаимосвязей между изучаемыми переменными, подразумевается либо общетеоретическое допущение, либо статистическая зависимость.
См. также
Wikimedia Foundation. 2010.
Определение, типы и примеры корреляционных исследований / наука | Thpanorama
Якорреляционное исследование это тип неэкспериментального исследования, в котором исследователи измеряют две переменные и устанавливают статистическую взаимосвязь между ними (корреляция), без необходимости включать внешние переменные для достижения соответствующих выводов. .
.
Есть две существенные причины, почему исследователи заинтересованы в этих статистических отношениях между переменными и мотивированы для проведения корреляционных исследований.
Во-первых, потому что они не верят, что связь между этими переменными является случайной, то есть исследователь будет применять опрос, использование которого известно группе ранее выбранных людей..
Вторая причина, по которой этот тип исследований проводится вместо экспериментов, заключается в причинно-следственной статистической взаимосвязи между переменными, таким образом, исследователи не могут управлять переменными независимо, поскольку это невозможно, нецелесообразно и неэтично.
Существует три типа корреляционных исследований (естественные наблюдения, опросы и анкетирование, анализ информации). Таким же образом, корреляция между переменными может быть положительной (прямо пропорциональной) или отрицательной (обратно пропорциональной). Указывает, каким образом одна переменная может влиять на другую.
Обычно считается, что корреляционные исследования должны включать две количественные переменные, такие как оценки, результаты числа событий, повторенных в течение определенного периода времени..
Тем не менее, наиболее важной особенностью корреляционного исследования является то, что две обработанные переменные измеряются (без манипуляций), и результаты верны независимо от типа переменной (количественной или категориальной) (Price, Jhangiani, & Chiang, 2017).
Вам также может быть интересно узнать о полевых исследованиях: что это такое, характеристики и этапы.
Определение корреляционного исследованияТермин корреляция определяется как отношение между двумя переменными. Основная цель использования корреляций в области исследований — выяснить, какие переменные связаны друг с другом. Таким образом, конкретное событие с научной точки зрения понимается как переменная.
Корреляционное исследование состоит в поиске разнообразных переменных, которые взаимодействуют друг с другом, и, таким образом, когда изменение одного из них очевидно, можно предположить, каким будет изменение другого, которое непосредственно связано с ним. .
.
Этот процесс требует от исследователя использовать переменные, которые он не может контролировать. Таким образом, исследователь может быть заинтересован в изучении переменной A, ее связи и влияния на переменную B.
Например, исследователь может изучить тип мороженого, предпочтительный в зависимости от возраста, и определить предпочтения потребителей на основе их возраста. Мир полон коррелированных событий, где, если переменная A затронута, есть большая вероятность, что переменная B также будет затронута..
В рамках корреляционного исследования есть два разных типа, один положительный и один отрицательный. Положительные корреляции означают, что переменная A увеличивается, а следовательно, и переменная B. С другой стороны, когда мы говорим об отрицательных корреляциях, когда переменная S увеличивается, переменная B уменьшается.
Корреляционные исследования основаны на многочисленных статистических тестах, которые указывают коэффициенты корреляции между переменными. Эти коэффициенты представлены численно, чтобы указать силу и направление отношений (Alston, 2017).
Эти коэффициенты представлены численно, чтобы указать силу и направление отношений (Alston, 2017).
В процессе корреляционного исследования исследователь не всегда имеет возможность выбрать переменные, которые он хочет изучать. Когда это происходит, говорят, что проводятся полуэкспериментальные исследования (Kowalczyk, 2015).
Существует три типа исследований корреляции, в рамках которых переменные могут или не могут контролироваться. Это зависит от типа вашего подхода к данной теме и того, как вы хотите провести исследование..
1- Естественное наблюдениеПервым из трех типов корреляционных исследований является естественное наблюдение. Таким образом, исследователь наблюдает и записывает переменные в естественной среде, не вмешиваясь в то же самое.
Примером этого может быть классная комната. Исследователь может проанализировать результаты и итоговые оценки, полученные студентами в отношении уровня отсутствия на рабочем месте. .
.
Этот тип исследования корреляции может занимать много времени и не всегда позволяет контролировать переменные.
2- Обзоры и вопросникиДругой тип корреляционного исследования возникает при проведении опросов и анкет, из которых собирается информация. В рамках этого типа исследований должна быть выбрана случайная выборка или группа участников.
Например, когда удовлетворительно завершен опрос о новом продукте в торговом центре, он участвует в исследовательском опросе с корреляционными целями. Этот тип опроса используется, чтобы предсказать, будет ли продукт успешным.
Использование опросов в рамках корреляционного исследования обычно очень удобно, однако, если участники не честны по этому поводу, они могут изменить конечные результаты исследования разными способами..
3- Анализ информацииПоследний тип корреляционных исследований, который можно провести, — это анализ данных, ранее собранных другими исследователями. Например, можно судить о судимости населения, чтобы предсказать, как криминальная статистика влияет на местную экономику..
Например, можно судить о судимости населения, чтобы предсказать, как криминальная статистика влияет на местную экономику..
Файлы запросов обычно доступны бесплатно в качестве инструментов запросов. Однако для того, чтобы установить существенную корреляционную связь, обычно необходимо иметь доступ к большим объемам информации..
В рамках этого типа исследований исследователи не контролируют тип информации, которая была записана (Раулин, 2013).
примеровГрузовик мороженогоХороший способ объяснить, как работает корреляционное исследование, — подумать о тележке для мороженого. Таким образом, человек может научиться распознавать особый звук грузовика с мороженым, уметь воспринимать его на расстоянии.
Когда звук грузовика становится громче, человек может распознать, что грузовик ближе.
Таким образом, переменная A будет звуком грузовика, а переменная B будет расстоянием, на котором находится грузовик. В этом примере корреляция положительная, в которой звук грузовика увеличивается, чем ближе расстояние от грузовика.
Если бы у нас были разные звуки грузовика, человек мог бы распознать их все и связать их с разными переменными (Ary, Jacobs, Razavieh, & Sorensen, 2009).
Выявление аутизма у детейВ рамках этого исследования использовалась исследовательская группа с тестом, предназначенным для выявления различий между различными группами населения, чтобы определить, существует ли какая-либо корреляция между анализируемыми переменными..
Была взята выборка из 66 участников, все они дети 12 месяцев. Среди этих участников 35 детей имели старших братьев и сестер с клиническим диагнозом аутизм. У оставшихся 31 ребенка были братья и сестры, у которых не было никакой степени аутизма.
Всех участников попросили манипулировать объектом для выполнения определенной задачи и, таким образом, иметь возможность идентифицировать какое-то нормальное и ненормальное поведение..
В возрасте 24 или 36 месяцев та же самая группа детей была снова проанализирована, чтобы определить, была ли склонность к аутизму или проблемы с развитием.
Результаты показали, что у 9 из детей, у которых были родные братья и сестры аутизма, также была диагностирована некоторая степень аутизма. Был рассчитан ряд корреляций для этих детей, включая их результаты в начальном тесте на манипуляции и последующем тесте..
Было доказано, что атипичная манипуляция предметом 12-месячного ребенка была положительно коррелирована с последующим диагнозом аутизма. Точно так же это было отрицательно связано с актуальным или нормальным развитием ребенка (Siegle, 2015).
Расизм в афро-американских женщинахВ рамках этого исследования были подняты три первоначальных вопроса об опыте, который афро-американские женщины могли иметь в прошлом..
Эти вопросы задавали вопросы о том, в каких пропорциях эти женщины сталкивались с расизмом..
Таким образом, ставится под сомнение взаимосвязь этого опыта с возможными психологическими условиями женщин и способностью этих женщин смягчать воздействие расизма на их психологическое состояние. .
.
Выборка включала 314 афроамериканских женщин, которые ответили на письменный опрос, предназначенный для оценки их опыта в отношении расизма, потенциальных психологических условий, вызванных этим явлением, и выбора поведения для решения ситуаций дискриминации..
Результаты показали проявление многочисленных форм расизма (оскорбления со стороны коллег, игнорирование продавцами в универмагах, расистские шутки и др.).
Об этих различных формах расизма сообщили более 70% участников. Стало очевидным, что расизм был распространенным опытом среди афро-американских женщин.
Коэффициенты корреляции выявили значительную положительную связь между зарегистрированным расизмом и событиями и возможными психологическими проблемами этих женщин. Этот вывод охватывает механизмы борьбы с расизмом, который они используют.
Другие результаты показали, что различные модели, используемые афро-американскими женщинами для борьбы с этими инцидентами, регулярно использовались частично успешно. .
.
Таким образом, многие женщины превратили бы негативный опыт в гораздо худший, пытаясь смягчить его психологическое воздействие (Goodwin & Goodwin, 2017)..
ссылки- Алстон, C. (2017). ком. Получено из корреляционных исследований в психологии: примеры, преимущества и типы: study.com.
- Ary, D., Jacobs, L.C., Razavieh, A. & Sorensen, C.K. (2009). Введение в исследования в области образования. Белмонт: Уодсворт.
- Гудвин, К. Дж. И Гудвин, К. А. (2017). Исследования в области психологии методов и дизайна. Источник Молнии Inc.: Уилли.
- Ковальчик Д. (2015). ком. Получено из корреляционных исследований: определение, цель и примеры: study.com.
- Price, P.C., Jhangiani, R.S., & Chiang, I.-C. А. (2017). Корреляционные исследования. Получено из Что такое корреляционное исследование?: Opentextbc.ca.
- Раулин Г. &. (2013). Методы исследования Грациано и Раулина (8-е издание).
 Получено на примере корреляционного исследования: graziano-raulin.com.
Получено на примере корреляционного исследования: graziano-raulin.com. - Siegle, D. (10 ноября 2015 г.). Университет Коннектикута. Получено от Основы образовательных исследований от Del Siegle: researchbasics.education.uconn.edu.
Важны и нужны ли ссылки в 2019? Корреляционное исследование + аналитика
Важная ремарка: корреляция — не означает наличия причинно-следственной связи, но, может говорить о её наличии или опровергать её.
В данной статье авторы пытаются, в том числе, понять, может ли текущая корреляция числа ссылок с позицией в Google носить случайный характер?
Мы рассмотрим исследование Stone Temple при поддержке MOZ, посвященное внешним ссылкам как фактору ранжирования. Это уже четвёртый эксперимент, но на этот раз объём данных значительно подрос, и западные коллеги затронули важную тему — влияние ссылок на различные тематики и секторы рынка в 2018-2019 годах.
Результаты
Данные были получены с помощью MOZ Link Explorer, индекс которого уже достаточно расширился и вполне репрезентативен. Ниже представлено количество найденных ссылок для 16 тысяч запросов, участвующих в предыдущих и последнем исследованиях Stone Temple:
Ниже представлено количество найденных ссылок для 16 тысяч запросов, участвующих в предыдущих и последнем исследованиях Stone Temple:
Количество ссылок на страницу как фактор ранжирования
Посмотрим на несколько диаграмм в рамках исследования «Нужны ли ссылки в 2019»? Первый набор данных основан на общем количестве внешних ссылок, ведущих на страницу и её позициями. Для них был рассчитан коэффициент корреляции Спирмена, который в общих чертах показывает линейную связь между случайными величинами. Ниже мы рассмотрим показатели подробнее.
Вот, как менялись коэффициенты для 6 000 одних и тех же запросов за последние 2 года:
На первый взгляд кажется, что зависимость со временем слабеет, но на самом деле такое отклонение вписывается в пределы обычной дисперсии, то есть, случайного разнообразия данных.
Обратить внимание скорее следует на то, что связь между количеством ссылок и ранжированием довольно сильна. Вот коэффициенты уже для 16 000 запросов, которые анализируются, начиная со второго исследования:
И наконец, для 27 000 запросов, изученных в рамках последнего анализа.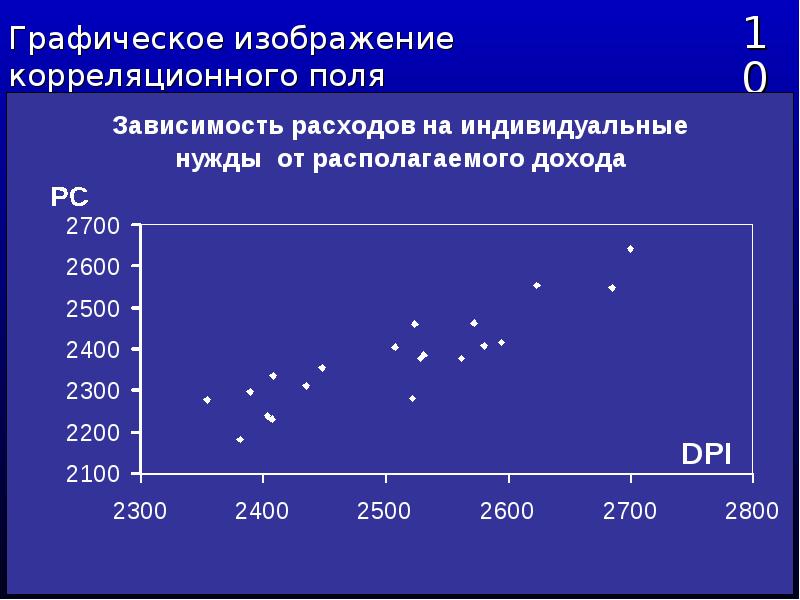 Связь между позициями и количеством ссылок по-прежнему очевидна:
Связь между позициями и количеством ссылок по-прежнему очевидна:
Ссылки как фактор ранжирования по типам запросов
Как обстоят дела с информационными и коммерческими запросами? У Stone Temple есть данные, показывающие корреляцию между количеством ссылок и позициями URL для разных типов запросов (для информационных зависимость чуть более сильная):
Не забывайте, проверить коммерциализацию и геозависимость можно с помощью нашего бесплатного инструмента.
Ссылки как фактор ранжирования в различных сферах
В рамках исследования также были выделены несколько сегментов коммерческих запросов: медицинская сфера, финансы, технологии и остальные.
Результаты следующие (финансовый сегмент более требователен к ссылочному):
Для информационных запросов в этих же тематиках картина несколько отличается:
Агрегация по нормализованному числу ссылок
Нормализация в данном случае означает, что количество ссылок для каждой позиции в выдаче по запросу разделили на самое большее число ссылок, найденных по этому же запросу. В результате наибольшая оценка ссылок для запроса будет иметь значение «1». Таким образом, было ограничено чрезмерное влияние запросов со слишком большим количеством найденных ссылок.
В результате наибольшая оценка ссылок для запроса будет иметь значение «1». Таким образом, было ограничено чрезмерное влияние запросов со слишком большим количеством найденных ссылок.
Причина применения такой методологии в том, что для поисковых систем важно не просто количество, но и качество и релевантность ссылочной массы. В агрегированном анализе мы получаем общее представление о влияние ссылок на большой массив данных.
Вот, какую корреляцию получили для 6 000 запросов, участвующих во всех четырех исследованиях:
Для 16 000, проанализированных трижды:
И для 27 000 запросов за 2018 год:
Заметили? Зависимость гораздо более очевидна, чем для ненормализованных значений.
Как взаимодействуют основные факторы ранжирования и ссылки в 2019?
Чтобы понять значимость корреляционных коэффициентов и сделать выводы о важности ссылок, необходимо выяснить, как именно факторы ранжирования взаимодействуют друг с другом.
Для примера авторы исследования выделили две категории факторов:
1. Актуальный и качественный контент. По-простому, если страница не имеет отношения к запросу, то она не должна ранжироваться. Это очевидно, но есть нюансы.
Чтобы их проиллюстрировать, представим, что у нас есть 10 «кусков» контента, которые достаточно релевантны для ранжирования по запросу, и присвоим им некие баллы релевантности (на картинке «Relevance Score»). Например:
Довольно неплохо в качестве алгоритма для ранжирования, верно? Обратите внимание, оценка релевантности установлена в очень узком диапазоне, и это не случайно (далее станет ясно почему).
Короче говоря, если контент не релевантен запросу, то он не должен ранжироваться, сколько бы внешних ссылок у него не было.
Проблема в том, что контент очень легко сделать релевантным, просто добавив в него ключевые слова. Поэтому нужно добавить ещё один показатель — качество («Quality Score»). Посмотрим, как это повлияет на наш алгоритм:
Уже лучше, но как и в случае оценки релевантности, анализ качества — сложная задача. Так давайте добавим ещё один показатель, отвечающий за оценку ссылок («Link Score» в таблице ниже):
Так давайте добавим ещё один показатель, отвечающий за оценку ссылок («Link Score» в таблице ниже):
Видите как меняются позиции («Rank») в трёх представленных сценариях? Довольно существенно, несмотря на узкий диапазон выбранных значений.
В этом упрощенном варианте алгоритма Google, ссылки играют значимую роль и нужны для ранжирования. Какой коэффициент корреляции Спирмена для результатов в последней таблице? 0,28. Довольно низкий, несмотря на ограниченное количество факторов в примере.
2. Другие факторы и алгоритмы вступают в игру. Например:
-
Локализация выдачи.
-
Результаты поиска по картинкам.
-
Видеорезультаты.
-
Query Deserves Diversity (QDD или «запрос заслуживает разнообразия»).
Перечисленное может повлиять примерно на 15% наших «лабораторных» результатов. Для иллюстрации, возьмём предыдущую таблицу и добавим в неё QDD (алгоритм «запрос заслуживает разнообразия»), чтобы «подмешать» в анализ ещё один алгоритм:
Как изменился коэффициент корреляции теперь? Упал до 0,03. Упс.
Упс.
Надеемся, что это даёт представление, почему коэффициент 0,3 для реальных данных из SERP (в начале статьи) показывает исключительную важность ссылок. Получается, их значение просто огромно.
Прогресс Google в борьбе со ссылочным спамом
Те, кто говорит о снижении роли ссылок в качестве фактора ранжирования, часто приводят в качестве аргумента ссылочный спам. Мол, Google больше не хочет участвовать в этой борьбе и просто снизил значение бэклинков.
Такая проблема действительно существовала с 2002 по 2013 годы, но с выходом алгоритм «Пингвин» и волны ручных санкций в 2012 ход битвы изменился. С релизом Penguin 4.0 в 2016 году, Google редко наказывает сайты за некачественные и спамные ссылки — он просто их не учитывает.
И если ранее одной из основных методик в SEO была массовая закупка ссылок, то теперь правила игры изменились и целая индустрия ушла в «подполье» — всё должно быть предельно аккуратно и качественно. Алгоритм «Пингвин» ещё раз доказывает — ссылки важны. Иначе какой прок Google от траты ресурсов на борьбу со спамом?
Иначе какой прок Google от траты ресурсов на борьбу со спамом?
Яндекс со своим Непот-фильтром также не исключение. Помните, что для диагностики у нас есть инструменты и надёжные способы проверки.
Почему ссылки такой ценный сигнал для поисковых систем?
Кратко можно обозначить две причины почему не хватает казалось бы очевидных метрик оценки качества:
-
Социальные сигналы (лайки, шеры). Google не может зависеть от сигналов сторонних платформ вроде Facebook. Даже LinkedIn перестали обмениваться с последними данными о лайках и шерах. Поисковым системам они также не кажутся достаточно ценными.
-
Поведенческие факторы и вовлечённость пользователей. Хотя споры о поведенческих как о факторах ранжирования не утихают, ПФ — всё же шумный сигнал и только его часто оказывается недостаточно для анализа качества страницы.
Так почему всё-таки ссылки?
-
Они требуют ресурсов, дополнительной работы и даже материальных вложений.
 Для Google это знак — к странице подошли с усердием. Добавить ссылку в пост социальной сети легко, куда сложнее овладеть аутрич-техниками и заслужить доверие вебмастеров.
Для Google это знак — к странице подошли с усердием. Добавить ссылку в пост социальной сети легко, куда сложнее овладеть аутрич-техниками и заслужить доверие вебмастеров. -
Когда вы размещаете ссылку на любую внешнюю страницу, вы волей-неволей идентифицируете свой сайт с брендом, на который ссылаетесь. Это говорит об ответственности перед пользователями и требует соответствующего качества.
-
Теперь самое главное — размещая ссылку на внешний ресурс, вы предлагаете своим пользователям покинуть ваш собственный сайт. Это ли не признак, заслуживающий доверия?
Важная ремарка: справедливости ради, стоит отметить, что все эти аргументы не помешали Яндексу существенно понизить значимость ссылочных факторов, начиная с 2014 года и сделать ставку на кликстрим и поведенческие факторы.
Укрепление результатов с помощью тематических кейсов
Stone Temple проводят множество маркетинговых кампаний для крупных клиентов. Их специалисты используют полученные результаты на практике, и вот какую выборку они представили (ключевая фраза / частотность запроса / позиция до / позиция после / количество новых ссылок):
Их специалисты используют полученные результаты на практике, и вот какую выборку они представили (ключевая фраза / частотность запроса / позиция до / позиция после / количество новых ссылок):
Успех! Ссылки работают и действительно имеют большое значение, но без прокаченного и релевантного запросу контента они бесполезны.
Для анализа входящих ссылок на собственные проекты используйте наши инструменты:
Всем побольше бэклинков и позиций повыше!
Исследование гемограмм пациентов
Исходные данные
Импорт из Excel в STATISTICA
Визуальный анализ
Диаграмма рассеяния
Способ 1
Способ 2
Средство Кисть
Диаграмма Вороного
Описательный (дескрипитивный) анализ гемограмм
Анализ выбросов
Корреляционный анализ
Корреляции Пирсона
Корреляции Спирмена и Кендалла
Исследование эффективности лечения: введение новой переменной
Цель дальнейшего исследования
Проверка гипотезы о нормальности
Сравнение выборок
Какой метод лечения более эффективен?
Есть ли существенное различие состояний пациентов до и после лечения?
Исходные данные
Исходная таблица данных содержится в формате Excel.
Таблица содержит информацию о 150 пациентах.
Четыре столбца содержат значения показателей их гемограмм – количество эритроцитов (в 1012/л), тромбоцитов (109/л), лейкоцитов (109/л), гемоглобин (г/л).
Импорт из Excel в
STATISTICAШаг 1. При попытке открытия файла в системе STATISTICA (через меню Файл/Открыть) программа предложит нам на выбор несколько вариантов.
Выберем второй пункт.
Шаг 2. Далее необходимо выбрать номер листа в таблице Excel, который содержит нужную нам информацию. Сделать это очень просто.
Выбреем Лист 1 и нажмём OK.
Шаг 3. Далее вам необходимо:
-
указать диапазон значений во внешнем файле данных, который будет импортирован;
-
решить, надо ли импортировать имена наблюдений и переменных;
-
сохранить (или нет) формат ячеек из исходной таблицы.

Поставим галочки во все поля и нажмём OK.
Шаг 4. Теперь в программе STATISTICA открыта таблица.
Сохраним её под именем Гемограмма.sta.
Шаг 4. Введём дополнительную информацию о переменных.
Для этого выберем в меню пункт Данные/Все спецификации переменных.
В появившемся диалоге Редактор спецификаций переменных можно: указать длинные имена, изменить типы данных, коды пропущенных данных, добавить новые переменные или удалить старые и т.д.
Визуальный анализ
Вначале данные нужно увидеть…
Система STATISTICA включает широкий спектр графических методов для визуального представления результатов исследований. Все графические средства системы STATISTICA обеспечивают возможность выбора встроенного аналитического интерактивного метода анализа и содержат большой набор программ настройки, позволяющих пользователю интерактивно управлять отображением информации на экране.
Диаграмма рассеяния
Построим диаграмму рассеяния для переменной Тромбоциты. Сделать это очень просто.
Из медицинской практики известно, что увеличение числа тромбоцитов в крови может привести к тромбозу.
Для выявления больных со слишком большим уровнем тромбоцитов в крови построим диаграмму рассеяния переменных Номер пациента и Тромбоциты.
Врач определяет критический уровень количества тромбоцитов в крови для проведения операции. Пусть это значение равно 250.
Проведём горизонтальную прямую, соответствующую данному значению.
Это можно сделать двумя способами.
Способ 1
Выберем из раскрывающегося списка пункт Параметры графика. В появившемся окне перейдём на закладку Ось: Дополнительные риски.
Выберем Ось – Левая Х, укажем Положение = 250, поставим галочку в окне сетка.
Можно также настроить тип и толщину линии. Для внесения изменений нажмём на кнопку Сетка.
Для внесения изменений нажмём на кнопку Сетка.
В итоге на диаграмме рассеяния отобразится прямая Тромбоциты = 250.
Способ 2
Воспользуемся панелью Графические инструменты.
Выберем рисование стрелки и проведём соответствующую прямую на графике
Как и раньше, можно настраивать опции построенного объекта.
Теперь выделим пациентов, количество тромбоцитов в крови которых превышает данный уровень.
Для этого воспользуемся средством Кисть.
Средство Кисть
Средство Кисть является очень удобным для визуального анализа данных.
Нажмём на кнопку 2M Закрашивание на панели инструментов.
Выделим точки, соответствующие наблюдениям, лежащим выше прямой Тромбоциты = 250.
Если мы теперь откроем таблицу Редактор данных графика, то отмеченные наблюдения будут выделены красным цветом.
Диаграмма Вороного
Построим диаграмму Вороного по переменным Гемоглобин и Тромбоциты. Сделать это очень просто.
На диаграмме Вороного значения двух переменных X и Y изображаются, как на диаграмме рассеяния, а затем пространство между отдельными точками данных делится границами, окружающими каждую точку данных, на области по следующему принципу: каждая точка области находится ближе к заключенной внутри точке данных, чем к любой другой соседней точке данных.
Приведем пример практического использования диаграммы Вороного.
Предположим, что на анализ поступил новый больной.
Для назначения лечения было бы полезно знать, какая гемограмма ему наиболее близка. Это можно сделать с помощью диаграммы Вороного.
Пусть в поступившей гемограмме указаны значения: Тромбоциты = 220 и Гемоглобин = 105. Проведём на графике соответствующие прямые; точка пересечения прямых будет соответствовать новому пациенту.
Выявим наблюдение, которое является «хозяином» области, в которое попадает данное наблюдение.
Для этого воспользуемся средством Кисть.
Описательный (дескриптивный) анализ гемограмм
Вычислим описательные статистики для переменных, содержащих информацию о гемограммах. Сделать это очень просто.
Шаг 1. Запустим модуль Основные статистики и таблицы.
Выберем пункт Описательные статистики. Нажмём OK.
Шаг 2. Выбор переменных
Шаг 3. На вкладке Дополнительно укажем интересующие нас статистики.
Нажав OK, получим таблицу с описательными статистиками.
Описательные статистики по группам
Достаточно часто возникает необходимость вычислить описательные статистики отдельно по каждой группе наблюдений.
Например, вычислим средние значения показателей гемограммы отдельно для каждой группы пациентов, а также для мужчин и для женщин.
Шаг 1. В диалоге Основные статистики и таблицы выберем пункт Группировка и однофакторный ДА.
В окне Внутригрупповые статистики и корреляции перейдём на вкладку Списки таблиц.
Шаг 2. Выберем группирующие переменные.
Шаг 3. Выберем зависимые переменные.
Нажмём на кнопку OK в диалоге Внутригрупповые статистики и таблицы.
В рабочей книге STATISTICA появится таблица, содержащая значения средних по группам.
Анализ выбросов
Выбросами являются резко выделяющиеся наблюдения, например, пациенты с избыточным числом тромбоцитов.
Выявление выбросов осуществляется посредством построения двумерных диаграмм размаха.
Построим диаграмму размаха по переменной Тромбоциты.
Выберем в меню пункт Графики/2M Графики/Диаграммы размаха. В появившемся окне перейдём на вкладку Дополнительно.
Укажем переменные.
Пока что мы не будем указывать группирующую переменную.
Отметим, что на вкладке Дополнительно окна 2M Диаграмма размаха Вы можем настроить опции для выявления наблюдений – выбросов (например, Вы можете указать Коэффициент выбросов).
Нажмём OK в диалоге 2M Диаграмма размаха.
На диаграмме размаха отмечены четыре выброса – три «слишком больших» значения и одно «слишком маленькое».
Визуально анализируя диаграмму размаха, Вы можете получить представление об изменчивости переменной.
Определим, какие именно наблюдения являются выбросами. Один из способов нам уже известен – можно построить диаграмму рассеяния для переменных Номер наблюдения и Тромбоциты и при помощи средства Кисть выделить нужные наблюдения.
Опишем другой способ. Расположим наблюдения по убыванию переменной Тромбоциты.
Для этого выберем из меню пункт Данные/Сортировка.
В появившемся окне укажем параметры Ключа 1.
После нажатия на кнопку OK наблюдения в исходной таблице данных будут расположены в порядке убывания переменной Тромбоциты.
Теперь мы можем определить, какие наблюдения являются выбросами – это будут первые три и последнее наблюдения в таблице. Итак, «нестандартный» уровень тромбоцитов в крови выявлен у пациентов номер 71, 87, 79 и 97.
Теперь вновь вызовем диалог 2M Диаграмма размаха и зададим в окне Переменные в качестве группирующей переменной переменную Пол.
Отметим, что наблюдения – выбросы, отмеченные на этой диаграмме, отличаются от наблюдений-выбросов на диаграмме, построенной без разбиения на группы.
Например, значение Тромбоциты = 300, являющееся выбросом для наблюдений, рассмотренных вместе, оказывается «нормальным» при рассмотрении только группы женщин. Есть и примеры обратного: значение Тромбоциты = 73 оказывается выбросом для группы мужчин, но при рассмотрении всех наблюдений оно оказывается «нормальным».
Корреляционный анализ
Вычислим корреляции между переменными Var4 – Var7. Сделать это очень просто.
Корреляции Пирсона
Запустим модуль Основные статистики и таблицы. В появившемся окне выберем пункт Парные и частные корреляции.
Отобразится окно Парные и частные корреляции.
Нажмём на кнопку Квадратная матрица и укажем переменные.
После нажатия на кнопку OK в диалоге Парные и Частные корреляции в рабочую книгу добавится таблица с коэффициентами корреляции между указанными переменными.
Итак, почти все переменные попарно зависимы; исключение составляет пара Эритроциты – Тромбоциты.
Корреляции Спирмена и Кендалла
Шаг 1. Запустим модуль Непараметрическая статистика. Выберем пункт Корреляции Спирмена, тау Кендалла, гамма.
В появившемся диалоге Ранговые корреляции перейдём на вкладку Дополнительно.
Шаг 2. Зададим переменные.
Шаг 3. Нажмём на кнопку Спирмена R в диалоге Ранговая корреляция.
Теперь вернёмся в окно Ранговая корреляция и нажмём на кнопку Тау Кендалла.
Обратите внимание: коэффициент корреляции Спирмена между переменными Эритроциты и Тромбоциты оказался статистически значимым, в то время как коэффициенты корреляции Кендалла – нет. Это объясняется тем, что коэффициент корреляции Спирмена сильнее реагирует на несогласие ранжировок.
Это объясняется тем, что коэффициент корреляции Спирмена сильнее реагирует на несогласие ранжировок.
Визуально проанализируем зависимость между переменными. С этой целью построим Матричный график.
Нажмём на кнопку Матричный график в диалоге Ранговые корреляции.
Другой способ построения подобного графика: можно выбрать из меню пункт Графика/Матричные графики.
Исследование эффективности лечения: введение новой переменной
Введем новую переменную, характеризующую эффективность лечения.
В качестве меры эффективности лечения выберем величину
,
где — состояние пациента до лечения (девятая переменная в таблице), — состояние пациента после лечения (десятая переменная в таблице).
Эта величина обладает следующими свойствами:
1) Чем ближе значение к 1, тем эффективнее лечение. В крайнем случае, когда пациент поступил в предсмертном состоянии (10), а после лечения оказался абсолютно здоров (100), значение величины равно 0.9.
2) Чем ближе значение к -1, тем менее эффективно лечение. В крайнем случае, когда пациент поступил абсолютно здоровым (100), а после лечения оказался в предсмертном состоянии (10), значение величины равно -0.9.
3) Значение = 0 означает, что состояние пациента не изменилось.
Добавим в таблицу новую переменную, назовём её Эффективностью, укажем формат отображения, зададим формулу для её вычисления.
В итоге в таблице появится новый столбец.
Цель дальнейшего исследования
Целью исследования, которое мы сейчас проведём, является получение ответов на следующие вопросы:
1) Какой метод лечения более эффективен?
2) Есть ли существенное различие состояний пациентов до и после лечения?
Проверка гипотезы о нормальности для переменной Эффективность
Для ответа на поставленные вопросы можно использовать T-критерий переменной Эффективность. Этот критерий требует нормальность распределения переменной, поэтому перед использованием проверим гипотезу о нормальности.
Сначала проверим визуальными методами.
Построим гистограмму по переменной Эффективность. Для этого выберем из меню пункт Графика/Гистограммы.
На вкладке Дополнительно укажем: Распределение = Нормальное, количество категорий – 7 (приблизительное значение двоичного логарифма от 150, то есть от количества наблюдений), выберем переменную – Эффективность.
Гипотеза о нормальности кажется очень неправдоподобной (особенно «плохо» выглядят крайние столбцы).
Тот же вывод следует сделать по нормальному вероятностному графику.
Если наблюдаемые значения (откладываемые по оси X) были бы распределены нормально, то все значения на графике должны были попасть на прямую линию. Однако этого не наблюдается.
Теперь вычислим некоторые описательные статистики для переменной Эффективность.
На вкладке Дополнительно диалога Описательные статистики поставим галочки в полях Асимметрия, стандартная ошибка асимметрии, Эксцесс, Стандартная ошибка эксцесса.
Нажмём OK.
Судя по значению Асимметрии, распределение переменной Эффективность можно считать нормальным (0 «почти что» содержится в интервале Ассиметрия ±Стандартная ошибка Асимметрии).
Но судя по значению Эксцесса, гипотезу о нормальности следует отклонить. Как правило, если найдена хотя бы одна существенная «нестыковка», гипотезу смело отклоняют, в то время как соответствие даже всем известным критериям ещё не влечёт справедливость гипотезы.
В заключении обратимся к модулю Подгонка распределений.
Выберем пункт Нормальное в левом столбце, нажмём OK.
В появившемся окне укажем в качестве переменной Эффективность.
Нажмём OK.
Обратите внимание: значение p = 0,00031, то есть значительно меньше 5%. Это значит, что гипотезу о нормальности следует отклонить.
Итак, окончательный вывод: Распределение переменной Эффективность существенно отличается от нормального распределения.
Сравнение выборок
И первый, и второй вопросы, поставленные в пункте Цели исследования, относятся к задаче сравнения выборок. Будем отвечать на вопросы в порядке их постановки.
1) Какой метод лечения более эффективен?
С точки зрения прикладной статистики, задача сводится к сравнению значений переменной Эффективность по группам I и II (сравнение независимых выборок).
Как мы уже выяснили, распределение отличается от нормального, поэтому мы воспользуемся методами непараметрической статистики.
Шаг 1. Запустим модуль Непараметрическая статистика.
Выберем пункт Сравнение двух независимых групп.
Шаг 2. Укажем переменные.
Обратите внимание: коды для группирующей переменной (I и II) автоматически появятся в соответствующих окошках.
Шаг 3. Нажмём на кнопку U-критерий Манна – Уитни.
Обратите внимание на p-уровень: 0,63. Гипотезу о равенстве функций распределения отклонить нельзя. Поэтому выявить явное преимущество одного из методов не удалось.
Неявное преимущество можно обнаружить на основе сравнения диаграмм размаха по переменной Эффективность.
Если мы хотим сравнить, вполне разумно рассмотрение категоризованных диаграмм размаха.
Для этого выберем в меню пункт Графики/категоризованные графики/Диаграмма размаха.
Укажем переменные для этого графика
На вкладке Дополнительно уменьшим количество Y-категорий до 4.
Нажмём OK.
2) Есть ли существенное различие состояний пациентов до и после лечения?
Это уже задача сравнения парных повторных наблюдений.
Как и при ответе на первый вопрос, мы воспользуемся непараметрическими методами.
Шаг 1. Запустим модуль Непараметрическая статистика.
Выберем пункт сравнение Двух зависимых переменных.
Шаг 2. Укажем переменные.
Шаг 3. Нажмём на кнопку Критерий знаков.
Вернёмся в диалог Сравнение двух переменных и нажмём на кнопку Критерий Вилкоксона.
Интерпретация результатов: гипотезу об однородности следует отвергнуть и принять альтернативу доминирования. Так как среднее значение состояния до лечения больше среднего значения состояния после лечения, то следует признать, что лечение существенно улучшает состояние пациентов.
Связанные определения:
Выборочное среднее, среднее значение выборки
Выброс
Дисперсия (рассеяние, разброс)
Дисперсия выборки (выборочная дисперсия)
Коэффициент вариации
Максимум
Математическое ожидание дискретной случайной величины
Математическое ожидание непрерывной случайной величины
Медиана
Меры дисперсии, меры разброса
Минимум
Мода
Описательные статистики
Описательный анализ
Параметры рассеяния
Параметры центральной тенденции
Среднее значение
Среднеквадратичное отклонение популяции
Стандартная ошибка среднего
Стандартное отклонение
В начало
Содержание портала
Что такое корреляционное исследование и как его проводить для успеха в бизнесе
Корреляционное исследование — это важная форма исследования, которую исследователи должны проводить на средних и поздних стадиях всего исследовательского процесса. Особенно это необходимо, если это касается новой темы.
Последовательно после описательного исследования, которое следует за поисковым исследованием, корреляционное исследование изучает взаимосвязь между двумя переменными. Это важно при попытке разобраться в переменных, обнаруженных в результате поисковых и описательных исследований.
Хотя корреляция не равняется причинно-следственной связи, понимание корреляции между двумя переменными имеет решающее значение для того, чтобы увидеть, как подобные отношения могут возникать и как они ведут себя в рамках существующего события, проблемы или явления.
В этой статье подробно рассказывается о корреляционных исследованиях, в том числе о том, почему важно проводить исследования для бизнеса, как их проводить и многое другое.
Определение корреляционного исследованияОдна из основных форм исследования, корреляционное исследование, отображает и объясняет взаимосвязь между двумя переменными. Эта форма исследования не является экспериментальной, поэтому исследователь практически не прилагает усилий для контроля или управления переменными .
переменных, изучаемых в этом виде исследования, могут быть количественными или категориальными.
Корреляционное исследование направлено на поиск неизвестных или предполагаемых взаимосвязей между переменными, поскольку это может указывать на аналогичное поведение или появление других переменных. Если нет, то такого рода исследования по-прежнему эффективны, так как рисует более четкую картину проблемы или явления, которое было обнаружено в ходе поисковых или описательных исследований.
В корреляционных исследованиях исследователи измеряют взаимосвязь между двумя переменными, не контролируя ни одну из них. Смысл такого исследования состоит в том, чтобы обнаружить:
- Положительная корреляция : Возникает, когда переменные изменяются одинаковым образом. Пример: По мере увеличения покупок увеличивается посещаемость магазина.
- Отрицательная корреляция : описывает переменные, которые изменяются противоположным образом. Пример: усиление выгорания сотрудников и сокращение производства.
- Нулевая корреляция: Когда нет связи между переменными. Пример: присутствие сотрудников в офисе не увеличивает количество подписанных контрактов с партнерами B2B.
Эта форма исследования имеет несколько определяющих характеристик, которые исследователи должны учитывать. Эти аспекты помогают идентифицировать эту форму исследования, помогая им использовать ее в будущем или противопоставлять ее причинным или экспериментальным исследованиям.
Ниже перечислены ключевые особенности этого исследования:
- Как и в случае неэкспериментального исследования , исследователям не нужно манипулировать переменными, чтобы либо согласиться, либо не согласиться с гипотезой.
- Он включает в себя измерение и наблюдение взаимосвязи между переменными, при этом не требует внешнего воздействия или каких-либо изменений .
- Он включает ретроспективные элементы, , поскольку он оглядывается на прошлые события и данные переменных, как средство для поиска и вычисления исторических закономерностей между ними.
- Это проводится, когда есть некоторые предварительные знания либо из исследовательских, либо из описательных исследований, так что по крайней мере один из факторов будет иметь отношение к прогнозируемому результату.
- Хотя он может показывать определенную корреляцию между переменными, например положительный, он может не остаться как таковой, так как он может измениться в будущем .
- Переменные можно наблюдать в закрытой среде или с помощью полевых исследований, то есть в общественном пространстве .
- Используется, когда переменные слишком сложны , чтобы их можно было исследовать с помощью экспериментального метода и контролируемых манипуляций.
- It одновременно измеряет переменные и их отношения в реальных условиях.
- Выполняется, когда подозревается, что связь является причинной , но исследователь не может манипулировать независимой переменной из-за сложности, невозможности или юридических ограничений.
- Применяется, когда одна или несколько целей требуют сбора некоторой степени прогноза.
Проведение корреляционных исследований выгодно для бизнеса несколькими способами. Во-первых, это исследование сосредотачивается на ранее неясных или нераскрытых аспектах всего исследовательского процесса, а именно на взаимосвязях между переменными .
Это исследование может c подтвердить или опровергнуть эти отношения, гипотезу об их существовании , а также гипотезу о том, как они связаны с предметом в целом .
Во-вторых, когда бизнес формирует четкое понимание взаимосвязей между определенными переменными — хорошими, плохими или несуществующими, он эффективно вооружается знаниями о том, как двигаться вперед. Например, корреляционное исследование может потребовать дальнейших корреляционных исследований, причинно-следственных или экспериментальных исследований.
Или это может потребовать меньшего количества исследований при представлении практических идей о том, как действовать с исследуемыми переменными и их средами.
Более того, он помогает исследователям понять изучаемые ими переменные по отношению к прошлому, сравнивая текущее поведение и другие атрибуты переменных с ретроспективными. Опираясь на эту концепцию, корреляционное исследование также помогает предприятиям формировать прогнозы .
Эти прогнозы относятся к другим аналогичным переменным или тем же переменным и могут иметь отношение к ближайшему и более позднему будущему. Корреляционные предсказания особенно полезны для обнаружения закономерностей.
Пример корреляционного исследования для бизнесаХотя в науке и научных ответвлениях существует множество различных вертикалей (например, психология, медицина), которые, по-видимому, требуют этого исследования, часто бывает не так ясно, как это можно сделать. помочь бизнесу.
Однако, как разъяснялось выше, корреляционное исследование имеет решающее значение для исследования бизнеса и рынка. Вот пример того, как компания использовала корреляционное исследование в своей общей исследовательской кампании:
Компания заметила снижение продаж при проведении поисковых исследований.Они заметили, что в корреляционном исследовании были определенные товары, продажи которых особенно резко упали.
Таким образом, они провели корреляционное исследование и обнаружили, что есть две переменные, которые могут иметь корреляцию: рост количества кухонной техники и снижение продаж этой техники.
Соответственно, компания развернула опросы для своего целевого рынка и постоянных клиентов, чтобы понять, действительно ли существует отрицательная корреляция. Опросы подтвердили, что это действительно так.Обладая этими знаниями, компания предложила скидку на бытовую технику, также рассмотрев возможность снижения цен через некоторое время.
Примеры корреляционного исследования- Качественный опрос
- Помогает лучше понять переменные.
- Может объяснить различное поведение по отношению к их среде / контексту.
- Ретроспективный обзор
- Вникает в прошлые события, происшествия и отношения в отношении переменных.
- Показывает, изменились ли переменные и как.
- Перспективный опрос
- Может найти связи между переменными за определенный период времени.
- Полезно для изучения переменных, чтобы формировать прогнозы и понимать результаты.
- Опрос лояльности клиентов
- Отлично подходит для сравнения постоянных клиентов с теми, кто не покупает у вас, но находится на вашем целевом рынке.
- Измеряет переменную постоянных покупок.
- Опрос удовлетворенности сотрудников
- Измеряет взаимосвязь между удовлетворенностью сотрудников и условиями работы или политикой компании.
- Помогает сравнить счастливых и недовольных сотрудников.
Корреляционные исследования значительно отличаются от других основных типов методов исследования, таких как исследовательские, описательные и экспериментальные исследования.
Тем не менее, исследование причинно-следственных связей часто объединяют с исследованием причинно-следственных связей . Хотя оба вида исследований касаются изучения взаимосвязей между переменными и проводятся на средних и поздних стадиях исследования, они изучают очень разные аспекты. Таким образом, они следуют разным подходам и измеряют разные вещи.
В то время как корреляционное исследование просто направлено на понимание того, как две переменные соотносятся друг с другом, исследование причинно-следственных связей пытается найти причинно-следственную связь между двумя переменными. Этот тип исследования больше связан с проведением сравнений.
Исследовательское исследование полностью контрастирует с корреляционным исследованием, поскольку оно обеспечивает саму основу исследовательской проблемы и формирует гипотезу для последующего исследования без привлечения переменных.
Описательное исследование углубляется в , описывая что-то уже установленное, обнаруженное или подозреваемое в поисковых исследованиях . Таким образом, он составляется после поисковых исследований в общем процессе.Это все еще ранняя часть всего исследовательского процесса.
В отличие от корреляционного исследования, он пытается более подробно описать то, что уже было установлено исследовательским, с появлением новых аспектов. Это не касается изучения переменных.
Экспериментальное исследование отличается от корреляционного исследования тем, что оно включает в себя манипулирование и контроль переменных , тогда как корреляционное исследование не оказывает абсолютно никакого контроля или изменений изучаемых переменных.
Как следует из названия, экспериментальное исследование представляет собой эксперименты с переменными как средство выявления причинно-следственных связей. Используя план научного исследования, это исследование включает в себя контролируемую среду, в которой переменные могут быть измерены, рассчитаны и затем сравнены.
Преимущества и недостатки корреляционного исследованияКорреляционное исследование предлагает ряд преимуществ для исследователей и предприятий. Однако, как и в случае со всеми другими методами исследования, у этого типа исследований есть несколько неудач.
Преимущества- Позволяет исследователям определять статистическую взаимосвязь между двумя переменными.
- Недорогой и эффективный (не трудоемкий) метод исследования.
- Предоставляет исследование, чтобы понять переменную в неизменном виде, существующую в ее естественном состоянии, чтобы полностью понять ее.
- Переменные в их естественном состоянии больше подходят для повседневных ситуаций.
- Хотя это не может доказать причинно-следственную связь, большой объем собранных и проанализированных корреляционных данных может подтвердить причинную гипотезу.
- Позволяет исследователям понять продолжительность и силу отношений.
- Используя коэффициент корреляции для измерения силы отношений (от 1,00 до -1,00), результаты легко классифицировать.
- Обеспечивает наиболее идеальный переход к проведению причинно-следственных или экспериментальных исследований.
- Обеспечивает понимание того, как переменные работают и существуют друг с другом, что другие методы не могут найти.
- Может быть получено путем быстрого исследования, например опросов или наблюдений.
- Он ограничен, так как он может только собрать статистическую информацию не более чем из двух переменных.
- Не принимает во внимание причинно-следственные связи, так как не определяет, какая из 2 переменных создает статистический образец.
- Не показывает, какая переменная имеет наибольшее влияние.
- Нельзя полностью полагаться на дальнейшие исследования, поскольку для определения взаимосвязи используются прошлые статистические закономерности.
Сравнительно простой и быстрый способ проведения исследования, корреляционное исследование может быть проведено с использованием полевых исследований, то есть естественных наблюдений, опросов и вторичных исследований. Вот как выполнить это исследование, используя все эти методы.
- Опросы: Позвольте исследователям быстро и легко получить обратную связь (через платформу для онлайн-опросов).
- Задайте вопросы о переменных.Используйте как открытые, так и закрытые вопросы. Первый вариант лучше подходит для более глубокого понимания переменных.
- Затем статистически проанализируйте ответы.
- Полевые исследования: Наблюдать за переменными в их естественной среде.
- Изучите покупателей и прохожих в обычных магазинах, используйте инструмент воспроизведения сеансов в интернет-магазинах.
- Запишите поведение, связанное с переменными.
- Проведите вторичное исследование : Найдите всю применимую литературу и доступные источники.
- Это зависит от вашей специальности и предмета обучения.
- Сложите их вместе и сравните со своими собственными выводами.
Корреляционное исследование, хотя и находится на средней стадии исследования, формирует самое начало исследования взаимосвязи переменных. Подобно описательному исследованию, корреляционное исследование описывает переменные, идя дальше, поскольку оно отслеживает, как одно связано с другим.
Важно провести это исследование, чтобы понять виды взаимосвязей, которые существуют между двумя переменными, прежде чем проводить какое-либо тестирование на них, будь то сравнение в причинно-следственных исследованиях или экспериментирование в экспериментальных исследованиях.
Мощный инструмент онлайн-опросов делает это возможным и практичным. Как упоминалось выше, существуют различные опросы, которые можно использовать для корреляционных исследований. Опытный провайдер онлайн-опросов сделает возможным реализовать все формы в вашем исследовании, а также отправить их в предполагаемый пул выборки.
Важность и использование корреляционных исследований
Фон: О важности корреляционных исследований сообщалось в литературе, однако в некоторых исследовательских текстах дизайн обсуждается подробно.
Цель: Обсудить важные вопросы и соображения в корреляционных исследованиях и предложить способы предотвращения потенциальных проблем во время подготовки и применения дизайна.
Обсуждение: В данной статье рассматривается выявленный в литературе пробел в отношении дизайна корреляционных исследований.В частности, обсуждается важность и цель корреляционных исследований, их применение, анализ и интерпретация с контекстуализацией медсестринского дела и медицинских исследований.
Заключение: Результаты корреляционных исследований можно использовать для определения распространенности и взаимосвязей между переменными, а также для прогнозирования событий на основе текущих данных и знаний. Несмотря на множество вариантов использования, требуется осмотрительность при использовании методологии и анализе данных.Чтобы помочь исследователям уменьшить количество ошибок, для обсуждения выделены важные вопросы и предложено несколько вариантов анализа данных.
Значение для практики: Корреляционные исследования широко используются, и эта статья должна быть особенно полезна для начинающих медсестер-исследователей. Кроме того, результаты корреляционных исследований могут использоваться, например, для информирования при принятии решений, а также для улучшения или инициирования деятельности или изменений, связанных со здоровьем.
Ключевые слова: корреляция; корреляционное исследование; анализ данных; инструменты измерения; медсестры; сестринские исследования; количественный; переменные.
Введение в корреляционные исследования | Основы образовательных исследований Дель Сигл
Презентация PowerPoint содержит важную информацию для этого модуля о корреляциях. Свяжитесь с инструктором, [email protected] … если у вас проблемы с его просмотром.
Некоторое содержимое этого веб-сайта может потребовать использования подключаемого модуля, например Microsoft PowerPoint.
Когда используются методы корреляции?
- Они используются для определения степени, в которой две или более переменных связаны между одной группой людей (хотя иногда каждая пара оценок не исходит от одного человека… корреляция между ростом отца и сына не будет).
- Нет попытки манипулировать переменными (случайными величинами)
Чем корреляционное исследование отличается от экспериментального исследования?
В корреляционных исследованиях мы не влияем (или, по крайней мере, не пытаемся) влиять на какие-либо переменные, а только измеряем их и ищем взаимосвязи (корреляции) между некоторым набором переменных, такими как артериальное давление и уровень холестерина.В экспериментальных исследованиях мы манипулируем некоторыми переменными, а затем измеряем влияние этой манипуляции на другие переменные; например, исследователь может искусственно повысить кровяное давление, а затем записать уровень холестерина. Анализ данных в экспериментальных исследованиях также сводится к вычислению «корреляций» между переменными, в частности, теми, которыми манипулируют, и теми, на которые манипулируют. Однако экспериментальные данные могут потенциально предоставить качественно лучшую информацию: только экспериментальные данные могут окончательно продемонстрировать причинно-следственные связи между переменными.Например, если мы обнаружили, что всякий раз, когда мы меняем переменную A, тогда изменяется и переменная B, мы можем сделать вывод, что «A влияет на B.» Данные корреляционных исследований можно «интерпретировать» только в причинно-следственных терминах, основываясь на некоторых имеющихся у нас теориях, но корреляционные данные не могут окончательно доказать причинную связь. Источник: http://www.statsoft.com/textbook/stathome.html
Хотя взаимосвязь между двумя переменными не доказывает, что одна из них вызвала другую, если нет взаимосвязи между двумя переменными, то одна не может быть причиной другой.
Исследование корреляции задает вопрос: какая связь существует?
- Корреляция имеет направление и может быть как положительным, так и отрицательным (обратите внимание на исключения, перечисленные ниже). При положительной корреляции люди, которые набирают больше (или ниже) среднего (среднего) по одному показателю, как правило, получают аналогичный результат выше (или ниже) среднего по другому показателю. Диаграмма рассеяния положительной корреляции возрастает (слева направо). При отрицательных отношениях, человек, который набирает баллы выше среднего по одному критерию, имеет тенденцию набирать ниже среднего по другому (или наоборот).Диаграмма рассеяния отрицательной корреляции падает (слева направо).
- Корреляция может различаться степенью или силой взаимосвязи (с коэффициентом корреляции произведения-момента Пирсона эта взаимосвязь является линейной). Ноль означает отсутствие взаимосвязи между двумя показателями, а r = 1,00 или r = -1,00 указывает на идеальную взаимосвязь. Сила может быть от 0 до +1,00. Примечание. Символ r используется для обозначения коэффициента корреляции произведения Пирсона и момента для выборки.Греческая буква rho (r) используется для обозначения населения. Чем сильнее корреляция — чем ближе значение r (коэффициент корреляции) к +1,00 — тем больше график рассеяния будет построен вдоль линии.
Когда нет связи между мерами (переменными), мы говорим, что они не связаны, некоррелированы, ортогональны или независимы.
Некоторая математика для двумерной корреляции моментов произведения (не требуется для EPSY 5601):
Умножьте значения z каждой пары и сложите все эти произведения.Разделите это число на единицу меньше, чем количество пар оценок. (довольно просто)
—или—
Каждая пара имеет две оценки… по одной от каждой из двух переменных. Для каждой пары вычтите среднее значение для каждой переменной из оценки пары по этой переменной и умножьте результаты друг на друга–> (Оценка1 — Среднее1) * (Оценка2 — Среднее2). Суммируйте эти результаты для всех пар -> СУММ ((Score1 — Mean1) * (Score2 — Mean2)). Разделите это на количество пар минус 1–> СУММ ((Score1 — Mean1) * (Score2 — Mean2)) / (n — 1).Умножьте стандартное отклонение для каждой из двух переменных друг на друга и разделите свой предыдущий ответ на это -> (SUM ((Score1 — Mean1) * (Score2 — Mean2)) / (n — 1)) / (SD1 * SD2) .
Вместо того, чтобы рассчитывать коэффициент корреляции по любой из приведенных выше формул, вы можете просто следовать этим связанным инструкциям для использования функции, встроенной в Microsoft Excel.
Некоторые вопросы корреляции, которые могут задать ученики начальной школы:
Какая связь между…
- посещаемость школы и оценки в школе?
- часов тратят каждую неделю на выполнение домашних заданий и школьных оценок?
- размах рук и рост?
- количество детей в семье и количество спален в доме?
Корреляции только описывают взаимосвязь, они не доказывают причинно-следственную связь.Корреляция — необходимое, но не достаточное условие для определения причинности.
Существуют три требования для установления причинно-следственной связи
- Статистически значимая взаимосвязь между переменными
- Причинная переменная произошла до другой переменной
- Нет других факторов, которые могли бы объяснить причину
(Корреляционные исследования не соответствуют последнему требованию и могут не соответствовать второму требованию.Однако отсутствие связи означает, что одна переменная не вызывала другую.)
Существует тесная взаимосвязь между количеством проданных рожков мороженого и количеством людей, которые тонут каждый месяц. То, что существует связь (сильная корреляция), не означает, что одно вызвало другое.
Если существует взаимосвязь между A (продажи рожков мороженого) и B (утопление), это может быть потому, что
- A-> B (Поедание мороженого вызывает утопление)
- A <-B (В результате утопления люди едят мороженое - возможно, скорбящие настолько расстроены, что покупают рожки мороженого, чтобы подбодрить себя)
- A <-C-> B (Что-то еще связано как с продажами мороженого, так и с количеством утопающих — теплая погода будет хорошим предположением)
Дело в том, что… только потому, что существует корреляция, вы НЕ МОЖЕТЕ сказать, что одна переменная вызывает другую.С другой стороны, если нет корреляции, вы можете сказать, что одно НЕ вызвало другое (при условии, что меры действительны и надежны).
Формат для вопросов и гипотез исследования корреляций:
Вопрос: Существует ли (статистически значимая) взаимосвязь между ростом и размахом рук?
H O : Нет (статистически значимой) зависимости между ростом и размахом рук (H0: r = 0).
H A : существует (статистически значимая) взаимосвязь между ростом и размахом рук (HA: r <> 0).
Коэффициент детерминации (общая вариация)
Один из способов, которым исследователи часто выражают силу связи между двумя переменными, — это возведение их коэффициентов корреляции в квадрат. Этот квадрат коэффициента корреляции называется КОЭФФИЦИЕНТОМ ОПРЕДЕЛЕНИЯ . Коэффициент детерминации полезен, потому что он дает долю дисперсии одной переменной, которая предсказуема от другой переменной.
Факторы, которые могут ограничивать коэффициент корреляции продукта и момента (PowerPoint демонстрирует эти факторы)
- Однородная группа (испытуемые очень похожи по переменным)
- Ненадежный измерительный прибор (вашим измерениям нельзя доверять, и они будут колебаться повсюду)
- Нелинейная зависимость (r Пирсона основано на линейных отношениях… в этом случае можно использовать другие формулы)
- Потолок или пол с измерением (множество оценок сгруппировано вверху или внизу… следовательно, нет разброса, который создает проблему, аналогичную однородной группе)
Допущения, которые необходимо выполнить, чтобы использовать корреляцию момента произведения Пирсона
- Меры примерно нормально распределены
- Дисперсия двух показателей одинакова (гомоскедастичность , ) — проверьте диаграмму рассеяния
- Отношение линейное — проверьте диаграмму рассеяния
- Выборка представляет население
- Переменные измеряются по шкале интервалов или отношений
Существуют различные типы отношений: Линейные — Нелинейные или Криволинейные — Немонотонные (вогнутые или циклические).Для измерения разных типов отношений с использованием разных типов шкал используются разные процедуры. Для этого класса очень важен вопрос измерительных шкал. Убедитесь, что вы их понимаете.
Переменные-предикторы и критерии (НЕ НУЖНЫ ДЛЯ EPSY 5601)
- Множественная корреляция — множество предикторов и один критерий ( R )
- Частичная корреляция — корреляция двух переменных после удаления их корреляции с другими переменными
- Последовательная или автокорреляция — корреляция набора чисел с самим собой (только с шахматной точностью)
- Каноническая корреляция — множество предикторов и множество критериев R c
При использовании таблицы критических значений для корреляции произведение-момент Пирсона значение, полученное через пересечение степени свободы ( n — 2) и тестируемого альфа-уровня ( p =.05) — это минимальное значение r , необходимое для того, чтобы отношения были выше случайности.
Статистический пакет SPSS, а также Microsoft Excel можно использовать для расчета корреляции.
Мы будем использовать Microsoft Excel.
Чтение таблицы корреляций в журнале Статья
Большинство исследований сообщают о корреляциях между набором переменных. Результаты представлены в таблице, подобной приведенной ниже.
Пересечение строки и столбца показывает корреляцию между переменной, указанной для строки, и переменной, указанной для столбца.Например, пересечение математики строки и науки столбца показывает, что корреляция между математикой и естествознанием была 0,874. В сноске указано, что три *** после 0,874 указывают на то, что связь была статистически значимой при p <0,001.
Большинство таблиц не сообщают об идеальной корреляции по диагонали, которая возникает, когда переменная коррелирует сама с собой. В приведенном выше примере диагональ использовалась для определения корреляции четырех факторов с другой переменной.Поскольку корреляцию между чтением и математикой можно определить в верхнем разделе таблицы, корреляции между этими двумя переменными не повторяются в нижней половине таблицы. Это верно для всех отношений, указанных в таблице. .
Дель Сигл, доктор философии
Neag School of Education — Университет Коннектикута
[email protected]
www.delsiegle.com
Последнее обновление 11.10.2015
Методология исследования онлайн, CHD / EDU / PSY 6691
Дизайн корреляционных исследований
Интерактивное оглавление (щелкните любой блок)
- Цель корреляционного исследования
Как определить этот тип дизайна
Описание коэффициента корреляции
Статистическая значимость коэффициентов корреляции
Краткий обзор двумерной корреляционной статистики
Более подробный взгляд на исследования прогнозирования
Оценка исследований корреляционных исследований
Оценка выборочного исследования № 15 (Выгорание и советник…)Задание на 6 неделю
Цель корреляционного исследования
В отличие от других исследовательских проектов, которые мы будем изучать в этом курсе, корреляционное исследование может преследовать любую из двух целей. Одна из целей проведения корреляционного исследования — определить степень, в которой существует связь между двумя или более переменными. Обратите внимание, что я НЕ говорил о причинно-следственной связи. Дизайн корреляционных исследований не может установить причинно-следственную связь.Какая разница? Что ж, это действительно очень просто. Переменные могут относиться друг к другу, при этом одна из них не приводит к возникновению другой.
Вот простой пример: когда вы перемещаете выключатель света в определенное положение, свет в комнате включается; когда вы перемещаете выключатель света в противоположное положение, свет гаснет. Существует взаимосвязь между перемещением переключателя света и включением и выключением света. Однако выключатель света не заставляет свет включаться и выключаться.Не верите мне? Может ли свет в комнате выключиться, не поворачивая выключатель? Можете ли вы перевести выключатель света в положение «включено», а свет не загорится? Ответ на оба вопроса, конечно, положительный. Выключатель света НЕ вызывает включение или выключение света — он контролирует поток электричества, а электричество — это то, что заставляет свет включаться или выключаться. Итак, между переключателем света и светом существует связь, но не причинно-следственная связь. Но что кто-то не знал об электричестве? Они увидят, как кто-то поворачивает выключатель, и свет включается и выключается.Этот человек заключил бы, что выключатель света заставляет свет включаться и выключаться. И, конечно, ошиблись бы. Так как же узнать, действительно ли это происходит из-за чего-то, что связано с чем-то еще? Невозможно без специального контролируемого исследования. Подводя итог, просто у статистиков есть поговорка: «корреляция не подразумевает причинно-следственную связь» , что означает, что то, что две переменные коррелируют друг с другом, не обязательно означает, что одна вызывает другую.
Вторая цель корреляционных исследований — разработать модели прогнозирования, позволяющие предсказать будущее значение переменной на основе текущего значения одной или нескольких других переменных. Распространенной моделью прогнозирования, используемой в образовании, является использование результатов вступительных экзаменов в колледж, чтобы помочь спрогнозировать успехи будущего студента в колледже. Колледжи и университеты прилагают все усилия, чтобы разработать наилучшие модели прогнозирования, которые они могут сделать, чтобы обеспечить зачисление наиболее потенциально успешных студентов.Чтобы повысить предсказательную силу своих моделей, они используют методы корреляционного исследования, некоторые из которых мы обсудим немного позже в этом уроке.
Как определить этот тип конструкции
Корреляционные исследования почти всегда выдаются заявлением о цели (или гипотезе, или цели). Обычно где-то в этих утверждениях появляется фраза «определить отношения между…». Это ключ к тому, что это корреляционный дизайн.Вы также заметите, что корреляционные исследования НЕ формируют группы. В этом отношении они похожи на планы описательных исследований. Итак, если вы посмотрите в разделе «Методология» отчета об исследовании и обнаружите, что группы не сформированы, то вы поймете, что это не может быть причинно-сравнительное исследование. Он должен быть описательным или корреляционным. Разницу между этими двумя конструкциями можно найти только в заявлении о целях.
Описание коэффициента корреляции
Прежде чем переходить к различным статистическим данным, давайте удостоверимся, что вы понимаете, что такое коэффициент корреляции.Коэффициент корреляции может принимать значение от -1 до +1 (включая ноль). Знак коэффициента просто означает, является ли корреляция прямой (положительной) или обратной (отрицательной). Сила коэффициента определяется его числовым значением. То есть коэффициент корреляции -,75 и один из 0,75 имеют одинаковую силу. Примечание: коэффициенты положительной корреляции обычно отображаются без какого-либо знака перед числом.
Прямая (положительная) корреляция возникает, когда переменная B увеличивается при увеличении переменной A, а переменная B уменьшается при уменьшении переменной A.Пример прямой корреляции — это соотношение между высотой столбика ртути в стеклянной трубке (термометре) и температурой окружающего воздуха.
Обратная (отрицательная) корреляция возникает, когда переменные A и B действуют противоположно друг другу (когда A увеличивается, B уменьшается, и наоборот). Например, рассмотрим взаимосвязь между усталостью и отдыхом. Чем больше человек отдыхает, тем меньше он устает, и наоборот (обычно).
«Обычно» — важное слово, когда мы говорим о корреляциях, потому что существует очень, очень мало переменных (если таковые имеются), которые идеально коррелируют друг с другом.Следовательно, подавляющее большинство корреляций меньше 1 (или больше -1) и обычно указываются в десятичной форме. Вы можете проверить практически любой текст элементарной статистики и найти практическое правило относительно того, что составляет сильную и слабую корреляцию. Вот типичный диапазон значений, который подойдет для наших нужд:
От 0,7 до 1,0 — сильная корреляция
От 0,4 до 0,69 — умеренная корреляция
От 0,1 до 0,39 — слабая корреляция
0.0 — нет корреляции
Статистическая значимость коэффициентов корреляции
Мы обсуждали понятие статистической значимости в Неделя 3. Мы узнали, что когда результат статистического теста является значимым, это означает, что это не произойдет случайно чаще, чем определенный процент времени (5 раз или 1 раз из 100). Мы можем применить эту концепцию и к коэффициентам корреляции. Но иногда это сбивает студентов с толку.Итак, давайте не будем останавливаться на достигнутом, чтобы прояснить это. Значение коэффициента корреляции (из предыдущего абзаца) не имеет отношения к тому, является ли он статистически значимым. То есть коэффициент корреляции 0,1 вполне может быть статистически значимым. Это будет означать, что две переменные очень мало связаны друг с другом, и этот результат, скорее всего, НЕ является случайным явлением. С другой стороны, коэффициент корреляции 0,95 не может быть статистически значимым.Это означало бы, что хотя в этом исследовании связь между двумя переменными была очень сильной, на самом деле, это, скорее всего, произошло случайно в этом конкретном исследовании и вряд ли повторится в другой выборке из той же популяции. Итак, НЕ предполагайте, что большие коэффициенты автоматически статистически значимы, а маленькие коэффициенты — нет. Нет связи между размером коэффициента корреляции и его статистической значимостью. Статистическая значимость корреляционного значения во многом зависит от размера выборки. Просто сконцентрируйтесь на значении «p», связанном с каждым коэффициентом корреляции, и если оно меньше альфа-уровня, установленного исследователем, то коэффициент будет статистически значимым, независимо от его числового значения.
Краткий обзор двумерной корреляционной статистики
Существует две категории корреляционной статистики: двумерная (две переменные) и многомерная (много переменных).Коэффициенты корреляции, используемые для достижения первой из целей, упомянутых выше (для определения силы и направления взаимосвязи между переменными), являются двумерными по своей природе. Это означает, что мы можем использовать эту статистику для одновременной корреляции только двух переменных. Многовариантная корреляционная статистика используется для поддержки второй цели (для разработки моделей прогнозирования). Они намного сложнее, поэтому мы не будем вдаваться в подробности о них. Мы разберемся с ними в следующем разделе.
А пока давайте посмотрим на двумерную корреляционную статистику. В вашем тексте таблица 12.3 на стр. 273 отображает десять различных двумерных статистических данных. Можете ли вы сказать, какие из них являются параметрическими? Проверьте свой ответ, если вы не уверены. Обратите внимание на различные формы, которые могут принимать переменные, и на то, что для каждого типа данных существует своя статистика. Большинство статистических данных в таблице непараметрические и по своей природе довольно слабые. Безусловно слабее своих параметрических аналогов.На самом деле они настолько слабы, что их ограниченная сила должна быть сосредоточена вокруг узких диапазонов, чтобы быть эффективными. Например, посмотрите на коэффициенты rho и tau . Оба они используются, когда коррелируемые переменные имеют форму рангов. Но tau предпочтительнее, когда размер выборки меньше 10, тогда как rho предпочтительнее, когда размер выборки больше 10 и меньше 30.
Из нашего обсуждения статистических инструментов на третьей неделе напомним, что мы обсуждали 4 основных типа данных: соотношение и интервал (вместе называемые непрерывными), ранги и номинальные (или категориальные).В этой таблице, по-видимому, есть два новых типа: искусственная и истинная дихотомии. Фактически, это особые типы категориальных данных. У дихотомий есть только две возможности — значит, только две категории. Истинная дихотомия встречается в природе (не созданная исследователем), как и пол (мужской и женский). Искусственная дихотомия определяется произвольно (обычно какой-либо точкой отсечения), например, точка «прошел-не прошел тест» или «богатый-бедный» (кто-то произвольно определяет разделительную линию) и т. Д.Уловили идею?
Почему так много разных коэффициентов? Подходит почти для любой комбинации данных. Скажем, например, вы хотели измерить степень корреляции (или взаимосвязи) между академическими достижениями учащихся в стандартизированном математическом тесте 12-го класса и их оценками IQ, измеренными Стэнфордским Бине (проверка гипотезы о том, что более высокие IQ имеют положительную связь для достижения результатов тестов). Какой коэффициент корреляции лучше всего использовать? Ваш ответ должен выглядеть примерно так: «Поскольку результаты тестов академической успеваемости и оценки IQ являются непрерывными, я бы использовал либо коэффициент Пирсона r (корреляция момента продукта), либо коэффициент eta .«Понятно? Хорошо (надеюсь, вы сказали« да »!) Давайте попробуем еще один пример. Допустим, вы хотели узнать, существует ли связь между полом и успеваемостью в старшей школе (опять же, измеренная с помощью теста академической успеваемости). наиболее подходящая статистика для использования? Проверить таблицу 12.3 (стр. 273) в тексте, проверьте свой ответ здесь. Вы правильно поняли? Если нет, поговорите со своими одноклассниками или с инструктором.
Попробуем еще один пример. Допустим, вы хотели определить взаимосвязь между цветом волос (например, блондинки, брюнетки и рыжие) и успеваемостью по математике (чтобы проверить гипотезу о том, что блондинки лучше разбираются в математике, чем брюнетки или рыжие).Какая статистика будет наиболее подходящей? Что ж, мы знаем, что академическая успеваемость — это непрерывная переменная. Мы должны осознать, что цвет волос — это категориальная переменная (в этом примере всего три категории). Однако, просматривая таблицу, мы не можем найти коэффициент корреляции, который работает с этой комбинацией типов данных. Что теперь?
Теперь мы воспользуемся техникой, известной как сокращение данных. Вернуться на неделю 3, когда я перечислил четыре типа данных в следующем порядке:
- Соотношение — (Вместе эти два
- Interval — назывались непрерывными)
- Порядковый номер — (Здесь называются ранги)
- Номинальный — (здесь называется категориальным)
Итак, до сих пор мы видели, что даже несмотря на то, что нет коэффициента корреляции для каждой возможной пары данных. Путем обработки данных можно создать набор данных, для которого существует соответствующая корреляционная статистика. В следующем разделе мы немного поговорим о многомерной корреляционной статистике, используемой в исследованиях прогнозирования.
Более пристальный взгляд на исследования в области прогнозирования
Предпосылка, лежащая в основе исследований прогнозирования в исследованиях социальных наук, заключается в том, что степень, в которой переменная A коррелирует с переменной B, позволяет нам с некоторой степенью уверенности сделать прогноз относительно значения переменной B на основе значения переменной A. Примечание это предсказание не то же самое, что причинно-следственная связь. То, что одно может предсказать возникновение чего-то другого, не обязательно означает, что одно вызывает другое.
То, что определяет, насколько хорошо одна переменная может предсказать другую, — это то, что называется общей (или объясненной, или общей) дисперсией . Способ определения количества общей дисперсии, существующей между двумя переменными, легко вычислить: просто возведите в квадрат коэффициент корреляции. То, что вы делаете, иногда поражает. Например, предположим, что баллы учащихся на вступительных экзаменах в колледж по SAT коррелируют с их средним баллом за первый семестр (GPA) в колледже, и мы обнаруживаем, что коэффициент корреляции имеет значение 0.70. Это сильная корреляция, что означает, что эти две переменные сильно связаны друг с другом. Но насколько хорошим предиктором среднего балла колледжа является результат теста SAT? Чтобы определить это, возводим в квадрат 0,70 и получаем (0,70 x 0,70 =) 0,49. Это означает, что 49% расхождений в оценках среднего балла колледжа можно объяснить баллами на вступительном экзамене SAT. Если подумать, это довольно плохой прогноз. Я мог бы подбросить честную монету и делать более точные прогнозы, чем это!
Итак, чем объясняется другой 51 процент дисперсии в баллах GPA? Это другие переменные.Сложнее всего определить, что это за переменные. Вот почему в социальных науках нет действительно хороших моделей двумерного прогнозирования. Люди слишком сложны, чтобы их можно было предсказать такими простыми способами. Это основа прогнозных исследований — поиск наборов переменных, которые объясняют как можно большую дисперсию одной переменной. Вот небольшая терминология, с которой вы можете столкнуться при изучении планов корреляционных исследований (особенно в исследованиях прогнозирования). Независимые переменные часто называются переменными-предикторами , а зависимая переменная обычно называется критериальной переменной .
Чтобы провести исследование прогнозирования, исследователь должен сначала провести исследование взаимосвязи всех переменных, которые, по его мнению, участвуют в модели прогнозирования. Итак, первая часть исследования — это выявление взаимосвязей между интересующими переменными. Затем вторая часть заключается в использовании этих отношений (коэффициентов) для создания модели. Мы не будем вдаваться в подробности создания модели, потому что они слишком подробны для этого курса. Достаточно обратить ваше внимание на методы многомерной корреляции в вашем тексте в таблице. 12.4 на стр. 274. Каждый из этих методов обеспечивает средства разработки модели прогнозирования на основе коэффициентов корреляции, вычисленных из набора переменных. Сами коэффициенты вычисляются с использованием двумерных методов, перечисленных в таблице. 12.3 в вашем тексте.
Оценка корреляционных исследований
На что следует обратить внимание при оценке корреляционного исследования? Прежде всего, обратите внимание на общие вещи, которые мы оценивали во всех предыдущих исследованиях: методика выборки; наличие действительной исследовательской гипотезы, цели или вопросов; и достоверность и надежность соответствующих мер, используемых для сбора данных.Вам также следует обратить внимание на то, использует ли исследователь соответствующие корреляционные статистические тесты.
Есть еще одна вещь, на которую нужно обратить внимание, которая не попадает ни в одну из этих категорий. Это относится к уровню альфа-ошибки, который мы обсуждали на неделе 2. Напомним, что альфа-ошибка — это уровень ошибки, которую исследователь готов принять или допустить и по-прежнему оставаться уверенным в том, что результаты исследования верны. Что ж, каждый раз, когда исследователь повторяет один и тот же статистический тест на одном и том же наборе данных, альфа-ошибка увеличивается.Это чрезвычайно важно в корреляционных исследованиях, потому что компьютеры способны коррелировать десятки, сотни и даже тысячи переменных за очень короткое время.
Например, предположим, исследователь хочет определить, существуют ли значимые отношения между пятью переменными (A, B, C, D и E). Взаимосвязь этих пяти переменных обычно отображается в виде матрицы с тем же количеством строк и столбцов, что и количество коррелируемых переменных.В нашем примере это будет матрица «5 на 5», которая может выглядеть так:
| A | B | C | D | E | |||||
| A | — | .27 | .78 | .65 * | . 27 | — | .56 | .88 | .76 |
| C | .78 | .56 | — | .02 | .32 * | ||||
| D | .65 * | .88 | .02 | — | .09 * | ||||
| E | .43 | .76 | .09 * | — |
* р <0,05
Обратите внимание на знаки «-» внизу диагонали (называемой главной диагональю ) матрицы. Обычно их игнорируют, потому что они являются идеальной корреляцией каждой переменной с самой собой.Также обратите внимание, что корреляции выше и справа от главной диагонали (называемые верхней треугольной матрицей ) являются зеркальным отображением корреляций ниже и слева от главной диагонали (называемой нижней треугольной матрицей ). Часто в исследовательских отчетах отображается верхняя или нижняя треугольная матрица, чтобы избежать путаницы в таблице.
Общее количество коэффициентов корреляции в этой матрице (включая коэффициенты по диагонали) составляет 5 x 5 = 25 взаимных корреляций.Здесь мы имеем тот же статистический тест (коэффициент корреляции), повторенный на одном и том же наборе данных (тот же набор из 5 переменных) 25 раз. Теперь вспомним наше обсуждение уровня ошибки альфа (0,05). Это количество ошибок, которые мы готовы терпеть и при этом быть уверены, что результаты верны. Что ж, учитывая этот уровень ошибки, мы можем ожидать, что некоторые из этих коэффициентов корреляции будут статистически значимыми — чисто случайно. Сколько и каких их будет. Мы не можем точно знать, какие коэффициенты окажутся ложно статистически значимыми.Но мы можем оценить, сколько их будет. Мы можем сделать это, просто умножив общее количество взаимных корреляций на уровень альфа-ошибки для исследования и округлив результат. В нашем текущем примере мы должны ожидать, что 1 (25 x 0,05 = 1,25 = 1 (округлено)) из этих 25 коэффициентов будет статистически значимым только случайно. Взгляд на корреляционную матрицу выше показывает, что 6 коэффициентов статистически значимы на уровне 0,05. Это намного больше, чем число, которое можно было бы ожидать случайно, учитывая количество коррелируемых переменных.Итак, эти корреляции — больше, чем просто случайность.
Если бы было, скажем, только два статистически значимых коэффициента. Было бы очень мало поводов для волнения, поскольку по крайней мере одно из них могло произойти случайно. При оценке корреляционных исследований постарайтесь определить количество потенциальных случайных корреляций, как мы делали выше, чтобы вы лучше почувствовали истинное значение результатов, сообщенных исследователем.
Оценка выборки исследования № 15
( эмоциональное выгорание и ожидания консультанта-практикующего надзора, )
- 1.Что это за дизайн исследования?
- Поскольку цель (последнее предложение введения) исследования — «изучить взаимосвязь между удовлетворенностью супервизором и выгоранием консультанта», это, несомненно, корреляционное исследование.
- 2. Какова исследовательская гипотеза, цель или вопрос (вопросы), или, если их нет, укажите так.
- Заявление о цели, указанное выше, на самом деле является хорошей целью исследования, поскольку оно краткое, основано на предыдущем исследовании (описанном ранее во введении) и определяет переменные, которые необходимо изучить.
- 3. На какую группу населения вы бы чувствовали себя комфортно, обобщая результаты этого исследования?
- Была получена довольно большая неслучайная выборка субъектов из Орегонской ассоциации персонала и руководства. Однако только 24% были возвращены в пригодном для использования состоянии. У меня очень мало уверенности, что эти 24 процента представляют собой первоначальные 500 человек, не говоря уже о более крупном населении. Поэтому мне неудобно делать обобщения на какую-либо популяцию из-за очень низкой скорости возврата.
- 4. Определите сильные стороны и угрозы достоверности в этом исследовании.
- Сильные стороны:
- Проверена надежность MBI и CSI. Были рассмотрены также оценки валидности (на странице 236).
- Если вы пришли к выводу, что как MBI, так и CSI генерируют непрерывные оценки, то вы должны были увидеть использование корреляции момента произведения Пирсона в качестве подходящей статистики в этом исследовании.
- Угрозы:
- Неслучайный выбор предметов.
- Низкий процент возврата и никаких доказательств того, что исследователи попытаются увеличить процент ответов.
- Анкеты не апробированы.
- Если вы пришли к выводу, что MBI или CSI генерировали непостоянные (категориальные или ранговые) оценки, то вы должны были рассматривать использование корреляции моментов произведения Пирсона как неподходящую статистику для использования в этом исследовании.
Наконец, просмотрите Таблицу 1 на странице 237 исследования.Обратите внимание, что отображается нижняя треугольная матрица (верхняя часть треугольника может содержать повторяющуюся информацию и поэтому не является необходимой. Сколько переменных коррелируется? Можете ли вы определить 9 переменных? — 3 для неудовлетворенности, 3 для идеального и 3 для Фактический. Это означает, что существует 81 возможная взаимная корреляция (9 x 9). Используя уровень ошибки альфа 0,05 (что нормально, потому что нам не сказали, какой был уровень альфа), возможное количество случайных статистически значимых корреляций составляет 4 (81 х.05). Сколько коэффициентов на самом деле оказалось статистически значимым? Подсчет всех корреляций, отмеченных звездочками, показывает 27. Поскольку это только для нижней треугольной матрицы, нам пришлось бы удвоить это число, чтобы получить общую сумму для всей матрицы. Это будет 54 статистически значимых корреляции (фактических). Сравнение этого числа с 4, ожидаемыми случайно, приводит нас к выводу, что есть причина для волнения по поводу значимых взаимосвязей, обнаруженных между переменными супервизии в этом исследовании.
- 5. Есть ли в этом исследовании какие-либо этические проблемы?
- В этом исследовании нет этических проблем, потому что с испытуемыми ничего не делается. Проверяются только их академические баллы. Единственные этические проблемы, связанные с корреляционными исследованиями, скорее всего, связаны со сбором данных.
Если у вас есть какие-либо вопросы относительно этой оценки (если вы нашли то, что я здесь не обсуждал, или если вы не понимаете то, что я здесь обсуждал), поговорите с другими участниками курса, чтобы узнать, сможете ли вы решить проблемы с ними.Если нет, обсудите свои вопросы с преподавателем в классе. или по электронной почте.
Конец недели 5 Урок
| Назначение на следующую неделю |
| Галл: Глава 13 (Истинные и квазиэкспериментальные проекты) |
| SB: Исследование 16 |
| Руководство: Глава 3 |
| Дополнительная практика оценки: попробуйте свои силы в оценке этих
сценарные исследования (я называю их мини-исследованиями.) Для каждого
проблема, прочтите сценарий (первая страница) и попробуйте оценить его, используя 5
оценочные вопросы в формате типичной оценочной викторины, который мы использовали
выше. Не смотрите ответы на второй странице, пока не ответите
все вопросы сами. Затем сравните свои ответы с приведенными в
эта проблема. Если у вас есть вопросы, вы не согласны или не понимаете
предоставленные ответы, напишите мне, и давайте обсудим это. Пакет сценариев 2 (документы MS Word): Сценарий А, Сценарий B, Сценарий C, Сценарий D, Сценарий E, Сценарий F, Сценарий G, Сценарий H. |
| Срок погашения на следующей неделе |
| Подготовка к оценочной викторине 2 |
Каковы преимущества и недостатки исследования корреляции?
Университеты и частные исследовательские фирмы по всему миру постоянно проводят исследования, которые открывают захватывающие открытия о мире и людях в нем. Корреляционное исследование исследует взаимосвязь между двумя переменными и то, как они взаимодействуют друг с другом.Корреляционные исследования популярны и полезны во многих научных исследованиях, особенно в области здравоохранения и социальных наук. Однако, как и в большинстве видов исследований, у корреляционных исследований есть как плюсы, так и минусы.
1 Эксперименты и корреляция
Корреляция — одно из двух основных средств проведения исследования. Другой — экспериментирование. В большинстве случаев экспериментирование предпочтительнее, потому что экспериментатор может манипулировать интересующей переменной и напрямую измерять результат.Например, исследователь, изучающий влияние гребли на потерю веса, может определить точное время и технику гребли, а затем измерить результат через заданный промежуток времени; Кроме того, исследователь может контролировать посторонние переменные, которые могут повлиять на результат. С другой стороны, корреляционные исследования не имеют такого контроля.
2 Принципы исследования корреляции
Корреляция измеряет взаимосвязь между двумя переменными. В отличие от экспериментов, отношения наблюдаются в более естественной среде.Нет экспериментатора, который бы контролировал переменные; скорее, переменные взаимодействуют вне лаборатории. Поскольку нет экспериментатора, который мог бы контролировать взаимодействие переменных, никакое корреляционное исследование не может определить, как вызвано явление. Это привело к важной мантре о том, что корреляция не обязательно указывает на причинно-следственную связь. Тем не менее, для широких, но все же значимых наблюдений, коррелятивные результаты могут дать хорошее понимание.
3 Преимущества корреляционных исследований
Корреляционные исследования позволяют исследователям собирать гораздо больше данных, чем эксперименты.Кроме того, поскольку корреляционные исследования обычно проводятся вне лаборатории, их результаты, как правило, более применимы к повседневной жизни. Еще одно преимущество корреляционных исследований состоит в том, что они открывают большие возможности для дальнейших исследований другим ученым. Когда исследователи впервые начинают исследовать явление или взаимосвязь, корреляционное исследование является хорошей отправной точкой. Это позволяет исследователям определить силу и направление отношений, чтобы более поздние исследования могли сузить результаты и, если возможно, определить причинно-следственную связь экспериментально.
4 Недостатки исследования корреляции
Исследование корреляции только раскрывает взаимосвязь; он не может предоставить убедительную причину, по которой существуют отношения. Корреляционный результат не показывает, какая переменная влияет на другую. Например, обнаружение того, что богатство сильно коррелирует с образованием, не объясняет, ведет ли богатство к большему образованию или образование ведет к большему благосостоянию. Причины любого из них можно предположить, но до тех пор, пока не будут проведены дополнительные исследования, причинно-следственная связь не может быть определена.Кроме того, обе причины могут быть вызваны третьей, неизвестной переменной. Например, проживание в штате Нью-Йорк может привести как к богатству, так и к образованию.
Использование в корреляционных исследованиях | BetterHelp
Автор: Joanna Smykowski
Обновлено 26 октября 2021 г.
Медицинское заключение: Chante ’Gamby, LCSW
Источник: rawpixel.com
Психологическое исследование обычно проводится в двух формах: экспериментальное исследование и корреляционное исследование . Эксперименты обычно проводятся в лабораторных условиях и включают манипулирование измеряемой переменной.
Корреляционное исследование , с другой стороны, не может определить причинно-следственную связь. Тот факт, что две вещи происходят одновременно, не означает, что A обязательно вызывает B.Может быть третья переменная, C, которая фактически заставляет A и B встречаться вместе.
Корреляционное исследование исследует взаимосвязи между задействованными переменными. Это исследование используется, чтобы узнать больше о том, что вместе связано с переменными. Одним из примеров является исследование соответствия Asch, о котором вы можете прочитать здесь.
Когда использовать корреляционное исследованиеХотя они не могут определить причинно-следственную связь, корреляционные исследования весьма полезны. Некоторыми переменными, такими как инвалидность или психическое заболевание, нельзя манипулировать с этической точки зрения.Например, с этической точки зрения нельзя вызвать у кого-то депрессию, даже если намерение состоит в том, чтобы помочь ему выздороветь — это просто неэтично и аморально. Другими переменными, которыми нельзя управлять, являются порядок рождения, пол и возраст.
Корреляции также полезны для прогнозирования. Как только психолог узнает, что две переменные, A и B, коррелируют. Он или она может более точно измерить одно из другого. Знание того, насколько изменение B вызвано изменением A, позволяет психологу предсказать изменение B, просто зная значение A.
В-третьих, если это приемлемо с этической и моральной точек зрения, корреляционные свидетельства могут привести к гипотезам и экспериментам. Психолог может захотеть выяснить, участвует ли третья переменная, C, или A является причиной B. .
Типы корреляционных исследованийСуществуют различные способы сбора информации для корреляционного исследования .Некоторые из самых известных — это опросы и натуралистические наблюдения.
Опросы полезны, когда исследователь хочет выбрать большую популяцию при невысоких затратах. Однако опросы обычно дают низкий процент откликов, и нет возможности подтвердить, что ответы являются честными.
Натуралистическое наблюдение предполагает, что исследователи просто наблюдают за своими объектами в их естественной среде обитания, не взаимодействуя с ними. Это полезно, когда исследователь хочет изучить конкретную популяцию.Узнайте больше на сайте AP Psychology.
Получение необходимой помощи
Вам доступна профессиональная психологическая помощь. Вы не должны бояться обращаться к ресурсам, которые могут помочь вам, и индивидуально подбирать лечение, чтобы вы были на высоте. Один из таких ресурсов — BetterHelp.
Источник: rawpixel.com
BetterHelp — это компания, которая предлагает платные, но доступные онлайн-консультации и терапию.Это компания, которая стремится оказывать психиатрическую помощь тем, кто хочет избежать стигмы, связанной с обращением за помощью в связи с болезнями. Эта компания также профессиональна, доступна и удобна. Узнайте больше на нашем сайте.
Что такое корреляционный анализ в маркетинговых исследованиях?
Корреляционный анализ в исследовании рынка — это статистический метод, который определяет силу взаимосвязи между двумя или более переменными.Вкратце, процесс выявляет закономерности во многих переменных набора данных.
Используя одну из нескольких формул, конечным результатом будет числовой результат от -1 до +1.
Допустим, вас интересует связь между двумя переменными, переменной A и переменной B.
Результаты, близкие к +1, указывают на положительную корреляцию, то есть, когда переменная A увеличивается, переменная B также увеличивается.
Напротив, выходы, близкие к -1, являются признаком отрицательной корреляции.Эти результаты означают, что по мере увеличения переменной A значение переменной B уменьшается.
Значение около 0 в корреляционном анализе указывает на менее значимую связь между переменной A и переменной B.
Пока вы технически тестируете две переменные одновременно, вы можете просматривать любое количество переменных в выходных данных сетки с теми же переменными, указанными как в столбцах, так и в строках.
В приведенном ниже примере выходных данных вы можете посмотреть на соответствующее поле, чтобы увидеть взаимосвязь между двумя переменными.
Обратите внимание, что значения для корреляционного анализа одной и той же переменной равны 1. Это имеет смысл, поскольку значения одной и той же переменной будут увеличиваться и уменьшаться полностью синхронно.
Как измерить корреляцию в маркетинговых исследованиях
Первым шагом в проведении корреляционного анализа в маркетинговых исследованиях является разработка опроса. Вам нужно будет планировать заранее, учитывая вопросы для анализа.
Сюда входят все, что дает данные как числовые, так и порядковые.Подумайте о таких показателях, как:
- Весы договорные
- Шкала важности
- Шкала удовлетворенности
- Деньги
- Температура
- Возраст
После завершения опроса вам нужно будет запрограммировать и протестировать его, чтобы убедиться, что вопросы работают правильно. Неправильная маркировка шкал или неправильная проверка данных при программировании испортят данные, используемые для корреляционного анализа.
Следующим шагом будет проведение полевых исследований в рамках исследования.
Очистите данные для анализа после достижения целевого количества ответов. Это также защищает целостность данных для анализа.
Затем вы можете запустить корреляционный анализ одним из нескольких методов.
Двумя наиболее распространенными способами проведения корреляционного анализа являются корреляция Пирсона r и ранговая корреляция Спирмена.
В большинстве программ для анализа данных есть инструмент для запуска корреляционного анализа после автоматического ввода входных данных.Анализ переменных также можно рассчитать вручную, но вы сэкономите время и избежите человеческих ошибок, используя программу.
Наконец, просмотрите результаты, чтобы увидеть, как связаны разные переменные.
Преимущества корреляционного анализа при исследовании рынка
Есть несколько причин рассмотреть возможность проведения корреляционного анализа в вашем следующем исследовании рынка.
Например, планирование корреляционного анализа мотивирует исследователей рынка задавать более точные вопросы в опросе.
Зная, что в ходе анализа будут изучены многие переменные, исследователи будут тратить больше времени на обдумывание всех наиболее важных и актуальных данных, которые необходимо собрать.
После получения данных корреляционный анализ поможет вам определить, какие переменные имеют самые сильные взаимосвязи. Непредвиденные отрицательные или положительные корреляции могут помочь предприятиям принимать более обоснованные решения.
Даже несмотря на то, что результаты корреляционного анализа сами по себе не являются отличным предсказателем, они все же могут использоваться для будущих качественных или количественных исследований.
Например, вы можете обнаружить значительную закономерность между переменными, которая вдохновит на дополнительные исследования.
Корреляционный анализ также хорошо ведет к регрессионному анализу. Для сравнения, регрессионный анализ показывает, как может выглядеть переменная A на основе определенного значения переменной B.
Другими словами, корреляция говорит вам, что существует связь, но регрессия показывает, как эта связь выглядит.
Когда использовать корреляционный анализ в исследовании рынка
Корреляционный анализ полезен для всех видов наборов данных, но он часто используется в маркетинговых исследованиях.
Вы, вероятно, найдете для них полезное приложение в опросах об удовлетворенности клиентов, опросах сотрудников, программах взаимодействия с клиентами (CX) или исследованиях рынка.
Эти опросы обычно включают много вопросов, которые делают переменные идеальными для корреляционного анализа.
Как упоминалось ранее, существует несколько различных подходов к корреляционному анализу, включая формулы Пирсона и Спирмена.
- Для корреляции Пирсона каждая переменная должна иметь нормальное распределение и предполагаемую линейную зависимость.
- При использовании корреляции Спирмена переменные должны содержать порядковые данные, в которых их положение важно.
Используйте корреляционный анализ только в том случае, если вы понимаете и можете объяснить клиенту, что корреляция не является причиной.
Заманчиво прийти к выводу, что две переменные напрямую влияют друг на друга, но этот анализ предназначен для выявления связей, а не для их прогнозирования.
Тем не менее, когда есть интерес к обнаружению взаимосвязей между двумя или более переменными, корреляционный анализ отлично подходит для проекта исследования рынка.
Свяжитесь с нашей компанией по исследованию рынка для измерения корреляционного анализа
Drive Research — национальная компания по исследованию рынка, расположенная в центре Нью-Йорка. Хотите включить корреляционный анализ в свое следующее исследование?
Ознакомьтесь с нашими услугами по исследованию рынка или свяжитесь с нами любым из указанных ниже способов.
- Напишите нам на нашем сайте
- Напишите нам по адресу [email protected]
- Позвоните нам по телефону 888-725-DATA
- Напишите нам по телефону 315-303-2040
Тим Гелл
В качестве аналитика-исследователя Тим участвует на всех этапах проекта исследования рынка для наших клиентов.Впервые он проявил интерес к исследованиям рынка во время учебы в Бингемтонском университете на основе сочетания бизнеса, статистики и психологии.




 Более того в этом случае знаки и k совпадают:
Более того в этом случае знаки и k совпадают:
 Получено на примере корреляционного исследования: graziano-raulin.com.
Получено на примере корреляционного исследования: graziano-raulin.com. Для Google это знак — к странице подошли с усердием. Добавить ссылку в пост социальной сети легко, куда сложнее овладеть аутрич-техниками и заслужить доверие вебмастеров.
Для Google это знак — к странице подошли с усердием. Добавить ссылку в пост социальной сети легко, куда сложнее овладеть аутрич-техниками и заслужить доверие вебмастеров.