Основной психофизический закон фехнера вебера: основной психофизический закон — это… Что такое основной психофизический закон?

Автор: | 10.03.1978
Нет комментариев

Содержание

основной психофизический закон — это… Что такое основной психофизический закон?

        ОСНОВНОЙ ПСИХОФИЗИЧЕСКИЙ ЗАКОН — функция зависимости величины ощущения от величины раздражителя. Единой формулы О. п. з. нет, но есть его варианты: логарифмический (Фехнера), степенной (Стивенса), обобщенные (Бэрда, Экмана, Забродина и др.). Наибольшую степень обобщения имеет закон Забродина, включающий не только логарифмическую и степенную функции, но и все промежуточные между ними.

        Закон Стивенса — вариант О. п. з. (С. Стивене, 1957) — степенная зависимость величины ощущения от величины стимула. Он установлен эмпирически на материале субъективного шкалирования, а также выводится теоретически аналогично закону Фехнера. Степенной закон Стивенса получил широкое распространение по той же причине, что и логарифмический закон Фехнера: он хорошо описывает многие эмпирические данные. По Сти-венсу, его закон справедлив для любых раздражителей: как измеряемых объективно (интенсивность звука или света, вес, температура, длина или наклон линий и т.

п.), так и не измеряемых (разборчивость почерков, серии рисунков и т.п.). Закон экспериментально проверен для более чем 20 стимульных признаков. Установлено, что показатели степени варьировали от 0, 3 (громкость) до 3, 5 (электрический удар). Степенная функция в логарифмическом масштабе на обеих осях координат имеет линейный вид с наклоном, зависящим от показателя степени.

        Все же обнаружено, что данный закон индивидуально варьирует, зависит от диапазона стимулов, плотности их расположения в диапазоне, вероятности их предъявления; крутизна степенной функции в двойных логарифмических координатах неодинакова в разных участках стимульной оси. Предложен ряд модификаций закона Стивенса, но неясно, какая из них лучше. На сегодня установлено, что он хорошо описывает в первом приближении субъективные оценки сенсорных стимулов. Однако он не универсален, так как не охватывает обнаружение и различение сигналов, неудовлетворительно описывает интервальное и категориальное шкалирование и т.

д.

        Закон Фехнера — вариант О. п. з. ( Г. Фехнер, 1860) — логарифмическая зависимость величины ощущения от величины стимула, выраженной в единицах порога.

        Он выведен автором теоретически на основе ряда априорных постулатов (за недоказанность которых не раз подвергнут критике) и закона Вебера. Несмотря на критику, закон Фехнера сохраняет свое значение и сегодня, так как хорошо соответствует многим экспериментальным фактам, особенно полученным для простых функций, близких к биологическим, а также для шкал едва заметных различий, накопленных над абсолютным порогом.

        В.А. Барабанщиков

Энциклопедия эпистемологии и философии науки. М.: «Канон+», РООИ «Реабилитация». И.Т. Касавин. 2009.

Научная суббота «Закон Э. Вебера – Г. Фехнера в жизни человека»

11 апреля 2020 года в Российской академии образования состоится интерактивная 

лекция «Закон Э. Вебера – Г. Фехнера в жизни человека. В чём сила маркетинга, рекламы и эргономики?»

Ведущие: Варвара Ильинична Моросанова, член-корреспондент РАО, доктор психологических наук, профессор; Сергей Владимирович Молчанов, кандидат психологических наук.

Участники узнают, как применяется на практике основной психофизический закон Вебера – Фехнера, и каким образом особенности человеческих ощущений и восприятия используются в эргономике, охране труда, маркетинге, рекламе. Во время обсуждения слушатели смогут найти ответы на вопросы о том, почему однообразная реклама быстро приедается и не замечается; почему на концертах и в вещании музыкальных телеканалов чередуются быстрые и медленные композиции, и почему сладкое лучше есть после первого и второго блюда, а не наоборот?

Вход на мероприятие по предварительной регистрации на сайте проекта «Субботы московского школьника» в соответствии с правилами регистрации и обозначенной для мероприятия целевой аудиторией.

Обучающиеся, прошедшие регистрацию, получат материалы занятий в видеоформате на адрес электронной почты, указанной при регистрации.

Лекция организована в рамках проекта “Субботы московского школьника”. Она станет одной из “Научных суббот”, которую организует РАО. Встречи с известными учеными и популяризаторами науки, которые показывают исследовательские будни изнутри, служат качественным дополнением к основной школьной программе. Каждый подросток сможет соприкоснуться с миром большой науки и увидеть связь теорий, теорем и гипотез с реальной жизнью.

Время проведения: с 14:45 до 16:20

Формат участия: дистанционный

Психофизика ощущений. Основной психофизический закон

Психофизика — это наука об измерении ощущений, изучающая количественные отношения между интенсивностью раздражителя и силой ощущения.

Основной психофизический закон

Густав Фехнер предпринял попытку разработать точный количественный метод измерения ощущений (душевных явлений). То, что сильные раздражители вызывают сильные ощущения, а слабые раздражители – слабые, было известно давно. Задача состояла в том, чтобы определить величину ощущения для каждого предъявляемого раздражителя. Попытка сделать это в количественной форме восходит к исследованиям греческого астронома Гиппарха (ок. 180 или 190-125 до н.э.). Он разработал шкалу звездных величин, делящую видимые невооруженным глазом звезды на шесть категорий: от самых слабых (шестой величины) до самых ярких (первой величины).

Эрнст Генрих Вебер на основе экспериментов по различению силы давления на кожу (веса поднимаемых на ладони грузов) установил, что вместо того, чтобы просто воспринимать разницу между раздражителями, мы воспринимаем отношение этой разницы к величине исходного раздражителя. До него аналогичный вывод уже был сделан в середине XIX в. французским физиком и математиком Пьером Бугером в отношении яркости зрительных ощущений. Г. Фехнер выразил сформулированную Э. Вебером закономерность в математической форме:

ΔR — изменение раздражителя, необходимое для обнаружения едва заметного различия в стимуляции;
R – величина раздражителя;
k – константа, значение которой зависит от вида ощущений.

Конкретное числовое значение k называют отношением Э. Вебера. В последующем было обнаружено, что величина k не остается постоянной во всем диапазоне интенсивности раздражителя, а увеличивается в области низких и высоких значений. Тем не менее отношение приращения величины раздражителя и силы ощущения (или отношение увеличения стимула к исходному его значению) остается постоянным для средней области диапазона интенсивности раздражителей, вызывающих практически все виды ощущений (закон Бугера – Вебера).

В дальнейшем измерение ощущений стало предметом исследований Г. Фехнера. Опираясь на закон Бугера – Вебера, а также на собственное допущение о том, что ощущение раздражителя представляет собой накопленную сумму равных приращений ощущения, Г. Фехнер сначала выразил все это в дифференциальной форме как dR=adI/I, затем проинтегрировал [принимая R=О при интенсивности раздражителя, равной абсолютному порогу (Iο)] и получил следующее уравнение:

R=clog Iο/I

где R – величина ощущения;
с – константа, величина которой зависит от основания логарифма и от отношения Вебера;
I – интенсивность раздражителя;
Iο — величина абсолютного порога интенсивности.

Приведенное выше уравнение получило название основного психофизического закона, или закона Вебера – Фехнера, согласно которому ощущения описываются кривой уменьшающегося прироста (или логарифмической кривой). Например, увеличение яркости, ощущаемое при замене одной лампочки десятью, будет таким же, как и в случае замены десяти лампочек сотней. Иначе говоря, возрастанию величины раздражителя в геометрической прогрессии соответствует прирост ощущения в арифметической прогрессии.

Позже были сделаны попытки уточнить основной закон психофизики. Так, американский психофизик С. Стивенс выявил степенной, а не логарифмический характер зависимости между силой ощущения и интенсивностью раздражителя:

где R – сила ощущения;
с – константа;
I – интенсивность раздражителя;
Iο —  величина абсолютного порога ощущения;
n – показатель степени, зависящий от модальности ощущений (значения приводятся в справочниках).

Обобщенный психофизический закон, предложенный Ю. Забродиным, учитывал тот факт, что характер зависимости между ощущениями и воздействующими раздражителями обусловлен осведомленностью человека о процессах ощущения. Исходя из этого, Ю. Забродин ввел в формулу закона С. Стивенса показатель z, характеризующий степень осведомленности:

Из формулы видно, что при z=0 формула обобщенного закона Ю. Забродина принимает вид закона Вебера – Фехнера, а при 2=1 — закона Стивенса.

Современные исследования шкалирования указывают, что уравнение Ю. Забродина не является обобщенным «в последней инстанции» психофизическим законом, т.е. оно не может охватить все существующее многообразие психофизических функций. В целом же Ю. Забродиным разработан системно-динамический подход к анализу сенсорных процессов.

Ставя перед собой задачу измерения ощущений, Г. Фехнер предполагал, что человек не способен непосредственно количественно оценить их величины. Поэтому он предложил косвенный способ измерения – в единицах физической величины стимула. Величина ощущения представлялась как сумма едва заметных его приращений над исходной точкой. Для ее обозначения Г. Фехнер ввел понятие порога ощущений, измеряемого в единицах стимула. Он различал абсолютный порог чувствительности и различительный (дифференциальный) порог.

Закон Вебера-Фехнера – основной психофизический закон. Основные психофизические законы (по Веккеру)

раздражителя к базовой величине раздражения; то же самое с ощущениями (слева)

 Закон Вебера — Фехнера

установлены закономерные функциональные взаимосвязи между величиной силовой характеристики физического раздражения и соответствующей ей субъективной величиной ощущения: интенсивность ощущения пропорциональна логарифму интенсивности стимула (раздражителя).

Закон Стивенса – это модификация закона Вебера — Фехнера. Между рядом ощущений и рядом физических раздражителей существует не логарифмическая, а степенная зависимость.

где R – сила ощущения;

с – константа;

I – интенсивность раздражителя;

Iο —  величина абсолютного порога ощущения;

n – показатель степени, зависящий от модальности ощущений

Обобщенный психофизический закон Ю.

Забродина:

Характер зависимости между ощущениями и воздействующими раздражителями обусловлен осведомленностью человека о процессах ощущения.

Введение показателя z, характеризующего степень осведомленности.

Основные психофизические законы (по Веккеру).

Оказалось, что интенсивность как универсальная количественная энергетическая характеристика явлений природы была распространена на сферу психических процессов и были установлены закономерные функциональные взаимосвязи между величиной силовой характеристики физического раздражения и соответствующей ей субъективной величиной ощущения. В этом выражается содержание

психофизического логарифмического закона Вебера — Фехнера. Принимая R=О при интенсивности раздражителя, равной абсолютному порогу (Iο)], получается следующее уравнение:

R=clog Iο/I,

где R – величина ощущения; с – константа, величина которой зависит от основания логарифма и от отношения Вебера; I – интенсивность раздражителя; Iο — величина абсолютного порога интенсивности.

По данному уравнению ощущение описывается кривой уменьшающегося прироста. Вывод логарифмического закона Фехнера основывается, как известно, на допущении о субъективном равенстве <едва заметных различий> раздражителей.

Интенсивность является универсальной характеристикой, она, конечно, не может не быть представленной на уровне нервного возбуждения, что и находит свое прямое выражение в нейрофизиологических фактах (прежде всего, например, в амплитудной характеристике градуальных сигналов).

Между ощущением как <первым> психическим сигналом и сигналом <чисто> нервным особый интерес представляет соотношение между психологической и нейрофизиологической величинами интенсивности (в их отношении к исходной интенсивности раздражения).

Современные психофизические исследования Стивенса и его школы открывают доступ к сущности психофизиологического <порога> или границы в рамках общих психофизических отношений. Он выявил степенной характер зависимости между силой ощущения и интенсивностью раздражителя (психофизический закон Стивенса).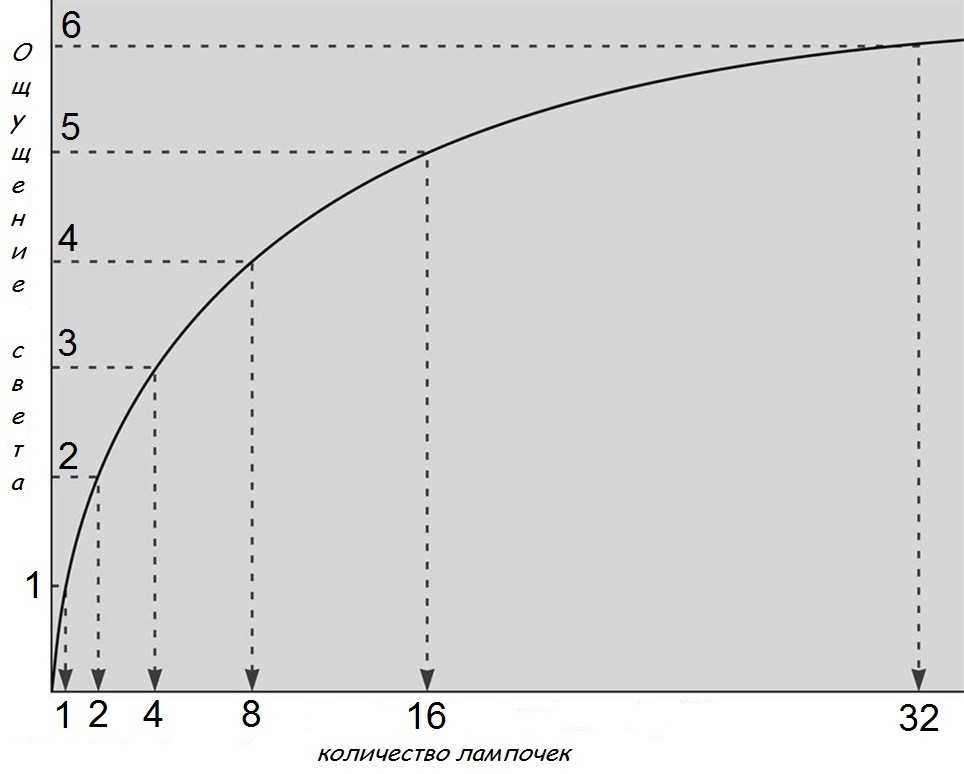

, где R – сила ощущения; с – константа; I – интенсивность раздражителя; Iο —  величина абсолютного порога ощущения; n – показатель степени, зависящий от модальности ощущений

Многочисленные данные свидетельствуют о том, что периферическая реакция анализатора действительно является именно логарифмической функцией интенсивности раздражителя. Периферическая реакция анализатора на раздражение есть реакция кодирования, преобразующего физическое воздействие источника информации в нервный сигнал-код, то сделанное Экманом заключение фактически означает

закон бугера-вебера. закон фехнера

В 1760 г. французский ученый, создатель фотометрии П.Бугер исследовал свою способность различать тень, отбрасываемую свечой, если экран, на который падает тень, одновременно освещается другой свечой. Его измерения доволь-

но точно установили, что отношение л К/К (где л К — минимальный воспринимаемый прирост освещения, К — исходное освещение) — величина сравнительно постоянная.

В 1834 г. немецкий психофизик Э.Вебер повторил и подтвердил опыты П.Бугера. Э.Вебер, изучая различение веса, показал, что минимально воспринимаемая разница в весе представляет собой постоянную величину, равную приблизительно 1/30. Груз в 31 г различается от груза в 30, груз в 62 г от груза в 60 г; 124 г от 120 г.

В историю исследования по психофизике ощущений это соотношение вошло под названием закона Бугера-Вебера: дифференциальный порог ощущений для разных органов чувств различен, но для одного и того же анализатора он представляет собой постоянную величину, т.о. л R/R = const.

Это отношение показывает, какую часть первоначальной величины стимула необходимо прибавить к этому стимулу, чтобы получить едва заметное изменение ощущения.

Дальнейшие исследования показали, что закон В ебера действителен лишь для раздражителей средней величины: при приближении к абсолютным порогам величина прибавки перестает быть постоянной. Закон Вебера применим не только к едва заметным, но и ко всяким различиям ощущений. Различие между парами ощущений кажутся нам равными, если равны геометрические соотношения соответствующих раздражителей. Так, увеличение силы освещения от 25 до 50 свечей дает субъективно такой же эффект, как увеличение от 50 до 100.

Исходя из закона Бугера-Вебера, Фехнер сделал допущение, что едва заметные различия (е.з.р.) в ощущениях можно рассматривать как равные, поскольку все они — величины бесконечно малые. Если приращение ощущения, соответствующее едва заметной разнице между стимулами, обозначить как л Е, то постулат Фехнера можно записать как л Е = const.

Фехнер принял е.з.р. (лЕ) как единицу меры, при помощи которой можно численно выразить интенсивность ощущений как сумму (или интеграл) едва заметных (бесконечно малых) увеличений, считая от порога абсолютной чувствительности. В результате он получил два ряда переменных величин — величины раздражителей и соответствующие им величины ощущений. Ощущения растут в арифметической прогрессии, когда раздражители растут в геометрической прогрессии.

Как это понимать? Берем, например, такие раздражители, как 10 свечей, увеличиваем их количество: 10 — 100 — 1000 -10000 и т.д. Это геометрическая прогрессия. Когда было 10 свечей, у нас имелось соответствующее ощущение. При увеличении раздражителей до 100 свечей ощущение увеличилось вдвое; появление 1000 свечей вызвало увеличение ощущения в три раза и т.д. Увеличение ощущений идет в арифметической прогрессии, т.е. намного медленнее увеличения самих раздражителей. Отношение этих двух переменных величин можно выразить в логарифмической формуле: Е = К lg R + С, где Е — сила ощущения, R — величина действующего раздражителя, К — коэффициент пропорциональности, С — константа, различная для ощущений разных модальностей.

Эта формула получила название основного психофизического закона, который по сути дела представляет собой закон Вебера-Фехнера. Согласно этому закону, изменение силы ощущения пропорционально десятичному логарифму изменения силы воздействующего раздражителя (рис.8).

Рис. 8. Логарифмическая кривая зависимости величины ощущения от силы раздражителя, иллюстрирующая закон Вебера-Фехнера

Ряд явлений, вскрытых исследованиями чувствительности, не укладывается в рамки закона Вебера-Фехнера. Например, ощущения в области протопатической чувствительности не обнаруживают постепенного нарастания по мере усиления раздражения, а по достижении известного порога сразу же появляются в максимальной степени. Они приближаются по своему характеру к типу реакций «все или ничего».

Спустя примерно полстолетия после открытия основного психофизического закона он вновь привлек к себе внимание и, на основе новых экспериментальных данных, породил дискуссию об истинном, точно выраженном математической формулой характере связи между силой ощущения и величиной раздражителя. Американский ученый С.Стивенс рассуждал следующим образом: что происходит при удвоении освещенности пятна света и, с другой стороны, силы тока (частота 60 гц), пропускаемого через палец? Удвоение освещенности пятна на темном фоне удивительно мало влияет на его видимую яркость. По оценке типичного наблюдателя кажущееся увеличение составляет всего лишь 25%. При удвоении же силы тока ощущение удара увеличивается в десять раз. С.Стивенс отвергает постулат Фехнера (лЕ = const.) и заявляет, что константной является другая величина, а именно отношение л Е/Е. Распространяя закон Бугера-Вебера на сенсорные величины (лЕ/Е = const), С.Стивенс через ряд математических преобразований получает степенную зависимость между ощущением и стимуляцией: Е= кРД где к — константа, определяемая избранной единицей измерения, Е — сила ощущения, R — значение воздействующего раздражителя, п- показатель, зависящий от модальности ощущения. Показатель п принимает значение 0,33 для яркости и 3,5 для электрическо-г2о удара. Эта закономерность получила название закона Стивенса.

По мнению С.Стивенса, степенная функция имеет то преимущество, что при использовании логарифмического масштаба на обеих осях, она выражается прямой линией, наклон которой соответствует значению показателя (п). Это видно на рис.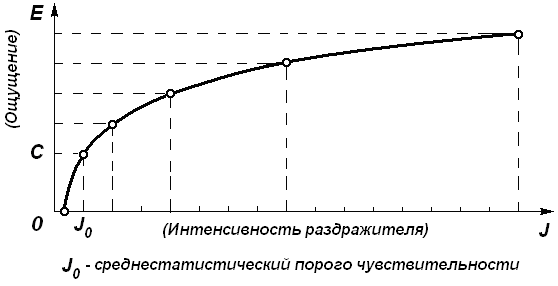 9: медленное увеличение яркостного контраста и быстрое усиление ощущения удара электрическим током.

J 235 Ю 203050 100 200500500″1000

Рис. 9. Степенная кривая зависимости величины ощущения от силы раздражителя, иллюстрирующая закон Стивенса. 1.Электрический удар. 2. Яркость.

Сто с лишним лет не прекращаются споры между сторонниками логарифмической зависимости силы ощущения от величины стимула (закон Фехнера) и степенной (закон Сти-венса). Если пренебречь чисто психофизическими тонкостями этого спора, то оба закона по своему психологическому смыслу окажутся весьма близкими: тот и другой утверждают, во-первых, что ощущения меняются непропорционально силе физических стимулов, действующих на органы чувств, и, во-вторых, что сила ощущения растет гораздо медленнее, чем величина физических стимулов.

Вопросы для самопроверки

1. Докажите несостоятельность на сегодняшний день методологической основы исследований Фехнера.

2.В чем состоит различие между психофизикой-I и психофизикой-П, классической и современной психофизикой?

3. Какие методы измерения психических процессов (ощущений) получили почетное наименование классических?

4.Что такое порог исчезновения ощущения и порог появления ощущения?

З.Приведите примеры влияния на человека допороговых сигналов.

6.В чем состоит сущность центральной проблемы психофизики-1?

У.Как зависит величина ощущения от силы раздражителя (по Фехнеру и по Стивенсу)?

В 1760 г. французский ученый, создатель фотометрии П.Бугер исследовал свою способность различать тень, отбрасываемую свечой, если экран, на который падает тень, одновременно освещается другой свечой. Его измерения довольно точно установили, что отношение л R/R (где л R — минимальный воспринимаемый прирост освещения, R — исходное освещение) — величина сравнительно постоянная.

В 1834 г. немецкий психофизик Э.Вебер повторил и подтвердил опыты П.Бугера. Э.Вебер, изучая различение веса, показал, что минимально воспринимаемая разница в весе представляет собой постоянную величину, равную приблизительно 1/30. Груз в 31 г различается от груза в 30, груз в 62 г от груза в 60 г; 124 г от 120 г.

В историю исследования по психофизике ощущений это соотношение вошло под названием закона Бугера-Вебера: дифференциальный порог ощущений для разных органов чувств различен, но для одного и того же анализатора он представляет собой постоянную величину, т.о. л R/R = const.

Это отношение показывает, какую часть первоначальной величины стимула необходимо прибавить к этому стимулу, чтобы получить едва заметное изменение ощущения.

Дальнейшие исследования показали, что закон Вебера действителен лишь для раздражителей средней величины: при приближении к абсолютным порогам величина прибавки перестает быть постоянной. Закон Вебера применим не только к едва заметным, но и ко всяким различиям ощущений. Различие между парами ощущений кажутся нам равными, если равны геометрические соотношения соответствующих раздражителей. Так, увеличение силы освещения от 25 до 50 свечей дает субъективно такой же эффект, как увеличение от 50 до 100.

Исходя из закона Бугера-Вебера, Фехнер сделал допущение, что едва заметные различия (е.з.р.) в ощущениях можно рассматривать как равные, поскольку все они — величины бесконечно малые. Если приращение ощущения, соответствующее едва заметной разнице между стимулами, обозначить как лЕ, то постулат Фехнера можно записать как лЕ = const.

Фехнер принял е.з.р. (лЕ) как единицу меры, при помощи которой можно численно выразить интенсивность ощущений как сумму (или интеграл) едва заметных (бесконечно малых) увеличений, считая от порога абсолютной чувствительности. В результате он получил два ряда переменных величин — величины раздражителей и соответствующие им величины ощущений. Ощущения растут в арифметической прогрессии, когда раздражители растут в геометрической прогрессии.

Как это понимать? Берем, например, такие раздражители, как 10 свечей, увеличиваем их количество: 10 — 100 — 1000 — 10000 и т.д. Это геометрическая прогрессия. Когда было 10 свечей, у нас имелось соответствующее ощущение. При увеличении раздражителей до 100 свечей ощущение увеличилось вдвое; появление 1000 свечей вызвало увеличение ощущения в три раза и т.д. Увеличение ощущений идет в арифметической прогрессии, т.е. намного медленнее увеличения самих раздражителей. Отношение этих двух переменных величин можно выразить в логарифмической формуле: Е = К lg R + C, где Е — сила ощущения, R — величина действующего раздражителя, К — коэффициент пропорциональности, С — константа, различная для ощущений разных модальностей.

Эта формула получила название основного психофизического закона, который по сути дела представляет собой закон Вебера-Фехнера.

Согласно этому закону, изменение силы ощущения пропорционально десятичному логарифму изменения силы воздействующего раздражителя (рис.8).

Ряд явлений, вскрытых исследованиями чувствительности, не укладывается в рамки закона Вебера-Фехнера. Например, ощущения в области протопатической чувствительности не обнаруживают постепенного нарастания по мере усиления раздражения, а по достижении известного порога сразу же появляются в максимальной степени. Они приближаются по своему характеру к типу реакций «все или ничего».

раздражителя, иллюстрирующая закон Вебера-Фехнера

Спустя примерно полстолетия после открытия основного психофизического закона он вновь привлек к себе внимание и, на основе новых экспериментальных данных, породил дискуссию об истинном, точно выраженном математической формулой характере связи между силой ощущения и величиной раздражителя. Американский ученый С.Стивенс рассуждал следующим образом: что происходит при удвоении освещенности пятна света и, с другой стороны, силы тока (частота 60 гц), пропускаемого через палец? Удвоение освещенности пятна на темном фоне удивительно мало влияет на его видимую яркость. По оценке типичного наблюдателя кажущееся увеличение составляет всего лишь 25%. При удвоении же силы тока ощущение удара увеличивается в десять раз. С.Стивенс отвергает постулат Фехнера (лЕ = const.) и заявляет, что константной является другая величина, а именно отношение л Е/Е. Распространяя закон Бугера-Вебера на сенсорные величины (л Е/Е = const. , где к — константа, определяемая избранной единицей измерения, Е — сила ощущения, R — значение воздействующего раздражителя, n — показатель, зависящий от модальности ощущения. Показатель n принимает значение 0,33 для яркости и 3,5 для электрического удара. Эта закономерность получила название закона Стивенса.

По мнению С.Стивенса, степенная функция имеет то преимущество, что при использовании логарифмического масштаба на обеих осях, она выражается прямой линией, наклон которой соответствует значению показателя (n). Это видно на рис. 9: медленное увеличение яркостного контраста и быстрое усиление ощущения удара электрическим током.

раздражителя, иллюстрирующая закон Стивенса. 1.Электрический удар. 2. Яркость.

Сто с лишним лет не прекращаются споры между сторонниками логарифмической зависимости силы ощущения от величины стимула (закон Фехнера) и степенной (закон Сти- венса). Если пренебречь чисто психофизическими тонкостями этого спора, то оба закона по своему психологическому смыслу окажутся весьма близкими: тот и другой утверждают, во-первых, что ощущения меняются непропорционально силе физических стимулов, действующих на органы чувств, и, во- вторых, что сила ощущения растет гораздо медленнее, чем величина физических стимулов.

Наряду с этим различаются оперативные пороги ощущений – величина сигнала, при которой точность и скорость его различения достигает максимума. Эта величина на порядок больше, чем величина порога различения, и применяется в различных практических расчетах.

Основной психофизический закон

Опираясь на положение о равенстве минимальных различий между ощущениями и соотношением Вебера, немецкий ученый Г. Т. Фехнер вывел психофизическую закономерность, которая получила именование основной психофизический закон . На основании этого закона сила ощущения пропорциональна логарифму величины действующего раздражителя:

R = C (lg S – lg S o),

где: R – интенсивность ощущения; С – константа, связанная с соотношением Вебера; S – интенсивность действующего стимула; S o – абсолютный порог.

Примерно через сто лет после этого американский ученый С. Стивенс выдвинул идею возможности непосредственной количественной оценки человеком своих ощущений. Он уточнил основной психофизический закон и установил, что зависимость между ощущением и физическим стимулом имеет не логарифмический , а степенной характер , и вывел следующую формулу:

R = C (S – S o) 2 .

Позднее были предложены другие уточнения основного психофизического закона, в частности отечественным психологом Ю. М. Забродиным, который ввел дополнительную константу, учитывающую условия наблюдения и задачи, стоящие перед субъектом.

Понятие и основные характеристики

Сенсорного ряда

Диапазон наших ощущений образует сенсорный ряд . Несмотря на то, что абсолютный и дифференциальный пороги представляют собой явно различные характеристики, за этими понятиями стоит общий принцип или одно и то же допущение.

Данное допущение состоит в следующем. Предполагается, что сенсорный ряд дискретен (т. е. прерывен). Это означает: до определенных пределов ощущение есть, а потом пропадает.

Представление, что наша сенсорная система устроена по пороговому, прерывистому принципу, получило название концепции дискретности сенсорного ряда, а ее автором является Г. Т. Фехнер. Причем эта точка зрения распространяется как на абсолютный, так и на дифференцированный пороги.

Психофизики, воодушевленные идеей «абсолютного слуха», или точкой исчезновения ощущений, провели сотни экспериментов, чтобы определить пороги чувствительности. Они с удивлением установили, что порог как бы плавает. Иными словами, даже для очень слабых раздражителей существует некоторая вероятность их обнаружения, а для относительно сильных – возможна вероятность их необнаружения.

Зависимость вероятности обнаружения (различения) стимулов от их интенсивности получила название психометрической функции.

Если сенсорная система работает по дискретному принципу, психометрическая функция будет выглядеть следующим образом. До определенного уровня интенсивности стимула вероятность обнаружения равна нулю, потом – единице (рис. 13).

В последующем, основываясь на результатах психофизических исследований, И. Мюллер предложил идею о непрерывности сенсорного ряда. Ее суть состоит в том, что не существует порога как такового: любой стимул в принципе может вызвать ощущения. Реальная психометрическая функция в этом случае показана нарис.14.

Теория непрерывности объясняет причину необнаружения некоторых слабых сигналов. Она состоит в том, что на возможность обнаружения стимула влияет не только его физическая интенсивность, но и расположенность сенсорной системы к ощущению. Данная расположенность зависит от множества случайных, плохо контролируемых факторов: усталость человека, степень его внимательности, мотивации, опыта и т.п.

При этом одни факторы благоприятно действуют на способность наблюдателя к обнаружению сигнала (например, большой опыт), а другие – неблагоприятно (например, усталость). Соответственно, неблагоприятные факторы уменьшают способность к обнаружению, а благоприятные – увеличивают. Отсюда нет оснований говорить о существовании какой-то особой точки на оси ощущений, где они прерываются, исчезают. Сенсорный ряд непрерывен, и если бы мы могли создать идеальные условия наблюдения, то сенсорная система восприняла бы насколько угодно малый сигнал.

Психометрическая кривая может быть получена для различных органов чувств и всех видов ощущений, причем для каждого вида ощущений существуют свои пороги.

Со времени научной дискуссии, проходившей между Г. Т. Фехнером и И. Мюллером, прошло уже более ста лет, но проблема дискретности – непрерывности сенсорного ряда до сих пор находится в поле зрения психологов. Исходные психофизические идеи вдохновили многих исследователей и позволили им создать массу психофизических концепций, интересных как для теории, так и полезных в практическом плане.

Современные концепции порогов чувствительности характеризуются двумя особенностями. Первая из них состоит в том, что различение и обнаружение трактуется как процесс, неотъемлемой частью которого является неопределенность и случайность. Вторая – в том, что все глубже исследуются механизмы несенсорного порядка, в широком смысле – механизмы принятия решений, которые «приходят на помощь» сенсорной системе и позволяют различным способом решать сенсорные задачи.

Адаптация

Чувствительность анализатора нестабильна и изменяется в зависимости от различных условий. Например, находясь в помещении с какими-то запахами, мы через некоторое время перестаем замечать эти запахи, т. к. чувствительность анализатора постепенно понижается. Изменение чувствительности анализатора в результате его приспособления к силе и продолжительности действующего раздражителя называется адаптацией.

Закон Бугера-Вебера

(иногда — за кон Вебера) — один из основных законов психофизики — установленная для случая различения одномерных раздражителей сенсорных прямо пропорциональная зависимость порога дифференциального от величины раздражителя I, к коей адаптирована (см. ) данная система сенсорная: 1Л=К (const). Коэффициент К, получивший название отношения Вебера, различен для разных раздражителей сенсорных: 0.003 — для высоты звука; 0.02 — для видимой яркости; 0.09 — для громкости звуков и пр. Он фиксирует величину, на которую нужно увеличить или уменьшить раздражитель, чтобы получить едва заметное изменение ощущения. Эту зависимость установил в XVIII в. французский ученый П. Бугер и позднее — независимо — детально изучил немецкий физиолог Э. Г. Вебер, проводивший эксперименты на различение весов, длин линий и высоты звукового тона, в коих тоже показал постоянство отношения едва заметного изменения раздражителя к его исходной величине. В дальнейшем было показано, что выявленный закон не универсален, но справедлив лишь для средней части диапазона восприятия системы сенсорной, где чувствительность дифференциальная имеет максимальное значение. За пределами этой части диапазона порог дифференциальный возрастает, особенно в диапазонах абсолютных нижнего и верхнего порогов.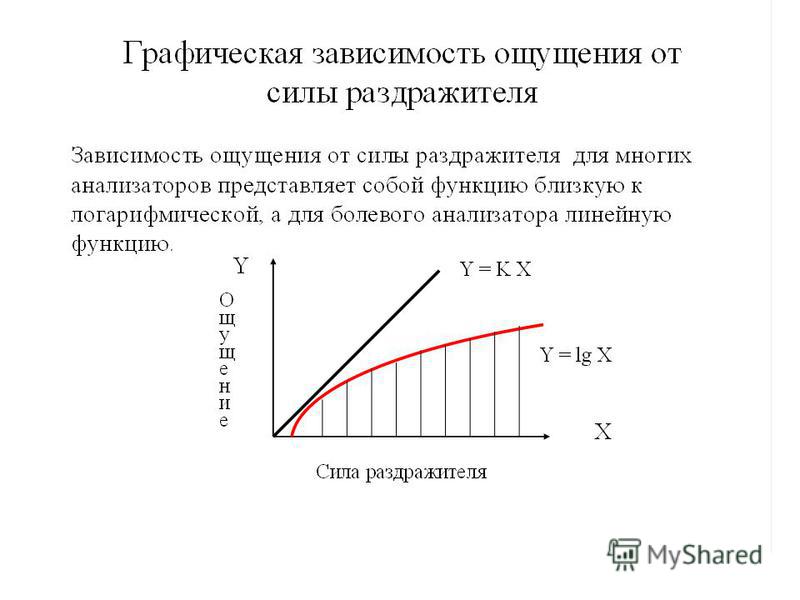 Дальнейшим развитием и отчасти интерпретацией закона Бугера-Вебера стал закон Вебера-Фехнера.

Словарь практического психолога. — М.: АСТ, Харвест . С. Ю. Головин . 1998 .

Впервые открыт французским ученым П.Бугером.

Категория.

Один из основных психофизических законов.

Специфика.

Согласно этому закону, едва заметное изменение ощущения при изменении интенсивности раздражителя возникает при увеличении исходного раздражителя на некоторую постоянную его долю. Так, исследуя способность человека распознавать тень на экране, который одновременно освещался другим источником света, Бугер показал, что минимальный прирост освещения предмета (дельта I), необходимый для того, чтобы вызвать ощущение едва заметного различия тени от освещенного экрана, зависит от уровня освещенности экрана I, но отношение (дельта I/I) — величина постоянная. К выявлению такой же закономерности пришел несколько позднее, но независимо от Бугера, Э.Вебер. Он проводил эксперименты на различение весов, длин линий и высоты звукового тона, в которых также показал постоянство отношения едва заметного изменения раздражителя к его исходной величине. Это отношение (дельта I/I), характеризующее величину дифференциального порога, зависит от модальности ощущения: для зрения она равна 1/100, для слуха — 1/10, для осязания — 1/30.

Критика.

В дальнейшем было показано, что выявленный закон не имеет универсального распространения, а справедлив только для средней части диапазона сенсорной системы, в котором дифференциальная чувствительность имеет максимальное значение. За пределами же этой части диапазона дифференциальный порог возрастает, особенно в диапазонах абсолютных нижнего и верхнего порогов.

Психологический словарь . И.М. Кондаков . 2000 .

Смотреть что такое «закон Бугера-Вебера» в других словарях:

    Закон Бугера – Вебера — Закон Бугера Вебера один из основных законов психофизики, открытый французским ученым П. Бугером, согласно которому едва заметное изменение ощущения при изменении интенсивности раздражителя возникает при увеличении исходного раздражит … Психологический словарь

    — (иногда закон Вебера) установленная для случая различения одномерных сенсорных раздражителей прямо пропорциональная зависимость разностного порога (см. порог ощущения) dI от величины раздражителя I, к которой адаптирована (см. адаптация… …

    Бугера-Вебера закон — (Р. Bouguer, 1698 1758, франц. математик и астроном; Е. Н. Weber, 1795 1878, нем. анатом и физиолог) отношение порога ощущения прироста раздражителя к исходной величине последнего есть величина постоянная … Большой медицинский словарь

    — (или закон Бугера Вебера; англ. Weber s law) один из законов классической психофизики, утверждающий постоянство относительного дифференциального порога (во всем сенсорном диапазоне варьируемого свойства стимула). В 1729 г. фр. физик, «отец»… … Большая психологическая энциклопедия — логарифмическая зависимость силы ощущения Е от физической интенсивности раздражителя Р: Е = к log P + с, где k и с некие постоянные, определяемые данной сенсорной системой. Зависимость была выведена немецким психологом и физиологом Г. Т. Фехнером … Большая психологическая энциклопедия

    Ощущение — Эта статья об отражении сигналов органов чувств. Об отражении эмоциональных процессов см. Переживание (психология). Ощущение, чувственный опыт простейший психический процесс, представляющий собой психическое отражение… … Википедия

М. Бугер в конце XVIII века исследовал способность человека различать близкие между собой уровни освещенности. Оборудо­вание, используемое Бугером в его экспериментах, вполне соот­ветствовало тому времени: это стол с измерительной линейкой, на котором размещались две свечи, и экран, освещаемый этими свечами. Передвигая каждую из свечей на разное расстояние отно­сительно экрана, Бугер пытался измерить то, что мы сейчас назы­ваем разностным (дифференциальным) порогом восприятия осве­щенности. Бугер пришел к выводу, что величина едва заметного различия (ЕЗР) между двумя освещенностями непостоянна, она возрастает пропорционально исходной освещенности: ΔL=kL. Другими словами, отношение ЕЗР (ΔL) к исходному уровню осве­щенности есть величина постоянная; ΔL/L= const. Аналогичные исследования для стимулов других сенсорных модальностей были проведены в середине XIX столетия Э. Вебером. Так, в одном из сво­их опытов Вебср предлагал испытуемым определять разницу между тяжестью двух грузов, поднимаемых одновременно. Было уста­новлено, в частности, что если в качестве исходного служил груз массой в 100 граммов, то испытуемый воспринимал едва замет-ное приращение тяжести при добавлении груза в 3 грамма. Если вес исходного груза увеличивался в 2, 3, 5… раз, то и величина разностного порога ΔР = P1 — Р2 повышалась в той же пропорции. Для веса в 200 граммов величина разностного порога составляла 6 граммов, для 300 — 9 граммов и т. д. Не трудно заметить, что и в этом случае соблюдается правило ΔР/P = const.

Данное отношение, выраженное в обобщенном виде:

ΔS/S= const,

где S — величина раздражителя (безотносительно к его сенсорной модальности), позднее стали называть правилом Вебера (или Бу­гера — Вебера). Как будет показано дальше, эта закономерность сыграла немаловажную роль в формулировке Фехнером его основ­ного психофизического закона.

Несмотря на то, что возникновение психофизики как науки обычно датируют 1860 годом (год выхода в свет книги Г. Фехнера «Элементы психофизики»), некоторые авторы называют более ран­нюю дату — 22 октября 1850 года. Именно в этот день Фехнеру пришла в голову мысль о законе количественной связи между физическими и психическими величинами. Как уже отмечалось ранее, Фехнер ничуть не сомневался в возможности количествен­ного измерения субъективных процессов. По его мнению, не только элементарные психические процессы (в частности, ощущения), но и процессы Орлее высокого порядка: «…живость воспомина­ний, образы фантазии, интенсивность отдельных мыслей и т. д.» могут быть выражены количественно. Что же касается измерения ощущений, то рассуждения Фехнера в основном сводились к сле­дующему.

1. Признавая справедливость правила Бугера — Вебера А5/5 — сош1, можно получить элементарную единицу измерения ощущений. Другими словами, величина дифференциального порога, которая является величиной постоянной и не зависит от абсолютного зна­чения раздражителя, есть не что иное, как элементарный «квант» ощущения, и он может быть использован как единица измерения субъективных величин. Фехнер предложил следующую формулу:

ΔS/S=ΔR

где ΔR — величина едва заметного ощущения.

Это было довольно смело — математически приравнять отно­шение двух физических величин к субъективной (психической) величине. Справедливости ради необходимо отметить, что вели чина ΔS/S не имеет размерности и не может быть выражена в ка­ких-либо физических единицах.

2. Принимая, что величины ΔS и ΔR являются бесконечно малыми (а это наиболее уязвимый пункт фехнеровской концепции), можно записать психофизическое отношение в виде дифференциального уравнения следующего вида:

3. Интегрируя выражение dS/S=dR, можно вывести закон взаимосвязи между величиной R (ощущением) и S (силой раздражителя):

R=klnS+C, или R=k’lgS+ С’.

Как уже отмечалось, выведенный путем математических рас­суждений логарифмический закон (величина ощущения пропор­циональна логарифму силы раздражения) Фехнер возвел в ранг основного психофизического закона. В 1877 году в своем послесло­вии к «Элементам психофизики» Фехнер писал так: «Вавилонская башня в свое время не была построена, так как рабочие не могли договориться, как се строить. Мое психофизическое сооружение (имеется в виду основной психофизический закон) никогда не будет разрушено, так как ученые никогда не договорятся, как его разру­шать».

Но сколь бы ни было амбициозным такое утверждение, надо отдать должное прозорливости Фехнера. Несмотря на многочис­ленные и продолжительные нападки со стороны противников Фех­нера, логарифмический закон доказал свою жизнеспособность не только в психофизике, но и в нейрофизиологии, сенсорной фи­зиологии и т. д. Было, в частности, показано, что физическая шка­ла интенсивности раздражителя на уровне рецепторов действитель­но претерпевает логарифмическое преобразование.

Волею судеб логарифмический закон Фехнера вошел практи­чески во все учебники и пособия по психологии и сенсорной физи­ологии. В то же время возражения против этого закона и альтер­нативные варианты психофизической зависимости, выдвигаемые современниками Фехнера и последующими поколениями психо­физиков, до недавнего времени оставались малоизвестными. Нам же представляется, что этот вопрос достаточно важен и заслуживает подробного рассмотрения.

Появление в 1860 году «Элементов психофизики» Фехнера совершило поистине революцию в психологии. Крупнейшие психологи второй половины XIX века размежевались на два лагеря.

Одни из них правильно поняли и оценили сущность концепции Фехнера о возможности количественного подхода к описанию психических явлений и процессов и форсировали свои усилия именно в этом направлении. Крупнейший ученый того времени Вильгельм Вундт стал основателем первой в мире лаборатории экспериментальной психологии, в которой проводились исследо­вания времени двигательной реакции, предпринимались попытки расчленить психику на отдельные элементарные психические акты, зарегистрировать, измерить, рассчитать их и уже после этого скон­струировать целостную картину психической деятельности. Дру­гие же (ярким примером может служить Уильям Джеймс) встре­тили в штыки саму идею о возможности количественного подхода в психологии.

И среди сторонников, и среди противников Фехнера нашлись такие, когорыс попытались разрушить «вавилонскую башню». При этом «подкоп» под психофизическое сооружение делался с разных сторон. Одни утверждали, что неправомерно принимать за основу правило Бугера — Вебера, поскольку оно справедливо только в обла­сти средних значений силы раздражителя, а при низких и высо­ких интснсивностях нарушается. Другие (а их было большинство) указывали на неправомерность дифференцирования величин А5 и ДД, поскольку они не являются бесконечно малыми (о том, что это на самом деле так, мы поговорим в следующих разделах). Наконец, третьи считали, что ΔR (субъективная величина едва за­метного различия) не является постоянной. Джеймс, в частности, писал: «Едва заметное ощущение приращения тяжести восприни­мается сильнее при добавлении нескольких фунтов к стофунтовому весу, нежели при добавлении нескольких унций к весу в один фунт. Фехнер игнорировал этот факт».

В качестве альтернативы закону Фехнера Ф. Брептано предло­жил уравнение следующего вида:

ΔR/R =k (ΔS/S)

Другими словами, он предположил, что правило Бугера — Всбср справедливо не только для физических параметров стимул (ΔS=kS), но и для ощущений (ΔR=k’R). Дифференцировани этого уравнения дает следующее выражение:

dR/R=k’/k (dS/S),

а интегрирование его приводит к двойной логарифмической (или степенной) зависимости типа:

lnR=(k’/k)lnS + С, или R = k’’Sk’/k

Экспериментальные подтверждения такой формы зависимости были получены в конце прошлого века П. Брстоном, И. Меркелем и другими исследователями.

Помимо двух приведенных выше трактовок основного психофи­зического закона (логарифмической и степенной форм зависимос­ти) были предложены и другие его модификации: экспоненциаль­ная (А. Пюттер), тангенциальная (Э. Зиннср), арктангенциальная (Г. Бснсш), фи-гамма-функция (Р. Хьюстон) и т. д.

Закон Вебера — Фехнера — Блог Викиум

    • Дмитрий Ершов

      Автор Викиум

Закон Вебера — Фехнера гласит о том, что сила звука увеличивается в геометрической прогрессии, а громкость — в арифметической. В этой статье вы узнаете, как расшифровывается формулировка психофизического закона, и как он был создан.

Согласно закону, интенсивность ощущений прямо пропорциональна логарифму интенсивности стимула. Его авторами являются специалист в области психологии Г. Фехнер и психофизиолог Э. Вебер. В ходе своих экспериментов Вебер пришел к выводу, что новый раздражитель принесет другие ощущения, если он будет по интенсивности отличаться от старого, воздействуя на величину, пропорциональную интенсивности первоначального раздражителя.

Стоит отметить, что фундаментальной основой для закона Вебера — Фехнера стали законы физика Бугера и Стивенса, имеющие тесную связь.

Как расшифровывается закон?

Чтобы лучше понять суть закона, надо рассмотреть пример. Так, если в комнате будет находиться 3 люстры с 2, 4 и 8 включенными лампочками, то каждая из люстр будет светиться одинаково ярче предыдущей. Чтобы у человека было ощущение, что яркость становится больше, количество ламп должно в разы увеличиваться. Например, если человек будет смотреть на люстру с десятью лампочками, а потом посмотрит сразу же на люстру с одиннадцатью включенными лампами, то практически ничего не заметит. В ходе наблюдений выявили, что человек способен реагировать не на любой раздражитель, а только на достаточно интенсивный.

Понятие порогов чувствительности

Если порог чувствительности слишком мал, действие раздражителя будет практически незаметно. Также стоит отметить, что если в чувствительности есть нижний показатель, то существует и верхний. Ощущение изменений происходит при нахождении между этими двумя показателями.

Если говорить о порогах чувствительности, то тут различие очевидно. Например, если взять в одну руку пустую сумку, а в другую — сумку с листом бумаги, человек этого абсолютно не заметит, так как лист весит мало. В данном случае происходит допороговое раздражение. Если же раздражитель имеет значительный вес, то раздражение можно назвать запороговым. Чем выше будет чувствительность, тем ниже эффект различения.

Закон Вебера — Фехнера имеет формулу: Y(ощущение) = k(константа) * S(стимул) и n(показатель степени функции). При этом показатель степени функции может изменяться в зависимости от ощущений.

Основным отличием сенсорной системы является умение замечать различия при одновременно или постепенно действующих раздражителях. Сенсорная адаптация бывает глобальной и селективной. Если при глобальной адаптации происходит снижение абсолютной и повышение дифференциальной чувствительности, то при селективной происходит постепенное привыкание к раздражителю. Селективная адаптация распространяется на всю нервную систему, снижая чувствительность.

То, как человек воспринимает различные раздражители, влияет на его понимание окружающей действительности. А восприятие во многом зависит от активности и эффективности работы мозга. Тренажеры Викиум помогают держать мозг в тонусе и развивать когнитивные функции.

Читайте нас в Telegram — wikium

contemporary psychology: Биографии психологов: Г. Т. Фехнер

Фехнер известен как создатель эмпирического закона (которых в психологии плюс минус 3-4), который говорит о том, что интенсивность ощущения пропорциональна логарифму интенсивности раздражителя. Для общего понимания вопроса стоит вернуться к дроби Вебера (или закону Вебера), которая говорит о том, что новый раздражитель, чтобы отличаться по ощущениям от предыдущего, должен отличаться от исходного на величину, пропорциональную исходному раздражителю. То бишь если изначально на руку испытуемому мы кладем грузик весом 75 грамм, то надо прибавить к нему 2,7 грамм (прирост груза), чтобы человек почувствовал различия. В тоже время если мы кладем 150 грамм на руку, то надо добавить 5,4 грамм, чтобы появилось ощущение различия по весу. Кстати говоря, эти прибавки веса принято называть едва различными различиями (ЕЗР). 

С учетом дроби Вебера, Фехнер в 1860 году экспериментально выявил основной психофизический закон. Стоит отметить, что многие авторы утверждают, что изначально закон Фехнеру приснился. Тем не менее, экспериментально он его все равно подтвердил. Суть закона Фехнера можно пояснить на таком примере, что люстра из 8 лампочек (при чем лампочки должны быть одинаковыми по яркости и другим характеристикам) кажется нам настолько же ярче люстры из 4-х лампочек, как люстра из 4-х лампочек ярче люстры из 2-х лампочек. То бишь логарифм. Кстати, мне больше нравится такая формулировка закона Фехнера: Для того чтобы интенсивность ощущения могла увеличиться в арифметической прогрессии, стимул должен увеличиться в геометрической. 

Дробь Вебера и Закон Фехнера (иногда называемый законом Вебера-Фехнера) легли в основу психофизики и стали предметами ее изучения. В 20-м веке наработки Вебера и Фехнера подвергались как критике, так и корректировке. На сегодняшний день они принимаются в учет при работе со стимулами средней величины. Было показано что они не очень верно работают с очень малой и очень большой интенсивностью стимулов. Что отчасти связано со Стивенсоном, который сделал свой закон (с блэкджеком и распутными женщинами), тем не менее, это совсем другая история. 

В 1860 году Фехнер опубликовал свой основной двухтомный труд — «Элементы психофизики». После чего он стал заниматься эстетикой. Основная идея тут была в том, что если ощущения поддаются измерению как относительные величины, то скорее всего можно будет измерить и красоту аналогичными методами. Фехнер стал измерять эстетику художественного искусства. Основной метод работы в исследованиях эстетики Фехнера состоял в том, чтобы сравнивать оценки, которые давали не профессионалы. Также была проведена серия экспериментов, на которых испытуемым предлагали разные прямоугольники. Испытуемые выбирали те, которые им нравились. Также была проведена связь с золотым сечением. Тем не менее, эта попытка не удалась, и у него ничего толком не вышло. В 1889 году, в возрасте 86 лет, Густав Теодор Фехнер умер. 

Основной вклад Г.Т. Фехнера в науку сводится к демонстрации экспериментальных процедур, многие из которых до сих пор актуальны и используются, например, для измерения величины ощущений. Также он первым показал, что психология может следовать общепринятой логике науки и давать количественные результаты. Однако на сегодняшний день психофизика по большей части является умершей наукой. Исследования в ее русле все еще проводятся, но сейчас она лучше воспринимается как важная, но не самая большая часть экспериментальной психологии.

Как обычно после биографии интересные факты о Г.Т. Фехнере: 

1) Фехнер интересен тем, что в своей ранней работе о сновидениях Зигмунд Фрейд ссылался только на одного ученого-психолога экспериментатора. И им был Фехнер. Тут стоит отметить, что в популярной психологии за Фрейдом закреплено открытие бессознательного. Это естественно не так. О неосознаваемых процессах психики писали еще классические философы. Но именно Фехнер внес самый большой вклад в эту тему до Фрейда. По его работам можно предположить, что бессознательным является все то, что меньше ЕЗР. А с учетом того, что ЕЗР вычисляется достаточно точно в цифровых значениях, то нельзя отрицать вклад Фехнера в понимание бессознательного. Кстати говоря, и вклад Фрейда я не отрицаю. В оправдание своего мнения отмечу, что Фрейд предельно любил и уважал Фехнера. Основатель психоанализа посещал психофизические лекции в середине 70-х годов. 

2) Кстати принцип удовольствия также впервые был выдвинут Фехнером. Правда, немного в иной формулировке, чем у Фрейда. Стоит отметить, что принцип Фехнера был чем-то вроде провозглашения личного выздоровления и метафизической философской конструкцией. Есть и другие заимствования Фрейда у Фехнера, но это слишком большая тема. 

3) А вот Уильям Джеймс, основатель американской функциональной психологии, терпеть не мог работы Фехнера. Он считал, что психофизика это сотонинское угодье для ученых, которые не хотят видеть никаких психологических результатов. 

4) Традиционно работы Фехнера относят к махровому материализму (особенно на моей памяти этим злоупотребляют практики), тем не менее, сам Фехнер считал себя оппонентом материалистичного миропонимания. 

5) Также Фехнер открыл цветовой эффект, заключающийся в том, что мы видим цвета при определенном движении черного и белого. Этот эффект используется во многих гифках в интернете. 

6) Фехнер ввел понятие медианы, которое на данные момент используется в статистике и анализе данных. 

7) Фехнер считал, что если разрезать мозолистое тело, соединяющее 2 полушария, то мозга станет 2. Он был уверен, что экспериментально его гипотезу никто не проверит. 

8) 22 октября 1850 года, Фехнеру приснился его закон. С 2001 года психофизики стали называть этот день именем Фехнера. 

9) Фехнер признавал идеи о духовности всего мира. Эта концепция достаточно хорошо проработана в его статьях, тем не менее, автор блога читал это с большим трудом, и пересказывать не собирается. По сути, там говорится, что есть разные духи и все мы едины. Ну никак не формат этого блога). 

10) После своей болезни он опубликовал много необычных работ, в том числе и сборник о психологии растений. 

В заключении отмечу, что я не рассказал про юмористические работы Фехнера об эволюции ангелов и много всего другого. Но я и не ставил перед собой задачу написания полной биографии замечательного ученого Густава Теодора Фехнера. Эта статья по большей части должна замотивировать читателей на повторение основного психофизического закона и вызвать интерес к личности его создателя. 

Конец.

Читайте все посты с биографиями известных психологов:

Психофизические законы

Психофизические законы

Психофизические законы:
Фехнер против

Стивенса

Фон:

Психофизика — это изучение связи между стимулами реального мира и их восприятием. Один из главных Целью психофизики является определение математических формул, позволяющих предсказать перцептивную реакцию на физический объект. Например, психофизика позволит вам предсказать, насколько ярким будет свет определенной физической интенсивности.Два общих психофизическими законами являются закон Фехнера и степенной закон Стивенса.

В этом исследовании вы оцените яркость нескольких цветных пятен. Согласно закону Фехнера воспринимаемое (психологическое) яркость цветовых пятен должна быть логарифмической функцией физической интенсивности цветовых пятен:

ψ = k ln (I / I 0 )

Где ψ — психологическая яркость цветового пятна, I — физическая интенсивность цветового пятна (измеренная люксметр), I 0 — это физическая интенсивность едва заметного цветового пятна, а k — постоянная величина (постоянная Вебера.) Закон Фехнера основан на предположении, что каждое просто заметное различие (JND) психологически эквивалентно. Следовательно, JND могут быть используется как линейка для определения психологической интенсивности раздражителя.

Согласно степенному закону Стивенса воспринимаемая яркость цветных пятен должна быть степенной функцией физической интенсивности. кол-во цветов:

ψ = c I n

Где ψ — психологическая яркость цветового пятна, I — физическая интенсивность цветового пятна (измеренная люксметр), n — мощность, до которой увеличивается интенсивность, а c — постоянная величина.Степенной закон Стивенса не основан на предположении — скорее, он основан на эмпирических наблюдениях за взаимосвязью между психологической яркостью и физической интенсивностью многих различных типы раздражителей.

Цель этого исследования — определить, какой из этих двух законов, Фехнера или Стивенса, лучше описывает взаимосвязь между психологической яркостью и физической интенсивностью цветовых пятен на основе предоставленных вами данных.

Исследование:

Ниже вы увидите три круга на синем фоне. Два меньших круга — это якоря для ваших оценок яркости. большего круга. Меньший черный кружок произвольно настроен на яркость, равную единице, а меньший белый кружок произвольно настроен на яркость. яркость 100. По отношению к двум меньшим кружкам вы должны ввести целое (целое) число от 1 до 100 включительно, которое указывает насколько ярким, по вашему мнению, является больший круг.Например, если вы думали, что яркость большого круга находится ровно посередине между яркость черного и белого круга, вы должны ввести 50 (на полпути между 1 и 100). Если вы думали, что яркость большего яркость круга была на три четверти яркости меньшего белого круга, вы должны ввести 75 (три четверти от 100).

Во время испытаний большой круг будет иметь несколько разную физическую интенсивность.Каждая из разных физических нагрузок будут представлены четыре раза. После того, как вы оценили психологическую яркость каждого цветового пятна (это не должно занять слишком много времени — не более пару минут, чтобы оценить яркость всех цветовых пятен), вы увидите таблицу результатов. Таблица будет включать приблизительная физическая интенсивность и каждое из ваших четырех оценок яркости каждой физической интенсивности. В таблице также будут указаны среднее из четырех ваших суждений о каждой физической интенсивности.

Будет представлен график приблизительной физической интенсивности (ось X) по сравнению со средним значением вашей психологической напряженности (ось Y). На графике будут две кривые. Красная кривая — наиболее подходящая функция логарифма (кривая регрессии наименьших квадратов) для ваших данных — это указание того, насколько хорошо закон Фехнера описывает ваши данные. Синяя кривая — наиболее подходящая степенная функция (кривая регрессии наименьших квадратов) для ваши данные — это показатель того, насколько хорошо закон Стивенса описывает ваши данные.

Чтобы количественно оценить, насколько хорошо каждая кривая описывает ваши данные, коэффициент детерминации r 2 , сообщается для каждой кривой. r 2 сообщает нам долю изменчивости переменной оси Y, которая объясняется изменчивостью переменной оси X. В этом случае r 2 говорит нам, сколько различий в психологической напряженности объясняется различиями в физической напряженности. Доводчик r 2 к 1.000, тем лучше кривая описывает данные.

Собери данные !:

Психофизика III: Психофизические законы

Лабораторная сессия III: Психофизические законы

Фон:

  1. Цель и задачи
    1. Чтобы проиллюстрировать, как разные люди описывали отношения между физическим миром и нашим опыт, т.е., проиллюстрировать различные предлагаемые психофизические законы
    2. Для сбора данных, которые позволят нам протестировать некоторые из эти законы
    3. На основе двух последних лабораторий
  2. Оценка звездной величины
    1. Все методы до сих пор что-то измерили о восприятии на наших границах или рядом с ними обнаружить раздражитель или его изменение.
    2. Требовался метод, чтобы попытаться научиться что-то о стимулах, которые легко обнаружить или разница между двумя стимулами, которые легко один стимул вдвое ярче, чем еще один стимул?
    3. Гарвардский психолог С.С. Стивенс задумался над этим. вопрос и в основном развитая оценка величины вне лифта разговор с другим Гарвардом профессор (не психолог).
    4. Простая основная идея. Представьте стимул, имейте участники дают стимулу число, которое они указывает на сенсорную силу стимула.
    5. Модуль: в некоторых версиях стандартный стимул используется, назовите модуль. Этот стимул дан стандартное число, независимо от того, какой исследователь хочет, скажем, 50.Затем участник назначает числа к другому стимулу, который принимает модуль в учетную запись. Например, если участник думает, что только что представленный стимул вдвое сильнее поскольку модуль и модуль равны 50, то субъект должен дать стимул 100.
    6. Подробнее в главе 2 текста.
  3. Что такое научный закон?
    1. Описание закономерности, наблюдаемой в данных
    2. Они не подразумевают объяснения регулярность
  4. Закон Вебера
    1. Разработано, чтобы описать, как JND меняется как изменение интенсивности фона
    2. Это попытка описать, как наша чувствительность изменение относится к интенсивности фона стимул
    3. Вопросы:
      1. Все ли пороги разницы одинакового размера независимо от интенсивности фона стимул?
      2. Если нет, существует ли какой-либо систематический способ размер этой разницы порогов меняются?
    4. Вебер ответил на эти вопросы так:
      1. Нет, пороги становятся больше фона интенсивность становится больше
      2. Более того, рост JND при том же пропорциональная ставка в качестве фона
      3. Он резюмировал свои заявления с следующее уравнение (оно говорит то же самое вещь, как указано выше):

    к =

    Δ I
    Я

k — постоянная величина.

I — интенсивность фона

ΔI — это разница между интенсивностью JND стимул и интенсивность фона

  1. Закон Фехнера (Нет в тексте)
    1. Посмотрите логарифмы сами
    2. Наблюдения:
      1. Фехнер начинает с закона Вебера
      2. Закон Вебера предполагает, что мы постепенно менее чувствителен к изменению стимула, так как интенсивность увеличивается
    3. Гипотеза:
      1. Что такое закон Вебера относится не только к нашему способность обнаруживать изменения, но в целом чувствительность к раздражителям
      2. По сути, порог восприятия и надпороговое восприятие то же
    4. приводит к следующему закону

      S = k лог ( I )


      S — это сила нашего сенсорного опыта
      k — постоянная и такая же k, как в законе Вебера
      . I — интенсивность стимула

  2. Степенной закон Стивенса
    1. Начинает свою разработку Magnitude Оценка
    2. Это прямая мера надпорогового восприятие, которое является объектом закона Фехнера
    3. Во многих случаях закон Фехнера является разумным для данных оценки величины, скажем, яркости или громкость
    4. В некоторых случаях закон Фехнера вообще не подходит, е.г., боль
    5. Стивенс хотел, чтобы общий закон охватил все ситуаций — это одно уравнение, а не набор несколько
    • Наука любит использовать общее описание, как возможно
  3. Стивенс разработал следующий закон, также называемый просто степенной закон

    S = cI b
    S и I такие же, как для Закона Фехнера
    c — константа и может быть любым
    b — показатель степени, изменяющий форму функция.См. Текст для получения дополнительной информации.

Задач на следующей неделе:

  1. Проведите следующие эксперименты из главы 2 на сайте СМИ:
    1. Эксперимент по закону Вебера: используйте принудительный выбор: Частотная дискриминация: ОСТРОВ 2.8b
      1. Бежит 6 раз
      2. При изменении вкладки настроек стимула (один раз за запустить):
        1. Стандартная частота:
          • Лаборатория 1 (AM): 100, 200, 400, 800, 1600, & 3200 Гц (Это будет твое I)
          • Лаборатория 2 (PM): 200, 400, 800 1600, 3200, & 6400 Гц (Это будет твое I)
        2. Никаких других настроек не менять
      3. В настройках метода:
        1. Оставить все настройки кроме:
        2. Максимальное значение разности частот (Гц): 75
      4. Это метод принудительного выбора (помните, как для расчета этих порогов)
    2. Оценка величины: Громкость тона & Оценка звездной величины : длина линии из главы 2 СМИ
      1. Количество уровней для тестирования: 10
      2. Количество повторов: 7
      3. Используйте модуль (оставьте отмеченным, что дефолт).Обратите внимание на значение.
  2. Проблемы:
    1. Эксперимент по закону Вебера: метод константы Стимулы: частотная дискриминация
      1. Поместите данные в отчет.
      2. Рассчитайте JND для каждого стандартная частота
      • Используйте уравнение порога принудительного выбора
    2. Ваш JND уже будет ΔI
    3. Преобразовать в ΔI / I
    4. Постройте гистограмму (то, что Excel называет столбцом график)
    • Ось X = I (стандартная частота (Гц))
    • Ось Y = ΔI / I
  3. Так 6 бар
  4. Ответьте на следующий вопрос: Данные соответствует закону Вебера или нет? Почему или почему нет?
  • Использование данных оценки магнитуды за 2-ю неделю
    1. Пункт с описанием процедуры
    2. Постройте результат оценки величины эксперименты на том же графике.
    3. График лучше согласуется с Фехнером или Предсказания Стивенса? Посмотрите на форма. Учитывайте все данные вместе. Не отвечайте за каждый набор данных по отдельности, но ответ должен относиться к обоим результаты вместе.
  • Стоит 25 очков
  • Балл: Развивайте навыки интерпретации графиков, в частности, как данные соотносятся с теоретическими идеи.

    • Границы | Единая теория психофизических законов восприятия силы звука

    Введение

    Психофизические законы пытаются связать амплитуду физического стимула с его воспринимаемой величиной, например громкость как функцию звукового давления или яркость как функцию яркости. Классический подход к раскрытию психофизических законов был предложен Фехнером (1966) в середине 18 века (оригинальная работа опубликована в 1860 году).Фехнер предположил, что едва заметная разница (jnd), выраженная как доля Вебера (Δ I / I ), где I — стандартная интенсивность звука, а Δ I — изменение интенсивности, необходимое для jnd, производит такое же приращение ощущения громкости (Δ L ). Интегрируя это уравнение, а именно Δ L = Δ I / I , он получил так называемый закон Фехнера: громкость является логарифмической функцией интенсивности звука ( L = log I ).

    Логарифмический закон Фехнера был заменен не только степенным законом Стивенса или L = I θ , где θ — константа (Stevens, 1961), но и его общий подход был поставлен под сомнение из-за невозможности интегрировать jnd-функции два разных звука, чтобы предсказать их соответствующие функции громкости (Newman, 1933; Miller, 1947). Таким образом, неудивительно, что некоторые исследователи отказались от фехнеровского подхода к установлению связи между стимулом jnd и субъективной величиной.Что было удивительно, так это основания отказа от фехнеровского подхода. Например, Стивенс (1961) утверждал, что метод прямой оценки величины устарел различение интенсивности как меру отношения между стимулом и ощущением. Он рассматривал меру дискриминации как «инженер говорит… разброс некоторых настроек шкалы». С совершенно противоположной точкой зрения Вимейстер и Бэкон (1988) заявили, что данные оценки громкости были мерой с «вероятно сильным участием несенсорных факторов», (и) мы не пытались связать эти данные с данными для различения интенсивности.”

    Были и другие исследователи, которые продолжали продвигать фехнеровский подход в поисках единой теории, связывающей различение интенсивности с функцией громкости. Первоначальное предположение Фехнера иногда называли теорией «наклона», потому что оно предсказывало, что чем круче функция громкости, тем меньше jnd или доля Вебера для постоянного увеличения громкости. Этот простой прогноз наклона оказался неверным, по крайней мере, в случаях набора громкости, когда потеря слуха улитки или частичная маскировка повышали порог слышимости, но вызывали аномально резкий рост громкости, так что нормальная громкость воспринималась при высоких уровнях звука (Fowler, 1937). .Чтобы объяснить несостоятельность теории наклона Фехнера, несколько исследователей предложили теорию «пропорционального jnd», в которой размер jnd необходимо нормировать на общее число jnd в динамическом диапазоне стимула (Riesz, 1933; Teghtsoonian, 1971; Lim и др., 1977). С другой стороны, теория «равной громкости, равной-jnd» утверждала, что jnd не имеет никакого отношения к наклону функции громкости, а скорее определяется общей громкостью (Zwislocki and Jordan, 1986). Несмотря на значительные усилия по тестированию этих соотношений громкость-jnd, консенсуса пока не достигнуто (Houtsma et al., 1980; Hellman et al., 1987; Schlauch and Wier, 1987; Ранкович и др., 1988; Джонсон и др., 1993; Стиллман и др., 1993; Schlauch et al., 1995; Аллен и Нили, 1997; Хеллман и Хеллман, 2001).

    Здесь я представляю единую теорию, начиная с общей формы функции громкости Zwislocki (1965), чтобы вывести общую форму закона Брентано, и я приду к общей форме отношения громкость-jnd, которая объединяет предыдущие теории громкости-jnd. . В частности, я считаю, что предыдущие теории «наклона», «пропорционального jnd» и «равной громкости, равного jnd» являются тремя дополнительными терминами в новой единой теории.Я также показываю, что новая теория способна предсказывать громкость и данные jnd в широком диапазоне слуховых ситуаций, включая нейросенсорную тугоухость, одновременную маскировку, прямую маскировку и электрический слух.

    Вывод единой теории

    Вывод общей формы закона Брентано или Экмана

    Я начинаю с общей формы функции громкости, предложенной Zwislocki (1965; уравнение 212):

    L = k [(I + cI0) θ- (cI0) θ] (1)

    , где I 0 — порог обнаружения для определенного типа звука, c представляет масштабный коэффициент внутреннего шума, а k — постоянная величина.

    Общность и симметрия — две причины выбора функции громкости Цвислока. Во-первых, при высоких интенсивностях ( I ≫ I o ) функцию Цвислока можно упростить до степенного закона Стивенса, а именно: L = kI θ . При низкой интенсивности Цвислоки сделал неявное, но важное предположение для учета набора громкости вблизи порога: наклон (θ) функции громкости не увеличивается, как первоначально предполагалось (Fowler, 1937), вместо этого увеличивается громкость на пороге.Установка I = I o в уравнении. (1), громкость на пороге, или L o = k [( I o + cI o ) θ — ( cI o ) θ ] = k [( 1 / c + 1 ) θ — 1)] ( cI o ) θ ∼ k [θ ( 1 / c ) 1 – θ ] ( I o ) θ , прямо пропорционально пороговому значению и «должно быть больше нуля (Zwislocki, 1965; p. .87) ». Математически громкость на пороге бесконечна, когда внутренний шум равен нулю ( c = 0), и наоборот. Это фундаментальный аргумент в пользу того, почему мозг имеет или нуждается во внутреннем шуме, потому что бесконечная громкость явно биологически неприемлема. Концепция внутреннего шума Цвислоки также была расширена, чтобы сформировать основу для рассмотрения набора громкости как «невосприятия мягкости» (Buus and Florentine, 2002), а тиннитуса как «дополнительного центрального шума» (Zeng, 2013). В интересах простоты я определяю громкость на пороге как: L o = k ( cI o ) θ (или c = 0.125 для θ = 0,27).

    Во-вторых, математическую симметрию можно показать, дифференцируя уравнение. (1):

    ΔLΔI = θk (I + cI0) θ-1 = θk (I + cI0) θI + cI0 (2)

    Складывая и вычитая тот же компонент в приведенном выше уравнении, я получаю:

    ΔLΔI = θk (I + cI0) θ- (cI0) θ + (cI0) θI + cI0 = θL + L0I + cI0 (3)

    Переписывая приведенное выше уравнение, я получаю общую форму закона Брентано или закона Экмана, а именно ΔLL = ΔII (обсуждение этих законов см. В Stevens, 1961):

    ΔLL + L0 = θΔII + cI0 (4)

    Уравнение (4) математически симметрично и сбалансировано, имеет общую форму закона Вебера, включающую пороговый поправочный член как в области ощущений ( L o ), так и в области стимула (c I ). o ).

    В первом приближении закон Вебера в области стимулов был «воспроизведен в сотнях исследований с использованием всех сенсорных модальностей и многих видов животных за последние два столетия (Pardo-Vazquez et al., 2019)». При распознавании интенсивности звука доля Вебера постоянна для широкополосного шума, но немного уменьшается с увеличением интенсивности, что приводит к «близкому нарушению» закона Вебера (McGill and Goldberg, 1968). Следовательно, уравнение. (4) можно записать как:

    ΔLL + L0 = wIα (5)

    , где w и α — константы, причем α = 0 указывает на полное соответствие закону Вебера.

    Согласно теории «пропорционального jnd» (Лим и др., 1977), константа w обратно пропорциональна количеству jnds ( N ) в динамическом диапазоне стимула. Другими словами, w = 1/ N , что можно рассматривать как коэффициент масштабирования, чтобы учесть тот факт, что разные субъекты или разные типы стимулов могут иметь разное количество различимых шагов в их соответствующем динамическом диапазоне (например, , у слушателя с нормальным слухом есть 100 шагов, а у пользователя кохлеарного имплантата — только 10), но все они имеют одинаковый рост громкости от тихого на пороговом уровне до неприятно громкого на верхнем пределе диапазона.Теория «пропорционального jnd» утверждает, что 10 шагов jnd у слушателя с нормальным слухом вызовут такое же изменение громкости, как и шаг jnd у пользователя кохлеарного имплантата. Хотя теория «пропорционального jnd» не предполагала и не требовала какой-либо конкретной функции jnd-громкости, Лим и др. (1977) намекнули, что закон Брентано «почти правильный» (см. Сноску 7 на стр. 1264 в Lim et al., 1977). В этом случае относительное изменение громкости обратно пропорционально количеству jnds с поправкой на интенсивность, происхождение которой будет рассмотрено в разделе «Обсуждение»:

    ΔLL + L0 = 1NIα (6)

    Прогнозирование функции jnd на основе функции баланса громкости

    Предположим, что функция громкости для тихого тона равна: L = f (I) , и что получена функция баланса громкости между тихим тоном и тоном в маскировке: I = г (Я м ). По определению, при I = g (I m ) громкость сбалансирована, так что функция громкости может быть получена для частично замаскированного тона:

    Lm = L = f (I) = f [g (Im)] (7)

    Дифференцируя приведенное выше уравнение, получаем:

    ΔLmΔIm = f ′ (I) g ′ (Im) = ΔLΔIg ′ (Im) (8)

    Перепишите приведенное выше уравнение:

    ΔIm = ΔI1g ′ (Im) ΔLmΔL (9)

    Заменить Δ L м и Δ L формулой.(6) чтобы получить:

    ΔIm = ΔI1g ′ (Im) NNmImαIαLm + LmoL + Lo (10)

    Для прогнозирования jnd в виде доли Вебера при той же интенсивности, то есть I m = I , чтобы можно было исключить поправочный член интенсивности (Imα / Iα) и разделить вышеприведенное уравнение по ( I ):

    ΔImI = ΔII1g ′ (Im) NNmLm + LmoL + Lo (11)

    Используя логарифмическое преобразование, можно вычислить jnd через долю Вебера в дБ (WFdB):

    WFmdB (I) = WFdB (I) -10log⁡g ′ (Im) + 10logNNm + 10logLm + LmoL + Lo (12)

    , где WF м дБ (I) = 10log (Δ I m / I ), что является долей Вебера для замаскированного тона, и WFdB (I) = 10log ( Δ I / I ), которая является логарифмической долей Вебера для тона в тишине.

    Уравнение (12) указывает, что, если WFdB (I) известно при данной интенсивности ( I ), то можно предсказать WF m дБ (I) с той же интенсивностью из трех дополнительных измеряет: (1) локальный наклон функции баланса громкости [ g ‘ ( I m )], (2) коэффициент масштабирования ( N / N m ) и (3) локальное соотношение громкости между замаскированным тоном и тоном в тишине [( L m + L mo ) / (L + L o )].Интересно, что теоретически нет необходимости точно знать порог обнаружения, точную форму увеличения громкости или функцию распознавания интенсивности для тона в тишине.

    Я рассматриваю уравнение. (12) в качестве единой теории психофизических законов восприятия интенсивности звука, потому что последние три члена в уравнении содержат три предыдущие теории, которые пытались связать функцию jnd с функцией громкости. Член 10log г ’ ( I м ) представляет собой первоначальную теорию« наклона »Фехнера; термин 10log ( N / N m ) представляет собой «пропорциональную» теорию Рисса; а последний термин представляет теорию Цвислоцкого «равной громкости, равной громкости».

    Подтверждение единой теории

    Прогнозирование jnd-функций при одновременном маскировании

    Одновременное маскирование не только повышает порог чистого тона, но также влияет на восприятие его громкости, подобно набору громкости при нейросенсорной тугоухости. Функции баланса громкости и распознавания интенсивности были измерены в одной и той же группе слушателей для чистых тонов в тишине и при одновременном маскировании шума (Houtsma et al., 1980; Rankovic et al., 1988; Schlauch et al., 1995).

    Здесь я использую Schlauch et al. (1995) данные для предсказания замаскированного jnd из тихого jnd, поскольку Schlauch et al. (1995) имел наиболее полный набор данных. Рисунок 1 иллюстрирует относительные вклады трех специальных членов в уравнении. (12) к предсказаниям jnd-данных при одновременном маскировании. На рисунке 1A показаны три функции баланса громкости: сплошная линия представляет гипотетическое состояние, при котором один и тот же тон идеально сбалансирован по громкости (т.е., соотношение 1: 1) между двумя ушами в тишине, пунктирная линия представляет измеренную функцию баланса для замаскированного тона в широкополосном шуме 15-SPL / Гц, а пунктирная линия для замаскированного тона в SPL / 40-дБ / Широкополосный шум Гц (из рисунка 3 в Schlauch et al., 1995). Затем дифференцируется интерполяция функции баланса громкости для получения наклонов в зависимости от интенсивности (X представляют маскировку 15 дБ SPL / Гц, а O представляют условие маскировки 40 дБ SPL / Гц). На рисунке 1B показана функция увеличения громкости для тона 1000 Гц в тишине (сплошная линия), основанная на модели Цвислока [уравнение.(1), используя k = 3,1; θ = 0,27; c = 2,5; I o = 10 — 12 Вт / м 2 или 0 дБ SPL], а также две функции замаскированного увеличения громкости, полученные путем применения функций баланса громкости на рисунке 1A к функция увеличения громкости в тишине. Значки X и O представляют собой соотношение громкости между соответствующими условиями тишины и маскировки. На рисунке 1C показаны измеренные jnd-функции в тихом режиме (сплошная линия), маскировке 15 дБ (пунктирная линия) и маскировке 40 дБ (пунктирная линия).Значки X и O представляют собой предсказанные значения jnd в двух вышеупомянутых условиях маскирования на основе уравнения. (12). В дополнение к использованию значений наклона на рисунке 1A и значений отношения громкости на рисунке 1B, уравнение. (12) использует коэффициент нормализации 4 дБ и 8 дБ для условий маскирования 15 дБ и 40 дБ соответственно. Коэффициенты нормализации 4 дБ и 8 дБ были оценены как по динамическому диапазону, так и по значениям jnd (Nelson et al., 1996; см. Их рисунок 9), при этом тихое состояние было в 2,5 раза больше и 6.В 3 раза больше шагов jnd, чем при условии маскирования 15 дБ и 40 дБ соответственно. В этом прогнозе не было свободного параметра. Что касается относительного вклада в успешное предсказание, теория «равной громкости, равной-jnd» была существенной для предсказания общей тенденции (та же нисходящая картина на рисунках 1B, C), в то время как теория наклона (относительно пологая Образец символов X и O на рисунке 1A) ведет себя аналогично теории пропорционального jnd в качестве константы для сдвига предсказанной функции вверх или вниз.

    Рисунок 1. Прогнозы при одновременном маскировании с данными (линиями), полученными Schlauch et al. (1995). Панель (A) показывает функции баланса громкости между тоном в тишине (ось y ) и тоном в шуме (ось x ): сплошная линия представляет состояние управления, при котором один и тот же тон был сбалансирован между два уха в тишине, пунктирная линия представляет функцию баланса для тона, маскируемого широкополосным шумом 15 дБ SPL / Гц, а пунктирная линия представляет функцию баланса громкости для тона шумом 40 дБ SPL / Гц.Символы представляют значения наклона для функции баланса. Значения наклона используют тот же масштаб, что и функция баланса от 0 до 100, за исключением того, что наклоны безразмерны. Панель (B) показывает производные функции увеличения громкости. Символы представляют значения отношения громкости между тихими и замаскированными тонами и тонами в тихом режиме. Панель (C) показывает измеренные функции jnd (линии) и прогнозируемые значения jnd (символы).

    Прогнозирование функции jnd при прямом маскировании

    На громкость и ее jnd-функции стимула также может влиять прямая и обратная маскировка.Увеличивается громкость и снижается различение интенсивности при прямом и обратном маскировании, особенно при средней интенсивности (Zeng et al., 1991; Plack and Viemeister, 1992; Zeng and Turner, 1992). Хотя ранняя попытка связать «горб среднего уровня» (функция jnd) с повышением громкости не увенчалась успехом (Zeng, 1994), Оберфельд (2008) обнаружил значительную корреляцию между повышенным jnd и повышенной громкостью при широком диапазоне маскирующих звуков. тестировались разности уровней сигнала.

    Используя те же этапы обработки, что и на рисунках 1, 2, показана функция баланса громкости между тоном длительностью 25 мс в тишине и при наличии 90 дБ УЗД, 100 мс прямого маскера (рисунок 2A), полученное увеличение громкости функция (рисунок 2B), а также измеренные и прогнозируемые функции jnd в тихом режиме и с маскированием (рисунок 2C).Теория наклона (рисунок 2A) предсказывала, что прямое маскирование будет давать меньшие, чем нормальные jnds для стандартных уровней ниже 50 дБ SPL, но большие jnds для уровней выше 50 дБ SPL. Теория «равной громкости, равного jnd» (рис. 2B) предсказала среднеуровневую функцию горба jnd из-за повышенной громкости при прямом маскировании. Коэффициент нормализации 7 дБ, или в пять раз меньше jnd шагов при прямом маскировании, был использован в окончательном успешном прогнозе (рис. 2C), который объединил все три специальные теории в формуле. (12).Подобная картина на рисунках 2B, C в целом согласуется с наблюдаемой корреляцией между повышенной громкостью и повышенным jnd (Oberfeld, 2008), но количественный прогноз требует дальнейшего изучения. Было бы также интересно узнать, может ли существующая объединенная теория предсказать аналогичную функцию jnd, наблюдаемую для коротких высокочастотных тонов в условиях режекторного шума (Carlyon and Moore, 1984). Оксенхэм и Мур (1995) намекнули на такую ​​возможность, предложив «новую теорию, [объясняющую] резкое отклонение от закона Вебера с точки зрения как дисперсии…, так и громкости частично замаскированных сигналов.”

    Рисунок 2. Прогнозы при прямой маскировке с данными (линиями) из Zeng (1994). Панель (A) показывает функции баланса громкости между тоном в тишине ( y -ось) и тоном с прямой маскировкой ( x -ось): сплошная линия представляет состояние управления, при котором один и тот же тон был сбалансирован между два уха в тишине, а пунктирная линия представляет функцию баланса для тона при прямой маскировке. Символы * представляют значения наклона для функции баланса, которая использует ту же шкалу, что и функция баланса от 0 до 100, за исключением того, что наклоны безразмерны.Панель (B) показывает производные функции увеличения громкости. Символы представляют значения отношения громкости между замаскированным тоном и тоном в тишине. Панель (C) показывает измеренные функции jnd (линии) и прогнозируемые значения jnd (символы).

    Предсказания jnd-функций в электрическом слухе

    В электрическом слухе, где волосковые клетки отсутствуют, а волокна слухового нерва напрямую стимулируются электрическим током, громкость обычно имеет узкий динамический диапазон 10–20 дБ (Zeng and Galvin, 1999).Зенг и Шеннон (1994) обнаружили, что у пользователей кохлеарных имплантатов громкость растет как традиционная степенная функция электрического тока для частот стимула ниже 300 Гц, но как экспоненциальная функция для частот стимула выше 300 Гц. Эти две разные функции увеличения громкости будут производить функцию логарифмического баланса громкости между низко- и высокочастотными электрическими стимулами. На рисунке 3A действительно показана такая функция логарифмического баланса (сплошные линии) между стимулом 100 Гц (синусоида или амплитуда импульса на оси y ) и синусоидой 1000 Гц (ось x ).

    Рис. 3. Баланс громкости (A) и функции JND (B) у пользователей кохлеарных имплантатов. (A) Функции баланса громкости были получены между синусоидальным импульсом 100 Гц или импульсом 100 Гц и синусоидальным электрическим стимулом 1000 Гц, адаптированным из рисунков 2D, E в Zeng and Shannon (1994). Печатается с разрешения AAAS. Символы представляют индивидуальные данные, а сплошная линия представляет функцию логарифмического баланса. Пунктирная линия представляет функцию линейного баланса, которая явно не соответствовала действительности. (B) Данные JND (символы) и предсказанные функции (линии) с использованием одних и тех же стимулов от одних и тех же субъектов в (A) , адаптировано из рисунка 4 в Zeng and Shannon (1999). Печатается с разрешения Wolters Kluwer Health.

    E1000 Гц = θlog⁡E100 Гц (13)

    , где θ — наклон функции логарифмического баланса громкости. Дифференцируя приведенное выше уравнение, чтобы получить следующую функцию JND между высокочастотными и низкочастотными электрическими стимулами:

    ΔE1000 Гц = θΔE100 ГцE100 Гц (14)

    Зенг и Шеннон (1999) измерили jnds этих стимулов у тех же пациентов с имплантатом (символы на рисунке 3B) и обнаружили, что не только эта функция jnd сохраняется, но, что более важно, функция jnd была почти постоянной (сплошная линия на рисунке 3B). .Учитывая такую ​​же функцию увеличения громкости мощности для электрических стимулов с частотой 100 Гц, неудивительно, что их доля Вебера также была постоянной. Но почему абсолютная разница (Δ E 1000 Гц ) была постоянной для стимула с частотой 1000 Гц? Зенг и Шеннон (1999) показали, что эта постоянная абсолютная разница является результатом функции экспоненциального роста громкости.

    L1000Hz = exp⁡ (E1000Hz) (15)

    Дифференцируя приведенное выше уравнение, получаем:

    ΔL1000HzΔE1000Hz = exp⁡ (E1000Hz) = L1000Hz (16)

    Переписывая приведенное выше уравнение, получаем:

    ΔL1000ГцL1000Гц = ΔE1000Гц (17)

    Уравнение (17) означает, что коэффициент Брентано также постоянен при электростимуляции.Единственная разница между уравнениями. (17) и (4) состоит в том, что (17) не содержит порогового члена, вероятно, из-за отсутствия спонтанной нервной активности в глухом ухе (Kiang and Moxon, 1972).

    Обсуждение

    Ни один из отдельных компонентов существующей единой теории не является новым. Предыдущие исследования предлагали эти отдельные теории и оценивали их по отдельности (например, Zwislocki and Jordan, 1986; Hellman and Hellman, 1990, 2001; Schlauch, 1994; Schlauch et al., 1995; Allen and Neely, 1997).Настоящее исследование является новым в двух отношениях. Во-первых, настоящее исследование объединяет ранее отключенные отдельные компоненты с помощью единой теоретической основы, а именно общей формы закона Брентано в формуле. (4). Во-вторых, настоящее исследование предлагает новую формулу, а именно уравнение. (12), который специально сочетает эти отдельные термины для успешного прогнозирования соотношений громкости и jnd при одновременной и прямой маскировке, а также у пользователей кохлеарных имплантатов. Настоящая единая теория и ее успешные применения предполагают, что, хотя закон Вебера необходимо заменить общей формой закона Брентано, первоначальная идея Фехнера об использовании jnds для вывода психофизических законов действительна, по крайней мере, в широком диапазоне рассматриваемых здесь слуховых ситуаций.

    Общая форма закона Брентано может быть использована для проверки того, насколько близко фактические данные jnd соответствуют закону Вебера и его потенциальным механизмам, путем комбинирования уравнений. (4) и (5):

    ΔLL + L0 = θΔII + cI0 = wIαилиΔII + cI0 = w′Iα (18)

    , где и w ’ (= w / θ), и α являются свободными параметрами, подлежащими оценке, причем α = 0 указывает на полное соответствие закону Вебера. На рисунке 4 показаны данные jnd и оценка модели для тона 1 кГц (Schlauch et al., 1995), широкополосного шума 8 кГц (6–14 кГц) и того же шума на фоне шума с зазубринами (Viemeister, 1983). .Все три набора данных могут быть смоделированы двухэтапной функцией с крутым первым этапом (∼10–20 дБ SPL), отражающим пороговое влияние, и более мелким вторым этапом (∼20–100 дБ SPL) с крутизной α в формуле. (16). Все три набора данных подчиняются закону Вебера (McGill and Goldberg, 1968), где α составляет -0,09 для тона, -0,03 для шума и 0,04 для шума на фоне шума с зазубринами. Ближайший промах находится в диапазоне от -9% до 4% и составляет в среднем 3% для трех рассматриваемых здесь стимулов.

    Рисунок 4. Прогнозирование JND для шумовых и тональных стимулов. Данные JND для широкополосного шума (сплошные треугольники) и того же шума на фоне шума с надрезом (сплошные квадраты) были взяты из Viemeister (1983; те же символы на его рисунке 1) и данных JND тона 1000 Гц (светлые кружки) ) взяты из Schlauch et al. (1995; кружки на рис. 2 в правом нижнем углу). Пунктирная линия представляет собой прогноз функции JND шума, пунктирная линия представляет шум на фоне шума с выемками, а сплошная линия представляет функцию JND тона.

    Чтобы найти решение почти пропуска закона Вебера, Макгилл и Голдберг использовали процесс, подобный Пуассону, в котором среднее значение громкости ( L ) и его дисперсия (σ 2 ) равны, где σ — величина среднеквадратичное отклонение. Для достижения 75% правильного обнаружения в jnd задаче теория обнаружения сигналов требует: d ′ = ΔLσ = ΔLL0,5 = 1 (Green and Swets, 1966). Замена Δ L = L 0,5 в уравнении. (19) произвести:

    ΔLL + L0 = L0.5L + L0∝L-0.5∝ (I0,27) -0,5∝I-0,14 (19)

    По сравнению с крутизной -0,14, предсказанной пуассоновским процессом, расчетная крутизна составляла 5% для тона, 11% для шума и 18% для шума на фоне режекторного шума. В качестве чрезмерной коррекции решение Макгилла и Голдберга создало гораздо большую разницу (в среднем = 11%), чем исходная проблема, то есть почти полное отсутствие (в среднем = 3%) закона Вебера. С другой стороны, использование распространения сигнала возбуждения является более вероятным механизмом, лежащим в основе почти несоблюдения закона Вебера (Florentine and Buus, 1981; Viemeister, 1983), но количественная обработка его предсказательной точности все еще отсутствует.По крайней мере, в первом приближении закон Вебера справедлив для различения интенсивности звука.

    Несмотря на то, что это непросто, поиск единого психофизического закона продолжает привлекать внимание, особенно его биологическая основа (например, Shepard, 1987; Nieder and Miller, 2003; Dehaene et al., 2008; Джафаров, Колониус, 2011; Техцунян, 2012; Pardo-Vazquez et al., 2019). Во влиятельной статье, которая привлекла 30 открытых комментариев коллег, Крюгер (1989) попытался примирить Фехнера и Стивенса, предложив единый психофизический закон, в котором (1) «каждый jnd имеет одинаковую субъективную величину для данной модальности» (2). ) «Субъективная величина увеличивается приблизительно как степенная функция физической величины» и (3) «субъективная величина зависит в первую очередь от периферических сенсорных процессов, то есть не происходит никаких нелинейных центральных преобразований.Что касается (1), Крюгер предпочел Δ S или в настоящем термине Δ L = c (константа) для закона экономии, но был готов принять Δ L / L = c (закон Брентано) или даже Δ L / L = L −0,5 (процесс Пуассона Макгилла и Голдберга). Настоящее исследование отдает предпочтение закону Брентано с пороговым поправочным коэффициентом. Второй момент был главной задачей единого закона Крюгера, в котором он не только пытался согласовать различные способы измерения величины ощущений (например,g., оценка величины по сравнению с категориальным рейтингом), но также вывести функцию субъективной величины из данных jnd. Он подробно исследовал «теорию пропорционального jnd» (стр. 260), неявно обсуждал теорию «наклона» (его таблица 1 на стр. 261), но, вероятно, не знал о «равной громкости, равном-jnd» теории, не говоря уже о том, чтобы рассматривать их как три независимых фактора, которые в совокупности вносят вклад в функцию jnd-громкости (настоящее исследование). Третий пункт Крюгера, относящийся к мозгу как к линейному устройству, неверен, потому что настоящее исследование (B3) не только показывает, что электрическая стимуляция слухового нерва, которая обходит слуховые волосковые клетки, вызывает экспоненциальную функцию громкости у пользователей кохлеарных имплантатов, но и что еще более важно, многие исследования нейропластичности обнаружили аномально повышенный прирост в головном мозге в ответ на снижение входного сигнала на периферии (например,г., Qiu et al., 2000; Норена, 2011; Chambers et al., 2016).

    Заявление о доступности данных

    Наборы данных, созданные для этого исследования, доступны по запросу соответствующему автору.

    Заявление об этике

    Этическое одобрение для этого исследования не требовалось, так как данные на людях были взяты из ранее опубликованных исследований. Пациенты / участники предоставили письменное информированное согласие на участие в этом исследовании.

    Взносы авторов

    F-GZ несет полную ответственность за представленные здесь работы.

    Конфликт интересов

    Автор заявляет, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могут быть истолкованы как потенциальный конфликт интересов.

    Благодарности

    Джо Цвислоки стимулировал мой интерес к этому предмету, когда я был аспирантом, посещающим его классы в Сиракузском университете. Я многому научился, а также получил пользу от интеллектуальных дискуссий с Крисом Тернером, Нилом Вимейстером, Бертом Шлаухом, Адрианом Хаутсмой, Бобом Шенноном, Уолтом Джестедтом, Джонтом Алленом, Брайаном Муром, Бобом Карлайоном, Крисом Плэком, Дунканом Люсом, Биллом МакГиллом, Бертом. Шарф, Рона и Билл Хеллман.Маике ван Экхаутте послужила мотивацией для обсуждения закона Вебера (рис. 4), Даниэль Оберфельд и Вольфганг Эллермайер сделали критические комментарии, которые помогли связать несколько неясных концов и расширить рамки обсуждения в этой статье. Однако я несу полную ответственность за представленные здесь работы.

    Список литературы

    Аллен, Дж. Б., и Нили, С. Т. (1997). Моделирование отношения между едва заметной разницей в интенсивности и громкостью для чистых тонов и широкополосного шума. Дж.Акуст. Soc. Являюсь. 102, 3628–3646. DOI: 10.1121 / 1.420150

    CrossRef Полный текст | Google Scholar

    Buus, S., и Florentine, M. (2002). Рост громкости у слушателей с улитковой тугоухостью: пересмотр набора. J. Assoc. Res. Отоларингол. 3, 120–139. DOI: 10.1007 / s101620010084

    PubMed Аннотация | CrossRef Полный текст | Google Scholar

    Карлайон Р. П. и Мур Б. С. (1984). Дискриминация по интенсивности: серьезный отход от закона Вебера. J. Acoust. Soc. Являюсь. 76, 1369–1376. DOI: 10.1121 / 1.3

    CrossRef Полный текст | Google Scholar

    Чемберс, А. Р., Резник, Дж., Юань, Ю., Уиттон, Дж. П., Эдж, А. С., Либерман, М. К. и др. (2016). Усиление по центру восстанавливает слуховую обработку после почти полной денервации улитки. Нейрон 89, 867–879. DOI: 10.1016 / j.neuron.2015.12.041

    PubMed Аннотация | CrossRef Полный текст | Google Scholar

    Дехаене, С., Изард, В., Спелке, Э., и Пика, П. (2008). Логарифмический или линейный? Четкое интуитивное понимание числовой шкалы в культурах коренных народов Запада и Амазонки. Наука 320, 1217–1220. DOI: 10.1126 / science.1156540

    PubMed Аннотация | CrossRef Полный текст | Google Scholar

    Фехнер, Г. Т. (1966). Elemente der Psychophysik [Элементы психофизики]. Нью-Йорк, Нью-Йорк: Холт, Райнхарт и Уинстон, Инк.

    Google Scholar

    Florentine, M., and Buus, S. (1981). Модель возбуждающего паттерна для распознавания интенсивности. J. Acoust. Soc. Являюсь. 70, 1646–1654. DOI: 10.1121 / 1.387219

    CrossRef Полный текст | Google Scholar

    Фаулер, Э. П. (1937). Измерение ощущения громкости — новый подход к физиологии слуха, функциональным и дифференциально-диагностическим тестам. Arch. Отоларингол. 26, 514–521. DOI: 10.1001 / archotol.1937.00650020568002

    CrossRef Полный текст | Google Scholar

    Грин Д. М. и Светс Дж. А. (1966). Теория обнаружения сигналов и психофизика. Нью-Йорк, Нью-Йорк: Wiley.

    Google Scholar

    Хеллман Р., Шарф Б., Техцунян М. и Техцунян Р. (1987). О связи между ростом громкости и различением интенсивности чистых тонов. J. Acoust. Soc. Являюсь. 82, 448–453. DOI: 10.1121 / 1.395445

    CrossRef Полный текст | Google Scholar

    Хеллман, В. С., и Хеллман, Р. П. (1990). Дискриминация по интенсивности как движущая сила громкости. Применение к чистым тонам в тишине. J. Acoust. Soc. Являюсь. 87, 1255–1265. DOI: 10.1121 / 1.398801

    CrossRef Полный текст | Google Scholar

    Хеллман, У. С., и Хеллман, Р. П. (2001). Пересмотр отношений между громкостью и различением интенсивности. J. Acoust. Soc. Являюсь. 109 (5 Pt 1), 2098–2102. DOI: 10.1121 / 1.1366373

    CrossRef Полный текст | Google Scholar

    Хаутсма, А. Дж., Дурлах, Н. И., и Брейда, Л. Д. (1980). Восприятие интенсивности XI. Экспериментальные результаты по отношению разрешения по интенсивности к согласованию громкости. J. Acoust. Soc. Являюсь. 68, 807–813. DOI: 10.1121 / 1.384819

    CrossRef Полный текст | Google Scholar

    Джонсон, Дж. Х., Тернер, К. У., Цвислоки, Дж. Дж. И Марголис, Р. Х. (1993). Просто заметные различия в интенсивности и их отношении к громкости. J. Acoust. Soc. Являюсь. 93, 983–991. DOI: 10.1121 / 1.405404

    CrossRef Полный текст | Google Scholar

    Кианг, Н. Ю. и Моксон, Э. К. (1972). Психологические соображения при искусственной стимуляции внутреннего уха. Ann. Отол. Ринол. Ларингол. 81, 714–730. DOI: 10.1177 / 000348947208100513

    PubMed Аннотация | CrossRef Полный текст | Google Scholar

    Крюгер, Л. Э. (1989). Примирение Фехнера и Стивенса — к единому психофизическому закону. Behav. Brain Sci. 12, 251–267. DOI: 10.1017 / S0140525x0004855x

    CrossRef Полный текст | Google Scholar

    Лим, Дж. С., Рабиновтиз, В. М., Брейда, Л. Д., и Дурлах, Н. И. (1977). Восприятие интенсивности.VIII. Сравнение громкости между разными типами стимулов. J. Acoust. Soc. Являюсь. 62, 1256–1267. DOI: 10.1121 / 1.381641

    CrossRef Полный текст | Google Scholar

    Макгилл, У. Дж., И Голдберг, Дж. (1968). Исследование близких к неудачам с участием закона Вебера и дискриминации по интенсивности тона. Восприятие. Психофизика. 4, 105–109. DOI: 10.3758 / bf03209518

    CrossRef Полный текст | Google Scholar

    Миллер, Г. (1947). Чувствительность к изменениям интенсивности белого шума и его отношение к маскировке и громкости. J. Acoust. Soc. Являюсь. 19, 609–619. DOI: 10.1121 / 1.1916528

    CrossRef Полный текст | Google Scholar

    Нельсон Д. А., Шмитц Дж. Л., Дональдсон Г. С., Вимейстер Н. Ф. и Джавел Э. (1996). Распознавание интенсивности в зависимости от уровня раздражителя при электрическом раздражении. J. Acoust. Soc. Являюсь. 100 (4 Pt 1), 2393–2414. DOI: 10.1121 / 1.417949

    CrossRef Полный текст | Google Scholar

    Ньюман, Э. (1933). В справедливости просто заметна разница как единица психологической величины. Пер. Kansas Acad. Sci. 36, 172–175. DOI: 10.2307 / 3625353

    CrossRef Полный текст | Google Scholar

    Нидер, А., Миллер, Э. К. (2003). Кодирование когнитивной величины: сжатое масштабирование числовой информации в префронтальной коре приматов. Нейрон 37, 149–157. DOI: 10.1016 / s0896-6273 (02) 01144-1143

    CrossRef Полный текст | Google Scholar

    Норена А. Дж. (2011). Интегративная модель тиннитуса, основанная на центральном усилении, контролирующем нервную чувствительность. Neurosci. Biobehav. Ред. 35, 1089–1109. DOI: 10.1016 / j.neubiorev.2010.11.003

    PubMed Аннотация | CrossRef Полный текст | Google Scholar

    Оберфельд Д. (2008). Горбинка средней разницы при замаскированной в прямом направлении дискриминации по интенсивности. J. Acoust. Soc. Являюсь. 123, 1571–1581. DOI: 10.1121 / 1.2837284

    CrossRef Полный текст | Google Scholar

    Оксенхэм, А.Дж., и Мур, Б.С.Дж. (1995). Превышение и серьезное отклонение от закона о веберах. Дж.Акуст. Soc. Являюсь. 97, 2442–2453. DOI: 10.1121 / 1.411965

    CrossRef Полный текст | Google Scholar

    Pardo-Vazquez, J. L., Castineiras-de Saa, J. R., Valente, M., Damiao, I., Costa, T., Vicente, M. I., et al. (2019). Механистическая основа закона Вебера. Нат. Neurosci. 22, 1493–1502. DOI: 10.1038 / s41593-019-0439-7

    PubMed Аннотация | CrossRef Полный текст | Google Scholar

    Плак, К. Дж., И Вимейстер, Н. Ф. (1992). Дискриминация по интенсивности при обратной маскировке. J. Acoust. Soc. Являюсь. 92, 3097–3101. DOI: 10.1121 / 1.404205

    CrossRef Полный текст | Google Scholar

    Цю К., Салви Р., Дин Д. и Буркард Р. (2000). Потеря внутренних волосковых клеток приводит к увеличению амплитуды ответа в слуховой коре неанестезированных шиншилл: свидетельство увеличения системного усиления. Слушай. Res. 139, 153–171. DOI: 10.1016 / s0378-5955 (99) 00171-9

    CrossRef Полный текст | Google Scholar

    Ранкович, К. М., Вимейстер, Н.Ф., Фантини Д. А., Чизман М. Ф. и Учияма К. Л. (1988). Соотношение между громкостью и разницей интенсивности составляет величину для тонов на тихом и шумном фоне. J. Acoust. Soc. Являюсь. 84, 150–155. DOI: 10.1121 / 1.396981

    CrossRef Полный текст | Google Scholar

    Riesz, R. (1933). Отношение между громкостью и минимальным заметным приращением интенсивности. J. Acoust. Soc. Являюсь. 4, 211–216. DOI: 10.1121 / 1.11

    CrossRef Полный текст | Google Scholar

    Schlauch, R.С. (1994). Разрешение по интенсивности и громкость в высокочастотном шуме. J. Acoust. Soc. Являюсь. 95, 2171–2179. DOI: 10.1121 / 1.410017

    CrossRef Полный текст | Google Scholar

    Шлаух Р. С., Харви С. и Лантье Н. (1995). Разрешение по интенсивности и громкость в широкополосном шуме. J. Acoust. Soc. Являюсь. 98, 1895–1902. DOI: 10.1121 / 1.413375

    CrossRef Полный текст | Google Scholar

    Стивенс, С. С. (1961). Чтобы почтить память Фехнера и отменить его закон: степенная функция, а не логарифмическая функция, описывает рабочие характеристики сенсорной системы. Наука 133, 80–86. DOI: 10.1126 / science.133.3446.80

    PubMed Аннотация | CrossRef Полный текст | Google Scholar

    Стиллман, Дж. А., Цвислоки, Дж. Дж., Чжан, М., и Чефаратти, Л. К. (1993). Просто заметные различия в интенсивности при одинаковой громкости в нормальном и патологическом ушах. J. Acoust. Soc. Являюсь. 93, 425–434. DOI: 10.1121 / 1.405622

    CrossRef Полный текст | Google Scholar

    Техцунян Р. (2012). Стандартная модель воспринимаемой величины: основа для (почти) всего, что о ней известно. Am. J. Psychol. 125, 165–174. DOI: 10.5406 / amerjpsyc.125.2.0165

    PubMed Аннотация | CrossRef Полный текст | Google Scholar

    Вимейстер, Н. Ф., и Бэкон, С. П. (1988). Распознавание интенсивности, обнаружение приращения и оценка амплитуды для тонов с частотой 1 кГц. J. Acoust. Soc. Являюсь. 84, 172–178. DOI: 10.1121 / 1.396961

    CrossRef Полный текст | Google Scholar

    Цзэн Ф. Г. (1994). Рост громкости при прямой маскировке: отношение к различению интенсивности. J. Acoust. Soc. Являюсь. 96, 2127–2132. DOI: 10.1121 / 1.410154

    CrossRef Полный текст | Google Scholar

    Цзэн, Ф. Г. (2013). Модель активной громкости, предполагающая, что шум в ушах — это повышенный центральный шум, а гиперакузия — как усиление нелинейного усиления. Слушай. Res. 295, 172–179. DOI: 10.1016 / j.heares.2012.05.009

    PubMed Аннотация | CrossRef Полный текст | Google Scholar

    Цзэн Ф. Г. и Шеннон Р. В. (1994). Механизмы кодирования громкости, полученные в результате электростимуляции слуховой системы человека. Наука 264, 564–566. DOI: 10.1126 / science.8160013

    PubMed Аннотация | CrossRef Полный текст | Google Scholar

    Цзэн Ф. Г. и Тернер К. В. (1992). Дискриминация по интенсивности при прямой маскировке. J. Acoust. Soc. Являюсь. 92 (2 Pt 1), 782–787. DOI: 10.1121 / 1.403947

    CrossRef Полный текст | Google Scholar

    Цзэн Ф. Г., Тернер К. В. и Релкин Э. М. (1991). Восстановление после предшествующей стимуляции. II: влияние на различение интенсивности. Слушай. Res. 55, 223–230. DOI: 10.1016 / 0378-5955 (91)-k

    CrossRef Полный текст | Google Scholar

    Zwislocki, J. (1965). «Анализ некоторых слуховых характеристик», в Справочнике по математической психологии , , ред. Р. Люс, Р. Р. Буш и Э. Галантер (Нью-Йорк, штат Нью-Йорк: John Wiley and Sons, Inc.), 79–97.

    Google Scholar

    Zwislocki, J. J., and Jordan, H. N. (1986). Об отношении интенсивности jnd к громкости и нейронному шуму. J. Acoust. Soc. Являюсь. 79, 772–780. DOI: 10.1121 / 1.393467

    CrossRef Полный текст | Google Scholar

    Объединение психофизических явлений: полная форма закона Фехнера

  • Бэрд, Дж. К., и Нома, Э. (1978). Основы шкалирования и психофизики . Нью-Йорк: Вили.

    Google ученый

  • Бекеси, Г. фон (1960). Эксперименты со слухом (E.G. Weaver, Ed.и Пер.). Нью-Йорк: Макгроу-Хилл.

    Google ученый

  • Дельбёф, Дж. Р. Л. (1873). Étude Psychophysique: Recherches théoriques et expérimentales sur la mesure des sensations et spécialement des sensations de lumière et de fatigue [Психофизическое исследование: теоретические и экспериментальные исследования по измерению ощущений, и особенно ощущения света и усталости]. В Mémoires Couronnés et autres mémoires, publiés par l’Academie Royale des Sciences, des Lettres, et des Beaux-arts de Belgique (Vol.23, с. 1–116). Брюссель: Хайез.

    Google ученый

  • Экман, Г. (1959). Закон Вебера и связанные с ним функции. Психологический журнал , 47 , 343–352.

    Артикул Google ученый

  • Гулик, В. Л., Гешайдер, Г. А., и Фрисина, Р. Д. (1989). Слух: физиологическая акустика, нейронное кодирование и психоакустика . Нью-Йорк: Издательство Оксфордского университета.

    Google ученый

  • Харрис, Дж. Д. (1963). Дискриминация по громкости. Журнал нарушений речи и слуха: Приложение к монографии (№ 11).

  • Hellman, R.P., & Zwislocki, J. (1961). Некоторые факторы, влияющие на оценку громкости. Журнал Акустического общества Америки , 33 , 687–694.

    Артикул Google ученый

  • Хеллман, В.С., & Хеллман, Р. П. (1990). Дискриминация по интенсивности как движущая сила громкости: применение к чистым тонам в тишине. Журнал акустического общества Америки , 87 , 1255–1265.

    Артикул PubMed Google ученый

  • Гельмгольц, Х. фон (1924). Трактат Гельмгольца по физиологической оптике (Том 2; Дж. П. С. Саутхолл, ред.). Менаша, Висконсин: Оптическое общество Америки. (Оригинальная работа опубликована в 1856-1866 гг.)

    Google ученый

  • Хаутсма, А.Дж. М., Дурлах, Н. И., и Брейда, Л. Д. (1980). Восприятие интенсивности XI: экспериментальные результаты по отношению разрешения интенсивности к согласованию громкости. Журнал Акустического общества Америки , 68 , 807–813.

    Артикул PubMed Google ученый

  • Джестедт В., Виер К. Дж. И Грин Д. М. (1977). Распознавание интенсивности в зависимости от частоты и уровня чувствительности. Журнал акустического общества Америки , 61 , 169–177.

    Артикул PubMed Google ученый

  • Кинг, М. К., и Локхед, Г. Р. (1981). Шкалы отклика и последовательные эффекты в суждении. Восприятие и психофизика , 30 , 599–603.

    Google ученый

  • Кох, К., и Мейер, Д. Э. (1991). Функциональное обучение: индукция непрерывных отношений стимула и реакции. Журнал экспериментальной психологии: обучение, память и познание , 17 , 811–836.

    Артикул Google ученый

  • Крюгер, Л. Э. (1989). Примирение Фехнера и Стивенса: к единому психофизическому закону. Поведенческие и мозговые науки , 12 , 251–320.

    Артикул Google ученый

  • Леманн, А. (1905). Elemente der Psychodynamik [Элементы психодинамики]. Лейпциг: О. Р. Рейсланд.

    Google ученый

  • Лим, Дж.С., Рабинович, В. М., Брейда, Л. Д., и Дурлах, Н. И. (1977). Восприятие интенсивности VIII: Сравнение громкости между различными типами стимулов. Журнал акустического общества Америки , 65 , 1256–1267.

    Артикул Google ученый

  • Marks, L.E. (1974a). По шкале ощущений: Пролегомены любой будущей психофизики, которая сможет стать наукой. Восприятие и психофизика , 16 , 358–376.

    Google ученый

  • Marks, L.E. (1974b). Сенсорные процессы: новая психофизика . Нью-Йорк: Academic Press.

    Google ученый

  • Marks, L. E., Galanter, E., & Baird, J. C. (1995). Бинауральное суммирование после изучения психофизических функций громкости. Восприятие и психофизика , 57 , 1209–1216.

    Google ученый

  • McGill, W.Дж. (1960). Наклон функции громкости: загадка. В Х. Гулликсен и С. Мессик (ред.), Психологическое масштабирование: теория и приложения (стр. 67–81). Нью-Йорк: Вили.

    Google ученый

  • МакГилл, У. Дж., И Голдберг, Дж. П. (1968). Исследование близких к неудачам с участием закона Вебера и дискриминации по интенсивности тона. Восприятие и психофизика , 4 , 105–109.

    Google ученый

  • Мюррей, Д.Дж. (1993). Перспектива для просмотра истории психофизики. Поведенческие и мозговые науки , 16 , 115–186.

    Артикул Google ученый

  • Николас С., Мюррей Д. Дж. И Фарахманд Б. (в печати). Психофизика Дж. Р. Л. Дельбёфа (1831–1896). Восприятие .

  • Норвич, К. Х. (1993). Информация, ощущение и восприятие . Сан-Диего: Academic Press.

    Google ученый

  • Норвич К. Х. и Вонг У. (1995). Универсальная модель действия единичных сенсорных рецепторов. Математические биологические науки , 125 , 83–108.

    Артикул PubMed Google ученый

  • Nutting, P. G. (1907). Полная форма закона Фехнера. Бюллетень Бюро стандартов , 3 , 59–64.

    Google ученый

  • Рис, Р. Р. (1928). Дифференциальная чувствительность уха к чистым тонам. Physical Review: Series 2 , 31 , 867–875.

    Google ученый

  • Робинсон Д. У. и Дадсон Р. С. (1956). Повторное определение отношения равной громкости для чистых тонов. Британский журнал прикладной физики , 7 , 166–181.

    Артикул Google ученый

  • Шакоу, П., и Рааб, Д. Х. (1973). Различение интенсивности тональных пакетов и формы функции Вебера. Восприятие и психофизика , 14 , 449–450.

    Google ученый

  • Шарф Б. (1978). Громкость. В E. Carterette & M. P. Friedman (Eds.), Handbook of Perception (Vol.4. С. 188–189). Нью-Йорк: Academic Press.

    Google ученый

  • Зиберт, В. М. (1968). Стимул трансформации в периферической слуховой системе. В P. A. Kolers & M. Eden (Eds.), Recognizing patterns (chap. 4, pp. 104–133). Кембридж, Массачусетс: M.I.T. Нажмите.

    Google ученый

  • Стивенс, С. С. (1936). Шкала для измерения психологической величины: Громкость. Психологический обзор , 43 , 405–416.

    Артикул Google ученый

  • Вимейстер, Н. Ф. (1988). Психофизические аспекты кодирования звуковой интенсивности. В Г. М. Эдельман, У. Э. Галл и В. М. Коуэн (ред.), Слуховая функция: нейробиологические основы слуха (глава 7, стр. 213). Нью-Йорк: Вили.

    Google ученый

  • Уорд, Л.М. и Дэвидсон К. П. (1993). Где действие: фракции Вебера как функция звукового давления на низких частотах. Журнал акустического общества Америки , 94 , 2587–2594.

    Артикул PubMed Google ученый

  • Вест, Р. Л. (1996). Ограниченное масштабирование: калибровка отдельных субъектов по оценке величины . Опубликовал докторскую диссертацию в Университете Британской Колумбии, Ванкувер.

    Google ученый

  • Вест, Р. Л., и Уорд, Л. М. (1994). Ограниченное масштабирование. В Л. М. Уорд (ред.), Труды десятого ежегодного собрания Международного общества психофизиков (стр. 225). Ванкувер, Британская Колумбия: Международное психофизическое общество.

    Google ученый

    • Идея Фехнера в JSTOR

    Абстрактный

    Из того принципа, что субъективное различие между двумя стимулами определяется их соотношением, Фехнер выводит свой логарифмический закон двумя способами.В одном из выводов, игнорируемых и забытых в современных интерпретациях теории Фехнера, он формулирует рассматриваемый принцип как функциональное уравнение и сводит его к уравнению с известным решением. В другом выводе, хорошо известном и часто критикуемом, он решает то же функциональное уравнение путем дифференцирования. Оба вывода математически достоверны (часто высмеянный «целесообразный принцип», упомянутый Фехнером, можно рассматривать как просто неумелый способ указать на определенное свойство дифференциации, которую он использует).Ни в одном из этих выводов не используется понятие едва заметных различий. Но если принять закон Вебера в дополнение к рассматриваемому принципу, то несходство между двумя стимулами приблизительно пропорционально количеству только что заметных различий, которые соответствуют между этими стимулами: чем меньше доля Вебера, тем лучше приближение, а дробь Вебера может всегда быть произвольно маленьким по соответствующему соглашению. Однако мы утверждаем, что ни два вывода закона Фехнера, ни связь этого закона с порогами не составляют суть подхода Фехнера.Мы видим эту суть в идее аддитивной кумуляции значений чувствительности. Работа Фехнера содержит удивительно современное определение чувствительности к данному стимулу: скорость роста функции вероятности большего, причем этот стимул служит стандартом. Идея аддитивной кумуляции значений чувствительности поддается широкому обобщению фехнеровской шкалы.

    Информация о журнале

    Американский журнал психологии (AJP) был основан в 1887 году Дж.Стэнли Холла, и в первые годы его редактировали Титченер, Боринг и Далленбах. Журнал опубликовал одни из самых новаторских и формирующих статей в области психологии за всю свою историю. AJP исследует науку о разуме и поведении, публикуя отчеты об оригинальных исследованиях в области экспериментальной психологии, теоретические презентации, комбинированный теоретический и экспериментальный анализ, исторические комментарии и подробные обзоры значимых книг.

    Информация об издателе

    Основанная в 1918 г., University of Illinois Press (www.press.uillinois.edu) считается одним из крупнейших и наиболее известных университетских изданий страны. Ежегодно The Press публикует более 120 новых книг и 30 научных журналов по множеству предметов, включая историю Америки, историю труда, историю спорта, фольклор, еду, фильмы, американскую музыку, американскую религию, афроамериканские исследования, женские исследования и Авраама. Линкольн. The Press является одним из основателей Ассоциации прессов американских университетов, а также History Cooperative, онлайновой коллекции из более чем 20 журналов по истории.

    Права и использование

    Этот предмет является частью коллекции JSTOR.
    Условия использования см. В наших Положениях и условиях
    Авторское право 2011 г. Попечительским советом Иллинойского университета.
    Запросить разрешения

    Психофизика

    Психофизика
    Следующая: Самоанализ Up: Психология Лекция 1 Предыдущая: Ассоциация & nbsp Содержание

    Психофизика

    Психофизика доминировала в ранней научной психологии — в период с позднего XIX век и начало XX века.Цель — сделать объективные измерения содержание разума через физический стимул, за которым следует отчет о психологическом опыте. Сегодняшние выставки когнитивной науки сильные методологические параллели с психофизикой.

    Вдохновленный Бенедикт Спиноза (1632-1677) — психофизический параллелизм: каждое физическое событие имеет ментальный аналог, и порок наоборот.

    Предположение снизу вверх: полное восприятие объектов происходит вне « элементарные ощущения », отражающие простые аспекты окружающая среда: например.вес, цвет, яркость, высота, громкость. Эти последние являются строительными блоками восприятия.

    Эрнст Вебер (1795-1878) Чувство осязания (двухточечный порог для на ощупь: самый маленький для языка — 1мм, самый большой для спины — 60мм). Показано это прикосновение состоит из ощущений давления, температуры и боли.

    Пороги наименьшего количества ощущений, обнаруживаемых органом чувств: порог — это уровень звука, света или прикосновения, при котором кто-то сообщает о том, что слышит, видит или ощущает какие-то ощущения в 50% случаев.(установленный первым Вебером?)

    Подтвержденное наличие кинестезии (опыт мышечной положение и движение).

    Закон Вебера: Вебер измерял воспринимаемую интенсивность стимула (например, вес, яркость, громкость, сладость), сочетая похожие стимулы а запись просто заметная разница в интенсивности — обнаружили, что jnd пропорционален величине стимула. (Одна свеча добавляется к 1 или к 100) Этот закон относится к физическим стимулам. с умственным опытом.1/40 для гирь в руке.

    6 # 6

    ( Reiz по-немецки « стимул »)

    Густав Фехнер (1801-1887) Элементы психофизики , 1860 г., основал « … точную науку о функциональных отношениях … между телом и разумом ».

    В 1860 году было введено математическое выражение закона Веберса:

    Пусть интенсивность стимула будет 7 # 7, а ощущения — 8 # 8.

    С

    9 # 9

    10 # 10

    Воспринимаемая интенсивность стимула (например,яркость и громкость) есть пропорциональна логарифму его физической интенсивности (закон Фехнера).

    Психологическое событие выражается в измеряемом физическом событии!

    Закон Вебера-Фехнера был заменен в современной психофизике на Закон мощности Стивена:

    11 # 11


    12 # 12

    (Отношение логарифм — логарифмическая интенсивность стимула против логарифмического восприятия дает прямую линию.)

    Герман Гельмгольц (1850-70) разработал способ измерения скорости передачи нервных импульсов (165–330 футов в секунду у людей).

    Провел эксперименты по цветовому зрению, восприятию (например, постэффект ношения). искажающие линзы; исследование восстановленного зрения) — представления о космосе нет врожденный.

    Разработал идею бессознательного вывода — прошлое знание влияет на восприятие (например, при оптических иллюзиях). Противопоставьте силлогистическому выводу .

    (Таким образом, Гельмгольц использовал b-u (молекулярный), а также t-d (молярный) подход)

    F.C. Дондерс (1868) измерил время, необходимое для высших умственных способностей. операции.

    Франц Брентано (священник-философ) 1874 выступил против молекулярного / механистический подход психофизиков и стресс-исследования феноменологические аспекты, такие как умственные действия — суждение, ощущение, воображение, слух; Итак, намерения, цели, цели. Этот т-д подход не был очень популярен до его возрождения в гештальте, а затем в символический взгляд AI.


    Следующая: Самоанализ Up: Психология Лекция 1 Предыдущая: Ассоциация & nbsp Содержание

    % PDF-1.7 % 137 0 объект > эндобдж xref 137 94 0000000016 00000 н. 0000002905 00000 н. 0000003147 00000 н. 0000003205 00000 н. 0000003241 00000 н. 0000003834 00000 н. 0000003983 00000 н. 0000004115 00000 п. 0000004539 00000 н. 0000004959 00000 н. 0000004996 00000 н. 0000005110 00000 н. 0000005222 00000 п. 0000005477 00000 н. 0000005504 00000 н. 0000006134 00000 н. 0000006584 00000 н. 0000007753 00000 н. 0000008168 00000 п. 0000008493 00000 п. 0000008742 00000 н. 0000009721 00000 н. 0000010334 00000 п. 0000010934 00000 п. 0000011350 00000 п. 0000012013 00000 н. 0000012124 00000 п. 0000013407 00000 п. 0000013842 00000 п. 0000014337 00000 п. 0000014714 00000 п. 0000014799 00000 н. 0000016183 00000 п. 0000017454 00000 п. 0000017587 00000 п. 0000017952 00000 п. 0000018218 00000 п. 0000018496 00000 п. 0000018765 00000 п. 0000018792 00000 п. 0000019205 00000 п. 0000020571 00000 п. 0000020947 00000 п. 0000021332 00000 п. 0000021641 00000 п. 0000023238 00000 п. 0000024513 00000 п. 0000032661 00000 п. 0000041331 00000 п. 0000041578 00000 п. 0000064150 00000 п. 0000064251 00000 п. 0000081799 00000 п. 0000081869 00000 п. 0000084519 00000 п. 0000089462 00000 п. 0000115951 00000 п. 0000116213 00000 н. 0000116283 00000 н. 0000116384 00000 н. 0000139622 00000 н. 0000139885 00000 н. 0000140369 00000 н. 0000146647 00000 н. 0000149313 00000 н. 0000149614 00000 н. 0000181206 00000 н. 0000181271 00000 н. 0000181364 00000 н. 0000183982 00000 н. 0000184275 00000 н. 0000184556 00000 н. 0000184583 00000 н. 0000184985 00000 н. 0000203526 00000 н. 0000203782 00000 н. 0000204220 00000 н. 0000229281 00000 п. 0000229556 00000 н. 0000229907 00000 н.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *