Корреляция — Википедия
Для графического представления корреляционной связи можно использовать прямоугольную систему координат с осями, которые соответствуют обеим переменным. Каждая пара значений маркируется при помощи определённого символа. Такой график называется диаграммой рассеяния.Корреля́ция (от лат. correlatio «соотношение, взаимосвязь»), или корреляционная зависимость — статистическая взаимосвязь двух или более случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин.[1]
Математической мерой корреляции двух случайных величин служит корреляционное отношение η{\displaystyle \mathbf {\eta } }
Впервые в научный оборот термин корреляция ввёл французский палеонтолог Жорж Кювье в XVIII веке. Он разработал «закон корреляции» частей и органов живых существ, с помощью которого можно восстановить облик ископаемого животного, имея в распоряжении лишь часть его останков. В статистике слово «корреляция» первым стал использовать английский биолог и статистик Фрэнсис Гальтон в конце XIX века
Значительная корреляция между двумя случайными величинами всегда является свидетельством существования некоторой статистической связи в данной выборке, но эта связь не обязательно должна наблюдаться для другой выборки и иметь причинно-следственный характер. Часто заманчивая простота корреляционного исследования подталкивает исследователя делать ложные интуитивные выводы о наличии причинно-следственной связи между парами признаков, в то время как коэффициенты корреляции устанавливают лишь статистические взаимосвязи. Например, рассматривая пожары в конкретном городе, можно выявить весьма высокую корреляцию между ущербом, который нанёс пожар, и количеством пожарных, участвовавших в ликвидации пожара, причём эта корреляция будет положительной. Из этого, однако, не следует вывод «увеличение количества пожарных приводит к увеличению причинённого ущерба», и тем более не будет успешной попытка минимизировать ущерб от пожаров путём ликвидации пожарных бригад
В то же время, отсутствие корреляции между двумя величинами ещё не значит, что между ними нет никакой связи. Например, зависимость может иметь сложный нелинейный характер, который корреляция не выявляет.
Некоторые виды коэффициентов корреляции могут быть положительными или отрицательными. В первом случае предполагается, что мы можем определить только наличие или отсутствие связи, а во втором — также и её направление. Если предполагается, что на значениях переменных задано отношение строгого порядка, то отрицательная корреляция
Метод вычисления коэффициента корреляции зависит от вида шкалы, к которой относятся переменные. Так, для измерения переменных с интервальной и количественной шкалами необходимо использовать коэффициент корреляции Пирсона (корреляция моментов произведений). Если по меньшей мере одна из двух переменных имеет порядковую шкалу, либо не является нормально распределённой, необходимо использовать ранговую корреляцию Спирмена или τ{\displaystyle \mathbf {\tau } } (тау) Кендалла. В случае, когда одна из двух переменных является дихотомической, используется точечная двухрядная корреляция, а если обе переменные являются дихотомическими — четырёхполевая корреляция. Расчёт коэффициента корреляции между двумя недихотомическими переменными не лишён смысла только тогда, когда связь между ними линейна (однонаправлена).
Параметрические показатели корреляции[править | править код]
Ковариация[править | править код]
Важной характеристикой совместного распределения двух случайных величин является ковариация (или корреляционный момент). Ковариация является совместным центральным моментом второго порядка.[6] Ковариация определяется как математическое ожидание произведения отклонений случайных величин
где M{\displaystyle \mathbf {M} } — математическое ожидание (в англоязычной литературе принято обозначение E{\displaystyle \mathbf {E} } от expected value).
Свойства ковариации:
- Ковариация двух независимых случайных величин X{\displaystyle \mathbf {X} } и Y{\displaystyle \mathbf {Y} } равна нулю[8].
Доказательство
- Абсолютная величина ковариации двух случайных величин X{\displaystyle \mathbf {X} } и Y{\displaystyle \mathbf {Y} } не превышает среднего геометрического их дисперсий: |covXY|⩽DXDY{\displaystyle |\mathrm {cov} _{XY}|\leqslant {\sqrt {\mathrm {D} _{X}\mathrm {D} _{Y}}}}
Доказательство
Введём в рассмотрение случайную величину Z1=σYX−σXY{\displaystyle \mathbf {Z} _{1}=\mathbf {\sigma } _{Y}\mathbf {X} -\mathbf {\sigma } _{X}\mathbf {Y} } (где σ{\displaystyle \mathbf {\sigma } } — среднеквадратическое отклонение) и найдём её дисперсию D(Z1)=M[Z−mZ1]2{\displaystyle \mathbf {D} (Z_{1})=\mathbf {M} [\mathbf {Z} -m_{Z1}]^{2}}. Выполнив выкладки получим:
D(Z1)=2σ2Xσ2Y−2σXσYcovXY.{\displaystyle \mathbf {D} (Z_{1})=2\mathbf {\sigma ^{2}} _{X}\mathbf {\sigma ^{2}} _{Y}-2\mathbf {\sigma } _{X}\mathbf {\sigma } _{Y}\mathrm {cov} _{XY}.}
Любая дисперсия неотрицательна, поэтому
2σ2Xσ2Y−2σXσYcovXY⩾0{\displaystyle 2\mathbf {\sigma ^{2}} _{X}\mathbf {\sigma ^{2}} _{Y}-2\mathbf {\sigma } _{X}\mathbf {\sigma } _{Y}\mathrm {cov} _{XY}\geqslant 0}
Отсюда
covXY⩽σXσY.{\displaystyle \mathrm {cov} _{XY}\leqslant \mathrm {\sigma } _{X}\mathrm {\sigma } _{Y}.}
Введя случайную величину Z2=σYX+σXY{\displaystyle \mathbf {Z} _{2}=\mathbf {\sigma } _{Y}\mathbf {X} +\mathbf {\sigma } _{X}\mathbf {Y} }, аналогично
covXY⩾−σXσY.{\displaystyle \mathrm {cov} _{XY}\geqslant -\mathrm {\sigma } _{X}\mathrm {\sigma } _{Y}.}
Объединив полученные неравенства имеем
−σXσY⩽covXY⩽σXσY.{\displaystyle -\mathrm {\sigma } _{X}\mathrm {\sigma } _{Y}\leqslant \mathrm {cov} _{XY}\leqslant \mathrm {\sigma } _{X}\mathrm {\sigma } _{Y}.}
Или
|covXY|⩽σXσY.{\displaystyle |\mathrm {cov} _{XY}|\leqslant \mathrm {\sigma } _{X}\mathrm {\sigma } _{Y}.}
Итак,
|covXY|⩽DXDY.{\displaystyle |\mathrm {cov} _{XY}|\leqslant {\sqrt {\mathrm {D} _{X}\mathrm {D} _{Y}}}.}
- Ковариация имеет размерность, равную произведению размерности случайных величин, то есть величина ковариации зависит от единиц измерения независимых величин. Данная особенность ковариации затрудняет её использование в целях корреляционного анализа[8].
Линейный коэффициент корреляции[править | править код]
Для устранения недостатка ковариации был введён линейный коэффициент корреляции (или коэффициент корреляции Пирсона), который разработали Карл Пирсон, Фрэнсис Эджуорт и Рафаэль Уэлдон в 90-х годах XIX века. Коэффициент корреляции рассчитывается по формуле[10][8]:
rXY=covXYσXσY=∑(X−X¯)(Y−Y¯)∑(X−X¯)2∑(Y−Y¯)2.{\displaystyle \mathbf {r} _{XY}={\frac {\mathbf {cov} _{XY}}{\mathbf {\sigma } _{X}{\sigma }_{Y}}}={\frac {\sum (X-{\bar {X}})(Y-{\bar {Y}})}{\sqrt {\sum (X-{\bar {X}})^{2}\sum (Y-{\bar {Y}})^{2}}}}.}где X¯=1n∑t=1nXt{\displaystyle {\overline {X}}={\frac {1}{n}}\sum _{t=1}^{n}X_{t}}, Y¯=1n∑t=1nYt{\displaystyle {\overline {Y}}={\frac {1}{n}}\sum _{t=1}^{n}Y_{t}} — среднее значение выборок.
Коэффициент корреляции изменяется в пределах от минус единицы до плюс единицы[11].
Доказательство
Разделив обе части двойного неравенства −σXσY⩽covXY⩽σXσY{\displaystyle -\mathrm {\sigma } _{X}\mathrm {\sigma } _{Y}\leqslant \mathrm {cov} _{XY}\leqslant \mathrm {\sigma } _{X}\mathrm {\sigma } _{Y}} на σXσY{\displaystyle \mathbf {\sigma } _{X}\mathbf {\sigma } _{Y}} получим
−1⩽rXY⩽ 1.{\displaystyle -1\leqslant \mathbf {r} _{XY}\leqslant \ 1.}
Линейный коэффициент корреляции связан с коэффициентом регрессии в виде следующей зависимости:rXY=aiσXiσY,{\displaystyle \mathbf {r} _{XY}=\mathbf {a} _{i}{\frac {{\sigma }_{Xi}}{{\sigma }_{Y}}},} где ai{\displaystyle \mathbf {a} _{i}} — коэффициент регрессии, σXi{\displaystyle \mathbf {\sigma } _{Xi}} — среднеквадратическое отклонение соответствующего факторного признака[12]. Отношение коэффициента регрессии к среднеквадратичному отклонению Y не зависит от единиц измерения Y.
Непараметрические показатели корреляции[править | править код]
Коэффициент ранговой корреляции Кендалла[править | править код]
Применяется для выявления взаимосвязи между количественными или качественными показателями, если их можно ранжировать. Значения показателя X выставляют в порядке возрастания и присваивают им ранги. Ранжируют значения показателя Y и рассчитывают коэффициент корреляции Кендалла:
τ=2Sn(n−1){\displaystyle \tau ={\frac {2S}{n(n-1)}}},
где S=P−Q{\displaystyle S=P-Q}.
P{\displaystyle P} — суммарное число наблюдений, следующих за текущими наблюдениями с большим значением рангов Y.
Q{\displaystyle Q} — суммарное число наблюдений, следующих за текущими наблюдениями с меньшим значением рангов Y. (равные ранги не учитываются!)
τ∈[−1;1]{\displaystyle \tau \in [-1;1]}
Если исследуемые данные повторяются (имеют одинаковые ранги), то в расчетах используется скорректированный коэффициент корреляции Кендалла:
τ=S[n(n−1)2−Ux][n(n−1)2−Uy]{\displaystyle \tau ={\frac {S}{{\sqrt {[{\frac {n(n-1)}{2}}-U_{x}][{\frac {n(n-1)}{2}}-U_{y}}}]}}}
Ux=∑t(t−1)2{\displaystyle U_{x}={\frac {\sum {t(t-1)}}{2}}}
Uy=∑t(t−1)2{\displaystyle U_{y}={\frac {\sum {t(t-1)}}{2}}}
t{\displaystyle t} — число связанных рангов в ряду X и Y соответственно.
Коэффициент ранговой корреляции Спирмена[править | править код]
Степень зависимости двух случайных величин (признаков) X{\displaystyle X} и Y{\displaystyle Y} может характеризоваться на основе анализа получаемых результатов (X1,Y1),…,(Xn,Yn){\displaystyle (X_{1},Y_{1}),\ldots ,(X_{n},Y_{n})}. Каждому показателю X{\displaystyle X} и Y{\displaystyle Y} присваивается ранг. Ранги значений X{\displaystyle X} расположены в естественном порядке i=1,2,…,n{\displaystyle i=1,2,\ldots ,n}. Ранг Y{\displaystyle Y} записывается как Ri{\displaystyle R_{i}} и соответствует рангу той пары (X,Y){\displaystyle (X,Y)}, для которой ранг X{\displaystyle X} равен i{\displaystyle i}. На основе полученных рангов Xi{\displaystyle X_{i}} и Yi{\displaystyle Y_{i}} рассчитываются их разности di{\displaystyle d_{i}} и вычисляется коэффициент корреляции Спирмена:
ρ=1−6∑di2n(n2−1){\displaystyle \rho =1-{\frac {6\sum d_{i}^{2}}{n(n^{2}-1)}}}
Значение коэффициента меняется от −1 (последовательности рангов полностью противоположны) до +1 (последовательности рангов полностью совпадают). Нулевое значение показывает, что признаки независимы.
Коэффициент корреляции знаков Фехнера[править | править код]
Подсчитывается количество совпадений и несовпадений знаков отклонений значений показателей от их среднего значения.
i=C−HC+H{\displaystyle i={\frac {C-H}{C+H}}}
C — число пар, у которых знаки отклонений значений от их средних совпадают.
H — число пар, у которых знаки отклонений значений от их средних не совпадают.
Множественный коэффициент корреляции[править | править код]
Коэффициент множественной ранговой корреляции (конкордации)[править | править код]
W=12Sm2(n3−n){\displaystyle W={\frac {12S}{m^{2}(n^{3}-n)}}}
S=∑i=1n(∑j=1mRij)2−(∑i=1n∑j=1mRij)2n{\displaystyle S=\sum _{i=1}^{n}{(\sum _{j=1}^{m}{R_{ij}})^{2}}-{\frac {(\sum _{i=1}^{n}{\sum _{j=1}^{m}{R_{ij}}})^{2}}{n}}}
m{\displaystyle m} — число групп, которые ранжируются.
n{\displaystyle n} — число переменных.
Rij{\displaystyle R_{ij}} — ранг i{\displaystyle i}-фактора у j{\displaystyle j}-единицы.
Значимость:
χ2=m(n−1)∗W{\displaystyle \chi ^{2}=m(n-1)*W}
χ2kp=(α;(n−1)(m−1)){\displaystyle {\chi ^{2}}_{kp}=(\alpha ;(n-1)(m-1))}
χ2>χ2kp{\displaystyle \chi ^{2}>{\chi ^{2}}_{kp}}, то гипотеза об отсутствии связи отвергается.
В случае наличия связанных рангов:
W=12Sm2(n3−n)−m∑j=1m(t3j−tj){\displaystyle W={\frac {12S}{m^{2}(n^{3}-n)-m\sum _{j=1}^{m}{({t^{3}}_{j}-t_{j})}}}}
χ2=12Smn(n+1)−∑j=1m(t3j−tj)n−1{\displaystyle \chi ^{2}={\frac {12S}{mn(n+1)-{\frac {\sum _{j=1}^{m}{({t^{3}}_{j}-t_{j})}}{n-1}}}}}
Свойства коэффициента корреляции[править | править код]
- если принять в качестве скалярного произведения двух случайных величин ковариацию ⟨X,Y⟩=cov(X,Y){\displaystyle \langle X,Y\rangle =\mathrm {cov} (X,Y)}, то норма случайной величины будет равна ‖X‖=D[X]{\displaystyle \|X\|={\sqrt {\mathrm {D} [X]}}}, и следствием неравенства Коши — Буняковского будет:
- −1⩽RX,Y⩽1{\displaystyle -1\leqslant \mathbb {R} _{X,Y}\leqslant 1}.
- Коэффициент корреляции равен ±1{\displaystyle \pm 1} тогда и только тогда, когда X{\displaystyle X} и Y{\displaystyle Y} линейно зависимы (исключая события нулевой вероятности, когда несколько точек «выбиваются» из прямой, отражающей линейную зависимость случайных величин):
- RX,Y=±1⇔Y=kX+b,k≠0{\displaystyle \mathbb {R} _{X,Y}=\pm 1\Leftrightarrow Y=kX+b,k\neq 0},
- где k,b∈R{\displaystyle k,b\in \mathbb {R} }. Более того в этом случае знаки RX,Y{\displaystyle \mathbb {R} _{X,Y}} и k{\displaystyle k} совпадают:
- sgnRX,Y=sgnk{\displaystyle \operatorname {sgn} \mathbb {R} _{X,Y}=\operatorname {sgn} k}.
Виды корреляции
Виды корреляционной связи между измеренными переменными могут быть различны: так корреляция бывает линейной и нелинейной, положительной и отрицательной. Она линейна, если с увеличением или уменьшением одной переменной, вторая переменная также растёт, либо убывает. Она нелинейна, если при увеличении одной величины характер изменения второй не линеен, а описывается другими законами (полиномиальная, гиперболическая).
Если повышение уровня одной переменной сопровождается повышением уровня другой, то речь идет о положительной корреляции. Чем выше личностная тревожность, тем больше риск заболеть язвой желудка. Возрастание громкости звука сопровождается ощущением повышения его тона.
Если рост уровня одной переменной сопровождается снижением уровня другой, то мы имеем дело с отрицательной корреляцией. По данным Зайонца, число детей в семье отрицательно коррелирует с уровнем их интеллекта. Чем боязливей особь, тем меньше у нее шансов занять доминирующее положение в группе. Нулевой называется корреляция при отсутствии связи переменных.
Отрицательная и положительная корреляция
Некоторые виды коэффициентов корреляции могут быть положительными или отрицательными (возможна также ситуация отсутствия статистической взаимосвязи — например, для независимых случайных величин). Если предполагается, что на значениях переменных задано отношение строгого порядка, то отрицательная корреляция—корреляция, при которой увеличение одной переменной связано с уменьшением другой переменной, при этом коэффициент корреляции может быть отрицательным;положительная корреляцияв таких условиях —корреляция, при которой увеличение одной переменной связано с увеличением другой переменной, при этом коэффициент корреляции может быть положительным. В практической деятельности, когда число коррелируемых пар признаков Х и Y невелико, то при оценке зависимости между показателями используется следующую градацию: 1) высокая степень взаимосвязи – значения коэффициента корреляции находится в пределах от 0,7 до 0,99; 2) средняя степень взаимосвязи – значения коэффициента корреляции находится в пределах от 0,5 до 0,69; 3) слабая степень взаимосвязи – значения коэффициента корреляции находится от 0,2 до 0,49.
Самостоятельное вычисление корреляции
Интересно было посмотреть, зависит ли каким-либо образом количество медалистов от заработной платы преподавателей школ в субъектах РФ. Чтобы это посмотреть, нужно самостоятельно вычислить корреляции. Процесс вычисления можно упростить, воспользовавшись Microsoft Excel: достаточно лишь ввести численные данные различных стран по уровню доходов и уровню рождаемости за какой-либо период и воспользоваться специальной функцией.
Опишем процесс подсчета корреляции. Для начала соберем численные данные интересующих нас показателей и сгруппируем их в таблицу, состоящую из двух столбцов. Первый из них содержит данные о средней заработной плате преподавателей, а второй — об количественном соотношении числа медалистов к числу всех выпускников. Каждая строка таблицы будет соответствовать определенному субъекту РФ. В конце столбцов в пустой ячейке впишем «=КОРРЕЛ». Затем выделим данные в одном столбце, поставим знак “;” и выделим второй столбец. Полученная цифра соответствует искомому значению корреляции.
ТОП 10: |
Взаимосвязь между временем, посвященным занятиям, и оценками является примером положительной корреляции. Приведенные ниже данные, полученные в ходе гипотетического исследования восьми студентов, говорят о наличии положительной корреляции. В данном случае первой переменной является время, операционально определенное как количество часов в неделю, потраченных на учебу, а второй — средний балл (СБ), варьирующийся от 0,0 до 4,0.
Значительное время, потраченное на учебу (42 часа), связано с высоким средним баллом (3,3), а самое малое время (16 часов) — с низким баллом (1,9). Примером отрицательной корреляции может быть взаимосвязь между бесполезно потраченным временем и средним баллом. Бесполезно потраченное время можно операционально определить как количество часов в неделю, потраченное на определенные занятия, например на игру в видеоигры, просмотр телесериалов или игру в гольф (конечно, эти виды деятельности можно назвать и «терапией»). Ниже приведены гипотетические данные для других восьми студентов. На этот раз вы увидите обратную взаимосвязь между количеством часов в неделю, потраченных впустую, и средним баллом:
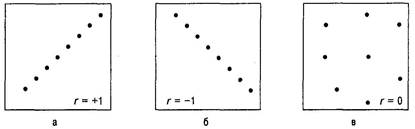
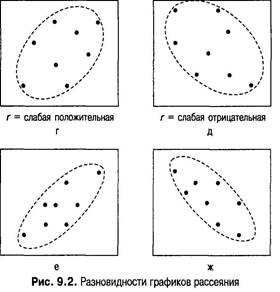
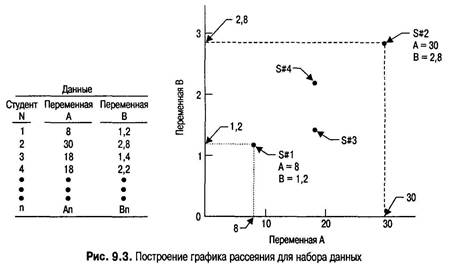
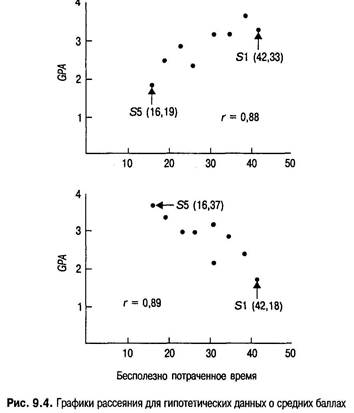
Обратите внимание, что при отрицательной корреляции переменные имеют обратную взаимосвязь: большое количество потраченного зря времени (42) связано с низким средним баллом (1,8), а небольшое (16) — с более высоким (3,7). Силу корреляции показывает особая величина описательной статистики, носящая название «коэффициент корреляции». Коэффициент корреляции равен-1,00 в случае прямой отрицательной корреляции, 0,00 при отсутствии взаимосвязи и +1,00 при полной положительной корреляции. Наиболее распространенным коэффициентом корреляции является пирсоново г (о нем упоминалось во вставке 9.1), названное так в честь британского ученого, соперничающего в известности с сэром Рональдом Фишером. Пирсоново г вычисляется для данных, полученных с помощью интервальной шкалы или шкалы отношений. В случае других шкал измерений рассматриваются другие виды корреляции. К примеру, для порядковых данных (т. е. упорядоченных) вычисляется «ро» Спирмена. В приложении С показано, как вычислять пирсоново г. Так же как среднее арифметическое и стандартное отклонение, коэффициент корреляции является величиной описательной статистики. В ходе заключительного анализа определяется, является ли конкретная корреляция значимо большей (или меньшей) нуля. Таким образом, для корреляционных исследований нулевая гипотеза (Н0) говорит, что действительное значение г равно 0 (т. е. нет никаких взаимосвязей), а альтернативная гипотеза (Н,) — что г№ 0. Отвергнуть нулевую гипотезу — значит решить, что между двумя переменными существует значимая взаимосвязь. В приложении График рассеяния Силу корреляции можно обнаружить, рассмотрев современную версию построенной Гальтоном таблицы (рис. 9.1) — график рассеяния.Он является графическим отображением взаимосвязи, на которую указывает корреляция. Как показано на рис. 9.2, в случае полной положительной (9.2, а) или полной отрицательной (9.2, б) корреляции точки образуют прямую линию, а нулевая корреляция дает график рассеяния (9.2, в), точки которого распределены случайным образом. По сравнению с относительно слабой корреляцией (9.2, гид) точки сравнительно сильной расположены ближе друг к другу (9.2, ж и з). В целом, по мере ослабления корреляции точки на графике рассеяния все больше удаляются от диагонали, связывающей точки при полной корреляции, равной +1,00 или -1,00. На рис. 9.3 показано, как по набору данных создается график рассеяния, а на рис. 9.4 приведены графики рассеяния для гипотетических примеров со средними баллами. Они отображают сильную положительную корреляцию между временем, потраченным на учебу, и средним баллом, а также сильную отрицательную корреляцию между бесполезно потраченным временем и средним баллом. Значения коэффициента корреляции равны +0,88 и -0,89 соответственно. Преподаватель может попросить вас проверить эти значения пирсонова
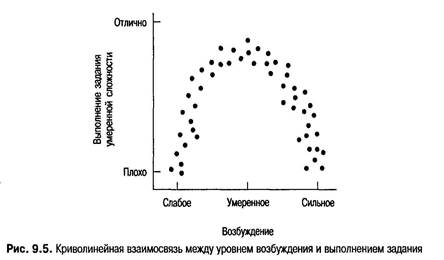
Допущение линейности До сих пор изучаемые нами графики рассеяния состояли из точек, несколько отклоняющихся от прямой линии, которая образуется при полной корреляции со значениями -1,00 или +1,00. Однако не все взаимосвязи линейны, а вычисление пирсонова г для нелинейного случая не поможет выявить природу такой взаимосвязи. На рис. 9.5 показан гипотетический пример, отражающий одно известное психологическое открытие: взаимосвязь между возбуждением и выполнением задания. Сложные задания выполняются хорошо при среднем уровне возбуждения, но гораздо хуже при очень низком или очень высоком (см., например, Anderson, 1990). При очень низком уровне возбуждения у человека недостаточно сил, чтобы работать над заданием, а очень высокое возбуждение мешает эффективной обработке информации, требующейся для выполнения работы. Из графика рассеяния видно, что точки ложатся вдоль определенной кривой, но при попытке применить линейную корреляционную процедуру вы получите, что г равно нулю или очень близко к нему. Анализ криволинейных взаимосвязей, подобных изображенной на рис. 9.5, проводится особыми методами, рассмотрение которых не входит в задачу данной книги.
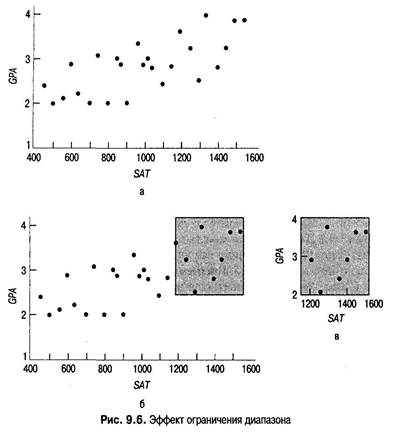
Ограничение диапазона При проведении корреляционного исследования важно учитывать людей, оценки которых попадают в широкий диапазон. Ограничение диапазонаодной или обеих переменных снижает корреляцию. Подобный эффект показан на рис. 9.6. Предположим, вы изучаете взаимосвязь между оценками SA Т (американский школьный тест проверки способностей) и успеваемостью в колледже (последняя оценивается по средним баллам, полученным первокурсниками в конце года). На рис. 9.6, а показано, каким может быть график рассеяния при исследовании 25 студентов. Коэффициент корреляции равен +0,70. Допустим далее, что вы решили изучить эту взаимосвязь на примере студентов, получивших 1200 и более баллов по тесту SAT На рис. 9.6, б выделены точки графика рассеяния для таких студентов — как показано на рис. 9.6, в, по ним можно построить отдельный график. Если вы теперь сравните рис. 9.6, а и 9.6, в, вам станет ясно, что для 9.6, в корреляция ниже. Действительно, она падает до +0,26. Этот пример имеет интересное следствие для колледжей, которые не учитывают студентов, чьи суммарные оценки теста SAT меньше 1200 баллов. Различные исследования (например, Schrader, 1971) показали, что общая корреляция между оценками SATn баллами, полученными в конце первого курса, равная приблизительно +4,0, является статистически значимой, но не высокой. Корреляцию находили, используя студентов с самыми разными оценками теста SAT. Если диапазон оценок SAT ограничен 1200 баллами и выше, то корреляция заметно снижается. Существуют особые процедуры для «коррекции» корреляции с учетом проблемы ограничения, но необходимо осознавать, что ограничение диапазона непосредственно влияет на возможность строить предположения о дальнейших событиях. Учебные заведения, проводящие строгий отбор и отсеивающие абитуриентов с результатами теста 5!А Г ниже 1200 баллов, без сомнения получат хороших студентов, но их возможность предсказать учебную успеваемость на основании оценок SAT будет не такой высокой, как у заведений, не предъявляющих таких высоких требо- ваний к абитуриентам. В вузах, имеющих меньше ограничений по отбору студентов, корреляция оценок SAТп академической успеваемости будет выше, чем в учебных заведениях со строгими ограничениями.
Коэффициент детерминации — г2 Довольно легко неверно понять смысл конкретного значения пирсонова г. Если оно равняется +0,70, то взаимосвязь действительно является относительно сильной, но студенты иногда думают, что +0,70 каким-то образом связано с 70%, и считают, что в таком случае взаимосвязь установлена на 70%. Это неверно. Для интерпретации значения корреляции гораздо правильнее использовать коэффициент детерминации (г2). Он находится возведением в квадрат пирсонова г, а поэтому вне зависимости от типа корреляции (положительной или отрицательной) его значение никогда не бывает отрицательным. Данный коэффициент формально определяется как степень изменчивости одной переменной корреляции, вызванная изменчивостью другой переменной. Поясним это на конкретном примере. Предположим, вы проводите исследование, в ходе которого у 100 участников измеряется уровень эмоциональной депрессии и средний балл. Вы проверяете вза-
|
имосвязь между двумя переменными и обнаруживаете отрицательную корреляцию: чем выше уровень депрессии, тем ниже средний балл, и наоборот, чем слабеедепрессия тем выше средний балл. Рассмотрим два значения корреляции, которыемогут быть получены в результате этого исследования, 1,00 и -0,50. Коэффициент детерминации будет равен 1,00 и 0,25 соответственно. Чтобы понять смыслэтих значений, для начала обратим внимание на то, что средний балл у 100 изучаемых людей, скорее всего, будет варьироваться от 0,0 до 4,0. Как исследователи, мыхотим выяснить причину такой изменчивости — почему один человек получает 3,8балла, а другой 2,4 и т. д. Другими словами, мы хотим узнать, что вызывает индивидуальные различия в средних баллах? В действительности, причиной этомуможет быть несколько факторов: учебные привычки, общий уровень интеллекта,эмоциональная устойчивость, склонность к выбору легких предметов для изучения и т. д. Как показывают оценки теста на депрессию, в нашем гипотетическомисследовании изучается один из этих факторов — эмоциональная устойчивость. Нпоказывает, насколько изменчивость средних баллов может быть связана непосредственно с депрессией. В первом случае, когда г = -1,00, а г2 = 1,00, мы можемприйти к выводу, что 100% изменчивости средних баллов связана с изменчивостьюоценок депрессии. Следовательно, можно сказать, что 100% различий между средними баллами (3,8 и 2,4 и др.) вызваны депрессией. В реальном исследовании такой результат, конечно, невозможно получить. Во втором случае, когда г = -0,5,а г2 = 0,25, только одна четверть (25%) изменчивости средних баллов будет связанас депрессией. Остальные 75% связаны с другими факторами, подобными перечисленным выше. Говоря кратко, коэффициент детерминации лучше характеризуетсилу отношений, чем пирсоново г.Корреляции в дипломных работах по психологии
Термин «корреляция» активно используется в гуманитарных науках, медицине; часто мелькает в СМИ. Ключевую роль корреляции играют в психологии. В частности, расчет корреляций выступает важным этапом реализации эмпирического исследования при написании ВКР по психологии.
Материалы по корреляциям в сети слишком научны. Неспециалисту трудно разобраться в формулах. В то же время понимание смысла корреляций необходимо маркетологу, социологу, медику, психологу – всем, кто проводит исследования на людях.
В этой статье мы простым языком объясним суть корреляционной связи, виды корреляций, способы расчета, особенности использования корреляции в психологических исследованиях, а также при написании дипломных работ по психологии.
Содержание
Что такое корреляция
Численное выражение корреляционной связи
Корреляционный анализ в психологии
Коэффициенты корреляции Пирсона и Спирмена
Как рассчитать коэффициент корреляции
Использование корреляционного анализа в дипломных работах по психологии
Что такое корреляция
Корреляция – это связь. Но не любая. В чем же ее особенность? Рассмотрим на примере.
Представьте, что вы едете на автомобиле. Вы нажимаете педаль газа – машина едет быстрее. Вы сбавляете газ – авто замедляет ход. Даже не знакомый с устройством автомобиля человек скажет: «Между педалью газа и скоростью машины есть прямая связь: чем сильнее нажата педаль, тем скорость выше».
Это зависимость функциональная – скорость выступает прямой функцией педали газа. Специалист объяснит, что педаль управляет подачей топлива в цилиндры, где происходит сжигание смеси, что ведет к повышению мощности на вал и т.д. Это связь жесткая, детерминированная, не допускающая исключений (при условии, что машина исправна).
Теперь представьте, что вы директор фирмы, сотрудники которой продают товары. Вы решаете повысить продажи за счет повышения окладов работников. Вы повышаете зарплату на 10%, и продажи в среднем по фирме растут. Через время повышаете еще на 10%, и опять рост. Затем еще на 5%, и опять есть эффект. Напрашивается вывод – между продажами фирмы и окладом сотрудников есть прямая зависимость – чем выше оклады, тем выше продажи организации. Такая же это связь, как между педалью газа и скоростью авто? В чем ключевое отличие?
Правильно, между окладом и продажами заисимость не жесткая. Это значит, что у кого-то из сотрудников продажи могли даже снизиться, невзирая на рост оклада. У кого-то остаться неизменными. Но в среднем по фирме продажи выросли, и мы говорим – связь продаж и оклада сотрудников есть, и она корреляционная.
В основе функциональной связи (педаль газа – скорость) лежит физический закон. В основе корреляционной связи (продажи – оклад) находится простая согласованность изменения двух показателей. Никакого закона (в физическом понимании этого слова) за корреляцией нет. Есть лишь вероятностная (стохастическая) закономерность.
Численное выражение корреляционной зависимости
Итак, корреляционная связь отражает зависимость между явлениями. Если эти явления можно измерить, то она получает численное выражение.
Например, изучается роль чтения в жизни людей. Исследователи взяли группу из 40 человек и измерили у каждого испытуемого два показателя: 1) сколько времени он читает в неделю; 2) в какой мере он считает себя благополучным (по шкале от 1 до 10). Ученые занесли эти данные в два столбика и с помощью статистической программы рассчитали корреляцию между чтением и благополучием. Предположим, они получили следующий результат -0,76. Но что значит это число? Как его проинтерпретировать? Давайте разбираться.
Полученное число называется коэффициентом корреляции. Для его правильной интерпретации важно учитывать следующее:
- Знак «+» или «-» отражает направление зависимости.
- Величина коэффициента отражает силу зависимости.
Прямая и обратная
Знак плюс перед коэффициентом указывает на то, что связь между явлениями или показателями прямая. То есть, чем больше один показатель, тем больше и другой. Выше оклад — выше продажи. Такая корреляция называется прямой, или положительной.
Если коэффициент имеет знак минус, значит, корреляция обратная, или отрицательная. В этом случае чем выше один показатель, тем ниже другой. В примере с чтением и благополучием мы получили -0,76, и это значит, что, чем больше люди читают, тем ниже уровень их благополучия.
Сильная и слабая
Корреляционная связь в численном выражении – это число в диапазоне от -1 до +1. Обозначается буквой «r». Чем выше число (без учета знака), тем корреляционная связь сильнее.
Чем ниже численное значение коэффициента, тем взаимосвязь между явлениями и показателями меньше.
Максимально возможная сила зависимости – это 1 или -1. Как это понять и представить?
Рассмотрим пример. Взяли 10 студентов и измерили у них уровень интеллекта (IQ) и успеваемость за семестр. Расположили эти данные в виде двух столбцов.
Испытуемый | IQ | Успеваемость (баллы) |
1 | 90 | 4,0 |
2 | 91 | 4,1 |
3 | 92 | 4,2 |
4 | 93 | 4,3 |
5 | 94 | 4,4 |
6 | 95 | 4,5 |
7 | 96 | 4,6 |
8 | 97 | 4,7 |
9 | 98 | 4,8 |
10 | 99 | 4,9 |
Посмотрите внимательно на данные в таблице. От 1 до 10 испытуемого растет уровень IQ. Но также растет и уровень успеваемости. Из любых двух студентов успеваемость будет выше у того, у кого выше IQ. И никаких исключений из этого правила не будет.
Перед нами пример полного, 100%-но согласованного изменения двух показателей в группе. И это пример максимально возможной положительной взаимосвязи. То есть, корреляционная зависимость между интеллектом и успеваемостью равна 1.
Рассмотрим другой пример. У этих же 10-ти студентов с помощью опроса оценили, в какой мере они ощущают себя успешными в общении с противоположным полом (по шкале от 1 до 10).
Испытуемый | IQ | Успех в общении с противоположным полом (баллы) |
1 | 90 | 10 |
2 | 91 | 9 |
3 | 92 | 8 |
4 | 93 | 7 |
5 | 94 | 6 |
6 | 95 | 5 |
7 | 96 | 4 |
8 | 97 | 3 |
9 | 98 | 2 |
10 | 99 | 1 |
Смотрим внимательно на данные в таблице. От 1 до 10 испытуемого растет уровень IQ. При этом в последнем столбце последовательно снижается уровень успешности общения с противоположным полом. Из любых двух студентов успех общения с противоположным полом будет выше у того, у кого IQ ниже. И никаких исключений из этого правила не будет.
Это пример полной согласованности изменения двух показателей в группе — максимально возможная отрицательная взаимосвязь. Корреляционная связь между IQ и успешностью общения с противоположным полом равна -1.
А как понять смысл корреляции равной нулю (0)? Это значит, связи между показателями нет. Еще раз вернемся к нашим студентам и рассмотрим еще один измеренный у них показатель – длину прыжка с места.
Испытуемый | IQ | Длина прыжка с места (м) |
1 | 90 | 2,5 |
2 | 91 | 1,2 |
3 | 92 | 2,0 |
4 | 93 | 1,7 |
5 | 94 | 1,9 |
6 | 95 | 1,3 |
7 | 96 | 1,7 |
8 | 97 | 2,3 |
9 | 98 | 1,1 |
10 | 99 | 2,6 |
Не наблюдается никакой согласованности между изменением IQ от человека к человеку и длинной прыжка. Это и свидетельствует об отсутствии корреляции. Коэффициент корреляции IQ и длины прыжка с места у студентов равен 0.
Мы рассмотрели крайние случаи. В реальных измерениях коэффициенты редко бывают равны точно 1 или 0. При этом принята следующая шкала:
- если коэффициент больше 0,70 – связь между показателями сильная;
- от 0,30 до 0,70 – связь умеренная,
- меньше 0,30 – связь слабая.
Если оценить по этой шкале полученную нами выше корреляцию между чтением и благополучием, то окажется, что эта зависимость сильная и отрицательная -0,76. То есть, наблюдается сильная отрицательная связь между начитанностью и благополучием. Что еще раз подтверждает библейскую мудрость о соотношении мудрости и печали.
Приведенная градация дает очень приблизительные оценки и в таком виде редко используются в исследованиях.
Чаще используются градации коэффициентов по уровням значимости. В этом случае реально полученный коэффициент может быть значимым или не значимым. Определить это можно, сравнив его значение с критическим значением коэффициента корреляции, взятым из специальной таблицы. Причем эти критические значения зависят от численности выборки (чем больше объем, тем ниже критическое значение).
Корреляционный анализ в психологии
Корреляционный метод выступает одним из основных в психологических исследованиях. И это не случайно, ведь психология стремится быть точной наукой. Получается ли?
В чем особенность законов в точных науках. Например, закон тяготения в физике действует без исключений: чем больше масса тела, тем сильнее оно притягивает другие тела. Этот физический закон отражает связь массы тела и силы притяжения.
В психологии иная ситуация. Например, психологи публикуют данные о связи теплых отношений в детстве с родителями и уровня креативности во взрослом возрасте. Означает ли это, что любой из испытуемых с очень теплыми отношениями с родителями в детстве будет иметь очень высокие творческие способности? Ответ однозначный – нет. Здесь нет закона, подобного физическому. Нет механизма влияния детского опыта на креативность взрослых. Это наши фантазии! Есть согласованность данных (отношения – креативность), но за ними нет закона. А есть лишь корреляционная связь. Психологи часто называют выявляемые взаимосвязи психологическими закономерностями, подчеркивая их вероятностный характер — не жесткость.
Пример исследования на студентах из предыдущего раздела хорошо иллюстрирует использование корреляций в психологии:
- Анализ взаимосвязи между психологическими показателями. В нашем примере IQ и успешность общения с противоположным полом – это психологические параметры. Выявление корреляции между ними расширяет представления о психической организации человека, о взаимосвязях между различными сторонами его личности – в данном случае между интеллектом и сферой общения.
- Анализ взаимосвязей IQ с успеваемостью и прыжками – пример связи психологического параметра с непсихологическими. Полученные результаты раскрывают особенности влияния интеллекта на учебную и спортивную деятельность.
Вот как могли выглядеть краткие выводы по результатам придуманного исследования на студентах:
- Выявлена значимая положительная зависимость интеллекта студентов и их успеваемости.
- Существует отрицательная значимая взаимосвязь IQ с успешностью общения с противоположным полом.
- Не выявлено связи IQ студентов с умением прыгать с места.
Таким образом, уровень интеллекта студентов выступает позитивным фактором их академической успеваемости, в то же время негативно сказываясь на отношениях с противоположным полом и не оказывая значимого влияния на спортивные успехи, в частности, способность к прыгать с места.
Как видим, интеллект помогает студентам учиться, но мешает строить отношения с противоположным полом. При этом не влияет на их спортивные успехи.
Неоднозначное влияние интеллекта на личность и деятельность студентов отражает сложность этого феномена в структуре личностных особенностей и важность продолжения исследований в этом направлении. В частности, представляется важным провести анализ взаимосвязей интеллекта с психологическими особенностями и деятельностью студентов с учетом их пола.
Коэффициенты Пирсона и Спирмена
Рассмотрим два метода расчета.
Коэффициент Пирсона – это особый метод расчета взаимосвязи показателей между выраженностью численных значений в одной группе. Очень упрощенно он сводится к следующему:
- Берутся значения двух параметров в группе испытуемых (например, агрессии и перфекционизма).
- Находятся средние значения каждого параметра в группе.
- Находятся разности параметров каждого испытуемого и среднего значения.
- Эти разности подставляются в специальную форму для расчета коэффициента Пирсона.
Коэффициент ранговой корреляции Спирмена рассчитывается похожим образом:
- Берутся значения двух индикаторов в группе испытуемых.
- Находятся ранги каждого фактора в группе, то есть место в списке по возрастанию.
- Находятся разности рангов, возводятся в квадрат и суммируются.
- Далее разности рангов подставляются в специальную форму для вычисления коэффициента Спирмена.
В случае Пирсона расчет шел с использованием среднего значения. Следовательно, случайные выбросы данных (существенное отличие от среднего), например, из-за ошибки обработки или недостоверных ответов могут существенно исказить результат.
В случае Спирмена абсолютные значения данных не играют роли, так как учитывается только их взаимное расположение по отношению друг к другу (ранги). То есть, выбросы данных или другие неточности не окажут серьезного влияния на конечный результат.
Если результаты тестирования корректны, то различия коэффициентов Пирсона и Спирмена незначительны, при этом коэффициент Пирсона показывает более точное значение взаимосвязи данных.
Как рассчитать коэффициент корреляции
Коэффициенты Пирсона и Спирмена можно рассчитать вручную. Это может понадобиться при углубленном изучении статистических методов.
Однако в большинстве случаев при решении прикладных задач, в том числе и в психологии, можно проводить расчеты с помощью специальных программ.
Расчет с помощью электронных таблиц Microsoft Excel
Вернемся опять к примеру со студентами и рассмотрим данные об уровне их интеллекта и длине прыжка с места. Занесем эти данные (два столбца) в таблицу Excel.
Переместив курсор в пустую ячейку, нажмем опцию «Вставить функцию» и выберем «КОРРЕЛ» из раздела «Статистические».
Формат этой функции предполагает выделение двух массивов данных: КОРРЕЛ (массив 1; массив»). Выделяем соответственно столбик с IQ и длиной прыжков.
Далее нажимаем галочку (то есть, рассчитать) и получаем значение , в нашем случае 0,038. Как видим, коэффициент не равен нулю, хотя и очень близок к нему.
В таблицах Excel реализована формула расчета только коэффициента Пирсона.
Расчет с помощью программы STATISTICA
Заносим данные по интеллекту и длине прыжка в поле исходных данных. Далее выбираем опцию «Непараметрические критерии», «Спирмена». Выделяем параметры для расчета и получаем следующий результат.
Как видно, расчет дал результат 0,024, что отличается от результата по Пирсону – 0,038, полученной выше с помощью Excel. Однако различия незначительны.
Использование корреляционного анализа в дипломных работах по психологии (пример)
Большинство тем выпускных квалификационных работ по психологии (дипломов, курсовых, магистерских) предполагают проведение корреляционного исследования (остальные связаны с выявлением различий психологических показателей в разных группах).
Сам термин «корреляция» в названиях тем звучит редко – он скрывается за следующими формулировками:
- «Взаимосвязь субъективного ощущения одиночества и самоактуализации у женщин зрелого возраста»;
- «Особенности влияния жизнестойкости менеджеров на успешность их взаимодействия с клиентами в конфликтных ситуациях»;
- «Личностные факторы стрессоустойчивости сотрудников МЧС».
Таким образом, слова «взаимосвязь», «влияние» и «факторы» — верные признаки того, что методом анализа данных в эмпирическом исследовании должен быть корреляционный анализ.
Рассмотрим кратко этапы его проведения при написании дипломной работы по психологии на тему: «Взаимосвязь личностной тревожности и агрессивности у подростков».
1. Для расчета необходимы сырые данные, в качестве которых обычно выступают результаты тестирования испытуемых. Они заносятся в сводную таблицу и помещаются в приложение. Эта таблица устроена следующим образом:
- каждая строка содержит данные на одного испытуемого;
- каждый столбец содержит показатели по одной шкале для всех испытуемых.
№ испытуемого | Личностная тревожность | Агрессивность |
1 | 12 | 24 |
2 | 14 | 25 |
3 | 11 | 13 |
4 | 17 | 19 |
5 | 21 | 29 |
6 | 26 | 29 |
7 | 13 | 16 |
8 | 16 | 20 |
8 | 13 | 24 |
9 | 18 | 21 |
10 | 23 | 31 |
2. Необходимо решить, какой из двух типов коэффициентов — Пирсона или Спирмена — будет использоваться. Напоминаем, что Пирсон дает более точный результат, но он чувствителен к выбросам в данных Коэффициенты Спирмена могут использоваться с любыми данными (кроме номинативной шкалы), поэтому именно они чаще всего используют в дипломах по психологии.
3. Заносим таблицу сырых данных в статистическую программу.
4. Рассчитываем значение.
5. На следующем этапе важно определить, значима ли взаимосвязь. Статистическая программа подсветила результаты красным, что означает, что корреляция статистически значимы при уровне значимости 0,05 (указано выше).
Однако полезно знать, как определить значимость вручную. Для этого понадобится таблица критических значений Спирмена.
Таблица критических значений коэффициентов Спирмена
Уровень статистической значимости | |||
Число испытуемых | р=0,05 | р=0,01 | р=0,001 |
5 | 0,88 | 0,96 | 0,99 |
6 | 0,81 | 0,92 | 0,97 |
7 | 0,75 | 0,88 | 0,95 |
8 | 0,71 | 0,83 | 0,93 |
9 | 0,67 | 0,8 | 0,9 |
10 | 0,63 | 0,77 | 0,87 |
11 | 0,6 | 0,74 | 0,85 |
12 | 0,58 | 0,71 | 0,82 |
13 | 0,55 | 0,68 | 0,8 |
14 | 0,53 | 0,66 | 0,78 |
15 | 0,51 | 0,64 | 0,76 |
Нас интересует уровень значимости 0,05 и объем нашей выборки 10 человек. На пересечении этих данных находим значение критического Спирмена: Rкр=0,63.
Правило такое: если полученное эмпирическое значение Спирмена больше либо равно критическому, то он статистически значим. В нашем случае: Rэмп (0,66) > Rкр (0,63), следовательно, взаимосвязь между агрессивностью и тревожностью в группе подростков статистически значима.
5. В текст дипломной нужно вставлять данные в таблице формата word, а не таблицу из статистической программы. Под таблицей описываем полученный результат и интерпретируем его.
Таблица 1
Коэффициенты Спирмена агрессивности и тревожности в группе подростков
| Агрессивность |
Личностная тревожность | 0,665* |
* — статистически достоверна (р≤0,05)
Анализ данных, приведенных в таблице 1, показывает, что существует статистически значимая положительная связьмежду агрессивностью и тревожностью подростков. Это означает, что чем выше личностная тревожность подростков, тем выше уровень их агрессивности. Такой результат дает основание предположить, что агрессия для подростков выступает одним из способов купирования тревожности. Испытывая неуверенность в себе, тревогу в связи с угрозами самооценке, особенно чувствительной в подростковом возрасте, подросток часто использует агрессивное поведение, таким непродуктивным способом снижая тревогу.
6. Можно ли при интерпретации связей говорить о влиянии? Можно ли сказать, что тревожность влияет на агрессивность? Строго говоря, нет. Выше мы показали, что корреляционная связь между явлениями носит вероятностный характер и отражает лишь согласованность изменений признаков в группе. При этом мы не можем сказать, что эта согласованность вызвана тем, что одно из явлений является причиной другого, влияет на него. То есть, наличие корреляции между психологическими параметрами не дает оснований говорить о существовании между ними причинно-следственной связи. Однако практика показывает, что термин «влияние» часто используется при анализе результатов корреляционного анализа.
© СтудентуПсихологу.рф
Линейный коэффициент корреляции Пирсона | statanaliz.info
Обнаружение взаимосвязей между явлениями – одна из главных задач статистического анализа. На то есть две причины. Первая. Если известно, что один процесс зависит от другого, то на первый можно оказывать влияние через второй. Вторая. Даже если причинно-следственная связь отсутствует, то по изменению одного показателя можно предсказать изменение другого.
Взаимосвязь двух переменных проявляется в совместной вариации: при изменении одного показателя имеет место тенденция изменения другого. Такая взаимосвязь называется корреляцией, а раздел статистики, который занимается взаимосвязями – корреляционный анализ.
Корреляция – это, простыми словами, взаимосвязанное изменение показателей. Она характеризуется направлением, формой и теснотой. Ниже представлены примеры корреляционной связи.
Далее будет рассматриваться только линейная корреляция. На диаграмме рассеяния (график корреляции) изображена взаимосвязь двух переменных X и Y. Пунктиром показаны средние.
При положительном отклонении X от своей средней, Y также в большинстве случаев отклоняется в положительную сторону от своей средней. Для X меньше среднего, Y, как правило, тоже ниже среднего. Это прямая или положительная корреляция. Бывает обратная или отрицательная корреляция, когда положительное отклонение от средней X ассоциируется с отрицательным отклонением от средней Y или наоборот.
Линейность корреляции проявляется в том, что точки расположены вдоль прямой линии. Положительный или отрицательный наклон такой линии определяется направлением взаимосвязи.
Крайне важная характеристика корреляции – теснота. Чем теснее взаимосвязь, тем ближе к прямой точки на диаграмме. Как же ее измерить?
Складывать отклонения каждого показателя от своей средней нет смысла, получим нуль. Похожая проблема встречалась при измерении вариации, а точнее дисперсии. Там эту проблему обходят через возведение каждого отклонения в квадрат.
Квадрат отклонения от средней измеряет вариацию показателя как бы относительно самого себя. Если второй множитель в числителе заменить на отклонение от средней второго показателя, то получится совместная вариация двух переменных, которая называется ковариацией.
Чем больше пар имеют одинаковый знак отклонения от средней, тем больше сумма в числителе (произведение двух отрицательных чисел также дает положительное число). Большая положительная ковариация говорит о прямой взаимосвязи между переменными. Обратная взаимосвязь дает отрицательную ковариацию. Если количество совпадающих по знаку отклонений примерно равно количеству не совпадающих, то ковариация стремится к нулю, что говорит об отсутствии линейной взаимосвязи.
Таким образом, чем больше по модулю ковариация, тем теснее линейная взаимосвязь. Однако значение ковариации зависит от масштаба данных, поэтому невозможно сравнивать корреляцию для разных переменных. Можно определить только направление по знаку. Для получения стандартизованной величины тесноты взаимосвязи нужно избавиться от единиц измерения путем деления ковариации на произведение стандартных отклонений обеих переменных. В итоге получится формула коэффициента корреляции Пирсона.
Показатель имеет полное название линейный коэффициент корреляции Пирсона или просто коэффициент корреляции.
Коэффициент корреляции показывает тесноту линейной взаимосвязи и изменяется в диапазоне от -1 до 1. -1 (минус один) означает полную (функциональную) линейную обратную взаимосвязь. 1 (один) – полную (функциональную) линейную положительную взаимосвязь. 0 – отсутствие линейной корреляции (но не обязательно взаимосвязи). На практике всегда получаются промежуточные значения. Для наглядности ниже представлены несколько примеров с разными значениями коэффициента корреляции.
Таким образом, ковариация и корреляция отражают тесноту линейной взаимосвязи. Последняя используется намного чаще, т.к. является относительным показателем и не имеет единиц измерения.
Диаграммы рассеяния дают наглядное представление, что измеряет коэффициент корреляции. Однако нужна более формальная интерпретация. Эту роль выполняет квадрат коэффициента корреляции r2, который называется коэффициентом детерминации, и обычно применяется при оценке качества регрессионных моделей. Снова представьте линию, вокруг которой расположены точки.
Линейная функция является моделью взаимосвязи между X иY и показывает ожидаемое значение Y при заданном X. Коэффициент детерминации – это соотношение дисперсии ожидаемых Y (точек на прямой линии) к общей дисперсии Y, или доля объясненной вариации Y. При r = 0,1 r2 = 0,01 или 1%, при r = 0,5 r2 = 0,25 или 25%.
Выборочный коэффициент корреляции
Коэффициент корреляции обычно рассчитывают по выборке. Значит, у аналитика в распоряжении не истинное значение, а оценка, которая всегда ошибочна. Если выборка была репрезентативной, то истинное значение коэффициента корреляции находится где-то относительно недалеко от оценки. Насколько далеко, можно определить через доверительные интервалы.
Согласно Центральное Предельной Теореме распределение оценки любого показателя стремится к нормальному с ростом выборки. Но есть проблемка. Распределение коэффициента корреляции вблизи придельных значений не является симметричным. Ниже пример распределения при истинном коэффициенте корреляции ρ = 0,86.
Предельное значение не дает выйти за 1 и, как бы «поджимает» распределение справа. Симметричная ситуация наблюдается, если коэффициент корреляции близок к -1.
В общем рассчитывать на свойства нормального распределения нельзя. Поэтому Фишер предложил провести преобразование выборочного коэффициента корреляции по формуле:
Распределение z для тех же r имеет следующий вид.
Намного ближе к нормальному. Стандартная ошибка z равна:
Далее исходя из свойств нормального распределения несложно найти верхнюю и нижнюю границы доверительного интервала для z. Определим квантиль стандартного нормального распределения для заданной доверительной вероятности, т.е. количество стандартных отклонений от центра распределения.
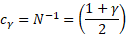
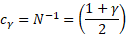
cγ – квантиль стандартного нормального распределения;
N-1 – функция обратного стандартного распределения;
γ – доверительная вероятность (часто 95%).
Затем рассчитаем границы доверительного интервала.
Нижняя граница z:
Верхняя граница z:
Теперь обратным преобразованием Фишера из z вернемся к r.
Нижняя граница r:
Верхняя граница r:
Это была теоретическая часть. Переходим к практике расчетов.
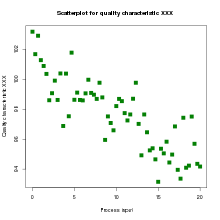
Как посчитать коэффициент корреляции в Excel
Корреляционный анализ в Excel лучше начинать с визуализации.
На диаграмме видна взаимосвязь двух переменных. Рассчитаем коэффициент парной корреляции с помощью функции Excel КОРРЕЛ. В аргументах нужно указать два диапазона.
Коэффициент корреляции 0,88 показывает довольно тесную взаимосвязь между двумя показателями. Но это лишь оценка, поэтому переходим к интервальному оцениванию.
Расчет доверительного интервала для коэффициента корреляции в Excel
В Эксель нет готовых функций для расчета доверительного интервала коэффициента корреляции, как для средней арифметической. Поэтому план такой:
— Делаем преобразование Фишера для r.
— На основе нормальной модели рассчитываем доверительный интервал для z.
— Делаем обратное преобразование Фишера из z в r.
Удивительно, но для преобразования Фишера в Excel есть специальная функция ФИШЕР.
Стандартная ошибка z легко подсчитывается с помощью формулы.
Используя функцию НОРМ.СТ.ОБР, определим квантиль нормального распределения. Доверительную вероятность возьмем 95%.
Значение 1,96 хорошо известно любому опытному аналитику. В пределах ±1,96σ от средней находится 95% нормально распределенных величин.
Используя z, стандартную ошибку и квантиль, легко определим доверительные границы z.
Последний шаг – обратное преобразование Фишера из z назад в r с помощью функции Excel ФИШЕРОБР. Получим доверительный интервал коэффициента корреляции.
Нижняя граница 95%-го доверительного интервала коэффициента корреляции – 0,724, верхняя граница – 0,953.
Надо пояснить, что значит значимая корреляция. Коэффициент корреляции статистически значим, если его доверительный интервал не включает 0, то есть истинное значение по генеральной совокупности наверняка имеет тот же знак, что и выборочная оценка.
Несколько важных замечаний
1. Коэффициент корреляции Пирсона чувствителен к выбросам. Одно аномальное значение может существенно исказить коэффициент. Поэтому перед проведением анализа следует проверить и при необходимости удалить выбросы. Другой вариант – перейти к ранговому коэффициенту корреляции Спирмена. Рассчитывается также, только не по исходным значениям, а по их рангам (пример показан в ролике под статьей).
2. Синоним корреляции – это взаимосвязь или совместная вариация. Поэтому наличие корреляции (r ≠ 0) еще не означает причинно-следственную связь между переменными. Вполне возможно, что совместная вариация обусловлена влиянием третьей переменной. Совместное изменение переменных без причинно-следственной связи называется ложная корреляция.
3. Отсутствие линейной корреляции (r = 0) не означает отсутствие взаимосвязи. Она может быть нелинейной. Частично эту проблему решает ранговая корреляция Спирмена, которая показывает совместный рост или снижение рангов, независимо от формы взаимосвязи.
В видео показан расчет коэффициента корреляции Пирсона с доверительными интервалами, ранговый коэффициент корреляции Спирмена.
↓ Скачать файл с примером ↓
Поделиться в социальных сетях:
Корреляционный анализ или Почему существуют странные корреляции / Habr
На данный опус меня навела публикация «Деньги, товар и немного статистики. Часть вторая», в которой автор исследовал зависимости между ценами на различные товары. Несколько смутило то, что несмотря на мастерское обращение с MatLab’ом, автор ни разу не упомянул об уровне значимости полученных корреляций. Ведь, связь между двумя величинами может и существовать, но если она статистически не значима, говорить о ней мы можем лишь в контексте рассуждений и домыслов.Пощупать данные «руками» долго не получалось, но вот выдался свободный час, и я, вооружившись R, двинулся в путь.
d = read.csv("data.csv", sep = ";") # загружаем данные
names(d) <- c("time","oil", "gold", "iron", "logs", "maize", "beef",
"chicken", "gas", "liquid_gas", "tea", "tobacco", "wheat", "sugar", "soy", "silver",
"rice", "platinum", "cotton", "copper", "coffee", "coal", "aluminum") # присваиваем удобочитаемые имена
# в своем посте автор использовал среднее геометрическое (СГ) - я пошел проторенной им тропой.
# так как в базовой комплектации R нет функции для расчета СГ, набросал свою:
gm_mean = function(x, na.rm=TRUE){
exp(sum(log(x[x > 0]), na.rm=na.rm) / length(x)) }
d.gm = apply(d[,2:23], 2, gm_mean) # получаем значение СГ для всех групп товаров
d.t = d[,2:23]/d.gm # получаем относительные цены
apply(d.t, 2, shapiro.test) # проверяем нормальность распределения
cor.m = cor(d.t, method = "spearman") # строим корреляционную матрицу
Немаловажный момент — распределение нормированных цен на все товары отличалось от нормального (р-значение для критерия Шапиро-Уилка значительно меньше 0.001), что неумолимо приводит нас к тому, что использование относительно «доброго» для поиска взаимосвязей коэффициента корреляции Пирсона не представляется возможным. К счастью, существует его непараметрический аналог — тест Спирмена.
Итак, корреляционная матрица получена. Взглянем на нее:
Окей, корреляции имеют место быть, хотя значения rho уже поменьше. Найдем наиболее высокие уровни и проверим их значимость:
out <- data.frame(X1 = rownames(cor.m)[-1],
X2 = head(colnames(cor.m), -1),
Value = cor.m[row(cor.m) == col(cor.m) + 1])
for(x in 1:length(out$X1)) {
print(
cor.test(
d.t[as.character(out[x,1])][[1]],
d.t[as.character(out[x,2])][[1]],
method = "sp")$p.value)
}
Для экономии места скажу, что для всех обнаруженных корреляционных взаимосвязей р-значение было меньше 0.0001, что говорит о статистически значимом явлении. Корреляционная матрица представлена ниже:
1 gold oil 0.2451402
2 iron gold 0.2503873
3 logs iron 0.2446200
4 maize logs 0.2547667
5 beef maize 0.2398418
6 chicken beef 0.2385301
7 gas chicken 0.2481030
8 liquid_gas gas 0.2544752
9 tea liquid_gas 0.2367907
10 tobacco tea 0.2416664
11 wheat tobacco 0.2553935
12 sugar wheat 0.2505641
13 soy sugar 0.2440920
14 silver soy 0.2589974
15 rice silver 0.2403048
16 platinum rice 0.2418105
17 cotton platinum 0.2343923
18 copper cotton 0.2498545
19 coffee copper 0.2321891
20 coal coffee 0.2482226
21 aluminum coal 0.2423581
Как видим, полученные rho не превышают 0.3, что указывает на слабую силу связи (согласно шкале Чеддока). Фактически, оперировать такими данными можно, но всегда нужно понимать, что колебания цен одного товара будет не боле чем на 10% сказываться на цене своего «партнера» по корреляции.
Хотелось бы отметить, что похожая линия рассуждений должна использоваться при анализе других странных корреляций. Цифры могут играть с нами злые шутки.
Спасибо jatx за то, что дал повод поиграть с цифрами!
Корреляция как показатель взаимосвязи между параметрами.
Научные термины пугают и притягивают одновременно. Термин «корреляция» все чаще можно встретить на страницах газет, по радио, на телевидении. Им козыряют экономисты, политологи, аналитики. Но, похоже, частота использования этого термина в СМИ отрицательно коррелирует с уровнем его понимания потребителями.
В переводе на простой язык, сказанная фраза означает следующее: «Чем чаще используется термин «корреляция», тем менее точным становится содержание этого понятия в сознании людей». В реальности, возможно, это и не так – исследования не проводились. Но важно другое – корреляция в обыденном понимании отражает взаимосвязь между явлениями.
Взаимосвязи вокруг нас
В человеке живет интуитивное ощущение взаимосвязи всех явлений. В фантастическом рассказе Рэя Брэдбери герой попадает в далекое прошлое и, нарушая запрет, сходит с тропы. Он лишь раздавил бабочку. Но вернулся в другой мир, с другим языком и даже президентом. Все связано вокруг…
При чем здесь корреляция? А при том, что пытливое сознание человека пытается выявлять корреляции. Зная взаимосвязи между явлениями, на них можно влиять, ими можно управлять.
Я не буду «грузить» вас математической терминологией, сложными формулами. Давайте разберемся в сути этого понятия; уясним что значит отрицательная и положительная корреляция; значимая и незначимая.
Понятие корреляции
Слово «корреляция» происходит от латинского «correlatio», что означает «соотношение» или «взаимосвязь».
Взаимосвязь присуща многим явлениям. Например, кепка, надетая на голову, связана с ней – куда голова, туда и кепка. Или палочка в руке дирижёра – они взаимосвязаны, и она послушна руке хозяина, полету его вдохновения. Но можно ли говорить, что их движения коррелируют между собой? Нет, и вот почему.
Функциональная связь
Палочка и рука взаимосвязаны и эта связь – функциональная. Она детерминирующая – жестко связывает между собой объекты. Если дирижёр сосредоточен и крепко держит палочку, то в их согласованном движении не будет моментов, когда которых рука движется в одну сторону, а палочку – в другую. Корреляционная связь совсем иной природы.
Посмотрим за спину нашего дирижёра. В зале сидят слушатели, любители музыки. Они испытывают какие-то эмоции. Их переживания, возможно, как-то связаны с уровнем их музыкального образования. Чем больше они знают про музыку, тем выше их эмоциональный отклик. Эта связь — корреляционная.
Корреляционная связь
В отличие от функциональной связи, корреляция отражает не жесткую зависимость между явлениями. Кто-то очень подкован теоретически, но эмоциональный отклик на музыку слабый. Другой мало образован, но его «пробило» на эмоции. Такая связь называется случайной, стохастической. И это сфера статистики – науки, занимающейся не отдельными явлениями, а массовыми.
Итак, корреляция отражает не функциональную, а статистическую случайную связь между явлениями (переменными). Почему случайную? Потому что заранее не известно, кто и как из слушателей будет реагировать на музыку. Но если статистический (массовый) расчет показал положительную корреляцию между образованностью и эмоциональным откликом, то это дает основания для важных выводов. Знание корреляционной связи позволяет предсказывать.
В данном примере мы с большой долей вероятности сможем утверждать, что из двух слушателей более эмоционально слушал тот, кто более образован. Это не будет однозначный вывод, ведь связь у нас не функциональная. Это будет вывод статистический, вероятностный – мы всегда можем ошибиться. Но вероятность этой ошибки не велика и заранее известна. Она называется «уровень статистической значимости». Как видим, без математики в этом вопросе все-таки не обойтись.
Коэффициент корреляции
В повседневной жизни, говоря о корреляции, например, успеха и затраченных усилий или ощущения счастья и материального достатка, мы опираемся на мифы, интуицию или досужие домыслы. Эти величины трудно измерить, перевести на язык цифр потом строго доказать их взаимосвязи. Но если мы имеем дело с явлениями, которые можно измерить, то здесь корреляцию можно рассчитать и получить коэффициент, который будет отражать силу и направление взаимосвязи.
Например, мы взяли группу из 20-ти человек и определили для каждого два параметра: возраст (посмотрели паспорт) и уровень оптимизма (провели психологический тестирование). Эти данные нужно занести в так называемую таблицу исходных данных и загрузить в статистическую программу. В итоге получим значение коэффициента корреляции. Не стоит пугаться этого числа, разгадать его тайны не так сложно.
Коэффициент корреляции может принимать численные значения в диапазоне от -1 до +1. Для анализа важны два показателя:
- Знак коэффициента корреляции (положительный или отрицательный).
- Абсолютное значение коэффициента корреляции (то есть, без учета знака, «по модулю»).
Отрицательная связь не значит плохая, положительная не значит хорошая
Если расчет корреляции между возрастом и оптимизмом среди испытуемых дал отрицательный показатель, это значит следующее: с годами растет оптимизм. То есть, чем выше возраст испытуемого, тем более оптимистично он смотрит на жизнь (мудрецы).
Но мы могли получить и обратный результат – отрицательную корреляцию между возрастом и оптимизмом. То есть, чем больше прожитых лет, тем меньше хорошего видится вокруг (скептики).
Если выборка подобрана правильно (репрезентативна), то она отражает ключевые особенности всех людей (или почти, например, живущих в большом городе). Тогда, полученные коэффициенты корреляции, дают важную информацию. Ее можно использовать, например, при приеме на работу. В случае положительной корреляции на должность менеджеров по продажам стоит брать людей постарше – они будут оптимистичны и доброжелательны.
Сила взаимосвязи – большая сила
Вы, наверное, уже догадались, что величина коэффициента корреляции отражает силу взаимосвязи между показателями. Чем больше численное значение по абсолютной величине (без учета знака), тем сила взаимосвязи больше.
Представим, что в нашей группе корреляция между возрастом и оптимизмом равна +1. Это значит, что, взяв любых двух человек из этой группы и узнав их возраст, мы точно сможем предсказать, кто из них более оптимистичен? Кстати, вы уже поняли кто? … Правильно, тот, кто старше.
А если корреляция равна -1, то в этой группе тот, кто моложе, более позитивно смотрит на мир. И это без всяких исключений! А вот если корреляция будет -0,9, значит в закономерности есть сбой — один или два человека в преклонных годах имеют высокий оптимизм. Они и нарушают общую закономерность и «снижают» коэффициент корреляции.
А теперь попробуйте сами объяснить, что значит, если коэффициент корреляции равен 0? Правильно, в этом случае никакой связи между переменными нет. Невозможно, зная возраст, предсказать позитивность взгляда на мир. И, наоборот, нельзя, зная оптимизм двоих испытуемых, сказать, кто старше. Но и эту информацию можно использовать. При поиске оптимистов для работы в «отделе бесперспективных проектов» не стоит смотреть на возраст.
Вывод
Надеюсь, теперь термин «корреляция» вас не пугает. Уверен, что вы сможете отличить функциональную связь (движение мышки и курсора) и корреляционную (время тренировок и высота прыжка). Имейте в виду, что, когда в обыденной речи просто говорят о корреляции, то имеют в виду положительную и значимую (достаточно высокую) взаимосвязь.
Этих знаний вполне хватит, чтобы понимать других и самому к месту ввернуть этот термин. Для более глубокого изучения необходимо разобраться, какие бывают коэффициенты корреляции, как их рассчитывать, как интерпретировать результаты. Это может быть полезно студентам, при проведении эмпирических исследований по психологии или социологии; при написании дипломных и курсовых.
Корреляции в дипломах по психологии
Коэффициент корреляции Пирсона
Коэффициент корреляции Спирмена
Надеюсь, эта статья поможет вам написать работу по психологии самостоятельно. Если понадобится помощь, обращайтесь (все виды работ по психологии; статистические расчеты). Заказать