Положительная корреляция отрицательная корреляция: Корреляция и коэффициент корреляции, корреляционная зависимость — inakhan.ru

Содержание

Корреляция — Психологос

Корреляция — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения одной или нескольких из этих величин приводят к систематическому изменению другой или других величин. Математической мерой корреляции двух случайных величин служит коэффициент корреляции.

Наличие корреляции ничего не говорит о том, что является причиной, а что следствием

Корреляция или причинно-следственная связь

Коэффицие́нт корреля́ции или парный коэффицие́нт корреля́ции в теории вероятностей и статистике — это показатель характера изменения двух случайных величин.

Корреляция может быть положительной и отрицательной (возможна также ситуация отсутствия статистической взаимосвязи — например, для независимых случайных величин).

Отрицательная корреляция — корреляция, при которой увеличение одной переменной связано с уменьшением другой переменной, при этом коэффициент корреляции отрицателен.

Положительная корреляция — корреляция, при которой увеличение одной переменной связано с увеличением другой переменной, при этом коэффициент корреляции положителен.

Автокорреляция — статистическая взаимосвязь между случайными величинами из одного ряда, но взятых со сдвигом, например, для случайного процесса — со сдвигом по времени.

Метод обработки статистических данных, заключающийся в изучении коэффициентов (корреляции) между переменными, называется корреляционным анализом.

Корреляция — что это такое простыми словами

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Когда некоторые люди слышат слово «корреляция», то зачастую просто впадают в ступор. Оно и понятно: жуткий термин из мира высшей математики и статистики.

Сразу представляются унылые графики, многоэтажные формулы, при взгляде на которые хочется забиться в угол и плакать. На самом деле все гораздо проще.

Потратив несколько минут на прочтение этой статьи, вы узнаете, что такое корреляция и как ее использовать в повседневной жизни.

Определение корелляции — что это

Простыми словами корреляция – это взаимосвязь двух или нескольких случайных параметров. Когда одна величина растет или уменьшается, другая тоже изменяется.

Объясним на примере: существует корреляция между температурой воздуха и потреблением мороженого. Чем жарче погода, тем больше холодного лакомства покупают люди. И наоборот.

Такие закономерности устанавливаются путем исследования больших объемов статистических данных. Собираем информацию о потреблении мороженого за несколько лет и сведения о колебаниях температуры за тот же период. А дальше сопоставляем и ищем зависимость.

Коррелировать – это значит быть взаимосвязанным с чем-то. Существует положительная и отрицательная корреляции.

При положительной чем больше один параметр, тем больше и другой. Например, чем масштабнее траты фермера на удобрения, тем обильнее урожай. При обратной корреляции рост одной величины сопровождается уменьшением другой. Чем выше здание, тем хуже оно противостоит землетрясениям.

Корреляция — это взаимосвязь без гарантий

Рассмотрим пример прямой корреляции: чем выше уровень благосостояния человека, тем больше его продолжительность жизни. Обеспеченные люди питаются качественной пищей и своевременно получают врачебную помощь. В отличие от бедняков.

Однако нельзя с уверенностью сказать, что определенный олигарх проживет дольше вот этого нищего.

Это лишь статистическая вероятность, которая может не сработать для одного конкретного случая. Этим корреляция отличается от линейной зависимости, где исход известен со 100-процентной вероятностью.

Но если мы возьмем выборку из сотни тысяч богачей и такого же числа малоимущих, сравним их продолжительность жизни, то общая тенденция будет верна.

Коэффициент корреляции

Это число, которое обозначается как «r». Оно находится в промежутке от -1 до 1. Отражает силу и полюс взаимосвязи величин. Посмотрим на примере:

Значение коэффициента	Какая корреляция?	О чем это говорит?
r=1	Сильная положительная корреляция	Люди, которые едят чернику, обладают острым зрением. Ешьте чернику!
r	Слабая положительная корреляция	Некоторые люди, которые любят чернику, обладают острым зрением. Но это не точно. Короче, ничего не пока понятно. Но лучше есть чернику на всякий случай.
r=0	Корреляция отсутствует	Черника и зрение никак не связаны.
r	Слабая отрицательная корреляция	Бывают случаи ухудшения зрения из-за черники. Не стоит рисковать.
r=-1	Сильная отрицательная корреляция	Практически все, кто ел чернику, ослепли. Берегитесь черники!

Величина коэффициента корреляции рассчитывается по формуле:

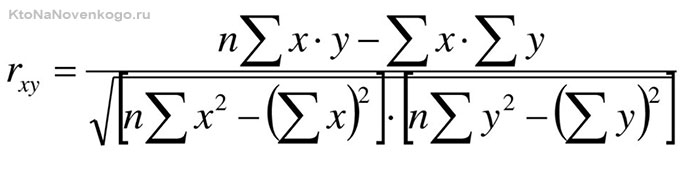
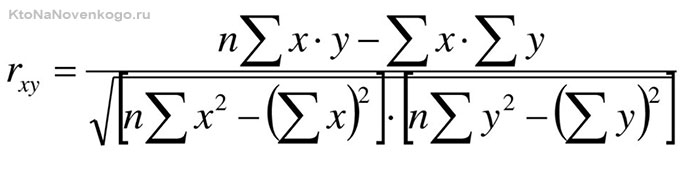
Если внезапно потемнело в глазах и возникло непреодолимое желание закрыть статью (синдром гуманитария), то есть вариант попроще. Microsoft Exel все выполнит сам при помощи функции «КОРРЕЛ». Делается это так:

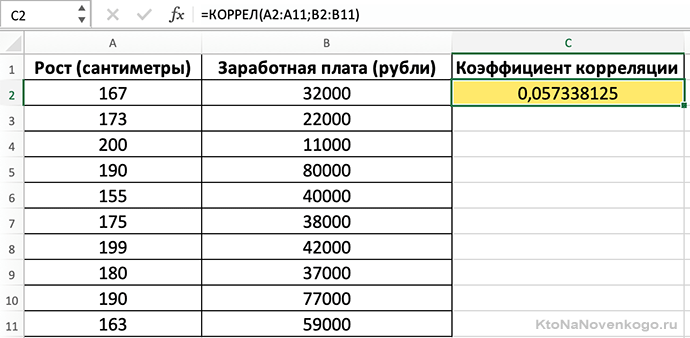
Судя по расчетам, рост человека практически никак не влияет на уровень зарплаты.

Реальные причины корреляции и возможные гипотезы

Курс доллара и стоимость нефти отрицательно коррелируют. Можем выдвинуть гипотезу: повышение цен на черное золото вызывает падение стоимости американской валюты. Но почему так происходит? Откуда взялась связь между этими явлениями?

Определение причины корреляции – это очень сложная задача. Переплетаются тысячи различных факторов, часть из которых скрыта.

Возможно, дело в том, что США – крупнейший потребитель нефти в мире. Каждый день они импортируют около 7,2 миллиона баррелей. Снижение цены на черное золото – хорошо для американской экономики, ведь позволяет тратить меньше денег. Следовательно, доллар растет.

Корреляция предоставляет возможность сделать вывод из статистических данных.

Например, мы выяснили, что существует отрицательная взаимосвязь между доходом персонала и его эффективностью в работе. Наша гипотеза: «Лентяи и бездельники получают больше, чем ответственные сотрудники». Тогда мы пересмотрим систему мотивации и избавимся от бесполезных людей.

Гипотеза – это лишь статистический вывод, предположение. Она вполне может оказаться ошибочной.

Согласно статистике, чем больше пожарных участвует в тушении огня, тем существенней размер ущерба. Какую гипотезу можем сделать отсюда? Пожарные приносят вред, давайте сократим их! Но если разобраться, то настоящая причина повреждения – это огонь. А увеличение числа лиц, задействованных в его тушении, – следствие масштаба пожара.

Наша вселенная бесконечна, а значит всегда можно найти несколько переменных, которые будут коррелировать между собой, несмотря на полное отсутствие причинно-следственных связей. Даже самое буйное воображение не сможет объяснить, что объединяет сыр и одеяло-убийцу:

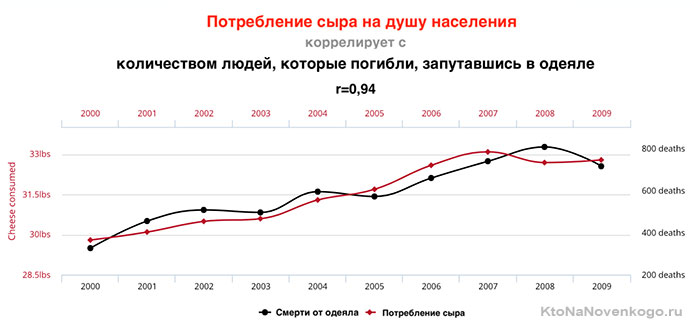
Более подробно на эту тему смотрите в видео:

Как при помощи корреляции люди становятся богаче

Главное правило любого инвестора: не класть все яйца в одну корзину. Вложения рекомендуется диверсифицировать (что это?) – распределять. Поэтому люди покупают акции не одной компании, а десятка разных, формируя инвестиционные портфели. Если котировки какой-то фирмы упадут, то оставшиеся девять смогут отыграть падение или хотя бы уменьшить убытки.

Но это в теории, а на практике все портит корреляция. Проблема в том, что стоимости акций разных компаний внутри отрасли или даже всей страны могут сильно коррелировать. Проблемы огромной корпорации провоцируют панику на рынке, снижают стоимость иных активов, на первый взгляд не связанных между собой. В 2008 году случился крах Lehman Brothers, который вызвал цепную реакцию и обвал на мировых рынках.

Поэтому при инвестировании нужно стараться выбирать направления, которые не связаны между собой (r стремится к 0).

Например, пара «золото – облигации США» = -0,13. Если собрать портфель из совершенно независимых частей, риски финансовых потерь сократятся.

Территориальное приближение активов друг к другу усиливает корреляцию. Значит, нужно рассматривать варианты в разных точках мира, максимально удаленных друг от друга.

В жизни этот принцип тоже действует. Если ваши навыки и знания позволяют трудиться программистом, таксистом, сантехником и журналистом – вы хорошо защищены от риска безработицы.

Памятка

Корреляция – это соотношение, взаимозависимость нескольких переменных.
Связь бывает положительной и отрицательной.
Коэффициент корреляции определяет степень взаимозависимости одной переменной от другой.
На основании корреляции люди выдвигают гипотезы (часто ошибочные).
Истинная причина корреляции порою скрыта под множеством факторов и внешних сил.
Бывает ложная корреляционная зависимость.
Раскладывая яйца по корзинам, помните о том, что они не должны коррелироваться друг с другом.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Использую для заработка

Рубрика: ЧАстые ВОпросы

Корреляция, корреляционная зависимость

Корреляция (от лат. correlatio), корреляционная зависимость — взаимозависимость двух или нескольких случайных величин. Суть ее заключается в том, что при изменении значения одной переменной происходит закономерное изменение (уменьшению или увеличению) другой(-их) переменной(-ых).

При расчете корреляций пытаются определить, существует ли статистически достоверная связь между двумя или несколькими переменными в одной или нескольких выборках. Например,

взаимосвязь между ростом и весом детей, взаимосвязь между успеваемостью и результатами выполнения теста IQ, между стажем работы и производительностью труда.

Важно понимать, что корреляционная зависимость отражает только взаимосвязь между переменными и не говорит о причинно-следственных связях. Например, если бы исследуемой выборке между ростом и весом человека существовала корреляционная зависимость то, это не значило бы, что вес является причиной роста человека, иначе сбрасывая лишние килограммы рост человека также уменьшался. Корреляционная связь лишь говорит о взаимосвязанности данных параметров, причем в данной конкретной выборке, в другой выборке мы можем не наблюдать полученные корреляции.

Показатель корреляции. Коэффициент корреляции (r) характеризует величину отражающую степень взаимосвязи двух переменных между собой. Он может варьировать в пределах от -1 (отрицательная корреляция) до +1 (положительная корреляция). Если коэффициент корреляции равен 0 то, это говорит об отсутствии корреляционных связей между переменными. Причем если коэффициент корреляции ближе к 1 (или -1) то говориться о сильной корреляции, а если ближе к 0, то о слабой.

При

положительной корреляции увеличение (или уменьшение) значений одной переменной ведет к закономерному увеличению (или уменьшению) другой переменной т.е. взаимосвязи типа увеличение-увеличение (уменьшение-уменьшение).

При отрицательной корреляции увеличение (или уменьшение) значений одной переменной ведет к закономерному уменьшению (или увеличению) другой переменной т.е. взаимосвязи типа увеличение-уменьшение (уменьшение-увеличение).

Корреляция (синонимы): соотношение, соотнесение, взаимосвязь, взаимозависимость, взаимообусловленность, взаимосоответствие.

Проведите корреляционный анализ за 5 минут

Онлайн сервис расчета статистики

17. Коэффициент корреляции Пирсона. — Нет здесь никого — LiveJournal

Функциональная и корреляционная зависимости.

Корреляция — связь между двумя переменными. Расчёт корреляции основан на формировании парных значений, которые образовываются из рассматриваемых зависимых выборок.

Метод вычисления коэффициента корреляции зависит от вида шкалы, к которой относятся переменные.

Переменные с метрической шкалой: коэффициент корреляции Пирсона.
По меньшей мере, одна из двух переменных имеет порядковую шкалу либо не является нормально распределённой: ранговая корреляция Спирмена.

Если данному значению одной величины соответствует вполне определенное значение другой, то говорят, что между этими величинами имеет место функциональная зависимость. Например, общий стаж работы y и стаж работы на данном предприятии x.

Часто случается так, что определенному значению одной величины соответствует целый комплекс значений другой, представляющий собой ряд распределения, причем при изменении данной величины меняется ряд распределения и его среднее. В таких случаях говорят о корреляционной зависимости. Она отражает тенденцию возрастания (положительная корреляция) или убывания (отрицательная корреляция) одной переменной величины при возрастании другой. Например, связь между ростом отцов и детей.

Корреляция Пирсона.

Данный коэффициент корреляции можно применять для метрических нормально распределенных переменных. Коэффициент корреляции говорит о том, насколько близко наблюдения лежат к некоторой прямой.

Основная гипотеза — об отсутствие линейной связи между переменными. При p < 0,05 гипотезу отвергаем.

Коэффициент корреляции может принимать значения от -1 до +1. При этом отрицательный коэффициент корреляции позволяет принять гипотезу о наличии линейной отрицательной связи, т.е. увеличение значения одной переменной в большинстве случаев соответствует уменьшению значения коррелирующей с ней переменной. Положительный коэффициент корреляции свидетельствует о положительной связи переменных: увеличение одной переменной соответствует увеличению

Механизм расчета тесноты и направленности корреляционной зависимости.

Корреляционная зависимость имеет место также между количеством удобрений и урожайностью, размером предприятий и себестоимостью, спросом на товары и ценой на рынке и т.д.

Корреляционная зависимость не является абсолютно точной, полной. В ней отражается множественность причин и следствий. Каждое явление находится под влиянием большого числа причин, действующих с разной силой. Изучая влияние Х на мы выделяем один фактор, но на данный признак Y оказывают влияние и многие другие, что обусловливает корреляционный характер зависимости.

Например, станем рассматривать влияние стажа на производительность труда рабочего Ясно, что стаж влияет на производительность, но не может определять ее полностью» так как на производительность влияют квалификация и образование, возраст и состояние здоровья и другие факторы. Таким образом, стаж далеко не единственный фактор производительности, связь между этими переменными корреляционная. И вообще: в силу сложности, многофакторности общественной жизни связи между социальными переменными практически всегда корреляционные.

Функциональная и корреляционная связи могут быть, а могут не быть причинно-следственными. Логическая природа рассматриваемых «сечений» (функциональная — корреляционная и причинно-следственная — не причинно-следственная) принципиально различна.

Рассмотрим пример. Как известно, между давлением Р, объемом V, абсолютной температурой Т и массой газа М существует функциональная зависимость

PV= CМT

(здесь С — константа)

Четыре величины P, V, Ч Т связаны функционально и вопрос о том, какая из них причина, какая следствие в общем случае лишен смысла. Однако в конкретной физической ситуации он может быть правомерным. допустим, что данная масса газа находится под постоянным давлением. (Сосуд закрыт поршнем с определенным «гнетом»). Начинаем нагревать сосуд. С увеличением Т будет увеличиваться V, причем каждому Т1 соответствует свое вполне определенное V_i. Значит, в случае функциональной зависимости такого рода причиной является нагревание, следствием — расширение объема. В упрощенной ситуации (при абстрагировании от ряда явлений, что часто законно) можно говорить о причинной зависимости между одной причиной и одним следствием.

В случае корреляционной связи все значительно сложнее. Здесь, как уже подчеркивалось, имеет место множественность причин: любое явление находится под влиянием большого числа факторов, каждый из которых имеет, вообще говоря, различную «силу». Наличие корреляции свидетельствует, что либо одно из двух выделяемых явлений есть частичная причина другого, либо оба явления — следствие общих причин. При этом «статистик, как таковой, будучи вполне компетентным в установлении корреляции между любыми величинами, к какой бы области они ни принадлежали, не компетентен в высказывании причинных суждений. для этого мало быть статистиком, а нужно быть биологом, медиком, метеорологом, экономистом и т.д., смотря по области исследования». Таким образом, установление корреляции еще не служит само по себе показателем существования причинно-следственной связи.

Проиллюстрируем эту мысль на примере. Для признаков X и Y задаваемых таблицей 13 коэффициент корелляции r=0.98, т.е. между X и Y есть значимая прямая связь. Здесь X — заработная плата школьных работников в миллионах долларов, а Y — общее потребление вина и ликеров в США в миллионах галлонов. Едва ли можно утверждать, что заработная плата школьных работников непосредственно зависит от потребления вина и ликеров или потребление винно-ликерных изделий от зарплаты школьных работников. Высокий коэффициент корреляции означает тесную линейную статистическую связь между двумя переменными и указывает лишь на возможную причинную связь.

Измерение корреляции — это часть проблемы, интерпретация результатов — другая, зачастую более трудная. Обсуждаемую корреляцию можно объяснить, обратившись к истории США. Период с 1870 г. по 1910 г. характеризовался бурным развитием экономики этой страны. Быстро увеличивалось население, развивались торговля, промышленность, сельское хозяйство. Росло число занятых во всех сферах хозяйства, росла и заработная плата (в частности — учителей). Росло потребление вообще (в частности — вин и ликеров).

Гипотеза критерия, значение и уровень значимости.

Основная гипотеза — об отсутствие линейной связи между переменными. При p < 0,05 гипотезу отвергаем.

Смысл и расчет доверительного интервала для значения.

Колонка Asymp. std. Error (стандартная ошибка) позволяет построить доверительный интервал для полученного значения r/

Недостатки коэффициента.

Корреляция · Loginom Wiki

Разделы: Бизнес-задачи, Алгоритмы
Loginom: Корреляционный анализ (обработчик), Статистика (визуализатор)

Статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения одной или нескольких из них приводят к систематическому изменению других. Математической мерой корреляции двух случайных величин служит коэффициент корреляции.

Некоторые виды корреляционных связей могут быть положительными или отрицательными (возможна также ситуация отсутствия статистической взаимосвязи, например, для независимых случайных величин).

Отрицательная корреляция имеет место, когда увеличение одной переменной связано с уменьшением другой. При положительной корреляции возрастание одной переменной вызывает увеличение другой.

Разновидностью корреляции является автокорреляция, которая характеризует статистическую взаимосвязь между случайными величинами из ряда, взятыми со сдвигом, например, временным. Модели, использующие автокорреляцию, широко применяются при прогнозировании временных рядов.

Исследования корреляционных зависимостей являются очень важными при построении аналитических моделей. Так, корреляция между входной и выходной переменными характеризует объясняющую способность модели.

Если поведение выходной переменной никак не связано с поведением входной (т.е. корреляционная связь между ними отсутствует), то такая модель обычно оказывается бесполезной. С другой стороны, наличие корреляции между входными переменными может вызвать серьезные проблемы, связанные с низкой точностью и неустойчивостью модели (мультиколлинеарность в регрессии), излишней размерностью и ее сложностью.

Впервые термин «корреляция» ввел в научный обиход французский палеонтолог Жорж Кювье. Значительный вклад в развитие теории корреляционного анализ внесли Френсис Гальтон, Карл Пирсон, Чарльз Спирмен, Морис Кендалл и другие.

Что такое корреляция и как ее считают?

Что такое корреляция?

Начнем с такого примера. Вы наполняете свой инвестиционный портфель различными инструментами (акциями, облигациями, чем-то еще), но неожиданно замечаете, что в процессе инвестирования все результаты движутся преимущественно в одну сторону. Т.е. вы получаете либо заметную доходность, либо существенный убыток.

Если первая ситуация нас радует, то вторая сильно печалит и мы начинаем задумываться, все ли сделали правильно. И хотя убытки, даже порой затяжные, это неизбежная ситуация реального инвестирования, при составлении нашего портфеля действительно была допущена ошибка, исправление которой поможет заметно улучшить суммарную доходность. Причем решение в данной ситуации представляется достаточно очевидным — портфель должен состоять из активов, которые ведут себя по возможности независимо друг от друга, хотя каждый по отдельности способен быть источником денежного потока.

Корреляция описывается числом в интервале от 1 до -1. Единица со знаком плюс означает абсолютно идентичное движение активов (к такой ситуации, например, близки котировки USD/RUB и EUR/RUB), и в этом случае говорят о полной или максимальной положительной корреляции. Минус один описывает полностью противоположенное поведение, когда рост одного актива всегда вызывает убыток другого — это максимально отрицательная корреляция. Оба варианта скорее идеальные случаи, так что отрицательной корреляцией считается любое негативное значение.

Значение около нуля говорит об отсутствии зависимости между котировками. Т.е. в общем корреляция рассчитывается на основании эмпирических данных — подобная функция есть в Экселе — и поэтому зависит от интервала рассмотрения активов. Корреляция финансовых инструментов имеется как на форекс, так и на фондовом рынке — рассмотрим их отдельно.

Корреляция на рынке форекс

На форекс представлено не такое уж большое число значимых соотношений — семь главных валютных пар уже охватят около 80% валютного рынка. Однако при хаотичном изменении котировок говорить о каком-то постоянном значении коэффициента корреляции валютных пар не приходится — оно полностью зависит от выбранного диапазона. Для иллюстрации этого подойдут две ссылки. Вот первая https://www.home.saxo/insights/tools/fx-correlations-table/tool-details:

Как видно, на настоящий момент тут можно оценить коэффициенты корреляции почти за три года. Причем над таблицей слева находится ползунок, перемещая который можно увидеть, как менялась корреляция валютных пар с периода отсчета (сейчас это 17 ноября 2012) до произвольной даты в течение последнего года. При перемещении этого ползунка будет заметно, что ряд валют не только сильно меняет свое значение, но порой изменяется и сам знак корреляции.

Аналогично можно выбрать периоды за последние 30 и 90 дней — почти наверняка многие показатели в ячейках не будут иметь ничего общего с прежними значениями. Кроме того, очень наглядно корреляция на форекс показана здесь: https://www1.oanda.com/lang/ru/forex-trading/analysis/currency-correlation:

Видно, что в большинстве случаев в течение года валютные пары меняли не только величину, но и знак корреляции к выбранной для сравнения паре (евро/доллар) на противоположенный. Щелчком по другой валютной паре в таблице можно выбрать ее в качестве эталона сравнения.

Корреляция на фондовом рынке

Переходя к фондовому рынку, в первую очередь необходимо обратить внимание на несравненно большее число инструментов, поскольку в принципе каждую акцию (и облигацию) можно рассматривать как отдельный актив. Таблица корреляции каждой акции друг к другу только на американском рынке привела бы к совершенно астрономическим цифрам — слава богу, в распоряжении инвестора есть такой инструмент как ETF, который помогает вложиться в произвольный индекс, отражающий экономику целого государства или даже региона, например Европы.

ETF позволяет широко диверсифицировать капитал — например, биржевой фонд с тикером SPY включает в себя 500 акций компаний США. Но не менее важным является то, что имея простой инструмент для вложения мы можем сравнить индексы различных стран друг с другом (пример — американский S&P500, российский РТС, немецкий DAX и др.) и на выходе получить относительную простую таблицу с достаточно ясными возможностями для инвестирования.

Ложка (и немалая) дегтя в том, что и на фондовом рынке коэффициенты корреляции финансовых инструментов не отличаются постоянством. Однако, в отличие от валютных пар, эти изменения обычно происходят медленнее и находятся в менее широком диапазоне (как будет показано ниже, историческая корреляция американских акций и облигаций с 1930 года описывалась интервалом от +0.5 до -0.5). Рассмотрим корреляцию российских и зарубежных активов (расчеты Сергея Наумова):

Здесь приведена корреляция российских и зарубежных активов на периоде в 17 лет до 2014 года. Из нее видно, что например российские акции и облигации имеют высокую корреляцию друг с другом (их котировки движутся как правило в одном направлении), тогда как золото и зарубежные облигации имели к российским акциям скорее противоположенное движение, т.е. отрицательную корреляцию.

Следовательно, разбавляя американские активы российскими с включением доли золота, можно было бы на первый взгляд добиться сглаживания доходности — однако на практике мы получили бы не просто более ровную кривую, а заметный дополнительный бонус. Посмотрим на таблицу ниже:

Так называемый «портфель лежебоки» — это портфель, включающий равные доли российских акций, облигаций и золота. При этом сравнивая доходность всех четырех портфелей можно увидеть, что она оказалась заметно выше, чем просто арифметическое среднее активов по отдельности! Как такое возможно?

Объяснение этому было дано еще в начале 50-х годов Г. Марковицем, который 30 лет спустя получил за свою теорию Нобелевскую премию — а сама теория стала основой портфельного инвестирования, наряду с понятием о корреляции активов. Согласитесь, что получать в течение 17 лет доходность на уровне 35% в год не позволяет ни один банк — такие предложения делаются лишь откровенными пирамидами. Тем не менее следующий слайд, берущий те же активы, но за другой период, хорошо иллюстрирует высказывание, как прошлая доходность не гарантирует будущей:

Как видно, здесь доходность портфелей представляет уже скорее среднее значение, хотя и лежащее гораздо ближе к верхней границе, чем к нижней; причем риски в этом случае оказываются ниже, чем в прошлой таблице. Откуда такие расхождения? В плане доходности стоит вспомнить огромный рывок российского рынка в 1999 году, когда паи облигаций выросли на невероятные 1800% — и вплоть до 2008 года российский рынок почти непрерывно рос, давая по несколько десятков процентов годовых.

Основной пик пришелся именно на 1999-2000 год. Однако после кризиса 2008 года последовала почти обратная ситуация — несколько восстановившись в 2009 году, в следующие годы даже рублевый индекс ММВБ не сумел достичь своего максимума, а номинированный в долларах РТС и вовсе после декабря 2014 отправился почти к уровню просадки 2008 года. Следовательно, несмотря на отрицательную корреляцию к американскому, российский рынок просто оказался не самым удачным активом, который с 2003 по 2014 годы показал среднюю доходность даже чуть ниже инфляции.

И это является важным фактором, который необходимо учесть — только нулевая или отрицательная корреляция не обеспечит кумулятивный эффект, если хотя бы один из активов будет показывать стагнацию или тем более негативную доходность. Идея именно в том, что в целом доходны оба актива, но проявляется это в разные периоды времени. Поэтому если в качестве развивающегося рынка в дополнение к американскому и европейскому добавлять российские активы, то нужно иметь в виду, что должный эффект, показанный в первой таблице, проявится лишь в случае возобновления роста.

Следовательно, нужно не только учитывать корреляцию, но и в идеальном случае представлять экономические возможности своих активов. При этом на американском рынке аналогичный портфель за почти 50 лет показал те же результаты, что и акции, однако с заметно меньшим риском:

Если же рассмотреть те же данные с 1925 года, то картина немного изменится: хотя доходность по акциям останется почти на том же уровне (9%, т.е. только на 10% меньше), но золото даст результат, близкий к 5% (что меньше почти на 40%). Соответственно, пострадает и портфельный результат: американский «лежебока» с 1925 года даст доходность лишь немногим более 7%, уже заметнее уступая акциям. Поэтому вывод ожидаем: волшебного портфеля нет, а российский лежебока в ближайшие годы скорее всего будет постепенно терять свой громадный отрыв, приближаясь к средним рыночным значениям.

Зависимость корреляции от времени

Как уже упоминалось выше, корреляция не является константой и сама меняется в зависимости от времени. К примеру, корреляция между акциями США и пятилетними гос. облигациями с 1926 по 2013 годы была равна 0.07 — т.е. зависимость почти не прослеживалась. Однако на истории корреляция колебалась от -0,5 до +0,5, причем в XX веке после Великой Депрессии она находилась в отрицательной зоне лишь с середины 50-х по середину 60-х годов. В период с 1970-1985 корреляция акций и облигаций была равна 0.3%, тогда как с 2002-2013 обратной по знаку:

Таким образом, задача поиска доходности зависит от двух неизвестных: корреляции и доходности активов на рассматриваемом промежутке, причем эта доходность достигается с различным риском (отклонением от среднего значения). Отрицательная корреляция в общем случае позволяет достигать большей доходности с меньшим риском по сравнению с менее доходным активом:

Фонд А — менее волатильный и менее доходный актив (облигации), фонд Б — более волатильный и доходный (акции). Стандартное отклонение определяет размах колебаний относительно среднего значения актива. Такое соотношение, как на рисунке выше, наблюдается на длинной истории — однако в пределах десятилетий может довольно сильно меняться:

Видно, что на протяжении 2000-2009 годов американские акции даже ушли в минус, в результате чего кривая получила движение вниз, а не вверх. Следовательно, корреляция ничего не говорит об абсолютной доходности — первая может мало меняться на протяжении 20 лет, однако результаты одинаковых портфелей на следующих друг за другом 10-летних промежутках разойдутся.

Так, в кризисные 70-е и растущие 80-е корреляция американских акций и 5-летних облигаций была в среднем одинакова (около 0.25), однако доходность портфеля 50 на 50 во втором случае была 15% годовых, а в первом лишь около 7%. Ниже отдельно показаны наилучшее и наихудшее американское десятилетие с 1950 года:

Как видим, отрицательная корреляция с 2000 года явилась причиной заметного выгиба кривой влево, в результате чего 5% доходности могли быть достигнуты с очень низким риском. Несомненно важным для инвестора является и корреляция других активов — в первую очередь американского и европейского рынков, стран Азии и пр. Детальный подход показывает разницу в их движениях — и следовательно, необходимость учитывать в своем портфеле рынки разных стран.

Корреляционный анализ или Почему существуют странные корреляции / Хабр

На данный опус меня навела публикация «Деньги, товар и немного статистики. Часть вторая», в которой автор исследовал зависимости между ценами на различные товары. Несколько смутило то, что несмотря на мастерское обращение с MatLab’ом, автор ни разу не упомянул об уровне значимости полученных корреляций. Ведь, связь между двумя величинами может и существовать, но если она статистически не значима, говорить о ней мы можем лишь в контексте рассуждений и домыслов.

Пощупать данные «руками» долго не получалось, но вот выдался свободный час, и я, вооружившись R, двинулся в путь.

d = read.csv("data.csv", sep = ";") # загружаем данные
names(d) <- c("time","oil", "gold", "iron", "logs", "maize", "beef",
              "chicken", "gas", "liquid_gas", "tea", "tobacco", "wheat", "sugar", "soy", "silver",
              "rice", "platinum", "cotton", "copper", "coffee", "coal", "aluminum") # присваиваем удобочитаемые имена

# в своем посте автор использовал среднее геометрическое (СГ) - я пошел проторенной им тропой.
# так как в базовой комплектации R нет функции для расчета СГ, набросал свою:
gm_mean = function(x, na.rm=TRUE){
  exp(sum(log(x[x > 0]), na.rm=na.rm) / length(x)) }

d.gm = apply(d[,2:23], 2, gm_mean) # получаем значение СГ для всех групп товаров
d.t = d[,2:23]/d.gm # получаем относительные цены
apply(d.t, 2, shapiro.test) # проверяем нормальность распределения
cor.m = cor(d.t, method = "spearman") # строим корреляционную матрицу

Немаловажный момент — распределение нормированных цен на все товары отличалось от нормального (р-значение для критерия Шапиро-Уилка значительно меньше 0.001), что неумолимо приводит нас к тому, что использование относительно «доброго» для поиска взаимосвязей коэффициента корреляции Пирсона не представляется возможным. К счастью, существует его непараметрический аналог — тест Спирмена.

Итак, корреляционная матрица получена. Взглянем на нее:

Окей, корреляции имеют место быть, хотя значения rho уже поменьше. Найдем наиболее высокие уровни и проверим их значимость:

out <- data.frame(X1 = rownames(cor.m)[-1],
                  X2 = head(colnames(cor.m), -1),
                  Value = cor.m[row(cor.m) == col(cor.m) + 1])

for(x in 1:length(out$X1)) {
  print(
    cor.test(
      d.t[as.character(out[x,1])][[1]],
      d.t[as.character(out[x,2])][[1]],
      method = "sp")$p.value)
  }

Для экономии места скажу, что для всех обнаруженных корреляционных взаимосвязей р-значение было меньше 0.0001, что говорит о статистически значимом явлении. Корреляционная матрица представлена ниже:

1 gold oil 0.2451402
2 iron gold 0.2503873
3 logs iron 0.2446200
4 maize logs 0.2547667
5 beef maize 0.2398418
6 chicken beef 0.2385301
7 gas chicken 0.2481030
8 liquid_gas gas 0.2544752
9 tea liquid_gas 0.2367907
10 tobacco tea 0.2416664
11 wheat tobacco 0.2553935
12 sugar wheat 0.2505641
13 soy sugar 0.2440920
14 silver soy 0.2589974
15 rice silver 0.2403048
16 platinum rice 0.2418105
17 cotton platinum 0.2343923
18 copper cotton 0.2498545
19 coffee copper 0.2321891
20 coal coffee 0.2482226
21 aluminum coal 0.2423581

Как видим, полученные rho не превышают 0.3, что указывает на слабую силу связи (согласно шкале Чеддока). Фактически, оперировать такими данными можно, но всегда нужно понимать, что колебания цен одного товара будет не боле чем на 10% сказываться на цене своего «партнера» по корреляции.

Хотелось бы отметить, что похожая линия рассуждений должна использоваться при анализе других странных корреляций. Цифры могут играть с нами злые шутки.

Спасибо jatx за то, что дал повод поиграть с цифрами!

Что такое корреляция? | Примеры корреляции

Корреляция — это термин, который является мерой силы линейной связи между двумя количественными переменными (например, ростом, весом). Этот пост определит положительных и отрицательных корреляций, проиллюстрированных примерами и объяснениями того, как измерить корреляцию. Наконец, будут обсуждены некоторые подводные камни, связанные с использованием корреляции.

P Позитивная корреляция — это взаимосвязь между двумя переменными, в которой обе переменные движутся в одном направлении. Это когда одна переменная увеличивается, а другая увеличивается, и наоборот. Например, положительная корреляция может означать, что чем больше вы тренируетесь, тем больше калорий вы сжигаете. В то время как отрицательная корреляция, — это соотношение, при котором одна переменная увеличивается, а другая уменьшается, и наоборот.

Там, где возможно с достаточно высоким уровнем точности предсказать значения одной переменной на основе значений другой, взаимосвязь между двумя переменными описывается как сильная корреляция . Слабая корреляция — это та, где в среднем значения одной переменной связаны с другой, но есть много исключений.

Корреляция продукта и момента Пирсона

Наиболее распространенной мерой корреляции является корреляция продукта-момента Пирсона , которую обычно называют просто корреляцией , , коэффициентом корреляции , или просто буквой r (всегда курсивом).Коэффициент корреляции Коэффициент r измеряет силу и направление линейной зависимости, например:

1 указывает на идеальную положительную корреляцию.
-1 указывает на идеальную отрицательную корреляцию.
0 указывает на отсутствие связи между различными переменными.

Значения от -1 до 1 обозначают силу корреляции, как показано в примере ниже.

Неправильная интерпретация корреляций

Практически все общие проблемы, которые могут сделать статистический анализ бессмысленным, могут возникнуть из-за корреляций.

Одним из примеров распространенной проблемы является то, что с небольшими выборками корреляции могут быть ненадежными. Чем меньше размер выборки, тем больше вероятность того, что мы увидим корреляцию, которая дальше от 0, даже если истинная корреляция (полученная, если бы у нас были данные для всей генеральной совокупности) была равна 0. Стандартный способ количественной оценки — использовать р-значение. В академических исследованиях распространено практическое правило: когда p больше 0,05, корреляции нельзя доверять.

Другая проблема, проиллюстрированная на верхнем левом графике ниже, заключается в том, что одно необычное наблюдение (выброс) может сильно ввести в заблуждение вычисленный коэффициент корреляции. Корреляции показывают только степень, в которой одна переменная может быть предсказана другой. Они не учитывают ситуации, когда разница в прогнозных значениях слишком мала, чтобы считаться полезной. Например, в ситуациях, когда размер эффекта может оказаться слишком маленьким, как показано в правом верхнем углу диаграммы ниже.

Другая проблема с корреляцией заключается в том, что она суммирует линейную зависимость. Если истинная зависимость нелинейна, то этого можно упустить. Еще одна проблема заключается в том, что очень высокие корреляции часто отражают тавтологию, а не интересующие результаты.

Хотите узнать больше? Узнайте, как визуализировать корреляцию с помощью корреляционной матрицы!

Создайте свою собственную корреляционную матрицу

Корреляция

Когда два набора данных прочно связаны друг с другом, мы говорим, что они имеют High Correlation .

Слово «Корреляция» состоит из Co- (что означает «вместе») и Relation

Корреляция Положительная , когда значения увеличиваются вместе на , и
Корреляция Отрицательная , когда одно значение уменьшается, , а другое увеличивается

Предполагается, что корреляция — линейная (после линии).

Корреляция может иметь значение:

1 — идеальная положительная корреляция
0 — корреляция отсутствует (значения вообще не связаны)
-1 — идеальная отрицательная корреляция

Значение показывает, насколько хороша корреляция (не насколько крутой является линия), и положительна она или отрицательна.

Пример: Продажа мороженого

В местном магазине мороженого отслеживается, сколько мороженого они продают, в зависимости от температуры в тот день. Вот их цифры за последние 12 дней:

Температура ° C	Продажа мороженого
*Продажи мороженого в зависимости от температуры*
14.2 °	$ 215
16,4 °	$ 325
11,9 °	$ 185
15,2 °	$ 332
18,5 °	406 долларов США
22,1 °	$ 522
19,4 °	$ 412
25,1 °	$ 614
23.4 °	$ 544
18,1 °	$ 421
22,6 °	445 долларов США
17,2 °	$ 408

А вот те же данные, что и точечная диаграмма:

Мы легко видим, что теплая погода и более высокие продажи идут рука об руку. Отношения хорошие, но не идеальные.

Фактически корреляция составляет 0,9575 …посмотрим в конце, как я это рассчитал.

Также попробуйте Калькулятор корреляции.

Неудовлетворительная корреляция на кривых

Вычисление корреляции правильно работает только для прямолинейных отношений.

Наше мороженое Пример: была жара!

Становится так жарко, что люди не подходят к магазину, и продажи начинают падать на .

Вот последний график:

Теперь значение корреляции 0 : «Нет корреляции»…!

Рассчитанное значение корреляции равно 0 (я вычислил), что означает «отсутствие корреляции».

Но мы видим, что данные следуют красивой кривой , которая достигает пика около 25 ° C.

Но вычисление корреляции недостаточно «умно», чтобы увидеть это.

Мораль истории: создайте точечный график и посмотрите на него!
Вы можете увидеть связь, которой нет в вычислении.

«Корреляция не является причинно-следственной связью»

Распространенная поговорка — «Корреляция не является причинно-следственной связью».

На самом деле означает , что корреляция не доказывает : одно вызывает другое:

Одно может вызвать другое
Другой может привести к первому
Они могут быть связаны разными вещами
Или это может быть случайность!

Может быть много причин, по которым данные имеют хорошую корреляцию.

Пример: солнцезащитные очки и мороженое

Наш магазин мороженого определяет, сколько солнцезащитных очков было продано в большом магазине за день, и сравнивает их с продажами мороженого:

Корреляция между продажами солнцезащитных очков и мороженого высока

Означает ли это, что солнцезащитные очки заставляют людей хотеть мороженого?

Пример. В бедных пригородах выше вероятность высокого уровня загрязнения.

Почему?

Бедные люди загрязняют окружающую среду?
Загрязненные пригороды — единственное место, которое могут себе позволить бедные люди?
Это обычное звено, такое как фабрики с низкооплачиваемой работой и большим загрязнением окружающей среды?

Пример: реальный случай!

Несколько лет назад опрос сотрудников выявил сильную положительную корреляцию между «Изучение внешнего курса» и больничных дней .

Означает ли это:

Учеба вызывает у них тошноту?
Больные много учатся?
Или они солгали о том, что заболели, чтобы больше учиться?

Без дополнительных исследований мы не можем понять, почему.

Как рассчитать

Как я вычислил значение 0,9575 вверху?

Я использовал «Корреляцию Пирсона». Существует программное обеспечение, которое может его вычислить, например функция CORREL () в Excel или LibreOffice Calc…

… а вот как рассчитать самому:

Назовем два набора данных «x» и «y» (в нашем случае температура x , а продажи мороженого y ):

Шаг 1. Найдите среднее значение x и среднее значение y

.
Шаг 2. Вычтите среднее значение x из каждого значения x (назовите их « a ») и вычтите среднее значение y из каждого значения y (назовите их « b »).
Шаг 3: Вычислить: ab , a ² и b ² для каждого значения
Шаг 4: Суммируем ab , суммируем a ² и суммируем b ²
Шаг 5. Разделите сумму ab на квадратный корень из [(сумма ²) × (сумма b ²)]

Вот как я рассчитал первый пример мороженого (значения округлены до 1 или 0 знаков после запятой):

В виде формулы это:

Где:

Σ — это сигма, символ «суммирования»
— каждое значение x минус среднее значение x (обозначенное выше «a»)
— каждое значение y за вычетом среднего значения y (выше обозначено буквой b)

Вам, вероятно, не придется так вычислять, но, по крайней мере, вы знаете, что это не «волшебство», а просто набор рутинных вычислений.

Примечание для программистов

Вы можете рассчитать это за один проход через данные. Просто просуммируйте x , y , x ² , y ² и xy (нет необходимости в a или b расчетах выше), затем используйте формулу:

Другие методы

Есть и другие способы вычисления коэффициента корреляции, например, «коэффициент ранговой корреляции Спирмена».

,
Примеры положительной корреляции
Чем больше времени вы проводите на беговой дорожке, тем больше калорий вы сжигаете.
Более высокие люди имеют больший размер обуви, а более низкие — меньшие.
Чем дольше растут волосы, тем больше шампуня вам понадобится.
Чем меньше времени я трачу на маркетинг своего бизнеса, тем меньше у меня будет новых клиентов.
Чем больше часов вы проводите под прямыми солнечными лучами, тем сильнее ваш солнечный ожог.
Чем больше денег она откладывает, тем в большей финансовой безопасности она себя чувствует.
С повышением температуры растут и продажи мороженого.
Когда сотрудник работает больше часов, его зарплата увеличивается пропорционально.
Чем больше бензина вы заправляете в машину, тем дальше он может проехать.
Чем дольше кто-то инвестирует, тем больше сложных процентов он заработает.
Чем больше времени вы проводите в ванне, тем более морщинистой становится ваша кожа.
По мере того, как идет больше снега, продажи антиобледенителей растут.
Чем больше вы пьете кофе, тем больше часов, в течение которых вы не спите.
По мере роста ребенка растет и размер его одежды.
По мере роста ее заработной платы увеличивались и ее расходы.
Чем больше идет дождь, тем выше продажи зонтов.
Более высокие люди обычно весят больше, а более низкие — меньше.
По мере того, как уровень счастья человека уменьшается, уменьшается и его полезность.
Люди, страдающие депрессией, чаще совершают самоубийства, чем те, кто этого не делает.
Чем больше людей идет в кино, тем больше денег тратится на билеты.
Когда рабочие получают повышение, моральный дух повышается.
По мере уменьшения протектора на шинах вашего автомобиля сцепление с дорогой уменьшается.
По мере снижения уровня воды в аквариуме, объем среды обитания рыб уменьшается.
Чем быстрее летит пилот реактивного самолета, тем выше перегрузки.
Чем больше вы тренируете мышцы, тем сильнее они становятся.
Когда сотрудники получают высокую зарплату, эффективность увеличивается.
По мере увеличения мощности лампочек световой поток увеличивается.
.
Примеры отрицательной корреляции
Отрицательная корреляция означает, что между двумя переменными существует обратная зависимость — когда одна переменная уменьшается, другая увеличивается. И наоборот, существует отрицательная корреляция, при которой одна переменная увеличивается, а другая уменьшается. Эти корреляции изучаются в статистике как средство определения взаимосвязи между двумя переменными.
У ученика, который много прогуливал, снижаются оценки.
По мере похолодания расходы на кондиционирование воздуха снижаются.
Если поезд увеличивает скорость, время, необходимое для достижения конечной точки, уменьшается.
Если курица становится старше, количество яиц, которые она производит, уменьшается.
Если солнце светит больше, дом с солнечными батареями требует меньше другого электричества.
Если на улице темнее, внутри требуется больше света.
Если автомобиль снижает скорость, время в пути до пункта назначения увеличивается.
Если в автомобильной шине больше воздуха, автомобиль может расходовать меньше бензина на милю.
Чем теплее на улице, тем меньше слоев одежды приходится носить, чтобы согреться.
Чем больше человек тренируется, тем меньше его вес.
Чем старше становится мужчина, тем меньше у него волос.
Чем больше человек работает, тем меньше у него свободного времени.
По мере взросления головастика его хвост становится меньше.
Чем дальше бежишь, тем медленнее может быть темп.
По мере повышения температуры продается меньше изделий из горячего шоколада.
По мере увольнения большего числа сотрудников удовлетворенность оставшихся сотрудников снижается.
По мере снижения температуры покупается больше нагревателей.
По мере того, как скорость байкера увеличивается, его время, чтобы добраться до финиша, уменьшается.
По мере увеличения наклона холма скорость, которую достигает пешеход, может уменьшаться.
Чем больше человек ест, тем меньше у него голод.
По мере увеличения влажности желание людей находиться на улице может уменьшаться.
По мере увеличения количества снегопадов количество людей, управляющих автомобилем, уменьшается.
С возрастом часто снижается ловкость.
Если температура на улице резко снизится, счета за отопление увеличатся.
Если житель использует больше мышеловок в доме, количество мышей в доме, вероятно, уменьшится.
Чем больше человек потребляет алкоголя, тем меньше у него рассудительности.
Чем больше окно закрыто занавесками, тем меньше света проникает в дом.
Чем больше убирается в доме, тем меньше вероятность появления вредителей.
Чем больше человек тренируется в тренажерном зале, тем меньше у него жира.
Чем больше человек выкурит сигарет, тем меньше лет ему придется прожить.
Чем больше человек бегает, тем меньше вероятность возникновения сердечно-сосудистых заболеваний.
Чем больше витаминов человек принимает, тем меньше вероятность дефицита.
Чем больше железа потребляет анемичный человек, тем меньше он устает.
Не каждое изменение дает положительный результат. Эти различные примеры отрицательной корреляции показывают, как многие вещи в реальном мире реагируют обратным образом.
.