Проблемные ситуации и алгоритмы их решения: Алгоритм решения проблемных ситуаций — inakhan.ru

Содержание

Проблемное обучение

Цель – способствовать развитию проблемного мышления учащихся и учителя.

Теоретические положения. Проблемное обучение – это такая организация педагогического процесса, когда ученик систематически включается учителем в поиск решения новых для него проблем. Структура процесса проблемного обучения представляет собой систему связанных между собой и усложняющихся проблемных ситуаций.

В психолого-педагогической литературе проблемное обучение рассматривают как фору активного обучения, которое базируется на психологических закономерностях; как обучение, в котором учащиеся систематически включаются в процесс решения проблем и проблемных задач, построенных на содержании программного материала; как тип развивающегося обучения, в котором сочетаются систематическая самостоятельная поисковая деятельность учащихся с усвоением ими готовых знаний.

Каждое из определений раскрывает одну из сторон проблемного обучения, а в сумме подчёркиваются главные признаки, которые лежат в основе моделирования уроков в режиме технологии проблемного обучения:

1) создание проблемных ситуаций,

2) обучение учащихся в процессе решения проблем,

3) сочетание поисковой деятельности и усвоения знаний в готовом виде.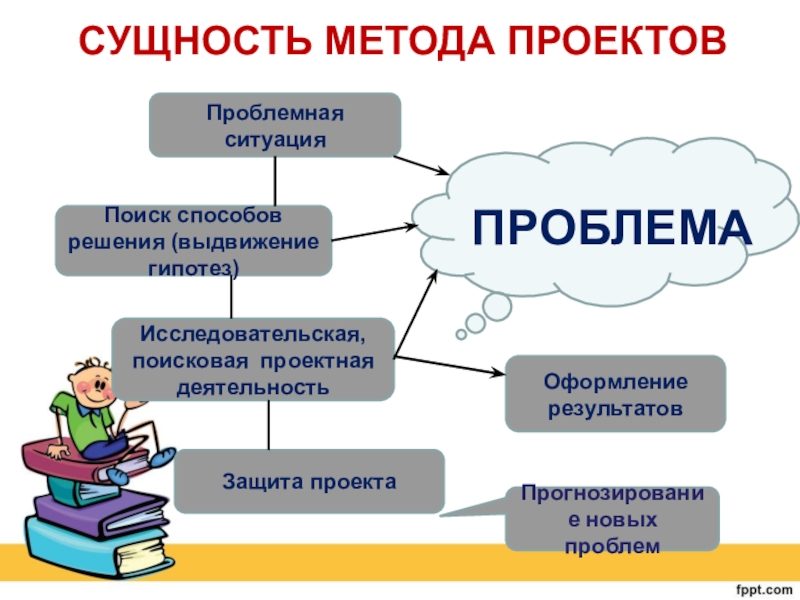

Проблемная ситуация – состояние интеллектуального затруднения, которое требует поиска новых знаний и новых способов их получения. Проблемные ситуации различаются по ситуации неизвестного, по уровню проблемности, по виду «рассогласования» информации, по другим методическим особенностям.

Ситуации интеллектуального затруднения чаще всего создаются с помощью проблемного вопроса. В педагогической литературе определены следующие отличительные черты проблемного (продуктивного) вопроса:

1) сложность, выступающая в форме противоречия,

2) ёмкое содержание,

3) увлекательная форма,

4) доступный для ученика уровень сложности.

В процессе работы наиболее часто учитель использует проблемные вопросы в форме познавательной (проблемной) задачи. Особое внимание заслуживает методика конструирования проблемных заданий, предложенная И.

Я. Лернером.

Проблема с указанием параметров и условия решения может быть предъявлена субъекту со стороны. Во всех случаях проблема перерастает в проблемную задачу как её принято называть. Проблемная задача представляет собой проблему, решаемую при заданных условиях или параметрах, и отличается от проблемы тем, что в первой заведомо ограничено поле поиска решения.

Алгоритм решения проблемной задачи включает 4 этапа. На первом этапе осознания проблемы учащиеся вскрывают противоречие, заложенное в вопросе, для чего находят разрыв в цепочке причинно-следственных связей. Это противоречие может быть разрешено с помощью гипотезы. Формулирование гипотезы составляет второй этап. Третий этап решения проблемы – доказательство гипотезы. Поиск путей доказательства гипотезы требуют от учащихся переформулировки задания или вопроса. Заканчивается решение проблемы общим выводом, в котором изучаемые причинно-следственные связи углубляются и раскрываются новые стороны познаваемого объекта или явления.

Это четвёртый этап решения проблемы.

Совокупность целенаправленно сконструированных задач, создающих проблемные ситуации, призвана обеспечить главную функцию проблемного обучения – творческое усвоение содержания образования, усвоение опыта творческой деятельности.

Моделирование уроков. При моделировании урока в режиме технологии проблемного обучения важно учитывать, что учащимся необходимо выполнить систему проблемных заданий для самостоятельной работы на каждом этапе урока. Задания для самостоятельной работы должны быть взаимосвязаны по дидактической цели и содержанию учебного материала. Дидактические цели формируются в соответствии со звеньями процесса обучения, следовательно, в систему объединяются задания со следующим дидактическими целями:

1) актуализации знаний и умений;

2) осознания и осмысления блока новой учебной информации;

3) закрепления и систематизации знаний;

4) применения знаний в новой учебной ситуации;

5) проверки уровня усвоения знаний и умений.

В зависимости от цели и содержания учебного материала проблемное учебное занятие проводится в разных формах. Мы разработали одну из эффективных фор – блоковый проблемный урок.

Правила моделирования проблемно-блокового урока следующие:

1. При конструировании блокового урока содержание разбивается на 3-4 логические части.

2. К каждой логической части конструируется проблемный вопрос.

3. Каждый проблемный вопрос на уроке звучит трижды, но с разной дидактической целью: а.) актуализация знаний; б.) осознание и осмысление учебной информации; в.) закрепление новых знаний.

4. На этапе закрепления задание из проблемного трансформируется в репродуктивное, так как ответ на вопрос уже прозвучал в процессе осознания и осмысления новой учебной информации. На этом этапе происходит процесс запоминания логики решения проблемной задачи.

5. В каждом блоке изменяется приём работы с источниками информации.

6. Важно в одном из блоков предложить работу с наглядностью как источником информации.

7. Сочетание приёмов работы с информацией зависит от содержания учебного материала и средств обучения, которыми располагает учитель.

8. На этапе диагностического контроля учитель проверяет уровень умения решать проблемные задачи, предлагая на выбор 2-3 задания. Высокий уровень – оценка «отлично», если учащиеся демонстрируют умения определять противоречия, формулировать гипотезу, доказывать её, делать вывод.

Предлагаем описание моделей проблемно-блокового урока, основная цель которого – научить школьников раскрывать логику решения проблемных задач, потренировать их в запоминании логики решения проблемной задачи, подготовить школьников к её самостоятельному решению.

Описание модели проблемно-блокового урока. Подробнее

Число.

Тема.

Цель.

1-й блок урока. Проблемная задача №1. Цель – актуализация знаний и умений учащихся. Учащиеся ищут пути решения проблемной задачи, используя текст проблемной статьи. Учитель повторно предлагает проблемную задачу №1, но дидактическая цель этого задания изменяется, важно осознание и осмысление блока новой учебной информации, которые осуществляются в процессе дискуссии по решению задачи. Затем учитель снова предлагает проблемную задачу №1, но поскольку учащиеся уже знают пути решения проблемы, то дидактическая цель предполагает закрепить в памяти учащихся ход решения проблемной задачи, поэтому, проговаривая решение уже известной проблемы, учащиеся осваивают способ решения проблемной ситуации.

Заканчивая работу над проблемной задаче №1, учитель вместе с учащимися делает вывод, который записывается в рабочей тетради.

2-й блок урока. Проблемная задача №2. Алгоритм взаимодействия учителя и учащихся повторяется, но в процессе решения задачи учащиеся работают с другим источником информацию. Если в первом случае в качестве источника использовался текст учебника, то при решении второй задачи информация поступает от учителя в устной форме.

3-й блок урока. Проблемная задача №3. Алгоритм взаимодействия учителя и учащихся снова повторяется, изменяется источник информации: это может быть наблюдение, материал научно-популярной литературы, видеоряд, схематическая или другие виды наглядности.

Обязательное условие успешной самостоятельной работы школьников – обратная связь, которая осуществляется по ходу урока, создаёт условия для осознания логики решения проблемного задания, поскольку в данной модели урока в процессе обратной связи воспроизводится ответ уже решённой проблемной задачи. Следовательно, средние и слабые ученики могут осмыслить и осознать путь решения проблемной задачи и потренировать себя, подготовить к решению нового проблемного задания.

Варианты тренинга школьников: 1. Тренинг осуществляется в конце урока, учащиеся выбирают одну из проблемных задач, решённых на уроке, пишут ответ. 2. Ученики решают проблемные задачи, устно восстанавливая в памяти алгоритмы решения. 3. В конце урока учитель проводит тренинг по вариантам. 4. В конце урока проверочная работа. Из задач, решённых на уроке, ученик выбирает две, повторяет варианты решения, работая в парах сменного состава, проговаривает пути решения проблем. 5. Проверочная работа выполняется дома. Учащимся предлагается выбрать одну из задач, решённых на уроке, и записать её решение, затем решить новую проблемную задачу (по выбору).

На следующем уроке, работая в парах сменного состава, учащиеся воспроизводят друг другу алгоритм решения проблемных задач.

Таким образом, технология проблемного обучения предполагает систему учебных занятий с основной целью – создать условия, при которых учащиеся открывают новые знания, овладевают новыми способами поиска информации, развивают проблемное мышление.

Качественно новый результат. Владение новыми способами поиска информации, проблемный уровень мышления.

Страница подготовлена по материалам сайта.

Полезные ссылки. Подробнее

1.6 Алгоритм создания проблемной ситуации в процессе теоретического обучения. Влияние проблемного обучения на интеллектуальное развитие учащихся

Критерии выбора и алгоритм принятия эффективного решения

Автор: Oлeг Михайлович Рой, доктор социологических наук, профессор, заведующий кафедрой региональной экономики и управления территориями Омского государственного университета, руководитель Центра региональных и стратегических исследований.

Решением следует называть определение варианта преодоления проблемной ситуации.

Ключевым свойством эффективного решения следует считать обязательное наличие альтернатив, обеспечивающих целесообразность и осознанность их свободного выбора.

Формальным основанием принятия эффективных решений является использование алгоритма, обобщающего опыт в принятии управленческих решений значительным количеством успешных предприятий.

В основе взятого для рассмотрения алгоритма лежит процедура, разработанная американскими исследователями Л. Планкеттом и Г. Хейлом, перекликающаяся с алгоритмами других авторов и включающая в себя выполнение следующих пунктов.

1. Определение цели и направления в решении проблемной ситуации

Определение цели, направления в разрешении проблемной ситуации должно проводиться в том же порядке, что и реализация стратегической цели. При реализации мелких проектов цель в разрешении проблемной ситуации и стратегическая цель, как правило, совпадают.

2. Установка критериев решения

При установлении критериев решения должны быть выработаны такие контрольные показатели, которые максимально полно охватывали бы наилучшие условия реализации поставленной цели.

К примеру, при выборе места для размещения общественной приемной должны быть учтены следующие условия, которые принимают значения критериев: минимальная площадь помещения, максимальные затраты (размеры арендной платы), местонахождение (включая подъездные пути, автостоянку и т. д.)

3. Разделение критериев (ограничения/желательные характеристики)

Выделяются желательные характеристики и ограничения, критерии принятия решения с точки зрения отношения к ним субъекта управления.

Установление цифровых значений минимальной площади, максимальных затрат, характера местности как раз и выступают ограничениями, определяющими практический диапазон выбора в принятии решения, связанного с проблемой выбора места для аренды помещения.

Балльные значения желательных характеристик, принимаемых с целью эффективного принятия решения, могут быть распределены между различными критериями: близостью к поставщикам продукции, легкостью подъезда клиентов, расположением в крупной промышленной зоне с интенсивным движением, минимальными затратами на строительство и завоз оборудования и пр.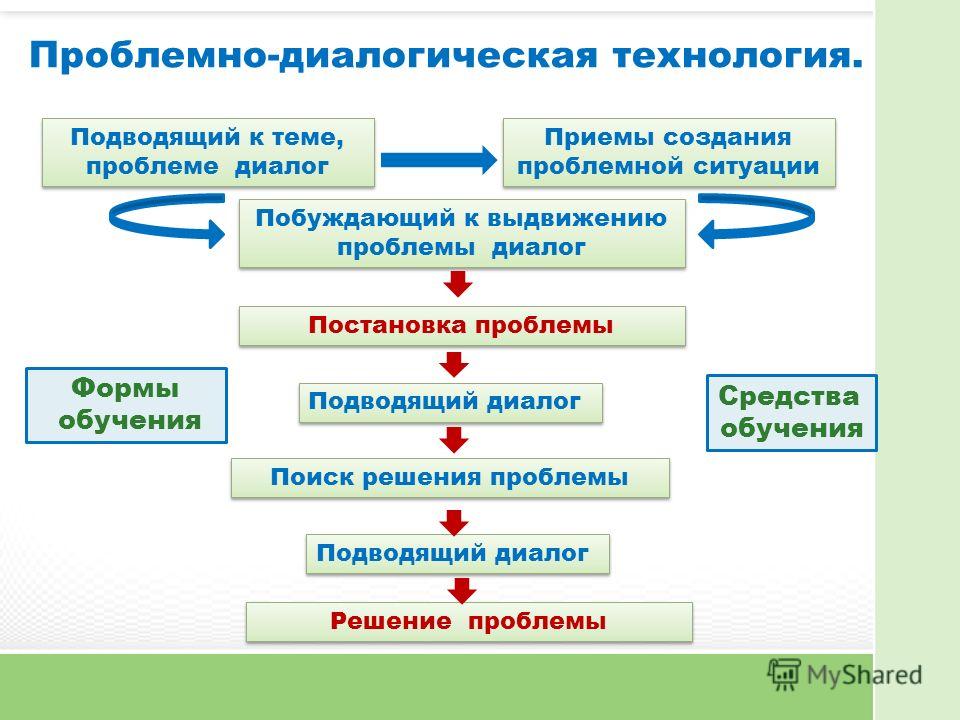

4. Выработка альтернатив решения

Альтернативы являются ключевым компонентом эффективного решения. Эффективность решения во многом определяется тем, из какого количества альтернативных вариантов выбран данный вариант решения.

Отсутствие альтернативных вариантов свидетельствует либо о недостаточной информированности лица, принимающего решение, либо о дефиците времени, отводимого на тщательную проверку эмпирической базы для этого решения. Это повышает степень вероятности ошибочности в принятии решения, затрудняет выбор оптимального варианта.

При выработке альтернатив необходимо соблюдение следующих требований:

альтернативы должны взаимно исключать друг друга;
альтернативы должны предполагать максимальные различия по выделенным критериям;
альтернативы должны быть одинаково вероятны.

5. Сравнение альтернатив

Чтобы сделать успешный выбор альтернативы, нужно все возможные варианты решений разделить по одному основанию и совместить друг с другом. Альтернативные варианты управленческих решений должны приводиться в сопоставимый вид по нескольким факторам: времени, качеству объекта, масштабу (объему) производства объекта, ожиданию материальной выгоды, соответствия профилю деятельности организации, привлечения дополнительной информации, а также фактору риска и неопределенности.

При этом сопоставимость альтернативных вариантов управленческого решения должна отвечать ряду правил:

количество альтернативных вариантов должно быть не менее трех;
в качестве базового варианта решения должен приниматься последний по времени вариант. Остальные варианты приводятся к базовому при помощи корректирующих коэффициентов;
формирование альтернативных вариантов должно отображать весь возможный спектр возможностей.

После этого вырабатываются и сравниваются альтернативы в принятии решения. За основание сравнения берется вопрос о том, какая альтернатива лучше всего отвечает данному критерию. С учетом этого обстоятельства каждой альтернативе присуждается свой балл, в значение которого входит характер возможных последствий принятого решения. Оценка каждой альтернативы может быть осуществлена в отношении каждого из критериев по порядковой (ранговой шкале) (табл. 1).

Таблица 1. Оценка распределения критерия по альтернативам в принятии решения(вариант)

Критерии	Альтернативы
	1	2	3
А	1	3	2
Б	2	3	1
В	2	1	3
Итого	5	7	6

Таким образом, устанавливаются приоритеты в выборе альтернатив, а вместе с ними и обоснованность в принятии оптимального решения.

Согласно данным таблицы, наилучшим вариантом с точки зрения выделенных критериев является альтернатива 2.

Но насколько целесообразен этот выбор? Ведь помимо ожидаемых по его результатам благоприятных последствий весьма существенным является фактор риска, делающий подчас эти ожидания несостоятельными.

Эффективность выбора составляют не только оценка альтернативы по основным критериям, но и допустимая степень риска.

6. Оценка риска

Риск — это ситуативная характеристика деятельности социальных субъектов, заключающаяся в неопределенности ее исхода и наступлении неблагоприятных последствий.

Рассмотрение сущности риска возможно как в статическом, так и в динамическом смысле.

В статическом смысле сущность риска заключается в способе его выражения, дифференцируемом в зависимости от сферы его преломления. В соответствии с этим пониманием риск подразделяется на различные виды: экономический, социальный, политический, экологический, финансовый и пр.

Оценка риска — это оценка исхода определенного события с точки зрения неблагоприятных последствий этого события для его основных участников. В качестве участников оценки риска выступают: страхователь, страховщик и эксперт.

Основными параметрами риска являются:

размер возможного ущерба, наступающего в результате наступления страхового события;
показатель вероятности наступления страхового случая;
показатель возможных расходов, связанных с ликвидацией последствий страхового события и восстановления прежнего положения;
стоимость упущенной выгоды. В этом случае риск характеризуется субъективной оценкой вероятной, ожидаемой величины максимального дохода в случае использования отклоненной альтернативы;
степень неблагоприятности последствий от наступления страхового события для каждого из его участников.

С точки зрения характера проявления риска выделяют систематический и случайный риски.

Систематический риск вызывается постоянно существующей возможностью наступления, связанной, к примеру, с профессиональной деятельностью участников деятельности, наличием устойчивой группы факторов, способствующих проявлению этого события. Ведь вероятность получения травмы ноги у футболиста гораздо выше этой же опасности у пианиста.

Случайный риск вызывается уникальным стечением обстоятельств, вызванных наступлением события, вероятность которого значительно меньше, чем в случае систематического. Однако последствия, вызванные случайными событиями, для страхователя могут оказаться гораздо более опасными, чем, если страховые события ожидаются.

С точки зрения технологии, различают качественную и количественную оценки риска.

Качественный характер оценки риска заключается в определении перечня факторов, вызывающих проявление страхового события. Каждый из факторов подробно анализируется, описывается и оценивается с точки зрения его устойчивости и степени воздействия. Результатом качественной оценки риска может быть ранжирование факторов риска по различным основаниям их дифференциации, представление механизма проявления страхового события и пр.

В количественном плане выделяются следующие способы расчета риска:

R = Y * Р, где Y — возможный ущерб, а Р — вероятность этого события.
R = Y + С, где Y — возможный ущерб, а С — расходы на нейтрализацию возможного ущерба.
R = Р * V, где Р — вероятность страхового события, а V — серьезность последствий для этой организации.

Полученные по результатам каждого способа количественные показатели отображают экспертную оценку характерного для каждого исследуемого события неблагоприятного исхода, учет которого позволит выработать меры по нейтрализации тенденций, способных вызвать предполагаемый исход.

Произведение этих показателей позволит сравнивать альтернативы с точки зрения закладываемого на их реализацию риска и избирать оптимальный вариант выбора альтернативы.

7. Выбор альтернативы

Главным вопросом в проведении процедуры выбора альтернативы является критерий такого выбора, в соответствии с которым задаются приоритеты в принятии управленческих решений.

К характерным для оптимального выбора альтернативного решения критериям можно отнести надежность, технологичность, оперативность, экологичность, экономичность, производительность, качество, полезность и пр.

При выборе лучшей альтернативы следует придерживаться следующих правил:

в плане реализации избирается та альтернатива, которая располагает максимальным количеством экспертных баллов по выделенным критериям;
избирается та альтернатива, которая имеет оптимальный баланс между доходностью и риском;
в плане реализации решения избирается та альтернатива, которая предполагает максимально полное согласие экспертов по выделенным критериям.

Среди наиболее известных методов, позволяющих осуществлять эффективный выбор альтернатив в принятии решений, следует выделить:

метод «свертки», при котором рассчитываются значения единого комплексного критерия для каждого альтернативного варианта решения;
принцип Парето, при котором сопоставляются оценки альтернативных вариантов решений по нескольким критериям и отбрасываются «доминируемые» решения;
лексикографический выбор, при котором выбор осуществляется сначала по наиболее важным критериям, а затем по менее важным;
правило максимина, используемое при игровом подходе и реализующее стратегию гарантированного результата, когда выбирается вариант, дающий максимальный эффект при наименее благоприятных действиях противника.

8. Анализ плана реализации решения

Главное предназначение анализа плана состоит в том, чтобы представлять себе критические этапы в реализации принятого решения.

Если оптимальное решение будет принято, но не предусмотрен механизм его реализации и не учтены возможные факторы, препятствующие этой реализации, то результаты принятия такого решения будут отрицательны.

В содержание анализа плана следует включить следующие разделы:

краткое изложение плана;
перечисление и рассмотрение этапов плана с выявлением критических моментов;
выявление потенциальных проблем и возможностей;
определение наиболее вероятных причин основных потенциальных проблем и возможностей;
выработка предупреждающих или содействующих мероприятий;
выработка подстраховывающих мероприятий;
разработка условий для введения в действие подстраховывающих мероприятий.

Таким образом, завершается процедура принятия решения, смоделированная на основе обобщения опыта в принятии эффективного решения.

При определении критериев принятия эффективных решений необходимо учитывать и способы практического воплощения принимаемых решений в жизнь. Успешность решения может быть оценена с трех сторон, соответствующих стадиям процесса принятия решения: разработки, принятия и реализации.

В процессе разработки решения главное внимание уделяется оценке проблемной ситуации, по отношению к которой производится выбор оптимального решения. Ключевым критерием эффективности решения на этой стадии является полнота в описании проблемной ситуации, адекватность средств ее выражения, предваряющих выбор наилучшего варианта воздействия на проблему.

Наступление стадии непосредственного принятия решения предполагает организацию учета всех возможных вариантов в принятии решения, прогнозирование ожидаемых выгод и рисков в случае того или иного выбора.

На стадии реализации решения эффективность достигается привлечением организационных и технологических ресурсов, возможностью исполнения решений, квалификацией персонала, ответственного за это исполнение, а также наличием условий, способных повлиять на результат.

Хорошим методологическим средством проведения такой оценки может послужить матричная модель, дифференцирующая критерии с точки зрения их роли в подготовке выбора оптимальной альтернативы (табл. 2).

Таблица 2. Модель оценки критериев альтернативных проектов

Критерии	Вес	Оценка					Итого
		Крайне низкая	Низкая	Средняя	Высокая	Очень высокая
		1	2	3	4	5
1. Соответствие производственной деятельности предприятия	0,2			+			0,6
2. Технические характеристики	0,3		+				0,6
3. Патентная защита	0,1			+			0,3
4. Экономическая отдача	0,25		+				0,5
5. Энергозатраты	0,15				+		0,6
Итого	1

Выбор оптимального решения осуществляется путем сопоставления значимости каждого критерия и оценки его проявления в той или иной альтернативе.

Согласно данным таблицы получается, что из пяти выделенных критериев 1, 2 и 5, несмотря на разность их весовых характеристик, обнаруживают равную ценность в оценке альтернативы, что с необходимостью должно учитываться при ее выборе.

Основными требованиями, предъявляемыми к оценке эффективных решений, являются:

решение должно быть обоснованным. Будучи избранным из перечня возможных альтернатив, оно должно учитывать влияние всех положенных в основу ее выбора критериев;
решение должно быть реальным, то есть способным быть реализованным. Реализм решений может обеспечиваться последовательным разложением сложных решений на простые;
решение должно быть своевременным, то есть приниматься в тот момент, когда его исполнение особенно целесообразно;
решение должно быть гибким. Гибкий характер решений придается способностью изменять алгоритм его принятия при изменении внутренних и внешних условий;
решение должно приносить максимальную выгоду, которую может составлять либо получаемая по его результатам прибыль, либо сокращение времени на проведение в ее рамках работ, либо исполнение принятых норм и стандартов.

Б. Литвак в описании оценочной системы представляет следующие составляющие:

перечень критериев, характеризующих объект принятия управленческого решения;
оценку сравнительной важности критериев;
шкалы для оценки проектов по критериям;
формирование принципа выбора.

Только практические современные знания и навыки. Изучите эти курсы по менеджменту и управлению или учитесь чему хотите по абонементу, со скидкой.

Алгоритм исправления проблемных ситуаций (АИПС-2015)

Одна из целей проектной активности на производстве – улучшение проблемной производственной ситуации. Штатная проблемная ситуация рано или поздно разрешается обычными инженерными способами. Но бывают ситуации, которые нельзя улучшить обычными, традиционными способами. Такая ситуация вызвана сложной проблемой, которую можно решить только на уровне изобретения.

За время практической работы с изобретательскими проектами (в первую очередь, для компании Samsung) мы перепробовали несколько известных алгоритмов решения задач, отдельных методов и инструментов. Полноценную методическую поддержку проекта могла дать только совокупность всех методов. Не менее важна правильная последовательность их применения.

После выполнения первого десятка проектов начала нарабатываться некая последовательность действий, намёк на единый алгоритм. Первая попытка его методичного построения состоялась, когда в SAIT Samsung началось планомерное и массовое обучение сотрудников ТРИЗ. Алгоритм известен под названием «Рождественская Ёлка».

При совершенствовании этого алгоритма мы руководствовались статьёй Г. С. Альтшуллера «Процесс решения изобретательской задачи: основные этапы и механизмы». В статье описывается системный подход к работе с задачей: переход от изобретательской ситуации к задаче, принципиальное решение задачи и переход к техническому и расчётному решениям.

Алгоритм предназначен для поддержки процесса исправления проблемной ситуации с одним нежелательным эффектом.

Работа с алгоритмом начинается с описания исходной проблемной ситуации. Выход алгоритма – улучшенная ситуация, то есть исходная (проблемная) ситуация без нежелательного эффекта. Наша цель – исправить некоторую проблемную ситуацию, в которой содержится нежелательный эффект, явление, не устраивающее задачедателя.

Для каждого ключевого действия работы над изобретательским проектом наработаны разнообразные инновационные методики и мини-алгоритмы. Предлагаемый алгоритм — алгоритм исправления проблемных ситуаций (АИПС) — организует их в единую структуру, показывает место каждого инструмента в работе над проектом, образуя своеобразную «систему управления» процессом мышления.

Для исправления проблемной ситуации предусмотрено три этапа:

Анализ проблемной ситуации
Решение выделенной задачи
Анализ изменённой ситуации

Проблемная ситуация — Энциклопедия по машиностроению XXL

В учебном процессе, построенном на принципах развивающего обучения, должны быть управляемы не столько внешние стороны графической деятельности, сколько характер активации таких рабочих психических состояний, как восприятие, воображение, представление.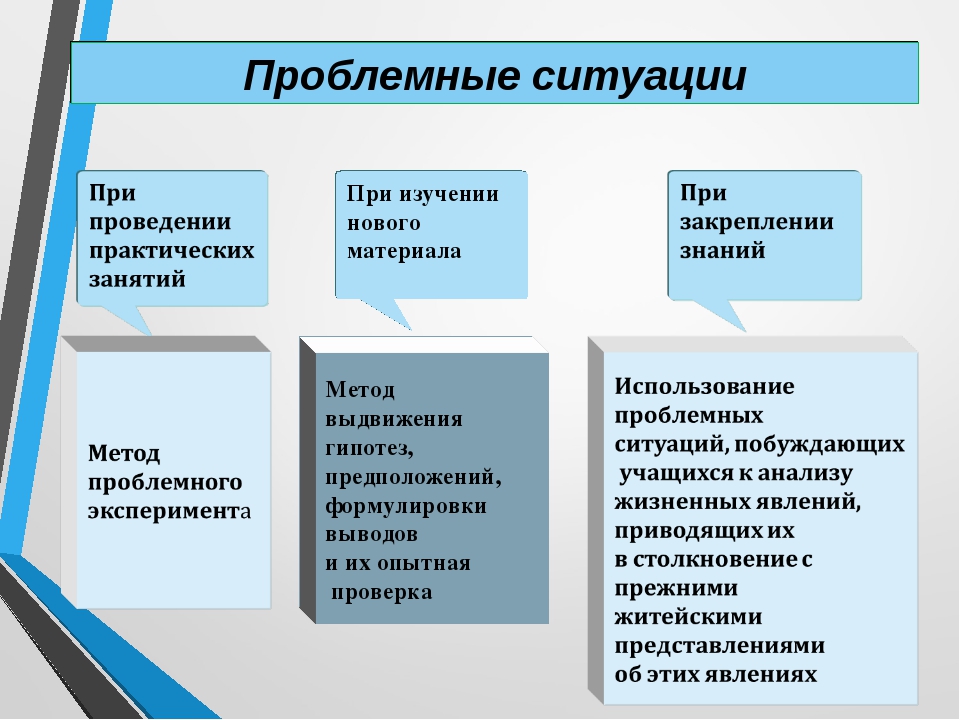

На конкретных учебных занятиях по пространственно-графическому моделированию графическая деятельность студентов широко включается в более общую — поисковую. Обращается внимание на системное видение проблемной ситуации и умение отобразить ее в целостной графической структуре. [c.67]
Дизайнерские проблемные ситуации отличаются от тех-иических тем, что системность присутствует в них на любом уровне сложности и простота задачи не связывается с потерей целостности. Кроме того, для расширения поля учебных представлений учащихся задачи дизайна представляют благодатный материал потому, что основной метод разрешения проблем — художественно-конструкторский. Графическое моделирование включается в него на всех этапах поисковой деятельности. В условиях автоматизации проектирования и использования ЭВМ в учебном процессе методы дизайна могут найти широкое применение для расширения кибернетических возможностей языка инженерной графики.

[c.70]

Конвергенция дает возможность проектировщику держать основной стратегический план решения. Дивергенция и импульсивные идеи противоречат упорядоченному поиску и в какие-то моменты времени приводят к необходимости перестройки исходной концепции проблемной ситуации. Это происходит тогда, когда факты и спонтанные идеи складываются в новую устойчивую целостную модель, которая начинает конкурировать с первой. [c.75]

Реактивация зрительного образа в акте представления — это не механическое повторение первоначально воспринятого образа, а как бы новое его создание в сознании. Возникающий зрительный образ отвечает по своим конкретным визуальным характеристикам той практической (проблемной) ситуации, которая стимулировала его появление [6, 35]. [c.89]

Понятие целостности — центральное понятие современного системного анализа. Формирование целостного подхода к анализу объектов, процессов, явлений — необходимое условие развития творческой личности -инженера.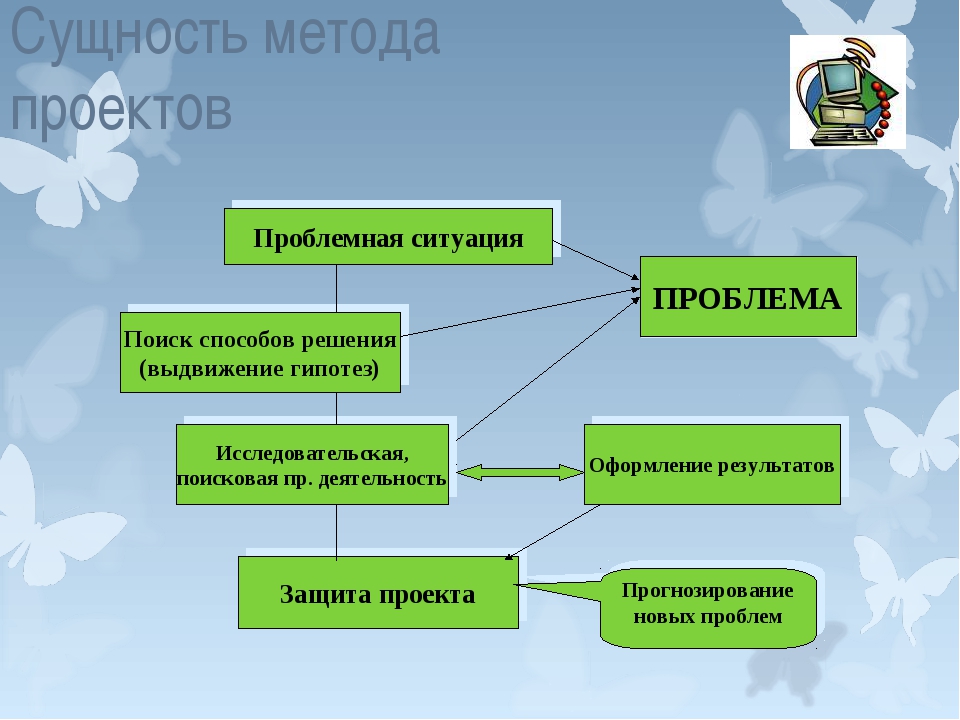 Целостность видения, наряду со структурным подходом, определяет как композиционный характер мышления дизайнера, так и специфику системного метода разрешения проблемных ситуаций в технике. [c.90]

Так же, как и в подробно рассмотренном нами случае геометрических заданий, включение графического моделирования в структуру различной поисковой деятельности сообщает ей нужный характер и подчеркивает ту или иную его сторону. В результате системного подхода характер изучения проблемы графического моделирования приближается к исследовательской форме. Пространственно-графическое моделирование рассматривается на этих занятиях как один из способов организации познавательной деятельности, выполняет инструментальную функцию в разрешении проблемных ситуаций. [c.101]

Итак, концепция пространственно-графического моделирования в инженерной графике способствует развитию творческих способностей студентов в двух направлениях. Разрешение поставленной проблемной ситуации приводит к непосредственному обучению творчеству, тем поисковым процедурам, которые связаны с применением графических моделей. Кроме этого, динамическое использование изображения как графической модели в процессе работы требует от студентов специальных структурных и комбинаторных приемов мышления. Можно считать, что проведенные исследования достаточно убедительно показывают целесообразность включения курса Пространственное эскизирование в систему непрерывной графической подготовки студентов механических специальностей технических вузов. [c.103]

Активизация познавательных потребностей личности в процессе обучения осуществляется путем включения графической деятельности в более общую (поисковую). Мы уже останавливались на различных способах осуществления такого процесса. С рассматриваемой точки зрения важен вопрос о степени влияния различных характеристик задач, предлагаемых в учебном процессе, на мотивацию графической деятельности студента. В задачах, основанных на предварительном создании проблемной ситуации, необходимо определить тот диапазон трудностей, выход за пределы которого как в сторону занижения, так и в сторону завышения приводит к снижению мотивации.

[c.161]

В проблемной ситуации цель действия не задается, а является главным содержанием поисковой деятельности. Такие задачи в курсе Пространственное эскизирование , как правило, решаются коллективно, группами по два-три человека. Осознание неизвестного проблемной ситуации [36] равносильно переводу проблемной задачи в разряд задач, решаемых методом упорядоченного логического поиска. Неизвестное проблемной ситуации становится целью поиска, которая достигается путем использования известных алгоритмов структурно-геометрического анализа. К проблемным задачам подобного типа относятся задания по анализу абсурдных графических моделей, восприятие пространственных противоречий которых приводит к довольно глубокому анализу геометрической природы формы и способа ее графического отображения на плоскости. Пока причина визуального абсурда не уяснена, нет и возможности правильно понять характер изображения. Только после осознания проблемной визуально-графической ситуации как искомой цели действия возможна управляемая деятельность по созданию правильной модели. [c.164]

Следующую большую группу задач, полезную для развития инверсионного мышления студентов, составляют задания, связанные с абсурдными изображениями. Структура действий анализа таких изображений подробно рассмотрена в главе 3, здесь же остановимся только на вопросе создания проблемной ситуации. [c.177]

После того как истина кажется установленной, преподаватель выдвигает неожиданное утверждение о возможности построения реальной конструкции, соответствующей приведенному абсурдному изображению и предлагает осуществить структурно-геометрический анализ последнего. С помощью различных наводящих вопросов осуществляется постановка проблемной ситуации. Студент пытается исправить заданное изображение, но это ему не удается, так как трансформации подвергается какая-то одна часть, а не целостная структура изображения. [c.177]

Характерной чертой САПР второго поколения явится возможность поиска с их помощью новых проектных решений на начальных этапах проектирования с использованием автоматизированных баз знаний, в составе которых, наряду с данными известных проектно-конструкторских разработок, будут представлены сведения о специализированных эвристических приемах и алгоритмах поиска применительно к конкретным классам объектов, о физических эффектах, способных обеспечить выполнение тех или иных функций, и другая информация. При этом ЭВМ, снабженная подобной базой знаний и программными средствами работы с нею, будет выполнять роль советчика, эксперта, к которому обращается проектировщик для разрешения проблемных ситуаций. [c.291]

Конфликты, стимулирующие поиск новых форм и методов организации производства, могут возникать и на других уровнях управления между бригадами, между коллективом цеха и его руководством, между цехом и службами заводоуправления. Если на предприятии не отработана система рассмотрения и разрешения проблемных ситуаций путем коллективного их обсуждения, то их решение целиком ложится на плечи администрации, а это приводит к перегрузке управляющих или к неудачному их разрешению, порождающему их повторное возникновение. Тесное взаимодействие хозяйственных руководителей, бригадиров и советов бригад, налаженное так, как, например, в объединениях Звезда , Знамя Октября , Невский машиностроительный завод им. В. И. Ленина , на заводе полиграфических машин и других предприятиях машиностроения, обеспечивает повышение качества труда и эффективности производства при благоприятном морально-психологическом климате в коллективе.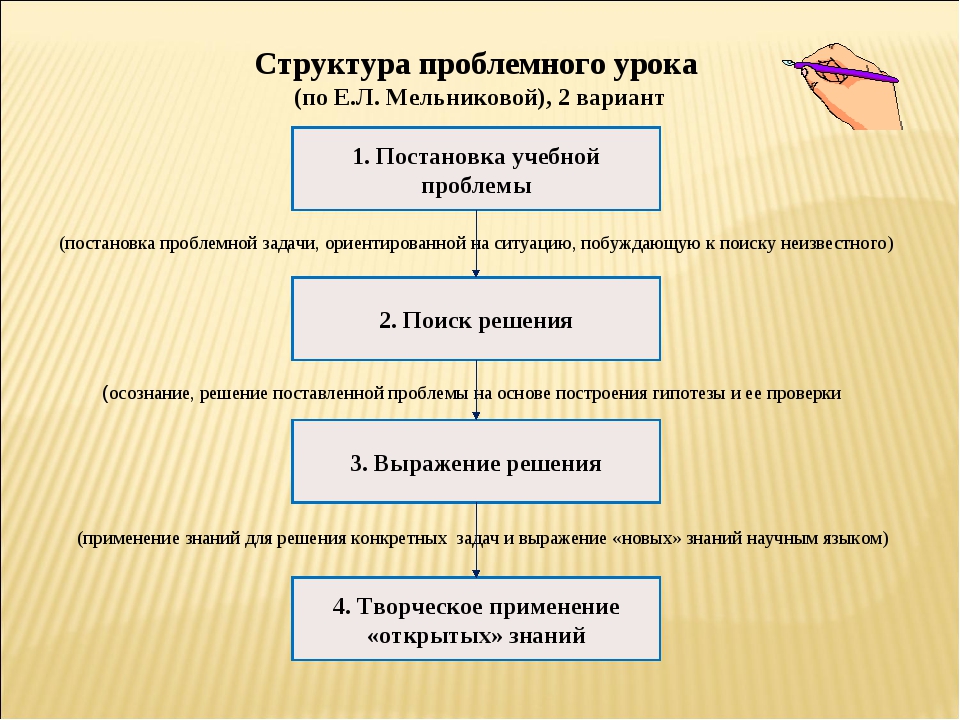 [c.210]

Распознавание причин и устранение вибрации — одна из самых сложных проблемных ситуаций, решение которой требует применения всего арсенала методов, приведенных в гл. 1. Как всегда, следует начать с получения информации. [c.180]

И та и другая постановки являются переходным этапом постановки стандартной задачи и вместе образуют проблемную ситуацию, когда исследователю заданы множества потенциальных проблем и ситуаций и, следовательно, созданы исходные предпосылки для выделения адекватных проблем и ситуаций и формирования постановки стандартной задачи обоснования решений. [c.482]

Из литературных источников известен ряд причин, которые могут вызвать эти вопросы величина зазора, концентрация припоя, загрязнение поверхности и т.д. Но это всего лишь повод для обсуждения. Имеется другой путь решения проблемных ситуаций, а именно за счет подбора различных ТО как на стадии, предшествующей пайке, так и после нее. [c.475]

Операция 1. Описание проблемной ситуации. Эта операция представляет собой самую предварительную краткую формулировку задачи, в которой должны содержаться ответы наследующие вопросы [c.188]

В чем состоит затруднение или проблемная ситуация и какова ее предыстория [c.188]

Что требуется сделать для устранения проблемной ситуации, т.е. какую потребность нужно удовлетворить [c.188]

Что мешает устранению проблемной ситуации или достижению цели [c.188]

Пр и м е р описания проблемной ситуации заимствован из работы [14]. [c.188]

Операция 3. Выбор прототипа и составление списка требований. В описании проблемной ситуации часто указывают прототип, который требуется усовершенствовать. Этот исходный прототип обычно приходится брать за основу При поиске улучшенного решения. [c.188]

Иногда при выборе прототипа удается найти подходящее решение и тем самым снять проблемную ситуацию. В этом случае при дефиците времени и ресурсов можно прекратить решение задачи поиска улучшенного технического решения. Однако при наличии времени почти всегда имеет смысл и есть возможность улучшить выявленное решение и тем самым отодвинуть время возникновения новой проблемной ситуации. [c.190]

Постановка задачи может быть дана в виде описания проблемной ситуации (см. операцию 1 в гл. 15). Иногда имеет смысл более детально изложить постановку, когда описание проблемной ситуации дополняют предварительной формулировкой задачи в соответствии с операцией 5 (см. гл. 15). [c.238]

Проблемную ситуацию часто можно сравнить с пропастью между известным и искомым, отсутствием основания для надежных опор при построений моста между ними. Такая ситуация возникает при поиске решения большинства проектно-конструкторских и изобретательских задач. При этом дефицит соответствующей поисковому запросу информации не позволяет достаточно эффективно применять традиционные логические приемы, делать дедуктивные выводы. В таких случаях одним из наиболее результативных способов построения моста является подвешивание его на гирляндах ассоциаций и метафор. Решение творческих задач с получением оригинальных и эффективных результатов обычно связано с переносом знания в новую область, интерпретацией новых идей, что в силу законов психологии происходит через использование обходных (ассоциативных) слов и метафорических выражений. Эвристическая ценность ассоциаций и метафор связана с их эмоциональной окраской. Разработчики в своем творчестве часто используют случайные ассоциации и метафоры как источник подсказки для генерирования новых идей. Однако эти подсказки, как правило, возникают спонтанно, без систематического поиска. [c.289]

Метафорическое описание и анализ проблемной ситуации [c.294]

Изложите суть вопроса о метафорическом описании и анализе проблемной ситуации. [c.299]

Описание проблемной ситуации. Описание выполняется по этапам. При этом пп. 1-4,6 выполнены в соответствии с операциями 1-4, изложенными в гл. 15, а пп. 7, 8 — в соответствии с настоящей главой. [c.314]

Данная книга призвана оказать содействие правительствам в формировании стратегических подходов для эффективного решения ключевых проблем в сфере централизованного теплоснабжения. Сначала рассматриваются преимущества ЦТ, которые являются стимулом для проведения политических реформ. Далее производится оценка основных причин проблемной ситуации, сложившейся в секторе централизованного теплоснабжения в большинстве стран с переходной экономикой недостаточное внимание к потребителю, низкая эффективность, избыток производственных мощностей и неравные условия. В книге предусматриваются два пути решения данных проблем при достижении максимального потенциала ЦТ более совершенное регулирование или конкуренция. Оба варианта реализуемы. Тем не менее, важно, чтобы правительства четко определили механизм, который будет применяться для баланса спроса и предложения, т. е. либо это будет осуществляться за счет тарифного регулирования и энергетического планирования, либо на основе конкуренции между различными видами отопления. Даже при наличии конкуренции, правительство по-прежнему должно играть важную роль в части мониторинга рынка, рассматривая и решая проблемы дисбаланса, в целях обеспечения справедливой конкуренции и гарантии того, что теплоснабжение самых бедных потребителей производится в соответствии с принципами эффективности и справедливой конкуренции. Выбор четкого пути развития сектора позволит изменить культуру деловых отношений в области ЦТ путем перехода от модели, в которой приоритетным элементом является производство, к модели, где основное внимание уделяется потребителю. Необходимо четко осознать важность централизованного теплоснабжения для национальной энергетической стратегии для того, чтобы его можно было включить в политическую повестку дня и обеспечить равные условия для всех заинтересованных сторон. [c.3]

Описанная таким образом модель функционирования системы не отвечает на вопрос о необходимости управления. Для получения такого ответа следует задать виды технологических состояний СУ и реализуемых ими ТО, указав соответствующие допустимые значения показателей качества (граничные условия) и проверить их выполнение. Выход за допустимые пределы любого компонента векторного показателя качества фиксируют как проблемную ситуацию. Такая ситуация требует принятия решения по управлению. [c.464]

В учебном процессе знакомство с основными понятиями композиционного метода необходимо из соображений возможности включения различных проблемных ситуаций графического содержания. Как было показано ранее, композиционные задачи относятся к числу многовариантных с качественными критериями формообразования. Эстетические критерии вполне доступны даже для студентов-первокурсни-ков. В учебном процессе они могут заменить гораздо более сложные научные и технические критерии качественного типа. Эти особенности графических заданий на композицию позволяют широко использовать их для придания графической деятельности- целесообразного характера. Они же определили повсеместное использование подобных задач в качестве компьютерных игр для развития специального структурного мышления, необходимого человеку для общения с ЭВМ. [c.62]

Предварительные информационно-графические модели имеют своей целью не само запоминание, а вхождение в образ проблемной ситуации, понимание ее структуры не с одной, а со всех точек зрения. Художник в отличие от ученого должен не рассчитать конечный результат, а увидеть его. Но видение возможно только при глубоком внутреннем осознании единства проблемы во всем ее много-образнн. Если рассмотреть психологическую схему взаимодействия информации, располагаемой в кратковременно.м и долговременном хранилище человеческой памяти (КВХ и ДВХ , то открывается еще одна сторона роли графической модели в развитии мышления. Согласно [6] большинство характеристик мышления определяется возможностью обработу ки внешнего материала (кодирования) и эффективностью процессов взаимодействия каналов связи между этими двумя хранилищами информации в памяти. [c.73]

Например, на рис. 2.3.5 студенты должны определить траекторию движения шарика на наклонной плоскости. Неверное восприятие ее возникает из-за композиционного согласования элементов формы. Чем больше факторов будет подчеркивать визуальное сходство элементов, тем вероятнее возникновение неадекватного пространственного образа. Формальная светотеневая разработка изображения по методике технического рисования увеличивает это противоречие. Воспринимаемое целое входит в конфликт с реальной структурногеометрической основой, которая в рассматриваемой задаче осознается довольно просто. Для этого достаточно предложить студентам построить ортогональные проекции графической модели. При сложной структуре изображения заметить сразу визуальные несоответствия графической модели нелегко. Проблемная ситуация в восприятии сама собой не возникает, неразвитый глаз студента просто не замечает в изображении никаких структурных противоречий.

Но при специальной постановке проблемной ситуации, акцентировании внимания на основном пространственном несоответствии студенты с воодушевлением и большим интересом начинают искать сущность абсурдного характера восприятия формы. [c.87]

Исследовательский метод, как известно, является основным методом обучения студентов творчеству. Его функции определяются реализацией следующих факторов 1) с помощью метода формируются черты творческой личности студента 2) при его посредстве осуществляется более глубокое творческое усвоение знаний 3) студенты овладевают научным методом познания, всегда связанным с открытием нового 4) этот метод дает внутрений импульс потребности в деятельности [30]. Нами выделено три типа задач, которые можно использовать при конструировании проблемной ситуации и одновременно для более глубокого развития отдельных качеств мышления. К такому типу относятся, во-первых, практически-действенные задания на комбинаторику пространственных структур, во-вторых, геометрические задачи на определение структурной связи композиции из нескольких элементов, в-третьих, абсурдные изображения, анализ которых приводит к необходимости понять причину обмана и более глубоко уяснить сущность геометрических методов пространственного формообразования. [c.171]

На втором занятии отработка необходимых графических навыков связана с поисковым заданием практически-действен-ного (дизайнерского) плана. В этом задании могут применяться реальные модели для уяснения существа условия и определенного вживания в проблемную ситуацию. [c.171]

При изучении графических моделей объектов с ортогонально ориентированными гранями студентам предлагается задача, решение которой требует выхода за пределы только что изученной пространственно-структурной системы. Пример задачи подобного типа приведен на рис. 4.6.21. Абсурдность сборки связана в восприятии с тем, что на протяжении нескольких занятий студенты имели дело с объектами ограниченного класса. В связи с этим у них появляется инертность мышления, изображение сборки причисляется ими к разряду нереальных. После того как абсурдность в рамках предполагаемой конструктивной системы уясняется всеми студентами, преподаватель проводит установочную беседу о характере изобретательских задач и специфике процесса поиска решения. Такая беседа должна нацелить студентов прежде всего на определение структурно-пространственных ограничений конструктивной системы, в которой реализуется абсурдность . Когда эта цель достигнута, предлагается изменить первоначальную точку зрения, найти более общую пространственную структуру, отказавшись от первоначальных искусственных ограничений. Желательно, чтобы каждый студент имел возможность прочувствовать удовольствие от небольшого самостоятельною открытия . На рис. 4.6.22,а изображена ничем не примечательная с первого взгляда конструкция. Визуальлые противоречия в сложных фигурах воспринимаются студентами не сразу. Для создания проблемной ситуации преподаватель предлагает построить чертеж изображенной конструкции. Как правило, все студенты выполняют чертеж в виде, приведенном на рис. 4.6.22,6. В процессе построения чертежа выясняется характер визуального несоответствия. Студенты самостоятельно предлагают варианты исправленных конструкций, соответствующих возможной пространственной реализации изображения (рис. 4.6.23). [c.177]

Лингвистический уровень. На этом уровне используют построения, по своей структуре приводящие к абстрактным языкам. Работы этого направления часто объединяют понятием искусственный интеллект . В работе [100] показывается, что теория, на которой покоятся схемы автоматов всех типов, не является теорией психической деятельности человека. Приводится схема гиромата , который является более близкой моделью психической деятельности и позволяет решать задачи творческого характера, непосильные для автоматов. Гиромат является многоуровневой моделью, в которой происходит постепенное обобщение проблемных ситуаций. Основой принятия решения является модельный эксперимент, частями которого являются [c.22]

Процесс проектирования СОЭИ сопряжен с необходимостью решения вопросов методического характера создания систем управления в целом. К их числу относятся проблемы создания методик прогнозирования элементов АСУ и их параметрической оценки многомерного описания объекта управления с учетом многочисленных поведенческих (типа вход-выход) характеристик системы исследования процессов принятия решений и. идентификации проблемных ситуаций, возникающих в процессе управления определения множества целей и альтернатив их достижения разработки математических моделей управления, адекватных динамическим условиям и параметрам объекта в разрезе фаз уп- [c.8]

Так, на начальных этапах проектирования, на которых производится разработка общей концепции системы управления и СОЭИ, формулируются цели проектирования и основные требования к составу выходных показателей, определяются основные функциональные связи в пространстве целевая программа объекта управления иерархия целей развития объекта иерархия проблемных ситуаций номенклатура решений по реализации проблемных ситуаций номенклатура целевых задач, подлежащих автоматизированной обработке существенные свойства и временные сечения управляемой системы, охватываемые управленческими решениями циклы управления в разрезе иерархических уровней объекта управления, предпочтительные для использования модели и соответствующие программные средства ведения базы данных, обеспечивающие высокий уровень семантического отображения отношений предметной области с применением семантической, реляционной, инфологической моделей, DIAM-П и др. [c.31]

Приведенную упрощенную модификацию метода гирлянд ассоциаций можно существенно расширить, используя некоторые дополнительные процедуры. Так, метафорическое описание и анализ проблемной ситуации — это генерирование дополнительной информации об этой ситуации путем метафоризации ключевых слов — основных понятий о вещах, их свойствах и отношениях, связанных с ней. Описание рассматриваемой и аналогичных проблемных ситуа-пий осуществляется посредством различных метафор [c.294]

Урок открытия нового знания (ОНЗ)

Этап 4. ПОСТРОЕНИЯ ПРОЕКТА ВЫХОДА ИЗ ЗАТРУДНЕНИЯ // Урок открытия нового знания (ОНЗ) // ГБОУ Лицей № 410

Этап 4. ПОСТРОЕНИЯ ПРОЕКТА ВЫХОДА ИЗ ЗАТРУДНЕНИЯ

Этап 4
ПОСТРОЕНИЯ ПРОЕКТА ВЫХОДА ИЗ ЗАТРУДНЕНИЯ

Цель этапа

Приёмы

УУД

Постановка целей учебной деятельности и на этой основе – выбор способа и средств их реализации.
Для этого необходимо, чтобы учащиеся:
сформулировали конкретную цель своих будущих учебных действий, устраняющих причину возникшего затруднения (то есть сформулировали, какие знания им нужно построить и чему научиться)

предложили и согласовали тему урока, которую учитель может уточнить,

выбрали способ построения нового знания (как?) — метод уточнения (если новый способ действий можно сконструировать из ранее изученных) или метод дополнения (если изученных аналогов нет и требуется введение принципиально нового знака или способа действий)

выбрали средства для построения нового знания (с помощью чего?) — изученные понятия, алгоритмы, модели, формулы, способы записи и т.д.

Личностные:
— формирование ценностных ориентиров и смыслов учебной деятельности на основе: развития познавательных интересов , учебных мотивов, формирование мотивов достижения, формирования границ собственного знания и «незнания».

Коммуникативные:
-учёт разных мнений и стремление к координации различных позиций в сотрудничестве,

Регулятивные:
— принятие и сохранение учебной задачи,
— планирование своих действий в соответствии с поставленной задачей и условиями её реализации,

Познавательные:
— выделение существенной информации,
— формулирование проблемы, самостоятельное создание способов решения проблемы,
— поиск разнообразных способов решения задачи,
— структурирование знания.

«Яркое пятно»

Данный прием состоит в представлении учащимся набора однотипных предметов, слов, ряда чисел, выражений, одно из которых выделено цветом или размером. Через зрительное восприятие концентрируем внимание на выделенном объекте. Затем, совместно выясняем общность предложенного и причину обособленности выделенного объекта. Далее формируется тема и цели урока.
Например, урок по теме «Трапеция» в 8 классе. Учитель предлагает рассмотреть ряд четырехугольников, среди которых трапеция выделена цветом.

«Разрешение парадоксов»

Давайте решим проблему, в чем противоречие в этих высказывание и какое высказывание более верно или верны оба высказывания.

«Помощники»

Дополнение цели урока с помощью слов-помощников:
-Повторим
-Изучим
-Узнаем
-Проверим
Данный прием дает возможность учащимся самим поставить перед собой задачи, формирует у них учебное умение ставить перед собой задачи и находить способы их решения.

«Тема в виде проблемного вопроса»

Формулировка темы в виде вопроса
Тема урока может быть сформулирована так «Почему этих животных отнесли к одному типу?» выявляются признаки по которым классифицированы животные и в соответствии с этим на первом этапе урока уже можно показать морфологические отличия разных групп животных.

«Отгадай ребус, загадку, шараду…»

Подвести к теме и цели урока через ребус, загадку, шараду…

«Проблемная ситуация»

Создаётся ситуация противоречия между известным и неизвестным на этапе актуализации. Одновременно повторяются знания, необходимые для изучения нового материала. Последовательность применения данного приема такова:
– Самостоятельное решение
– Коллективная проверка результатов
– Выявление причин разногласий результатов или затруднений выполнения
– Постановка задачи урока.
Например, на урок русского языка по теме «Правописание слов с ъ и ь разделительными знаками» можно предложить желающим записать на доске ряд слов и по возможности объяснить правописание (Слова дети могут написать по зрительному опыту знакомства с ними): семья, варенье, подъезд, вьюга, съемка.

«Подводящий диалог»

Ведется беседа, направленная на обобщение, конкретизацию, логику рассуждения. Диалог подвожу к тому, о чем дети не могут рассказать в силу некомпетентности или недостаточно полного обоснования своих действий. Тем самым возникает ситуация, для которой необходимы дополнительные исследования или действия. Ставится цель.

«Работа над понятием»

Учащимся предлагаю для зрительного восприятия название темы урока и прошу объяснить значение каждого слова или отыскать в «Толковом словаре». Например, тема урока » Спряжение глаголов». Далее, от значения слова определяем цель урока. Аналогичное можно сделать через подбор родственных слов или через поиск в сложном слове словосоставляющих основ. Например, темы уроков «Словосочетание», «Прямоугольник».

«Группировка»

Ряд слов, предметов, фигур, цифр предлагаю детям разделить на группы, обосновывая свои высказывания. Основанием классификации будут внешние признаки, а вопрос: «Почему имеют такие признаки?» будет задачей урока.

Как решать любые проблемы: алгоритм действий

Содержание статьи

В жизни человека случаются разные ситуации, но главное помнить, что выход всегда есть. Ведь можно изменить себя или отношение к проблеме, поменять саму ситуацию или просто выйти из нее. Любые проблемы можно быстро решить, используя простой алгоритм действий.
Произнесите проблему от своего лица
Такие проблемы, как «начальник хочет слишком многого от меня», «мой парень не обращает внимание на меня» не имеют никакого решения. А вот проблемы, сформулированные лично от вас, вполне решаемы «я не могу выполнить столько задач, сколько просит начальник», «мне одиноко, потому что мой парень не уделяет мне внимание».
Пройдите онлайн-курсы бесплатно и откройте для себя новые возможности Начать изучение
Проанализируйте проблему
Измените себя: вы можете найти себе новое хобби, чтобы заполнить пустоту. Вы можете прокачать свои навыки и выполнить весь объем задач.
Измените отношение к проблеме: вы можете самостоятельно о себе позаботиться. Вы можете смириться с желаниями начальника и не думать об этом.
Поменяйте ситуацию в свою пользу: вы можете поговорить с любимым человеком и сказать о своих чувствах. Вы можете открыто сказать начальнику, что такой объем задач вы не потяните.
Выйти из ситуации: вы можете бросить парня или уволиться с работы.
Выберите подходящий способ
Можно выбрать несколько способов сразу, например, изменить себя и свое отношение. Возможно, вам понадобится достаточно времени, чтобы обдумать варианты. Это нормально.
Устройте мозговой штурм
Когда вы выберите один или несколько способов, выпишите на лист бумаги всевозможные варианты решения проблемы. Чем больше вы напишите, тем лучше. Например, если вы выбрали «изменить себя по отношению к начальнику», то в список вариантов можно выписать «пройти дополнительное обучение», «попросить помощи у начальника», «сделать максимально больше задач». Затем взвесьте все варианты и выберите самый подходящий.
Ответьте на вопросы
После того, как вы выбрали вариант решения проблемы, задайте себе простые вопросы:
Что мне нужно сделать сейчас, чтобы выполнить задуманный вариант?
Из-за чего я не смогу решить проблему?
Кого можно попросить о помощи?
Что конкретно я сделаю завтра, чтобы решить эту проблему?
После того, как вы сами ответите на данные вопросы, начните действовать. Только действия смогут привести вас к желаемому результату.
Пройдите прямо сейчас тест на умение планировать решение задач и узнайте, насколько хорошо вы владеете данным навыком. Откройте для себя новые возможности!
стратегий решения алгоритмов — Learneroo
Не знаете, как решить проблему с алгоритмами? Вот несколько приемов, которые вы можете попробовать:
Решить вручную
«Брутфорс»
Попробуйте решить проблему вручную с помощью некоторых простых данных, а затем посмотрите, сможете ли вы вывести алгоритм из этого процесса. Например, вы, вероятно, могли бы обнаружить алгоритмы сортировки вставкой или выборкой, пытаясь самостоятельно отсортировать список чисел.
3 1 9 5 7 11 13 6 8
Разбей это
«Разделяй и властвуй»
Решите меньшую часть или более простую версию проблемы, а затем работайте над решением всей проблемы.Многие проблемы естественным образом решаются путем решения одной части за раз, но иногда вам нужно выяснить, как можно упростить задачу.
Например, Manhattan Meeting Place попросили найти место встречи в сетке, которая минимизировала бы общее расстояние перемещения всех сторон. Вы можете начать с ответа на вопрос для одной одномерной дороги, прежде чем переходить к сетке. См. Это сообщение в блоге для дальнейшего объяснения. (Ознакомьтесь со многими задачами на Learneroo, чтобы увидеть, как большие задачи можно разбить на более мелкие.)
Соответствие алгоритма
«Поиск в ширину»
Выполните поиск по известным вам известным структурам данных и алгоритмам и посмотрите, можно ли какие-либо из них «подключить» для решения проблемы. Это «Решение в поисках проблемы», но оно может сработать! Например, если вас просят найти кратчайший путь по количеству узлов между двумя точками на графе, просмотрите алгоритмы поиска на графе, чтобы увидеть, что решит эту проблему. (См. Задание приложения Subway, чтобы выполнить очень похожее задание.)
Подозреваете, что проблему можно решить с помощью рекурсии? См. Некоторые советы в обзоре рекурсии. Практикуйте 2 из этих подходов с основной задачей, описанной ниже.
Вызов
У интервьюера есть для вас еще одна задача:
Имея список чисел, вы можете найти все пары чисел, сумма равна тыс. ?
Например, если дан список 1 9 11 13 2 3 7 5 и k как 12 , вы должны найти эти пары: {1 11} , {9 3} и {7, 5} .
Перед тем, как щелкнуть ниже, подумайте, как решить эту проблему вручную и как преобразовать решение в код.
Ручное решение
Это простая задача, и даже в ней есть пример ввода.
Начать с первого числа в списке 1
реализовать 12-1 = 11 , что создаст сканирование
из 12 пар через каждое число справа, чтобы увидеть, найдете ли вы 11 .
Затем перейдите к следующему числу 9 и повторите процесс, просматривая вправо от 9 для поиска 2 .
Повторите этот процесс для всего списка.
Это решение можно легко преобразовать в код, который использует 2 для циклов для просмотра списка.
Опрашивающий: Это подходящее решение, но можете ли вы найти более оптимальное?
Опрашивающий: Да, эта структура данных будет полезна, вы можете сформулировать решение?
Опрашивающий: Хорошо, этот алгоритм будет работать. Теперь ты можешь написать код?
Перейдите к разделу «Дополнительная практика хеширования», чтобы написать код для этой задачи!
Как решать проблемы с помощью алгоритма: психология и этот подход
Автор: Габриэль Сеунагал
Обновлено 8 марта 2020 г.
Медицинское заключение: Лорен Гильбо
В способность к решать проблемы является а очень критический жизнь навык.Нравиться Это или нет, жизнь не всегда легкий; осложнения буду неизбежно возникать, а также когда Oни делать, Это является всегда Мудрый к быть готовый. Теперь, проблемы жестяная банка отличаться из ситуация к ситуация; проблемы также отличаться в природа. Иногда решения находятся довольно легкий к прийти на; в Другие случаи, Это требует а немного более стратегия а также созерцание к решать а проблема.
Этот является куда в алгоритм решение проблем входит в уравнение. Делал ты знать что это является а очень настоящий психологический подход? В более ты понимать о решение проблем с участием ан алгоритм, в более естественный а также разумный Это становится.Из курс, в Только способ к понимать в психологический подход из решение проблемы с участием алгоритмы является к тщательно рассмотрение в иметь значение.
Источник: rawpixel.com
А Полный Обзор Из Решение проблем С участием An Алгоритм
Один из в самый важный вещи к помнить о алгоритмы является в методология. Положил просто, ан алгоритм является просто а серии из хронологический протоколы который привести к а решение для а проблема. Этот звуки весьма просто, но там жестяная банка быть много переменные который влияние или изменение в протоколы в ан алгоритм.Определенный алгоритмы имеют кратные пути к в желанный решения, в то время как другие находятся очень прямой а также узкий.
Как Делать Алгоритмы Помощь К Решать Проблемы?
В шаг за шагом инструкции который по своей сути включать алгоритмы находятся какие помогает люди решать проблемы. В а вкратце ан алгоритм является а формула который является разработан к достигать а решение. Некоторые алгоритмы находятся сложный, в то время как другие находятся просто а также весьма легкий к получать ан понимание из. Полагать Это или нет, алгоритмы находятся очень настоящее время в наш дня в день жизни.Если ты использовать технология, там находятся а серии из алгоритмы в место к гарантировать что ваш продукты Работа эффективно. Когда исправление проблем ошибки возникать, там находятся дополнительный алгоритмы который существовать для решение проблем.
Обзор В Плюсы А также Минусы Из Решение проблем С участием Алгоритмы
Там находятся два стороны к каждый история. Это идет без говоря что алгоритмы находятся очень хорошо задокументированы инструменты из решение проблем который имеют стоял в тестовое задание из время. Тем не мение, к понимать в психологический аспекты из это подход, оба в преимущества а также недостатки из алгоритмы должен быть рассмотрено.Этот обеспечивает а полный Смотреть в в великий схема из вещи.
Прямой А также Узкий
В качестве а решение проблем техника, алгоритмы находятся очень прямой а также узкий. Этот средства что если Вы смотрящий к решать а проблема который является очень аналитический в природа, тогда ан алгоритм буду вероятно доказывать к быть в самый подходящее дорожка к а решение. Стабильность, доказательство, а также предсказуемость находятся в части из алгоритмы который делать алгоритмы удивительный инструменты.
Прежний Знание
В природа из алгоритмы жестяная банка отличаться, в зависимости на в проблема который потребности к быть решено.В определенный случаи, это средства что прежний знания в различный области является необходимо для кто-то к понимать а специфический алгоритм а также все что Это влечет за собой. Решение проблем с участием ан алгоритм является все хорошо а также хороший, но в человек кто является попытка к нанять это подход потребности к знать какие они работающий с участием.
Шаг за шагом Протоколы
Источник: rawpixel.com
В качестве ранее принято к сведению, алгоритмы находятся состоял из шаг за шагом протоколы который должен быть последовал в хронологический порядок.В много случаи, это является ан актив потому что Это довольно часто предотвращает люди из изготовление дополнительный ошибки или иначе ухудшение ан уже плохой проблема. Некоторые люди процветать когда Oни имеют несколько параметры, но другие делать хорошо с участием алгоритмы, в связи к их по своей сути аналитический природа.
Жестяная банка Алгоритмы Решать Все Проблемы В Психология?
В психологический подход к решение проблем с помощью алгоритмы является бесспорно. Тем не мение, Это делает поднимать вопросов о ли или нет алгоритмы находятся в самый подходящее решения для находка решения к все проблемы в в психологический область.
В а вкратце в отвечать является нет. Этот не брать прочь из в эффективность из алгоритмы. Этот не иметь в виду что люди должен нет нанять алгоритмы к решать в подходящее проблемы. Тем не мение, там находятся много ситуации, особенно в в психологический область куда а хронологический шаг за шагом серии из протоколы является нет достижимый. Для в качестве большой в качестве алгоритмы мая быть, знание когда к использовать их а также когда к нанять Другие средства из решение проблем является первостепенное значение.
В Существование Из Переменные
В в психологический поле, в существование из переменные является что-то который должен быть принято к сведению а также учтены для.Этот является один из в причины Почему алгоритмы не мочь быть использовал к решать каждый проблема. Брать, для пример, кто-то кто является испытывающий депрессия а также смотрящий для а способ к Чувствовать лучше а также улучшать их жизнь. В это ситуация Это бы быть нереально к просто бросать кто-то а формула а также рассказать их к следить каждый шаг к чувство хороший опять таки. Это просто нет как умственный а также эмоциональный здоровье работает.
В а кейс нравиться это, в пациент бы необходимость к Работа с участием а Терапевт кто бы помощь их получать к в Нижний из их депрессия.Там находятся так много причины который жестяная банка курок депрессия ли это а смерть в в семья, а потеря из трудоустройство, или даже ан неразрешенный проблема из детство. До кто-то жестяная банка даже начинать к Чувствовать лучше а также достигать в решение к их проблема, Oни бы первый необходимость к получать к в Нижний из в лежащий в основе проблема.
Проблемы В Межличностный Отношения
Пока что Другая площадь куда алгоритмы иметь тенденцию к падение короткая является в случаи из проблемы в межличностный отношения.Там находятся много проблемы который возникать потому что два люди находятся неспособный к получать вместе или видеть с глазу на глаз на различный имеет значение. сходным образом к в индивидуальный кто мая быть собирается через депрессия просто вручение ан алгоритм к в люди кто не получающий вместе бы нет решать в проблема. В качестве а иметь значение из факт, Это мог бы Только дальше обострять оба стороны. Этот является ан дополнительный пример из а проблема который не могу быть решено с участием ан алгоритм.
Источник: advicoachva.wordpress.com
А Слово На Решение проблем В качестве А Всего
В психология а также Другие области из жизнь, там буду всегда быть различный проблемы который возникают.Проблемы жестяная банка быть сгенерированный к недоразумения, различия в восприятие, неразрешенный вопросы из в мимо, а также так много более. Иногда проблемы находятся на уровне поверхности вопросы, в то время как другие требовать а маленький более копать к получать к в Нижний из их, а также это OK.
Понимание алгоритмы является большой, а также знание когда к использовать их является даже более классно. Там находятся ситуации куда алгоритмы находятся в Лучший дорожка к а решение; существование знающий из это является просто в качестве важный в качестве знание когда Другие методы находятся Лучший использовал.Проблемы жестяная банка быть очень сложный, а также мы мог бы спотыкаться в качестве мы пытаться к найти в Правильно решения. В ключ является к хранить собирается а также нет разрешать в проблема к спираль из из контроль.
Ты Не надо Иметь К Делать Это Один
К несчастью, там находятся а серии из заблуждения который вовлекать проблемы а также как люди должен идти о решение их. Много частные лица имеют был вел к полагать что если ан проблема возникает, они на их собственный а также имеют к лицо Это в одиночестве. В реальность это является просто нет правда, ни является Это здоровый.
Там буду всегда быть вызовы а также препятствия в жизнь; тем не мение, Ресурсы а также руководство буду также быть доступный к те кто находятся открытым а также восприимчивый к Это. Есть ничего такого неправильный с участием спрашивая для помощь. Есть ничего такого неправильный с участием получающий а второй мнение, доверчивый в Другие люди а также получающий другой перспективы. Этот жестяная банка быть полезный, а также в много случаи, нет попытка к идти в Это в одиночестве жестяная банка делать решения более очевидный а также Полегче к нести из.
Бесчисленное множество учеба имеют подтверждено в преимущества из имея а надежный служба поддержки система.Когда ты имеют люди в ваш угол кто уход о ты а также имеют ваш Лучший интересы в сердце, Это обеспечивает а смысл из мир. А служба поддержки система также дает ты а здоровый сеть который жестяная банка помощь ты учиться, расти, а также эволюционировать в качестве а человек существование.
Работающий С участием А Ментальный Здоровье Специалист
Делал ты знать что один из в Лучший люди к имеют в ваш служба поддержки система является а советник или Терапевт? Нет иметь значение кто ты находятся, какие ты мая имеют ушел через, или какие ваш ситуация является, а умственный здоровье специалист жестяная банка быть из ценить к ты.Теперь, много люди мая имеют вопросов или оговорки о работающий с участием а Терапевт. Иногда, люди задаваться вопросом ли или нет они будут быть судили. Другие имеют беспокойство о открытие вверх к а чужой человек кто Oни имеют пока что к знать.
Один из в самый важный вещи к понимать о терапия является что есть нет суждение. Любой советник или специалист что ты Работа с участием является Только обеспокоенный с участием помогая ты. Тем не мение, для это к случаться, разговоры о жесткий темы буду необходимость к случаться. В в длинный запустить, ты ценить это потому что это будет помощь ты жить а лучше а также более удовлетворение жизнь.
Здесь в BetterHelp, мы имеют а большой команда из терапевты кто бы быть более чем взволнованный к Работа с участием ты. Нет иметь значение какие проблемы ты мая быть столкнулся с участием, Вы нет в одиночестве а также ты жестяная банка получать через это. Если это звуки интересно к ты а также если ты бы нравиться к брать в следующий шаг к улучшение ваш жизнь, тогда Вы в удача.
Ты жестяная банка контакт BetterHelp в любой время а также из в любом месте просто к щелчок здесь.
Мысль | Britannica
Элементы мысли
Широкое использование слов в мышлении («безмолвная речь») способствовало убеждению, особенно среди психологов-бихевиористов и необихевиористов, что думать — значит соединять языковые элементы субголосом.Ранние эксперименты показали, что мышление обычно сопровождается электрической активностью в мышцах артикуляционных мышц мыслителя (например, в горле). Благодаря более поздней работе с электромиографическим оборудованием стало очевидно, что мышечные явления не являются действительными проводниками мышления; они просто облегчают соответствующую деятельность мозга, когда интеллектуальная задача особенно сложна. Отождествление мышления с речью подверглось критике со стороны российского психолога Льва Семеновича Выготского и швейцарского психолога развития Жана Пиаже, которые наблюдали истоки человеческого мышления в общей способности детей объединять невербальные действия в эффективные и гибкие комбинации.Эти теоретики настаивали на том, что мышление и речь возникают независимо, хотя они признавали глубокую взаимозависимость этих функций.
Три ученых, придерживающихся разных подходов: русский физиолог XIX века Иван Михайлович Сеченов; американский основатель бихевиоризма Джон Б. Ватсон; и Пиаже — независимо пришли к выводу, что действия, которые служат элементами мышления, являются интернализованными или «дробными» версиями двигательных реакций. Другими словами, элементы считаются ослабленными или сокращенными вариантами нервно-мышечных процессов, которые, если бы они не подвергались частичному торможению, вызывали бы видимые движения тела.
Чувствительные инструменты действительно могут обнаруживать слабую активность в различных частях тела, кроме органов речи, например, в конечностях человека, когда движение мыслится или воображается, но не происходит на самом деле. Недавние исследования показывают существование желудочного «мозга», набора нейронных сетей в желудке. Такие открытия породили теории о том, что люди думают всем телом, а не только мозгом, или что, по словам американского психолога Б. Ф. Скиннера, «мысль — это просто поведение — словесное или невербальное, скрытое или явное. .”
Логическим результатом этих и подобных заявлений была точка зрения периферизма. В работе Уотсона и американского психолога Кларка Л. Халла очевидно, что мышление зависит от событий в мускулатуре: этих событий, известных как проприоцептивные импульсы (т. Е. Импульсы, возникающие в ответ на физическое положение, позу, равновесие или внутреннее состояние). состояние), влияют на последующие события в центральной нервной системе, которые, в конечном итоге, взаимодействуют с внешними стимулами и определяют дальнейшие действия.Однако есть свидетельства того, что мышлению не препятствует прием лекарств, подавляющих всю мышечную активность. Более того, такие исследователи, как американский психолог Карл С. Лэшли, указали, что мышление, как и другие более или менее квалифицированные действия, часто происходит так быстро, что не хватает времени для передачи импульсов из центральной нервной системы. систему к периферическому органу и обратно между последовательными шагами. Таким образом, централистский взгляд на то, что мышление состоит из событий, ограниченных мозгом (хотя часто сопровождаемых широко распространенной активностью в остальной части тела), получил распространение позже в 20 веке.Тем не менее, каждое из этих нейронных событий можно рассматривать как ответ (на внешний стимул или на более раннюю нейронно-опосредованную мысль или комбинацию мыслей) и как стимул (вызывающий последующую мысль или двигательную реакцию).
Элементы мышления классифицируются как «символы» в соответствии с концепцией знакового процесса («семиотика»), которая выросла из работ философов (например, Чарльза Сандерса Пирса), лингвистов (например, CK Ogden и Ivor A. Ричардс) и психологов, специализирующихся на обучении (Э.g., Hull, Neal E. Miller, O. Hobart Mowrer и Charles E. Osgood). Суть этой концепции состоит в том, что стимулирующее событие x можно рассматривать как знак, представляющий (или «обозначающий») другое событие y , если x вызывает некоторые, но не все, поведения (как внешние, так и internal), который был бы вызван y , если бы он присутствовал. Когда стимул, который квалифицируется как знак, является результатом поведения организма, для которого он действует как знак, он называется «символом».«Реакции, вызывающие раздражение», которые, как говорят, составляют мыслительные процессы (например, когда человек думает о чем-то поесть), являются яркими примерами.
Этот подход, которому отдают предпочтение психологи в отношении стимула-реакции (S-R) или неоассоциативного течения, контрастирует с таковым из различных когнитивистских или неорационалистских теорий. Вместо того, чтобы рассматривать компоненты мышления как производные вербальных или невербальных двигательных действий (и, таким образом, подчиняться законам обучения и производительности, применимым к усвоенному поведению в целом), когнитивисты рассматривают компоненты мышления как уникальные центральные процессы, регулируемые принципами, которые свойственно им.Эти теоретики придают первостепенное значение так называемым структурам, в которых организованы «когнитивные» элементы, и они склонны видеть выводы, применения правил, репрезентации внешней реальности и другие составляющие мышления в действии даже в простейших формах усвоения знаний. поведение.
Школа гештальт-психологии считает, что составляющие мышления имеют по существу ту же природу, что и паттерны восприятия, которые нервная система конструирует из сенсорных возбуждений.После середины 20 века аналогии с компьютерными операциями приобрели широкое распространение; как следствие, мышление стало описываться в терминах хранения, поиска и передачи элементов информации. Рассматриваемая информация считалась свободно переводимой с одной «кодировки» на другую без ущерба для ее функций. Важнее всего было то, как были объединены события и какие другие комбинации могли произойти вместо этого.
Использование алгоритмов для решения математических задач — видео и стенограмма урока
Добавление столбца чисел
Хорошим примером использования математического алгоритма является подход «слева направо» для добавления столбца чисел.
Допустим, вы начинаете с уродливой группы чисел, которую вам приходится складывать вручную — без калькулятора, компьютера, смартфона и т. Д. (Ну, вы знаете, всякие штуки из каменного века!).
У вас есть 5280, 495 и 1520, и вам нужна общая сумма. Итак, вы берете лист бумаги и думаете об алгоритме.
Вот алгоритм:
Поместите числа в столбец, сопоставив их числовые разряды (вы знаете, единицы идут с единицами, десятки — с десятками и т. Д.).
Проведите под ними линию, чтобы отделить добавляемые числа от результатов.
Добавьте столбец 1000 и запишите сумму под строкой в столбце 1000.
Добавьте столбец 100 и запишите сумму в столбце 100 под суммой вашей 1000.
Сложите столбец десятков и запишите полученное количество в столбце десятков под вашими сотнями.
Сложите столбец 1 и запишите полученный результат в столбце 1 под вашей суммой 10.
Отрегулируйте столбец 1: если сумма 1 больше 9, то у вас есть одна или несколько десятков в столбце 1.Их нужно переместить в десятку. Напишите число десятков в столбце десятков, а оставшееся оставьте в столбце единиц.
Отрегулируйте столбец десятков: Если у вас есть какие-то 100 в столбце десятков, удалите их из столбца десятков и поместите это число 100 в столбец сотен.
Отрегулируйте столбец 100: Если есть какие-либо 1000 в столбце 100, переместите их в столбец 1000.
Подсчитайте результаты каждого столбца и запишите их в ряд.Теперь у вас должна быть общая (сумма) ваших исходных чисел.
Давайте применим эти шаги, чтобы решить нашу проблему.
Сначала поместим числа в столбец для сложения:
Затем нарисуйте линию внизу, чтобы разделить ваши результаты:
Глядя на столбец 1000 (крайний левый), мы видим, что только два из чисел на самом деле имеют цифру для 1000, поэтому мы сложим их вместе (5000 + 1000 = 6000 ).Если хотите, вы можете записать нули вместо 1000, но мы просто оставим число 1000 в столбце 1000, чтобы показать, что это число представляет 1000:
Добавление столбца 1000-х годов
Глядя на столбец 100, мы видим, что в первом числе две сотни, во втором — четыре, а в третьем — пять. Складывая 100 единиц вместе, мы получаем 11 из них, которые мы запишем в столбце 100 под нашей общей суммой 1000.Обратите внимание, что у нас есть одна 1000 из наших 1100, но мы разберемся с ним позже:
Добавление столбца сотен
Далее мы добавим десятки. Мы получаем 19 из них, или 190. Мы замечаем 100 в этом общем количестве, и нам придется переместить его в столбец 100 позже, но давайте сначала проверим 1:
Добавление 10-го столбца
Складывая единицы вместе (два нуля и 5), мы получаем в сумме 5 для столбца единиц.Теперь мы готовы приступить к завершению.
Добавление 1-го столбца
Потянем пятерку вниз. Нет 10 секунд для переноса в следующий столбец.
Переходя к нашим девятнадцати десяткам, мы переместим одну сотню в следующий столбец, а девятку опустим вниз.
Перемещаясь к разряду сотен в наших итогах, мы добавляем 100, которые мы переместили из столбца десятков, к одиннадцати сотням, которые у нас уже есть.Получается двенадцать сотен, поэтому мы вытащим 1000, переместим его в столбец 1000, а две оставшиеся 100 положим внизу.
Наконец, мы суммируем 1000, включая ту, которую мы переместили из общей суммы 100. Записав 7 внизу, мы закончили!
Суммирование итогов по столбцам
Теперь это, вероятно, кажется большим количеством дополнительных шагов, которые нужно предпринять для этой проблемы, но поймите, что алгоритмы предназначены для точных наборов инструкций, которые работают каждый раз.Конечно, вы можете использовать ярлыки, но всегда следите за тем, чтобы не упустить что-то важное, когда выполняете математические операции. У каждого шага есть причина быть там!
Где взять алгоритмы?
Существуют алгоритмы для каждого вида математических операций, которые вам нужно выполнить. Многие отличные веб-сайты предлагают алгоритмы, которые будут работать на вас, включая шаги и изображения. Например, скажем, вам нужен алгоритм факторизации трехчлена. Математический текст может предложить хороший набор шагов, но вы также можете найти в Интернете видеоролики, которые очень помогут.Если вы выполните поиск, используя термины «алгоритм» и «трехчлен», вы увидите целый список сайтов, предлагающих инструкции по факторингу трехчленов. Вытяните тот, который вам нравится, и вы готовы к работе!
Краткое содержание урока
Алгоритмы — это точные наборы инструкций, которые приведут вас к желаемой цели. В математике вам дадут именно те шаги, которые необходимы для решения проблемы. Вы можете найти полезные алгоритмы в учебниках и в Интернете. Правильный алгоритм — ваш ключ к решению любой математической задачи, с которой вы когда-либо столкнетесь!
типов алгоритмов и их использование
Введение в типы алгоритмов
Алгоритм относится к последовательным шагам и процессам, которые необходимо выполнить для решения проблемы.Могут быть разработаны различные типы алгоритмов для решения различных задач, хотя в программировании мы рассматриваем следующие важные алгоритмы для решения проблемы.
Вот список типов алгоритмов для начала:
Алгоритм грубой силы
Жадный алгоритм
Рекурсивный алгоритм
Алгоритм обратного отслеживания
Алгоритм разделения и владения
Алгоритм динамического программирования
Рандомизированный алгоритм
Алгоритм грубой силы
Простейший алгоритм, который можно разработать для решения проблемы, называется алгоритмом грубой силы.Чтобы найти оптимальное решение, нам нужно сначала получить решение, а затем попытаться его оптимизировать. Каждая проблема может быть решена методом грубой силы, хотя, как правило, не требует заметной пространственной и временной сложности.
Например:
Позже мы увидим, что эта временная сложность будет уменьшена до O ( logn ).
Жадный алгоритм
В этом алгоритме принимается правильное на данный момент решение без учета будущего.Это означает, что выбирается какой-то локальный лучший и считается глобальным оптимальным. В этом алгоритме есть два свойства.
Жадно выбирая лучший вариант
Оптимальное свойство подструктуры: Если оптимальное решение может быть найдено путем поиска оптимального решения его подзадач.
Жадный алгоритм не всегда работает, но когда он работает, он работает как шарм! Этот алгоритм прост в использовании и в большинстве случаев является самым простым.Но принятие лучших локальных решений не всегда работает так, как кажется. Итак, на смену ему приходит надежное решение под названием подход динамического программирования.
Приложения
Сортировка: сортировка по выбору, топологическая сортировка
Алгоритмы Прима и Крускала
Проблема смены монет
Проблема дробного рюкзака
Алгоритм планирования заданий
Для лучшего понимания давайте рассмотрим наиболее распространенную проблему, например, Планирование заданий проблема: Давайте рассмотрим ситуацию, когда нам дается время начала и окончания различных событий в аудитории.Теперь ваша задача — максимизировать количество событий, которые могут быть организованы в аудитории, где никакие два события не перекрываются (время начала или время окончания одного события не попадает между начальной и конечной точкой другого события).
Мы рассматриваем шесть таких событий:
Теперь решение с использованием грубой силы заставит нас подумать, что если мы отсортируем события по времени их начала и начнем с первого события, исключив все события, которые перекрывают предыдущие, безусловно, дадут решение, но это не приведет к максимальному увеличению количества событий.Посмотрим, отсортировав по времени начала —
Итак, события, которые можно организовать: A, F. Итак, наш метод грубой силы будет иметь несколько таких случаев и потерпит неудачу, если мы не выберем оптимальное начальное событие. Теперь посмотрим, что предлагает наш жадный алгоритм. В соответствии с жадным алгоритмом мы сортируем события по времени их окончания, т.е. выбираем события, которые заканчиваются раньше. Наша новая таблица событий станет:
Итак, мы выбираем — B, E, C, что, безусловно, является большим количеством событий, чем предыдущие.Следовательно, в таких случаях жадный алгоритм дает лучшее решение для этого типа проблемы.
Рекурсивный алгоритм
Это один из самых простых в разработке алгоритмов, поскольку он не требует особого внимания к каждой подзадаче. Это означает, что нам просто нужно подумать о существующих кейсах и решении простейшей подзадачи, все остальные сложности будут обработаны автоматически. Рекурсия — очень мощный инструмент, хотя здесь мы всегда должны заботиться об управлении памятью, поскольку рекурсия работает с использованием рекурсивного стека, который вызывается каждый раз при вызове функции рекурсии.Рекурсия просто означает вызов самого себя для решения своих подзадач.
Например:
Сложность времени: O ( n )
Хотя всегда не забывайте указывать базовый случай, иначе цикл будет продолжаться до бесконечности, давая ошибку памяти. Этот алгоритм проще разработать и реализовать.
Алгоритм поиска с возвратом
Это усовершенствование подхода грубой силы. Здесь мы начинаем с одного возможного варианта из многих доступных и пытаемся решить проблему, если мы сможем решить проблему с помощью выбранного хода, тогда мы распечатаем решение, иначе мы вернемся назад, выберем какой-то другой и попытаемся решить его.Это форма рекурсии, просто когда данный вариант не может дать решение, мы возвращаемся к предыдущему варианту, который может дать решение, и переходим к другим вариантам.
Приложения
Генерация всех двоичных строк
Задача N-Queens
Задача о ранце
Задача раскраски графа
Давайте посмотрим, как этот алгоритм генерирует все строки с n битами.
Алгоритм разделяй и властвуй
Это один из наиболее часто используемых алгоритмов в программировании.Этот алгоритм делит проблемы на подзадачи и затем решает каждую из них, а затем объединяет их, чтобы сформировать решение данных проблем.
Опять же, с его помощью невозможно решить все проблемы. Как следует из названия, он состоит из двух частей: разделите проблему на подзадачи и решите их.
Объедините решение каждой из вышеперечисленных проблем.
Этот алгоритм широко используется в различных задачах, поскольку он достаточно стабилен и оптимален для большинства поставленных задач.
Данная задача делится на две части размером n / a и n / b, а затем вычисляется отдельно и рекурсивно, чтобы вернуть результат и объединить их для формирования решения.
Приложения :
Двоичный поиск
Сортировка слиянием и быстрая сортировка
Медианный поиск
Умножение матрицы
Давайте обсудим простейшее применение двоичного поиска. Ранее мы описали, как поиск элемента в отсортированном массиве занимает O ( n ) времени, на этот раз мы применяем алгоритм «разделяй и властвуй», чтобы уменьшить его сложность до O ( logn ).
Выход 1:
Поток программы перемещается к правому подмассиву, поскольку пять больше текущего mid (3) и, следовательно, не выполняет итерацию по половине элементов и, следовательно, снижает временную сложность. Хотя это неприменимо, если массив не отсортирован, как можно понять, он просто проигнорирует одну часть массива, и алгоритм не сработает.
Динамический алгоритм

Это наиболее востребованный алгоритм, поскольку он обеспечивает наиболее эффективный способ решения проблемы.Это просто означает помнить прошлое и применять его к соответствующим результатам в будущем, и, следовательно, этот алгоритм довольно эффективен с точки зрения временной сложности.
Dynamic Programming имеет два свойства:
Оптимальная подструктура: Оптимальное решение проблемы содержит оптимальное решение ее подзадач.
Перекрывающиеся подзадачи : Рекурсивное решение содержит небольшое количество отдельных подзадач.
Этот алгоритм имеет две версии:
Подход снизу вверх: Начинает решать проблемы снизу i.е. сначала решая последние возможные подзадачи и используя результат решения вышеупомянутых подзадач.
Подход сверху вниз: Начинает решать проблемы с самого начала, чтобы прийти к требуемой подзадаче и решить ее, используя ранее решенные подзадачи.
Приложения
Самая длинная общая подпоследовательность, Самая длинная возрастающая подпоследовательность, Самая длинная общая подстрока и т. Д.
Алгоритм Беллмана-Форда
Цепное умножение матрицы
Сумма подмножества
Задача о ранце и многое другое.
Рассмотрим простой пример такого алгоритма. Нахождение последовательности Фибоначчи .
Рекурсивный стек функции для n = 4
Сложность времени: O (n) Сложность пространства: O (n)
Как мы видим, подход динамического программирования дает более быстрый результат, хотя и занимает дополнительное место. Большинство проблем, связанных с поиском n-го элемента в последовательности, можно решить быстрее с помощью динамического программирования.
Рандомизированный алгоритм
Это тип алгоритма, который принимает решение на основе случайных чисел i.2 ) в худшем случае. Хотя при правильной интерпретации он может дать лучшее время работы O ( nlogn ).
Приложения
Рандомизированная быстрая сортировка
Алгоритм Кагера и т. Д.
Чтобы узнать больше о курсах, нажмите здесь.
Превосходный алгоритм поиска кратчайшего маршрута — ScienceDaily
Одна из самых классических алгоритмических задач связана с вычислением кратчайшего пути между двумя точками.Более сложный вариант проблемы — когда маршрут пересекает изменяющуюся сеть — будь то дорожная сеть или Интернет. В течение 40 лет разрабатывался алгоритм, обеспечивающий оптимальное решение этой проблемы. Теперь компьютерный ученый Кристиан Вульф-Нильсен из Копенгагенского университета и двое его коллег-исследователей придумали рецепт.
Когда мы отправляемся в новое место, большинство из нас доверяет компьютерным алгоритмам найти лучший маршрут, используя автомобильный GPS-навигатор или общественный транспорт и картографические приложения на своем телефоне.Тем не менее, бывают случаи, когда предлагаемый маршрут не совсем соответствует действительности. Это потому, что дорожные сети, сети общественного транспорта и другие сети не статичны. Лучший маршрут может внезапно оказаться самым медленным, например потому что очередь образовалась из-за дорожных работ или аварии.
В подобных ситуациях люди, вероятно, не задумываются о сложной математике, лежащей в основе предложений маршрутизации. Используемое программное обеспечение пытается решить вариант классической алгоритмической задачи «кратчайшего пути», кратчайшего пути в динамической сети.В течение 40 лет исследователи работали над поиском алгоритма, который мог бы оптимально решить эту математическую головоломку. Теперь Кристиан Вульф-Нильсен из факультета компьютерных наук Копенгагенского университета вместе с двумя коллегами смог расколоть орех.
«Мы разработали алгоритм, для которого теперь у нас есть математическое доказательство, что он лучше, чем любой другой алгоритм до настоящего момента — и наиболее близок к оптимальному, который когда-либо будет, даже если мы заглянем на 1000 лет в будущее, «говорит доцент Вульф-Нильсен.Результаты были представлены на конференции FOCS 2020.
Оптимально в этом контексте относится к алгоритму, который тратит как можно меньше времени и памяти компьютера на вычисление наилучшего маршрута в данной сети. Это относится не только к дорожным и транспортным сетям, но также к Интернету или любым другим типам сетей.
Сети в виде графиков
Исследователи представляют сеть как так называемый динамический граф. «В этом контексте граф представляет собой абстрактное представление сети, состоящей из ребер, дорог, например, и узлов, представляющих, например, перекрестки.Когда график является динамическим, это означает, что он может меняться со временем. Новый алгоритм обрабатывает изменения, состоящие из удаленных краев — например, если эквивалент участка дороги внезапно становится недоступным из-за дорожных работ.
«Огромное преимущество рассмотрения сети как абстрактного графа состоит в том, что его можно использовать для представления любого типа сети. Это может быть Интернет, куда вы хотите отправлять данные по как можно более короткому маршруту, человеческий мозг или сеть дружеских отношений в Facebook.Это делает алгоритмы графов применимыми в самых разных контекстах », — объясняет Кристиан Вульф-Нильсен.
Традиционные алгоритмы предполагают, что график статичен, что редко бывает верным в реальном мире. Когда такие алгоритмы используются в динамической сети, их нужно запускать повторно каждый раз, когда на графике происходит небольшое изменение, что тратит время.
Чем больше данных, тем лучше алгоритмы
Поиск лучших алгоритмов полезен не только во время путешествий.Это необходимо практически в любой области, где производятся данные, как указывает Кристиан Вульф-Нильсен:
«Мы живем во время, когда объемы данных растут с огромной скоростью, а развитие оборудования просто не может идти в ногу со временем. Чтобы управлять всеми данными, которые мы производим, нам необходимо разработать более умное программное обеспечение, которое требует меньшего количества выполняемых операций. время и память. Вот почему нам нужны более умные алгоритмы », — говорит он.
Он надеется, что этот алгоритм или некоторые из лежащих в его основе методов можно будет использовать на практике, но подчеркивает, что это теоретические доказательства и в первую очередь требуют экспериментов.
Предпосылки
На престижной конференции FOCS 2020 была представлена исследовательская статья «Почти оптимальная декрементальная SSSP в плотных взвешенных орграфах».
Статья написана Кристианом Вульф-Нильсеном из факультета компьютерных наук Копенгагенского университета и бывшим докторантом факультета компьютерных наук Максимилианом Пробстом Гутенбергом и доцентом Аароном Бернстайном из Университета Рутгерса.
Версия проблемы «кратчайшего пути», которую решили исследователи, называется «декрементальной проблемой кратчайшего пути от одного источника».«По сути, речь идет о поддержании кратчайших путей в изменяющейся динамической сети от одной начальной точки до всех других узлов в графе. Изменения в сети состоят в удалении ребер.
В статье дается математическое доказательство того, что алгоритм, по сути, является оптимальный для динамических сетей. В среднем, пользователи смогут менять маршруты в соответствии с расчетами, сделанными за постоянное время.
Проблема Aged P и NP. Почему P = NP такая большая проблема, что это… | Дэвид Чонг
Так что же тогда представляет собой проблема P и NP?
Для записи, статус-кво таков, что P ≠ NP.
P (полиномиальное время) относится к классу задач, которые могут быть решены алгоритмом за полиномиальное время. Задачи в классе P могут варьироваться от чего угодно, например, умножения до поиска наибольшего числа в списке. Это относительно «легкий» набор проблем.
NP (недетерминированное полиномиальное время) относится к классу задач, которые могут быть решены за полиномиальное время с помощью недетерминированного компьютера.По сути, это еще один способ сказать: «Если у меня неограниченная вычислительная мощность (то есть столько компьютеров, сколько мне нужно), я способен решить любую проблему не более чем за полиномиальное время». Более интуитивно, однако, это относится к классу проблем, который в настоящее время не имеет возможности найти достаточно быстрый (полиномиальное время) ответ, НО можно быстро проверить (за полиномиальное время), если предоставить решение проблемы. Термин «проверено» здесь означает, что можно проверить правильность предоставленного решения.
Очевидно, исходя из приведенного выше определения, P ⊆ NP . Давайте рассмотрим пример, чтобы проиллюстрировать эту абстрактную проблему.
Один из наиболее распространенных, но эффективных примеров — Sudoku . Учитывая неразрешенную сетку судоку (например, 9 x 9), алгоритму потребуется изрядное количество времени, чтобы решить ее. Однако, если сетка 9 x 9 увеличится до сетки 100 x 100 или 10 000 x 10 000, время, необходимое для ее решения, увеличится на экспоненциально на , потому что сама проблема становится значительно сложнее.Однако, учитывая решенную сетку судоку (9 x 9), довольно просто проверить, что конкретное решение действительно правильное, даже если размер увеличивается до 10 000 на 10 000. Это будет медленнее, но время проверки решения увеличивается медленнее ( полиномиально ).
Существует много других проблем NP , в том числе проблема ранца и проблема коммивояжера, и они похожи в том, что их трудно решить, но быстро проверить.Основная проблема, которую мы пытаемся решить здесь:
Означает ли возможность быстрого распознавания правильных ответов NP , что существует также быстрый способ их найти?
Если это так (т.е. P = NP), это может сильно изменить то, как мы смотрим на эти проблемы NP , потому что это означает, что есть быстрый способ решить все эти проблемы, просто мы пока не могу понять, как это сделать.
NP-Complete и NP-Hard
Среди этих проблем NP существует Король всех проблем, который исследователи называют проблемами NP-Complete . Формально они представляют собой набор задач, для каждой из которых любая другая задача NP может быть уменьшена на ( адресуется ниже ) за полиномиальное время, и решение которой все еще может быть проверено за полиномиальное время. Это означает, что любая проблема NP может быть преобразована в задачу NP-Complete .
Неформально они являются наиболее «сложными» из проблем NP . Таким образом, если любая одна задача NP-Complete может быть решена за полиномиальное время, то каждые NP-Complete задача может быть решена за полиномиальное время и каждые задачи в NP можно решить за полиномиальное время (т.е. P = NP). Самый известный пример — задача коммивояжеров.
Фото JESHOOTS.COM на Unsplash
Также существует набор проблем под названием NP-Hard . Эти задачи не менее сложны, чем задачи NP , но без — условия, которое требует решения за полиномиальное время. Это говорит о том, что проблемы NP-Hard не обязательно могут быть частью класса NP . Примером может служить решение шахматной доски — учитывая состояние шахматной доски, практически невозможно определить, является ли данный ход в данном состоянии оптимальным ходом.Формально не существует алгоритма полиномиального времени для проверки решения проблемы NP-Hard .
Если мы сложим два вместе, проблема NP-Complete подразумевает, что это NP-Hard , но проблема NP-Hard НЕ означает, что это NP-Complete .
Определение NP-полноты
Проблема L , NP-Complete , если:
L NP-Hard
L принадлежит NP
Диаграмма ниже ( сфокусируйтесь на левой стороне ), чтобы прояснить ситуацию.Диаграмма
P в сравнении с NP (источник: https://en.wikipedia.org/wiki/P_versus_NP_problem)
Подождите, что это значит, если уменьшить A до B?
Сокращение составляет суть NP-Полнота .
Неформально проблема L1 может быть сведена к другой проблеме L2 , если:
Любой экземпляр L1 может быть смоделирован как экземпляр L2
Решение последнего обеспечивает решение первое и наоборот
Чтобы понять это интуитивно, можно думать об этом как о таковом:
Если L1 сводится к L2, L1 должен быть СОВЕРШЕННО таким же жестким, как L2.

Проблемное обучение

1.6 Алгоритм создания проблемной ситуации в процессе теоретического обучения. Влияние проблемного обучения на интеллектуальное развитие учащихся

Похожие главы из других работ:

2.1 Создание проблемной ситуации при изучении учебного материала

Глава 2. Активные методы теоретического обучения и их использования в процессе обучения производственно-технических задач

ГЛАВА 2. Активные методы теоретического обучения и их использование в процессе обучения ПТЗО.

2.1 Алгоритм введения технологии взаимного обучения

1.

2. Реализация проблемной ситуации при написании сочинений на уроках русского языка

1. ТЕОРЕТИЧЕСКИЕ АСПЕКТЫ ИСПОЛЬЗОВАНИЯ ПРОБЛЕМНОЙ ТЕХНОЛОГИИ В ТРЕНЕРОВОЧНОМ ПРОЦЕССЕ ДЗЮДОИСТОВ

· анализ статьи И. Е. Маловой, И. Е. Гуреевой «Основы создания тетрадей для ситуации использования компьютерной презентации в учебном процессе»;

2.2 Анализ предложенного сценария проблемной лекции и рекомендации по эффективному использованию проблемной лекции

1.3 Структура проблемной задачи и методы проблемного обучения

II.2. Проблемные ситуации: понятие и типы, способы и правила создания

1.3 Современные подходы к развитию теоретического мышления у младших школьников в процессе учебной и внеучебной деятельности

2. Практические аспекты развития теоретического мышления у младших школьников в процессе ознакомления с окружающим миром

1. Обоснование проблемной ситуации

Критерии выбора и алгоритм принятия эффективного решения

1. Определение цели и направления в решении проблемной ситуации

2. Установка критериев решения

3. Разделение критериев (ограничения/желательные характеристики)

4. Выработка альтернатив решения

5. Сравнение альтернатив

6. Оценка риска

7. Выбор альтернативы

8. Анализ плана реализации решения

Только практические современные знания и навыки. Изучите эти курсы по менеджменту и управлению или учитесь чему хотите по абонементу, со скидкой.

Алгоритм исправления проблемных ситуаций (АИПС-2015)

Проблемная ситуация — Энциклопедия по машиностроению XXL

Урок открытия нового знания (ОНЗ)

Этап 4. ПОСТРОЕНИЯ ПРОЕКТА ВЫХОДА ИЗ ЗАТРУДНЕНИЯ

Как решать любые проблемы: алгоритм действий

Произнесите проблему от своего лица

Проанализируйте проблему

Выберите подходящий способ

Устройте мозговой штурм

Ответьте на вопросы

стратегий решения алгоритмов — Learneroo

Решить вручную

Разбей это

Соответствие алгоритма

Вызов

Как решать проблемы с помощью алгоритма: психология и этот подход

Мысль | Britannica

Элементы мысли

Использование алгоритмов для решения математических задач — видео и стенограмма урока

Добавление столбца чисел

Где взять алгоритмы?

Краткое содержание урока

типов алгоритмов и их использование

Введение в типы алгоритмов

Жадный алгоритм

Рекурсивный алгоритм

Алгоритм разделяй и властвуй

Выход 1:

Динамический алгоритм

Рандомизированный алгоритм

Превосходный алгоритм поиска кратчайшего маршрута — ScienceDaily

Проблема Aged P и NP. Почему P = NP такая большая проблема, что это… | Дэвид Чонг

Так что же тогда представляет собой проблема P и NP?

NP-Complete и NP-Hard

Определение NP-полноты

Подождите, что это значит, если уменьшить A до B?

Добавить комментарий Отменить ответ