Релаксация (Физика) — это… Что такое Релаксация (Физика)?
Релаксация (от лат. relaxatio — ослабление, уменьшение) — процесс установления термодинамического, а следовательно, и статистического равновесия в физической системе, состоящей из большого числа частиц.
Свойства и виды
Релаксация — многоступенчатый процесс, так как не все физические параметры системы (распределение частиц по координатам и импульсам, температура, давление, концентрация в малых объёмах и во всей системе и другие) стремятся к равновесию с одинаковой скоростью. Обычно сначала устанавливается равновесие по какому-либо параметру (частичное равновесие), что также называется релаксацией. Все процессы релаксации являются неравновесными процессами, при которых в системе происходит диссипация энергии, то есть производится энтропия (в замкнутой системе энтропия возрастает). В различных системах релаксация имеет свои особенности, зависящие от характера взаимодействия между частицами системы; поэтому процессы релаксации
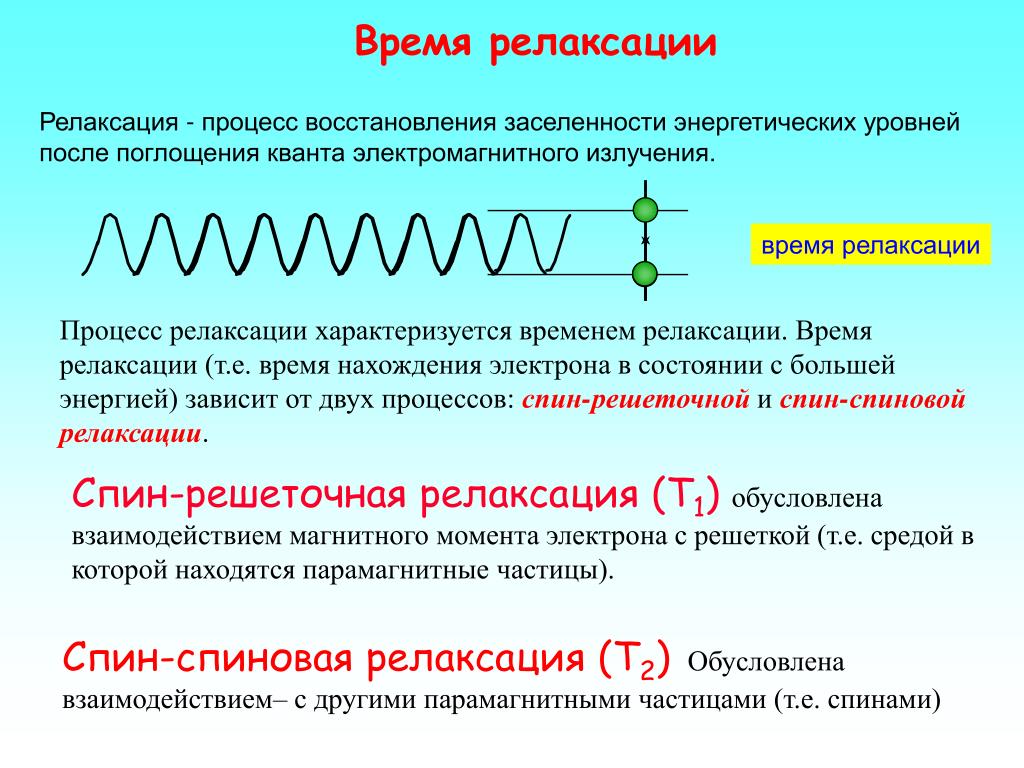 Время установления равновесия (частичного или полного) в системе называется временем релаксации. Процесс установления равновесия в газах определяется длиной свободного пробега частиц и временем свободного пробега (среднее расстояние и среднее время между двумя последовательными столкновениями молекул). Отношение имеет порядок величины скорости частиц. Величины и очень малы по сравнению с макроскопическими масштабами длины и времени. С другой стороны, для газов время свободного пробега значительно больше времени столкновения . Только при этом условии релаксация определяется лишь парными столкновениями молекул.
Время установления равновесия (частичного или полного) в системе называется временем релаксации. Процесс установления равновесия в газах определяется длиной свободного пробега частиц и временем свободного пробега (среднее расстояние и среднее время между двумя последовательными столкновениями молекул). Отношение имеет порядок величины скорости частиц. Величины и очень малы по сравнению с макроскопическими масштабами длины и времени. С другой стороны, для газов время свободного пробега значительно больше времени столкновения . Только при этом условии релаксация определяется лишь парными столкновениями молекул.Описание процесса релаксации
Для одноатомных газов
В одноатомных газах (без внутренних степеней свободы, то есть обладающих только поступательными степенями свободы) релаксация происходит в два этапа.
На первом этапе за короткий промежуток времени, порядка времени столкновения молекул то, начальное, даже сильно неравновесное, состояние хаотизируется таким образом, что становятся несущественными детали начального состояния и оказывается возможным так называемое «сокращённое описание» неравновесного состояния системы, когда не требуется знания вероятности распределения всех частиц системы по координатам и импульсам, а достаточно знать распределение одной частицы по координатам и импульсам в зависимости от времени, то есть одночастичную функцию распределения молекул.
На втором этапе за время порядка времени свободного пробега молекул и в результате всего нескольких столкновений в макроскопически малых объёмах системы устанавливается локальное равновесие; ему соответствует локально-равновесное, или квазиравновесное, распределение, которое характеризуется такими же параметрами, как и при полном равновесии системы, но зависящими от пространственных координат и времени. Эти малые объёмы содержат ещё очень много молекул, а поскольку они взаимодействуют с окружением лишь на своей поверхности, их можно считать приближённо изолированными. Параметры локально-равновесного распределения в процессе

Такие процессы (вязкость, теплопроводность, диффузия, электропроводность и т. п.) называются медленными. Соответствующее время релаксации зависит от размеров системы и велико по сравнению с : , что имеет место при , то есть для не сильно разреженных газов.
Для многоатомных газов
В многоатомных газах (с внутренними степенями свободы) может быть замедлен обмен энергией между поступательными и внутренними степенями свободы, и возникает процесс релаксации, связанный с этим явлением. Быстрее всего — за время порядка времени между столкновениями — устанавливается равновесие по поступательным степеням свободы; такое равновесное состояние можно охарактеризовать соответствующей температурой. Равновесие между поступательными и вращательными степенями свободы устанавливается значительно медленнее. Возбуждение колебательных степеней свободы может происходить лишь при высоких температурах. Поэтому в многоатомных газах возможны многоступенчатые процессы
Для смесей газов
В смесях газов с сильно различающимися массами молекул замедлен обмен энергией между компонентами, вследствие чего возможно возникновение состояния с различными температурами компонент и процессы релаксации
 Например, в плазме сильно различаются массы ионов и электронов. Быстрее всего устанавливается равновесие электронной компоненты, затем приходит в равновесие ионная компонента, и значительно большее время требуется для установления равновесия между электронами и ионами; поэтому в плазме могут длительное время существовать состояния, в которых ионные и электронные температуры различны а, следовательно, происходят процессы релаксации температур компонент.
Например, в плазме сильно различаются массы ионов и электронов. Быстрее всего устанавливается равновесие электронной компоненты, затем приходит в равновесие ионная компонента, и значительно большее время требуется для установления равновесия между электронами и ионами; поэтому в плазме могут длительное время существовать состояния, в которых ионные и электронные температуры различны а, следовательно, происходят процессы релаксации температур компонент.Для жидкостей
В жидкостях теряет смысл понятие времени и длины свободного пробега частиц (а следовательно, и кинетического уравнения для одночастичной функции распределения). Аналогичную роль для жидкости играют величины и — время и длина корреляции динамических переменных, описывающих потоки энергии или импульса;
 В макроскопически малых объёмах жидкости, но ещё достаточно больших по сравнению с длиной корреляции , локально-равновесное распределение устанавливается за время порядка времени корреляции в результате интенсивного взаимодействия между молекулами (а не парных столкновений, как в газе), но эти объёмы по-прежнему можно считать приближённо изолированными. На гидродинамическом этапе
В макроскопически малых объёмах жидкости, но ещё достаточно больших по сравнению с длиной корреляции , локально-равновесное распределение устанавливается за время порядка времени корреляции в результате интенсивного взаимодействия между молекулами (а не парных столкновений, как в газе), но эти объёмы по-прежнему можно считать приближённо изолированными. На гидродинамическом этапе 
Для твёрдых тел и квантовых жидкостей
В твёрдых телах, как и в квантовых жидкостях, релаксацию можно описывать как релаксацию в газе квазичастиц. В этом случае можно ввести время и длину свободного пробега соответствующих квазичастиц (при условии малости возбуждения системы). Например, в кристаллической решётке при низких температурах упругие колебания можно трактовать как газ фононов. Взаимодействие между фононами приводит к квантовым переходам, то есть к столкновениям между ними.

На втором этапе за счёт слабого спин-орбитального взаимодействия магнитный момент медленно ориентируется вдоль оси лёгкого намагничивания; этот этап аналогичен гидродинамическому этапу релаксации в газах.
См. также
Литература
Лит.: Уленбек Д., форд Дж., Лекции по статистической механике, пер. с англ., М., 1965.
Ссылки
Wikimedia Foundation. 2010.
Релаксация (Физика) — это… Что такое Релаксация (Физика)?
Релаксация (от лат. relaxatio — ослабление, уменьшение) — процесс установления термодинамического, а следовательно, и статистического равновесия в физической системе, состоящей из большого числа частиц.
Свойства и виды
Релаксация — многоступенчатый процесс, так как не все физические параметры системы (распределение частиц по координатам и импульсам, температура, давление, концентрация в малых объёмах и во всей системе и другие) стремятся к равновесию с одинаковой скоростью. Обычно сначала устанавливается равновесие по какому-либо параметру (частичное равновесие), что также называется релаксацией. Все процессы релаксации являются неравновесными процессами, при которых в системе происходит диссипация энергии, то есть производится энтропия (в замкнутой системе энтропия возрастает). В различных системах релаксация имеет свои особенности, зависящие от характера взаимодействия между частицами системы; поэтому процессы релаксации весьма многообразны. Время установления равновесия (частичного или полного) в системе называется временем релаксации. Процесс установления равновесия в газах определяется длиной свободного пробега частиц и временем свободного пробега (среднее расстояние и среднее время между двумя последовательными столкновениями молекул). Отношение имеет порядок величины скорости частиц. Величины и очень малы по сравнению с макроскопическими масштабами длины и времени. С другой стороны, для газов время свободного пробега значительно больше времени столкновения .
Обычно сначала устанавливается равновесие по какому-либо параметру (частичное равновесие), что также называется релаксацией. Все процессы релаксации являются неравновесными процессами, при которых в системе происходит диссипация энергии, то есть производится энтропия (в замкнутой системе энтропия возрастает). В различных системах релаксация имеет свои особенности, зависящие от характера взаимодействия между частицами системы; поэтому процессы релаксации весьма многообразны. Время установления равновесия (частичного или полного) в системе называется временем релаксации. Процесс установления равновесия в газах определяется длиной свободного пробега частиц и временем свободного пробега (среднее расстояние и среднее время между двумя последовательными столкновениями молекул). Отношение имеет порядок величины скорости частиц. Величины и очень малы по сравнению с макроскопическими масштабами длины и времени. С другой стороны, для газов время свободного пробега значительно больше времени столкновения . Только при этом условии релаксация определяется лишь парными столкновениями молекул.
Только при этом условии релаксация определяется лишь парными столкновениями молекул.
Описание процесса релаксации
Для одноатомных газов
В одноатомных газах (без внутренних степеней свободы, то есть обладающих только поступательными степенями свободы) релаксация происходит в два этапа.
На первом этапе за короткий промежуток времени, порядка времени столкновения молекул то, начальное, даже сильно неравновесное, состояние хаотизируется таким образом, что становятся несущественными детали начального состояния и оказывается возможным так называемое «сокращённое описание» неравновесного состояния системы, когда не требуется знания вероятности распределения всех частиц системы по координатам и импульсам, а достаточно знать распределение одной частицы по координатам и импульсам в зависимости от времени, то есть одночастичную функцию распределения молекул. (Все остальные функции распределения более высокого порядка, описывающие распределения по состояниям двух, трёх и т. д. частиц, зависят от времени лишь через одночастичную функцию). Одночастичная функция удовлетворяет кинетическому уравнению Больцмана, которое описывает процесс релаксации. Этот этап называется кинетическим и является очень быстрым процессом релаксации.
д. частиц, зависят от времени лишь через одночастичную функцию). Одночастичная функция удовлетворяет кинетическому уравнению Больцмана, которое описывает процесс релаксации. Этот этап называется кинетическим и является очень быстрым процессом релаксации.
На втором этапе за время порядка времени свободного пробега молекул и в результате всего нескольких столкновений в макроскопически малых объёмах системы устанавливается локальное равновесие; ему соответствует локально-равновесное, или квазиравновесное, распределение, которое характеризуется такими же параметрами, как и при полном равновесии системы, но зависящими от пространственных координат и времени. Эти малые объёмы содержат ещё очень много молекул, а поскольку они взаимодействуют с окружением лишь на своей поверхности, их можно считать приближённо изолированными. Параметры локально-равновесного распределения в процессе релаксации медленно стремятся к равновесным, а состояние системы обычно мало отличается от равновесного. Время релаксации для локального равновесия . После установления локального равновесия для описания релаксации неравновесного состояния системы служат уравнения гидродинамики (уравнения Навье — Стокса, уравнения теплопроводности, диффузии и т. п.). При этом предполагается, что термодинамические параметры системы (плотность, температура и т. д.) и массовая скорость (средняя скорость переноса массы) мало меняются за время и на расстоянии . Этот этап релаксации называется гидродинамическим. Дальнейшая релаксация системы к состоянию полного статистического равновесия, при котором выравниваются средние скорости частиц, средняя температура, средняя концентрация и т. д., происходит медленно в результате очень большого числа столкновений.
Время релаксации для локального равновесия . После установления локального равновесия для описания релаксации неравновесного состояния системы служат уравнения гидродинамики (уравнения Навье — Стокса, уравнения теплопроводности, диффузии и т. п.). При этом предполагается, что термодинамические параметры системы (плотность, температура и т. д.) и массовая скорость (средняя скорость переноса массы) мало меняются за время и на расстоянии . Этот этап релаксации называется гидродинамическим. Дальнейшая релаксация системы к состоянию полного статистического равновесия, при котором выравниваются средние скорости частиц, средняя температура, средняя концентрация и т. д., происходит медленно в результате очень большого числа столкновений.
Такие процессы (вязкость, теплопроводность, диффузия, электропроводность и т. п.) называются медленными. Соответствующее время релаксации зависит от размеров системы и велико по сравнению с : , что имеет место при , то есть для не сильно разреженных газов.
Для многоатомных газов
В многоатомных газах (с внутренними степенями свободы) может быть замедлен обмен энергией между поступательными и внутренними степенями свободы, и возникает процесс релаксации, связанный с этим явлением. Быстрее всего — за время порядка времени между столкновениями — устанавливается равновесие по поступательным степеням свободы; такое равновесное состояние можно охарактеризовать соответствующей температурой. Равновесие между поступательными и вращательными степенями свободы устанавливается значительно медленнее. Возбуждение колебательных степеней свободы может происходить лишь при высоких температурах. Поэтому в многоатомных газах возможны многоступенчатые процессы релаксации энергии колебательных и вращательных степеней свободы.
Для смесей газов
В смесях газов с сильно различающимися массами молекул замедлен обмен энергией между компонентами, вследствие чего возможно возникновение состояния с различными температурами компонент и процессы релаксации их температур. Например, в плазме сильно различаются массы ионов и электронов. Быстрее всего устанавливается равновесие электронной компоненты, затем приходит в равновесие ионная компонента, и значительно большее время требуется для установления равновесия между электронами и ионами; поэтому в плазме могут длительное время существовать состояния, в которых ионные и электронные температуры различны а, следовательно, происходят процессы релаксации температур компонент.
Например, в плазме сильно различаются массы ионов и электронов. Быстрее всего устанавливается равновесие электронной компоненты, затем приходит в равновесие ионная компонента, и значительно большее время требуется для установления равновесия между электронами и ионами; поэтому в плазме могут длительное время существовать состояния, в которых ионные и электронные температуры различны а, следовательно, происходят процессы релаксации температур компонент.
Для жидкостей
В жидкостях теряет смысл понятие времени и длины свободного пробега частиц (а следовательно, и кинетического уравнения для одночастичной функции распределения). Аналогичную роль для жидкости играют величины и — время и длина корреляции динамических переменных, описывающих потоки энергии или импульса; t1 и l1 характеризуют затухание во времени и в пространстве взаимного влияния молекул, то есть корреляции. При этом полностью остаётся в силе понятие гидродинамического этапа релаксации и локально-равновесного состояния. В макроскопически малых объёмах жидкости, но ещё достаточно больших по сравнению с длиной корреляции , локально-равновесное распределение устанавливается за время порядка времени корреляции в результате интенсивного взаимодействия между молекулами (а не парных столкновений, как в газе), но эти объёмы по-прежнему можно считать приближённо изолированными. На гидродинамическом этапе релаксация в жидкости термодинамические параметры и массовая скорость удовлетворяют таким же уравнениям гидродинамики, как и для газов (при условии малости изменения термодинамических параметров и массовой скорости за время и на расстоянии ). Время релаксации к полному термодинамическому равновесию (так же, как в газе и твёрдом теле) можно оценить с помощью кинетических коэффициентов. Например, время релаксации концентрации в бинарной смеси в объёме порядка , где — коэффициент диффузии, время релаксации температуры , где — коэффициент температуропроводности, и т. д. Для жидкости с внутренними степенями свободы молекул возможно сочетание гидродинамического описания поступательных степеней свободы с дополнительными уравнениями для описания релаксации внутренних степеней свободы (релаксационная гидродинамика).
В макроскопически малых объёмах жидкости, но ещё достаточно больших по сравнению с длиной корреляции , локально-равновесное распределение устанавливается за время порядка времени корреляции в результате интенсивного взаимодействия между молекулами (а не парных столкновений, как в газе), но эти объёмы по-прежнему можно считать приближённо изолированными. На гидродинамическом этапе релаксация в жидкости термодинамические параметры и массовая скорость удовлетворяют таким же уравнениям гидродинамики, как и для газов (при условии малости изменения термодинамических параметров и массовой скорости за время и на расстоянии ). Время релаксации к полному термодинамическому равновесию (так же, как в газе и твёрдом теле) можно оценить с помощью кинетических коэффициентов. Например, время релаксации концентрации в бинарной смеси в объёме порядка , где — коэффициент диффузии, время релаксации температуры , где — коэффициент температуропроводности, и т. д. Для жидкости с внутренними степенями свободы молекул возможно сочетание гидродинамического описания поступательных степеней свободы с дополнительными уравнениями для описания релаксации внутренних степеней свободы (релаксационная гидродинамика).
Для твёрдых тел и квантовых жидкостей
В твёрдых телах, как и в квантовых жидкостях, релаксацию можно описывать как релаксацию в газе квазичастиц. В этом случае можно ввести время и длину свободного пробега соответствующих квазичастиц (при условии малости возбуждения системы). Например, в кристаллической решётке при низких температурах упругие колебания можно трактовать как газ фононов. Взаимодействие между фононами приводит к квантовым переходам, то есть к столкновениям между ними. Релаксация энергии в кристаллической решётке описывается кинетическим уравнением для фононов. В системе спиновых магнитных моментов ферромагнетика квазичастицами являются магноны; Релаксацию (например, намагниченности) можно описывать кинетическим уравнением для магнонов. Релаксация магнитного момента в ферромагнетике происходит в два этапа: на первом этапе за счёт относительно сильного обменного взаимодействия устанавливается равновесное значение абсолютной величины магнитного момента.
На втором этапе за счёт слабого спин-орбитального взаимодействия магнитный момент медленно ориентируется вдоль оси лёгкого намагничивания; этот этап аналогичен гидродинамическому этапу релаксации в газах.
См. также
Литература
Лит.: Уленбек Д., форд Дж., Лекции по статистической механике, пер. с англ., М., 1965.
Ссылки
Wikimedia Foundation. 2010.
Релаксация (Физика) — это… Что такое Релаксация (Физика)?
Релаксация (от лат. relaxatio — ослабление, уменьшение) — процесс установления термодинамического, а следовательно, и статистического равновесия в физической системе, состоящей из большого числа частиц.
Свойства и виды
Релаксация — многоступенчатый процесс, так как не все физические параметры системы (распределение частиц по координатам и импульсам, температура, давление, концентрация в малых объёмах и во всей системе и другие) стремятся к равновесию с одинаковой скоростью. Обычно сначала устанавливается равновесие по какому-либо параметру (частичное равновесие), что также называется релаксацией. Все процессы релаксации являются неравновесными процессами, при которых в системе происходит диссипация энергии, то есть производится энтропия (в замкнутой системе энтропия возрастает). В различных системах релаксация имеет свои особенности, зависящие от характера взаимодействия между частицами системы; поэтому процессы релаксации весьма многообразны. Время установления равновесия (частичного или полного) в системе называется временем релаксации. Процесс установления равновесия в газах определяется длиной свободного пробега частиц и временем свободного пробега (среднее расстояние и среднее время между двумя последовательными столкновениями молекул). Отношение имеет порядок величины скорости частиц. Величины и очень малы по сравнению с макроскопическими масштабами длины и времени. С другой стороны, для газов время свободного пробега значительно больше времени столкновения .
Обычно сначала устанавливается равновесие по какому-либо параметру (частичное равновесие), что также называется релаксацией. Все процессы релаксации являются неравновесными процессами, при которых в системе происходит диссипация энергии, то есть производится энтропия (в замкнутой системе энтропия возрастает). В различных системах релаксация имеет свои особенности, зависящие от характера взаимодействия между частицами системы; поэтому процессы релаксации весьма многообразны. Время установления равновесия (частичного или полного) в системе называется временем релаксации. Процесс установления равновесия в газах определяется длиной свободного пробега частиц и временем свободного пробега (среднее расстояние и среднее время между двумя последовательными столкновениями молекул). Отношение имеет порядок величины скорости частиц. Величины и очень малы по сравнению с макроскопическими масштабами длины и времени. С другой стороны, для газов время свободного пробега значительно больше времени столкновения . Только при этом условии релаксация определяется лишь парными столкновениями молекул.
Только при этом условии релаксация определяется лишь парными столкновениями молекул.
Описание процесса релаксации
Для одноатомных газов
В одноатомных газах (без внутренних степеней свободы, то есть обладающих только поступательными степенями свободы) релаксация происходит в два этапа.
На первом этапе за короткий промежуток времени, порядка времени столкновения молекул то, начальное, даже сильно неравновесное, состояние хаотизируется таким образом, что становятся несущественными детали начального состояния и оказывается возможным так называемое «сокращённое описание» неравновесного состояния системы, когда не требуется знания вероятности распределения всех частиц системы по координатам и импульсам, а достаточно знать распределение одной частицы по координатам и импульсам в зависимости от времени, то есть одночастичную функцию распределения молекул. (Все остальные функции распределения более высокого порядка, описывающие распределения по состояниям двух, трёх и т. д. частиц, зависят от времени лишь через одночастичную функцию). Одночастичная функция удовлетворяет кинетическому уравнению Больцмана, которое описывает процесс релаксации. Этот этап называется кинетическим и является очень быстрым процессом релаксации.
д. частиц, зависят от времени лишь через одночастичную функцию). Одночастичная функция удовлетворяет кинетическому уравнению Больцмана, которое описывает процесс релаксации. Этот этап называется кинетическим и является очень быстрым процессом релаксации.
На втором этапе за время порядка времени свободного пробега молекул и в результате всего нескольких столкновений в макроскопически малых объёмах системы устанавливается локальное равновесие; ему соответствует локально-равновесное, или квазиравновесное, распределение, которое характеризуется такими же параметрами, как и при полном равновесии системы, но зависящими от пространственных координат и времени. Эти малые объёмы содержат ещё очень много молекул, а поскольку они взаимодействуют с окружением лишь на своей поверхности, их можно считать приближённо изолированными. Параметры локально-равновесного распределения в процессе релаксации медленно стремятся к равновесным, а состояние системы обычно мало отличается от равновесного. Время релаксации для локального равновесия . После установления локального равновесия для описания релаксации неравновесного состояния системы служат уравнения гидродинамики (уравнения Навье — Стокса, уравнения теплопроводности, диффузии и т. п.). При этом предполагается, что термодинамические параметры системы (плотность, температура и т. д.) и массовая скорость (средняя скорость переноса массы) мало меняются за время и на расстоянии . Этот этап релаксации называется гидродинамическим. Дальнейшая релаксация системы к состоянию полного статистического равновесия, при котором выравниваются средние скорости частиц, средняя температура, средняя концентрация и т. д., происходит медленно в результате очень большого числа столкновений.
Время релаксации для локального равновесия . После установления локального равновесия для описания релаксации неравновесного состояния системы служат уравнения гидродинамики (уравнения Навье — Стокса, уравнения теплопроводности, диффузии и т. п.). При этом предполагается, что термодинамические параметры системы (плотность, температура и т. д.) и массовая скорость (средняя скорость переноса массы) мало меняются за время и на расстоянии . Этот этап релаксации называется гидродинамическим. Дальнейшая релаксация системы к состоянию полного статистического равновесия, при котором выравниваются средние скорости частиц, средняя температура, средняя концентрация и т. д., происходит медленно в результате очень большого числа столкновений.
Такие процессы (вязкость, теплопроводность, диффузия, электропроводность и т. п.) называются медленными. Соответствующее время релаксации зависит от размеров системы и велико по сравнению с : , что имеет место при , то есть для не сильно разреженных газов.
Для многоатомных газов
В многоатомных газах (с внутренними степенями свободы) может быть замедлен обмен энергией между поступательными и внутренними степенями свободы, и возникает процесс релаксации, связанный с этим явлением. Быстрее всего — за время порядка времени между столкновениями — устанавливается равновесие по поступательным степеням свободы; такое равновесное состояние можно охарактеризовать соответствующей температурой. Равновесие между поступательными и вращательными степенями свободы устанавливается значительно медленнее. Возбуждение колебательных степеней свободы может происходить лишь при высоких температурах. Поэтому в многоатомных газах возможны многоступенчатые процессы релаксации энергии колебательных и вращательных степеней свободы.
Для смесей газов
В смесях газов с сильно различающимися массами молекул замедлен обмен энергией между компонентами, вследствие чего возможно возникновение состояния с различными температурами компонент и процессы релаксации их температур. Например, в плазме сильно различаются массы ионов и электронов. Быстрее всего устанавливается равновесие электронной компоненты, затем приходит в равновесие ионная компонента, и значительно большее время требуется для установления равновесия между электронами и ионами; поэтому в плазме могут длительное время существовать состояния, в которых ионные и электронные температуры различны а, следовательно, происходят процессы релаксации температур компонент.
Например, в плазме сильно различаются массы ионов и электронов. Быстрее всего устанавливается равновесие электронной компоненты, затем приходит в равновесие ионная компонента, и значительно большее время требуется для установления равновесия между электронами и ионами; поэтому в плазме могут длительное время существовать состояния, в которых ионные и электронные температуры различны а, следовательно, происходят процессы релаксации температур компонент.
Для жидкостей
В жидкостях теряет смысл понятие времени и длины свободного пробега частиц (а следовательно, и кинетического уравнения для одночастичной функции распределения). Аналогичную роль для жидкости играют величины и — время и длина корреляции динамических переменных, описывающих потоки энергии или импульса; t1 и l1 характеризуют затухание во времени и в пространстве взаимного влияния молекул, то есть корреляции. При этом полностью остаётся в силе понятие гидродинамического этапа релаксации и локально-равновесного состояния. В макроскопически малых объёмах жидкости, но ещё достаточно больших по сравнению с длиной корреляции , локально-равновесное распределение устанавливается за время порядка времени корреляции в результате интенсивного взаимодействия между молекулами (а не парных столкновений, как в газе), но эти объёмы по-прежнему можно считать приближённо изолированными. На гидродинамическом этапе релаксация в жидкости термодинамические параметры и массовая скорость удовлетворяют таким же уравнениям гидродинамики, как и для газов (при условии малости изменения термодинамических параметров и массовой скорости за время и на расстоянии ). Время релаксации к полному термодинамическому равновесию (так же, как в газе и твёрдом теле) можно оценить с помощью кинетических коэффициентов. Например, время релаксации концентрации в бинарной смеси в объёме порядка , где — коэффициент диффузии, время релаксации температуры , где — коэффициент температуропроводности, и т. д. Для жидкости с внутренними степенями свободы молекул возможно сочетание гидродинамического описания поступательных степеней свободы с дополнительными уравнениями для описания релаксации внутренних степеней свободы (релаксационная гидродинамика).
В макроскопически малых объёмах жидкости, но ещё достаточно больших по сравнению с длиной корреляции , локально-равновесное распределение устанавливается за время порядка времени корреляции в результате интенсивного взаимодействия между молекулами (а не парных столкновений, как в газе), но эти объёмы по-прежнему можно считать приближённо изолированными. На гидродинамическом этапе релаксация в жидкости термодинамические параметры и массовая скорость удовлетворяют таким же уравнениям гидродинамики, как и для газов (при условии малости изменения термодинамических параметров и массовой скорости за время и на расстоянии ). Время релаксации к полному термодинамическому равновесию (так же, как в газе и твёрдом теле) можно оценить с помощью кинетических коэффициентов. Например, время релаксации концентрации в бинарной смеси в объёме порядка , где — коэффициент диффузии, время релаксации температуры , где — коэффициент температуропроводности, и т. д. Для жидкости с внутренними степенями свободы молекул возможно сочетание гидродинамического описания поступательных степеней свободы с дополнительными уравнениями для описания релаксации внутренних степеней свободы (релаксационная гидродинамика).
Для твёрдых тел и квантовых жидкостей
В твёрдых телах, как и в квантовых жидкостях, релаксацию можно описывать как релаксацию в газе квазичастиц. В этом случае можно ввести время и длину свободного пробега соответствующих квазичастиц (при условии малости возбуждения системы). Например, в кристаллической решётке при низких температурах упругие колебания можно трактовать как газ фононов. Взаимодействие между фононами приводит к квантовым переходам, то есть к столкновениям между ними. Релаксация энергии в кристаллической решётке описывается кинетическим уравнением для фононов. В системе спиновых магнитных моментов ферромагнетика квазичастицами являются магноны; Релаксацию (например, намагниченности) можно описывать кинетическим уравнением для магнонов. Релаксация магнитного момента в ферромагнетике происходит в два этапа: на первом этапе за счёт относительно сильного обменного взаимодействия устанавливается равновесное значение абсолютной величины магнитного момента.
На втором этапе за счёт слабого спин-орбитального взаимодействия магнитный момент медленно ориентируется вдоль оси лёгкого намагничивания; этот этап аналогичен гидродинамическому этапу релаксации в газах.
См. также
Литература
Лит.: Уленбек Д., форд Дж., Лекции по статистической механике, пер. с англ., М., 1965.
Ссылки
Wikimedia Foundation. 2010.
Что это такое Релаксация (физика). Энциклопедия
1.1. Описание процесса релаксации Для одноатомных газов
В одноатомных газах без внутренних степеней свободы, то есть обладающих только поступательными степенями свободы релаксация происходит в два этапа.
На первом этапе за короткий промежуток времени, порядка времени столкновения молекул то, начальное, даже сильно неравновесное, состояние хаотизируется таким образом, что становятся несущественными детали начального состояния и оказывается возможным так называемое «сокращённое описание» неравновесного состояния системы, когда не требуется знания вероятности распределения всех частиц системы по координатам и импульсам, а достаточно знать распределение одной частицы по координатам и импульсам в зависимости от времени, то есть одночастичную функцию распределения молекул.
Одночастичная функция удовлетворяет кинетическому уравнению Больцмана, которое описывает процесс релаксации. Этот этап называется кинетическим и является очень быстрым процессом релаксации.
На втором этапе за время порядка времени свободного пробега молекул и в результате всего нескольких столкновений в макроскопически малых объёмах системы устанавливается локальное равновесие; ему соответствует локально-равновесное, или квазиравновесное, распределение, которое характеризуется такими же параметрами, как и при полном равновесии системы, но зависящими от пространственных координат и времени. Эти малые объёмы содержат ещё очень много молекул, а поскольку они взаимодействуют с окружением лишь на своей поверхности, их можно считать приближённо изолированными. Параметры локально-равновесного распределения в процессе релаксации медленно стремятся к равновесным, а состояние системы обычно мало отличается от равновесного. Время релаксации для локального равновесия t p ≫ t 0 {\displaystyle t_{p}\gg t_{0}}. После установления локального равновесия для описания релаксации неравновесного состояния системы служат уравнения гидродинамики. При этом предполагается, что термодинамические параметры системы плотность, температура и т. д. и массовая скорость средняя скорость переноса массы мало меняются за время t {\displaystyle t} и на расстоянии l {\displaystyle l}. Этот этап релаксации называется гидродинамическим. Дальнейшая релаксация системы к состоянию полного статистического равновесия, при котором выравниваются средние скорости частиц, средняя температура, средняя концентрация и т. д., происходит медленно в результате очень большого числа столкновений.
После установления локального равновесия для описания релаксации неравновесного состояния системы служат уравнения гидродинамики. При этом предполагается, что термодинамические параметры системы плотность, температура и т. д. и массовая скорость средняя скорость переноса массы мало меняются за время t {\displaystyle t} и на расстоянии l {\displaystyle l}. Этот этап релаксации называется гидродинамическим. Дальнейшая релаксация системы к состоянию полного статистического равновесия, при котором выравниваются средние скорости частиц, средняя температура, средняя концентрация и т. д., происходит медленно в результате очень большого числа столкновений.
Такие процессы называются медленными. Соответствующее время релаксации t p {\displaystyle t_{p}} зависит от размеров L {\displaystyle L} системы и велико по сравнению с t {\displaystyle t}: t 0 ≈ t L / l 2 ≫ t {\displaystyle t_{0}\approx tL/l2\gg t}, что имеет место при l ≪ L {\displaystyle l\ll L}, то есть для не сильно разреженных газов. {- {\ frac {t} {RC}}} \,}
{- {\ frac {t} {RC}}} \,}
Постоянная называется временем релаксации или постоянной времени RC цепи. Схема нелинейного генератора , которая генерирует повторяющуюся форму волны путем повторяющегося разряда конденсатора через сопротивление, называется релаксационным генератором . τ знак равно р C {\ Displaystyle \ тау = RC \}
В физике конденсированного состояния
В физике конденсированного состояния релаксация обычно рассматривается как линейный отклик на небольшое внешнее возмущение. Поскольку лежащие в основе микроскопические процессы активны даже в отсутствие внешних возмущений, можно также изучать «релаксацию в равновесии» вместо обычной «релаксации в равновесие» (см. Теорему о флуктуации-диссипации ).
Снятие стресса
В механике сплошных сред , релаксации напряжений являются постепенным исчезновением напряжений от вязкоупругой среды после того, как она была деформирована.
Время диэлектрической релаксации
В диэлектрических материалов, диэлектрическая поляризация Р зависит от электрического поля Е . Если E изменяется, P (t) реагирует: поляризация релаксирует к новому равновесию. Это важно в диэлектрической спектроскопии . За диэлектрическое поглощение ответственны очень большие времена релаксации .
Время диэлектрической релаксации тесно связано с электропроводностью . В полупроводнике это мера того, сколько времени требуется, чтобы нейтрализовать проводимость. Это время релаксации мало в металлах и может быть большим в полупроводниках и изоляторах .
Жидкости и аморфные твердые тела
Аморфная твердое вещество , такие как аморфный индометацин дисплеи температурная зависимость молекулярного движения, которая может быть определены количественно как среднее время релаксации для твердого вещества в метастабильном переохлажденной жидкости или стекла , чтобы подойти к молекулярной характеристике движения кристалла . Дифференциальная сканирующая калориметрия может использоваться для количественной оценки изменения энтальпии из-за релаксации молекулярной структуры.
Дифференциальная сканирующая калориметрия может использоваться для количественной оценки изменения энтальпии из-за релаксации молекулярной структуры.
Термин «структурная релаксация» был введен в научную литературу в 1947/48 г. без какого-либо объяснения, применительно к ЯМР и означающий то же самое, что и «тепловая релаксация».
Спиновая релаксация в ЯМР
В ядерном магнитном резонансе (ЯМР) различные релаксации — это свойства, которые он измеряет.
Методы химической релаксации
В химической кинетике методы релаксации используются для измерения очень высоких скоростей реакций . Система, первоначально находящаяся в равновесии, нарушается быстрым изменением параметра, такого как температура (чаще всего), давление, электрическое поле или pH растворителя. Затем наблюдают возврат к равновесию, обычно с помощью спектроскопических средств, и измеряют время релаксации. В сочетании с константой химического равновесия системы это позволяет определять константы скорости прямой и обратной реакций.
Мономолекулярная обратимая реакция первого порядка
Мономолекулярная обратимая реакция первого порядка, близкая к равновесной, может быть представлена следующей символической структурой:
А → k B → k ′ А {\ displaystyle {\ ce {A -> [k] B -> [k ‘] A}}}
А ↽ — — ⇀ B {\ displaystyle {\ ce {A <=> B}}}
Другими словами, реагент A и продукт B превращаются друг в друга на основании констант скорости реакции k и k ‘.
Чтобы найти концентрацию A, учтите, что прямая реакция ( ) вызывает уменьшение концентрации A с течением времени, тогда как обратная реакция ( ) приводит к увеличению концентрации A с течением времени. А → k B {\ displaystyle {\ ce {A -> [{k}] B}}} B → k ′ А {\ displaystyle {\ ce {B -> [{k ‘}] A}}}
Следовательно, где скобки вокруг A и B указывают концентрации. d [ А ] d т знак равно — k [ А ] + k ′ [ B ] {\ displaystyle {d [A] \ over dt} = — k [A] + k ‘[B]}
Если мы говорим, что при , и применяя закон сохранения массы, мы можем сказать, что в любое время сумма концентраций A и B должна быть равна концентрации , принимая объем, в котором растворены A и B не меняется: т знак равно 0 , [ А ( т ) ] знак равно [ А ] 0 {\ displaystyle t = 0, [A (t)] = [A] _ {0}} А 0 {\ displaystyle A_ {0}}
[ А ] + [ B ] знак равно [ А ] 0 ⇒ [ B ] знак равно [ А ] 0 — [ А ] {\ Displaystyle [A] + [B] = [A] _ {0} \ Rightarrow [B] = [A] _ {0} — [A]}
Подставляя это значение вместо [B] через A (0) и A (t), получаем
d [ А ] d т знак равно — k [ А ] + k ′ [ B ] знак равно — k [ А ] + k ′ ( [ А ] 0 — [ А ] ) знак равно — ( k + k ′ ) [ А ] + k ′ [ А ] 0 {\ displaystyle {d [A] \ over dt} = — k [A] + k ‘[B] = — k [A] + k’ ([A] _ {0} — [A]) = — (k + k ‘) [A] + k’ [A] _ {0}} , которое становится сепарабельным дифференциальным уравнением 1 — ( k + k ′ ) [ А ] + k ′ [ А ] 0 d [ А ] знак равно d т {\ displaystyle {1 \ over — (k + k ‘) [A] + k’ [A] _ {0}} d [A] = dt}
Это уравнение можно решить заменой, чтобы получить [ А ] знак равно k ′ — k е — ( k + k ′ ) т k + k ′ [ А ] 0 {\ displaystyle [A] = {k’-ke ^ {- (k + k ‘) t} \ над k + k’} [A] _ {0}}
В атмосферных науках
Обесцвечивание облаков
Рассмотрим перенасыщенную часть облака. Затем отключите восходящие потоки, унос и любые другие источники / стоки пара и вещи, которые могут вызвать рост частиц (лед или вода). Затем подождите, пока это перенасыщение не уменьшится и не станет просто насыщением (относительная влажность = 100%), что является состоянием равновесия. Время, необходимое для рассеяния пересыщения, называется временем релаксации. Это произойдет, когда кристаллы льда или жидкая вода будут расти в облаке и, таким образом, будут поглощать содержащуюся в нем влагу. Динамика релаксации очень важна в физике облаков для точного математического моделирования .
Затем отключите восходящие потоки, унос и любые другие источники / стоки пара и вещи, которые могут вызвать рост частиц (лед или вода). Затем подождите, пока это перенасыщение не уменьшится и не станет просто насыщением (относительная влажность = 100%), что является состоянием равновесия. Время, необходимое для рассеяния пересыщения, называется временем релаксации. Это произойдет, когда кристаллы льда или жидкая вода будут расти в облаке и, таким образом, будут поглощать содержащуюся в нем влагу. Динамика релаксации очень важна в физике облаков для точного математического моделирования .
В водяных облаках, где концентрации выше (сотни на см 3 ) и температура выше (что позволяет значительно снизить скорость перенасыщения по сравнению с ледяными облаками), время релаксации будет очень низким (от секунд до минут).
В ледяных облаках концентрации ниже (всего несколько единиц на литр), а температуры ниже (очень высокие скорости перенасыщения), поэтому время релаксации может достигать нескольких часов. Время релаксации представлено как
Время релаксации представлено как
- T = (4π DNRK ) −1 секунда, где:
- D = коэффициент диффузии [м 2 / с]
- N = концентрация (кристаллов льда или капель воды) [м −3 ]
- R = средний радиус частиц [м]
- K = емкость [безразмерная].
В астрономии
В астрономии время релаксации относится к скоплениям гравитационно взаимодействующих тел, например, к звездам в галактике . Время релаксации — это мера времени, которое требуется для того, чтобы один объект в системе («тестовая звезда») был значительно возмущен другими объектами в системе («звездами поля»). Чаще всего это время определяется как время, в течение которого скорость тестовой звезды изменяется по порядку.
Предположим, что пробная звезда имеет скорость v . Когда звезда движется по своей орбите, ее движение будет случайным образом возмущено гравитационным полем ближайших звезд. {\! -1} \! \ Mathrm {yr}}
{\! -1} \! \ Mathrm {yr}}
где ρ — средняя плотность, m — масса тестовой звезды, σ — 1d дисперсия скоростей звезд поля, а ln Λ — кулоновский логарифм .
Во временных масштабах, связанных со временем релаксации, происходят различные события, включая коллапс ядра , равнораспределение энергии и образование каспа Бахколла-Вольфа вокруг сверхмассивной черной дыры .
Смотрите также
Рекомендации
Пермский государственный национальный исследовательский университет
Кафедра теоретической физики Пермского государственного университета организована в 1951 году профессором Иваном Григорьевичем Шапошниковым после разделения кафедры теоретической физики и металлофизики, основанной в 1948 г.
За прошедшие годы по профилю кафедры окончили университет около 400 выпускников, из них свыше 100 человек защитили кандидатские диссертации, докторами наук стали более 30 человек.
На протяжении ряда лет кафедра занимает лидирующее положение в университете по научной работе и количеству грантов, в 2000 и 2001 годах заняла второе, а в 2002 году первое место в областном конкурсе кафедр вузов.
Ежегодно сотрудники и студенты кафедры публикуют более ста печатных работ по современным направлениям физики, в том числе стати в рецензируемых зарубежных и российских научных журналах, материалах конференций различных уровней, тезисов докладов конференций. Регулярно издаются учебно-методические пособия по общим и специальным курсам, закрепленным за кафедрой. Профессор В.К. Хеннер является автором двух учебников, изданных и активно используемых в вузах США и внедрённых в учебную программу физического факультета ПГНИУ.
Основными направлениями научно-исследовательской работы кафедры теоретической физики являются гидродинамика и гидродинамическая устойчивость, физика наномагнитных структур и материалов, магнитный резонанс и релаксация, теория динамических систем.
На базе кафедры создан Научно-образовательный центр «Неравновесные переходы в сплошных средах».
Кафедра обучает студентов по направлению «Физика» в области теоретической физики, ведет обучение по двум программам подготовки магистров по направлению «Физика», готовит аспирантов по специальности «Механика жидкости, газа и плазмы».
Кафедра теоретической физики ведёт цикл дисциплин по математике (векторный и тензорный анализ, дифференциальные уравнения, методы математической физики), теоретической физике (теоретическая механика, механика сплошных сред, электродинамика и электродинамика сплошных сред, квантовая теория). Также читаются спецкурсы для студентов химического, механико-математического и геологического факультетов.
Для студентов, специализирующихся по теоретической физике, читается большое количество спецкурсов общей направленности (астрофизика, общая теория относительности, квантовая электродинамика) и отражающих сложившиеся на кафедре научные направления (физическая гидродинамика, динамика аномальных жидкостей, теория колебаний, теория волновых процессов, физика акустических явлений).
Кафедра обладает высококвалифицированным профессорско-преподавательским составом: из 10 преподавателей кафедры 3 — доктора физико-математических наук, 7 — кандидаты физико-математических наук. Преподаватели кафедры являются ведущими и всемирно известными исследователями. В разное время на кафедре работали четыре заслуженных деятеля науки РФ – И.Г. Шапошников, Г.З. Гершуни, Д.В. Любимов и Т.П. Любимова.
Студенты активно привлекаются к научным исследованиям через курсовые и дипломные работы и гранты Научно-образовательного центра «Неравновесные переходы в сплошных средах», участвуют в работе Городского гидродинамического семинара имени Г. З. Гершуни и Е. М. Жуховицкого, Семинара по физике конденсированного состояния.
Научные исследования студентов и сотрудников кафедры в области физической гидродинамики и теории гидродинамической устойчивости, теории магнитной спиновой релаксации и физике магнитных наноматериалов, выполняемые при поддержке Российского научного фонда (РНФ), Российского фонда фундаментальных исследований (РФФИ), U..JPG) S. Civilian Research and Development Foundation (CRDF), Правительства Пермского края (проекты Международных исследовательских групп) и других.
S. Civilian Research and Development Foundation (CRDF), Правительства Пермского края (проекты Международных исследовательских групп) и других.
Кафедра теоретической физики ежегодно проводит Всероссийскую конференцию «Пермские гидродинамические научные чтения», ранее проводилась молодых учёных «Неравновесные процессы в сплошных средах», принимает активное участие в работе конференции студентов и молодых учёных «Физика для Пермского края», Зимней школе по механике сплошных сред ИМСС УрО РАН и других мероприятиях различных уровней. На протяжении более 50 лет кафедра теоретической физики руководит Пермским городским гидродинамическим семинаром им. Г.З. Гершуни и Е.М. Жуховицкого.
Коллектив кафедры теоретической физики, 2018 г.
Релаксация индуцированного ориентационного порядка в изотропной фазе нематического полимера
TY — JOUR
T1 — Релаксация индуцированного ориентационного порядка в изотропной фазе нематического полимера
AU — Рогожин, В. Б.
Б.
AU — Полушин, С.Г.
AU — Лезова, И.Е.
AU — Полушина, Г.Е.
AU — Рюмцев, Е.И.
AU — Никонорова, Н.А.
N1 — В. Б. Рогожин, С. Г. Полушин, И. Е. Лезова, Г. Е. Полушина, Е. И. Рюмцев, Н. А. Никонорова, “Релаксация индуцированного ориентационного порядка в изотропной фазе нематического полимера”, Письма в ЖЭТФ, 110:8 (2019), 521–525
PY — 2019/10/25
Y1 — 2019/10/25
N2 — Методами эффекта Керра и диэлектрической спектроскопии исследована ориентационная динамика в изотропной фазе гребнеобразного нематического полимера с мезогенными и функциональными боковыми группами. Впервые установлено, что в мезогенном полимере, в отличие от низкомолекулярных мезогенов, процесс релаксации электрического двойного лучепреломления расплава выше температуры фазового перехода нематик–изотропная фаза может быть представлен суммой нескольких экспоненциальных процессов, два из которых играют определяющую роль. Эти процессы сменяют друг друга на интервале температур порядка 50 градусов. Диэлектрическая спектроскопия также позволила выделить два процесса ориентационной релаксации, один обусловлен вращением боковых мезогенных групп, а второй связан с движением сегментов основной цепи.
Диэлектрическая спектроскопия также позволила выделить два процесса ориентационной релаксации, один обусловлен вращением боковых мезогенных групп, а второй связан с движением сегментов основной цепи.
AB — Методами эффекта Керра и диэлектрической спектроскопии исследована ориентационная динамика в изотропной фазе гребнеобразного нематического полимера с мезогенными и функциональными боковыми группами. Впервые установлено, что в мезогенном полимере, в отличие от низкомолекулярных мезогенов, процесс релаксации электрического двойного лучепреломления расплава выше температуры фазового перехода нематик–изотропная фаза может быть представлен суммой нескольких экспоненциальных процессов, два из которых играют определяющую роль. Эти процессы сменяют друг друга на интервале температур порядка 50 градусов. Диэлектрическая спектроскопия также позволила выделить два процесса ориентационной релаксации, один обусловлен вращением боковых мезогенных групп, а второй связан с движением сегментов основной цепи.
KW — эффект Керра
KW — жидкокристаллический полимер
KW — изотропный расплав
KW — релаксация
UR — http://www.mathnet.ru/php/archive.phtml?wshow=paper&jrnid=jetpl&paperid=6022&option_lang=rus
M3 — статья
VL — 110
SP — 521
EP — 525
JO — ПИСЬМА В «ЖУРНАЛ ЭКСПЕРИМЕНТАЛЬНОЙ И ТЕОРЕТИЧЕСКОЙ ФИЗИКИ»
JF — ПИСЬМА В «ЖУРНАЛ ЭКСПЕРИМЕНТАЛЬНОЙ И ТЕОРЕТИЧЕСКОЙ ФИЗИКИ»
SN — 0370-274X
IS — 8
ER —
3.6.2 Модель времени релаксации
3.6.2 Модель времени релаксацииДалее: 3.7 Генерация и рекомбинация Up: 3.6 Время релаксации энергии Предыдущее: 3.6.1 Методология
Подразделы
Следующее выражение используется для моделирования времени релаксации электронов как функция температуры носителя и температуры решетки:
| (3,138) |
В случае дырок предполагается постоянное время релаксации энергии.

| (3,139) |
Гибкость этой функции позволяет легко адаптировать ее ко всем рассматриваемым материалы. Для бинарных материалов Si, Ge и III-V все параметры в (3.138) сведены в Таблицу 3.33.
Для полупроводниковых сплавов AIIIBV зависимость на материальный состав включен.и моделируются как квадратичная функция от. Параметры приведены в таблице 3.34.
3.6.2.1 Элементарные и двоичные полупроводники
Прямой метод используется для Si, Ge и GaAs, а непрямой — для AlAs. и InAs, в зависимости от имеющихся данных MC. На рис. 3.40 показаны значения для в Si, полученные из модели (линии) и результатов Монте-Карло (кружки и треугольники) при разных температурах решетки. Время релаксации энергии
немного уменьшается с повышением температуры решетки.Также наблюдается
что для высоких температур электронов,
имеет тенденцию к насыщению.
Время релаксации энергии
немного уменьшается с повышением температуры решетки.Также наблюдается
что для высоких температур электронов,
имеет тенденцию к насыщению. При очень низкой температуре электронов
начинает увеличиваться. Этот эффект
не воспроизводится моделью. Когда температура электронов близка к
температура решетки, член
появляясь в энергии
баланс стремится к нулю [183], поэтому влияние
является
незначительна, поэтому ее повышением можно пренебречь.
В GaAs и Ge подобное поведение наблюдалось при очень низкой электронной температуре,
и сделаны те же предположения, что и для Si.В случае Ge рис. 3.41
показывает, что
практически не зависит от температуры решетки, за исключением
для очень низкой электронной температуры. Следовательно, любая температура решетки
зависимостью не учитывается (в (3.138)). Резкое начальное
падение объясняется увеличением оптического и междолинного рассеяния как
электроны нагреваются полем [186].
Результаты для GaAs показаны на рис. 3.42. При высоком электронном
температуры
стремится к некоторому насыщенному значению и становится независимым от
температура решетки.Для низких и промежуточных электронных температур
поведение можно объяснить переходом электронов из
долины. Электронная температура, для которой
достигает пика
значение не зависит от температуры решетки. Соответствующая средняя энергия,
эВ, близко к разнице энергий между двумя долинами, эВ.
3.42. При высоком электронном
температуры
стремится к некоторому насыщенному значению и становится независимым от
температура решетки.Для низких и промежуточных электронных температур
поведение можно объяснить переходом электронов из
долины. Электронная температура, для которой
достигает пика
значение не зависит от температуры решетки. Соответствующая средняя энергия,
эВ, близко к разнице энергий между двумя долинами, эВ.
3.
 6.2.2 Полупроводниковые сплавы Аналогичное поведение времени релаксации энергии
в
InGaAs и AlGaAs к GaAs можно увидеть в
Инжир.3.43 и рис. 3.44. Таким образом,
материалов сплава моделируется сохраняя стандартное отклонение и амплитуду полученной функции
для GaAs прямым методом и корректировкой положения с помощью
зависимость от состава материала (
) и (
).
6.2.2 Полупроводниковые сплавы Аналогичное поведение времени релаксации энергии
в
InGaAs и AlGaAs к GaAs можно увидеть в
Инжир.3.43 и рис. 3.44. Таким образом,
материалов сплава моделируется сохраняя стандартное отклонение и амплитуду полученной функции
для GaAs прямым методом и корректировкой положения с помощью
зависимость от состава материала (
) и (
). За
и из сплава (AB) модель
предлагает квадратичную интерполяцию между значениями из таблицы 3.33
для основных материалов (A и B) в зависимости от состава материала.
и называются параметрами изгиба. Значения, используемые в этом модели приведены в Таблице 3.34.
Косвенный метод применим для всех полупроводниковых сплавов, как описано в Раздел 2.2. Температурная зависимость решетки GaAs составляет сохраняется для обоих рассмотренных полупроводниковых сплавов, AlGaAs и InGaAs.
 Это приближение более точное для материалов с низким содержанием материала.
состав, который используется чаще ().
Это приближение более точное для материалов с низким содержанием материала.
состав, который используется чаще (). На рис. 3.43 результаты модели для при 300 К для разных составов материалов. Обратите внимание на сдвиг
температура электронов, при которой
достигает максимума до более низких значений
с увеличением. Для высоких значений () нет пикового значения наблюдается. Такое поведение можно объяснить зависимостью
, и долинные минимумы. Когда доля Al изменяется с на
, разница энергий между долинами и варьируется
между и эВ.Соответствующее изменение энергии электронов
связано с пиком
, варьируется от до
эВ. Кроме того, по содержанию Al впадины самые низкие,
и запрещенная зона становится косвенной. Этим объясняется отсутствие пика за .
Для InGaAs аналогичные результаты получены на рис. 3.44. Есть
сдвиг максимума
к более высоким значениям с увеличением
Состав индия до. Это можно объяснить электронным
изменение населения из-за
переходы. Для InAs быстрый переход к
наблюдаются более низкие значения, не объясняемые зависимостью энергетических долин
на .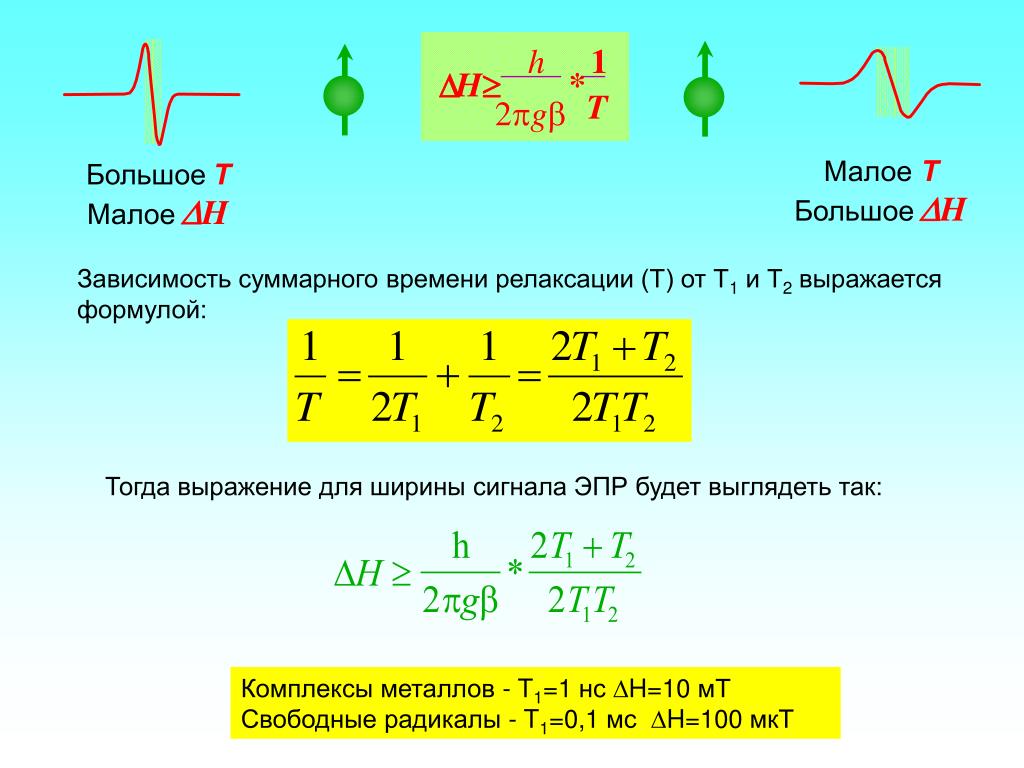 Результаты моделирования методом Монте-Карло показывают, что при очень высоком содержании индия
средняя энергия электронов уменьшается, а скорость дрейфа насыщения
увеличивается очень сильно, но в этом случае нет четких результатов.
Результаты моделирования методом Монте-Карло показывают, что при очень высоком содержании индия
средняя энергия электронов уменьшается, а скорость дрейфа насыщения
увеличивается очень сильно, но в этом случае нет четких результатов.
3.6.2.3 Применение модели
Времена релаксации энергии используются в модели подвижности HD. (3.129) и в релаксационных условиях баланса энергии уравнения (3.8) и (3.9). Кроме того, если включен самонагрев, времена релаксации энергии используются в релаксационные члены уравнения решеточного теплового потока (3. 17).
17).Используя непостоянные времена релаксации энергии электронов в (3.129) позволяет правильно моделировать выброс скорости в характеристики поля скоростей для материалов III-V.Кроме того, это помогает должна быть достигнута лучшая точность зависимости параметров слабого сигнала от смещения. Хорошее согласие с результатами моделирования МК и его простая Аналитическая структура делает его привлекательным для моделирования устройств.
Далее: 3.7 Генерация и рекомбинация Up: 3.6 Время релаксации энергии Предыдущее: 3.6.1 Методология Васил Паланковский
28.02.2001
Явление релаксации | физика и химия
Явление релаксации , в физике и химии, эффект, связанный с задержкой между приложением внешнего напряжения к системе, то есть к скоплению материи, и ее реакцией.Это может происходить в ядерных, атомных и молекулярных системах. Химики и физики используют эффекты релаксации для изучения процессов, которые занимают доли секунды. Когда уравновешенная ядерная, атомная или молекулярная система подвергается резкому физическому изменению, например, внезапному повышению температуры или давления, системе требуется время, чтобы повторно уравновеситься в новых условиях. Эффект релаксации может быть вызван перераспределением энергии между ядерными, электронными, колебательными и вращательными энергетическими состояниями атомов и молекул, составляющих систему, или может быть результатом сдвига в соотношении количества молекул продукта к количество молекул реагента (тех, которые изначально принимают участие) в химической реакции.Измерение времени релаксации может дать много сведений об атомных и молекулярных структурах, а также о скоростях и механизмах химических реакций.
Когда уравновешенная ядерная, атомная или молекулярная система подвергается резкому физическому изменению, например, внезапному повышению температуры или давления, системе требуется время, чтобы повторно уравновеситься в новых условиях. Эффект релаксации может быть вызван перераспределением энергии между ядерными, электронными, колебательными и вращательными энергетическими состояниями атомов и молекул, составляющих систему, или может быть результатом сдвига в соотношении количества молекул продукта к количество молекул реагента (тех, которые изначально принимают участие) в химической реакции.Измерение времени релаксации может дать много сведений об атомных и молекулярных структурах, а также о скоростях и механизмах химических реакций.
Исторический очерк
Слово релаксация было первоначально применено к молекулярному процессу английским физиком Джеймсом Клерком Максвеллом. В статье «О динамической теории газов», которую он представил в 1866 году, Максвелл сослался на время, необходимое для упругой силы, возникающей при искажении или распаде жидкости, до 1/ e ( e — основа системы натурального логарифма), умноженное на ее начальное значение как «время релаксации» упругой силы. Самое раннее предположение о химическом релаксационном эффекте содержится в диссертации (Берлин, 1910), основанной на исследованиях, проведенных немецким физико-химиком Вальтером Нернстом. Измерения распространения звука через газообразный четырехокись азота, который распадается или диссоциирует на двуокись азота, привели Нернста к выводу, что эксперименты на частотах, при которых реакция диссоциации не успевала за изменениями температуры и давления, происходящими в звуковой волне. позволит оценить скорость диссоциации.Десять лет спустя на заседании Прусской академии наук Альберт Эйнштейн представил доклад, в котором описал различные теоретические аспекты этого релаксационного эффекта.
Самое раннее предположение о химическом релаксационном эффекте содержится в диссертации (Берлин, 1910), основанной на исследованиях, проведенных немецким физико-химиком Вальтером Нернстом. Измерения распространения звука через газообразный четырехокись азота, который распадается или диссоциирует на двуокись азота, привели Нернста к выводу, что эксперименты на частотах, при которых реакция диссоциации не успевала за изменениями температуры и давления, происходящими в звуковой волне. позволит оценить скорость диссоциации.Десять лет спустя на заседании Прусской академии наук Альберт Эйнштейн представил доклад, в котором описал различные теоретические аспекты этого релаксационного эффекта.
Обнаружение эффекта химической релаксации, предсказанного Нернстом и Эйнштейном, стало технически возможным только во второй половине 20-го века. В первой половине века физики и химики, изучающие релаксацию, сосредоточились на физических релаксационных процессах. Питер Дебай назвал время, необходимое дипольным молекулам (те, чьи заряды неравномерно распределены) в переменном электрическом поле, диэлектрической релаксацией. Поглощение звука газами использовалось для исследования передачи энергии от поступательной (или смещения в пространстве) к вращательной (вращение и кувырок) и колебательной (колебания внутри молекулы) степеням свободы, трем независимым формам движения молекулы. В первом случае требуется всего несколько столкновений молекул, но для передачи энергии между поступательными и колебательными модами могут потребоваться тысячи столкновений. Поскольку процессы не мгновенные, а зависят от времени, наблюдаются релаксационные эффекты.Их измерение дает информацию о молекулярных связях и структуре. Химическая релаксация была заново открыта немецким физико-химиком Манфредом Эйгеном в 1954 году. С тех пор технический прогресс позволил разработать методы измерения времен релаксации, охватывающие весь диапазон молекулярных процессов и химической реакционной способности.
Поглощение звука газами использовалось для исследования передачи энергии от поступательной (или смещения в пространстве) к вращательной (вращение и кувырок) и колебательной (колебания внутри молекулы) степеням свободы, трем независимым формам движения молекулы. В первом случае требуется всего несколько столкновений молекул, но для передачи энергии между поступательными и колебательными модами могут потребоваться тысячи столкновений. Поскольку процессы не мгновенные, а зависят от времени, наблюдаются релаксационные эффекты.Их измерение дает информацию о молекулярных связях и структуре. Химическая релаксация была заново открыта немецким физико-химиком Манфредом Эйгеном в 1954 году. С тех пор технический прогресс позволил разработать методы измерения времен релаксации, охватывающие весь диапазон молекулярных процессов и химической реакционной способности.
Большое разнообразие явлений релаксации и методов, разработанных для их изучения, не позволяет провести всесторонний обзор.Для облегчения общего обсуждения расслабляющая система, ее начальное и конечное состояния, природа возмущения и реакция системы рассматриваются отдельно. Приведены примеры, которые подчеркивают важные особенности явлений релаксации и иллюстрируют разнообразие информации, которую можно получить в результате их изучения. Для подведения итогов обсуждения используется умеренно подробное описание одного метода релаксации, метода температурных скачков.
Приведены примеры, которые подчеркивают важные особенности явлений релаксации и иллюстрируют разнообразие информации, которую можно получить в результате их изучения. Для подведения итогов обсуждения используется умеренно подробное описание одного метода релаксации, метода температурных скачков.
Механизмы релаксации
Химическую релаксацию четырехокиси азота легко визуализировать, и она иллюстрирует принципы, общие для всех явлений релаксации. Четырехокись азота (формула N 2 O 4 ; также называемая четырехокись азота) на самом деле представляет собой димер (молекулу, образованную из двух одинаковых компонентов, называемых мономерами), который диссоциирует на две молекулы двуокиси азота (формула NO 2 ). Мономер и димер легко различить: первый представляет собой коричневый газ; последний — бесцветный газ.Продукт и реагенты находятся в равновесии, представленное обратимой реакцией:
При температуре окружающей среды (комнатной) и атмосферном давлении примерно 80 процентов молекул в смеси являются димерами, а остальные молекулы являются мономерами. Распределение молекул между двумя формами остается неизменным, пока температура и давление остаются постоянными. Но когда система нарушается из-за внезапного изменения температуры или давления, газы в конечном итоге достигают новых равновесных концентраций, соответствующих новым условиям.Если внешние условия изменятся, то соотношение мономеров и димеров изменится до нового значения. Зависимость равновесия от давления интуитивно понятна следующим образом: в хорошем приближении объем, который занимает газ при заданном давлении и температуре, напрямую зависит от количества молекул газа. Диссоциация одной молекулы четырехокиси азота на две молекулы двуокиси азота влечет за собой расширение газа — удвоение молекул, — которому противодействует внешнее давление.Если внешнее давление увеличивается, система снимает напряжение, уменьшая свой объем, то есть объединяя мономеры с образованием димеров и, таким образом, уменьшая количество молекул. Равновесие смещается в пользу димеров при повышенном давлении и в пользу мономеров при пониженном давлении.
Распределение молекул между двумя формами остается неизменным, пока температура и давление остаются постоянными. Но когда система нарушается из-за внезапного изменения температуры или давления, газы в конечном итоге достигают новых равновесных концентраций, соответствующих новым условиям.Если внешние условия изменятся, то соотношение мономеров и димеров изменится до нового значения. Зависимость равновесия от давления интуитивно понятна следующим образом: в хорошем приближении объем, который занимает газ при заданном давлении и температуре, напрямую зависит от количества молекул газа. Диссоциация одной молекулы четырехокиси азота на две молекулы двуокиси азота влечет за собой расширение газа — удвоение молекул, — которому противодействует внешнее давление.Если внешнее давление увеличивается, система снимает напряжение, уменьшая свой объем, то есть объединяя мономеры с образованием димеров и, таким образом, уменьшая количество молекул. Равновесие смещается в пользу димеров при повышенном давлении и в пользу мономеров при пониженном давлении. При любом постоянном давлении соотношение двух форм в конечном итоге становится постоянным.
При любом постоянном давлении соотношение двух форм в конечном итоге становится постоянным.
Химическая релаксация возникает из-за неспособности систем в состоянии равновесия мгновенно реагировать на изменения внешних условий.Скорость восстановления равновесия или повторного уравновешивания ограничивается концентрациями реагентов и их реакционной способностью. При любой заданной температуре и давлении существует определенная вероятность того, что в единицу времени молекула четырехокиси азота распадется на две молекулы двуокиси азота и что последняя рекомбинирует с образованием димера. Например, среднее время жизни молекулы четырехокиси азота при температуре окружающей среды и атмосферном давлении составляет около одной трети микросекунды (одна миллионная секунды).Произведение обратной величины среднего времени жизни на концентрацию молекул четырехокиси азота дает скорость, с которой они диссоциируют. При равновесии нет чистого изменения числа молекул тетроксида азота, потому что скорость их диссоциации точно уравновешивается скоростью, с которой они реформируются за счет ассоциации молекул диоксида азота. Если внешние условия изменяются, реакционная способность мономера и димера изменяется мгновенно, но их концентрации изменяются с конечной скоростью, пока не будет восстановлен баланс между скоростями ассоциации и диссоциации.Определив время релаксации, можно получить скорость, с которой диоксид азота объединяется с образованием тетроксида диазота, а также скорость обратной реакции.
Если внешние условия изменяются, реакционная способность мономера и димера изменяется мгновенно, но их концентрации изменяются с конечной скоростью, пока не будет восстановлен баланс между скоростями ассоциации и диссоциации.Определив время релаксации, можно получить скорость, с которой диоксид азота объединяется с образованием тетроксида диазота, а также скорость обратной реакции.
Звук, распространяющийся в газе, можно представить как волну давления, чередующееся увеличение и уменьшение давления, называемое синусоидальным изменением давления, со временем в любой точке среды сопровождается соответствующим колебанием температуры. Влияние изменения температуры и давления звуковой волны, движущейся через газообразный четырехокись азота, на диссоциацию четырехокиси азота зависит от частоты этой звуковой волны.Когда давление колеблется достаточно медленно, реакция диссоциации будет оставаться в равновесии с колебанием; то есть крайние значения соотношения мономер-димер будут совпадать с крайними значениями давления и температуры.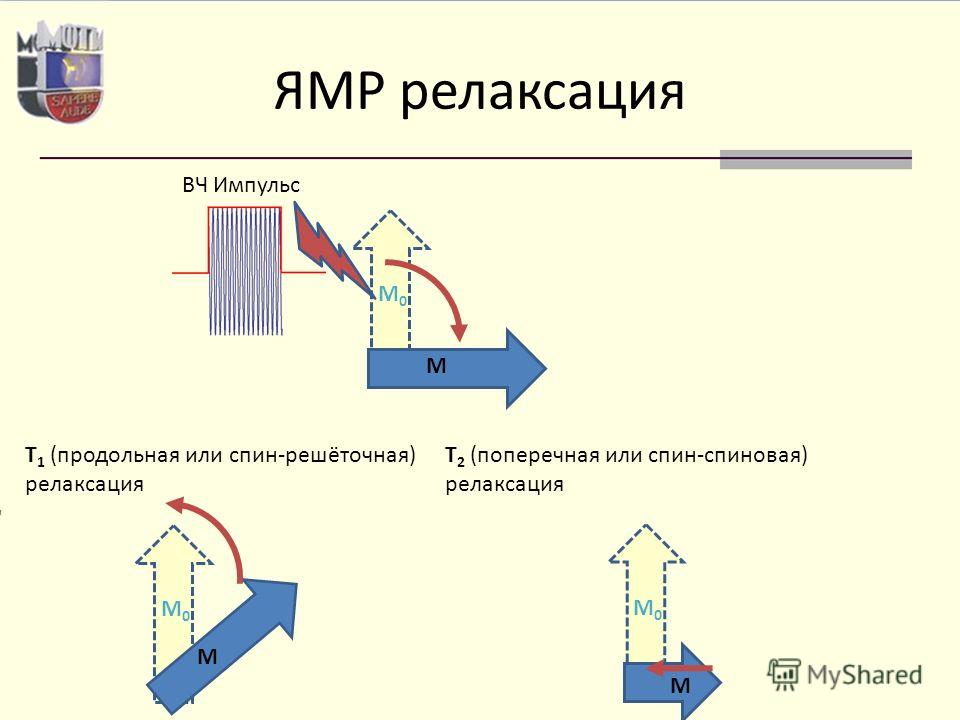 Если, с другой стороны, давление колеблется слишком быстро, чтобы реакция могла последовать, отношение мономеров к димерам будет оставаться постоянным на уровне равновесия для температуры и давления окружающей среды; но на промежуточных частотах может наблюдаться эффект релаксации, и восстановление химического равновесия будет отставать от изменения давления внутри газа.
Если, с другой стороны, давление колеблется слишком быстро, чтобы реакция могла последовать, отношение мономеров к димерам будет оставаться постоянным на уровне равновесия для температуры и давления окружающей среды; но на промежуточных частотах может наблюдаться эффект релаксации, и восстановление химического равновесия будет отставать от изменения давления внутри газа.
Релаксирующее химическое равновесие приводит как к поглощению звука газом, так и к рассеиванию или изменению скорости звука. Измерение любого из этих эффектов позволяет оценить время релаксации. Максимальное поглощение звука происходит, например, когда угловая частота (два π раза в секунду) звуковой волны равна обратной величине времени релаксации. Время релаксации, в свою очередь, может быть связано с механизмом химической реакции и реакционной способностью реагентов.
время релаксации τ — обзор
2.2 Уравнение Ланжевена
Экспериментально известно, что времена релаксации для жидкостей имеют порядок 10 −14 с . Как будет установлено в ближайшее время, соответствующие масштабы времени для броуновских частиц составляют по крайней мере 10 −9 с . Такое разделение во временных масштабах является следствием очень большой массы броуновской частицы по сравнению с массой молекулы растворителя и существенно для достоверности ланжевеновского описания.
Как будет установлено в ближайшее время, соответствующие масштабы времени для броуновских частиц составляют по крайней мере 10 −9 с . Такое разделение во временных масштабах является следствием очень большой массы броуновской частицы по сравнению с массой молекулы растворителя и существенно для достоверности ланжевеновского описания.
Взаимодействие сферической броуновской частицы с молекулами растворителя разделено на две части. Прежде всего, существует быстро меняющаяся сила f ( t ) со временем t в результате случайных столкновений молекул растворителя с броуновской частицей. Эта сила колеблется в вышеупомянутой временной шкале растворителя 10 -14 с . Во-вторых, когда броуновская частица достигает скорости v = p / M ( p — координата импульса броуновской частицы, а M — ее масса), возникает сила трения, обусловленная систематическим . столкновения с молекулами растворителя.Когда объем броуновской частицы намного больше, чем объем молекул растворителя, эта систематическая сила равна силе гидродинамического трения макроскопически большой сферы. Для не слишком больших скоростей эта сила трения прямо пропорциональна скорости броуновской частицы, а константа пропорциональности γ является константой трения: сила трения = −γ p / M . Коэффициент трения макроскопически большой сферы, как показано в главе 5 по гидродинамике, равен,
столкновения с молекулами растворителя.Когда объем броуновской частицы намного больше, чем объем молекул растворителя, эта систематическая сила равна силе гидродинамического трения макроскопически большой сферы. Для не слишком больших скоростей эта сила трения прямо пропорциональна скорости броуновской частицы, а константа пропорциональности γ является константой трения: сила трения = −γ p / M . Коэффициент трения макроскопически большой сферы, как показано в главе 5 по гидродинамике, равен,
(2.1) γ = 6πη0a,
с η 0 сдвиговой вязкостью растворителя и a радиусом броуновской частицы. Коэффициент трения в уравнении (2.1) обычно называют коэффициентом трения Стокса. Таким образом, уравнение движения Ньютона для сферической броуновской частицы записывается как
(2.2) dp / dt = −γp / M + f (t).
Координата положения r броуновской частицы по определению связана с координатой импульса следующим образом:
(2. 3) dr / dt = p / M.
3) dr / dt = p / M.
Поскольку систематическое взаимодействие с молекулами растворителя явно выражено (первый член в правой части уравнения (2.2)), среднее по ансамблю флуктуирующей силы f равно нулю,
(2,4)
Из-за вышеупомянутого большого разделения во временных масштабах для расчета теплового движения броуновской частицы достаточно использовать дельта-коррелированную случайную силу во времени, то есть
(2.5)
, где δ — дельта-распределение, а G — постоянная 3 × 3-мерная матрица, которую можно рассматривать как мера силы колебания и называется силой колебаний . Такая дельта-коррелированная случайная сила ограничивает описание временным разрешением, которое велико по отношению к шкале времени растворителя 10 -14 с .
Уравнение (2.2) представляет собой уравнение движения Ньютона для макроскопической частицы с флуктуирующей случайной силой, добавленной для учета тепловых столкновений молекул растворителя с броуновской частицей. Такое уравнение называется уравнением Ланжевена . Это стохастическое уравнение движения в том смысле, что координата импульса броуновской частицы, а также координата ее положения теперь являются стохастическими переменными. Нет смысла просить детерминированное решение уравнений. (2.2,3), поскольку заданы только усредненные по ансамблю свойства случайной силы f . Усилия должны быть направлены на вычисление условной функции плотности вероятности для p и r в момент времени t , учитывая их начальные значения в момент времени t = 0.В дальнейшем «функция плотности вероятности» сокращенно обозначается как pdf . Решение уравнения Ланжевена — это спецификация PDF для стохастической переменной ( p, r ). Обратите внимание, что уравнение (2.2) математически бессмысленно, поскольку оно стоит без спецификаций (2.4,5 статистических свойств случайной силы f .
Такое уравнение называется уравнением Ланжевена . Это стохастическое уравнение движения в том смысле, что координата импульса броуновской частицы, а также координата ее положения теперь являются стохастическими переменными. Нет смысла просить детерминированное решение уравнений. (2.2,3), поскольку заданы только усредненные по ансамблю свойства случайной силы f . Усилия должны быть направлены на вычисление условной функции плотности вероятности для p и r в момент времени t , учитывая их начальные значения в момент времени t = 0.В дальнейшем «функция плотности вероятности» сокращенно обозначается как pdf . Решение уравнения Ланжевена — это спецификация PDF для стохастической переменной ( p, r ). Обратите внимание, что уравнение (2.2) математически бессмысленно, поскольку оно стоит без спецификаций (2.4,5 статистических свойств случайной силы f .
Интегрирование уравнения (2. 2) дает,
2) дает,
(2,6) p (t) = p (0) exp {−γMt} + ∫0tdt’f (t ‘) exp {−γM (t − t’)}.
Теперь пусть τ будет временным интервалом, намного большим, чем шкала времени растворителя 10 −14 с .Случайная сила развивается через множество независимых реализаций в течение этого временного интервала. С другой стороны, пусть τ настолько мало, что exp {−γ t / M } почти постоянна на временах порядка τ, то есть возьмем τ ≪ M / γ. При таком выборе τ уравнение (2.6) можно переписать как
(2.7) p (t) = p (0) exp {−γMt} + Σj = 0N − 1exp {−γM (t − jτ)} ∫jτ (j + 1) τdt’f (t ‘),
, где N = t / τ. Поскольку случайная сила развивается через множество независимых реализаций в течение интервала времени τ, каждый интеграл в уравнении.(2.7) — гауссова переменная со средним нулем. Это следствие центральной предельной теоремы, поскольку каждый интеграл можно рассматривать как сумму многих статистически эквивалентных и независимых членов (центральная предельная теорема сформулирована в (1. 80) во вводной главе). Кроме того, поскольку сумма независимых гауссовских переменных также является гауссовой переменной, как показано в упражнении 1.17 в главе 1, из представления (2.7) следует, что,
80) во вводной главе). Кроме того, поскольку сумма независимых гауссовских переменных также является гауссовой переменной, как показано в упражнении 1.17 в главе 1, из представления (2.7) следует, что,
X1 = p (t) −p (0) exp {−γMt},
, является гауссовой переменной.
А как насчет координаты положения r броуновской частицы? Приведенное выше рассуждение легко расширить, включив координату положения. Используя уравнение (2.3), интегрирование уравнения (2.6) дает (см. Упражнение 2.1),
(2,8) r (t) = r (0) + p (0) γ [1 − exp {−γMt}] + 1γ∫0tdt’f (t ‘) [1 − exp {−γM (t − t ‘)}].
Следуя тем же рассуждениям, что и ранее, показывает, что,
X2≡r (t) −r (0) −p (0) γ [1 − exp {−γMt}],
, — гауссовская переменная со средним значением, равным нулю.
Рассмотрим стохастическую переменную ( p, r ).Определим переменную,
(2.9) X≡ (X1, X2) = (∫0tdt’f (t ‘) exp {−γM (t − t’)}, 1γ∫0tdt’f (t ‘) [1 − exp {−γM (t − t ‘)}]),
где ур. (2.6) и (2.8) используются во второй строке. Согласно приведенному выше обсуждению, X является гауссовой переменной. Для заданных начальных значений импульса и координат положения p (0) и r (0) pdf переменной X явно идентичен pdf ( p, r ). Следовательно, pdf-файл ( p, r ) имеет вид (обозначения см. В подразделе 1.3.1 об условных PDF-файлах во вводной главе),
(2.6) и (2.8) используются во второй строке. Согласно приведенному выше обсуждению, X является гауссовой переменной. Для заданных начальных значений импульса и координат положения p (0) и r (0) pdf переменной X явно идентичен pdf ( p, r ). Следовательно, pdf-файл ( p, r ) имеет вид (обозначения см. В подразделе 1.3.1 об условных PDF-файлах во вводной главе),
(2.10) P (p, r, t | p (0), r (0), t = 0) = 1 (2π) n / 2detDexp {−12X.D − 1.X},
с,
(2.11) D =
det D обозначает определитель D , а n = 6 — размер X . Обратите внимание, что каждая из матриц < x i x j >, i, j = 1, 2, является 3 × 3-мерной, так что D является 6 × 6-мерным.Используя ур. (2.4,5) средние по ансамблю < x i x j > легко вычисляются,
(2. 12)
12)
(2.13)
(2.14)
Теперь можно идентифицировать матрицу G , используя теорему о равнораспределении, которая гласит (см. Упражнение 2.2),
(2,15) limt → ∞
= IˆMβ,
, где β = 1/ k B T , с k B постоянная Больцмана и T температура и Î единичная матрица.Сила колебаний теперь следует из определения переменной x 1 (ниже уравнения (2.7)) и среднего по ансамблю (2.12). Для времен t ≫ M / γ уравнение (2.12) сводится к
(2,16)
= GM2γ.
Сравнение с уравнением (2.15) определяет силу колебаний,
(2.17) G = Iˆ2γβ.
Это соотношение часто называют теоремой о флуктуационной диссипации, поскольку она связывает флуктуационную силу с коэффициентом трения, который определяет диссипацию кинетической энергии в тепло. С идентификацией силы флуктуации G , pdf гауссовой переменной ( p, r ) полностью определен.
С идентификацией силы флуктуации G , pdf гауссовой переменной ( p, r ) полностью определен.
Время релаксации
Время релаксацииСледующий: Обратимость и необратимость Up: Статистическая механика Предыдущая: Теорема
Время релаксации Теорема гарантирует, что изолированная система многих частиц в конечном итоге достичь равновесия независимо от его исходного состояния.Типичная шкала времени для этого процесса называется временем релаксации и детально зависит от природы из межчастичные взаимодействия. Принцип равных априорных вероятностей имеет вид действительно только для состояний равновесия. Отсюда следует, что мы можем только безопасно применить это принцип для систем, которые оставались нетронутыми в течение многих времен релаксации с момента их установки или последнего взаимодействия с внешним миром. Время релаксации на воздухе в типичном классе составляет намного меньше одной секунды.
 Это говорит о том, что такой воздух, вероятно, находится в
равновесие большую часть времени и, следовательно, должно регулироваться
принцип равных априорных вероятностей . На самом деле это известно
быть так. Рассмотрим другой пример. Наша галактика Млечный Путь — это
Изолированная динамическая система, состоящая из примерно звезд. Фактически,
можно подумать
как самогравитирующий « газ » звезд. На первый взгляд
« Млечный путь »
казалось бы, идеальная система, на которой
проверить идеи статистической механики.Звезды в Галактике взаимодействуют через случайные события, близкие к промахам, в которых они
обмениваются энергией и импульсом. Фактические столкновения действительно очень редки. К несчастью,
такие взаимодействия происходят очень редко, потому что
между звездами очень много пустого пространства. Лучшая оценка для
Время релаксации Млечного Пути составляет около лет.
Это следует сравнить с предполагаемым возрастом Галактики, который составляет всего лишь
около лет. Понятно, что, несмотря на солидный возраст, « Млечный путь »
не существует достаточно долго, чтобы достичь равновесия
государственный.
Это говорит о том, что такой воздух, вероятно, находится в
равновесие большую часть времени и, следовательно, должно регулироваться
принцип равных априорных вероятностей . На самом деле это известно
быть так. Рассмотрим другой пример. Наша галактика Млечный Путь — это
Изолированная динамическая система, состоящая из примерно звезд. Фактически,
можно подумать
как самогравитирующий « газ » звезд. На первый взгляд
« Млечный путь »
казалось бы, идеальная система, на которой
проверить идеи статистической механики.Звезды в Галактике взаимодействуют через случайные события, близкие к промахам, в которых они
обмениваются энергией и импульсом. Фактические столкновения действительно очень редки. К несчастью,
такие взаимодействия происходят очень редко, потому что
между звездами очень много пустого пространства. Лучшая оценка для
Время релаксации Млечного Пути составляет около лет.
Это следует сравнить с предполагаемым возрастом Галактики, который составляет всего лишь
около лет. Понятно, что, несмотря на солидный возраст, « Млечный путь »
не существует достаточно долго, чтобы достичь равновесия
государственный. Это говорит о том, что
принцип равных априорных вероятностей не может быть использован для
описывают звездную динамику. Неудивительно, что наблюдаемое распределение скоростей
звезд в окрестностях Солнца не подчиняется этому принципу.
Это говорит о том, что
принцип равных априорных вероятностей не может быть использован для
описывают звездную динамику. Неудивительно, что наблюдаемое распределение скоростей
звезд в окрестностях Солнца не подчиняется этому принципу. Следующий: Обратимость и необратимость Up: Статистическая механика Предыдущая: Теорема Ричард Фицпатрик 2006-02-02
2.1.4: Методы релаксации — Химия LibreTexts
Многие химические реакции завершаются менее чем за несколько секунд, что затрудняет определение скорости реакции.В этих случаях методы релаксации могут использоваться для определения скорости реакции.
Введение
Термин релаксация используется для описания возврата реакции к равновесию. Равновесная система подвергается внешнему возмущению, например, изменению температуры. Когда изменение применяется внезапно, время запаздывания, необходимое системе для достижения нового положения равновесия, связано с константами \ (k_f \) и \ (k_r \) и называется временем релаксации , , \ (\ tau \) . Для определения метода релаксации можно использовать реакции с периодом полураспада от 1 с до 10 10 с. Есть три разных метода (каждый из которых представляет собой разные процессы, которые внезапно нарушают реакцию), которые используются для наблюдения за временем релаксации. Их:
Для определения метода релаксации можно использовать реакции с периодом полураспада от 1 с до 10 10 с. Есть три разных метода (каждый из которых представляет собой разные процессы, которые внезапно нарушают реакцию), которые используются для наблюдения за временем релаксации. Их:
Можно найти, что:
\ [T = \ dfrac {1} {k_f ([A] _ {eq} + [B] _ {eq}) + k_r} \ label {1} \]
где \ ([A] _ {eq} \) и \ ([B] _ {eq} \) — значения в новом равновесии при конечной температуре. Эти значения можно измерить в отдельных экспериментах.Таким образом, константа равновесия \ (K \) также может быть вычислена из
\ [K = \ dfrac {[C] _ {eq}} {[A] _ {eq} [B] _ {eq}} \ label {2} \]
но
\ [K = \ dfrac {k_f} {k_r} = \ dfrac {[C] _ {eq}} {[A] _ {eq} [B] _ {eq}} \ label {3} \]
Следовательно, мы можем найти \ (k_f \) и \ (k_r \).
Время релаксации \ (\ tau \) является функцией констант скорости \ (k_f \) и \ (k_r \) химической системы в состоянии равновесия с равновесными концентрациями [A] экв. и [B] экв.
и [B] экв.
Скачок температуры
\ ([A] _ {eq} \) и \ ([B] _ {eq} \) — новые равновесные концентрации, которые возникли после того, как система подверглась температурному скачку, когда она находилась в состоянии покоя при таком же другом равновесии. государственный.
\ [T = \ dfrac {1} {k_f ([A] _ {eq} + [B] _ {eq}) + k_r} \ label {4} \]
\ [A + B \ rightleftharpoons C + Q \ label {5} \]
при новой более высокой температуре.
k f , k r , [A] eq , [B] eq , [C] eq — значения при новой более высокой температуре.
Новые условия (более высокая температура) могут применяться так быстро, что можно проследить движение даже очень отзывчивых систем (очень быстро движущихся к новому равновесию) к новому состоянию равновесия.Скачок температуры, например, до 10 o ° C может быть произведен в водном растворе электрическим разрядом, который длится не более 1 мкс. {(- t / T)} \ label {6} \]
{(- t / T)} \ label {6} \]
, где \ (X \) — такое свойство, как электрическая проводимость или спектроскопическое поглощение, пропорциональное степени реакции.\ (X_t \) и \ (X_0 \) — значения линейного свойства в момент времени \ (t = t \) и \ (t = 0 \), соответственно, а \ (T \) — время релаксации. Когда \ (τ = t \),
\ [X_t = \ dfrac {X_o} {e} = \ dfrac {X_o} {2.718} \ label {7} \]
Таким образом, время релаксации может быть определено путем измерения времени, за которое X 0 уменьшится до X 0 / 2.718. Другими словами, это время, за которое процесс релаксации переносит систему на долю 1 / е в сторону положения равновесия.- \ rightleftharpoons H_2O + Q \ label {10a} \]
Оба новых равновесия в k f и k r при более высокой температуре с \ ([A] _ {eq} \), \ ([B] _ {eq} \), \ ([C] _ {eq } \). Конечно, до эксперимента с температурным скачком существовало старое равновесие, k f ‘и k r ‘, отличное от k f и k r , с \ ([A] _o \), \ ([B] _o \), \ ([C] _o \) при начальной температуре. 2 -X_t (k_f [B] _] {eq} X_t + k_f [A] _ {eq} + k_r) \ label {15} \]
2 -X_t (k_f [B] _] {eq} X_t + k_f [A] _ {eq} + k_r) \ label {15} \]
Начиная с:
\ [\ dfrac {d [C]} {dt} = 0 = k_f [A] _ {eq} [B] _ {eq} — k_r [C] _ {eq} \ label {16} \]
k f Xt 2 можно пренебречь из-за небольшой степени реакции.{-Lt}) \ rightarrow \ dfrac {-t} {T} = -L \ rightarrow T = 1 / L \]
Получаем:
\ [T = \ dfrac {1} {k_f [A] _ {eq} + k_f [B] _ {eq} + k_r} \ label {22} \]
В целом константы скорости обратимой реакции можно определить с помощью релаксационного метода.
Время релаксации и скорость охлаждения жидкости в интервале стеклования
Сандитов Д.С., Бартенев Г.М., Физические свойства неупорядоченных структур, Новосибирск: Наука, 1982. ].
Google ученый

Мазурин О.В., Стеклование , Ленинград: Наука, 1986.
Google ученый
Ростиашвили В.Г., Иржак В.И., Розенберг Б.А. Стеклование полимеров . Л .: Химия, 1987. 272 с.
Google ученый
Волькенштейн, М.В. , Птицын О.Б. Релаксационная теория стеклования // Докл. Акад. АН СССР , 1955, т. 103, нет. 5. С. 795–798.
CAS Google ученый
Бартенев Г.М. , Лукьянов И.А. Зависимость температуры стеклования от скорости нагрева аморфных материалов и связь температуры стеклования с энергией активации // Журн. Физ. Хим. , 1955, т.29, нет. 8. С. 1486–1498.
8. С. 1486–1498.
CAS Google ученый
Бартенев Г.М. Ю., Ломовской В.А. Молекулярные механизмы стеклования неорганических стекол. Физ. Хим. , 2003, т. 77, нет. 12. С. 2266–2276. J. Phys. Chem. , 2003, т. 77, нет. 12. С. 2045–2054].
CAS Google ученый
Бартенев Г.М., Бартенева А.Г., Релаксационные свойства полимеров, , М .: Химия, 1992.
Google ученый
Tool, A.Q., Релаксация между неупругой деформацией и тепловым расширением стекла в диапазоне отжига, J. Am. Ceram. Soc. , 1946, т. 29, нет. 9. С. 240–253.
Артикул CAS Google ученый
Нарайнасвами О.С. Модель структурной релаксации в стекле. Chem. , 1971, т. 54, нет. 10. С. 491–498.
Google ученый
Мойнихан К.Т., Истил А.Дж., Уайлдер Дж. И Тиккер Дж. Зависимость температуры стеклования от скорости нагрева и охлаждения, J. Phys. Chem. , 1974, т. 78, нет. 26. С. 2673–2677.
Артикул CAS Google ученый
Олемской, А. , Хоменко А.В. Синергетическая теория стеклования в жидкостях. Тех. Физ. , 2000, т. 70, нет. 6. С. 10–13. [ Tech. Phys. , 2000, т. 70, нет. 6. С. 677–682].
Google ученый
Привен А.И. Расчет температурных зависимостей вязкости и времени объемной релаксации оксидных стеклообразующих расплавов по химическому составу и температуре дилатометрического стеклования.Хим. Стекла , 2001, т. 27, нет. 6. С. 772–793. [ Glass Phys. Chem. , 2001, т. 27, нет. 6. С. 527–542].
Google ученый
Френкель Я.И., Кинетическая теория жидкостей, . Л .: Наука, 1975.
Google ученый
Glasstone, S., Laidler, K., and Eyring, H., The Theory of Rate Processes , New York: Princeton University Press, 1941. Перевод под заглавием Теория абсолютных скоростей реакции , М .: Иностранная литература, 1948.
Google ученый
Cohen, M.H. и Тернбулл Д. Молекулярный транспорт в жидкостях и стеклах, J. Chem. Phys. , 1959, т. 31, нет. 5. С. 1164–1169.
Артикул CAS Google ученый
Сандитов Д.С. Энтропия активации возбуждения атомов вблизи стеклования // Докл. Акад. НАУК .2005. 403, нет. 4. С. 213–217. [ Докл. Phys. Chem. , 2005, т. 403, нет. 4. С. 146–149].
Google ученый
Бурштейн А.И. О происхождении псевдоактивационной температурной зависимости вязкости // Докл. Акад. АН СССР , 1973, т. 213, нет. 5, стр.1109–1112.
Google ученый
Маседо, П. Б. и Литовиц Т.А., Об относительной роли свободного объема и энергии активации в вязкости жидкостей, J. Chem. Phys. , 1965, т. 42, нет. 1. С. 245–256.
Артикул CAS Google ученый
Сандитов Д.С. К теории молекулярной подвижности жидкостей и стекол в широком диапазоне температур и давлений // Изв.Высш. Учебн. Завед., Физ. , 1971, № 2. С. 17–23.
Мацуока С., Алоизио С.Дж., Баир Х.Э. Падение температуры в стеклообразных полимерах во время деформации, J. Appl. Phys. , 1977, т. 48, вып. 10. С. 4058–4062.
Артикул CAS Google ученый
Сандитов Д.С. Условие стеклования жидкостей и критерий Линдеманна плавления в модели возбужденного атома // Докл.Акад. НАУК .2003. 390, нет. 2. С. 209–213. [ Докл. Phys. Chem. , 2003, т. 390, нет. 2. С. 122–125].
Google ученый
Сандитов Д.С. Модель возбужденных атомов и вязкоупругие свойства полимеров и стекол // Высокомол. Журн. Соедин., Сер. А , 2005 г., т. 47, нет. 3. С. 478–489. [ Polym. Наук, сер. А , 2005, т. 47, нет. 3. С. 289–298].
CAS Google ученый
Сандитов Д.С., Байнова А.Б. Вязкое течение и пластическая деформация стекол в модели возбужденных атомов // Физ. Мезомех. Хим. Стекла , 2004, т. 30, нет. 2. С. 153–177. [ Glass Phys. Chem. , 2004, т. 30, нет. 2. С. 113–131].
[ Glass Phys. Chem. , 2004, т. 30, нет. 2. С. 113–131].
Google ученый
Адам Дж., Гиббс Дж. Х. О температурной зависимости свойств кооперативной релаксации в стеклообразующих жидкостях, J. Chem. Phys., 1965, т. 43, вып. 1. С. 139–146.
Артикул CAS Google ученый
Немилов С.В. Вязкое течение стекол в зависимости от их структуры: применение теории скоростных процессов // Физ. Мезомех. Хим. Стекла , 1992, т. 18, нет. 1. С. 3–44. [ Сов. J. Glass Phys. Chem. , 1992, т. 18, нет. 1. С. 1-21].
CAS Google ученый

Немилов С.В., Термодинамические и кинетические аспекты стекловидного состояния , Бока-Ратон: CRC, 1995.
Google ученый
Ferry, J.D., Вязко-упругие свойства полимеров , Нью-Йорк: Wiley, 1961. Перевод под названием Вязкоупругие свойства полимеров , М .: Иностранная литература, 1963.
Google ученый
Дуров, В.А. , Шахпаронов М.И. Теория коллективных реакций в жидких фазах. VI. Уравнение Вильямса-Лэнделла-Ферри, Ж. Физ. Хим. , 1979, т. 53, нет. 10. С. 2456–2459.
CAS Google ученый
Мазурин О.В., Стрельцина М.В., Швайко-Швайковская Т. П., Своя стекла и стеклообразующих расплавов. Справочник . Свойства стекол и стеклообразующих расплавов. Справочник. Л .: Наука, вып.1, 1977.
П., Своя стекла и стеклообразующих расплавов. Справочник . Свойства стекол и стеклообразующих расплавов. Справочник. Л .: Наука, вып.1, 1977.
Google ученый
Судзуки К., Фудзимори Х., Хасимото К., Аморфные металлы, , М .: Металлургия, 1987.
Google ученый
Борнхофт Х. и Брукнер Р. Упругие и неупругие свойства натронно-известково-силикатных расплавов, Glass Sci. Technol. (Франкфурт-на-Майне), 1999, т. 72, нет. 10, стр.315–321.
CAS Google ученый
Мельниченко Т.Д., Ризак В.М., Мельниченко Т.Н., Феделеш В.И. Параметры теории флуктуационного свободного объема стекол в системе Ge-As-Se // Физ. Мезомех. Хим. Стекла , 2004, т. 30, нет. 5. С. 553–564. [ Glass Phys. Chem. , 2004, т. 30, нет. 5. С. 406–414].
Мезомех. Хим. Стекла , 2004, т. 30, нет. 5. С. 553–564. [ Glass Phys. Chem. , 2004, т. 30, нет. 5. С. 406–414].
Google ученый
Сандитов Д.С., Козлов Г.В. О природе корреляции между упругими постоянными и температурой стеклования аморфных полимеров // Физ. Мезомех. Хим. Стекла , 1993, т. 19, нет. 4. С. 561–571. [ Glass Phys. Chem. , 1993, т. 19, нет. 4. С. 289–294].
CAS Google ученый
Сандитов Д.С., Сангадиев С.Ш., Козлов Г.В. О связи модуля упругости стекловидных тел и температуры стеклования расплавов // Физ. Мезомех.Хим. Стекла , 1998, т. 24, вып. 6. С. 758–766. [ Glass Phys. Chem. , 1998, т. 24, вып. 6. С. 539–545].
Google ученый
Мазурин О.В. Ю., Клюев В.П. Дилатометрическое исследование структурного гистерезиса в некоторых многокомпонентных стеклах // Физ. мезомех. Хим. Стекла , 1975, т. 1, вып. 3. С. 245–250.
CAS Google ученый
Клюев В.П. В., Булаева А.В. Вязкость и термическое расширение свинцоборатных стекол в интервале стеклования // Физ. Хим. Стекла , 1980, т. 6, вып. 6. С. 674–678.
CAS Google ученый
Мазурин О.В. Ю., Столяр С.В. О связи между температурами стеклования и температурой ликвидуса для некоторых эвтектических составов боросиликатной системы натрия // Физ. Хим. Стекла , 1984, т.10, вып. 2. С. 163–166.
CAS Google ученый
В ЯМР сильное магнитное поле используется для частичной поляризации ядерных спинов. Если взять протоны в качестве наиболее распространенного примера, то избыток спина протона в направлении магнитного поля составляет небольшую суммарную намагниченность материала. Чтобы создать условия для наблюдения сигнала ЯМР, к образцу прикладывают сильное радиочастотное излучение на соответствующей частоте, чтобы вызвать «перевороты спина».С квантовой точки зрения, радиочастотные фотоны поглощаются некоторыми протонами, переводя их из параллельного магнитному полю в антипараллельное состояние с более высокой энергией. Когда возбуждающее РЧ-поле выключено, протоны стремятся вернуться в свое более низкое энергетическое состояние. Эта «релаксация» обратно в состояние, когда их спины параллельны статическому магнитному полю, производит небольшое количество радиочастотного излучения, которое регистрируется как сигнал ЯМР. Обычно наблюдаются две разные постоянные времени затухания.
| |||||||||||||||||||||||||||