Таблица плюс минус: Таблица сложения чисел (1, 2 класс) и игра – Табличное сложение / Сложение / Справочник по математике для начальной школы — inakhan.ru

Содержание

Табличное сложение / Сложение / Справочник по математике для начальной школы

Главная
Справочники
Справочник по математике для начальной школы
Сложение
Табличное сложение

Прежде чем познакомиться с таблицами сложения чисел, мы рассмотрим случаи сложения разных видов.

Например, 7 + 6 = ?

Мы видим, что сумма будет больше 10, потому что 10 — это 7 и 3. Мы будем прибавлять число 6 по частям.

Сначала прибавляем столько, чтобы получить 10: 7 + 3 = 10.

Дальше мы вспоминаем, что 6 — это 3 и 3.

Число 3 мы уже прибавили, значит, надо прибавить ещё 3: 10 + 3 = 13.

Тогда наш пример 7 + 6 можно записать по-другому:

или так:

Значит, 7 + 6 = 13

Рассуждая так, можно решить любой пример на сложение в пределах 20.

Случаи табличного сложения

11 — это 1 и 10

11 — это 2 и 9

11 — это 3 и 8

11 — это 4 и 7

11 — это 5 и 6

12 — это 2 и 10

12 — это 3 и 9

12 — это 4 и 8

12 — это 5 и 7

12 — это 6 и 6

13 — это 3 и 10

13 — это 4 и 9

13 — это 5 и 8

13 — это 6 и 7

14 — это 4 и 10

14 — это 5 и 9

14 — это 6 и 8

14 — это 7 и 7

15 — это 5 и 10

15 — это 6 и 9

15 — это 7 и 8

16 — это 6 и 10

16 — это 7 и 9

16 — это 8 и 8

17 — это 7 и 10

17 — это 8 и 9

18 — это 8 и 10

18 — это 9 и 9

19 — это 9 и 10

Таблицы сложения

Таблица сложения нужна, чтобы научиться быстрому сложению чисел.

Существует несколько таблиц сложения чисел. Одна из первых таблиц такого рода — таблица сложения в пределах 10, но если ты хорошо знаешь состав чисел, тебе она не понадобится.

Как пользоваться такой таблицей?

Например, тебе нужно узнать, сколько будет 4 + 5.

Есть очень простая таблица сложения чисел с переходом через десяток. Вот она.

Пользоваться ею, конечно, очень легко.

Но наиболее полная таблица сложения чисел в от 1 до 20 представлена ниже.

Как ею пользоваться? Очень просто.

Например, тебе нужно к 7 + 6:

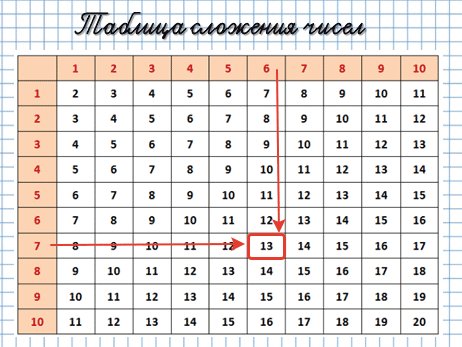
А это сводная таблица, которой можно прользоваться, пока не заучишь её наизусть.

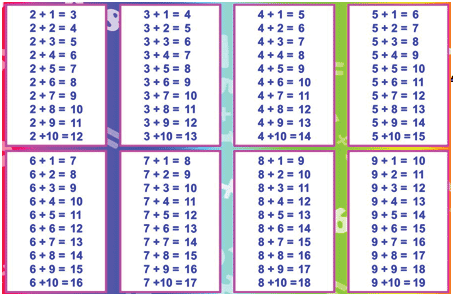
А такими таблицами можно пользоваться при заучивании результатов сложения наизусть.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Письменное сложение в столбик

Сложение

Правило встречается в следующих упражнениях:

1 класс

Страница 45. Вариант 2. № 2, Волкова, Проверочные работы

Страница 69, Моро, Волкова, Степанова, Учебник, 2 часть

Страница 71, Моро, Волкова, Степанова, Учебник, 2 часть

Страница 76, Моро, Волкова, Степанова, Учебник, 2 часть

Страница 79, Моро, Волкова, Степанова, Учебник, 2 часть

Страница 80, Моро, Волкова, Степанова, Учебник, 2 часть

Страница 89, Моро, Волкова, Степанова, Учебник, 2 часть

Страница 92, Моро, Волкова, Степанова, Учебник, 2 часть

Страница 34, Моро, Волкова, Рабочая тетрадь, 2 часть

Страница 45, Моро, Волкова, Рабочая тетрадь, 2 часть

2 класс

Страница 28, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 34, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 65, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 67, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Задание 15, Моро, Волкова, Рабочая тетрадь, 1 часть

Задание 22, Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 5. Вариант 2. № 1, Моро, Волкова, Проверочные работы

Страница 4, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 64, Моро, Волкова, Рабочая тетрадь, 2 часть

Страница 76, Моро, Волкова, Рабочая тетрадь, 2 часть

3 класс

Страница 6, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 14, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 65, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 6, Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 8, Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 11, Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 5, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 14, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 7, Моро, Волкова, Рабочая тетрадь, 2 часть

Страница 12, Моро, Волкова, Рабочая тетрадь, 2 часть

5 класс

Упражнение 166, Мерзляк, Полонский, Якир, Учебник

Пользовательское соглашение

Таблица сложения — распечатать для 1 класса

Распечатать для школы Скачать и распечатать

Скачать бесплатно и распечатать таблицы сложения. Математика 1 класс.

Таблица сложения до 10

Скачать таблицу сложения от 1 до 10 для распечатки в формате А4:

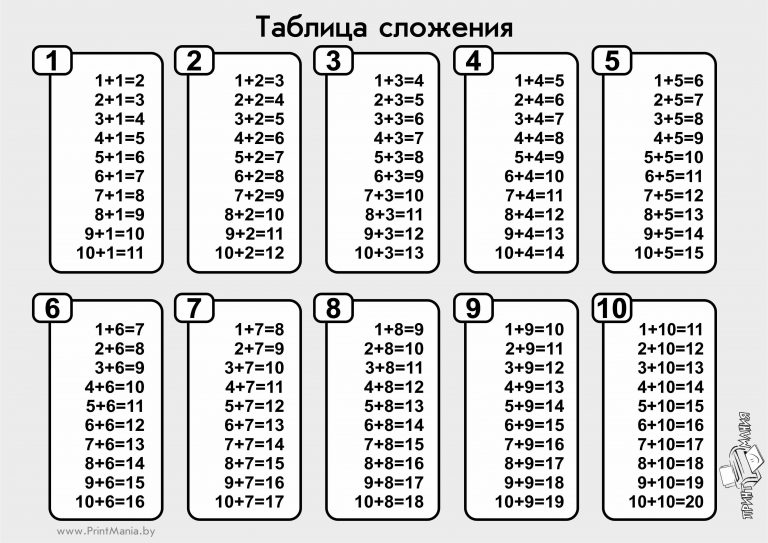
Таблица сложения до 20

Скачать и распечатать таблицу сложения от 1 до 20:

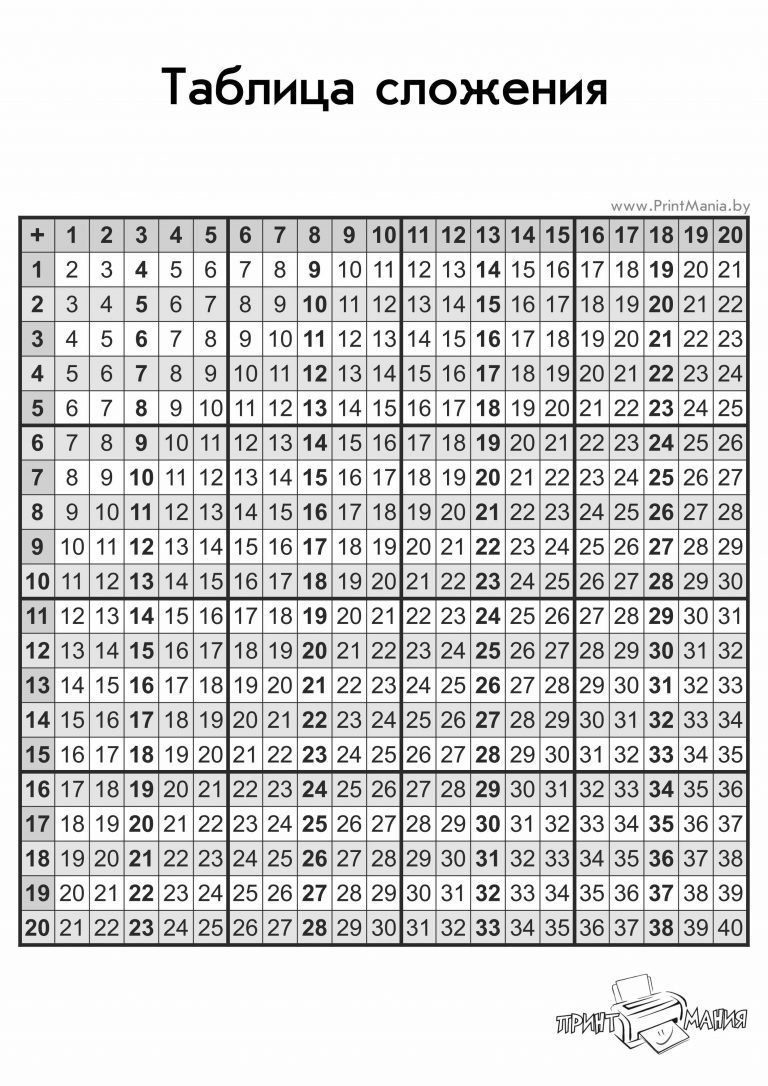
Таблица сложения — тренажеры

Готовые тренажеры таблицы сложения по математике для 1 класса — распечатать на А4.

Тренажер таблицы сложения в пределах 10:

Тренажер таблицы сложения в пределах 20:

± — Знак плюс-минус (U+00B1) plusmn

Описание символа

Знак плюс-минус (±) используется для указания интервала. От трёх до семи можно написать так: 5±2. На клавиатуре набрать можно комбинацией Alt+0177. Число 0177 вводятся на цифровом блоке с включённым Num Lock.

Этот текст также доступен на следующих языках: English; Deutsch;

Кодировка

Кодировка	hex	dec (bytes)	dec	binary
UTF-8	C2 B1	194 177	49841	11000010 10110001
UTF-16BE	00 B1	0 177	177	00000000 10110001
UTF-16LE	B1 00	177 0	45312	10110001 00000000
UTF-32BE	00 00 00 B1	0 0 0 177	177	00000000 00000000 00000000 10110001
UTF-32LE	B1 00 00 00	177 0 0 0	2969567232	10110001 00000000 00000000 00000000

Наборы с этим символом:

Знак плюс-минус — Википедия

Материал из Википедии — свободной энциклопедии

∓

Знак плюс-минус (±) — математический символ, который ставится перед некоторым выражением и означает, что значение этого выражения может быть как положительным, так и отрицательным. Часто используется, например, для указания:

пределов изменения каких-либо параметров;
инструментальной точности измерения физической величины;
ожидаемого разброса значений статистически измеренного параметра;
интервала значений результата в приближённых математических вычислениях.

Пример 1: фраза «напряжение в сети должно быть 220 ± 4,5 вольт» означает, что напряжение должно быть в диапазоне от 215,5 до 224,5 вольт.

Пример 2, где символ «плюс-минус» надо понимать буквально, как указание альтернативы из двух вариантов — известная формула для вычисления двух корней квадратного уравнения ax2+bx+c=0{\displaystyle ax^{2}+bx+c=0}:

x=−b±b2−4ac2a.{\displaystyle \displaystyle x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}.}

Эта формула — компактная запись, объединяющая формулы для первого и второго корня:

x1=−b+b2−4ac2a;x2=−b−b2−4ac2a{\displaystyle \displaystyle x_{1}={\frac {-b+{\sqrt {b^{2}-4ac}}}{2a}};\quad x_{2}={\frac {-b-{\sqrt {b^{2}-4ac}}}{2a}}}

Пример 3, аналогичный второму, тригонометрический:

sin⁡(x±y)=sin⁡(x)cos⁡(y)±cos⁡(x)sin⁡(y){\displaystyle \sin(x\pm y)=\sin(x)\cos(y)\pm \cos(x)\sin(y)}

Пример 4. Здесь истолкование символа плюс-минус иное: надо выбрать знак одночлена в зависимости от его номера в ряду:

sin⁡(x)=x−x33!+x55!−x77!+⋯±1(2n+1)!x2n+1+⋯{\displaystyle \sin \left(x\right)=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots \pm {\frac {1}{(2n+1)!}}x^{2n+1}+\cdots }

Знак плюс-минус появился у Альбера Жирара (1626), который записывал этот символ следующим образом: ou+− {\displaystyle {\boldsymbol {{\underset {-}{\overset {+}{\operatorname {\scriptscriptstyle ou} }}}\ \ }}} (французское слово ou в переводе означает «или»). Современный вид символу придал Уильям Отред в 1631 году^[1].

У знака плюс-минус есть вариант: знак ∓{\displaystyle \mp } (минус-плюс). Он используется совместно с одним или несколькими знаками плюс-минус и означает, что знаку плюс в плюс-минусе строго соответствует знак минус в минус-плюсе, и обратно. Пример:

cos⁡(x±y)=cos⁡xcos⁡y∓sin⁡xsin⁡y{\displaystyle \cos(x\pm y)=\cos x\cos y\mp \sin x\sin y}

Это компактная запись двух формул:

cos⁡(x+y)=cos⁡xcos⁡y−sin⁡xsin⁡y; cos⁡(x−y)=cos⁡xcos⁡y+sin⁡xsin⁡y{\displaystyle \cos(x+y)=\cos x\cos y-\sin x\sin y;~\cos(x-y)=\cos x\cos y+\sin x\sin y}

В шахматной нотации символ ± означает, что после соответствующего хода преимущество имеют белые, а символ ∓ — что преимущество у чёрных.

Символ	Код в Юникоде	Название в Юникоде	Название	HTML шестн.	HTML десят.	HTML обозн.
±{\displaystyle \pm }	U+00B1	Plus-minus sign	Символ плюс-минус	±	±	±
∓{\displaystyle \mp }	U+2213	Minus-or-Plus sign	Символ минус-плюс	∓	∓

В ISO 8859-1 символ плюс-минус имеет код 0xB1.
В TeX знаки плюс-минус и минус-плюс кодируются как \pm и \mp соответственно.
В системе Microsoft Windows для ввода символа плюс-минус можно, прижав клавишу Alt, ввести на цифровой клавиатуре число 0177.
В системах Linux/Unix сформировать символ плюс-минус можно последовательностью compose +-.
На компьютерах Макинтош плюс-минус кодируется вводом символов ⌥ Option ⇧ Shift = .

↑ Александрова Н. В. История математических терминов, понятий, обозначений: Словарь-справочник. — 3-е изд. — СПб.: ЛКИ, 2008. — С. 127. — 248 с. — ISBN 978-5-382-00839-4.


Плюс (+) Минус (−) Знак умножения (· или ×) Знак деления (: или /) Обелюс (÷) Знак корня (√) Факториал (!) Знак интеграла (∫) Набла (∇) Знак равенства (=, ≈, ≡ и др.) Знаки неравенства (≠, >, < и др.) Пропорциональность (∝) Скобки (( ), [ ], ⌈ ⌉, ⌊ ⌋, { }, ⟨ ⟩) Вертикальная черта (\|) Косая черта, слеш (/) Обратная косая черта, бэкслеш (\) Знак бесконечности (∞) Знак градуса (°) Штрих (′, ″, ‴, ⁗) Звёздочка (*) Процент (%) Промилле (‰) Тильда (~) Карет (^) Циркумфлекс (ˆ) Плюс-минус (±) Знак минус-плюс (∓) Десятичный разделитель (, или .) Символ конца доказательства (∎)

Плюс (+)
Минус (−)
Знак умножения (· или ×)
Знак деления (: или /)
Обелюс (÷)
Знак корня (√)
Факториал (!)
Знак интеграла (∫)
Набла (∇)
Знак равенства (=, ≈, ≡ и др.)
Знаки неравенства (≠, >, < и др.)
Пропорциональность (∝)
Скобки (( ), [ ], ⌈ ⌉, ⌊ ⌋, { }, ⟨ ⟩)
Вертикальная черта (|)
Косая черта, слеш (/)
Обратная косая черта, бэкслеш (\)
Знак бесконечности (∞)
Знак градуса (°)
Штрих (′, ″, ‴, ⁗)
Звёздочка (*)
Процент (%)
Промилле (‰)
Тильда (~)
Карет (^)
Циркумфлекс (ˆ)
Плюс-минус (±)
Знак минус-плюс (∓)
Десятичный разделитель (, или .)
Символ конца доказательства (∎)

Сложение и вычитание отрицательных и положительных чисел. Решение примеров.

Существуют разные типы чисел — четные числа, нечетные числа, простые числа, составные числа. Также на основе знака числа могут быть двух видов — положительные числа и отрицательные числа. Эти числа могут быть представлены на числовой линией. Среднее число в этой строке равно нулю. С левой стороны от нуля находятся отрицательные числа, а с правой стороны — положительные.

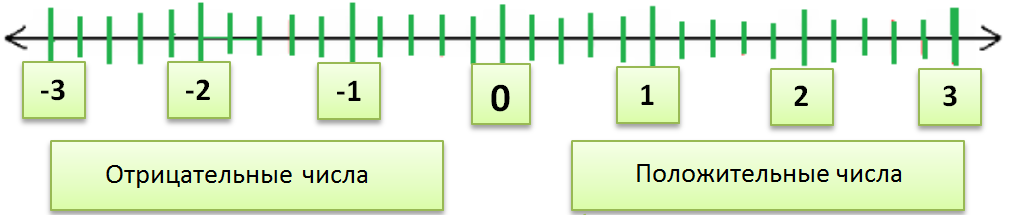
Ноль — это нейтральный элемент относительно сложения целых чисел. В основном в этой статье мы будем изучать операции сложения и вычитания с отрицательными числами. Существуют определенные правила для знаков при сложении и вычитании:

Правила для знаков при сложении и вычитании

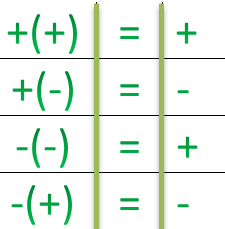
Для того чтобы сложить два отрицательных числа, надо сложить два числа и поставить знак минус.

\((-2)+(-3)=-5\)

Если первое число положительное, а второе отрицательное, смотрим, какое число по модулю больше, отнимаем от большего меньшее число и ставим знак большего числа:

\((-8)+4=4-8=-4\)

\(9+(-4)=9-4=5\)

Для каждого числа кроме \(0\) существует противоположный элемент, при сумме с ним образуется ноль:

\(-9+9=0\) \(7,1+(-7,1)=0\)

При вычитания двух чисел, в которых оба отрицательные, следует знать правило: минус на минус дает плюс. То есть, если стоят рядом два минуса, в сумме получается плюс.

\((-7)-(-6)=(-7)+6=(-1)\)

Если первое число положительное, а второе отрицательное, вычитаем по тому же принципу, что и складываем: смотрим, какое число по модулю больше, отнимаем от большего меньшее число и ставим знак большего числа.

\(7-9=-2\) так как \(9>7\)

Также не стоит забывать минус на минус дает плюс:

\(7-(-9)=7+9=16\)

Задача 1. Вычислите:

\(4+(-5)\)
\(-36+15\)
\((-17)+(-45)\)
\(-9+(-1)\)

Решение:

\(4+(-5)=4-5=-1\)
\(-36+15=-21\)
\((-17)+(-45)\) \(=-17-45=-62\)
\(-9+(-1)=-9-1=-10\)

Задача 2. Вычислите:

\(3-(-6)\)
\(-16-35\)
\(-27-(-5)\)
\(-94-(-61)\)

Решение:

\(3-(-6)=3+6=9\)
\(-16-35=-51\)
\(-27-(-5)=-27+5=-22\)
\(-94-(-61)=-94+61=-33\)

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Таблица сложения | Таблица умножения

В первом столбце и в первой строке записаны слагаемые, в ячейках на пересечении соответствующих столбцов и строк записаны результаты.
Например, если первое слагаемое равно 4, а второе равно 3, то сумма будер равна 7:

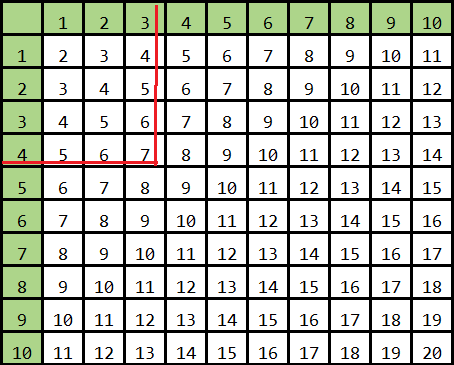
Другие варианты, в том числе до 20, таблицу в другом цветовом оформлении можно найти и скачать для распечатывания в конце статьи. Кроме таблиц для удобного счета с древних времен используют также и другие способы, они описаны в соответствующем разделе, в этой же статье речь пойдет прежде всего о таблицах.

Прежде чем приступать к описанию этой темы, следует определиться с основными понятиями.

Например, что значит запись «4 + 5 = 9», и как это отразить в таблице сложения. В большинстве современных книг по математике приняты определенные названия для каждого из этих чисел. Мы будем применять на этой странице наиболее распространенные на сегодняшний день. Согласно общепринятой терминологии, в вышеприведенном примере 4 и 5 – это слагаемые, 9 – сумма. Сложение также иногда называют прибавлением и суммированием, нахождением суммы. Также в математике есть термин «операция сложения». Слагаемые иногда называют суммируемыми, а результат — результатом сложения или результатом суммирования.

Часто начинают изучение со сложения простых чисел. Первым этапом является сложение чисел до 10, далее от 10 до 20. На этих этапах для более быстрого запоминания пользуются таблицами, которые, как и таблицу умножения, можно найти на оборотах некоторых тетрадей. Существует два вида таких таблиц сложения. Первый – это, собственно говоря, не совсем таблица, а скорее сгруппированные простые равенства.

Таблица сложения равенства.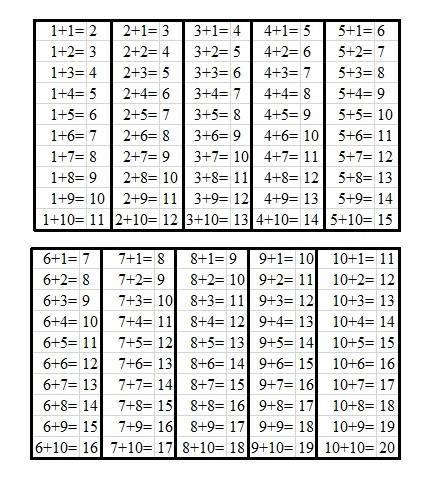

Расширенный вариант обычно представляют в следующем виде.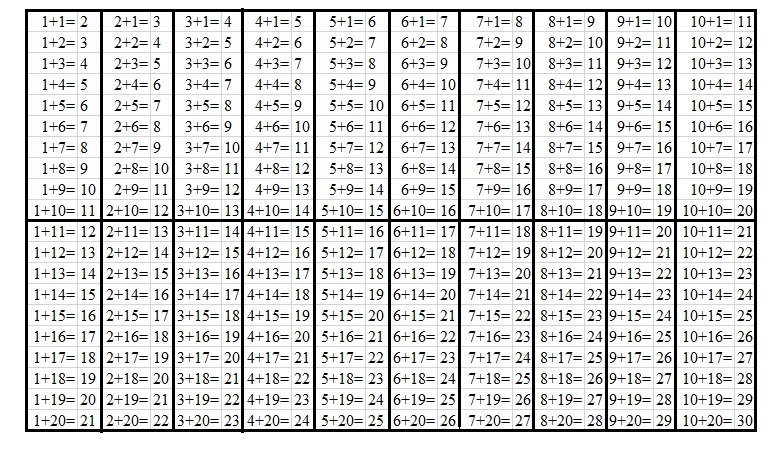

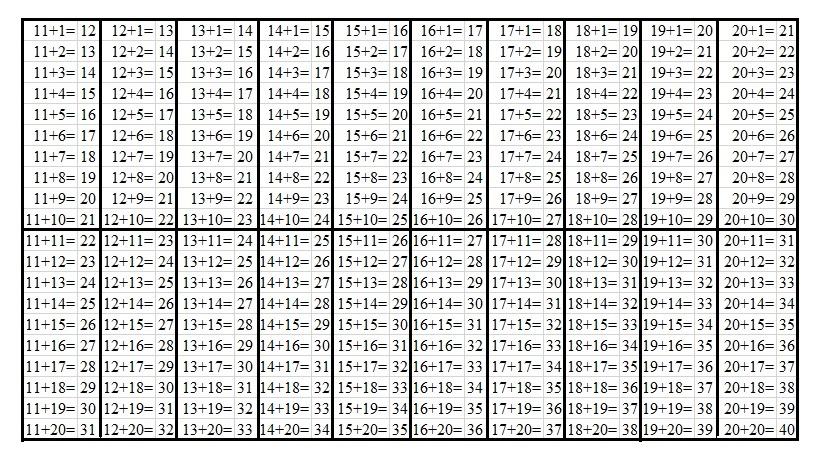
Есть и другой способ. В представленной ниже таблице в первой строке и в первом столбце находятся слагаемые, в ячейках на пересечении соответствующих столбцов и строк записаны суммы двух этих чисел. Рассмотрим на конкретных примерах, как можно пользоваться таблицей сложения.

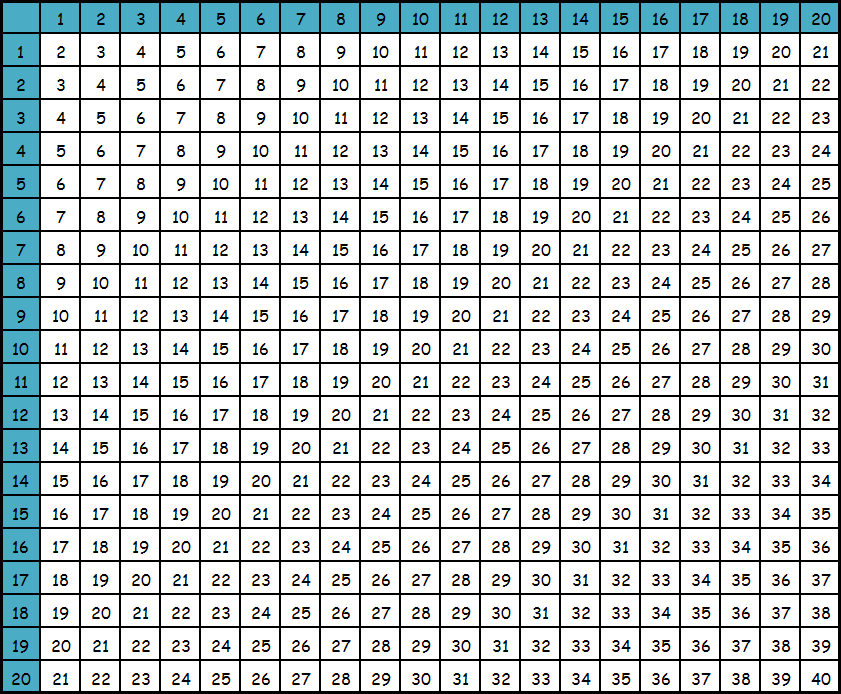
Сложим 3 и 4. Находим число 3 по горизонтали и число 4 по вертикали. Мысленно проводим линии до места пересечения. Это и есть искомое значение. Нетрудно заметить, что если мы поменяем местами значения и отыщем по горизонтали 4, а по вертикали — 3, то также в ячейке будет 7.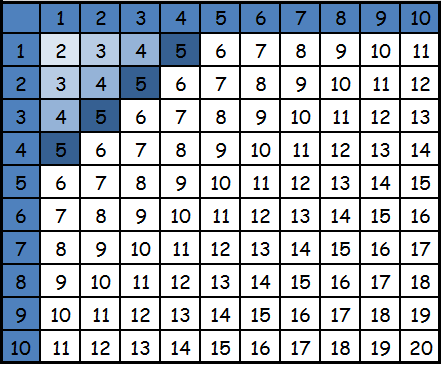

Отсюда вытекает одно из свойств, справедливых для суммы чисел. Звучит оно так: «От перестановки мест слагаемых сумма не меняется». Это свойство справедливо и для большего количества слагаемых. Разберемся в вопросе о том, можно ли данной таблицей пользоваться в случае сложения нескольких слагаемых. Ответ: можно, но до определенных значений. В этом случае действия нужно производить постепенно. Сначала складываем первые два слагаемых, получаем некое число. Если это простое число, которое входит в таблицу, то мы находим его и к нему прибавляем оставшееся и так далее. То есть, ориентируемся на наличие значений в таблице. Например, 4+5+6. Начала находим результат для действия 4 + 5, в ячейке на пересечении их столбца и строки находится 9. Далее выполняем действие 9+6. Находим в таблице 9 и 6. Далее все аналогично. Для больших чисел обычно таблицы не составляются. Таблица вычитания. Этой же таблицей можно пользоваться и для операции вычитания. В этом случае производим обратные действия. В самой таблице находим значение, из которого нужно вычесть число. Затем проводим линию до того числа, которое вычитается, остается мысленно дойти до оставшегося значения. Оно и будет искомым. Совсем просто это можно осуществить при помощи линейки. В данном случае линейка подставляется от вычитаемого числа сначала вертикально, затем горизонтально. Или наоборот. Для быстрого устного счета часто запоминают результаты сложения, и со временем уже нет необходимости наличия таблицы перед глазами.

Для ознакомления также ниже представлены более старые варинты таблицы.

Таблицы сложения значительно упрощают повседневный счет, поэтому много лет назад люди начали их использовать и некоторые из них мы можем видеть в сохранившихся книгах. Например, так выглядела таблица сложения в книге «Арифметика» Магницкого Л. Ф. 1703 года издания.

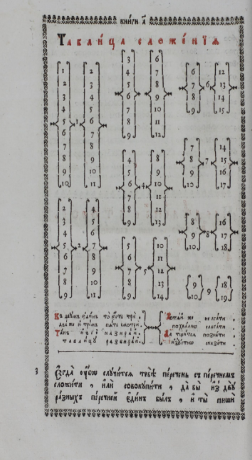
(на картинке фото фрагмента из оцифрованной версии книги, саму книгу найти было достаточно сложно, поэтому использована сканированная версия, которая есть в широком доступе) Так выглядит эта таблица в воспроизведении (переиздании) той же книги, сделанном в 1914 году под редакцией П. Баранова: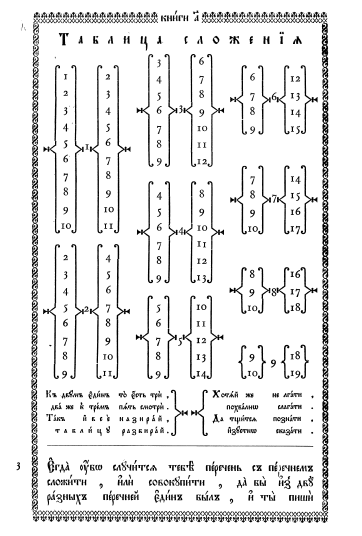

(на картинке как раз фотография тоже сканированной версии переиздания 1914 года).

Сложение и вычитание однозначных чисел с переходом через разряд. Таблица сложения до 20

На данном уроке вы научитесь складывать и вычитать однозначные числа с переходом через разряд. Решая интересные задания, вы изучите алгоритм сложения и вычитания чисел с переходом через десяток и познакомитесь с таблицей сложения однозначных чисел до 20. У вас будет возможность попрактиковать изученный ранее материал на интересных примерах.

Тема: Знакомство с основными понятиями в математике

Урок: Сложение и вычитание однозначных чисел с переходом через разряд. Таблица сложения до 20

С помощью графической модели можно объяснить сложение однозначных чисел с переходом через десяток.

Каким способом можно сложить 9 и 7? (рис. 1)

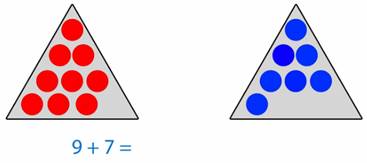
Рис. 1

На графической модели видно, что первое слагаемое 9 надо дополнить до 10. Для этого разобьем второе слагаемое на две части, одна из которых равна числу 1, так как

9 + 1 = 10, значит 7 = 1 + 6. (рис. 2)

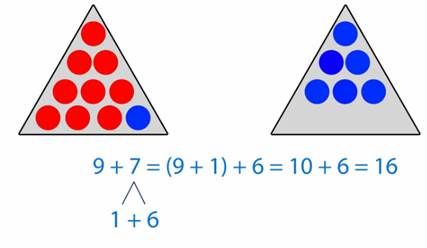
Рис. 2

Выполним сложение по частям:

9 + 7 = (9 + 1) + 6 = 10 + 6 = 16

Ответ: 9 + 7 = 16.

Можно сложить эти числа по-другому. (рис. 3)

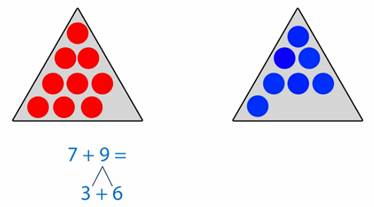
Рис. 3

Второе слагаемое 7 можно дополнить до 10. Для этого первое слагаемое разобьем на две части, одна из которых равна числу 3. Следовательно, 9 = 3 + 6.

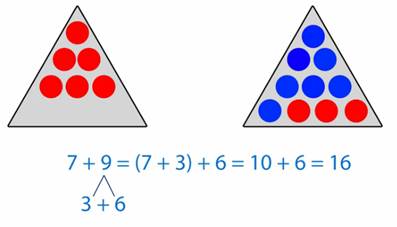
Рис. 4

Выполним сложение по частям:

7 + 9 = (7 + 3) + 6 = 10 + 6 = 16

Ответ: 7 + 9 = 16.

Чтобы сложить однозначные числа с переходом через десяток, необходимо до десяти добавить одно из слагаемых, а затем прибавить оставшиеся единицы.

9 + 5

Первое слагаемое – 9, ему недостаёт до 10 одной единицы, поэтому второе слагаемое разбиваем на части. 5 – это 1 и 4. Добавляем к 9 сначала одну единицу, а потом оставшиеся четыре единицы.

9 + 5 = 9 + (1 + 4 ) = 14

Ответ: 9 +5 = 14.

6 + 6

Первое слагаемое – 6, ему недостаёт до 10 четырёх единиц, поэтому второе слагаемое разбиваем на части: 4 и 2. Добавляем к 6 сначала 4 и получаем десять единиц, а потом оставшиеся две единицы.

6 + 6 = 6 + (4 + 2) = 12

Ответ: 6 + 6 = 12

4 + 8

Первое слагаемое – 4, ему недостаёт до 10 шести, поэтому второе слагаемое 8 разбиваем на части: 6 и 2. Добавляем к 4 сначала шесть единиц и получаем десять единиц, а потом оставшиеся две единицы.

4 + 8 = 4 + (6 + 2) = 12

Ответ: 4 + 8 = 12

Чтобы выполнить вычитание с переходом через десяток по частям, необходимо определить число единиц в уменьшаемом и разбить вычитаемое на две части, одна из которых равна числу единиц. А потом выполнить вычитание по частям.

С помощью графической модели можно объяснить и вычитание однозначного числа из двузначного числа до 20.

11 – 6

В уменьшаемом 11 один десяток и одна единица. (рис. 5)

Рис. 5

Вычитаемое 6 разбиваем на части: 1 и 5. Вычитаем сначала из 11 одну единицу, получаем 10, а потом из 10 вычитаем оставшиеся пять единиц. (рис. 6)

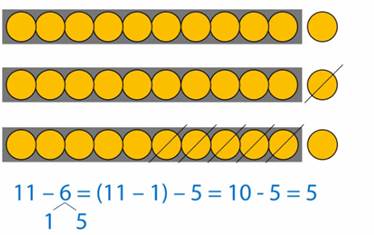
Рис. 6

Ответ:11 – 6 = 5

15 – 7

В уменьшаемом 15 – пять единиц, поэтому вычитаемое 7 разбиваем на части: 5 и 2. Вычитаем из 15 сначала пять единиц, получится 10. Потом из десяти вычитаем оставшиеся две единицы.

15 – 7 = 15 – (5 + 2) = 8

Ответ: 15 – 7 = 8.

16 – 9

В уменьшаемом 16 – шесть единиц, поэтому вычитаемое 9 разбиваем на части: 6 и 3. Вычитаем сначала из 16 шесть единиц, получится 10. А потом из 10 вычитаем оставшиеся три единицы.

16 – 9 = 16 – (6 + 3) = 7

Ответ: 16 – 9 = 7.

12 – 4

В уменьшаемом 12 – две единицы, поэтому вычитаемое 4 разбиваем на части: 2 и 2. Из 12 вычитаем 2, получится 10. И от 10 отнимаем 2.

12 – 4 = 12 – (2 + 2) = 8

Ответ: 12 – 4 = 8.

Использовать прием сложения и вычитания по частям с переходом через десяток не всегда удобно, поэтому необходимо выучить таблицу сложения однозначных чисел до 20 наизусть.

На рисунке изображена таблица, с помощью которой вам будет легче выучить случаи сложения однозначных чисел до 20. (рис. 7)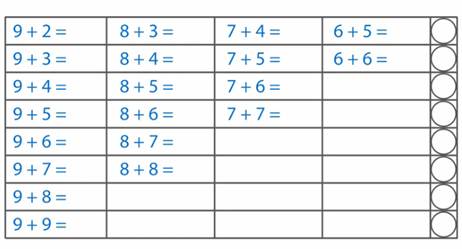

Рис. 7

В каждом столбике первое слагаемое – одинаковое, а второе – увеличивается на один, значит сумма тоже будет увеличиваться на один. Найдём значение данных сумм.

9 + 2 = 11, следовательно: 9 + 3 = 12, рассуждая так, заполняем всю таблицу. (рис. 8)

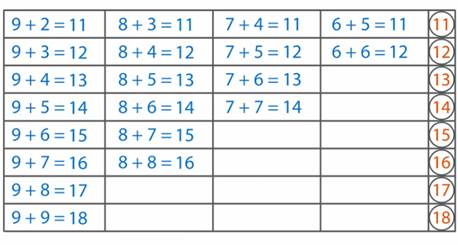
Рис. 8

В каждой строке записаны суммы с одинаковыми ответами. Выберите способ, как вам легче будет запомнить ответы: по столбикам или по строкам. Если вы хорошо выучите таблицу сложения однозначных чисел до 20, то вам будет нетрудно выполнять и вычитание однозначных чисел в пределах 20.

На уроке мы учились складывать и вычитать однозначные числа с переходом через десяток до 20. Знания таблицы сложения до 20 поможет вам при решении примеров и задач.

Список литературы

Александрова Л.А., Мордкович А.Г. Математика 1 класс. – М: Мнемозина, 2012.
Башмаков М.И., Нефедова М.Г. Математика. 1 класс. – М: Астрель, 2012.
Беденко М.В. Математика. 1 класс. – М7: Русское слово, 2012.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

Социальная сеть работников образования (Источник).
5klass.net (Источник).
Самоучка (Источник).

Домашнее задание

1. Вспомните как правильно складывать и вычитать однозначные числа с переходом через разряд.

2. Помогите лягушке решить примеры.

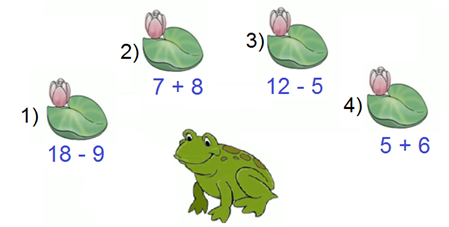
3. Решите примеры и раскрасьте рисунок.