| | Навигация по справочнику TehTab.ru: главная страница / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Детский сад — 7 класс. / / Таблица сложения от 1 до 10. Таблица сложения до 20.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| TehTab.ru Реклама, сотрудничество: [email protected] | Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Правила знаков
Минус и плюс – это признаки отрицательных и положительных чисел в математике. Они по-разному взаимодействую с собой, поэтому при выполнении каких-либо действий с числами, например, деление, умножение, вычитание, сложение и т.д., необходимо учитывать правила знаков. Без этих правил вы никогда не сможете решить даже самую простую алгебраическую или геометрическую задачу. Без знания этих правил, вы не сможете изучить не только математику, но и физику, химию, биологию, и даже географию.
Рассмотрим подробней основные правила знаков.
Деление.
Если мы делим «плюс» на «минус», то получаем всегда «минус». Если мы делим «минус» на «плюс», то получаем всегда также «минус». Если мы делим «плюс» на «плюс», то получаем «плюс». Если же мы делим «минус» на «минус», то получим, как ни странно, также «плюс».
Умножение.
Если мы умножаем «минус» на «плюс», то получаем всегда «минус». Если мы умножаем «плюс» на «минус», то получаем всегда также «минус». Если мы умножаем «плюс» на «плюс», то получаем положительно число, то есть «плюс». Тоже самое касается и двух отрицательных чисел. Если мы умножаем «минус» на «минус», то получим «плюс».
Вычитание и сложение.
Они базируются уже на других принципах. Если отрицательное число будет больше по модулю, чем наше положительное, то результат, конечно же, будет отрицательный. Наверняка, вам интересно, что же такое модуль и зачем он тут вообще. Все очень просто. Модуль – это значение числа, но без знака. Например -7 и 3. По модулю -7 будет просто 7 , а 3 так и останется 3. В итоге мы видим, что 7 больше, то есть выходит, что наше отрицательное число больше. Вот и выйдет -7+3 = -4. Можно сделать еще проще. Просто на первое место ставить положительное число, и выйдет 3-7 = -4, возможно кому-то так более понятно. Вычитание действуют полностью по такому же принципу.
Например -7 и 3. По модулю -7 будет просто 7 , а 3 так и останется 3. В итоге мы видим, что 7 больше, то есть выходит, что наше отрицательное число больше. Вот и выйдет -7+3 = -4. Можно сделать еще проще. Просто на первое место ставить положительное число, и выйдет 3-7 = -4, возможно кому-то так более понятно. Вычитание действуют полностью по такому же принципу.
Правила при умножении (делении) чисел | |||||||||||||||
| |||||||||||||||
Урок математики в 1 классе «Плюс 3, минус 3»
Урок математики в 1 классе
Тема: +3,-3
Цели и задачи:
1. Знать состав числа «3», приёмы сложения и вычитания для случаев +3,-3, таблицу сложения для случаев + 1, +2.
Знать состав числа «3», приёмы сложения и вычитания для случаев +3,-3, таблицу сложения для случаев + 1, +2.
2. Уметь прибавлять и вычитать «3»
3. Развивать умение анализировать, познавательную мотивацию
4. Воспитывать интерес к устному народному творчеству, чувство товарищества.
Ход урока:
Орг. момент
Встало солнышко давно,
Заглянуло к нам в окно.
Нас оно торопит в класс,
Математика у нас!
Сегодня у нас необычный урок математики. На нём мы все отправимся в волшебный мир сказки. Сказка – в загадочный таинственный мир. В сказках совершаются самые невероятные чудеса. Здесь можно увидеть быстро несущийся под облаками ковер-самолет, набрести на ветхую избушку Бабы Яги, встретить говорящих зверей и птиц и много других чудес.
И так, готовы вы отправиться в сказку?
Чтобы в сказку попасть надо после 3 звонков:
3 раза топнуть левой ногой, 3 раза хлопнуть над головой.
3 раза покружиться вокруг себя. Произнести: 1, 2, 3 — сказка в гости приходи!
Звучит сказочная музыка.
Вот мы и в сказочной стране. Здесь всё покрыто волшебством, даже числа. А особенно число три.
Работа в тетради. Повторение написания цифры 3.
А как вы думаете, почему в сказках это число волшебное. Вспомните сказочных героев, сказочные предметы, которых в сказках было три.
Актуализация опорных знаний:
Устный счёт:
Песенка о трёх поросятах или загадка:
Возле леса на опушке
Трое их живёт в избушке.
Вместо носа – пятачок,
Вместо хвостика – крючок.
Угадайте без подсказки,
Кто герои этой сказки?
Что строили в сказке поросята?
Каким должен быть их дом? Почему?
Построим дом для трёх поросят. На доске план дома с примерами, по классу развешаны кирпичики и детали крыши с ответами. Дети решают примеры и прикрепляют соответствующий кирпичик.
На доске план дома с примерами, по классу развешаны кирпичики и детали крыши с ответами. Дети решают примеры и прикрепляют соответствующий кирпичик.
(Примеры читаем по-разному)
5+2=
7-1=
7-2=
6+1=
7+1
8+2=
Молодцы, ребята, хороший дом получился у нас, но чтобы выполнить задания следующих героев, надо вспомнить состав числа три:
3 3 3
Загадка про Бабу Ягу.
В самой чаще есть избушка.
В ней живёт одна старушка.
Чёрный кот ей верно служит.
Царь Кощей с ней с детства дружит.
Узнала Баба Яга, что есть в самом густом лесу яблонька волшебная. Яблочки на неё растут молодильные. Кто их съест — сразу помолодеет. Отправилась она в лес, сорвала несколько яблок. Давайте посчитаем, сколько яблок в её корзинке. А сколько ещё на яблоне висит? Как узнать, сколько всего яблок выросло на яблоне?
Давайте найдём разные способы, как можно к 6 прибавить 3.
6+3=6+1+1+1=9
6+3=6+1+2=9
6+3=6+2+1=9
Сколько было яблок? Сколько ещё сорвали? Как прибавили 3? Может кто-то назовёт свой способ, как можно прибавить число 3?
Решение обратной задачи.
Баба Яга решила три яблока отправить своему другу – Кощею Бессмертному. Давайте узнаем, сколько у неё останется яблок.
9-3=9-1-2=6
9-3=9-1-1-1=6
9-3=9-2-1=6
Физкультминутка:
Вы устали, засиделись?
Вам размяться захотелось?
Отложите вы тетрадки,
Приступаем мы к зарядке.
Раз – подняться, потянуться,
Два – согнуться, разогнуться,
Три – в ладоши три хлопка,
Головою три кивка,
На четыре – руки шире,
Пять – руками помахать,
Шесть – за парту тихо сесть.
Семь, восемь — лень отбросим.
Работа с карточками
Впереди Змей Горыныч, дышит огнём, чтобы его обойти, надо по мостику пройти. Пройти сможет лишь тот, кто правильно сосчитает все примеры, расположенные на мостике. Работа в паре:
Работа в паре:
Увеличь каждое число на 3:
Уменьши каждое число на 3:
Мы оказались в дремучем лесу, сможем выбраться, если решим все примеры.
Самостоятельная работа:
Решение примеров:
6
0
7
о
7
+3=1
м
9
0-3=5
и
10
+3=4
м
9
л
8
+3=7
д
4
-3=9-3=
2
ц
6
ы
5
+3=Самопроверка. Самооценка. Дети проверяют и собирают из флажков слово: МОЛОДЦЫ
Вот и закончилась сказка, закончился наш урок.
Подведение итогов.
-Мы узнали…,
-Мы учились…,
-Мы смогли…,
-У нас не получилось…,
-На уроке было легко…,
-На уроке было трудно…
«Плюс-минус-интересно» — Документ
Рефлексия в конце урока
1. Ребята по кругу высказываются одним
предложением, выбирая начало фразы из
рефлексивного экрана на доске:
Ребята по кругу высказываются одним
предложением, выбирая начало фразы из
рефлексивного экрана на доске:
сегодня я узнал…
было интересно…
было трудно…
я выполнял задания…
я понял, что…
теперь я могу…
я почувствовал, что…
я приобрел…
я научился…
у меня получилось …
я смог…
я попробую…
меня удивило…
урок дал мне для жизни…
мне захотелось…
2. «Плюс-минус-интересно».
Это упражнение можно выполнять как
устно, так и письменно, в зависимости
от наличия времени. Для письменного
выполнения предлагается заполнить
таблицу из трех граф. В графу «П» — «плюс»-
записывается все, что понравилось на
уроке, информация и формы работы, которые
вызвали положительные эмоции, либо, по
мнению ученика, могут быть ему полезны
для достижения каких-то целей. В графу
«М» — «минус»- записывается все, что не
понравилось на уроке, показалось скучным,
вызвало неприязнь, осталось непонятным,
или информация, которая, по мнению
ученика, оказалась для него не нужной,
бесполезной . В графу «И» — «интересно»-
учащиеся вписывают все любопытные
факты, о которых узнали на уроке, что бы
еще хотелось узнать по данной проблеме,
вопросы к учителю.
В графу
«М» — «минус»- записывается все, что не
понравилось на уроке, показалось скучным,
вызвало неприязнь, осталось непонятным,
или информация, которая, по мнению
ученика, оказалась для него не нужной,
бесполезной . В графу «И» — «интересно»-
учащиеся вписывают все любопытные
факты, о которых узнали на уроке, что бы
еще хотелось узнать по данной проблеме,
вопросы к учителю.
Плюс | Минус | Интересно |
3.Анкета.
Школьникам предлагается небольшая анкета, наполнение которой можно менять, дополнять в зависимости от того, на какие элементы урока обращается особое внимание. Можно попросить обучающихся аргументировать свой ответ.
1.
 На уроке я работал
На уроке я работал2. Своей работой на уроке я
3. Урок для меня показался
4. За урок я
5. Мое настроение
6. Материал урока мне был
7. Домашнее задание мне кажется
активно / пассивно
доволен / не доволен
коротким / длинным
не устал / устал
стало лучше / стало хуже
понятен / не понятен
полезен / бесполезен
интересен / скучен
легким / трудным
интересным / неинтересным
4. «Мои ответы».
На протяжении урока отмечать условно свои ответы:
«V» — ответил по просьбе учителя, но ответ не правильный;
«W» — ответил по просьбе учителя, ответ правильный;
«| » — ответил по своей инициативе, но ответ не правильный;
«+» — ответил по своей инициативе, ответ правильный;
«0» — не ответил.
5. «Комплимент».
Комплимент-похвала, комплимент деловым качествам, комплимент в чувствах, в котором учащиеся оценивают вклад друг друга в урок и благодарят друг друга и учителя за проведенный урок. Такой вариант окончания урока дает возможность удовлетворения потребности в признании личностной значимости каждого.
6. «Три лица».
Учитель показывает учащимся карточки с изображением трех лиц: веселого, нейтрального и грустного.
Учащимся предлагается выбрать рисунок, который соответствует их настроению.
7. «Цветные карточки».
У учащихся две карточки: синяя и красная. Они показывают карточку в соответствии с их настроением в начале и в конце урока. В данном случае мы можем проследить, как меняется эмоциональное состояние ученика в процессе занятия.
8.«Пейзаж». Учащимся
предлагаются две картины с изображением
пейзажа. Одна картина проникнута
грустным, печальным настроением, другая
— радостным, веселым. Ученики выбирают
ту картину, которая соответствует их
настроению.
Одна картина проникнута
грустным, печальным настроением, другая
— радостным, веселым. Ученики выбирают
ту картину, которая соответствует их
настроению.
9.Приём «Что, если…?»
Приём «Что, если…?» предполагает включение на этапе рефлексии вопросов, которые начинаются со слов: «Что, если…?» Данные вопросы позволяют учащимся по-новому, с другой стороны посмотреть на проблему, выдвинуть свои предположения, свои гипотезы развития событий, расширяя тем самым опыт спонтанного общения, способствуя развитию гипотетического мышления учащихся. (Что, если бы Вася не познакомился с Валеком и Марусей?(Владимир Галактионович Короленко «В дурном обществе»).
10.Подбор афоризма пословицы, стихотворения к уроку.
11. Оценка «приращения» знаний и достижения целей (высказывания Я не знал… — Теперь я знаю…).
12. Решение проблемы на уроке
можно оформить в виде графического
организатора, например «грабли» или «гроздь». Они приемлемы на стадии рефлексии, когда
учащиеся ещё раз пересматривают,
осмысливают то, что узнали, расширяют
сферу своих знаний, выдвигают новые
идеи.
Они приемлемы на стадии рефлексии, когда
учащиеся ещё раз пересматривают,
осмысливают то, что узнали, расширяют
сферу своих знаний, выдвигают новые
идеи.
Итог совместной работы в группе можно выполнить в виде схемы-паутины.
Что нового ты узнал на уроке?
Какие уже имеющиеся у тебя знания понадобились в решении задачи (или на уроке)?
Кто и как тебе помогал(и) на уроке при решении задач?
Какие знания, полученные на уроке, понадобятся тебе в будущем?
Где ты применишь полученные знания?
В какой момент урока ты чувствовал себя особенно успешным?
Благодаря каким инструментам ты нашел решение?
Какие способы и приемы работы ты использовал на уроке (составлял таблицу, рисовал схему, составлял тезисы и т.д.)?
С кем тебе было интереснее всего работать в паре/группе? Почему?
За что бы ты себя похвалил на уроке?
Что изменил бы в своих действиях на уроке?
Что бы ты изменил на уроке в последующем?
Что тебе понравилось на уроке больше всего?
И т. д.
д.
13.Аргументированные ответы на один из вопросов:
1. Что вы ожидали от урока и что получилось?
2. Какие этапы урока вы считаете наиболее удачными и почему?
3. Какие события (действия, мнения и т.п.) вызвали наиболее яркие ощущения?
4. Была ли польза от такого рода работы?
5. В чем вы видите собственное приращение?
6. Что вам более всего удалось во время урока, какие виды деятельности были выполнены наиболее успешно? Назовите наиболее эффективные из них.
7. Перечислите в порядке убывания основные проблемы и трудности, которые вы испытывали во время урока. Какими способами вы их преодолевали?
8. Что мы делали нерационально? Назовите одно действие, которое можно добавить, чтобы завтра сделать нашу работу на уроке более успешной.
9. На основании каких критериев
можно оценить нашу деятельность?
На основании каких критериев
можно оценить нашу деятельность?
10.Какой этап урока вы бы опустили, вычеркнули? Почему?
14.Резюме, эссе, мини-сочинения.
15. «Три М».
Учащимся предлагается назвать три момента, которые у них получились хорошо в процессе урока, и предложить одно действие, которое улучшит их работу на следующем уроке.
16.»График».
Учащимся предлагается начертить в течение урока график
-изменения их интереса;
-уровня познания,
— личной активности.
17. «Дерево моего успеха».
Предлагается на индивидуальном дереве успеха с помощью условных знаков показать, насколько оказался доступным и усвоенным тот или иной фрагмент темы.
18. Техника «рефлексивная мишень».
На доске рисуется мишень, которая
делится на сектора. В каждом из секторов
записываются параметры- вопросы рефлексии
состоявшейся деятельности. Например,
оценка содержания, оценка форм и методов
проведения урока, оценка деятельности
педагога, оценка своей деятельности.
Участник ставит метки в сектора
соответственно оценке результата: чем
ближе к центру мишени, тем ближе к
десятке, на краях мишени оценка ближе
к нулю. Затем проводят её краткий анализ.
В каждом из секторов
записываются параметры- вопросы рефлексии
состоявшейся деятельности. Например,
оценка содержания, оценка форм и методов
проведения урока, оценка деятельности
педагога, оценка своей деятельности.
Участник ставит метки в сектора
соответственно оценке результата: чем
ближе к центру мишени, тем ближе к
десятке, на краях мишени оценка ближе
к нулю. Затем проводят её краткий анализ.
19. Вопросы, требующие многовариантных ответов:
Почему было трудно?
Что открыли, узнали на уроке?
Оправдались ли ваши ожидания от урока?
Что вы взяли с сегодняшнего урока?
Над чем заставил задуматься урок?
20. «Благодарю…».
В конце урока учитель предлагает
каждому ученику выбрать только одного
из ребят, кому хочется сказать спасибо
за сотрудничество и пояснить, в чем
именно это сотрудничество проявилось. Учителя из числа выбираемых следует
исключить. Благодарственное слово
педагога является завершающим. При этом
он выбирает тех, кому досталось наименьшее
количество комплиментов, стараясь найти
убедительные слова признательности и
этому участнику событий.
Учителя из числа выбираемых следует
исключить. Благодарственное слово
педагога является завершающим. При этом
он выбирает тех, кому досталось наименьшее
количество комплиментов, стараясь найти
убедительные слова признательности и
этому участнику событий.
21.»А напоследок я скажу».
Школьникам предлагается последовательно ответить на три вопроса:
Насколько оправдались ваши ожидания и кому за это спасибо (исключая учителя)?
Что не оправдалось и почему?
Мои и наши перспективы?
22.»Ассоциация».
Обучающимся предлагается из
картинок, разложенных на столе, выбрать
по две: первую – которая максимально
иллюстрирует его состояние на начало
урока, вторую – на его окончание. Затем
каждый желающий может объяснить свой
выбор (по одному – два предложения на
картинку). Любые комментарии со стороны
других одноклассников или учителя
исключаются. Педагог комментирует свои
картинки последним, подводя итоги урока.
23. «Синквейн».
В конце урока обучающимся предлагается написать синквейн на основе изученного материала. Синквейн – это пятистрочная строфа.
1-я строка – одно ключевое слово, определяющее содержание синквейна;
2-я строка – два прилагательных, характеризующих данное понятие;
3-я строка – три глагола, обозначающих действие в рамках заданной темы;
4-я строка – короткое предложение, раскрывающее суть темы или отношение к ней;
5-я строка – синоним ключевого слова (существительное).
Пушкин
Великий, талантливый.
Думает, страдает, любит.
Чувства добрые пробуждает.
Гений.
24.Оценочный лист.
Рефлексия
Выполнил ли я то, что задумал?
__________________________________________________________________
Получилось ли сделать то, что я записал как главный результат проекта?
____________________________________________________________________________________________________________________________________
Всё ли получилось так, как я задумывал?
____________________________________________________________________________________________________________________________________
Что было сделано хорошо?
______________________________________________________________________________________________________________________________________________________________________________________________________
Что было сделано плохо?
____________________________________________________________________________________________________________________________________
Что было выполнить легко, а что оказалось неожиданно трудно?
______________________________________________________________________________________________________________________________________________________________________________________________________
Кто мог бы сказать мне СПАСИБО за проект?
____________________________________________________________________________________________________________________________________
Попрошу взрослых оценить мою работу:
ч т о с к а з а л а м а м а:
__________________________________________________________________
ч т о с к а з а л а у ч и т е л ь н и ц а:
__________________________________________________________________
к а к о ц е н и л и п р о е к т д р у з ь я:
____________________________________________________________________________________________________________________________________
В ч ё м я с н и м и с о г л а с е н, в ч ё м — н е т ?
__________________________________________________________________
25. “Букет
настроения”. В начале
урока учащимся раздаются бумажные
цветы: красные и голубые. На доске
изображена ваза. В конце урока я говорю:
“ Если вам понравился урок, и вы узнали
что-то новое, то прикрепите к вазе красный
цветок, если не понравился – голубой”.
Можно предложить ребятам более
разнообразный спектр цветов: красный,
желтый, синий. В конце урока собрать
цветы в корзинку или вазочку. Хочу
напомнить, какому настроению соответствует
какой цвет:
“Букет
настроения”. В начале
урока учащимся раздаются бумажные
цветы: красные и голубые. На доске
изображена ваза. В конце урока я говорю:
“ Если вам понравился урок, и вы узнали
что-то новое, то прикрепите к вазе красный
цветок, если не понравился – голубой”.
Можно предложить ребятам более
разнообразный спектр цветов: красный,
желтый, синий. В конце урока собрать
цветы в корзинку или вазочку. Хочу
напомнить, какому настроению соответствует
какой цвет:
красный — восторженное;
оранжевый — радостное, теплое;
желтый — светлое, приятное;
зеленый – спокойное;
синий — неудовлетворенное, грустное;
фиолетовый — тревожное, напряженное;
черный — упадок, уныние.
26.«Волшебная палочка».
-Если я найду волшебную палочку, я порошу ее помочь…(кому?)
27. Анализ своих ошибок.
Анализ своих ошибок.
28. Шкала настроения.
У каждого ученика лежит листок со шкалой настроение (10 баллов). Ученик отмечает свое настроение на протяжении всего урока. Можно сделать общую шкалу для всего класс. Одна ломаная линия покажет настроение в начале урока, вторая – в конце.
29. Слова-напутствия.
И пусть в вашей жизни не будет ни одного дня, когда бы вы не прочли хоть одной страницы новой книги.
К.Паустовский
Суди себя сам. Это самое трудное. Себя судить куда труднее, чем других. Если ты сумеешь правильно судить себя, значит, ты поистине мудр.
А.де Сент-Экзюпери
30.Работа с сигнальными карточками.
Зеленая карточка. Я удовлетворен уроком. Урок был полезен
для меня. Я с пользой и хорошо работал
на уроке. Я понимал все, о чем говорилось
и что делалось на уроке.
Урок был полезен
для меня. Я с пользой и хорошо работал
на уроке. Я понимал все, о чем говорилось
и что делалось на уроке.
Желтая карточка. Урок был интересен. Я принимал в нем участие. Урок был в определенной степени полезен для меня. Я отвечал с места, выполнил ряд заданий. Мне было на уроке достаточно комфортно.
Красная карточка. Пользы от урока я получил мало. Я не очень понимал, о чем идет речь. Мне это не нужно. К ответу на уроке я был не готов.
31. Лучики солнца.
Детям можно предложить представить себя лучиками солнца. В конце урока дать задание разместить лучики на солнце согласно своему настроению. Учащиеся подходят к доске и вставляют лучики.
32. «Дерево чувств». Если чувствую себя хорошо, комфортно, то вешаю на дерево яблоки красного цвета, если нет, зелёного.
33. «Светофор».
«Светофор».
Оцените свою деятельность на уроке с помощью «Светофора» (зелёный – все понятно, желтый – есть затруднения, красный – много непонятного – карточки данных цветов даны учащимся еще до урока).
34.«Яблоко и стрелы» .
35.Эмоционально-музыкальная концовка. Учащиеся слушают фрагменты из двух музыкальных произведений (желательно указать композитора произведения). Звучит тревожная музыка и спокойная, восторженная. Учащиеся выбирают музыкальный фрагмент, который соответствует их настроению.
36.Если есть время, то можно предложить учащимся выразить свое эмоциональное настроение в виде рисунка, а в конце провести выставку рисунков.
37. «Лестница успеха».
Если учитель ведёт урок в
традиционном плане, то можно выделить
и написать на доске этапы деятельности.
В конце урока предложить учащимся
оценить свою работу на каждом этапе в
виде ступенек, ведущих к успеху.
38.»Бортовой журнал» — форма фиксации информации с помощью ключевых слов, графических моделей, кратких предложений и умозаключений, вопросов. В качестве задаваемых преподавателем частей «бортового журнала», которые будут заполняться учащимися, могут быть: ключевые понятия темы, связи, которые может установить студент, важные вопросы.
39.Различные виды дневников: обычный, дневник — художественный альбом, двухчастный дневник (в одной графе — наблюдаемые факты, цитаты из высказываний, в другой — комментарии) и другие. В отличие от эссе и «бортового журнала», дневник ведется в течение длительного промежутка времени и позволяет ученику осуществить более вдумчивую рефлексию, отслеживая как непосредственный процесс, так и сравнивая свои действия во времени («отложенная» рефлексия).
40. «Письменное интервью» — вариант групповой письменной рефлексии
в форме вопросов и ответов участников
группы. Данный способ позволяет в
достаточно короткий промежуток времени
провести письменную рефлексию с целью
взаимообмена мнениями.
Данный способ позволяет в
достаточно короткий промежуток времени
провести письменную рефлексию с целью
взаимообмена мнениями.
41. «Лист самоконтроля». Ведется на протяжении всего урока.
Фамилия, имя ученика_____________________________
Вид задания | Отметка |
42. «Кто веселее?».
Выберите рисунок, соответствующий вашему настроению.
43.Определите свое настроение, поставив кляксу любого цвета.
44. «Одним словом». Закончите одним словом:
Сегодняшний урок – это…
Сегодня на уроке я …
45. Выберите
1 фразу для соседа по парте:
Выберите
1 фразу для соседа по парте:
Ты молодец.
Я доволен твоей работой на уроке.
Ты мог бы поработать лучше.
46. «Острова».
На доске или у каждого ученика карта настроения. Поставьте знак √, на каком из островов вы сегодня пребывали: о.Страха, Познания, Уверенности, Скуки, Мечты, Будущего, Радости.
47.Запустите корабль в море Знаний. Те ребята, которые считают, что хорошо усвоили тему, помещают свой кораблик в море, а те, кто не уверен в этом, остаются в заливе правил.
ЗАЛИВ ПРАВИЛ
МОРЕ ЗНАНИЙ
48.Стихотворение.
Мне интересно знать, о чем мечтает каждый,
Оставшись сам с собой наедине,
К чему стремится и чего он жаждет,
О чем мечтает дома в тишине,
О чем порою думает ночами,
Какого чуда он от жизни ждет,
И грезит вдруг какими миражами,
Какие замки строит он в мечтах,
О чем тоскует, мается, грустит,
Какими тайнами воспоминаний
Он
раны сердца часто бередит.
Но, к сожаленью, это невозможно
Узнать, что человек в себе хранит:
Все чувства его спрятаны надежно,
И мир души не каждому открыт.
Н.Петренко
-Ваша «душа» сегодня ленилась или трудилась?
Во всем мне хочется дойти
До самой сути
В работе, в поисках пути,
В сердечной смуте.
До сущности протекших дней,
До их причины,
До оснований, до корней,
До сердцевины.
Все время схватывая нить
Судеб, событий,
Жить, думать, чувствовать, любить,
Свершать открытья.
Б.Пастернак
Думайте, чувствуйте, любите, фантазируйте, анализируйте, исследуйте, философствуйте – живите!!!
В добрый час, ребята!
Будем, ребята, беречь доброту,
Будет, ребята, беречь красоту,
Будем дерзать, будем творить,
Улыбку познанья Уроку дарить!
Учитель: Пожелайте всего доброго друг другу!
Ученики желают друг другу добра.
Нашим гостям.
Чтобы гости захотели
К нам на урок прийти опять.
Ученики приветствуют учителей.
49.«Кораблик».
-Какое настроение у вас после урока? Прикрепите флажок на соответствующий корабль. Если урок понравился – алый парус, если на душе «тоска зеленая» -зеленый парус, если урок никак не тронул – черный парус.
50.«Лист самооценки».
Узнал что-то новое Научился Расстроился Я Получил радость Удивился Ничего не понял |
51.«Акрослово».
Опишите при помощи эпитетов образ цветаевской Москвы.
М-манящая
О –огненно-купольная, отвергнутая Петром
С – святая
К – колокольная, краснокупольная
В – возвеличенная, вольная
А
– алтарная.
52.«Релаксация».
Закройте глаза и вспомните приятные моменты нашего занятия.
Я рада, что на протяжении всего занятия вы были внимательны.
Я хочу, чтобы все, кто работал хорошо – улыбнулись мне, а кто чувствует в себе потенциал работать еще лучше – поаплодировали себе.
53.«Пожелание».
Давайте возьмемся за руки и пожелаем друг другу:
-Избавляйся от…
-Будь всегда…
-Помни…
Желаю вам цвести, расти,
Копить, крепить здоровье.
Оно для дальнего пути –
Главнейшее условие.
Пусть каждый день и каждый час
Вам новой добудет,
Пусть добрым будет ум у вас.
А сердце будет умным.
Вам от души желаю я,
Друзья, всего хорошего.
А все хорошее, друзья,
Дается нам недешево.
С.Маршак
54.«Подбор стихотворения».
Выберите стихотворение, которое наиболее близкое вам сейчас.
И любо мне, и сладко мне,
И мир в моей груди,
Дремотою обвеян я –
О, время, погоди!
Ф. Тютчев
Тютчев
С души как бремя скатится,
Сомненье далеко – и верится, и плачется,
И так легко, легко.
М.Лермонтов
Земля дрожит в огнях заката,
Любви прекрасная звезда,
А на душе легко и свято,
Легко, как в детские года.
И.Тургенев
И с отвращением читаю жизнь свою,
Я трепещу и проклинаю.
И горько жалуюсь. И горько слезы лью,
Но строк печальных не смываю.
А.Пушкин
Проходят дни, проходят сроки,
Свободы тщетно жаждем мы,
Мы беспощадно одиноки
На дне своей души-тюрьмы.
В.Брюсов
Смешать печаль, которой нет острей,
С восторгами, которых не бывало.
К.Бальмонт
Чемодан, мясорубка,корзина
На доске вывешиваются рисунки чемодана, мясорубки, корзины.
Чемодан – всё, что пригодится в дальнейшем.
Мясорубка – информацию переработаю.
Корзина – всё выброшу.
Ученикам
предлагается выбрать, как они поступят
с информацией, полученной на уроке.
Анализ урока учащимися
Назовите, чем вы занимались на уроке?
Какие трудности ты испытывал на уроке?
Какие формы работы на уроке тебе нравятся больше всего?
Поставь баллы от 1 до 5:
Индивидуальная — работа в парах —
По карточкам — самостоятельная работа —
Работа в группах — коллективная работа —
Необычные уроки ( сказки, экскурсия, путешествия) —
Маятник настроения
Маятник- подвижный, например, деревянная рейка, жёстко закреплённая вверху ватмана. Слева на картинке- хмурый день, тучи, дождь. Справа солнце, безоблачное небо. В зависимости от того, «солнечное» или «дождливое» настроение, маятник в конце дня отклоняется влево или вправо. При этом внизу, в секторе, до которого отклонился маятник, отмечается число и причина.
Цветик- многоцветик
Дети
выбирают для себя лепесток, цвет которого
наиболее подходит к цвету настроения. Затем все лепестки собирают в один общий
цветок.
Затем все лепестки собирают в один общий
цветок.
Мишень настроения
День это выстрел. В какую область настроения учащийся попал сегодня? В зависимости от этого наклеивается кружок – попадание в одной из цветовых зон. Внутри дата и мотивация
Состояние моей души
Крайне скверно
Плохо
Ученик берёт изображение человека и ставит её на ту ступеньку, которая соответствует состоянию его души.
SMS
Ученикам предлагается на бумажных сотовых телефонах написать SMS –сообщение другу о том, как прошёл урок, оценить как плодотворно он работал.
Автор: Соловьёва Наталья Сергеевна
Источник:
/shkola/rodnoi-yazyk-i-literatura/library/refleksiya-v-konce-uroka
Почему минус на минус дает плюс?
«Враг моего врага — мой друг».
Проще всего ответить: «Потому что таковы правила действий над отрицательными числами». Правила, которые мы учим в школе и применяем всю жизнь. Однако учебники не объясняют, почему правила именно такие. Мы сначала постараемся понять это, исходя из истории развития арифметики, а потом ответим на этот вопрос с точки зрения современной математики.
Давным-давно людям были известны только натуральные числа: 1, 2, 3, … Их использовали для подсчета утвари, добычи, врагов и т. д. Но числа сами по себе довольно бесполезны — нужно уметь с ними обращаться. Сложение наглядно и понятно, к тому же сумма двух натуральных чисел — тоже натуральное число (математик сказал бы, что множество натуральных чисел замкнуто относительно операции сложения). Умножение — это, по сути, то же сложение, если мы говорим о натуральных числах. В жизни мы часто совершаем действия, связанные с этими двумя операциями (например, делая покупки, мы складываем и умножаем), и странно думать, что наши предки сталкивались с ними реже — сложение и умножение были освоены человечеством очень давно. Часто приходится и делить одни величины на другие, но здесь результат не всегда выражается натуральным числом — так появились дробные числа.
Часто приходится и делить одни величины на другие, но здесь результат не всегда выражается натуральным числом — так появились дробные числа.
Без вычитания, конечно, тоже не обойтись. Но на практике мы, как правило, вычитаем из большего числа меньшее, и нет нужды использовать отрицательные числа. (Если у меня есть 5 конфет и я отдам сестре 3, то у меня останется 5 – 3 = 2 конфеты, а вот отдать ей 7 конфет я при всем желании не могу.) Этим можно объяснить, почему люди долго не пользовались отрицательными числами.
В индийских документах отрицательные числа фигурируют с VII века н.э.; китайцы, видимо, начали употреблять их немного раньше. Их применяли для учета долгов или в промежуточных вычислениях для упрощения решения уравнений — это был лишь инструмент для получения положительного ответа. Тот факт, что отрицательные числа, в отличие от положительных, не выражают наличие какой-либо сущности, вызывал сильное недоверие. Люди в прямом смысле слова избегали отрицательных чисел: если у задачи получался отрицательный ответ, считали, что ответа нет вовсе. Это недоверие сохранялось очень долго, и даже Декарт — один из «основателей» современной математики — называл их «ложными» (в XVII веке!).
Это недоверие сохранялось очень долго, и даже Декарт — один из «основателей» современной математики — называл их «ложными» (в XVII веке!).
Рассмотрим для примера уравнение 7x – 17 = 2x – 2. Его можно решать так: перенести члены с неизвестным в левую часть, а остальные — в правую, получится 7x – 2x = 17 – 2, 5x = 15, x = 3. При таком решении нам даже не встретились отрицательные числа.
Но можно было случайно сделать и по-другому: перенести слагаемые с неизвестным в правую часть и получить 2 – 17 = 2x – 7x, (–15) = (–5)x. Чтобы найти неизвестное, нужно разделить одно отрицательное число на другое: x = (–15)/(–5). Но правильный ответ известен, и остается заключить, что (–15)/(–5) = 3.
Что демонстрирует этот нехитрый пример? Во-первых, становится понятна логика, которой определялись правила действий над отрицательными числами: результаты этих действий должны совпадать с ответами, которые получаются другим путем, без отрицательных чисел. Во-вторых, допуская использование отрицательных чисел, мы избавляемся от утомительного (если уравнение окажется посложнее, с большим числом слагаемых) поиска того пути решения, при котором все действия производятся только над натуральными числами. Более того, мы можем больше не думать каждый раз об осмысленности преобразуемых величин — а это уже шаг в направлении превращения математики в абстрактную науку.
Во-вторых, допуская использование отрицательных чисел, мы избавляемся от утомительного (если уравнение окажется посложнее, с большим числом слагаемых) поиска того пути решения, при котором все действия производятся только над натуральными числами. Более того, мы можем больше не думать каждый раз об осмысленности преобразуемых величин — а это уже шаг в направлении превращения математики в абстрактную науку.
Правила действий над отрицательными числами сформировались не сразу, а стали обобщением многочисленных примеров, возникавших при решении прикладных задач. Вообще, развитие математики можно условно разбить на этапы: каждый следующий этап отличается от предыдущего новым уровнем абстракции при изучении объектов. Так, в XIX веке математики поняли, что у целых чисел и многочленов, при всей их внешней непохожести, есть много общего: и те, и другие можно складывать, вычитать и перемножать. Эти операции подчиняются одним и тем же законам — как в случае с числами, так и в случае с многочленами. А вот деление целых чисел друг на друга, чтобы в результате снова получались целые числа, возможно не всегда. То же самое и с многочленами.
А вот деление целых чисел друг на друга, чтобы в результате снова получались целые числа, возможно не всегда. То же самое и с многочленами.
Потом обнаружились другие совокупности математических объектов, над которыми можно производить такие операции: формальные степенные ряды, непрерывные функции… Наконец, пришло понимание, что если изучить свойства самих операций, то потом результаты можно будет применять ко всем этим совокупностям объектов (такой подход характерен для всей современной математики).
В итоге появилось новое понятие: кольцо. Это всего-навсего множество элементов плюс действия, которые можно над ними производить. Основополагающими здесь являются как раз правила (их называют аксиомами), которым подчиняются действия, а не природа элементов множества (вот он, новый уровень абстракции!). Желая подчеркнуть, что важна именно структура, которая возникает после введения аксиом, математики говорят: кольцо целых чисел, кольцо многочленов и т. д. Отталкиваясь от аксиом, можно выводить другие свойства колец.
Мы сформулируем аксиомы кольца (которые, естественно, похожи на правила действий с целыми числами), а затем докажем, что в любом кольце при умножении минуса на минус получается плюс.
Кольцом называется множество с двумя бинарными операциями (т. е. в каждой операции задействованы два элемента кольца), которые по традиции называют сложением и умножением, и следующими аксиомами:
- сложение элементов кольца подчиняется переместительному (A + B = B + A для любых элементов A и B) и сочетательному (A + (B + C) = (A + B) + C) законам; в кольце есть специальный элемент 0 (нейтральный элемент по сложению) такой, что A + 0 = A, и для любого элемента A есть противоположный элемент (обозначаемый (–A)), что A + (–A) = 0;
- умножение подчиняется сочетательному закону: A·(B·C) = (A·B)·C;
- сложение и умножение связаны такими правилами раскрытия скобок: (A + B)·C = A·C + B·C и A·(B + C) = A·B + A·C.

Заметим, что кольца, в самой общей конструкции, не требуют ни перестановочности умножения, ни его обратимости (т. е. делить можно не всегда), ни существования единицы — нейтрального элемента по умножению. Если вводить эти аксиомы, то получаются другие алгебраические структуры, но в них будут верны все теоремы, доказанные для колец.
Теперь докажем, что для любых элементов A и B произвольного кольца верно, во-первых, (–A)·B = –(A·B), а во-вторых (–(–A)) = A. Из этого легко следуют утверждения про единицы: (–1)·1 = –(1·1) = –1 и (–1)·(–1) = –((–1)·1) = –(–1) = 1.
Для этого нам потребуется установить некоторые факты. Сперва докажем, что у каждого элемента может быть только один противоположный. В самом деле, пусть у элемента A есть два противоположных: B и С. То есть A + B = 0 = A + C. Рассмотрим сумму A + B + C. Пользуясь сочетательным и переместительным законами и свойством нуля, получим, что, с одной стороны, сумма равна B: B = B + 0 = B + (A + C) = A + B + C, а с другой стороны, она равна C: A + B + C = (A + B) + C = 0 + C = C. Значит, B = C.
Значит, B = C.
Заметим теперь, что и A, и (–(–A)) являются противоположными к одному и тому же элементу (–A), поэтому они должны быть равны.
Первый факт получается так: 0 = 0·B = (A + (–A))·B = A·B + (–A)·B, то есть (–A)·B противоположно A·B, значит, оно равно –(A·B).
Чтобы быть математически строгими, объясним еще, почему 0·B = 0 для любого элемента B. В самом деле, 0·B = (0 + 0) B = 0·B + 0·B. То есть прибавление 0·B не меняет сумму. Значит, это произведение равно нулю.
А то, что в кольце ровно один ноль (ведь в аксиомах сказано, что такой элемент существует, но ничего не сказано про его единственность!), мы оставим читателю в качестве несложного упражнения.
Ответил: Евгений Епифанов
Таблица «Плюс — минус — интересно»
Всем доброго времени суток!
Как приятно, что постепенно увеличивается количество постоянных читателей моего блога! Огромное Вам спасибо за внимание к этому блогу! Постараюсь и дальше оправдывать Ваши надежды.
Сегодня, уважаемые мои читатели, хочу Вас познакомить с универсальным (на мой взгляд) приемом технологии РКМЧП — таблица «Плюс — минус — интересно». Эту таблицу придумал Эдвард де Боно, доктор медицинских наук, доктор философии Кембриджского университета, специалист в области развития практических навыков в области мышления.
Почему считаю его универсальным? Дело в том, что данный прием можно использовать на разных стадиях урока и в любом классе, в устной или письменной форме в зависимости от наличия времени.
На стадии осмысления новая информация заносится в таблицу из трех граф: «П» — «плюс»; «М» — «минус»; «И» — «интересно». По ходу чтения текста учебника или прослушивания рассказа учителя (а в старших классах прослушивания лекции) учащимся предлагается фиксировать в соответствующих графах таблицы информацию, отражающую:
«П» — информация, которая, с точки зрения ученика носит позитивный характер, известна ученику, вызывает у него положительные эмоции; факты, которые могут отвечать на вопрос «Что в этом хорошего?»;
«М» — негативный характер, которая отвечает на вопрос «Что в этом плохого?», или все то, что у них отсутствует или осталось непонятным;
«И» — наиболее интересные и спорные факты или все то, о чем хотелось бы узнать подробнее.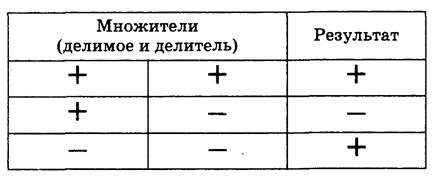
В конце работы можно провести обсуждение спорных вопросов. При использовании таблицы «П — М — И» внимание намеренно направляется сначала на «Плюс», потом на «Минус», затем на «Интересно».
Это один из приемов активной работы с текстом. Цель этого приема – формирование разнообразного отношения к тексту. Данный прием формирует навыки анализа и классификации изучаемой информации. Заполняя такую таблицу, учащиеся учатся точно работать с информацией, не искажая ее смысла.
На стадии рефлексии в графу «П» — «плюс» записывается все, что понравилось на уроке, информация и формы работы, которые вызвали положительные эмоции, либо по мнению ученика могут быть ему полезны для достижения каких-то целей. В графу «М» — «минус» записывается все, что не понравилось на уроке, показалось скучным, вызвало неприязнь, осталось непонятным, или информация, которая, по мнению ученика, оказалась для него не нужной, бесполезной с точки зрения решения жизненных ситуаций. В графу «И» — «интересно» учащиеся вписывают все любопытные факты, о которых узнали на уроке и что бы еще хотелось узнать по данной проблеме, вопросы к учителю.
В графу «И» — «интересно» учащиеся вписывают все любопытные факты, о которых узнали на уроке и что бы еще хотелось узнать по данной проблеме, вопросы к учителю.
Это упражнение позволяет учителю взглянуть на урок глазами учеников, проанализировать его с точки зрения ценности для каждого ученика. Для учащихся наиболее важными будут графы «П» и «И», так как в них будут содержаться памятки о той информации, которая может им когда-нибудь пригодиться. В данном случае информация не только более активно воспринимается, но и систематизируется, и оценивается.
Данный прием можно использовать так же при защите проектов. Но об этом я расскажу позже.
Хотелось бы знать и Ваше мнение по поводу данного приема.
Таблица математических знаков (символов): значения, распечатать
Ниже представлена таблица с основными математическими символами и знаками: корень (√), больше (>), меньше (<), равенство (=) и др. Также приведено их краткое описание и примеры для лучшего понимания.
Также приведено их краткое описание и примеры для лучшего понимания.
| Символ / знак | Название | Значение / описание | Пример |
| = | равно | равенство | е. 4 плюс 3 равно 7</nobr>» data-order=»<nobr>7 = 4 + 3,</nobr><br><nobr>т.е. 4 плюс 3 равно 7</nobr>»>7 = 4 + 3, |
| ≠ | не равно | неравенство | 7 ≠ 10, 7 не равно 10 |
| ≈ | приблизительно равно | приближенное равенство/округление | равно 0,36</nobr>» data-order=»<nobr>0,35765 ≈ 0,36,</nobr><br><nobr>0,35765 прибл. равно 0,36</nobr>»>0,35765 ≈ 0,36, |
| > | больше | A больше, чем B | 15 > 10, 15 больше 10 |
| < | меньше | A меньше, чем B | 6 < 8, 6 меньше 8 |
| ≥ | больше или равно | A больше или равно B | 10 ≥ 4, 10 больше или равно 4 |
| ≤ | меньше или равно | A меньше или равно B | 3 ≤ 7, 3 меньше или равно 7 |
| ( ) | круглые скобки | сначала считается выражение внутри скобок | 3 ⋅ (4 + 6) = 30 |
| [ ] | квадратные скобки | сначала считается выражение внутри скобок | [(1 + 3) ⋅ (2 + 4)] = 24 |
| + | плюс | знак сложения | 1 + 2 = 3 |
| − | минус | знак вычитания | 3 − 2 = 1 |
| ± | плюс-минус | выполняются оба действия: и сложение, и вычитание | 4 ± 6 = 10 или -2 |
| ± | минус-плюс | выполняются оба действия: и вычитание, и сложение | 5 ∓ 8 = -3 или 13 |
| * | звездочка | умножение | 3 * 3 = 9 |
| × | икс | умножение | 3 × 3 = 9 |
| ⋅ | точка | умножение | 3 ⋅ 3 = 9 |
| ÷ | обелюс | деление | 8 ÷ 2 = 4 |
| / | косая черта | деление | 8 / 2 = 4 |
| : | двоеточие | деление | 8 : 2 = 4 |
| — | горизонтальная линия | дробь (деление) | 1/2 |
| mod | modulo | остаток от деления | 7 mod 2 = 1, 7 : 2 = 3 (остаток 1) |
| » data-order=».»>. | точка | десятичный разделитель | 3.45 = 3 + 45/100 |
| , | запятая | десятичный разделитель | 6,12 = 6 + 12/100 |
| ab | степень | число А в степени B | 32 = 9 |
| a^b | циркумфлекс | число А в степени B | 4^3 = 64 |
| √a | квадратный корень | √a ⋅ √a = a | √16 = ±4 |
| 3√a | кубический корень | 3√a ⋅ 3√a ⋅ 3√a = a | 3√27 = 3 |
| n√a | корень n-й степени | n√8 = 2 для n=3 | |
| % | процент | 1% = 1/100 | 10% × 50 = 5 |
| ‰ | промилле | 1%</nobr>» data-order=»<nobr>1‰ = 1/1000 = 0.1%</nobr>»>1‰ = 1/1000 = 0.1% | 5‰ × 40 = 0.2 |
microexcel.ru
Как составить таблицу средних значений плюс / минус стандартных ошибок и других функций — Подача на конкурс таблиц — таблицы
Как составить таблицу средних значений плюс / минус стандартных ошибок и других функций
Авторы : Эрик Смит, Байрон Смит
Принадлежности : Технологический институт Вирджинии, клиника Мэйо
Abstract : В этом примере показано, как составить научную таблицу со средними значениями плюс или минус стандартные ошибки. Пример включает другие функции, такие как среднее и стандартное отклонения и среднее значение с диапазоном. Производимая таблица похожа на ту, что была опубликована в недавнем экологическом журнале. Это сообщение обновляет исходное сообщение, добавляя две дополнительные функции.
Производимая таблица похожа на ту, что была опубликована в недавнем экологическом журнале. Это сообщение обновляет исходное сообщение, добавляя две дополнительные функции.
Полное описание : В научных публикациях данные часто обобщаются в виде таблицы или рисунка, который включает средние значения и стандартные ошибки (или стандартные отклонения). Вдобавок эти таблицы могут иметь другие функции, включая некоторые вычисленные значения, отступы, отсутствующие ячейки и т. Д. В этом примере показано, как создать таблицу с помощью kableExtra, в которой переменные являются столбцами, а строки соответствуют уровням обработки.Также обсуждается экспорт таблицы в Excel или Word. Таблица аналогична таблице 6 в Wilson et.al., Импульсы солености взаимодействуют с сезонным высыханием, увеличивая потери углерода экосистемой в болотах во Флориде Эверглейдс, Ecological Applications 2018, 2092-2108. Доступ к данным можно получить через веб-ссылку. Даются ссылки на файл Rmd и полученный файл html.
Тип таблицы: static-HTML
Тип отправки: Пример одной таблицы
Таблица: https: //htmlpreview.github.io /? https: //github.com/another-smith/meanSE/blob/main/mean-and-se-table10-12with-functions.html
Repo: https://github.com/another-smith/meanSE /blob/main/mean%20and%20se%20table10-12with%20functions.Rmd
RStudio Cloud:
Используемый пакет DT :
gt Используемый пакет:
Reactable Используемый пакет:
используемый флэш-пакет :
huxtable используемый пакет:
kableExtra используемый пакет: true
Другие пакеты:
Невозможно поместить знак плюса или минуса в таблицу — TeX
Поскольку в строке заголовка табличной среды не используются буквы «пишущей машинки» (они же моноширинные), я бы также не стал использовать буквы пишущей машинки в теле табличной среды .Удаление директив \ verb и включение чисел, по мере необходимости, в математические инициаторы / терминаторы $ , похоже, было бы правильным решением. При необходимости используйте директивы
При необходимости используйте директивы \ phantom для точной настройки вертикального выравнивания чисел до и после символа \ pm .
Я бы также удалил директивы \ small и особенно \ footnotesize , поскольку материал помещается внутри текстового блока.
В приведенном ниже примере я отключил загрузку всех пакетов, которые не имеют отношения к рассматриваемому примеру.
В сторону: инструкция
\ usepackage [повесить, маленький, labelfont = bf, up, textfont = it, up] {caption}
кажется противоречивым, так как форма шрифта для текстовой части подписи должна быть как вверх [форма] , так и она [alics]. В любом случае второй вариант для labelfont и textfont игнорируется в обоих случаях. Лучше было бы написать инструкцию как
\ usepackage [зависнуть, labelfont = bf, textfont = it] {caption}
\ documentclass [twoside] {article}
\ usepackage [T1] {fontenc}
% \ linespread {1. 05}% Межстрочный интервал - Палатино требуется больше места между строками
\ usepackage {microtype}
\ usepackage [hmarginratio = 1: 1, top = 32mm, columnsep = 20pt] {geometry}
% \ usepackage {multicol}% Используется для двухколоночного макета документа.
\ usepackage [hang, labelfont = bf, textfont = it] {caption}% Пользовательские подписи под / над плавают в таблицах или на рисунках
\ usepackage {booktabs}% Горизонтальные правила в таблицах
% \ usepackage {float}% Требуется для таблиц и рисунков в среде с несколькими столбцами - они должны быть размещены в определенных местах с помощью [H] (e.грамм. \ begin {table} [H])
% \ usepackage {lettrine}% Lettrine - это первая увеличенная буква в начале текста
% \ usepackage {paralist}% Используется для среды compactitem, которая создает маркеры с меньшим пространством между ними
% \ usepackage {esvect}
% \ usepackage {abstract}% Разрешает абстрактную настройку
% \ Renewcommand {\ abstractnamefont} {\ normalfont \ bfseries}% Установите полужирный текст "Аннотация"
% \ refreshcommand {\ abstracttextfont} {\ normalfont \ small \ itshape}% Установите для самой аннотации мелкий курсив
%
% \ usepackage {titlesec}% Позволяет настраивать заголовки
% \ Renewcommand \ thesection {\ Roman {section}}% Римские цифры для разделов
% \ Renewcommand \ thesubsection {\ Roman {subsction}}% Римские цифры для подразделов
% \ titleformat {\ section} [блок] {\ large \ scshape \ centering} {\ thesection.
05}% Межстрочный интервал - Палатино требуется больше места между строками
\ usepackage {microtype}
\ usepackage [hmarginratio = 1: 1, top = 32mm, columnsep = 20pt] {geometry}
% \ usepackage {multicol}% Используется для двухколоночного макета документа.
\ usepackage [hang, labelfont = bf, textfont = it] {caption}% Пользовательские подписи под / над плавают в таблицах или на рисунках
\ usepackage {booktabs}% Горизонтальные правила в таблицах
% \ usepackage {float}% Требуется для таблиц и рисунков в среде с несколькими столбцами - они должны быть размещены в определенных местах с помощью [H] (e.грамм. \ begin {table} [H])
% \ usepackage {lettrine}% Lettrine - это первая увеличенная буква в начале текста
% \ usepackage {paralist}% Используется для среды compactitem, которая создает маркеры с меньшим пространством между ними
% \ usepackage {esvect}
% \ usepackage {abstract}% Разрешает абстрактную настройку
% \ Renewcommand {\ abstractnamefont} {\ normalfont \ bfseries}% Установите полужирный текст "Аннотация"
% \ refreshcommand {\ abstracttextfont} {\ normalfont \ small \ itshape}% Установите для самой аннотации мелкий курсив
%
% \ usepackage {titlesec}% Позволяет настраивать заголовки
% \ Renewcommand \ thesection {\ Roman {section}}% Римские цифры для разделов
% \ Renewcommand \ thesubsection {\ Roman {subsction}}% Римские цифры для подразделов
% \ titleformat {\ section} [блок] {\ large \ scshape \ centering} {\ thesection. } {1em} {}% Изменить внешний вид заголовков разделов
% \ titleformat {\ subsction} [block] {\ large} {\ thesubsection.} {1em} {}% Изменить внешний вид заголовков разделов
\ usepackage {fancyhdr}% Верхние и нижние колонтитулы
\ pagestyle {fancy}% У всех страниц есть верхние и нижние колонтитулы.
\ fancyhead {}% Убрать заголовок по умолчанию
\ fancyfoot {}% Очистить нижний колонтитул по умолчанию
\ fancyhead [C] {CH 341: Биохимия I $ \ bullet $ Ноябрь 2015 г. $ \ bullet $ Vol. XXI, No. 1}% Пользовательский текст заголовка
\ fancyfoot [RO, LE] {\ thepage}% Пользовательский текст нижнего колонтитула
% \ usepackage {tabularx}
% \ usepackage {pgfplots}
% \ usepackage {caption}
% \ usepackage {graphicx}% позволяет импортировать изображения
% \ usepackage {float}% позволяет управлять положением поплавка
% \ usepackage {mhchem}
% \ usepackage {textgreek}
% \ usepackage {siunitx}
% \ usepackage {textcomp}
% \ usepackage {multirow}
% \ usepackage {grffile}
% \ usepackage [экспорт] {adjustbox}
% \ usepackage {placeins}
% Обычно рекомендуется загружать "hyperref" последней.
} {1em} {}% Изменить внешний вид заголовков разделов
% \ titleformat {\ subsction} [block] {\ large} {\ thesubsection.} {1em} {}% Изменить внешний вид заголовков разделов
\ usepackage {fancyhdr}% Верхние и нижние колонтитулы
\ pagestyle {fancy}% У всех страниц есть верхние и нижние колонтитулы.
\ fancyhead {}% Убрать заголовок по умолчанию
\ fancyfoot {}% Очистить нижний колонтитул по умолчанию
\ fancyhead [C] {CH 341: Биохимия I $ \ bullet $ Ноябрь 2015 г. $ \ bullet $ Vol. XXI, No. 1}% Пользовательский текст заголовка
\ fancyfoot [RO, LE] {\ thepage}% Пользовательский текст нижнего колонтитула
% \ usepackage {tabularx}
% \ usepackage {pgfplots}
% \ usepackage {caption}
% \ usepackage {graphicx}% позволяет импортировать изображения
% \ usepackage {float}% позволяет управлять положением поплавка
% \ usepackage {mhchem}
% \ usepackage {textgreek}
% \ usepackage {siunitx}
% \ usepackage {textcomp}
% \ usepackage {multirow}
% \ usepackage {grffile}
% \ usepackage [экспорт] {adjustbox}
% \ usepackage {placeins}
% Обычно рекомендуется загружать "hyperref" последней. \ usepackage {hyperref}% Для гиперссылок в PDF
\ newcommand {\ head} [1] {\ textnormal {\ textbf {# 1}}}
\ begin {document}
\ begin {table}
\ caption {Концентрации продуктов и скорости ферментативных реакций для 5 концентраций субстрата в различных средах с ингибиторами}
\ центрирование
\ begin {tabular} {lcc}
\ toprule [1.5pt]
\ head {Металл} & \ head {SD средней скорости}
& \ head {Средняя концентрация продукта, образованная SD} \\
\ midrule
Магний и $ 1,30 \ pm 0,67 \ phantom {0} $ & 25,97 $ \ pm 13,33 $ \\
Цинк и $ 0,40 \ pm 0,049 $ & $ \ phantom {0} 8,06 \ pm \ phantom {0} 0,97 $ \\
\ bottomrule [1.5pt]
\ end {tabular}
\ end {table}
\ конец {документ}
\ usepackage {hyperref}% Для гиперссылок в PDF
\ newcommand {\ head} [1] {\ textnormal {\ textbf {# 1}}}
\ begin {document}
\ begin {table}
\ caption {Концентрации продуктов и скорости ферментативных реакций для 5 концентраций субстрата в различных средах с ингибиторами}
\ центрирование
\ begin {tabular} {lcc}
\ toprule [1.5pt]
\ head {Металл} & \ head {SD средней скорости}
& \ head {Средняя концентрация продукта, образованная SD} \\
\ midrule
Магний и $ 1,30 \ pm 0,67 \ phantom {0} $ & 25,97 $ \ pm 13,33 $ \\
Цинк и $ 0,40 \ pm 0,049 $ & $ \ phantom {0} 8,06 \ pm \ phantom {0} 0,97 $ \\
\ bottomrule [1.5pt]
\ end {tabular}
\ end {table}
\ конец {документ}
Сложение и вычитание положительных и отрицательных чисел
Числа могут быть положительными или отрицательными
Это числовая строка:
| Отрицательные числа (-) | Положительные числа (+) |
«-» — отрицательный знак. | «+» — положительный знак |
Отсутствие знака означает положительный результат
Если число имеет без знака , это обычно означает, что это положительное число .
Воздушные шары и гири
Давайте подумаем о числах как о воздушных шарах (положительных) и весах (отрицательных):
К этой корзине привязаны воздушные шары и гири: |
Добавление положительного числа
Сложение положительных чисел — это просто сложение.
Мы можем добавить шары (мы добавляем положительное значение ) корзина тянется вверх (положительно) |
Пример: 2 + 3 = 5
действительно говорит
«Положительное 2 плюс Положительное 3 равно Положительное 5»
Мы могли бы записать это как (+2) + (+3) = (+5)
Вычитание положительного числа
Вычитание положительных чисел — это просто вычитание.
Воздушные шары можно забрать ( вычитаем положительное значение ) корзина тянется вниз (минус) |
Пример: 6 — 3 = 3
действительно говорит
«Положительное 6 минус Положительное 3 равно Положительное 3»
Мы могли бы записать это как (+6) — (+3) = (+3)
Добавление отрицательного числа
Теперь давайте посмотрим, как выглядит сложение и вычитание отрицательных чисел :
Мы можем складывать веса ( добавляем отрицательные значения ) корзина тянется вниз (минус) |
Пример: 6 + (−3) = 3
действительно говорит
«Положительные 6 плюс отрицательные 3 равны положительным 3»
Мы могли бы записать это как (+6) + (−3) = (+3)
Последние два примера показали нам, что удаление воздушных шаров (вычитание положительного числа) или прибавление веса (добавление отрицательного числа) заставляет корзину опускаться.
Итак, имеют тот же результат :
- (+6) — (+3) = (+3)
- (+6) + (−3) = (+3)
Другими словами, , вычитая положительное значение , совпадает с , добавляя отрицательное значение .
Вычитание отрицательного числа
Наконец, мы можем убрать веса (мы вычитаем отрицательных значений ) корзина тянется вверх (положительно) |
Пример: Что такое 6 — (−3)?
6 — (- 3) = 6 + 3 = 9
Да, действительно! Вычесть отрицание — это то же самое, что добавить!
Два отрицания — плюс
Что мы нашли?
Добавление положительного числа — это простое сложение…
Добавление положительного значения Добавление
Положительное и отрицательное вместе …
Вычитание положительного
или
Сложение отрицательного
равно
Вычитание
Пример: Что такое 6 — (+3)?
6 — (+ 3) = 6 — 3 = 3
Пример: Что такое 5 + (−7)?
5 + (- 7) = 5 — 7 = −2
Вычитание негатива.
 ..
..Вычитание отрицательного аналогично Добавление
Пример: Что такое 14 — (−4)?
14 — (- 4) = 14 + 4 = 18
Правила:
Все это можно поместить в два правила :
| Правило | Пример | ||||
|---|---|---|---|---|---|
| + (+) | Два одинаковых знака становятся положительным знаком | 3 + (+ 2) = 3 + 2 = 5 | |||
| — (-) | 6 — (- 3) = 6 + 3 = 9 | ||||
| + (-) | Два непохожих знака превращаются в знак минуса | 7 + (- 2) = 7 — 2 = 5 | |||
| — (+) | 8 — (+ 2) = 8 — 2 = 6 | ||||
Они «как знаки», когда они похожи друг на друга (другими словами: одинаковые).
Итак, все, что вам нужно запомнить, это:
Два знака типа становятся положительным знаком
Два знака в отличие от становятся отрицательным знаком
Пример: Что такое 5 + (- 2)?
+ (-) — это в отличие от знаков (они не совпадают), поэтому они становятся отрицательным знаком .
5 + (- 2) = 5 — 2 = 3
Пример: Что такое 25 — (- 4)?
— (-) — это , как знаки , поэтому они становятся положительным знаком .
25 — (- 4) = 25 + 4 = 29
Пример: Что такое −6 + (+ 3)?
+ (+) — это , как знаков, поэтому они становятся положительным знаком .
−6 + (+ 3) = −6 + 3 = −3
Начните с −6 на числовой прямой, двигайтесь вперед на 3, и вы получите −3
А теперь поиграйся!
| Попробуйте сыграть в Casey Runner, вам нужно знать правила положительного и отрицательного, чтобы добиться успеха! |
Объяснение здравого смысла
И есть объяснение «здравого смысла»:
Если я скажу «Ешь!» Я призываю вас поесть (позитив)
Если я скажу «Не ешьте!» Я говорю об обратном (отрицательном).
Теперь, если я скажу: «Не ешь ли , а не !», Я говорю, что не хочу, чтобы вы умерли с голоду, поэтому я снова говорю: «Ешь!» (положительный).
Итак, два отрицания дают положительный результат, и если это вас устраивает, тогда вы сделали!
Другое объяснение здравого смысла
Друг +, враг —
| + + ⇒ + | .друг друга мой друг | |
| + — ⇒ — | друг врага — мой враг | |
| — + ⇒ — | враг друга — мой враг | |
| — — ⇒ + | .враг врага мой друг |
Пример банка
Пример. В прошлом году банк по ошибке снял с вашего счета 10 долларов, и они хотят это исправить.
Таким образом, банк должен забрать отрицательные 10 долларов.
Допустим, ваш текущий баланс составляет 80 долларов, поэтому у вас будет:
80 долларов — (- 10 долларов) = 80 долларов + 10 долларов = 90 долларов
Итак, вы получаете $ 10, еще на свой счет.
Длинный пример, который вам может понравиться
Очки союзника
Элли может быть непослушным или милым. Итак, родители Элли сказали
«Если вы любезны, мы добавим 3 балла (+3).
Если непослушны, снимаем 3 балла (−3).
Когда вы набираете 30 очков, вы получаете игрушку ».
| Ally начинает день с 9 очками: | 9 | |
| Мама Элли обнаруживает пролитое молоко: | 9 — 3 = 6 | |
Тогда папа признается, что пролил молоко и пишет «отменить». Как «отменить» минус 3? | ||
| Итак, мама вычисляет: | 6 — (−3) = 6 + 3 = 9 |
Итак, когда мы вычитаем отрицательное, мы получаем
баллов (т. е.е. так же, как добавление очков).
е.е. так же, как добавление очков).
Таким образом, вычитание отрицательного числа аналогично Добавление
| Несколько дней спустя. У Элли 12 очков. | ||
| | | |
| Мама добавляет 3 очка, потому что комната Элли чистая. | 12 + 3 = 15 | |
| | | |
| Папа говорит: «Я убрал эту комнату» и пишет «отменить» на диаграмме.Мама считает: | 15 — (+3) = 12 | |
| | | |
Папа видит, как Элли чистит собаку. Записывает на графике «+3». Мама считает: Записывает на графике «+3». Мама считает: | 12 + (+3) = 15 | |
| | | |
| Элли бросает камень в окно. Папа пишет на диаграмме «−3».Мама считает: | 15 + (−3) = 12 |
См .: как « 15 — (+3) », так и « 15 + (−3) » дают 12.
Итак:
Неважно, вычтите ли вы
положительных очков или добавите отрицательные
, вы все равно потеряете очки.
Итак, вычитание положительного
или
Добавление отрицательного
равно
Вычитание
Попробуйте эти упражнения…
Теперь попробуйте этот рабочий лист и посмотрите, как у вас дела.
А еще попробуйте эти вопросы:
Выравнивание символов плюс / минус (Microsoft Word)
Обратите внимание: Эта статья написана для пользователей следующих версий Microsoft Word: 97, 2000, 2002 и 2003. Если вы используете более позднюю версию (Word 2007 или новее), этот совет может вам не подойти .Чтобы посмотреть версию этого совета, написанного специально для более поздних версий Word, щелкните здесь: Выравнивание символов плюс / минус.
Если вы используете более позднюю версию (Word 2007 или новее), этот совет может вам не подойти .Чтобы посмотреть версию этого совета, написанного специально для более поздних версий Word, щелкните здесь: Выравнивание символов плюс / минус.
Для научного письма числовые данные часто представлены в таблицах в формате среднего +/- стандартного отклонения (с ‘+/-‘, представленным одним символом, достигается удерживанием клавиши Alt и нажатием 0177 на числовом значении. клавиатура).Чтобы таблица выглядела привлекательно, часто желательно, чтобы символы +/- в разных строках были выровнены друг с другом.
Есть несколько способов выровнять символы в зависимости от характеристик данных, которые вы представляете. Одно из решений — использовать в таблице несколько столбцов, чтобы символ +/- отображался в отдельном столбце. Отформатируйте столбец слева от столбца +/-, чтобы содержащиеся в нем числа были выровнены по правому краю. Отформатируйте столбец +/- так, чтобы он был выровнен по левому краю.Информация в двух столбцах теперь должна быть совмещена друг с другом, и вы можете изменить свойства таблицы (в частности, левое и правое поля ячеек), чтобы отрегулировать видимый интервал между ними. При желании вы также можете удалить границу, которую Word автоматически добавляет между столбцами.
Одно из решений — использовать в таблице несколько столбцов, чтобы символ +/- отображался в отдельном столбце. Отформатируйте столбец слева от столбца +/-, чтобы содержащиеся в нем числа были выровнены по правому краю. Отформатируйте столбец +/- так, чтобы он был выровнен по левому краю.Информация в двух столбцах теперь должна быть совмещена друг с другом, и вы можете изменить свойства таблицы (в частности, левое и правое поля ячеек), чтобы отрегулировать видимый интервал между ними. При желании вы также можете удалить границу, которую Word автоматически добавляет между столбцами.
Если все это звучит как много шагов, это действительно может быть — это зависит от того, как именно вы хотите, чтобы информация в двух столбцах выглядела. Более простым решением может быть просто установить позиции табуляции внутри самого столбца.Если в числах +/- нет десятичной точки, вы можете установить десятичную табуляцию в столбце. Word автоматически выравнивает значения, как если бы символ +/- был десятичной точкой.
Если значения имеют десятичные точки, то вы можете установить несколько вкладок в столбце, а затем использовать Ctrl + Tab для фактической вставки символа табуляции перед числом (для выравнивания числа) и между значением и + / — символ (для выравнивания символа).
Если данные не обязательно должны быть в таблице, вам также следует рассмотреть возможность использования редактора формул для представления значений +/-.Редактор формул имеет метку выравнивания — непечатаемый символ, расположенный на второй палитре в верхнем ряду палитр редактора формул. Просто поместите метку выравнивания слева или справа от символа +/- и нажмите Введите в конце каждого числа. Не имеет значения, находится ли знак выравнивания слева или справа от символа +/-, если вы согласны для каждого числа.
WordTips — ваш источник экономичного обучения работе с Microsoft Word.(Microsoft Word — самая популярная программа для обработки текстов в мире. )
Этот совет (290) применим к Microsoft Word 97, 2000, 2002 и 2003. Вы можете найти версию этого совета для ленточного интерфейса Word (Word 2007 и более поздних версий) здесь: Выравнивание символов плюс / минус .
)
Этот совет (290) применим к Microsoft Word 97, 2000, 2002 и 2003. Вы можете найти версию этого совета для ленточного интерфейса Word (Word 2007 и более поздних версий) здесь: Выравнивание символов плюс / минус .
Автор Биография
Аллен Вятт
Аллен Вятт — всемирно признанный автор, автор более чем 50 научно-популярных книг и многочисленных журнальных статей.Он является президентом Sharon Parq Associates, компании, предоставляющей компьютерные и издательские услуги. Узнать больше о Allen …
Условная обработка во время слияния почты
На первый взгляд возможности слияния могут показаться ограниченными. Одна вещь, которую часто упускают из виду (и которая делает …
Открой для себя большеВосстановление сочетания клавиш
Word использует сочетания клавиш для всех видов задач. Иногда вы можете создать ярлык, который сбивает один из другого …
Иногда вы можете создать ярлык, который сбивает один из другого …
Советы Excel: время и дата
Excel отлично подходит для хранения всех типов данных, включая время и дату. ExcelTips: время и дата предоставляет …
Открой для себя большеКод ASCII Знак плюс-минус, Американский стандартный код для обмена информацией, Полная таблица ASCII, символы, буквы, гласные с акцентами, согласные, знаки, символы, числа плюс, минус, знак, ascii, 241, ascii art, ascii table , код ascii, символ ascii, текст ascii, диаграмма ascii, символы ascii, коды ascii, символы, коды, таблицы, символы, список, alt, клавиши, клавиатура, правописание, управление, для печати, расширенный, буквы, послания, почерк, скрипты , надписи, majuscules, заглавные буквы, minuscules, нижний, регистр, маленький, острый, ударение, острый, гравировка, диарезис, циркумфлекс, тильда, седилья, анилло, круг, eñe, enie, arroba, фунт, фунт, цент, тип, написать , заклинание, испанский, английский, ноутбуки, ноутбуки, ascii, asci, asccii, asqui, askii, aski, aschi, aschii, 20210212
ASCII для печати
символов
часто используемые
(испанский язык)
гласные с острым ударением
(испанский язык)
коммерческий / торговый
символов
Краткая история кода ASCII:
Американский стандартный код для обмена информацией, или код ASCII, был создан в 1963 году Комитетом «Американской ассоциации стандартов» или «ASA», агентство изменило свое название в 1969 году на «Американский национальный институт стандартов» или «ANSI» как оно известно с тех пор.
Этот код возникает в результате изменения порядка и расширения набора символов и знаков, уже использовавшихся в то время в телеграфии компанией Bell.
Сначала включались только заглавные буквы и цифры, но в 1967 году были добавлены строчные буквы и некоторые управляющие символы, образующие так называемый US-ASCII, то есть символы от 0 до 127.
Таким образом, с этим набором из 128 символов было опубликовано в 1967 г. в стандартной комплектации и содержит все необходимое для написания на английском языке.
В 1981 году IBM разработала расширение 8-битного кода ASCII, названное «кодовой страницей 437», в этой версии были заменены некоторые устаревшие управляющие символы на графические символы.Также было добавлено 128 символов, с новыми символами, знаками, графикой и латинскими буквами, все знаки препинания и символы, необходимые для написания текстов на других языках, таких как испанский.
Таким образом были добавлены символы ASCII в диапазоне от 128 до 255.
IBM включает поддержку этой кодовой страницы в аппаратном обеспечении своей модели 5150, известной как «IBM-PC», считающейся первым персональным компьютером.
Операционная система этой модели, «MS-DOS», также использовала этот расширенный код ASCII.
Почти все компьютерные системы сегодня используют код ASCII для представления символов и текстов.(283).
Как использовать код ASCII:
Не зная об этом, вы используете его все время, каждый раз, когда используете компьютерную систему, но если все, что вам нужно, это получить некоторые символы, не включенные в вашу клавиатуру, следует сделать следующее, например:
Как печатать: знак плюс-минус?
WINDOWS: на компьютерах с операционной системой Windows, например Windows 8, Win 7, Vista, Windows XP и т. Д.
Чтобы получить букву, знак, знак или символ «±» : (знак плюс-минус) на компьютерах с операционной системой Windows:
1) Нажмите клавишу «Alt» на клавиатуре и не отпускайте.

2) Удерживая нажатой клавишу «Alt», введите на клавиатуре число «241», которое является номером буквы или символа «±» в таблице ASCII.
3) Тогда перестаньте нажимать клавишу «Alt» и … у вас все получилось! (284)
Полный список символов, букв, символов и знаков ASCII с описанием:
управляющих символа ASCII непечатаемых:
код ASCII 00 = NULL (нулевой символ)
код ASCII 01 = SOH (начало заголовка)
код ASCII 02 = STX (начало текста)
код ASCII 03 = ETX (конец текста , масть карты червы)
код ASCII 04 = EOT (конец передачи, масть бубновой карты)
код ASCII 05 = ENQ (запрос, масть трефовой карты)
код ASCII 06 = ACK (подтверждение, пиковая карта костюм)
код ASCII 07 = BEL (звонок)
код ASCII 08 = BS (Backspace)
код ASCII 09 = HT (горизонтальная табуляция)
код ASCII 10 = LF (перевод строки)
ASCII код 11 = VT (вертикальная табуляция, мужской символ, символ Марса)
Код ASCII 12 = FF (подача формы, женский символ, символ Венеры)
Код ASCII 13 = CR (возврат каретки)
ASCII код 14 = SO (Shift Out)
Код ASCII 15 = SI (Shift In)
Код ASCII 16 = DLE (Выход канала данных)
Код ASCII 17 = DC1 (Управление устройством 1)
Код ASCII 18 = DC2 (Управление устройством 2)
Код ASCII 19 = DC3 (управление устройством 3)
код ASCII 20 = DC4 (управление устройством 4)
код ASCII 21 = NAK (отрицательное подтверждение NAK)
код ASCII 22 = SYN (синхронный режим ожидания)
ASCII код 23 = ETB (Конец транс. блок)
блок)
код ASCII 24 = CAN (отмена)
код ASCII 25 = EM (конец носителя)
код ASCII 26 = SUB (замена)
код ASCII 27 = ESC (Escape)
ASCII код 28 = FS (разделитель файлов)
код ASCII 29 = GS (разделитель групп)
код ASCII 30 = RS (разделитель записей)
код ASCII 31 = US (разделитель единиц)
код ASCII 127 = DEL (Удалить)
Печатаемые символы ASCII:
(буквенно-цифровые, символы и знаки)
код ASCII 32 = пробел (пробел)
код ASCII 33 = ! (восклицательный знак)
код ASCII 34 = « (двойные кавычки; кавычки; речевые знаки)
код ASCII 35 = # (цифровой знак)
код ASCII 36 = $ (знак доллара)
код ASCII 37 = % (знак процента)
код ASCII 38 = и (амперсанд)
код ASCII 39 = ‘ (одинарная кавычка или апостроф)
код ASCII 40 = ( (круглые скобки или круглые скобки, открывающий раунд) скобка)
код ASCII 41 = ) (круглые или круглые скобки, закрывающие скобки)
код ASCII 42 = * (звездочка)
код ASCII 43 = + (знак плюс)
код ASCII 44 = , (Запятая)
Код ASCII 45 = — (Дефис, знак минус)
Код ASCII 46 = . (точка, точка)
(точка, точка)
код ASCII 47 = / (косая черта, косая черта, дробная черта, делительная косая черта)
код ASCII 48 = 0 (ноль)
код ASCII 49 = 1 (номер один )
код ASCII 50 = 2 (число два)
код ASCII 51 = 3 (число три)
код ASCII 52 = 4 (число четыре)
код ASCII 53 = 5 (число пять)
Код ASCII 54 = 6 (число шесть)
Код ASCII 55 = 7 (число семь)
Код ASCII 56 = 8 (число восемь)
Код ASCII 57 = 9 (число девять)
код ASCII 58 = : (двоеточие)
код ASCII 59 = ; (точка с запятой)
код ASCII 60 = < (знак меньше)
код ASCII 61 = = (знак равенства)
код ASCII 62 = > (знак больше, неравенство)
код ASCII 63 = ? (вопросительный знак)
код ASCII 64 = @ (знак at)
код ASCII 65 = A (заглавная буква A)
код ASCII 66 = B (заглавная буква B)
код ASCII 67 = C (заглавная буква C)
код ASCII 68 = D (заглавная буква D)
код ASCII 69 = E (заглавная буква E)
код ASCII 70 = F (заглавная буква F)
код ASCII 71 = G (заглавная буква G)
код ASCII 72 = H (заглавная буква H)
код ASCII 73 = I (заглавная буква I)
код ASCII 74 = J (заглавная буква J)
код ASCII 75 = K (заглавная буква K)
код ASCII 76 = L (заглавная буква L)
код ASCII 77 = M (заглавная буква M)
код ASCII 78 = N (заглавная буква N)
Код ASCII 79 = O (Заглавная буква O)
Код ASCII 80 = P ( Заглавная буква P)
код ASCII 81 = Q (заглавная буква Q)
код ASCII 82 = R (заглавная буква R)
код ASCII 83 = S (заглавная буква S)
код ASCII 84 = T (заглавная буква T)
код ASCII 85 = U (заглавная буква U)
код ASCII 86 = V (заглавная буква V)
код ASCII 87 = W (заглавная буква W)
код ASCII 88 = X (заглавная буква X)
код ASCII 89 = Y (заглавная буква Y)
код ASCII 90 = Z (заглавная буква Z)
код ASCII 91 = [ (квадратные скобки или квадратные скобки, открытие скобка)
код ASCII 92 = \ (обратная косая черта, обратная косая черта)
код ASCII 93 = ] (квадратные или квадратные скобки, закрывающая скобка)
код ASCII 94 = ^ (круговой акцент или каретка)
ASCII код 95 = _ (подчеркивание, подчеркивание, нижнее штрих или нижняя линия)
код ASCII 96 = ` (серьезный удар)
код ASCII 97 = a (строчная буква a, минускула a)
код ASCII 98 = b (строчная буква b, минус b)
Код ASCII 99 = c (строчная буква c, минускула c)
код ASCII 100 = d (строчная буква d, минускула d)
код ASCII 101 = e (строчная буква e, минускула e)
код ASCII 102 = f (строчная буква f, минускула f)
код ASCII 103 = g (строчная буква g, минускула g)
код ASCII 104 = h (строчная буква h, минускула h)
код ASCII 105 = i (строчная буква i, минускула i)
код ASCII 106 = j (строчная буква j, минускула j)
код ASCII 107 = k (строчная буква k, минускула k)
код ASCII 108 = l (строчная буква l, минускул l)
код ASCII 1 09 = м (строчная буква m, минускула m)
код ASCII 110 = n (строчная буква n, минускула n)
код ASCII 111 = o (строчная буква o, минускула o)
код ASCII 112 = p (строчная буква p, минускула p)
код ASCII 113 = q (строчная буква q, минускула q)
код ASCII 114 = r (строчная буква r, минускула r)
код ASCII 115 = с (строчная буква s, минускул s)
код ASCII 116 = t (строчная буква t, минускула t)
код ASCII 117 = u (строчная буква u, минускула u)
код ASCII 118 = v ( Строчная буква v, минускула v)
Код ASCII 119 = w (Строчная буква w, минускула w)
Код ASCII 120 = x (строчная буква x, минускула x)
Код ASCII 121 = y (строчная буква y, minuscule y)
Код ASCII 122 = z (строчная буква z, минускула z)
код ASCII 123 = { (фигурные или фигурные скобки, открывающие скобки)
код ASCII 124 = | (вертикальная черта, vbar, вертикальная линия или вертикальная косая черта)
код ASCII 125 = } (фигурные скобки или скобки, закрывающие фигурные скобки)
код ASCII 126 = ~ (тильда; повернутое тире)
Расширенные символы ASCII:
код ASCII 128 = Ç (Majuscule C-cedilla)
код ASCII 129 = ü (буква u с умлаутом или диэрезисом, u-умляут)
код ASCII 130 = é (буква e с острым ударением или e -acute)
код ASCII 131 = â (буква a с диакритическим ударением или a-циркумфлекс)
код ASCII 132 = ä (буква a с умляутом или диэрезисом, a-умляут)
код ASCII 133 = à (буква a с тупым ударением)
код ASCII 134 = å (буква a с кольцом)
код ASCII 135 = ç (минускульная c-седилья)
код ASCII 136 = ê (буква e с диакритическим знаком акцента) или e-циркумфлекс)
код ASCII 137 = ë (буква e с умлаутом или диэрезисом; e-умляуты)
код ASCII 138 = è (буква e с тупым ударением)
код ASCII 139 = ï (буква i с умлаутом или тремой; i-умлаут)
Код ASCII 140 = î (буква i с акцент с циркумфлексом или i-циркумфлекс)
код ASCII 141 = ì (буква i с тупым ударением)
код ASCII 142 = Ä (буква A с умляутом или диэрезисом; A-умлаут)
код ASCII 143 = Å (заглавная буква A с кольцом)
код ASCII 144 = É (заглавная буква E с острым ударением или E-острым ударением)
код ASCII 145 = æ (латиница дифтонг ae в нижнем регистре)
код ASCII 146 = Æ (латинский дифтонг AE в верхнем регистре)
код ASCII 147 = ô (буква o с акцентом или o-циркумфлексом)
код ASCII 148 = ö (буква o с умляутом или диэрезисом; о-умляут)
код ASCII 149 = ò (буква o с тупым ударением)
код ASCII 150 = û (буква u с диакритическим ударением или u-циркумфлексом)
код ASCII 151 = ù (буква u с тупым ударением)
код ASCII 152 = ÿ (строчная буква y с диэрезисом)
код ASCII 153 = Ö (буква O с умляутом или диэрезисом; O-умляут)
код ASCII 154 = Ü (буква U с умляутом или диэрезисом; U-умляут)
ASCII cod e 155 = ø (ноль с косой чертой в нижнем регистре или пустой набор)
код ASCII 156 = £ (знак фунта; символ фунта стерлингов)
код ASCII 157 = Ø (ноль с косой чертой в верхнем регистре или пустой набор)
код ASCII 158 = × (знак умножения)
код ASCII 159 = ƒ (знак функции; f со знаком крючка ; знак флорина)
код ASCII 160 = á (строчная буква a с острым ударением или острым ударением)
код ASCII 161 = í (строчная буква i с острым ударением или i-острым ударением)
код ASCII 162 = ó (строчная буква o с острым ударением или o-острым ударением)
код ASCII 163 = ú (строчная буква u с острым ударением или u-острым ударением)
код ASCII 164 = — (eñe, enie, испанская буква enye , нижний регистр n с тильдой)
код ASCII 165 = Ñ (испанская буква enye, верхний регистр N с тильдой, EÑE, enie)
код ASCII 166 = ª (женский порядковый номер)
код ASCII 167 = º ( мужской порядковый номер)
код ASCII 168 = ¿900 06 (перевернутые вопросительные знаки)
код ASCII 169 = ® (зарегистрированный символ товарного знака)
код ASCII 170 = ¬ (символ логического отрицания)
код ASCII 171 = ½ (половина)
код ASCII 172 = ¼ (четверть, одна четверть)
код ASCII 173 = ¡ (перевернутые восклицательные знаки)
код ASCII 174 = « (угловые кавычки, гильеметы, кавычки, указывающие вправо)
код ASCII 175 = » ( Гильметы, угловые кавычки, кавычки, указывающие влево)
код ASCII 176 = ░ (графический символ, пунктирная низкая плотность)
код ASCII 177 = ▒ (графический символ, пунктирная средняя плотность)
код ASCII 178 = ▓ (графический символ, пунктир с высокой плотностью точек)
код ASCII 179 = │ (символ рисования прямоугольником, одиночная вертикальная линия)
код ASCII 180 = ┤ (символ рисования прямоугольником, одиночная вертикальная и левая линия)
код ASCII 18 1 = Á (заглавная буква A с острым ударением или A с острым ударением)
код ASCII 182 = Â (буква A с диакритическим ударением или A-циркумфлекс)
код ASCII 183 = À (буква A с тупым ударением )
код ASCII 184 = © (символ авторских прав)
код ASCII 185 = ╣ (прямоугольный символ двойной вертикальной и левой линии)
код ASCII 186 = ║ (прямоугольный символ двойной вертикальной линии)
код ASCII 187 = ╗ (двойная линия символа прямоугольника в верхнем правом углу)
код ASCII 188 = ╝ (двойная линия символа прямоугольника в нижнем правом углу)
код ASCII 189 = ¢ (символ центов)
код ASCII 190 = ¥ (знак YEN и YUAN)
код ASCII 191 = ┐ (символ рисования прямоугольника, однострочный верхний правый угол)
код ASCII 192 = └ (символ рисования прямоугольника, однострочный нижний левый угол)
код ASCII 193 = ┴ (символ рисования прямоугольником, одинарная линия по горизонтали и вверх)
код ASCII 194 = ┬ (символ рисования прямоугольником, одинарная линия, горизонтальная вниз)
код ASCII 195 = ├ (символ рисования прямоугольником, одинарная линия по вертикали и справа)
код ASCII 196 = ─ (символ рисования прямоугольником, одинарная горизонтальная линия)
код ASCII 197 = ┼ (символ рисования прямоугольника, одинарная горизонтальная линия, вертикальный)
код ASCII 198 = ã (строчная буква a с тильдой или a-тильдой)
Код ASCII 199 = Ã (заглавная буква A с тильдой или A-тильдой)
Код ASCII 200 = ╚ (двойная линия символа прямоугольника в нижнем левом углу)
код ASCII 201 = ╔ (двойная линия символа рисования прямоугольника верхний левый угол)
код ASCII 202 = ╩ (символ рисования прямоугольником, двойная линия по горизонтали и вверх)
код ASCII 203 = ╦ (символ рисования прямоугольником, двойная линия горизонтально вниз)
код 204 = ╠ (двойная линия символа рисования прямоугольником, вертикальная и правая)
код ASCII 205 = = (двойная горизонтальная линия символа рисования прямоугольника)
код ASCII 206 = ╬ (двойная линия символа рисования прямоугольника, горизонтальная вертикальная)
ASCII код 207 = ¤ (общий знак валюты)
код ASCII 208 = ð (строчная буква eth)
код ASCII 209 = Ð (заглавная буква Eth)
код ASCII 210 = Ê (буква E с циркумфлексом ударение или E-циркумфлекс)
код ASCII 211 = Ë (буква E с умлаутом или диэрезисом, E-умляут)
код ASCII 212 = È (заглавная буква E с тупым ударением)
код ASCII 213 = ı (Строчная точка без i)
Код ASCII 214 = Í (Заглавная буква I с острым ударением или I-акутом)
Код ASCII 215 = Î (Буква I с диакритическим ударением или I-циркумфлексом)
Код ASCII 216 = Ï (Пусть тер I с умлаутом или диэрезисом; I-умлаут)
ASCII-код 217 = ┘ (прямоугольный однострочный нижний правый угол)
ASCII-код 218 = ┌ (прямоугольный однострочный символ в верхнем левом углу)
ASCII-код 219 = █ (блок , графический символ)
код ASCII 220 = (нижняя половина блока)
код ASCII 221 = ¦ (вертикальная пунктирная полоса)
код ASCII 222 = Ì (заглавная буква I с серьезным ударением)
код ASCII 223 = ▀ (верхняя половина блока)
код ASCII 224 = Ó (заглавная буква O с острым ударением или острым ударением O)
код ASCII 225 = ß (буква Eszett; scharfes S или диез S)
код ASCII 226 = Ô (буква O с циркумфлексом или O-циркумфлексом)
код ASCII 227 = Ò (заглавная буква O с серьезным ударением)
код ASCII 228 = x (строчная буква o с тильдой или o-тильдой )
код ASCII 229 = Õ (на душу населения l буква O с тильдой или O-тильдой)
Код ASCII 230 = µ (строчная буква Mu; микрознак или микрон)
код ASCII 231 = (строчная буква Thorn)
код ASCII 232 = Þ (заглавная буква Thorn)
код ASCII 233 = Ú (заглавная буква U с острым ударением или U-острый )
код ASCII 234 = (буква U с циркумфлексом или U-циркумфлекс)
код ASCII 235 = Ù (заглавная буква U с тупым ударением)
код ASCII 236 = ý (строчная буква y с острым ударением акцент)
код ASCII 237 = Ý (заглавная буква Y с острым ударением)
код ASCII 238 = ¯ (символ Макрона)
код ASCII 239 = ´ (острый ударение)
код ASCII 240 = ≡ (Символ отношения сравнения)
Код ASCII 241 = ± (знак плюс-минус)
(объект HTML = & plusmn;) Код ASCII 242 = ‗ (подчеркивание или подчеркивание)
Код ASCII 243 = ¾ (три четверти , три четверти)
код ASCII 244 = ¶ (Знак абзаца или pilcrow; знак конца абзаца)
код ASCII 245 = § (знак раздела)
код ASCII 246 = ÷ (знак деления; Обелус)
код ASCII 247 = ¸ (седилья)
код ASCII 248 = ° (Символ градуса)
код ASCII 249 = (диарез)
код ASCII 250 = · (вставка или пробел)
код ASCII 251 = ¹ (верхний индекс один, показатель степени 1, первая степень)
код ASCII 252 = ³ (верхний индекс три, показатель степени 3, куб, третья степень)
код ASCII 253 = ² (верхний индекс два, показатель степени 2, квадрат, вторая степень)
код ASCII 254 = ■ (черный квадрат)
Код ASCII 255 = nbsp (неразрывный или непрерывный пробел)
Ключевые слова для этой страницы — код ASCII Знак плюс-минус: ±
Как ввести или написать код ASCII Знак плюс-минус, ± плюс, минус, знак, ascii, 241, ascii art, ascii table, code ascii, ascii character , текст ascii, таблица ascii, символы ascii, коды ascii, символы, коды, таблицы, символы, список, alt, клавиши, клавиатура, правописание, управление, для печати, расширенный, буквы, послания, почерк, сценарии, надписи, маюскулы, заглавные буквы , minuscules, нижний, падеж, маленький, острый, ударение, острый, гравировать, диарезис, циркумфлекс, тильда, седилья, анилло, круг, eñe, enie, arroba, фунт, стерлинг, цент, тип, написать, заклинание, испанский, английский , ноутбуки, ноутбуки, ascii, asci, asccii, asqui, askii, aski, aschi, aschii, (285).
Интерпретация методом плюс-минус
Задача 11.13
Интерпретируйте данные в таблице 11.13a, используя метод плюс-минус.
Фон
Принцип Ферма (проблема 4.13) гласит, что путь луча между двумя точками A {\ displaystyle A} и B {\ displaystyle B} таков, что время пробега является либо минимумом (например, прямые волны, отражения и встречные волны), либо максимумом. . Следовательно, путь лучей между A {\ displaystyle A} и B {\ displaystyle B} уникален, так что tAB = tBA = tr = взаимное время {\ displaystyle t_ {AB} = t_ {BA} = t_ {r} = обратное время}.В результате, когда мы перевернули профили, мы можем найти рефрактор, нарисовав волновые фронты из двух источников: A {\ displaystyle A} и B {\ displaystyle B}; когда сумма времен пробега для двух пересекающихся волновых фронтов равна tr {\ displaystyle t_ {r}}, точка пересечения должна лежать на рефракторе (см. задачу 11.14c). Это основная концепция метода плюс-минус (Hagedoorn, 1959).
Построение волновых фронтов обсуждается в задаче 11.14c.
На основе записанных данных мы рисуем и маркируем волновые фронты с интервалами Δ {\ displaystyle \ Delta}, как показано на рисунке 11.13а. Если угол падения равен нулю, они находятся под углами ± θc {\ displaystyle \ pm \ theta _ {c}} к рефрактору, а пересечения дают ромбовидные параллелограммы. Горизонтальная диагональ параллелограмма равна V2Δ {\ displaystyle V_ {2} \ Delta}, а вертикальная диагональ — V1Δ / cosθc {\ displaystyle V_ {1} \ Delta / \ cos \ theta _ {c}}. Строки постоянной суммы времен пробега за вычетом tr {\ displaystyle t_ {r}} ( плюс значения ) дают конфигурацию рефрактора, а различия ( минус значения ) позволяют проверить значение V2 {\ displaystyle V_ {2} }.{\ circ}} с интервалом Δ = 0.20 {\ displaystyle \ Delta = 0.20} s. Поскольку tr = 2.30 {\ displaystyle t_ {r} = 2.30} s, а рефракция от источника B {\ displaystyle B} начинается около 0,8 с, мы рисуем волновые фронты для источника B {\ displaystyle B} для tB = 0. 80 {\ displaystyle t_ {B} = 0.80}, 1.00, 1.20, 1.40 и 1.60 с. Для источника A {\ displaystyle A} мы рисуем волновые фронты для tA = 1,48 {\ displaystyle t_ {A} = 1,48}, 1,28, 1,08, 0,88 и 0,68 с. Мы интерполируем, чтобы найти начальные точки этих волновых фронтов.
80 {\ displaystyle t_ {B} = 0.80}, 1.00, 1.20, 1.40 и 1.60 с. Для источника A {\ displaystyle A} мы рисуем волновые фронты для tA = 1,48 {\ displaystyle t_ {A} = 1,48}, 1,28, 1,08, 0,88 и 0,68 с. Мы интерполируем, чтобы найти начальные точки этих волновых фронтов.
Горизонтальная и вертикальная диагонали параллелограммов имеют длину 1.{\ circ} /0.20=2.92 \ {\ rm {км / с}}. \ end {выравнивается}}}
Эти значения согласуются со значениями на рисунке 11.13b в пределах погрешности.
Рефрактор показан на рисунке 11.13b пунктирной линией. Различия в интервале вертикальных минусовых линий очень незначительны, поэтому мы можем предположить, что V2 {\ displaystyle V_ {2}} является постоянным.
Читать далее
Также в этой главе
Внешние ссылки
Правила для положительных и отрицательных чисел
Положительные и отрицательные числа — это два широких класса чисел, которые используются в математике, а также в повседневных транзакциях, таких как управление деньгами или измерение веса.
- Положительное число имеет значение больше нуля. Его знак положительный, но обычно он пишется без знака плюс перед ним (например, 4, 51, а не +4, +51).
- Отрицательное число имеет значение меньше нуля. Его знак считается отрицательным и пишется со знаком минус перед ним (например, -2, -23).
- Сумма положительного числа и равного ему отрицательного числа равна нулю.
- Ноль не является ни положительным, ни отрицательным числом.
Существуют правила сложения, вычитания, умножения и деления положительных и отрицательных чисел.Как правило, легче выполнять операции с отрицательными числами, если они заключены в скобки, чтобы разделять их. Числовые линии также упрощают понимание положительных чисел и чисел.
Сложение и вычитание положительных и отрицательных чисел
Когда вы складываете или вычитаете положительные и отрицательные числа, знак ответа зависит от того, похожи ли знаки или какое число имеет большее значение. Сложить положительные и отрицательные числа просто, если оба числа имеют одинаковый знак. Просто найдите сумму чисел и держите знак. Например:
Просто найдите сумму чисел и держите знак. Например:
- 3 + 2 = 5
- (-4) + (-2) = -6
Найдите сумму положительного и отрицательного числа, вычтя число с меньшим значением из числа с большее значение. Знак — это знак большего числа.
- (-7) + 2 = -5
- 4 + (-8) = 4-8 = -4
- (-3) + 8 = 5
- 10 + (-2) = 10-2 = 8
- (-5) + 4 = -1
Правила вычитания аналогичны правилам сложения.Для двух положительных чисел, если первое число больше второго, результатом будет другое положительное число.
Если вы вычтите большое положительное число из меньшего положительного числа, вы получите отрицательное число.
Легкий способ сделать это — вычесть меньшее число из большего числа и изменить знак ответа на минус.
Когда вы вычитаете положительное число из отрицательного числа, это то же самое, что прибавлять отрицательное число. Другими словами, это делает отрицательное число более отрицательным.
- (-4) — 3 = (-4) + (-3) = -7
- (-10) — 12 = (-10) + (-12) = -24
Вычитание отрицательного числа из положительного числа отменяет отрицательные знаки и становится простым сложением. Это делает положительное число более положительным.
- 4 — (-3) = 4 + 3 = 7
- 5 — (-2) = 5 + 2 = 7
Когда вы вычитаете отрицательное число из другого отрицательного числа, отрицательные знаки снова отменяют каждое другое, чтобы стать знаком плюс.Ответ имеет знак большего числа.
- (-2) — (-7) = (-2) + 7 = 5
- (-5) — (-3) = (-5) + 3 = -2
Умножение и деление положительных и отрицательные числа
Если вы умножите или разделите одинаковые знаки, вы получите положительное число. Умножение или деление положительных и отрицательных чисел дает отрицательное число.Правила умножения и деления просты:
- Если оба числа положительные, результат будет положительным.
- Если оба числа отрицательны, результат положительный.
 (По сути, два отрицательных значения компенсируют друг друга).
(По сути, два отрицательных значения компенсируют друг друга). - Если одно число положительное, а другое отрицательное, результат будет отрицательным.
- Если вы умножаете или делите несколько чисел знаками, сложите, сколько положительных чисел и сколько отрицательных чисел. Знак избытка — знак ответа.
- Умножение любого числа (положительного или отрицательного) на ноль дает ответ 0.
- Ноль, деленный на любые числа, равен 0.
- Любое число, деленное на ноль, равно бесконечности.
Вот несколько примеров. В этих примерах используются целые числа (целые числа), но те же правила применяются к десятичным и дробным числам.
- 4 x 5 = 20
- (-2) x (-3) = 6
- (-6) x 3 = -18
- 7 x (-2) = -14
- 2 x (-3 ) x 4 = -24
- (-2) x 2 x (-3) = 12
- 12/2 = 6
- (-10) / 5 = -2
- 14 / (-7) = -2
- (-6) / (-2) = 3
 На уроке я работал
На уроке я работал
 05}% Межстрочный интервал - Палатино требуется больше места между строками
\ usepackage {microtype}
\ usepackage [hmarginratio = 1: 1, top = 32mm, columnsep = 20pt] {geometry}
% \ usepackage {multicol}% Используется для двухколоночного макета документа.
\ usepackage [hang, labelfont = bf, textfont = it] {caption}% Пользовательские подписи под / над плавают в таблицах или на рисунках
\ usepackage {booktabs}% Горизонтальные правила в таблицах
% \ usepackage {float}% Требуется для таблиц и рисунков в среде с несколькими столбцами - они должны быть размещены в определенных местах с помощью [H] (e.грамм. \ begin {table} [H])
% \ usepackage {lettrine}% Lettrine - это первая увеличенная буква в начале текста
% \ usepackage {paralist}% Используется для среды compactitem, которая создает маркеры с меньшим пространством между ними
% \ usepackage {esvect}
% \ usepackage {abstract}% Разрешает абстрактную настройку
% \ Renewcommand {\ abstractnamefont} {\ normalfont \ bfseries}% Установите полужирный текст "Аннотация"
% \ refreshcommand {\ abstracttextfont} {\ normalfont \ small \ itshape}% Установите для самой аннотации мелкий курсив
%
% \ usepackage {titlesec}% Позволяет настраивать заголовки
% \ Renewcommand \ thesection {\ Roman {section}}% Римские цифры для разделов
% \ Renewcommand \ thesubsection {\ Roman {subsction}}% Римские цифры для подразделов
% \ titleformat {\ section} [блок] {\ large \ scshape \ centering} {\ thesection.
05}% Межстрочный интервал - Палатино требуется больше места между строками
\ usepackage {microtype}
\ usepackage [hmarginratio = 1: 1, top = 32mm, columnsep = 20pt] {geometry}
% \ usepackage {multicol}% Используется для двухколоночного макета документа.
\ usepackage [hang, labelfont = bf, textfont = it] {caption}% Пользовательские подписи под / над плавают в таблицах или на рисунках
\ usepackage {booktabs}% Горизонтальные правила в таблицах
% \ usepackage {float}% Требуется для таблиц и рисунков в среде с несколькими столбцами - они должны быть размещены в определенных местах с помощью [H] (e.грамм. \ begin {table} [H])
% \ usepackage {lettrine}% Lettrine - это первая увеличенная буква в начале текста
% \ usepackage {paralist}% Используется для среды compactitem, которая создает маркеры с меньшим пространством между ними
% \ usepackage {esvect}
% \ usepackage {abstract}% Разрешает абстрактную настройку
% \ Renewcommand {\ abstractnamefont} {\ normalfont \ bfseries}% Установите полужирный текст "Аннотация"
% \ refreshcommand {\ abstracttextfont} {\ normalfont \ small \ itshape}% Установите для самой аннотации мелкий курсив
%
% \ usepackage {titlesec}% Позволяет настраивать заголовки
% \ Renewcommand \ thesection {\ Roman {section}}% Римские цифры для разделов
% \ Renewcommand \ thesubsection {\ Roman {subsction}}% Римские цифры для подразделов
% \ titleformat {\ section} [блок] {\ large \ scshape \ centering} {\ thesection. } {1em} {}% Изменить внешний вид заголовков разделов
% \ titleformat {\ subsction} [block] {\ large} {\ thesubsection.} {1em} {}% Изменить внешний вид заголовков разделов
\ usepackage {fancyhdr}% Верхние и нижние колонтитулы
\ pagestyle {fancy}% У всех страниц есть верхние и нижние колонтитулы.
\ fancyhead {}% Убрать заголовок по умолчанию
\ fancyfoot {}% Очистить нижний колонтитул по умолчанию
\ fancyhead [C] {CH 341: Биохимия I $ \ bullet $ Ноябрь 2015 г. $ \ bullet $ Vol. XXI, No. 1}% Пользовательский текст заголовка
\ fancyfoot [RO, LE] {\ thepage}% Пользовательский текст нижнего колонтитула
% \ usepackage {tabularx}
% \ usepackage {pgfplots}
% \ usepackage {caption}
% \ usepackage {graphicx}% позволяет импортировать изображения
% \ usepackage {float}% позволяет управлять положением поплавка
% \ usepackage {mhchem}
% \ usepackage {textgreek}
% \ usepackage {siunitx}
% \ usepackage {textcomp}
% \ usepackage {multirow}
% \ usepackage {grffile}
% \ usepackage [экспорт] {adjustbox}
% \ usepackage {placeins}
% Обычно рекомендуется загружать "hyperref" последней.
} {1em} {}% Изменить внешний вид заголовков разделов
% \ titleformat {\ subsction} [block] {\ large} {\ thesubsection.} {1em} {}% Изменить внешний вид заголовков разделов
\ usepackage {fancyhdr}% Верхние и нижние колонтитулы
\ pagestyle {fancy}% У всех страниц есть верхние и нижние колонтитулы.
\ fancyhead {}% Убрать заголовок по умолчанию
\ fancyfoot {}% Очистить нижний колонтитул по умолчанию
\ fancyhead [C] {CH 341: Биохимия I $ \ bullet $ Ноябрь 2015 г. $ \ bullet $ Vol. XXI, No. 1}% Пользовательский текст заголовка
\ fancyfoot [RO, LE] {\ thepage}% Пользовательский текст нижнего колонтитула
% \ usepackage {tabularx}
% \ usepackage {pgfplots}
% \ usepackage {caption}
% \ usepackage {graphicx}% позволяет импортировать изображения
% \ usepackage {float}% позволяет управлять положением поплавка
% \ usepackage {mhchem}
% \ usepackage {textgreek}
% \ usepackage {siunitx}
% \ usepackage {textcomp}
% \ usepackage {multirow}
% \ usepackage {grffile}
% \ usepackage [экспорт] {adjustbox}
% \ usepackage {placeins}
% Обычно рекомендуется загружать "hyperref" последней. \ usepackage {hyperref}% Для гиперссылок в PDF
\ newcommand {\ head} [1] {\ textnormal {\ textbf {# 1}}}
\ begin {document}
\ begin {table}
\ caption {Концентрации продуктов и скорости ферментативных реакций для 5 концентраций субстрата в различных средах с ингибиторами}
\ центрирование
\ begin {tabular} {lcc}
\ toprule [1.5pt]
\ head {Металл} & \ head {SD средней скорости}
& \ head {Средняя концентрация продукта, образованная SD} \\
\ midrule
Магний и $ 1,30 \ pm 0,67 \ phantom {0} $ & 25,97 $ \ pm 13,33 $ \\
Цинк и $ 0,40 \ pm 0,049 $ & $ \ phantom {0} 8,06 \ pm \ phantom {0} 0,97 $ \\
\ bottomrule [1.5pt]
\ end {tabular}
\ end {table}
\ конец {документ}
\ usepackage {hyperref}% Для гиперссылок в PDF
\ newcommand {\ head} [1] {\ textnormal {\ textbf {# 1}}}
\ begin {document}
\ begin {table}
\ caption {Концентрации продуктов и скорости ферментативных реакций для 5 концентраций субстрата в различных средах с ингибиторами}
\ центрирование
\ begin {tabular} {lcc}
\ toprule [1.5pt]
\ head {Металл} & \ head {SD средней скорости}
& \ head {Средняя концентрация продукта, образованная SD} \\
\ midrule
Магний и $ 1,30 \ pm 0,67 \ phantom {0} $ & 25,97 $ \ pm 13,33 $ \\
Цинк и $ 0,40 \ pm 0,049 $ & $ \ phantom {0} 8,06 \ pm \ phantom {0} 0,97 $ \\
\ bottomrule [1.5pt]
\ end {tabular}
\ end {table}
\ конец {документ}
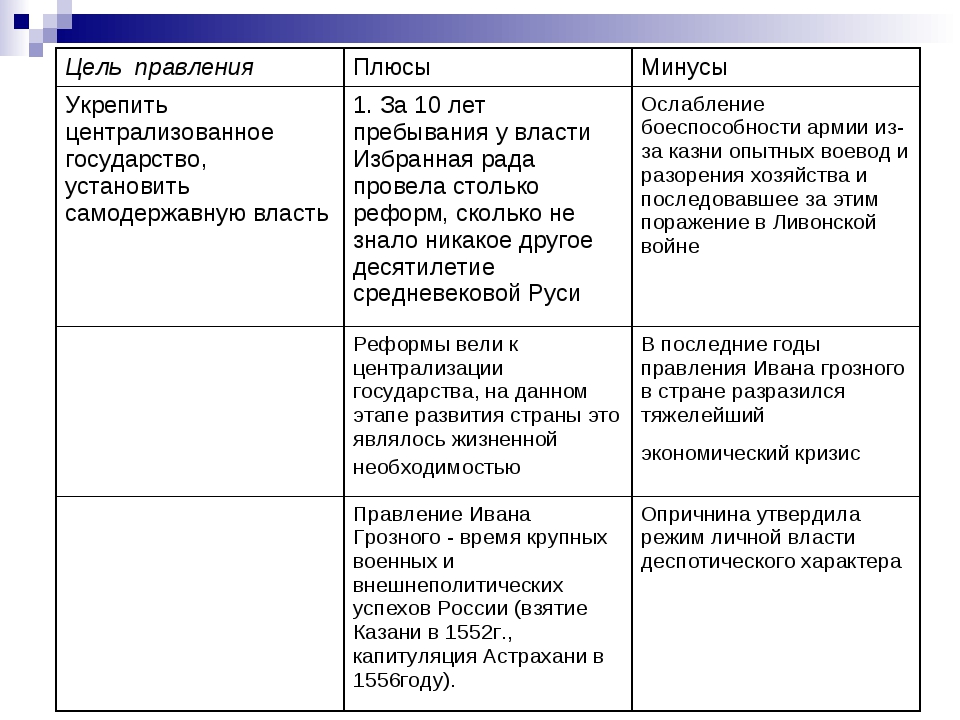
 (По сути, два отрицательных значения компенсируют друг друга).
(По сути, два отрицательных значения компенсируют друг друга).