|
Формальная логика — это широкая область логических исследований, изучающая идеализированные рассуждения и их системы посредством логических исчислений на основе метода формализации (см. Формализация). Метод формализации подразумевает, что логические рассуждения изучаются в отвлечении от их конкретного содержания; при этом сами логические рассуждения формулируются на некотором точном (формализованном) языке при помощи специального аппарата символов (см. Язык формализованный). Такие точные языки имеют две составляющие: синтаксис (см. Синтактика) и семантику (см. Семантика). Синтаксисом называется совокупность правил построения объектов языка (обычно называемых формулами). Семантикой называется совокупность соглашений, описывающих наше понимание формул (или некоторых из них) и позволяющих считать одни формулы верными, а другие — нет. Формализованный язык позволяет избежать двусмысленной и логической неясности естественного языка, которым пользовалась при описании рассуждений Способность человеческого мышления к конструктивной языковой деятельности порождает возможность оперировать следующими логическими формами: В связи с различием логических форм выделяют два основных направления формальной логики:
Кроме того, формальная логика затрагивает и такие вопросы, например, как формализация содержательных теорий, проблема смысла и значения, логические ошибки и парадоксы и многие другие. Самостоятельное выделение этих вопросов достаточно условно, все они погружаются в проблематику основных направлений и тесно переплетены друг с другом. Логика возникла в Древней Греции в рамках философии (см. Философия). История её развития насчитывает около двух с половиной тысячелетий и делится на два основных периода:
Античную и схоластическую логику сейчас объединяет общее название «традиционной логики». Она, кроме историко-философского, по-прежнему имеет важное пропедевтическое значение и, будучи своеобразным стержнем интеллектуальной культуры человека, признается неотъемлемым элементом широкого гуманитарного образования. Новый этап в развитии логики (со второй половины XIX века) был связан с её формализацией и последующей математизацией. В связи с этим новая логика получила название математической (или символической) логики (см. Логика символическая, Логика математическая). Современные логические системы в большинстве своём полностью опираются на формальные математические методы и являются логически интерпретированными исчислениями. Важным разделом современной формальной логики является металогика (см. |
ФОРМАЛЬНАЯ ЛОГИКА — это… Что такое ФОРМАЛЬНАЯ ЛОГИКА?
наука о мышлении, предметом к-рой является исследование умозаключений и доказательств с т. зр. их формы (формы логической) и в отвлечении от их конкретного содержания. Ф. л. является базисной наукой – ее идеи и методы используются как в повседневной практике, напр. в качестве средства от логич. ошибок, так и в особенности в теории для логического анализа науч. знания и для дедуктивного (синтетического) построения на базе логических исчислений любых «нелогических» науч. дисциплин.
Историч. основу Ф. л. образует т.н. т р а д и ц и о н н а я Ф. л., к к-рой относят обычно учение о понятии, учение о мышления законах, учение о суждении и теорию силлогистич. вывода – учение о силлогизме, или силлогистику, учения о непосредственных умозаключениях и несиллогистических умозаключениях, учение о логических ошибках и, наконец, традиц. логику индуктивную. Основоположником традиц. Ф. л. является Аристотель: обобщив опыт повседневного и отчасти науч. мышления тогда только формировавшейся науки, Аристотель создал учение о силлогизме и дал первые примеры анализа рассуждений с т. зр. их формы. Однако уже сам Аристотель сознавал, что в силлогистич. схемы нельзя уложить многие рассуждения, в особенности математические. Это побудило мегариков и ранних стоиков исследовать др.
в качестве средства от логич. ошибок, так и в особенности в теории для логического анализа науч. знания и для дедуктивного (синтетического) построения на базе логических исчислений любых «нелогических» науч. дисциплин.
Историч. основу Ф. л. образует т.н. т р а д и ц и о н н а я Ф. л., к к-рой относят обычно учение о понятии, учение о мышления законах, учение о суждении и теорию силлогистич. вывода – учение о силлогизме, или силлогистику, учения о непосредственных умозаключениях и несиллогистических умозаключениях, учение о логических ошибках и, наконец, традиц. логику индуктивную. Основоположником традиц. Ф. л. является Аристотель: обобщив опыт повседневного и отчасти науч. мышления тогда только формировавшейся науки, Аристотель создал учение о силлогизме и дал первые примеры анализа рассуждений с т. зр. их формы. Однако уже сам Аристотель сознавал, что в силлогистич. схемы нельзя уложить многие рассуждения, в особенности математические. Это побудило мегариков и ранних стоиков исследовать др.

 Для совр. Ф. л. характерно построение формальных теорий логич. вывода (см. Вывод в математической логике) в рамках тех или иных логич. «формализмов» (исчислений), а следовательно, и особое внимание к построению самих этих формализмов и применяемых при этом формально-дедуктивных методов. В зависимости от того, какие осн. понятия и методы используются для построения формальных теорий логич. вывода [в том числе и в зависимости от того, как интерпретируются осн. логич. константы: дизъюнкция, конъюнкция, импликация, отрицание (в логике), эквиваленция] различают: классическую (иначе двузначную) логику, интуиционистскую логику, конструктивную логику, модальную логику, многозначную логику и др. Каковы бы ни были различия в построении этих теорий, каждая теория состоит из двух осн. разделов: логики высказываний и логики предикатов. Классич. вариант последней непосредственно примыкает к традиц. силлогистике (логике «одноместных» предикатов), хотя в многочисленных и различных предикатов исчислениях (см.
Для совр. Ф. л. характерно построение формальных теорий логич. вывода (см. Вывод в математической логике) в рамках тех или иных логич. «формализмов» (исчислений), а следовательно, и особое внимание к построению самих этих формализмов и применяемых при этом формально-дедуктивных методов. В зависимости от того, какие осн. понятия и методы используются для построения формальных теорий логич. вывода [в том числе и в зависимости от того, как интерпретируются осн. логич. константы: дизъюнкция, конъюнкция, импликация, отрицание (в логике), эквиваленция] различают: классическую (иначе двузначную) логику, интуиционистскую логику, конструктивную логику, модальную логику, многозначную логику и др. Каковы бы ни были различия в построении этих теорий, каждая теория состоит из двух осн. разделов: логики высказываний и логики предикатов. Классич. вариант последней непосредственно примыкает к традиц. силлогистике (логике «одноместных» предикатов), хотя в многочисленных и различных предикатов исчислениях (см. также ст. Натуральное исчисление, Секвенций исчисление) формализуется субъектно-предикатная структура предложений, понимаемая в более широком, чем в традиц. Ф. л., смысле: помимо свойств («одноместных» предикатов), в них формализуются и отношения («многоместные» предикаты), что делает излишней особую логику отношений в ее традиц. филос. истолковании.
Каждая из указанных выше формальных теорий имеет определ. филос. смысл, являясь логической реализацие й тех или иных методологич. подходов в науке. Связь совр. Ф. л. и философии стимулируется прежде всего актуальной задачей обоснования математики – науч. направлением, имеющим как логический, так и филос. характер (см. ст. Алгоритм, Интуиционизм, Исчисление задач, Конструктивное направление, Логицизм, Математическая бесконечность, Математическая логика, Метод аксиоматический, Минимальная логика, Номинализм в философии математики, Положительная логика, Принцип исключенного третьего, Проверяемость, Теория множеств, формализм, Эффективизм). Примером обогащения и углубления логич.
также ст. Натуральное исчисление, Секвенций исчисление) формализуется субъектно-предикатная структура предложений, понимаемая в более широком, чем в традиц. Ф. л., смысле: помимо свойств («одноместных» предикатов), в них формализуются и отношения («многоместные» предикаты), что делает излишней особую логику отношений в ее традиц. филос. истолковании.
Каждая из указанных выше формальных теорий имеет определ. филос. смысл, являясь логической реализацие й тех или иных методологич. подходов в науке. Связь совр. Ф. л. и философии стимулируется прежде всего актуальной задачей обоснования математики – науч. направлением, имеющим как логический, так и филос. характер (см. ст. Алгоритм, Интуиционизм, Исчисление задач, Конструктивное направление, Логицизм, Математическая бесконечность, Математическая логика, Метод аксиоматический, Минимальная логика, Номинализм в философии математики, Положительная логика, Принцип исключенного третьего, Проверяемость, Теория множеств, формализм, Эффективизм). Примером обогащения и углубления логич. исследований, вызванных стимулирующим влиянием проблем обоснования математики, может служить возникновение металогики – в узком (гильбертовском) смысле как теории формальных систем, ограниченной рамками финитизма, и в широком смысле как метатеории Ф. л. вообще, включающей логический синтаксис (см. Синтаксис в логике, Метаязык), логическую семантику (см. такжеСемантика в логике и примыкающие к ней ст. Взаимозаменимости отношение, Знак, Значение, Имя, Интерпретация, Контрфактические предложения, Логическая истинность, Модель, Название, Описания операторы, Реализуемость, Синтетические и аналитические суждения, Тавтология, Тождественная истинность, Фактическая истинность, Экстенсиональные и неэкстенсиональные языки), теории определения и определимости и теорию тождества (см. А=А, Правило замены равного равным, Принцип замещения, Равенство в логике и математике). Дальнейшим расширением металогич. проблематики явилось выделение в особую дисциплину прагматики, развивавшейся первоначально в рамках логико-семантич.
исследований, вызванных стимулирующим влиянием проблем обоснования математики, может служить возникновение металогики – в узком (гильбертовском) смысле как теории формальных систем, ограниченной рамками финитизма, и в широком смысле как метатеории Ф. л. вообще, включающей логический синтаксис (см. Синтаксис в логике, Метаязык), логическую семантику (см. такжеСемантика в логике и примыкающие к ней ст. Взаимозаменимости отношение, Знак, Значение, Имя, Интерпретация, Контрфактические предложения, Логическая истинность, Модель, Название, Описания операторы, Реализуемость, Синтетические и аналитические суждения, Тавтология, Тождественная истинность, Фактическая истинность, Экстенсиональные и неэкстенсиональные языки), теории определения и определимости и теорию тождества (см. А=А, Правило замены равного равным, Принцип замещения, Равенство в логике и математике). Дальнейшим расширением металогич. проблематики явилось выделение в особую дисциплину прагматики, развивавшейся первоначально в рамках логико-семантич. и психологич. анализа (см. Психологизм в логике), и, наконец, появление семиотики. Т.о., связь между мышлением и языком как «практической действительностью мысли» (К. Маркс) нашла отражение во взаимосвязи философии, психологии, лингвистики и логики.
В развитии совр. Ф. л. особую роль играют вопросы ее приложений, особенно в вычислит. математике и технике, кибернетике и теории информации, лингвистике математической и пр. (см., напр., ст. Логические машины, Логические схемы автоматов). Связующим звеном между Ф. л. и вычислит. математикой исторически явилась логика классов, к-рая развилась в результате попыток свести силлогистич. методы решения логич. задач к алгебраич. методам их решения, образовав, т.о., первое алгебраич. направление в совр. Ф. л. – алгебру логики (см. также Теоретико-множественная логика). Дальнейшим развитием алгебраич. направления явилось объединение алгебры логики и логики предикатов в теории конечных автоматов, расширение алгебры логики в сторону «алгебраизации» логики предикатов – теория моделей и математич.
и психологич. анализа (см. Психологизм в логике), и, наконец, появление семиотики. Т.о., связь между мышлением и языком как «практической действительностью мысли» (К. Маркс) нашла отражение во взаимосвязи философии, психологии, лингвистики и логики.
В развитии совр. Ф. л. особую роль играют вопросы ее приложений, особенно в вычислит. математике и технике, кибернетике и теории информации, лингвистике математической и пр. (см., напр., ст. Логические машины, Логические схемы автоматов). Связующим звеном между Ф. л. и вычислит. математикой исторически явилась логика классов, к-рая развилась в результате попыток свести силлогистич. методы решения логич. задач к алгебраич. методам их решения, образовав, т.о., первое алгебраич. направление в совр. Ф. л. – алгебру логики (см. также Теоретико-множественная логика). Дальнейшим развитием алгебраич. направления явилось объединение алгебры логики и логики предикатов в теории конечных автоматов, расширение алгебры логики в сторону «алгебраизации» логики предикатов – теория моделей и математич. теория структур. Другую – «арифметическую» – ветвь, связавшую Ф. л. и вычислит. математику, образуют теория рекурсивных функций и предикатов (см. также ст. Алгоритм, Массовая проблема, Разрешимое и перечислимое множества, Сводимость), исчисление λ-конверсии (см. Оператор абстракции, Функция), логика комбинаторная и др. Из общих науч. приложений Ф. л. следует отметить вопросы, связанные с задачами уточнения понятия науч. закона (см. Диспозициональный предикат, Каузальная импликация, Номологические высказывания, Связь), с попытками применения логики в биологии и физике (см. Логика квантовой механики), в этике и юриспруденции (см. Нормативная логика). Успехи, достигнутые в формальной теории дедукции, способствовали применению точных методов в разработке широкого комплекса проблем теории индукции и индуктивной логики (см. ст. Логика индуктивная, раздел Современная логика индуктивная, ст. Научная индукция, Неполная индукция, Популярная индукция), и вероятностной логики.
Т.о., ответ на вопрос «Что такое Ф.
теория структур. Другую – «арифметическую» – ветвь, связавшую Ф. л. и вычислит. математику, образуют теория рекурсивных функций и предикатов (см. также ст. Алгоритм, Массовая проблема, Разрешимое и перечислимое множества, Сводимость), исчисление λ-конверсии (см. Оператор абстракции, Функция), логика комбинаторная и др. Из общих науч. приложений Ф. л. следует отметить вопросы, связанные с задачами уточнения понятия науч. закона (см. Диспозициональный предикат, Каузальная импликация, Номологические высказывания, Связь), с попытками применения логики в биологии и физике (см. Логика квантовой механики), в этике и юриспруденции (см. Нормативная логика). Успехи, достигнутые в формальной теории дедукции, способствовали применению точных методов в разработке широкого комплекса проблем теории индукции и индуктивной логики (см. ст. Логика индуктивная, раздел Современная логика индуктивная, ст. Научная индукция, Неполная индукция, Популярная индукция), и вероятностной логики.
Т.о., ответ на вопрос «Что такое Ф. л.?» можно дать, лишь опираясь на историч. анализ ведущих тенденций развития логики, а также принимая во внимание, что термин «Ф. л.» употребляется неоднозначно, что в рамках Ф. л. в широком смысле можно говорить о различных разделах и дисциплинах, к-рые также носят имя «Ф. л.». Такая дифференциация Ф. л., с др. стороны, дополняется интеграцией, появлением новых теорий и концепций, в к-рых Ф. л. рассматривается с к.-л. единой, общей т. зр.
л.?» можно дать, лишь опираясь на историч. анализ ведущих тенденций развития логики, а также принимая во внимание, что термин «Ф. л.» употребляется неоднозначно, что в рамках Ф. л. в широком смысле можно говорить о различных разделах и дисциплинах, к-рые также носят имя «Ф. л.». Такая дифференциация Ф. л., с др. стороны, дополняется интеграцией, появлением новых теорий и концепций, в к-рых Ф. л. рассматривается с к.-л. единой, общей т. зр.М. Новосёлов, Г. Рузавин, П. Таванец. Москва.
Философская Энциклопедия. В 5-х т. — М.: Советская энциклопедия. Под редакцией Ф. В. Константинова. 1960—1970.
Формальная логика
Формальная логика- Введение
3
- § 1. Марксистская философия о мышлении 3
- § 2. Мышление и язык 4
- § 3. Определение формальной логики 5
- § 4. Логика и психология 9
- § 5. Из истории логики 10
- § 6.
 Практическое значение формальной логики
16
Практическое значение формальной логики
16 - § 7. Структура формальной логики 19
- Часть первая. ОБЩАЯ ЛОГИКА ОСНОВНЫЕ ЛОГИЧЕСКИЕ ФОРМЫ И МЕТОДЫ МЫШЛЕНИЯ
20
- Глава I. Понятие
20
- § 8. Об определении и структуре понятия 20
- § 9. Основные методы образования понятий 26
- § 10. Соотношение между содержанием и объемом понятия 26
- § 11. Виды понятий 32
- § 12. Формально-логические отношения между понятиями по содержанию и по объему 36
- § 13. Обобщение и ограничение понятий …….. З9
- Глава II. Суждение
42
- § 14. Сущность суждения и его строение 42
- § 15. Суждение и предложение 46
- § 16. Суждение и вопрос 48
- § 17. Деление суждений по качеству и количеству 54
- § 18. Объединенная классификация суждений по качеству и количеству 57
- § 19. Распределенность терминов в категорических суждениях 58
- § 20.
 Отношения между суждениями
61
Отношения между суждениями
61 - § 21. Деление суждений по модальности 63
- § 22. Сложные суждения 69
- Глава III. Основные формально — логические законы
75
- § 23. Общие замечания 75
- § 24. Закон тождества 76
- § 25. Закон противоречия 79
- § 26. Закон исключенного третьего 81
- § 27. Закон достаточного основания 84
- Глава IV. Умозаключение
87
- § 28. Определение умозаключения 87
- § 29. Непосредственные умозаключения 89
- § 30. Простой категорический силлогизм 98
- § 31. Сокращенные, сложные и сложносокращенные категорические силлогизмы 111
- § 32. Условные, разделительные и условно — разделительные силлогизмы 114
- § 33. Индуктивные умозаключения 120
- § 34. Аналогия 127
- Глава V. Логические методы научного мышления
138
- § 35. Методы классификации объектов исследования 138
- § 36.
 Определение
147
Определение
147 - § 37. Доказательство 156
- § 38. Доказательство (продолжение: паралогизмы, софизмы и парадоксы) 168
- § 39. Аксиоматический метод 174
- § 40. Индуктивные методы установления причинной связи явлений 179
- § 41. Гипотеза 185
- § 42. Вероятностные методы в логике 192
- Глава I. Понятие
20
- Часть вторая. СИМВОЛИЧЕСКАЯ ЛОГИКА
200
- Глава I. Табличное построение логики высказываний
200
- § 1. Высказывания и формы высказываний 200
- § 2. Язык логики высказываний 203
- § 3. Семантика логических знаков 208
- § 4. Таблицы формул логики высказываний 214
- § 5. Равносильные формулы 219
- § б. Правило равносильной замены 224
- § 7. Полные системы логических знаков 227
- § 8. Закон двойственности 234
- § 9. Тождественно — истинные и тождественно — ложные формулы 236
- Глава II.
 Нормальные формы формул логики высказываний
241
Нормальные формы формул логики высказываний
241- § 10. Нормальная форма 241
- § 11. Проблема разрешения 242
- § 12. Конъюнктивная нормальная форма и совершенная конъюнктивная нормальная форма 246
- § 13. Логическое следование и логические следствия 251
- § 14. Сокращенная конъюнктивная нормальная форма 254
- § 15. Дизъюнктивные нормальные формы 260
- Глава III. Естественный вывод в логике высказываний
267
- § 16. Понятия логического вывода 267
- § 17. Производные правила 284
- § 18. Чисто прямое доказательство 287
- § 19. Слабое косвенное доказательство 291
- § 20. Квазисильное косвенное доказательство 295
- § 21. Сильное (классическое) косвенное доказательство 297
- § 22. Полнота классического нечисления высказываний 302
- § 23. Аксиоматическое представление логики высказываний 308
- Глава IV.
 Формализованная силлогистика
322
Формализованная силлогистика
322 - Глава V. Естественный вывод в логике предикатов 330
- Глава VI. Модальная логика 345
- Глава I. Табличное построение логики высказываний
200
В основу учебника положен курс логики, читавшийся на философском факультете Ленинградского университета в течение ряда лет. В нем освещаются вопросы, относящиеся к общей и символической логике. Учебник предназначен для студентов-философов и студентов других гуманитарных факультетов и педагогических вузов.
Загрузка…
Основы формальной логики: как не дать собой манипулировать
Мы начинаем серию материалов о манипулятивных техниках, автором которой выступил известный журналист, редактор (и преподаватель философии) Дмитрий Шишкин. В первой части разберёмся, как связаны казахстанские медийные скандалы последнего времени с древними греками Протагором и Аристотелем.
А связаны они очень даже явно — через приёмы словесного мошенничества, названного 2500 лет назад «софизмом». Древние греки научились распознавать ложь по формальным признаками, пора бы заново овладеть этим знанием и нам.
Древние греки научились распознавать ложь по формальным признаками, пора бы заново овладеть этим знанием и нам.
Искусство манипуляции людьми появилось вместе с речью. Правильно подобранными словами можно отправлять в атаку на врага или обращать в бегство, ввергать в депрессию или мотивировать к свершениям. Но в целом смысл манипуляции всегда один — заставлять делать или думать что-то, что мы делать и думать не собирались — то есть, использовать нас.
Что не так в противостоянии людей, желающих сохранить урочище Кок-Жайляу диким местом, и теми, кто хочет его застроить? На первый взгляд обычный гражданский конфликт — урбанистов и экологов. Но если обратить внимание на нюансы: когда «экологи» приводят аргументы против застройки, а их в ответ называют «экологическим талибаном», и взглянуть на список логических уловок, составленный древними, становится понятно, что это классический пример применения уловки Argumentum ad hominem («аргумент к человеку/личности» или «атака на человека»).
Такие примеры встречаются ежедневно. И мы предлагаем вам учиться разбираться в них не по наитию, а научно.
Содержание / Мазмұны
Немного истории
Софистика
Более 2500 лет назад в Древней Греции активно распространились школы софистики. Там давали уроки начинающим политикам: как при помощи ораторского искусства добиваться своих целей. От философов, также процветавших в древних полисах, софисты отличались в основном тем, что не считали важными какие-то универсальные задачи и теоретические размышления, а главным признавали достижение практической цели.
Интересно, что софистика появилась раньше логики как оформленной науки, и, скорее всего, именно софисты подтолкнули философов к её созданию (в качестве инструмента противодействия демагогам, вводившим народ в заблуждение ради собственных целей).
«Он (Протагор, живший примерно в период 485 – 410 годов до нашей эры, за сто лет до Аристотеля – прим. авт.) первый заявил, что о всяком предмете можно сказать двояко и противоположным образом… о мысли он не заботился, спорил о словах, и повсеместное нынешнее племя спорщиков берёт своё начало от него», – писал о самом ярком представителе софистов Диоген Лаэртский в своей книге «О жизни, учениях и изречениях знаменитых философов».
Аристотель побеждает всех
Софистов ругал ещё Платон, а его ученик Аристотель решил положить конец одурачиванию народа (по крайней мере, попытался — мы и сейчас попадаемся на те же самые уловки, что были известны ещё 2500 лет назад). Он создал научную базу формальной логики (которую сам он называл «Аналитикой») и классифицировал логические ошибки, используемые софистами.
В принципе, логическая ошибка и логическая уловка — это одно и то же, просто ошибка допускается несознательно, а уловка специально вводится в речь.
Аристотель в своём труде «О софистических опровержениях» наглядно показал, что если разложить любой софизм, будет видна специально внедрённая в него ошибка, благодаря которой выводы софиста кажутся логичными.
После Аристотеля немало в развитие формальной логики внесли римляне Цицерон и Квинтилиан, а затем и средневековые схоласты – мы будем в дальнейшем пользоваться их типологией логических ошибок, так что пусть вас не удивляют латинские термины.
Немного теории
Теория — это самая скучная часть формальной логики, и передо мной стоит трудная задача: уложить в рамки современного «лонгрида» курс, который в институте преподаётся в течение года. Поэтому отсечём всё ненужное современному человеку, имеющему интернет и способному самостоятельно найти недостающие фрагменты.
Главное, что есть в формальной логике — это её четыре основных закона
Три из них сформулировал ещё Аристотель:
— закон тождества,
— закон противоречия,
— закон исключённого третьего.
А четвертый закон – достаточного основания — был добавлен немецким математиком и философом Лейбницем в начале XVIII века.
Закон тождества
«…иметь не одно значение — значит не иметь ни одного значения», писал по этому поводу Аристотель в своей «Метафизике».
То есть каждая мысль и каждый термин в процессе рассуждения должны иметь одно и то же значение. Подмена понятия в ходе рассуждения — это классическая логическая ошибка (или уловка).
Например:
– Гражданин N хороший человек, скромный и любит ездить на велосипеде.
– Из него получится хороший аким города!
Здесь мы видим, как в первой части утверждения говорится о личных качествах человека, а вывод делается о его профессиональных качествах — что далеко не тождественно.
Закон противоречия
Два противоречащих друг другу суждения не могут быть одновременно истинными. По крайней мере, одно из них ложно.
… невозможно, чтобы одно и то же в одно и то же время было и не было присуще одному и тому же в одном и том же отношении (Аристотель, «Метафизика»)
Например:
Мы часто встречаем заявления от официальных лиц и даже целых институтов о том, что:
– Народ Казахстана неоднократно демонстрировал свою политическую зрелость, отдавая голоса на выборах президента и депутатов парламента за стабильность!
– Вместе с тем, наш народ не готов пока к выборности акимов и прочим демократическим преобразованиям.
Налицо явное противоречие: получается, народ Казахстана с одной стороны политически подкован, а с другой — настолько дремуч, что не готов к такому элементарному процессу, как выборы акима.
Закон исключённого третьего
Два противоречащих друг другу суждения не могут быть одновременно оба истинными или оба ложными.
…ничего не может быть посредине между двумя противоречивыми суждениями об одном, каждый отдельный предикат необходимо либо утверждать, либо отрицать (Аристотель, «Метафизика»)
Противоречащими называют такие два суждения, в одном из которых что-либо утверждается о предмете, а в другом то же самое об этом же предмете отрицается.
Например:
– Цензура запрещена!
– Если в интересах общества, то цензура разрешена.
Оба эти утверждения об одном и том же явлении не могут быть одновременно правдивыми или ложными. Если делается исключение, то первое утверждение ложное – «третьего не дано».
Закон достаточного основания
Всякая правильная мысль должна быть обусловлена другими мыслями, истинность которых доказана.
…ни одно явление не может оказаться истинным или действительным, ни одно утверждение справедливым, – без достаточного основания, почему именно дело обстоит так, а не иначе, хотя эти основания в большинстве случаев вовсе не могут быть нам известны (Готфрид Вильгельм Лейбниц, «Монадология»)
Это, в общем — именно то, чем занимается «Фактчек в Казахстане» — поиском достаточных оснований для публикаций. В отличие от первых трёх законов, которые можно применять формальными методами, просто соотнося какие-то утверждения с правилами, для установки достаточности основания необходимо включать критическое мышление и затем прилагать усилия для проверки суждений, в которых вы засомневались.
Например, самые яркие примеры мы встречаем довольно часто в виде панических слухов, распространяемых через мессенджеры и социальные сети.
В случае со скандалом вокруг заболеваемости менингитом: неверными оказались как утверждения об эпидемии, так и «рецепт», в котором утверждалось, что для профилактики менингита всем необходимо пропить курс антибиотиков (что, как пояснили затем врачи, назначается только людям, контактировавшим с больными).
На законе достаточного основания также базируется важный юридический принцип: «презумпция невиновности», гласящий, что никто не виновен, пока его вина не была доказана.
В соцсетях и даже СМИ он нарушается настолько часто, практически ежедневно, что примеры вы легко найдёте сами. Людей называют ворами и убийцами до судов, друг друга лжецами безо всяких доказательств и опровержений и т.д.
В следующей части читайте о логических уловках, построенных на нарушении этих законов логики:
- Ignoratio elenchi или «подмена тезиса»
- Argumentum Ad Hominem или «переход на личности»
Проблема взаимоотношений логики формальной и философской (неформальной и воображаемой Н. А. Васильева)
%PDF-1.3 % 1 0 obj > endobj 5 0 obj /Title >> endobj 2 0 obj > endobj 3 0 obj > endobj 4 0 obj > stream
 А. Васильева)
А. Васильева)зачем она менеджеру продуктов и как развивать логическое мышление
Менеджер продуктов должен умело коммуницировать, и логика здесь — хороший помощник. Нам только кажется, что мы говорим и мыслим логически — на самом деле большинство наших поступков алогичны. Сергей Руденко, Principal Product Manager в Amazon, ex-Riot Games, рассказал, как и зачем менеджеру продуктов использовать логическое мышление.
Нам только кажется, что мы говорим и мыслим логически — на самом деле большинство наших поступков алогичны. Сергей Руденко, Principal Product Manager в Amazon, ex-Riot Games, рассказал, как и зачем менеджеру продуктов использовать логическое мышление.
Рассмотрим простую ситуацию. Мы спим и всё происходящее во сне нам кажется логичным. А наутро мы пытаемся пересказывать сон любимому человеку и он тут же рассыпается, теряются логические связи, слушателю наш рассказ кажется бредом.
Это экстремальный пример того, как мы становимся заложниками собственного понимания какого-то явления. Теперь рассмотрим, как это происходит в работе с продуктом: мы день и ночь думаем о продукте, за который отвечаем, в наших головах уже кристаллизовался его образ. Но когда нужно рассказать о нем другому человеку, мы с трудом можем выстроить логические связи. Именно поэтому в менеджменте продуктов так важна документация — ведь излагая свои мысли на бумаге, мы вынуждены логично выстраивать и структурировать их.
С логикой как наукой я познакомился, когда учился на военного переводчика в Москве. Преподаватель курса по формальной логике объяснил нам, студентам, для чего нужна логика в жизни и нашей профессии, буквально за 10 минут — и мы с удовольствием слушали курс в течение года. Все, что мы считали простым, вдруг оказалось сложным. Я понял, что логика — базовая дисциплина и постигать ее нужно перед другими предметами. Она помогает мне на протяжении всей карьеры: в научных работах, программировании, менеджменте продуктов.
Формальная логика дает в руки менеджеру продуктов несколько полезных инструментов.
- Установление связи между причиной и следствием.
- Обобщение, или «зачем я это делаю?»
На мой взгляд, менеджер продуктов как минимум должен быть хорошим коммуникатором — анализировать и логически доносить информацию, мыслить абстракциями, переключаться между разными уровнями понимания. Логика как раз заставляет осмыслять слова и поступки. С ее помощью мы можем дойти до истоков своего высказывания, понять причины и следствия, задуматься, насколько наши мысли — действительно наши, и верим ли мы в них на самом деле. Благодаря логике мы можем посмотреть на свою презентацию со стороны, осознать проблемы и сделать ее более логичной и понятной для собеседника.
Логика как раз заставляет осмыслять слова и поступки. С ее помощью мы можем дойти до истоков своего высказывания, понять причины и следствия, задуматься, насколько наши мысли — действительно наши, и верим ли мы в них на самом деле. Благодаря логике мы можем посмотреть на свою презентацию со стороны, осознать проблемы и сделать ее более логичной и понятной для собеседника.
Логика помогает менеджеру продуктов избежать многих ловушек. Например, компания нанимает меня, чтобы я сделал приложение безопасным. Компания доверяет мне как эксперту. Но я новый сотрудник и чтобы вникнуть в суть дела, мне понадобится несколько месяцев. Поэтому я вынужден принимать на веру утверждение о том, что задача, которую мне поручили, важна для компании. И если я не сомневаюсь в этом, не пытаюсь понять, действительно ли продукту нужна система авторизации, которую я делаю, то я могу полгода или год потратить на то, в чем просто нет необходимости. А ведь за это время я мог бы сделать для компании что-то более ценное и инновационное.
Работая над продуктом, мы должны заносить в Jira пользовательские истории и сценарии, включая мотивационную часть («Как пользователь я авторизуюсь в приложении, чтобы работать со своими личными документами»), но часто из-за нехватки времени или лени не делаем этого. В хорошей команде деструктивные последствия такого пренебрежения могут и не проявиться. Но опытный менеджер продуктов должен убедиться, что все детали и мотивация пользователя были хотя бы проговорены вслух и команда ничего не упустила.
Второй инструмент логики — обобщение, или «зачем я это делаю?»Мы пишем о менеджменте продуктов и развитии в телеграм-каналах make sense и Продуктовое мышление.
Второй инструмент — это обобщение (generalizations). Для удобства работы с ним я применяю три дополнительных полезных инструмента.
- So that (для того чтобы). Когда мы спрашиваем себя, для чего мы делаем то, что делаем. Например, если в команде мы изучаем пользовательские истории, важно убедиться, что все действительно понимают, о чем идет речь.
 И тут опять же помогает обобщение. Нужно задать себе и коллегам вопрос: «Частью какого большого проекта является эта история? Для чего мы это делаем?» Даже если нам кажется, что мы все это давно знаем, нужно еще раз проговорить вслух задачи и цели, отстраниться от деталей, выйти на более высокий уровень. И делать это не разово, а периодически. Так обобщение помогает избежать рутинности и потери смысла. Когда мы задаем себе вопрос, что мы вообще делаем в этой жизни, то мы не скатываемся на уровень, где наша работа — скучная и механическая.
И тут опять же помогает обобщение. Нужно задать себе и коллегам вопрос: «Частью какого большого проекта является эта история? Для чего мы это делаем?» Даже если нам кажется, что мы все это давно знаем, нужно еще раз проговорить вслух задачи и цели, отстраниться от деталей, выйти на более высокий уровень. И делать это не разово, а периодически. Так обобщение помогает избежать рутинности и потери смысла. Когда мы задаем себе вопрос, что мы вообще делаем в этой жизни, то мы не скатываемся на уровень, где наша работа — скучная и механическая. - Zoom in zoom out. Это своего рода микроскоп и телескоп, то есть переход от частного к общему и обратно. Всем участникам команды нужно иметь широкое видение — смотреть на происходящее сверху, обобщать и свободно перемещаться от частного к общему. Как в фильме «Особое мнение» с Томом Крузом — он использует модный на тот момент интерфейс: руками распределяет информационные элементы в пространстве, как с помощью pinch zoom на айфоне, погружается в детали, а потом снова возвращается на уровень обобщения.
 Мы должны делать примерно то же самое в своем уме. Ведь часто, особенно в больших корпорациях, мы работаем в режиме zoom in. Помню, в Microsoft мы отвечали за конкретный сегмент — Евразию, смотрели, каких приложений не хватает пользователям. Работая в таком узком сегменте, можно упустить из виду большую задачу. Например, нам надо, чтобы новый Windows Phone стал жизнеспособной экосистемой для пользователей, которым полюбился его дизайн и интерфейс. Если не держать эту большую задачу в голове, можно попасть в ловушку KPI — мы достигаем поставленные перед нами задачи, но не понимаем, зачем.
Мы должны делать примерно то же самое в своем уме. Ведь часто, особенно в больших корпорациях, мы работаем в режиме zoom in. Помню, в Microsoft мы отвечали за конкретный сегмент — Евразию, смотрели, каких приложений не хватает пользователям. Работая в таком узком сегменте, можно упустить из виду большую задачу. Например, нам надо, чтобы новый Windows Phone стал жизнеспособной экосистемой для пользователей, которым полюбился его дизайн и интерфейс. Если не держать эту большую задачу в голове, можно попасть в ловушку KPI — мы достигаем поставленные перед нами задачи, но не понимаем, зачем. - Десинтезатор. Это образ мышления, который мы можем использовать, когда строим новый продукт на базе имеющихся решений. К примеру, нам нужно было запустить сервисы по всему миру, включая Китай, и использовать для этого внутренний облачный продукт компании Riot. Мы могли бы поступить, как владелец машины с автоматической коробкой передач, который просто нажимает на педаль и едет, не понимая, как все работает.
 Но это недостаточно зрелый подход. В какой-то момент мы рискуем столкнуться с трудностями и не понять их причины. Поэтому сначала мы изучаем, что представляет собой этот продукт, из чего он состоит, как он хотя бы примерно работает. Это способно защитить нас от многих рисков и проблем в будущем.
Но это недостаточно зрелый подход. В какой-то момент мы рискуем столкнуться с трудностями и не понять их причины. Поэтому сначала мы изучаем, что представляет собой этот продукт, из чего он состоит, как он хотя бы примерно работает. Это способно защитить нас от многих рисков и проблем в будущем.
Как тренировать навыки логического мышленияКак развивать стратегическое мышление в бизнесе и жизни и правильно смотреть в будущее
Все эти инструменты эффективны, когда нужно разобраться с какой-то сложной задачей или концепцией. Они похожи на фреймворк и скорее всего, даже не понадобятся, если перед нами простая проблема. К примеру, в детстве я легко сколотил табуретку из доски и четырех стоек с помощью гвоздей и молотка и был очень горд собой. Но если бы надо было создать более сложный продукт, например, стул или кресло-качалку, мне бы пришлось поломать голову и применить какое-то подобие фреймворка.
Навыки логического мышления полезно тренировать даже в ситуациях, когда кажется, что все и так понятно. Около года назад я приобрел большой автомобиль — настоящий монстр-трак. И в нем не было ступенек. Сначала, как обыватель, я расстроился: нужно будет каждый раз прыгать с приличной высоты, одежда испачкается. Но потом применил продуктовое мышление: записал видео о том, как крепить ступени, где их купить, как ими пользоваться. Готовя видео, я нашел ответы на много интересных вопросов, которые в противном случае даже передо мной даже не встали.
Около года назад я приобрел большой автомобиль — настоящий монстр-трак. И в нем не было ступенек. Сначала, как обыватель, я расстроился: нужно будет каждый раз прыгать с приличной высоты, одежда испачкается. Но потом применил продуктовое мышление: записал видео о том, как крепить ступени, где их купить, как ими пользоваться. Готовя видео, я нашел ответы на много интересных вопросов, которые в противном случае даже передо мной даже не встали.
Также инструменты логического мышления можно оттачивать на ресурсах вроде Product Hunt, где стартапы презентуют свои продукты. Глядя на какой-нибудь маленький проект, который решает точечную задачу, мы анализируем, какая у него аудитория, в чем ошибки и удачные ходы его создателей.
С помощью таких тренировок со временем мы выходим на тот уровень, где уже можем без особых усилий и подсознательно применять логические инструменты. Когда я работал в Microsoft, мой ментор с самого начала стал выводить меня из себя постоянными вопросами «для чего мы это делаем (so that)». Казалось, все и так понятно. Но уже через несколько месяцев я увидел положительные результаты такого подхода и сейчас требую этого ото всех, с кем работаю.
Казалось, все и так понятно. Но уже через несколько месяцев я увидел положительные результаты такого подхода и сейчас требую этого ото всех, с кем работаю.
Визуализация и выстраивание командной цепочкиКак в менеджменте продуктов работают карьерные треки менеджера и individual contributor?
В менеджменте продуктов инструменты логики помогают визуализировать связи между командами и выстраивать цепочки. Мы видим: одна команда делает это, чтобы другая команда могла сделать то и так далее.
Компания Riot Games одной из первых заявила о том, что ее миссия — максимально фокусироваться на нуждах заказчиков, то есть пользователей игр. Конечно, все компании, которые создают популярные игры, ориентируются на клиентов. Но важно проговорить это вслух, чтобы стрелка вашего компаса всегда указывала верное направление.
И к этому нужно возвращаться снова и снова. В Riot Games мы, казалось бы, уже проговорили цели, знаем, что делает каждая команда, и все в хорошем смысле слова одержимы потребностями клиента. Но все равно часто приходилось дискутировать о том, какова же наша миссия. Ведь дьявол кроется в деталях. Иногда второстепенные вещи выходят на первый план, а более важные моменты остаются в тени — просто потому, что их никто не проговорил.
Но все равно часто приходилось дискутировать о том, какова же наша миссия. Ведь дьявол кроется в деталях. Иногда второстепенные вещи выходят на первый план, а более важные моменты остаются в тени — просто потому, что их никто не проговорил.
Итак, важно помнить, что наш общий заказчик, для которого мы все делаем — это пользователь игр, конечный потребитель. Однако не нужно пренебрегать и интересами внутренних заказчиков. Например, мы заказываем у одной из наших команд внутреннюю облачную платформу. То есть одна команда выступает заказчиком для другой. Для моей команды ключевым заказчиком была команда магазина «Лиги легенд». Мы работали в тесной связи друг с другом, и нам очень помогала визуализация.
Несколько лет назад я сделал визуализацию для всего нашего отдела, расписал, чем занимается каждая команда, кто от кого и как зависит. В процессе общался с коллегами, просил помочь. И многие из них обнаружили, что какие-то старые интеграции уже не работают, а про какие-то они просто забыли. Так мы выявили много несоответствий и начали с ними работать.
Так мы выявили много несоответствий и начали с ними работать.
Визуализация полезна и в том случае, когда мы говорим о KPI команды. Мы должны понимать, каковы показатели каждой команды, каковы наши общие цели, и перемещаться между разными уровнями. Тогда в компании не будет проблем и перекосов.
Формальная логика может быть увлекательным, полезным и совсем не формальным делом
Анна МЕХЕД, учитель математики школы № 2030, учитель года Москвы-2007: – Когда я думала, как представить свой опыт работы, то столкнулась с огромной проблемой выбора. Выбор для меня был на конкурсе очень мучительным и невероятно сложным. Говорить о формах и методах? Да, наверное, это важно, но все учителя используют новые формы и методы работы, часто свои формы и методы. Тогда я и решила тоже представить что-то свое, что было бы любопытным для моих коллег. В результате на конкурсе я представила свою программу по логике для старших классов средней школы.
Почему я написала эту программу? Логика – важный инструмент любой науки, который регламентирует формы и методы научного познания. Мы все, особенно естественники (впрочем, и гуманитарии тоже), подчиняем все свои рассуждения законам логики: анализ данных, построение теории, явные и неявные доказательства.
Мы все, особенно естественники (впрочем, и гуманитарии тоже), подчиняем все свои рассуждения законам логики: анализ данных, построение теории, явные и неявные доказательства.
Работая в школе, я часто сталкиваюсь с тем, что дети не умеют правильно рассуждать. Мало того, произнося слова, они не понимают той смысловой нагрузки, которую несет каждое слово. Часто они попадают в ситуацию, которая кажется им безвыходной только потому, что они не могут сделать верные выводы или принимают желаемое за действительное.
На зачетах по геометрии я обязательно прошу ребенка нарисовать картинку, иллюстрирующую его ответ. Особенно это связано с многогранниками и телами вращения. Я прошу ребенка использовать в рисунке те термины и слова, которые он употребил. Сразу выплывает то, что он сказал неправильно. Сказал лишнее слово, получил не ту фигуру, а не сказал – вообще не получил никакой фигуры. Именно поэтому лет семь назад (спасибо Московскому педагогическому университету, который подумал о том, что логика – необходимый предмет в школе) я разработала такую программу.
Но программа – это не самое интересное. Я столкнулась с большой проблемой, как подобрать проверочные работы к этой программе. Здесь, поскольку это старшая школа, мне пришлось уже придумывать, как заинтересовать детей, у которых интересы явно лежат вне сферы формальной логики, такими заданиями, чтобы они захотели правильно рассуждать и делать верные выводы. Я опиралась на теорию множеств, потом уже появился учебник для 9-10-х классов, в котором и комбинаторика, и теория вероятности, и элементы математической логики иллюстрируются с помощью теории множеств. Я пошла по тому же пути, может быть, чуть-чуть пораньше, и мне было приятно увидеть, что мой путь рассуждения был верен.
Теперь мы с учениками учимся красиво и правильно записывать наши мысли, следуя законам логики, начинаем выяснять отношения между понятиями, ограничивая или обобщая, и здесь мои ученики видят, что логика, как и математика, всеобъемлюща и с ее помощью можно описать абсолютно все. Мы учимся определять логические связки и записывать все в виде логических цепочек, что помогает нам систематизировать полученные знания.
На самом деле программу по логике я писала для того, чтобы собрать все те части логики, которые используются в средней школе. Мы следуем законам логики в информатике, в стереометрии и в матанализе, но вот как общую дисциплину мы логику не рассматриваем. Я вела эту программу три года в экономическом классе и получила результаты, которые меня порадовали.
Формальная логика | Britannica
Формальная логика , абстрактное изучение предложений, утверждений или утвержденно используемых предложений и дедуктивных аргументов. Дисциплина абстрагируется от содержания этих элементов структур или логических форм, которые они воплощают. Логики обычно используют символические обозначения для четкого и недвусмысленного выражения таких структур, а также для упрощения манипуляций и проверок достоверности. Хотя в следующем обсуждении свободно используются технические обозначения современной символической логики, ее символы вводятся постепенно и с сопровождающими пояснениями, чтобы серьезный и внимательный читатель мог следить за развитием идей.
Формальная логика — это априорное, а не эмпирическое исследование. В этом отношении он контрастирует с естественными науками и всеми другими дисциплинами, данные которых зависят от наблюдения. Его ближайшая аналогия — чистая математика; действительно, многие логики и чистые математики сочли бы свои соответствующие предметы неразличимыми или просто двумя ступенями одной и той же единой дисциплины. Поэтому формальную логику не следует путать с эмпирическим изучением процессов мышления, которое принадлежит психологии.Его также следует отличать от искусства правильного рассуждения, которое представляет собой практический навык применения логических принципов к конкретным случаям; и, что еще более резко, его следует отличать от искусства убеждения, в котором неверные аргументы иногда более эффективны, чем веские.
Общие наблюдения
Вероятно, наиболее естественный подход к формальной логике основан на идее обоснованности аргумента, известного как дедуктивный. Дедуктивный аргумент можно грубо охарактеризовать как аргумент, в котором утверждается, что какое-то предложение (вывод) следует со строгой необходимостью из некоторого другого предложения или предложений (посылок) — i. е., что было бы непоследовательно или противоречиво утверждать посылки, но отрицать вывод.
е., что было бы непоследовательно или противоречиво утверждать посылки, но отрицать вывод.
Если дедуктивный аргумент должен преуспеть в установлении истинности его вывода, должны быть выполнены два совершенно разных условия: во-первых, вывод должен действительно следовать из посылок, т. Е. Вывод заключения из посылок должен быть логически правильным. — и, во-вторых, сами посылки должны быть верными. Аргумент, удовлетворяющий обоим этим условиям, называется обоснованным. Из этих двух условий логик как таковой занимается только первым; второй, определение истинности или ложности посылок, является задачей некой специальной дисциплины или общего наблюдения, соответствующего предмету аргументации.Когда вывод аргумента правильно выводится из его посылок, вывод из посылок к заключению считается (дедуктивно) достоверным, независимо от того, истинны ли посылки. Другие способы выразить тот факт, что вывод является дедуктивно достоверным, — это сказать, что истинность посылок дает (или дала бы) абсолютную гарантию истинности вывода или что это повлечет за собой логическую несогласованность (в отличие от простой ошибка факта), чтобы предположить, что посылки были верными, а вывод — ложным.
Дедуктивные умозаключения, с которыми связана формальная логика, как следует из названия, имеют силу, действительность которых зависит не от каких-либо особенностей их предмета, а от их формы или структуры. Таким образом, два вывода: (1) Каждая собака — млекопитающее. Некоторые четвероногие — собаки. ∴ Некоторые четвероногие — млекопитающие. и (2) Каждый анархист верит в свободную любовь. Некоторые члены правительственной партии — анархисты.∴ Некоторые члены правительственной партии верят в свободную любовь. различаются по предмету и, следовательно, требуют различных процедур для проверки истинности или ложности своих предпосылок. Но их достоверность обеспечивается тем, что у них общего, а именно тем, что аргумент в каждом из них имеет форму (3) Каждые X — это Y . Некоторые Z имеют размер X . ∴ Некоторые Z являются Y .
Строка (3) выше может называться формой вывода, а (1) и (2) тогда являются экземплярами этой формы вывода.Буквы X , Y и Z в (3) обозначают места, в которые могут быть вставлены выражения определенного типа. Символы, используемые для этой цели, известны как переменные; их использование аналогично использованию x в алгебре, которое отмечает место, в которое может быть вставлено число. Экземпляр формы вывода создается путем замены всех переменных в ней подходящими выражениями (т.е., подставляя одно и то же выражение везде, где повторяется одна и та же переменная). Особенность (3), которая гарантирует, что каждый его экземпляр будет действительным, заключается в его построении таким образом, что каждый единообразный способ замены его переменных, чтобы сделать посылки истинными, автоматически делает и вывод истинным, или, другими словами, что ни один его пример не может иметь истинных посылок, кроме ложного заключения. В силу этой особенности форма (3) называется действительной формой вывода. Напротив, (4) Каждые X — это Y .Некоторые Z являются Y . ∴ Некоторые Z имеют размер X . не является допустимой формой вывода, поскольку, хотя могут быть получены его примеры, в которых все посылки и заключение верны, могут быть также получены его примеры, в которых посылки истинны, но заключение ложно — например, (5) Каждый собака — млекопитающее. Некоторые крылатые существа — млекопитающие. ∴ Некоторые крылатые существа — собаки.
Напротив, (4) Каждые X — это Y .Некоторые Z являются Y . ∴ Некоторые Z имеют размер X . не является допустимой формой вывода, поскольку, хотя могут быть получены его примеры, в которых все посылки и заключение верны, могут быть также получены его примеры, в которых посылки истинны, но заключение ложно — например, (5) Каждый собака — млекопитающее. Некоторые крылатые существа — млекопитающие. ∴ Некоторые крылатые существа — собаки.
Формальная логика как исследование имеет дело с формами вывода, а не с их конкретными примерами.Одна из его задач — различать действительные и недействительные формы вывода, а также исследовать и систематизировать отношения, существующие между действительными.
Идея действительной формы вывода тесно связана с идеей действительной формы предложения. Форма предложения — это выражение, экземпляры которого (созданные, как и раньше, соответствующими и единообразными заменами переменных) не являются выводами из нескольких предложений к заключению, а скорее предложениями, взятыми индивидуально, а допустимая форма предложения — это форма, для которой все экземпляры истинные суждения. Простой пример: (6) Nothing одновременно является X и отличным от X . Формальная логика связана с формами предложений, а также с формами вывода. Фактически, изучение форм предложения может быть включено в исследование форм вывода следующим образом: пусть посылки любой данной формы вывода (вместе взятые) будут обозначены аббревиатурой альфа (α), а ее заключение — бета (β). . Тогда указанное выше условие действительности формы вывода «α, следовательно, β» сводится к утверждению, что ни один экземпляр формы высказывания «α и не-β» не является истинным — i.е., что каждый пример формы предложения (7) Не оба: α и не-β истинны — или эта строка (7), полностью прописанная, конечно, является действительной формой предложения. Однако изучение форм высказываний не может быть подобным образом приспособлено к изучению форм вывода, и поэтому из соображений полноты формальной логики принято рассматривать формальную логику как изучение форм высказываний. Поскольку работа логика с формами предложений во многом аналогична работе математика с числовыми формулами, системы, которые он конструирует, часто называют исчислениями.
Простой пример: (6) Nothing одновременно является X и отличным от X . Формальная логика связана с формами предложений, а также с формами вывода. Фактически, изучение форм предложения может быть включено в исследование форм вывода следующим образом: пусть посылки любой данной формы вывода (вместе взятые) будут обозначены аббревиатурой альфа (α), а ее заключение — бета (β). . Тогда указанное выше условие действительности формы вывода «α, следовательно, β» сводится к утверждению, что ни один экземпляр формы высказывания «α и не-β» не является истинным — i.е., что каждый пример формы предложения (7) Не оба: α и не-β истинны — или эта строка (7), полностью прописанная, конечно, является действительной формой предложения. Однако изучение форм высказываний не может быть подобным образом приспособлено к изучению форм вывода, и поэтому из соображений полноты формальной логики принято рассматривать формальную логику как изучение форм высказываний. Поскольку работа логика с формами предложений во многом аналогична работе математика с числовыми формулами, системы, которые он конструирует, часто называют исчислениями.
Большая часть работы логика происходит на более абстрактном уровне, чем в предыдущем обсуждении. Даже формула, такая как (3) выше, хотя и не относится к какому-либо конкретному предмету, но содержит такие выражения, как «каждый» и «является а», которые считаются имеющими определенное значение, а переменные предназначены для обозначения мест. для выражений одного вида (грубо говоря, нарицательные существительные или названия классов). Однако возможно — а для некоторых целей это необходимо — изучать формулы, не придавая им даже такой степени значимости.Построение системы логики, по сути, включает два различных процесса: первый состоит в создании символического аппарата — набора символов, правил их объединения в формулы и правил манипулирования этими формулами; второй заключается в придании этим символам и формулам определенного значения. Если выполняется только первое, система считается неинтерпретируемой или чисто формальной; если последнее также выполняется, система называется интерпретируемой. Это различие важно, потому что системы логики обладают определенными свойствами совершенно независимо от любых интерпретаций, которые могут быть им наложены.В качестве примера можно взять аксиоматическую систему логики, то есть систему, в которой определенные недоказанные формулы, известные как аксиомы, принимаются в качестве отправных точек, а дальнейшие формулы (теоремы) доказываются на их основе. Как будет показано позже ( см. Ниже Аксиоматизация ПК), вопрос о том, является ли последовательность формул в аксиоматической системе доказательством или нет, зависит исключительно от того, какие формулы принимаются в качестве аксиом и каковы правила вывода теорем из аксиом. , а вовсе не о том, что означают теоремы или аксиомы.Более того, данная неинтерпретируемая система в целом может быть одинаково хорошо интерпретирована множеством различных способов; следовательно, изучая неинтерпретируемую систему, изучается структура, которая является общей для множества интерпретируемых систем.
Это различие важно, потому что системы логики обладают определенными свойствами совершенно независимо от любых интерпретаций, которые могут быть им наложены.В качестве примера можно взять аксиоматическую систему логики, то есть систему, в которой определенные недоказанные формулы, известные как аксиомы, принимаются в качестве отправных точек, а дальнейшие формулы (теоремы) доказываются на их основе. Как будет показано позже ( см. Ниже Аксиоматизация ПК), вопрос о том, является ли последовательность формул в аксиоматической системе доказательством или нет, зависит исключительно от того, какие формулы принимаются в качестве аксиом и каковы правила вывода теорем из аксиом. , а вовсе не о том, что означают теоремы или аксиомы.Более того, данная неинтерпретируемая система в целом может быть одинаково хорошо интерпретирована множеством различных способов; следовательно, изучая неинтерпретируемую систему, изучается структура, которая является общей для множества интерпретируемых систем. Обычно логик, конструирующий чисто формальную систему, действительно имеет в виду конкретную интерпретацию, и его мотивом для построения этого является вера в то, что, когда ему дается такая интерпретация, формулы системы смогут выразить истинные принципы в некоторой области. мысли; но, среди прочего, по указанным выше причинам он обычно заботится о том, чтобы описать формулы и сформулировать правила системы без ссылки на интерпретацию и указать в качестве отдельного вопроса интерпретацию, которую он имеет в виду.
Обычно логик, конструирующий чисто формальную систему, действительно имеет в виду конкретную интерпретацию, и его мотивом для построения этого является вера в то, что, когда ему дается такая интерпретация, формулы системы смогут выразить истинные принципы в некоторой области. мысли; но, среди прочего, по указанным выше причинам он обычно заботится о том, чтобы описать формулы и сформулировать правила системы без ссылки на интерпретацию и указать в качестве отдельного вопроса интерпретацию, которую он имеет в виду.
Многие идеи, используемые при изложении формальной логики, включая некоторые из них, упомянутые выше, поднимают проблемы, относящиеся скорее к философии, чем к самой логике. Примеры: Каков правильный анализ понятия истины? Что такое суждение и как оно связано с предложением, которым оно выражено? Существуют ли какие-то здравые рассуждения, которые не являются ни дедуктивными, ни индуктивными? К счастью, можно научиться выполнять формальную логику, не получив удовлетворительных ответов на такие вопросы, точно так же, как можно заниматься математикой, не отвечая на вопросы, относящиеся к философии математики, такие как: являются ли числа реальными объектами или умственными конструкциями?
Формальная логика | Britannica
Формальная логика , абстрактное изучение предложений, утверждений или утвержденно используемых предложений и дедуктивных аргументов. Дисциплина абстрагируется от содержания этих элементов структур или логических форм, которые они воплощают. Логики обычно используют символические обозначения для четкого и недвусмысленного выражения таких структур, а также для упрощения манипуляций и проверок достоверности. Хотя в следующем обсуждении свободно используются технические обозначения современной символической логики, ее символы вводятся постепенно и с сопровождающими пояснениями, чтобы серьезный и внимательный читатель мог следить за развитием идей.
Дисциплина абстрагируется от содержания этих элементов структур или логических форм, которые они воплощают. Логики обычно используют символические обозначения для четкого и недвусмысленного выражения таких структур, а также для упрощения манипуляций и проверок достоверности. Хотя в следующем обсуждении свободно используются технические обозначения современной символической логики, ее символы вводятся постепенно и с сопровождающими пояснениями, чтобы серьезный и внимательный читатель мог следить за развитием идей.
Формальная логика — это априорное, а не эмпирическое исследование. В этом отношении он контрастирует с естественными науками и всеми другими дисциплинами, данные которых зависят от наблюдения. Его ближайшая аналогия — чистая математика; действительно, многие логики и чистые математики сочли бы свои соответствующие предметы неразличимыми или просто двумя ступенями одной и той же единой дисциплины. Поэтому формальную логику не следует путать с эмпирическим изучением процессов мышления, которое принадлежит психологии. Его также следует отличать от искусства правильного рассуждения, которое представляет собой практический навык применения логических принципов к конкретным случаям; и, что еще более резко, его следует отличать от искусства убеждения, в котором неверные аргументы иногда более эффективны, чем веские.
Его также следует отличать от искусства правильного рассуждения, которое представляет собой практический навык применения логических принципов к конкретным случаям; и, что еще более резко, его следует отличать от искусства убеждения, в котором неверные аргументы иногда более эффективны, чем веские.
Общие наблюдения
Вероятно, наиболее естественный подход к формальной логике основан на идее обоснованности аргумента, известного как дедуктивный. Дедуктивный аргумент можно грубо охарактеризовать как аргумент, в котором утверждается, что какое-то предложение (вывод) следует со строгой необходимостью из некоторого другого предложения или предложений (посылок) — i.е., что было бы непоследовательно или противоречиво утверждать посылки, но отрицать вывод.
Если дедуктивный аргумент должен преуспеть в установлении истинности его вывода, должны быть выполнены два совершенно разных условия: во-первых, вывод должен действительно следовать из посылок, т. Е. Вывод заключения из посылок должен быть логически правильным. — и, во-вторых, сами посылки должны быть верными. Аргумент, удовлетворяющий обоим этим условиям, называется обоснованным. Из этих двух условий логик как таковой занимается только первым; второй, определение истинности или ложности посылок, является задачей некой специальной дисциплины или общего наблюдения, соответствующего предмету аргументации.Когда вывод аргумента правильно выводится из его посылок, вывод из посылок к заключению считается (дедуктивно) достоверным, независимо от того, истинны ли посылки. Другие способы выразить тот факт, что вывод является дедуктивно достоверным, — это сказать, что истинность посылок дает (или дала бы) абсолютную гарантию истинности вывода или что это повлечет за собой логическую несогласованность (в отличие от простой ошибка факта), чтобы предположить, что посылки были верными, а вывод — ложным.
— и, во-вторых, сами посылки должны быть верными. Аргумент, удовлетворяющий обоим этим условиям, называется обоснованным. Из этих двух условий логик как таковой занимается только первым; второй, определение истинности или ложности посылок, является задачей некой специальной дисциплины или общего наблюдения, соответствующего предмету аргументации.Когда вывод аргумента правильно выводится из его посылок, вывод из посылок к заключению считается (дедуктивно) достоверным, независимо от того, истинны ли посылки. Другие способы выразить тот факт, что вывод является дедуктивно достоверным, — это сказать, что истинность посылок дает (или дала бы) абсолютную гарантию истинности вывода или что это повлечет за собой логическую несогласованность (в отличие от простой ошибка факта), чтобы предположить, что посылки были верными, а вывод — ложным.
Дедуктивные умозаключения, с которыми связана формальная логика, как следует из названия, имеют силу, действительность которых зависит не от каких-либо особенностей их предмета, а от их формы или структуры. Таким образом, два вывода: (1) Каждая собака — млекопитающее. Некоторые четвероногие — собаки. ∴ Некоторые четвероногие — млекопитающие. и (2) Каждый анархист верит в свободную любовь. Некоторые члены правительственной партии — анархисты.∴ Некоторые члены правительственной партии верят в свободную любовь. различаются по предмету и, следовательно, требуют различных процедур для проверки истинности или ложности своих предпосылок. Но их достоверность обеспечивается тем, что у них общего, а именно тем, что аргумент в каждом из них имеет форму (3) Каждые X — это Y . Некоторые Z имеют размер X . ∴ Некоторые Z являются Y .
Таким образом, два вывода: (1) Каждая собака — млекопитающее. Некоторые четвероногие — собаки. ∴ Некоторые четвероногие — млекопитающие. и (2) Каждый анархист верит в свободную любовь. Некоторые члены правительственной партии — анархисты.∴ Некоторые члены правительственной партии верят в свободную любовь. различаются по предмету и, следовательно, требуют различных процедур для проверки истинности или ложности своих предпосылок. Но их достоверность обеспечивается тем, что у них общего, а именно тем, что аргумент в каждом из них имеет форму (3) Каждые X — это Y . Некоторые Z имеют размер X . ∴ Некоторые Z являются Y .
Строка (3) выше может называться формой вывода, а (1) и (2) тогда являются экземплярами этой формы вывода.Буквы X , Y и Z в (3) обозначают места, в которые могут быть вставлены выражения определенного типа. Символы, используемые для этой цели, известны как переменные; их использование аналогично использованию x в алгебре, которое отмечает место, в которое может быть вставлено число. Экземпляр формы вывода создается путем замены всех переменных в ней подходящими выражениями (т.е., подставляя одно и то же выражение везде, где повторяется одна и та же переменная). Особенность (3), которая гарантирует, что каждый его экземпляр будет действительным, заключается в его построении таким образом, что каждый единообразный способ замены его переменных, чтобы сделать посылки истинными, автоматически делает и вывод истинным, или, другими словами, что ни один его пример не может иметь истинных посылок, кроме ложного заключения. В силу этой особенности форма (3) называется действительной формой вывода. Напротив, (4) Каждые X — это Y .Некоторые Z являются Y . ∴ Некоторые Z имеют размер X . не является допустимой формой вывода, поскольку, хотя могут быть получены его примеры, в которых все посылки и заключение верны, могут быть также получены его примеры, в которых посылки истинны, но заключение ложно — например, (5) Каждый собака — млекопитающее.
Экземпляр формы вывода создается путем замены всех переменных в ней подходящими выражениями (т.е., подставляя одно и то же выражение везде, где повторяется одна и та же переменная). Особенность (3), которая гарантирует, что каждый его экземпляр будет действительным, заключается в его построении таким образом, что каждый единообразный способ замены его переменных, чтобы сделать посылки истинными, автоматически делает и вывод истинным, или, другими словами, что ни один его пример не может иметь истинных посылок, кроме ложного заключения. В силу этой особенности форма (3) называется действительной формой вывода. Напротив, (4) Каждые X — это Y .Некоторые Z являются Y . ∴ Некоторые Z имеют размер X . не является допустимой формой вывода, поскольку, хотя могут быть получены его примеры, в которых все посылки и заключение верны, могут быть также получены его примеры, в которых посылки истинны, но заключение ложно — например, (5) Каждый собака — млекопитающее. Некоторые крылатые существа — млекопитающие. ∴ Некоторые крылатые существа — собаки.
Некоторые крылатые существа — млекопитающие. ∴ Некоторые крылатые существа — собаки.
Формальная логика как исследование имеет дело с формами вывода, а не с их конкретными примерами.Одна из его задач — различать действительные и недействительные формы вывода, а также исследовать и систематизировать отношения, существующие между действительными.
Идея действительной формы вывода тесно связана с идеей действительной формы предложения. Форма предложения — это выражение, экземпляры которого (созданные, как и раньше, соответствующими и единообразными заменами переменных) не являются выводами из нескольких предложений к заключению, а скорее предложениями, взятыми индивидуально, а допустимая форма предложения — это форма, для которой все экземпляры истинные суждения.Простой пример: (6) Nothing одновременно является X и отличным от X . Формальная логика связана с формами предложений, а также с формами вывода. Фактически, изучение форм предложения может быть включено в исследование форм вывода следующим образом: пусть посылки любой данной формы вывода (вместе взятые) будут обозначены аббревиатурой альфа (α), а ее заключение — бета (β). . Тогда указанное выше условие действительности формы вывода «α, следовательно, β» сводится к утверждению, что ни один экземпляр формы высказывания «α и не-β» не является истинным — i.е., что каждый пример формы предложения (7) Не оба: α и не-β истинны — или эта строка (7), полностью прописанная, конечно, является действительной формой предложения. Однако изучение форм высказываний не может быть подобным образом приспособлено к изучению форм вывода, и поэтому из соображений полноты формальной логики принято рассматривать формальную логику как изучение форм высказываний. Поскольку работа логика с формами предложений во многом аналогична работе математика с числовыми формулами, системы, которые он конструирует, часто называют исчислениями.
. Тогда указанное выше условие действительности формы вывода «α, следовательно, β» сводится к утверждению, что ни один экземпляр формы высказывания «α и не-β» не является истинным — i.е., что каждый пример формы предложения (7) Не оба: α и не-β истинны — или эта строка (7), полностью прописанная, конечно, является действительной формой предложения. Однако изучение форм высказываний не может быть подобным образом приспособлено к изучению форм вывода, и поэтому из соображений полноты формальной логики принято рассматривать формальную логику как изучение форм высказываний. Поскольку работа логика с формами предложений во многом аналогична работе математика с числовыми формулами, системы, которые он конструирует, часто называют исчислениями.
Большая часть работы логика происходит на более абстрактном уровне, чем в предыдущем обсуждении. Даже формула, такая как (3) выше, хотя и не относится к какому-либо конкретному предмету, но содержит такие выражения, как «каждый» и «является а», которые считаются имеющими определенное значение, а переменные предназначены для обозначения мест. для выражений одного вида (грубо говоря, нарицательные существительные или названия классов). Однако возможно — а для некоторых целей это необходимо — изучать формулы, не придавая им даже такой степени значимости.Построение системы логики, по сути, включает два различных процесса: первый состоит в создании символического аппарата — набора символов, правил их объединения в формулы и правил манипулирования этими формулами; второй заключается в придании этим символам и формулам определенного значения. Если выполняется только первое, система считается неинтерпретируемой или чисто формальной; если последнее также выполняется, система называется интерпретируемой. Это различие важно, потому что системы логики обладают определенными свойствами совершенно независимо от любых интерпретаций, которые могут быть им наложены.В качестве примера можно взять аксиоматическую систему логики, то есть систему, в которой определенные недоказанные формулы, известные как аксиомы, принимаются в качестве отправных точек, а дальнейшие формулы (теоремы) доказываются на их основе.
для выражений одного вида (грубо говоря, нарицательные существительные или названия классов). Однако возможно — а для некоторых целей это необходимо — изучать формулы, не придавая им даже такой степени значимости.Построение системы логики, по сути, включает два различных процесса: первый состоит в создании символического аппарата — набора символов, правил их объединения в формулы и правил манипулирования этими формулами; второй заключается в придании этим символам и формулам определенного значения. Если выполняется только первое, система считается неинтерпретируемой или чисто формальной; если последнее также выполняется, система называется интерпретируемой. Это различие важно, потому что системы логики обладают определенными свойствами совершенно независимо от любых интерпретаций, которые могут быть им наложены.В качестве примера можно взять аксиоматическую систему логики, то есть систему, в которой определенные недоказанные формулы, известные как аксиомы, принимаются в качестве отправных точек, а дальнейшие формулы (теоремы) доказываются на их основе. Как будет показано позже ( см. Ниже Аксиоматизация ПК), вопрос о том, является ли последовательность формул в аксиоматической системе доказательством или нет, зависит исключительно от того, какие формулы принимаются в качестве аксиом и каковы правила вывода теорем из аксиом. , а вовсе не о том, что означают теоремы или аксиомы.Более того, данная неинтерпретируемая система в целом может быть одинаково хорошо интерпретирована множеством различных способов; следовательно, изучая неинтерпретируемую систему, изучается структура, которая является общей для множества интерпретируемых систем. Обычно логик, конструирующий чисто формальную систему, действительно имеет в виду конкретную интерпретацию, и его мотивом для построения этого является вера в то, что, когда ему дается такая интерпретация, формулы системы смогут выразить истинные принципы в некоторой области. мысли; но, среди прочего, по указанным выше причинам он обычно заботится о том, чтобы описать формулы и сформулировать правила системы без ссылки на интерпретацию и указать в качестве отдельного вопроса интерпретацию, которую он имеет в виду.
Как будет показано позже ( см. Ниже Аксиоматизация ПК), вопрос о том, является ли последовательность формул в аксиоматической системе доказательством или нет, зависит исключительно от того, какие формулы принимаются в качестве аксиом и каковы правила вывода теорем из аксиом. , а вовсе не о том, что означают теоремы или аксиомы.Более того, данная неинтерпретируемая система в целом может быть одинаково хорошо интерпретирована множеством различных способов; следовательно, изучая неинтерпретируемую систему, изучается структура, которая является общей для множества интерпретируемых систем. Обычно логик, конструирующий чисто формальную систему, действительно имеет в виду конкретную интерпретацию, и его мотивом для построения этого является вера в то, что, когда ему дается такая интерпретация, формулы системы смогут выразить истинные принципы в некоторой области. мысли; но, среди прочего, по указанным выше причинам он обычно заботится о том, чтобы описать формулы и сформулировать правила системы без ссылки на интерпретацию и указать в качестве отдельного вопроса интерпретацию, которую он имеет в виду.
Многие идеи, используемые при изложении формальной логики, включая некоторые из них, упомянутые выше, поднимают проблемы, относящиеся скорее к философии, чем к самой логике. Примеры: Каков правильный анализ понятия истины? Что такое суждение и как оно связано с предложением, которым оно выражено? Существуют ли какие-то здравые рассуждения, которые не являются ни дедуктивными, ни индуктивными? К счастью, можно научиться выполнять формальную логику, не получив удовлетворительных ответов на такие вопросы, точно так же, как можно заниматься математикой, не отвечая на вопросы, относящиеся к философии математики, такие как: являются ли числа реальными объектами или умственными конструкциями?
Формальная логика | Britannica
Формальная логика , абстрактное изучение предложений, утверждений или утвержденно используемых предложений и дедуктивных аргументов.Дисциплина абстрагируется от содержания этих элементов структур или логических форм, которые они воплощают. Логики обычно используют символические обозначения для четкого и недвусмысленного выражения таких структур, а также для упрощения манипуляций и проверок достоверности. Хотя в следующем обсуждении свободно используются технические обозначения современной символической логики, ее символы вводятся постепенно и с сопровождающими пояснениями, чтобы серьезный и внимательный читатель мог следить за развитием идей.
Логики обычно используют символические обозначения для четкого и недвусмысленного выражения таких структур, а также для упрощения манипуляций и проверок достоверности. Хотя в следующем обсуждении свободно используются технические обозначения современной символической логики, ее символы вводятся постепенно и с сопровождающими пояснениями, чтобы серьезный и внимательный читатель мог следить за развитием идей.
Формальная логика — это априорное, а не эмпирическое исследование. В этом отношении он контрастирует с естественными науками и всеми другими дисциплинами, данные которых зависят от наблюдения. Его ближайшая аналогия — чистая математика; действительно, многие логики и чистые математики сочли бы свои соответствующие предметы неразличимыми или просто двумя ступенями одной и той же единой дисциплины. Поэтому формальную логику не следует путать с эмпирическим изучением процессов мышления, которое принадлежит психологии.Его также следует отличать от искусства правильного рассуждения, которое представляет собой практический навык применения логических принципов к конкретным случаям; и, что еще более резко, его следует отличать от искусства убеждения, в котором неверные аргументы иногда более эффективны, чем веские.
Общие наблюдения
Вероятно, наиболее естественный подход к формальной логике основан на идее обоснованности аргумента, известного как дедуктивный. Дедуктивный аргумент можно грубо охарактеризовать как аргумент, в котором утверждается, что какое-то предложение (вывод) следует со строгой необходимостью из некоторого другого предложения или предложений (посылок) — i.е., что было бы непоследовательно или противоречиво утверждать посылки, но отрицать вывод.
Если дедуктивный аргумент должен преуспеть в установлении истинности его вывода, должны быть выполнены два совершенно разных условия: во-первых, вывод должен действительно следовать из посылок, т. Е. Вывод заключения из посылок должен быть логически правильным. — и, во-вторых, сами посылки должны быть верными. Аргумент, удовлетворяющий обоим этим условиям, называется обоснованным. Из этих двух условий логик как таковой занимается только первым; второй, определение истинности или ложности посылок, является задачей некой специальной дисциплины или общего наблюдения, соответствующего предмету аргументации. Когда вывод аргумента правильно выводится из его посылок, вывод из посылок к заключению считается (дедуктивно) достоверным, независимо от того, истинны ли посылки. Другие способы выразить тот факт, что вывод является дедуктивно достоверным, — это сказать, что истинность посылок дает (или дала бы) абсолютную гарантию истинности вывода или что это повлечет за собой логическую несогласованность (в отличие от простой ошибка факта), чтобы предположить, что посылки были верными, а вывод — ложным.
Когда вывод аргумента правильно выводится из его посылок, вывод из посылок к заключению считается (дедуктивно) достоверным, независимо от того, истинны ли посылки. Другие способы выразить тот факт, что вывод является дедуктивно достоверным, — это сказать, что истинность посылок дает (или дала бы) абсолютную гарантию истинности вывода или что это повлечет за собой логическую несогласованность (в отличие от простой ошибка факта), чтобы предположить, что посылки были верными, а вывод — ложным.
Дедуктивные умозаключения, с которыми связана формальная логика, как следует из названия, имеют силу, действительность которых зависит не от каких-либо особенностей их предмета, а от их формы или структуры. Таким образом, два вывода: (1) Каждая собака — млекопитающее. Некоторые четвероногие — собаки. ∴ Некоторые четвероногие — млекопитающие. и (2) Каждый анархист верит в свободную любовь. Некоторые члены правительственной партии — анархисты. ∴ Некоторые члены правительственной партии верят в свободную любовь. различаются по предмету и, следовательно, требуют различных процедур для проверки истинности или ложности своих предпосылок. Но их достоверность обеспечивается тем, что у них общего, а именно тем, что аргумент в каждом из них имеет форму (3) Каждые X — это Y . Некоторые Z имеют размер X . ∴ Некоторые Z являются Y .
∴ Некоторые члены правительственной партии верят в свободную любовь. различаются по предмету и, следовательно, требуют различных процедур для проверки истинности или ложности своих предпосылок. Но их достоверность обеспечивается тем, что у них общего, а именно тем, что аргумент в каждом из них имеет форму (3) Каждые X — это Y . Некоторые Z имеют размер X . ∴ Некоторые Z являются Y .
Строка (3) выше может называться формой вывода, а (1) и (2) тогда являются экземплярами этой формы вывода.Буквы X , Y и Z в (3) обозначают места, в которые могут быть вставлены выражения определенного типа. Символы, используемые для этой цели, известны как переменные; их использование аналогично использованию x в алгебре, которое отмечает место, в которое может быть вставлено число. Экземпляр формы вывода создается путем замены всех переменных в ней подходящими выражениями (т.е., подставляя одно и то же выражение везде, где повторяется одна и та же переменная). Особенность (3), которая гарантирует, что каждый его экземпляр будет действительным, заключается в его построении таким образом, что каждый единообразный способ замены его переменных, чтобы сделать посылки истинными, автоматически делает и вывод истинным, или, другими словами, что ни один его пример не может иметь истинных посылок, кроме ложного заключения. В силу этой особенности форма (3) называется действительной формой вывода. Напротив, (4) Каждые X — это Y .Некоторые Z являются Y . ∴ Некоторые Z имеют размер X . не является допустимой формой вывода, поскольку, хотя могут быть получены его примеры, в которых все посылки и заключение верны, могут быть также получены его примеры, в которых посылки истинны, но заключение ложно — например, (5) Каждый собака — млекопитающее. Некоторые крылатые существа — млекопитающие. ∴ Некоторые крылатые существа — собаки.
Особенность (3), которая гарантирует, что каждый его экземпляр будет действительным, заключается в его построении таким образом, что каждый единообразный способ замены его переменных, чтобы сделать посылки истинными, автоматически делает и вывод истинным, или, другими словами, что ни один его пример не может иметь истинных посылок, кроме ложного заключения. В силу этой особенности форма (3) называется действительной формой вывода. Напротив, (4) Каждые X — это Y .Некоторые Z являются Y . ∴ Некоторые Z имеют размер X . не является допустимой формой вывода, поскольку, хотя могут быть получены его примеры, в которых все посылки и заключение верны, могут быть также получены его примеры, в которых посылки истинны, но заключение ложно — например, (5) Каждый собака — млекопитающее. Некоторые крылатые существа — млекопитающие. ∴ Некоторые крылатые существа — собаки.
Формальная логика как исследование имеет дело с формами вывода, а не с их конкретными примерами. Одна из его задач — различать действительные и недействительные формы вывода, а также исследовать и систематизировать отношения, существующие между действительными.
Одна из его задач — различать действительные и недействительные формы вывода, а также исследовать и систематизировать отношения, существующие между действительными.
Идея действительной формы вывода тесно связана с идеей действительной формы предложения. Форма предложения — это выражение, экземпляры которого (созданные, как и раньше, соответствующими и единообразными заменами переменных) не являются выводами из нескольких предложений к заключению, а скорее предложениями, взятыми индивидуально, а допустимая форма предложения — это форма, для которой все экземпляры истинные суждения.Простой пример: (6) Nothing одновременно является X и отличным от X . Формальная логика связана с формами предложений, а также с формами вывода. Фактически, изучение форм предложения может быть включено в исследование форм вывода следующим образом: пусть посылки любой данной формы вывода (вместе взятые) будут обозначены аббревиатурой альфа (α), а ее заключение — бета (β). . Тогда указанное выше условие действительности формы вывода «α, следовательно, β» сводится к утверждению, что ни один экземпляр формы высказывания «α и не-β» не является истинным — i. е., что каждый пример формы предложения (7) Не оба: α и не-β истинны — или эта строка (7), полностью прописанная, конечно, является действительной формой предложения. Однако изучение форм высказываний не может быть подобным образом приспособлено к изучению форм вывода, и поэтому из соображений полноты формальной логики принято рассматривать формальную логику как изучение форм высказываний. Поскольку работа логика с формами предложений во многом аналогична работе математика с числовыми формулами, системы, которые он конструирует, часто называют исчислениями.
е., что каждый пример формы предложения (7) Не оба: α и не-β истинны — или эта строка (7), полностью прописанная, конечно, является действительной формой предложения. Однако изучение форм высказываний не может быть подобным образом приспособлено к изучению форм вывода, и поэтому из соображений полноты формальной логики принято рассматривать формальную логику как изучение форм высказываний. Поскольку работа логика с формами предложений во многом аналогична работе математика с числовыми формулами, системы, которые он конструирует, часто называют исчислениями.
Большая часть работы логика происходит на более абстрактном уровне, чем в предыдущем обсуждении. Даже формула, такая как (3) выше, хотя и не относится к какому-либо конкретному предмету, но содержит такие выражения, как «каждый» и «является а», которые считаются имеющими определенное значение, а переменные предназначены для обозначения мест. для выражений одного вида (грубо говоря, нарицательные существительные или названия классов). Однако возможно — а для некоторых целей это необходимо — изучать формулы, не придавая им даже такой степени значимости.Построение системы логики, по сути, включает два различных процесса: первый состоит в создании символического аппарата — набора символов, правил их объединения в формулы и правил манипулирования этими формулами; второй заключается в придании этим символам и формулам определенного значения. Если выполняется только первое, система считается неинтерпретируемой или чисто формальной; если последнее также выполняется, система называется интерпретируемой. Это различие важно, потому что системы логики обладают определенными свойствами совершенно независимо от любых интерпретаций, которые могут быть им наложены.В качестве примера можно взять аксиоматическую систему логики, то есть систему, в которой определенные недоказанные формулы, известные как аксиомы, принимаются в качестве отправных точек, а дальнейшие формулы (теоремы) доказываются на их основе. Как будет показано позже ( см.
Однако возможно — а для некоторых целей это необходимо — изучать формулы, не придавая им даже такой степени значимости.Построение системы логики, по сути, включает два различных процесса: первый состоит в создании символического аппарата — набора символов, правил их объединения в формулы и правил манипулирования этими формулами; второй заключается в придании этим символам и формулам определенного значения. Если выполняется только первое, система считается неинтерпретируемой или чисто формальной; если последнее также выполняется, система называется интерпретируемой. Это различие важно, потому что системы логики обладают определенными свойствами совершенно независимо от любых интерпретаций, которые могут быть им наложены.В качестве примера можно взять аксиоматическую систему логики, то есть систему, в которой определенные недоказанные формулы, известные как аксиомы, принимаются в качестве отправных точек, а дальнейшие формулы (теоремы) доказываются на их основе. Как будет показано позже ( см. Ниже Аксиоматизация ПК), вопрос о том, является ли последовательность формул в аксиоматической системе доказательством или нет, зависит исключительно от того, какие формулы принимаются в качестве аксиом и каковы правила вывода теорем из аксиом. , а вовсе не о том, что означают теоремы или аксиомы.Более того, данная неинтерпретируемая система в целом может быть одинаково хорошо интерпретирована множеством различных способов; следовательно, изучая неинтерпретируемую систему, изучается структура, которая является общей для множества интерпретируемых систем. Обычно логик, конструирующий чисто формальную систему, действительно имеет в виду конкретную интерпретацию, и его мотивом для построения этого является вера в то, что, когда ему дается такая интерпретация, формулы системы смогут выразить истинные принципы в некоторой области. мысли; но, среди прочего, по указанным выше причинам он обычно заботится о том, чтобы описать формулы и сформулировать правила системы без ссылки на интерпретацию и указать в качестве отдельного вопроса интерпретацию, которую он имеет в виду.
Ниже Аксиоматизация ПК), вопрос о том, является ли последовательность формул в аксиоматической системе доказательством или нет, зависит исключительно от того, какие формулы принимаются в качестве аксиом и каковы правила вывода теорем из аксиом. , а вовсе не о том, что означают теоремы или аксиомы.Более того, данная неинтерпретируемая система в целом может быть одинаково хорошо интерпретирована множеством различных способов; следовательно, изучая неинтерпретируемую систему, изучается структура, которая является общей для множества интерпретируемых систем. Обычно логик, конструирующий чисто формальную систему, действительно имеет в виду конкретную интерпретацию, и его мотивом для построения этого является вера в то, что, когда ему дается такая интерпретация, формулы системы смогут выразить истинные принципы в некоторой области. мысли; но, среди прочего, по указанным выше причинам он обычно заботится о том, чтобы описать формулы и сформулировать правила системы без ссылки на интерпретацию и указать в качестве отдельного вопроса интерпретацию, которую он имеет в виду.
Многие идеи, используемые при изложении формальной логики, включая некоторые из них, упомянутые выше, поднимают проблемы, относящиеся скорее к философии, чем к самой логике. Примеры: Каков правильный анализ понятия истины? Что такое суждение и как оно связано с предложением, которым оно выражено? Существуют ли какие-то здравые рассуждения, которые не являются ни дедуктивными, ни индуктивными? К счастью, можно научиться выполнять формальную логику, не получив удовлетворительных ответов на такие вопросы, точно так же, как можно заниматься математикой, не отвечая на вопросы, относящиеся к философии математики, такие как: являются ли числа реальными объектами или умственными конструкциями?
Формальная логика | Britannica
Формальная логика , абстрактное изучение предложений, утверждений или утвержденно используемых предложений и дедуктивных аргументов.Дисциплина абстрагируется от содержания этих элементов структур или логических форм, которые они воплощают. Логики обычно используют символические обозначения для четкого и недвусмысленного выражения таких структур, а также для упрощения манипуляций и проверок достоверности. Хотя в следующем обсуждении свободно используются технические обозначения современной символической логики, ее символы вводятся постепенно и с сопровождающими пояснениями, чтобы серьезный и внимательный читатель мог следить за развитием идей.
Логики обычно используют символические обозначения для четкого и недвусмысленного выражения таких структур, а также для упрощения манипуляций и проверок достоверности. Хотя в следующем обсуждении свободно используются технические обозначения современной символической логики, ее символы вводятся постепенно и с сопровождающими пояснениями, чтобы серьезный и внимательный читатель мог следить за развитием идей.
Формальная логика — это априорное, а не эмпирическое исследование. В этом отношении он контрастирует с естественными науками и всеми другими дисциплинами, данные которых зависят от наблюдения. Его ближайшая аналогия — чистая математика; действительно, многие логики и чистые математики сочли бы свои соответствующие предметы неразличимыми или просто двумя ступенями одной и той же единой дисциплины. Поэтому формальную логику не следует путать с эмпирическим изучением процессов мышления, которое принадлежит психологии.Его также следует отличать от искусства правильного рассуждения, которое представляет собой практический навык применения логических принципов к конкретным случаям; и, что еще более резко, его следует отличать от искусства убеждения, в котором неверные аргументы иногда более эффективны, чем веские.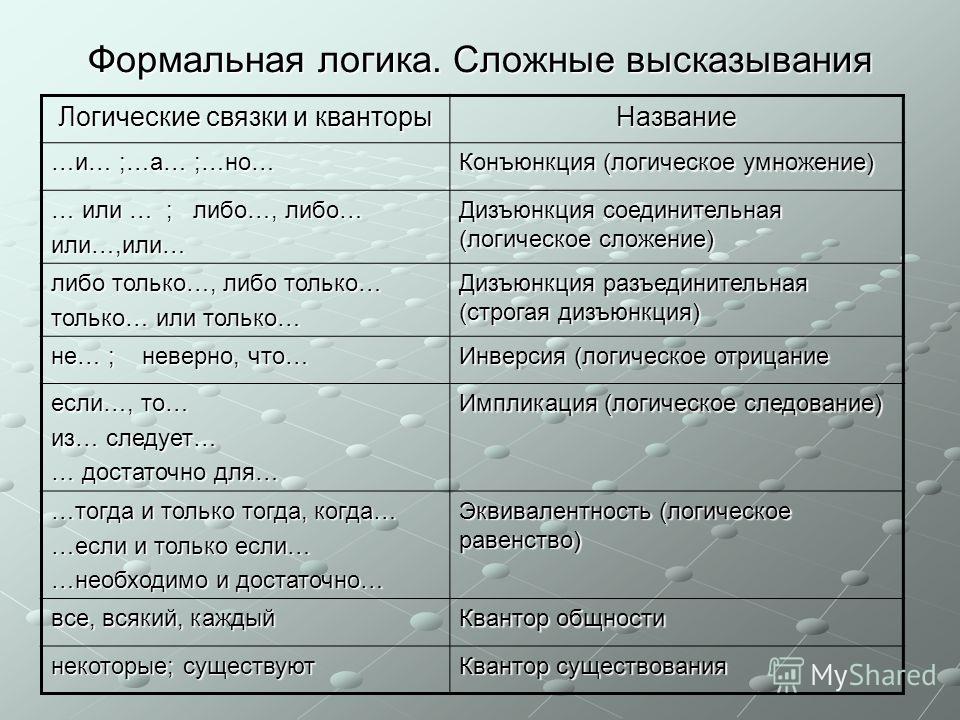
Общие наблюдения
Вероятно, наиболее естественный подход к формальной логике основан на идее обоснованности аргумента, известного как дедуктивный. Дедуктивный аргумент можно грубо охарактеризовать как аргумент, в котором утверждается, что какое-то предложение (вывод) следует со строгой необходимостью из некоторого другого предложения или предложений (посылок) — i.е., что было бы непоследовательно или противоречиво утверждать посылки, но отрицать вывод.
Если дедуктивный аргумент должен преуспеть в установлении истинности его вывода, должны быть выполнены два совершенно разных условия: во-первых, вывод должен действительно следовать из посылок, т. Е. Вывод заключения из посылок должен быть логически правильным. — и, во-вторых, сами посылки должны быть верными. Аргумент, удовлетворяющий обоим этим условиям, называется обоснованным. Из этих двух условий логик как таковой занимается только первым; второй, определение истинности или ложности посылок, является задачей некой специальной дисциплины или общего наблюдения, соответствующего предмету аргументации. Когда вывод аргумента правильно выводится из его посылок, вывод из посылок к заключению считается (дедуктивно) достоверным, независимо от того, истинны ли посылки. Другие способы выразить тот факт, что вывод является дедуктивно достоверным, — это сказать, что истинность посылок дает (или дала бы) абсолютную гарантию истинности вывода или что это повлечет за собой логическую несогласованность (в отличие от простой ошибка факта), чтобы предположить, что посылки были верными, а вывод — ложным.
Когда вывод аргумента правильно выводится из его посылок, вывод из посылок к заключению считается (дедуктивно) достоверным, независимо от того, истинны ли посылки. Другие способы выразить тот факт, что вывод является дедуктивно достоверным, — это сказать, что истинность посылок дает (или дала бы) абсолютную гарантию истинности вывода или что это повлечет за собой логическую несогласованность (в отличие от простой ошибка факта), чтобы предположить, что посылки были верными, а вывод — ложным.
Дедуктивные умозаключения, с которыми связана формальная логика, как следует из названия, имеют силу, действительность которых зависит не от каких-либо особенностей их предмета, а от их формы или структуры. Таким образом, два вывода: (1) Каждая собака — млекопитающее. Некоторые четвероногие — собаки. ∴ Некоторые четвероногие — млекопитающие. и (2) Каждый анархист верит в свободную любовь. Некоторые члены правительственной партии — анархисты. ∴ Некоторые члены правительственной партии верят в свободную любовь. различаются по предмету и, следовательно, требуют различных процедур для проверки истинности или ложности своих предпосылок. Но их достоверность обеспечивается тем, что у них общего, а именно тем, что аргумент в каждом из них имеет форму (3) Каждые X — это Y . Некоторые Z имеют размер X . ∴ Некоторые Z являются Y .
∴ Некоторые члены правительственной партии верят в свободную любовь. различаются по предмету и, следовательно, требуют различных процедур для проверки истинности или ложности своих предпосылок. Но их достоверность обеспечивается тем, что у них общего, а именно тем, что аргумент в каждом из них имеет форму (3) Каждые X — это Y . Некоторые Z имеют размер X . ∴ Некоторые Z являются Y .
Строка (3) выше может называться формой вывода, а (1) и (2) тогда являются экземплярами этой формы вывода.Буквы X , Y и Z в (3) обозначают места, в которые могут быть вставлены выражения определенного типа. Символы, используемые для этой цели, известны как переменные; их использование аналогично использованию x в алгебре, которое отмечает место, в которое может быть вставлено число. Экземпляр формы вывода создается путем замены всех переменных в ней подходящими выражениями (т.е., подставляя одно и то же выражение везде, где повторяется одна и та же переменная). Особенность (3), которая гарантирует, что каждый его экземпляр будет действительным, заключается в его построении таким образом, что каждый единообразный способ замены его переменных, чтобы сделать посылки истинными, автоматически делает и вывод истинным, или, другими словами, что ни один его пример не может иметь истинных посылок, кроме ложного заключения. В силу этой особенности форма (3) называется действительной формой вывода. Напротив, (4) Каждые X — это Y .Некоторые Z являются Y . ∴ Некоторые Z имеют размер X . не является допустимой формой вывода, поскольку, хотя могут быть получены его примеры, в которых все посылки и заключение верны, могут быть также получены его примеры, в которых посылки истинны, но заключение ложно — например, (5) Каждый собака — млекопитающее. Некоторые крылатые существа — млекопитающие. ∴ Некоторые крылатые существа — собаки.
Особенность (3), которая гарантирует, что каждый его экземпляр будет действительным, заключается в его построении таким образом, что каждый единообразный способ замены его переменных, чтобы сделать посылки истинными, автоматически делает и вывод истинным, или, другими словами, что ни один его пример не может иметь истинных посылок, кроме ложного заключения. В силу этой особенности форма (3) называется действительной формой вывода. Напротив, (4) Каждые X — это Y .Некоторые Z являются Y . ∴ Некоторые Z имеют размер X . не является допустимой формой вывода, поскольку, хотя могут быть получены его примеры, в которых все посылки и заключение верны, могут быть также получены его примеры, в которых посылки истинны, но заключение ложно — например, (5) Каждый собака — млекопитающее. Некоторые крылатые существа — млекопитающие. ∴ Некоторые крылатые существа — собаки.
Формальная логика как исследование имеет дело с формами вывода, а не с их конкретными примерами. Одна из его задач — различать действительные и недействительные формы вывода, а также исследовать и систематизировать отношения, существующие между действительными.
Одна из его задач — различать действительные и недействительные формы вывода, а также исследовать и систематизировать отношения, существующие между действительными.
Идея действительной формы вывода тесно связана с идеей действительной формы предложения. Форма предложения — это выражение, экземпляры которого (созданные, как и раньше, соответствующими и единообразными заменами переменных) не являются выводами из нескольких предложений к заключению, а скорее предложениями, взятыми индивидуально, а допустимая форма предложения — это форма, для которой все экземпляры истинные суждения.Простой пример: (6) Nothing одновременно является X и отличным от X . Формальная логика связана с формами предложений, а также с формами вывода. Фактически, изучение форм предложения может быть включено в исследование форм вывода следующим образом: пусть посылки любой данной формы вывода (вместе взятые) будут обозначены аббревиатурой альфа (α), а ее заключение — бета (β). . Тогда указанное выше условие действительности формы вывода «α, следовательно, β» сводится к утверждению, что ни один экземпляр формы высказывания «α и не-β» не является истинным — i. е., что каждый пример формы предложения (7) Не оба: α и не-β истинны — или эта строка (7), полностью прописанная, конечно, является действительной формой предложения. Однако изучение форм высказываний не может быть подобным образом приспособлено к изучению форм вывода, и поэтому из соображений полноты формальной логики принято рассматривать формальную логику как изучение форм высказываний. Поскольку работа логика с формами предложений во многом аналогична работе математика с числовыми формулами, системы, которые он конструирует, часто называют исчислениями.
е., что каждый пример формы предложения (7) Не оба: α и не-β истинны — или эта строка (7), полностью прописанная, конечно, является действительной формой предложения. Однако изучение форм высказываний не может быть подобным образом приспособлено к изучению форм вывода, и поэтому из соображений полноты формальной логики принято рассматривать формальную логику как изучение форм высказываний. Поскольку работа логика с формами предложений во многом аналогична работе математика с числовыми формулами, системы, которые он конструирует, часто называют исчислениями.
Большая часть работы логика происходит на более абстрактном уровне, чем в предыдущем обсуждении. Даже формула, такая как (3) выше, хотя и не относится к какому-либо конкретному предмету, но содержит такие выражения, как «каждый» и «является а», которые считаются имеющими определенное значение, а переменные предназначены для обозначения мест. для выражений одного вида (грубо говоря, нарицательные существительные или названия классов). Однако возможно — а для некоторых целей это необходимо — изучать формулы, не придавая им даже такой степени значимости.Построение системы логики, по сути, включает два различных процесса: первый состоит в создании символического аппарата — набора символов, правил их объединения в формулы и правил манипулирования этими формулами; второй заключается в придании этим символам и формулам определенного значения. Если выполняется только первое, система считается неинтерпретируемой или чисто формальной; если последнее также выполняется, система называется интерпретируемой. Это различие важно, потому что системы логики обладают определенными свойствами совершенно независимо от любых интерпретаций, которые могут быть им наложены.В качестве примера можно взять аксиоматическую систему логики, то есть систему, в которой определенные недоказанные формулы, известные как аксиомы, принимаются в качестве отправных точек, а дальнейшие формулы (теоремы) доказываются на их основе. Как будет показано позже ( см. Ниже Аксиоматизация ПК), вопрос о том, является ли последовательность формул в аксиоматической системе доказательством или нет, зависит исключительно от того, какие формулы принимаются в качестве аксиом и каковы правила вывода теорем из аксиом. , а вовсе не о том, что означают теоремы или аксиомы.Более того, данная неинтерпретируемая система в целом может быть одинаково хорошо интерпретирована множеством различных способов; следовательно, изучая неинтерпретируемую систему, изучается структура, которая является общей для множества интерпретируемых систем. Обычно логик, конструирующий чисто формальную систему, действительно имеет в виду конкретную интерпретацию, и его мотивом для построения этого является вера в то, что, когда ему дается такая интерпретация, формулы системы смогут выразить истинные принципы в некоторой области. мысли; но, среди прочего, по указанным выше причинам он обычно заботится о том, чтобы описать формулы и сформулировать правила системы без ссылки на интерпретацию и указать в качестве отдельного вопроса интерпретацию, которую он имеет в виду.
Однако возможно — а для некоторых целей это необходимо — изучать формулы, не придавая им даже такой степени значимости.Построение системы логики, по сути, включает два различных процесса: первый состоит в создании символического аппарата — набора символов, правил их объединения в формулы и правил манипулирования этими формулами; второй заключается в придании этим символам и формулам определенного значения. Если выполняется только первое, система считается неинтерпретируемой или чисто формальной; если последнее также выполняется, система называется интерпретируемой. Это различие важно, потому что системы логики обладают определенными свойствами совершенно независимо от любых интерпретаций, которые могут быть им наложены.В качестве примера можно взять аксиоматическую систему логики, то есть систему, в которой определенные недоказанные формулы, известные как аксиомы, принимаются в качестве отправных точек, а дальнейшие формулы (теоремы) доказываются на их основе. Как будет показано позже ( см. Ниже Аксиоматизация ПК), вопрос о том, является ли последовательность формул в аксиоматической системе доказательством или нет, зависит исключительно от того, какие формулы принимаются в качестве аксиом и каковы правила вывода теорем из аксиом. , а вовсе не о том, что означают теоремы или аксиомы.Более того, данная неинтерпретируемая система в целом может быть одинаково хорошо интерпретирована множеством различных способов; следовательно, изучая неинтерпретируемую систему, изучается структура, которая является общей для множества интерпретируемых систем. Обычно логик, конструирующий чисто формальную систему, действительно имеет в виду конкретную интерпретацию, и его мотивом для построения этого является вера в то, что, когда ему дается такая интерпретация, формулы системы смогут выразить истинные принципы в некоторой области. мысли; но, среди прочего, по указанным выше причинам он обычно заботится о том, чтобы описать формулы и сформулировать правила системы без ссылки на интерпретацию и указать в качестве отдельного вопроса интерпретацию, которую он имеет в виду.
Многие идеи, используемые при изложении формальной логики, включая некоторые из них, упомянутые выше, поднимают проблемы, относящиеся скорее к философии, чем к самой логике. Примеры: Каков правильный анализ понятия истины? Что такое суждение и как оно связано с предложением, которым оно выражено? Существуют ли какие-то здравые рассуждения, которые не являются ни дедуктивными, ни индуктивными? К счастью, можно научиться выполнять формальную логику, не получив удовлетворительных ответов на такие вопросы, точно так же, как можно заниматься математикой, не отвечая на вопросы, относящиеся к философии математики, такие как: являются ли числа реальными объектами или умственными конструкциями?
Формальная логика | Britannica
Формальная логика , абстрактное изучение предложений, утверждений или утвержденно используемых предложений и дедуктивных аргументов.Дисциплина абстрагируется от содержания этих элементов структур или логических форм, которые они воплощают. Логики обычно используют символические обозначения для четкого и недвусмысленного выражения таких структур, а также для упрощения манипуляций и проверок достоверности. Хотя в следующем обсуждении свободно используются технические обозначения современной символической логики, ее символы вводятся постепенно и с сопровождающими пояснениями, чтобы серьезный и внимательный читатель мог следить за развитием идей.
Формальная логика — это априорное, а не эмпирическое исследование. В этом отношении он контрастирует с естественными науками и всеми другими дисциплинами, данные которых зависят от наблюдения. Его ближайшая аналогия — чистая математика; действительно, многие логики и чистые математики сочли бы свои соответствующие предметы неразличимыми или просто двумя ступенями одной и той же единой дисциплины. Поэтому формальную логику не следует путать с эмпирическим изучением процессов мышления, которое принадлежит психологии.Его также следует отличать от искусства правильного рассуждения, которое представляет собой практический навык применения логических принципов к конкретным случаям; и, что еще более резко, его следует отличать от искусства убеждения, в котором неверные аргументы иногда более эффективны, чем веские.
Общие наблюдения
Вероятно, наиболее естественный подход к формальной логике основан на идее обоснованности аргумента, известного как дедуктивный. Дедуктивный аргумент можно грубо охарактеризовать как аргумент, в котором утверждается, что какое-то предложение (вывод) следует со строгой необходимостью из некоторого другого предложения или предложений (посылок) — i.е., что было бы непоследовательно или противоречиво утверждать посылки, но отрицать вывод.
Если дедуктивный аргумент должен преуспеть в установлении истинности его вывода, должны быть выполнены два совершенно разных условия: во-первых, вывод должен действительно следовать из посылок, т. Е. Вывод заключения из посылок должен быть логически правильным. — и, во-вторых, сами посылки должны быть верными. Аргумент, удовлетворяющий обоим этим условиям, называется обоснованным. Из этих двух условий логик как таковой занимается только первым; второй, определение истинности или ложности посылок, является задачей некой специальной дисциплины или общего наблюдения, соответствующего предмету аргументации.Когда вывод аргумента правильно выводится из его посылок, вывод из посылок к заключению считается (дедуктивно) достоверным, независимо от того, истинны ли посылки. Другие способы выразить тот факт, что вывод является дедуктивно достоверным, — это сказать, что истинность посылок дает (или дала бы) абсолютную гарантию истинности вывода или что это повлечет за собой логическую несогласованность (в отличие от простой ошибка факта), чтобы предположить, что посылки были верными, а вывод — ложным.
Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчасДедуктивные умозаключения, с которыми связана формальная логика, как следует из названия, имеют силу, действительность которых зависит не от каких-либо особенностей их предмета, а от их формы или структуры. Таким образом, два вывода: (1) Каждая собака — млекопитающее. Некоторые четвероногие — собаки. ∴ Некоторые четвероногие — млекопитающие. и (2) Каждый анархист верит в свободную любовь. Некоторые члены правительственной партии — анархисты.∴ Некоторые члены правительственной партии верят в свободную любовь. различаются по предмету и, следовательно, требуют различных процедур для проверки истинности или ложности своих предпосылок. Но их достоверность обеспечивается тем, что у них общего, а именно тем, что аргумент в каждом из них имеет форму (3) Каждые X — это Y . Некоторые Z имеют размер X . ∴ Некоторые Z являются Y .
Строка (3) выше может называться формой вывода, а (1) и (2) тогда являются экземплярами этой формы вывода.Буквы X , Y и Z в (3) обозначают места, в которые могут быть вставлены выражения определенного типа. Символы, используемые для этой цели, известны как переменные; их использование аналогично использованию x в алгебре, которое отмечает место, в которое может быть вставлено число. Экземпляр формы вывода создается путем замены всех переменных в ней подходящими выражениями (т.е., подставляя одно и то же выражение везде, где повторяется одна и та же переменная). Особенность (3), которая гарантирует, что каждый его экземпляр будет действительным, заключается в его построении таким образом, что каждый единообразный способ замены его переменных, чтобы сделать посылки истинными, автоматически делает и вывод истинным, или, другими словами, что ни один его пример не может иметь истинных посылок, кроме ложного заключения. В силу этой особенности форма (3) называется действительной формой вывода. Напротив, (4) Каждые X — это Y .Некоторые Z являются Y . ∴ Некоторые Z имеют размер X . не является допустимой формой вывода, поскольку, хотя могут быть получены его примеры, в которых все посылки и заключение верны, могут быть также получены его примеры, в которых посылки истинны, но заключение ложно — например, (5) Каждый собака — млекопитающее. Некоторые крылатые существа — млекопитающие. ∴ Некоторые крылатые существа — собаки.
Формальная логика как исследование имеет дело с формами вывода, а не с их конкретными примерами.Одна из его задач — различать действительные и недействительные формы вывода, а также исследовать и систематизировать отношения, существующие между действительными.
Идея действительной формы вывода тесно связана с идеей действительной формы предложения. Форма предложения — это выражение, экземпляры которого (созданные, как и раньше, соответствующими и единообразными заменами переменных) не являются выводами из нескольких предложений к заключению, а скорее предложениями, взятыми индивидуально, а допустимая форма предложения — это форма, для которой все экземпляры истинные суждения.Простой пример: (6) Nothing одновременно является X и отличным от X . Формальная логика связана с формами предложений, а также с формами вывода. Фактически, изучение форм предложения может быть включено в исследование форм вывода следующим образом: пусть посылки любой данной формы вывода (вместе взятые) будут обозначены аббревиатурой альфа (α), а ее заключение — бета (β). . Тогда указанное выше условие действительности формы вывода «α, следовательно, β» сводится к утверждению, что ни один экземпляр формы высказывания «α и не-β» не является истинным — i.е., что каждый пример формы предложения (7) Не оба: α и не-β истинны — или эта строка (7), полностью прописанная, конечно, является действительной формой предложения. Однако изучение форм высказываний не может быть подобным образом приспособлено к изучению форм вывода, и поэтому из соображений полноты формальной логики принято рассматривать формальную логику как изучение форм высказываний. Поскольку работа логика с формами предложений во многом аналогична работе математика с числовыми формулами, системы, которые он конструирует, часто называют исчислениями.
Большая часть работы логика происходит на более абстрактном уровне, чем в предыдущем обсуждении. Даже формула, такая как (3) выше, хотя и не относится к какому-либо конкретному предмету, но содержит такие выражения, как «каждый» и «является а», которые считаются имеющими определенное значение, а переменные предназначены для обозначения мест. для выражений одного вида (грубо говоря, нарицательные существительные или названия классов). Однако возможно — а для некоторых целей это необходимо — изучать формулы, не придавая им даже такой степени значимости.Построение системы логики, по сути, включает два различных процесса: первый состоит в создании символического аппарата — набора символов, правил их объединения в формулы и правил манипулирования этими формулами; второй заключается в придании этим символам и формулам определенного значения. Если выполняется только первое, система считается неинтерпретируемой или чисто формальной; если последнее также выполняется, система называется интерпретируемой. Это различие важно, потому что системы логики обладают определенными свойствами совершенно независимо от любых интерпретаций, которые могут быть им наложены.В качестве примера можно взять аксиоматическую систему логики, то есть систему, в которой определенные недоказанные формулы, известные как аксиомы, принимаются в качестве отправных точек, а дальнейшие формулы (теоремы) доказываются на их основе. Как будет показано позже ( см. Ниже Аксиоматизация ПК), вопрос о том, является ли последовательность формул в аксиоматической системе доказательством или нет, зависит исключительно от того, какие формулы принимаются в качестве аксиом и каковы правила вывода теорем из аксиом. , а вовсе не о том, что означают теоремы или аксиомы.Более того, данная неинтерпретируемая система в целом может быть одинаково хорошо интерпретирована множеством различных способов; следовательно, изучая неинтерпретируемую систему, изучается структура, которая является общей для множества интерпретируемых систем. Обычно логик, конструирующий чисто формальную систему, действительно имеет в виду конкретную интерпретацию, и его мотивом для построения этого является вера в то, что, когда ему дается такая интерпретация, формулы системы смогут выразить истинные принципы в некоторой области. мысли; но, среди прочего, по указанным выше причинам он обычно заботится о том, чтобы описать формулы и сформулировать правила системы без ссылки на интерпретацию и указать в качестве отдельного вопроса интерпретацию, которую он имеет в виду.
Многие идеи, используемые при изложении формальной логики, включая некоторые из них, упомянутые выше, поднимают проблемы, относящиеся скорее к философии, чем к самой логике. Примеры: Каков правильный анализ понятия истины? Что такое суждение и как оно связано с предложением, которым оно выражено? Существуют ли какие-то здравые рассуждения, которые не являются ни дедуктивными, ни индуктивными? К счастью, можно научиться выполнять формальную логику, не получив удовлетворительных ответов на такие вопросы, точно так же, как можно заниматься математикой, не отвечая на вопросы, относящиеся к философии математики, такие как: являются ли числа реальными объектами или умственными конструкциями?
Formal Logic — Broadview Press
Формальная логика — это текст для бакалавриата, подходящий для вводных, промежуточных и продвинутых курсов по символической логике.Девять глав книги предлагают исчерпывающее освещение функциональной и количественной логики истинности, а также основ более сложных тем, таких как теория множеств и модальная логика. Сложные идеи объясняются простым языком, который не предполагает какого-либо знания в области логики или математики, а стратегии вывода проиллюстрированы многочисленными примерами. Переводам, таблицам, деревьям, естественной дедукции и простым мета-доказательствам можно научиться с помощью более 400 упражнений. Сопутствующий веб-сайт предлагает дополнительное программное обеспечение для практики и обучающие видеоролики.
Комментарии
“ Formal Logic — ясный, доступный и интуитивно понятный, но он также точный, ясный и исчерпывающий. Сложные и часто сбивающие с толку концепции раскрываются в серьезной и прямой манере с забавной и демистифицирующей терминологией и полезными аналогиями. Это педагогическая жемчужина ». — Мэри Кейт Макгоуэн, колледж Уэллсли
«Это отличный вводный текст по символической логике. Он доступен, с ясными и краткими объяснениями ключевых понятий, а также с множеством полезных примеров и практических задач, но также достаточно строг, чтобы подготовить студентов ко второму курсу логики; действительно, я не знаю ни одной книги, в которой бы лучше сочетались эти достоинства.Я с нетерпением жду возможности использовать Formal Logic в своих курсах ». — Кевин Моррис, Тулейнский университет
«Эта книга делает идеи логики высказываний, логики предикатов и формального доказательства легко доступными, переходя непосредственно к сути каждого из них на естественном, нетехническом языке. Лаконично, но никогда не торопился. Он получает детали правильно, не сосредотачиваясь на них как на деталях, а благодаря ясному пониманию того, почему они такие, какие они есть ». — Колин Макларти, Западный резервный университет Кейса.
«Формальная логика Пола Грегори заслуживает внимательного рассмотрения любому, кто принимает новый логический текст.Включение глав по теории множеств и модальной логике делает его ценным ресурсом для студентов, которые хотят выйти за рамки стандартного введения в логику ». — Майкл Хикс, Университет Майами
I: Неформальные понятия
1: Неформальное введение
II: Истинно-функциональная логика
2: Язык S
3: Формальная семантика для S
- 3.1 Присвоение истинных значений и таблицы истинности
3.2 семантические свойства отдельных WFF3.3 Семантические свойства наборов WFF
3.4 Семантические свойства, их взаимосвязь и простая металогика
3.5 Деревья истины
- 3.5.1 Тесты с деревьями истины
3.5.2 Упражнения3.6 Глоссарий глав
4: SD: Естественное вычитание в S
- 4.1 Основная идея
- 4.1.1 Повторение
4.1.2 Правила клина
4.1.3 Правила стрелок
4.1.4 Правила хуков
4.1.5 Правила Vee
4.1.6 Правила двойной стрелки
4.1.7 Упражнения4.2 Выводы: стратегии и примечания
4.3 Теория доказательств в SD4,4 SDE , расширение до SD
- 4.4.1 Правила вывода SDE
4.4.2 Упражнения
4.4.3 Правила замены SDE
4.4.4 Упражнения4.5 Глоссарий глав
III: Количественная логика
5: Язык P
6: Формальная семантика для P
- 6.1 Семантика и интерпретация
- 6.1.1 Основы интерпретаций
6.1.2 Интерлюдия: немного теории множеств
6.1.3 Формальная интерпретация P
6.1.4 Построение интерпретаций6.2 Семантические свойства отдельных WFF
6.3 Семантические свойства наборов WFF
6.4 Объем и распределение квантора
6.5 Свойства отношений
6.6 Глоссарий глав
7: PD: естественное удержание в
песо- 7.1 Правила вывода квантификаторов
- 7.1.1 Универсальное исключение
7.1.2 Экзистенциальное исключение
7.1.3 Универсальное введение
7.1.4 Экзистенциальное исключение
7.1.5 Упражнения7.2 Выводы: стратегии и примечания
7.3 Теория доказательств в PD7.4 PDE, расширение PD
- 7.4.1 Отрицание квантора
7.4.2 Упражнения7.4 Глоссарий глав
IV: Расширенные темы
8: Базовая теория множеств, парадокс и бесконечность
- 8.1 Основы множеств
8.2 Парадокс Рассела
8.3 Схема аксиом разделения
8.4 Подмножество, пересечение, объединение, различие8.5 Пары, упорядоченные пары, наборы степеней, отношения и функции
8.6 Бесконечные множества и доказательство Кантора8.7 Глоссарий глав
9: Модальная логика
V: Приложения
A: Ответы на упражнения
B: Глоссарий
C: Таблицы истинности, древовидные правила и правила вывода
- C.1 Таблицы истинности характеристик
C.2 правила дерева истинности для S
C.3 Система деривации SD
C.4 Система деривации SDE
C.5 Система деривации PD
Пол А. Грегори — адъюнкт-профессор и глава философии в Университете Вашингтона и Ли.
Formal Logic имеет два дополнительных веб-сайта: один для студентов и один для преподавателей.
Студенческий веб-сайт содержит средство проверки для языка SD, обсуждаемого в книге, а также серию видеоуроков.Бесплатный код доступа к этому веб-сайту прилагается ко всем новым копиям Formal Logic . Если вы приобрели бывшую в употреблении копию, вы можете получить доступ за символическую плату здесь.
На веб-сайте инструктора есть набор дополнительных вопросов, связанных с главами 1-7 книги Formal Logic .
Чтобы просмотреть образец главы Formal Logic , щелкните здесь. (Открывается в формате PDF.)
Формальная логика — обзор
One: Inferences in Science
Логика Милля подверглась критике со стороны британских идеальных философов в конце XIX — начале XX века.Ф. Х. Брэдли и Бернар Бозанке написали книги по логике, в которых пытались опровергнуть Милля.
Они критиковали почти все аспекты философии Милля и все аспекты его логики. В их глазах Милль мало что мог сделать из того, что было правильным. Среди прочего, они критиковали рассуждения Милля о дизъюнкции и дизъюнктивном силлогизме, а следовательно, и о той роли, которую Милль приписывал отрицательным примерам в научном методе. В частности, они утверждали, что формальная логика сама по себе не может объяснить, как негативные примеры функционируют в научной практике.
Вот как Бозанке проанализировал один случай. Пример из биологии. Это касается некоего растения — пчелы Офрис; вопрос в том, удобряется ли он самооплодотворением или удобряется насекомыми. Гипотеза Дарвина заключалась в том, что растение самооплодотворяется под действием ветра, выдувающего массы пыльцы, которые развиваются на растении, пока они не коснутся стигмы. Альтернативная гипотеза заключалась в том, что для оплодотворения требовались насекомые. Обратите внимание, что это причинные гипотезы, и поэтому, как утверждает Милль, подразумевают закономерности.Бозанке не признает этого. Во всяком случае, в своем эксперименте Дарвин, чтобы подтвердить свою гипотезу, изолировал колос цветов в воде в комнате. В этой ситуации было отсутствие насекомых (не и ). Это сделало невозможным оплодотворение насекомыми. Это также обеспечило отсутствие ветра. В этом контексте массы пыльцы не соприкасались со стигмой. Таким образом, в этой ситуации мы имеем как отсутствие ветра (не- w ), так и отсутствие контакта (не- c ).Согласно Бозанке, Дарвин заключает, что его гипотеза верна, что пчела Офрис самооплодотворяется под действием ветра.
Босанке сообщает об этом примере, что
Здесь мы оставили основу формальной логики, в которой «не w не c » могло основываться только на знании того, что « c есть w». В рассматриваемом сейчас процессе « c — это w » фактически основывается на знании того, что «not — w — это не c ».Подтверждающая сила отрицательного примера в индукции зависит от того факта, что он имеет положительное содержание в той же системе конечной , что и c, и w, , и в рамках этой системы связано с ними посредством определенного отрицания. 26
Таким образом, он утверждает, что формальная логика не может объяснить вывод Дарвина. Но Бозанке ошибается. Фактически, есть способ, которым формальная логика может справиться с этим примером. Действительно, именно так Милль работал с такими примерами.
Поскольку Бозанке понимает утверждение «не w не c », мы имеем
Бесплатные кадки без ветра не дают контакта
Из этого он делает вывод, что
c — это w = контакт осуществляется ветром
Во-первых, мы должны признать, что для эмпирика вывод не столько « c — это w », сколько по Бозанке. претензии, а скорее это
ветер производит контакт
или
Всякий раз, когда ветер контактирует
То есть следует сделать вывод, что ветер является достаточным условием для контакта: это причинная закономерность.То, как Бозанке формулирует этот вопрос, подразумевает, что вывод происходит путем противопоставления: «не w, не равно c », мы заключаем « c равно w». Это разновидность немедленного вывода. Но на самом деле вывод, по крайней мере, с точки зрения формальной логики, более сложен. В самом деле, мы видим, что все должно быть сложнее. Поскольку то, что наблюдается, — это частные вещи, единичные случаи, из которых мы хотим заключить обобщение.
Бозанке фактически отмечает только одно из наблюдений Дарвина. Дело в том, что Дарвин также гарантировал, что при наличии ветра (w) в отсутствии насекомых (i) имеется наличие контакта ( c ). Он сделал это, поместив аналогичный шип Bee Ophrys на открытом воздухе в присутствии ветра, но прикрытый сеткой, которая гарантировала отсутствие насекомых. Фактический отчет Босанке о выводе, когда переход от «not- w is not c » к « c is w», опускает эту информацию.Но это очень важно для эмпирического анализа примера. Согласно эмпирическому объяснению этого вывода, на самом деле есть два доказательства: в обоих насекомых отсутствуют, в то время как в одном присутствуют ветер и контакт, а в другом — ветер и контакт отсутствуют. Мы можем суммировать эти результаты в небольшой таблице, где « a » указывает на отсутствие, а « p » указывает на присутствие:
iwcevent one: appevent two: aaa
А теперь, просто применив метод разности , мы можем сделать вывод, что
Если w , затем c .
Или, по крайней мере, мы можем сделать это при условии, что у нас есть основания для принятия как принципа детерминизма , , что существует по крайней мере одно достаточное условие, так и принципа ограниченного разнообразия , что это условие относится к числу определенный детерминированный набор. То есть нам нужно знать общее утверждение о том, что
- (*)
Существует свойство f такое, что всякий раз, когда f затем c , и оно находится в наборе, состоящем из w и i
Это закон; В конце концов, утверждает общую истину.Но он также утверждает существование определенного свойства. Поскольку этот закон также заявляет о существовании, он включает конкретный количественный показатель. Фактически, это смешанная количественная форма. Милль видит необходимость в таком дополнительном принципе, если его элиминирующие методы должны работать — хотя его дедуктивная логика, как мы видели, слишком примитивна, чтобы позволить ему полностью сформулировать свои идеи; но он видит, подчеркнем, что такой «закон о законах» необходим. Более того, опять же, как увидел Милль, поскольку закон (*) утверждает существование свойства определенного вида, он делает абстрактное родовое утверждение , а не конкретное: он утверждает, что существует как свойство объекта. определенный родовой тип , и этого свойства достаточно для наличия обусловленного свойства c.
Этот закон (*) направляет исследователя. Он утверждает, что существует определенный закон, который необходимо открыть, и что этот закон будет иметь определенную общую форму. Задача исследователя — в данном случае Дарвина — найти закон, который (*) утверждает, что существует.
Что касается самого (*), то, как правило, можно вывести истинность такого абстрактного общего закона из некоторой фоновой теории такого рода:
- (**)
Для всех систем г общего вида G существует свойство f , такое, что оно является универсальным видом F и такое, что всякий раз, когда f затем g .
Из закона такого рода вместе с помещениями
c имеет вид GF = {i, w}
, можно вывести закон (*), которым руководствуются исследования. (**) имеет тот же общий вид, что и наша теория (T), о которой мы говорили выше. Что (**) утверждает, так это то, что для всех систем определенного общего вида для этих систем существуют особые законы некоторого другого общего вида. Основанием для принятия (**) является прошлый опыт: насколько мы можем судить, когда мы рассматривали системы соответствующего родового типа, мы действительно преуспели в открытии законов того вида, которые (**) могли бы заставить нас поверить, что есть.В самом общем виде (**) — это, конечно, то, что Милль называл законом универсальной причинности.
Принимая (**), мы можем вывести закон типа (*) для интересующих нас систем, в случае Дарвина — пчелы Офрис. Закон (*) указывает нам не только на то, где искать, но и на то, что если мы действительно посмотрим достаточно внимательно, мы сможем открыть закон соответствующего типа для этих систем. Наши предварительные знания о (**) и, следовательно, о (*), таким образом, обеспечивают телеологию для исследовательского процесса.Цель состоит в том, чтобы открыть особый закон определенного рода; наши знания, полученные из теории, говорят нам, что цель может быть достигнута . И наша логика подсказывает нам, что средство достижения этой цели — это метод различия. Таким образом, цель должна быть достигнута с помощью данных наблюдений, записанных в карте присутствия и отсутствия.
Эмпирическая логика, которую защищает Милль, проводит четкие границы между утверждениями об отдельных фактах, положительных и отрицательных, которые записаны в карте присутствия и отсутствия.Эти факты онтологически и логически отделимы и независимы друг от друга. Это означает, в частности, что эти констатации отдельных фактов сами по себе не подразумевают констатацию закона или закономерности, которая является заключением вывода. Конечно, они подтверждают этот закон, но не они его самым решительным образом поддерживают. Эта поддержка, скорее, исходит из работы устраняющих механизмов, которые служат для того, чтобы показать, что возможные альтернативы не могут быть истинными, то есть показывают, что, учитывая эти данные наблюдений, ничто иное, как вывод, возможно, не может быть истинным.
Босанке, однако, имеет несколько иное представление об этом процессе. Он рассматривает только событие, которое мы обозначили как событие два. Это событие он записывает как «not-w is not c», из чего затем выводит контрапозитив «c is w». Последнее он принимает за причинное заключение заключения Дарвина. Резкое различие, проводимое эмпириком между констатацией отдельных фактов в предпосылках и законом, то есть заключением, не является частью теории Бозанке.Бозанке также не интерпретирует этот пример с точки зрения элиминационных механизмов. Если утверждения об отсутствии сами по себе для эмпирика не подразумевают какой-либо закон, то для Бозанке, напротив, утверждение об отсутствии становится утверждением, что «не w не является c », и только из этого следует причинный вывод. подразумевается, что ‘ c — это w’ . Bosanquet как бы обнаруживает причинную претензию в самих конкретных событиях.И я теперь буду утверждать, что это вовсе не случайно: Бозанке на самом деле преследует точку зрения, которую многие сочли роковой критикой эмпирического подхода к законам и научным выводам.
Давайте посмотрим на то, что Бозанке сказал ранее.
Милль утверждал, что универсальное суждение
Все A — B
— изложение отдельных фактов.
a — это A & a, — это B, b — — это A & b, — это B,…
Как он выразился,
… общая истина — это совокупность частных истин; всеобъемлющее выражение, которым одновременно подтверждается или опровергается неопределенное количество отдельных фактов. 27
На самом деле, однако, как мы видели аргумент Милля, это не просто соединение : это само по себе вывод: форма языка такова, что позволяет нам записывать в одном утверждении.
… все, что мы наблюдали, вместе со всем, что мы делаем из наших наблюдений…. 28
На этот счет силлогизм, такой как
Все люди смертны, Сократ человек, следовательно, Сократ смертен
не дает новых знаний в заключении, помимо того, что содержится в предпосылках.Или, скорее, поскольку он дает новое знание, он делает это только путем вывода фактов из второстепенной посылки и вывода из наблюдаемых фактов, которые входят в число тех фактов, которые зафиксированы в основной посылке. То, что делают дедуктивные связи, — это гарантия того, что наша мысль непротиворечива; они не позволяют нам сделать вывод, что все люди смертны, а затем отрицать смертность человека, Сократа. По словам Милля, дедуктивная логика сама по себе является логикой последовательности, а не логикой истины.Именно индуктивный вывод составляет логику истины.
Босанке поднимает этот вопрос. 29 Он рассматривает вывод от частностей к частностям:
a — это B, b — это B, c — это B, d — это B; , следовательно, e равно B
Например, a — хорошая книга, b — хорошая книга, c — хорошая книга, d — хорошая книга, и поэтому e — хорошая книга. Он справедливо отмечает, что это не лучший вывод.Однако, в отличие от этого, вывод
Айвенго, Уэверли и Роб Рой — хорошие книги; следовательно, Guy Mannering — хорошая книга
разумно. Это разумно, потому что «существует самоочевидный отрывок посредством идентичности авторства, который слишком очевиден, чтобы быть выраженным, но который мог бы сформировать предпосылку в любом явном изложении вывода».
Босанке отмечает, что
… невозможно сформулировать вывод [к частностям из частных] в форме, которая будет казаться убедительной, если мы не добавим второй посылкой элемент единства между частностями, всегда действующий в уме, который необходимо привязать частные отличия к отличиям от универсального. 30
Обратите внимание на точку: что нужно, так это «элемент единства между частностями, всегда действующий в уме, который необходим, чтобы связать частные различия в различия универсального»: есть элемент единства; это связывает различия, то есть различные различия, в различия внутри универсального; и этот элемент единства действует в уме. Вернемся к этим пунктам.
В любом случае, принимая это, мы видим, что вывод, который должен быть сделан на частностях из частных, на самом деле
Все романы Скотта — хорошие книги Гай Мэннеринг — это роман Скотта Хенса, Гай Мэннеринг — хорошая книга
, где основная посылка подтверждается умозаключением.
(@) Айвенго, Уэверли и Роб Рой — это романы, написанные Скоттом Иванхо, Уэверли и Роб Рой — хорошие книги. Следовательно, все романы Скотта — хорошие книги.
Пока что это выглядит довольно близко к мнению Милля.На самом деле, однако, Бозанке очень важным образом квалифицирует вывод вывода (@). Вот один из примеров Бозанке 31 :
a, b, c, d рациональны, b, c, d — люди, следовательно, все ли люди рациональны? или, Люди могут быть рациональными
Заключение вывода (@) следует воспринимать как предположение, а не как что-то продемонстрированное.
Бозанке отмечает, что здесь есть телеология:
В общем, совпадение нескольких атрибутов в одном или нескольких объектах… является отправной точкой для сознательного предположения и исследования.И эта отправная точка — все, что воплощает в себе нынешняя форма вывода. Гипотеза или чистое «открытие» отличается от доказательства только степенью. 32
Опять же, это не сильно отличается от того, что мог бы сказать Милль. Но оказывается, что телеология на самом деле совсем другая: представление Милля об этой телеологии основано на абстрактных общих теориях, законах о законах, которые направляют исследования. Для Бозанке, напротив, телеология, как и в случае с Уэвеллом, направлена на раскрытие как бы реальной объективной необходимости в вещах, которые сначала не кажутся нам очевидными, но которые становятся явными по мере продвижения процесса открытия.
Босанке комментирует (@) следующим образом:
Основание для аргументации, являющееся характерным единством неанализируемого индивидуального объекта или события, естественно, занимает место субъекта в суждении — конкретного индивида, принимаемого как реальный, — и, следовательно, порождает ту силлогистическую форму, в которой средний срок является предметом обеих предпосылок. 33
Здесь он снова подчеркивает «единство», которое можно найти в аргументе. Только теперь это единство, которое находится в «неанализируемом индивидуальном объекте», а не, как раньше, «действует в уме».Или, скорее, элемент единства присутствует одновременно в субъекте, о котором идет речь, и действует в уме человека, делающего вывод. Эта точка зрения, конечно, действительно похожа на точку зрения Уэвелла. В любом случае, это «единство», которое, как утверждает Бозанке, мы обнаруживаем в отдельных фактах, является основанием аргумента.
Что касается понятия земли, Бозанке ранее объяснил, что это такое. Он отличал чисто коллективные суждения от действительно универсальных.Первые имеют дело с агрегатом, возникающим в результате перечисления 34 . Из них выделяются квазиколлективные суждения, которые являются действительно общими и применимы к неопределенному числу людей, то есть к открытому классу, как теперь можно было бы сказать. Они не могут быть результатом простого перечисления, иначе они не могли бы быть действительно общими, а не резюме уже наблюдаемых. Следовательно, эти суждения должны «получать [свое] значение из какого-то другого источника». 35 Среди этих суждений есть такие, как «Все люди смертны», то есть те, которые мы только что рассматривали.Эти квазиколлективные суждения — больше, чем просто резюме уже наблюдаемых, но, тем не менее, их можно опровергнуть с помощью единственного контрпримера; как выразился Бозанке, они «беспомощны перед самым банальным исключением». 36 Помимо этого, существуют действительно универсальные суждения, такие как «Человек смертен». На практике они эквивалентны утверждениям типа «Все люди смертны». Тем не мение,
Очевидно, что к утверждению универсальной связи, которую мы считаем в таком случае почти оправданной, прибегают не со стороны отдельных единиц, а со стороны общей или непрерывной природы, которая связывает их в единое целое. весь. 37
Поскольку такого рода универсальное суждение подтверждается связью между атрибутами, оно является абстрактным и, следовательно, гипотетическим. 38 Гипотетическое суждение содержит следствие и основание; второе гарантирует первое. Он делает это благодаря тому, что он связан с ним, связан внутренне, в самом его существовании.
Основание подразумевает следствие, отличное от самого себя, хотя по существу одно с ним. 39
Эти два связаны как части в целом, что устанавливает связь между ними.
… содержание гипотетического суждения состоит из основания и следствия, каждое из которых относится к чему-то отличному от себя и, следовательно, по существу является частью….
Речь идет только о деталях, насколько система, в которой существует связь, и посредством которой существует эта связь, сама выражается в явном виде в качестве содержания в рамках гипотетического суждения. 40 .
Эти нексу сами по себе являются фактами в мире.
… каждый набор отношений, в котором сохраняется определенная взаимосвязь атрибутов, сам в конечном счете является фактом или данным, без сомнения относительным в пределах некоторой дальнейшей совокупности, но абсолютным относительно выводов, сделанных внутри него. 41
Следовательно, «все гипотетические суждения основываются на категориальной основе». 42 .
Таким образом, Бозанке предположил, что вывод вывода
a, b, c, d являются рациональными, b, c, d являются мужчинами Следовательно, …….
не было
Все люди рациональны
но
Все ли люди рациональны? или, Люди могут быть рациональными.
Вывод от частностей к частностям в действительности формирует гипотезу , которая не готова для обоснованного утверждения, пока она не будет основана на категориальной основе.На том уровне, где останавливается эмпирик, — «люди могут быть рациональными», мы, согласно Бозанке, все еще находимся на уровне невежества в отношении подлинной структуры реальности. Эмпирик хотел бы, чтобы мы остановились на той точке, где необходимо продолжить подлинное исследование.
Таким образом, по сути, Бозанке утверждает, что Милль ошибается в своем взгляде на общие положения, когда рассматривает их все как квазиколлективные суждения. Напротив, основание для истинно универсальных суждений, суждений, которые не могут быть опровергнуты или опровергнуты единичным случаем, лежит в связи, существующей между атрибутами.Как также утверждал Уэвелл, суждение действительно универсально только в том случае, если оно не поддается опровержению — только если, другими словами, оно каким-то образом истинно a priori.
 Логика), развивавшаяся в рамках философии (см. Философия). Методы формализации дали логике такие преимущества, как высокая точность формулировок, возможность изучения более сложных, с точки зрения логической формы, объектов. Определение «формальная логика» было введено И. Кантом с намерением подчеркнуть её ведущую особенность в подходе к изучаемым объектам и отграничить её тем самым от других возможных логик.
Логика), развивавшаяся в рамках философии (см. Философия). Методы формализации дали логике такие преимущества, как высокая точность формулировок, возможность изучения более сложных, с точки зрения логической формы, объектов. Определение «формальная логика» было введено И. Кантом с намерением подчеркнуть её ведущую особенность в подходе к изучаемым объектам и отграничить её тем самым от других возможных логик. Эта иерархия недостаточно ясна, и её обоснования порой легко подвергаются критике, однако она часто используется в качестве удобной схемы изложения предметной области формальной логики, что, собственно, подкрепляется многовековой традицией преподавания этой дисциплины. Эти логические формы и лежащие в основе операций с ними законы и принципы, то есть так называемый логический аппарат, составляют основную область исследований формальной логики, а выработка самих эффективных логических аппаратов — её основную цель.
Эта иерархия недостаточно ясна, и её обоснования порой легко подвергаются критике, однако она часто используется в качестве удобной схемы изложения предметной области формальной логики, что, собственно, подкрепляется многовековой традицией преподавания этой дисциплины. Эти логические формы и лежащие в основе операций с ними законы и принципы, то есть так называемый логический аппарат, составляют основную область исследований формальной логики, а выработка самих эффективных логических аппаратов — её основную цель. Здесь формулируются способы корректного получения суждения, называющегося заключением, из некоторых исходных суждений, называющихся посылками, посредством рассуждения. В рамках теории вывода выделяют логику, рассматривающую дедуктивные рассуждения (см. Дедукция), то есть определённые способы доказательств, и логику, занимающуюся правдоподобными рассуждениями: индукция, аналогия и другие.
Здесь формулируются способы корректного получения суждения, называющегося заключением, из некоторых исходных суждений, называющихся посылками, посредством рассуждения. В рамках теории вывода выделяют логику, рассматривающую дедуктивные рассуждения (см. Дедукция), то есть определённые способы доказательств, и логику, занимающуюся правдоподобными рассуждениями: индукция, аналогия и другие.
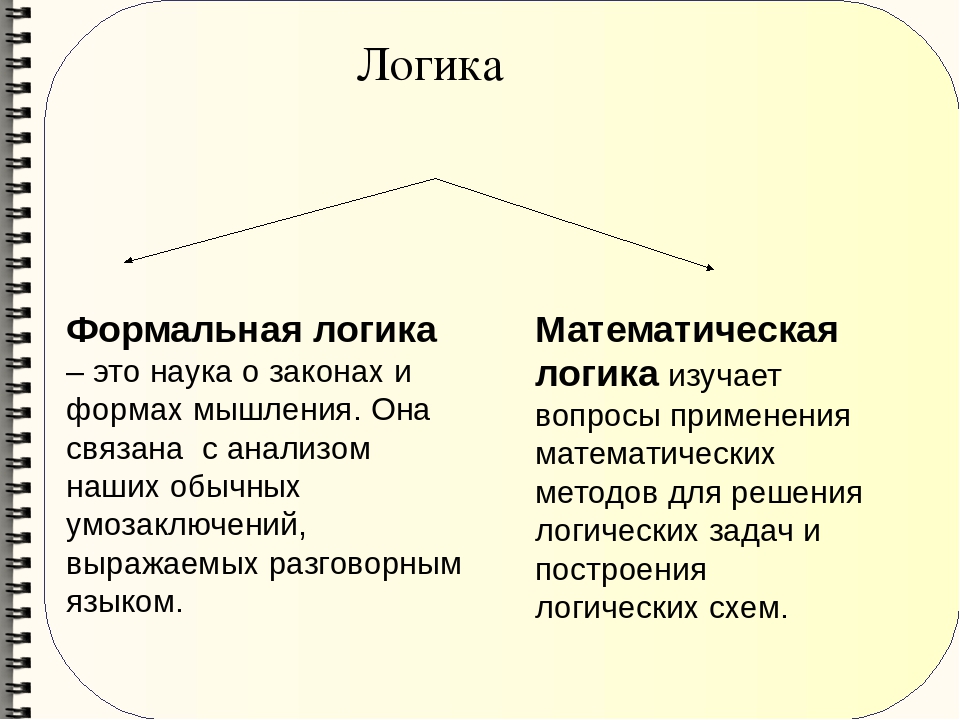 Основные разделы математической логики — классические логика высказываний (см. Логика высказываний) и логика предикатов (см. Логика предикатов). Широкое распространение получили исследования
Основные разделы математической логики — классические логика высказываний (см. Логика высказываний) и логика предикатов (см. Логика предикатов). Широкое распространение получили исследования  Металогика), в которой исследуются различные проблемы, относящиеся к логическим теориям. Основными здесь являются вопросы о тех свойствах, которыми обладают логические теории: о непротиворечивости, полноте, наличии разрешающих процедур, независимости исходных дедуктивных принципов, а также о различных отношениях между теориями и так далее. В этом смысле металогика является своего рода саморефлексией логики относительно своих построений. Все метатеоретические исследования проводятся на специальном метаязыке, в качестве которого используется естественный язык, обогащённый специальной терминологией и метатеоретическими дедуктивными средствами.
Металогика), в которой исследуются различные проблемы, относящиеся к логическим теориям. Основными здесь являются вопросы о тех свойствах, которыми обладают логические теории: о непротиворечивости, полноте, наличии разрешающих процедур, независимости исходных дедуктивных принципов, а также о различных отношениях между теориями и так далее. В этом смысле металогика является своего рода саморефлексией логики относительно своих построений. Все метатеоретические исследования проводятся на специальном метаязыке, в качестве которого используется естественный язык, обогащённый специальной терминологией и метатеоретическими дедуктивными средствами. Практическое значение формальной логики
16
Практическое значение формальной логики
16 Отношения между суждениями
61
Отношения между суждениями
61 Определение
147
Определение
147 Нормальные формы формул логики высказываний
241
Нормальные формы формул логики высказываний
241 Формализованная силлогистика
322
Формализованная силлогистика
322 И тут опять же помогает обобщение. Нужно задать себе и коллегам вопрос: «Частью какого большого проекта является эта история? Для чего мы это делаем?» Даже если нам кажется, что мы все это давно знаем, нужно еще раз проговорить вслух задачи и цели, отстраниться от деталей, выйти на более высокий уровень. И делать это не разово, а периодически. Так обобщение помогает избежать рутинности и потери смысла. Когда мы задаем себе вопрос, что мы вообще делаем в этой жизни, то мы не скатываемся на уровень, где наша работа — скучная и механическая.
И тут опять же помогает обобщение. Нужно задать себе и коллегам вопрос: «Частью какого большого проекта является эта история? Для чего мы это делаем?» Даже если нам кажется, что мы все это давно знаем, нужно еще раз проговорить вслух задачи и цели, отстраниться от деталей, выйти на более высокий уровень. И делать это не разово, а периодически. Так обобщение помогает избежать рутинности и потери смысла. Когда мы задаем себе вопрос, что мы вообще делаем в этой жизни, то мы не скатываемся на уровень, где наша работа — скучная и механическая.  Мы должны делать примерно то же самое в своем уме. Ведь часто, особенно в больших корпорациях, мы работаем в режиме zoom in. Помню, в Microsoft мы отвечали за конкретный сегмент — Евразию, смотрели, каких приложений не хватает пользователям. Работая в таком узком сегменте, можно упустить из виду большую задачу. Например, нам надо, чтобы новый Windows Phone стал жизнеспособной экосистемой для пользователей, которым полюбился его дизайн и интерфейс. Если не держать эту большую задачу в голове, можно попасть в ловушку KPI — мы достигаем поставленные перед нами задачи, но не понимаем, зачем.
Мы должны делать примерно то же самое в своем уме. Ведь часто, особенно в больших корпорациях, мы работаем в режиме zoom in. Помню, в Microsoft мы отвечали за конкретный сегмент — Евразию, смотрели, каких приложений не хватает пользователям. Работая в таком узком сегменте, можно упустить из виду большую задачу. Например, нам надо, чтобы новый Windows Phone стал жизнеспособной экосистемой для пользователей, которым полюбился его дизайн и интерфейс. Если не держать эту большую задачу в голове, можно попасть в ловушку KPI — мы достигаем поставленные перед нами задачи, но не понимаем, зачем. Но это недостаточно зрелый подход. В какой-то момент мы рискуем столкнуться с трудностями и не понять их причины. Поэтому сначала мы изучаем, что представляет собой этот продукт, из чего он состоит, как он хотя бы примерно работает. Это способно защитить нас от многих рисков и проблем в будущем.
Но это недостаточно зрелый подход. В какой-то момент мы рискуем столкнуться с трудностями и не понять их причины. Поэтому сначала мы изучаем, что представляет собой этот продукт, из чего он состоит, как он хотя бы примерно работает. Это способно защитить нас от многих рисков и проблем в будущем.