Слово КОНГРУЭНТНЫЙ — Что такое КОНГРУЭНТНЫЙ?
Слово состоит из 12 букв: первая к, вторая о, третья н, четвёртая г, пятая р, шестая у, седьмая э, восьмая н, девятая т, десятая н, одиннадцатая ы, последняя й,
Слово конгруэнтный английскими буквами(транслитом) — kongrentnyi
Значения слова конгруэнтный. Что такое конгруэнтный?
Конгруэнтное число
Конгруэ́нтное число — натуральное число, равное площади прямоугольного треугольника со сторонами, длины которых выражаются рациональными числами. Конгруэнтные числа образуют последовательность: Например…
ru.wikipedia.org
КОНГРУЭНТНЫЕ ФИГУРЫ
КОНГРУЭНТНЫЕ ФИГУРЫ (от лат. congruens — родительный падеж congruentis — соответствующий, совпадающий), геометрические фигуры, переходящие друг в друга при движении.
Большой энциклопедический словарь
КОНГРУЭНТНЫЕ ФИГУРЫ (от лат congruens, род. п. congruentis — соответствующий, совпадающий), геом. фигуры, переходящие друг в друга при движении.
Словарь естествознания
Конгруэнтное плавление
Конгруэнтное плавление Congruent melting — Конгруэнтное плавление. Изотермическое или изобарическое плавление, при котором твердая и жидкая фазы имеют один и тот же состав от начала и до конца превращения. Металлы и сплавы. Справочник. — 2003
Справочник. — 2003Конгруэнтное изменение отношений
Конгруэнтное изменение отношений — (лат. congruentis — соразмерный, соответствующий, совпадающий) — изменение межличностных отношений в сторону развития существующих.
Жмуров В.А. Большой толковый словарь терминов по психиатрии
Конгруэнтное изменение отношений (лат. congruentis — соразмерный, соответствующий, совпадающий) – в социальной психологии — изменение межличностных отношений в сторону развития уже существующих.
vocabulary.ru
Линейный конгруэнтный метод
Линейный конгруэнтный метод — один из алгоритмов генерации псевдослучайных чисел. Применяется в простых случаях и не обладает криптографической стойкостью. Входит в стандартные библиотеки различных компиляторов.
ru.wikipedia.org
Валидность конгруэнтная
Валидность конгруэнтная (лат. congruens – соразмерный, соответствующий, совпадающий) – метод установления валидности теста посредством корреляции значений, полученных по нему, со значениями…
vocabulary.ru
Русский язык
Конгруэ́нт/н/ый.
Морфемно-орфографический словарь. — 2002
- конгресс
- конгруенция
- конгруэнтность
- конгруэнтный
- конгруэнция
- кондакарный
- кондак
Что такое конгруэнтность, и как ее развить? — Блог Викиум
Знаете ли вы, что согласование ваших мыслей и действий показывает конгруэнтность или неконгруэнтность? Насколько часто вы скрываете свои эмоции? Наверняка каждому хоть раз приходилось демонстрировать натянутую улыбку, когда на душе скребли кошки.
Обычно такое чувство приносит сильнейший дискомфорт. В этой статье вы узнаете о понятии конгруэнция и о том, и как ее достичь.
Что такое конгруэнтность?
В психологии под определением конгруэнтности понимается открытое выражение своих чувств, когда мысли и действия человека полностью совпадают. Конгруэнтность является полной противоположностью инконгруэнтности, при которой поступки и чувства человека не имеют согласованности.
Конгруэнтный человек спокойно говорит обо всем, что думает, даже если его что-то тревожит. Определение данному термину дал Карл Роджерс, по мнению которого конгруэнтность вместе с эмпатией являются очень важной частью для психотерапевтической связи.
Примеры конгруэнтности
Конгруэнтность, согласно Роджерсу, является характеристикой коммуникации. Среди признаков конгруэнтности:
- искренность;
- гармония с самим собой;
- полное совпадение действий и чувств;
- честность.
Люди с развитой конгруэнтностью всегда привлекают окружающих и быстро находят с ними общий язык. Например, если парню приглянулась девушка, и он конгруэнтно развит, то сразу же подойдет к ней и расскажет о своих чувствах. Если же он относиться к неконгруэнтным личностям, то максимум, что он сможет сделать — заговорить на отдаленные темы.
Для поведения неконгруэнтных людей характерны:
- постоянное вранье;
- несоответствие чувств и действий.
Такие личности всегда скрывают свои настоящие чувства, чем очень сильно отталкивают окружающих.
Причины неконгруэнтности
По мнению специалистов в области психологической медицины, существует несколько причин, которые приводят людей к неконгруэнтному состоянию. Например, человек просто хочет произвести на окружающих впечатление, поэтому часто ведет себя не так, как ощущает внутри. Обычно такие люди очень быстро говорят и часто нервничают, а значит вскоре такое общение надоедает окружающим.
Еще одна причина — желание показаться окружающим расслабленным и игривым. Такое состояние очень быстро утомляет самого человека и он испытывает эмоциональную усталость. В данном случает отношения с окружающими тоже очень быстро прекращаются. Также к этому списку можно добавить поведение человека, когда он хочет произвести эффект личности с высоким статусом, которого на самом деле нет.
Преимущества конгруэнтности
Конгруэнтность имеет ряд преимуществ:
- индивид всегда ведет себя естественно;
- такими людьми нет возможности манипулировать;
- человек привлекает окружающих;
- конгруэнтный человек испытывает только здоровые эмоции;
Как достичь конгруэнтности?
Развить данное состояние можно так:
- никогда не лгите и оставайтесь честным перед самим собой;
- общайтесь с окружающими максимально просто и расслабленно;
- не старайтесь скопировать поведение другого человека;
- не бойтесь проявлять эмоции;
- при общении не следует очень резко менять интонацию.
Чтобы способствовать развитию конгруэнтности, психологи придумали упражнение, при котором человеку необходимо пойти туда, где есть люди, и начать с ними общение. Основной целью является проявление естественности. Не следует проводить анализ поведения, чтобы выглядеть так, как кто-то вас хочет видеть, нужно придерживаться принципов и оставаться самим собой. А также правильно строить коммуникации научит курс Викиум «Эффективное общение. Онлайн-интенсив«.
Конгруэнтные фигуры | Математика
Конгруэнтные фигуры.
Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. СБОРНИК СТАТЕЙ.
Текст для быстрого ознакомления (формулы и чертежи качественнее отображаются в PDF файле ниже):
Скачать бесплатно: Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. ИЗБРАННЫЕ ВОПРОСЫ ТЕОРИИ ПРЕОБРАЗОВАНИЙ ПОДОБИЯ ПЛОСКОСТИ И ЕЕ ПРИМЕНЕНИЕ К РЕШЕНИЮ ЗАДАЧ. З. А. Скопец, Л. И. Кузнецова
(стр. 227-246)
На главную страницу Библиотека учителя математики.
ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. СБОРНИК СТАТЕЙ.
§ 4. Конгруэнтные фигуры. А. М. Абрамов НАЧАЛЬНЫЕ ПОНЯТИЯ ГЕОМЕТРИИ.
П е р в о е о п р е д е л е н и е . Фигура Фх конгруэнтна фигуре
Ф, если существует сохраняющее расстояния отображение
фигуры Ф на Фх.
Так как перемещения сохраняют расстояния, часто употребляется
такой метод доказательства конгруэнтности фигур Ф и Фх:
находится перемещение, при котором образом фигуры Ф является
Фх.
В т о р о е о п р е д е л е н и е . Если существует перемещение,
Ф.
Замечание, сделанное перед этим определением, показывает,
что если фигура Фх конгруэнтна фигуре Ф в смысле второго определения,
то Фх конгруэнтна Фив смысле первого определения.
257 Конгруэнтные фигуры.
Для доказательства эквивалентности этих двух определений
остается показать, что если существует сохраняющее расстояния
отображение G, область определения которого — фигура Ф, а
множество значений — Фх, то существует и перемещение F (изометрическое
отображение всей плоскости, а не ее подмножества Ф),
при котором образ фигуры Ф — фигура Фх.
. Возьмем отличную от Л и Б
точку Xфигуры Ф. НапрямойЛхбх имеется ровно одна точка Х1г
для которой |ЛХ| = |ЛхХх|, |fiX| =|SxXx|. Поэтому и F, и G
переводят X в X’, т. е. F — продолжение G на всю плоскость.
Второй случай: Ф содержит точки А, В, С, не принадлежащие
одной прямой.
Так как G сохраняет расстояния, точки Ах — G (Л), Вх — G (В),
Сх = G (С) также не принадлежат одной прямой, причем | Лх-SxN
= | АВ\, |ВхСх1 = |ВС|, |ЛхСх1 =|ЛС|. Как показано при доказательстве
теоремы 2.1 существует перемещение F, которое, как и
С, переводит Л в Аг, В в Въ С в Сх. Если Ф не содержит других
точек, кроме Л, б и С, теорема доказана. Пусть X — произвольная
точка Ф, отличная от Л, Б, С.
В этом случае мы докажем, что F (X) = G (X), показав, что существует
не более одной точки плоскости, удаленной от Л’ на расстояние
| ЛХ|, от В’ — на |fiX| и от С’— на |СХ|.
В самом деле, имеется не более двух точек Y1 и Y» плоскости,
для каждой из которых расстояние от Ах равно |ЛХ|, а от Вх —
|£Х| (теорема 1.
Z . 3 (рис. 9).
Угол 2 при симметрии Sa отображается на конгруэнтный ему
угол. Но луч ОА при симметрии Sa отображается на себя и по условию
Z. 1 Z. 2. Так как по теореме 4.2 от луча О А можно отложить
в данной полуплоскости лишь один угол, конгруэнтный данному,
$а _____
то [ОБ) ==> [ОС). Следовательно, и прямая р при симметрии Sa
отображается на’себя.
Из теоремы 3.4 вытекает, что Sp (а) — а. Поэтому угол 1 при
симметрии Sp отображается на угол 3, т. е. Z. 1 Ш АЗ.
Если две прямые пересекаются, то, как известно, они задают
четыре выпуклых угла. Из доказанной корректности определения
прямого угла следует, что если один из этих четырех углов прямой,
то и все четыре угла прямые.
О п р е д е л е н и е . Дее прямые, образующие при пересечении
прямые углы, называются взаимно перпендикулярными.
Т е о р е м а 4.4. Для любой точки О плоскости и любой прямой
р существует одна и только одна прямая, проходящая через О
и перпендикулярная р.
Д о к а з а т е л ь с т в о . Рассмотрим два случая.
Первый случай’. О $ р.
а) С у щ е с т в о в а н и е . Пусть О* = Sp (О) и М — точка
пересечения прямых 00′ и р (рис. 10, а). При еимметрии Sp лучи
МО и МО’ отображаются друг на друга, луч MN — на себя. Поэтому
углы OMN и O’MN — смежные и конгруэнтные углы. Это
означает, что прямые 00′ и р перпендикулярны.
б) Е д и н с т в е н н о с т ь . Допустим, что через точку О
260 Конгруэнтные фигуры.
проходят два перпендикуляра к прямой
р (рис. 11,6). Тогда, как это следует из
теоремы 4.2, прямые О А и О В при симметрии
Sp отображаются на себя. Так как эти
прямые пересекаются в точке О, отсюда получаем,
что эти прямые имеют вторую общую
точку O’— Sp (О). Но через две точки
проходит единственная прямая, поэтому
(ОА) = (ОВ). Это противоречит сделанному
допущению.
Конгруэнтные фигуры 2
Второй случай1. О £ р.
а) С у щ е с т в о в а н и е .
Z.2,
в силу транзитивности отношения конгруэнтности
фигур Z. Г Z. 2′, т. е. (ОА’) J. р.
б) Е д и н с т в е н н о с т ь . Допустим, что через точку О € р
проходят два перпендикуляра р и р’ к прямой а (рис. 11, б). Тогда
луч ОР’ содержится в одном из углов АОР и РОВ. Пусть для определенности
[OP’) а Z-РОВ. При симметрии с осью ОР угол РОВ
отображается на угол РОА (эти углы прямые), луч ОР’ — на некоторый
луч ОР», содержащийся в угле РОА и отличный от луча
ОР. При этом Z-P»OA /-Р’ОВ. Это противоречит теореме 4.2:
от луча ОА в полуплоскости с границей ОА отложены два угла
(Z-P’OA и Z.POA), конгруэнтные углу Р’ОВ.
С доказательством этой теоремы нетрудно сделать вывод, что
медиатриса любого отрезка является серединным перпендикуляром
этого отрезка.
О п р е д е л е н и е . Луч ОМ угла АО В называется биссектрисой
этого угла, если углы АОМ и ВОМ, являющиеся подмножествами
данного угла, конгруэнтны.
Т е о р е м а .
4 . 5 . Для любого угла плоскости, отличного от развернутого,
существует биссектриса этого угла и притом только
одна.
Д о к а з а т е л ь с т в о . 1. Существование. Если прямая АВ —
граница развернутого угла, то любой луч с началом О € (А В),
перпендикулярный к прямой АВ и содержащийся в данном развернутом
угле (рис. 12, а), является его биссектрисой. Отметим, что
неединственность биссектрисы развернутого угла вытекает из того
обстоятельства, что в отличие от других углов вершина (край->;
няя точка) развернутого угла не единственна.
261 Конгруэнтные фигуры.
Если угол АО В — выпуклый (рис. 12, б), его биссектриса —
луч с началом О, содержащий середину М отрезка CD (С (: [ОА),
D (; [ОВ), |ОС|= |OD|). Действительно, \ОМ\ — ось симметрии
угла АОВ, а точка М — внутренняя точка этого угла, так как
Z-AOB — выпуклая фигура.
Луч ON, противоположный лучу ОМ, — биссектриса невыпуклого
угла АОВ.
2.
Единственность. Если ОК и ОМ — различные биссектрисы
угла АОВ (рис. 13), то симметрии Sok и Som отображают угол на
себя. Кроме того, Е (/L.AOB) = Z.AOB. Но существует не более
двух перемещений, отображающих один из данных конгруэнтных
углов на другой (см. доказательство теоремы 4.2.) Противоречие.
Допустив, что существует более одной биссектрисы у невыпуклого
угла, приходим к противоречию с только что доказанной единственностью
биссектрисы выпуклого угла.
262 Конгруэнтные фигуры.
На главную страницу Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. СБОРНИК СТАТЕЙ.
Школьная математика. Математика в школе.
РАЗНИЦА МЕЖДУ КОНГРУЭНТНЫМ И РАВНЫМ | СРАВНИТЕ РАЗНИЦУ МЕЖДУ ПОХОЖИМИ ТЕРМИНАМИ — НАУКА
Конгруэнтный против равного Конгруэнтность и равенство — схожие понятия в геометрии, но их часто неправильно понимают и путают.РавноРавный означает, что величины или размеры любых двух сравниваемых о
Конгруэнтный против равного
Конгруэнтность и равенство — схожие понятия в геометрии, но их часто неправильно понимают и путают.
Равно
Равный означает, что величины или размеры любых двух сравниваемых одинаковы. Концепция равенства знакома в нашей повседневной жизни; однако как математическое понятие его следует определять с помощью более строгих мер. В разных полях используется другое определение равенства. В математической логике это определяется с помощью аксиом Паэно. Равенство относится к числам; часто числа, представляющие свойства.
В контексте геометрии равенство имеет те же значения, что и в обычном использовании термина «равно». В нем говорится, что если атрибуты двух геометрических фигур одинаковы, то эти две фигуры равны. Например, площадь треугольника может быть равна площади квадрата. Здесь речь идет только о размере «площади» собственности, и они совпадают. Но сами цифры нельзя считать одинаковыми.
Конгруэнтный
В контексте геометрии конгруэнтность означает равенство как фигур (формы), так и размеров. Или, проще говоря, если одно можно рассматривать как точную копию другого, тогда объекты конгруэнтны, независимо от их расположения.
Это эквивалентное понятие равенства, используемое в геометрии. В случае сравнения в аналитической геометрии также даются гораздо более строгие определения.
Независимо от ориентации показанных выше треугольников, их можно расположить так, чтобы они полностью перекрывали друг друга. Следовательно, они одинаковы по размеру и форме. Следовательно, они являются конгруэнтными треугольниками. Фигура и ее зеркальное отображение также совпадают. (Их можно перекрывать после поворота вокруг оси, лежащей в плоскости формы).
В приведенном выше примере, хотя фигуры являются зеркальными отражениями, они совпадают.
Конгруэнтность в треугольниках важна при изучении геометрии плоскости. Чтобы два треугольника были равны, соответствующие углы и стороны должны быть равны. Треугольники можно считать конгруэнтными, если выполняются следующие условия.
• SSS (сторона сторона сторона) если все три соответствующие стороны равны по длине.
• SAS (сторона бокового угла) Пара соответствующих сторон и включенный угол равны.
• ASA (Угол стороны угла) Пара соответствующих углов и включенная сторона равны.
• AAS (Angle Angle Side) Пара соответствующих углов и не включенная сторона равны.
• HS (катет гипотенузы прямоугольного треугольника) Два прямоугольных треугольника конгруэнтны, если гипотенуза и одна сторона равны.
Случай AAA (Angle Angle Angle) НЕ является случаем, когда соответствие всегда действительно. Например, следующие два треугольника имеют равные углы, но не совпадают, потому что размеры сторон разные.
В чем разница между конгруэнтным и равным?
• Если некоторые атрибуты геометрических фигур одинаковы по величине, то они считаются равными.
• Если и размеры, и фигуры равны, то цифры считаются совпадающими.
• Равенство касается величины (чисел), в то время как конгруэнтность касается как формы, так и размера фигуры.
Одним из наиболее распространенных ПРНГ является линейный конгруэнтный генератор, который использует рекуррентность. | |
| Другие результаты | |
| Треугольник ABD построен конгруэнтно треугольнику ABC с AD = BC и BD = AC. Перпендикуляры от D и C встречают основание AB на E и F соответственно. | |
| Для p, конгруэнтного 1 mod 4, избыток равен нулю, так как -1 является квадратичным остатком, а остатки симметричны при r ↔ p−r. | |
| Для p, конгруэнтного 3 mod 4, избыток E всегда положителен. | |
| Бред может быть классифицирован как настроение конгруэнтное или несогласованное, в зависимости от того, соответствует ли природа бреда настроению человека. | |
| На рубеже XIX века Карл Фридрих Гаусс разработал знак тождества для отношения конгруэнтности и, в квадратичной взаимности, интегральной части. | |
| Эта концепция намекает на важность конгруэнтности между эмоциями, оценкой и познанием. | |
Основные подгруппы конгруэнтности, определенные триплетом простых чисел, порождают Фуксовы группы, соответствующие триплету римановых поверхностей. | |
| Были получены смешанные результаты конгруэнтности по пользователям. | |
| Тогда решение системы одновременной конгруэнтности задается полиномом. | |
| Сочетание свободной задачи и конгруэнтности, как было сказано, представляет собой лучший сценарий, чтобы понять его влияние, так как он ближе к реальной жизни привычки просмотра. | |
| Остеотомия для восстановления или изменения конгруэнтности суставов также является одной из форм артропластики. | |
| Таким образом, алгоритм дает два решения для нашей конгруэнтности. | |
| Подразумевается, что критикуемое выражение или пропозиция лишены субстанции или конгруэнтности, в противоположность тому, что они просто являются различными взглядами. | |
| Ресурсы и дефицит сосуществуют, как это концептуализируется в модели ресурсной конгруэнтности. | |
В 1991 году Линда Бак и Ричард Аксель обнаружили молекулярную конгруэнтность обонятельных рецепторов — работа, впоследствии награждённая Нобелевской премией. | |
| Конгруэнтность Целлера-это алгоритм, разработанный Кристианом Целлером для вычисления дня недели для любой даты юлианского или григорианского календаря. | |
| Таким образом, чтобы реализовать конгруэнтность Зеллера на компьютере, формулы должны быть слегка изменены, чтобы обеспечить положительный числитель. | |
| Они включают в себя эмпатию, безусловное позитивное отношение, конгруэнтность и отношение к технике. | |
| Конгруэнтность-это отношение содержания объявления к веб-контенту. | |
| Редфилд обнаружил удивительную конгруэнтность между химией глубокого океана и химией живых существ, таких как фитопланктон в поверхностном океане. | |
| Реальная конгруэнтность текста и опыта признается невозможной. | |
| Конгруэнтность оказывает большее влияние, когда пользователь просматривает меньше веб-страниц. | |
При принудительном воздействии, как всплывающая реклама, конгруэнтность улучшает память. | |
| В частности, конгруэнтность Целлера и алгоритм Судного дня широко используют арифметику по модулю 7. | |
| При синдроме чужой руки нейронные механизмы, участвующие в установлении того, что эта конгруэнтность произошла, могут быть нарушены. | |
| Очень хорошим примером такого альтернативного формата является CREAC, который, как говорят, обеспечивает большую ясность и конгруэнтность. | |
| Класс остатков, соответствующий a, обозначается a. равенство классов остатков называется конгруэнтностью и обозначается. | |
| Если производные Дарбу двух фреймов равны, то версия фундаментальной теоремы исчисления утверждает, что кривые конгруэнтны. | |
| Поскольку стороны обоих треугольников имеют одинаковые длины a, b и c, треугольники конгруэнтны и должны иметь одинаковые углы. | |
Точка конгруэнтная — Энциклопедия по машиностроению XXL
Два множества называются равными лишь в том случае, если они состоят из одних II тех же элементов или оба не имеют элементов.
Поэтому, например, два треугольника АВС и ВЕР. имеющие одинаковые стороны и углы, не являются равными. Они называются конгруэнтными (обозначение ). О П р е д е л е ни е Фигура Ф называется конгруэнтной фигуре Ф, если существует перемещение, отображающее Ф на Ф1 . (Определение перемещения см. в п. П). Конгруэнтность фигур обладает свойствами рефлексивности (Ф Ф), симметричности (если Ф1 = Ф, то Ф = Ф )у транзитивности (если Ф] = Ф и Ф = Ф2, то Ф Ф2). Это надо иметь в виду, например, при определении свойств поступательного движения тела (траектории его точек конгруэнтны), а также, при решении задач.
[c.38]
Поэтому В (у (t)) = 3f t+ a, g g,), gi- VgW, = —7 Ф, g — константа. В этом случае дискриминант A=gl — 27g — =3 -4 (2U —9Ф ) > О, так как для системы (16) корни 1, 2, 3 уравнения 4x —gg = О — вещественные. Поэтому 2й —9Ф >0 в случае системы (16) с вещественными yj, р, q, г. В случае системы (16) с вещественными yj, р, q, г форма B y(t)) принимает конечные вещественные значения при всех i.
Поэтому мнимая часть константы Сз в формуле для B y t)) равна (2га+1)(Оз (где (Од —чисто мнимый примитивный полупериод функции i (z g , g-g)) и может быть заменена на (Од. Для системы (15) функция B x[t)) вещественна при всех t. Из формулы B x(t)) = = 3 tс gi, gi), полученной чисто алгебраически, и вещественности B x t)) следует, что 2 = ira((0i—(02)-f 2, где (Oj и (Oj —комплексно-сопряженные примитивные полупериоды для (г gi, gs), n—целое, /г —вещественное. Для любого такого прямая i+ g (—ооотносительно решетки периодов (порожденной 2а> , 2(и . Вблизи точки 2 = 0, (z g , gi) z . Поэтому любое решение x t) системы (15) (отличное от х = 0) за конечное время уходит на бесконечность и возвращается из бесконечности.
[c.294]Из этого частного случая вытекает, что если плоская фигура ограничена прямыми одного уровня, то она проецируется на параллельную плоскость проекций в конгруэнтную фигуру — без искажения, а в остальных случаях — с искажением. [c.11]
Проецирующие прямые — прямые, перпендикулярные к одной из плоскостей проекций (или параллельные одновременно двум плоскостям проекций — рис.
24). Следовательно, на комплексном чертеже одна из проекций проецирующей прямой превращается в точку, а другие — совпадают с линиями связи и конгруэнтны самой прямой.
[c.30]
Поэтому при перемещении горизонтальная проекция треугольника свою форму не меняет. Следовательно, справедлива теорема при плоскопараллельном движении фигуры относи тельно горизонтальной плоскости проекций фронтальные проекции ее точек перемещаются по прямым, пер пендикулярным линиям связи, а гори зонтальная проекция фигуры остается конгруэнтной самой себе. [c.85]
Для построения случайных точек в примере удобно использовать горизонтальные плоскости уровня у(у2). Плоскость у(у2) рассекает конус по параллели га(1П2 —> 1П ), а призму по треугольнику п(п2 -> П1), конгруэнтному основанию. Пересечение их горизонтальных проекций определяет точки 81 82 и 6 ->б2. Аналогично определены точки 5 ->52,31 32,41->42. [c.183]
Аналогично можно показать, что при перемещении, параллельном плоскости ,, расстояния между горизонтальными проекциями любой пары точек произвольной фигуры Ф остаются постоянными.
Таким образом, проекции Ф в начальный и Ф[ в конечный моменты перемещения конгруэнтны.
[c.64]
Замечая, что линии контура плана могут быть разделены на два пучка параллельных прямых, определяем перспективы несобственных точек (F и F ) каждого из пучков, причем точка F является перспективой несобственной точки пучка параллельных прямых направления I, а точка F — направления II. Обе точки найдены при помощи лучей SF и SF», соответственно параллельных прямым направлений I и II. Лучи SF и SF , будучи параллельными прямым, расположенным в горизонтальной плоскости, пересекут картину в точках, лежащих на линии горизонта h (черт. 355). При построении перспективы без увеличения отрезки PF и PF на черт. 355 конгруэнтны соответственно отрезкам PoF и PqF] на черт. 354. [c.166]
Справедлива аналогичная теорема о плоскопараллельном перемещении относительно 112. при плоскопараллельном движении фигуры относительно фронтальной плоскости проекций горизонтальные проекции ее точек перемещаются по прямым, перпендикулярным линиям связи, а фронтальная проекция фигуры остается конгруэнтной самой себе.
[c.57]
Движение образующей т может быть определено перемещением какой-либо ее точки М по бесконечно малым хордам направляющей п. Покажем, что образующие и направляющие поверхности параллельного переноса взаимозаменяемы, т. е. поверхность, образованная движением линии п по линии т, конгруэнтна поверхности, образованной движением линии т по линии п. [c.95]
Пусть линейчатая поверхность Ф определена двумя конгруэнтными пространственными кривыми а, а и взаимно однозначным соответствием Г, установленным между точками А А этих кривых. Пусть [c.108]
Поэтому, в отличие от скорости материальной точки или точки произвольно движущегося тела, которая есть вектор, приложенный к этой точке в данном ее положении, скорость твердого тела, движущегося поступательно, есть вектор свободный, ибо он может быть приложен к любой точке тела. Только в случае поступательного движения и можно говорить о скорости тела как целого. Траектории всех точек тела в этом случае суть конгруэнтные кривые, т.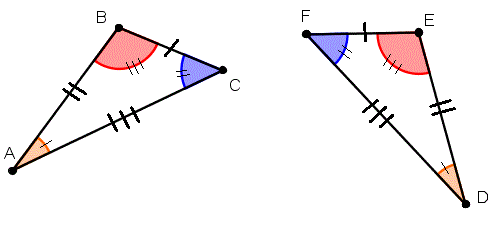
е. такие кривые, которые при наложении совпадают всеми своими точками.
[c.95]
При поступательном движении твердого тела траектории всех его точек при наложении совпадают (т. е. траектории конгруэнтны). [c.100]
Если колеса катятся по рельсу без скольжения, то точки Л и В, а следовательно, и точка Лi описывают укороченные циклоиды. Эти циклоиды одинаковой формы, параллельны в соответствующих точках и конгруэнтны. [c.102]
Развёртка конгруэнтна поверхности, т. е. если её наложить на поверхность, то соответствующие точки совпадут. Это значит, что между множествами точек поверхности и развёртки устанавливается взаимно однозначное соответствие, которое позволяет сформулировать следующие основные свойства развёрток [c.225]
T. e. точки описывают траектории (являющиеся конгруэнтными) по одному п тому же закону движения. [c.172]
Перенесем векторы скоростей у и ув1 в точки и В и найдем векторы приращения скоростей Ау и Ауд.
Рассмотрим треугольники АММ и BM N. Эти треугольники конгруэнтны (равны), и их равные стороны попарно параллельны, следовательно,
[c.100]
Соединим точки А а Аи В и В прямыми линиями и из середин полученных отрезков (точек М и М) восставим перпендикуляры до их взаимного пересечения в точке О. Эту точку соединим прямыми линиями с концами отрезков АВ и A Bt и получим два конгруэнтных (равных) треугольника, имеющих общую вершину О [c.116]
При поступательном движении твердого тела все его точки описывают конгруэнтные траектории и в каждый момент времени имеют одинаковые скорости и ускорения. [c.33]
Для нахождения постоянных р и Pi рассмотрим главный вектор всех сил, действующих вдоль некоторой дуги АВ, соединяющей две конгруэнтные точки. Выражение для,главного вектора имеет вид [187] [c.186]
Горизонтальная проекция Ai точки А описывает при этом кривую Ai Ai Ai …, конгруэнтную кривой А А А .
.., а во фронтальной проекции точка Аа перемещается по горизонтальной прямой Г А Аг Аг .,. (рис. 121, а и б).
[c.124]
При изменении момента сопротивления на валу гидромотора будет изменяться и мощность Л д при весьма незначительном изменении Ид = /4 ((>) (за счет изменения утечек с изменением напора). Кривая Мд = /д Q) будет перемещаться конгруэнтно по оси ординат, а Нц = /5 ( ) образует пучок кривых с несколько размытой общей точкой за счет изменения Qy (штрих-пунктир). [c.223]
Предположим, что в результате перемещения некоторая точка подвижной сферы из положения А (фиг. 1) в пространстве переместилась в точку В, в то время как та точка, которая раньше находилась в Вг заняла теперь новое положение С. Плоскость AB пересекает неподвижную сферу по окружности (обыкновенно, но не обязательно, малого круга). Если У—один из полюсов этого круга на сфере, то равнобедренные сферические треугольники AJB и BJ конгруэнтны.
Действительно, дуги АВ и ВС равны, так как они являются двумя положениями одной и той же дуги большого круга подвижной сферы. Таким образом дуга АВ может быть совмещена с дугой ВС при помощи вращения вокруг оси 0J на угол равный AJB 1).
[c.9]На основе данных работ [3, 4] дистектическая точка конгруэнтного плавления Nb отвечает температуре 3600 50° С и находится при 48% (ат.) С. [c.249]
V14.3. Прямыми уровня называют прямые, параллельные одной нз плоскостей проекций (см. рис. 3, б 22). На двухпроекцион-ном чертеже одна из проекций такой прямой будет перпендикулярна к линиям связи, так как одинаково удаление всех ее точек от параллельной плоскости проекций, а вторая — будет направлена под углом к линиям связи и конгруэнтна самой прямой (см. 2, п. 2.8). [c.30]
Построения на чертеже (рис. 78, б). Из точки В проведем перпен дикуляр к проекции А В, отложим на нем отрезок В Во = В В» и соединим прямой точки А и В .
Построенный треугольник А ВдВ конгруэнтен — треугольнику АВВ (см. рис. 78, а), так как конгруэнтны их катеты и угол между ними равен 90 . Следовательно, отрезок А Во конгруэнтен отрезку АВ и угол В А Во определяет угол наклона отрезка АВ к горизонтальной плоскости проекций.
[c.96]
Справедлива аналогичная теорема о плоскопараллельном перемещении относительно П2 при плоскопара.т лельном движении фигуры относи тельно фронтальной плоскости проек ций горизонтальные проекции ее то чек перемещаются по прямым, пер пендикулярным линиям связи, а фронтальная проекция фигуры оста ется конгруэнтной самой себе. [c.85]
Меридиан (A BD) и экватор (параллель точки А) сферы являются конгруэнтными линиями. Для построения любой точки поверхности используются параллели. [c.144]
Для определения положения плоскости в пространстве одной горизонтали ее недостаточно. Необходимо знать еще, например, положение какой-нибудь ее точки, не лежащей на горизонтали.
За такую точку проще всего принять точку D окружности, горизонтальная про—екция d которой на чертеже имеется и расстояние которой от горизонтали ОА известно точка D удалена от нее на расстояние радиуса окружности, который равен отрезку Ос. Фронтальная проекция d определится из прямоугольного треугольника Odd, построенного на отрезке Od, как на катете, гипотенуза которого Odx равна большой полуоси Ос. Катет ddi равен разности апликат точек D и О. Фронтальная проекция d будет удалена от фронтальной проекции горизонтали на расстояние dd. Задача имеет два решения в зависимости от того, вверх или вниз по отношению к фронтальной проекции Горизонтали отложить величину катета dd -, эти два решения представляют конгруэнтные фигуры, симметрично расположенные по отношению к плоскости, параллельной горизонтальной плоскости проекций и проходящей через горизонталь.
[c.10]
Горизонтальной плоскости проекций, и, следовательно, перпендикулярную проецирующим лучам, в виде треугольника, подобного треугольнику а Ь С.
Остается выполнить следующее к одной и, вершин треугольника аЬс, а Ь с, данного в исходном его положении, пристроить прямую — искомое направление косоугольного проецирования (относительно данной системы плоскостей проекций), соответствующее ортогонально проецирующему лучу, проходящему через одноименную вершину треугольника во вспомогательном его положении. Иначе говоря, на одном из ортогонально проецирующих лучей, например на луче, проходящем через точку В2 во вспомогательном положении треугольника А2В2С2, взять произвольную точку Л 2 и к данному треугольнику AB в точке В пристроить отрезок ВК так, чтобы фигуры АВСК и А2В2С2К2 были конгруэнтны. Тогда любая плоскость, перпендикулярная к прямой ВК, будет удовлетворять требованиям задачи.
[c.107]
Рассмотрим плоскопараллельное движение треугольника. Пусть треугольник AB совершает плоскопараллельное движение относительно горизонтальной плоскости проекций. То1да его вершины перемешаются в горизонтальных плоскостях, и угол наклона плоскости греугольника к плоскости IIi остается неизменным.
Следовательно, справедлива теорема 5 при плоскопараллельном движении фигуры относительно горизонтальной плоскости проекций фронтальные проекции ее точек перемещаются по прямым, перпендикулярным линиям связи, а горизонтальная проекция фигуры остается конгруэнтной самой себе.
[c.57]
Расчет любого зубчатого зацепления предполагает использование двух станочных зацеплений с соответствующими производящими колесами и производящими механизмами огибания. Если производящие поверхности могут быть приведены в такое положение, что они совпадают между собой при наложении друг с другом во всех точках, то такие поверхности называются конгруэнтной производящей парой. На рис. 12.8 показаны кисходные контуры I н 2 реечного профиля. Использование принципа конгруэнтной производящей пары упрощает анализ сопряженности боковых поверхностей в зацеплении, рода контакта, наличия или отсутствия интерференции профилей. [c.357]
Поступательным движением плоской фигуры будет такое движение, при котором любая прямая, взятая в плоскости движущейся фигуры, перемещается параллельно самой себе.
Из этого определения следует, так же как и в случае твердого тела (см. 8), что все точки фигуры (подвижной плоскости) в этом случае имеют равные скорости и ускоретя и описывают конгруэнтные траектории.
[c.101]
II равномерно. Конгруэнтность в этом случае означает параллельность нрямолиненных траекторий, по которым точки тела движутся с одинаковой скоростью. Такое движение может быть названо прямолинейным равномерным поступательным движением тела. [c.173]
Пусть точка М совершает плоскопараллельное движение относительно плоскости П,. Тогда траектория М М М … ее движения лежит в горизонтальной плоскости Е (рис. 180, а). Горизонтальная проекция М1 точки М описывает при этом кщъую М М М. .., конгруэнтную кривой а во фронтальной проекции точка М2 перемещается по горизонтальной прямой Е2=УИ УИ УИф.. (рис. 180, а и б). [c.141]
Мы можем рассматривать вопрос и с другой точки зрения. Рассмотрим точки тела, которые первоначально лежат на некоторой плоскости ш. Пусть ш та плоскость, иа которой эти же точки будут находиться после бесконечно малого перемещения. Пусть далее а какая-нибудь фигура на Л, а а ее положение в плоскости ш. Ортогональная проекция с» фигуры о на плоскость й может считаться конгруэнтной з, так как при бесконечно малом перемещении мы можем пренебрегать бесконечно малыми количествами второго порядка. Фигуры а и а» в общем случае не будут совпадать, но могут быгь совмещены при помощи некоторого вращения вокруг определенной точки О в плоскости Л ( Статика, 14, 15). Пусть т есть нормаль к плоскости 5 в точке О, а и — прямая пересечения плоскостей ш и й. Очевидно, что перемещение тела может рассматриваться, как последовательное вращение на определенные бесконечно малые углы поворота вокруг осей тип. Отсюда следует, что все нулевые прямые плоскости должны будут пересекать чак прямую т, так и прямую л, а следовательно, должны будут проходить и через точку О. Заметим, что прямые т я п представляют две сопряженные прямые, перпендикулярные между собою. Прямая п называется характеристикою» плоскости 3). [c.23]
Что такое нарушение прикуса — причины и рекомендации
Для того чтобы понять, что такое нарушение прикуса, следует определиться, каким должен быть естественный или физиологический прикус?
Во-первых, верхние зубы всегда крупнее нижних, поэтому они формируют бОльшую по площади зубную дугу. При смыкании верхних и нижних зубов между собой верхние передние зубы (резцы) перекрывают нижние, а верхние и нижние резцы контактируют между собой. Глубина перекрытия зубов составляет от 1/5 до 2/3 высоты коронки, при этом нет контакта нижних резцов с нёбом.
Во-вторых, каждый зуб контактирует с двумя зубами на противоположной челюсти (антагонистами).
В-третьих, жевательные зубы имеют выраженный рельеф – бугры и естественные ямочки (фиссуры). Соприкасаясь между собой, верхние и нижние зубы встречаются конгруэнтными (совмещаемыми) поверхностями: бугры взаимодействуют с ямками зубов-антагонистов, формируя фиссуро-бугорковый контакт. Все остальное – уже нарушение нормы.
Неправильный прикус вызывает у пациента проблемы трех типов:
- Психосоциальные проблемы, связанные с ухудшенной челюстно-лицевой эстетикой: человек с неровными зубами чаще всего, прячет свою улыбку, испытывает сложности в коммуникации с другими людьми и часто не считает себя достаточно симпатичным.
- Функциональные проблемы. Для адекватного измельчения пищи перед проглатыванием требуется определенное количество жевательных движений. Если существует проблема прикуса, эффективность жевания снижена, поскольку не все зубы контактируют с антагонистами (зубами противоположной челюсти). Из-за этого человеку приходится совершать большее число жевательных движений или проглатывать плохо пережеванную пищу. Кроме того, возможны расстройства височно-нижнечелюстного сустава: когда нарушается прикус, то естественная нагрузка на зубы, мышцы, костные структуры и сустав становится неравномерной. А это сильный дискомфорт или боль при открывании и закрывании рта, шум или щелчки при движении нижней челюсти, боль при пережевывании твёрдой пищи, головные боли.
- Нарушение прикуса часто способствует разрушению зубов и развитию заболеваний пародонта.
Остатки пищи между передними зубами; нижние резцы упираются в нёбо, и, тем самым, травмируют слизистую оболочку.
Преждевременные контакты между зубами чреваты повышенной стираемостью и, как следствие, появлением повышенной чувствительности от кислых, сладких и температурных раздражителей. Отклонение верхних зубов вперёд увеличивает вероятность травм; травмирующая глубокая окклюзия, при которой нижние передние зубы соприкасаются с небом, и /или верхние зубы касаются десны противоположной челюсти, могут привести к значительным дефектам ткани.
Верхние передние зубы полностью перекрывают нижние и касаются десны противоположной челюсти, вызывая травму пародонта
В результате постоянной травмы десны произошло обнажение части корней нижних зубов.
В некоторых случаях нарушение прикуса у взрослых делает невозможным протезирование зубов, поэтому требуется предварительная ортодонтическая подготовка.
Ортопантомограмма пациента И., 43 года. Вследствие потери нижнего зуба (на снимке справа) произошло наклонное смещение позади стоящих зубов, отсутствует пространство для имплантации.
Более 80% населения во всём мире имеет нарушение прикуса. Неутешительная статистика. Однако с каждым годом растет число людей, готовых начать лечение. Все, кто решился исправить прикус, отмечают заметные перемены по окончании терапии: заметно улучшается форма лица и профиль, в некоторых случаях контур губ становится объемнее, сам человек в целом выглядит намного привлекательнее. Кроме того, естественный процесс пережевывания пищи после исправления прикуса не вызывает никаких сложностей, прекращаются головные боли, щелчки в нижнечелюстном суставе и прочие сопутствующие неправильному прикусу проблемы. Качество жизни заметно улучшается!
Почему неправильный прикус надо исправлять?
Определение конгруэнтности по Merriam-Webster
con · gru · ent | \ kən-ˈgrü-ənt , ˈKäŋ-grü-ənt \ 1 : совпадающие … Установить стимулы и вознаграждения, соответствующие профессиональному положению.- Тимоти С. Хили2 : совмещаются так, чтобы полностью совпадать. конгруэнтные треугольники
3 : с разницей, кратной данному модулю 12 сравнимо с 2 (по модулю 5), так как 12−2 = 2 · 5.
конгруэнтных треугольников — открытый справочник по математике
конгруэнтный треугольник — открытый справочник по математикеОпределение: треугольники — это конгруэнтный когда все соответствующие стороны и внутренние углы конгруэнтный.Треугольники будут иметь одинаковую форму и размер, но один может быть зеркальным отражением другого.
В простом случае ниже два треугольника PQR и LMN равны конгруэнтный потому что каждая соответствующая сторона имеет одинаковую длину и каждый соответствующий угол имеет одинаковую меру. Угол в точке P имеет ту же величину (в градусах), что и угол в точке L, сторона PQ имеет такую же длину, что и сторона LM и т.
Попробуйте Перетащите любую оранжевую точку на P, Q, R. Другой треугольник LMN изменится, чтобы оставаться конгруэнтным ему.
На схеме выше треугольники нарисованы рядом друг с другом, и очевидно, что они идентичны. Однако один треугольник можно повернуть, перевернуть (отразить) или два треугольника могут иметь общую сторону. Эти случаи обсуждаются далее на других страницах:
Представьте себе треугольники картонные
Один из способов представить себе соответствие треугольников — представить, что они сделаны из картона. Они совпадают, если вы можете перемещать их, вращать и переворачивать различными способами, чтобы они сделайте кучу там, где они точно ложатся друг на друга.
Как определить, совпадают ли треугольники
Любой треугольник определяется шестью мерками (три стороны, три угла). Но вам не нужно знать их все, чтобы показать, что два треугольника конгруэнтны. Подойдут разные группы по три человека. Треугольники конгруэнтны, если:- SSS (боковая сторона)
Все три соответствующие стороны равны по длине.
См. Конгруэнтность треугольника (боковая сторона). - SAS (сторона бокового угла)
Пара соответствующих сторон и включенный угол равны.
См. Конгруэнтность треугольника (сторона бокового угла). - ASA (угол стороны угла)
Пара соответствующих углов и включенная сторона равны.
См. Конгруэнтность треугольника (боковой угол). - AAS (сторона углового угла)
Пара соответствующих углов и невключенная сторона равны.
См. Конгруэнтность треугольника (сторона угла). - HL (катет гипотенузы прямоугольного треугольника)
Два прямоугольных треугольника равны, если гипотенуза и один катет равны.
См. Конгруэнтность треугольника (катет гипотенузы).
AAA не работает.
Если все соответствующие углы треугольника одинаковы, треугольники будут одной формы, но не обязательно одинакового размера. Подробнее об этом см. Почему AAA не работает.
Они называются подобными треугольниками (см. Подобные треугольники).
SSA не работает.
Учитывая две стороны и не включенный угол, можно нарисовать два разных треугольника, удовлетворяющих указанным значениям.Следовательно, недостаточно доказать конгруэнтность. См. Почему не работает SSA.
Конструкции
Еще один способ подумать об этом — спросить, можно ли построить уникальный треугольник, исходя из того, что вы знаете. Например, если вам даны длины двух сторон и включенный угол (SAS), вы можете нарисовать только один возможный треугольник. Если бы вы нарисовали два из них, они были бы одинаковой формы и размера — определение конгруэнтности. Для получения дополнительной информации о конструкциях см. Введение в конструкции.Свойства конгруэнтных треугольников
Если два треугольника конгруэнтны, то каждая часть треугольника (сторона или угол) конгруэнтна соответствующей части другого треугольника.В этом истинная ценность концепции; как только вы докажете, что два треугольника совпадают, вы можете найти углы или стороны одного из них от другого.
Чтобы запомнить эту важную идею, некоторые считают полезным использовать аббревиатуру CPCTC, что означает « C или соответствующие P art of C ongruent T ongruent являются C ongruent».
Помимо сторон и углов, все остальные свойства треугольника такие же, такие как площадь, периметр, расположение центров, окружностей и т. Д.
Другие темы сравнения
Конгруэнтные треугольники
Конгруэнтные многоугольники
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
Конгруэнтные формы — Преобразования — Edexcel — GCSE Maths Revision — Edexcel
Две формы одинакового размера и одинаковой формы равны конгруэнтным .
Формы A, B, E и G совпадают. Они идентичны по размеру и форме.
Конгруэнтные треугольники
Для того, чтобы два треугольника были конгруэнтными, необходимо выполнение одного из 4 критериев.
Три стороны равны (SSS: сторона, сторона, сторона)
Два угла одинаковы и соответствующая сторона одинакова (ASA: угол, сторона, угол)
Две стороны равны, и угол между две стороны равны (SAS: сторона, угол, сторона)
Прямой угол, гипотенуза и соответствующая сторона равны (правая сторона, прямой угол, гипотенуза, сторона)
Пример 1
Укажите, совпадают ли два треугольника .Укажите причину в поддержку своего ответа.
Да — SSS, три стороны равны.
Пример 2
Укажите, совпадают ли два треугольника. Укажите причину в поддержку своего ответа.
Да — ПРАВ.
- Вопрос
Укажите, совпадают ли два треугольника. Укажите причину в поддержку своего ответа.
- Показать ответ
Нет — на левой диаграмме длина 7 см находится между углами 40 ° и 60 °.На правой диаграмме это не так.
Конгруэнтное определение. Что означает конгруэнтность?
Конгруэнт имеет два значения. Это может относиться к двум или более предметам, находящимся в гармонии. Когда вещи конгруэнтны, они согласуются и пропорциональны друг другу. Когда вещи совпадают, это означает, что они находятся в мирном консенсусе. В этих терминах часто говорят о поощрении и вознаграждении.
Стимул к чему-либо должен соответствовать тому, что человека просят сделать.Стимул может быть денежным или любым, что требуется человеку, которого просят выполнить задание. Например, зарплата должна соответствовать той работе, которую кого-то просят сделать.
Другой пример того, что что-то конгруэнтно, можно использовать для описания дружбы или других отношений.
- Политические взгляды двух людей не совпадали.
- Результаты лабораторных исследований не соответствовали образцу подозреваемого, поэтому он был освобожден.
- Несмотря на наши различия, нам необходимо согласованно работать вместе.
У этого определения конгруэнтности много синонимов. Вот некоторые из самых популярных.
Согласие — означает, что две или более вещи согласуются или совместимы. Это означает, что две вещи идут вместе или хорошо работают вместе.
- Нам нужно найти музыку, соответствующую битве, которая происходит на экране.
- После расследования полиция определит, соответствуют ли доказательства показаниям свидетелей.
Совпадающий — означает, что две или более вещи находятся в согласии или находятся в гармонии. Конгруэнтное может использоваться как синоним конгруэнтного.
- Квотербек и принимающий не соответствовали друг другу, что привело к перехвату.
- Речи и язык тела близнецов совпадали.
Соглашение — относится к двум или более вещам или людям, находящимся в гармонии или соответствии в своих мнениях или чувствах.Это также может относиться к результату того, что два или более людей или организаций пришли к соглашению или согласились с условиями.
- Обе компании пришли к соглашению о дальнейших действиях по слиянию.
- Теперь, когда мы уладили спор, согласны ли мы.
Гармоничный — означает, что что-то свободно от разногласий или несогласий. Это также относится к чему-то приятному.
- Они вместе уже 20 лет, и их связывают удивительно гармоничные отношения.
- После долгих лет гармонии они наконец высказали свое мнение, и завязался спор.
Несоответствующий — относится к чему-то, что не гармонично, и не соответствует или не соответствует своему окружению. По сути, то, что несовместимо, не принадлежит.
- Когда она появилась в джинсах и увидела, что все остальные носят бальные платья, она почувствовала себя несовместимой со своим окружением.
- Комната была такой красивой, но искусственное растение в ванной казалось несовместимым с окружающей ее элегантностью.
Несоответствующее — относится к чему-то или кому-то, что не подходит или не подходит для данных обстоятельств. Когда что-то неуместно, это может быть правильным для другой ситуации, но это не подходит для текущей ситуации, в которой он находится.
- Комментарий, сделанный за ужином, был неуместным, учитывая, что она впервые встречает этих людей.
- Во что ты наденешь завтра? Я хочу убедиться, что не ношу что-то неуместное.
Конгруэнтное значение также обычно используется в геометрии. Это означает, что две формы или фигуры идентичны, и они точно совпадают, когда они накладываются друг на друга или помещаются друг на друга. Проще говоря, это означает, что две вещи имеют одинаковый размер и форму.
- Два треугольника равны.
- Вы можете сказать, что треугольники совпадают, потому что все три угла одинаковы.
- У правильного многоугольника восемь совпадающих сторон, а также восемь совпадающих углов.
Есть несколько синонимов для этого определения конгруэнтности. Вот некоторые из самых популярных.
Соответствие — означает, что что-то соответствует правилам. Это также может означать, что поведение человека соответствует тому, как должно быть.
- Дисциплина и соответствие своим ценностям — две характеристики, которые родители искали в школе.
- Требуется соответствие доктрине.
Match- относится к людям или предметам, которые похожи или соответствуют друг другу.
- Для близнецов очень типично носить подходящие наряды.
- Пожалуйста, убедитесь, что две ткани совпадают.
Вот самый распространенный антоним этого определения конгруэнтности.
Конфликт- имеет много значений, как антоним конгруэнтности, он относится к несовместимости между двумя или более идеями, интересами или вещами.
- Убедитесь, что эти цвета не конфликтуют друг с другом.
- Надеюсь, на сегодняшней встрече не будет конфликта.
Что такое конгруэнтная форма? [Видео и практические вопросы]
Соответствующие формы
Привет, ребята! Добро пожаловать в этот видеоролик о подходящих объектах.
Что происходит, когда я беру этот объект
и переворачиваю его?
Выглядит по-другому, правда? Но разве не все стороны одинаковы? Если я переверну его, мы ясно увидим, что эти два объекта одинаковы.
Это то, что мы называем конгруэнтными объектами — формами, которые можно переворачивать, поворачивать, сдвигать, чтобы получить ту же форму. Все стороны каждой фигуры должны быть одинаковыми.
Есть несколько различных способов перемещения конгруэнтных объектов. Перемещение объекта с помощью одного из этих трех движений может изменить положение или способ внешнего вида формы, но сама форма всегда останется прежней.
Первое движение, о котором мы поговорим, — это вращение на . Один из способов перемещения конгруэнтной формы — это ее повернуть или повернуть.
Второй механизм — это отражение . Отражение происходит, когда объект переворачивается по воображаемой линии или оси. Это похоже на то, как если бы объект смотрел на себя в зеркало.
Третья и последняя часть — это перевод . Перевод происходит, когда вы перемещаете фигуру, просто перемещая ее в любом направлении. Таким образом, вы не поворачиваете его или переворачиваете, вы просто скользите.
Хорошо, теперь пора взглянуть.
Эти два треугольника совпадают, но они перевернуты по оси y.Итак, это отражение. Это все тот же треугольник, с той лишь разницей, что он перевернут.
Эти два треугольника тоже совпадают, но они были повернуты или повернуты.
Эти две стрелки идентичны по форме и размеру; Итак, мы знаем, что они совпадают. Однако они были сдвинуты вверх. Это движение — перевод.
Хорошо, теперь ваша очередь практиковаться.
Определите, совпадают ли следующие формы. Если они совпадают, то определите, как они были перемещены — отражением, вращением или перемещением.
Эти две формы совпадают?
Нет, они не совпадают. Мы видим, что они разных размеров: одна звезда имеет шесть точек, а другая — пять. Чтобы увидеть это более четко, мы можем разместить их друг на друге.
Эти две формы совпадают?
Ага! Мы видим, что они идентичны; однако они были перемещены. Что это за движение? Ну, похоже, их просто перевернули, не так ли? Если мы представим, что есть линия через середину, мы увидим, что они были перевернуты через линию.Эта форма была отражена.
Эти две формы совпадают?
Нет. Мы можем увидеть, что они разного размера, поместив их друг на друга.
Хорошо, последний. Эти две формы совпадают?
Ага! Они идентичны по форме и размеру, но какой тип механизма был сделан? Он был перевернут, как последний? Нет, это не отражение. Он был повернут или повернут? Нет, значит, это не ротация. Его сдвинули? Да, поэтому мы знаем, что это перевод.
Что такое конгруэнтные числа? — Определение и примеры — Видео и стенограмма урока
Примеры конгруэнтности
Конгруэнтность — это то, что имеют две цифры, если они конгруэнтны. Эти формы явно демонстрируют соответствие, потому что они абсолютно одинаковы:
А как насчет этих форм?
Один треугольник указывает вверх, а другой — вниз.Однако, если бы вы измерили их, вы бы обнаружили, что соответствующие стороны обоих треугольников абсолютно одинаковы. Фактически, второй треугольник такой же, как и первый; его только что повернули. Итак, эти формы совпадают.
Важно помнить, что направления фигур не влияют на их конгруэнтность. Пока они одинаковой формы и имеют одинаковые размеры, они конгруэнтны.
Теперь посмотрим на квадраты:
Это оба квадрата, но один намного меньше другого.Хотя они одинаковой формы, эти две фигуры не одинакового размера. Следовательно, эти квадраты неконгруэнтны или не конгруэнтны.
Последний пример:
Хотя эти фигуры не совсем те формы, которые мы привыкли видеть, они состоят из одних и тех же линий и кривых и имеют одинаковый размер. Единственная разница в том, что одно является отражением другого, но они все равно конгруэнтны, поскольку имеют точно такие же формы и размеры.
Резюме урока
Любые фигуры (даже если их больше двух) одинаковой формы и размера, совпадают с . Неважно, смотрят ли они в разные стороны или одно является отражением другого. Пока форма и размер точно такие же, фигуры совпадают.
Конгруэнтные цифры Словарь и определения
| Словарь | Определения |
|---|---|
| Конгруэнтное | фигуры, даже если они отражены или повернуты, одинаковой формы и размера |
| Неконгруэнтный | фигурки, различающиеся по размеру и форме |
| Соответствие | что имеют две цифры, если они совпадают |
Результаты обучения
По завершении этого урока учащиеся готовы:
- Описывать совпадающие цифры
- Уметь определять соответствие
- Определите, когда формы несовместимы
FAQ: Что означает конгруэнтность?
Что означает конгруэнтность в математике?
Конгруэнтность означает одинаковый размер и форму.Не имеет значения, являются ли они зеркальным отображением друг друга или перевернутыми. Если бы вы могли вырезать их и положить друг на друга, чтобы показать, что они одного размера и формы, они будут считаться конгруэнтными.
Что означает конгруэнтность?
1: качество или состояние согласия, совпадения или совпадения… счастливое совпадение природы и разума… — Гертруда Химмельфарб. 2: утверждение, что два числа или геометрические фигуры совпадают.
Как мне узнать свой SSS SAS ASA AAS?
Есть пять способов определить, совпадают ли два треугольника: SSS, SAS, ASA, AAS и HL.SSS (сторона, сторона, сторона) SSS означает «сторона, сторона, сторона» и означает, что у нас есть два треугольника, все три стороны которых равны. SAS (сторона, угол, сторона) ASA (угол, сторона, угол) AAS (угол, угол, сторона) HL (гипотенуза, катет)
Что такое конгруэнтный угол?
Конгруэнтные углы — это углы с точно такой же мерой. Пример: На показанном рисунке A конгруэнтно B; они оба измеряют 45 °.
Как доказать конгруэнтность формы?
Конгруэнтные формы Три стороны равны (SSS: сторона, сторона, сторона) Два угла одинаковы и соответствующая сторона одинакова (ASA: угол, сторона, угол) Две стороны равны, а угол между двумя сторонами равен равный (SAS: сторона, угол, сторона)
Какой пример конгруэнтной формы?
Обычно мы оставляем за собой конгруэнтность для двухмерных фигур, но трехмерные фигуры, такие как наши шахматные фигуры, тоже могут быть конгруэнтными.Подумайте обо всех пешках на шахматной доске. Все они совпадают. Подводя итог, конгруэнтные фигуры идентичны по размеру и форме; длина сторон и углы одинаковы.
Что означает конгруэнтная форма?
В геометрии две фигуры или объекта являются конгруэнтными, если они имеют одинаковую форму и размер, или если один имеет такую же форму и размер, что и зеркальное отображение другого. Это означает, что любой объект можно перемещать и отражать (но не изменять размер) так, чтобы он точно совпадал с другим объектом.
Какое еще слово обозначает конгруэнтность?
Какое еще слово означает конгруэнтность?
| совместимый | совпадающие |
|---|---|
| гармоничный | идентичный |
| неконфликтный | приятный |
| одновременно | совпадают |
| согласование UK | согласование США |
Какой знак конгруэнтности?
Символ ≡ означает «соответствует».Два треугольника похожи, если имеют одинаковую форму. Два одинаковых треугольника равноугольные, т. Е. Соответствующие углы равны.
Что такое правило сравнения ASA?
ASA (Угол-Сторона-Угол) Если любые два угла и сторона, включенные между углами одного треугольника, эквивалентны соответствующим двум углам и стороне, включенной между углами второго треугольника, то два треугольника считаются конгруэнтными по формуле Как правило .
Что такое SSS SAS ASA AAS?
Эти 5 условий: — SSS (сторона, сторона, сторона) — SAS (сторона, угол, сторона) — ASA (угол, сторона, угол) — AAS (угол, угол, сторона) — HL (гипотенуза, катет) Конгруэнтно треугольники не следует путать с аналогичными треугольниками (треугольники, размер которых увеличивается относительно друг друга) Музыка Адриана фон Циглера.Показать больше.
Что доказывает SSS?
Сторона-Сторона-Сторона — это правило, используемое для доказательства того, что данный набор треугольников конгруэнтен. Правило SSS гласит: Если три стороны одного треугольника равны трем сторонам другого треугольника, то треугольники равны.
Как определить, конгруэнтен ли угол?
Углы совпадают, если у них одинаковая угловая величина в градусах. Они могут быть в любой ориентации на плоскости. На рисунке выше есть два совпадающих угла.Обратите внимание, они указывают в разных направлениях.
Как узнать, совпадают ли углы?
Два угла конгруэнтны, если имеют одинаковую величину.