18,9% людей имеют акцентуацию «Циклоид»
Акцентуации характера как чрезмерные проявления определенных черт характера являются крайним состоянием нормы, хотя излишняя выраженность некоторых из них и может быть предпосылкой к определенного рода психическим расстройствам.
Считается, что больше всего акцентуаций у молодежи и с возрастом некоторые из них проходят или смягчаются, оказывая все меньше воздействия на повседневную жизнь.
Давайте узнаем, у кого каких акцентуаций больше
Для этого использовался тест Личко на акцентуации характера. В опросе приняло участие 6 092 человека разного пола и возраста.
Оказалось, что самые распространенные акцентуации это:
- Циклоид (18,19%) – смена настроения с определенной периодичностью.
- Психастеник (12,25%) – высокая склонность к самоанализу и «самокопанию».
-
Лабильный (10,67%) – резкие спонтанные перепады настроения.

- Параноик (8,01%) – глубокая фиксация на какой-либо идее.
И это в процентном соотношении к общему количеству опрощенных. Получается, что каждый пятый человек – «Циклоид».
Акцентуации и возраст
Почти половина всех опрошенных оказалась в возрасте от 25 до 34 лет.
Как и говорила теория, с возрастом количество акцентуаций у людей уменьшается и это можно увидеть на диаграмме самой часто встречаемой акцентуации «Циклоид»:
Стоит отметить, что это именно процентное отношение обладателей данной акцентуации к общему количеству человек данного возраста, соответственно тот факт, что больше всего прошедших опрос имеют возраст 25-34 года на результат не повлиял. Как мы можем увидеть, к 35-44 годам у половины людей акцентуация «Циклоид» проходит, причем такая картина характерна почти всем акцентуациям, а некоторым даже в большей степени.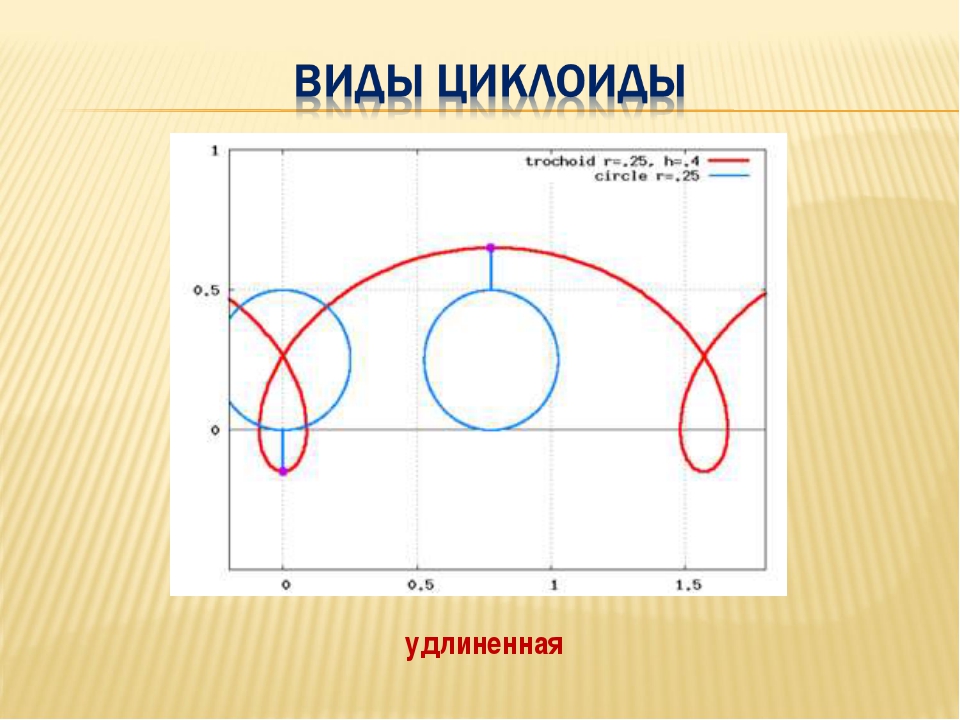
- «Дистимный тип» в возрасте до 17 лет имеют 9,05% человек, а в 35-45 лет уже только 1,45%, то есть в 6 раз меньше людей.
- «Эпилептоид» – в возрасте до 17 лет 5,83% а к 35-45 годам только 0,48.
- Единственным исключением из всех является гипертимный тип – только в 45-60 лет их количество снижается в 2 раза, в остальных возрастах это в среднем 3,5%.
Акцентуации и пол
У мужчин и женщин, как известно особенности характера значительно отличаются, и, как следовало ожидать, преобладающие акцентуации различны.
Среди мужчин больше:
- Параноик – 11,1% (у женщин – 7,18%).
- Шизоид – 10,07% (у женщин – 5,89%).
- Гипертим – 5,05% (у женщин – 3,81%).
А у женщин:
- Циклоид – 19,84% (мужчины – 12,03%).
- Психастеник – 13,09% (мужчины – 9,08).
-
Лабильный – 12,03% (мужчины – 5,59%).

Акцентуации и образование
При увеличении уровня образования результаты теста показали, что количество акцентуаций уменьшается, хотя это может и быть влиянием возраста.
Акцентуации и семейное положение
Почти по всем акцентуациям среди людей, состоящих в официальном браке независимо от возраста количество имеющих акцентуации в полтора-два раза меньше. Но особо стоит отметить тех, кто никогда еще не был в браке – у них, количество людей с акцентуациями в 2-3 раза больше, чем у остальных.
Акцентуации и среднемесячный доход
С ростом дохода количество большинства акцентуаций уменьшается, но некоторые увеличивается (параноик, гипертим), или остаются неизменными (астенический, неустойчивый, истероид, эпилептоид).
Что интересного можно сказать об акцентуациях?
- с возрастом их количество уменьшается в 2-3 раза;
- у каждого пятого человека есть акцентуация «Циклоид»;
- у женщин чаще встречаются, чем у мужчин акцентуации: лабильный, циклоид, психастеник;
- у мужчин чаще чем у женщин встречаются акцентуации: параноик, шизоид, гипертим;
-
у людей в браке в 1.

- те, кто больше зарабатывает чаще имеют акцентуации параноик и гипертим.
Изображение в шапке — Lidya Nada, Unsplash.
Изображение –
ЦИКЛОИДА | Энциклопедия Кругосвет
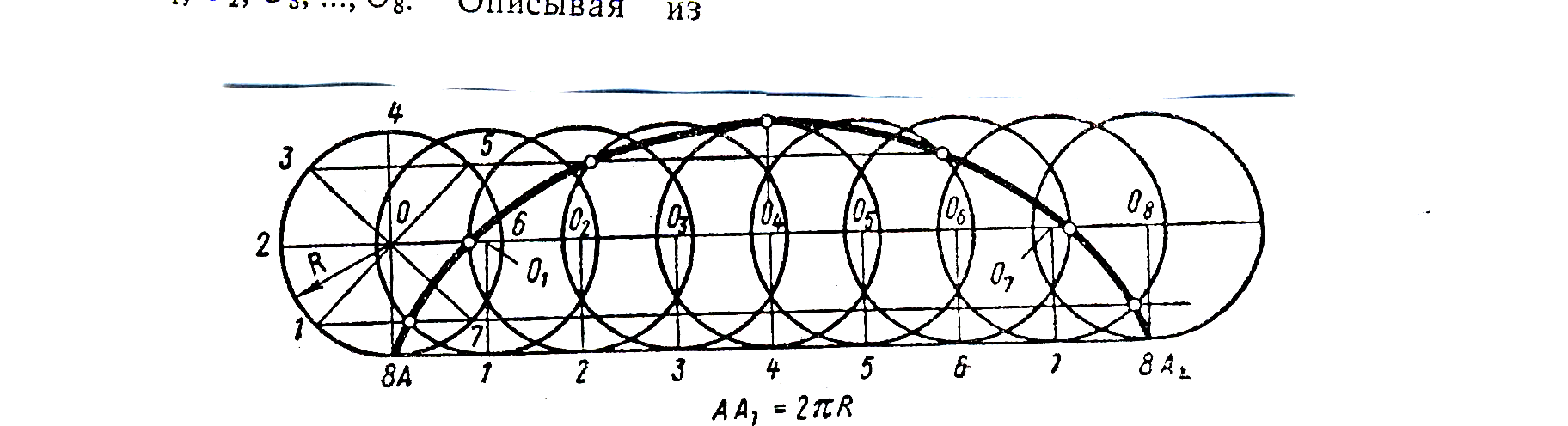
ЦИКЛОИДА (в переводе с греч. кругообразный) – плоская трансцендентная кривая, которую описывает точка окружности радиуса r, катящейся по прямой без скольжения (трансцендентной кривой называется кривая, которая в прямоугольных координатах не может быть описана алгебраическим уравнением). Ее параметрическое уравнение
x = rt – r sin t,
y = r – r cos t
Точки пересечения циклоиды с прямой, по которой катится окружность (эта окружность называется производящей, а прямая, по которой она катится, – направляющей), называются точками возврата, а самые высокие точки на циклоиде, расположенные посредине между соседними точками возврата, называются вершинами циклоиды.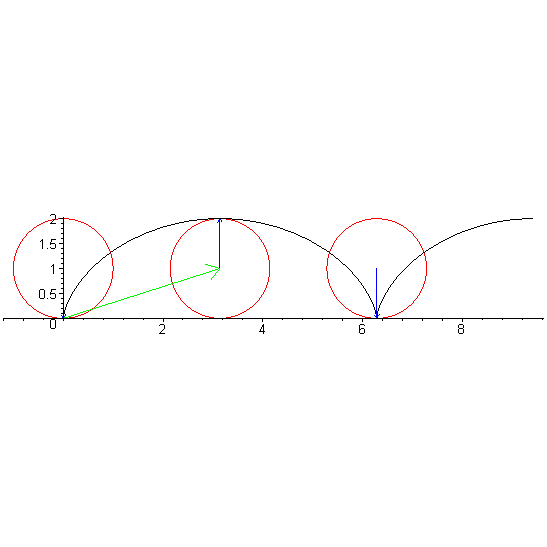
Первым изучать циклоиду начал Галилео Галилей. Длина одной арки циклоиды была определена в 1658 английским архитектором и математиком Кристофером Реном, автором проекта и строителем купола собора Святого Павла в Лондоне. Оказалось, что длина циклоиды равна 8-ми радиусам производящей окружности.
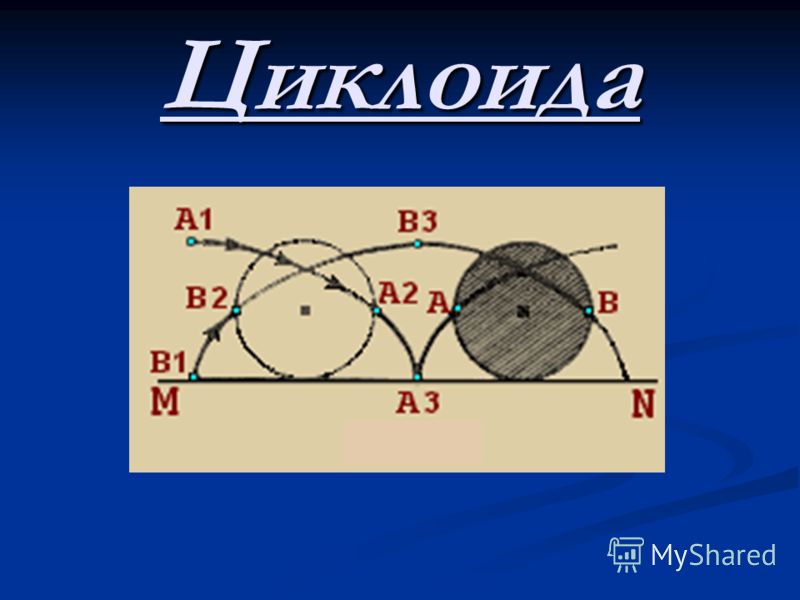
Одно из замечательных свойств циклоиды, давшее ей название – брахистохрона (от греческих слов «кратчайший» и «время) связано с решением задачи о наискорейшем спуске. Встал вопрос, какую форму надо придать хорошо отшлифованному (чтобы практически исключить трение) желобу, соединяющему две точки, чтобы шарик скатился вниз от одной точки к другой в кратчайшее время. Братья Бернулли доказали, что желоб должен иметь форму опрокинутой вниз циклоиды.
Родственные циклоиде кривые можно получить, рассматривая траектории точек, не находящихся на производящей окружности.
Пусть точка С0 находится внутри окружности.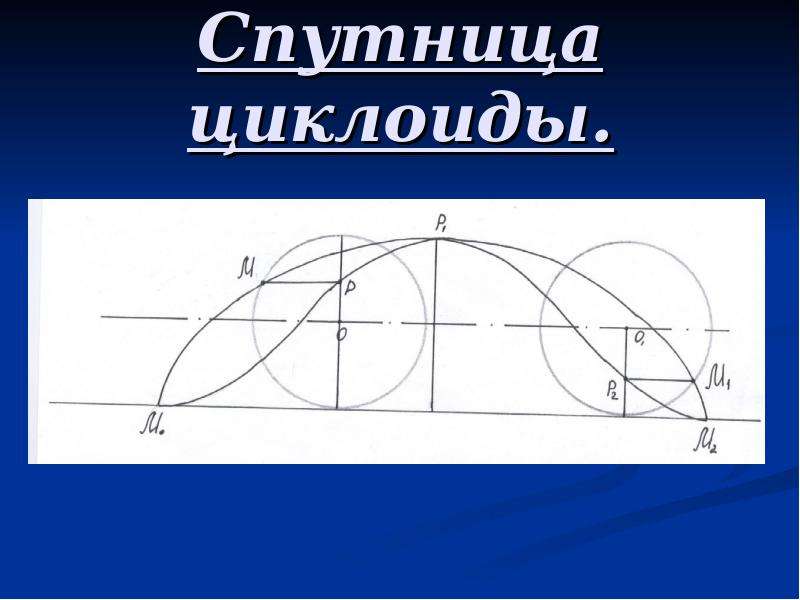 Если провести через С0 вспомогательную окружность с тем же центром, что и у производящей окружности, то при качении производящей окружности по прямой АВ маленькая окружность будет катиться по прямой A´В´, но ее качение будет сопровождаться скольжением, и точка
Если провести через С0 вспомогательную окружность с тем же центром, что и у производящей окружности, то при качении производящей окружности по прямой АВ маленькая окружность будет катиться по прямой A´В´, но ее качение будет сопровождаться скольжением, и точка
Аналогичным образом определяется удлиненная циклоида – это траектория точки, расположенной на продолжении радиуса производящей окружности, при этом качение сопровождается скольжением в противоположном направлении.
Циклоидальные кривые применяются при многих технических расчетах и свойства их используются, например, при построении профилей зубьев шестерен, в циклоидальных маятниках, в оптике и, таким образом, изучение этих кривых важно с прикладной точки зрения. Не менее важно и то, что, изучая эти кривые и их свойства, ученые 17 в. разрабатывали приемы, которые привели к созданию дифференциального и интегрального исчислений, а задача о брахистохроне явилась шагом к изобретению вариационного исчисления.
Елена Малишевская
Проверь себя!
Ответь на вопросы викторины «Математика»
Как звали математика, который в 19 лет решил задачу, не поддававшуюся усилиям лучших геометров со времен Евклида?
Циклоидный тип. Психология и психоанализ характера
Циклоидный тип
Как известно, этот тип был описан Кречмером и сперва стал широко использоваться в психиатрических исследованиях. П. Б. Ганнушкин включил в «группу циклоидов» четыре типа психопатов — «конституционально-депрессивных», «конституционально-возбужденных» (гипертимных), циклотимиков и эмотивно-лабильных. Циклотимия им рассматривалась как тип психопатии. Однако в дальнейшем под этим понятием стали подразумевать относительно легкие случаи маниакально-депрессивного психоза. Существование циклоидности за рамками этого заболевания было поставлено под сомнение. С 40-х годов термин циклоидная психопатия исчез из психиатрических руководств. И лишь в редких современных работах циклоиды упоминаются как преморбидныи тип больных эндогенными психозами, причем они не дифференцируются от гипертимов.
Между тем существует особая группа случаев, когда циклические изменения эмоционального фона никогда даже не приближаются к психотическому уровню. Г.Е.Сухарева отметила, что такие непсихотические циклотимические колебания у подростков с наступлением зрелости могут полностью сгладиться. Подобные случаи, с нашей точки зрения, правомерно было бы рассматривать как циклоидную акцентуацию.
Наши исследования показали, что в подросковом возрасте можно видеть два варианта циклоидной акцентуации — типичные и лабильные циклоиды.
Типичные циклоиды в детстве ничем не отличаются от сверстников или чаще производят впечатление гипертимов. С наступлением пубертатного периода (у девочек это может совпасть с менархе) возникает первая субдепрессивная фаза. Ее отличает склонность к апатии и раздражительности. С утра ощущается вялость и упадок сил, все валится из рук. То, что раньше давалось легко и просто, теперь требует неимоверных усилий. Труднее становится учиться. Людское общество начинает тяготить, компании сверстников избегаются, приключения и риск теряют всякую привлекательность. Прежде шумные и бойкие подростки в эти периоды становятся вялыми домоседами. Падает аппетит, но вместо свойственной выраженным депрессиям бессонницы нередко наблюдается сонливость. Созвучно настроению все приобретает пессимистическую окраску. Мелкие неприятности и неудачи, которые обычно начинают сыпаться из-за падения работоспособности, переживают крайне тяжело. На замечания и укоры нередко отвечают раздражением, порою грубостью и гневом, но в глубине души впадая еще в большее уныние. Серьезные неудачи и нарекания окружающих могут углубить субдепрессивное состояние или вызвать острую аффективную реакцию с суицидными попытками. Обычно лишь только в этом случае циклоидные подростки попадают под наблюдение психиатра.
Прежде шумные и бойкие подростки в эти периоды становятся вялыми домоседами. Падает аппетит, но вместо свойственной выраженным депрессиям бессонницы нередко наблюдается сонливость. Созвучно настроению все приобретает пессимистическую окраску. Мелкие неприятности и неудачи, которые обычно начинают сыпаться из-за падения работоспособности, переживают крайне тяжело. На замечания и укоры нередко отвечают раздражением, порою грубостью и гневом, но в глубине души впадая еще в большее уныние. Серьезные неудачи и нарекания окружающих могут углубить субдепрессивное состояние или вызвать острую аффективную реакцию с суицидными попытками. Обычно лишь только в этом случае циклоидные подростки попадают под наблюдение психиатра.
У типичных циклоидов фазы обычно непродолжительны и длятся две-три недели. Субдепрессия может смениться обычным состоянием или периодом подъема, когда циклоид снова превращается в гипертима, стремится в компании, заводит знакомства, претендует на лидерство и легко наверстывает упущенное в занятиях. Периоды подъема случаются реже, чем субдепрессивные фазы, и по выраженности бывают менее ярки. Лишь несвойственные им обычно рискованные шутки над старшими, да стремление везде и всюду острить бросается в глаза окружающим в эти периоды.
Периоды подъема случаются реже, чем субдепрессивные фазы, и по выраженности бывают менее ярки. Лишь несвойственные им обычно рискованные шутки над старшими, да стремление везде и всюду острить бросается в глаза окружающим в эти периоды.
У циклоидных подростков имеются свои «места наименьшего сопротивления». Важнейшим из них, вероятно, является неустойчивость к коренной ломке жизненного стереотипа. Этим, видимо, объясняются присущие циклоидам затяжные субдепрессивные реакции на первом курсе высших учебных заведений. Резкое изменение характера учебного процесса, обманчивая легкость первых студенческих дней, отсутствие ежедневного контроля со стороны преподавателей, сменяющееся необходимостью усвоить в короткий период зачетно-экзаменационной сессии гораздо больший, чем в школе, материал — все это ломает привитый предшествующим десятилетием учебный стереотип. Способность в период подъема на лету усваивать материал школьной программы здесь оказывается недостаточной. Упущенное приходится наверстывать усиленными занятиями, а в субдепрессивной фазе и это не приводит к желаемым результатам.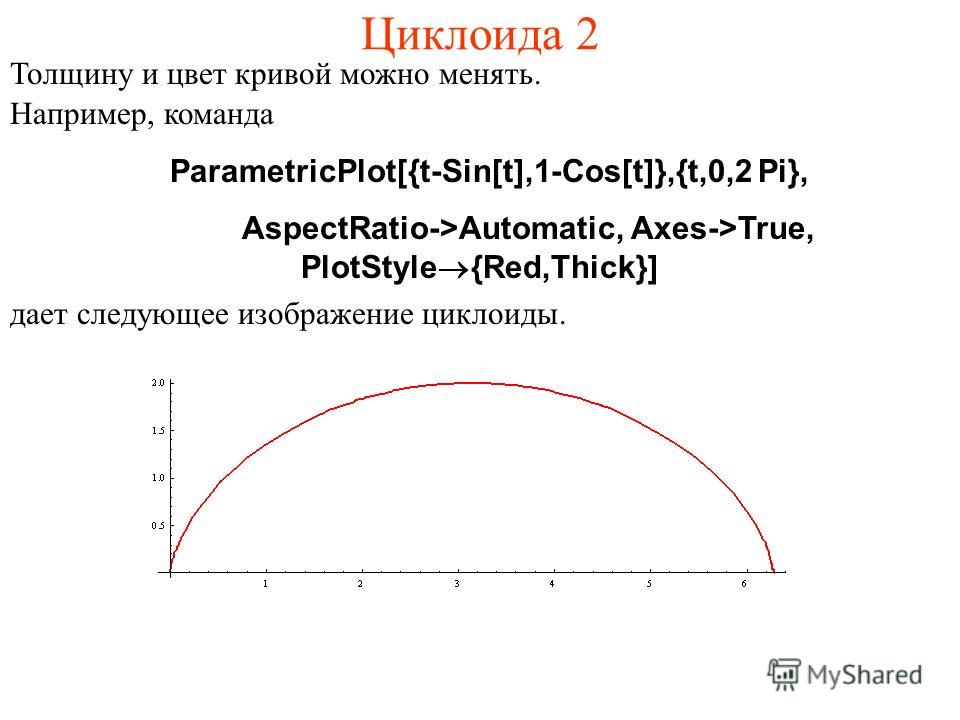 Переутомление и астения затягивают субдепрессивную фазу, появляется отвращение к учебе и к умственной работе вообще.
Переутомление и астения затягивают субдепрессивную фазу, появляется отвращение к учебе и к умственной работе вообще.
Лабильные циклоиды, в отличие от типичных, во многом приближаются к лабильному (эмоционально-лабильному или реактивно-лабильному) типу. Фазы здесь гораздо короче — несколько «хороших» дней сменяют несколько «плохих». «Плохие» дни более отмечены дурным настроением, чем вялостью, упадком сил или неудовлетворительным самочувствием. В пределах одного периода возможны короткие перемены настроения, вызванные соответствующими известиями или событиями. Но в отличие от описываемого далее лабильного типа нет чрезмерной эмоциональной реактивности, постоянной готовности настроения легко и круто меняться от незначительных причин.
Подростковые поведенческие реакции у циклоидов как типичных, так и лабильных, обычно выражены умеренно. Эмансипационные устремления и реакции группирования со сверстниками усиливаются в период подъема. Увлечения отличаются нестойкостью — в субдепрессивные периоды их забрасывают, в период подъема находят новые или возвращаются к прежним заброшенным. Заметного снижения сексуального влечения в субдепрессивной фазе сами подростки обычно не отмечают, хотя, по наблюдению близких, сексуальные интересы в «плохие дни» гаснут. Выраженные нарушения поведения (делинквентность, побеги из дому, знакомство с наркотиками) мало свойственны циклоидам. К алкоголизации в компаниях они обнаруживают склонность в периоды подъема.
Заметного снижения сексуального влечения в субдепрессивной фазе сами подростки обычно не отмечают, хотя, по наблюдению близких, сексуальные интересы в «плохие дни» гаснут. Выраженные нарушения поведения (делинквентность, побеги из дому, знакомство с наркотиками) мало свойственны циклоидам. К алкоголизации в компаниях они обнаруживают склонность в периоды подъема.
Суицидальное поведение в виде аффективных (но не демонстративных) попыток или истинных покушений возможны в субдепрессивной фазе.
Самооценка характера у циклоидов формируется постепенно, по мере того, как накапливается опыт «хороших» и «плохих» периодов. У подростков этого опыта еще нет и поэтому самооценка может быть еще очень неточна.
Циклоидная акцентуация, как указывалось, лишь изредка попадает под наблюдение психиатра. Однако среди здоровых подростков ее удается выявить в 2-5%. Причем из них половина может быть отнесена к типичным, а другая половина — к лабильным циклоидам.
Данный текст является ознакомительным фрагментом.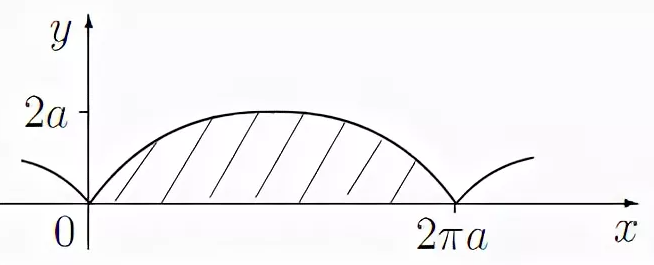
Чем отличается циклоид от шизоида — ЗдоровьеИнфо
Что делает человека индивидуумом? Особой, непохожей на других личностью? Конечно, его характер. Какие черты характера наследуются, а какие приобретаются в социуме? Каким образом рождается неповторимая индивидуальность каждого конкретного человека? Все это изучает наука характерология.
Антонина Камышенкова / «Здоровье-инфо»
Классификация характеров с античности до XX века
Попытки классифицировать каким-то образом всю богатую палитру человеческих характеров и темпераментов предпринимались еще со времен античности, и были на протяжении столетий крайне разнообразны. Тип темперамента связывали с особым составом крови, телесными «соками», влиянием звезд, линиями на ладонях, звучанием собственного имени и т. д.
д.
Отдельно стоит выделить физиогномику, сторонники которой за основу определения характера человека брали особенности строения его лица и мимики. К XIX веку физиогномика дала новое ответвление – френологию, которая рассматривала не только черты лица, но и строение черепа человека. В Новом периоде истории физиогномика, френология, а также другие более или менее внятные теории объяснения характера, такие как графология (связь характера с почерком) и конституциональный подход – (связь характера и строения тела) оформились в психогностику, являющуюся донаучным преддверием познания человеческой психики. И она ценна уже тем, что дала истоки для развития весьма интересных теорий. Таких, например, как теория Эрнеста Кречмера. По ней характер находится в тесной связи с физическим строением тела, которое, в свою очередь, во многом обеспечивается эндокринными факторами.
Подробнее об Эрнесте Кречмере
Эрнест Кречмер – немецкий психиатр, живший и работавший в конце XIX – начале XX века, именно тогда, когда собственно и появился сам термин Charakterkunde – в переводе с немецкого означающий «Характерология».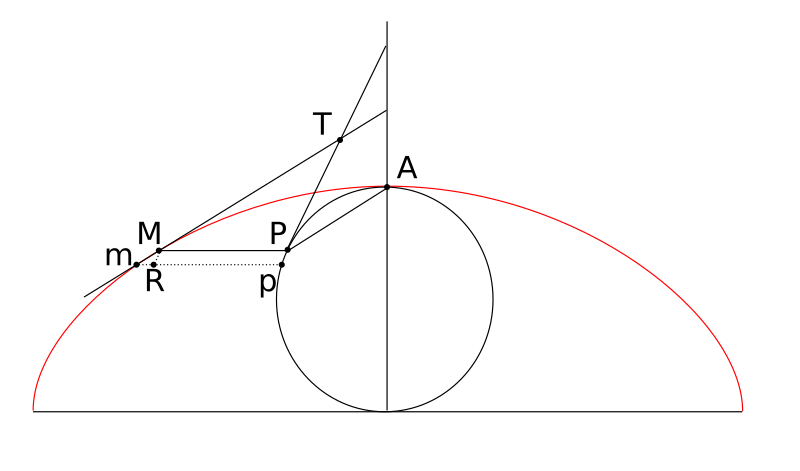 На основании экспериментов в своей богатой врачебной практике он написал научный труд «Строение тела и характер», где классифицировал характеры, тесно увязав их типы с особенностями телесного строения, и эта классификация вызывает неослабевающий интерес и споры по сей день.
На основании экспериментов в своей богатой врачебной практике он написал научный труд «Строение тела и характер», где классифицировал характеры, тесно увязав их типы с особенностями телесного строения, и эта классификация вызывает неослабевающий интерес и споры по сей день.
Кречмер полагал, что психические аппараты, а значит и темперамент каждого человека, имеют свой телесный коррелят – мозговой центр, и находится в неразрывной связи с органами чувств, всеми двигательными центрами и эндокринными железами.
Типы характеров по Кречмеру
Кречмер определил три основных типа характеров, причем все, конечно же, в зависимости от двух различных групп «химических гормонов», которые, в свою очередь, определяют телосложение.
- Пикнический тип. Это человек приземистый, с широкой костью, с толстой шеей и основательным туловищем. По характеру – циклоид. Спокоен, добросердечен, радостно относится к жизни.
- Астенический тип.
 Человек худощавый, невысокий, лептосомный (узкий). По характеру т.н. шизоид. Молчаливый и замкнутый в себе интроверт.
Человек худощавый, невысокий, лептосомный (узкий). По характеру т.н. шизоид. Молчаливый и замкнутый в себе интроверт. - Атлетический, смешанный тип. Наиболее распространенный тип – следствие смешения двух разных групп гормонов. Высок и физически крепок, по характеру может иметь черты и от циклического и от шизоидного типа.
При этом, конечно же, эта классификация не подразумевала, что люди одной группы все как один похожи между собой, ибо внутри каждой из них происходит дальнейшее разделение в зависимости, например, от того «направлен ли циклоидный темперамент больше к полюсу веселого и печального, а шизоидный – к полюсу раздражительного или холодного». Точно так же циклоидный тип по своему психическому темпу может тяготеть к полюсу подвижного или же флегматичного, а шизоидный – от порывистого до тягуче-замедленного. От этих данных как раз зависит множество индивидуальных оттенков каждой личности.
Дальнейшее развитие характерологии Кречмера
Эти идеи, конечно, не могли остаться не подхваченными. В дальнейшем кречмеровские типы были дополнены выдающимся русским психиатром Петром Ганнушкиным (конец XIX – начало ХХ вв.) и нашим современником, профессором психиатрии Марком Евгеньевичем Бурно. Правда, нельзя не сказать и о гонениях на эту науку в нашей стране в 30-40 годы. К тому времени она изменила название, став педологией, и, как и многие другие науки (генетика, кибернетика) была «предана анафеме», будучи обозначена как «буржуазная лженаука», и лишь в 60-е годы была реабилитирована.
В дальнейшем кречмеровские типы были дополнены выдающимся русским психиатром Петром Ганнушкиным (конец XIX – начало ХХ вв.) и нашим современником, профессором психиатрии Марком Евгеньевичем Бурно. Правда, нельзя не сказать и о гонениях на эту науку в нашей стране в 30-40 годы. К тому времени она изменила название, став педологией, и, как и многие другие науки (генетика, кибернетика) была «предана анафеме», будучи обозначена как «буржуазная лженаука», и лишь в 60-е годы была реабилитирована.
Ганнушкин, собственно, рассматривал область психических расстройств, пограничных между нормой и патологией. Однако его выводы оказались далеко за рамками рассмотрения психопатий, ибо какие-то типы характеров явно были ближе к норме, нежели к не норме. Среди его типов были такие красноречивые как «мечтатели», «антисоциальные» и «патологические лгуны». Атлетический тип Кречмера он назвал «эпилептоидом». По Бурно же внес в палитру типов характеров, такие как: «застенчиво-раздражительный», «педантичный» , «тревожно-сомневающийся» и др. Таким образом, сегодня типология основных типов характера, берущая исток от Кречмера, и прошедшая через Ганнушкина и Бурно, выглядит так:
Таким образом, сегодня типология основных типов характера, берущая исток от Кречмера, и прошедшая через Ганнушкина и Бурно, выглядит так:
- Если вы добры, общительны, реалистичны. Адекватно реагируете на события, а внешне – широки и склонны к полноте, то вы циклоид-сангвиник. Из литературных героев самые яркие примеру, это барон Дю Валлон, больше известный нам как Портос, а также Санчо Панса, бравый солдат Швейк и другие добродушные толстяки.
- Если вы худощавы и невысоки, являетесь реалистом, но при этом склонны к тревоге и сомнениям, и порой переживаете за что-либо до абсурда, то вы психастеник. Вспомним чиновника из рассказа Чехова, который умер от после того, как чихнул на лысину какому-то высокому чину. Не выдержал своей рефлексии по этому поводу. Такому человеку свойственна гипертрофированная порядочность и мнительность. Он склонен мучительно обдумывать уже произошедшее, терзая себя, порой совершенно попусту. «Быть или не быть?» – мучается он.
 Да-да, шекспировский Гамлет тоже был психастеником.
Да-да, шекспировский Гамлет тоже был психастеником. - Вы нормального телосложения и обычного роста. Для вас важна жизнь напоказ, чтобы окружающие знали о ваших переживаниях и были в курсе вашей жизни. Значит, вы принадлежите к т.н. истерикам. Этот тип порой склонен даже выдавать себя не за себя самого, и живет в выдуманной им реальности. Бывает аферистом, но при этом такой убедительный актер, что ему все верят. Как, например, гоголевскому Хлестакову или даме из рассказа Сомерсета Моэма, которая играла роль больной сердечницы и до того вжилась в нее, что в самом деле умерла.
- Вам повезло иметь атлетическое телосложение, обладать сильной волей и авторитарным характером? Вы не витаете в облаках и являетесь приземленным прагматиком, при этом умеете руководить людьми? Вы эпилептоид. Иллюстрация такого типа – это известный российский политик Александр Лебедь или генерал Де Голль. Хотя данный тип может быть и немного иным. Например, мольеровский Тартюф прячет стремление управлять людьми за угодливой и подобострастной манерой поведения.
 Будучи приживалом, умело манипулирует своими благодетелями, внося смуту и раздор и тем самым приближая себя к заветной цели – власти.
Будучи приживалом, умело манипулирует своими благодетелями, внося смуту и раздор и тем самым приближая себя к заветной цели – власти. - Вы замкнуты в себе, предпочитаете свой богатый внутренний мир внешнему? Внешне астеничны и легки? Практически не нуждаетесь в общении, и кое-кто даже считает вас аутистом? Это характеризует вас как шизоида. Такой человек склонен творить или заниматься наукой, перенося все сложные переживания внутреннего мира в свою деятельность. Художники кубисты – вот образцы шизоидных устремлений. Они пишут так «как видят», перенося, например, на холст разноцветные кубики и шары и объясняя, что это «портрет юноши». Из литературных героев это набоковский Лужин, живущий в своем мире шахматных партий, и параллельно проживающий реальную, второстепенную для него жизнь.
- Вам скучна реальная жизнь, вы порой не знаете, чего хотели бы, интересуетесь сегодня физикой, а завтра историей Древнего Египта? Это полифонический (мозаичный) характер, который может сочетать разные, порой несовместимые черты.
 Человек внешне может быть похожим на любой из других типов, при этом противоречив и непоследователен. Яркий пример полифонического творчества – это пьесы абсурда Годе, фильмы Бунюэля или картины Сальвадора Дали. В них тесно увязан реализм с вымыслом, концовка может опережать начало, поступки людей зачастую совершенно необъяснимы. Литературный герой мозаичного характера – это мистер Рочестер из «Джейн Эйр» или Настасья Филипповна Достоевского.
Человек внешне может быть похожим на любой из других типов, при этом противоречив и непоследователен. Яркий пример полифонического творчества – это пьесы абсурда Годе, фильмы Бунюэля или картины Сальвадора Дали. В них тесно увязан реализм с вымыслом, концовка может опережать начало, поступки людей зачастую совершенно необъяснимы. Литературный герой мозаичного характера – это мистер Рочестер из «Джейн Эйр» или Настасья Филипповна Достоевского.
Многообразие ветвей характерологии
Мы рассмотрели лишь одну ветку развития характерологии, при том, что веток и веточек этой науки существует великое множество, причем каждая из них, как правило, берет свое начало в прошлых столетиях, а чаще всего – в XIX веке. Есть французские, немецкие и американские и другие течения. Характер рассматривается в соответствии с элементами духовности, с типом форм реагирования на раздражители, со спецификой его поведения и т.д. Существуют также понятия социальной и национальной характерологии.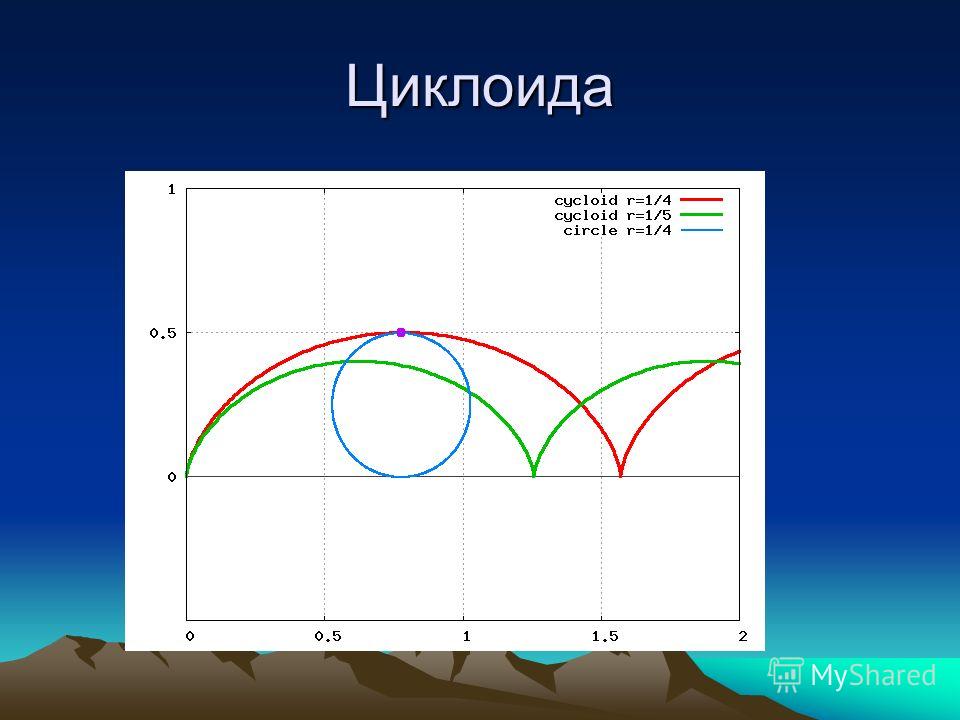
Из всех этих разновидностей можно выделить психоаналитическую характерологию, и прежде всего тем, что она также рассматривает характер в тесной связи с «телесным». Здесь характер тесно связан и с либидо, и с эго, а они в свою очередь связаны с детскими переживаниями. Так «оральный» тип человека – это тот в прошлом ребенок, которого мать мало кормила грудью, анальный – переживший унижения, генитальный – прошедшие детские комплексы Эдипа или Электры (влечение к своему родителю противоположного пола) и фаллический – «жертва» излишне жесткого давления со стороны родителей. Но кроме «телесного» и там и здесь, больше ничего общего психоаналитическая и кречмерианская характерологии не имеют. Более того, с точки зрения психического анализа характер можно изменить, адаптировав его к своему существованию, а с точки зрения характерологии по Кречмеру – человек не может изменить нечто, данное ему при рождении, поэтому надо помочь ему приспособиться к внешним условиям с учетом особенностей его характера.
Стоит сказать также, что сегодня есть масса попыток классификации характеров, которые можно было бы назвать «попсой», настолько примитивно и настолько далеко от мало-мальски научного обоснования они лежат. Например, некоторые психологи предлагают дифференцировать характер человека по цвету его глаз.
В завершение
Конечно, нельзя сказать, что кречмерианская характерология идеальна и неопровержима. На протяжении многих лет ее справедливо критиковали и за перенос закономерностей, установленных в психиатрической клинике, на среду нормальных людей, и за недостаточность убедительных статистических доказательств, и за то, что «телесных» данных явно недостаточно для изучения всех разновидностей человеческих характеров. Сегодня, конечно, имеется масса новых возможностей классификаций характера и установления, от чего именно зависит тот или иной тип. Сегодня ученые могут использовать такие величины, как нейродинамическая конституция мозга, а также данные молекулярной биологии и генетики. Все это раскрывает новые возможности для исследования и познания. Одно остается непреложным – именно Кречмер дал этому изначальный импульс, будучи передовым исследователем человеческой психики для своего времени.
Все это раскрывает новые возможности для исследования и познания. Одно остается непреложным – именно Кречмер дал этому изначальный импульс, будучи передовым исследователем человеческой психики для своего времени.
Циклоида / Этюды // Математические этюды
Зимой Вы можете построить во дворе горку изо льда и проверить это свойство вживую.
Задача о таутохроне состоит в нахождении такой кривой, что, начиная с любого начального положения, время спуска в заданную точку будет одинаковым.
Христиан Гюйгенс доказал, что единственной таутохроной является циклоида.
Конечно же, Гюйгенса не интересовал спуск по ледяным горкам. В то время учёные не имели такой
роскоши заниматься науками из любви к искусству. Задачи, которые изучались, исходили из жизни
и запросов техники того времени. В XVII веке совершаются уже дальние морские плавания. Широту
моряки умели определять уже достаточно точно, но удивительно, что долготу не умели определять
совсем. И один из предлагавшихся способов измерения широты был основан на наличии точных хронометров.
И один из предлагавшихся способов измерения широты был основан на наличии точных хронометров.
Первым, кто задумал делать маятниковые часы, которые были бы точны, был Галилео Галилей. Однако в тот момент, когда он начинает их реализовывать, он уже стар, он слеп, и за оставшийся год своей жизни учёный не успевает сделать часы. Он завещает это сыну, однако тот медлит и начинает заниматься маятником тоже лишь перед смертью и не успевает реализовать замысел. Следующей знаковой фигурой был Христиан Гюйгенс.
Он заметил, что период колебания обычного маятника, рассматривавшегося Галилеем, зависит
от изначального положения, т.е. от амплитуды. Задумавшись о том, какова должна быть
траектория движения груза, чтобы время качения по ней не зависело от амплитуды, он
решает задачу о таутохроне. Но как заставить груз двигаться по циклоиде? Переводя
теоретические исследования в практическую плоскость, Гюйгенс делает «щёчки», на которые
наматывается веревка маятника, и решает ещё несколько математических задач. Он доказывает,
что «щёчки» должны иметь профиль той же самой циклоиды, тем самым показывая, что эволютой
циклоиды является циклоида с теми же параметрами.
Он доказывает,
что «щёчки» должны иметь профиль той же самой циклоиды, тем самым показывая, что эволютой
циклоиды является циклоида с теми же параметрами.
Не удается найти страницу | Autodesk Knowledge Network
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}}*
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}}/500 {{l10n_strings.TAGS}} {{$item}} {{l10n_strings.PRODUCTS}} {{l10n_strings.DRAG_TEXT}}{{l10n_strings. DRAG_TEXT_HELP}}
DRAG_TEXT_HELP}}
{{article.content_lang.display}}
{{l10n_strings.AUTHOR}}{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$select.selected.display}} {{l10n_strings. CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}}
{{l10n_strings.CREATE_A_COLLECTION_ERROR}}
CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}}
{{l10n_strings.CREATE_A_COLLECTION_ERROR}}Циклоидные подростки: любить, поддерживать, не навредить
Как человек минует подростковый период, во многом определит его характер и судьбу во взрослой жизни. Статьи о подростковых проблемах раздают советы, но большинство рецептов не работает. Как подобрать ключик к подростку, чтобы помочь, а не навредить?
С другой планеты?
Родители детей предпубертатного возраста заранее готовятся к трудностям: активно читают книги и статьи по психологии. Друзья, у которых дети постарше, рассказывают страшные истории и сетуют: перепробовали многое, а результата нет.
Отчего популярные прикладные советы по воспитанию подростков по большей части не помогают? Может, потому, что подходят к проблемам важного в жизни человека возраста чересчур упрощённо и обобщённо.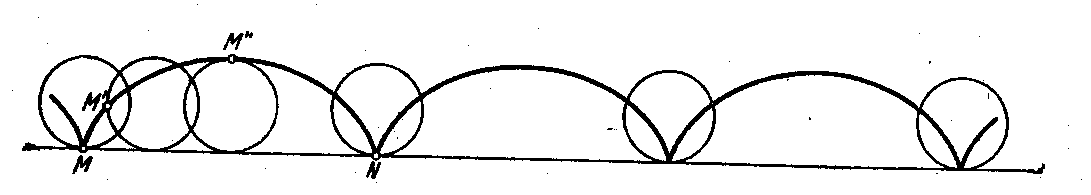
Почитаешь поверхностную литературу – и создаётся впечатление, что подростки – особенные люди, почти инопланетяне и отличаются определённым набором психоэмоциональных качеств. Это сумрачные, раздражительные, стремящиеся к уединению существа с частой сменой настроений, склонные к суицидным мыслям, и, не дай-то Бог, даже к попыткам свести счёты с жизнью.
Обобщённый портрет получается жутковатым, и его, якобы, создаёт только одно обстоятельство – типичный для этой возрастной категории гормональный всплеск. Мол, физиология вступает в реакцию с психологией, тело и душа ребёнка – в постоянном конфликте. Делайте так, говорите вот это, и вскоре будет положительный результат. Но эти утверждения далеки от реальности.
Обобщённого среднестатистического подростка, к которому применимы популярные обобщённые психологические советы, в природе не существует.

Наши дети в подростковый период развиваются по совершенно разным траекториям, поэтому к каждой замочной скважине души ключик свой.
Но есть и вполне типичные поведенческие проявления. Благодаря им можно попытаться свести многообразие внутреннего мира и характеров подростков к определённым психологическим типам. Это поможет нам разобраться, как лучше вести себя с теми или иными подростками, чтобы не нанести им душевных ран и способствовать развитию их положительных сторон.
На языке психологов разные поведенческие типы подростков – это разные акцентуации характеров. Разобраться не так-то просто. В поведении подростка много показного и скрываемого внутри.
Так, например, откровенно демонстративное поведение молодого человека с уверенной бравадой и оглушительной самопрезентацией, чаще всего, говорит как раз об обратном – о его природной робости, нерешительности и комплексе неполноценности. Их он и пытается скрыть за эффектным показным фейерверком.
Их он и пытается скрыть за эффектным показным фейерверком.
Не гусеница и не бабочкаНа самом деле накачанный парень в татуировках и шипах с ирокезом на голове, ведущий себя нагло и вызывающе, скорее всего, очень стеснителен и во что бы то ни стало хочет понравиться.
Сразу оговоримся: мы говорим о нормальных детях, а не о психопатах. Акцентуации характера – это варианты нормы. Подросток похож на окуклившуюся гусеницу: он уже не гусеница, но ещё и не бабочка, растёт неравномерно – как снаружи – телом, так и изнутри – душой, поэтому иногда проявления его характера принимают крайние формы.
При подростковых акцентуациях некоторые черты характера особенно усилены. Это значит, что в чем-то подросток очень силен, а в чем-то – уязвим.
Некоторые воздействия на психику он переносит легко и хорошо, другие – гораздо тяжелее, что усложняет его взаимодействие с окружающим миром.

При этом психика растущего ребёнка очень пластична, и опытный психолог вместе с мудрым родителем, поняв эти особенности, помогут подростку преодолеть то, что для него трудно и вовремя перерасти то, что следует перерасти. А значит, нормально адаптироваться в обществе сверстников и взрослых.
Почему вовремя? Потому что подростковый возраст в силу современных социальных установок у молодых людей затягивается надолго. В том возрасте, когда их отцы и деды уже были отцами семейств и считались мужчинами, наши сыновья зачастую остаются детьми.
Им позволено подолгу очно учиться, не работать, посвящать досуг играм и клубным тусовкам. Так подростковые проблемы не «перерастаются» порой до сорока, а то и до пятидесяти лет.
Явные и скрытыеАкцентуации бывают явные и скрытые. Иногда акценты характера отчётливые, и в поведении ребёнка легко установить причины и следствия.
Со скрытой акцентуацией сложнее: распознать её можно только в критические моменты.
Она же и опасней: мы не знаем, что и в какой момент времени может повлиять на подростка и произвести неожиданный эффект. Что причинит ему кратковременную душевную боль или глубокую психологическую травму.
Но даже скрытые акцентуации поддаются диагностике, и опытный психолог, побеседовав с ребёнком и родителями, поможет разобраться в проблеме.
Ошибки на этом пути могут дорого стоить. Если специалист вовремя не отличит акцентуацию от психопатии, здоровый ребёнок может стать пациентом психиатра. Поэтому родители проблемного подростка должны не отгораживаться от трудного ребёнка, а напротив, вдумчиво наблюдать за его поведением, анализировать свои наблюдения и что-то подсказывать психологу.
Циклоидный тип подросткаОткрываем небольшой цикл статей о подростках с различными акцентуациями характера.
И сегодня мы поговорим, что такое циклоидный тип и как воспитывать с любовью подростков с такими особенностями, чтобы помочь им, а не навредить.
Акцентуация характера у подростков именно этого типа, кстати, редко тревожит психиатров. Это ребята с циклическими колебаниями настроения, которых среди здоровых сверстников примерно пять процентов.
Дети до наступления подросткового возраста ничем не отличаются от ровесников, кажутся активными, подвижными и общительными. Но их душевное состояние ухудшается с приходом взросления и гормональных перемен.
Ухудшение состояния проявляется так. Как и многие подростки, эти дети начинают страдать придирчивостью и раздражительностью. Но если у обычных подростков раздражение направлено на старших, то у циклоидных подростков гнев и раздражительность изливаются на всех окружающих – родных и посторонних, педагогов и наставников, друзей и одноклассников.
Субдепрессивная фаза (время особенно сильных негативных проявлений характера) у этих подростков имеет такие последствия: вялость, усталость, повышенная утомляемость и ипохондрия.
Кажется, что сил на учёбу и любимые занятия больше нет, что всё болит, а выйти из дома просто невозможно.
На две-три недели подростки «окапываются» в своей комнате и не желают участвовать во внешней жизни: отказываются от общения, меньше выходят в соцсети, иногда, если не удаётся получить больничный, откровенно прогуливают учёбу.
Мамы и папы часто недоумевают, что с ребёнком, а может, он действительно серьёзно болен, раз утратил интерес к друзьям, развлечениям и окружающему миру. Нет, скорее всего, это не болезнь. Но это и не здоровье и благополучие.
Надо понимать: своё состояние дети не симулируют. В эти дни и недели они чувствуют себя действительно плохо, и это ухудшение самочувствия – психосоматическое.
Болит душа, а тело реагирует по-своему.
Но, пока близкие беспокоятся и ищут пути решения проблемы, такое состояние проходит. Обычно через пару недель всё возвращается на круги своя.
Больше того: подростки вдруг ощущают душевный подъем и даже эйфорию, но и это ненадолго. Вскоре у них устанавливается спокойное, нейтральное настроение.
Привязанные к привычному
Проявить беспокойство следует, когда состояния, похожие на депрессию, утяжеляются и становятся продолжительнее. Значит, есть некие внешние факторы, которые усугубляют это состояние.
«Больная мозоль» подростка-циклоида – это ситуация, когда происходит слом его жизненного стереотипа.
Кардинальные перемены его сильно травмируют. Такой ребёнок сильно привыкает, прочно привязывается к определённому порядку вещей. Если этот порядок меняется, если разрушаются привычные для него отношения, наступает кризис.
Если этот порядок меняется, если разрушаются привычные для него отношения, наступает кризис.
Причин может быть множество: развод родителей, долгое отсутствие близкого человека или друга, переезд, изменение расписания занятий, переход на вторую смену, и прочие, гораздо менее серьёзные с нашей точки зрения, но ощутимые для него.
Умом понимая, что вернуть всё обратно невозможно, подросток сердцем, то есть эмоционально, не может принять изменений и старается сделать так, чтобы всё было по-прежнему.
Скажем, он пытается заменить отсутствующего друга по переписке или по общению в соцсетях, создавая иллюзию, что говорит не с новым человеком, а со старым другом. Для него это механизм психологической защиты, точка опоры, чтобы не потерять равновесие и не уйти с головой в субдепрессивное состояние.
Если сверстники не ощущают никакой проблемы и препятствия в подобных переменах, то эти подростки видят перед собой не ветку, которую можно перешагнуть, а упавшее дерево полутораметровой толщины – непреодолимый психологический барьер.
Пытаясь приспосабливаться к новому, они теряют много эмоциональных сил и чувствуют сильное душевное истощение.
Например, такие ощущения подростки и молодые люди испытывают при переходе со школьного образования на средне-специальное или высшее. На первом курсе возникают новые отношения: теперь не спрашивают на каждом уроке, а читают лекции, контролируют меньше, а требуют больше: зачёты и экзамены происходят чаще. Это – полная ломка учебного стереотипа.
Муки ученьяПодростку становится трудно усваивать материал. В школе всё было по-другому: в свои светлые периоды-циклы школьник мог успешно отвечать у доски, зарабатывать хорошие оценки, вдохновляться классной и внеклассной работой.
Теперь не так. Приходится напрягаться, переписывать и заучивать пропущенное, подтягивать хвосты, причём не только тогда, когда твой эмоциональный фон на подъёме. На стадии упадка сил и ипохондрии эти задачи кажутся абсолютно нерешаемыми. Наступает переутомление, слабость, астенический синдром.
На стадии упадка сил и ипохондрии эти задачи кажутся абсолютно нерешаемыми. Наступает переутомление, слабость, астенический синдром.
Отвращение к учёбе и любому умственному труду – вполне логичное следствие передозировок с занятиями у подростков-циклоидов.
Именно поэтому такие учащиеся и студенты уходят с первого курса, заболевают накануне экзаменов, не выдерживают нагрузок и демонстративно заваливают сессии, к которым они готовились.
Рано или поздно эти дети находят в себе ресурсы, берут волю в кулак и преодолевают свои барьеры, но это даётся им гипер-усилием, после которого неизбежен эмоциональный спад и кризис.
Усугубить и без того критическое состояние подростка-циклоида в момент его трудностей с учёбой может бестактное поведение родителей и непрофессионализм педагогов, а также отсутствие душевной тонкости и чуткости у тех и других.

Публично призывать подростка к совести на виду у всего класса или группы, стыдить его в соцсетях или при знакомых и друзьях – это самое плохое, что можно придумать. С совестью и прилежностью у этих ребят как раз всё в порядке, просто их эмоциональный склад, их акцентуация характера мешает им в некоторые моменты быть продуктивными.
Обычно и мамы с папами, и учителя обосновывают жёсткие воспитательные меры желанием пользы и оправдывают себя самыми лучшими намерениями. На деле же они наносят растущим детям неисцелимые сердечные раны, которые только усугубляют их и без того тяжёлое душевное состояние и ещё сильнее ухудшают настроение.
Не доводите до пределаЧего мы добьёмся такими методами? Того, что совесть подростка, которая у него как раз присутствует, будет мучить его с болезненной силой.
Самоуничижение, самообвинение молодого человека захлестнут его с головой, что полностью лишит его воли к действию, желания жить и учиться, и даже может привести к попыткам суицида.

Получается как в одной популярной рок-песенке: «В общем, известное дело, что у нас с тобой впереди: не доводи до предела – до предела не доводи…»
Родителям и педагогам надо внимательно наблюдать за подростком и отнестись к проблеме с пониманием: лучше недожать, чем пережать. Если возможно, помочь ему адаптироваться в новой учебной ситуации.
Если у подростка в данный момент ни на что нет сил, не грех разок написать за него сочинение или нанять спокойного репетитора. Терпеливо объяснить, как браться за курсовик.
Не требовать прыгнуть выше его возможностей и сил и продемонстрировать головокружительные успехи. Да, пусть первый курс будет с троечки на четвёрочку, но уже через год у него наступит адаптация к новому учебному процессу и учёба пойдёт в гору.
Учебные трудности циклоидного подростка мы привели в качестве примера. На самом деле, похожие проблемы могут возникнуть в любой сфере его деятельности – в семье, в неформальных отношениях с ровесниками.
Главная беда таких подростков – снижение эмоционального тонуса. Эти ребята теряют силы при забеге на длинной дистанции, если применить такой образ к душевной сфере.
Поэтому им необходимы не ежовые рукавицы: не жёсткая критика домочадцев и не повышенные требования педагогов, а, напротив, тепло, поддержка, поощрение, умеренная похвала маленьких успехов, искренний интерес к их делам, мыслям и настроению.
Бывает, что фазы подъёма и спада по времени намного короче и чередуются гораздо чаще. Психика испытывает перегрузки, потому что такие американские горки не проходят для неё даром. Следом начинают страдать здоровье, иммунитет, общий физический тонус, и в этом нет ничего удивительного.
Ведь, как писал в своей книге «Дух, душа, тело» святитель Крымский Лука (Войно-Ясенецкий), практикующий врач-хирург и знаток человеческих душ, – человек по своей природе трехсоставен, все элементы его существа взаимодействуют, и болезни зарождаются не на физическом, а на душевном и духовном уровнях.
От перегрузок и усиления следующего за ними субдепрессивного состояния подросток или молодой человек может по-настоящему заболеть, получить нервное истощение, а это гораздо опаснее, чем остаться в школе на второй год, не перейти с курса на курс.
Поэтому нам, взрослым, надо пристально наблюдать за подростками с такими особенностями душевной организации и не посматривать за ними в пол-глаза, а смотреть широко открытыми глазами.
И пусть в ваших глазах они читают не гневное осуждение, не порицание их временной и вынужденной неуспешности, а готовность вовремя поддержать, сочувствие, понимание и любовь.
О других типах акцентуаций характера подростков читайте в следующих статьях.
Валентина Патронова
по материалам методического сборника Ленинградского (ныне – Санкт-Петербургского) психоневрологического НИИ им. Бехтерева
Бехтерева
Определение циклоиды по Merriam-Webster
cy · cloid | \ Sī-klȯid \ : кривая, образованная точкой на окружности круга, когда он катится по прямой линии.
1 : гладкая с концентрическими линиями роста циклоидные весы также : , имеющие циклоидные чешуйки или состоящие из них
2 : характеризуется чередованием высокого и низкого настроения циклоидная личность
Елена Геометрия
Исследуйте циклоиды
Najia Bao
Доброе утро! Каждый. Сегодня давайте
исследуйте и исследуйте Елену Геометрическую, то есть циклоиду. Это было
Впервые я услышал о циклоиде, когда мне было 12 лет. Мой отец,
инженер-механик, который как раз конструировал некую систему циклоидальных передач,
рассказал мне историю циклоиды от Галилея, одного из первых людей,
изучите циклоиду до двух известных проблем о циклоиде — Кристиан Гюйгенс
проблема таутохроны и проблема брахистохрон Джона Бернуллиса. Также он объяснил разницу между
циклоидные и эвольвентные шестерни, а также их сила и слабость.Честно говоря, в то время меня не интересовало то, что он сказал. Однако после того, как я
прошел курс Дифференциальная геометрия (в аспирантуре), осваиваю циклоиды.
Сегодня давайте
исследуйте и исследуйте Елену Геометрическую, то есть циклоиду. Это было
Впервые я услышал о циклоиде, когда мне было 12 лет. Мой отец,
инженер-механик, который как раз конструировал некую систему циклоидальных передач,
рассказал мне историю циклоиды от Галилея, одного из первых людей,
изучите циклоиду до двух известных проблем о циклоиде — Кристиан Гюйгенс
проблема таутохроны и проблема брахистохрон Джона Бернуллиса. Также он объяснил разницу между
циклоидные и эвольвентные шестерни, а также их сила и слабость.Честно говоря, в то время меня не интересовало то, что он сказал. Однако после того, как я
прошел курс Дифференциальная геометрия (в аспирантуре), осваиваю циклоиды.
А циклоида — это геометрическое место точки на окружности, катящейся по прямой. Писать параметрические уравнения для циклоиды и построение графика с помощью GSP.
Циклоида — геометрическое место точки P на ободе окружности радиуса r , катящейся по прямой (см. Рисунок 1).Предположим, что круг катится по оси x .
и одна позиция P — это
origin, давайте найдем параметрические уравнения для циклоиды.
Рисунок 1).Предположим, что круг катится по оси x .
и одна позиция P — это
origin, давайте найдем параметрические уравнения для циклоиды.
Теперь мы Рассмотрите угол поворота t круга как параметр. Как известно, t = 0 , когда P находится в начале. Когда круг повернулся на t радиан, пройденное расстояние составит OT = arc. PT = RT . Предположим, что координаты P равны (x, y) , получаем, что x = OT — PQ = rt — r sint = r (t — sint) , , что есть, x = r (t -sint) .Сходным образом, получаем, что y = r (1-стоимость) (см. инжир. 1). Следовательно, циклоида — путь подвижная точка P — имеет параметрические уравнения x = a (t — sint), y = a (1-стоимость).
Рисунок 1
Теперь мы построить циклоиду по GSP.
Рисунок 2
Теперь давайте дальше
исследовать циклоиды. Хочу представить вам гипоциклоиды и эпициклоиды. А
гипоциклоида — это кривая, очерченная фиксированной точкой P на окружности C с радиусом b , когда C катится по внутренней части окружности с центром O и радиусом a . Его параметрическое уравнение: Если
окружность C катится по внешней стороне фиксированного круга, кривая, начерченная номером P , называется эпициклоидой (см. рис. 3). Затем
его параметрическое уравнение
Хочу представить вам гипоциклоиды и эпициклоиды. А
гипоциклоида — это кривая, очерченная фиксированной точкой P на окружности C с радиусом b , когда C катится по внутренней части окружности с центром O и радиусом a . Его параметрическое уравнение: Если
окружность C катится по внешней стороне фиксированного круга, кривая, начерченная номером P , называется эпициклоидой (см. рис. 3). Затем
его параметрическое уравнение
Рисунок 3
Может быть, кто-то из
Вы бы сказали, что циклоида кажется такой простой и распространенной, но почему ее называют Еленой Геометрии.Это потому, что
связана с одной из самых известных пар проблем в истории
исчисление. Первая задача, получившая название таутохронной задачи , началась с Галилея и завершена Кристианом.
Гюйгенс. Проблема таутохрон состоит в том, что время, необходимое для полного поворота данного маятника, равно
примерно одинаково, делает ли он большое движение на высоких скоростях или
небольшое движение на более низких скоростях. Вторая проблема — брахистохрона.
проблема , это определить путь вниз
частица скользит из точки A в точку B за кратчайшее время.Этот
проблема была предложена Джоном Бернулли в 1696 году как вызов
математики Европы. Ньютон, Лейбниц, Гопиталь, Джон и Джеймс
Баэрнулли все нашел правильное решение. Просто потому, что две проблемы
привлекла так много великих математиков и физиков, что циклоида называется Еленой геометрии.
Вторая проблема — брахистохрона.
проблема , это определить путь вниз
частица скользит из точки A в точку B за кратчайшее время.Этот
проблема была предложена Джоном Бернулли в 1696 году как вызов
математики Европы. Ньютон, Лейбниц, Гопиталь, Джон и Джеймс
Баэрнулли все нашел правильное решение. Просто потому, что две проблемы
привлекла так много великих математиков и физиков, что циклоида называется Еленой геометрии.
— Как найти параметрическое уравнение циклоиды?
Эта книга — отличный ресурс. См. Pdf страницу 599, актуальную страницу 567.
http://www.marystarhigh.com/apps/download/7vb7ETI4n4RtLFWDnZw0xNfQRUSB1swoBHQpP7i1l9pXZS1Y.pdf/Precalculus%20Book.pdf
Вам следует перейти на страницу перед чтением и во время прочтения остальной части сообщения.
В нем он объясняет все очень связно и разбивает вывод на 4 этапа: нахождение уравнения для местоположения центра круга (координаты x и y), а затем нахождение уравнения для точки P в в ссылке.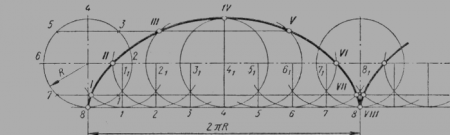 до центра.
до центра.
Мы начнем с попытки найти центр круга под углом $ \ theta $. Координата x будет равна пройденному расстоянию, что совпадает с длиной уже пройденного сектора круга. Сектор равен радиусу, умноженному на центральный угол, поэтому центр будет в точке $ x = a \ theta $
.Координата y центра в любое время очень проста, потому что центром всегда является высота радиуса, которая равна $ a $. Следовательно, центр находится в координатах $ (a \ theta, a) $ под углом $ \ theta $.
Теперь давайте попробуем найти местоположение точки P относительно центра . Начнем с координаты x.
Под углом $ \ theta $ P сначала будет отставать, затем прыгать вперед, а затем возвращаться туда, откуда он начался. Следовательно, мы хотим начать с вычитания $ 0a $, затем $ 1a $, затем $ 0a $, затем — $ 1a $, а затем снова вернуться к $ 0 $. Такое поведение демонстрирует $ a \ sin \ theta $, поэтому наша координата x теперь завершена: $ x = a \ theta — a \ sin \ theta = a (\ theta — \ sin \ theta) $
Теперь о координате y.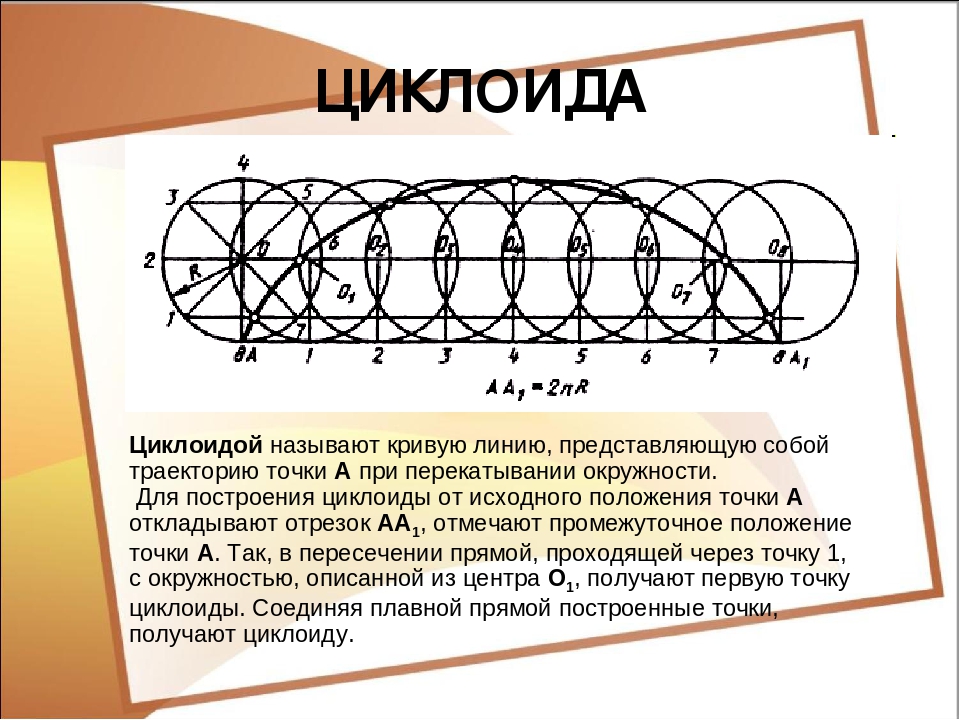 Чтобы получить высоту точки P под углом $ \ theta $, мы замечаем, что она начинается ниже центра, затем идет выше центра, а затем снова ниже. Следовательно, мы хотим вычесть $ 1a $, затем $ 0a $, затем $ -1a $ (добавить $ 1a $), а затем снова вернуться к $ 0a $. Образец $ (1, 0, -1, 0, 1) $ демонстрируется $ a \ cos \ theta $, поэтому мы хотим вычесть это из центра, давая нам $ y = a — a \ cos \ theta $ или $ y = a (1 — \ cos \ theta) $.
Чтобы получить высоту точки P под углом $ \ theta $, мы замечаем, что она начинается ниже центра, затем идет выше центра, а затем снова ниже. Следовательно, мы хотим вычесть $ 1a $, затем $ 0a $, затем $ -1a $ (добавить $ 1a $), а затем снова вернуться к $ 0a $. Образец $ (1, 0, -1, 0, 1) $ демонстрируется $ a \ cos \ theta $, поэтому мы хотим вычесть это из центра, давая нам $ y = a — a \ cos \ theta $ или $ y = a (1 — \ cos \ theta) $.
Итак, мы закончили. Наши два уравнения: $$ x = a (\ theta — \ sin \ theta) $$ $$ y = a (1 — \ cos \ theta) $$.
Циклоида
Педаль циклоиды.Блокнот Mathematica для этой страницы .
радиальный эволюционировать отрицательная педаль педаль едкий параллельный инверсия производная циссоид по линии раковина строфоид
История
Описание
Циклоида (таутохрона, брахистохрона) — член циклоидального семейства кривых. (См .: Curve Family Index) Выпуклые (расширенные) или свернутые (сжатые) циклоиды также известны как трохоиды. На этой странице мы используем самое узкое определение термина циклоида, определяемого как след точки на окружности круга, катящийся по линии без проскальзывания.
На правом рисунке c — катящийся круг. P — точка отслеживания. A — точка соприкосновения с линией. PA — нормаль в точке P. E — отражение P через A. Географическое место E — эволюция циклоиды.
По следам циклоиды По следам циклоиды по касательнойФормула
- Параметрический: {t — Sin [t], 1 — Cos [t]}
Недвижимость
Каустик
Катакостика циклоиды относительно параллельных лучей, проходящих под ее дугой, — это две меньшие циклоиды.(Или диакустика циклоиды с лучами, падающими сверху.)
Катакостик с вертикальными лучамиЭволют и инволют
Эволюция циклоиды — это другая циклоида. На первом рисунке показаны последовательные эволюции циклоиды. Второй соединяет точки на кривой с их центром соприкасающихся кругов.
Слева: зеленая циклоида — это эволюция красной циклоиды, эволюция синей циклоиды. Справа: нормали желтой циклоиды (зеленые) приведены к центру соприкасающегося круга.Окончания образуют его эволюционную кривую, представляющую собой еще одну циклоиду. Построение эволюции циклоидыЭвольвента циклоиды также является циклоидой. И эвольвентные, и эвольвентные свойства легко подтверждаются прямым применением формулы и упрощают результат.
Радиальный
Радиал циклоиды — это круг.
Создание радиального Радиал циклоидыСвязанные веб-сайты
См .: Веб-сайты на плоских кривых, книги о плоских кривых .
Роберт Йейтс: кривые и их свойства .
Архив истории математики MacTutor
Brombacher Aarnout, с фильмами GSP и QuickTime. http://jwilson.coe.uga.edu/EMT668/EMT668.Student.Folders/BrombacherAarnout/EMT669/cycloids/cycloids.html
Джозеф Портни. Довольно подробное изложение свойства циклоиды быть кривой наивысшего качества. (называется брахистохромом) http://www.navworld.com/navcerebrations/millennium/millennium.htm
Калькулятор циклоиды
Калькулятор циклоиды позволяет вычислить необходимые параметры, необходимые для создания циклоиды.Нашему инструменту в основном требуется радиус окружности, по которому он может найти площадь, длину дуги, длину горба, высоту и периметр каждой дуги циклоиды. Мы уверены, что вы хотели бы знать, как построить циклоиду или как выполняется трассировка циклоидной кривой? Мы рассмотрим все эти темы, поэтому продолжайте читать ниже.
Что такое циклоида?
Попытайтесь представить упавшую монету, катящуюся по прямой линии. Теперь представьте точку где-нибудь на краю монеты. Эта точка движется по кривой.Вы смогли это представить? Потому что это циклоида. Другими словами или более техническими словами, циклоида — это кривая, образованная окружностью, вращающейся вдоль прямой линии. История циклоиды противоречива, поскольку многие математики утверждали, что ее открыли. Но Галилей был первым, кто методично изучил эту кривую и дал ей название циклоида.
На рисунке показана циклоида, образованная катящимся кругом по прямой. По Komal RafayУравнение циклоиды
Циклоида состоит из различных компонентов, наиболее важным из которых является радиус катящейся окружности, образующей циклоиду.Все компоненты циклоиды вместе с их уравнениями приведены ниже:
Полярное уравнение циклоиды
Полярное уравнение циклоиды имеет вид:
x = r * (θ - sin (θ))
y = r * (1 - cos (θ))Где,
- r — Радиус; и
- θ — Угловое смещение окружности.
Декартово уравнение
Декартово уравнение циклоиды имеет вид:
x = r * cos ⁻1 (1 - y / r) - √ y * (2 r - y)Длина дуги циклоиды
Длина дуги циклоиды — это криволинейное расстояние между двумя выступами.Он обозначается S и его формула:
S = 8 * rПлощадь циклоиды
Площадь циклоиды — это площадь под аркой, которая создается за один оборот окружности. В калькуляторе циклоиды используется формула:
A = 3 * π * r²Длина горба циклоиды
Длина горба — это расстояние по прямой между двумя выступами. Это также длина катящегося круга, и его формула:
C = 2 * π * rВысота горба циклоиды
Высота горба циклоиды — это высота дуги, и она эквивалентна диаметру вращающейся окружности.Его формула:
d = 2 * rПериметр циклоиды Периметр циклоиды — это сумма длин всех ее сторон. Циклоида состоит из двух сторон: арки и основания. Чтобы получить периметр, нам понадобятся длины горба и дуги. Его формула:
p = C + S
Как построить циклоиду
Теперь, когда вы использовали наш калькулятор циклоид, вы знаете, какие параметры используются для трассировки циклоидной кривой.Но некоторым из вас будет интересно, как бы вы построили циклоиду на бумаге, если бы это было необходимо. Следуйте инструкциям ниже, чтобы построить свою собственную циклоиду:
Возьмем диаметр круга 5 см или 50 мм.
Нарисуйте круг радиусом 2,5 см или 25 мм и отметьте его центр как
C.Теперь нарисуйте горизонтальную линию той же длины, что и окружность круга от основания и центра,
C.Теперь разделите круг, горизонтальную линию и базовую линию на 12 равных частей.Назовите точки на горизонтальной линии от C1, C2, C3 до C12 и от 1,2,3 до 12 на базовой линии.
Соедините C1 с 1, C2 с 2, C3 с тремя, и продолжайте делать это до C12 по 12.
Проведите горизонтальные линии из всех точек круга в том же направлении, что и горизонтальная линия, проведенная из центра ранее.
Взяв центр C1 и радиус 2,5 см или 25 мм, нарисуйте дугу на прямой, проходящей через 1. Затем взяв центр C2 и радиус 2.5 см или 25 мм, нарисуйте дугу, проходящую через 2. Аналогичным образом, взяв центр C3 и радиус 2,5 см или 25 мм, нарисуйте дугу на линии, проходящей через 3. Продолжайте следовать той же процедуре для всех точек на главной горизонтальной линии до C12.
Используя полученные дуги, нарисуйте плавную кривую от руки.
На рисунке показано построение циклоиды с помощью геометрических инструментов. По Komal Rafay
Это кривая, очерченная точкой на окружности окружности, если она катится по прямой без скольжения, также известная как ваша циклоида.
Циклоидная кривая
Циклоидная кривая следует простым гармоническим движениям, что означает, что она периодическая и будет повторять идентичный образец для каждого оборота. Концепция циклоидной кривой или циклоидальной дуги использовалась в архитектурном проекте Художественного музея Кимбел в Техасе.
Вариации циклоиды
Есть несколько разновидностей циклоиды. Обычно они различаются точкой катящегося круга, образующей кривую. В некоторых случаях точка может находиться внутри или за пределами круга, что дает соответственно сокращенную или вытянутую циклоиду.
Список разновидностей циклоиды приведен ниже:
- Куртат циклоида;
- циклоид пролатный;
- трохоид;
- Гипоциклоид;
- эпициклоида;
- гипотрохоид; и
- Эпитрохоид.
Как найти длину дуги циклоиды?
Формула для определения длины дуги циклоиды имеет следующий вид: S = 8 × г Где S — длина дуги, а r — радиус окружности.
Какова формула площади циклоиды?
Площадь циклоиды — это площадь под сводом циклоиды.Его формула:
A = 3 × π × r²
Что вычисляет циклоидный калькулятор?
Калькулятор циклоиды принимает радиус катящейся окружности в качестве входных данных и вычисляет следующие компоненты циклоиды:
- Длина дуги;
- Площадь;
- Длина горба;
- Высота горба; и
- Периметр.
циклоида
Кривая образована геометрическим местом точки, прикрепленной к окружности (цикл -> циклоида), которая катится по
прямая 1) .Другими словами:
сочетание линейного (термин t) и кругового движения (термины sin t и cos
т).
В уравнении Уивелла кривую можно записать как s = sinφ.
Старый грек уже знал эту кривую.
Значение параметра ‘a’ определяет начальную точку относительно окружности:
- (обыкновенная) циклоида
Начальная точка находится на окружности (a = 1).
Когда начальная точка не находится на окружности, кривая называется трохоидой: - циклоида вытянутая (фр.циклод
аллонж)
Начальная точка находится вне круга (a> 1). - куртатная циклоида (фр. Cyclode raccourcie)
Начальная точка находится внутри круга (a <1).
Если у вас есть твердая рука, вы можете сделать свою собственную циклоиду на доске, совмещение линейного и кругового движения.
Когда циклоида катится по линии, путь центра представляет собой эллипс. Для обычной циклоиды результатом является круг.
(обыкновенная) циклоида
В Голландии мы используем для этой кривой также название «колесная линия» 2) , быть в трек, за которым следует точка на велосипедное колесо.
Кривая имеет два замечательных качества:
Первое качество состоит в том, что циклоида является брахистохрона 3) , то есть кривая между двумя точками в
вертикальная плоскость, по которой бусине нужно пройти наименьшее время 4) . Галилей (который дал кривой название в 1699 г.) заявил в 1638 г. (ложно), что
брахистохрона должна быть дугой окружности. А в июне 1696 г. Иоганн Бернулли бросил вызов своему брату Якобу Бернулли — оба были соперниками — решить
проблема. Декабрь 1696 г.Иоганн 5) повторил свое
в «Acta eruditorum» с просьбой прислать решения до Пасхи 1697 года. Иоганн и Якоб , а также Лейбниц , Ньютон и де Л’Эпиталь решены
эта проблема.
Это одна из первых вариационных задач, подлежащих изучению.
Фактически, эта кривая противоположна (отражается по оси x) показанной
изгиб. Без всякой формулы можно понять, что по этой кривой путь быстрее
чем по прямой. Для циклоиды результирующая составляющая силы тяжести равна
побольше, а так разгон и скорость, сразу после старта. Также легко
экспериментально проверить, что путь по прямой занимает больше времени.
Эти знания можно использовать во время катания на лыжах: быстрее выбрать спуск, чтобы
вы набираете скорость, чем избегаете склонов.
Второе качество — циклоида таутохрона (иногда называется: изохрона ) 6) . Это означает, что бусинка вдоль кривой требует
в то же время, чтобы спуститься, независимо от отправной точки. Замечательный! Это был христианин г.
Гюйгенс , открывший этот факт в 1659 году. В своем трактате «Horologium Oscilatorium»
(1673) он конструирует часы с маятником переменной длины.Маятник движется между
две щеки, обе в форме циклоиды. Раскачиваясь наружу, маятник
укорачивает. Huygens использовал идею о том, что эвольвента
циклоиды — это та же циклоида (конечно, справедливо и для эволюции).
Эта конструкция компенсировала неравномерность нормального маятника. Для нормального
маятника время колебания только в первом приближении не зависит от
положение в сторону 7) . Гюйгенс был весьма впечатлен, он написал над доказательством: «magna nec ingenijsvestigata priorum», чтобы быть
переводится как: «это что-то великое, никогда прежде не исследованное гением».
В своих экспериментах Гюйгенс также использовал эвольвентный
круга в его маятниковых часах, чтобы приблизиться к циклоидальному пути.
Однако использование принципа таутохрон при проектировании маятниковых часов тоже оказалось актуальным.
много механических проблем, чтобы сделать это обычным явлением.
О таутохронах можно также прочитать в «Моби Дике», книге Германа Мелвилла, в трактате о котле для кипячения китового жира.
Вот некоторые интересные свойства циклоиды:
Cusa был первым, кто изучил кривую в наше время, пытаясь
найти площадь круга. Mersenne (1599) дал первое правильное определение
циклоида, он попытался найти область под кривой, но потерпел неудачу. Он поставил
вопрос Робервалю , который решил его в 1634 году.Позже Торричелли независимо нашел площадь кривой.
Декарт нашел, как провести касательную к циклоиде, он бросил вызов Роберваль найти решение Робервалю не удалось, а вот Ферма удалось. Также Viviani нашел касательную.
В августе 1658 года компания Pascal опубликовала задание с двумя призами под именем Amos Dettonville .
Он задал 9 вопросов о циклоиде, спрашивая площадь и центр тяжести ее сегмента.
Говорят, что для Паскаля изучение кривой было хорошим развлечением от сильной зубной боли. Введены
Wallis и Laloure , обе попытки не увенчались успехом. Sluze , г. Ricci , Huygens , Wren и Fermat не участвовали в конкурсе,
но все написали свое решение на Паскале. 10 октября 1658 г. Паскаль опубликовал свой собственный
решения, вместе с расширением результата Wren .
Газета называлась «Histoire de la Roulette, appel autrement Trochoide ou Cycloide».
Desargues предложил зубья для шестерен в форме циклоиды (около 1635 г.).
Якоб и Иоганн Бернулли показали (1692 г.), что циклоида — это катакостический
круга, где световые лучи исходят от окружности.
Циклоидная дуга с лучами, перпендикулярными оси x, дает две циклоидные дуги.
Итак, циклоида была очень популярна среди математиков 17 века.Поэтому в дальнейшем кривая получила название кривая ссоры , Елена Геометров и Яблоко раздора 9) .
В музее фортепиано в Хопкинтоне 10) можно найти пианино, задний край которого имеет форму циклоиды. В
Создатель Генри Линдеман назвал инструмент «Циклоида».
Гранд », конец 1800-х гг.
Но при взгляде сверху видно, что его форма отличается от реальной циклоиды:
Шестерни имеют циклоидную форму, могут быть приближены серией дуг окружности.Также можно использовать числовые таблицы, например, George Одонтограф Гранта , который также является названием инструмента для прекращения очертания зубьев шестерен.
Кривая представляет собой пойнт-рулетку.
Теперь отслеживаемая точка не лежит на окружности. Когда точка лежит снаружи круг, кривая называется вытянутой циклоидой (или расширенная циклоида ). Когда точка лежит внутри катящейся окружности, кривая называется скрученной циклоидой . (или сжатая циклоида ).Последняя кривая следует клапаном велосипеда. Вот откуда наименование клапана , кривая для циклоиды от.
Первыми исследовали кривую Drer (1525) и Rmer (1674).
с винтом Voith-Schneider (VSP),
Впервые испытанный в 1927 году, корабль способен точно маневрировать и уходить в сторону.
Пропеллеры вращаются вокруг оси, перпендикулярной движению, так что они
следовать по пути циклоиды.Положение лопастей определяет направление
судна, и в его основе лежит тот же принцип действия плавника рыбы.
Пропеллер называется циклоидальным или трохоидальным винтом.
банкноты
1) Пусть есть круг с центром (0, R)
и точка (p, 0) в качестве отправной точки для броска. Тогда координаты
циклоида в зависимости от угла наклона t составляет
2) На голландском языке: radlijn
3) Брахисто (Греч.) или brachus (лат.) = короткий, chronos (Гр.) = Время
4) На высоте y шарик приобретает скорость √gy, поэтому
что минимизация времени пробега означает минимизацию интеграла
.
Решение этого уравнения приводит к дифференциальному уравнению y (1 + y ‘ 2 ) = c
к циклоиде.
5) В то время профессор математики в Гронингене, Голландия
6) Тауто = равно, хронос = время: кривая, которой следует следовать за равное время.
7) Правильное соотношение дает полный эллиптический интеграл первого рода.
8) На английском языке: История игры в рулетку, также называемая трохоидой или циклоидой.
9) Елена и яблоко раздора относятся к Троянской войне.
Голландский для кривой ссоры: kibbelkromme.
10) Хопкинтон, штат Массачусетс, около 1/2 часа. к западу от Бостона, см. веб-сайт Музея фортепиано.
11) Trochus (лат.) = Обруч.
Иногда значения циклоиды и трохоиды меняют местами: трохоид для общего
случай, циклоида только для ситуации, когда начальная точка лежит на окружности.
Циклоида — Mathonline
Циклоида — это особый тип параметрической кривой, которая очерчивается точкой на окружности круга, когда он катится по прямой линии. График циклоиды выглядит так:
Сначала определим центр круга. Что касается координаты x, обратите внимание, что дуга, образованная, когда точка P катится вдоль оси x, равна расстоянию между началом координат и центром круга (это расширено в следующем разделе), а также обратите внимание, что y -координата окружности никогда не меняется и остается на длине r.Таким образом, мы получаем, что, поскольку длина дуги равна rΘ, то центр окружности равен C (rΘ, r)
.x-Координаты циклоиды
Чтобы определить параметрическое уравнение для циклоиды, давайте воспользуемся углом тета, образованным перпендикуляром, опущенным из центра круга, и положением некоторой точки P, которая очерчивает круг по мере увеличения теты. Мы будем использовать тэту, потому что она меняется так же, как t со временем. На диаграмме ниже наглядно показано, как мы определим циклоиду
.Сначала давайте найдем функцию x (t), чтобы описать, как x-координата циклоиды изменяется при изменении теты.Обратите внимание, что точка P начинается в начале координат и удаляется на расстояние, равное длине отрезка OC. Однако также обратите внимание, что дуга окружности, образованной тета, также равна отрезку OC, потому что он перекатился по оси x. Напомним, что длина дуги окружности:
(1)\ begin {align} s = r \ theta \ end {align}
Нам не нужно знать точное измерение радиуса, а тета варьируется. Так просто:
(2)\ begin {align} OC = r \ theta \ end {align}
Однако длина OC — это не то, что нам нужно.Нам нужно вычесть длину сегмента PC, чтобы получить длину OP = x. В этом случае мы можем использовать тригонометрию:
(3)\ begin {align} \ sin \ theta = \ frac {PC} {r} \\ r \ sin \ theta = PC \ end {align}
Таким образом, координаты x при изменении теты равны:
(4)\ begin {align} OC — PC \\ = r \ theta — r \ sin \ theta \\ = r (\ theta — \ sin \ theta) \ end {align}
Координаты Y циклоиды
Мы будем использовать аналогичные методы для определения координаты y при изменении теты.Сначала мы признаем, что длина опущенного перпендикуляра от центра круга до оси x равна r, поскольку это просто радиус круга. Теперь мы хотим вычесть расстояние от центра до координаты y. Еще раз, мы можем использовать тригонометрию, чтобы получить длину rcosΘ. Таким образом, получаем, что координата y равна:
(5)\ begin {align} y = r — r \ cos \ theta \\ y = r (1 — \ cos \ theta) \ end {align}
Мы узнали, что циклоиду можно определить двумя параметрическими уравнениями, а именно:
(6)\ begin {align} x = r (\ theta — \ sin \ theta) \ quad, \ quad y = r (1 — \ cos \ theta) \ end {align}
Поскольку точка, очерчивающая циклоиду, P, начинается на оси x и вращается от оси x, имеет смысл, что циклоиде требуется расстояние 2πr, чтобы снова пересечь ось x.Таким образом, одна дуга циклоиды возникает после того, как происходит расстояние 2πr бросков цикла.
Давайте теперь проанализируем, являются ли эти арки полукругами. Мы знаем, что максимальная высота круга будет вдвое больше радиуса, или 2r, что также будет максимальной высотой арки.


 Человек худощавый, невысокий, лептосомный (узкий). По характеру т.н. шизоид. Молчаливый и замкнутый в себе интроверт.
Человек худощавый, невысокий, лептосомный (узкий). По характеру т.н. шизоид. Молчаливый и замкнутый в себе интроверт. Да-да, шекспировский Гамлет тоже был психастеником.
Да-да, шекспировский Гамлет тоже был психастеником.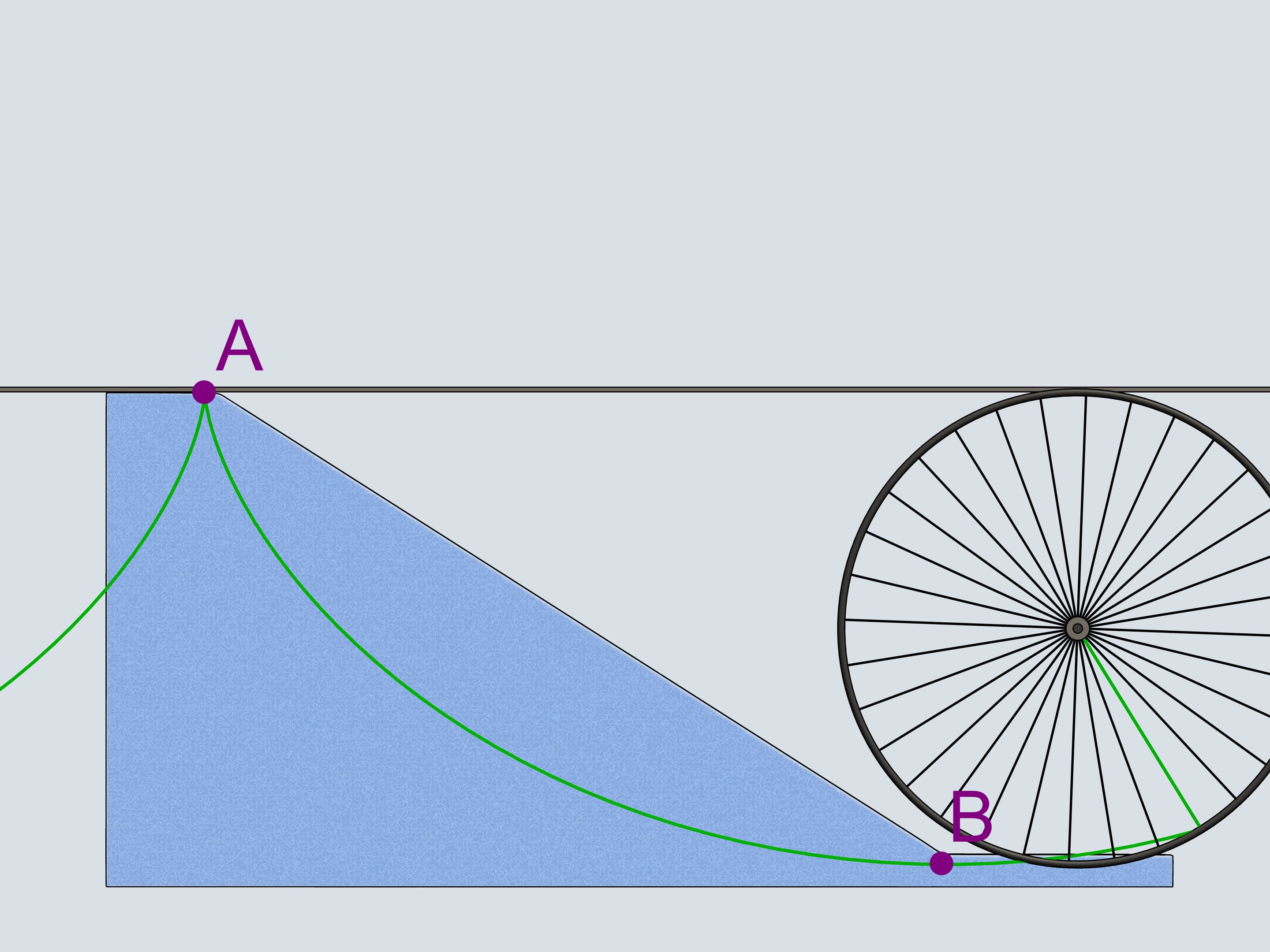 Будучи приживалом, умело манипулирует своими благодетелями, внося смуту и раздор и тем самым приближая себя к заветной цели – власти.
Будучи приживалом, умело манипулирует своими благодетелями, внося смуту и раздор и тем самым приближая себя к заветной цели – власти. Человек внешне может быть похожим на любой из других типов, при этом противоречив и непоследователен. Яркий пример полифонического творчества – это пьесы абсурда Годе, фильмы Бунюэля или картины Сальвадора Дали. В них тесно увязан реализм с вымыслом, концовка может опережать начало, поступки людей зачастую совершенно необъяснимы. Литературный герой мозаичного характера – это мистер Рочестер из «Джейн Эйр» или Настасья Филипповна Достоевского.
Человек внешне может быть похожим на любой из других типов, при этом противоречив и непоследователен. Яркий пример полифонического творчества – это пьесы абсурда Годе, фильмы Бунюэля или картины Сальвадора Дали. В них тесно увязан реализм с вымыслом, концовка может опережать начало, поступки людей зачастую совершенно необъяснимы. Литературный герой мозаичного характера – это мистер Рочестер из «Джейн Эйр» или Настасья Филипповна Достоевского.

 И сегодня мы поговорим, что такое циклоидный тип и как воспитывать с любовью подростков с такими особенностями, чтобы помочь им, а не навредить.
И сегодня мы поговорим, что такое циклоидный тип и как воспитывать с любовью подростков с такими особенностями, чтобы помочь им, а не навредить. Болит душа, а тело реагирует по-своему.
Болит душа, а тело реагирует по-своему.