Инструменты качества: контрольные карты Шухарта
Есть совершенно конкретный инструментарий работы с качеством на предприятии. Совокупность средств, которые в него входят, принято обобщать понятием «инжиниринг качества». Сейчас речь пойдет о том, как представить имеющиеся у вас данные в виде контрольной карты Шухарта.
Для чего нужно: карта позволяет анализировать причины появления брака. Идея карты состоит в том, что статистические вариации числа дефектных изделий не должны превышать или быть меньше определенных значений. Если это все-таки происходит, то значит, на процесс влияют некоторые субъективные факторы, не связанные с естественными флуктуациями (колебаниями) вероятности, свойственными для любой системы.
Что понадобится: идеально подойдет программа «Excel» из стандартного пакета программ ОС «Windows».
Итак, начнем!
Предположим, у нас есть данные по количеству бракованных деталей по одним и тем же месяцам за несколько лет.
| Месяц | Количество бракованных деталей за разные годы |
| 1 месяц | 25, 23, 26, 22, 27, 22, 20 |
| 2 месяц | 29, 28, 29, 28, 30, 30, 31 |
| 3 месяц | 20, 20, 20, 21, 21, 21, 20 |
| 4 месяц | 19, 20, 21, 22, 23, 24, 19 |
| 5 месяц | 37, 37, 38, 38, 36, 36, 30 |
| 6 месяц | 35, 34, 35, 34, 35, 34, 35 |
| 7 месяц | 19, 19, 20, 20, 16, 19, 20 |
Находим среднее арифметическое по каждому месяцу и строим гистограмму.
Теперь перед нами стоит задача определить границы, в которых колебания количества дефектов можно признать «нормальными». Это можно сделать по формулам, которые приводит ГОСТ 50779.42-99, специально посвященный контрольным картам Шухарта. Вот они:
UCL (верхняя граница – Upper Control Limit, – ред.) = X +A2 * R
LCL (нижняя граница – Low Control Limit, – ред. ) = X – A2 * R
) = X – A2 * R
A2 – это специальный инженерный коэффициент, необязательно знать, что это такое, чтобы пользоваться им. Таблица значений этой переменной дана в стандарте ГОСТ 50779.42-99. Конкретное значение переменной зависит от количества данных в подгруппе. В нашем случае речь идет о том, сколько чисел есть по каждому из месяцев. Например, за 1 месяц у нас есть 7 цифр.
R – это размах. Он представляет собой разность между самым большим и самым маленьким значением в подгруппе. Получившиеся результаты по разным месяцам нужно, опять-таки сложить и получить среднее арифметическое.
X – среднее арифметическое средних арифметических по количеству дефектов. Проще говоря, нужно сначала найти среднее значение дефектов по каждой подгруппе, а затем среднее для всех подгрупп в общем. X представляет собой еще и среднюю линию, равноудаленную от верхней и нижней границ «допустимых значений».
У нас получилось, что X = 26,29, R = 4,14, A2 = 0,219.
UCL = 28.02
LCL = 24.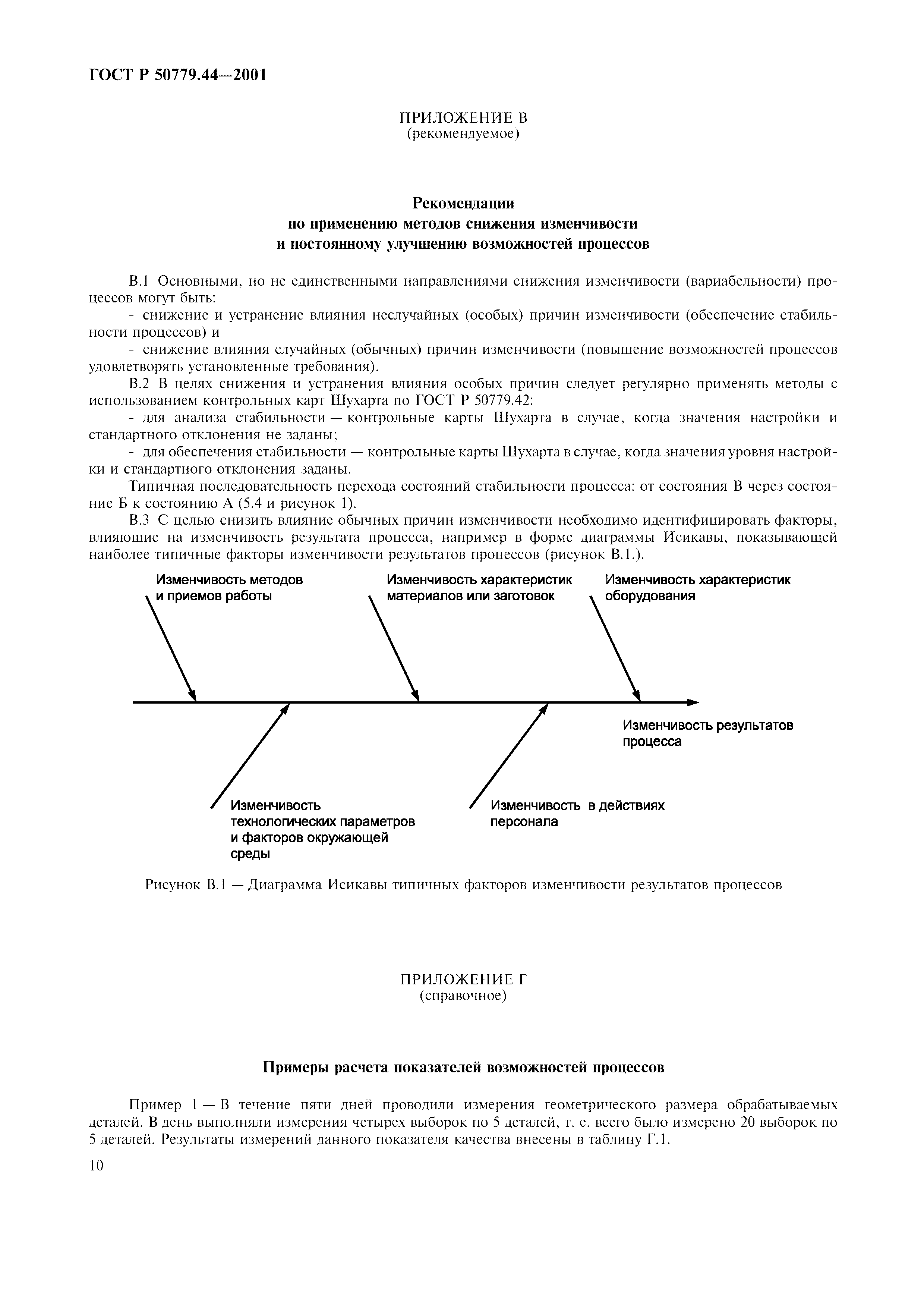 56
56
Показатели по дефектам за 1, 3, 4, 5, 6, 7 месяцы выходят за границу «нормальных» вариаций. Получается, есть много субъективных факторов, влияющих на процессы. Необходимо их найти и устранить. Тогда с конвейера будет выходить гораздо более качественная продукция.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Аспекты управления качеством
УДК 658.562:664Табл. 1. Ил. 1. Библ. 14.
DOI: 10.21323/2071-2499-2020-6-14-17
Аспекты управления качеством
Никитина М.А., канд. техн. наук, Захаров А.Н., канд. техн. наукФНЦ пищевых систем им. В.М. Горбатова
Ключевые слова: Шухарт, SCADA, управление качеством, теория управления,
Реферат:
Рассматриваются основные принципы построения систем управления качеством при производстве пищевых продуктов. Дан анализ управленческих производственных систем для управления качеством с точки зрения концепции статистического управления качеством Шухарта.
Aspects of quality management
Nikitina M.A., Zakharov A.N.Gorbatov Research Center for Food Systems
Key words: Shewhart, SCADA, quality management, management theory
Summary:
The main principles of the development of quality management systems in food production are examined. Analysis of management production systems for quality management from the viewpoint of the Shewhart’s concept of statistical quality control is given.
СПИСОК ЛИТЕРАТУРЫ / REFERENCES:
Nikitina, M.A. Berezhlivoye proizvodstvo kak instrument povysheniya proizvoditel’nosti truda i povysheniya kachestva produktsii [Lean production as an instrument of increasing labor productivity and improving product quality] / M. A. Nikitina, A.N. Zakharov // Vsyo o myase. – 2020. – № 1. – P. 25–29. DOI: 10.21323/2071–2499–2020–1–25–29.
A. Nikitina, A.N. Zakharov // Vsyo o myase. – 2020. – № 1. – P. 25–29. DOI: 10.21323/2071–2499–2020–1–25–29.
2. Shewhart, W.A. Economic Control of Quality of Manufactured Product / W.A. Shewhart. – New York: D. Van Nostrand Company, Inc, 1931. – 501 p.
3. Волошина, Е.С. Оценка результативности системы менеджмента качества на мясоперерабатывающем предприятии / Е.С. Волошина, Н.И. Дунченко // Теория и практика переработки мяса. – 2017. – Т. 2. – № 3. – С. 21–30. https://doi.org/10.21323/2414–438X‑2017–2–3–21–30.
Voloshina, E.S. Otsenka rezul’tativnosti sistemy menedzhmenta kachestva na myasopererabatyvayushchem predpriyatii [Measurement of quality management system performance in meat processing] / E.S. Voloshina, N.I. Dunchenko // Theory and practice of meat processing. – 2017. – V. 2. – № 3. – P. 21–30. https://doi.org/10.21323/2414–438X‑2017–2–3–21–30.
4. Feigenbaum A.V. Total Quality Control. – New York: McGraw-Hill, 1961. – 896 p.
5. Shewhart, W.A. Statistical method. From the viewpoint of quality control / W.A. Shewhart, W.E. Deming. – Washington: The Graduate school the department of agriculture, 1939. – 155 p.
From the viewpoint of quality control / W.A. Shewhart, W.E. Deming. – Washington: The Graduate school the department of agriculture, 1939. – 155 p.
6. Клячкин, В.Н. Статистические методы в управлении качеством: компьютерные технологии / В.Н. Клячкин. – М.: Финансы и статистика, 2009. – 304 с. ISBN978–5–279–03046–0.
Klyachkin, V.N. Statisticheskiye metody v upravlenii kachestvom: komp’yuternyye tekhnologii [Statistical methods in quality management: computer technologies] / V.N. Klyachkin, Moscow: Finance and statistics, 2009. – 304 p. ISBN978–5–279–03046–0.
7. ГОСТ Р ИСО 7870–2–2015. «Статистические методы. Контрольные карты. Часть 2. Контрольные карты Шухарта». – М.: Стандартинформ, 2019. – 57 с.
GOST R ISO 7870–2–2015. «Statisticheskiye metody. Kontrol’nyye karty. Chast’ 2. Kontrol’nyye karty Shukharta» [GOST R ISO 7870–2–2015 “Control charts. Part 2: Shewhart control charts”]. – Moscow: Standartinform. 2019. – 57 p.
8. Гиссин, В.И. Управление качеством / В. И. Гиссин. – М.: Март, 2003. – 400 с. ISBN5–241–00269–3.
И. Гиссин. – М.: Март, 2003. – 400 с. ISBN5–241–00269–3.
Gissin, V.I. Upravleniye kachestvom [Management of quality] / V.I. Gisin. – Moscow: Mart, 2003. – 400 p. ISBN5–241–00269–3.
9. ГОСТ Р ИСО 9000–2008. «Системы менеджмента качества. Основные положения и словарь». – М.: Стандартинформ, 2008. – 70 с.
GOST R ISO 9000–2008. «Sistemy menedzhmenta kachestva. Osnovnyye polozheniya i slovar’» [GOST R ISO 9000–2008. “Quality management systems. Fundamentals and vocabulary”]. – Moscow: Standartinform. 2008. – 70 p.
10. Чем Вам поможет программный продукт «1С: Мясопереработка MES. Модуль для 1С: ERP». Электронный ресурс – Режим доступа: [http://mesbymeat.ru/program/chem-vam-pomozhetmesbymeat/]. (Дата обращения: 08.12.2020).
Chem Vam pomozhet programmnyy produkt «1S: Myasopererabotka MES. Modul’ dlya 1S: ERP» [How the program module “1С: Meat processing MES. Module for 1С: ERP” can help you?]. Electronic resource. – Access mode: [http://mesbymeat.ru/program/chem-vam-pomozhet-mesbymeat/]. (Accessed: 08.12.2020).
(Accessed: 08.12.2020).
11. Мясной Эксперт на «Окраине». Тестируем MES на прочность, изучаем пользу от внедрения. Электронный ресурс – Режим доступа: [https://meat-expert.ru/articles/95-myasnoy-ekspertna-okraine-testiruem-mes-na-prochnost-izuchaem-polzu-otvnedreniya]. (Дата обращения: 08.12.2020).
Myasnoy Ekspert na «Okraine». Testiruyem MES na prochnost’, izuchayem pol’zu ot vnedreniya [Meat Expert in “Okraina”. Testing MES for strength, studying benefits from introduction]. Electronic resource. – Access mode: [https://meat-expert.ru/articles/95-myasnoyekspert-na-okraine-testiruem-mes-na-prochnost-izuchaem-polzu-otvnedreniya]. (Accessed: 08.12.2020).
12. ГОСТ Р ИСО 9001–2015. «Системы менеджмента качества. Требования». – М.: Стандартинформ, 2015. – 64 с.
GOST R ISO 9001–2015. «Sistemy menedzhmenta kachestva. Trebovaniya » [GOST R ISO 9001–2015. “Quality Management System. Requirements”]. – Moscow: Standartinform. 2015. – 64 p.
13. Лисицын, А.Б. Качество и безопасность продукции: создание и развитие систем управления / А.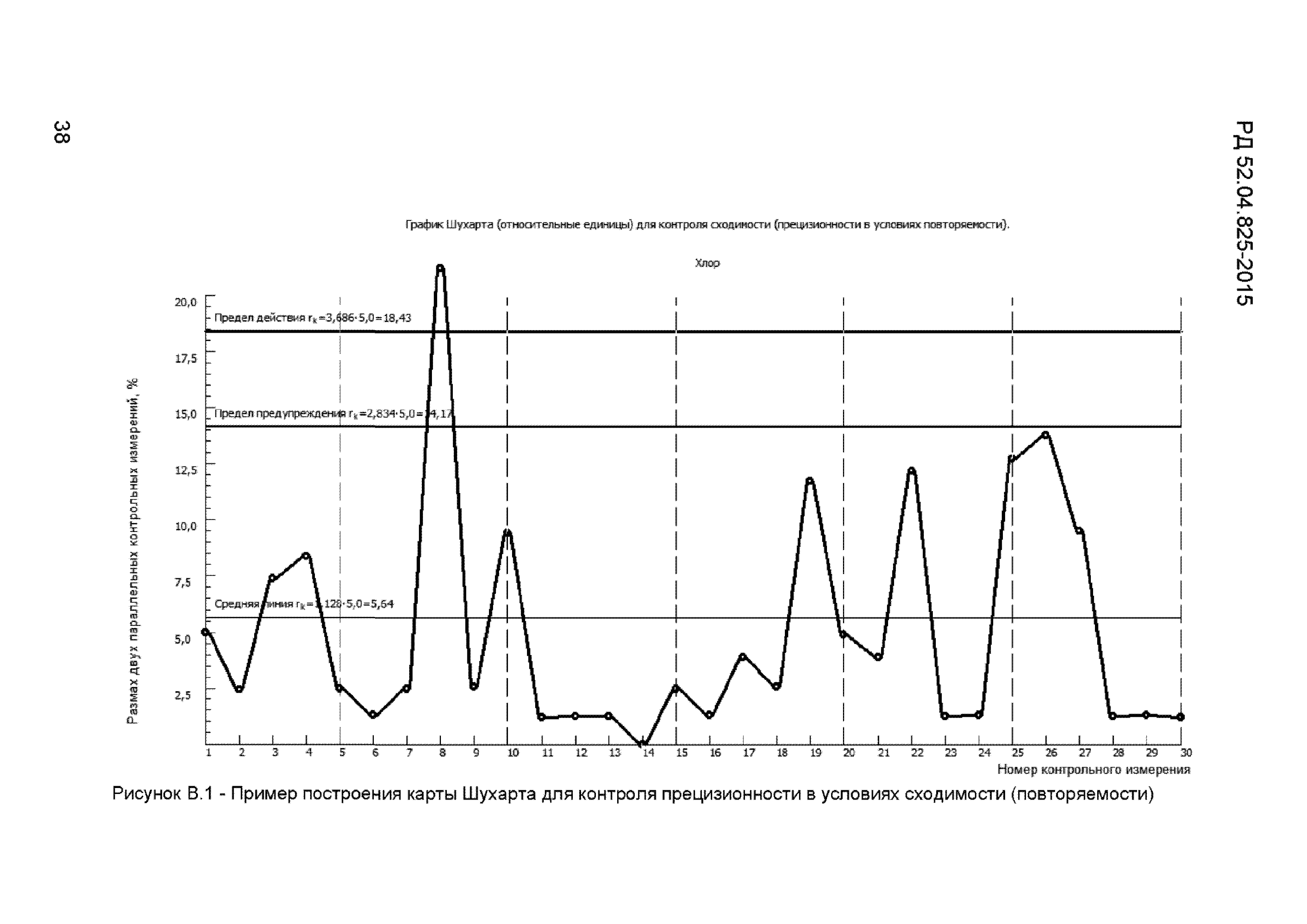
Lisitsyn, A.B. Kachestvo i bezopasnost’ produktsii: sozdaniye i razvitiye sistem upravleniya [Quality and safety of products: creation and development of management systems] / A.B. Lisitsyn, I.M. Chernukha, G. Yu. Makarenkova, G.A. Berlova, O.A. Kuznetsova / / under the ed. A.B. Lisitsyn. – Moscow: Editorial Service, 2010. – 312 p. ISBN978–5–9901348–3–6.
14. Конкурс «Гарантия качества». Электронный ресурс. – Режим доступа: [https://www.vniimp.ru/press-centr/news/news_977.html]. (Дата обращения: 16.09.2020).
Konkurs «Garantiya kachestva» [Competition “Quality Assurance”]. Electronic resource. – Access mode: [https://www.vniimp.ru/press-centr/news/news_977.html] (Accessed: 16.09.2020).
Контакты:
Никитина Марина Александровна[email protected]
Захаров Александр Николаевич
a.
 [email protected]
[email protected]Для цитирования:
Никитина, М.А. Аспекты управления качеством / М.А. Никитина, А.Н. Захаров // Все о мясе. – 2020. – № 6. – С. 14-17. DOI: 10.21323/2071-2499-2020-6-14-17.For citation:
Nikitina, M.A. Aspects of quality management / M.A. Nikitina, A.N. Zakharov // Vsyo o myase. – 2020. – № 6. – Р. 14-17. DOI: 10.21323/2071-2499-2020-6-14-17.Россельхознадзор — Официальный сайт — Версия для печати
Россельхознадзор — Официальный сайт — Версия для печатиОфициальный сайт
Федеральной службы по ветеринарному и фитосанитарному надзору
(http://www.fsvps.ru)
Россельхознадзор / Новости
13 ноября 2020 г.
ФГБУ ЦНМВЛ проведет вебинар по внутрилабораторному контролю качества химических исследований
В период с 7 по 11 декабря Учебный центр подведомственного Россельхознадзору ФГБУ «Центральная научно-методическая ветеринарная лаборатория» (ФГБУ ЦНМВЛ) проведет курсы повышения квалификации по теме «Внутрилабораторный контроль качества химических исследований».
Курсы повышения квалификации будут организованы в очной форме с использованием дистанционных образовательных технологий (вебинар).
В рамках обучающей программы слушатели ознакомятся с основными направлениями организации контроля качества, нормативно-правовой базой по внутрилабораторному контролю: ГОСТ Р 50779.42-99 «Контрольные карты Шухарта», ГОСТ 8.315-97 «Государственная система обеспечения единства измерений. Стандартные образцы состава и свойств веществ и материалов. Основные положения», ГОСТ Р ИСО 31000 «Менеджмент риска. Принципы и руководство», ГОСТ Р ИСО/МЭК 31010 «Менеджмент риска. Методы оценки риска». Также слушатели получат навыки контроля стабильности результатов проведенных измерений и управления рисками при обеспечении контроля качества.
В завершение обучения состоится итоговая аттестация. Слушатели, успешно прошедшие итоговую аттестацию, получат удостоверение о повышении квалификации.
Дополнительную информацию о порядке зачисления можно получить по телефону: 8 (905) 167-46-64, а также по электронной почте: Elenav.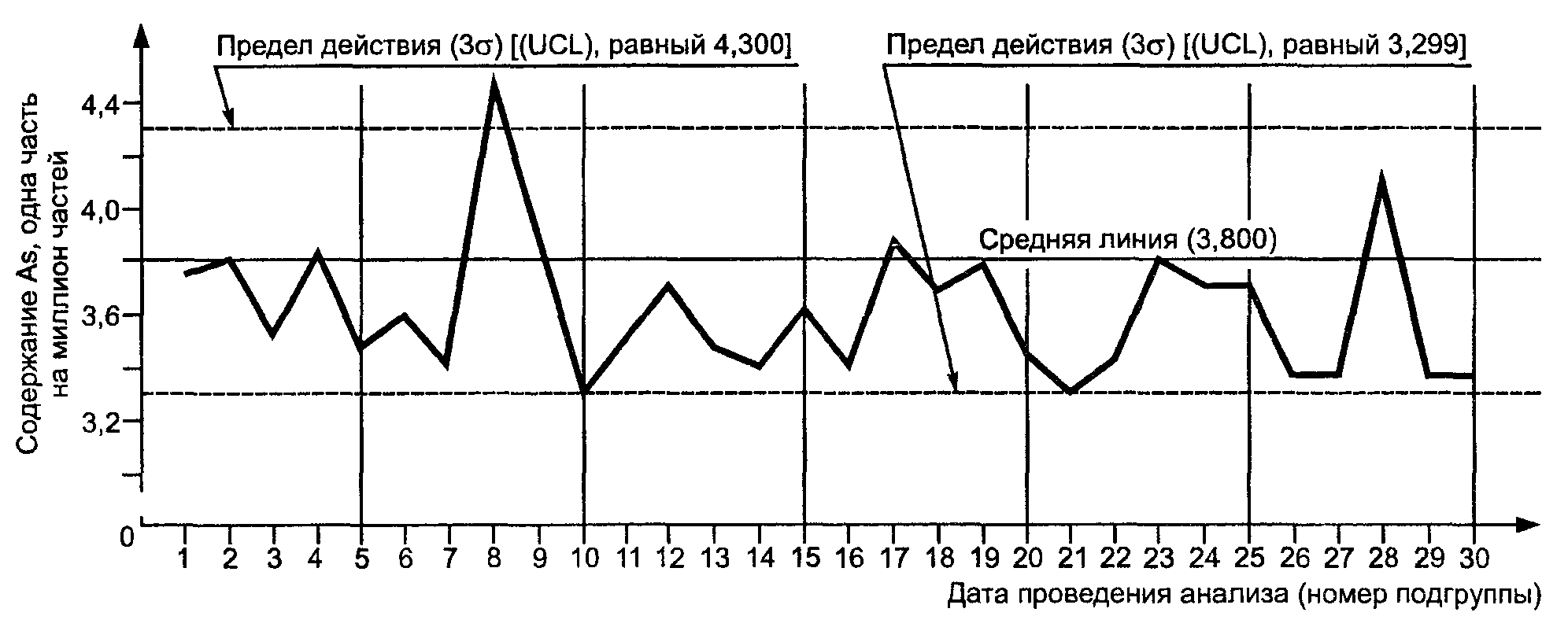 [email protected] .
[email protected] .
Россельхознадзор / Новости / http://www.fsvps.ru/fsvps/news/38382.html
Стратегия решения проблемы конфиденциальности
Конфиденциальность данных является серьезной проблемой и поэтому требует нашего внимания. В этом исследовании мы предлагаем маскирование с помощью методов рандомизированного ответа (RRT), чтобы обеспечить конфиденциальность и, таким образом, избежать фальсификации. Мы предполагаем, что характеристика процесса носит конфиденциальный характер, и из-за проблем с конфиденциальностью фактические измерения не могут быть переданы группе мониторинга. В таких ситуациях производитель с большой долей вероятности может сфальсифицировать измерения. Следовательно, обычные методы построения контрольных диаграмм могут ввести в заблуждение относительно статуса процесса.Мы обсуждаем различные стратегии маскирования данных, которые будут использоваться с контрольными диаграммами типа Шухарта. Обычная контрольная диаграмма типа Шухарта выглядит как часть предложенных диаграмм. Средняя продолжительность выполнения (ARL) используется в качестве показателя эффективности предложений по исследованию. Мы оценили производительность предложенных графиков для разных размеров смены и при различной интенсивности маскировки. Мы также провели сравнительный анализ различных моделей при различных параметрах чувствительности. Мы также сравнили эффективность предложений с традиционной диаграммой Шухарта.Замечено, что контрольная диаграмма B-L в модели RRT работает лучше для небольших смен, а для больших размеров смены диаграмма G-B в модели несвязанных вопросов работает лучше. Также рассматривается практическое применение предложения по исследованию, когда представляет интерес мониторинг толщины краски на холодильниках.
Обычная контрольная диаграмма типа Шухарта выглядит как часть предложенных диаграмм. Средняя продолжительность выполнения (ARL) используется в качестве показателя эффективности предложений по исследованию. Мы оценили производительность предложенных графиков для разных размеров смены и при различной интенсивности маскировки. Мы также провели сравнительный анализ различных моделей при различных параметрах чувствительности. Мы также сравнили эффективность предложений с традиционной диаграммой Шухарта.Замечено, что контрольная диаграмма B-L в модели RRT работает лучше для небольших смен, а для больших размеров смены диаграмма G-B в модели несвязанных вопросов работает лучше. Также рассматривается практическое применение предложения по исследованию, когда представляет интерес мониторинг толщины краски на холодильниках.
1. Введение
Метод контрольных диаграмм предназначен для раннего обнаружения особых причин вариаций в процессе. Идея была предложена Шухартом для мониторинга производственного процесса, а также широко применяется в других областях, таких как здравоохранение, социальные науки и принятие деловых решений. Например, Мухаммад и др. [1] исследовали различные явления, такие как количество операций и время пребывания в больнице, и интерпретировали различные контрольные диаграммы для непрерывных и атрибутивных данных. Sherlaw-Johnson и Beardsley [2] использовали k-сигму и диаграммы переменных контроля для выявления изменений в ежеквартальной наблюдаемой экстренной госпитализации людей определенной возрастной группы в больницу по поводу различных заболеваний. В своей работе они подчеркнули необходимость частого и непрерывного сбора данных по различным показателям с помощью опросов пациентов.В других медицинских учреждениях SPC использовался для мониторинга смертности [3, 4], частоты инфицирования, приобретенной в результате оказания медицинской помощи [5] и [6, 7], а также ряда технологических показателей, включая частоту повторных госпитализаций, продолжительность пребывания или койко-дни [8, 9].
Например, Мухаммад и др. [1] исследовали различные явления, такие как количество операций и время пребывания в больнице, и интерпретировали различные контрольные диаграммы для непрерывных и атрибутивных данных. Sherlaw-Johnson и Beardsley [2] использовали k-сигму и диаграммы переменных контроля для выявления изменений в ежеквартальной наблюдаемой экстренной госпитализации людей определенной возрастной группы в больницу по поводу различных заболеваний. В своей работе они подчеркнули необходимость частого и непрерывного сбора данных по различным показателям с помощью опросов пациентов.В других медицинских учреждениях SPC использовался для мониторинга смертности [3, 4], частоты инфицирования, приобретенной в результате оказания медицинской помощи [5] и [6, 7], а также ряда технологических показателей, включая частоту повторных госпитализаций, продолжительность пребывания или койко-дни [8, 9].
Что касается расширенных методов контрольных диаграмм, мотивированных утверждением Шухарта (1939, стр. 134), «единственный способ ощутить любую характеристику качества количественно — это с помощью операции измерения», Линна и Вудалл [10 ] рассмотрел вопрос об ошибке измерения в производственном процессе и количественно оценил ее влияние на мощность контрольной диаграммы Шухарта для мониторинга исследуемой характеристики.В социальных науках и науках о здоровье эти измерения для целей мониторинга могут собираться непосредственно у лиц в популяции или извлекаться из записей. В обеих ситуациях есть переменные, по которым могут потребоваться данные, но из-за проблем с конфиденциальностью получить точные данные становится сложно. Например, кто-то может быть заинтересован в мониторинге частоты абортов, среднего количества заниженных сведений в отчете о подоходном налоге, количества неудачных операций и количества случаев приема запрещенных наркотиков, но наблюдение за данными непосредственно по этим вопросам приведет к недостоверным результатам. , см., например, Horvitz et al.[11], Эйххорн и Хайр [12], а также Бар-Лев и др.
134), «единственный способ ощутить любую характеристику качества количественно — это с помощью операции измерения», Линна и Вудалл [10 ] рассмотрел вопрос об ошибке измерения в производственном процессе и количественно оценил ее влияние на мощность контрольной диаграммы Шухарта для мониторинга исследуемой характеристики.В социальных науках и науках о здоровье эти измерения для целей мониторинга могут собираться непосредственно у лиц в популяции или извлекаться из записей. В обеих ситуациях есть переменные, по которым могут потребоваться данные, но из-за проблем с конфиденциальностью получить точные данные становится сложно. Например, кто-то может быть заинтересован в мониторинге частоты абортов, среднего количества заниженных сведений в отчете о подоходном налоге, количества неудачных операций и количества случаев приема запрещенных наркотиков, но наблюдение за данными непосредственно по этим вопросам приведет к недостоверным результатам. , см., например, Horvitz et al.[11], Эйххорн и Хайр [12], а также Бар-Лев и др. [13]. Методы рандомизированного отклика (RRT), впервые разработанные Уорнером [14], предоставляют инструменты, с помощью которых можно собирать достоверные данные для получения выводов об истинных величинах с высокой степенью достоверности, но с низкой точностью.
[13]. Методы рандомизированного отклика (RRT), впервые разработанные Уорнером [14], предоставляют инструменты, с помощью которых можно собирать достоверные данные для получения выводов об истинных величинах с высокой степенью достоверности, но с низкой точностью.
В настоящее время конфиденциальность данных является основной проблемой для производственных предприятий и организаций, связанных с бизнесом. В обеих областях широко предлагаются методы построения контрольных диаграмм для повышения качества и принятия бизнес-решений соответственно.Один из возможных способов получения данных — замаскировать фактическое измерение процесса перед его сохранением или, по крайней мере, при выдаче информации для целей мониторинга. Простой и вероятностный способ маскировки характеристики — это сделать это с помощью моделей рандомизированного отклика. Как и в случае с методами построения диаграмм контроля качества, данные могут быть качественными или количественными. Модели рандомизированных ответов обеспечивают механизм маскировки как для качественных, так и для количественных данных.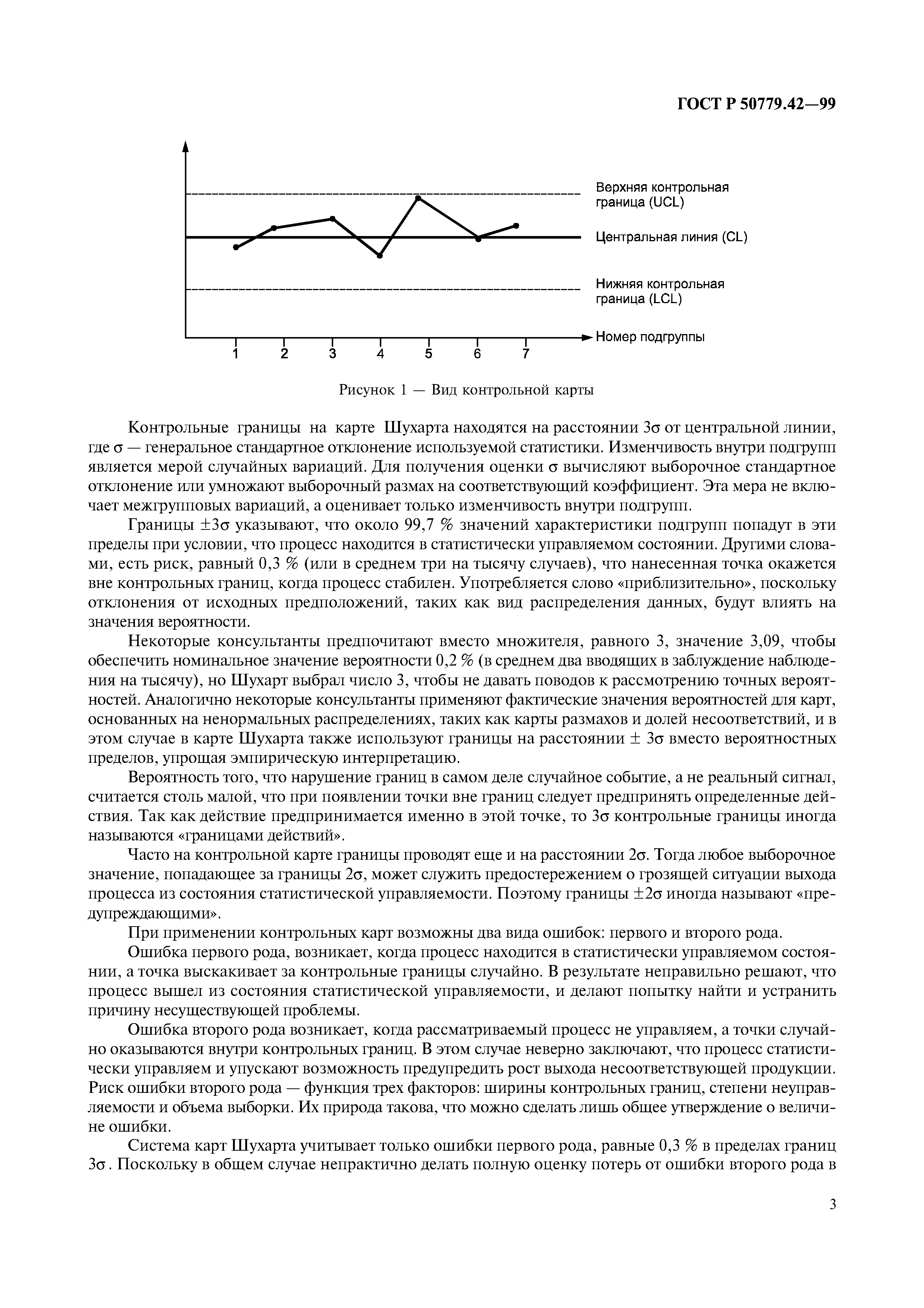 Важно отметить, что индивидуальное рандомизированное наблюдение не может использоваться для определения истинного наблюдения, но фактическое среднее поведение поддается оценке.
Важно отметить, что индивидуальное рандомизированное наблюдение не может использоваться для определения истинного наблюдения, но фактическое среднее поведение поддается оценке.
В нынешнюю эпоху электронных подключений контроль качества в производственном процессе силами внешних специалистов не является чем-то необычным; обмен точной информацией с другими организациями может представлять серьезную угрозу безопасности данных в ситуациях, когда участие внешних инспекторов неизбежно, а обмен точными данными представляет собой угрозу конфиденциальности. Модель RR очень способна решить эту проблему; то есть, нужно просто замаскировать данные с помощью модели RR, прежде чем передавать их в отдел контроля качества, и в этой статье мы показываем, что отдел контроля качества по-прежнему способен контролировать параметры процесса, не зная фактических измерений характеристика процесса.
Целью данной статьи является рассмотрение проблемы ложных отчетов и конфиденциальности данных в методах построения контрольных диаграмм с помощью включения рандомизированных ответов. Предпосылки исследования приведены в Разделе 2, и, следовательно, дается введение в RRT и статистический контроль процессов. В разделе 3 предлагаются стратегии маскирования данных и результирующие контрольные диаграммы типа Шухарта для мониторинга среднего значения процесса. В разделе 4 дается оценка эффективности предложенных диаграмм. Раздел 5 посвящен сравнительному анализу предложенных графиков с существующими.В Разделе 6 представлено применение предложений по исследованию. Исследование завершено, и некоторые аспекты будущих исследований перечислены в Разделе 7.
Предпосылки исследования приведены в Разделе 2, и, следовательно, дается введение в RRT и статистический контроль процессов. В разделе 3 предлагаются стратегии маскирования данных и результирующие контрольные диаграммы типа Шухарта для мониторинга среднего значения процесса. В разделе 4 дается оценка эффективности предложенных диаграмм. Раздел 5 посвящен сравнительному анализу предложенных графиков с существующими.В Разделе 6 представлено применение предложений по исследованию. Исследование завершено, и некоторые аспекты будущих исследований перечислены в Разделе 7.
2. Предпосылки
Это исследование основано на двух известных статистических методах, а именно, методе рандомизированного ответа и диаграмме статистического контроля процесса. Итак, краткий обзор этих двух приведен в следующих разделах.
2.1. Метод рандомизированного ответа
Около полувека назад Уорнер [14] предложил метод рандомизированного ответа в качестве метода исследования для уменьшения потенциальной предвзятости из-за отсутствия ответа и социальной желательности при задании вопросов о деликатном поведении и убеждениях. В этом методе респондентам предлагается использовать устройство рандомизации, такое как подбрасывание монеты, результат которого интервьюер не наблюдает. В зависимости от конкретной конструкции устройство рандомизации определяет, на какой вопрос респондент должен ответить [14–17], тип выражения, который респондент использует для ответа на деликатный вопрос [18], или должен ли респондент дать заранее определенный ответ [19]. , 20]. За счет введения случайного шума метод рандомизированного ответа скрывает индивидуальные ответы и защищает конфиденциальность респондентов.В результате респонденты могут быть более склонны отвечать правдиво.
В этом методе респондентам предлагается использовать устройство рандомизации, такое как подбрасывание монеты, результат которого интервьюер не наблюдает. В зависимости от конкретной конструкции устройство рандомизации определяет, на какой вопрос респондент должен ответить [14–17], тип выражения, который респондент использует для ответа на деликатный вопрос [18], или должен ли респондент дать заранее определенный ответ [19]. , 20]. За счет введения случайного шума метод рандомизированного ответа скрывает индивидуальные ответы и защищает конфиденциальность респондентов.В результате респонденты могут быть более склонны отвечать правдиво.
Метод рандомизированного ответа — это в основном метод генерации данных, который расширяется различными способами. В зависимости от типа параметра мы хотим оценить через данные; RRT делятся на два основных типа: качественные RRT и количественные RRT. В качественных RRT оценка пропорций оставалась основным интересом, а когда дело доходит до оценки среднего населения или подобного, то используются количественные RRT. По поводу последних достижений в области RRT мы отсылаем к Shah et al. [21] и Blair et al. [22]. С другой стороны, RRT были эффективно объединены с другими инструментами, и были предложены новые области исследований. Например, Du и Zhan [23] объединили RRT для сохранения конфиденциальности при интеллектуальном анализе данных, а Shah et al. [24] успешно объединили модели RRT и парного сравнения, чтобы гарантировать конфиденциальность судей в эксперименте парных сравнений и, следовательно, уменьшить влияние смещения социальной желательности.
По поводу последних достижений в области RRT мы отсылаем к Shah et al. [21] и Blair et al. [22]. С другой стороны, RRT были эффективно объединены с другими инструментами, и были предложены новые области исследований. Например, Du и Zhan [23] объединили RRT для сохранения конфиденциальности при интеллектуальном анализе данных, а Shah et al. [24] успешно объединили модели RRT и парного сравнения, чтобы гарантировать конфиденциальность судей в эксперименте парных сравнений и, следовательно, уменьшить влияние смещения социальной желательности.
Существуют различные другие поля, с которыми RRT может быть объединен для получения результатов, менее подверженных ложным сообщениям, и мы думаем, что статистические контрольные диаграммы являются одним из них.Таким образом, в следующем подразделе мы кратко объясним это с кратким обзором.
2.2. Графики статистического контроля
В настройках статистического управления процессом (SPC) вариации в измерениях подразделяются на два типа: вариации по особой причине и вариации по общей причине, последний никогда не может быть устранен полностью, и поэтому они приемлемы.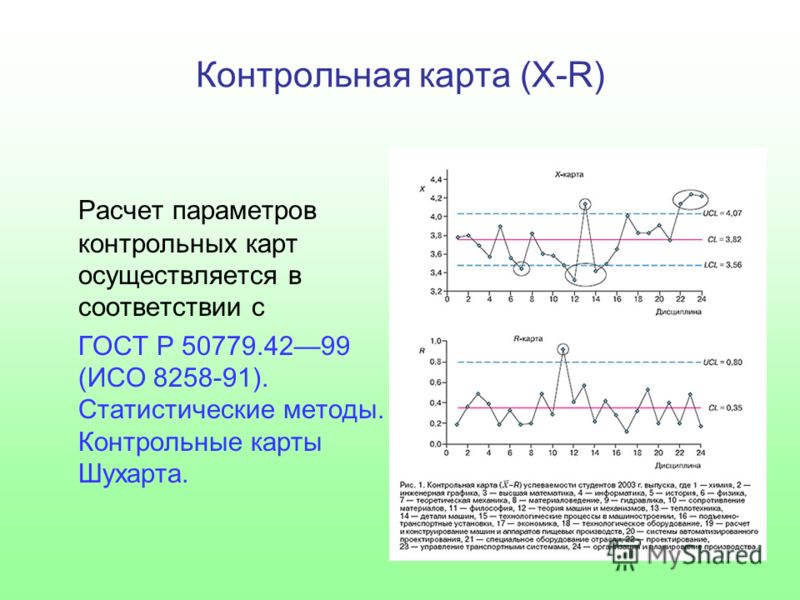 Первый считается плохим, и если он присутствует, процесс классифицируется как неконтролируемый. Кроме того, эти изменения объясняются изменением параметров процесса.Для обеспечения качества рекомендуется раннее обнаружение сдвига. Контрольная диаграмма (CC) — один из статистических инструментов, используемых для раннего обнаружения сдвига. Идея была разработана Шухартом [25] около века назад в Америке для мониторинга производственного процесса. В настоящее время в этих техниках есть достойный прогресс. Например, предлагаются контрольные диаграммы экспоненциального скользящего среднего (EWMA) и совокупной суммы (CUSUM) с учетом важности величины сдвига, а p-диаграмма, u-диаграмма, s-диаграмма и многие другие предлагаются с учетом различного качества. характеристики, представляющие интерес.Кроме того, много литературы посвящено настройке границ диаграммы Шухарта для различных сред. Например, Raji et al. [26] оценивают влияние выбросов на диаграмму Шухарта и оценивают применимость с помощью данных из промышленности по производству полупроводников; и Челано и Чакраборти [27] предложили нераспространяемую контрольную диаграмму Шухарта для мониторинга продуктивности с конечным горизонтом.
Первый считается плохим, и если он присутствует, процесс классифицируется как неконтролируемый. Кроме того, эти изменения объясняются изменением параметров процесса.Для обеспечения качества рекомендуется раннее обнаружение сдвига. Контрольная диаграмма (CC) — один из статистических инструментов, используемых для раннего обнаружения сдвига. Идея была разработана Шухартом [25] около века назад в Америке для мониторинга производственного процесса. В настоящее время в этих техниках есть достойный прогресс. Например, предлагаются контрольные диаграммы экспоненциального скользящего среднего (EWMA) и совокупной суммы (CUSUM) с учетом важности величины сдвига, а p-диаграмма, u-диаграмма, s-диаграмма и многие другие предлагаются с учетом различного качества. характеристики, представляющие интерес.Кроме того, много литературы посвящено настройке границ диаграммы Шухарта для различных сред. Например, Raji et al. [26] оценивают влияние выбросов на диаграмму Шухарта и оценивают применимость с помощью данных из промышленности по производству полупроводников; и Челано и Чакраборти [27] предложили нераспространяемую контрольную диаграмму Шухарта для мониторинга продуктивности с конечным горизонтом.
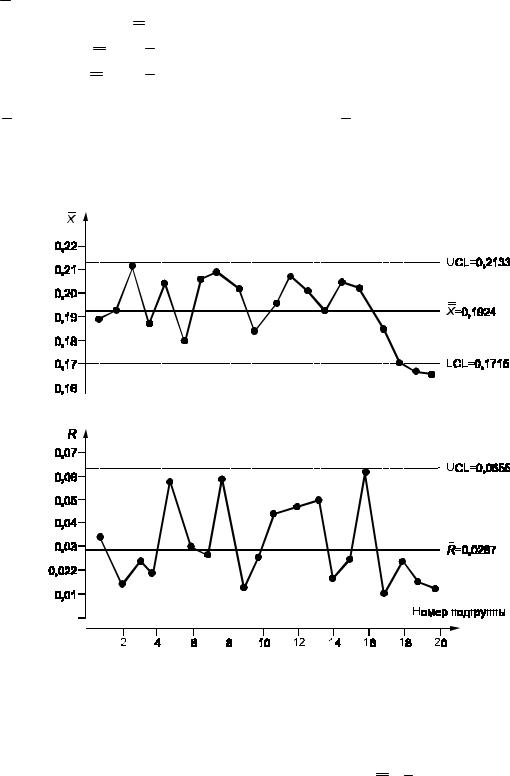
Теперь мы переходим к обсуждению базовой и простой контрольной диаграммы Шухарта [25] для мониторинга среднего значения непрерывной случайной величины X , известной как контрольная диаграмма x-столбца.Установленные компоненты этой диаграммы: (1) средство оценки параметра процесса, называемое статистикой построения графика, функция выборочного наблюдения (наблюдений), (2) центральная линия, соответствующая среднему значению средства оценки, и (3 ) контрольный предел, верхний контрольный предел (UCL) и нижний контрольный предел (LCL), обычно устанавливаются как 3 стандартных ошибки вокруг среднего значения. Для математических формулировок предположим, что характеристика качества следует распределению со средним значением и дисперсией, и рассмотрим, что это статистика построения графика, тогда верхний и нижний пределы k-сигмы, соответственно, определены как
Существует несколько правил для классификации процесс выходит из-под контроля или под контролем, называемое правилом запуска s, но самым простым из них является то, что если значение статистики построения графика выходит за эти контрольные пределы, то процесс считается неконтролируемым; в противном случае нет никаких доказательств вариаций по особой причине. Одним из критериев измерения производительности CC является ARL, определяемый как среднее количество подвыборок, необходимых для CC для обнаружения сдвига в параметрах процесса. Вариации по общей причине могут привести к подаче сигнала CC; в таких ситуациях вычисленный ARL классифицируется как контролируемый ARL и обозначается ARL 0 . Частота ложных тревог, обратная ARL 0 , представляет собой вероятность того, что значение статистики построения графика выходит за контрольные пределы, учитывая, что параметры процесса находятся в контролируемом состоянии, то есть где, как говорят, значение для который считается, что базовый процесс находится в контролируемом состоянии.В (1) и (2) k — положительная константа, обычно используемая равной 3 для процесса, в котором предполагается, что распределение базовой характеристики качества подчиняется нормальному распределению. В таких случаях k , равное 3, дает 0 ARL, равное 370. Когда статистика построения графика не соответствует нормальному распределению, а затем для измерения производительности, можно зафиксировать частоту ложных тревог на 0,0027 (или любое другое значение) и значение k должно быть найдено.
Одним из критериев измерения производительности CC является ARL, определяемый как среднее количество подвыборок, необходимых для CC для обнаружения сдвига в параметрах процесса. Вариации по общей причине могут привести к подаче сигнала CC; в таких ситуациях вычисленный ARL классифицируется как контролируемый ARL и обозначается ARL 0 . Частота ложных тревог, обратная ARL 0 , представляет собой вероятность того, что значение статистики построения графика выходит за контрольные пределы, учитывая, что параметры процесса находятся в контролируемом состоянии, то есть где, как говорят, значение для который считается, что базовый процесс находится в контролируемом состоянии.В (1) и (2) k — положительная константа, обычно используемая равной 3 для процесса, в котором предполагается, что распределение базовой характеристики качества подчиняется нормальному распределению. В таких случаях k , равное 3, дает 0 ARL, равное 370. Когда статистика построения графика не соответствует нормальному распределению, а затем для измерения производительности, можно зафиксировать частоту ложных тревог на 0,0027 (или любое другое значение) и значение k должно быть найдено. Подробнее см. Mehmood et al.[28] и Haridy et al. [29].
Подробнее см. Mehmood et al.[28] и Haridy et al. [29].
3. Различные типы маскирования и предлагаемые диаграммы
Этот раздел посвящен построению обобщенной техники построения контрольных диаграмм, которая в широком смысле использует методику Шухарта и приводит к гибкому способу мониторинга чувствительного персонажа. Этот механизм использует как количественные модели рандомизированного отклика, так и методы, используемые для мониторинга среднего значения процесса в статистическом управлении процессом. Мы начинаем с того, что представляем производителю механизм маскировки, который он может выбрать для маскировки данных.Затем мы предоставляем контрольные пределы диаграмм типа Шухарта, и они способны удовлетворить интенсивность маскировки, используемую производителями. Наконец, мы проводим теоретическое сравнение с традиционной диаграммой Шухарта.
В следующих разделах давайте обозначим интересующий чувствительный характер случайной величиной X , пусть S будет случайной величиной, используемой для маскировки ответа, сгенерированного из произвольного распределения, и пусть Z будет наблюдаемым рандомизированным отклик. В исследованиях RR S также называют переменной скремблирования.
В исследованиях RR S также называют переменной скремблирования.
3.1. Маскировка с помощью Greenberg et al. [30] Модель и диаграмма G-B
В исследовании Greenberg et al. [30], они придумали идею сбора количественных данных при выборке для опроса по чувствительным вопросам. Мы используем исследование Гринберга и др. [30] и заявляют, что производитель / респондент сообщает фактическое измерение X с вероятностью P или значение S с вероятностью (1-P). Таким образом, замаскированные данные могут быть смоделированы, как где p определяется таким же образом, как определено Warner [14], известен как параметр маскирования, выбирается производителем и известен группе мониторинга.Кроме того, предположим, что X следует распределению со средним значением и дисперсией, а S не зависит от X со средним значением и дисперсией. Теперь нетривиально показать, что среднее значение и дисперсия Z равны
. Затем несмещенная оценка, предложенная Гринбергом и др. [30] равно
[30] равно
И его дисперсия дается следующим образом:
Используя приведенные выше факты, мы имеем контрольную диаграмму типа Шухарта для мониторинга среднего значения X с нижним и верхним доверительным пределом, соответственно. , as
Если мы посмотрим на модель (3) и ограничения (7) и (8), то нетривиально заметить, что для, у нас есть немаскированные данные, и эта диаграмма сокращается до обычных пределов диаграммы типа Шухарта. приведенные в (1) и (2).В следующих разделах мы будем называть эту диаграмму диаграммой G-B.
3.2. Маскировка с помощью Эйххорна и Хайра [12] и Бар-Лев и др. [13] Модели и диаграмма B-L
Эйххорн и Хайр [12] предложили новую технику рандомизированного ответа для оценки среднего отклика населения количественно-чувствительного характера. Каждое измерение записывается в замаскированной форме. То есть производителю предписывается предоставить закодированные или скремблированные наблюдения, полученные путем умножения истинного значения измерения на некоторые случайные числа, неизвестные контролирующим органам. Группа мониторинга не знает, какое случайное число производитель использовал для кодирования, но известно распределение, по которому это случайное число было сгенерировано.
Группа мониторинга не знает, какое случайное число производитель использовал для кодирования, но известно распределение, по которому это случайное число было сгенерировано.
Пусть X — это переменная, представляющая ответы на чувствительный количественный символ, S — это переменная, представляющая случайное число, используемое для целей кодирования ответов, а Z E = XS представляет закодированный ответ, где S и X независимы друг от друга.Тогда где — коэффициент вариации.
Таким образом, несмещенная оценка, предложенная Эйххорном и Хайром [12], задается как и ее дисперсия равна
. Обозначим интересующий нас чувствительный характер случайной величиной X , пусть S — случайная величина. используется для маскировки ответа, сгенерированного из произвольного распределения, а Z — наблюдаемый рандомизированный ответ. Для простоты и без потерь мы предполагаем независимость между X и S . Согласно Бар-Леву и соавт. [13], Z распределяется так же, как и та же роль, определенная Уорнером [14], известная как параметр маскировки и представленная исследователем. Кроме того, предположим, что X следует распределению со средним значением и дисперсией, а S не зависит от X со средним значением и дисперсией. Теперь нетривиально показать, что среднее значение и дисперсия Z равны
Согласно Бар-Леву и соавт. [13], Z распределяется так же, как и та же роль, определенная Уорнером [14], известная как параметр маскировки и представленная исследователем. Кроме того, предположим, что X следует распределению со средним значением и дисперсией, а S не зависит от X со средним значением и дисперсией. Теперь нетривиально показать, что среднее значение и дисперсия Z равны
. Используя приведенную выше информацию, Bar-Lev et al. [13] предложили несмещенную оценку истинного среднего значения, поскольку где — выборочное среднее рандомизированных данных.Стандартная ошибка оценки, приведенной в (14), составляет
Используя уравнения (14) и (15), нижний контрольный предел k-сигмы (LCL 2 ), центральную линию (CL 2 ) и верхний контрольный предел. предел (UCL 2 ) контрольной диаграммы Шухарта для мониторинга среднего значения чувствительного процесса X , определяется, соответственно, как
Эта модель является общей формой прямых откликов и моделью, предложенной Эйххорном и Хайром [12 ], то есть для этой модели сводится к механизму прямого отклика, а для, это становится мультипликативной моделью рандомизированного отклика, предложенной Эйххорном и Хайром. Для простоты в следующих разделах мы обозначим эту предложенную схему как B-L (Bar-Lev).
Для простоты в следующих разделах мы обозначим эту предложенную схему как B-L (Bar-Lev).
3.3. Маскирование с помощью аддитивных моделей и диаграммы G-A
Для повышения эффективности оценок было рассмотрено несколько методов. Такие улучшения стоят простоты модели, но аддитивные модели рандомизированного отклика являются одними из тех, которые просты в применении и лучше с точки зрения дисперсии оценок. Гупта и др. [31] предложили дополнительную модель рандомизированного аддитивного отклика, которая, с увеличением эффективности, также способна производить информацию для оценки уровня чувствительности.Здесь мы упрощаем Gupta et al. [31] модель как
В этой упрощенной версии Gupta et al. [31] модель, если, то мы получаем модель, предложенную Поллоком и Беком [32]. Несмещенная оценка чувствительного среднего может быть представлена как
. Нетривиально показать, что дисперсия (18) равна
. Установив в (17), (18) и (19), можно получить модель , оценка и ее дисперсия, предложенные Поллоком и Беком [32] соответственно.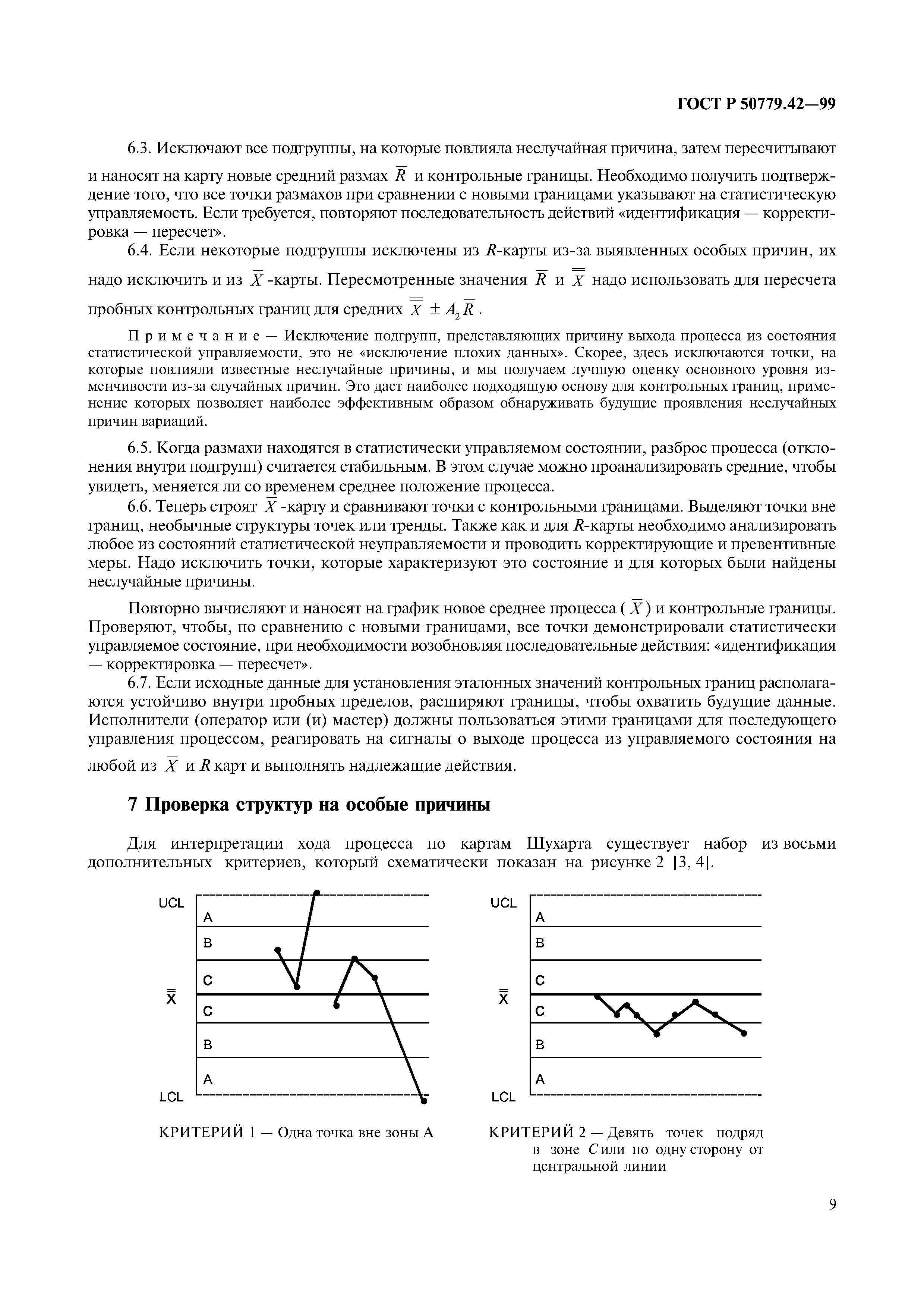
Верхний контрольный предел (UCL 3 ) и нижний контрольный предел (LCL 3 ) для этой модели, соответственно, дается как
Кроме того, эта диаграмма называется диаграммой GA, что означает добавление Гупты. диаграмму, и, положив, диаграмма GA сводится к обычной диаграмме Шухарта.
4. Оценка производительности
Производительность предложенной диаграммы оценивается с помощью традиционного моделирования Монте-Карло для различных значений параметра маскирования ( p ). Мы предположили, что X следует нормальному распределению со средним значением 3 и дисперсией 1. Распределение маскирующей переменной S предполагается пуассоновским со средним значением. Сначала мы провели поиск значений k для различных значений, установив ARL 0 приблизительно равным 370, а затем мы ввели сдвиг различной величины и вычислили неконтролируемую среднюю длину пробега (ARL) и стандартное отклонение длины прогона (SDRL) для оценки мощности обнаружения сдвига в X предлагаемой диаграммы. Размер сдвига в среднем X определяется как, где — среднее значение сдвига X . Результаты представлены в Таблице 1–3 для различных настроек. Мы сравнили производительность с традиционной диаграммой Шухарта.
Размер сдвига в среднем X определяется как, где — среднее значение сдвига X . Результаты представлены в Таблице 1–3 для различных настроек. Мы сравнили производительность с традиционной диаграммой Шухарта.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4.
 1. Диаграмма G-B
1. Диаграмма G-BСогласно результатам, приведенным в таблице 2, эта диаграмма страдает смещенной проблемой ARL для меньших размеров смен.Как следует из (5), статистика построения графиков не существует для, что означает, что полностью несвязанные данные (когда Z = S ) не могут использоваться для мониторинга среднего значения процесса. Кроме того, для больших сдвигов (больше или равных 1) производительность диаграммы улучшается с увеличением и сходится к обычной диаграмме Шухарта, когда становится 1.
4.2. График B-L
Как обсуждалось в разделе 3.2, что модель B-L является обобщенной формой модели Эйхорна и Хайра [12], мы рассматриваем модель B-L для оценки.Значения ARL, представленные в таблице 2, показывают обычное поведение; то есть по мере увеличения размера сдвига мы ожидаем более раннего обнаружения. Также наблюдается отсутствие линейной зависимости между p и характеристиками контрольной диаграммы, но диаграмма работает лучше при крайних значениях p ; то есть, когда или, то ARL уменьшается раньше, чем увеличивается размер сдвига. Стоит отметить, что при мы полностью замаскировали данные; то есть конфиденциальность полностью обеспечивается; когда, то у нас есть полностью демаскированные данные, и предлагаемая контрольная диаграмма сводится к обычной диаграмме Шухарта; Следует убедиться в общности предложенной схемы.Кроме того, когда p уменьшается с 0,9 до 0,1 (с размером шага, равным 0,1), тогда мощность обнаружения диаграммы увеличивается. Кроме того, в данной настройке наблюдается, что для некоторых комбинаций p и размера сдвига предложенная диаграмма смещена по ARL, и эти ситуации выделены в таблице 2.
Стоит отметить, что при мы полностью замаскировали данные; то есть конфиденциальность полностью обеспечивается; когда, то у нас есть полностью демаскированные данные, и предлагаемая контрольная диаграмма сводится к обычной диаграмме Шухарта; Следует убедиться в общности предложенной схемы.Кроме того, когда p уменьшается с 0,9 до 0,1 (с размером шага, равным 0,1), тогда мощность обнаружения диаграммы увеличивается. Кроме того, в данной настройке наблюдается, что для некоторых комбинаций p и размера сдвига предложенная диаграмма смещена по ARL, и эти ситуации выделены в таблице 2.
4.3. График G-A
Контрольные пределы представлены в таблице 1 для различных значений параметра маскирования, p , путем фиксации ARL 0 равным 370.Проблема смещения ARL снова возникает для небольших смен. Связь между степенью маскировки и средней длиной тиража не является линейной; то есть существует тенденция к увеличению ARL для меньших размеров смены, но постепенно тенденция к снижению для больших размеров смен (больше или равных 1). Точно так же эта диаграмма является обобщением простых диаграмм Шухарта, Поллока и Бека [32].
Точно так же эта диаграмма является обобщением простых диаграмм Шухарта, Поллока и Бека [32].
5. Сравнительный анализ
В этом разделе приводится сравнение предложенных диаграмм данного исследования с традиционной диаграммой Шухарта.
5.1. Сравнение предложенных диаграмм
В этом разделе графическое сравнение предложенных диаграмм G-B, G-A и B-L дается для различных размеров смен. На рисунке 1 изображена взаимосвязь между, δ, и ARL предложенных диаграмм. Замечено, что график B-L превосходит графики G-B и G-A, когда он меньше или равен 0,7 для разных сдвигов. По мере увеличения размера сдвига производительность диаграммы G-A увеличивается по сравнению с диаграммой G-B для меньших значений.Если зафиксировать значение больше 0,7, диаграмма G-B работает лучше, чем две другие диаграммы, а когда, то все диаграммы сходятся к простой диаграмме Шухарта.
5.2. Предложенная диаграмма в сравнении с диаграммой Шухарта
Как мы видели, предлагаемые диаграммы являются обобщенной формой традиционной диаграммы Шухарта. Стоит отметить, что маскирование имеет два факта: (i) оно обеспечивает конфиденциальность и (ii) оно вносит дополнительный шум в дисперсии оценок. В связи с последним фактом можно сказать, что традиционная диаграмма, представленная в (1) и (2), имеет более узкие пределы, чем предлагаемая, и, следовательно, имеет больше возможностей для обнаружения сдвига.Однако мы не верим в этот аргумент и утверждаем, что традиционная диаграмма Шухарта неспособна обнаружить фальсифицированные ответы, свидетелями которых мы стали в Таблице 2. Для дальнейшего уточнения применимости предлагаемой работы мы рассматриваем ситуацию, когда предполагается, что процесс состоит из чувствительный характер, и группа мониторинга не знает, что измерения сфальсифицированы. Из-за чувствительности производитель сфальсифицировал ответы как, где X — фактическое значение, а S — переменная скремблирования, определенная ранее.Из-за отсутствия предварительной информации группа мониторинга должна использовать традиционную контрольную диаграмму типа Шухарта (с ограничениями, указанными в (1) и (2)) для целей мониторинга. Если это так, то можно увидеть ухудшающуюся природу этого явления на диаграмме Шухарта в последних строках таблицы 2; без изменения параметров процесса диаграмма объявила процесс неконтролируемым. С другой стороны, предложенная методика способна уменьшить влияние фальсифицированных ответов и способна обнаруживать изменение параметра процесса.
Стоит отметить, что маскирование имеет два факта: (i) оно обеспечивает конфиденциальность и (ii) оно вносит дополнительный шум в дисперсии оценок. В связи с последним фактом можно сказать, что традиционная диаграмма, представленная в (1) и (2), имеет более узкие пределы, чем предлагаемая, и, следовательно, имеет больше возможностей для обнаружения сдвига.Однако мы не верим в этот аргумент и утверждаем, что традиционная диаграмма Шухарта неспособна обнаружить фальсифицированные ответы, свидетелями которых мы стали в Таблице 2. Для дальнейшего уточнения применимости предлагаемой работы мы рассматриваем ситуацию, когда предполагается, что процесс состоит из чувствительный характер, и группа мониторинга не знает, что измерения сфальсифицированы. Из-за чувствительности производитель сфальсифицировал ответы как, где X — фактическое значение, а S — переменная скремблирования, определенная ранее.Из-за отсутствия предварительной информации группа мониторинга должна использовать традиционную контрольную диаграмму типа Шухарта (с ограничениями, указанными в (1) и (2)) для целей мониторинга. Если это так, то можно увидеть ухудшающуюся природу этого явления на диаграмме Шухарта в последних строках таблицы 2; без изменения параметров процесса диаграмма объявила процесс неконтролируемым. С другой стороны, предложенная методика способна уменьшить влияние фальсифицированных ответов и способна обнаруживать изменение параметра процесса.
6. Приложение
В этом разделе мы рассматриваем набор данных от Wild и Seber [33] и рандомизируем эти отдельные наблюдения, используя модель, предложенную Bar-Lev et al. [13] (фактически можно рассматривать любую другую модель). Маскированные и немаскированные данные приведены в таблице 4 для различных значений = 0, 0,1, 0,5, 0,8, 0,9 и 1,0. Толщина краски, указанная в первой строке таблицы 1, не маскируется; то есть измерения, соответствующие, являются исходными измерениями.Мы полагаем, что из-за деликатных ситуаций производитель может фальсифицировать эти наблюдения перед тем, как предоставить их инспекторам по качеству. Наша процедура позволяет производителю маскировать эти измерения с помощью модели рандомизированного ответа, описанной в предыдущих разделах. Таким образом инспектор не сможет отследить исходные измерения и, следовательно, конфиденциальность измерений будет обеспечена. Здесь мы рассмотрели отрицательное биномиальное распределение со средним значением 3 и дисперсией 7,5 при маскировании наблюдений для различных значений параметра маскирования P.И из значений видно, что истинные измерения замаскированы; кроме того, интенсивность маскирования увеличивается, когда значение p уменьшается, и, следовательно, для, данные полностью маскируются; то есть каждое измерение, скорее всего, будет отличаться от фактического. На рисунке 2 мы показали, что после маскировки наблюдения группа мониторинга все еще может объявить процесс вышедшим из-под контроля, что на самом деле вышло из-под контроля.
7. Заключение и рекомендацииКонфиденциальность данных в настоящее время является серьезной проблемой, и мы считаем, что если конфиденциальность не защищена, то весьма вероятно, что Владельцам данных (производителям и пациентам) не остается ничего другого, как фальсифицировать данные. Установлено, что сфальсифицированные ответы приводят к неверным выводам. Чтобы справиться с этой ситуацией, в данной работе предлагается беспроигрышная стратегия.Производителю разрешается выполнять маскирование вероятностным способом в любой степени, чтобы обеспечить конфиденциальность и поделиться значением параметра маскирования с группой мониторинга. Эмпирическое исследование показало, что по мере увеличения степени маскировки разница между фактическим и замаскированным наблюдением увеличивается, и в максимальной степени диаграмма все еще способна определять фактическое (неконтролируемое) состояние процесса. Предлагаемый метод разработан для контрольной диаграммы типа Шухарта для мониторинга среднего значения процесса.Следовательно, есть возможность распространить предложенную стратегию на диаграммы управления памятью, а также на атрибуты. Что касается механизма маскировки, существует множество продвинутых моделей, но базовые модели были рассмотрены, чтобы избежать осложнений для практикующих. Поэтому будет интересно провести сравнительное исследование с разными моделями RR. Доступность данныхДанные, использованные для подтверждения выводов этого исследования, включены в статью. Конфликт интересовАвторы заявляют об отсутствии конфликта интересов. Понимание вариаций в зарегистрированных случаях смерти от COVID-19 с помощью нового приложения «Диаграмма Шухарта»Int J Qual Health Care. 26 июня 2020 г .: mzaa069. Рокко Дж Перла1 Health Initiative, Population and Quantitative Health Sciences, Медицинская школа Массачусетского университета Shannon M Provost2 Департамент информации, управления рисками и операциями, Техасский университет в Остине Гарет Дж. Парри3 Институт улучшения здравоохранения Гарвардской медицинской школы Кевин Литтл4 ООО «Информатор Экологический Дизайн» Ллойд П Провост5 Партнеры по совершенствованию процессов, 1 Инициатива в области здравоохранения, народонаселение и количественные науки о здоровье, Медицинская школа Массачусетского университета 2 Департамент информации, управления рисками и операциями, Техасский университет в Остине 3 Институт улучшения здравоохранения Гарвардской медицинской школы 4 ООО «Информационный Экологический Дизайн» 5 Партнеры по совершенствованию процессов, Запросы на перепечатку адресов: Shannon M.Провост, Школа бизнеса Маккомбса, 2110 Speedway, Stop B6500, Остин, Техас, 78712. Тел .: 512-913-2040, Факс: 512-471-0587; Эл. Почта: ude.saxetu@tsovorpsЗапрошены изменения, 10 июня 2020 г .; Принято 2020 16 июня. Авторские права © Автор (ы) 2020. Опубликовано Oxford University Press совместно с Международным обществом качества в здравоохранении. Все права защищены. Для получения разрешений обращайтесь по электронной почте: [email protected]. Эта статья доступна через подмножество открытого доступа PMC для неограниченного повторного использования и анализа в любой форме и любыми средствами с указанием первоисточника.Эти разрешения предоставляются на время пандемии COVID-19 или до тех пор, пока разрешения не будут отозваны в письменной форме. По истечении срока действия этих разрешений PMC предоставляется бессрочная лицензия на предоставление этой статьи через PMC и Europe PMC в соответствии с существующими средствами защиты авторских прав. Эта статья цитируется в других статьях в PMC.AbstractObjectiveВдохновленные пандемией коронавирусного заболевания 2019 (covid-19), мы разработали новую диаграмму Шухарта, чтобы визуализировать и извлекать уроки из вариаций регистрируемых смертей во время эпидемии. КонтекстБез метода, позволяющего понять, можно ли объяснить ежедневные вариации результатов значимыми сигналами изменений — а не вариативностью, которую мы ожидали бы — поставщиками медицинских услуг, лидерами в области улучшения, лицами, определяющими политику, и общественностью. изо всех сил пытаются понять, улучшаются ли эпидемические условия. МетодыМы разработали новую гибридную диаграмму C- и диаграмму I для обнаружения в пределах географической области начала и конца экспоненциального роста зарегистрированных смертей.Зарегистрированные случаи смерти были единицей анализа из-за ошибочного сообщения о случаях из-за вариабельности местных стратегий тестирования. Мы использовали моделирование и тематические исследования для оценки производительности диаграммы и определения технических параметров. Этот подход также применяется к другим критическим мерам, связанным с пандемией, когда доступны высококачественные данные. ВыводыГибридная диаграмма обнаружила начало экспоненциального роста и определила ранние сигналы об окончании фазы роста. Во время пандемии своевременные надежные сигналы о нарастании или ослаблении эпидемии могут иметь смертельные последствия.Эта новая диаграмма предлагает практический инструмент, доступный для руководителей системы и оперативных групп, для визуализации и извлечения уроков из ежедневно регистрируемых случаев смерти во время эпидемии. Без диаграмм Шухарта и, в более широком смысле, теории вариаций в нашем эпидемиологическом арсенале нам не хватает научного метода для оценки местных условий в реальном времени. Диаграммы Шухарта должны стать стандартным методом изучения данных в контексте пандемии или эпидемии. Ключевые слова: Контрольная карта Шухарта, пандемия covid-19, статистическая публичная отчетность по данным здравоохранения, статистический контроль процессов ВведениеВо время пандемии коронавируса 2019 (covid-19) преобладали сообщения о новых случаях заболевания и смерти СМИ.В районах, наиболее пострадавших от вируса, жители и их руководители с нетерпением ждут последних ежедневных данных. Увеличение числа зарегистрированных смертей по сравнению с предыдущим днем может вызвать отчаяние или панику; уменьшение дает надежду на то, что ситуация меняется. Каждый день приносит новую и, казалось бы, значимую историю, которая может повлиять на индивидуальный выбор поведения, повлиять на организационное планирование и / или исказить процесс принятия решений на местном и национальном уровнях. Международные средства массовой информации склонны делать сенсацию пандемией с заголовками, фиксирующими повседневные различия, о чем свидетельствует выборка заголовков в СМИ, характеризующих траекторию смертности от COVID-19 в Великобритании () весной 2020 года.Этот слишком распространенный тип репортажей в прессе затмевает целостный системный взгляд на эпидемический ландшафт. Вместо этого он вызывает гиперреактивную реакцию со стороны политиков и граждан. Динамическая диаграмма зарегистрированных случаев смерти от COVID-19 в Великобритании с примерами заголовков в СМИ. Мы знаем, что количество регистрируемых смертей каждый день — как и все, что мы измеряем — будет колебаться. Не имея метода, позволяющего понять, отражают ли эти «взлеты и падения» просто естественную изменчивость, нам будет трудно распознать сигналы значимого улучшения [1] в условиях эпидемии.Чтобы смоделировать распространение и влияние пандемии covid-19, мы сосредотачиваемся на публично зарегистрированных случаях смерти (а не на случаях заболевания), поскольку вариативность местных стратегий тестирования приводит к ошибочной оценке подтвержденных случаев [2, 3]. Приведенную здесь диаграмму Шухарта можно применять для отслеживания других мер, связанных с эпидемией, таких как госпитализации, госпитализации в ОИТ и интубации. Фундаментальный постулат науки о совершенствовании состоит в том, что понимание источников вариаций в системе является важным аспектом любых усилий, направленных на улучшение этой системы.В 1931 году Уолтер Шухарт предположил, что вариация меры имеет два потенциальных источника: общие причины и особые причины [4]. «Общие причины» присущи системе с течением времени, влияя на всех в системе и на все результаты системы. «Особые причины» не являются частью обычной системы, но возникают из-за определенных обстоятельств или некоторого «особого» источника вариации, который может быть отнесен к идентифицируемой причине. Шухарт создал инструмент «контрольная диаграмма» для практического применения этой теории [5], предоставив экспертам в предметной области (людям с глубокими знаниями местной системы) формальный метод выявления особых причин и оценки вмешательств, которые они предпринимают для изменения системы. общих причин.Теория и диаграммы Шухарта были успешно применены к многочисленным проблемам здравоохранения, промышленности, правительства, образования и благосостояния людей [6–11], но их применение к эпидемиям было ограниченным. Большая часть предыдущих исследований с использованием диаграмм Шухарта в эпидемиологическом контексте была сосредоточена на инфекционном контроле и больничной эпидемиологии [12–16]. Более актуальным для нашего подхода является относительно немногочисленная литература, основанная на использовании контрольных диаграмм, позволяющих своевременно обнаруживать необычные закономерности в данных общественного здравоохранения [17, 18].В исследовании 1946 года эпидемия полиомиелита отслеживалась с помощью столбчатых диаграмм размером х , предполагая, что «таблица промышленного контроля может оказаться полезной для многих видов эпидемиологической работы» [19, с. 1510]. Диаграммы Shewhart U использовались для отслеживания случаев заболеваний и направлений в больницы в качестве динамической системы предупреждения для органов здравоохранения, поставщиков медицинских услуг и населения в целом и, таким образом, «снижали возможность ускорения неблагоприятных событий, указывая соответствующие реакции на нормальные изменения» [ 20, p280]. Исследователи использовали скользящие средние, экспоненциально взвешенные скользящие средние и / или графики кумулятивных сумм для сигнализации о начале или окончании вспышек [21–24], что позволяет быстро обнаруживать и «последующие своевременные меры общественного здравоохранения для снижения ненужной заболеваемости и смертности» [ 25, p3309]. Обзор Вудалла за 2006 г. подчеркнул возможности наблюдения за общественным здоровьем и призвал к дальнейшему исследованию приложений общественного здравоохранения с помощью контрольных диаграмм [26]. Предыдущие исследования показали, что «из многих инструментов, используемых для постоянного улучшения качества, возможно, наиболее важным для понимания эпидемиологом является контрольная диаграмма» [27, p102].Тем не менее, его потенциал для поддержки инициатив в области общественного здравоохранения до сих пор остается непризнанным. В этом документе описывается применение теории вариаций Шухарта для разработки новой контрольной диаграммы для отслеживания ежедневных зарегистрированных смертей в определенной географической области во время пандемии covid-19. МетодыМы разработали новую гибридную диаграмму Шухарта для оценки траектории зарегистрированных смертей с использованием типичной эпидемиологической кривой (), но это приложение не требует теоретических предположений, обычно связанных с этой моделью [28]. Гипотетический пример типичной эпидемиологической кривой с тремя фазами. Наша гибридная диаграмма Шухарта моделирует три фазы эпидемии (до роста, роста и после роста). Соответствующие спецификации диаграммы для каждого этапа описаны в этом разделе. Технические подробности приведены в Приложении. Фаза 1 (до роста)Фаза до роста начинается в первый день зарегистрированной смерти в географическом регионе. Диаграмма Шухарта для этой фазы представляет собой базовую диаграмму C [1] для данных подсчета в период, когда количество смертей, регистрируемых в день в определенной географической области, невелико и стабильно.Основное внимание в нашем анализе на этом этапе уделяется обнаружению, когда характер регистрируемых смертей указывает на то, что эпидемия начала переходить в фазу экспоненциального роста. Во-первых, мы наносили ежедневные сообщения о смертях на график прогона до тех пор, пока не будет достаточно наблюдений, чтобы удовлетворить минимальным требованиям для эффективной диаграммы C . Мы рекомендуем рассчитывать контрольные пределы только после того, как будет зарегистрировано не менее восьми смертей. Стандартная диаграмма C используется для мониторинга фазы, предшествующей росту, и для обнаружения сигнала об особых причинах вариации (количество смертей выше верхнего предела (UL) или смещение на 8 дней подряд выше средней линии (CL) .Любой из этих сигналов предполагает переход в фазу экспоненциального роста. Диаграмма C для зарегистрированных случаев смерти от COVID-19 в Сингапуре () была стабильной, без признаков экспоненциального роста, пример местоположения, где эпидемия оставалась в фазе, предшествующей росту (по состоянию на 25 апреля 2020 г.). Пример диаграммы для страны на этапе, предшествующем росту. Сигнал особой причины на диаграмме C указывает на то, что, возможно, начался период экспоненциального роста.Подходящее время для начала второй фазы I- Диаграмма обозначается следующим образом:
Мы продолжили наносить ежедневные наблюдения на C — диаграмму, пока не будут выполнены все вышеперечисленные критерии.Например, диаграмма C из Южной Кореи () показала сигнал особой причины выше верхнего предела при наблюдении девяти смертей 20 марта. указывает на начало фазы экспоненциального роста (по состоянию на 25 апреля 2020 г.). Итак, мы продолжили график C- и обновили центральную линию и пределы графика после добавления каждой точки данных. Пример диаграммы для страны, которая еще не перешла в фазу экспоненциального роста. Фаза 2 (рост)Фаза роста начинается, когда структура зарегистрированных эпидемических смертей перестает быть стабильной и начинает экспоненциально расти (). Диаграмма I используется для наблюдения за фазой роста и определения сигнала об окончании экспоненциального роста. Фаза 2 потенциально начинается в тот день, когда диаграмма C впервые обнаруживает сигнал особой причины. Однако мы продолжаем наносить данные на диаграмму C в течение следующих 5 дней, после чего мы устанавливаем регрессию логарифма по основанию 10 ежедневных зарегистрированных смертей по количеству последовательных дней, начиная с данных, представленных в тот день, когда вызвал сигнал особой причины на диаграмме предварительного роста C [29].Когда нижняя граница 95% доверительного интервала для наклона регрессии неотрицательна, мы начинаем моделировать фазу роста, нанося результаты наблюдений на диаграмму I и используя коэффициенты регрессии для расчета ее наклонной центральной линии и контроля. пределы [30]. Пример диаграммы для страны, находящейся в фазе экспоненциального роста. Гибридная диаграмма C- и диаграмма I- для Перу () показывают пример страны, которая начала экспоненциальный рост и остается в фазе 2 (по состоянию на 25 апреля 2020 г.).Нелинейная изогнутая центральная линия и контрольные пределы являются результатом преобразования логарифмических расчетов обратно в шкалу зарегистрированных смертей. Отправной точкой для диаграммы I для Перу было наблюдение 17 смертей 2 апреля, которое первоначально вызвало сигнал особой причины на диаграмме C . Мы продолжали строить графики новых зарегистрированных смертей и каждый день обновляли расчеты центральной линии регрессии и контрольных пределов. После того, как фаза экспоненциального роста в Перу продолжалась более 20 дней (22 апреля), мы «заморозили» центральную линию и контрольные пределы (то есть мы перестали включать последующие данные для подгонки регрессии и расчета пределов диаграммы).Этот процесс «замораживания» контрольных пределов после 20 наблюдений является стандартной практикой для карт Шухарта [1]. Замороженные пределы следует расширить в будущем в качестве руководства для интерпретации последующих наблюдений, нанесенных на карту. Это важное различие по сравнению со многими эпидемиологическими моделями, которые не используют контрольные пределы для оценки стабильности случаев или смертей во времени и, следовательно, не оснащены для обнаружения двухточечных вариаций, которые отражают значимое изменение в представляющих интерес показателях. .Мы продолжаем наносить ежедневные наблюдения в фазу роста, ища сигналы особых причин вариаций. Наблюдения за верхним контрольным пределом или смещение восьми последовательных наблюдений над средней линией указывают на то, что скорость роста увеличивается по сравнению с предыдущими днями. Наблюдения ниже нижнего контрольного предела или смещение восьми последовательных наблюдений ниже средней линии являются показателями уменьшения скорости роста или, возможно, конца периода роста. Фаза 3 (после роста)Фаза после роста начинается, когда траектория зарегистрированных смертей больше не демонстрирует экспоненциальный рост, после чего мы ожидаем, что в последующие дни картина выйдет на плато или снизится.Если сигнал особой причины ниже нижнего предела возникает до того, как фаза роста сохраняется в течение 20 дней, мы приостанавливаем расчет пределов и наносим на график количество зарегистрированных смертей на следующий день. Если это следующее ежедневное наблюдение также упадет ниже нижнего контрольного предела, мы сделаем вывод, что фаза роста, вероятно, закончилась. Мы продолжаем наносить на диаграмму последующие подсчеты зарегистрированных смертей, но не обновляем лимиты. Нанесение зарегистрированных случаев смерти от эпидемии COVID-19 в Испании на нашу гибридную диаграмму () указывает на то, что предварительная фаза роста закончилась 10 марта с сигналом особой причины, вызванным наблюдением за 23 случаями смерти.Расчеты графика I были заморожены 29 марта после 20 дней экспоненциального роста в Испании. Особая причина ниже нижнего предела 3 апреля сигнализировала об окончании фазы роста. После того, как наблюдение ниже нижней границы диаграммы I 4 апреля сигнализировало о начале фазы 3 в Испании, модель зарегистрированных смертей продолжила (по состоянию на 25 апреля 2020 г.) тенденцию к снижению. Пример диаграммы для страны, которая вышла из фазы экспоненциального роста. Гибридная диаграмма Шухарта для зарегистрированных смертейВ отличие от линейных контрольных пределов, которые чаще всего связаны с контрольными диаграммами, центральная линия и пределы для фазы роста на гибридной диаграмме Шухарта нелинейны ().Траекторию развития эпидемии в нескольких фазах можно более четко визуализировать в логарифмической шкале (), поскольку количество зарегистрированных смертей охватывает разные порядки величины (от десятков до тысяч). Чтобы вернуться к исходной шкале с подсчетом зарегистрированных смертей (), мы возведем в степень логарифмические значения для центральной линии, верхнего и нижнего пределов. Пример диаграммы в логарифмическом масштабе для страны, которая прошла фазу экспоненциального роста. Наши диаграммы Шухарта обновляются с каждым ежедневным отчетом о новых случаях смерти от COVID-19 в других странах, а также в штатах и территориях США.Дисплеи доступны для общественности через интерактивное онлайн-приложение для создания диаграмм covid-19, разработанное компанией Informing Ecological Design, и комплексную панель данных по covid-19, размещенную Институтом улучшения здравоохранения [31, 32]. На этих платформах могут быть небольшие различия в отношении источников данных и реализации нашего метода. Наш мир в данных был источником данных, который использовался для создания диаграмм, представленных в этой статье [33]. ОбсуждениеЭто приложение диаграмм Шухарта предлагает по крайней мере четыре различных возможности для обучения во время эпидемии. Первый , это полезный метод для привлечения экспертов в предметной области на местах и для улучшения понимания того, в какой степени работают бесчисленные изменения в практике и политике, внедренные правительствами и выполняемые непосредственным персоналом. Второй , графики предоставляют нам сигналы, позволяющие определить, когда количество новых смертей в местности (например, городе, округе, штате или стране) начало экспоненциально расти. Третий , он позволяет нам использовать начальные модели экспоненциального роста в качестве основы для определения того, когда ежедневная смертность перестала расти, что указывает на то, что траектория зарегистрированных смертей в районе входит в пологую часть эпидемиологической кривой или, возможно, начинает иметь тенденцию вниз. Четвертый , наш подход сводит к минимуму риск и психологические потери, которые могут возникнуть, когда люди подталкивают людей к реагированию на каждую точку данных, как если бы это был значимый сигнал об улучшении или ухудшении условий (когда они могут не измениться). меняется вообще). Например, заголовки газет из Великобритании () изображают различия в сообщениях о смерти от COVID-19, как если бы каждое ежедневное число представляло собой особый рассказ о значительных изменениях в условиях эпидемии. Визуализация этих данных на нашей гибридной диаграмме Шухарта () показывает, что изменения в смертности от COVID-19 в Великобритании в течение этого периода времени (6 марта — 15 апреля 2020 г.) являются вариациями по общей причине. Диаграмма Шухарта нового гибрида для ежедневных зарегистрированных смертей от COVID-19 в Великобритании. Доступны многочисленные методы для моделирования роста эпидемии и прогнозирования пикового числа смертей в определенных областях, но нам неизвестны другие методы, которые определяют первый день, когда область либо входит в начальную фазу экспоненциального роста, либо выходит из нее. Наш подход предоставляет инструмент для поддержки практикующих врачей и экспертов в данной области в распознавании условий, связанных с различными фазами эпидемии, и для информирования о стратегиях сдерживания и решениях в области политики общественного здравоохранения.Способность обнаруживать в географической зоне начало и конец экспоненциального роста имеет важные последствия для планирования и готовности к чрезвычайным ситуациям. Например, было бы трудно оправдать ослабление процедур социального дистанцирования, в то время как статистика ежедневных смертей еще не выявила значимого сигнала к снижению. Следующие этапы нашей работы по применению диаграмм Шухарта к кривой эпидемии будут сосредоточены на моделировании плато вокруг вершины, отслеживании снижения числа зарегистрированных смертей и мониторинге заключительных стадий, на которых количество смертей находится на низком уровне, стабильный уровень.Например, диаграмма C может быть полезна для быстрого определения, если зарегистрированные случаи смерти начинают расти после ослабления или прекращения мер по сдерживанию эпидемии. Диаграмма G- для количества дней между зарегистрированными смертельными случаями [1] также может использоваться в качестве простой системы наблюдения для мониторинга условий на пост-ростовой фазе. Наш подход к этим диаграммам ограничен достоверностью данных. Различия в регистрируемых случаях смерти включают вариации в методах отчетности и рабочих определениях в разных местах и во времени [34–36].Поскольку изменчивость измерений встроена в расчет контрольных пределов, метод Шухарта является менее реактивным и, следовательно, выгодным в таком контексте. Проблемы с качеством и непротиворечивостью эпидемических данных усиливают аргументы в пользу привлечения экспертов в предметной области (тех, кто знает местные условия или клинический опыт) для руководства интерпретацией диаграмм. ЗаключениеВо время пандемии ранние и надежные сигналы о том, что число зарегистрированных смертей растет или уменьшается, могут иметь последствия для жизни и смерти.Наука об улучшении предлагает методы для представления и интерпретации вариаций, которые будут необходимы для успешных организационных изменений в ответ на covid-19 [37]. Новая гибридная контрольная диаграмма, описанная в этом документе, представляет собой практический инструмент для поддержки обучения на основе отчетных данных во время эпидемии или пандемии, а также подход, который доступен и полезен для руководителей системы и оперативных групп. Без диаграмм Шухарта — и, в более широком смысле, теории вариаций — в нашем эпидемиологическом арсенале нам не хватает научного метода для оценки в реальном времени степени улучшения эпидемических условий.Диаграммы Шухарта должны стать стандартной частью того, как мы учимся и визуализируем данные в контексте пандемии или эпидемии. Приложение: Расчеты для гибридной карты ШухартаФаза 1 (до роста) — количество смертей каждый день низкое и стабильное Для построения эпидемических данных для местоположения, находящегося на стадии до роста, мы используем диаграмму C-. Эта диаграмма полезна для подсчета инцидентов в определенном регионе, в котором общая вероятность инцидента мала [1].Расчет контрольных пределов для диаграммы C- основан на стандартной ошибке для распределения Пуассона. Мы использовали следующий процесс для создания диаграммы фазы 1 C-:
Пример линейных и логарифмических гибридных диаграмм Шухарта с фазами эпидемии. Фаза 2 (рост) — смертей в день растут с каждым днем. Чтобы отобразить эпидемические данные для региона, находящегося в фазе экспоненциального роста, мы используем диаграмму I- (также известную как диаграмма X- или диаграмма Xmr-) для индивидуальных измерений подсчета объема [1].Расчет CL основан на линейной регрессии [1, 30] логарифма зарегистрированных случаев смерти от эпидемий ( Y ) при последовательных подсчетах дней ( X ). Диапазон перемещения, рассчитываемый как разница между последовательными остатками регрессии данных, используется для определения контрольных пределов с использованием только вариации по общей причине путем отсеивания отдельных диапазонов перемещения, которые завышены вариацией по особой причине:
Фаза 3 диаграммы (после роста) — ежедневно регистрируемых смертей остаются неизменными или падают. Фаза 3 наступает, когда область достигла и / или прошла пик смертности, после чего ожидается снижение количества зарегистрированных смертей. Продолжайте графически отображать количество смертей, не обновляя пределы для фазы 1 или фазы 2. БлагодарностиМы хотели бы поблагодарить Яна Перла и Наташи Скерган за поддержку при подготовке этой статьи. Список литературы1. Провост LP, Мюррей С. Руководство по данным здравоохранения: изучение данных для улучшения. Сан-Франциско: John Wiley & Sons, 2011. [Google Scholar] 2. Суббараман Н. Почему ежедневные подсчеты погибших стали необычайно важны для понимания пандемии коронавируса. Nature 2020, 10.1038 / d41586-020-01008-1. [PubMed] [Google Scholar] 4. Шухарт WA. Экономический контроль качества выпускаемой продукции. Нью-Йорк: D Van Nostrand Company, 1931, (перепечатано ASQC Quality Press, 1980).[Google Scholar] 5. Шухарт WA, Деминг МЫ. Статистические методы с точки зрения контроля качества. Вашингтон: Высшая школа Министерства сельского хозяйства США, 1939 г. (переиздано Dover Publications, 1986 г.). [Google Scholar] 6. Мохаммед М.А., Ченг К.К., Роуз А., Маршалл Т. Бристоль, судоводитель и клиническое управление: забытые уроки Шухарта. Ланцет 2001; 357: 463–7. [PubMed] [Google Scholar] 7. Berwick DM. Контроль различий в медицинском обслуживании: консультация Уолтера Шухарта.Med Care 1991; 29: 1212–25. [PubMed] [Google Scholar] 8. Деминг МЫ. Новая экономика для промышленности, правительства, образования. Кембридж, Массачусетс: Центр перспективных инженерных исследований Массачусетского технологического института, 1994 г. [Google Scholar] 9. Нолан Т., Перла Р.Дж., Провост Л. Понимание вариаций. Qual Prog 2016; 49: 28–37. [Google Scholar] 10. Нолан Т.В., Провост Л.П. Понимание вариаций. Qual Prog 1990; 23: 70–8. [Google Scholar] 11. Теннант Р., Мохаммед М.А., Коулман Дж. Дж. И др. . Мониторинг пациентов с использованием контрольных карт: систематический обзор.Int J Qual Health Care 2007; 19: 187–94. [PubMed] [Google Scholar] 12. Беннеян JC. Статистические методы контроля качества в инфекционном контроле и госпитальной эпидемиологии, введение в часть I и основы теории. Инфекционный контроль Hosp Epidemiol 1998; 19: 194–214. [PubMed] [Google Scholar] 13. Арантес А., Карвалью Э.Д., Медейрос Э.А. и др. . Использование статистических контрольных карт процесса в эпидемиологическом надзоре за внутрибольничными инфекциями. Rev Saude Publica 2003; 37: 768–74. [PubMed] [Google Scholar] 14. IC Gomes, Mingoti SA, Oliveira CD.Новый опыт использования контрольных карт для выявления вспышек внутрибольничных инфекций. Клиники 2011; 66: 1681–9. [Бесплатная статья PMC] [PubMed] [Google Scholar] 15. Селлик JA. Использование статистических диаграмм контроля процессов в госпитальной эпидемиологии. Инфекционный контроль Hosp Epidemiol 1993; 14: 649–56. [PubMed] [Google Scholar] 16. Брюэр Дж. Х., Гассер К. С.. Сходство между постоянным повышением качества и эпидемиологическим надзором. Инфекционный контроль Hosp Epidemiol 1993; 14: 95–8. [PubMed] [Google Scholar] 17.Qian YH, Su J, Shi P et al. . Попытка раннего выявления пандемии гриппа a (h2N1) с использованием данных эпиднадзора за гриппоподобными заболеваниями и необъяснимой пневмонией. Другие респирные вирусы гриппа 2011; 5: e479–86. [Бесплатная статья PMC] [PubMed] [Google Scholar] 18. Хашимото С., Мураками Ю., Танигучи К. и др. . Выявление эпидемий на ранней стадии посредством эпиднадзора за инфекционными заболеваниями. Int J Epidemiol 2000; 29: 905–10. [PubMed] [Google Scholar] 19. Рич WH, Терри MC. Промышленная «контрольная карта» применяется для изучения эпидемий.Public Health Rep 1946; 61: 1501–11. [PubMed] [Google Scholar] 20. Hanslik T, Boelle PY, Flahault A. Контрольная карта: эпидемиологический инструмент для мониторинга здоровья населения. Общественное здравоохранение 2001; 115: 277–81. [PubMed] [Google Scholar] 21. Сонессон С, Бок Д. Обзор и обсуждение проспективного статистического наблюдения в общественном здравоохранении. J R Stat Soc Ser A Stat Soc 2003; 166: 5–21. [Google Scholar] 22. Штайнер Ш., Грант К., Кури М. и др. . Обнаружение начала вспышки гриппа с использованием графиков экспоненциально взвешенных скользящих средних.BMC Med Inform Decis Mak 2010; 10: 37. [Бесплатная статья PMC] [PubMed] [Google Scholar] 23. Уильямсон Г.Д., Уэтерби Хадсон Г. Система мониторинга для обнаружения аберраций в отчетах наблюдения за общественным здоровьем. Stat Med 1999; 18: 3283–98. [PubMed] [Google Scholar] 24. Bjerkedal T, Bakketeig LS. Наблюдение за врожденными пороками и другими состояниями новорожденного. Int J Epidemiol 1975; 4: 31–6. [PubMed] [Google Scholar] 25. Vanbrackle L, Уильямсон GD. Исследование характеристик средней продолжительности тиража национальной системы надзора за подлежащими регистрации заболеваниями.Stat Med 1999; 18: 3309–19. [PubMed] [Google Scholar] 26. Woodall WH. Использование контрольных карт в здравоохранении и надзоре за общественным здоровьем. J Qual Technol 2006; 38: 89–104. [Google Scholar] 27. Симмонс Б.П., Кричевский С.Б. Эпидемиологические подходы к оценке качества. Инфекционный контроль Hosp Epidemiol 1995; 16: 101–4. [PubMed] [Google Scholar] 29. Фаррингтон С.П., Эндрюс, штат Нью-Джерси, Бил А.Д., Кэтчпол, Массачусетс. Статистический алгоритм раннего выявления вспышек инфекционных заболеваний. J R Stat Soc Ser A Stat Soc 1996; 159: 547–63.[Google Scholar] 30. Грант Э.Л., Ливенворт Р.С. Статистический контроль качества, 7 изд. Нью-Йорк: МакГроу-Хилл, 1980, 298–302. [Google Scholar] 36. Аткинс К.Э., Венцель Н.С., Ндеффо-Мбах М. и др. . Недостаточная отчетность и оценки летальности для возникающих эпидемий. BMJ 2015; 350: h2115. [Бесплатная статья PMC] [PubMed] [Google Scholar] 37. Staines A, Amalberti R, Berwick DM et al. . COVID-19: навыки безопасности пациентов и повышения качества, которые необходимо использовать во время всплеска. Int J Qual Health Care 2020. 10.1093 / intqhc / mzaa050.[Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 60071
60071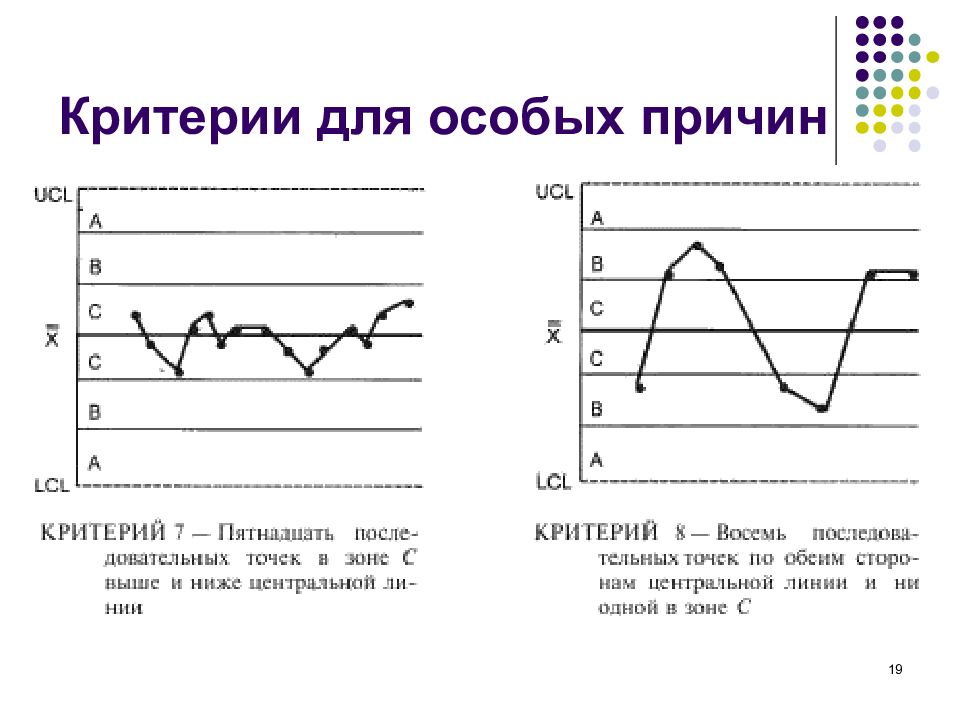 1972
1972 А.
А. 7171
7171 4872
4872 1005
1005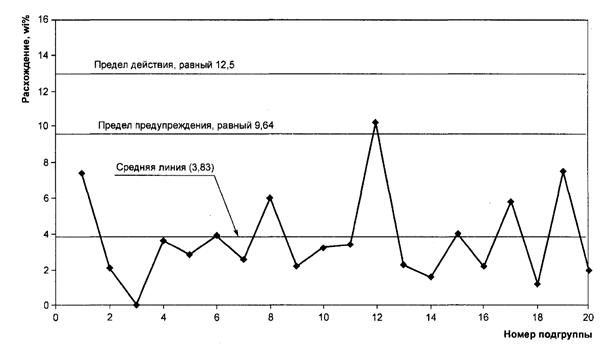 3311
3311  00
00 3532
3532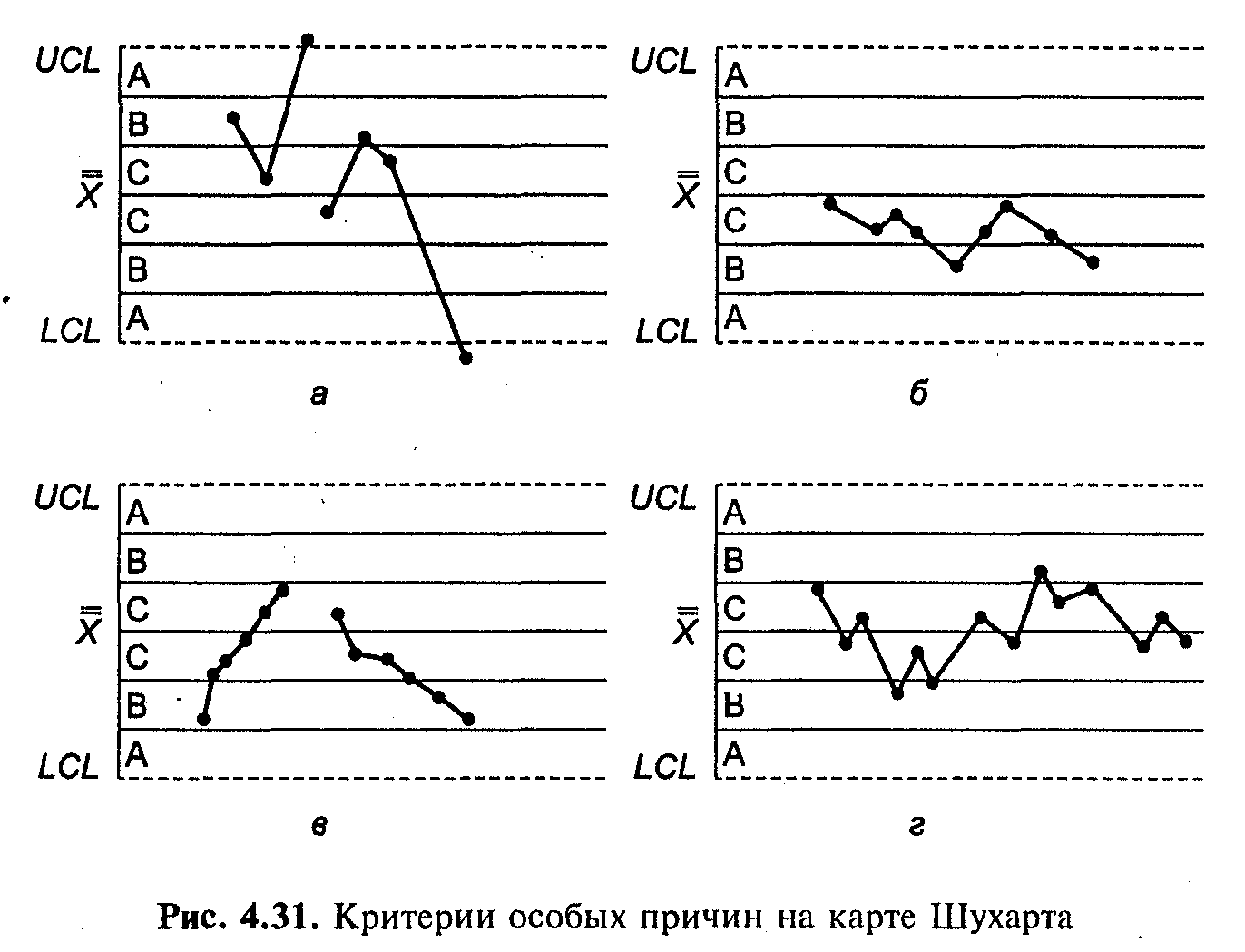 0251
0251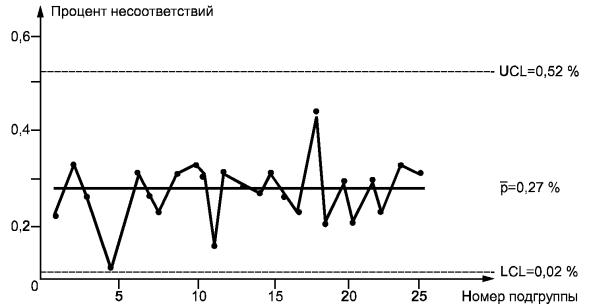 4328
4328 +68841
+68841 А.
А.