Отрицательная корреляция положительная корреляция: Корреляция, корреляционная зависимость

Корреляция, корреляционная зависимость

Корреляция (от лат. correlatio), корреляционная зависимость — взаимозависимость  двух или нескольких случайных величин. Суть ее заключается в том, что при изменении значения одной переменной происходит закономерное изменение (уменьшению или увеличению) другой(-их) переменной(-ых).

При расчете корреляций пытаются определить, существует ли статистически достоверная связь между двумя или несколькими переменными в одной или нескольких выборках. Например, взаимосвязь между ростом и весом детей, взаимосвязь между успеваемостью и результатами выполнения теста IQ, между стажем работы и производительностью труда.

Важно понимать, что корреляционная зависимость отражает только взаимосвязь между переменными и не говорит о причинно-следственных связях. Например, если бы исследуемой выборке между ростом и весом человека существовала корреляционная зависимость то, это не значило бы, что вес является причиной роста человека, иначе сбрасывая лишние килограммы рост человека также уменьшался.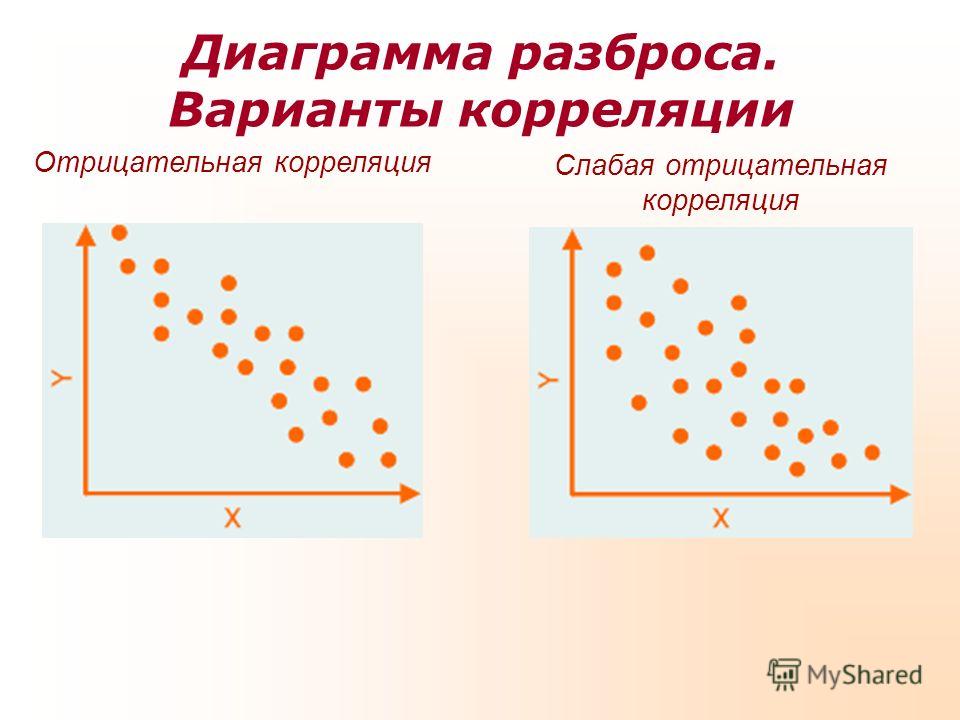

Корреляционная связь лишь говорит о взаимосвязанности данных параметров, причем в данной конкретной выборке, в другой выборке мы можем не наблюдать полученные корреляции.

Показатель корреляции. Коэффициент корреляции (r) характеризует величину отражающую степень взаимосвязи двух переменных между собой. Он может варьировать в пределах от -1 (отрицательная корреляция) до +1 (положительная корреляция). Если коэффициент корреляции равен 0 то, это говорит об отсутствии корреляционных связей между переменными. Причем если коэффициент корреляции ближе к 1 (или -1) то говориться о сильной корреляции, а если ближе к 0, то о слабой.

При положительной корреляции увеличение (или уменьшение) значений одной переменной ведет к закономерному увеличению (или уменьшению) другой переменной т.е. взаимосвязи типа увеличение-увеличение (уменьшение-уменьшение).

При отрицательной корреляции увеличение (или уменьшение) значений одной переменной ведет к закономерному уменьшению (или увеличению) другой переменной т.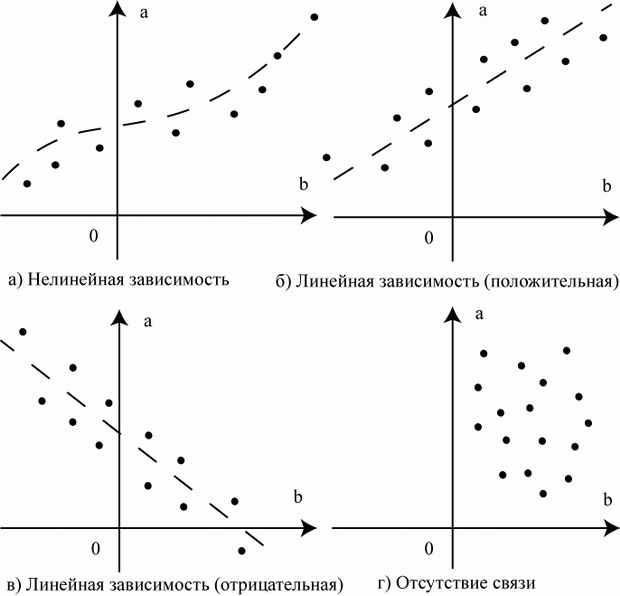 е. взаимосвязи типа увеличение-уменьшение (уменьшение-увеличение).

Корреляция (синонимы):

соотношение, соотнесение, взаимосвязь, взаимозависимость, взаимообусловленность, взаимосоответствие.

Проведите корреляционный анализ за 5 минут

Онлайн сервис расчета статистики

 

Отрицательная корреляция ⋆ FINAN$I$TEM

Одна переменная растет, другая падает

Что такое отрицательная корреляция?

Отрицательная корреляция — это взаимосвязь между двумя переменными, которые движутся в противоположных направлениях. Другими словами, когда переменная A увеличивается, переменная B уменьшается. Отрицательная корреляция также известна как обратная корреляция.

Две переменные могут иметь разную степень отрицательной корреляции. Переменная A может иметь сильную отрицательную корреляцию с B и может иметь коэффициент корреляции -0,9. Это означает, что при каждом положительном изменении единицы переменной B переменная A уменьшается на 0,9.

В качестве другого примера, эти переменные также могут иметь слабую отрицательную корреляцию. Коэффициент -0,2 означает, что на каждую единицу изменения переменной B, переменная A уменьшается, но незначительно, на 0,2.

Примеры отрицательной, положительной и низкой корреляции

Начнем с графика идеальной отрицательной корреляции. Как вы можете видеть на графике ниже, уравнение линии y = -0,8x. Это означает, что если Акция Y выросла на 1,0%, то Акция X упала на 0,8%. Эти отношения совершенно противоположны, поскольку они всегда движутся в противоположных направлениях.

Теперь давайте посмотрим на график с идеальной положительной корреляцией. На графике ниже вы можете видеть, что если Акция Y выросла на 1,0%, Акция X выросла на 1,6%.

Наконец, давайте рассмотрим другой пример, на этот раз двух низко коррелированных активов. Как видите, точки сильно разбросаны, и ни одна из них не лежит на линии наилучшего соответствия. Для этих двух акций практически нет корреляции между доходностью Акции Y и доходностью Акции X.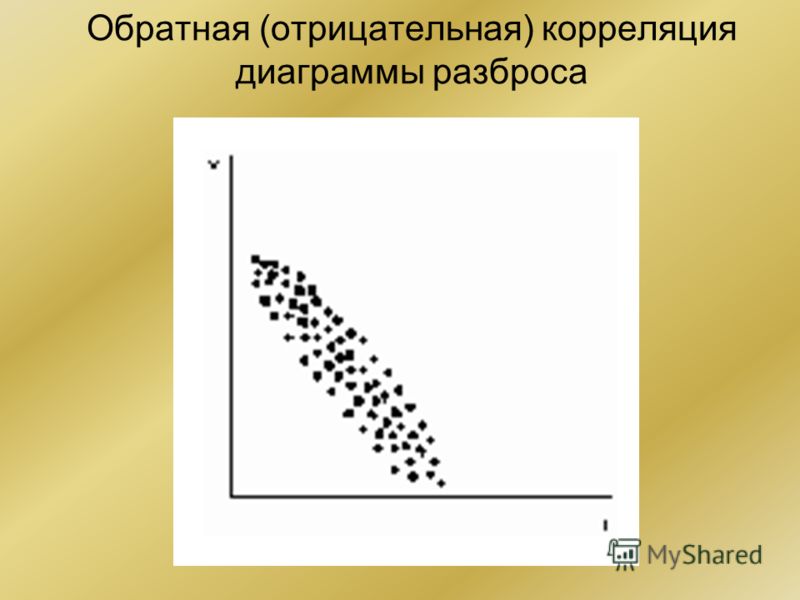 Эти две ценные бумаги движутся совершенно независимо друг от друга.

Преимущества отрицательно коррелированных активов в портфелях

Концепция отрицательной корреляции важна для инвесторов или аналитиков, которые рассматривают возможность добавления новых инвестиций в свой портфель. Когда рыночная неопределенность высока, общим соображением является перебалансировка портфелей путем замены некоторых ценных бумаг, имеющих положительную корреляцию, на те, которые имеют отрицательную корреляцию.

Движение портфеля компенсирует друг друга, снижая риск, а также доходность. После того, как неопределенность на рынке уменьшится, инвесторы могут начать закрывать офсетные позиции. Примером отрицательно коррелированных ценных бумаг может быть опцион на акции и пут на акции, стоимость которых растет по мере падения цены акции.

Отрицательный коэффициент

У пары инструментов всегда будет коэффициент от -1 до 1. Коэффициент ниже нуля указывает на отрицательную корреляцию.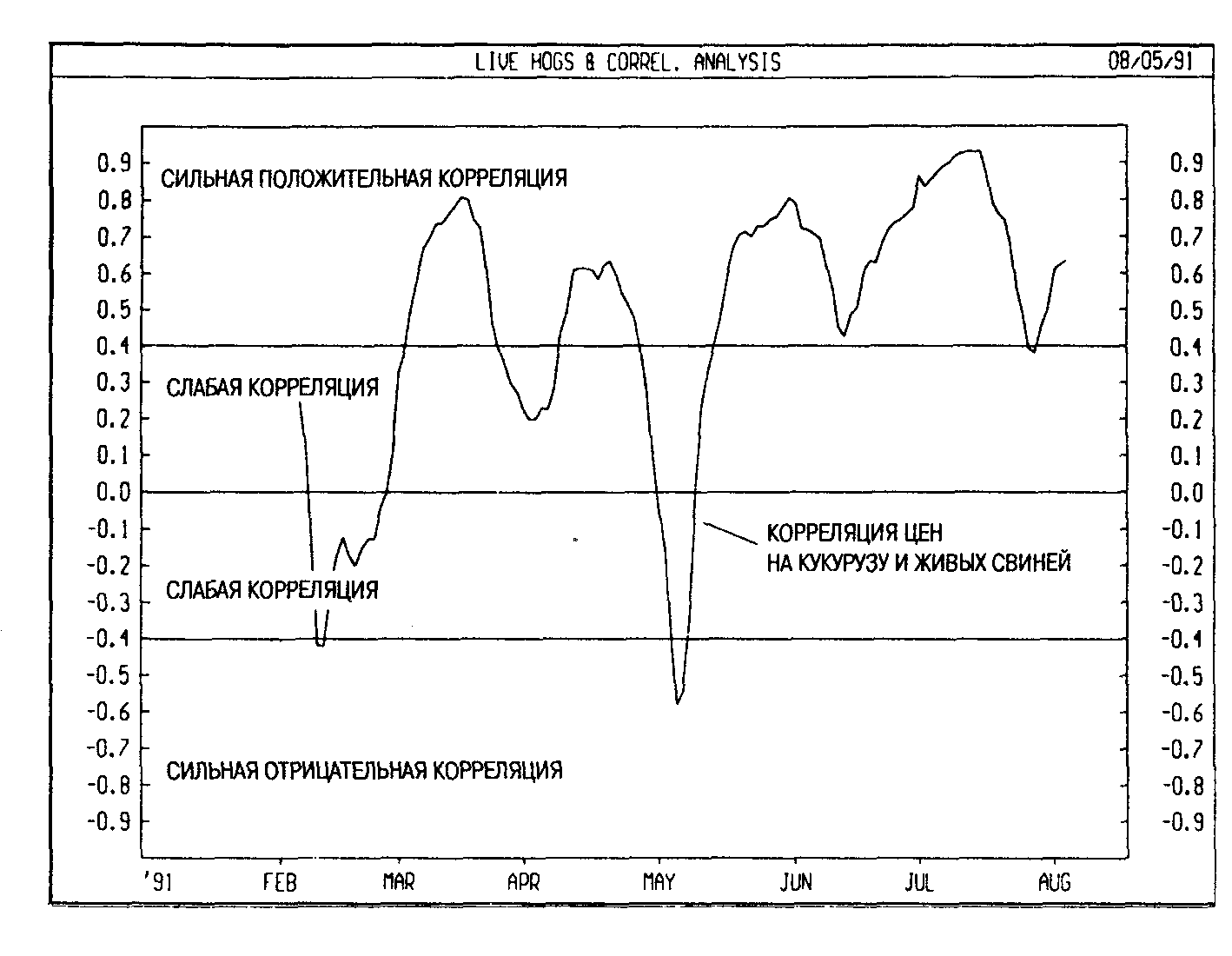

Когда два инструмента имеют корреляцию -1, эти инструменты имеют совершенно обратную зависимость. Если инструмент A поднимется на 1 доллар, инструмент B опустится на 1 доллар.

В другом примере, если корреляция между обменным курсом EUR / USD и обменным курсом USD / CHF имеет коэффициент -0,85, на каждые 100 пунктов EUR / USD движется вверх, USD / CHF опускается на 85.

Примеры активов с отрицательной корреляцией

Вот несколько распространенных примеров отрицательной корреляции между активами:

• Цены на нефть и акции авиакомпаний
• Цены на золото и фондовые рынки (большую часть времени, но не всегда)
• Любой вид страховой выплаты

Дополнительные ресурсы:

Спасибо за то, что прочитали руководство Finansistem по обратно пропорциональным активам в инвестициях и финансах. Чтобы продолжить обучение, Finansistem настоятельно рекомендует:

Корреляция полная отрицательная — Энциклопедия по экономике

Коэффициент корреляции может изменяться в диапазоне 1,0. Коэффициент +1,0 (полная положительная корреляция) означает, что изменения независимой переменной приведут к идентичным изменениям зависимой (т.е. изменение индикатора вызовет такое же изменение цены бумаги). Коэффициент 1,0 (полная отрицательная корреляция) означает, что изменения независимой переменной вызовут идентичные изменения зависимой, но в противоположном направлении. Коэффициент, равный нулю, свидетельствует об отсутствии связи между переменными, то есть изменения независимой переменной не влияют на изменения зависимой.  [c.104]

Коэффициент корреляции всегда лежит в интервале между -1 и +1. Если он равен — 1, то это означает полную отрицательную корреляцию, если +1 — полную положительную корреляцию. В большинстве случаев он находится между этими двумя экстремальными значениями.  [c.182]

Коэффициент корреляции — зто статистическая мера степени корреляции между двумя рядами показателей. Изменяется от -1 в случае полной отрицательной корреляции до +1 в случае полной положительной корреляции.  [c.811]

Из гл. 2 мы знаем, что коэффициент корреляции может принимать значения от + 1 (полная положительная корреляция) до —1 (полная отрицательная корреляция). Положительная корреляция означает, что доходности каждой пары активов в основном изменяются в одном направлении. Это соотношение тем сильнее, чем ближе коэффициент корреляции к + 1. Отрицательная корреляция показывает, что доходности изменяются в противоположных направлениях, при этом соотношение становится сильнее по мере того, как коэффициент приближается к — 1.  [c.187]

При полной отрицательной корреляции доходов динамика квадратического отклонения доходов от портфеля более сложная. По мере движения от точки Л к точке К эта величина сначала сокращается и доходит до нуля в точке В, затем растет (см. рис. 8.4). Следует обратить внимание на то, что при движении от Л1 до В рост дохода сопровождается уменьшением риска (квадратического отклонения).  [c.175]

При полной отрицательной корреляции находим  [c. 179]

Для интерпретации коэффициента корреляции необходимо знать область его существования 0 коэффициента корреляции может быть достигнуто, если положительные и отрицательные произведения отклонений признаков от их средних величин в числителе полностью уравновесят друг друга. Это свидетельствовало бы о полном отсутствии связи, но вероятность такого абсолютно точного взаимопогашения крайне мала для любой реальной, не бесконечно большой совокупности. Поэтому и при отсутствии реальной связи коэффициент корреляции на практике не равен нулю. Например, коэффициент корреляции между надоем молока от коров и числом букв в названии предприятия в совокупности хозяйств, указанных в табл. 8.1, равен +0,216. Как отделить реальные, надежно установленные связи от таких случайных, незначимых величин коэффициента корреляции, рассматривается в следующем разделе этой главы.  [c.246]

Как мы уже знаем (см. главу 2), добавление рыночных систем увеличивает среднее геометрическое по портфелю в целом. Однако возникает проблема каждая следующая рыночная система вносит все меньший и меньший вклад в среднее геометрическое и все больше ухудшает его, понижая эффективность из-за одновременных, а не последовательных результатов. Поэтому не следует торговать слишком большим числом рыночных систем. Более того, реальное применение теоретически оптимальных портфелей осложняется из-за залоговых требований. Другими словами, вам лучше торговать 3 рыночными системами при полном оптимальном f, чем 300 рыночными системами при значительно пониженных уровнях, согласно уравнению (8.08). Скорее всего вы придете к выводу, что оптимальное число рыночных систем для торговли должно быть невелико. Особенно это обстоятельство важно, когда у вас много ордеров к исполнению и увеличивается вероятность ошибок. Если одна или несколько рыночных систем в портфеле имеют оптимальные веса больше единицы, может возникнуть еще одна проблема. Рассмотрим рыночную систему с оптимальным f=0,8 и наибольшим проигрышем, составляющим 4000 долларов. Для этой рыночной системы f = 5000 долларов. Давайте предположим, что оптимальный вес данного компонента в портфеле равен 1,25, поэтому вы будете торговать одной единицей компонента на каждые 4000 долларов ( 5000/1,25) баланса счета. Как только компонент столкнется с наибольшим проигрышем, весь активный баланс на счете будет обнулен, если прибылей в других рыночных системах не хватит для сохранения активного баланса. Рассмотренная проблема наиболее актуальна для систем, которые редко генерируют сделки. Если бы у нас были две рыночные системы с отрицательной корреляцией и положительным ожиданием, необходимо было бы открывать бесконечное количество контрактов на рынке. Когда один из компонентов проигрывает, другой выигрывает равную или большую сумму. Таким образом, мы получаем прибыль в каждой игре, однако только в том случае, когда рыночные системы ведут игру одновременно. Рассматриваемая же торговля аналогична гипотетической ситуации, когда один из компонентов в игре не активен, но используется другая рыночная система с бесконечным числом контрактов. Проигрыш может быть катастрофическим. Проблему можно решить следующим образом разделите единицу на наибольший вес компонента портфеля и используйте полученное значение в качестве верхней границы активного баланса, если оно меньше, чем значение, найденное из уравнения (8.08). В таком случае, если в будущем произойдет проигрыш той же величины, что и наибольший проигрыш (на основе которого рассчитано f), мы не потеряем все деньги. Например, наибольший вес компонента в нашем портфеле составляет 1,25. Если значение из уравнения (8.08) будет больше 1 / 1,25 = 0,8, следует использовать 0,8 в качестве верхней границы для доли активного баланса. Если первоначальная доля активного баланса небольшая, вышеописанная проблема может и не возникнуть, однако более агрессивному трейдеру следует всегда принимать ее во внимание. Альтернативное решение состоит в введении дополнительных ограничений в матрице портфеля (например, для каждой рыночной системы можно ограничить максимальные веса единицей и ввести дополнительные ограничения по залоговым средствам). Подобные дополнительные ограничения  [c.241]

Коэффициент корреляции доходности по двум финансовым инструментам инвестирования может принимать значения от +1 (означающего полную и положительную корреляцию между рассматриваемыми величинами) до -1 (означающего полную и отрицательную корреляцию между рассматриваемыми величинами). Используя различия в ковариации инвестиционного дохода, можно подобрать в формируемый портфель такие виды финансовых инструментов, которые, не меняя уровня средней доходности портфеля, позволяют существенно снизить уровень его риска.  [c.389]

Коэффициент корреляции может принимать любые значения от 0 до 1. Если коэффициент корреляции равен нулю, то это означает отсутствие связи между х и у. Если его абсолютная величина составляет единицу, то, следовательно, существует полная зависимость между исследуемыми факторами, т, е, корреляционная зависимость совпадает с функциональной. Чем ближе коэффициент корреляции к единице, тем теснее зависимость между х и у чем ближе к нулю, тем связь слабее. Положительное значение коэффициента корреляции указывает на прямую зависимость, отрицательное значение — обратную.  [c.115]

К = -I, т. с. четвертое свойство коэффициентов ранговой корреляции. Это означает, что ранжированные показатели по признакам X и Y полностью противоположны, разнонаправленны. В таком случае аудитор может утверждать, что один ранжированный ряд (например, исчисленный по фактическим показателям функционирования данной хозяйственной системы в конкретном квартале) полностью «переставлен», инвертирован по отношению к другому, эталонному. Из всех возможных режимов функционирования, моделируемых и контролируемых при помощи данного набора п показателей, этот — единственный абсолютно отрицательный. Он означает не только замедление, но практически полное торможение развития системы, ее деградацию, отсутствие какого бы то ни было, даже медленного продвижения от предыдущего состояния к другому, более высокому состоянию.  [c.127]

Если доходы по обоим видам ценных бумаг явно коррелируют (т. е. положительный эффект по одному виду всегда сопровождается положительным эффектом по другому виду, а отрицательный эффект — всегда отрицательным), это означает полную корреляцию с коэффициентом корреляции +1. Аналогичным образом возможна противоположная ситуация, когда положительному эффекту по одному виду всегда соответствует отрицательный эффект по другому виду ценных бумаг, и наоборот. В этом случае коэффициент корреляции между двумя видами равен — 1.  [c.158]

Наше исследование коэффициента корреляции предполагает, что для полного устранения риска предприятие должно вкладывать средства в проекты, доходы от которых совершенно отрицательно коррелированны. Если это так, изменчивость доходов от различных проектов взаимно сокращается, и поэтому риск полностью устраняется. Однако, к сожалению, возможность следовать подобной инвестиционной политике встречается редко. В реальном мире крайне сложно  [c.224]

Этот коэффициент может принимать значения от минус единицы до плюс единицы. Коэффициент, равный минус единице, указывает на полную отрицательную корреляцию, коэффициент, равный плюс единице, — на полную положительную корреляцию, коэффициент, равный нулю,— на отсутствие связи. Заключенные между этими крайними величинами значения указывают на степень взаимосвязи. Обратите внимание на то, что коэффициент отражает степень только линейной взаимосвязи переменных. Например, две переменные могут быть тесно связаны нелинейным соотношением (скажем, у =х2), а значение г будет невысоким. (См. также rank orrelation.)  [c.102]

Определим доход и дисперсию для портфеля с долями, равными, допустим, 0,3 и 0,7. Получим по формулам (8.6) и (8.7) D = 0,651 + 0,37лху и А — 2,7. Таким образом, при полной положительной корреляции D = 1,021, при полной отрицательной корреляции О = 0,281. В итоге с вероятностью 95% можно утверждать, что суммарный доход находится в первом случае в преде-  [c.176]

Плотность ковариации между уровнями доходности по двум видам финансовых инструментов можно определить, рассчитав коэффициент корреляции, который может принимать значения от +1 до —1. Значение коэффициента корреляции, равное +1, означает полную и положительную корреляцию между уровнями доходности изучаемых финансовых инструментов, т. е. однонаправленное совпадающее изменение. Значение, равное —1, показывает полную и отрицательную корреляцию между уровнями доходности рассматриваемых финансовых инструментов. Следовательно, когда доходность одной ценной бумаги наиболее высока, велика вероятность того, что доходность второй ценной бумаги принимает наиболее низкие значения. Расчет коэффициента корреляции осуществляется по следующей формуле  [c.392]

Что произойдет, если добавлять в портфель все большее количество новых акций Как правило, риск портфеля будет уменьшаться по мере увеличения числа акций Если дополнить портфель достаточно большим количеством акций, можно ли полностью свести риск к нулю В целом ответ на этот вопрос отри цательный, однако степень воздействия добавления новых акций на снижение риска портфеля зависит от уровня корреляции между отдельными акциями чем меньше значение коэффициента корреляции, тем ниже риск крупного портфеля. На самом деле если бы в распоряжении инвестора имелось достаточно акций с коэффициентом корреляции, равным нулю (или отрицательным), риск можно было бы полностью элиминировать. Однако в большинстве случаев коэффици енты корреляции между отдельными акциями положительны, но не достигают +1.0, поэтому можно лишь снизить риск портфеля, но не устранить его полно стью  [c.58]

Некоторая (не слишком существенная) часть из сочетаний Коткл и КИНБ> приведенных в табл. 6.10, и особенно те из сочетаний, в которых исчислено значение KPA3B при положительных и отрицательных значениях исходных коэффициентов ранговой корреляции (такие случаи редки), на практике может оказаться бессодержательной. Но без их значений данная таблица не давала бы полной системной картины математической зависимости между различными значениями этих коэффициентов, а потому она приведена именно в этом виде.  [c.148]

Мы провели собственное исследование ротации секторов и обнаружили, что есть негативная корреляция между результатами последовательных лет, по крайней мере для не- которых из секторов рынка. В период с 1987 по 1998 год индекс Nasdaq после года, в котором наблюдалось падение на 10%, в среднем вырастал на 25%. В 2000-2001 годах произошла практически полная смена лучших и худших секторов, входящих в индекс S P 500. Два лучших и два худших сектора по итогам 2000 года в 2001 году поменялись местами, и корреляция рейтингов между двумя годами оказалась высокой и отрицательной -0,8. Это соответствует предположению о том, что для покупки акций существует лишь ограниченный запас энергии (первый закон термодинамики), и одновременно второму закону термодинамики — закону энтропии, который постулирует, что потенциальная энергия спонтанно стремится высвободиться.  [c.427]

Отрицательная корреляция — Энциклопедия по экономике

Когда уровень вертикальной интеграции скорректированным коэффициентом добавленной стоимости, возникает слабая отрицательная корреляция между вертикальной интеграцией и эффективностью. Коэффици-корреляции для 102 компаний обрабатывающей про-  [c.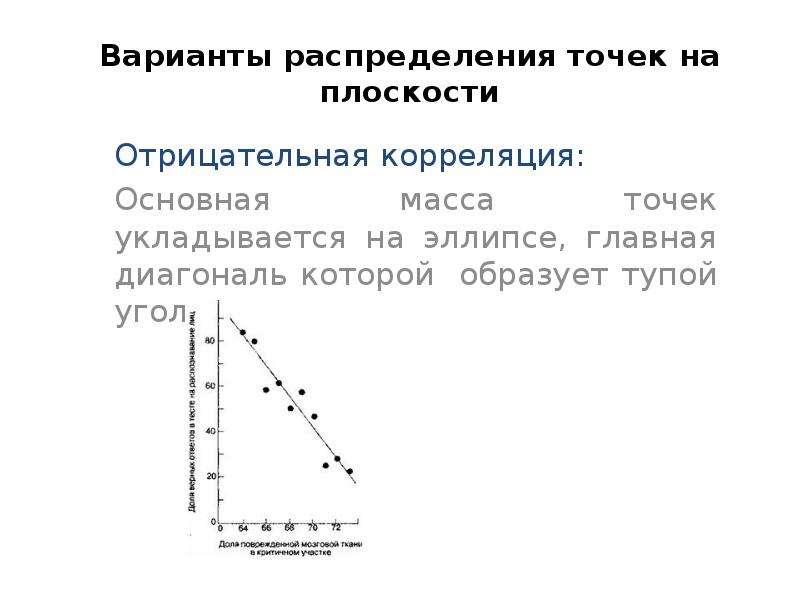 171]

При —1 имеет место отрицательная корреляция. Проекты реагируют на экономические воздействия в противоположных направлениях.  [c.424]

Если фирмы имеют проекты с отрицательной корреляцией, происходит диверсификация.  [c.424]

Заметим, что риск полностью устраняется при линейной отрицательной корреляции проектов.  [c.425]

Положительная связь увеличивает риск. Если бы в рассматриваемом примере имела место отрицательная корреляция между доходами, то коэффициент вариации составил бы 9,07% и риск был бы существенно ниже.  [c.122]

При таком количестве источников такая теснота отрицательной корреляции невозможна.  [c.123]

Зарубежной статистикой доказано, что в долговременных расчетах формула Пааше занижает, а индекс Ласпейреса завышает изменение цен. Вследствие наличия отрицательной корреляции между индивидуальными индексами цен и количествами относительный вес товаров падает, если цена возрастает. Чем дальше отдаляется базисный год, тем больше, как правило, становится вариация индивидуальных цен и количеств, а также разность между индексами Ласпейреса и Пааше. Достижение неравенства /л > /п, называемого эффектом Ласпейреса, может в силу ряда причин превратиться в свою противоположность (7Л замены товаров, ошибка выборки и др.).  [c.562]

Для выбора вариантов диверсификации следует по годам реализации проектов определить индивидуальную экономическую рентабельность производства продуктов А, Б и В, среднюю рентабельность по каждому виду продукции, отклонения текущих значений рентабельности от средней и определить корреляцию между выпуском продуктов А и Б, А и В. Знак корреляции покажет наиболее предпочтительный вариант диверсификации. Диверсификация с отрицательной корреляцией, в основном, несколько уменьшает совокупную отдачу от проектов, но в то же время сокращает риск резкого уменьшения доходов.  [c.264]

При отрицательной корреляции всегда существует стратегия формирования портфеля (представленная особым набором акций в нем), позволяющая полностью исключить риск». Очень жаль, что в реальности такой совершенно отрицательной корреляции между обыкновенными акциями не бывает.  [c.152]

Статистическим анализом доказано, что в долговременном аспекте формула Пааше занижает реальное изменение цен вследствие отрицательной корреляции проданного количества товара и цены, а в случае долгосрочных и международных сопоставлений разница между индексами, взвешенными разными способами, составляет несколько процентов. Значения индексов, вычисленных по формулам Ласпейреса и Пааше, совпадают лишь в случае почти невозможного ка практике совпадения структуры товарной массы базисного и отчетного периодов.  [c.310]

Коэффициент корреляции может изменяться в диапазоне 1,0. Коэффициент +1,0 (полная положительная корреляция) означает, что изменения независимой переменной приведут к идентичным изменениям зависимой (т.е. изменение индикатора вызовет такое же изменение цены бумаги). Коэффициент 1,0 (полная отрицательная корреляция) означает, что изменения независимой переменной вызовут идентичные изменения зависимой, но в противоположном направлении. Коэффициент, равный нулю, свидетельствует об отсутствии связи между переменными, то есть изменения независимой переменной не влияют на изменения зависимой.  [c.104]

В случае сравнения индикатора и цены бумаги высокий положительный коэффициент корреляции (скажем, больше 0,70) означает, что за изменением индикатора должно последовать соответствующее изменение цены. Высокая отрицательная корреляция (напр., меньше 0,70) говорит о том, что изменение индикатора обычно вызывает изменение цены в противоположном направлении. Низкий (т.е. близкий к нулю) коэффициент корреляции означает слабую взаимосвязь цены и индикатора.  [c.104]

СИЛЬНАЯ ОТРИЦАТЕЛЬНАЯ КОРРЕЛЯЦИЯ  [c.105]

Высокая положительная корреляция свидетельствует о том, что за выигрышем чаще следует очередной выигрыш и реже следует проигрыш и наоборот. При высокой отрицательной корреляции за выигрышем чаще следует проигрыш и реже — очередной выигрыш и наоборот.  [c.214]

За выигрышем чаще следует проигрыш, за проигрышем -выигрыш. В этом случае мы имеем отрицательную корреляцию между результатами сделок  [c.217]

Рассмотрим результаты последовательных сделок торговой системы. Назовем серией несколько следующих подряд прибыльных сделок или несколько следующих подряд убыточных сделок. В случае положительной корреляции количество серий на периоде тестирования будет меньше, чем количество серий при независимом чередовании прибылей и убытков. При отрицательной корреляции ситуация будет обратной. Заметим, что при расчете серий учитывается только знак дохода по сделке, а не его абсолютная величина, при этом сделки с нулевым доходом учитываются как убыточные.  [c.217]

Рисунок 1-3 Отрицательная корреляция (г = -1,00)

Теперь посмотрите на рисунок 1-3. Он показывает две последовательности, которые находятся точно в противофазе. Когда одна линия идет вверх, другая следует вниз (и наоборот). Мы называем это отрицательной корреляцией. Формула для коэффициента линейной корреляции г двух последовательностей X и Y такова (черта над переменной обозначает среднее арифметическое значение)  [c.20]

Средние значения различаются, потому что вы усредняете только те X и Y, которые частично перекрывают друг друга, поэтому последнее значение Y (3) не вносит вклад в среднее Y, а первое значение X (1) не вносит вклад в среднее X. Числитель является суммой всех значений из столбца Е (0,8). Чтобы найти знаменатель, мы извлечем квадратный корень из итогового значения столбца F, то есть 8,555699, затем извлечем квадратный корень из итогового значения столбца G, то есть 8,258329, и перемножим их, что даст в результате 70,65578. Теперь разделим числитель 0,8 на знаменатель 70,65578 и получим 0,011322. Это наш коэффициент линейной корреляции г. В данном случае коэффициент линейной корреляции 0,011322 едва ли о чем-то говорит, но для многих торговых систем он может достигать больших значений. Высокая положительная корреляция (по крайней мере, 0,25) говорит о том, что большие выигрыши редко сменяются большими проигрышами, и наоборот. Отрицательные значения коэффициента корреляции (между -0,25 и -0,30) подразумевают, что после больших проигрышей следуют большие выигрыши, и наоборот. Для заданного количества сделок с помощью метода, известного как Трансформация Z Фишера , коэффициент корреляции можно преобразовать в доверительный уровень. Эта тема рассматривается в приложении С. Отрицательную корреляцию так же, как и положительную, можно использовать в своих интересах. Например, если обнаружена отрицательная корреляция и система показала большой проигрыш, то в следующей сделке можно ожидать большой выигрыш и таким образом открыть больше контрактов, чем обычно. Если и эта сделка принесет убыток, то он не должен быть очень большим (из-за отрицательной корреляции).  [c.22]

До настоящего момента мы ограничивали сумму процентных весов 100 процентами. Однако возможно, что сумма процентных размещений для портфеля, который будет иметь наивысший геометрический рост, превысит 100%. Рассмотрим, например, две рыночные системы, А и В, которые идентичны во всех отношениях, за тем исключением, что у них отрицательная корреляция (R среднего геометрического — это портфель, который размещает 50% в каждую из двух рыночных систем. Это означает, что вам следует торговать 1 контрактом на каждые 10 000 долларов баланса для рыночной системы А, и для системы В. Однако когда есть отрицательная корреляция, можно показать, что оптимальный рост счета в действительности будет достигнут при торговле 1 контрактом для баланса, меньшего 10 000 долларов для рыночной системы А и/или рыночной системы В. Другими словами, когда есть отрицательная корреляция, сумма процентных весов может превышать 100%. Более того, возможно, что процентные размещения в рыночные системы могут по отдельности превысить 100%.  [c.47]

Важно помнить, что исторически ваш проигрыш может быть такой же большой, как и процент f (в смысле возможного уменьшения баланса). В действительности вам следует ожидать, что в будущем он будет выше, чем данное значение. Это означает, что комбинация двух рыночных систем, даже если они имеют отрицательную корреляцию, может привести к уменьшению баланса на 44%. Это больше, чем в системе с положительным математическим ожиданием, в которой оптимальное f= 0,25, и поэтому максимальный исторический проигрыш уменьшит баланс только на 25%. Мораль такова диверсификация, если она произведена правильно, является методом, который повышает прибыли. Она не обязательно уменьшает проигрыши худшего случая, что абсолютно противоречит популярному представлению. Диверсификация смягчает многие мелкие проигрыши, но она не уменьшает проигрыши худшего случая. При оптимальном f максимальные проигрыши могут быть существенно больше, чем думают многие. Поэтому, даже если вы хорошо диверсифицировали портфель, следует быть готовым к значительным уменьшениям баланса. Однако давайте вернемся и посмотрим на результаты, когда коэффициент корреляции между двумя играми равен 0. В такой ситуации, какими бы ни были результаты одного броска, они не влияют на результаты другого броска. Таким образом, есть четыре возможных результата  [c.49]

Очевидно, что при диверсификации вы должны использовать такие рыночные системы, которые имеют самую низкую корреляцию прибылей друг к другу, и желательно отрицательную корреляцию. Вы должны понимать, что уменьшение баланса худшего случая едва ли будет смягчено диверсификацией, хотя вы сможете смягчать многие более слабые уменьшения баланса. Наибольшая польза диверсификации состоит в улучшении среднего геометрического. Метод поиска оптимального портфеля путем рассмотрения чистых дневных HPR упраздняет необходимость смотреть за тем, сколько сделок в каждой рыночной системе произошло. Использование этого метода позволит вам наблюдать только за средним геометрическим независимо от частоты сделок. Таким образом, среднее геометрическое становится единственной статистической оценкой того, насколько прибыльным является портфель. Главная цель диверсификации — это получение наивысшего среднего геометрического.  [c.50]

Отметьте, что в случае комбинированного счета и в случае отдельных счетов прибыль одна и та же 42,38. Мы рассматривали положительную корреляцию между двумя системами. Теперь рассмотрим случай с отрицательной корреляцией между теми же системами, для двух отдельных денежных счетов (Таблица III)  [c.62]

Как мы уже знаем (см. главу 2), добавление рыночных систем увеличивает среднее геометрическое по портфелю в целом. Однако возникает проблема каждая следующая рыночная система вносит все меньший и меньший вклад в среднее геометрическое и все больше ухудшает его, понижая эффективность из-за одновременных, а не последовательных результатов. Поэтому не следует торговать слишком большим числом рыночных систем. Более того, реальное применение теоретически оптимальных портфелей осложняется из-за залоговых требований. Другими словами, вам лучше торговать 3 рыночными системами при полном оптимальном f, чем 300 рыночными системами при значительно пониженных уровнях, согласно уравнению (8.08). Скорее всего вы придете к выводу, что оптимальное число рыночных систем для торговли должно быть невелико. Особенно это обстоятельство важно, когда у вас много ордеров к исполнению и увеличивается вероятность ошибок. Если одна или несколько рыночных систем в портфеле имеют оптимальные веса больше единицы, может возникнуть еще одна проблема. Рассмотрим рыночную систему с оптимальным f=0,8 и наибольшим проигрышем, составляющим 4000 долларов. Для этой рыночной системы f = 5000 долларов. Давайте предположим, что оптимальный вес данного компонента в портфеле равен 1,25, поэтому вы будете торговать одной единицей компонента на каждые 4000 долларов ( 5000/1,25) баланса счета. Как только компонент столкнется с наибольшим проигрышем, весь активный баланс на счете будет обнулен, если прибылей в других рыночных системах не хватит для сохранения активного баланса. Рассмотренная проблема наиболее актуальна для систем, которые редко генерируют сделки. Если бы у нас были две рыночные системы с отрицательной корреляцией и положительным ожиданием, необходимо было бы открывать бесконечное количество контрактов на рынке. Когда один из компонентов проигрывает, другой выигрывает равную или большую сумму. Таким образом, мы получаем прибыль в каждой игре, однако только в том случае, когда рыночные системы ведут игру одновременно. Рассматриваемая же торговля аналогична гипотетической ситуации, когда один из компонентов в игре не активен, но используется другая рыночная система с бесконечным числом контрактов. Проигрыш может быть катастрофическим. Проблему можно решить следующим образом разделите единицу на наибольший вес компонента портфеля и используйте полученное значение в качестве верхней границы активного баланса, если оно меньше, чем значение, найденное из уравнения (8.08). В таком случае, если в будущем произойдет проигрыш той же величины, что и наибольший проигрыш (на основе которого рассчитано f), мы не потеряем все деньги. Например, наибольший вес компонента в нашем портфеле составляет 1,25. Если значение из уравнения (8.08) будет больше 1 / 1,25 = 0,8, следует использовать 0,8 в качестве верхней границы для доли активного баланса. Если первоначальная доля активного баланса небольшая, вышеописанная проблема может и не возникнуть, однако более агрессивному трейдеру следует всегда принимать ее во внимание. Альтернативное решение состоит в введении дополнительных ограничений в матрице портфеля (например, для каждой рыночной системы можно ограничить максимальные веса единицей и ввести дополнительные ограничения по залоговым средствам). Подобные дополнительные ограничения  [c.241]

Таким образом, вам нужно найти п оптимальных значений f, по одному на каждый компонент. Заметьте также, что хотя значения / не могут быть меньше нуля, каждое из них может быть больше единицы. Причина этого в том, что если между двумя компонентами имеется достаточно высокая отрицательная корреляция, то соответствующие им значения/будут стремиться к бесконечности.  [c.66]

Обратите внимание, что вы можете назначить оптимальное /для этих двух потоков, равным бесконечности (тогда/ будет бесконечно мало, и у вас будет бесконечное количество единиц), ибо суммарно нет ни одного убыточного периода владения. Заметьте также, что торговля этим портфелем много агрессивнее торговли первого потока с оптимальным/ равным 0,25. Наконец, отметьте, что хотя поток 2 имеет отрицательное математическое ожидание, благодаря отрицательной корреляции с потоком 1, торгуя ими одновременно, вам следовало бы задействовать бесконечное количество единиц актива То есть иногда подключение компонента с отрицательным математическим ожиданием повышает общую эффективность портфеля.  [c.66]

Цены двух абсолютно положительно коррелированных групп акций будут одновременно двигаться вверх-вниз. Это значит, что диверсификация не сократит риск, если портфель состоит из абсолютно положительно коррелированных групп акций. В то же время риск может быть устранен полностью путем диверсификации при наличии абсолютной отрицательной корреляции.  [c.77]

Диверсификация является одним из способов защиты капитала, однако в разнообразии тоже должна быть мера. Допустим, трейдер одновременно открыл позиции на слишком большом количестве разных рынков. Может получиться так, что прибыль от одной или двух удачных сделок не сможет компенсировать убытков по остальным позициям. Всегда необходимо находить разумный компромисс между диверсификацией и концентрацией. Иногда трейдеры концентрируют средства всего на нескольких рынках и получают неплохую прибыль. Это вполне допустимо, во всяком случае, если эти рынки проявляют ярко выраженную направленность. Единого ответа на вопрос, в какой степени следует диверсифицировать капитал, не существует. Мой личный опыт подсказывает, что более или менее надежного распределения средств можно достичь, открывая позиции одновременно на четырех-шести рынках разных групп — не больше. Повторяю, рынках разных групп. Чем больше значение отрицательной корреляции, существующей между рынками, тем выше диверсификация вложенных в них средств. Так, длинные позиции на четырех рынках иностранных валют, открытые одновременно, — не самый удачный пример того, какой должна быть эффективная диверсификация.  [c.430]

Для измерения взаимосвязи между какими-либо видами деятельности предприятия используется показатель корреляции, показывающий связь между признаками, состоящую в изменении средней величины одного из них в зависимости от изменения значения другого. Если изменение одного признака в связи с изменением другого происходит в одном направлении, то корреляция считается положительной. Если же эти изменения разнонаправлены, то между данными признаками существует отрицательная корреляция.  [c.264]

В качестве иллюстрации рассмотрим компанию Multi rop, имеющую два подразделения, активы каждого из которых оцениваются в 1 млрд. долл. Предположим, что показатели доходности каждого из этих подразделений характеризуется достаточно высоким уровнем риска, но они связаны между собой отрицательной корреляцией. В связи с этим объединение этих двух подразделений в рамках одной компании приводит к тому, что доходность ценных бумаг Multi rop оказывается безрисковой. Безрисковая процентная ставка составляет 5% годовых, и эта же величина оказывается ожидаемой равновесной ставкой доходности для каждого из двух подразделений. Предположим, что Multi rop имеет долгосрочные долговые обязательства на сумму в 1 млрд. долл., по которым также начисляется процент в 5% годовых.  [c.311]

Предположим, что вместо абсолютной отрицательной корреляции показатели доходности двух подразделений фирмы Multi rop никак не коррелируют. Будет ли в j этом случае выделение дочерней фирмы Uni rop в виде отдельной фирмы приводить к повышению благосостояния акционеров  [c.312]

В примере показан расчет значения риска для портфеля инноваций. В данном случае рассмотрены сопутствующие товары, имеющие высокую корреляцию, поэтому величина риска для портфеля в целом получилась достаточно большой. Вывод на рынок товаров со значениями отрицательных корреляцияй привел бы к снижению совокупного риска.  [c.105]

Основные концепции современной теории портфеля изложены в монографии, написанной доктором Гарри Марковицем. Первоначально Маркович предположил, что управление портфелем является проблемой структурного, а не индивидуального выбора акций, что обычно практикуется. Марковиц доказывал, что диверсификация эффективна только тогда, когда корреляция между включенными в портфель рынками имеет отрицательное значение. Если у нас есть портфель, составленный из одного вида акций, то наилучшая диверсификация достигается в том случае, если мы выберем другой вид акций, которые имеют минимально возможную корреляцию с ценой первой акции. В результате этого, портфель в целом (если он состоит из этих двух видов акций с отрицательной корреляцией) будет иметь меньшую дисперсию, чем любой вид акций, взятый отдельно. Марковиц предположил, что инвесторы действуют рациональным способои и при наличии выбора предпочитают портфель с меньшим риском при равном уровне прибыльности или выбирают портфель с большей прибылью, при одинаковом риске. Далее Марковиц утверждает, что для данного уровня риска есть оптимальный портфель с наивысшей доходностью, и таким же образом для данного уровня доходности есть оптимальный портфель с наименьшим риском. Портфель, доходность которого может быть увеличена без сопутствующего увеличения риска или портфель, риск которого можно уменьшить без сопутствующего уменьшения доходности, согласно Марковичу, неэффективны. Рисунок 1-7 показывает все имеющиеся портфели, рассматриваемые в данном примере. Если у вас портфель С, то лучше заменить его на портфель А, где прибыль такая же, но с меньшим риском, или на портфель В, где вы получите большую прибыль при том же риске. Описывая эту ситуацию, Марковиц ввел понятие эффективная граница (effi ient frontier). Это набор портфелей, которые находятся в верхней левой части графика, то есть портфели, прибыль которых больше не может быть увеличена без увеличения риска, и риск которых не может быть уменьшен без уменьшения прибыли. Портфели, находящиеся на эффективной границе, называются эффективными портфелями (см. Рисунок 1-8). Портфели, которые находятся вверху справа и внизу слева, в целом недостаточно диверсифицированы по сравнению с другими портфелями. Те же портфели, которые находятся в середине эффективной границы, обычно очень хорошо диверсифицированы. Выбор портфеля инвестором зависит от степени неприятия риска инвестором — иначе говоря, от желания взять на себя риск. В модели Марковица любой портфель, который находится на эффективной границе, является хорошим выбором, но какой именно портфель выберет инвестор — это вопрос личного предпочтения (позднее мы увидим, что есть точное оптимальное расположение портфеля на эффективной границе для всех инвесторов). Модель Марковица первоначально была представлена для портфеля акций, который инвестор будет держать достаточно долго. Поэтому основными входными данными были ожидаемые доходы по акциям (определяется как ожидаемый прирост цены акции плюс дивиденды), ожидаемые дисперсии этих доходов и корреляции доходов между различными акциями. Если бы мы  [c.41]

GS I имеет сильную положительную корреляцию с инфляцией и сильную отрицательную корреляцию с доходностью акций и облигаций. Эти важный критерий для создания диверсифицированного портфеля. Академические исследования показали добавляя индекс к физическим биржевым товарам, портфельные менеджеры могут увеличивать доходность портфеля, содержащего традиционные американские акции и облигации, бе з увеличения его изменчивости.  [c.202]

Коэффициент корреляции (Correlation coefficient) · Loginom Wiki

Разделы: Метрики

Loginom: Корреляционный анализ (обработчик), Статистика (визуализатор)

В математической статистике — показатель, характеризующий силу статистической связи двумя или несколькими случайными величинами.

Если коэффициент корреляции описывает связь между двумя случайными величинами, то он называется простым, если между одной случайной величиной и их группой, то множественным.

Простой коэффициент корреляции (Пирсона) вычисляется по формуле:

r=n∑i=1(xn−¯x)(yn−¯y)nσxσy,

где n — число статистических наблюдений, x и y — случайные переменные. Значения коэффициента корреляции всегда расположены в диапазоне от -1 до 1 и интерпретируются следующим образом:

• если коэффициент корреляции близок к 1, то между переменными наблюдается положительная корреляция. Иными словами, отмечается высокая степень связи между переменными. В данном случае, если значения переменной x будут возрастать, то и выходная переменная также будет увеличиваться;
• если коэффициент корреляции близок к -1, это означает, что между переменными имеет место сильная отрицательная корреляция. Иными словами, поведение выходной переменной будет противоположным поведению входной. Если значение x будет возрастать, то y будет уменьшаться, и наоборот;
• промежуточные значения, близкие к 0, будут указывать на слабую корреляцию между переменными и, соответственно, низкую зависимость. Иными словами, поведение переменной x не будет совсем (или почти совсем) влиять на поведение y (и наоборот).

Коэффициент корреляции равен квадратному корню коэффициента детерминации, поэтому может применяться для оценки значимости регрессионных моделей.

Очевидно, что если корреляция между переменными высокая, то, зная поведение входной переменной, проще предсказать поведение выходной, и полученное предсказание будет точнее (говорят, что входная переменная хорошо «объясняет» выходную). Однако чем выше корреляция наблюдается между переменными, тем очевиднее связь между ними, например, взаимозависимость между ростом и весом людей.

Коэффициент корреляции Пирсона описывает только степень линейной связи и применим к непрерывным величинам. Для дискретных (качественных) данных используются коэффициенты ранговой корреляции Кендалла или Спирмена.

Коэффициент корреляции широко применяется в анализе данных для отбора переменных в аналитические модели и выявления наиболее значимых признаков с точки зрения решаемой задачи.

Корреляция как показатель взаимосвязи между параметрами.

Научные термины пугают и притягивают одновременно. Термин «корреляция» все чаще можно встретить на страницах газет, по радио, на телевидении. Им козыряют экономисты, политологи, аналитики. Но, похоже, частота использования этого термина в СМИ отрицательно коррелирует с уровнем его понимания потребителями.

В переводе на простой язык, сказанная фраза означает следующее: «Чем чаще используется термин «корреляция», тем менее точным становится содержание этого понятия в сознании людей». В реальности, возможно, это и не так – исследования не проводились. Но важно другое – корреляция в обыденном понимании отражает взаимосвязь между явлениями.

 

Взаимосвязи вокруг нас

В человеке живет интуитивное ощущение взаимосвязи всех явлений. В фантастическом рассказе Рэя Брэдбери герой попадает в далекое прошлое и, нарушая запрет, сходит с тропы. Он лишь раздавил бабочку. Но вернулся в другой мир, с другим языком и даже президентом. Все связано вокруг…

При чем здесь корреляция? А при том, что пытливое сознание человека пытается выявлять корреляции. Зная взаимосвязи между явлениями, на них можно влиять, ими можно управлять.

Я не буду «грузить» вас математической терминологией, сложными формулами. Давайте разберемся в сути этого понятия; уясним что значит отрицательная и положительная корреляция; значимая и незначимая.

 

Понятие корреляции

Слово «корреляция» происходит от латинского «correlatio», что означает «соотношение» или «взаимосвязь».

Взаимосвязь присуща многим явлениям. Например, кепка, надетая на голову, связана с ней – куда голова, туда и кепка. Или палочка в руке дирижёра – они взаимосвязаны, и она послушна руке хозяина, полету его вдохновения. Но можно ли говорить, что их движения коррелируют между собой? Нет, и вот почему.

 

Функциональная связь

Палочка и рука взаимосвязаны и эта связь – функциональная. Она детерминирующая – жестко связывает между собой объекты. Если дирижёр сосредоточен и крепко держит палочку, то в их согласованном движении не будет моментов, когда которых рука движется в одну сторону, а палочку – в другую. Корреляционная связь совсем иной природы.

Посмотрим за спину нашего дирижёра. В зале сидят слушатели, любители музыки. Они испытывают какие-то эмоции. Их переживания, возможно, как-то связаны с уровнем их музыкального образования. Чем больше они знают про музыку, тем выше их эмоциональный отклик. Эта связь — корреляционная.

 

Корреляционная связь

В отличие от функциональной связи, корреляция отражает не жесткую зависимость между явлениями. Кто-то очень подкован теоретически, но эмоциональный отклик на музыку слабый. Другой мало образован, но его «пробило» на эмоции. Такая связь называется случайной, стохастической. И это сфера статистики – науки, занимающейся не отдельными явлениями, а массовыми.

Итак, корреляция отражает не функциональную, а статистическую случайную связь между явлениями (переменными). Почему случайную? Потому что заранее не известно, кто и как из слушателей будет реагировать на музыку. Но если статистический (массовый) расчет показал положительную корреляцию между образованностью и эмоциональным откликом, то это дает основания для важных выводов. Знание корреляционной связи позволяет предсказывать.

В данном примере мы с большой долей вероятности сможем утверждать, что из двух слушателей более эмоционально слушал тот, кто более образован. Это не будет однозначный вывод, ведь связь у нас не функциональная. Это будет вывод статистический, вероятностный – мы всегда можем ошибиться. Но вероятность этой ошибки не велика и заранее известна. Она называется «уровень статистической значимости». Как видим, без математики в этом вопросе все-таки не обойтись.

 

Коэффициент корреляции

В повседневной жизни, говоря о корреляции, например, успеха и затраченных усилий или ощущения счастья и материального достатка, мы опираемся на мифы, интуицию или досужие домыслы. Эти величины трудно измерить, перевести на язык цифр потом строго доказать их взаимосвязи. Но если мы имеем дело с явлениями, которые можно измерить, то здесь корреляцию можно рассчитать и получить коэффициент, который будет отражать силу и направление взаимосвязи.

Например, мы взяли группу из 20-ти человек и определили для каждого два параметра: возраст (посмотрели паспорт) и уровень оптимизма (провели психологический тестирование). Эти данные нужно занести в так называемую таблицу исходных данных и загрузить в статистическую программу. В итоге получим значение коэффициента корреляции. Не стоит пугаться этого числа, разгадать его тайны не так сложно.

Коэффициент корреляции может принимать численные значения в диапазоне от -1 до +1. Для анализа важны два показателя:

• Знак коэффициента корреляции (положительный или отрицательный).
• Абсолютное значение коэффициента корреляции (то есть, без учета знака, «по модулю»).

 

Отрицательная связь не значит плохая, положительная не значит хорошая

Если расчет корреляции между возрастом и оптимизмом среди испытуемых дал положительный показатель, это значит следующее: с годами растет оптимизм. То есть, чем выше возраст испытуемого, тем более оптимистично он смотрит на жизнь (мудрецы).

Но мы могли получить и обратный результат – отрицательную корреляцию между возрастом и оптимизмом. То есть, чем больше прожитых лет, тем меньше хорошего видится вокруг (скептики).

Если выборка подобрана правильно (репрезентативна), то она отражает ключевые особенности всех людей (или почти, например, живущих в большом городе). Тогда, полученные коэффициенты корреляции, дают важную информацию. Ее можно использовать, например, при приеме на работу. В случае положительной корреляции на должность менеджеров по продажам стоит брать людей постарше – они будут оптимистичны и доброжелательны.

 

Сила взаимосвязи – большая сила

Вы, наверное, уже догадались, что величина коэффициента корреляции отражает силу взаимосвязи между показателями. Чем больше численное значение по абсолютной величине (без учета знака), тем сила взаимосвязи больше.

Представим, что в нашей группе корреляция между возрастом и оптимизмом равна +1. Это значит, что, взяв любых двух человек из этой группы и узнав их возраст, мы точно сможем предсказать, кто из них более оптимистичен? Кстати, вы уже поняли кто? … Правильно, тот, кто старше.

А если корреляция равна -1, то в этой группе тот, кто моложе, более позитивно смотрит на мир. И это без всяких исключений! А вот если корреляция будет -0,9, значит в закономерности есть сбой — один или два человека в преклонных годах имеют высокий оптимизм. Они и нарушают общую закономерность и «снижают» коэффициент корреляции.

А теперь попробуйте сами объяснить, что значит, если коэффициент корреляции равен 0? Правильно, в этом случае никакой связи между переменными нет. Невозможно, зная возраст, предсказать позитивность взгляда на мир. И, наоборот, нельзя, зная оптимизм двоих испытуемых, сказать, кто старше. Но и эту информацию можно использовать. При поиске оптимистов для работы в «отделе бесперспективных проектов» не стоит смотреть на возраст.

 

Вывод

Надеюсь, теперь термин «корреляция» вас не пугает. Уверен, что вы сможете отличить функциональную связь (движение мышки и курсора) и корреляционную (время тренировок и высота прыжка). Имейте в виду, что, когда в обыденной речи просто говорят о корреляции, то имеют в виду положительную и значимую (достаточно высокую) взаимосвязь.

Этих знаний вполне хватит, чтобы понимать других и самому к месту ввернуть этот термин. Для более глубокого изучения необходимо разобраться, какие бывают коэффициенты корреляции, как их рассчитывать, как интерпретировать результаты. Это может быть полезно студентам, при проведении эмпирических исследований по психологии или социологии; при написании дипломных и курсовых.

 

Корреляции в дипломах по психологии

 

Коэффициент корреляции Пирсона

Коэффициент корреляции Спирмена

 

 

 

---

Надеюсь, эта статья поможет вам написать работу по психологии самостоятельно. Если понадобится помощь, обращайтесь (все виды работ по психологии; статистические расчеты). Заказать

Интуиция за корреляцией

Дата публикации Jun 26, 2019

Когда вы погружаетесь в море знаний, которое является наукой о данных, одна из первых рыб, которую вы обнаружите, — это корреляция, и это двоюродный брат, автокорреляция. Если вы не потратите время на то, чтобы узнать их, невозможно сделать многое в науке о данных. Итак, давайте познакомимся с ними.

В самом общем смыслекорреляция между двумя переменными может рассматриваться как некая связь между ними.то есть, когда значение одной переменной изменяется, значение другой изменяется впредсказуемым образом, большую часть времени,

На практике слово корреляция обычно используется для описаниялинейные отношения (а иногда и нелинейные отношения)между переменными.

Я подойду к аспекту линейности через минуту.

Между тем вот пример двухвозможнокоррелированные переменные. Мы говорим ‘possiblу, потому что это гипотеза, которая должна быть проверена и доказана.

Взаимосвязь между городом и шоссе экономия топлива пассажирских транспортных средств. Источник: UC Irvine ML Repository

Давайте составим несколько неофициальных определений.

Линейные отношения

Линейная корреляция:Если значения двух коррелированных переменныхизменяться с постоянной скоростьюпо отношению друг к другу они, как говорят, имеютлинейная корреляциядруг с другом.

Имея в виду линейную корреляцию, давайте вернемся к нашему примеру:

Возможно, линейно коррелированные переменные. Источник:Автомобильный набор данных,UC Irvine ML Репозиторий

Есликорреляция в этом случае является линейной, аМодель линейной регрессии(то есть прямая линия) после того, как она будет подобрана к данным, должна быть в состоянии адекватнообъяснятьлинейный сигнал в этом наборе данных. Вот как будет выглядеть подобранная модель (черная линия) для этого набора данных:

Линейная регрессионная модель, подходящая для 80% точек данных в наборе данных City против Highway MPG

В приведенном выше примере теперь вы можете использовать подобранную модель для прогнозирования значений MPG для шоссе, соответствующих значениям MPG для городов, которые модель не виделано которые находятся в диапазоне набора данных обучения,

Вот график предсказаний подобранной линейной модели для набора данных удержания, который содержит 20% исходных данных, которые модель не видела во время процесса подгонки.

Фактическое против прогнозируемого MPG для автомагистрали на 20%

Для программно склонных следующий код Python дал эти результаты.

Вы можете получить данные, использованные в примере изВот, Если вы используете эти данные в своей работе, обязательно напишите людям наUC Irvine ML хранилище,

Нелинейные отношения

Теперь давайте посмотрим на нелинейные отношения.

Нелинейная корреляция:Если значения коррелированных переменных не изменяются с постоянной скоростью по отношению друг к другу, говорят, что они имеютнелинейные отношенияилинелинейная корреляциядруг с другом.

Вот пример того, что выглядит как случай длянелинейныйкорреляция.

Пример нелинейного отношения

До тех пор, пока кто-либо не преобразует зависимую переменную (в нашем примере — это Highway MPG), чтобы сделать отношение линейным, модель линейной регрессии не сможет адекватно «объяснить» информацию, содержащуюся в таких нелинейных отношениях.

Положительная и отрицательная корреляция

Положительная корреляция:Для двух коррелированных переменных, когда значение одной переменнойувеличивается (или уменьшается),тогдабольшую часть времениесли значение другой переменной также видно соответственноувеличение(или уменьшить), то две переменные можно сказать, чтоположительно коррелированный,

Вот пример, который предлагает положительную корреляцию между двумя переменными:

Две переменные, которые кажутся положительно коррелированными. Источник:Автомобильный набор данных,UC Irvine ML Репозиторий

Отрицательная корреляция:Для двух коррелированных переменных, когда значение одной переменнойувеличивается(или уменьшается),тогдабольшую часть времениесли значение другой переменной рассматривается соответственноснижение(или увеличение), то две переменные называютсяотрицательно коррелированный,

Вот пример, который предлагает отрицательную корреляцию:

Две переменные, которые кажутся отрицательно коррелированными. Источник:Автомобильный набор данных,UC Irvine ML Репозиторий

Как измерить корреляцию

Давайте посмотрим на следующие два графика рассеяния.

Оба графика предполагают положительную корреляцию между соответствующими переменными. Но корреляция сильнее на первом графике, поскольку точки более плотно упакованы вместе по воображаемой прямой линии, проходящей через точки.

коэффициент корреляциимежду двумя переменными количественно определяет, насколько тесно связаны перемещения двух переменных относительно друг друга

Формула для коэффициента Пирсона

Формула для коэффициента корреляции между двумя переменными, которые имеютлинейное отношениеявляется:

Формула для коэффициента корреляции между переменными X и Y

Две сигмы в знаменателе являются стандартными отклонениями соответствующих переменных. Мы будем анализироватьковариациив немного.

Между тем отметим, что при расчете по приведенной выше формуле коэффициент корреляции называетсяКоэффициент корреляции Пирсона.Он представлен символом ‘р’При использовании для образца и по символурокогда используется для всей совокупности ценностей.

Если вы хотите использовать «популяционную версию» этой формулы, обязательно используйте «популяционные формулы» для ковариации и стандартного отклонения.

Интерпретация значения г

— Значениер(илиро) плавно колеблется от[-1,0 до 1,0],
— Когда переменные отрицательно коррелированыr = [- 1, 0),
—г = -1подразумевает совершенную отрицательную корреляцию.
— когда они положительно коррелируютr = (0, +1],
—г = + 1подразумевает совершенную положительную корреляцию.
— Когдаr = [0]переменные не являются линейно коррелированными.

Теперь давайте вернемся к пониманиюковариационнаятермин в числителе.

Интуиция для формулы коэффициента Пирсона

Чтобы действительно понять, что происходит в формуле Пирсона, нужно сначала понятьковариационная, Как и корреляция, ковариация между двумя переменными измеряет, насколько тесно связаны значения двух переменных.

Когда используется для измерения герметичностилинейные отношенияКовариация рассчитывается по следующим формулам:

Давайте разберем эти формулы термин за термином:

Как упоминалось ранее, ковариация измеряет, насколько синхронно изменяются значения переменных с помощью w.r.t. друг друга. Поскольку мы хотим измерить изменение стоимости, изменение должно быть привязано к фиксированному значению. Это фиксированное значение является средним для ряда данных этой переменной. Для выборочной ковариации мы используем выборочное среднее, а для выборочной ковариации — среднее. Использование среднего значения в качестве целевой цели также центрирует каждое значение вокруг его среднего. Это объясняет вычитаниеИкса такжеYот их соответствующих средств в числителе.

Умножение центрированных значений в числителе гарантирует, что произведение будет положительным, когдаИкса такжеYоба поднимаются или падают относительно своих соответствующих средств. ЕслиИксподнимается ноYпадает ниже соответствующего среднего, продукт отрицательный.

Суммирование в числителе гарантирует, что если продукты с положительной оценкой более или менее уравновешивают продукты с отрицательной оценкой, чистая сумма будет крошечным числом, что означает отсутствие доминирующего положительного или отрицательного паттерна в движении двух переменных. WRT друг друга. В этом случае значение ковариации будет небольшим. С другой стороны, если положительные продукты доминируют над отрицательными, то сумма будет большим положительным или большим отрицательным числом, означающим чистый положительный или чистый отрицательный характер движения между двумя переменными.

Наконец,Nили(П-1)в знаменателе усредняет вещи по доступным степеням свободы. В выборке одна степень используется средним для выборки, поэтому мы делим на(П-1).

Ковариантность прекрасна, но …

Ковариантность — это прекрасный способ количественно оценить движение переменных относительно друг друга, но у него есть некоторые проблемы.

Отличающиеся единицы:Ковариацию трудно интерпретировать, когда единицы двух переменных различны. Например, еслиИксв долларах иYнаходится в фунтах стерлингов единица ковариации междуИкса такжеYстановитсядолларовые времена фунт стерлингов, Как можно это интерпретировать? Даже когда обаИкса такжеYимеют одну и ту же единицу, скажем, доллар, единицы ковариации становится …доллар раз доллар!Все еще не легко понять. Облом!

Отличающиеся весы:Существует также проблема дальности. когдаИкса такжеYварьируются в течение небольшого интервала, скажем[0,1]вы получите обманчиво крошечное значение ковариации, даже еслиИкса такжеYдвигаться вместе очень плотно.

Сложность со сравнением:Потому чтоИкса такжеYмогут иметь разные единицы измерения и разные диапазоны, зачастую невозможно объективно сравнить ковариацию между одной парой переменных и другой парой переменных. Скажи я хочу сравнитьнасколько сильнее или слабееэто линейная зависимость междуэкономия топлива и длина автомобиляпо сравнению с отношением междуэкономия топлива и снаряженная масса, Использование ковариации для этого сравнения потребует сравнения двух значений в двух разных единицах и двух разных диапазонах. Проблематично, если не сказать больше.

Если бы мы только могли масштабировать ковариацию, чтобы диапазон был стандартизирован, а также решить проблему «единиц» Введите «стандартное отклонение». Проще говоря, стандартное отклонение измеряет среднее отклонение данных от их среднего значения. Стандартное отклонение также имеет приятное свойство: он имеет ту же единицу, что и исходная переменная. Итак, давайте разделим ковариацию на стандартные отклонения двух переменных. Это приведет к изменению масштаба ковариации, так что теперь она выражается вкратные стандартному отклонениюи это будет такжеотмените единицы измерения из числителя, Все неприятности с ковариацией решаются в двух простых делениях! Вот полученная формула:

Где же мы видели эту формулу раньше? Это, конечно, коэффициент корреляции Пирсона!

Автокорреляция

Авто или самокорреляция — это корреляция переменной со значением, которое приняла переменная,Иксединиц (времени) в прошлом. Например, температура воздуха в месте может быть автоматически коррелирована с температурой воздуха того же места 12 месяцев назад. Автокорреляция имеет значение для переменных, которые индексируются по шкале, которая может быть упорядочена, то есть по порядковой шкале. Шкала времени является примером порядковой шкалы.

Так же, как корреляция, автокорреляция может быть линейной или нелинейной, положительной или отрицательной, или она может быть нулевой.

Формула для автокорреляции при использовании длялинейноАвтокоррелированная связь между переменной и k-lagged версией себя выглядит следующим образом:

Формула для k-лаговой автокорреляции Y

Давайте немного углубимся в понимание автокорреляции, посмотрев на другой набор данных:

Среднемесячная максимальная температура в Бостоне, штат Массачусетс, с января 1998 года по июнь 2019 года. Источник данных о погоде:Национальные центры экологической информации

На приведенном выше графике показана среднемесячная максимальная температура по городу Бостон. Он рассчитывается путем усреднения за каждый месяц максимальной суточной температуры, зарегистрированной метеостанцией в этом месяце, за период с января 1998 года по июнь 2019 года.

Давайте построим график зависимости температуры от времени для разных лагов.

Среднемесячная максимальная температура в Бостоне, штат Массачусетс, нанесена на график с лаговой версией самого себя. Источник:Национальные центры экологической информации

График LAG 12 показывает сильную положительную линейную зависимость между средней максимальной температурой за месяц и средней максимальной за тот же месяц год назад.

Существует также сильная отрицательная автокорреляция между точками данных, которые разнесены на шесть месяцев, то есть на LAG 6.

В целом в этих данных присутствует сильный сезонный сигнал, который можно ожидать в данных о погоде такого рода.

Ниже приведена автокорреляционная тепловая карта, показывающая корреляцию между каждой комбинациейTа такжеТ-к, Для нас интересная колонка выделена синим цветом.

Корреляционная тепловая карта

В первом столбце интересующий квадрат равен единице (среднемесячный максимум, TMINUS12) и, возможно, квадрату (среднемесячный максимум, TMINUS6). Теперь, если вы вернетесь к коллажу рассеянного графика, вы заметите, что отношение для всех других комбинаций лагов является нелинейным. Так в любомлинейная сезонная модельмы попытаемся построить для этих данных полезность значений коэффициента корреляции, которые были сгенерированы для этих нелинейных отношений (то есть для оставшихся квадратов на тепловой карте), строго ограничена, и их не следует использоватьдаже если некоторые из них имеют большие значения.

Помните, что (авто) коэффициенты корреляции при расчете с использованием формул, которые упоминались ранее, полезны только тогда, когда отношение является линейным Если связь нелинейная, нам нужен другой метод для количественной оценки силы нелинейной связи. Например,Ранговой коэффициент корреляции Спирменаможет быть использован для количественной оценки силы взаимосвязи между переменными, которые имеют нелинейные,монотонныйотношения.

Вот код Python для построения временных рядов температуры, коллажа рассеяния и тепловой карты:

Python-код для построения температурных рядов, автокорреляционных графиков рассеяния и корреляционной тепловой карты

А вот инабор данных,

Слово предостережения

Наконец, слово предостережения. Корреляция между двумя переменнымиИкса такжеYявляется ли оно линейным или нелинейным, не означает автоматически причинно-следственную связь междуИкса такжеY(пока верно обратное). Даже когда наблюдается большая корреляция междуИкса такжеY,Иксне может напрямую влиятьYили наоборот. Может быть, есть скрытая переменная, называемая смешанной переменной, которая одновременно влияет на обаИкса такжеYтак что они поднимаются и падают синхронно друг с другом. Для иллюстрации рассмотрим следующий график, который показывает два набора данных, нанесенных друг на друга

График зависимости общей рабочей силы с доступом к электричеству (Источник: Всемирный банк)

ВотИксЭто временной ряд, который варьируется от 1990 до 2016 года и содержит долю населения мира, имеющего доступ к электричеству в каждый из этих лет. ПеременнаяYЭто также временной ряд, который варьируется от 1990 до 2016 года и содержит численность рабочей силы во всем мире в каждый из этих лет.

Два набора данных явно сильно коррелированы. Вы будете судить, есть ли причина и следствие!

---

Я пишу о темах в науке о данных, уделяя особое внимание анализу временных рядов и прогнозированию.

Если вам понравилась эта статья, пожалуйста, следуйте за мной наСачин Свиданиеполучать советы, практические рекомендации и советы по программированию по темам, посвященным анализу временных рядов, моделированию и прогнозированию.

Оригинальная статья

Коэффициенты корреляции: положительный, отрицательный и нулевой

Коэффициенты корреляции — это индикаторы силы линейной связи между двумя разными переменными, x и y. Коэффициент линейной корреляции больше нуля указывает на положительную взаимосвязь. Значение меньше нуля означает отрицательную взаимосвязь. Наконец, нулевое значение указывает на отсутствие связи между двумя переменными x и y.

В этой статье объясняется значение коэффициента линейной корреляции для инвесторов, как рассчитать ковариацию для акций и как инвесторы могут использовать корреляцию для прогнозирования рынка.

Ключевые выводы:

• Коэффициенты корреляции используются для измерения силы линейной связи между двумя переменными.
• Коэффициент корреляции больше нуля указывает на положительную взаимосвязь, а значение меньше нуля означает отрицательную взаимосвязь.
• Нулевое значение указывает на отсутствие связи между двумя сравниваемыми переменными.
• Отрицательная корреляция или обратная корреляция — ключевая концепция при создании диверсифицированных портфелей, которые могут лучше противостоять волатильности портфеля.
• Расчет коэффициента корреляции занимает много времени, поэтому данные часто загружаются в калькулятор, компьютер или статистическую программу, чтобы найти коэффициент.

Понимание корреляции

Коэффициент корреляции ( ρ ) — это мера, определяющая степень, в которой связано движение двух разных переменных. Наиболее распространенный коэффициент корреляции, генерируемый корреляцией произведения-момента Пирсона, используется для измерения линейной связи между двумя переменными.Однако в нелинейной зависимости этот коэффициент корреляции не всегда может быть подходящей мерой зависимости.

Возможный диапазон значений коэффициента корреляции от -1,0 до 1,0. Другими словами, значения не могут превышать 1,0 или быть меньше -1,0. Корреляция -1,0 указывает на абсолютную отрицательную корреляцию, а корреляция 1,0 указывает на идеальную положительную корреляцию. Если коэффициент корреляции больше нуля, это положительная связь. И наоборот, если значение меньше нуля, это отрицательная связь.Нулевое значение указывает на отсутствие связи между двумя переменными.

При интерпретации корреляции важно помнить, что наличие корреляции между двумя переменными не означает, что одна вызывает другую.

Корреляция и финансовые рынки

На финансовых рынках коэффициент корреляции используется для измерения корреляции между двумя ценными бумагами. Например, когда две акции движутся в одном направлении, коэффициент корреляции положительный.И наоборот, когда две акции движутся в противоположных направлениях, коэффициент корреляции отрицательный.

Если коэффициент корреляции двух переменных равен нулю, линейной зависимости между переменными нет. Однако это только для линейной зависимости. Возможно, что переменные имеют сильную криволинейную связь. Когда значение ρ близко к нулю, обычно между -0,1 и +0,1, считается, что переменные не имеют линейной зависимости (или очень слабой линейной зависимости).

Например, предположим, что цены на кофе и компьютеры наблюдаются и обнаруживают корреляцию +,0008. Это означает, что между двумя переменными нет корреляции или взаимосвязи.

Инвестопедия / Хьюго Линь

Расчет ρ

Ковариация двух рассматриваемых переменных должна быть рассчитана до определения корреляции. Затем требуется стандартное отклонение каждой переменной. Коэффициент корреляции определяется делением ковариации на произведение стандартных отклонений двух переменных.

Стандартное отклонение — это мера разброса данных от среднего значения. Ковариация — это мера того, как две переменные изменяются вместе. Однако его масштабы безграничны, поэтому его трудно интерпретировать. Нормализованная версия статистики вычисляется путем деления ковариации на произведение двух стандартных отклонений. Это коэффициент корреляции.

Корреляция знак равно ρ знак равно cov ( Икс , Y ) σ Икс σ Y \ text {Корреляция} = \ rho = \ frac {\ text {cov} (X, Y)} {\ sigma_X \ sigma_Y} Корреляция = ρ = σX σY cov (X, Y)

Положительная корреляция

Положительная корреляция — когда коэффициент корреляции больше 0 — означает, что обе переменные движутся в одном направлении.Когда ρ равно +1, это означает, что две сравниваемые переменные имеют идеальную положительную взаимосвязь; когда одна переменная перемещается выше или ниже, другая переменная перемещается в том же направлении с той же величиной.

Чем ближе значение ρ к +1, тем сильнее линейная зависимость. Например, предположим, что стоимость цен на нефть напрямую связана с ценами на авиабилеты с коэффициентом корреляции +0,95. Связь между ценами на нефть и ценами на авиабилеты имеет очень сильную положительную корреляцию, так как значение близко к +1.Таким образом, если цена на нефть снижается, стоимость авиабилетов также снижается, а если цена на нефть возрастает, то же самое происходит и с ценами на авиабилеты.

На приведенной ниже диаграмме мы сравниваем один из крупнейших банков США, JPMorgan Chase & Co. (JPM), с биржевым фондом Financial Select SPDR Exchange Traded Fund (ETF) (XLF). Как вы понимаете, компания JPMorgan Chase & Co. должна иметь положительную корреляцию с банковской отраслью в целом. Мы видим, что коэффициент корреляции в настоящее время составляет 0,98, что свидетельствует о сильной положительной корреляции.Значение выше 0,50 обычно свидетельствует о положительной корреляции.

Понимание корреляции между двумя акциями (или одной акцией) и отраслью может помочь инвесторам оценить, как акции торгуются по сравнению с аналогами. Все типы ценных бумаг, включая облигации, сектора и ETF, можно сравнить с помощью коэффициента корреляции.

Отрицательная корреляция

Отрицательная (обратная) корреляция возникает, когда коэффициент корреляции меньше 0. Это указывает на то, что обе переменные движутся в противоположном направлении.Короче говоря, любое значение от 0 до -1 означает, что две ценные бумаги движутся в противоположных направлениях. Когда ρ равно -1, связь считается полностью отрицательно коррелированной.

Короче говоря, если одна переменная увеличивается, другая уменьшается с той же величиной (и наоборот). Однако степень отрицательной корреляции между двумя ценными бумагами может меняться со временем (и они почти никогда не коррелируют точно все время).

Примеры отрицательной корреляции

Например, предположим, что проводится исследование для оценки взаимосвязи между наружной температурой и счетами за отопление.В исследовании сделан вывод об отрицательной корреляции между ценами на отопление и температурой наружного воздуха. Коэффициент корреляции равен -0,96. Эта сильная отрицательная корреляция означает, что по мере снижения температуры на улице цены на отопление увеличиваются (и наоборот).

Когда дело доходит до инвестирования, отрицательная корреляция не обязательно означает, что следует избегать ценных бумаг. Коэффициент корреляции может помочь инвесторам диверсифицировать свой портфель, включив в него набор инвестиций, имеющих отрицательную или низкую корреляцию с фондовым рынком.Короче говоря, при снижении риска волатильности в портфеле иногда все же привлекаются противоположности.

Например, предположим, что у вас есть сбалансированный портфель на 100 000 долларов, который инвестируется на 60% в акции и 40% в облигации. В год высоких экономических показателей доходность акционерного компонента вашего портфеля может составить 12%, в то время как компонент облигации может принести -2%, поскольку процентные ставки растут (что означает, что цены на облигации падают).

Таким образом, общая доходность вашего портфеля составит 6.4% ((12% x 0,6) + (-2% x 0,4). В следующем году, когда экономика заметно замедлится и процентные ставки будут снижены, ваш портфель акций может составить -5%, в то время как ваш портфель облигаций может принести 8%, что дает вам общую доходность портфеля в размере 0,2%.

Что, если бы вместо сбалансированного портфеля ваш портфель состоял на 100% из акций? Используя те же предположения о доходности, ваш портфель, полностью состоящий из акций, будет иметь доходность 12% в первый год и -5% во второй год. Эти цифры явно более изменчивы, чем доходность сбалансированного портфеля, равная 6.4% и 0,2%.

Коэффициент линейной корреляции

Коэффициент линейной корреляции — это число, вычисленное на основе заданных данных, которое измеряет силу линейной связи между двумя переменными: x и y. Знак коэффициента линейной корреляции указывает направление линейной зависимости между x и y. Когда r (коэффициент корреляции) близок к 1 или -1, линейная зависимость сильная; когда он близок к 0, линейная зависимость слабая.

Даже для небольших наборов данных вычисления коэффициента линейной корреляции могут оказаться слишком длинными, чтобы их можно было выполнять вручную.Таким образом, данные часто загружаются в калькулятор или, что более вероятно, в компьютер или статистическую программу, чтобы найти коэффициент.

Коэффициент Пирсона

Как расчет коэффициента Пирсона, так и базовая линейная регрессия — это способы определить, как статистические переменные связаны линейно. Однако эти два метода различаются. Коэффициент Пирсона — это мера силы и направления линейной связи между двумя переменными без предположения о причинно-следственной связи.Коэффициент Пирсона показывает корреляцию, а не причинно-следственную связь. Коэффициенты Пирсона варьируются от +1 до -1, где +1 представляет положительную корреляцию, -1 представляет отрицательную корреляцию, а 0 означает отсутствие связи.

Простая линейная регрессия описывает линейную связь между переменной ответа (обозначенной y) и объясняющей переменной (обозначенной x) с использованием статистической модели. Статистические модели используются для прогнозов.

Упростите линейную регрессию, вычислив корреляцию с помощью такого программного обеспечения, как Excel.

В финансах, например, корреляция используется в нескольких анализах, включая расчет стандартного отклонения портфеля. Поскольку на это уходит много времени, корреляцию лучше всего рассчитать с помощью такого программного обеспечения, как Excel. Корреляция объединяет статистические концепции, а именно дисперсию и стандартное отклонение. Дисперсия — это дисперсия переменной вокруг среднего значения, а стандартное отклонение — это квадратный корень из дисперсии.

Поиск корреляции с помощью Excel

Существует несколько методов расчета корреляции в Excel.Самый простой — получить два набора данных рядом и использовать встроенную формулу корреляции:

Investopedia.com

Если вы хотите создать корреляционную матрицу для ряда наборов данных, в Excel есть подключаемый модуль анализа данных, который находится на вкладке «Данные» в разделе «Анализ».

Выберите таблицу доходов. В этом случае наши столбцы имеют заголовки, поэтому мы хотим установить флажок «Ярлыки в первой строке», чтобы Excel обрабатывал их как заголовки. Затем вы можете выбрать вывод на том же листе или на новом листе.

Investopedia.com

Как только вы нажмете Enter, данные будут созданы автоматически. Вы можете добавить текст и условное форматирование, чтобы очистить результат.

Investopedia.com

Коэффициент линейной корреляции Часто задаваемые вопросы

Что такое коэффициент линейной корреляции?

Коэффициент линейной корреляции — это число, вычисленное на основе заданных данных, которое измеряет силу линейной связи между двумя переменными, x и y.

Как найти коэффициент линейной корреляции?

Корреляция объединяет несколько важных и связанных статистических концепций, а именно дисперсию и стандартное отклонение.2)]}} r = [n∑x2− (∑x) 2] [n∑y2− (∑y) 2)] n (∑xy) — (∑x) (∑y)

Вычисления слишком длинные, чтобы их можно было выполнять вручную, и программное обеспечение, такое как Excel или статистическая программа, является инструментами, используемыми для вычисления коэффициента.

Что означает линейная корреляция?

Коэффициент корреляции — это значение от -1 до +1. Коэффициент корреляции +1 указывает на идеальную положительную корреляцию. Когда переменная x увеличивается, переменная y увеличивается. Когда переменная x уменьшается, переменная y уменьшается.Коэффициент корреляции -1 указывает на абсолютную отрицательную корреляцию. По мере увеличения переменной x переменная z уменьшается. Когда переменная x уменьшается, переменная z увеличивается.

Как найти коэффициент линейной корреляции на калькуляторе?

Графический калькулятор необходим для расчета коэффициента корреляции. Следующие инструкции предоставлены Statology.

Шаг 1. Включите диагностику

Вам нужно будет сделать этот шаг на калькуляторе только один раз.После этого вы всегда можете начать с шага 2 ниже. Если вы этого не сделаете, r (коэффициент корреляции) не будет отображаться при запуске функции линейной регрессии.

• Нажмите [2nd], а затем [0], чтобы войти в каталог вашего калькулятора. Прокрутите, пока не увидите «DiagnosticsOn».
• Нажимайте клавишу ВВОД, пока на экране калькулятора не появится сообщение «Готово».

Это важно повторить: вам никогда не придется делать это снова, если вы не перезагрузите калькулятор.

Шаг 2: Введите данные

Введите свои данные в калькулятор, нажав [STAT], а затем выбрав 1: Edit.Чтобы упростить задачу, вы должны ввести все свои «данные x» в L1 и все «данные y» в L2.

Шаг 3: Рассчитайте!

После того, как вы введете свои данные, вы перейдете к [STAT], а затем к меню CALC вверху. Наконец, выберите 4: LinReg и нажмите Enter.

Вот и все! Готово! Теперь вы можете просто считать коэффициент корреляции прямо с экрана (его r). Помните, что если r не отображается на вашем калькуляторе, необходимо включить диагностику.Это то же самое место на калькуляторе, где вы найдете уравнение линейной регрессии и коэффициент детерминации.

Итог

Коэффициент линейной корреляции может быть полезен при определении взаимосвязи между инвестициями и рынком в целом или другими ценными бумагами. Его часто используют для прогнозирования доходности фондового рынка. Это статистическое измерение полезно во многих отношениях, особенно в финансовой отрасли.

Например, это может быть полезно для определения того, насколько хорошо взаимный фонд ведет себя по сравнению с его эталонным индексом, или его можно использовать для определения того, как взаимный фонд ведет себя по отношению к другому фонду или классу активов.Добавляя взаимный фонд с низкой или отрицательной корреляцией к существующему портфелю, можно получить преимущества диверсификации.

Страница не найдена

• Образование

  • Общий

    • Словарь
    • Экономика
    • Корпоративные финансы
    • Рот ИРА
    • Акции
    • Паевые инвестиционные фонды
    • ETFs
    • 401 (к)

  • Инвестирование / Торговля

    • Основы инвестирования
    • Фундаментальный анализ
    • Управление портфелем
    • Основы трейдинга
    • Технический анализ
    • Управление рисками
• Рынки

  • Новости

    • Новости компании
    • Новости рынков
    • Торговые новости
    • Политические новости
    • Тенденции

  • Популярные акции

    • Яблоко (AAPL)
    • Тесла (TSLA)
    • Amazon (AMZN)
    • AMD (AMD)
    • Facebook (FB)
    • Netflix (NFLX)
• Симулятор
• Ваши деньги

  • Личные финансы

    • Управление благосостоянием
    • Бюджетирование / экономия
    • Банковское дело
    • Кредитные карты
    • Домовладение
    • Пенсионное планирование
    • Налоги
    • Страхование

  • Обзоры и рейтинги

    • Лучшие онлайн-брокеры
    • Лучшие сберегательные счета
    • Лучшие домашние гарантии
    • Лучшие кредитные карты
    • Лучшие личные займы
    • Лучшие студенческие ссуды
    • Лучшее страхование жизни
    • Лучшее автострахование
• Советники

  • Ваша практика

    • Управление практикой
    • Непрерывное образование
    • Карьера финансового консультанта
    • Инвестопедия 100

  • Управление благосостоянием

    • Портфолио Строительство
    • Финансовое планирование
• Академия

  • Популярные курсы

    • Инвестирование для начинающих
    • Станьте дневным трейдером
    • Торговля для начинающих
    • Технический анализ

  • Курсы по темам

    • Все курсы
    • Курсы трейдинга
    • Курсы инвестирования
    • Финансовые профессиональные курсы

Представлять на рассмотрение

Извините, страница, которую вы ищете, недоступна.Вы можете найти то, что ищете, используя наше меню или параметры поиска.

дом

• О нас
• Условия эксплуатации
• Словарь
• Редакционная политика
• Рекламировать
• Новости
• Политика конфиденциальности
• Свяжитесь с нами
• Карьера
• Уведомление о конфиденциальности для Калифорнии

• #
• А
• B
• C
• D
• E
• F
• г
• ЧАС
• я
• J
• K
• L
• M
• N
• О
• п
• Q
• р
• S
• Т
• U
• V
• W
• Икс
• Y
• Z

Investopedia является частью издательской семьи Dotdash.

Страница не найдена

• Образование

  • Общий

    • Словарь
    • Экономика
    • Корпоративные финансы
    • Рот ИРА
    • Акции
    • Паевые инвестиционные фонды
    • ETFs
    • 401 (к)

  • Инвестирование / Торговля

    • Основы инвестирования
    • Фундаментальный анализ
    • Управление портфелем
    • Основы трейдинга
    • Технический анализ
    • Управление рисками
• Рынки

  • Новости

    • Новости компании
    • Новости рынков
    • Торговые новости
    • Политические новости
    • Тенденции

  • Популярные акции

    • Яблоко (AAPL)
    • Тесла (TSLA)
    • Amazon (AMZN)
    • AMD (AMD)
    • Facebook (FB)
    • Netflix (NFLX)
• Симулятор
• Ваши деньги

  • Личные финансы

    • Управление благосостоянием
    • Бюджетирование / экономия
    • Банковское дело
    • Кредитные карты
    • Домовладение
    • Пенсионное планирование
    • Налоги
    • Страхование

  • Обзоры и рейтинги

    • Лучшие онлайн-брокеры
    • Лучшие сберегательные счета
    • Лучшие домашние гарантии
    • Лучшие кредитные карты
    • Лучшие личные займы
    • Лучшие студенческие ссуды
    • Лучшее страхование жизни
    • Лучшее автострахование
• Советники

  • Ваша практика

    • Управление практикой
    • Непрерывное образование
    • Карьера финансового консультанта
    • Инвестопедия 100

  • Управление благосостоянием

    • Портфолио Строительство
    • Финансовое планирование
• Академия

  • Популярные курсы

    • Инвестирование для начинающих
    • Станьте дневным трейдером
    • Торговля для начинающих
    • Технический анализ

  • Курсы по темам

    • Все курсы
    • Курсы трейдинга
    • Курсы инвестирования
    • Финансовые профессиональные курсы

Представлять на рассмотрение

Извините, страница, которую вы ищете, недоступна.Вы можете найти то, что ищете, используя наше меню или параметры поиска.

дом

• О нас
• Условия эксплуатации
• Словарь
• Редакционная политика
• Рекламировать
• Новости
• Политика конфиденциальности
• Свяжитесь с нами
• Карьера
• Уведомление о конфиденциальности для Калифорнии

• #
• А
• B
• C
• D
• E
• F
• г
• ЧАС
• я
• J
• K
• L
• M
• N
• О
• п
• Q
• р
• S
• Т
• U
• V
• W
• Икс
• Y
• Z

Investopedia является частью издательской семьи Dotdash.

Определение положительной корреляции

Что такое положительная корреляция?

Положительная корреляция — это взаимосвязь между двумя переменными, в которой обе переменные движутся в тандеме, то есть в одном направлении. Положительная корреляция существует, когда одна переменная уменьшается, когда другая переменная уменьшается, или одна переменная увеличивается, а другая увеличивается.

Ключевые выводы

• Положительная корреляция — это взаимосвязь между двумя переменными, в которой обе переменные движутся в тандеме, то есть в одном направлении.
• Положительная корреляция существует, когда одна переменная уменьшается, когда другая переменная уменьшается, или одна переменная увеличивается, а другая увеличивается.
• Акции могут иметь определенную положительную корреляцию друг с другом или с рынком в целом.
• Beta — это обычная мера того, насколько цена отдельной акции коррелирует с более широким рынком, часто с использованием индекса S&P 500 в качестве ориентира.

Понимание положительной корреляции

Совершенно положительная корреляция означает, что в 100% случаев рассматриваемые переменные перемещаются вместе в одном и том же процентном соотношении и в одном и том же направлении.Можно увидеть положительную корреляцию между спросом на продукт и связанной с ним ценой. В ситуациях, когда доступное предложение остается неизменным, цена вырастет, если возрастет спрос.

В статистике идеальная положительная корреляция представлена ​​значением коэффициента корреляции +1,0, в то время как 0 указывает на отсутствие корреляции, а -1,0 указывает на идеальную обратную (отрицательную) корреляцию.

Кроме того, прибыли или убытки на определенных рынках могут привести к аналогичным движениям на связанных рынках.По мере роста цен на топливо растут и цены на авиабилеты. Поскольку для работы самолетов требуется топливо, увеличение этой стоимости часто перекладывается на потребителя, что приводит к положительной корреляции между ценами на топливо и ценами на авиабилеты.

Положительная корреляция не гарантирует роста или выгоды. Вместо этого он используется для обозначения любых двух или более переменных, которые вместе движутся в одном направлении, поэтому, когда одна увеличивается, увеличивается и другая. Хотя корреляция существует, причинно-следственная связь может отсутствовать.Таким образом, хотя некоторые переменные могут перемещаться вместе, может быть неизвестно, почему это движение происходит.

Корреляция — это форма зависимости, где сдвиг в одной переменной означает, что изменение вероятно в другой, или что определенные известные переменные дают определенные результаты. Общий пример можно увидеть в спросе на дополнительные продукты. Если спрос на автомобили вырастет, возрастет и спрос на автомобильные услуги, такие как шины. Увеличение в одной области влияет на дополнительные отрасли.

В некоторых ситуациях положительные психологические реакции могут вызвать положительные изменения в определенной области. Это можно продемонстрировать на финансовых рынках в случаях, когда общие положительные новости о компании приводят к повышению курса акций.

Корреляция против причинно-следственной связи

Корреляция между переменными не (обязательно) подразумевает причинно-следственную связь.

Положительная корреляция в финансах

Простой пример положительной корреляции включает использование процентного сберегательного счета с установленной процентной ставкой.Чем больше денег добавляется на счет, будь то новые депозиты или заработанные проценты, тем больше процентов может быть начислено. Точно так же повышение процентной ставки будет коррелировать с ростом генерируемых процентов, в то время как снижение процентной ставки вызывает уменьшение фактически начисленных процентов.

Инвесторы и аналитики также смотрят на то, как движения акций коррелируют друг с другом и с рынком в целом. У большинства акций есть корреляция между движениями цен друг друга где-то в середине диапазона, с коэффициентом 0, указывающим на отсутствие какой-либо связи между двумя ценными бумагами.Например, акции в онлайн-магазине, скорее всего, мало коррелируют с запасами шин и автомастерских, в то время как у двух аналогичных розничных компаний корреляция будет выше. Это связано с тем, что предприятия, которые ведут очень разные операции, будут производить разные продукты и услуги с использованием разных ресурсов.

С другой стороны, у обычного книжного ритейлера, вероятно, будет отрицательная корреляция с акциями Amazon.com, поскольку популярность онлайн-ритейлера обычно является плохой новостью для традиционных книжных магазинов.Акции популярного платежного процессора PayPal, вероятно, будут положительно коррелировать с запасами интернет-магазинов, пользующихся его услугами. Если акции eBay, Amazon и Best Buy вырастут из-за увеличения онлайн-доходов, вполне вероятно, что PayPal испытает такой же рост, поскольку его доход, связанный с комиссионными сборами, возрастет, а положительные отчеты о прибылях будут поощрять инвесторов.

Бета и корреляция

Бета — это обычная мера того, насколько цена отдельной акции коррелирует с более широким рынком, часто с использованием индекса S&P 500 в качестве ориентира.Если у акции есть бета 1.0, это означает, что ее ценовая активность сильно коррелирована с рынком. Акция с бета-коэффициентом 1.0 имеет систематический риск, но расчет бета-версии не может обнаружить какой-либо несистематический риск. Добавление акций в портфель с бета-коэффициентом 1.0 не увеличивает риск для портфеля, но также не увеличивает вероятность того, что портфель обеспечит избыточную доходность.

Бета меньше 1,0 означает, что ценная бумага теоретически менее волатильна, чем рынок, а это означает, что портфель менее рискован с включенными акциями, чем без них.Например, акции коммунальных предприятий часто имеют низкие бета-ставки, потому что они, как правило, движутся медленнее, чем среднерыночные.

Бета, превышающая 1,0, указывает на то, что цена ценной бумаги теоретически более волатильна, чем рыночная. Например, если бета акции составляет 1,2, предполагается, что она на 20% более волатильна, чем рынок. Акции технологических компаний и компании с малой капитализацией, как правило, имеют более высокие значения бета, чем рыночный эталон. Это указывает на то, что добавление акций в портфель увеличит риск портфеля, но также увеличит его ожидаемую доходность.

У некоторых акций даже есть отрицательные беты. Бета -1,0 означает, что акции обратно коррелируют с рыночным эталоном, как если бы они были противоположным, зеркальным отображением тенденций эталонного теста. Опционы пут или обратные ETF предназначены для отрицательных бета-ставок, но есть несколько отраслевых групп, например, золотодобытчики, где отрицательная бета также является обычным явлением.

Положительная корреляция против обратной корреляции

В статистике положительная корреляция описывает взаимосвязь между двумя переменными, которые изменяются вместе, а обратная корреляция описывает взаимосвязь между двумя переменными, которые изменяются в противоположных направлениях.Обратную корреляцию иногда называют отрицательной корреляцией. Примеры положительной корреляции встречаются в повседневной жизни большинства людей. Например, чем больше часов работает сотрудник, тем больше будет его зарплата в конце недели. Чем больше денег тратится на рекламу, тем больше клиентов покупают у компании.

Обратные корреляции описывают два фактора, которые колеблются относительно друг друга. Примеры включают уменьшение баланса в банке по сравнению с увеличением привычки тратить и сокращение расхода бензина по сравнению с увеличением средней скорости движения.Одним из примеров обратной корреляции в мире инвестиций является связь между акциями и облигациями. По мере роста цен на акции рынок облигаций имеет тенденцию к снижению, так же как рынок облигаций чувствует себя хорошо, когда акции не работают.

Важно понимать, что корреляция не обязательно подразумевает причинно-следственную связь. Переменные A и B могут расти и падать вместе, или A может расти, когда B падает, но не всегда верно, что рост одного фактора напрямую влияет на рост или падение другого.И то, и другое может быть вызвано лежащим в основе третьим фактором, например ценами на сырьевые товары, или очевидная взаимосвязь между переменными может быть совпадением.

Например, количество людей, подключенных к Интернету, росло с момента его появления, и цена на нефть в целом за тот же период росла. Это положительная корреляция, но эти два фактора почти наверняка не имеют значимого отношения. То, что как количество пользователей Интернета, так и цены на нефть увеличились, можно объяснить третьим фактором, а именно общим ростом в связи с прошедшим временем.

Часто задаваемые вопросы

Что такое пример положительной корреляции?

Примером положительной корреляции является процентный сберегательный счет с установленной процентной ставкой. Чем больше денег добавляется на счет, будь то новые депозиты или заработанные проценты, тем больше процентов может быть начислено. Точно так же повышение процентной ставки будет коррелировать с ростом генерируемых процентов, в то время как снижение процентной ставки вызывает уменьшение фактически начисленных процентов.

Какая связь между бета и положительной корреляцией?

Бета — это обычная мера того, насколько цена отдельной акции коррелирует с более широким рынком, часто с использованием индекса S&P 500 в качестве ориентира. Любое значение бета выше нуля подразумевает некоторую степень положительной корреляции. Если у акции есть бета 1.0, это означает, что ее ценовая активность сильно коррелирована с рынком. Рынок и акции растут или падают пропорционально. Бета меньше 1.0 означает, что акция идет вверх или вниз меньше, чем рынок.Бета, превышающая 1.0, указывает на то, что акция будет расти или падать больше, чем рынок.

Что такое обратная корреляция?

В статистике положительная корреляция описывает взаимосвязь между двумя переменными, которые изменяются вместе, а обратная корреляция описывает взаимосвязь между двумя переменными, которые изменяются в противоположных направлениях. Обратную корреляцию иногда называют отрицательной корреляцией. В области инвестирования отрицательные бета-версии показывают обратную корреляцию.Акция с бета ниже нуля будет двигаться в направлении, противоположном рыночному ориентиру. Бета, равная -1,0, означает, что движение акций является зеркальным отражением тенденций теста. Опционы пут или обратные ETF предназначены для отрицательных бета-ставок, но есть несколько отраслевых групп, например, золотодобытчики, где отрицательная бета также является обычным явлением.

Подразумевает ли корреляция причинно-следственную связь?

Корреляция не обязательно подразумевает причинно-следственную связь. На самом деле было бы ошибкой предполагать обратное.Переменные A и B могут расти и падать вместе, или A может расти, когда B падает, но не всегда верно, что рост одного фактора напрямую влияет на рост или падение другого. Оба могут быть вызваны лежащим в основе третьим фактором или очевидная взаимосвязь между переменными может быть совпадением.

Определения корреляции, примеры и интерпретация

Определения корреляции, примеры и интерпретация

Д-р Саул МакЛеод, обновлено 2020 г.

---

Корреляция означает ассоциацию — точнее, это мера степени взаимосвязи двух переменных.Есть три возможных результата корреляционного исследования: положительная корреляция, отрицательная корреляция и отсутствие корреляции.

Положительная корреляция — это связь между двумя переменными, в которой обе переменные движутся в одном направлении. Следовательно, когда одна переменная увеличивается вместе с другой, или одна переменная уменьшается, а другая уменьшается. Примером положительной корреляции может быть рост и вес. Более высокие люди обычно тяжелее.

Отрицательная корреляция — это взаимосвязь между двумя переменными, в которой увеличение одной переменной связано с уменьшением другой.Примером отрицательной корреляции может служить высота над уровнем моря и температура. По мере подъема на гору (увеличение высоты) становится холоднее (температура снижается).

нулевая корреляция существует, когда нет связи между двумя переменными. Например, нет никакой связи между количеством выпитого чая и уровнем интеллекта.

Диаграммы рассеяния

Корреляцию можно выразить визуально. Это делается путем рисования диаграммы рассеяния (также известной как диаграмма рассеяния, диаграмма рассеяния, диаграмма рассеяния или диаграмма рассеяния).

Диаграмма рассеяния — это графический дисплей, который показывает отношения или связи между двумя числовыми переменными (или сопеременными), которые представлены в виде точек (или точек) для каждой пары оценок.

Диаграмма рассеяния показывает силу и направление корреляции между переменными.

Когда вы рисуете диаграмму рассеяния, не имеет значения, какая переменная идет по оси x, а какая — по оси y.

Помните, что в корреляциях мы всегда имеем дело с парными оценками, поэтому значения двух переменных, взятых вместе, будут использоваться для построения диаграммы.

Определите, какая переменная будет идти по каждой оси, а затем просто поставьте крестик в точке, где 2 значения совпадают.

Некоторые виды использования корреляций

Некоторые виды использования корреляций

Прогноз

• Если существует связь между двумя переменными, мы можем делать прогнозы относительно друг друга.

Срок действия

• Одновременное действие (корреляция между новым показателем и установленным показателем).

Надежность

• Тестирование-повторное тестирование надежности (согласованные измерения).
• Надежность между экспертами (согласны ли наблюдатели).

Проверка теории

---

Коэффициенты корреляции: определение силы корреляции

Коэффициенты корреляции: определение силы корреляции

Вместо построения диаграммы рассеяния корреляцию можно выразить численно в виде коэффициента в диапазоне от -1 до +1.При работе с непрерывными переменными следует использовать коэффициент корреляции r Пирсона.

Коэффициент корреляции ( r ) указывает степень, в которой пары чисел для этих двух переменных лежат на прямой линии. Значения больше нуля указывают на положительную корреляцию, а значения ниже нуля указывают на отрицательную корреляцию.

Корреляция –1 указывает на идеальную отрицательную корреляцию, означающую, что по мере того, как одна переменная растет, другая уменьшается.Корреляция +1 указывает на идеальную положительную корреляцию, что означает, что по мере увеличения одной переменной растет другая.

Нет правила для определения того, какой размер корреляции считается сильной, умеренной или слабой. Интерпретация коэффициента зависит от темы исследования.

При изучении вещей, которые трудно измерить, следует ожидать, что коэффициенты корреляции будут ниже (например, выше 0,4 будет относительно сильным). Когда мы изучаем вещи, которые легче измерить, например социально-экономический статус, мы ожидаем более высоких корреляций (например,г. выше 0,75, чтобы быть относительно сильным).)

В таких исследованиях мы редко видим корреляции выше 0,6. Для такого рода данных мы обычно считаем корреляцию выше 0,4 относительно сильной; корреляции между 0,2 и 0,4 являются умеренными, а корреляции ниже 0,2 считаются слабыми.

Когда мы изучаем вещи, которые легче поддаются подсчету, мы ожидаем более высоких корреляций. Например, для демографических данных мы обычно считаем корреляцию выше 0,75 относительно сильной; корреляции между 0.45 и 0,75 являются умеренными, а значения ниже 0,45 считаются слабыми.

---

Корреляция против причинности

Корреляция против причинности

Причинность означает, что одна переменная (часто называемая предиктивной переменной или независимой переменной) вызывает другую (часто называемую переменной результата или зависимой переменной).

Можно провести эксперименты для установления причинно-следственной связи. Эксперимент изолирует независимую переменную и манипулирует ею, чтобы наблюдать ее влияние на зависимую переменную, и контролирует среду, чтобы можно было исключить посторонние переменные.

Корреляция между переменными, однако, не означает автоматически, что изменение одной переменной является причиной изменения значений другой переменной. Корреляция показывает, только если существует связь между переменными.

Корреляция не всегда доказывает причинно-следственную связь, поскольку может быть задействована третья переменная. Например, пребывание пациента в больнице коррелирует со смертью, но это не означает, что одно событие вызывает другое, поскольку может быть задействована третья переменная (например, диета, уровень упражнений).

Резюме

«Корреляция не является причинно-следственной связью» означает, что наличие взаимосвязи между двумя переменными не обязательно означает, что одна вызывает другую.

Корреляция определяет переменные и ищет связь между ними. Эксперимент проверяет влияние, которое независимая переменная оказывает на зависимую переменную, но корреляция ищет взаимосвязь между двумя переменными.

Это означает, что эксперимент может предсказать причину и следствие (причинно-следственную связь), но корреляция может предсказать только взаимосвязь, поскольку может быть задействована другая посторонняя переменная, о которой она не знает.

---

Сила корреляций

Сила корреляций

1 . Корреляция позволяет исследователю исследовать встречающиеся в природе переменные, которые, возможно, неэтично или непрактично проверять экспериментально. Например, было бы неэтично проводить эксперимент по поводу того, вызывает ли курение рак легких.


2 . Корреляция позволяет исследователю ясно и легко увидеть, существует ли связь между переменными.Затем это можно отобразить в графической форме.

Ограничения корреляций

Ограничения корреляций

1 . Корреляция не подразумевает и не может подразумевать причинно-следственную связь. Даже если между двумя переменными существует очень сильная связь, мы не можем предположить, что одна вызывает другую.

Например, предположим, что мы обнаружили положительную корреляцию между просмотром насилия по телевизору и агрессивным поведением в подростковом возрасте. Возможно, причиной обоих этих факторов является третья (посторонняя) переменная — скажем, например, взросление в доме с насилием — и то, что наблюдение за Т.В. и агрессивное поведение являются результатом этого.


2 . Корреляция не позволяет нам выходить за рамки предоставленных данных. Например, предположим, что была обнаружена связь между временем, затраченным на домашнее задание (от 1/2 часа до 3 часов), и количеством G.C.S.E. проходит (с 1 по 6). Было бы неправомерно делать из этого вывод, что, потратив 6 часов на домашнее задание, можно получить 12 G.C.S.E. проходит.

Как ссылаться на эту статью:

Как ссылаться на эту статью:

McLeod, S.А. (2018, 14 января). Корреляционные определения, примеры и интерпретация . Просто психология. https://www.simplypsychology.org/correlation.html

сообщить об этом объявлении

корреляция

корреляция

корреляция

Корреляционный анализ измеряет, как две переменные связаны между собой. Коэффициент корреляции (r) — это статистика, которая сообщает вам силу и направление этой связи. Он выражается как положительное или отрицательное число от -1 до 1.Значение числа указывает на силу взаимосвязи:

• r = 0 означает отсутствие корреляции
• r = 1 означает идеальную положительную корреляцию
• r = -1 означает идеальную отрицательную корреляцию

Знак коэффициента корреляции указывает, является ли направление взаимосвязи положительным (прямым) или отрицательным (обратным).

Переменные, имеющие прямую связь (положительную корреляцию), увеличиваются вместе и уменьшаются вместе.

В обратной зависимости (отрицательная корреляция) одна переменная увеличивается, а другая уменьшается.

В то время как знак указывает, как одна переменная изменяется по отношению к другой переменной, величина числа указывает на силу взаимосвязи.

Важно помнить, что, хотя коэффициенты корреляции могут использоваться для прогнозирования (т. Е. Если мы знаем значение одной переменной и корреляцию, мы можем предсказать, каким будет значение второй переменной), они НЕ МОГУТ использоваться для причинно-следственной связи (т.е. .е. мы не можем сказать, что одна переменная вызывает другую).

Пример

Предположим, вы читаете исследование экзаменов Regents. Исследователь хотел знать, связана ли успеваемость в начальной школе с оценками на экзаменах по регентсексу. Он провел корреляционный анализ успеваемости в начальной школе и оценки Regentsexam и обнаружил, что r = 0,75 в своем исследовании. Это говорит вам о двух вещах:

1. r положительно, поэтому успеваемость в начальной школе и оценка на экзамене Риджентс имеют тенденцию увеличиваться и уменьшаться одновременно.
2. r довольно близко к 1, поэтому прямая связь довольно сильная.

Если существует корреляция между двумя переменными, это НЕ означает, что одна переменная вызывает другую. Причинно-следственная связь и корреляция — две очень разные вещи.

Два коэффициента корреляции, которые чаще всего встречаются в литературе, — это момент произведения Пирсона и сумма рангов Спирмана.

11. Корреляция и регрессия

Слово корреляция используется в повседневной жизни для обозначения некоторой формы ассоциации.Можно сказать, что мы заметили корреляцию между туманными днями и приступами хрипов. Однако в статистических терминах мы используем корреляцию для обозначения связи между двумя количественными переменными. Мы также предполагаем, что связь является линейной, что одна переменная увеличивает или уменьшает фиксированную величину для увеличения или уменьшения единицы другой. Другой метод, который часто используется в этих обстоятельствах, — это регрессия, которая включает в себя оценку наилучшей прямой линии для резюмирования ассоциации.

Коэффициент корреляции

Степень ассоциации измеряется коэффициентом корреляции, обозначаемым r. Иногда его называют коэффициентом корреляции Пирсона по имени автора, и он является мерой линейной связи. Если для выражения взаимосвязи необходима изогнутая линия, необходимо использовать другие, более сложные меры корреляции.

Коэффициент корреляции измеряется по шкале от + 1 до 0 до -1. Полная корреляция между двумя переменными выражается либо + 1, либо -1.Когда одна переменная увеличивается, а другая увеличивается, корреляция положительная; когда одно уменьшается, а другое увеличивается, оно отрицательно. Полное отсутствие корреляции обозначается цифрой 0. Рисунок 11.1 дает некоторые графические представления корреляции.

Рисунок 11.1 Иллюстрированная корреляция.

Просмотр данных: диаграммы рассеяния

Когда исследователь собрал две серии наблюдений и хочет выяснить, существует ли между ними связь, он или она должны сначала построить диаграмму рассеяния.Вертикальная шкала представляет один набор измерений, а горизонтальная шкала — другой. Если один набор наблюдений состоит из экспериментальных результатов, а другой — из временной шкалы или какой-либо наблюдаемой классификации, обычно результаты экспериментов наносят на вертикальную ось. Они представляют собой то, что называется «зависимой переменной». «Независимая переменная», такая как время или высота или какая-либо другая наблюдаемая классификация, измеряется по горизонтальной оси или базовой линии.

Слова «независимый» и «зависимый» могут озадачить новичка, потому что иногда непонятно, что от чего зависит.Эта путаница — триумф здравого смысла над вводящей в заблуждение терминологией, потому что часто каждая переменная зависит от какой-то третьей переменной, которая может или не может быть упомянута. Разумно, например, полагать, что рост детей зависит от возраста, а не наоборот, но учитывать положительную корреляцию между средним выходом смол и выходом никотина для определенных марок сигарет. в смоле: оба эти фактора изменяются параллельно с некоторыми другими факторами или факторами в составе сигарет.Урожайность одного не кажется «зависимым» от другого в том смысле, что в среднем рост ребенка зависит от его возраста. В таких случаях часто не имеет значения, какой масштаб на какой оси диаграммы разброса. Однако, если намерение состоит в том, чтобы сделать выводы об одной переменной из другой, наблюдения, из которых должны быть сделаны выводы, обычно помещаются в базовую линию. В качестве еще одного примера, график ежемесячной смертности от сердечных заболеваний по сравнению с ежемесячными продажами мороженого покажет отрицательную связь.Однако вряд ли поедание мороженого защитит от сердечных заболеваний! Просто уровень смертности от сердечных заболеваний обратно пропорционален, а потребление мороженого положительно связано с третьим фактором, а именно температурой окружающей среды.

Расчет коэффициента корреляции

Педиатрический регистратор измерил анатомическое мертвое пространство легких (в мл) и рост (в см) у 15 детей. Данные приведены в таблице 11.1 и диаграмме рассеяния, показанной на рисунке 11.2 Каждая точка представляет одного ребенка и помещается в точку, соответствующую измерению высоты (горизонтальная ось) и мертвого пространства (вертикальная ось). Регистратор теперь проверяет узор, чтобы определить, кажется ли вероятным, что область, покрытая точками, находится в центре прямой линии или нужна изогнутая линия. В этом случае педиатр решает, что прямая линия может адекватно описать общую тенденцию точек. Поэтому его следующим шагом будет вычисление коэффициента корреляции.

При построении диаграммы рассеяния (рисунок 11.2), чтобы показать рост и анатомические мертвые зоны легких у 15 детей, педиатр указал цифры, как в столбцах (1), (2) и (3) таблицы 11.1. Полезно расположить наблюдения в последовательном порядке независимой переменной, когда одна из двух переменных явно идентифицируется как независимая. Соответствующие цифры для зависимой переменной затем могут быть исследованы в отношении возрастающего ряда для независимой переменной.Таким образом мы получаем ту же картину, но в числовой форме, как показано на диаграмме разброса.

Рис. 11.2 Диаграмма разброса зависимости между ростом и анатомическим мертвым пространством легких у 15 детей.

Расчет коэффициента корреляции осуществляется следующим образом: x представляет значения независимой переменной (в данном случае высота), а y представляет значения зависимой переменной (в данном случае анатомическое мертвое пространство). Используемая формула:

, которая может быть представлена ​​как:

Процедура калькулятора

Найдите среднее значение и стандартное отклонение x, как описано в разделе Найдите среднее и стандартное отклонение y:

Вычтите 1 из n и умножьте на SD (x) и SD (y), (n — 1) SD (x) SD (y)

Это дает нам знаменатель формулы.(Не забудьте выйти из режима «Stat».)

Для числителя умножьте каждое значение x на соответствующее значение y, сложите эти значения и сохраните их.

110 x 44 = Min

116 x 31 = M +

и т. Д.

Сохраняется в памяти. Вычтите

MR — 15 x 144,6 x 66,93 (5426,6)

Наконец, разделите числитель на знаменатель.

r = 5426,6 / 6412,0609 = 0,846.

Коэффициент корреляции 0,846 указывает на сильную положительную корреляцию между размером легочного анатомического мертвого пространства и ростом ребенка.Но при интерпретации корреляции важно помнить, что корреляция не является причинно-следственной связью. Причинная связь между двумя коррелированными переменными может быть, а может и не быть. Причем, если есть связь, она может быть косвенной.

Часть вариации одной из переменных (измеряемая по ее дисперсии) может рассматриваться как обусловленная ее взаимосвязью с другой переменной, а другая часть — как следствие неопределенных (часто «случайных») причин. Часть, обусловленная зависимостью одной переменной от другой, измеряется Ро.Для этих данных Rho = 0,716, поэтому мы можем сказать, что 72% различий между детьми в размере анатомического мертвого пространства объясняется ростом ребенка. Если мы хотим обозначить силу связи, для абсолютных значений r 0-0,19 считается очень слабым, 0,2-0,39 — слабым, 0,40-0,59 — умеренным, 0,6-0,79 — сильным и 0,8-1 — очень сильным. корреляция, но это довольно произвольные пределы, и следует учитывать контекст результатов.

Тест значимости

Чтобы проверить, очевидна ли связь и могла ли она возникнуть случайно, используйте тест t в следующем расчете:

вводится при n — 2 степенях свободы.

Например, коэффициент корреляции для этих данных составил 0,846.

Количество пар наблюдений было 15. Применяя уравнение 11.1, мы имеем:

Вводя таблицу B при 15-2 = 13 степенях свободы, мы находим, что при t = 5,72, P <0,001, поэтому коэффициент корреляции может быть учтен. как очень значительный. Таким образом (как сразу видно из диаграммы рассеяния) мы имеем очень сильную корреляцию между мертвым пространством и высотой, которая вряд ли возникла случайно.

Предположения, управляющие этим тестом:

1. Что обе переменные правдоподобно Нормально распределены.
2. Что между ними существует линейная зависимость.
3. Нулевая гипотеза состоит в том, что между ними нет связи.

Тест не следует использовать для сравнения двух методов измерения одной и той же величины, например, двух методов измерения пиковой скорости выдоха. Его использование таким образом кажется распространенной ошибкой, поскольку значительный результат интерпретируется как означающий, что один метод эквивалентен другому.Причины широко обсуждались (2), но стоит напомнить, что значительный результат мало что говорит нам о прочности отношений. Из формулы должно быть ясно, что даже при очень слабой связи (скажем, r = 0,1) мы получим значительный результат с достаточно большой выборкой (скажем, n больше 1000).

Ранговая корреляция Спирмена

График данных может выявить отдаленные точки далеко от основной части данных, что может ненадлежащим образом повлиять на расчет коэффициента корреляции.Альтернативно переменные могут быть количественными дискретными, такими как количество родинок, или упорядоченными категориальными, такими как оценка боли. Непараметрическая процедура по Спирмену заключается в замене наблюдений их рангами при вычислении коэффициента корреляции.

Это приводит к простой формуле для ранговой корреляции Спирмена, Rho.

где d — разница в рангах двух переменных для данного человека. Таким образом, мы можем вывести таблицу 11.2 из данных в таблице 11.1.

Отсюда получаем, что

В этом случае значение очень близко к значению коэффициента корреляции Пирсона. Для n> 10 коэффициент ранговой корреляции Спирмена можно проверить на значимость с помощью t-критерия, приведенного ранее.

Уравнение регрессии

Корреляция описывает силу связи между двумя переменными и является полностью симметричной, корреляция между A и B такая же, как корреляция между B и A. Однако, если две переменные связаны, это означает что когда один изменяется на определенную величину, другой изменяется в среднем на определенную величину.Например, у детей, описанных ранее, больший рост в среднем связан с большим анатомическим мертвым пространством. Если y представляет зависимую переменную, а x — независимую переменную, эта связь описывается как регрессия y по x.

Взаимосвязь может быть представлена ​​простым уравнением, называемым уравнением регрессии. В этом контексте «регрессия» (термин — историческая аномалия) просто означает, что среднее значение y является «функцией» от x, то есть изменяется вместе с x.

Уравнение регрессии, показывающее, насколько изменяется y при любом заданном изменении x, можно использовать для построения линии регрессии на диаграмме рассеяния, и в простейшем случае предполагается, что это прямая линия. Направление наклона линии зависит от того, положительная или отрицательная корреляция. Когда два набора наблюдений увеличиваются или уменьшаются вместе (положительно), линия наклоняется вверх слева направо; когда один набор уменьшается, а другой увеличивается, линия наклоняется вниз слева направо.Поскольку линия должна быть прямой, она, вероятно, пройдет через несколько точек, если вообще пройдет. Учитывая, что ассоциация хорошо описывается прямой линией, мы должны определить две особенности линии, если мы хотим правильно разместить ее на диаграмме. Первый из них — это расстояние от базовой линии; второй — его наклон. Они выражаются в следующем уравнении регрессии :

С помощью этого уравнения мы можем найти ряд значений переменной, которые соответствуют каждому из ряда значений x, независимой переменной.Параметры α и β следует оценивать по данным. Параметр обозначает расстояние над базовой линией, на котором линия регрессии пересекает вертикальную ось (y); то есть, когда y = 0. Параметр β (коэффициент регрессии ) означает величину, на которую необходимо умножить изменение x, чтобы получить соответствующее среднее изменение y, или величину y, изменяющуюся на единицу увеличения x. Таким образом, он представляет собой степень наклона линии вверх или вниз. Уравнение регрессии часто более полезно, чем коэффициент корреляции.Это позволяет нам предсказать y по x и дает нам лучшее представление о взаимосвязи между двумя переменными. Если для конкретного значения x, x i уравнение регрессии предсказывает соответствие значения y, ошибка прогнозирования равна. Легко показать, что любая прямая линия, проходящая через средние значения x и y, даст полную ошибку предсказания, равную нулю, потому что положительные и отрицательные члены в точности сокращаются. Чтобы удалить отрицательные знаки, мы возводим в квадрат разности и выбираем уравнение регрессии, чтобы минимизировать сумму квадратов ошибок прогнозирования. Мы обозначаем выборочные оценки альфа и бета буквами a и b.Можно показать, что одна прямая линия, которая минимизирует, оценка методом наименьших квадратов, дается

и

, можно показать, что

, который используется, потому что мы вычислили все компоненты уравнения (11.2) в вычислении коэффициента корреляции.

Расчет коэффициента корреляции по данным в таблице 11.2 дал следующее:

Применяя эти цифры к формулам для коэффициентов регрессии, мы имеем:

Следовательно, в этом случае уравнение регрессии y на x становится

Это означает, что в среднем на каждое увеличение роста на 1 см увеличение анатомического мертвого пространства составляет 1.033 мл по всему диапазону измерений составила .

Линия, представляющая уравнение, наложена на диаграмму разброса данных на рисунке 11.2. Чтобы нарисовать линию, нужно взять три значения x, одно в левой части диаграммы рассеяния, одно в середине и одно справа, и подставить их в уравнение следующим образом:

Если x = 110 , y = (1,033 x 110) — 82,4 = 31,2

Если x = 140, y = (1,033 x 140) — 82,4 = 62,2

Если x = 170, y = (1.033 x 170) — 82,4 = 93,2

Хотя двух точек достаточно для определения линии, три лучше в качестве проверки. Поместив их на диаграмму разброса, мы просто проводим через них линию.

Рисунок 11.3 Линия регрессии, проведенная на диаграмме рассеяния, связывающая рост и анатомическое мертвое пространство легких у 15 детей

Стандартная ошибка наклона SE (b) определяется как:

, где — остаточное стандартное отклонение, определяемое как:

Это может будет показано, что алгебраически оно равно

. Мы уже должны передать все члены в этом выражении.Таким образом получается квадратный корень из. Знаменатель (11,3) равен 72,4680. Таким образом, SE (b) = 13,08445 / 72,4680 = 0,18055.

Мы можем проверить, существенно ли отличается наклон от нуля:

t = b / SE (b) = 1,033 / 0,18055 = 5,72.

Опять же, это n — 2 = 15 — 2 = 13 степеней свободы. Предположения, управляющие этим тестом:

1. Что ошибки предсказания приблизительно нормально распределены. Обратите внимание, это не означает, что переменные x или y должны быть нормально распределены.
2. Что отношения между двумя переменными линейны.
3. То, что разброс точек вокруг линии приблизительно постоянен — ​​мы не хотели бы, чтобы изменчивость зависимой переменной увеличивалась по мере увеличения независимой переменной. В этом случае попробуйте логарифмировать переменные x и y.

Обратите внимание, что критерий значимости наклона дает точно такое же значение P, что и критерий значимости коэффициента корреляции.Хотя эти два теста производятся по-разному, они алгебраически эквивалентны, что имеет интуитивный смысл.

Мы можем получить 95% доверительный интервал для b из

, где tstatistic from имеет 13 степеней свободы и равен 2,160.

Таким образом, 95% доверительный интервал составляет

от 1,033 — 2,160 x 0,18055 до 1,033 + 2,160 x 0,18055 = от 0,643 до 1,422.

Линии регрессии дают нам полезную информацию о данных, из которых они собираются. Они показывают, как одна переменная в среднем меняется с другой, и их можно использовать, чтобы узнать, какой может быть одна переменная, если мы знаем другую — при условии, что мы зададим этот вопрос в рамках диаграммы разброса.Спроектировать линию на любом конце — для экстраполяции — всегда рискованно, потому что отношения между x и y могут измениться или может существовать какая-то точка отсечения. Например, можно провести линию регрессии, связывающую хронологический возраст некоторых детей с их костным возрастом, и это может быть прямая линия, скажем, между возрастом от 5 до 10 лет, но спроецировать ее на возраст 30 лет. явно приведет к ошибке. Компьютерные пакеты часто производят перехват из уравнения регрессии без предупреждения, что это может быть совершенно бессмысленным.Рассмотрим регресс артериального давления по сравнению с возрастом у мужчин среднего возраста. Коэффициент регрессии часто бывает положительным, что свидетельствует о повышении артериального давления с возрастом. Перехват часто близок к нулю, но было бы неправильно делать вывод, что это надежная оценка артериального давления у новорожденных мальчиков мужского пола!

Дополнительные методы

Возможно использование нескольких независимых переменных — в этом случае метод известен как множественная регрессия. (3,4) Это наиболее универсальный из статистических методов, который может использоваться во многих ситуациях.Примеры включают: чтобы учесть более одного предиктора, возраст, а также рост в приведенном выше примере; чтобы учесть ковариаты — в клиническом исследовании зависимой переменной может быть результат после лечения, первая независимая переменная может быть бинарной, 0 для плацебо и 1 для активного лечения, а вторая независимая переменная может быть исходной переменной, измеренной до лечения, но может повлиять на результат.

Общие вопросы

Если две переменные взаимосвязаны, связаны ли они причинно?

Часто путают корреляцию и причинную связь.Все, что показывает корреляция, — это то, что две переменные связаны. Может быть третья переменная, смешивающая переменная, связанная с ними обоими. Например, ежемесячные смерти от утопления и ежемесячные продажи мороженого положительно коррелируют, но никто не скажет, что эта связь была причинной!

Как проверить допущения, лежащие в основе линейной регрессии?

Во-первых, всегда смотрите на диаграмму рассеяния и спрашивайте, линейна ли она? Получив уравнение регрессии, вычислите остатки. Гистограмма покажет отклонения от нормальности, а график зависимости покажет, увеличиваются ли остатки в размере по мере увеличения.

Ссылки

1. Russell MAH, Cole PY, Idle MS, Adams L. Выходы окиси углерода в сигаретах и ​​их связь с выходом никотина и типом фильтра. BMJ 1975; 3: 713.
2. Бланд Дж. М., Альтман Д. Г.. Статистические методы оценки соответствия между двумя методами клинического измерения. Lancet 1986; я: 307-10.
3. Браун Р.А., Свансон-Бек Дж. Медицинская статистика персональных компьютеров, 2-е изд. Лондон: Издательская группа BMJ, 1993.
4. Армитаж П., Берри Г. В: Статистические методы в медицинских исследованиях, 3-е изд.Оксфорд: Научные публикации Блэквелла, 1994: 312-41.

Упражнения

11.1 Было проведено исследование посещаемости больницы людей в 16 различных географических районах за фиксированный период времени. Расстояние центра от больницы каждого района измерялось в милях. Результаты были следующими:

(1) 21%, 6,8; (2) 12%, 10,3; (3) 30%, 1,7; (4) 8%, 14,2; (5) 10%, 8,8; (6) 26%, 5,8; (7) 42%, 2,1; (8) 31%, 3,3; (9) 21%, 4,3; (10) 15%, 9.0; (11) 19%, 3,2; (12) 6%, 12,7; (13) 18%, 8,2; (14) 12%, 7,0; (15) 23%, 5,1; (16) 34%, 4,1.

Каков коэффициент корреляции между посещаемостью и средней удаленностью географической области?

11.2 Найдите ранговую корреляцию Спирмена для данных, приведенных в 11.1.

11.3 Если значения x из данных в 11.1 представляют собой среднее расстояние от области до больницы, а значения y представляют уровень посещаемости, каково уравнение для регрессии y на x? Что это означает?

11.