Положительная корреляция отрицательная корреляция: Корреляция полная положительная — Энциклопедия по экономике

Корреляция полная положительная — Энциклопедия по экономике

Коэффициент корреляции может изменяться в диапазоне 1,0. Коэффициент +1,0 (полная положительная корреляция) означает, что изменения независимой переменной приведут к идентичным изменениям зависимой (т.е. изменение индикатора вызовет такое же изменение цены бумаги). Коэффициент 1,0 (полная отрицательная корреляция) означает, что изменения независимой переменной вызовут идентичные изменения зависимой, но в противоположном направлении. Коэффициент, равный нулю, свидетельствует об отсутствии связи между переменными, то есть изменения независимой переменной не влияют на изменения зависимой.  [c.104]

Как мы уже знаем (см. главу 2), добавление рыночных систем увеличивает среднее геометрическое по портфелю в целом. Однако возникает проблема каждая следующая рыночная система вносит все меньший и меньший вклад в среднее геометрическое и все больше ухудшает его, понижая эффективность из-за одновременных, а не последовательных результатов. Поэтому не следует торговать слишком большим числом рыночных систем. Более того, реальное применение теоретически оптимальных портфелей осложняется из-за залоговых требований. Другими словами, вам лучше торговать 3 рыночными системами при полном оптимальном f, чем 300 рыночными системами при значительно пониженных уровнях, согласно уравнению (8.08). Скорее всего вы придете к выводу, что оптимальное число рыночных систем для торговли должно быть невелико. Особенно это обстоятельство важно, когда у вас много ордеров к исполнению и увеличивается вероятность ошибок. Если одна или несколько рыночных систем в портфеле имеют оптимальные веса больше единицы, может возникнуть еще одна проблема. Рассмотрим рыночную систему с оптимальным f=0,8 и наибольшим проигрышем, составляющим 4000 долларов. Для этой рыночной системы f = 5000 долларов. Давайте предположим, что оптимальный вес данного компонента в портфеле равен 1,25, поэтому вы будете торговать одной единицей компонента на каждые 4000 долларов ( 5000/1,25) баланса счета. Как только компонент столкнется с наибольшим проигрышем, весь активный баланс на счете будет обнулен, если прибылей в других рыночных системах не хватит для сохранения активного баланса. Рассмотренная проблема наиболее актуальна для систем, которые редко генерируют сделки. Если бы у нас были две рыночные системы с отрицательной корреляцией и положительным ожиданием, необходимо было бы открывать бесконечное количество контрактов на рынке. Когда один из компонентов проигрывает, другой выигрывает равную или большую сумму. Таким образом, мы получаем прибыль в каждой игре, однако только в том случае, когда рыночные системы ведут игру одновременно. Рассматриваемая же торговля аналогична гипотетической ситуации, когда один из компонентов в игре не активен, но используется другая рыночная система с бесконечным числом контрактов. Проигрыш может быть катастрофическим. Проблему можно решить следующим образом разделите единицу на наибольший вес компонента портфеля и используйте полученное значение в качестве верхней границы активного баланса, если оно меньше, чем значение, найденное из уравнения (8. 08). В таком случае, если в будущем произойдет проигрыш той же величины, что и наибольший проигрыш (на основе которого рассчитано f), мы не потеряем все деньги. Например, наибольший вес компонента в нашем портфеле составляет 1,25. Если значение из уравнения (8.08) будет больше 1 / 1,25 = 0,8, следует использовать 0,8 в качестве верхней границы для доли активного баланса. Если первоначальная доля активного баланса небольшая, вышеописанная проблема может и не возникнуть, однако более агрессивному трейдеру следует всегда принимать ее во внимание. Альтернативное решение состоит в введении дополнительных ограничений в матрице портфеля (например, для каждой рыночной системы можно ограничить максимальные веса единицей и ввести дополнительные ограничения по залоговым средствам). Подобные дополнительные ограничения  [c.241]

Коэффициент корреляции всегда лежит в интервале между -1 и +1. Если он равен — 1, то это означает полную отрицательную корреляцию, если +1 — полную положительную корреляцию. В большинстве случаев он находится между этими двумя экстремальными значениями.  [c.182]

Для специального случая полной положительной корреляции (и только для этого случая) Var[fp] является возведенным во вторую степень  [c.151]

Прямая линия в области 0.1739 [c.152]

Коэффициент корреляции — зто статистическая мера степени корреляции между двумя рядами показателей. Изменяется от -1 в случае полной отрицательной корреляции до +1 в случае полной положительной корреляции.  [c.811]

Из гл. 2 мы знаем, что коэффициент корреляции может принимать значения от + 1 (полная положительная корреляция) до —1 (полная отрицательная корреляция). Положительная корреляция означает, что доходности каждой пары активов в основном изменяются в одном направлении. Это соотношение тем сильнее, чем ближе коэффициент корреляции к + 1. Отрицательная корреляция показывает, что доходности изменяются в противоположных направлениях, при этом соотношение становится сильнее по мере того, как коэффициент приближается к — 1.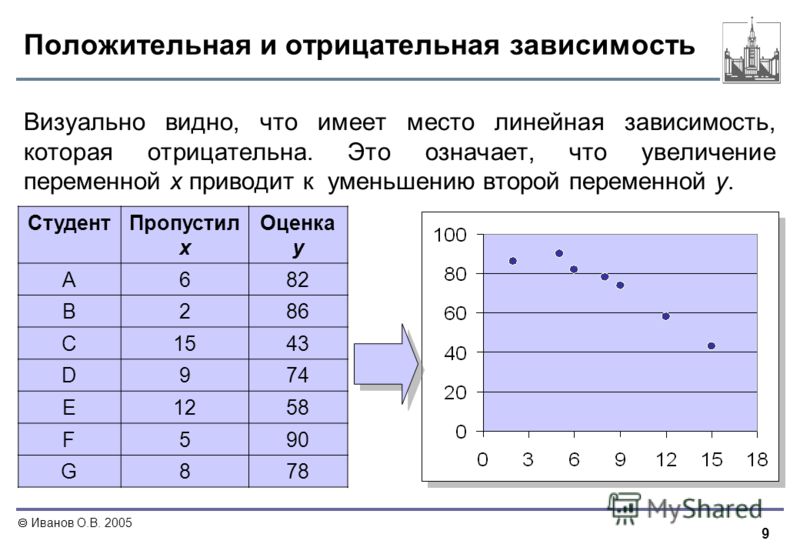  [c.187]

Для частного случая, когда ах = ау = о, получим по формуле (8.6) D = а2. Иначе говоря, при полной положительной корреляции «смешение» инвестиций не окажет никакого влияния на величину дисперсии.  [c.175]

При полной положительной корреляции расчетные значения доли первой бумаги составят по формуле (8.15)  [c.179]

Для интерпретации коэффициента корреляции необходимо знать область его существования 0 коэффициента корреляции может быть достигнуто, если положительные и отрицательные произведения отклонений признаков от их средних величин в числителе полностью уравновесят друг друга. Это свидетельствовало бы о полном отсутствии связи, но вероятность такого абсолютно точного взаимопогашения крайне мала для любой реальной, не бесконечно большой совокупности. Поэтому и при отсутствии реальной связи коэффициент корреляции на практике не равен нулю. Например, коэффициент корреляции между надоем молока от коров и числом букв в названии предприятия в совокупности хозяйств, указанных в табл. 8.1, равен +0,216. Как отделить реальные, надежно установленные связи от таких случайных, незначимых величин коэффициента корреляции, рассматривается в следующем разделе этой главы.  [c.246]

По этой причине необходимо ежедневно соединять подсчета при изменении их балансов. Сравним две похожие системы систему А и систему Б. Обе системы имеют 50% шанс выигрыша и обе имеют отношение выигрыша 2 1. Поэтому оптимальное f диктует, чтобы мы ставили 1 доллар на каждые 4 доллара баланса. Первый пример описывает ситуацию, когда эти две системы имеют положительную корреляцию. Мы начинаем со 100 долларов и разбиваем их на 2 подсчета по 50 долларов каждый. После регистрации сделки для этой системы изменится только столбец Полный капитал , так как каждая система имеет свой собственный отдельный счет. Размер денежного счета каждой системы используется для определения ставки для последующей игры  [c.61]

Коэффициент корреляции доходности по двум финансовым инструментам инвестирования может принимать значения от +1 (означающего полную и положительную корреляцию между рассматриваемыми величинами) до -1 (означающего полную и отрицательную корреляцию между рассматриваемыми величинами). Используя различия в ковариации инвестиционного дохода, можно подобрать в формируемый портфель такие виды финансовых инструментов, которые, не меняя уровня средней доходности портфеля, позволяют существенно снизить уровень его риска.  [c.389]

Коэффициент корреляции может принимать любые значения от 0 до 1. Если коэффициент корреляции равен нулю, то это означает отсутствие связи между х и у. Если его абсолютная величина составляет единицу, то, следовательно, существует полная зависимость между исследуемыми факторами, т, е, корреляционная зависимость совпадает с функциональной. Чем ближе коэффициент корреляции к единице, тем теснее зависимость между х и у чем ближе к нулю, тем связь слабее. Положительное значение коэффициента корреляции указывает на прямую зависимость, отрицательное значение — обратную.  [c.115]

Если доходы по обоим видам ценных бумаг явно коррелируют (т. е. положительный эффект по одному виду всегда сопровождается положительным эффектом по другому виду, а отрицательный эффект — всегда отрицательным), это означает полную корреляцию с коэффициентом корреляции +1. Аналогичным образом возможна противоположная ситуация, когда положительному эффекту по одному виду всегда соответствует отрицательный эффект по другому виду ценных бумаг, и наоборот. В этом случае коэффициент корреляции между двумя видами равен — 1.  [c.158]

При полной (то есть единичной) положительной корреляции между ценными бумагами диверсификация портфеля не даёт положительного эффекта. В этом случае, в соответствии с выражением (6.4.25), среднеквадратическое отклонение эффективности (то есть среднеквадратическое значение риска ) портфеля просто равно среднему риску от отдельных вложений и не стремится к нулю с увеличением числа ценных бумаг. По содержательному смыслу положительная корреляция имеет место, когда движение курсов ценных бумаг определяется действием одного и того же фактора, и это действие проявляется в движении курсов в одну и туже сторону.  [c.131]

Мы получаем прямую линию вида E[fp] = а — 0.6055 r[fp]. Кривая возможных действий, очевидно, образуется из двух прямых линий по абсолютной сумме одинакового наклона. Нам известны две координаты кривой. Они могут находиться на одной и той же прямой линии лишь при полной положительной корреляции, см. с. 152. При имею-  [c.154]

Этот коэффициент может принимать значения от минус единицы до плюс единицы. Коэффициент, равный минус единице, указывает на полную отрицательную корреляцию, коэффициент, равный плюс единице, — на полную положительную корреляцию, коэффициент, равный нулю,— на отсутствие связи. Заключенные между этими крайними величинами значения указывают на степень взаимосвязи. Обратите внимание на то, что коэффициент отражает степень только линейной взаимосвязи переменных. Например, две переменные могут быть тесно связаны нелинейным соотношением (скажем, у =х2), а значение г будет невысоким. (См. также rank orrelation.)  [c.102]

Определим доход и дисперсию для портфеля с долями, равными, допустим, 0,3 и 0,7. Получим по формулам (8.6) и (8.7) D = 0,651 + 0,37лху и А — 2,7. Таким образом, при полной положительной корреляции D = 1,021, при полной отрицательной корреляции О = 0,281.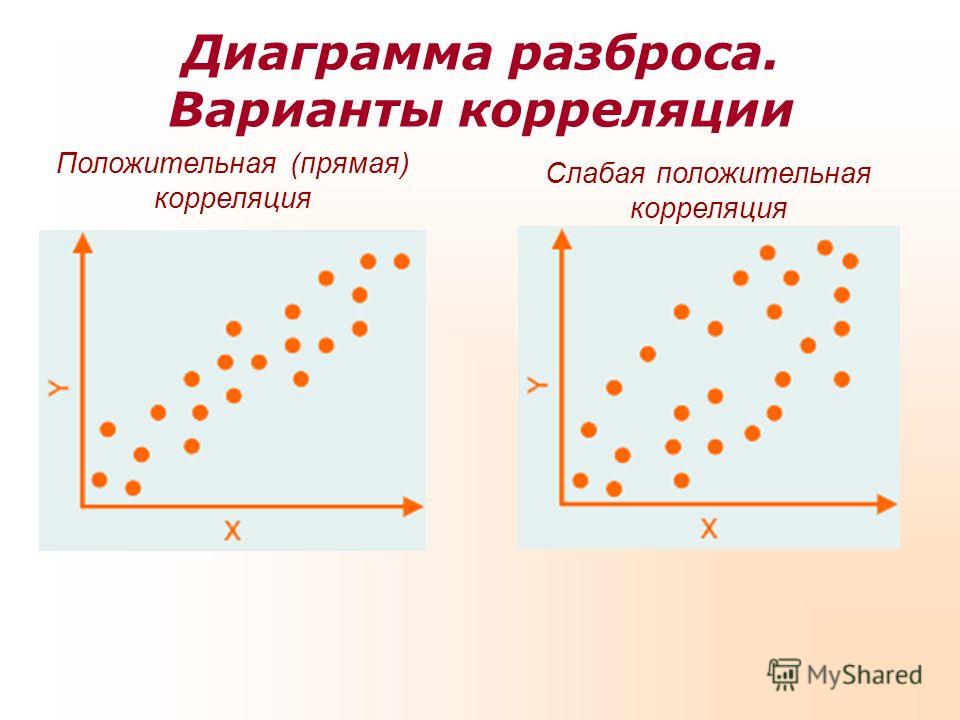 В итоге с вероятностью 95% можно утверждать, что суммарный доход находится в первом случае в преде-  [c.176]

Плотность ковариации между уровнями доходности по двум видам финансовых инструментов можно определить, рассчитав коэффициент корреляции, который может принимать значения от +1 до —1. Значение коэффициента корреляции, равное +1, означает полную и положительную корреляцию между уровнями доходности изучаемых финансовых инструментов, т. е. однонаправленное совпадающее изменение. Значение, равное —1, показывает полную и отрицательную корреляцию между уровнями доходности рассматриваемых финансовых инструментов. Следовательно, когда доходность одной ценной бумаги наиболее высока, велика вероятность того, что доходность второй ценной бумаги принимает наиболее низкие значения. Расчет коэффициента корреляции осуществляется по следующей формуле  [c.392]

Из рис 2 2 н 2 3 следует 1) если между акциями существует обратная функциональная связь (г = —1.0), риск портфеля может быть сведен к нулю, и 2) если между акциями имеет место прямая функциональная связь (г = +1 0), диверсификация не приводит к снижению риска В действительности больший ство акций положительно коррелируют друг с другом, но эта связь не является функциональной Коэффициент корреляции двух случайным образом выбран ных акций на Нью Йоркской фондовой бирже составляет около +0 6, а в боль шинстве случаев г лежит в пределах от +0 5 до +0.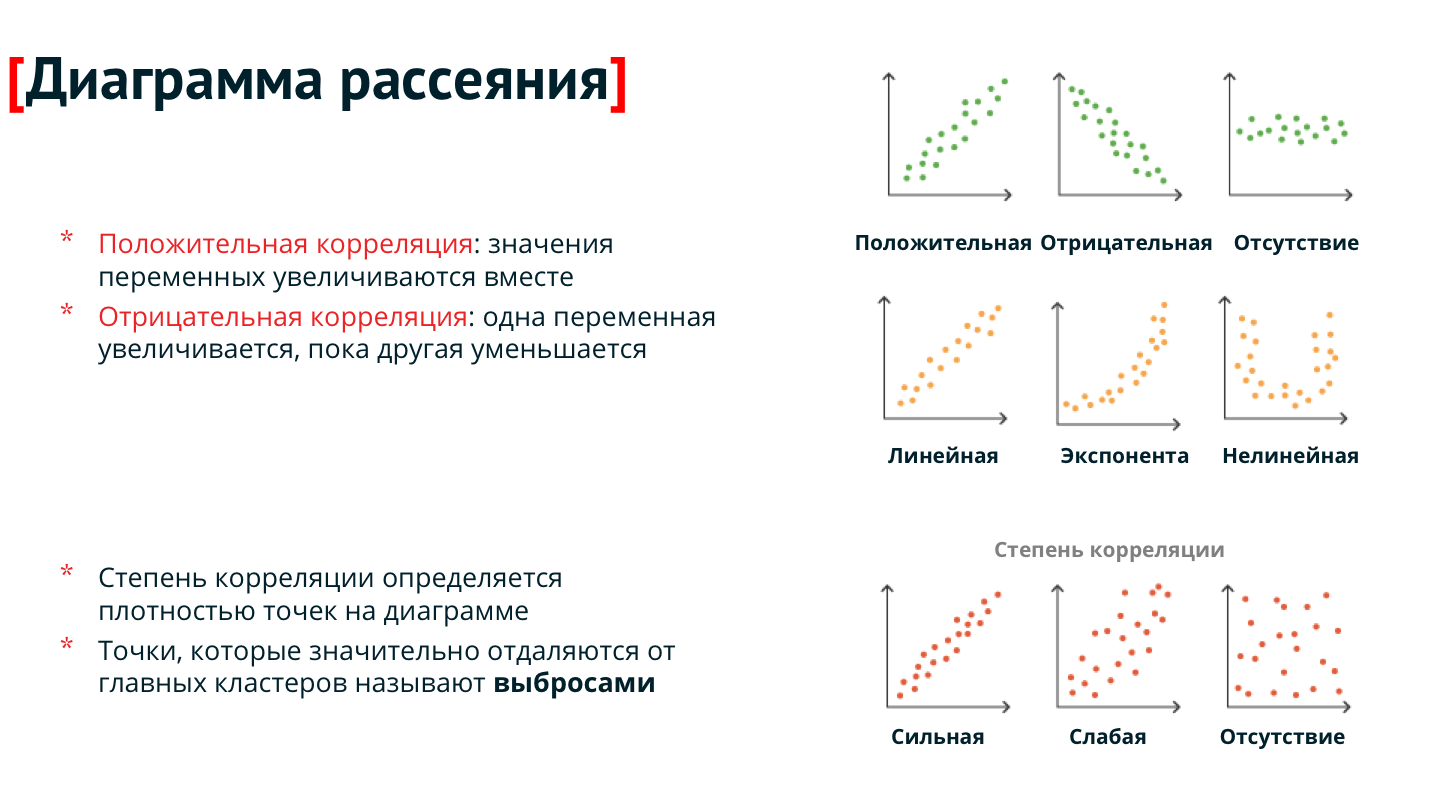 7 При таких условиях объединение акций в портфель снижает риск, однако полностью его не элими нирует Графически ситуация объединения в портфель двух акций с коэффи циентом корреляции г = +0 65 представлена на рис 2.4. Средняя фактическая доходность портфеля равна 15 0% и совпадает со средней фактической доход ностью каждой из акций. Между тем среднее квадратическое отклонение порт феля, равное 20 6%, меньше, чем среднее квадратическое отклонение любой из акций. Таким образом, риск портфеля не равен среднему из рисков составля ющих его акций, а диверсификация приводит к снижению, но не к полному устранению риска 7  [c.47]

Что произойдет, если добавлять в портфель все большее количество новых акций Как правило, риск портфеля будет уменьшаться по мере увеличения числа акций Если дополнить портфель достаточно большим количеством акций, можно ли полностью свести риск к нулю В целом ответ на этот вопрос отри цательный, однако степень воздействия добавления новых акций на снижение риска портфеля зависит от уровня корреляции между отдельными акциями чем меньше значение коэффициента корреляции, тем ниже риск крупного портфеля. На самом деле если бы в распоряжении инвестора имелось достаточно акций с коэффициентом корреляции, равным нулю (или отрицательным), риск можно было бы полностью элиминировать. Однако в большинстве случаев коэффици енты корреляции между отдельными акциями положительны, но не достигают +1.0, поэтому можно лишь снизить риск портфеля, но не устранить его полно стью  [c.58]

Некоторая (не слишком существенная) часть из сочетаний Коткл и КИНБ> приведенных в табл. 6.10, и особенно те из сочетаний, в которых исчислено значение KPA3B при положительных и отрицательных значениях исходных коэффициентов ранговой корреляции (такие случаи редки), на практике может оказаться бессодержательной. Но без их значений данная таблица не давала бы полной системной картины математической зависимости между различными значениями этих коэффициентов, а потому она приведена именно в этом виде.  [c.148]

РАЗНИЦА МЕЖДУ ПОЛОЖИТЕЛЬНОЙ И ОТРИЦАТЕЛЬНОЙ КОРРЕЛЯЦИЕЙ | СРАВНИТЕ РАЗНИЦУ МЕЖДУ ПОХОЖИМИ ТЕРМИНАМИ — НАУКА

Положительная корреляция против отрицательной корреляции Корреляция — это мера силы связи между двумя переменными. Коэффициент корреляции определяет степень изменения одной переменной на основе измен

Положительная корреляция против отрицательной корреляции

Корреляция — это мера силы связи между двумя переменными. Коэффициент корреляции определяет степень изменения одной переменной на основе изменения другой переменной. В статистике корреляция связана с понятием зависимости, которое представляет собой статистическую связь между двумя переменными.

Коэффициент корреляции Пирсона или коэффициент корреляции продукт-момент Пирсона, или просто коэффициент корреляции, получается по следующим формулам.

Для населения:

Для образца:

и следующее выражение эквивалентно приведенному выше выражению.

и стандартные баллы X и Y соответственно. это среднее и s_Икс и s_Y — стандартные отклонения X и Y.

Коэффициент корреляции Пирсона (или просто коэффициент корреляции) является наиболее часто используемым коэффициентом корреляции и действителен только для линейной связи между переменными. r — значение от -1 до 1 (-1 ≤ r ≤ +1). Если r = 0, отношения не существует, а если r ≥ 0, отношение прямо пропорционально, и значение одной переменной увеличивается вместе с другой. Если r ≤ 0, одна переменная уменьшается, а другая увеличивается, и наоборот.

Из-за условия линейности коэффициент корреляции r также можно использовать для установления наличия линейной зависимости между переменными.

 

В чем разница между положительной корреляцией и отрицательной корреляцией?

• Когда существует положительная корреляция (r> 0) между двумя случайными величинами, одна переменная перемещается пропорционально другой переменной. Если одна переменная увеличивается, другая увеличивается. Если одна переменная уменьшается, другая тоже уменьшается.

• Когда существует отрицательная корреляция (r <0) между двумя случайными величинами, переменные движутся в противоположном направлении. Если одна переменная увеличивается, другая уменьшается, и наоборот.

• Линия, приближающая положительную корреляцию, имеет положительный градиент, а линия, приближающая отрицательную корреляцию, имеет отрицательный градиент.

Корреляция — это… Что такое Корреляция?

Вообще, от того, что происходит здесь у нас, в Российской Федерации, — мало что зависит. Редко, когда какое-нибудь событие у нас в Российской Федерации вызовет какую-нибудь заметную реакцию на весь рынок. Я не имею в виду корпоративные новости, хотя и здесь тоже не всегда авария на каком-нибудь предприятии Лукойла отразиться на его акциях, но такая же авария на заводе Exxon (парадокс) вызовет падение акций Лукойла. Зато плохие данные по

занятости в США могут устроить настоящий обвал на российском рынке. Такие парадоксов на финансовом рынке полным полно.

Впрочем не одни мы такие. Практически любой рынок акций в мире тесно связан с американским рынком акций и реагирует прежде всего на то, что происходит там. И здесь помимо фундаментальных причин взаимодействия рынков капитала оказывает сильное влияние также широкое распространение средств автоматической торговли.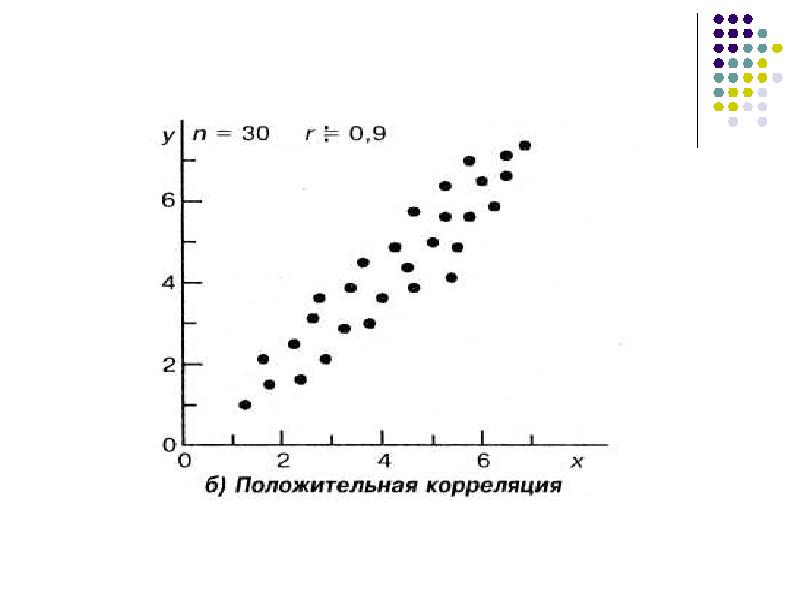 Это проявляется особенно отчетливо на микроуровне (тики). Каждое тиковое движение индекса S&P500 вверх или вниз тут же отзывается соответствующим изменением индексов FTSE, DAX, ММВБ, Bovespa. Подобная корреляция существует повсеместно и является основой для принятия трейдерами решений.

Далее идут несколько графиков, которые показывают, как взаимодействуют между собой индекс S&P500, индекс РТС и цены на нефть. На этих графиках показано изменение S&P500, индекса РТС и цен на нефть в процентах с заданного на графике момента отсчета.

На рисунке выделена ситуация в марте месяце, когда индекс РТС пошел за черным золотом, а не за индексом S&P500. Это был период обострения ситуации в Северной Африке и на Среднем Востоке. Повышение цен на нефть негативно отразилось на американском фондовом рынке, но в то же время привело к ралли на российском рынке акций. Обратите внимание еще на один факт: разворот на российском фондовом рынке почти всегда происходит чуть раньше, чем это делают цены на нефть.

На следующем графике показаны те же корреляции с момента выступления Бена Бернэйнк в Джексонхолле, где он объявил о предстоящей программе QE2.

Как мы видим, почти до Нового года S&P500, индекс РТС и нефть двигались практически синхронно. В январе – феврале случилась сезонная коррекция в черного золота, но российский рынок продолжал расти вместе с Америкой, осваивая деньги, которые обычно выделяют инвестиционным фондам в начале года. Следующий график показывает те же корреляции с момента пика американского фондового рынка в 2007 году. Впечатляющее параболическое ралли в черного золота все-таки несильно смогло утащить за собой российский рынок акций.

Обращает внимание на этом графике стабильность спрэда между ценами на нефть и индексом РТС. Следующий график показывает нам корреляции с января 2004 года. Инвестирование в американский фондовый рынок за этот период не принесло никакой профита.

И наконец самый впечатляющий график из этой серии: с начала 2000 года.

Как мы видим, в то время как нефть и индекс РТС выдали очень сильный рост за этот период, 450% и 1500% соответственно, американский фондовый рынок за это время практически не покидал отрицательную зону. Несомненно, есть и другие факторы, которые оказывают влияние на российский фондовый рынок. Например, курс рубля. Укрепление курса рубля приводит к притоку денег на российский рынок. Увеличение ставки

дополнительного вложения капитала приводит к росту рубля и соответственно способствует росту российского рынка ( обычно оно заранее отыгрывается инсайдерами).

Когда доллар дешевеет относительно рубля, то, если считать, что цены на активы в рублях остаются неизменны, следовательно они должны дорожать относительно доллара и других валют. Возможно, зависимость российского рынка от цен на нефть выражает взаимосвязь рынка с изменением курса национальной валюты с каким-нибудь коррелирующим коэффициентом. Поэтому хотя здесь тоже есть определенная корреляция, заниматься выявлением взаимодействия индекса РТС с курсом рубля или какой-то другой валюты нет смысла.

Корреляция (Correlation) — это

Вкратце: можно сделать следующие выводы: взаимодействие российского рынка акций с индексом S&P500 отражает глобальный рыночный сентимент по отношению к рынкам акций в целом; взаимодействие с ценами на нефть отражает как традиционное преобладание в российских индексах акций нефтегазового сектора, так и большую часть взаимосвязи с изменением курсов валют.

Существуют и другие корреляции, которые необходимо учитывать при инвестировании в российский рынок акций: например взаимодействие российского рынка с притоком/оттоком иностранного капитала.

       Корреляция ценных бумаг

Между доходностями ценных бумаг может наблюдаться функциональная зависимость. Это означает, что существует строгое правило, которое связывает значения их доходностей. Наиболее простой является линейная зависимость.

На финансовом рынке зависимость между доходностями ценных бумаг часто бывает не функциональной, т.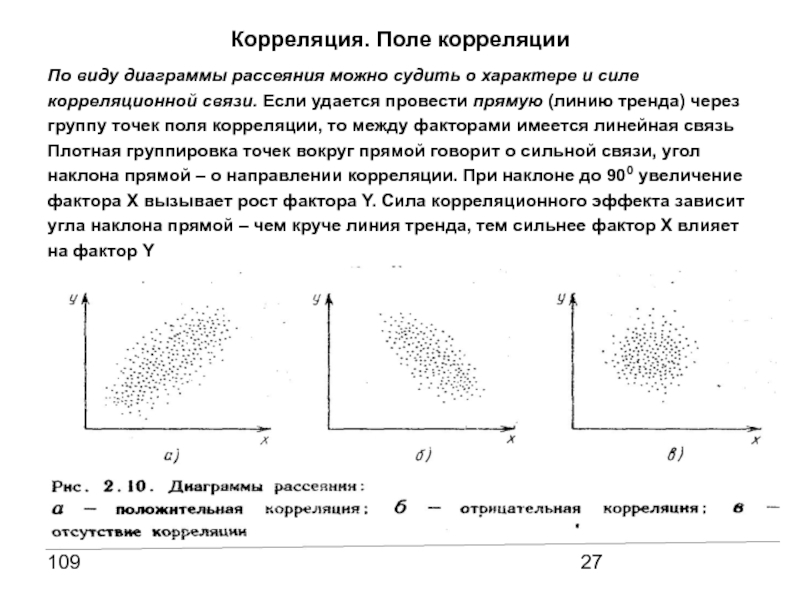

е. не жесткой. В этом случае одному значению доходности одной бумаги могут соответствовать разные значения доходности другой бумаги. Таким образом, не наблюдается строгого закона, который бы связывал значения их доходностей. Зависимость подобного рода называют стохастической или вероятностной, или статистической. Это означает, что при изменении доходности одной бумаги можно говорить лишь о том, какие значения доходности может принять другая бумага и с какой вероятностью. Такое положение вещей объясняется существованием большого количества факторов, влияющих на доходности конкретных активов и тем, что все их сложно учесть.

При формировании портфеля степень взаимосвязи между доходностями двух ценных бумаг можно определить с помощью таких показателей как ковариация и коэффициент корреляции.

Ковариация говорит о степени зависимости двух случайных величин. Она может принимать положительные, отрицательные значения и равняться нулю. Если ковариация положительна, это говорит о том, что при изменении значения одной переменной другая имеет тенденцию изменяться в том же направлении. Так, при положительной ковариации доходностей двух бумаг с ростом доходности первой бумаги доходность второй также будет расти. При падении доходности первой бумаги доходность второй также будет снижаться.

При отрицательной ковариации переменные имеют тенденцию изменяться в противоположных направлениях. В таком случае рост доходности первой бумаги будет сопровождаться падением доходности второй бумаги, и наоборот. Чем больше значение ковариации, тем сильнее зависимость между переменными. Если ковариация равна нулю, никакой зависимости между переменными не наблюдается.

Коэффициент корреляции характеризует степень тесноты линейной зависимости двух переменных и является безразмерной величиной. Тенденция к линейной зависимости двух переменных может иметь более или менее выраженный характер. Поэтому значения коэффициента изменяются в диапазоне от -1 до +1. Если коэффициент равен +1, между доходностями двух бумаг существует положительная функциональная зависимость. Если коэффициент корреляции положительный, но меньше чем +1, между доходностями двух бумаг также существует зависимость, но менее строгая.

Если коэффициент корреляции равен -1, между доходностями бумаг существует отрицательная функциональная зависимость. При коэффициенте корреляции равном нулю никакой зависимости между переменными нет.

       Корреляция инвестиций

Многие ли инвесторы — участники нашего форума корректируют свой набор инструментов с использованием диверсификации и корреляции. Думаю, что не многие. Если понятие диверсификации знакомо большинству хотя бы на уровне пословицы: «Не держите все яйца в одной корзине». То понятие корреляции активов, к примеру я, обнаружил совсем недавно.

Составление диверсификации инвестиционного портфеля из активов с некоррелированными результатами уменьшает риск, поскольку в то время, как прибыль на один актив падает, на другой она, вероятно, растет. При попытке строить диверсифицированный инвестиционный портфель из активов с ярко выраженной отрицательной корреляцией мы можем получить неожиданный и очень полезный для нас эффект. Суммарная доходность инвестиционного портфеля может оказаться выше доходности отдельных активов, а соответственно риск может оказаться ниже, чем риск того и другого активов.

О чем говорят данные фондовой биржи США по корреляционной зависимости между разными группами активов за 1926 — 2009: взаимная корреляция между акциями малых предприятий и акциями крупных предприятий — (+0.79). Это довольно высокая корреляция. Хотя и не 1. Все-таки крупные акции и малые акции ведут себя несколько по-разному. Между акциями и облигациями корреляция уже близка к нулю.

Корреляции между акциями и краткосрочными облигациями и казначейскими векселями тоже близки к нулю и даже несколько отрицательные.

Облигации друг с другом коррелируются достаточно высоко. Долгосрочные краткосрочные облигации имеют между собой корреляцию 0.8 — 0.9.

Долгосрочные облигации с казначейскими векселями напротив — резкое понижение корреляции.

Отдельно США, Канада, Япония и Великобритания, отдельно Европа, Азиатский регион и Тихоокеанский регион: корреляция между близко лежащими регионами достаточно высокая. Между Азией и Тихоокеанским регионом корреляция около 0.92. Между Канадой и США также достаточно высокая корреляция. А вот чем дальше друг от друга отстоят регионы, тем ниже между ними корреляция. Даже у Японии с Англией или Японии с Канадой и США корреляция меньше чем 0.5. Важно! При желании уменьшить риск инвестиционного портфеля мы можем включать в него акции из разных частей света.

Корреляция между индексом ММВБ, двумя ПИФами УК «Тройка Диалог», золотом, серебром, долларом, евро и московской недвижимым имуществом: корреляция между индексом акций и фондом акций, конечно, высокая. Корреляция между акциями и облигациями где то на уровне 0.5. Между ценными бумагами и золотом корреляция близка к нулю (даже немного отрицательная). Корреляция между золотом и серебром высокая. Поэтому пытаться включать в свой инвестиционный портфель и золото и серебро особого смысла не имеет.

Корреляция между долларом и евро и между акциями и облигациями опять же нулевая или даже отрицательная. Корреляция между жильем и индексом ММВБ в Российской Федерации даже отрицательная (на уровне минус 0.17-0.18). Что, кстати, довольно не типично по мировым меркам.

Выводы: Без правильной диверсификации активов с учетом их взаимной корреляции невозможно сформировать эффективный инвестиционный портфель, который позволит Вам приумножить Ваш капитал или, во всяком, случае сохранить его.

       Корреляция курса доллара и цены на нефть и обратная пропорциональность

Фундаментальные факторы являются основой торговли на валютном рынке, они позволяют установить взаимосвязь валютных курсов с теми или иными событиями. В этой статье пойдет речь о корреляции такого показателя как цена на нефть с курсом доллара Соединенных Штатов. Экономика Америки является одной из самых энергозависимых экономик мира. Соединенные Штаты Америки потребляют просто огромное количество нефтепродуктов, поэтому повышение цены на сырую нефть просто не может не сказаться на курсе национальной валюты.

Причина подобной связи лежит довольно глубоко, но изменения происходят буквально сразу, так как рынок склонен реагировать еще до фундаментальных изменений на основании психологических факторов. При рассмотрении влияния цены на нефть на курс доллара складывается довольно не однозначная ситуация ведь США являются одним из самых крупных производителей нефти, в тоже время выступают самым крупным приобретателем данного вида сырья.

По статистическим данным экономике Америки не хватает собственных запасов нефтепродуктов для обеспечения потребностей всего производства, при этом часть добытой черного золота внутри страны идет на экспорт. По этой причине Америка вынуждена ежегодно закупать около 9 миллиардов баррелей черного золота, что существенно отображается на увеличении стоимости американских товаров как внутри страны, так и на внешних рынках.

А увеличение стоимости товаров, как известно всегда ведет к негативным последствиям для национальной валюты. Кроме этого негативное влияние на курс американского доллара так же оказывает то, что для закупки черного золота компаниям приходится покупать другие иностранные валюты, так как экспортеры не всегда согласны на расчеты в долларах Соединенных Штатов. К примеру, ряд арабских стран не так давно полностью перешли в расчетах за нефть на евро. В результате этих двух факторов видим следующую картину, цена на нефть повышается, в результате увеличивается предложение доллара Соединенных Штатов Америки на валютном рынке Forex, в результате его курс идет вниз.

В то же время, при падение цены на нефть, наблюдается обратная ситуация, доллар Соединенных Штатов Америки начинает активно расти по отношению к таким валютам как евро, канадский доллар и некоторым другим валютам. Данную зависимость можно довольно удачно использовать в игре на валютной бирже forex, для торговли самым оптимальным выбором будет пара Доллар США-Канадский доллар, так как именно по этому инструменту будут наблюдаться наибольшая волатильность. При возможности можно использовать и такую валютную пару как USD/RUR, она будет реагировать аналогично предыдущему инструменту.

Ордера на покупку открываются в случае подорожания черного золота, ордера на продажу — в случае падения цены на черное золото. Так же иногда отслеживается и обратная пропорциональность, при укреплении американского доллара начинает заметно падать цена на нефтепродукты и сырую нефть, это свойство можно использовать при торговле на сырьевых ранках.

       Корреляция курса рубля и цены на нефть

О войне в Сирии говорят все, кто торгует черным золотом. Чёрное золото марки Brent очень долго находилась в диапазоне 100-110 долларов за баррель. Но на вероятности свержения американцами еще одного правительства фьючерс на нефть быстро поднялся до 117 долларов. Потом была логичная коррекция, и сейчас Brent торгуется около 115 долларов.

Как вел себя рубль? Очень часто у Analystov можно услышать: “рубль подорожал на фоне роста нефти”, или “рост доллара связан с падением цен на нефть”. Есть ли корреляция курса доллара к рублю и цен на нефть? Есть ли это корреляция сейчас? В этом году? Курс доллара к рублю коррелировал с ценами на нефть до июля, а в июле Brent пошел вверх, а рубль — нет. Почему так произошло?

Здесь несколько причин. Во-первых, бюджет, который зависит от цен на нефть и курса доллара к рублю. Этому бюджету чем выше курс доллара и цены на нефть, тем лучше. Во-вторых, не только нефтяники хотят видеть более слабый рубль. Отчетности многих экспортеров “просят” более выгодный для них курс. В-третьих, отток капитала никуда не девался. Отток идет и идет большой. В-четвертых, в курс доллара были еще заложены ожидания по покупке Банк России валюты для Минфина. В-пятых, доллар сейчас растет по отношению ко всем “слабым” валютам типа рубля (бразильскому риалу или индийской рупии).

Зависимость бюджета Российской Федерации от сырьевого экспортирования стала уже притчей во языцах. Федеральный бюджет на 45 процентов наполняется поступлениями от продажи черного золота и нефтепродуктов. Примерно половина добытой в Российской Федерации черного золота (246 млн. тонн) отправляется за границу, а вторая половина перерабатывается на Российских НПЗ. Расчеты по черного золота с импортерами проводятся в долларах. В результате, валютные поступления от продажи черного золота и определяют курс рубля относительно доллара. Чем больше цена черного золота, тем больше долларовых поступлений, тем больше на международный валютный рынок Forex поступает долларов, тем крепче рубль. И наоборот.

Наиболее удачное и образное определение стоимости рубля дал Сергей Гуриев, ректор Российской экономической школы: «Российский рубль — это бумажная версия черного золота. Какая нефть, такой и рубль». Мы решили проверить, с какой точностью совпадают между собой котировки рубля и доллара. Графики соотношения «баррель — рубль» за двухлетний период, включающий пик цены на нефть 146 долларов за баррель, пришедшийся налето 2008 года и спад цены до 40 долларов за баррель в зиму 2008-2009 годов, приведен на графике.

Степень соответствия стоимости рубля к цене черного золота можно охарактеризовать коэффициентом корреляции, устанавливающим статистическую взаимосвязь этих величин. Коэффициент корреляции (обычно используется коэффициент Пирсона) может принимать значения от минус единицы до единицы. Для независимых между собой процессов (величин) коэффициент корреляции принимает значение, близкое к нулю. И, наоборот, для функционально зависимых друг от друга процессов этот коэффициент приближается к единице или минус единице, в зависимости от сонаправленного или встречного характера движения исследуемых величин.

В нашем случае коэффициент корреляции, рассчитанный на периоде в один год (с 01 февраля 2009 года до 01 февраля 2010 года) составляет значение равное по модулю 0,935. Это очень высокая степень соответствия стоимости рубля и цены на нефть: с точки зрения математической статистики, функциональная связь существует. Построим простейшую математическую модель поведения курса рубля относительно доллара, предполагающую линейную зависимость одного от другого. Зеленая линия на графике отображает моделированное поведение курса рубля.

Не нужно знать слово «корреляция», чтобы оценить столь наглядный результат. Несовпадение с моделью в период максимальных цен на нефть, когда рубль укреплялся и становился тормозом для отечественных экспортеров, объясняется рублевыми интервенциями центрального банка на валютном рынке Форекс по сдерживанию усиления курса рубля. И наоборот — интенсивными долларовыми интервенциями при ослаблении рубля в период провальных цен на нефть.

Модель позволяет провести оценку будущего курса рубля, например, при цене барреля 90 долларов, курс рубля может подняться до 27 руб/долл., а при цене барреля 50 долларов может опуститься до 35 руб/долл. Следует признать, конкретная модель не учитывает множество факторов, в том числе, как уже показано, и вмешательство центральный банк, но, тем не менее наглядно иллюстрирует общий принцип.

Возникает вопрос, как долго сохранится жесткая связь «баррель-рубль»? Ответ: до тех пор, пока не изменится структура российского экспортирования или расчетной валютой по нефтяным контрактам останется доллар.

       Корреляция цен на нефть и ВВП России

В своей работе менеджера я постоянно использую различные показатели деятельности (KPI). Меня заинтересовали своего рода KPI макроэкономического уровня. Ранее я рассказал о том, каким является уровень коррупции в Российской Федерации и странах мира по оценкам Центра антикоррупционных исследований и инициатив Transparency International. Затем я рассмотрел динамику еще одного макроэкономического показателя — рейтинга экономической свободы, формируемого Американским исследовательским центром «Фонд наследия» (The Heritage Foundation ) и газетой The Wall Street Journal. И, наконец, представил показатели налоговой нагрузки в странах мира (tax misery), публикуемые журналом Forbes.

В последнее время в связи с падением цен на нефть заговорили о возможных проблемах с исполнением бюджета страны. И меня заинтересовал вопрос, насколько тесно коррелируют цены на нефть с макроэкономическими показателями отечественной экономики!?

Существует много различных видов цен на нефть, и данные, на которые я ссылаюсь, не самые распространенные… но, то, как они представлены, насколько полно и удобно, позволяет анализировать их с различных сторон. При том, что корреляция между различными видами цен на нефть, на мой взгляд, полнейшая. Нередко проблемы в экономике страны связывают с именем Ельцина, а успехи — Путина. На первый взгляд, зависимость однозначная, но, как покажет последующий анализ, поверхностная.

Корреляция цен на нефть и размера ВВП Российской Федерации меня просто поразила. Подсчитав коэффициент корреляции, я понял, что означает выражение «на нефтяной игле». Если 97% динамики ВВП Российской Федерации связано с ценой на нефть, то, что остается на другие факторы!? Играют ли они, хоть какую-то роль!?

Не подумайте, что столь высокая корреляция характерна для всех макроэкономических показателей. Так курс доллара показывает всего 50%-ную корреляцию со стоимостью черного золота. То есть, только половина изменений курса доллара может быть объяснена мировой конъюнктурой нефтяного рынка.

ВВП США также демонстрирует весьма умеренную корреляцию с ценами на нефть. Хотя и в США взаимосвязь также весьма тесная.

       Корреляция в психологии

Понятие иллюзорной корреляции. Иллюзорная корреляция (illusory correlation) — это психологическое явление, которое наблюдается практически у всех людей, подобно тому, как практически все люди подвержены иллюзии Мюллера-Лайера и другим оптическим иллюзиям.

Возможно, явление иллюзорной корреляции будет легче понять, если назвать его словами «иллюзия связи», а суть иллюзорной корреляции заключается в том, что человек по той или иной причине видит связь между параметрами, свойствами, явлениями, которой на самом деле нет. Обычно иллюзорная корреляция наблюдается в паре «свойство — признак наличия этого свойства». Например, если человек считает, что цвет волос может говорить о степени умственного развития человека, а жесткость волос — о жесткости характера, то речь идет как раз об иллюзорной корреляции. На самом же деле, понятно, никакой связи между цветом волос и интеллектом или между жесткостью волос и характером нет.

Экспериментально явление иллюзорной корреляции впервые исследовал Лорен Чепман (кстати, это однофамилец нашего знаменитого, хотя и провалившегося агента-нелегала Анны Чапман) еще в 1967 году. И именно этот исследователь ввел сам термин «иллюзорная корреляция». Исследование проводилось так. Испытуемым в течение определенного времени предъявлялись (проецировались на экран) пары слов, например, «бекон — яйца». Пары составлялись следующим образом: левым словом оказывалось одно из следующих четырех слов: бекон, лев, бутоны, лодка, а правым — одно из следующих трех слов: яйца, тигр, тетрадь.

Таким образом испытуемому предъявлялось 12 пар слов: «бекон — яйца», «бекон — тигр», «бекон — тетрадь» и т.д. Причем эти пары слов предъявлялись много раз и чередовались в случайном порядке, но каждая пара предъявлялась равное количество раз.

Затем испытуемых просили оценить частоту появления каждой пары слов. И это ключевой момент эксперимента. Не смотря на то, что объективно частота предъявления каждой пары слов была одинаковой, более высокой испытуемые объявили частоту предъявления пар слов, имеющих, по выражению автора эксперимента «сильную вербальную ассоциацию».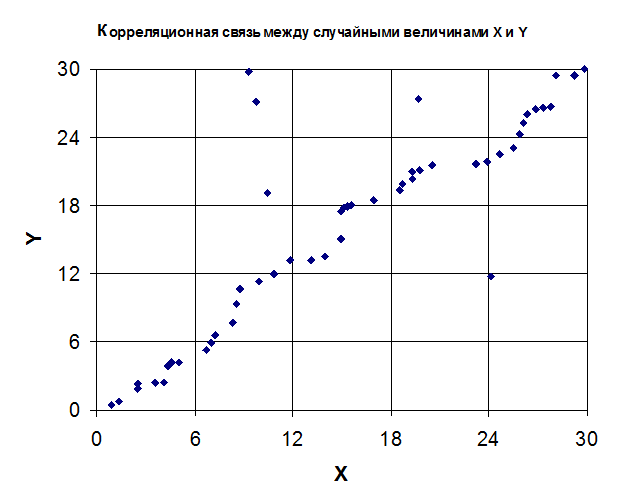 Это следующие пары слов: «бекон — яйца» (ассоциация по смежности) и «лев — тигр» (ассоциация по сходству).

Таким образом, испытуемые имели иллюзорные представления о том, что слово «бекон» теснее связано со словом «яйца», а слово «лев» со словом «тигр», чем другие слова друг с другом. Напомню, что на самом деле каждая из 12 пар слов предъявлялась равное количество раз.

Итак, при иллюзорной корреляции человек, как говорится, путает Божий дар с яичницей: видит связь там, где ее на самом деле нет.

Иллюзорная корреляция и проективные тесты. Исследовал Лорен Чепман (вместе со своей женой Джин Чепман) и роль иллюзорных корреляций в определении характера человека с помощью так называемых проективных тестов. Исследовались такие проективные тесты как «рисунок человека» и «тест Роршаха».

При этом супругов Чепман интересовал вопрос о том, почему психологи продолжают пользоваться проективными тестами, хотя в научных исследованиях многократно показывалась их несостоятельность (bankruptcy) как психодиагностического инструмента, т.е. отсутствие связи между предлагаемыми разработчиками этих тестов ключами и интерпретациями с психологическими характеристиками тестируемых индивидов. Чепманы предположили, что подобная настойчивость в использовании не валидных тестов обусловлена явлением иллюзорной корреляции, которому подвержены психологи (как и все люди).

Прежде чем перейти к описанию собственно экспериментов необходимо сказать несколько слов о проективных тестах.

Проективные тесты основаны на предположении о том, что при интерпретации бессодержательных визуальных стимулов (кляксы) или при выполнении неопределенного задания (нарисовать человека) испытуемый якобы обязательно проявит свои черты характера. Например, разработчик теста «Рисунок человека» Карен Маховер утверждала, что паранойяльный (подозрительный) субъект при рисовании человека особый акцент придаст глазам, озабоченный своей мужественностью — нарисует мускулистого человека, озабоченный собственным интеллектом — нарисует большую голову и пр. В ключах же к тесту Роршаха утверждается, например, что если человек имеет гомосексуальные склонности, то в кляксах он увидит: ягодицы, задний проход, гениталии, женскую одежду, людей неопределенного пола, людей с признаками обоих полов.

Я думаю, читатель легко заметил, что описанные выше связи между признаками и чертами характера чисто ассоциативные и основаны на бытовых, житейских, тривиальных представлениях. Действительно, почему бы человеку с сомнениями в своей мужественности и не рисовать мускулистых людей, а гомосексуалистам — не видеть в кляксах задние проходы? Но на самом деле никакой связи тут нет.

И Чепманы экспериментально показали что такого рода иллюзорным корреляциям при интерпретации упомянутыхпроективных тестов подвержены и профессиональные психологи, и не имеющие никакого отношения к психологии люди.

Схема эксперимента была несколько похожа на схему эксперимента по выявлению иллюзорных корреляций, который мы рассмотрели выше. Испытуемым предложили рисунки человека, выполненные как пациентами психиатрической клиники, так и здоровыми людьми, и соответствующие психологические характеристики. Например, к рисунку человека с большой головой прилагалась характеристика «обеспокоен уровнем своего интеллекта». При этом, обратите внимание (!), одни и те же психологические характеристики прилагались к разным рисункам. Например, характеристика «относится к людям с недоверием и подозрением» прилагалась как к рисункам с выраженным акцентом на глазах, так и к рисункам, не имеющим каких либо особенностей изображения глаз. Причем таких сочетаний было, как и в уже рассмотренном эксперименте, одинаковое количество.

Испытуемых попросили установить связь между особенностями рисунков и психологическими характеристиками авторов этих рисунков. И как читатель, должно быть, уже догадался, испытуемые продемонстрировали иллюзорную корреляцию: например, утверждали, что такая черта характера как подозрительность сочетается именно с выраженным акцентом на глазах. Более того: такая же картина наблюдалась и в следующей серии экспериметов, в которой эти две характеристики (выраженные глаза и подозрительность) вообще не встречались вместе!

Похожим образом проводился и эксперимент с пятнами Роршаха. К пятнам прилагались интерпретации, сформулированные лицами, прошедшими психодиагностику, и психологические характеристики этих людей. Например, интерпретация «задний проход» равное количество раз совпадала с каждым из следующих четырех психологических характеристик: он проявляет сексуальное влечение к другим мужчинам; он полагает, что окружающие сговорились вокруг него; он испытывает грусть и депрессию в течение длительного времени; он испытывает сильное чувство собственной неполноценности.

Как и в предыдущем эксперименте испытуемые вновь продемонстрировали явление иллюзорной корреляции, увязавинтерпретацию «задний проход» с психологической характеристикой «он проявляет сексуальное влечение к другим мужчинам».

Иллюзорная корреляция в нашей жизни. Конечно, иллюзорные корреляции искажают наше с Вами восприятие не только в лабораториях. Например, именно явление иллюзорной корреляции во многом определяет формирование стереотипов по отношению к тем или иным народам или социальным слоям.

На иллюзорных корреляциях построены многие лженауки (в особенности лженауки о душе), в частности, физиогномика, соционика, графология, типология преступников Чезаре Ломброзо, френология, измышления Б.Хигира о том, что имя человека определяет его характер, а также явно оккультные учения, такие как хиромантия. Многие аспекты психологического оккультизма также коренятся в иллюзорных корреляциях. На иллюзорных корреляциях основаны и многие представления современного психоанализа и других видов психотерапии (например, когда кашель объявляется проявлением тайного желания сказать гадость, а боль в спине — проявлением тяжелой психологической ноши, которую взвалил на себя человек).

       Корреляция в повседневной жизни

Усиление интереса в психологической науке к потенциалу корреляционного анализа обусловлено целым рядомпричин. Во-первых, становится допустимым изучение широкого круга переменных, экспериментальная проверка которых затруднена или невозможна. Ведь по этическим соображениям, к примеру, нельзя провести экспериментальные исследования самоубийств, наркомании, деструктивных родительских воздействий, влияния авторитарных сект. Во-вторых, возможно получение за короткое время ценных обобщений данных о больших количествах исследуемых лиц. В-третьих, известно, что многие феномены изменяют свою специфику во время строгих лабораторных экспериментов. А корреляционный анализ предоставляет исследователю возможность оперировать информацией, полученной в условиях, максимально приближенных к реальным. В-четвертых, осуществление статистического изучения динамики той или иной зависимости нередко создает предпосылки к достоверному прогнозированию психологических процессов и явлений.

Однако следует иметь в виду, что применение корреляционного метода связано и с весьма существенными принципиальными ограничениями.

Так, известно, что переменные вполне могут коррелировать и при отсутствии причинно-следственной связи между собой.

Это иногда возможно в силу действия случайных причин, при неоднородности выборки, из-за неадекватности исследовательского инструментария поставленным задачам. Такая ложная корреляция способна стать, скажем, «доказательством» того, что женщины дисциплинированнее мужчин, подростки из неполных семей более склонны к правонарушениям, экстраверты агрессивнее интровертов и т. п.

Необходимо запомнить: наличие корреляций не является показателем выраженности и направленности причинно-следственных отношений.

Другими словами, установив корреляцию переменных мы можем судить не о детерминантах и производных, а лишьо том, насколько тесно взаимосвязаны изменения переменных и каким образом одна из них реагирует на динамику другой.

Корреляция (Correlation) — это

Не со всеми проблемами можно справиться экспериментальным методом. Существует множество ситуаций, когда исследователь не может контролировать, какие испытуемые попадают в те или иные условия. Например, если надо проверить гипотезу, что люди с анорексией более чувствительны к изменениям вкуса, чем люди с нормальным весом, то не можем же мы собрать группу испытуемых с нормальным весом и потребовать, чтобы у половины из них появилась анорексия! На самом деле нам придется отобрать людей, уже страдающих анорексией, и тех, у кого вес в норме, и проверить, различаются ли они также по вкусовой чувствительности. Вообще говоря, можно использовать метод корреляций, чтобы определить связана ли некоторая переменная, которую мы не можем контролировать, с другой интересующей нас переменной, или, иначе говоря, коррелируют ли они между собой.

В вышеприведенном примере у переменной веса есть только два значения — нормальный и анорексичный. Чаще случается, что каждая из переменных может принимать много значений, и тогда надо определить, насколько величины одной и другой переменной коррелируют между собой. Определить это может статистический параметр, называемый коэффициентом корреляции и обозначаемый буквой r. Коэффициент корреляции позволяет оценить, насколько связаны две переменные, и выражается числом от -1 до +1. Ноль означает отсутствие связи; полная связь выражается единицей (+1, если отношение положительное, и -1, если оно отрицательное). По мере увеличения r от 0 до 1 сила связи возрастает.

Графики рассеивания, иллюстрирующие корреляцию. Эти гипотетические данные принадлежат 10 пациентам, каждый из которых имеет некоторое повреждение участков мозга, ответственных, насколько известно, за узнавание лиц. На рисунке пациенты располагаются вдоль горизонтали соответственно объему повреждения мозга, причем самая левая точка показывает пациента с наименьшим повреждением (10%), а самая правая точка показывает пациента с наибольшим повреждением (55%). Каждая точка на графике отражает показатель для отдельного пациента в тесте на узнавание лиц. Корреляция положительная и равна 0,90. На рисунке изображены те же самые данные, но теперь они показывают долю правильных ответов, а не ошибок. Здесь корреляция отрицательная, равная -0,90. На рисунке успехи пациентов в тесте на распознавание отображены в зависимости от их роста. Здесь корреляция равна нулю.

Суть коэффициента корреляции можно пояснить на примере графического представления данных гипотетического исследования. Как показано на рисунке, в исследовании участвуют пациенты, о которых заранее известно, что у них поврежден мозг, и это вызвало разной степени трудности в узнавании лиц (прозопагнозия). Предстоит выяснить, возрастает ли трудность, или ошибка узнавания лиц, с увеличением процента поврежденной мозговой ткани. Каждая точка на графике показывает результат для отдельного пациента при его тестировании на узнавание лиц. Например, пациент с 10%-ным повреждением ошибался в тесте на распознавание лиц в 15% случаев, а пациент с 55%-ным повреждением делал ошибки в 95% случаев. Если бы ошибка узнавания лиц постоянно возрастала с увеличением процента повреждения мозга, точки на графике располагались бы все время выше при движении слева направо; если бы они размещались на диагонали рисунка, коэффициент корреляции был бы r = 1,0. Однако несколько точек расположены по разные стороны этой линии, поэтому корреляция составляет около 90%. Корреляция 90% означает очень сильную связь между объемом поврежденного мозга и ошибками узнавания лиц. Корреляция на рисунке — положительная, поскольку большее повреждение мозга вызывает больше ошибок.

Если бы вместо ошибок мы решили отобразить долю правильных ответов в тесте на распознавание, то получили бы график, изображенный нарисунке. Здесь корреляция отрицательная (равная примерно -0,90), поскольку с увеличением повреждения мозга доля правильных ответов уменьшается. Диагональ на рисунке — это просто инверсный вариант той, что на предыдущем рисунке.

Корреляция (Correlation) — это

Наконец, обратимся к графику на рисунке. Здесь отображена доля ошибок пациентов в тесте на распознавание лиц в зависимости от их роста. Разумеется, нет оснований считать, что доля узнанных лиц связана с ростом пациента, и график подтверждает это. При движении слева направо точки не проявляют согласованного движения ни вниз, ни вверх, а разбросаны вокруг горизонтальной линии. Корреляция равна нулю.

Корреляция бывает положительной (+) и отрицательной (-). Знак корреляции показывает, связаны ли две переменные положительной корреляцией (величина обеих переменных растет или уменьшается одновременно) или отрицательной корреляцией (одна переменная растет при уменьшении другой). Предположим, например, что количество пропусков занятий студентом имеет корреляцию -0,40 с баллами в конце семестра (чем больше пропусков, тем меньше баллов). С другой стороны, корреляция между полученными баллами и количеством посещенных занятий будет +0,40. Прочность связи одна и та же, но знак ее зависит от того, считаем ли мы пропущенные или посещенные занятия.

По мере усиления связи двух переменных r увеличивается от 0 до 1. Чтобы лучше это представить, рассмотрим несколько известных положительных коэффициентов корреляции: коэффициент корреляции между баллами, полученными в первый год обучения в колледже, и баллами, полученными на втором году, составляет около 0,75, корреляция между показателями геста на интеллект в возрасте 7 лет и при повторном тестировании в 18 лет составляет примерно 0,70, корреляция между ростом одного из родителей и ростом ребенка во взрослом возрасте, составляет около 0,50, корреляция между результатами теста на способность к обучению, полученными в школе и в колледже, равна примерно 0,40, корреляция между баллами, полученными индивидуумами в бланковых тестах, и суждением психолога-эксперта об их личностных качествах составляет около 0,25.

В психологических исследованиях коэффициент корреляции 0,60 и выше считается достаточно высоким. Корреляция в диапазоне от 0,20 до 0,60 имеет практическую и теоретическую ценность и полезна при выдвижении предсказаний. К корреляции от 0 до 0,20 следует относиться осторожно, при выдвижении предсказаний ее польза минимальна.

Корреляция (Correlation) — это

Тесты. Знакомый пример использования корреляционного метода — тесты по измерению некоторых способностей, достижений и других психологических качеств. При тестировании группе людей, различающихся по какому-нибудь качеству (например, математическим способностям, ловкости рук или агрессивности), предъявляют некоторую стандартную ситуацию. Затем можно вычислить корреляцию между изменениями показателей данного теста и изменением другой переменной. Например, можно установить корреляцию между показателями группы студентов в тесте на математические способности и их оценками по математике при дальнейшем обучении в колледже; если корреляция значительная, то на основе результатов этого теста можно решить, кого из нового набора студентов можно перевести в группу с повышенными требованиями.

Тестирование — важный инструмент психологических исследований. Оно позволяет психологам получать большое количество данных о людях с минимальным отрывом их от повседневных дел и без применения сложного лабораторного оборудования. Построение тестов включает множество этапов, которые мы подробно рассмотрим в последующих главах.

Корреляция и причинно-следственные связи. Между экспериментальными и корреляционными исследованиями есть важное различие. Как правило, в экспериментальном исследовании систематически манипулируют одной переменной (независимой) с целью определить ее причинное воздействие на некоторые другие переменные (зависимые). Такие причинно-следственные связи нельзя вывести из корреляционных исследований. Ошибочное понимание корреляции как причинно-следственного отношения можно проиллюстрировать на следующих примерах. Может существовать корреляция между мягкостью асфальта на улицах города и количеством солнечных ударов, случившихся за день, но отсюда не следует, что размягченный асфальт выделяет какой-то яд, приводящий людей на больничную койку. На самом деле изменение обеих этих переменных — мягкости асфальта и числа солнечных ударов — вызывается третьим фактором — солнечным теплом. Еще один простой пример — высокая положительная корреляция между большим количеством аистов, гнездящихся во французских деревнях, и высокой рождаемостью, зарегистрированной там же. Предоставим изобретательным читателям самим догадываться о возможных причинах такой корреляции, не прибегая к постулированию причинно-следственной связи между аистами и младенцами. Эти примеры служат достаточным предостережением от понимания корреляции как причинно-следственного отношения. Если между двумя переменными есть корреляция, изменение одной может вызывать изменения другой, но без специальных экспериментов такой вывод будет неоправданным.

Источники и ссылки

ru.wikipedia.org — свободная энциклопедия Википедия

bank24.ru — круглосуточный банк деловой Российской Федерации

dic.academic.ru — портал словарей и эциклопедий

statsoft.ru — электронный учебник по статистике

superscalper.ru — сервис по скальпингу на FORTS и NYSE

machinelearning.ru — информационно-аналитический ресурс интеллектуального анализа данных

uchebnik.biz — студенческая библиотека гуманитарного направления

testent.ru — образовательный сайт Казахстана

fdvladimir.ru — Финансовый дом «Владимир» — брокер на рынке ценных бумаг

lib.qrz.ru — электронная библиотека технической направленности

uchimatchast.ru — сайт по прикладной математике

cito-web.yspu.org — Ярославский государственный педагогический университет

math.semestr.ru — он-лайн калькулятор математических и экономических величин

stathelp.ru — статистическая помощь, новости статистики

gaap.ru — теория и практика финансового учета

goldenfront.ru — сайт об инвестициях в золото

newsland.com — новости в Российской Федерации и мире

Энциклопедия инвестора. 2013.

Синонимы:

• Коррекция
• Коррупция

Полезное

Смотреть что такое «Корреляция» в других словарях:

• корреляция —    КОРРЕЛЯЦИЯ (с. 325) (от позднелат. correlatio соотношение) термин, применяемый в различных областях знания, в том числе и в психологии, для обозначения взаимного соотношения, соответствия понятий и явлений.    Большинство психологических… …   Большая психологическая энциклопедия

• КОРРЕЛЯЦИЯ — [лат. correlatio] взаимная связь, соотношение предметов или понятий. Словарь иностранных слов. Комлев Н.Г., 2006. КОРРЕЛЯЦИЯ новолатинск. от relata. Взаимное отношение, например, существующее между опекуном и опекаемым. Объяснение 25000… …   Словарь иностранных слов русского языка

• КОРРЕЛЯЦИЯ — (correlation) Степень зависимости между двумя переменными. Линейная корреляция между двумя переменными х и у определяется знаком и величиной Σi (xi μx )(yi μy), где μx и μy среднее значение х и у. Между двумя переменными существует положительная… …   Экономический словарь

• корреляция — соотношение, соотнесение, взаимосвязь, взаимозависимость, взаимообусловленность, взаимосоответствие Словарь русских синонимов. корреляция сущ., кол во синонимов: 8 • автокорреляция (1) …   Словарь синонимов

• КОРРЕЛЯЦИЯ — (от франц. correlation соотношение) в статистике понимается как взаимоотношение между изучаемыми статистическими величинами, рядами и группами; для определения наличия или отсутствия К. статистика пользуется особым методом. Метод К. применяется… …   Большая медицинская энциклопедия

• корреляция — — [http://www.rfcmd.ru/glossword/1.8/index.php?a=index d=23] корреляция Величина, характеризующая взаимную зависимость двух случайных величин X и Y — безразлично, определяется ли она некоторой причинной связью или просто случайным… …   Справочник технического переводчика

• Корреляция — взаимосвязь двух или нескольких величин, при которой изменения одной или нескольких из них приводят к изменению другой или других . К. считается простой, когда речь идет об отношениях между двумя величинами или переменными (например, между… …   Словарь бизнес-терминов

• КОРРЕЛЯЦИЯ — в математической статистике вероятностная или статистическая зависимость. В отличие от функциональной зависимости корреляция возникает тогда, когда зависимость одного из признаков от другого осложняется наличием ряда случайных факторов …   Большой Энциклопедический словарь

• КОРРЕЛЯЦИЯ — (от лат. correlatio соотношение) 1) в логике – отношение между двумя одинаковыми по форме связями. Если благодаря закономерному изменению структуры одна связь становится изоморфной (равной по форме) другой, тогда это отношение обеих связей… …   Философская энциклопедия

• корреляция — и, ж. corrélation f., нем. Korrelation &LT;лат. correlatio соотношение. Впервые отмечается в словаре Гавкина 1894 г. ЭС. Взаимная связь, соотношение предметов или понятий. Закон корреляции. Функциональная корреляция. БАС 1. Рост безработицы и… …   Исторический словарь галлицизмов русского языка

• Корреляция — [correlation] величина, характеризующая взаимную зависимость двух случайных величин X и Y безразлично, определяется ли она некоторой причинной связью или просто случайным совпадением (ложной корреляцией). Для того, чтобы определить эту… …   Экономико-математический словарь

Разница между положительной и отрицательной корреляцией (Наука и природа)

Положительная корреляция против отрицательной корреляции

Корреляция является мерой силы взаимосвязи между двумя переменными. Коэффициент корреляции количественно определяет степень изменения одной переменной на основе изменения другой переменной. В статистике корреляция связана с концепцией зависимости, которая представляет собой статистическую связь между двумя переменными.

Коэффициент корреляции Пирсона или Коэффициент корреляции Пирсона-Момента, или просто коэффициент корреляции получают по следующим формулам.

Для населения:

Для образца:

и следующее выражение эквивалентно приведенному выше выражению.

и являются стандартными баллами X и Y соответственно.  это среднее и с_Икс и с_Y стандартные отклонения X и Y.

Коэффициент корреляции Пирсона (или просто коэффициент корреляции) является наиболее часто используемым коэффициентом корреляции и действителен только для линейного отношения между переменными. r это значение между -1 и 1 (-1 ≤ r ≤ +1). Если r = 0, связь не существует, а если r ≥ 0, связь прямо пропорциональна, и значение одной переменной увеличивается вместе с другой. Если r ≤ 0, одна переменная уменьшается по мере увеличения другой, и наоборот.

Из-за условия линейности коэффициент корреляции r также можно использовать для установления наличия линейной зависимости между переменными.

 

В чем разница между положительной и отрицательной корреляцией?

• Когда существует положительная корреляция (r> 0) между двумя случайными переменными, одна переменная перемещается пропорционально другой переменной. Если одна переменная увеличивается, другая увеличивается. Если одна переменная уменьшается, другая уменьшается.

• Когда есть отрицательная корреляция

• Линия, аппроксимирующая положительную корреляцию, имеет положительный градиент, а линия, аппроксимирующая отрицательную корреляцию, имеет отрицательный градиент.

Корреляция — что это такое простыми словами

Обновлено 24 июля 2021

1. Что это такое
2. Коэффициент корреляции
3. Причины корреляции и гипотезы
4. Как с помощью этого становятся богаче
5. Памятка

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Когда некоторые люди слышат слово «корреляция», то зачастую просто впадают в ступор. Оно и понятно: жуткий термин из мира высшей математики и статистики.

Сразу представляются унылые графики, многоэтажные формулы, при взгляде на которые хочется забиться в угол и плакать. На самом деле все гораздо проще.

Потратив несколько минут на прочтение этой статьи, вы узнаете, что такое корреляция и как ее использовать в повседневной жизни.

Определение корелляции — что это

Простыми словами корреляция – это взаимосвязь двух или нескольких случайных параметров. Когда одна величина растет или уменьшается, другая тоже изменяется.

Объясним на примере: существует корреляция между температурой воздуха и потреблением мороженого. Чем жарче погода, тем больше холодного лакомства покупают люди. И наоборот.

Такие закономерности устанавливаются путем исследования больших объемов статистических данных. Собираем информацию о потреблении мороженого за несколько лет и сведения о колебаниях температуры за тот же период. А дальше сопоставляем и ищем зависимость.

Коррелировать – это значит быть взаимосвязанным с чем-то. Существует положительная и отрицательная корреляции.

При положительной чем больше один параметр, тем больше и другой. Например, чем масштабнее траты фермера на удобрения, тем обильнее урожай. При обратной корреляции рост одной величины сопровождается уменьшением другой. Чем выше здание, тем хуже оно противостоит землетрясениям.

Корреляция — это взаимосвязь без гарантий

Рассмотрим пример прямой корреляции: чем выше уровень благосостояния человека, тем больше его продолжительность жизни. Обеспеченные люди питаются качественной пищей и своевременно получают врачебную помощь. В отличие от бедняков.

Однако нельзя с уверенностью сказать, что определенный олигарх проживет дольше вот этого нищего.

Это лишь статистическая вероятность, которая может не сработать для одного конкретного случая. Этим корреляция отличается от линейной зависимости, где исход известен со 100-процентной вероятностью.

Но если мы возьмем выборку из сотни тысяч богачей и такого же числа малоимущих, сравним их продолжительность жизни, то общая тенденция будет верна.

Коэффициент корреляции

Это число, которое обозначается как «r». Оно находится в промежутке от -1 до 1. Отражает силу и полюс взаимосвязи величин. Посмотрим на примере:

Значение коэффициента	Какая корреляция?	О чем это говорит?
r=1	Сильная положительная корреляция	Люди, которые едят чернику, обладают острым зрением. Ешьте чернику!
r меньше 0,5	Слабая положительная корреляция	Некоторые люди, которые любят чернику, обладают острым зрением. Но это не точно. Короче, ничего не пока понятно. Но лучше есть чернику на всякий случай.
r=0	Корреляция отсутствует	Черника и зрение никак не связаны.
r меньше -0,5	Слабая отрицательная корреляция	Бывают случаи ухудшения зрения из-за черники. Не стоит рисковать.
r=-1	Сильная отрицательная корреляция	Практически все, кто ел чернику, ослепли. Берегитесь черники!

Величина коэффициента корреляции рассчитывается по формуле:

Если внезапно потемнело в глазах и возникло непреодолимое желание закрыть статью (синдром гуманитария), то есть вариант попроще. Microsoft Exel все выполнит сам при помощи функции «КОРРЕЛ». Делается это так:

Судя по расчетам, рост человека практически никак не влияет на уровень зарплаты.

Реальные причины корреляции и возможные гипотезы

Курс доллара и стоимость нефти отрицательно коррелируют. Можем выдвинуть гипотезу: повышение цен на черное золото вызывает падение стоимости американской валюты. Но почему так происходит? Откуда взялась связь между этими явлениями?

Определение причины корреляции – это очень сложная задача. Переплетаются тысячи различных факторов, часть из которых скрыта.

Возможно, дело в том, что США – крупнейший потребитель нефти в мире. Каждый день они импортируют около 7,2 миллиона баррелей. Снижение цены на черное золото – хорошо для американской экономики, ведь позволяет тратить меньше денег. Следовательно, доллар растет.

Корреляция предоставляет возможность сделать вывод из статистических данных.

Например, мы выяснили, что существует отрицательная взаимосвязь между доходом персонала и его эффективностью в работе. Наша гипотеза: «Лентяи и бездельники получают больше, чем ответственные сотрудники». Тогда мы пересмотрим систему мотивации и избавимся от бесполезных людей.

Гипотеза – это лишь статистический вывод, предположение. Она вполне может оказаться ошибочной.

Согласно статистике, чем больше пожарных участвует в тушении огня, тем существенней размер ущерба. Какую гипотезу можем сделать отсюда? Пожарные приносят вред, давайте сократим их! Но если разобраться, то настоящая причина повреждения – это огонь. А увеличение числа лиц, задействованных в его тушении, – следствие масштаба пожара.

Наша вселенная бесконечна, а значит всегда можно найти несколько переменных, которые будут коррелировать между собой, несмотря на полное отсутствие причинно-следственных связей. Даже самое буйное воображение не сможет объяснить, что объединяет сыр и одеяло-убийцу:

Более подробно на эту тему смотрите в видео:

Как при помощи корреляции люди становятся богаче

Главное правило любого инвестора: не класть все яйца в одну корзину. Вложения рекомендуется диверсифицировать (что это?) – распределять. Поэтому люди покупают акции не одной компании, а десятка разных, формируя инвестиционные портфели. Если котировки какой-то фирмы упадут, то оставшиеся девять смогут отыграть падение или хотя бы уменьшить убытки.

Но это в теории, а на практике все портит корреляция. Проблема в том, что стоимости акций разных компаний внутри отрасли или даже всей страны могут сильно коррелировать. Проблемы огромной корпорации провоцируют панику на рынке, снижают стоимость иных активов, на первый взгляд не связанных между собой. В 2008 году случился крах Lehman Brothers, который вызвал цепную реакцию и обвал на мировых рынках.

Поэтому при инвестировании нужно стараться выбирать направления, которые не связаны между собой (r стремится к 0).

Например, пара «золото – облигации США» = -0,13. Если собрать портфель из совершенно независимых частей, риски финансовых потерь сократятся.

Территориальное приближение активов друг к другу усиливает корреляцию. Значит, нужно рассматривать варианты в разных точках мира, максимально удаленных друг от друга.

В жизни этот принцип тоже действует. Если ваши навыки и знания позволяют трудиться программистом, таксистом, сантехником и журналистом – вы хорошо защищены от риска безработицы.

Памятка

1. Корреляция – это соотношение, взаимозависимость нескольких переменных.
2. Связь бывает положительной и отрицательной.
3. Коэффициент корреляции определяет степень взаимозависимости одной переменной от другой.
4. На основании корреляции люди выдвигают гипотезы (часто ошибочные).
5. Истинная причина корреляции порою скрыта под множеством факторов и внешних сил.
6. Бывает ложная корреляционная зависимость.
7. Раскладывая яйца по корзинам, помните о том, что они не должны коррелироваться друг с другом.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

NOT_SET | Tradimo

Корреляция между рынками возникает тогда, когда цена в двух или более рынках изменяется одновременно. Корреляция может быть положительной: если цена одного актива повышается, то и цена другого актива также повышается. Корреляция может также быть и отрицательной: если цена одного актива растет, то цена второго – падает.

Причины, лежащие в основе рыночной корреляции, различаются между рынками. Определение их может позволить трейдеру определить будущие ценовые маневры, в разумных пределах.

Важно заметить, что корреляция между рынками может нарушаться, если в более широкой экономической среде возникают потрясения или изменения условий, такие как финансовый кризис.

Капитал перемещается между рынками, вызывая корреляцию

Самый простой способ понять принципы рыночной корреляции заключается в том, чтобы подумать о движении капитала между рынками.

Положительная корреляция между золотом и австралийским долларом

Австралийский доллар положительно коррелирует с ценой золота. Это происходит, потому что Австралия – важный производитель золота, которое она экспортирует на мировой рынок. Чтобы купить золото у австралийских поставщиков, покупателю сначала необходимо конвертировать используемую им валюту в австралийский доллар.

Если цена золота растет, покупатель золота должен будет приобрести больше австралийских долларов для его покупки. Поскольку спрос на австралийские доллары теперь повысился из-за необходимости купить товар, их цена относительно других валют растет. Таким образом, существует корреляция между золотом и австралийскими долларами.

Отрицательная корреляция между долларами США и золотом

В нормальных рыночных условиях инвесторы ищут способы заработать деньги с помощью инвестирования капитала в финансовые рынки, например облигаций или акций в США. Подобные инвестиции считаются рискованными из-за потенциальных волатильности и потерь, которые могут произойти, однако, подобные предприятия могут принести существенную прибыль.

Хоть золото традиционно все еще и является ценным в наше время, инвесторы могут посчитать, что большую прибыль им принесет инвестирование в рынок акций США, что приводит к меньшему спросу на золото. Следовательно, капитал перемещается от золота к акциям США. Акции в США могут быть куплены лишь с использованием долларов США, поэтому при повышении спроса на акции, повышается спрос и на доллар США, в результате чего он растет в цене. Таким образом, существует отрицательная корреляция между долларом США и золотом.

В моменты экономической нестабильности инвесторы могут потерять интерес к рискованным предприятиям вроде акций США или облигаций, и искать способов для более безопасного вложения капитала, например, в золото. Инвесторы продают свои рискованные активы и получают доллары США, чтобы приобрести золото на мировом рынке. Тогда спрос на доллар США падает, а спрос на золото – растет. Таким образом, стоимость доллара США упала, а стоимость золота – возросла.

Рыночные корреляции могут разрушаться

Временами нормальные корреляции между рынками нарушаются.

Для примера вспомним корреляцию между долларом США и золотом. Было выяснено, что в периоды экономического спада инвесторы и трейдеры будут искать возможностей для более безопасных инвестиций в золото и продавать доллары.

Однако в аномальных условиях, таких как кризис, подобное поведение рынка может начать нарушаться. Экономические условия вполне могут стать настолько плохими, что инвесторы будут искать безопасных вложений в различные активы, которые могут включать и государственные облигации США, и золото. Чтобы приобрести государственные облигации США, необходимо приобрести доллар США, в результате чего растет их цена. Золото, будучи безопасным для вложений, также растет в цене из-за увеличения спроса.

В этом примере повышается цена и доллара США, и золота, в результате чего отрицательная корреляция между ними нарушается.

Использование рыночной корреляции в торговле

Трейдер может использовать коррелированные рынки, чтобы попробовать определить будущие ценовые маневры одного рынка, используя данные о другом.

AUD/USD и золото

Из примера с австралийским долларом и золотом ясно, что в нормальных рыночных условиях существует положительная корреляция между ними.

Скажем, было несколько отчетов с негативными данными об экономике США. Инвесторы могут решить, что подобные условия бизнеса стали более сложными для работы, и изъять капиталы с фондовых рынков. Капиталы затем перемещаются с фондового рынка, поскольку инвесторы ищут возможностей для вложения капитала в других местах.

Инвесторы понимают, что на золото может иметься спрос, когда инвесторы ищут безопасных вложений во время рыночной нестабильности. Трейдеры знают, что поскольку Австралия является крупным производителем золота, австралийский доллар вырастет в цене, чтобы была возможность купить все более дорогое золото. Трейдеры также понимают, что для этого, скорее всего, необходимо продать доллары США. В результате стоимость доллара США снижается, а стоимость австралийского доллара – растет.

В результате, трейдеры могут искать возможностей для покупки AUS/USD.

Нефть и CAD

В нормальных рыночных условиях существует положительная корреляция между канадским долларом и нефтью.

В настоящий момент США являются крупнейшим в мире потребителем нефти. Канада же является одним из крупнейших ее экспортеров. Экономика Канады сильно зависит от США – 75% суммарного экспорта Канады и почти вся производимая ей нефть идут в США.

Импортерам нефти в США приходится использовать канадские доллары, чтобы покупать канадскую нефть. Когда цена нефти растет, необходимо больше канадских долларов для ее покупки, так что импортерам приходится конвертировать больше долларов США в канадские. В результате этого повышается спрос на канадские доллары, снижается спрос на доллары США, и стоимость канадского доллара относительно доллара США растет.

Можно искать возможности для торговли канадским долларом, когда происходящее в мире с большой вероятностью приведет к подорожанию нефти. Например, когда ураган заставляет прекратить производство нефти в некоторых частях Соединенных Штатов. Поскольку производство остановилось, предложение нефти снижается. Спрос на нефть не снизился, поэтому цена нефти растет, а также растет спрос на канадские доллары, как было объяснено выше. Трейдеры теперь могут искать возможности для покупки канадских долларов.

Фондовые рынки и швейцарский франк

В нормальных рыночных условиях существует отрицательная корреляция между фондовыми рынками и швейцарским франком.

Швейцарский франк традиционно считается безопасным убежищем, поэтому в периоды экономической нестабильности инвесторы ищут способы вложения капитала в швейцарский франк вместо других, более рискованных активов, таких как фондовые рынки.

Таким образом, если, например, выпущены негативные отчеты об экономике США, инвесторы могут изъять капитал из фондовых рынков США и вложить его в безопасные активы вроде швейцарского франка.

В таком случае, инвесторы будут приобретать швейцарский франк, что увеличивает его цену из-за увеличения спроса. Поэтому когда трейдер наблюдает спад в экономике США, он может искать возможности для покупки швейцарского франка против других валют.

Из этого урока вы узнали, что …

• … рыночная корреляция означает, что два или более рынка изменяются одинаково.
• … положительная корреляция заключается в том, что цена одного актива растет, когда растет цена другого.
• … примером положительной корреляции может служить связь между золотом и австралийским долларом.
• … отрицательная корреляция – это снижение цены одного актива при повышении цены другого.
• … примером отрицательной корреляции может служить связь между долларом США и золотом.
• … в аномальных условиях, таких как экономический или финансовый кризис, корреляция между рынками может нарушаться.
• … трейдеры могут использовать рыночные корреляции для поиска возможности для торговли. Если выпускаются новости, которые повлияют на определенный рынок, имеет смысл искать возможности для торговли на коррелированных с ним.
• … пример подобного процесса: если на экономику США оказывается негативное влияние, трейдеры могут искать возможности для покупки австралийского доллара.

Линейный коэффициент корреляции Пирсона — statanaliz.info

Обнаружение взаимосвязей между явлениями – одна из главных задач статистического анализа. На то есть две причины. Первая. Если известно, что один процесс зависит от другого, то на первый можно оказывать влияние через второй. Вторая. Даже если причинно-следственная связь отсутствует, то по изменению одного показателя можно предсказать изменение другого.

Взаимосвязь двух переменных проявляется в совместной вариации: при изменении одного показателя имеет место тенденция изменения другого. Такая взаимосвязь называется корреляцией, а раздел статистики, который занимается взаимосвязями – корреляционный анализ.

Корреляция – это, простыми словами, взаимосвязанное изменение показателей. Она характеризуется направлением, формой и теснотой. Ниже представлены примеры корреляционной связи.

Далее будет рассматриваться только линейная корреляция. На диаграмме рассеяния (график корреляции) изображена взаимосвязь двух переменных X и Y. Пунктиром показаны средние.

При положительном отклонении X от своей средней, Y также в большинстве случаев отклоняется в положительную сторону от своей средней. Для X меньше среднего, Y, как правило, тоже ниже среднего. Это прямая или положительная корреляция. Бывает обратная или отрицательная корреляция, когда положительное отклонение от средней X ассоциируется с отрицательным отклонением от средней Y или наоборот.

Линейность корреляции проявляется в том, что точки расположены вдоль прямой линии. Положительный или отрицательный наклон такой линии определяется направлением взаимосвязи.

Крайне важная характеристика корреляции – теснота. Чем теснее взаимосвязь, тем ближе к прямой точки на диаграмме. Как же ее измерить?

Складывать отклонения каждого показателя от своей средней нет смысла, получим нуль. Похожая проблема встречалась при измерении вариации, а точнее дисперсии. Там эту проблему обходят через возведение каждого отклонения в квадрат.

Квадрат отклонения от средней измеряет вариацию показателя как бы относительно самого себя. Если второй множитель в числителе заменить на отклонение от средней второго показателя, то получится совместная вариация двух переменных, которая называется ковариацией.

Чем больше пар имеют одинаковый знак отклонения от средней, тем больше сумма в числителе (произведение двух отрицательных чисел также дает положительное число). Большая положительная ковариация говорит о прямой взаимосвязи между переменными. Обратная взаимосвязь дает отрицательную ковариацию. Если количество совпадающих по знаку отклонений примерно равно количеству не совпадающих, то ковариация стремится к нулю, что говорит об отсутствии линейной взаимосвязи.

Таким образом, чем больше по модулю ковариация, тем теснее линейная взаимосвязь. Однако значение ковариации зависит от масштаба данных, поэтому невозможно сравнивать корреляцию для разных переменных. Можно определить только направление по знаку. Для получения стандартизованной величины тесноты взаимосвязи нужно избавиться от единиц измерения путем деления ковариации на произведение стандартных отклонений обеих переменных. В итоге получится формула коэффициента корреляции Пирсона.

Показатель имеет полное название линейный коэффициент корреляции Пирсона или просто коэффициент корреляции.

Коэффициент корреляции показывает тесноту линейной взаимосвязи и изменяется в диапазоне от -1 до 1. -1 (минус один) означает полную (функциональную) линейную обратную взаимосвязь. 1 (один) – полную (функциональную) линейную положительную взаимосвязь. 0 – отсутствие линейной корреляции (но не обязательно взаимосвязи). На практике всегда получаются промежуточные значения. Для наглядности ниже представлены несколько примеров с разными значениями коэффициента корреляции.

Таким образом, ковариация и корреляция отражают тесноту линейной взаимосвязи. Последняя используется намного чаще, т.к. является относительным показателем и не имеет единиц измерения.

Диаграммы рассеяния дают наглядное представление, что измеряет коэффициент корреляции. Однако нужна более формальная интерпретация. Эту роль выполняет квадрат коэффициента корреляции r², который называется коэффициентом детерминации, и обычно применяется при оценке качества регрессионных моделей. Снова представьте линию, вокруг которой расположены точки.

Линейная функция является моделью взаимосвязи между X иY и показывает ожидаемое значение Y при заданном X. Коэффициент детерминации – это соотношение дисперсии ожидаемых Y (точек на прямой линии) к общей дисперсии Y, или доля объясненной вариации Y. При r = 0,1 r² = 0,01 или 1%, при r = 0,5 r² = 0,25 или 25%.

Выборочный коэффициент корреляции

Коэффициент корреляции обычно рассчитывают по выборке. Значит, у аналитика в распоряжении не истинное значение, а оценка, которая всегда ошибочна. Если выборка была репрезентативной, то истинное значение коэффициента корреляции находится где-то относительно недалеко от оценки. Насколько далеко, можно определить через доверительные интервалы.

Согласно Центральное Предельной Теореме распределение оценки любого показателя стремится к нормальному с ростом выборки. Но есть проблемка. Распределение коэффициента корреляции вблизи придельных значений не является симметричным. Ниже пример распределения при истинном коэффициенте корреляции ρ = 0,86.

Предельное значение не дает выйти за 1 и, как бы «поджимает» распределение справа. Симметричная ситуация наблюдается, если коэффициент корреляции близок к -1.

В общем рассчитывать на свойства нормального распределения нельзя. Поэтому Фишер предложил провести преобразование выборочного коэффициента корреляции по формуле:

Распределение z для тех же r имеет следующий вид.

Намного ближе к нормальному. Стандартная ошибка z равна:

Далее исходя из свойств нормального распределения несложно найти верхнюю и нижнюю границы доверительного интервала для z. Определим квантиль стандартного нормального распределения для заданной доверительной вероятности, т.е. количество стандартных отклонений от центра распределения.

c_γ – квантиль стандартного нормального распределения;
N^-1 – функция обратного стандартного распределения;
γ – доверительная вероятность (часто 95%).
Затем рассчитаем границы доверительного интервала.

Нижняя граница z:

Верхняя граница z:

Теперь обратным преобразованием Фишера из z вернемся к r.
Нижняя граница r:

Верхняя граница r:

Это была теоретическая часть. Переходим к практике расчетов.

Как посчитать коэффициент корреляции в Excel

Корреляционный анализ в Excel лучше начинать с визуализации.

На диаграмме видна взаимосвязь двух переменных. Рассчитаем коэффициент парной корреляции с помощью функции Excel КОРРЕЛ. В аргументах нужно указать два диапазона.

Коэффициент корреляции 0,88 показывает довольно тесную взаимосвязь между двумя показателями. Но это лишь оценка, поэтому переходим к интервальному оцениванию.

Расчет доверительного интервала для коэффициента корреляции в Excel

В Эксель нет готовых функций для расчета доверительного интервала коэффициента корреляции, как для средней арифметической. Поэтому план такой:

— Делаем преобразование Фишера для r.
— На основе нормальной модели рассчитываем доверительный интервал для z.
— Делаем обратное преобразование Фишера из z в r.

Удивительно, но для преобразования Фишера в Excel есть специальная функция ФИШЕР.

Стандартная ошибка z легко подсчитывается с помощью формулы.

Используя функцию НОРМ.СТ.ОБР, определим квантиль нормального распределения. Доверительную вероятность возьмем 95%.

Значение 1,96 хорошо известно любому опытному аналитику. В пределах ±1,96σ от средней находится 95% нормально распределенных величин.

Используя z, стандартную ошибку и квантиль, легко определим доверительные границы z.

Последний шаг – обратное преобразование Фишера из z назад в r с помощью функции Excel ФИШЕРОБР. Получим доверительный интервал коэффициента корреляции.

Нижняя граница 95%-го доверительного интервала коэффициента корреляции – 0,724, верхняя граница – 0,953.

Надо пояснить, что значит значимая корреляция. Коэффициент корреляции статистически значим, если его доверительный интервал не включает 0, то есть истинное значение по генеральной совокупности наверняка имеет тот же знак, что и выборочная оценка.

Несколько важных замечаний

1. Коэффициент корреляции Пирсона чувствителен к выбросам. Одно аномальное значение может существенно исказить коэффициент. Поэтому перед проведением анализа следует проверить и при необходимости удалить выбросы. Другой вариант – перейти к ранговому коэффициенту корреляции Спирмена. Рассчитывается также, только не по исходным значениям, а по их рангам (пример показан в ролике под статьей).

2. Синоним корреляции – это взаимосвязь или совместная вариация. Поэтому наличие корреляции (r ≠ 0) еще не означает причинно-следственную связь между переменными. Вполне возможно, что совместная вариация обусловлена влиянием третьей переменной. Совместное изменение переменных без причинно-следственной связи называется ложная корреляция.

3. Отсутствие линейной корреляции (r = 0) не означает отсутствие взаимосвязи. Она может быть нелинейной. Частично эту проблему решает ранговая корреляция Спирмена, которая показывает совместный рост или снижение рангов, независимо от формы взаимосвязи.

В видео показан расчет коэффициента корреляции Пирсона с доверительными интервалами, ранговый коэффициент корреляции Спирмена.

↓ Скачать файл с примером ↓

Поделиться в социальных сетях:

Корреляция

Корреляция

Адаптировано из: Вводная статистика: концепции, модели и приложения
Дэвид В. Стокбургер

Комментарии, выделенные курсивом, предоставлены Линдой Вульф

---

КОРРЕЛЯЦИЯ

ОПРЕДЕЛЕНИЕ

Коэффициент корреляции произведения Пирсона и момента (r) или коэффициент корреляции для краткости — это мера степени линейной связи между двумя переменными , обычно обозначаемыми X и Y.В то время как в регрессии акцент делается на предсказании одной переменной от другой, в корреляции акцент делается на степени, в которой линейная модель может описывать взаимосвязь между двумя переменными. В регрессии интерес является направленным, одна переменная является прогнозируемой, а другая является прогнозирующей; в корреляции интерес ненаправлен, отношения — критический аспект.

Коэффициент корреляции может принимать любое значение от плюс до минус единицы.

Знак коэффициента корреляции (+, -) определяет направление взаимосвязи, положительное или отрицательное.Положительный коэффициент корреляции означает, что по мере увеличения значения одной переменной значение другой переменной увеличивается; по мере того, как одно уменьшается, другое уменьшается. Отрицательный коэффициент корреляции указывает на то, что по мере увеличения одной переменной другая уменьшается, и наоборот.

Помните, что корреляция не означает причинно-следственную связь. На основании корреляции нельзя делать причинно-следственные выводы.

Есть две причины, по которым мы не можем сделать причинно-следственные утверждения:

1. Мы не знаем направления причины — X вызывает Y или Y вызывает X?
2. Может быть задействована третья переменная «Z», которая отвечает за ковариацию между X и Y

Абсолютное значение коэффициента корреляции измеряет силу взаимосвязи.Коэффициент корреляции r = 0,50 указывает на более сильную степень линейной зависимости, чем при r = 0,40. Точно так же коэффициент корреляции r = -. 50 показывает большую степень взаимосвязи, чем один из r = .40. Таким образом, нулевой коэффициент корреляции (r = 0,0) указывает на отсутствие линейной зависимости, а коэффициенты корреляции r = + 1,0 и r = -1,0 указывают на идеальную линейную зависимость.

ПОНИМАНИЕ И ИНТЕРПРЕТАЦИЯ КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ

Коэффициент корреляции можно понять различными способами, каждый из которых теперь будет рассмотрен по очереди.

Диаграммы рассеяния

Мы можем построить график данных, используемых при вычислении коэффициента корреляции. По сути, с помощью корреляции моментов продукта Пирсона мы исследуем взаимосвязь между двумя переменными — X и Y. Построив каждую пару данных (у вас будут наборы оценок для X и Y), вы создадите график, называющий диаграмму рассеяния или корреляционная диаграмма. Таким образом, если вы строили график роста и веса всех детей в первом классе с двадцатью учениками, вы бы поместили одну точку на график в точке пересечения роста и веса каждого ученика.Для корреляции не имеет значения, какая переменная идет по оси x, а какая — по оси y. Однако для линейной регрессии переменная, которая является предиктором, идет по оси x. Прогнозируемая переменная идет по оси ординат.

Чтобы оценить степень взаимосвязи, нужно смотреть как на наклон линии, которая лучше всего подходит для точек данных, так и на степень разброса от той же линии. В корреляции мы не проводим черту; в линейной регрессии мы вычисляем положение линии.Чем более разбросаны точки данных, тем ниже корреляция. Чем ближе все точки данных к линии, другими словами, чем меньше разброс, тем выше степень корреляции.

Диаграммы рассеяния, представленные ниже, возможно, лучше всего иллюстрируют, как изменяется коэффициент корреляции при изменении линейной зависимости между двумя переменными. При r = 0,0 точки сильно разбросаны по графику, большинство из которых имеют форму круга. По мере увеличения линейной зависимости круг становится все более и более эллиптическим по форме, пока не будет достигнут предельный случай (r = 1.00 или r = -1,00), и все точки попадают на прямую линию.

Ряд диаграмм рассеяния и связанных с ними коэффициентов корреляции представлены ниже для того, чтобы учащийся мог лучше оценить значение коэффициента корреляции на основе диаграммы рассеяния в соответствующем компьютерном упражнении.

При изучении диаграмм рассеяния ниже проверьте как размер (степень взаимосвязи), так и знак (положительная или отрицательная корреляция).

---

r = 1.00

---

г = -,54

---

r = 0,85

---

г = -,94

---

г = 0,42

---

г = -,33

---

r = 0,17

---

г = 0,39

---

Другие примеры

---

Наклон линии регрессии z-значений

Коэффициент корреляции — это наклон (b) линии регрессии, когда обе переменные X и Y были преобразованы в z-значения.Чем больше коэффициент корреляции, тем круче наклон. Это связано с различием между интуитивной линией регрессии и фактической линией регрессии, о которой говорилось выше.

Эту интерпретацию коэффициента корреляции, возможно, лучше всего проиллюстрировать на примере с числами. Необработанные значения оценок переменных X и Y представлены в первых двух столбцах следующей таблицы. Вторые два столбца — это столбцы X и Y, преобразованные с помощью преобразования z-оценки.

То есть из каждой исходной оценки в столбцах X и Y вычитается среднее значение, а затем результат делится на стандартное отклонение выборки. Таблица выглядит следующим образом:

	Х	Я	z X	z Y
	12	33	-1.07	-0,61
	15	31	-0,07	-1,38
	19	35	-0,20	0,15
	25	37	0.55	.92
	32	37	1,42	.92
	20.60	34,60	0.0	0,0
=	8,02	2,61	1.0	1.0

С приведенными выше числами следует отметить два момента: (1) коэффициент корреляции инвариантен при линейном преобразовании X и / или Y, и (2) наклон линии регрессии, когда и X, и Y были преобразованы в z-значения — коэффициент корреляции.

Сначала вычисление коэффициента корреляции с исходными оценками X и Y дает r = 0,85. Затем вычисление коэффициента корреляции с z _X и z _Y дает то же значение, r = 0,85. Поскольку преобразование z-оценки является частным случаем линейного преобразования (X ‘= a + bX), можно доказать, что коэффициент корреляции инвариантен (не изменяется) при линейном преобразовании X и / или Y Читатель может проверить это, вычислив коэффициент корреляции, используя X и z _Y или Y и z _X .По сути, это означает, что изменение масштаба переменной X или Y не изменит размер коэффициента корреляции, пока преобразование соответствует требованиям линейного преобразования.

Интерпретация отклонений

Квадрат коэффициента корреляции (r ² ) — это доля дисперсии по Y, которую можно учесть, зная X. И наоборот, это пропорция дисперсии по X, которую можно учесть, зная Y.

Квадрат коэффициента корреляции также известен как коэффициент детерминации . Это один из лучших способов оценки прочности отношений. Например, мы знаем, что корреляция между ростом и весом приблизительно равна r = 0,70. Если возвести это число в квадрат, чтобы найти коэффициент детерминации — r-квадрат = 0,49 Таким образом, 49 процентов веса человека напрямую приходится на его рост и наоборот.

Вернуться на главную страницу статистики

Понимание корреляций | Управление оценки образования

ScorePak® может вычислять коэффициенты корреляции моментов продукта Пирсона среди любого количества оценок любого типа.Результаты представлены в квадратной корреляционной матрице, каждая из которых содержит до десяти переменных. Если запрашиваются взаимные корреляции между более чем десятью переменными, будет создано несколько матриц.

Пример отчета о корреляции (9K PDF)

Коэффициенты корреляции

Коэффициенты корреляции показывают степень взаимосвязи двух оценок и направление этой взаимосвязи. Они отражают тенденцию переменных к «совместному изменению»; то есть, чтобы изменения значения одной переменной были связаны с изменениями значения другой.При интерпретации коэффициентов корреляции важны два свойства.

• Звездная величина . Значения корреляции варьируются от -1,00 до 1,00. Чем больше абсолютное значение коэффициента (размер числа без учета знака), тем больше величина отношения. Например, корреляции 0,60 и -60 имеют равную величину, и обе они больше, чем корреляция 0,30. Когда нет линейной зависимости, корреляция будет 0,00; когда существует идеальная линейная зависимость (взаимно однозначное соответствие между значениями переменных), корреляция будет равна 1.00 или -1.00.
• Направление . Направление связи (положительное или отрицательное) обозначается знаком коэффициента. Положительная корреляция означает, что увеличение значения одного балла обычно сопровождается увеличением значения другого. Отрицательная корреляция означает, что увеличение одного сопровождается уменьшением другого.

Устный перевод

Поскольку оценки ScorePak®, как правило, являются оценками за тесты, можно ожидать, что большинство взаимосвязей между ними будет положительным.Чем в большей степени тесты измеряют одно и то же, тем сильнее взаимосвязь между ними. Баллы часто взвешиваются и суммируются для создания сводного балла, который затем используется для выставления оценок. В таких приложениях желательны умеренные положительные корреляции (r> .30) между оценками. Отрицательная или небольшая положительная корреляция (r <0,20) между результатами тестов означает, что совокупная оценка может быть ненадежной.

Отсутствующие данные

При вычислении корреляций ScorePak® включает пары наблюдений, для которых не пропущен ни один результат теста.Однако ScorePak® не удаляет все дело только потому, что отсутствуют данные по одному или нескольким оценкам; если вы взаимно коррелируете несколько оценок, результаты тестов для конкретного человека будут включены в те коэффициенты, для которых присутствуют обе оценки, и исключены из тех коэффициентов, для которых одна или обе оценки отсутствуют.

Составные оценки создаются путем объединения оценок с использованием одного или нескольких шагов преобразования. Сводная оценка может отсутствовать, а может и не отсутствовать, если отсутствует одна или несколько оценок, на которых она основана.Проверьте описание пропущенных значений для каждого преобразования, если вы планируете коррелировать составные баллы. В общем, корреляция составной оценки с оценками, из которых она получена, обычно относительно велики из-за общей дисперсии оценок с составной оценкой. Однако эти «частичные-целые» корреляции могут быть обманчиво малыми, если в оценках, составляющих сводную оценку, много недостающих данных, и для составной оценки не устанавливается значение «пропущено», если она содержит недостающие оценки.

Затухание

Важно помнить, что результаты тестов сами по себе в некоторой степени ненадежны. Можно сопоставить только достоверные части двух наборов оценок; ненадежная часть является случайной ошибкой и, следовательно, не будет коррелированной. В результате величина корреляции между любыми двумя результатами тестов ограничивается или ослабляется ненадежностью каждого из них. Если достоверность результатов теста известна, корреляцию можно скорректировать на ослабление. ScorePak® не делает эту поправку, потому что коэффициент надежности недоступен в то время, когда программа вычисляет корреляции.Однако, если вы коррелируете необработанные оценки, вы можете использовать коэффициенты надежности, указанные в ScorePak® Item Analysis, чтобы исправить корреляции в соответствии со следующей формулой:

rxy ’= rxy / [(SQRT (rxx * ryy)], где

rxy ’= скорректированная корреляция результата теста« x »с оценкой теста« y »
rxy = нескорректированная корреляция
rxx = надежность результата теста« x »
ryy = надежность результата теста« y »

Психологическая статистика

Направление отношений

Мера корреляции говорит нам о направлении взаимосвязи между двумя переменными.Направление может быть положительным или отрицательным .

1. Положительный
: При положительной взаимосвязи обе переменные имеют тенденцию двигаться в одном направлении: если одна переменная увеличивается, другая имеет тенденцию также увеличиваться. Если один уменьшается, другой также имеет тенденцию.

В приведенном выше примере средний балл успеваемости и MathSAT положительно связаны. По мере увеличения GPA (или MathSAT) другая переменная также имеет тенденцию к увеличению.

2. Отрицательно
: При отрицательной взаимосвязи переменные имеют тенденцию двигаться в противоположных направлениях: если одна переменная увеличивается, другая имеет тенденцию уменьшаться, и наоборот.

Направление взаимосвязи между двумя переменными определяется знаком коэффициента корреляции для переменных. Положительные отношения имеют знак «плюс», а отрицательные — знак «минус».

Форма (форма) отношения

: Форма или форма отношения указывает на то, является ли отношение прямым или изогнутым.

1. Линейная
: прямая зависимость называется линейной , потому что она аппроксимирует прямую линию.Пример со средним баллом, MathSAT показывает взаимосвязь, которая является, грубо говоря, линейной.
2. Криволинейная
: криволинейная связь называется криволинейной , потому что она приближается к кривой линии. Пример взаимосвязи между количеством миль на галлон и рабочим объемом двигателя различных автомобилей, проданных в США в 1982 году, показан ниже. Это криволинейно (и отрицательно).

В этом курсе мы имеем дело только с коэффициентами корреляции, которые измеряют линейную зависимость.Существуют и другие коэффициенты корреляции, которые измеряют криволинейную взаимосвязь, но они выходят за рамки вводного уровня.

Степень (сила) родства

Наконец, коэффициент корреляции измеряет степень (сила) взаимосвязи между двумя переменными. Обсуждаемые нами меры только измеряют силу линейной связи между двумя переменными. Две особые сильные стороны:

1. Perfect Relationship
: Когда две переменные связаны точно (линейно), коэффициент корреляции равен +1.00 или -1.00. Говорят, что они связаны совершенно линейно, положительно или отрицательно.
2. Нет связи
: Когда две переменные вообще не имеют отношения, их корреляция равна 0,00.

Сильные стороны могут быть между -1,00, 0,00 и +1,00. Однако обратите внимание. +1.00 — это самая большая положительная корреляция, а -1.00 — самая большая отрицательная корреляция, которая возможна. Вот три примера:

Масса и мощность

Связь между весом и мощностью в лошадиных силах сильная, линейная и положительная, хотя и не идеальная.Коэффициент корреляции Пирсона равен +,92.

Передаточное число и мощность в лошадиных силах

Взаимосвязь между передаточным числом и мощностью в лошадиных силах еженедельно отрицательная, но не равна нулю. Коэффициент корреляции Пирсона равен -,59.

Передаточное число и мили на галлон

Связь между передаточным числом и MPG еженедельно положительна, но не равна нулю. Коэффициент корреляции Пирсона равен 0,42.

Отрицательная корреляция — обзор

Корреляция

Метод корреляции Пирсона является наиболее распространенным методом для числовых переменных; ему присваивается значение от — 1 до 1, где 0 — отсутствие корреляции, 1 — полная положительная корреляция, а — 1 — полная отрицательная корреляция.Это интерпретируется следующим образом: значение корреляции 0,7 между двумя переменными будет указывать на то, что между ними существует значимая и положительная взаимосвязь. Положительная корреляция означает, что если переменная A увеличивается, то B также будет расти, тогда как если значение корреляции отрицательное, то если A увеличивается, B уменьшается.

Для получения дополнительной информации о методе корреляции Пирсона см .:

Босло, Сара и Пол Эндрю Уоттерс. 2008. Статистика в двух словах: Краткий справочник на рабочем столе , гл.7. Севастополь, Калифорния: O’Reilly Media. ISBN-13: 978-0596510497.

Учитывая две переменные «возраст» и «зарплату», можно ожидать сильной положительной корреляции между ними: по мере того, как люди стареют, они, как правило, зарабатывают больше денег. Следовательно, корреляция между возрастом и заработной платой, вероятно, дает значение более 0,7. На рис. 6.2 показаны пары числовых переменных, нанесенные друг на друга, с соответствующим значением корреляции между двумя переменными, показанными на оси абсцисс. Крайний правый график показывает идеальную положительную корреляцию 1.0, тогда как средний график показывает две переменные, между которыми нет никакой корреляции. Крайний левый график показывает идеальную отрицательную корреляцию — 1,0.

Рисунок 6.2. Корреляции между двумя числовыми переменными

Корреляцию можно рассчитать между двумя числовыми значениями (например, возрастом и зарплатой) или между двумя значениями категорий (например, тип продукта и профессия). Однако компания может также захотеть рассчитать корреляции между переменными разных типов. Один из методов расчета корреляции числовой переменной с категориальной — это преобразование числовой переменной в категории.Например, возраст может быть разделен на диапазоны (или сегменты), например: от 18 до 30, от 31 до 40 и так далее.

Помимо корреляции, часто вычисляется ковариация двух переменных. В отличие от значения корреляции, которое должно быть между -1 и 1, ковариация может принимать любое числовое значение. Ковариация указывает степень синхронизации дисперсии (или волатильности) двух переменных.

Для получения дополнительной информации о ковариации см .:

Босло, Сара и Пол Эндрю Уоттерс.2008. Статистика в двух словах: Краткий справочник на рабочем столе , гл. 16. Севастополь, Калифорния: O’Reilly Media. ISBN-13: 978-0596510497.

В таблице 6.2 показаны корреляции между четырьмя бизнес-переменными, взятыми из таблицы 6.1. Две переменные, которые имеют самую высокую корреляцию, — это профессия с доходом (долл. США) с корреляцией 0,85 и возраст с доходом (долл. США) с корреляцией 0,81. Наименьшая корреляция — использование мобильного телефона с доходом (0,25) и использование мобильного телефона с профессией (0.28). Следовательно, первоначальный вывод заключается в том, что использование сотового телефона не имеет высокой корреляции с какой-либо другой переменной, поэтому его можно исключить из набора входных переменных. Таблица 6.1 также показывает, что использование сотового телефона имеет значительно более низкую надежность (0,3), чем другие переменные, и это может отразиться на его значении корреляции с остальными переменными. Кроме того, профессия имеет высокую корреляцию только с доходом; однако будет видно, что эта корреляционная пара (доход, профессия) важна для типа бизнеса.Учитывая, что каждая переменная коррелирует с любой другой переменной, значения повторяются по диагонали. Поэтому значения на одной стороне диагонали можно не указывать. Обратите внимание, что все значения равны 1 на диагонали, потому что это корреляции переменных сами с собой.

Таблица 6.2. Корреляции между переменными-кандидатами

	Возраст	Доход (долл. США)	Профессия	Использование мобильного телефона
Возраст	1	0.81	0,38	0,60
Доход (долл. США)	0,81	1	0,85	0,25
Профессия	0,38 1	0,85 использование телефона	0,60	0,25	0,28	1

Коэффициент корреляции — обзор

2 Измерение рыночной корреляции

Как уже сообщалось в другом месте, сэру Гальтону (1886) приписывают открытие скважины. известный коэффициент корреляции, который он использовал для анализа взаимосвязи между средним ростом родителей (как матерей, так и отцов) и их детей с целью разработки эволюционной теории наследственности.После этого Пирсон (1896) опубликовал первую строгую трактовку корреляции, в которой он ввел коэффициент корреляции момента произведения Пирсона для оценки степени линейной связи между двумя случайными величинами. Показатель, указанный в уравнении (1), дает стандартизированную оценку степени, в которой две переменные (временные ряды) перемещаются вместе во времени относительно их индивидуальных средних:

(1) ρX, Y = COV (X, Y) σXσY,

, где ρ символизирует корреляцию между двумя временными рядами; COV — ковариация между двумя переменными; а σX и σY — стандартное отклонение двух временных рядов X и Y.Условная корреляция определяется следующим образом:

(2) ρX, Y = Et-1COV (X, Y) Et-1 (σXσY),

, где условная корреляция основана на ранее известной информации. Законы вероятности требуют, чтобы все корреляции, указанные таким образом, лежали в диапазоне [-1,1].

Условные корреляции также удовлетворяют этому ограничению для всех возможных реализаций ранее известной информации. Это, по-видимому, позволяет легко и удобно донести до инвесторов значение корреляции.Стандартная интерпретация коэффициента корреляции заключается в том, что положительные (отрицательные) коэффициенты указывают степень, в которой переменные перемещаются вместе в одном (противоположном) направлении. Рассматривая это в контексте управления портфелем, Марковиц (1952) показывает, что дисперсия доходности портфеля равна средневзвешенному значению коэффициентов корреляции доходности активов, составляющих портфель. Учитывая, что все веса активов положительны, снижение риска портфеля требует включения активов с меньшей, чем идеально положительной корреляцией (+1), с предпочтением некоррелированных или отрицательно коррелированных активов.Это очень важно в структуре построения портфеля.

Критика этого традиционного показателя зависимости от активов заключается в том, что он представляет собой только среднее значение отклонений от среднего без какого-либо различия между большой и малой доходностью или отрицательной и положительной доходностью (Poon et al., 2004; Aloui et al., 2011). В результате асимметрия в зависимости доходности акций медвежьего и бычьего рынков, задокументированная в литературе, не может быть объяснена. Вслед за этим была разработана техническая и обширная литература, посвященная тому, как лучше всего оценивать корреляции и моделировать их изменяющиеся во времени характеристики с течением времени и во время рыночных потрясений.Мы кратко представляем здесь принципы некоторых из этих подходов — когерентность вейвлетов, модель GARCH с динамической условной корреляцией (DCC-GARCH), модели экстремальных значений и копул — и отсылаем заинтересованных читателей к источнику этих моделей.

При вейвлет-подходе практическая мера зависимости между двумя временными рядами получается путем вычисления квадрата когерентности вейвлета. Это делается путем возведения в квадрат мощности кросс-вейвлета и деления результата на произведение двух вейвлет-спектров, как представлено в уравнении (3).Торренс и Компо (1998 г.), Рэмси и Лэмпарт (1998 г.) и Гринстед и др. (2004) дают прекрасное и подробное описание вейвлет-анализа.

(3) Rn2 (s) = Ss-1WnXY (s) 2Ss-1WnX (s) 2 · Ss-1WnY (s) 2.

Числитель в уравнении (3) представляет собой квадрат модуля сглаженного кросс-вейвлет-спектра (где WnXY (s) = WnX (s), WnY (s) ∗, WnX и WnY — это вейвлет-преобразования xn и yn). Знаменатель представляет собой сглаженные спектры мощности вейвлетов. S обозначает сглаживающий оператор по времени и масштабу.Уравнение (3) аналогично квадрату коэффициента корреляции и дает величину от 0 до 1, причем высокое значение показывает сильную корреляцию между двумя временными рядами. Следовательно, квадратичная функция когерентности вейвлета как коэффициент корреляции для каждого момента времени и для каждой частоты. По этой причине его можно использовать для измерения степени, в которой два временных ряда перемещаются вместе во времени, фиксируя изменяющиеся во времени особенности и по частотам, которые эффективно отделяют краткосрочные корреляции от долгосрочных.

Энгл (2002) представил одну из наиболее практичных и простых многомерных моделей, DCC-GARCH, которую можно использовать для оценки изменяющихся во времени корреляций для большого класса активов. Мы кратко представляем модель здесь. Пусть rt обозначает вектор доходности инноваций nx1 в момент времени t, который предполагается условно нормальным с нулевым средним и ковариационной матрицей Ht:

(4) rtΦt-1∼N (0, Ht),

где Φt- 1 — информация, установленная в момент времени t-1. Матрица условной ковариации Ht может быть разложена следующим образом:

(5) Ht≡DtRtDt,

где Dt — (n × n) диагональная матрица изменяющихся во времени стандартных отклонений от одномерных моделей GARCH с попаданием на i-ю диагональ, i = 1,2,…, n.Rt — это (n × n) изменяющаяся во времени корреляционная матрица, содержащая условную корреляцию. Модель DCC-GARCH оценивается с использованием двухэтапной процедуры. Первоначально одномерные модели GARCH подбираются для каждого ряда доходности активов, и получаются остатки, стандартизированные по их расчетным стандартным отклонениям. Впоследствии стандартизованные остатки используются для оценки коэффициентов, управляющих динамическими корреляциями (более подробное описание см. В Engle, 2002).

Теория экстремальных значений и функции копулы также использовались для выявления асимметричных корреляций.Они имеют дело со структурой крайней зависимости как отрицательной, так и положительной доходности акций в многомерной структуре (см., Например, Longin and Solnik, 2001; Pais and Stork, 2011). Теория экстремальных значений включает в себя две особенности моделирования: хвосты предельных распределений и структуру зависимости экстремальных наблюдений. Теория демонстрирует, что распределение превышений доходности может сходиться только к обобщенному распределению Парето. При заданном пороге хвост распределения характеризуется тремя параметрами: вероятностью хвоста, параметром дисперсии и индексом хвоста.Теория также показывает, что распределение экстремальной доходности может сходиться только к распределению, характеризуемому обобщенными маржинальными распределениями Парето и функцией зависимости, форма которой четко не определена. Используя логистическую функцию, Лонгин и Сольник (2001) моделируют зависимость между экстремальной доходностью различных рынков. Они также обсуждают процедуру оценки корреляции экстремальных доходностей (более подробную информацию см. В Longin and Solnik, 2001). Aloui et al.(2011) также комбинируют условные многомерные копулы с теорией экстремальных значений, а также обобщенный авторегрессионный процесс условной гетероскедастичности для моделирования совместных превышений доходности акций выше и ниже заданного порога.

Мы не оспариваем полезность этих подходов. В этой главе мы также принимаем во внимание асимметрию и анализируем корреляцию между международными акциями и переменными тренда глобальных индексов акций. В отличие от технических моделей, кратко представленных выше, нас особенно интересуют разрывы тренда и то, как это можно использовать для повышения диверсификации портфеля.Таким образом, мы анализируем не корреляцию рыночной доходности или волатильности, а несоответствие тенденций между развивающимися и развитыми рынками. Учитывая, что направление отклонений от среднего значения двух временных рядов доходности капитала может отличаться от тенденции двух случайных величин двигаться либо в одном, либо в противоположном направлении, при анализе зависимости от рынка с использованием этого показателя необходимо учитывать тенденцию. (Lhabitant, 2011). Это добавляет практическое расширение к литературе.

Руководство по надлежащему использованию коэффициента корреляции в медицинских исследованиях

Malawi Med J. 2012 Сентябрь; 24 (3): 69–71.

MM Mukaka

¹ Программа клинических исследований Malawi-Liverpool Wellcome Trust

² Департамент общественного здравоохранения, Медицинский колледж, Университет Малави

³ Ливерпульская школа тропической медицины, Ливерпуль, L69 3GA , Великобритания, Ливерпульский университет

¹ Программа клинических исследований Malawi-Liverpool Wellcome Trust

² Департамент общественного здравоохранения, Медицинский колледж, Университет Малави

³ Ливерпульская школа тропической медицины, Ливерпуль, L69 3GA, Великобритания, Ливерпульский университет

Эта статья цитируется в других статьях в PMC.

Abstract

Корреляция — это статистический метод, используемый для оценки возможной линейной связи между двумя непрерывными переменными. Это просто и вычислить, и интерпретировать. Однако неправильное использование корреляции настолько распространено среди исследователей, что некоторые статистики хотели бы, чтобы этот метод вообще никогда не был изобретен. Цель этой статьи — предоставить руководство по правильному использованию корреляции в медицинских исследованиях и выявить некоторые злоупотребления. Были представлены примеры применения коэффициента корреляции с использованием данных статистического моделирования, а также реальных данных.Было предоставлено практическое правило для интерпретации величины коэффициента корреляции.

Определения корреляции и пояснения

Термин «корреляция» иногда используется в устном общении свободно. Среди ученых-коллег термин корреляция используется для обозначения ассоциации, связи или любой формы отношений, ссылки или переписки. Это широкое разговорное определение иногда приводит к неправильному использованию статистического термина «корреляция» среди ученых, участвующих в исследованиях.Неправильное использование корреляции настолько распространено, что некоторые статистики хотели бы, чтобы этот метод никогда не был изобретен. ¹

Интернет-словарь Вебстера определяет корреляцию как взаимную связь между двумя или более вещами; статистика, показывающая, насколько близко друг к другу изменяются две переменные; он может варьироваться от -1 (абсолютная отрицательная корреляция) до 0 (без корреляции) до +1 (идеальная положительная корреляция). ²

С точки зрения статистики корреляция — это метод оценки возможной двусторонней линейной связи между двумя непрерывными переменными. ¹ Корреляция измеряется статистикой, называемой коэффициентом корреляции, которая представляет силу предполагаемой линейной связи между рассматриваемыми переменными. Это безразмерная величина, принимающая значение в диапазоне от -1 до +1 ³ . Нулевой коэффициент корреляции указывает на отсутствие линейной зависимости между двумя непрерывными переменными, а коэффициент корреляции -1 или +1 указывает на идеальную линейную зависимость. Сила взаимосвязи может быть от -1 до +1.Чем сильнее корреляция, тем ближе коэффициент корреляции к ± 1. Если коэффициент является положительным числом, переменные напрямую связаны (т. Е. По мере увеличения значения одной переменной значение другой также имеет тенденцию к этому). Если, с другой стороны, коэффициент является отрицательным числом, переменные связаны обратно пропорционально (т. Е. По мере увеличения значения одной переменной значение другой имеет тенденцию уменьшаться). ³ Любая другая форма связи между двумя непрерывными переменными, которая не является линейной, не является корреляцией в статистическом смысле.Чтобы подчеркнуть этот момент, математическая взаимосвязь не обязательно означает наличие корреляции. Например, рассмотрим уравнение y = 2 × 2. С точки зрения статистики, неправильно говорить о корреляции между x и y. Это так, потому что, хотя взаимосвязь существует, она не является линейной в этом диапазоне указанных значений x. Можно точно предсказать y для каждого значения x в заданном диапазоне, но корреляция не равна ни -1, ни +1. Следовательно, это было бы несовместимо с определением корреляции, и поэтому нельзя сказать, что x коррелирован с y.

Типы коэффициентов корреляции

⁴

Существует два основных типа коэффициентов корреляции: коэффициент корреляции момента произведения Пирсона и коэффициент ранговой корреляции Спирмена. Правильное использование типа коэффициента корреляции зависит от типа исследуемых переменных. Мы сосредоточимся на этих двух типах корреляции; другие типы основаны на них и часто используются при рассмотрении нескольких переменных.

Коэффициент корреляции момента произведения Пирсона

Коэффициент корреляции момента произведения Пирсона обозначается как ϱ для параметра генеральной совокупности и как r для выборочной статистики.Он используется, когда обе изучаемые переменные имеют нормальное распределение. На этот коэффициент влияют экстремальные значения, которые могут преувеличивать или ослаблять силу взаимосвязи, и поэтому неуместен, когда одна или обе переменные не имеют нормального распределения. Для корреляции между переменными x и y формула для расчета коэффициента корреляции выборки Пирсона имеет вид ³

r = ∑i = 1n (xi − x) (yi − y) [∑i = 1n (xi− x¯) 2] [∑i = 1n (yi − y¯) 2]

где xi и yi — значения x и y для i-го человека.

Коэффициент ранговой корреляции Спирмена

Коэффициент ранговой корреляции Спирмена обозначается как ϱs для параметра совокупности и как rs для выборочной статистики. Это уместно, когда одна или обе переменные искажены или имеют порядковый номер ¹ и устойчивы, когда присутствуют экстремальные значения. Для корреляции между переменными x и y формула для расчета выборочного коэффициента корреляции Спирмена имеет вид

rs = 1−6∑i = 1ndi2n (n2−1), где di — разность рангов для x и y

Различие между коэффициентами корреляции Пирсона и Спирмена в приложениях будет обсуждаться на примерах ниже.

Связь между коэффициентом корреляции и диаграммами рассеяния с использованием статистического моделирования

Данные, изображенные на — были смоделированы из двумерного нормального распределения 500 наблюдений со средними значениями 2 и 3 для переменных x и y соответственно. Стандартные отклонения составляли 0,5 для x и 0,7 для y. Диаграммы разброса были построены для корреляций 0,2, 0,5, 0,8 и -0,8.

Диаграмма рассеяния x и y: корреляция Пирсона = 0,2

Диаграмма рассеяния x и y: корреляция Пирсона = -0.80

In диаграмма рассеяния показывает некоторый линейный тренд, но тенденция не так ясна, как у. Четко видна тенденция, и точки не так разбросаны, как у и. То есть, чем выше корреляция в любом направлении (положительном или отрицательном), тем более линейна связь между двумя переменными и тем очевиднее тенденция на диаграмме разброса. Для и сила линейной зависимости одинакова для рассматриваемых переменных, но направление другое. В значения y увеличиваются при увеличении значений x, тогда как значения y уменьшаются при увеличении значений x.

Диаграмма рассеяния x и y: корреляция Пирсона = 0,50

Диаграмма рассеяния x и y: корреляция Пирсона = 0,80

Практическое использование коэффициента корреляции

Простое применение коэффициента корреляции можно проиллюстрировать на примере данных из выборки из 780 женщин посещение их первых посещений женской консультации (ДРП). Мы можем ожидать положительной линейной зависимости между возрастом матери в годах и количеством детей, потому что количество детей не может уменьшаться с возрастом, но мы не можем предсказать силу этой взаимосвязи.Задача состоит в том, чтобы количественно оценить силу ассоциации. То есть нас интересует сила взаимосвязи между двумя переменными, а не направление, поскольку в этом случае направление очевидно. Материнский возраст непрерывен и обычно искажен, в то время как родство является порядковым и асимметричным. С этими шкалами измерения данных подходящий коэффициент корреляции — коэффициент Спирмена. Для этих данных коэффициент Спирмена равен 0,84. В этом случае возраст матери сильно коррелирует с паритетом, т.е.е. имеет высокую положительную корреляцию (). Коэффициент корреляции Пирсона для этих переменных равен 0,80. В этом случае два коэффициента корреляции схожи и приводят к одному и тому же выводу, однако в некоторых случаях они могут сильно отличаться, что приводит к разным статистическим выводам. Например, в той же группе женщин корреляция Спирмена между уровнем гемоглобина и паритетом составляет 0,3, а корреляция Пирсона — 0,2. В этом случае два коэффициента могут привести к разным статистическим выводам.Например, коэффициент корреляции 0,2 считается незначительной корреляцией, в то время как коэффициент корреляции 0,3 считается низкой положительной корреляцией (), поэтому было бы важно использовать наиболее подходящий. В этом случае наиболее подходящим коэффициентом является коэффициент Спирмена, поскольку четность искажена.

Таблица 1

Практическое правило для интерпретации размера коэффициента корреляции ⁴

Размер корреляции	Интерпретация
.От 90 до 1,00 (от -,90 до -1,00)	Очень высокая положительная (отрицательная) корреляция
от 0,70 до 0,90 (от -,70 до -,90)	Высокая положительная (отрицательная) корреляция
От 0,50 до 0,70 (от -,50 до -,70)	Умеренная положительная (отрицательная) корреляция
от 0,30 до 0,50 (от -,30 до -,50)	Низкая положительная (отрицательная) корреляция
от 0,00 до 0,30 (от 0,00 до −30)	незначительная корреляция

В другом наборе данных из 251 взрослой женщины возраст и вес были преобразованы с помощью логарифма.Причина преобразования заключалась в том, чтобы сделать переменные нормально распределенными, чтобы мы могли использовать коэффициент корреляции Пирсона. Затем мы проанализировали данные на предмет линейной связи между журналом возраста (agelog) и журналом веса (wlog). Обе переменные приблизительно нормально распределены в логарифмической шкале. В этом случае более уместен коэффициент корреляции Пирсона. Коэффициент 0,184. Это показывает, что существует незначительная корреляция между возрастом и весом по логарифмической шкале ().

В шаблоне изменяется при более высоких значениях четности.показывает, как меняются коэффициенты корреляции Спирмена и Пирсона при исключении семи пациентов с более высокими значениями паритета. Когда семь более высоких значений четности исключаются, коэффициент корреляции Пирсона существенно изменяется по сравнению с коэффициентом корреляции Спирмена. Хотя разница в коэффициенте корреляции Пирсона до и после исключения выбросов не является статистически значимой, интерпретация может быть разной. Коэффициент корреляции 0,2 до исключения выбросов считается незначительной корреляцией, в то время как 0.3 после исключения выбросов можно интерпретировать как слабую положительную корреляцию (). Интерпретация корреляции Спирмена остается той же до и после исключения выбросов с коэффициентом корреляции 0,3. Разница в изменении между коэффициентами Спирмена и Пирсона при исключении выбросов поднимает важный вопрос при выборе подходящей статистики. Данные с нестандартным распределением могут включать значения выбросов, которые требуют использования коэффициента корреляции Спирмена.

Диаграмма разброса гемоглобина относительно паритета для 783 женщин, посещавших ДРП номер 1 визита

Таблица 2

Коэффициенты корреляции Спирмена и Пирсона для гемоглобина и паритета

9075 9070

					Экстремальные значения включены		Экстремальные значения удалены
	n	r	n	r
Копейщик	783	0.3	776	0,3
Пирсона	783	0,2	776	0,3
							для оценки силы и направления линейных отношений между парами переменных. Если обе переменные распределены нормально, используйте коэффициент корреляции Пирсона, в противном случае используйте коэффициент корреляции Спирмена.Коэффициент корреляции Спирмена более устойчив к выбросам, чем коэффициент корреляции Пирсона. Коэффициенты корреляции не передают информацию о том, перемещается ли одна переменная в ответ на другую. Нет попытки установить одну переменную как зависимую, а другую как независимую. Таким образом, взаимосвязи, выявленные с помощью коэффициентов корреляции, следует интерпретировать так, как они есть: ассоциации, а не причинно-следственные связи. 5 Корреляцию нельзя использовать для оценки соответствия между методами.Согласованность методов следует оценивать с использованием графиков Бланда-Альтмана 6 . Благодарности Я хотел бы выразить признательность доктору Саре Уайт, доктору философии, за ее комментарии на протяжении всей разработки этой статьи и Нинке Р. ван ден Брук, доктору философии, FRCOG, DFFP, DTM & H, за то, что она позволила мне использовать подмножество ее данные для иллюстраций. Список литературы 1. Альтман Д.Г. Практическая статистика для медицинских исследований. Чепмен и Холл / CRC; [Google Scholar] 3. Swinscow TDV. В: Статистика на первом месте.Девятое издание. Кэмпбелл М. Дж., Редактор. Саутгемптонский университет; Авторские права BMJ Publishing Group 1997. [Google Scholar] 4. Hinkle DE, Wiersma W, Jurs SG. Прикладная статистика для поведенческих наук. 5-е изд. Бостон: Хоутон Миффлин; 2003. [Google Scholar] 5. Кларк Г.М., Кук Д. Базовый курс статистики. 3-е изд [Google Scholar] 6. Альтман Д.Г., Бланд Дж. М.. Измерение в медицине: анализ сравнительных исследований методов. Статистик. 1983; 32: 307–317. [Google Scholar] Корреляция | Введение в статистику Что такое корреляция? Корреляция — это статистическая мера, которая выражает степень, в которой две переменные линейно связаны (что означает, что они изменяются вместе с постоянной скоростью).Это распространенный инструмент для описания простых отношений без объяснения причин и следствий. Как измеряется корреляция? Коэффициент корреляции выборки, r , количественно определяет силу взаимосвязи. Корреляции также проверяются на статистическую значимость. Какие ограничения корреляционного анализа? Корреляция не может смотреть на присутствие или влияние других переменных за пределами двух исследуемых.Важно отметить, что корреляция не говорит нам о причине и следствии. Корреляция также не может точно описать криволинейные отношения. Корреляции описывают перемещение данных вместе Корреляции полезны для описания простых отношений между данными. Например, представьте, что вы просматриваете набор данных о кемпингах в горном парке. Вы хотите знать, есть ли связь между высотой кемпинга (насколько высоко он находится в горах) и средней высокой температурой летом. Для каждого отдельного кемпинга у вас есть два показателя: высота над уровнем моря и температура. Когда вы сравниваете эти две переменные в вашем образце с корреляцией, вы можете найти линейную зависимость: по мере увеличения высоты температура падает. Они отрицательно коррелируют с . Что означают числа корреляции? Мы описываем корреляции с помощью безразмерной меры, называемой коэффициентом корреляции, который находится в диапазоне от -1 до +1 и обозначается r .Статистическая значимость обозначается р-значением. Поэтому корреляции обычно записываются с двумя ключевыми числами: r = и p = . Чем ближе r к нулю, тем слабее линейная зависимость. Положительные значения r указывают на положительную корреляцию, при которой значения обеих переменных имеют тенденцию увеличиваться вместе. Отрицательные значения r указывают на отрицательную корреляцию, когда значения одной переменной имеют тенденцию увеличиваться, когда значения другой переменной уменьшаются. Значение p свидетельствует о том, что мы можем сделать осмысленный вывод о том, что коэффициент корреляции населения, вероятно, отличен от нуля, на основании того, что мы наблюдаем в выборке. «Измерение без единиц измерения» означает, что корреляции существуют по собственной шкале: в нашем примере число, указанное для r , не находится в той же шкале, что и высота над уровнем моря или температура. Это отличается от другой сводной статистики. Например, среднее значение измерений высоты находится в том же масштабе, что и его переменная. Как только мы получим значительную корреляцию, мы также можем посмотреть на ее силу. Идеальная положительная корреляция имеет значение 1, а идеальная отрицательная корреляция имеет значение -1. Но в реальном мире мы никогда не ожидаем увидеть идеальную корреляцию, если одна переменная на самом деле не является косвенной мерой для другой. Фактически, наблюдение за идеальным числом корреляции может предупредить вас об ошибке в ваших данных! Например, если вы случайно записали расстояние от уровня моря для каждого кемпинга вместо температуры, это будет идеально коррелировать с высотой над уровнем моря. Еще одна полезная информация — это N или количество наблюдений. Как и в случае с большинством статистических тестов, знание размера выборки помогает нам судить о силе нашей выборки и о том, насколько хорошо она представляет совокупность. Например, если мы измерили высоту и температуру только для пяти кемпингов, а в парке две тысячи кемпингов, мы бы хотели добавить в нашу выборку больше кемпингов. Визуализация корреляций с помощью диаграмм рассеяния Вернемся к нашему примеру сверху: по мере увеличения высоты лагеря температура падает.Мы можем посмотреть на это непосредственно с помощью диаграммы рассеяния. Представьте, что мы нанесли на график данные о нашем кемпинге: Каждая точка на графике представляет один кемпинг, который мы можем разместить на осях x и y по высоте и высокой температуре в летнее время. Коэффициент корреляции ( r ) также иллюстрирует нашу диаграмму рассеяния. Это говорит нам в числовом выражении, насколько близко точки, отображенные на диаграмме рассеяния, подходят к линейной зависимости. Более сильные взаимосвязи или более высокие значения или означают отношения, в которых точки очень близки к линии, которая соответствует данным. А как насчет более сложных отношений? Диаграммы рассеяния также полезны для определения того, есть ли в наших данных что-либо, что может нарушить точную корреляцию, например необычные закономерности, такие как криволинейная связь или экстремальный выброс. Корреляции не могут точно определить криволинейные отношения. В криволинейной взаимосвязи переменные коррелируют в заданном направлении до определенной точки, где взаимосвязь изменяется. Например, представьте, что мы смотрели на высоту нашего кемпинга и на то, насколько высоко отдыхающие в среднем оценивают каждый кемпинг.Возможно, поначалу высота и рейтинг кемпинга положительно коррелируют, потому что с кемпингов выше открывается лучший вид на парк. Но в какой-то момент более высокие высоты начинают отрицательно коррелировать с рейтингом кемпинга, потому что отдыхающим ночью холодно! Мы можем получить еще больше информации, добавив закрашенные эллипсы плотности на нашу диаграмму рассеяния. Эллипс плотности показывает наиболее плотную область точек на диаграмме рассеяния, что, в свою очередь, помогает нам увидеть силу и направление корреляции. Эллипсы плотности могут быть разных размеров. Один из распространенных вариантов для изучения корреляции — это эллипс плотности 95%, который захватывает приблизительно 95% самых плотных наблюдений. Если две переменные движутся вместе, например, высота и температура наших лагерей, мы ожидаем увидеть, что этот эллипс плотности отражает форму линии. И мы можем видеть, что в криволинейной зависимости эллипс плотности выглядит кругом: корреляция не дает нам содержательного описания этой связи. . Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт