Оптимизация
Оптимизация – это процесс приведения объекта (системы) в оптимальное (наилучшее) состояние. Для проведения оптимизации необходимы: математическая модель объекта, целевая функция и оптимизационный алгоритм (рисунок). Целевая функция формализует требования, предъявляемые к объекту (максимизация коэффициента усиления, увеличение надежности, снижение стоимости, максимизация прибыли и т.д.).Оптимизационный алгоритм ищет экстремум целевой функции.
Оптимизация осуществляется при помощи алгоритмов математического программирования
и бывает структурной, параметрической и структурно-параметрической.
В процессе структурной оптимизации оптимизируется структура объекта,
в процессе же параметрической – оптимизируются параметры (номиналы)
элементов, входящих в состав структуры. Эти задачи решаются при помощи
алгоритмов дискретного, непрерывного и дискретно-непрерывного математического
программирования, соответственно.
В зависимости от числа критериев, по которым выполняется оптимизация объекта, различают однокритериальную и многокритериальную оптимизацию. Так, если при синтезе усилителя необходимо лишь достичь максимального коэффициента усиления, то это будет задачей однокритериальной оптимизации. Если помимо максимального коэффициента усиления необходимо еще достичь минимального уровня шума (два критерия качества) – то это уже будет задачей многокритериальной оптимизации. Следует заметить, что обычно не удается достичь максимума сразу по нескольким критериям.
По наличию ограничений на целевую функцию и рабочие параметры различают
оптимизацию без ограничений и при наличии ограничений. Так, если при
синтезе усилителя необходимо, чтобы коэффициент усиления был не меньше
какой-то заданной величины, то говорят о наложении ограничения на соответствующий
критерий. Если же при этом требуется использовать номиналы элементов,
значения которых должны попасть в какой-то заданный интервал (например,
сопротивления должны быть не меньше 100 Ом и не больше 100 КОм), то
тогда мы имеем дело с ограничениями на рабочие параметры.
Если же при этом требуется использовать номиналы элементов,
значения которых должны попасть в какой-то заданный интервал (например,
сопротивления должны быть не меньше 100 Ом и не больше 100 КОм), то
тогда мы имеем дело с ограничениями на рабочие параметры.
И структурный, и параметрический синтез объектов может осуществляться при помощи оптимизационных алгоритмов: структурный синтез – при помощи методов дискретного математического программирования; параметрический – непрерывного; структурно-параметрический – при помощи алгоритмов дискретно-непрерывного математического программирования.
В случае параметрического синтеза при известной (заданной) структуре
объекта подбираются параметры (номиналы) элементов таким образом, чтобы
минимизировать (максимизировать) целевую функцию. Предположим, мы каким-то
образом определили структуру усилителя и хотим подобрать номиналы элементов
(значения сопротивлений, емкостей, индуктивностей и т.
Следует заметить, что существующие оптимизационные алгоритмы обычно
не гарантируют нахождение глобального оптимума, но это не является критическим.
Например, для увеличения вероятности нахождения глобального оптимума
можно значительно увеличить число итераций, использовать несколько алгоритмов,
многократно запускать соответствующие алгоритмы и т.д. Современные продвинутые
системы автоматизированного проектирования (САПР) имеют в своем составе
модули параметрического синтеза и оптимизации.
Если помимо подбора параметров необходимо еще и определить структуру объекта (например, усилителя), то мы будем уже иметь дело со структурно-параметрическим синтезом, который решается при помощи алгоритмов дискретно-непрерывного математического программирования. Если задача параметрической оптимизации сейчас решается практически для любых объектов, то развитие структурно-параметрической оптимизация сейчас находится лишь на начальной стадии развития.
С теорией оптимизации тесно связаны математическое программирование, теория исследования операций, теория принятия решений, динамическое программирование.
Дальнейшее развитие теории и практики оптимизации является очень важным для развития науки и техники.
Литература
- Батищев Д.И. Методы оптимального проектирования. М. Радио и связь 1984г.
- Батищев Д.
 И. Поисковые методы оптимального проектирования. М.: Сов.
Радио, 1975.
И. Поисковые методы оптимального проектирования. М.: Сов.
Радио, 1975. - Химмельблау Д. Прикладное нелинейное программирование. Пер. с англ. Мир, М., 1975.
- Емельянов В.В., Курейчик В.В., Курейчик В.М. Теория и практика эволюционного моделирования. М.: Физматлит, 2003.
- Сушков Ю.А. Об одном способе организации случайного поиска. Автоматика и вычислительная техника, 1974, № 6, 41-48.
- Фиакко А., Мак-Кормик Г. Нелинейное прогаммирование. Методы последовательной безусловной минимизации. Пер. с англ. М.: Мир, 1972.
- Соболь И.М., Статников Р.Б. Выбор оптимальных параметров в задачах со многими критериями. М.: Наука, 1981.
- Демьянов В.Ф., Малоземов В.Н. Введение в минимакс. М.: Наука, 1972.
Связанные понятия
Оптимизация
Оптимальный — наилучший в заданных условиях. Качество оценивается с помощью критерия оптимальности, а условия задаются в виде ограничений на дополнительные критерии.
Качество оценивается с помощью критерия оптимальности, а условия задаются в виде ограничений на дополнительные критерии.
Стремление к повышению эффективности труда, творчества, любой целенаправленной деятельности, это естественное стремление человека как бы нашло свое выражение, ясную и понятную форму в идее оптимальности. Различие между строго научным и «общепринятым», житейским пониманием оптимальности совсем невелико. Правда, встречающиеся выражения типа «наиболее оптимальный» или «добьемся максимального эффекта при минимуме затрат» математически некорректны, но лица, использующие эти выражения, на самом деле просто нестрого и неудачно выражают правильную мысль: как только дело касается конкретной оптимизации, они быстро и легко исправляют формулировки.
Оптимизация — в математике, информатике и исследовании операций задача нахождения экстремума (минимума или максимума) целевой функции в некоторой области конечномерного векторного пространства, ограниченной набором линейных и/или нелинейных равенств и/или неравенств.
Оптимизационные модели предназначены для определения оптимальных (наилучших) с точки зрения некоторого критерия параметров моделируемого объекта или же для поиска оптимального (наилучшего) режима управления некоторым процессом. Часть параметров модели относят к параметрам управления, изменяя которые можно получать различные варианты наборов значений выходных параметров. Как правило, данные модели строятся с использованием одной или нескольких дескриптивных моделей и включают некоторый критерий, позволяющий сравнивать различные варианты наборов значений выходных параметров между собой с целью выбора наилучшего. На область значений входных параметров могут быть наложены ограничения в виде равенств и неравенств, связанные с особенностями рассматриваемого объекта или процесса. Целью оптимизационных моделей является поиск таких допустимых параметров управления, при которых критерий выбора достигает своего «наилучшего значения».
Задача формулируется в виде математической модели. Типовая математическая модель исследования операций представлена в следующей формулировке:
Максимизация или минимизация целевой функции, при условии выполнения ограничений
Оптимальными называются решения которые по тем или другим признакам предпочтительнее других. Каждый выбор лучшего варианта конкретен, поскольку основан на соответствии установленным критериям. Говоря об оптимальном варианте, указывают эти критерии («оптимальный по…»). То, что оптимально при одном критерии, не обязательно будет таковым при другом.
Допустимое решение — если оно удовлетворяет всем ограничениям модели. Допустимых решений в отдельных случаях может быть бесконечное множество.
Оптимальное решение — если кроме того, что оно допустимо, целевая функция в этом решении достигает максимального или минимального значения.
Оптимизация — максимизация или минимизация целевой функции.
Оптимизационная модель — это модель принятия решения, содержащая показатель эффективности (целевую функцию), который необходимо оптимизировать при условии соблюдения набора заданных ограничений.
Оптимальное решение — допустимый набор значений переменных решения, оптимизирующий целевую функцию оптимизационной модели.
Модель оптимального выбораБольшое число встречающихся на практике задач выбора сводится к нахождению лучших или наиболее предпочтительных для человека вариантов, а нередко — к поиску единственно лучшего варианта. При этом у каждого лица принимающего решение (ЛПР) есть собственные субъективные представления о том, что для него является предпочтительным в конкретной ситуации выбора.
При этом у каждого лица принимающего решение (ЛПР) есть собственные субъективные представления о том, что для него является предпочтительным в конкретной ситуации выбора.
Имеется достаточно много задач, для которых можно построить математическую модель выбора, где понятие лучшего варианта формализуется путем задания одного или нескольких числовых показателей эффективности или критериев качества решения. Эти показатели, хотя и задаются ЛПР, носят объективный характер, определяемый содержанием решаемой задачи, и выражаются какими-либо функциями, зависящими от переменных, которыми измеряются свойства вариантов. В таких случаях наиболее предпочтительным для ЛПР вариантом решения задачи выбора принято считать так называемый оптимальный вариант, который соответствует экстремальному значению одного или нескольких показателей эффективности решения при существующих условиях.
Принципиальным моментом для формулировки задачи оптимального выбора является возможность описания проблемной ситуации и предпочтений ЛПР в количественной форме. Это означает, что, во-первых, возможные варианты решения (альтернативы, объекты, способы действия) определяются количественными признаками (переменными, параметрами, атрибутами), измеряемыми с помощью числовых шкал. Во-вторых, должны быть заданы количественные же показатели (критерии оптимальности, показатели эффективности, целевые функции, функции ценности), по величине которых оценивается качество выбранного варианта. Такого рода ситуации характерны для хорошо структурируемых проблем и повторяющихся ситуаций выбора, типичных для исследования операций и оптимального управления.
Это означает, что, во-первых, возможные варианты решения (альтернативы, объекты, способы действия) определяются количественными признаками (переменными, параметрами, атрибутами), измеряемыми с помощью числовых шкал. Во-вторых, должны быть заданы количественные же показатели (критерии оптимальности, показатели эффективности, целевые функции, функции ценности), по величине которых оценивается качество выбранного варианта. Такого рода ситуации характерны для хорошо структурируемых проблем и повторяющихся ситуаций выбора, типичных для исследования операций и оптимального управления.
Для анализа возможных вариантов решения проблемы (способов достижения цели) и выбора среди них одного или нескольких лучших вариантов строятся формальные модели оптимального выбора. Модель дает упрощенное представление реальной проблемы и должна отражать наиболее важные и объективно существующие зависимости и связи между вариантами, описывающими их признаками и ограничениями, которые задаются управляемыми и неуправляемыми факторами. Построение такой модели — задача консультантов-аналитиков и экспертов при участии ЛПР. При построении модели выбора нужно соизмерять адекватность и детальность модели с точностью требуемого решения реальной задачи выбора, а также с объемом необходимой для поиска решения информации — как имеющейся в наличии, так и получаемой дополнительно.
Построение такой модели — задача консультантов-аналитиков и экспертов при участии ЛПР. При построении модели выбора нужно соизмерять адекватность и детальность модели с точностью требуемого решения реальной задачи выбора, а также с объемом необходимой для поиска решения информации — как имеющейся в наличии, так и получаемой дополнительно.
Ограничения оптимизационного подхода
Оптимизационные проблемы являются строго формальными математическими задачами. Практическое значение решений таких задач прямо зависит от того, насколько хороша исходная математическая модель. В сложных системах математическое моделирование является затруднительным, приблизительным, неточным. Чем сложнее система, тем осторожнее следует относиться к ее оптимизации.
С позиций системного анализа отношение к оптимизации можно сформулировать следующим образом: это мощное средство повышения эффективности, но использовать его следует все более осторожно по мере возрастания сложности проблемы.
При всей очевидной полезности идеи оптимизации практика требует необходимости осторожного обращения с ней. Для такого заключения имеются достаточно веские основания.
- Оптимальное решение часто оказывается неустойчивым: незначительные на первый взгляд изменения в условиях задачи могут привести к выбору существенно отличающихся альтернатив.
- Рассматриваемая система является частью некоторой большей системы, и тогда локальная оптимизация совсем не обязательно приведет к тому же результату, который потребуется от подсистемы при оптимизации системы в целом. Это приводит к необходимости увязывать критерии подсистем с критериями системы, часто делая ненужной локальную оптимизацию.
- Критерии характеризуют цель лишь косвенно, иногда лучше, иногда хуже, но всегда приближенно. Максимизация критерия оптимальности часто отождествляется с целью, а на самом деле это разные вещи.
 Фактически критерий и цель относятся друг к другу как модель и оригинал, со всеми вытекающими отсюда особенностями. Многие цели трудно или даже невозможно количественно описать.
Фактически критерий и цель относятся друг к другу как модель и оригинал, со всеми вытекающими отсюда особенностями. Многие цели трудно или даже невозможно количественно описать. - Не задав всех необходимых ограничений, мы можем одновременно с максимизацией основного критерия получить непредвиденные и нежелательные сопутствуюшие эффекты.
Моделирование
Системный анализ
Исследование операций
Методология исследования операций
определение, способы оптимизации, типичные ошибки при проведении — Контур.
 Бухгалтерия
БухгалтерияДля любой хозяйственной деятельности важна эффективная оптимизация налогообложения: это помогает предпринимателю снизить выплаты в бюджет и сохранить больше денег в бизнесе.
Что такое налоговая оптимизация
Налоговая оптимизация — это комплекс методов и подходов для эффективного планирования (минимизации) налогов, перечисляемых в бюджет. Правильная оптимизация налогов (осуществляемая законными методами), а также прогнозирование различных рисков, помогают избежать больших убытков и сохранить стабильное положение фирмы на рынке.
Эксперты выделяют два способа минимизации налогов физических и юридических лиц:
- Налоговое планирование — это целенаправленные законные действия налогоплательщика, направленные на уменьшение его расходов на уплату налогов. Такой способ включает правило: «Разрешено все, что не запрещено законом». В налоговом планировании следует соблюдать основные принципы: законность, эффективность, надежность, безвредность, минимизация затрат.

- Уклонение от налогов — в этом случае для неплательщика предусмотрены суровые наказания. Поэтому лучше все-таки использовать легальные методы высвобождения от налогового бремени.
Легальные способы оптимизации налогов
Выбор подходящей системы налогообложения. Специальные налоговые режимы позволяют организациям выплачивать в бюджет небольшую часть своих доходов. Проведите расчеты, сравните выгодность разных налоговых режимов для вашего конкретного бизнеса. Воспользуйтесь нашим калькулятором систем налогообложения, чтобы рассчитать нагрузку на каждом режиме по своим параметрам.
Проверка добросовестности контрагентов. Если контрагент окажется недобросовестным, то расходы по сделке с ним не будут приниматься налоговой и вам придется заплатить больше налогов. Используйте системы проверки контрагентов на благонадежность. Например, в бухгалтерском веб-сервисе Контур.Бухгалтерия такая система есть.
Разработка правильной учетной политики. В зависимости от специфики бизнеса учетная политика поможет законными методами уменьшить налоговую базу и платежи в бюджет. Здесь читайте об учетной политике ООО на УСН.
Применение налоговых льгот. Это законные возможности уменьшить налоги или не платить их совсем. Но льготы есть не у всех. Льготы и послабления есть почти по всем налогам, кроме налога на игорный бизнес. Например, здесь мы рассказывали о налоговых льготах для IT-компаний.
Коронавирусная благотворительность. Если вы пожертвуете имущество или деньги на борьбу с коронавирусом, то сможете учесть их стоимость во внереализационных расходах при расчете налога на прибыль. Для УСН и ЕСХН это тоже актуально. Важно, что имущество должно быть предназначено для диагностики и лечения коронавируса, а также для предотвращения его распространения. Например, можно пожертвовать арматуру для строительства инфекционного отделения для коронавирусных больных. Право на учет расходов действует, если помощь получили некоммерческие медицинские организации, органы госвласти и управления или местного самоуправления, ГМУ или ГМУП.
Право на учет расходов действует, если помощь получили некоммерческие медицинские организации, органы госвласти и управления или местного самоуправления, ГМУ или ГМУП.
Дефорсирование двигателя. Транспортный налог зависит от мощности двигателя. Если ее уменьшить, ежегодные отчисления государству можно будет сократить. А побочный бонус — экономия на страховке. Чтобы получить эти преимущества, снизить мощность нужно официально и по закону, отметив изменения в ПТС, свидетельство и полис. Варианта два: исправить данные в паспорте, если они указаны неверно, или уменьшить мощность двигателя. Для уменьшения заменяют мотор или проводят дефорсирование с разрешения ГИБДД.
Нелегальные способы минимизации налогов: не используйте их
Многие организации для ухода от налогов применяют различные махинации. Налоговые органы, догадываясь об этом, исследуют схемы уклонения от уплаты налогов и довольно быстро приходят с проверками и наказаниями в неудачливую организацию. Вот самые простые противозаконные схемы, о которых хорошо известно налоговым работникам.
Вот самые простые противозаконные схемы, о которых хорошо известно налоговым работникам.
Дробление бизнеса. Это бизнес-процесс, в результате которого появляется несколько новых организаций, вместо одной крупной. Так, налогоплательщики пытаются сохранить право на спецрежимы, остаться в реестре МСП, одновременно работать с партнерами с НДС и без него. Однако если компания не имеет собственных источников дохода, не может самостоятельно выбирать направления расходов и свою прибыль передает в другую организацию, то штрафы здесь гарантированы.
Обналичивание средств организации. Иными словами, создание фирм-однодневок. Через такие организации недобросовестные предприниматели выводят деньги по фиктивным сделкам, переводя безналичные деньги в наличные.
Присоединение к организации убыточной компании. В результате такого присоединения снижаются налоги (НДС, налог на прибыль). Однако налоговый сотрудник, конечно, заострит свое внимание на приобретении убыточной компании и проверит, является ли убыток действительным, или же он фиктивный.
Типичные ошибки при проведении процедуры оптимизации
Использование налоговой оптимизации требует от организации серьезного подхода, так как ошибки, допущенные в налоговом учете, могут привести к незапланированным расходам в виде штрафов.
Отсутствие цели оптимизации. Ваши действия по сокращению налогов должны иметь обоснование — убедительную бизнес-цель, ради которой вы так или иначе преобразовали организацию. Это нужно будет при необходимости объяснить налоговой и подтвердить документально.
Изменение схемы работы задним числом. Переход на новую систему налогообложения занимает время, и большой организации потребуется больше времени. Побеспокойтесь заранее о переходе на новый налоговый режим.
Использование схем, которые стоят на особом контроле у государства. Воздержитесь от нелегальных приемов сокращения налогов. Опытные сотрудники налоговой службы занимаются исследованием махинаций налогоплательщиков, которые позже доводятся до всех сотрудников инспекций.
Недостаточный инструктаж работников. Применение схем оптимизации требует проработки. Поясните алгоритм новой схемы сотрудникам и создайте для них письменные инструкции. Тогда они смогут при необходимости дать актуальные пояснения налоговой службе.
Автор статьи: Александра Аверьянова
Оптимизируйте налоги законными способами с бухгалтерским сервисом Контур.Бухгалтерия. Здесь есть удобный налоговый и бухгалтерский учет, варианты учетной политики для малого бизнеса, проверка контрагентов. Наши эксперты помогут выбрать удобный налоговый режим и применять налоговые льготы. Первые 14 дней работы в сервисе — бесплатно.
Многокритериальная оптимизация|ИТММ ННГУ
Кафедра информатики и автоматизации научных исследований
Специальность: Прикладная информатика в области принятия решений
Преподаватель: Коротченко А.Г.
Содержание дисциплины направлено на ознакомление студентов с основными понятиями теории многокритериальной оптимизации и теории матричных игр, методами решения такого рода задач, а также с задачами принятия решений, когда цели задаются с помощью связанных с ними бинарных отношений предпочтений.
В результате изучения дисциплины студенты должны:
Знать определение эффективных и слабо-эффективных стратегий (точек), теорему их существования, способы скаляризации векторного критерия, специальные свойства бинарных отношений, принципы оптимальности, используемые в задачах принятия решений, когда цели задаются с помощью связанных с ними отношений предпочтений, определение бескоалиционной, антагонистической и матричной игры, теоремы о седловых точках, основную теорему теории матричных игр, достаточные признаки значения игры и оптимальных стратегий игроков.
Уметь находить множество эффективных стратегий для классов бикритериальных задач оптимизации, использовать алгоритмы, основанные на принципах оптимальности, для отыскания эффективных решений в задачах, когда цели задаются с помощью связанных с ними отношений предпочтений, решать частные классы матричных игр: 2*2 игры, 2*n и m*2 игры, 3*3 игры.
Иметь представление об алгоритмах выделения приближенно-эффективных точек при решении конкретных многокритериальных задач, о связи между разрешимостью пар двойственных задач линейного программирования и решениями матричных игр.
Содержание
1. Задачи оптимизации со многими критериями оптимальности. Эффективные и слабо эффективные стратегии (точки). Теорема существования эффективных точек. Множество Парето. Способы отыскания эффективных точек. Обобщенная функция цели. Скаляризация векторного критерия оптимальности при наличии дополнительной информации о важности частных критериев.
2. Линейные многокритериальные задачи. Методы отыскания эффективных точек в линейных многокритериальных задачах. Бикритериальная задача о ранце, бикритериальная задача на сети.
3. Приближенно-эффективные точки и алгоритмы их выделения. Понятие e-оптимального решения в задаче многокритериальной оптимизации и алгоритмы его отыскания. Вопросы сходимости множества приближенно-эффективных точек к множеству эффективных точек.
4. Задача принятия решений при задании целей с помощью связанных с ними бинарных отношений предпочтений. Аппарат теории отношений. Содержательное описание отношений. Специальные свойства отношений. Структура «доминирование-безразличие». Выявление предпочтений.
Содержательное описание отношений. Специальные свойства отношений. Структура «доминирование-безразличие». Выявление предпочтений.
5. Принципы оптимальности, используемые в задачах принятия решений, когда цели задаются с помощью связанных с ними отношений предпочтений. Принцип недоминируемости. Задача ранжирования при заданном транзитивном отношении предпочтения. Принцип Неймана-Моргенштерна. Понятие ядра отношения. Алгоритм выделения ядра. Принцип «грубого» ранжирования. Алгоритм выделения контуров графа бинарного отношения. Принцип «тонкого» ранжирования. Понятие предельного вектора, связь с числом Перрона-Фробениуса матрицы бинарного отношения.
6. Игровые задачи принятия решений. Определение бескоалиционной игры. Приемлемые ситуации и ситуации равновесия. Стратегическая эквивалентность игр. Антагонистические игры. Седловые точки. Равенство минимаксов.
7. Матричные игры. Смешанные стратегии. Смешанное расширение игры. Существование минимаксов в смешанных стратегиях.
Существование минимаксов в смешанных стратегиях.
8. Теорема о минимаксах. Лемма о двух альтернативах. Значение игры и оптимальные стратегии игроков. Три свойства значения игры. Достаточные признаки значения игры.
9. Частные классы матричных игр. 2х2 игры. Метод решения 2хn и mх2 игр. 3х3 игры.
10. Матричные игры и линейное программирование. Прямая и двойственная задача задачи линейного программирования. Связь между разрешимостью пар двойственных задач линейного программирования и решениями матричных игр.
Лабораторный практикум
- Линейные многокритериальные задачи. Реализация метода построения эффективных векторов и эффективных стратегий бикритериальной задачи, основанного на минимальном свойстве эффективных точек. Реализация метода динамического программирования решения бикритериальной задачи о ранце и бикритериальной задачи на сети.
- Реализация метода помеченных точек при приближенном решении многокритериальной задачи оптимизации.
 Демонстрация сходимости множества приближенных эффективных точек к множеству эффективных стратегий при различном задании аппроксимирующего множества. Решение контрольных примеров.
Демонстрация сходимости множества приближенных эффективных точек к множеству эффективных стратегий при различном задании аппроксимирующего множества. Решение контрольных примеров. - Реализация принципов выбора (недоминируемости, Неймана – Моргенштерна, ранжирования) в задачах принятия решений, когда цели задаются с помощью связанных с ними отношений предпочтений. Решение контрольных примеров.
Литература
а) основная литература:
- Батищев Д.И. Задачи и методы векторной оптимизации. – Изд. ГГУ, Горький, 1979
- Розен В.В. Цель- оптимальность- решение: Математические модели принятия оптимальных решений. – М.: Радио и связь, 1982
- Батищев Д.И. Методы оптимального проектирования. – М.: Радио и связь, 1984
- Воробьев Н.Н. Теория игр. Лекции для экономистов-кибернетиков. Изд. ЛГУ, Ленинград, 1974
- Воробьев Н.Н. Теория игр для экономистов-кибернетиков. М.: Наука, 1985
б) дополнительная литература:
- Никайдо Х.
 Выпуклые структуры и математическая экономика.– М.: Мир, 1972
Выпуклые структуры и математическая экономика.– М.: Мир, 1972 - Кини Р.Л., Райфа Х. Принятие решений при многих критериях: предпочтения и замещения.- М.: Радио и связь, 1981
- Соболь И.М., Статников Р.Б. Выбор оптимальных параметров в задачах со многими критериями. – М.: Наука, 1981
- Подиновский В.В., Ногин В.Д. Парето-оптимальные решения многокритериальных задач. – М.: Наука, 1982
- Морозов В.В., Сухарев А.Г., Федоров В.В. Исследование операций в задачах и упражнениях. – М.: Высшая школа, 1986
- Юдин Д.Б. Вычислительные методы теории принятия решений. – М.: Наука, 1989
- Емеличев В.А., Мельников О.И., Сарванов В.И., Тышкевич Р.И. Лекции по теории графов. – М.: Наука, 1990
- Штойер Р. Многокритериальная оптимизация. – М.: Радио и связь, 1992
- Батищев Д.И., Коган Д.И. Вычислительная сложность экстремальных задач переборного типа. – Изд. ННГУ, Н.Новгород, 1994
- Ашманов С.А. Линейное программирование. М.: Наука, 1981
- Воробьев Н.
 Н. Основы теории игр. Бескоалиционные игры. М.: Наука, 1984
Н. Основы теории игр. Бескоалиционные игры. М.: Наука, 1984 - Коротченко А.Г., Тихонов В.А. Методические указания (сборник задач) по курсу «Модели и методы принятия решений» — Изд. ННГУ, Н.Новгород, 2000
- Коротченко А.Г., Бобков А.Н. Принципы оптимальности в задачах принятия решений (методическая разработка) – Изд. ННГУ, Н.Новгород, 2002
Отчетность
Понятие оптимальной системы. Синтез и оптимизация параметров
Понятие оптимальной системы. Синтез и оптимизация параметровПонятие оптимальной системы. Синтез и оптимизация параметров |
Оглавление |
В системном анализе под «большой системой» понимают некоторую совокупность элементов, объединяемых между собой функциональными связями, нацеленными на решение единой задачи. «Большая система» понимается не с точки зрения ее географического размаха, а с точки зрения развитых функций составляющих ее элементов, необходимых для решения целевой задачи.
 Поэтому большая система может быть и сосредоточенной.
Поэтому большая система может быть и сосредоточенной.
Практически всегда большая система является дорогостоящей, поэтому при ее разработке необходимо спроектировать ее так, чтобы целевой эффект ее применения обеспечивался при минимальных затратах. Возможна также и обратная постановка задачи — проектировать систему так, чтобы вложенные в создание системы ограниченные ресурсы приносили максимальный целевой эффект.
Существует два подхода к проектированию больших систем. Первый и наиболее общий
— это синтез. В этом случае формируются самые общие требования к системе, определяется какой
должен быть целевой эффект, но сами элементы системы, их функции и связи не задаются.
В зависимости от типа системы применятся тот или иной математический аппарат: динамическое
программирование Беллмана, метод максимума Понтрягина и др. На этой основе синтезируются
элементы системы, их функции и связи, такие что целевой эффект работы системы является максимальным,
а требуемые для создания системы ресурсы не превышают заданных. Либо, при обратной
постановке задачи, целевой эффект достигает заданного уровня, а затрачиваемые ресурсы минимальны.
Метод синтеза хорош тем, что дает глобальный экстремум даже в том случае, если целевая функция носит периодический
характер. Графическое пояснение показано на рис.1.
Либо, при обратной
постановке задачи, целевой эффект достигает заданного уровня, а затрачиваемые ресурсы минимальны.
Метод синтеза хорош тем, что дает глобальный экстремум даже в том случае, если целевая функция носит периодический
характер. Графическое пояснение показано на рис.1.
Однако практические задачи с использованием упомянутого математического аппарата решить и довести до уровня реализации удается весьма редко. Поэтому на практике применяют более грубые методы, которые носят название «параметрический синтез» или «оптимизация параметров системы». В отличие от методов прямого синтеза, эти методы не всегда дают глобальный экстремум, однако в рамках задаваемых структуры системы и ее параметров полученные результаты являются приемлемыми для целей практики.
Рассмотрим абстрактный пример. Пусть имеется система, на входе которой действует вектор входных воздействий система имеет параметры выходная целевая функция имеет вид
В данном примере большая система имеет параметры z1,z2. ..zm
и отрабатывает входное воздействие с параметрами
x1,x2…xn. Очевидно, что результат функционирования системы, т.е целевая функция
зависят как от параметров {zi} самой системы, так и от параметров входного
воздействия {xi}. Оптимизация параметров системы состоит в том, что при
фиксированом (статическом) наборе параметров {xi} мы можем подбирать
параметры системы {zi} таким образом, что выходная целевая функция R достигает
экстремума. Однако, параметры системы должны быть связаны с ресурсными характеристиками,
например, со стоимостью. Поскольку изменение каждого из параметров {zi} системы требует внесения
вложения ресурсов: например мы должны увеличить пропускную способность каналов сети или
производительность узлов коммутации, а это требует определенных затрат.
Поэтому для того чтобы подбор параметров системы был оптимальным, необходимо
связать каждый из них с функцией стоимости: z 1 = f ( d1 ), z 2 = f ( d2 ) и т.
..zm
и отрабатывает входное воздействие с параметрами
x1,x2…xn. Очевидно, что результат функционирования системы, т.е целевая функция
зависят как от параметров {zi} самой системы, так и от параметров входного
воздействия {xi}. Оптимизация параметров системы состоит в том, что при
фиксированом (статическом) наборе параметров {xi} мы можем подбирать
параметры системы {zi} таким образом, что выходная целевая функция R достигает
экстремума. Однако, параметры системы должны быть связаны с ресурсными характеристиками,
например, со стоимостью. Поскольку изменение каждого из параметров {zi} системы требует внесения
вложения ресурсов: например мы должны увеличить пропускную способность каналов сети или
производительность узлов коммутации, а это требует определенных затрат.
Поэтому для того чтобы подбор параметров системы был оптимальным, необходимо
связать каждый из них с функцией стоимости: z 1 = f ( d1 ), z 2 = f ( d2 ) и т. д.,
где di i=1,2..m — стоимость изменения параметра. В этом случае, изменяя параметры системы zi,
мы будем изменять суммарную стоимость изменения параметров
и изменять их таким образом, чтобы стоимость системы была не выше заданной, а целевая функция
достигала экстремума. Либо в обратной постановке задачи, мы будем изменять
параметры системы так, чтобы ее сумарная стоимость была минимальной, а целевая функция соответствовала
заданной.
д.,
где di i=1,2..m — стоимость изменения параметра. В этом случае, изменяя параметры системы zi,
мы будем изменять суммарную стоимость изменения параметров
и изменять их таким образом, чтобы стоимость системы была не выше заданной, а целевая функция
достигала экстремума. Либо в обратной постановке задачи, мы будем изменять
параметры системы так, чтобы ее сумарная стоимость была минимальной, а целевая функция соответствовала
заданной.
Метод оптимизации параметров не дает глобального экстремума, по очень простой причине -
задавая структуру и состав параметров системы мы уже ограничили свой выбор, и полученный
оптимум будет носить частный характер. Однако для решения практических задач этот
метод является приемлемым.
|
Предыдущий |
Следующий |
Понятие оптимизация сайтов | leksimage.
 ru
ruПонятие оптимизация сайтов
В последнее время определение “оптимизация сайтов” на слуху у большинства компаний, которые предоставляют определенные услуги в глобальной интернет сети. Это совсем не удивительно, если учесть большую пользу, которую можно извлечь при правильном построении стратегии рекламы тех или иных товаров, либо услуг в интернете.Так что же являет собой процесс оптимизации сайтов, в чем состоит его суть?
Оптимизация сайтов является комплексом мероприятий направленных на повышение видимости конкретного сайта в результатах поисковых систем по набору ключевых слов или фраз. Проще говоря — это поднятие позиций сайта.
Оптимизация сайта состоит из нескольких этапов:
1) Начальный анализ сайта, сферы деятельности и анализ конкуренции.
На данном этапе надо провести тщательное изучение структуры построения сайта, его текстового содержания, при этом оценив уровень конкуренции и выявив возможные сложности с которыми придется сталкиваться.
2) Подбор ключевых запросов для поисковой оптимизации (иными словами составление семантического ядра). В процессе подбора ключевых фраз рекомендуют использовать статистику запросов пользователей конкретной поисковой системы. При подборе и формировании ключевых фраз стоит обратить внимание на запросы с сокращениями, ошибками в написании, написание фирм-производителей латиницей и кириллицей. Полезно также посмотреть на ключевые запросы, которые используют конкуренты.
3) Работа над структурой и содержимым сайта. Этот процесс может состоять из нескольких мероприятий, направленных на создание дополнительных страниц проекта в зависимости от ассортимента продукции компании, или ее услуг. Работа над содержимым сайта в основном исходит из оптимизации того, что пользователь будет видеть на странице: тексты, графические объекты и написание новых текстов на сайт.
4) Оптимизация мета-данных проекта. Основными мета-данными любой интернет страницы являются: Title (заглавие страницы), Description (описание страницы), Keywords (ключевые запросы). Полезным для продвижения проекта и привлечения целевой аудитории является составление мета-данных с разным написанием, для всех страниц проекта.
Полезным для продвижения проекта и привлечения целевой аудитории является составление мета-данных с разным написанием, для всех страниц проекта.
Оптимизация: определение и изучение концепции усиления воздействия инициатив в области общественного здравоохранения | Политика и системы исследований в области здравоохранения
Частота ответов и характеристики респондентов
Тридцать из 33 приглашенных лиц (91%) дали активное согласие и приняли участие в исследовании. Среди участников были мужчины ( n = 11) и женщины ( n = 19), эксперты в области политики и практики ( n = 16) и эксперты-исследователи ( n = 14). Участники семинара провели встречи в семи университетах или научно-исследовательских институтах по всему миру (Таблица 1).Неучастники жили за пределами Австралии и не смогли посетить семинар из-за конкурирующих требований.
Таблица 1 Учреждения, представленные на семинареЦель 1: Определение оптимизации в контексте общественного здравоохранения
В ходе последующих раундов Delphi рабочее определение оптимизации претерпело несколько изменений (рис. 2). После финального раунда согласованное определение оптимизации в контексте общественного здравоохранения было : « Оптимизация — это преднамеренный, повторяющийся и управляемый данными процесс для улучшения медицинского вмешательства и / или его реализации для удовлетворения потребностей общественности, определенной заинтересованными сторонами. воздействие на здоровье при ограниченных ресурсах ».
2). После финального раунда согласованное определение оптимизации в контексте общественного здравоохранения было : « Оптимизация — это преднамеренный, повторяющийся и управляемый данными процесс для улучшения медицинского вмешательства и / или его реализации для удовлетворения потребностей общественности, определенной заинтересованными сторонами. воздействие на здоровье при ограниченных ресурсах ».
Этапы уточнения определения
Цель 2: Ключевые аспекты оптимизации для общественного здравоохранения
В соответствии со второй целью в ходе семинара участники обсудили концептуальные и практические соображения при оптимизации вмешательств в области общественного здравоохранения . Они были сгруппированы по основным темам и соответствующим подтемам, которые обсуждаются в следующем разделе и обобщены в таблице 2.
Таблица 2 Ключевые соображения при оптимизации вмешательств в области общественного здравоохраненияТема 1: Параметры для оптимизации
Участники признали, что существуют различные параметры оптимизации, которые необходимо учитывать либо при рассмотрении вопроса об оптимизации, либо после принятия решения о продолжении с оптимизацией. Параметры, используемые при принятии решения об оптимизации, включают ряд предварительных условий, которые могут потребоваться для того, чтобы оптимизация была возможной или потенциально целесообразной. После принятия решения об оптимизации может потребоваться другой набор параметров. Они кажутся более сфокусированными на том, какой результат и как должен происходить процесс оптимизации.
Параметры, используемые при принятии решения об оптимизации, включают ряд предварительных условий, которые могут потребоваться для того, чтобы оптимизация была возможной или потенциально целесообразной. После принятия решения об оптимизации может потребоваться другой набор параметров. Они кажутся более сфокусированными на том, какой результат и как должен происходить процесс оптимизации.
Предварительные условия для оптимизации
- 1)
Доступны качественные данные о результатах и ресурсы для анализа / оценки результатов программы
Наличие данных хорошего качества для оценки воздействия вмешательства и / или стратегии реализации на результат, для которого они оптимизируются, необходимо для оптимизации.Некоторые участники отметили, что оптимизация особенно подходит для вмешательств, при которых собираются стандартные данные, которые можно недорого получить и использовать для оценки воздействия вмешательств по мере их итеративного изменения. Например, для этой цели можно использовать существующие медицинские записи, связанные наборы данных или данные из систем наблюдения за риском хронических заболеваний общественного здравоохранения. Однако участники отметили ограниченность многих из этих источников данных для обеспечения достаточно обоснованных мер по улучшению, а также значительную проблему, которая связана с определением легко доступных, достаточно надежных мер по оптимизации в области общественного здравоохранения.
Например, для этой цели можно использовать существующие медицинские записи, связанные наборы данных или данные из систем наблюдения за риском хронических заболеваний общественного здравоохранения. Однако участники отметили ограниченность многих из этих источников данных для обеспечения достаточно обоснованных мер по улучшению, а также значительную проблему, которая связана с определением легко доступных, достаточно надежных мер по оптимизации в области общественного здравоохранения.
Кроме того, учитывая, что процессы оптимизации могут занять значительное время (возможно, много лет), наличие постоянных стабильных ресурсов считалось важным предварительным условием для оптимизации. Участники признали, что, хотя многие службы общественного здравоохранения имеют постоянное регулярное финансирование для реализации программ здравоохранения и их оценки, многие другие этого не делают. В таких обстоятельствах, когда доступны только краткосрочные дискретные средства, оптимизация вмешательств или стратегий их реализации может оказаться невозможной или нецелесообразной.
- 2)
Существующие инициативы недостаточно эффективны, и от оптимизации ожидаются значимые воздействия на здоровье населения
Участники обсудили, что для того, чтобы гарантировать участие в процессах оптимизации, должно быть достаточно доказательств, чтобы продемонстрировать, что существующее вмешательство или подходы к реализации недостаточно эффективны. Кроме того, от процесса оптимизации следует ожидать значимых улучшений, чтобы оправдать продолжение оптимизации.
«[для оптимизации] у вас должна быть проблема, которую стоит решить ». (Специалист по внедрению)
“ Учитывайте минимальный стандарт… избегайте попыток оптимизировать вещи, которые того не стоят. »(специалист по внедрению)
Другими словами, чтобы приступить к процессу оптимизации, необходимо взвесить важность проблемы для общественного здравоохранения и потенциальные выгоды от оптимизированной стратегии вмешательства / реализации. Употребление табака, широко распространенное в обществе и являющееся причиной значительного вреда, является примером проблемы общественного здравоохранения, в результате которой со временем можно ожидать улучшения воздействия за счет оптимизации.
Употребление табака, широко распространенное в обществе и являющееся причиной значительного вреда, является примером проблемы общественного здравоохранения, в результате которой со временем можно ожидать улучшения воздействия за счет оптимизации.
- 3)
Доступна организационная поддержка и руководство для таких действий, как взаимодействие с конечными пользователями.
Оптимизация требует участия конечных пользователей. Некоторые участники предположили, что участие в процессах оптимизации может быть значительным вложением, требующим организационной поддержки и приверженности.Кроме того, постоянная оптимизация стратегии реализации может нанести ущерб агентству, ответственному за реализацию программы. В таких обстоятельствах лидерство и поддержка организации, а также готовность и готовность к постоянным изменениям в соответствующих организациях кажутся основополагающими.
Параметры, учитываемые после принятия решения об оптимизации (когда и на каком результате оптимизировать)
Помимо выделения различных предварительных условий для оптимизации, группа обсудила типы параметров, которые могут быть рассмотрены после принятия решения о продолжении оптимизации.
- 1)
Процессы оптимизации могут происходить по всему континууму преобразования общественного здравоохранения (разработка вмешательства посредством масштабного внедрения)
Группа обсудила, могут ли процессы оптимизации происходить на любом этапе преобразования общественного здравоохранения — во время разработки вмешательства, разработка стратегии реализации, активное распространение и реализация в масштабе — а также типы данных, которые необходимы для различных этапов.
“ Необходимо учитывать, что, возможно, оптимизация — это постоянный процесс, а не только в определенные моменты времени. ”(Практикующий)
« Может быть, оптимизация — это не конец и не начало, а происходит повсюду? »(эпидемиолог)
Тем не менее, существовали различные и расходящиеся мнения об относительной ценности процессов оптимизации на более ранних стадиях, применяемых к разработке вмешательств, и процессов оптимизации на более поздних стадиях, которые могут быть более сфокусированы на оптимизации их реализации в реальных контекстах, чтобы максимизировать их влияние. Некоторые участники усомнились в разнице между оптимизацией на ранних этапах разработки вмешательства и традиционным формирующим исследованием.
Некоторые участники усомнились в разнице между оптимизацией на ранних этапах разработки вмешательства и традиционным формирующим исследованием.
“ Что бы вы сделали по-другому в программе укрепления здоровья (например, хорошая формирующая оценка), чтобы оптимизировать предварительное вмешательство, помимо хорошего планирования? »(специалист по общественному здравоохранению / поведенческому поведению)
« Различие между хорошим дизайном… почему он должен охватывать то, что уже хорошо освещено? »(Практик)
Другие предположили, что ключевым отличием является конкретная направленность оптимизации на улучшение воздействия, цель оптимизации, согласованная с целями заинтересованных сторон, а не академическими целями или целями разработчика программ, и ориентация на непрерывное или постоянное улучшение. .
« Оптимизация выходит за рамки хорошего планирования… потому что в процессе оптимизации мы пытаемся добиться большей эффективности… большей эффективности ».
(Практик)
Обсуждение завершилось заявлением о том, что, хотя процессы оптимизации могут происходить на любой стадии разработки и реализации вмешательства, влияние вмешательства с большей вероятностью будет максимальным, если оптимизация будет происходить на протяжении всего процесса преобразования общественного здравоохранения. .
- 2)
Оптимизация должна быть направлена на улучшение воздействия на результаты, определенные и оцениваемые заинтересованными сторонами (или конечными пользователями)
Участники считали, что основной целью оптимизации является улучшение результатов, определенных и оцениваемых заинтересованными сторонами, включая затраты , эффективность, соответствие существующим программам и / или охват [36].Как правило, заинтересованными сторонами являются агентства или организации, ответственные за финансирование реализации вмешательства, или лица, ответственные за осуществление вмешательства. В зависимости от вовлеченных заинтересованных сторон и воздействия, которое они стремятся оптимизировать, процессы и результаты оптимизации могут различаться. Исходя из этого, группа согласилась с тем, что сначала важно определить, кто заинтересован в оптимизации.
Исходя из этого, группа согласилась с тем, что сначала важно определить, кто заинтересован в оптимизации.
При рассмотрении заинтересованных сторон участники подчеркнули необходимость различать лиц, определяющих политику (которые могут включать государственных или негосударственных лиц, принимающих решения), и конечных пользователей / потребителей (которые могут включать членов сообщества, пациентов и организации, такие как медицинские школы или общественные организации).
« Начните с заинтересованных сторон… оптимизируйте потребности заинтересованных сторон… политиков в сравнении с потребителями. Удовлетворили ли мы потребности заинтересованных сторон? Каковы их потребности ? » (Специалист по общественному здравоохранению / поведенческому поведению)
Четкое разъяснение того, кем являются заинтересованные стороны и чем они отличаются, может затем помочь в установлении того, как взаимодействовать с каждой группой в непрерывном процессе реализации общественного здравоохранения.
Участники признали, что необходимо учитывать различные и часто расходящиеся точки зрения и приоритеты заинтересованных сторон.Результаты оптимизации могут включать меры воздействия вмешательства на качество помощи, индивидуальное поведение в отношении здоровья, условия или качество жизни, а также результаты на уровне населения или системы здравоохранения, включая показатели неравенства, реализации, использования медицинских услуг или затрат.
Было достигнуто общее согласие с тем, что в контексте общественного здравоохранения, хотя могут существовать ожидания результатов на системном уровне лиц, определяющих политику и / или исследователей, и ожидания результатов на уровне организации руководителей ведомств и поставщиков услуг, на микроуровне всегда следует учитывать ожидания результатов и приоритеты конечных пользователей (такие как охват, справедливость, соответствие и качество жизни).
« Оптимизация [в общественном здравоохранении] идет с позитивным намерением » (специалист по внедрению)
«Например… оптимизация ухода за пациентами с переломом бедра.
Система оптимизирована с точки зрения затрат, снижения заражения [системный уровень] , но не с точки зрения качества жизни отдельного человека. Необходимо учитывать качество жизни. В настоящее время рамки не охватывают это »(специалист по общественному здравоохранению / поведенческим наукам)
Кажется, что при оптимизации вмешательств в области общественного здравоохранения первостепенное значение имеет соблюдение приоритетов конечных пользователей и не упускать из виду« позитивные намерения ». оптимизации.
« Основная мотивация — здоровье населения. Это должно быть в первую очередь при планировании »(Менеджер службы здравоохранения)
- 3)
Влияние оптимизации рассматривается относительно доступных ресурсов
Влияние оптимизации происходит в контексте и рассматривается относительно доступности ограниченных ресурсов.
« Использование ресурсов — ключевой ингредиент для осуществления деятельности » (методист)
Участники признали, что потребности в ресурсах являются важным фактором во всем процессе оптимизации в области общественного здравоохранения и что такие требования могут различаться на разных этапах разработка и внедрение интервенций.
« (…) в то время как на этапе исследования мы можем рассматривать высокий риск / высокую доходность; на этапе предоставления услуги вы можете начать с большим количеством ресурсов, чем возможно, а затем масштабировать их для реального мира; и на уровне населения нам необходимо учитывать эффективность и уязвимость населения »(специалист по внедрению)
Различные параметры, описанные выше, влияют на процесс и результаты оптимизации в общественном здравоохранении. Участники также обсудили некоторые соображения относительно потенциальных методов определения того, какие элементы программы следует оптимизировать.
Тема 2: Как оптимизировать
Обсуждение того, как проводить оптимизацию, отражало различные точки зрения участников, и не было достигнуто соглашения относительно «наилучшего подхода» для определения того, как следует изменить вмешательство или стратегию реализации, чтобы оптимизировать происходить.
Необходимо понять логику или причинно-следственную модель основной инициативы
Участники согласились с тем, что для оптимизации необходимо понимать основные компоненты и механизмы программы. Однако было отмечено, что многие программы не имеют логической модели и что существуют научные и практические соображения, ограничивающие возможности и возможности для проверки предполагаемых механизмов.
Однако было отмечено, что многие программы не имеют логической модели и что существуют научные и практические соображения, ограничивающие возможности и возможности для проверки предполагаемых механизмов.
“ Несмотря на то, что логика программы так важна для правильной оценки программы, большинство программ не имеют логики программы… мы не имеем представления о том, какие компоненты программы относятся к каким аспектам программы .”(Практикующий)
Для понимания механизмов инициативы могут использоваться факторные планы или аналоговые методы.
Некоторые предложили оптимизировать элементы стратегии вмешательства или реализации, используя количественные механистические методы (например, анализ посредничества) и планы исследований, включая рандомизированные и факторные испытания, а также другие более прагматичные подходы, такие как аналоговые методы (т. е. виньетки). Участники отметили, что аналоговые методы помогут избежать необходимости тестирования всего вмешательства в большом рандомизированном контрольном исследовании, поскольку они помогут определить — в небольшом масштабе — факторы, влияющие на воздействия.
е. виньетки). Участники отметили, что аналоговые методы помогут избежать необходимости тестирования всего вмешательства в большом рандомизированном контрольном исследовании, поскольку они помогут определить — в небольшом масштабе — факторы, влияющие на воздействия.
« Мы могли бы использовать основанные на нормах вмешательства для улучшения доставки… оптимизация в пространстве аналогов или виньеток для тестирования вмешательства с предполагаемыми конечными пользователями, например, тестирования того, как более эффективно доставлять / передавать сообщения конечным пользователям …» ( Ученый по внедрению)
Тема 3: Определение момента достижения оптимизации
Последняя группа соображений по оптимизации была связана с тем, как узнать, когда была оптимизирована стратегия вмешательства и / или реализации.
Мнения заинтересованных сторон, необходимо учитывать потенциал дополнительных значимых воздействий и уравновешивание нескольких результатов
Участники обсудили взаимосвязь между параметрами, упомянутыми выше (приоритеты или ожидаемые результаты, определенные заинтересованными сторонами, и ограничения ресурсов) и решением относительно точки, в которой программа (вмешательство или ее реализация) считается «оптимизированной».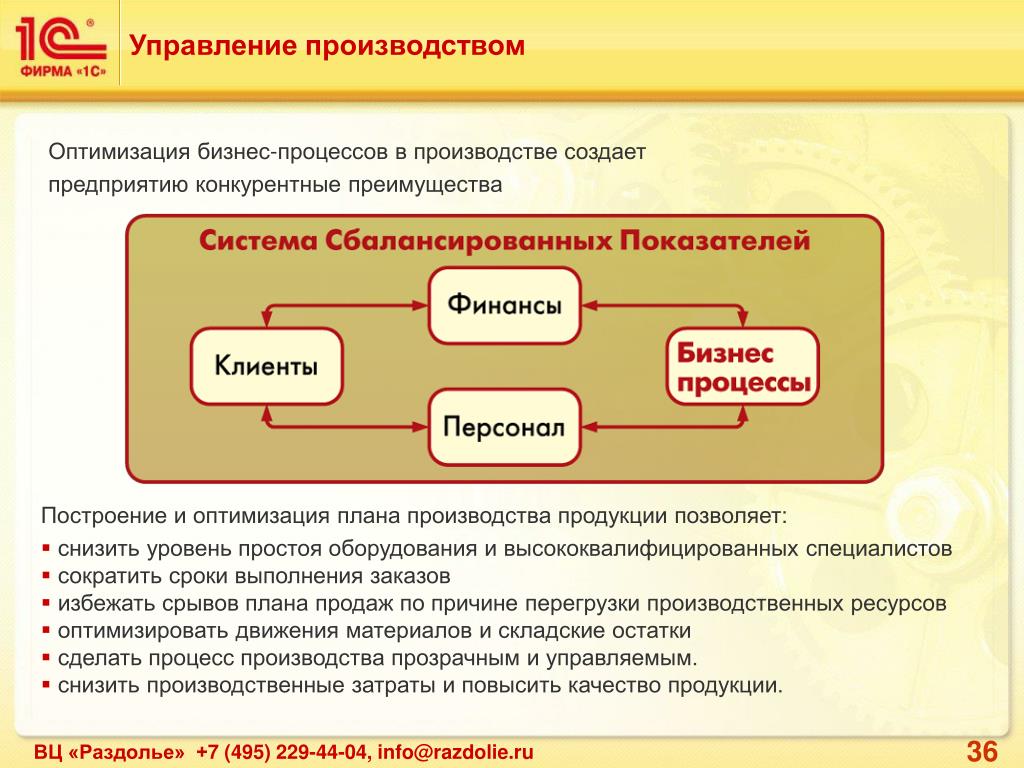 Не было достигнуто согласия относительно точной точки принятия решения или критериев.В частности, некоторые участники подчеркнули, что при принятии решения об оптимизации программы необходимо учитывать ценности и перспективы заинтересованных сторон. Другие предположили, что оптимизация была достигнута, когда заинтересованные стороны считают, что дальнейшие инвестиции в оптимизацию могут не привести к значительным улучшениям воздействия. Кроме того, некоторые участники относились к точке оптимизации более концептуально, как к «точке баланса». Эта «точка баланса» будет находиться между приемлемостью для заинтересованных сторон и такими аспектами программы, как рентабельность, влияние на бюджет, охват и эффективность, понимаемые в рамках ограничений конкретного контекста.
Не было достигнуто согласия относительно точной точки принятия решения или критериев.В частности, некоторые участники подчеркнули, что при принятии решения об оптимизации программы необходимо учитывать ценности и перспективы заинтересованных сторон. Другие предположили, что оптимизация была достигнута, когда заинтересованные стороны считают, что дальнейшие инвестиции в оптимизацию могут не привести к значительным улучшениям воздействия. Кроме того, некоторые участники относились к точке оптимизации более концептуально, как к «точке баланса». Эта «точка баланса» будет находиться между приемлемостью для заинтересованных сторон и такими аспектами программы, как рентабельность, влияние на бюджет, охват и эффективность, понимаемые в рамках ограничений конкретного контекста.
Оптимизация питательной среды для дифференциации индуцированных человеком плюрипотентных стволовых клеток с использованием дизайна экспериментов — доказательство концепции
DOI: 10. 1002 / btpr.3143.
Epub 2021 22 марта.
1002 / btpr.3143.
Epub 2021 22 марта.Принадлежности Расширять
Принадлежности
- 1 Колледж наук о здоровье и жизни, Школа биологических наук, Астонский университет, Бирмингем, Великобритания.
- 2 Департамент биохимической инженерии, Университетский колледж Лондона, Лондон, Великобритания.
Элемент в буфере обмена
Патрисия П. Эстебан и др.
Biotechnol Prog.
2021 июл.
Эстебан и др.
Biotechnol Prog.
2021 июл.
Показать варианты
Формат АннотацияPubMedPMID
DOI: 10.1002 / btpr.3143. Epub 2021 22 марта.Принадлежности
- 1 Колледж наук о здоровье и жизни, Школа биологических наук, Астонский университет, Бирмингем, Великобритания.

- 2 Департамент биохимической инженерии, Университетский колледж Лондона, Лондон, Великобритания.
Элемент в буфере обмена
Полнотекстовые ссылки Опции CiteDisplayПоказать варианты
Формат АннотацияPubMedPMID
Абстрактный
Использование индуцированных человеком плюрипотентных стволовых клеток (hiPSC) в клеточной терапии имеет огромный потенциал, но сталкивается со многими практическими проблемами, включая затраты, связанные со средой для культивирования клеток и факторами роста.Существует неотложная потребность в создании оптимизированной платформы для культивирования, чтобы направлять дифференциацию hiPSCs в зародышевые листки в определенной питательной микросреде для создания рентабельных и надежных терапевтических средств. Целью этого исследования было определение оптимальной среды питания путем имитации концентраций трех ключевых факторов (глюкозы, пирувата и кислорода) in vivo во время спонтанной дифференцировки hiPSCs, полученных из пуповинной крови, которые сильно отличаются от in vitro расширения и сценарии дифференциации.Более того, мы предположили, что высокие концентрации глюкозы, пирувата и кислорода, обнаруженные в типичных средах для выращивания, могут ингибировать дифференцировку определенных клонов. План экспериментов был использован для изучения взаимодействия между этими тремя переменными во время спонтанной дифференциации hiPSCs. Мы обнаружили, что более низкие концентрации кислорода и глюкозы усиливают экспрессию мезодермальных (Brachyury, KIF1A) и эктодермальных (нестин, β-тубулин) маркеров. Наши результаты представляют новый подход к эффективной направленной дифференциации hiPSCs посредством манипулирования компонентами среды, одновременно избегая использования факторов роста, что снижает затраты.
Целью этого исследования было определение оптимальной среды питания путем имитации концентраций трех ключевых факторов (глюкозы, пирувата и кислорода) in vivo во время спонтанной дифференцировки hiPSCs, полученных из пуповинной крови, которые сильно отличаются от in vitro расширения и сценарии дифференциации.Более того, мы предположили, что высокие концентрации глюкозы, пирувата и кислорода, обнаруженные в типичных средах для выращивания, могут ингибировать дифференцировку определенных клонов. План экспериментов был использован для изучения взаимодействия между этими тремя переменными во время спонтанной дифференциации hiPSCs. Мы обнаружили, что более низкие концентрации кислорода и глюкозы усиливают экспрессию мезодермальных (Brachyury, KIF1A) и эктодермальных (нестин, β-тубулин) маркеров. Наши результаты представляют новый подход к эффективной направленной дифференциации hiPSCs посредством манипулирования компонентами среды, одновременно избегая использования факторов роста, что снижает затраты.
Ключевые слова: дизайн экспериментов; дифференциация зародышевого листка; индуцированные человеком плюрипотентные стволовые клетки.
© 2021 Авторы. Прогресс биотехнологии, опубликованный Wiley Periodicals LLC от имени Американского института инженеров-химиков.
Похожие статьи
- Электроспрядные полистирольные каркасы в качестве синтетического субстрата для размножения и дифференцировки индуцированных человеком плюрипотентных стволовых клеток без ксенонов.
Леонг М.Ф., Лу Х.Ф., Лим ТК, Ду Ц, Ма НКЛ, Ван АКА. Леонг М.Ф. и др. Acta Biomater. 2016 декабрь; 46: 266-277. DOI: 10.1016 / j.actbio.2016.09.032. Epub 2016 22 сентября. Acta Biomater.
 2016 г.
PMID: 27667015
2016 г.
PMID: 27667015 - Дифференциация индуцированных человеком плюрипотентных стволовых клеток в мужские половые клетки.
Чжао Н, Шэн М., Ван Х, Ли И, Фарзане М.Чжао Н и др. Curr Stem Cell Res Ther. 2021; 16 (5): 622-629. DOI: 10,2174 / 1574888X15666200705214223. Curr Stem Cell Res Ther. 2021 г. PMID: 32628592 Рассмотрение.
- Оптимизированная последовательная экспансия индуцированных человеком плюрипотентных стволовых клеток с использованием инокуляции низкой плотности для получения клинически значимых количеств в биореакторах с вертикальным колесом.
Борис Б.С., Со Т., Колтер Дж., Данг Т., Робертс Е.Л., Ревей Т., Лариджани Л., Кравец Р., Льюис И., Аргиропулос Б., Ранкур Д.Е., Юнг С., Хашимура Ю., Ли Б., Каллос М.
 С.Борис Б.С. и др.
Стволовые клетки Transl Med. 2020 Сен; 9 (9): 1036-1052. DOI: 10.1002 / sctm.19-0406. Epub 2020 22 мая.
Стволовые клетки Transl Med. 2020.
PMID: 32445290
Бесплатная статья PMC.
С.Борис Б.С. и др.
Стволовые клетки Transl Med. 2020 Сен; 9 (9): 1036-1052. DOI: 10.1002 / sctm.19-0406. Epub 2020 22 мая.
Стволовые клетки Transl Med. 2020.
PMID: 32445290
Бесплатная статья PMC. - Надежная дифференциация мРНК-репрограммированных человеческих плюрипотентных стволовых клеток в направлении ретинального происхождения.
Шридхар А., Олемахер С.К., Лангер КБ, Мейер Дж. С.. Шридхар А. и др.Стволовые клетки Transl Med. 2016 Апрель; 5 (4): 417-26. DOI: 10.5966 / sctm.2015-0093. Epub 2016 1 марта. Стволовые клетки Transl Med. 2016 г. PMID: 26933039 Бесплатная статья PMC.
- Мини-обзор; Дифференциация плюрипотентных стволовых клеток человека в ооциты.
Ван Г, Фарзане М. Ван Г. и др. Curr Stem Cell Res Ther.
 2020; 15 (4): 301-307. DOI: 10.2174 / 1574888X15666200116100121.Curr Stem Cell Res Ther. 2020.
PMID: 31951188
Рассмотрение.
2020; 15 (4): 301-307. DOI: 10.2174 / 1574888X15666200116100121.Curr Stem Cell Res Ther. 2020.
PMID: 31951188
Рассмотрение.
использованная литература
ССЫЛКИ
- Мейер-младший. Значение индуцированных плюрипотентных стволовых клеток для фундаментальных исследований и клинической терапии. J Med Ethics. 2008; 34 (12): 849-851. https://doi.org/10.1136 / jme.2008.024786.
- Робинтон Д.А., Дейли GQ. Перспективы индуцированных плюрипотентных стволовых клеток в исследованиях и терапии. Природа. 2012; 481 (7381): 295-305. https://doi.org/10.1038/nature10761.
- Такахаши К.
 , Яманака С. Индукция плюрипотентных стволовых клеток из культур эмбриональных и взрослых фибробластов мыши с помощью определенных факторов.Клетка. 2006; 126: 663-676. https://doi.org/10.1016/j.cell.2006.07.024.
, Яманака С. Индукция плюрипотентных стволовых клеток из культур эмбриональных и взрослых фибробластов мыши с помощью определенных факторов.Клетка. 2006; 126: 663-676. https://doi.org/10.1016/j.cell.2006.07.024.
- Такахаши К.
- Такахаши К., Танабе К., Охнуки М. и др. Индукция плюрипотентных стволовых клеток из фибробластов взрослого человека определенными факторами. Клетка. 2007; 107 (5): 861-872. https://doi.org/10.1016/j.cell.2007.11.019.
- Крикс С., Шим Дж. В., Пиао Дж. И др.Дофаминовые нейроны, полученные из человеческих ES-клеток, эффективно приживаются в моделях болезни Паркинсона на животных. Природа. 2011; 480: 547-551. https://doi.org/10.1038/nature10648.
Показать все 55 ссылок
Типы публикаций
- Поддержка исследований, за пределами США.
 Правительство
Правительство
LinkOut — дополнительные ресурсы
Источники полных текстов
Другие источники литературы
цитировать
КопироватьФормат: AMA APA ГНД NLM
Преимущества Real Time Concept Optimization ™
Лучшие Лрактики
Преимущества Real Time Concept Optimization ™
Как и большинство компаний, ваша, скорее всего, находится под растущим давлением, требующим быстрого вывода новых идей на рынок.Когда дело доходит до фильтрации новых концепций, выявления победителей и внесения улучшений, которые повысят производительность, у вас не будет роскоши долгого времени выполнения заказа.
Вот почему концепция оптимизации в реальном времени ™ была разработана Radius. Он предоставляет вашей организации ориентированные на потребителя оценки, которые включают мгновенную обратную связь и немедленные рекомендации по развитию и совершенствованию идей. Преимущества этого подхода включают в себя:
- Получите немедленную реакцию от вашей целевой аудитории
- Получение отзывов о том, как быстро улучшить или усовершенствовать концепции
- Пересмотреть и усилить концепции в процессе
- Соедините концепции с прототипами, чтобы обеспечить согласованность между двумя
Оптимизатор концепций в реальном времени ™ работает, позволяя извлекать уроки из каждой фокус-группы для доработки концепций, которые затем представляются следующей фокус-группе.Этот процесс повторяется в нескольких фокус-группах (определяется на основе количества концепций, которые необходимо проверить, и количества включаемых подгрупп / сегментов). В частности, вот как это работает:
В частности, вот как это работает:
- Мы начинаем с проекта концепции (или концепций), а также можем включать прототипы.
- Эти концепции / прототипы представлены и обсуждаются в первой группе для оценки эмоциональных, интеллектуальных и внутренних реакций, а также симпатий, антипатий, степени интереса, того, что побуждает тех, кто заинтересован, релевантности, степени соответствия прототипам (если в наличии) и т. д.
- После этой первой группы следует формальная структурированная рабочая сессия с Radius и командой клиентов вместе с профессиональным автором концепции для доработки / обновления концепции (концепций) на основе отзывов.
- Эти переработанные концепции затем представляются следующей фокус-группе, и процесс повторяется по мере необходимости, как указано выше.
В конечном итоге, подход к оптимизации концепции в реальном времени ™ предлагает понимание:
- Концепции с наибольшим потенциалом по сравнению с теми, которые следует переосмыслить или отменить приоритетность
- Привлекательность концепции у целевой аудитории
- Возможности улучшения
- Степень, в которой целевой рынок идентифицируется с концептуальными преимуществами и основаниями верить
- Степень соответствия концепта и прототипа
- Уровень согласованности между концепцией и брендом
Radius Global Market Research привносит более чем 60-летний опыт разработки новых концепций, чтобы обеспечить достижение бизнес-целей с максимальной степенью возможностей и вниманием к деталям. Если вы хотите узнать больше о том, какие преимущества может получить ваша организация от Real Time Concept Optimizer ™ , свяжитесь с нами.
Если вы хотите узнать больше о том, какие преимущества может получить ваша организация от Real Time Concept Optimizer ™ , свяжитесь с нами.
Концепция прямой оптимизации пути волокна
Концепция выравнивания армирующих волокон в произвольных направлениях предлагает новый взгляд на использование анизотропных характеристик композитов из армированного углеродным волокном полимера (CFRP). В дополнение к концепции конструкции многоосных композитов, ламинат, армированный криволинейными волокнами, называется регулируемым осевым волокном (также известный как жгут с переменной жесткостью и регулируемым углом наклона).Технология Tailored Fiber Placement (TFP) хорошо подходит для производства текстильных преформ с изменяемой осевой конструкцией волокон с использованием адаптированных вышивальных машин. Эта работа представляет новую концепцию моделирования и оптимизации криволинейных армированных волокном композитов, где новинка основана на локальной оптимизации как угла волокна, так и нарастания внутренней толщины одновременно. Эта структура называется Direct Fiber Path Optimization (DFPO). Помимо описания DFPO, его возможности демонстрируются на примере оптимизации образца на растяжение в открытом стволе из углепластика.Ключевые результаты показывают явное улучшение по сравнению с часто используемым в настоящее время подходом к применению траекторий главных напряжений для модели армирования с переменным осевым сопротивлением.
Эта структура называется Direct Fiber Path Optimization (DFPO). Помимо описания DFPO, его возможности демонстрируются на примере оптимизации образца на растяжение в открытом стволе из углепластика.Ключевые результаты показывают явное улучшение по сравнению с часто используемым в настоящее время подходом к применению траекторий главных напряжений для модели армирования с переменным осевым сопротивлением.
1. Введение
В последнее время спрос на энергоэффективные системы обусловлен использованием легких композитов из углепластика в конструктивных элементах. Эти материалы все чаще используются в авиационной, космической и автомобильной промышленности. Из-за высокой стоимости углеродных волокон становится важным их эффективное использование [1].За счет использования конструкции волокна с переменной осью (VA) жесткость и прочностные свойства могут быть улучшены по сравнению с классическими конструкциями из углепластика [2]. Таким образом, термин VA означает изменение ориентации волокон на уровне слоя. Желаемые характеристики композитов из углепластика достигаются за счет направления нагрузок почти исключительно вдоль ориентации волокон и, таким образом, минимизации сдвигающей нагрузки матрицы. Для технической реализации хорошо подходит технология TFP, разработанная в Leibniz-Institut für Polymerforschung Dresden (Германия).Основы и некоторые приложения технологии TFP описаны в [3, 4]. Укладка углеродных волокон обычно выполняется сшиванием сухих ровингов, как показано на Рисунке 1. Ровинг направляется через вращающуюся ровничную трубу на основной материал, где швейная нить, нанесенная зигзагообразным узором, удерживает его на месте. .
Желаемые характеристики композитов из углепластика достигаются за счет направления нагрузок почти исключительно вдоль ориентации волокон и, таким образом, минимизации сдвигающей нагрузки матрицы. Для технической реализации хорошо подходит технология TFP, разработанная в Leibniz-Institut für Polymerforschung Dresden (Германия).Основы и некоторые приложения технологии TFP описаны в [3, 4]. Укладка углеродных волокон обычно выполняется сшиванием сухих ровингов, как показано на Рисунке 1. Ровинг направляется через вращающуюся ровничную трубу на основной материал, где швейная нить, нанесенная зигзагообразным узором, удерживает его на месте. .
Для оптимизации композитов VA было разработано несколько подходов. Обширный обзор криволинейных армированных волокном композитов был недавно выполнен Ribeiro et al.[5]. Под названием рулевого управления с регулируемым углом наклона Weaver et al. [6] улучшили характеристики последующего сцепления композитных панелей с компоновкой VA, в то время как Panesar и Weaver [7] оптимизировали смешанные бистабильные ламинаты, подходящие для морфинга клапанов. Duvaut et al. [8] реализовали переменную плотность волокна для учета интенсивности локальных напряжений. Для аналогичной цели толщина локального слоя варьировалась Parnas et al. [9] как дополнительный параметр конструкции. Гро и Уивер [10] предложили конструкцию с минимальной массой типичной панели крыла самолета при торцевом сжатии.Khani et al. [11] разработали математический алгоритм оптимизации панелей переменной жесткости с использованием параметров ламинирования. Ван Кампен и др. [12] предложили методологию преобразования известного распределения параметров ламинирования для композитного ламината VA в реалистичные углы волокон с минимальными потерями структурных характеристик. Чо и Роулендс [13] снизили концентрацию напряжений в ламинате открытого ствола с помощью генетического алгоритма.
Duvaut et al. [8] реализовали переменную плотность волокна для учета интенсивности локальных напряжений. Для аналогичной цели толщина локального слоя варьировалась Parnas et al. [9] как дополнительный параметр конструкции. Гро и Уивер [10] предложили конструкцию с минимальной массой типичной панели крыла самолета при торцевом сжатии.Khani et al. [11] разработали математический алгоритм оптимизации панелей переменной жесткости с использованием параметров ламинирования. Ван Кампен и др. [12] предложили методологию преобразования известного распределения параметров ламинирования для композитного ламината VA в реалистичные углы волокон с минимальными потерями структурных характеристик. Чо и Роулендс [13] снизили концентрацию напряжений в ламинате открытого ствола с помощью генетического алгоритма.
В отличие от процедур оптимизации, критерий главного напряжения часто использовался для построения криволинейных трасс волокна, например.г., [14–17]. Келли и др. [18], Waldmann et al. [19], а также Малахов и Полилов [20] разработали криволинейный путь волокна на основе концепции выравнивания волокон по пути нагрузки путем размещения волокон вдоль главных напряжений. Предполагалось, что оба подхода являются критериями оптимизации, хотя процесс математической оптимизации явно не выполнялся и применялся только критерий проектирования a priori . Кроме того, были разработаны процессы численной оптимизации на основе градиента [9, 21–23] и подходы к оптимизации, основанные на эволюционных алгоритмах [24–28] для проектирования композитов VA.
Предполагалось, что оба подхода являются критериями оптимизации, хотя процесс математической оптимизации явно не выполнялся и применялся только критерий проектирования a priori . Кроме того, были разработаны процессы численной оптимизации на основе градиента [9, 21–23] и подходы к оптимизации, основанные на эволюционных алгоритмах [24–28] для проектирования композитов VA.
Однако, из-за часто выбираемого подхода к изменению углов отдельных квазиизотропных конечных элементов (КЭ), количество проектных переменных значительно велико, что также увеличивает вычислительные затраты. Таким образом, большинство примеров было рассчитано с использованием КЭ-моделей с ограниченным числом конечных элементов. Повышенная свобода проектирования приводит к увеличению сложности проблемы проектирования. Например, Conti et al. [17] обнаружили, что использование углов волокна в качестве проектных переменных неизбежно приводит к плохому поведению целевой функции с множеством локальных минимумов.
Обычно узор из VA волокон может подразумеваться в различной плотности волокон, что приводит к неоднородной толщине сухих преформ. Следовательно, это неоднородное наращивание толщины чрезвычайно сложно учесть при анализе. Учитывая эту сложность, в современных подходах не учитывается накопление толщины и учитывается только изменение угла волокна.
Таким образом, основная критика многих современных подходов к оптимизации заключается в том, что не существует процедуры математической оптимизации, которую можно было бы начать или работать без необходимой информации о производственном процессе из-за отсутствия соответствующей процедуры моделирования.Однако знание распределения толщины и локальной ориентации волокон, соответствующих произвольной компоновке волокон, которая может быть произведена с помощью TFP, имеет важное значение для процесса проектирования детали. Spickenheuer et al. [1, 29] и Albers et al. [30] предприняли первые попытки отделить процесс оптимизации криволинейного армированного волокном композита, изготовленного с помощью TFP, от реальных численных моделей, чтобы ограничить количество требуемых конструктивных переменных, сделав их независимыми от применяемого разрешения сетки FE. Таким образом, как только установлено достаточно точное моделирование компоновки волокон VA, методы оптимизации могут быть применены к структуре волокон. Это позволяет полностью использовать высокие степени свободы в процессе проектирования и максимизировать характеристики анизотропных материалов углепластика.
Таким образом, как только установлено достаточно точное моделирование компоновки волокон VA, методы оптимизации могут быть применены к структуре волокон. Это позволяет полностью использовать высокие степени свободы в процессе проектирования и максимизировать характеристики анизотропных материалов углепластика.
С учетом выявленных пробелов в текущем состоянии дел в правильном моделировании композитов VA, в этой работе представлена новая процедура проектирования для иллюстрации возможности создания VA-рисунка для образца на растяжение в открытом стволе, где оптимальное волокно образец не может быть легко выведен.Таким образом, новый подход к оптимизации под названием Direct Fiber Path Optimization (DFPO) для композитов VA будет представлен и численно оценен на примере образца для растяжения в открытом стволе.
2. Конечно-элементное моделирование
2.1. Настройка модели
Согласно современному уровню техники, моделирование композитных структур в основном ограничивается укладкой слоев с постоянной толщиной и постоянным углом волокон внутри каждого слоя. Модели для структурного анализа однородных спиралей и одиночных изогнутых лент из параллельных волокон и постоянной толщины были успешно применены дополнительно за счет увеличения усилий по моделированию [31].В этом случае известно аналитическое описание локальной толщины преформы и ориентации волокна, которое можно использовать для построения соответствующих моделей КЭ для структурного моделирования. Однако существующие ограничения модели слишком сильны, если кто-то планирует применить стратегии оптимизации, чтобы полностью использовать потенциал углепластика, производимого TFP, и адаптировать производственные требования. Хотя существует много подходов к использованию математического описания алгоритма оптимизации для вывода числовой модели, например.g., геометрия каждого шага итерации, эта работа будет описывать моделирование независимо от оптимизации и, таким образом, как общий модуль для любой структуры VA с аналогичной характеристикой размещения, строго следуя производственным характеристикам TFP.
Модели для структурного анализа однородных спиралей и одиночных изогнутых лент из параллельных волокон и постоянной толщины были успешно применены дополнительно за счет увеличения усилий по моделированию [31].В этом случае известно аналитическое описание локальной толщины преформы и ориентации волокна, которое можно использовать для построения соответствующих моделей КЭ для структурного моделирования. Однако существующие ограничения модели слишком сильны, если кто-то планирует применить стратегии оптимизации, чтобы полностью использовать потенциал углепластика, производимого TFP, и адаптировать производственные требования. Хотя существует много подходов к использованию математического описания алгоритма оптимизации для вывода числовой модели, например.g., геометрия каждого шага итерации, эта работа будет описывать моделирование независимо от оптимизации и, таким образом, как общий модуль для любой структуры VA с аналогичной характеристикой размещения, строго следуя производственным характеристикам TFP. Целью моделирования является эластичное описание податливости ламината и прогнозирование начальных отказов на основе физически обоснованного критерия отказа. Мезомасштабная модель используется для оценки конкретных свойств процесса TFP в соответствии с рекомендациями Uhlig et al.[32].
Целью моделирования является эластичное описание податливости ламината и прогнозирование начальных отказов на основе физически обоснованного критерия отказа. Мезомасштабная модель используется для оценки конкретных свойств процесса TFP в соответствии с рекомендациями Uhlig et al.[32].
Для создания сплошных слоев с TFP ровницы необходимо размещать с небольшим перекрытием, чтобы не было зазоров между ними. При размещении с постоянной толщиной и ориентацией волокон можно производить параллельные ламинаты для небольшого диапазона расстояний между соседними ровингами. Толщина рассчитывается согласно следующему (см. Рисунок 2):
где — площадь поперечного сечения ровницы, расстояние между соседними ровингами, тонкость ровницы, объемная доля волокна и плотность волокна.
При произвольном непараллельном размещении ровницы оценка толщины усложняется. В качестве отправной точки для аналитического описания такой преформы используется путь укладки, который является основой для укладки волокна с помощью машины TFP. Этот путь или, в более общем смысле, последовательность путей будет называться шаблоном проектирования. Самое простое математическое описание — это последовательность прямых линий в двух измерениях. Изогнутые траектории размещения, например, содержащие примитивы, такие как дуги или шлицы, будут аппроксимированы последовательностью коротких прямых линий с точностью производства.Прямая линия определяется начальной и конечной точками внутри плоскости размещения. Все точки между ними описываются где — переменная параметризации в диапазоне от нуля до единицы. Обратите внимание, что либо полная последовательность прямых линий может быть соединена, в случае если имеется только один оптоволоконный тракт, либо, по крайней мере, некоторые последующие линии не соединены, что представляет собой полностью отдельные оптоволоконные тракты, как показано на Рисунке 3.
Этот тип шаблона проектирования содержит только информацию о путях размещения волокон, включая длину ровингов, но не информацию о ширине или площади поперечного сечения.Формальным расширением информации о прямом пути в сочетании с площадью поперечного сечения является линия распределения толщины линии для отрезков прямой с длиной:
Здесь концепция дельта-распределения Дирака использовалась для определения функции плотности. Эта функция распределения толщины линий является лишь промежуточным этапом, так как полный объем волокна сосредоточен вдоль бесконечно тонких линий, и бесконечно большая толщина получается на линиях и нулевая в других местах. Однако функция уже выполняет условие нормализации.Путем интегрирования по всему проектному пространству или любой области, содержащей все линейные сегменты, получается общий объем волокна:
Для практических целей такое распределение толщины не очень полезно, поскольку в нем отсутствует информация о ширине типичного ровинга, который размещается с помощью вышивальная машина. Эта ширина обычно зависит от типа используемой ровницы, например, количества нитей, плотности материала и, что наиболее важно, от параметра машины, ширины зигзагообразного стежка, используемого для закрепления ровницы на основном материале.
С помощью свертки с различными функциями сглаживания можно добавить информацию о ширине ровницы. Очень удобный подход — это крупнозернистая свертка с гауссовым центром в точке () ширины, определяемой шириной размещения, чтобы получить гауссово распределение толщины:
Крупнозернистое зерно выполняется путем интегрирования функции во всей плоскости. Используя определение распределения толщины линии, решение для этой свертки может быть выражено в терминах функций ошибок.Это делает численную реализацию очень быстрой. Это гауссовское распределение толщины представляет собой гауссовское средневзвешенное значение объемной плотности ровницы в области вокруг точки, в которой необходимо вычислить толщину. Для одиночных прямолинейных ровингов такое распределение толщины приводит к гауссовой площади поперечного сечения, которая примерно соответствует реальным площадям поперечного сечения для процесса TFP, как показано на микрошлифах Uhlig et al. [32]. Другие функции сглаживания, такие как среднее цилиндрическое, приближают поперечное сечение одиночной ровницы в большей степени.Однако полученные ламинаты демонстрируют множество неоднородностей, которые отрицательно влияют на сходимость моделирования. При гауссовом распределении толщины граница ламината должна определяться толщиной отсечки, так как гауссово нигде не является точно нулевым.
Основная задача численного моделирования — получить геометрию и ориентацию волокна на основе схемы размещения одного слоя. Последовательные слои накладываются друг на друга без учета эффекта драпирования, что нормально, если градиенты толщины нижних слоев достаточно малы.Описание ограничено слоями непересекающихся ровингов или, по крайней мере, размещениями ровинга, где перекрывающиеся ровницы пересекаются под небольшими углами, так что имеет смысл усреднение по элементам ориентации волокон. Обратите внимание, что для многих примеров, которые содержат самопересекающийся ровинг, слой можно разделить на более мелкие слои с непересекающимися ровингами. На рисунке 4 показано схематическое описание процедуры моделирования. На основе двумерной (2D) сетки плоского проектного пространства создается трехмерная модель конечных элементов с использованием локализованной информации о гауссовом распределении толщины и усредненной ориентации волокна.Толщина оценивается в каждом угловом узле и ориентация волокна в центре каждого элемента. Ориентация волокна хорошо определена для линейных сегментов. Ориентация элементарного волокна усредняется по средневзвешенной толщине всех линейных сегментов, которые вносят вклад в общую толщину в центральной точке каждого элемента.
Последовательные слои можно накладывать друг на друга. Результирующая трехмерная (3D) модель КЭ представляет собой кусочную линеаризацию по каждому элементу локально усредненных характеристик, а именно толщины и угла волокна.В качестве альтернативы, толщина и угол волокна могут быть объединены в центре КЭ в двухмерное описание многослойного элемента оболочки, чтобы получить модель для той же самой компоновки волокна с меньшими вычислительными затратами. Основное различие возникает из-за пренебрежения компонентом, не лежащим в плоскости ориентации волокна, и градиентами толщины внутри элемента.
Далее рассматриваются два числовых примера с использованием DFPO. Для обоих случаев используются следующие параметры: объемная доля волокна () 58%; тонкость ровницы () 400 текс; плотность () 1.76 г. см −3 ; и параметр сглаживания ширины () 1 мм.
2.2. Случай 1: Образец для растяжения в открытом отверстии
Образец в открытом отверстии под растягивающей нагрузкой выбран для демонстрации возможностей моделирования и оптимизации ламинатов VA с использованием подхода DFPO. Геометрия и размеры их образцов представлены на рисунке 5 (а). Чтобы напрямую оценить возможности предлагаемой структуры оптимизации, образец состоит из двух слоев, полученных путем наложения слоя TFP из углеродного волокна (слой, который необходимо оптимизировать) поверх основного материала (тканое полотно ± 45 ° с удельной массой 256 ).На рис. 6 подробно показан исследуемый двухслойный образец открытого ствола.
На основе двухмерной сетки опорной плоскости локальная толщина оценивается в каждом узле для каждого слоя ламината вдоль сетки FE, как показано на синей цветовой шкале (рис. 7 (b)). Кроме того, ориентация элементарного волокна (рис. 7 (а)) задается как усредненная ориентация волокна в центре каждого элемента. В областях, где текущая структура волокон не имеет ровницы, расчет толщины фактически дает ноль.Однако для обеспечения непрерывной сетки в этом случае в соответствующих узлах устанавливается очень маленькая толщина 0,001 мм, а соответствующие свойства материала элемента устанавливаются на свойства смолы (синие элементы на рисунке 6). Соответствующая модель FE дополнительно включает в нижнюю часть ламината слой основного материала постоянной толщины (0,24 мм), как показано на Рисунке 6.
Симметричные граничные условия применяются по всем осям образца. Нагрузка прилагается к верхнему краю образца.Эти детали можно увидеть на рисунке 6. Моделирование методом конечных элементов выполняется в ANSYS APDL с использованием квадратичных элементов SOLID186 и линейных элементов SOLID185 (справочник по библиотеке ANSYS).
2.3. Случай 2: Узко-средний растяжимый образец
Чтобы предоставить другой пример применимости предлагаемой структуры DFPO, был рассмотрен образец при тех же условиях нагружения. Для этого анализируется и оптимизируется образец с узкой серединой при растягивающей нагрузке. Подробная информация о геометрии и размерах узкого среднего образца на растяжение показаны на рисунке 5 (б).Чтобы оценить возможности DFPO, как и образец в открытом стволе, образец состоит из двух слоев, полученных путем наложения слоя TFP из углеродного волокна (слой, который необходимо оптимизировать) поверх основного материала (углеродное волокно ± 45 ° тканое полотно плотностью 256). Свойства материала как слоя углеродного волокна UD / эпоксидной смолы TFP, так и слоистых композитов из углеродного волокна / эпоксидной ткани, используемых в моделях FE и оптимизации, представлены в таблице 1.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||
 И. Поисковые методы оптимального проектирования. М.: Сов.
Радио, 1975.
И. Поисковые методы оптимального проектирования. М.: Сов.
Радио, 1975. Фактически критерий и цель относятся друг к другу как модель и оригинал, со всеми вытекающими отсюда особенностями. Многие цели трудно или даже невозможно количественно описать.
Фактически критерий и цель относятся друг к другу как модель и оригинал, со всеми вытекающими отсюда особенностями. Многие цели трудно или даже невозможно количественно описать.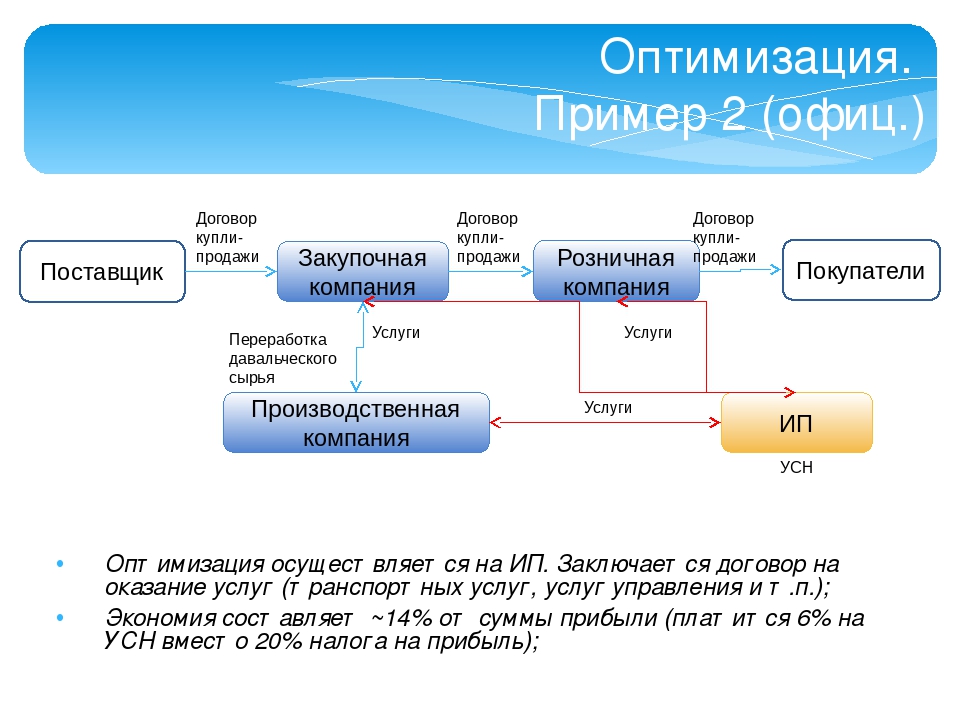
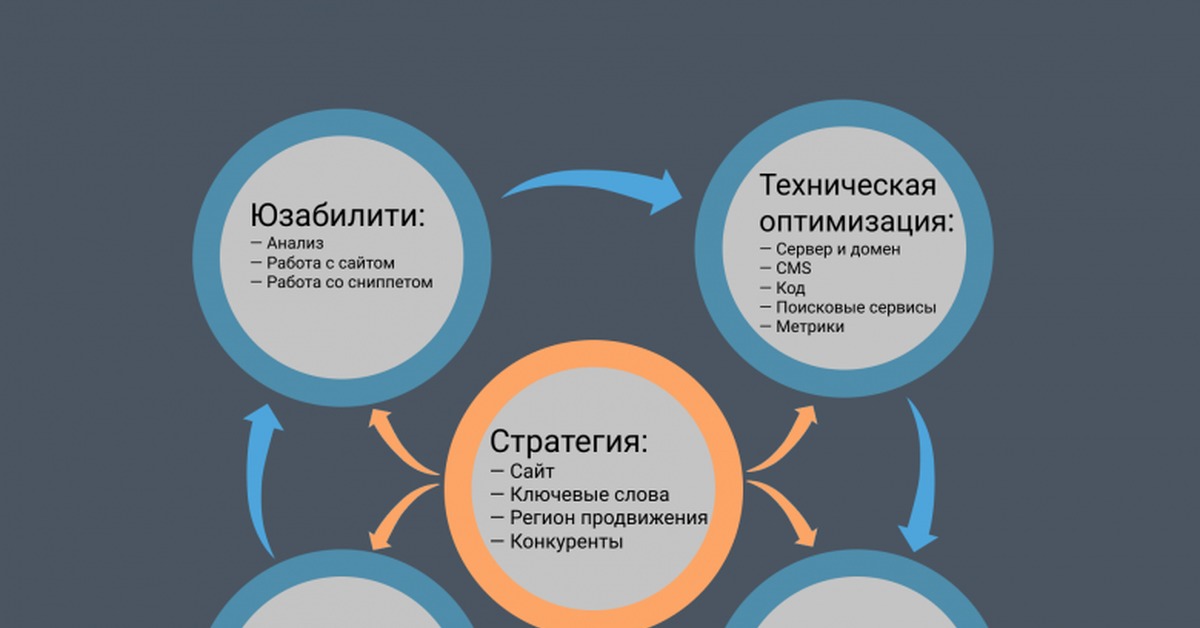 Демонстрация сходимости множества приближенных эффективных точек к множеству эффективных стратегий при различном задании аппроксимирующего множества. Решение контрольных примеров.
Демонстрация сходимости множества приближенных эффективных точек к множеству эффективных стратегий при различном задании аппроксимирующего множества. Решение контрольных примеров. Н. Основы теории игр. Бескоалиционные игры. М.: Наука, 1984
Н. Основы теории игр. Бескоалиционные игры. М.: Наука, 1984 (Практик)
(Практик) Система оптимизирована с точки зрения затрат, снижения заражения [системный уровень] , но не с точки зрения качества жизни отдельного человека. Необходимо учитывать качество жизни. В настоящее время рамки не охватывают это »(специалист по общественному здравоохранению / поведенческим наукам)
Система оптимизирована с точки зрения затрат, снижения заражения [системный уровень] , но не с точки зрения качества жизни отдельного человека. Необходимо учитывать качество жизни. В настоящее время рамки не охватывают это »(специалист по общественному здравоохранению / поведенческим наукам)
 2016 г.
PMID: 27667015
2016 г.
PMID: 27667015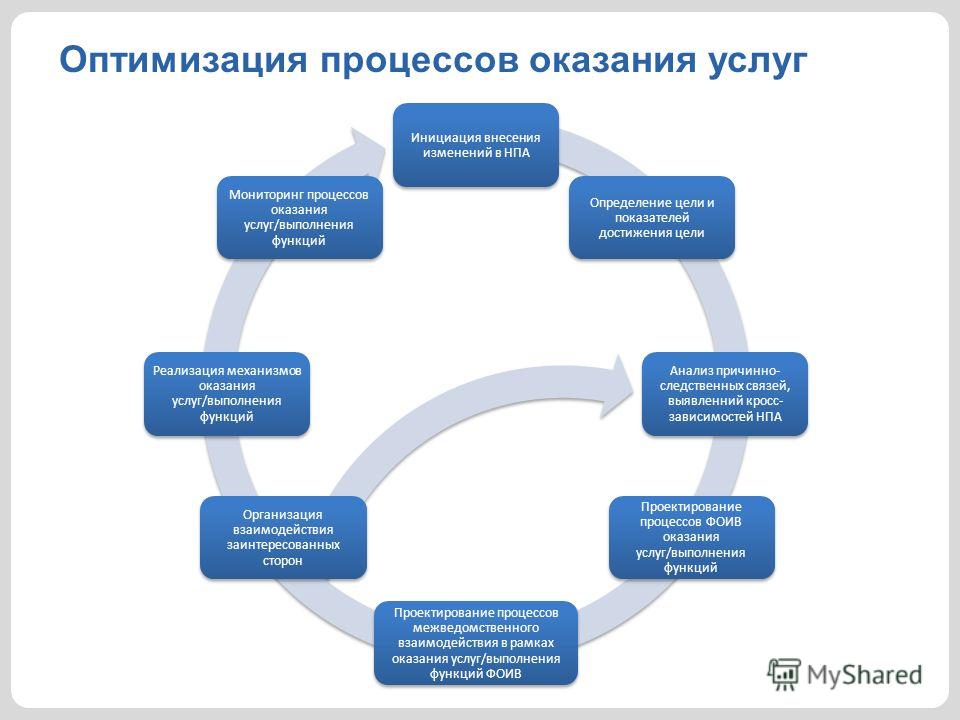 С.Борис Б.С. и др.
Стволовые клетки Transl Med. 2020 Сен; 9 (9): 1036-1052. DOI: 10.1002 / sctm.19-0406. Epub 2020 22 мая.
Стволовые клетки Transl Med. 2020.
PMID: 32445290
Бесплатная статья PMC.
С.Борис Б.С. и др.
Стволовые клетки Transl Med. 2020 Сен; 9 (9): 1036-1052. DOI: 10.1002 / sctm.19-0406. Epub 2020 22 мая.
Стволовые клетки Transl Med. 2020.
PMID: 32445290
Бесплатная статья PMC.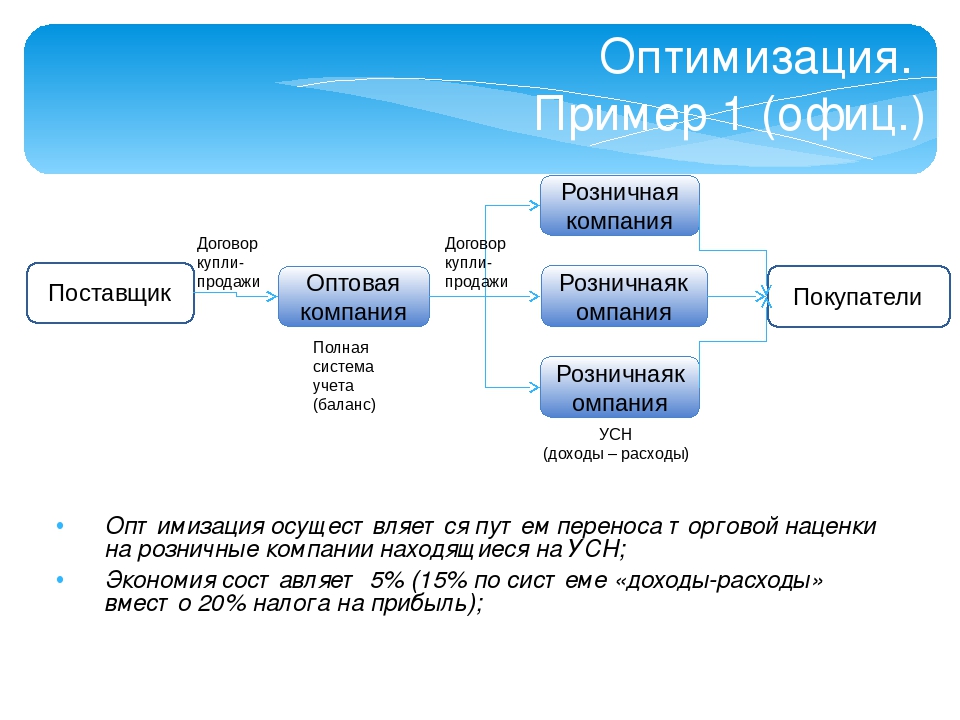 2020; 15 (4): 301-307. DOI: 10.2174 / 1574888X15666200116100121.Curr Stem Cell Res Ther. 2020.
PMID: 31951188
Рассмотрение.
2020; 15 (4): 301-307. DOI: 10.2174 / 1574888X15666200116100121.Curr Stem Cell Res Ther. 2020.
PMID: 31951188
Рассмотрение. , Яманака С. Индукция плюрипотентных стволовых клеток из культур эмбриональных и взрослых фибробластов мыши с помощью определенных факторов.Клетка. 2006; 126: 663-676. https://doi.org/10.1016/j.cell.2006.07.024.
, Яманака С. Индукция плюрипотентных стволовых клеток из культур эмбриональных и взрослых фибробластов мыши с помощью определенных факторов.Клетка. 2006; 126: 663-676. https://doi.org/10.1016/j.cell.2006.07.024. Правительство
Правительство