Причинно-следственная связь — вопрос права или вопрос факта?
Как известно, основаниями для удовлетворения требования о взыскании убытков является совокупность условий: факт их причинения, документально подтвержденный размер убытков и наличие причинно-следственной связи между понесенными убытками и нарушением.
Для деликтной ответственности чуть иначе, но причинно-следственная связь также необходима.
Чем же является причинно-следственная связь — вопросом права или вопросом факта? Вопрос о наличии либо отсутствии причинно-следственной связи часто ставят на разрешение эксперта. Но вопрос права на разрешение эксперта ставить нельзя.
Значит, вопрос факта. Но так ли это?
Как соотнести «причинно-следственная связь = вопрос факта» с презумпциями в п.5 постановления Пленума Верховного Суда от 24.03.16 № 7? С разрешением вопросов о причинно-следственной связи в инстанциях, следующих за апелляцией? С тем, что Верховный Суд недавно указал «причиненные истцу убытки были связаны с определением сторонами договора купли-продажи по своему усмотрению порядка оплаты квартиры, сама по себе не может служить основанием для отказа в иске, поскольку не свидетельствует об отсутствии вреда, причинной связи между противоправным поведением и наступившим вредом, вины причинителя вреда»?
Или все-таки именно причинно-следственная связь — это вопрос права, а уже «повлияло ли на возникшие убытки событие такое-то по мнению эксперта» — это вопрос факта, который и можно ставить перед экспертом. Аналогично и стороны вправе представлять доказательства причинной связи, но на их основании суд должен лишь промежуточно установить наличие либо отсутствие обстоятельств, которые будут далее использованы судом для разрешения вопроса о наличии причинно-следственной связи.
Обычные примеры — договорные убытки, ДТП. Можно ограничиться заключением эксперта, который прямо укажет «действия лица Х находились в прямой причинной связи с наступившими последствиями» или все-таки вопрос посложнее?!
Определение причинно-следственных связей и их представление в виде стратегической карты
Определение причинно-следственных связей и их представление в виде стратегической карты
Одним из основных элементов ССП является определение и документирование причинно-следственных взаимосвязей между отдельными стратегическими целями. Устанавливаемые причинно-следственные связи отражают наличие зависимостей между отдельными целями. При формировании данных зависимостей неявные связи между целями проявляются и становятся понятными менеджерам. А само вырисовывание причинно следственных зависимостей позволяет найти оптимальные пути реализации стратегии. Стратегические цели не являются независимыми и оторванными друг от друга, а наоборот, они тесно друг с другом связаны и влияют друг на друга. Для отражения причинно-следственных цепочек между стратегическими целями Каплан и Нортон используют термин «стратегические карты», а саму разработку причинно-следственной цепочки целей называют одним из самых сложных этапов процесса построения ССП.
Устанавливаемые причинно-следственные связи отражают наличие зависимостей между отдельными целями. При формировании данных зависимостей неявные связи между целями проявляются и становятся понятными менеджерам. А само вырисовывание причинно следственных зависимостей позволяет найти оптимальные пути реализации стратегии. Стратегические цели не являются независимыми и оторванными друг от друга, а наоборот, они тесно друг с другом связаны и влияют друг на друга. Для отражения причинно-следственных цепочек между стратегическими целями Каплан и Нортон используют термин «стратегические карты», а саму разработку причинно-следственной цепочки целей называют одним из самых сложных этапов процесса построения ССП.
При построении причинно-следственной цепочки необходимо учитывать основное правило ее построения, которое состоит в отсутствии необходимости изображения всех возможных связей между целями. Нечитабельное и слишком сложное изображение многочисленных связей теряет свой смысл с точки зрения управляемости. Попытка изобразить все мыслимые причинно-следственные связи означает необходимость построения слишком сложных и неуправляемых матриц. Но данные матрицы не смогут помочь в донесении стратегии сотрудникам, ни при осуществлении процесса управления. Лучшие же результаты будут получены тогда, когда на карте целей будут изображены только стратегически значимые причинно-следственные связи. Тем самым предпринимается попытка повысить информативность, сконцентрировать внимание на ключевых аспектах деятельности и обеспечение прозрачности стратегии.
Например, подразделение повышает уровень своего сервиса, чтобы тем самым достичь цели «повышение привязанности клиентов к компании». Однако от цели «повысить уровень сервиса» исходит только одна стрелочка, так как повышение качества обслуживания сначала способствует повышению удовлетворенности клиентов, а лишь затем – повышению привязанности клиентов к компании.
В процессе формирования причинно следственных цепочек взаимосвязей необходимо понимать, что не существует «правильных» причинно-следственных связей. Как только мы покидаем финансовые цели, то многие причинно-следственные зависимости уже невозможно установить математическим способом. Например, насколько лучший имидж компании приведет к росту доходов. Если мы улучшим имидж в 2 раза — во сколько возрастут доходы? Насколько повышение уровня удовлетворенности сотрудников может повысить готовность клиентов приобретать товары компании?
Как только мы покидаем финансовые цели, то многие причинно-следственные зависимости уже невозможно установить математическим способом. Например, насколько лучший имидж компании приведет к росту доходов. Если мы улучшим имидж в 2 раза — во сколько возрастут доходы? Насколько повышение уровня удовлетворенности сотрудников может повысить готовность клиентов приобретать товары компании?
Все из перечисленных причинно-следственных связей могут быть изучены с помощью корреляции, но лишь некоторые из них научно могут быть обоснованы и измерены количественно. Сами причинно-следственные связи являются индивидуальными для каждой компании и являются инструментом управления, при помощи которого менеджеры могут проверить свои предположения и сделать соответствующие выводы. Предположения же строятся на базе накопленного в компании опыта. Причинно следственные связи в ССП только тогда будут «правильными», когда они стали результатом консенсуса между менеджерами и позволяют построить целостную систему целей компании. Построение причинно-следственных связей между целями помогает менеджерам представить свои сделанные допущения наглядными и проверить наличие корреляции между отдельными целями. Поэтому рассмотренные методы не ставят во главу угла точность, которую, в силу названных причин, достичь просто невозможно.
Важно, чтобы все сотрудники компании обсуждали связи стратегической карты. Чем прочнее конкретная связь, тем в большей мере руководство должно уделять внимание опережающему индикатору. Когда руководители стараются управлять опережающими индикаторами, оно имеет больше шансов повлиять на последующий результат. Управление опережающими индикаторами означает, что они рассматриваются на равне с последующими результатами, если даже важнее.

Особенно важно проводить «разбор полетов» по индикаторам, которые не достигли своих целей. То есть, необходимо выделять зоны, требующие особого внимания – «центры внимания», на обсуждение которых руководство должно затратить определенное время, чтобы выработать идеи о том, как улучшить ситуацию.
Безусловно, чтобы стать настоящей системой управления Карты показателей должны использоваться в качестве повестки дня ежемесячных собраний для руководства компании. Также к ежемесячному собранию готовятся наиболее важные ключевые индикаторы, которые измеряются на постоянной основе и немедленно сообщаются по всей компании. Например, «своевременная доставка» является важным показателем, результат по которому может постоянно изображаться на внутренних мониторах компании. Желательно также отслеживать графическое представление динамики показателей по подразделению за прошлые года, а также в сравнении с целью, и в сравнении с лучшими подразделениями компании.
Помимо отчетов по достижению показателей в ежемесячном докладе должны содержаться пункты о том, что необходимо предпринять для исправления ситуации. На очередном собрании необходимо оценить, что произошло с момента последнего собрания. Когда установленные задачи выполнены — они вычеркиваются из списка. Список задач должен содержать лишь те пункты, по которым ведется работа. Предложения по улучшению, генерируемые на основе карты показателей, фокусируются на определенной перспективе или на определенном показателе. По каждому предпринятому мероприятию необходимо производить оценку. Это важная характеристика обучающейся компании – учиться на собственном опыте и отражать это в последующей деятельности. Если действие предпринимаются с определенной целью — важно проверить, привели ли они к достижению намеченных результатов.
Взаимосвязи между действиями и результатами, определенные на основе опыта компании очень важны при прогнозировании, но при условии четкого определения целей компании в стратегических картах.
Документирование причинно-следственных связей между отдельными целями осуществляется, как правило, вместе с их разработкой во время «стратегической сессии». Если их не документировать сразу, то потом бывает очень трудно вспомнить все мысли, которые возникали у участников команды по этому поводу. Также вырисовывание причинно-следственной цепочки предполагает нумерацию целей в зависимости, от какой проекции выписывается причинно-следственная цепочка. В том случае, если цепочка причинно-следственных связей вырисовывается громоздкой и малочитабельной, ее необходимо упростить для легкого понимания каждым сотрудником компании. Для того, чтобы эффективно использовать механизм причинно-следственных связей по донесению информации, нам нужно как графическое изображение данных связей, так и краткое сопроводительное описание данной стратегической карты.
Как уже отмечалось, сначала мы должны разработать показатели деятельности, а потом составлять карту причинно-следственных связей.
Предположим, что мы располагаем показателями для каждой из четырех составляющих. Но при разработке карты стратегии может выясниться, что некоторые из выбранных нами показателей не вписываются в описание стратегии. Данные показатели, возможно, понадобятся для Систем показателей нижних уровней, которые будут создаваться при каскадировании. Либо такие показатели могут служить операционными или диагностическими показателями и отслеживаться вне ССП. При составлении карты стратегии, для обеспечения логической последовательности могут потребоваться совершенно новые показатели. В этом заключается истинная ценность процесса составления причинно-следственных связей, так как он заставляет тщательно изучить и подобрать показатели, отражающие точное описание стратегии компании. Правильно составленная ССП должна содержать комплекс основных итоговых показателей (запаздывающих) и факторов деятельности (опережающих индикаторов), приводящих к улучшению результатов по этим параметрам.
Правильно составленная ССП должна содержать комплекс основных итоговых показателей (запаздывающих) и факторов деятельности (опережающих индикаторов), приводящих к улучшению результатов по этим параметрам.
Формирование причинно-следственных связей необходимо начинать в каждой из четырех составляющих с запаздывающих индикаторов деятельности. Ориентация этих показателей на результат легко позволяет их объединить в логическую последовательность, начиная с финансовых показателей, переходя к клиентским показателям, после к показателям процессов и в конечном итоге к показателям обучения и развития. После создания логической цепочки запаздывающих показателей во всех четырех составляющих, для каждого из показателей мы будем продумывать опережающие показатели деятельности. Опережающие показатели могут не быть логически связаны со всеми четырьмя составляющими ССП. Это связано с тем, что они являются узкоспециализированными для итоговых показателей. Хотя опережающие показатели (факторы деятельности) могут казаться несвязанными или необъединенными одной темой, при изучении их в контексте всей ССП мы видим, что они являются мощным фактором, приводящим в действие весь механизм ССП.
Например, мы выбрали стратегию предоставления комплексного решения клиентам. Исходя из такой стратегической направленности — компания предлагает клиентам не передовые продукты и не лучшую операционную деятельность, потому, что конкурентным преимуществом является комплексное решение для клиентов. А это, соответственно, потребует глубокого знания потребностей клиентов.
В финансовой составляющей компании, например, необходим рост доходов. Рост доходов не возможен без увеличения количества лояльных к компании клиентов и перекрестных продаж. Соответственно, лояльность клиентов может быть определена в качестве запаздывающего индикатора деятельности. Что будет являться фактором повышения лояльности клиентов? Так как мы избрали в качестве стратегического направления тесную связь с клиентом, а соответственно, для достижения успеха компании необходимо предоставить комплексное решение для клиентов. Для разработки комплексных решений вам необходимо как можно больше знать о трудностях и потребностях клиентов, конкурентную среду. Выполнение этой задачи потребует от компании большего присутствия у клиентов, общения с ними для выявления их потребностей. Поэтому компании необходимо данную цель измерять показателем «количество часов, проведенных с клиентами с целью выявления потребностей и запросов».
Для разработки комплексных решений вам необходимо как можно больше знать о трудностях и потребностях клиентов, конкурентную среду. Выполнение этой задачи потребует от компании большего присутствия у клиентов, общения с ними для выявления их потребностей. Поэтому компании необходимо данную цель измерять показателем «количество часов, проведенных с клиентами с целью выявления потребностей и запросов».
Следующим этапом после выбора финансовых и клиентских показателей является выбор показателей для внутренних бизнес-процессов, которые необходимо довести до совершенства, чтобы оправдать ожидания клиентов. В соответствии с предложением покупательной ценностью для клиентов мы можем определить знания потребностей клиентов в качестве основополагающего фактора их лояльности. Соответственно, количество разработанных клиентских решений является запаздывающим индикатором внутренних процессов. Мы понимаем, что сама по себе база клиентских решений не появиться. Если такая база решений должна стать основой лояльности клиентов, то у сотрудников необходимо создать мотивацию ее использовать. Основным фактором, способствующим генерированию клиентских решений, является обучение персонала в тех сферах компетенции, которые позволяют разрабатывать комплексные решения клиентов. Соответственно, запаздывающим индикатором обучения и развития будет «достижение компетентности». Результаты обучения это опережающий показатель обучения и развития.
Таким образом, создается карта стратегии, показывающая комплекс взаимосвязанных показателей по четырем составляющим ССП. Данная карта отражает самое обоснованное предположение о том, что необходимо для реализации своей стратегии. Она также послужит инструментом обеспечения единой направленности действий сотрудников для достижения общих целей компании.
Для того, чтобы максимально использовать информационный потенциал карты стратегии, необходимо описать сопроводительный рассказ, оживляющий карту стратегии в представлении сотрудников.
Источник:
Книга «Внедрение системы сбалансированных показателей: оценка деятельности компании»
Авторы: Немировский И., Старожукова И.
При использовании материалов статьи обязательна ссылка на сайт «Академия развития Лидеров» http://beleader.com.ua
Методологическое значение знания о причинно-следственной связи в криминалистической методике расследования преступлений Текст научной статьи по специальности «Право»
Д.П. Песенкова
МЕТОДОЛОГИЧЕСКОЕ ЗНАЧЕНИЕ ЗНАНИЯ О ПРИЧИННО-СЛЕДСТВЕННОЙ СВЯЗИ В КРИМИНАЛИСТИЧЕСКОЙ МЕТОДИКЕ РАССЛЕДОВАНИЯ ПРЕСТУПЛЕНИЙ
Исследуются вопрос специфики разработки знания о причинно-следственной связи как самостоятельной криминалистической теории, ее методологическое значение для теории криминалистической методики. Проблемы задействования знаний о причинно-следственной связи рассматриваются через призму современных приоритетов познания в криминалистической методике расследования преступлений, определяющих такие знания, как системообразующие, что дает возможность дальнейшего развития и укрепления основ в разработке криминалистических методик расследования преступлений.
Ключевые слова: причинность; причинно-следственная связь; криминалистическая методика расследования преступлений.
В современный период формирования и развития научных знаний криминалистики все более широко задействуется учение о причинно-следственной связи. Знания о причинно-следственной связи активно используется в криминалистической методологии. Такое пристальное внимание объяснимо тем, что современное представление и укоренение идеи причинности в научном и обыденном сознании вынуждает к углубленному рассмотрению относительно этой идеи. Данное рассмотрение с позиции современных разработок науки особенно необходимо на сегодняшний день, поскольку возникла ситуация, что само понятие «причинность» оказалось предметом научного рассмотрения.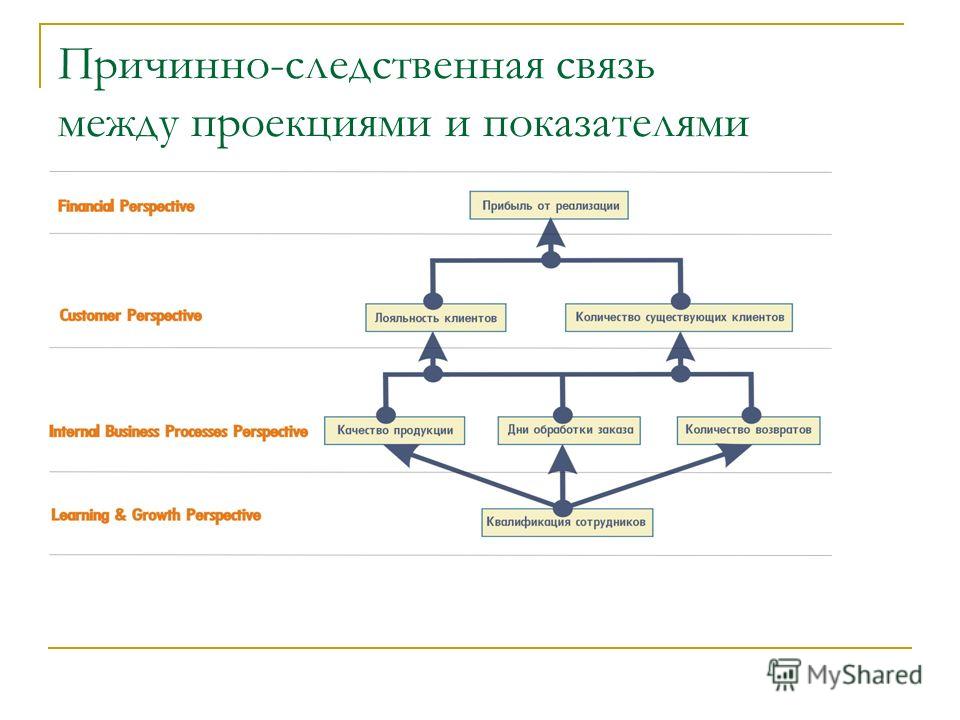 В рамках конкретной науки ее исследование приводит к особому представлению об общности идеи причинности, понятой не просто как принцип объяснения мира, а обладающей методологическим значением, позволяющим реализовать познавательный интерес.
В рамках конкретной науки ее исследование приводит к особому представлению об общности идеи причинности, понятой не просто как принцип объяснения мира, а обладающей методологическим значением, позволяющим реализовать познавательный интерес.
В современной криминалистике само представление о процессе раскрытия и расследования преступлений предполагает установление причинно-следственных связей. Данный подход диктует необходимость разработки средств и методов их познания, обусловливает внимательное отношение к проблеме причинной связи в научном и практическом аспектах, а также требует дальнейшего совершенствования уже существующих ее методов задействования.
Анализ литературы показал, что разработанные ранее теоретические знания о причинности, в современных условиях развития общественных и специальных наук, законодательной базы и жизни государства, выражают собой причинно-следственную связь как отношение причины и следствия, позволяют понять лишь внешний источник правового явления и процесса. Именно в этом состоит их основная роль в системе генетических методов познания [1. С. 33]. Однако это является не достаточным для криминалистического исследования в рамках методики расследования конкретного вида преступления, поскольку с данной позиции в процессе расследования и раскрытия преступлений раскрываются лишь отдельные причинноследственные связи и не дают оснований говорить о полноте познания событий прошлого, его механизма. Этого не достаточно для установления истины в раскрытии и расследовании преступного события.
Как известно, поиск источников любого конкретного научного знания, прежде всего, начинается с правильного понимания их соотношения с всеобщими научными знаниями, что связано с существованием всеобщих законов, не отрицающих существования зако-
номерностей объективной действительности на другом уровне. Высшим уровнем является исследование и познание общих основ — проблемы в сфере философии, где вопрос о причинной связи занимает значительное место и отражает одну из форм всеобщей связи и взаимодействия явлений — причины и следствия. Другим значимым источником формирования знаний о причинно-следственной связи методики расследования преступлений принято считать саму отраслевую науку.
Высшим уровнем является исследование и познание общих основ — проблемы в сфере философии, где вопрос о причинной связи занимает значительное место и отражает одну из форм всеобщей связи и взаимодействия явлений — причины и следствия. Другим значимым источником формирования знаний о причинно-следственной связи методики расследования преступлений принято считать саму отраслевую науку.
Анализ литературы показывает, что криминалистика, заимствуя понятия, до настоящего времени не имеет собственного определения причины и следствия, причинно-следственной связи, причинности применительно к специфике науки, а применение знаний теории о причинно-следственной связи основано на способности знаний адаптироваться к среде отдельной методики расследования преступлений [2. С. 392-404; 3. С. 207-210].
Первоначальное представление об идее причинности в методике расследования преступлений нашло применение в рамках «общих положений методики расследования преступлений» при разработке основных категорий криминалистики — криминалистической характеристики преступлений, с установлением обязательных структурных ее элементов — «преступная деятельность», «способ совершения преступления», «личность преступника», а также оснований криминалистических классификаций и методов структуризации изучаемых явлений.
Разрабатывая данное положение, была предпринята попытка свести всю некую систему, установить между ними корреляционные связи и зависимости, носящие закономерный характер и выраженные в количественных показателях [4. С. 179; 5. С. 130-132]. Безусловно, как нам представляется, перспективность данной позиции заключается в том, что в основу формирования систематизации сведений о криминалистической характеристике преступлений закладывается принцип причинности. Однако необходимо сделать некоторые пояснения.
Рассматривая в качестве источника нормы уголовного права и процесса, криминалисты в изучении проблем причинности сохраняют данный аспект проблем такого исследования. Последний заключается в изучении связей между доказательствами и предметом доказывания, т. е. в конечном счете, в исследовании связей между фактами вообще и доказательственных рядах в частности. Заметим, что ранее большинство ученых рассматривали связь между доказательствами только как связь причинную, нередко ставя между ними знак равенства. Именно на причинный характер связи дока-
Последний заключается в изучении связей между доказательствами и предметом доказывания, т. е. в конечном счете, в исследовании связей между фактами вообще и доказательственных рядах в частности. Заметим, что ранее большинство ученых рассматривали связь между доказательствами только как связь причинную, нередко ставя между ними знак равенства. Именно на причинный характер связи дока-
зательств с обстоятельствами, входящими в предмет доказывания, указывали в своих работах М.М. Грод-зинский [6. С. 79], М.С. Строгович [7. С. 351] и другие авторы. В этой связи А.А. Эйсман констатирует, что «что в процессуальной и криминалистической литературе связи между фактами обычно рассматриваются суммарно, не различаются на отдельные типы либо сводятся к одному типу — причинной связи» [8. С. 15].
Таким образом, в соответствии с принципом причинности устанавливается системно-функциональная зависимость структуры и содержания криминалистической характеристики от соответствующих норм уголовного процесса и уголовного права. Выделение такой конкретной и необходимой связи может свидетельствовать об оценочном суждении, о результате реализации идеи причинности в криминалистической методике расследования преступлений и в криминалистике в целом.
С начала 1960-х гг. это положение подверглось пересмотру. Однако, как показал анализ криминалистической литературы, все связующие нити между криминалистикой и уголовно-правовой теорией, между криминалистикой и уголовно-процессуальной теорией, криминалистикой и криминологией, существующие в прошлом, в целом сохранились и по сей день [9. С. 58].
Однако, как нам представляется, криминалистическая наука разрабатывает научные методы раскрытия преступлений на основе более глубокого познания сущности причинно-следственных связей, объективно существующих в области совершения и раскрытия преступлений. Изначальное представление о причинной связи создало предпосылки для криминалистического изучения проявлений категорий причины и следствия, причинно-следственной связи, причинности и послужило предпосылкой для разговора о формирующейся криминалистической теории причинности.
Изначальное представление о причинной связи создало предпосылки для криминалистического изучения проявлений категорий причины и следствия, причинно-следственной связи, причинности и послужило предпосылкой для разговора о формирующейся криминалистической теории причинности.
Начиная с середины 1960-х гг., в русле системных представлений стала активно разрабатываться и отечественная теория причинности. Закономерное отражение этой теории послужило закономерному заимствованию в криминалистической литературе самого понятия «причинно-следственная связь». В этой связи в рамках криминалистики предпринята попытка для формирования базовой теории применяемой в рамках науки криминалистики, в целом исходя из специфики предмета.
Объектом криминалистической теории причинности принято считать механизм преступления и содержательная сторона его установления. В окончательном виде в концепции общей криминалистической теории фигурируют закономерности механизма преступления, возникновения информации о преступлении и преступнике. В структуре информационно-познавательной деятельности следователя по раскрытию, расследованию и предупреждению преступлений выделяются такие элементы, как «уголовно-релевантные (т.е. содержащие информацию о предмете уголовного расследования) события, процессы, факты» и «механизм их отражения в окружающей среде» [10. С. 8].
Данная структура понятия предмета криминалистики предполагала разработки криминалистических характеристик преступлений, выражающих закономерности механизма преступления и содержательную сторо-
ну его отражения в окружающей среде. Однако сложность исследования этого вопроса была связана с тем, как нам представляется, что в виду специфики предмета криминалистическую науку интересуют в общем виде лишь те объекты, которые участвуют в акте отражения преступления и его участников, а также результаты этого отражения в окружающей среде, заключающей в себе информацию о всех существенных обстоятельствах аналогичных событий, т. е. только то, что составляет информационную основу для раскрытия, расследования и предупреждения преступлений. Таким образом, последняя информация является содержанием структуры механизма преступления, его причинных закономерностей.
е. только то, что составляет информационную основу для раскрытия, расследования и предупреждения преступлений. Таким образом, последняя информация является содержанием структуры механизма преступления, его причинных закономерностей.
В данном случае одной из главных задач криминалистического познания является установление не просто процесса как такового, а установление причинного взаимодействия всей совокупности элементов, составляющих механизм преступления в целом. В той связи, в нашем представлении, все элементы познания механизма нельзя сводить только к наблюдаемым следам -отражениям преступления. Дело в том, что в криминалистической методике расследования преступлений познание закономерностей, формирования ее предмета исследования нельзя уместить в виде одной прямой, поэтапно развивающейся линии. Это отношения всегда развивающиеся в плоскости, где исследуются не только наблюдаемые объекты, но и те явления, условия, которые скрыты от человеческого глаза, но о существовании которых возможно узнать только через установления отношений связи, в частности причинно-следственной.
Таким образом, говоря о криминалистическом познании причинно-следственной связи, представляется верным рассмотрение ее в качестве взаимодействия, что выводит нас на иной, более высокий порядок познания и использования в теории и практике расследования преступлений. Данный подход позволяет посредством раскрытия внутреннего содержания причинно-следственного взаимодействия выявить своеобразие соотношения компонентов такого взаимодействия и понять его механизм. Это позволит углубить наши представления о событийной стороне преступления, его механизме.
Следует сказать, что рассмотрение данной системной взаимообусловленности элементов причинноследственных взаимодействий позволит удовлетворять требования раскрытия, расследования и предупреждения преступлений. Это связано с тем, что в современной практике расследования одностороннего преставления о причинно-следственной связи не достаточно.
Это связано с тем, что в современной практике расследования одностороннего преставления о причинно-следственной связи не достаточно.
В литературе сказано, что необходимым условием использования принципа причинности для познания механизма события является правильное понимание значения причинно-следственных связей как частицы универсальной связи. Содержание же знаний в криминалистической методике, как и любой области научного знания, на сегодняшний день носит системноструктурный характер, который не исчерпывается особенностями составляющих его элементов, а коренится, прежде всего, в характере связей и отношений между отдельными элементами [11. С. 338]. Это, на наш
взгляд, позволяет задействовать знания о причинноследственной связи на новом уровне, определяя его как системообразующие.
Усиливая методологическое значение причинной связи, подчеркнем, что важным принципом в исследовании механизма совершения преступления сегодня является принцип единства положений методики расследования преступлений с положениями криминалистической теории причинности. Реализация положений причинности в криминалистической методике позволяет принять логические формы различных концепций, например, криминалистическая характеристика преступлений определенной категории (например дорожно-транспортных происшествий), правила адаптации частных криминалистических методик к особенностям и условиям расследования по уголовному делу и т. д. Таким образом, современное представление о реализации положений причинности в системе методики расследования преступлений легло и в основу криминалистической классификации преступлений.
До последнего времени классификации преступлений, построенные по различным основаниям, рассматривались в криминалистической литературе с точки зрения возможности их применения для систематизации частных криминалистических методик, обладающих оптимальной приспособляемостью к практике раскрытия аналогичных преступлений [4. С. 186-187; 12. С. 151-168; 13. С. 25-26]. Заметим, что по мере развития криминалистической теории и метода накопления эмпирического материала усиливалось тяготение к разработке конкретных частных методик расследования на основе криминалистической классификации преступлений [4. С. 182-190; 14. С. 90; 15. С. 347], но при одном обязательном условии: их система строится на основании анализа уголовно-правовых признаков [16. С. 197].
С. 186-187; 12. С. 151-168; 13. С. 25-26]. Заметим, что по мере развития криминалистической теории и метода накопления эмпирического материала усиливалось тяготение к разработке конкретных частных методик расследования на основе криминалистической классификации преступлений [4. С. 182-190; 14. С. 90; 15. С. 347], но при одном обязательном условии: их система строится на основании анализа уголовно-правовых признаков [16. С. 197].
Идея заключалась в том, что результаты исследования его проблем должны обеспечить получение того, что необходимо для его познания, а также раскрытия и расследования преступления. Таким требованиям данная проблема может отвечать при условии, что оно будет направлено на разработку криминалистической характеристики преступления в соответствии с его уголовно-правовой и криминалистической классификациями. При этом главным в исследовании данных проблем является познание качественной природы изучаемых явлений, получение конкретных эмпирических данных в их взаимозависимости и взаимообусловленности, в их реальных типологических причинноследственных отношениях. Таким образом, в исследованиях раскрывается возможность вскрыть глубинные вероятностно-статистические зависимости и на этой основе сформировать систематизированное знание о механизме преступления и методах его раскрытия, расследования и предупреждения.
В последние годы, обращаясь к проблеме задействования знания о причинно-следственной связи в рамках методик, некоторые авторы склоняются к выделению различных уровней закономерностей их познания. Например, в основании систематизации, по мнению В.Е. Корноухова, должны быть положены закономерности познавательных процессов при расследовании
преступлений, что дало автору возможность выделить классы методик. Классы методик отличаются друг от друга закономерностями познавательных процессов и стратегическими задачами [17. С. 144]. Например, в классе методик «Причинные отношения» закономерность познания состоит в том, что в начале изучаются последствия, затем — обстановка, предшествующая преступлению, а после этого — механизм. В качестве стратегической задачи, пронизывающей в целом процесс расследования, выступает задача познания прямой причинно-следственной связи между деянием (действием или бездействием) и наступившими последствиями.
С. 144]. Например, в классе методик «Причинные отношения» закономерность познания состоит в том, что в начале изучаются последствия, затем — обстановка, предшествующая преступлению, а после этого — механизм. В качестве стратегической задачи, пронизывающей в целом процесс расследования, выступает задача познания прямой причинно-следственной связи между деянием (действием или бездействием) и наступившими последствиями.
Каждый из выделенных классов на основе общности объекта посягательства подразделяется на отдельные роды, а они, в свою очередь, на виды (по вертикальному ряду) [3. С. 635]. Видовое деление методик в данной классификации по вертикали осуществляется с использованием непосредственного объекта посягательства, и уголовно-правовая характеристика классификации имеет большое значение. В этом роде причинно-следственная связь чаще носит непосредственный характер — невыполнение или ненадлежащее выполнение нормативных предписаний и наступление последствий, предусмотренных той или иной нормой уголовного права.
Таким образом, предложенная классификация методик, по мнению автора, в целом раскрывает закономерности процесса познания и свидетельствует о многообразии средств практической деятельности следственного аппарата более общего, чем предыдущие.
На наш взгляд, данная идея является интересной, однако необходимо сделать некоторые замечания, что в свете современного развития законодательства исследование причинно-следственной связи все чаще носит характер нарушений предписаний не только уголовноправовых норм, но и норм неуголовного права. Тем самым современное представление об исследовании должно приобретать комплексный, «межотраслевой» характер, что приводит к необходимости генетической разработки отдельных категорий конкретной методики расследования преступлений, отражающей специфику преступления. Однако нет необходимости создавать «с нуля» существующие концепции, а лишь внести некоторые изменения в соответствии с современным положением вещей практики.
Это дает возможность рассматривать причинно -следственные связи в рамках методики расследования преступлений в качестве систематизирующего критерия для самой внутренней структуры методики конкретного вида преступления, где знания о причинноследственной связи имеют интегрирующее значение, связывая структурные элементы всех компонентов в системе криминалистической методики расследования преступлений, и служат гносеологической основой ретроспективного процесса познания (расследования).
Таким образом, говоря о задействовании знаний о причинности внутри криминалистической методики расследования преступлений, следует подчеркнуть, что структуру последней возможно строить на реализации принципа причинности, на познании причинных связей между отдельными элементами структуры метода осу-
ществления расследования и научно-эмпирического его обеспечения. При этом определения знания о причинноследственной связи в качестве системообразующего центра имеют методологическое значение, т.к. они, исследуя особенности диалектических проявлений причины и следствия при познании механизма преступления и содержательной стороны процесса его установления,
формируют правильное понимание значения единичных и общих причинно-следственных связей в данной предметной области. Это находится в обратной связи с криминалистической методикой расследования преступлений, теорией причинности, более глубокого и всестороннего проникновения в сущность изучаемых криминалистически значимых объектов, явлений процессов.
ЛИТЕРАТУРА
1. Черненко А.К. Философия права. Новосибирск: Наука, 1997. 153 с.
2. Белкин Р.С. Курс криминалистики: В 3 т. Т. 2: Частные криминалистические теории. М.: Юристъ, 1997. 464 с.
М.: Юристъ, 1997. 464 с.
3. Курс криминалистики. Общая часть / Отв. ред. В.Е. Корноухов. М.: Юристъ, 2000. 784 с.
4. Белкин Р.С. Криминалистика: проблемы, тенденции, перспективы. От теории к практике. М., 1988. 302 с.
5. СеливановН.А. Советская криминалистика: система понятий. М.: Юрид. лит., 1982. 150 с.
6. ГродзинскийМ.М. Улика в советском уголовном процессе // Ученые труды ВИЮН. М., 1944. Вып. VII.
7. СтроговичМ.С. Материальная истина и судебные доказательства в советском уголовном процессе. М., 1955. 382 с.
8. Эйсман А.А. О формах связи косвенных доказательств // Вопросы криминалистики. 1964. № 11.
9. Лубин А.Ф. Механизм преступной деятельности. Методология криминалистического исследования. Н. Новгород, 1997. 334 с.
10. Колдин В.Я. Предмет, методология и система криминалистики // Криминалистика социалистических стран. М., 1986. 509 с.
11. Косарев С.Ю. История и теория криминалистических методик расследования преступлений / Под ред. В.И. Рохлина. СПб.: Юридический центр Пресс, 2008. 495 с.
12. ГерасимовИ.Ф. Некоторые проблемы раскрытия преступлений. Свердловск: Урал. книж. изд-во, 1975. 184 с.
13. Васильев А.Н. О криминалистической классификации преступлений // Методика расследования преступлений (общие положения): Материалы науч.-практ. конф. М., 1976. 302 с.
14. ОбразцовВ.А. О криминалистической классификации преступлений // Вопросы борьбы с преступностью. М., 1980. Вып. 33.
М., 1980. Вып. 33.
15. Peschak J. As Kollektiv. Kriminalistika. Obzor. Bratislava, 1981. 407 с.
16. Белкин Р.С. Курс советской криминалистики. М., 1979. Т. 3. 406 с.
17. Курс криминалистики / Под ред. В.Е. Корноухова. Красноярск, 1996. Т. 1. 441 с.
Статья представлена научной редакцией «Право» 15 октября 2010 г.
Моделирование причинно-следственных связей между целями [BS Docs 4]
Цели могут быть связаны друг с другом причинно-следственными связями. Моделирование этих связей может осуществляться:
Рисунок 1. Цели на диаграмме стратегической карты
Степень влияния одной цели на другую можно отразить при помощи параметра «Сила влияния», значения которого с соответствующими числовыми коэффициентами могут быть следующие:
Очень слабое влияние — 0,25;
Слабое влияние — 0,5;
Нормальное влияние — 1;
Сильное влияние — 2;
Очень сильное влияние — 4.
По умолчанию значение параметра «Сила влияния» задается как «Нормальное влияние». Изменить значение параметра можно в Окне свойств связи (стрелки) или в Окне свойств цели на вкладках Зависит от целей и Влияет на цели. Т.к. не все цели могут быть изображены на диаграмме стратегической карты, установить связь между такими целями можно непосредственно на вкладках Зависит от целей и Влияет на цели. На диаграмме стратегической карты изменение силы влияния графически отображается в виде толщины связующей стрелки: чем больше влияние, тем толще стрелка.
Заполнение списков «Зависит от целей» и «Влияет на цели» может осуществляться путем переноса одной цели из справочника «Цели» непосредственно в Окно свойств другой цели на вкладку Зависит от целей в параметр «Цель исходящая» или на вкладку Влияет на цели в параметр «Цель входящая». Или другим способом: в Окне свойств цели на вкладке Зависит от целей (Влияет на цели) в параметре «Цель исходящая» («Цель входящая») нажатием на кнопку выбрать к добавлению нужную цель. Более подробно работа с полями ввода описана в главе Руководство пользователя → Типы параметров и поля ввода их значений.
Или другим способом: в Окне свойств цели на вкладке Зависит от целей (Влияет на цели) в параметре «Цель исходящая» («Цель входящая») нажатием на кнопку выбрать к добавлению нужную цель. Более подробно работа с полями ввода описана в главе Руководство пользователя → Типы параметров и поля ввода их значений.
Внимание!
Указание причинно-следственной связи между целями на диаграмме стратегической карты меняет содержимое вкладок Влияет на цели и Зависит от целей в Окне свойств цели (см. Моделирование стратегических целей) только после сохранения диаграммы!
Причинно-следственную связь сделали одновременно прямой и обратной
Делитель луча света (beamsplitter)
Peeter Piksarv
Физики из Университета Вены и Австрийской академии наук показали, что в квантовой механике может существовать ситуация, в которой нельзя определить точную причинно-следственную связь между событиями в эксперименте. Это первый эксперимент такого рода, в котором неопределенность причинности измеряется напрямую. В его основе лежит установка, в которой реализуется суперпозиция порядка выполнения операций: над фотоном одновременно выполняют операцию A, потом B и операцию B, потом A. Подобные процессы могут найти применение в разработке алгоритмов для квантовых компьютеров. Исследование опубликовано в журнале Science Advances.
В зависимости от состояния управляющего параметра (сверху) либо Алиса делает операцию прежде Боба, либо Боб прежде Алисы. Если параметр оказывается квантовым, то он может находиться в суперпозиции значений — тогда возникает суперпозиция порядков операций. Одновременно и Алиса получает фотон раньше Боба и Боб раньше Алисы.
Giulia Rubino et al. / Science Advances, 2017
Принцип причинности (наличие причинно-следственной связи) — одно из фундаментальных свойств физики и других наук, позволяющее разделять один процесс на последовательность шагов, каждый из которых становится причиной последующего. Например, лампочка загорается после того, как мы замыкаем электрическую цепь выключателем, гром возникает из-за удара молнии, но не наоборот. Принцип причинности лежит в основе специальной теории относительности, запрещая чему-либо перемещаться быстрее скорости света.
В квантовой механике подобные свойства часто оказываются устроенными более сложно. К примеру, запутанные состояния специальным образом нарушают ее локальность: если взять две запутанные частицы и провести измерение над одной из них, это моментально (то есть быстрее скорости света) скажется на другой, как бы далеко она ни находилась. При этом не нарушаются причинно-следственные связи — моментальной передачи полезной информации не происходит.
Для того, чтобы доказать квантовую природу запутанности состояний были разработаны неравенства Белла. Это выражение, которое ограничивает частоту совпадений результатов двух случайных измерений двух запутанных частиц. Подробнее о них можно прочесть в описании недавнего эксперимента с участием космических генераторов случайных чисел. Кроме того, есть специальный математический аппарат, который позволяет определить, являются ли два состояния разделимыми или не разделимыми (запутанными) — «свидетель запутанности». Это некоторая функция (след специальной матрицы), которая оказывается больше или равна нулю для разделимых состояний и меньше нуля — для неразделимых.
Это некоторая функция (след специальной матрицы), которая оказывается больше или равна нулю для разделимых состояний и меньше нуля — для неразделимых.
Оказывается, в квантовой механике можно поставить эксперимент, в котором возникает неопределенность причинно-следственных связей. С помощью похожего математического аппарата («свидетеля причинности») можно показать, что процесс, лежащий в основе эксперимента, не разделим на последовательности элементарных операций.
Основу эксперимента можно пояснить на таком примере. Пусть у нас есть число (например, единица), над которым мы хотим провести две последовательные операции: умножить его на два и возвести в квадрат. В классической ситуации, в зависимости от порядка операций, мы получим два разных результата. Пусть порядок операций будет зависеть от того, выпадет орел или решка при броске монеты. Тогда мы будем получать с вероятностью 50 процентов «четыре» и с вероятностью 50 процентов «два». Очевидно, что зная результат вычисления мы можем восстановить порядок операций и представить все результаты эксперимента как сумму двух путей вычисления.
В квантовой версии эксперимента порядок операций связан с состоянием «Кота Шредингера» — суперпозицией двух состояний. Роль числа в эксперименте будет выполнять состояние фотона (поляризация), а вместо умножения и возведения в степень будут происходить изменения поляризации. Аналогами математических операций являются «отзеркаливание» плоскости поляризации и превращение линейной поляризации в круговую или эллиптическую. От порядка этих операций зависит конечное состояние фотона. Чтобы обеспечить два варианта порядка операций для фотона необходимо создать две возможных траектории: в одной он будет проходить сначала через прибор A, потом B, в другой — наоборот. Суперпозиция двух траекторий может возникнуть, например, если направить одиночный фотон на светоделитель, полупрозрачное зеркало.
Такие эксперименты уже проводились. Однако доказать, что две траектории находятся в суперпозиции удавалось лишь очень косвенно. Например, недавно физики построили вычислительный алгоритм, в основе которого лежит суперпозиция порядка квантовых операций. Он позволял определить, есть ли разница в последовательности выполнения двух неизвестных операций или нет, причем делал это эффективнее, чем алгоритмы с классическим порядком операций. Лишь по уменьшению сложности вычислений в эксперименте авторы подтвердили, что в установке реализуется неопределенный порядок операций.
Например, недавно физики построили вычислительный алгоритм, в основе которого лежит суперпозиция порядка квантовых операций. Он позволял определить, есть ли разница в последовательности выполнения двух неизвестных операций или нет, причем делал это эффективнее, чем алгоритмы с классическим порядком операций. Лишь по уменьшению сложности вычислений в эксперименте авторы подтвердили, что в установке реализуется неопределенный порядок операций.
Авторы новой работы поставили эксперимент, в котором суперпозицию последовательностей квантовых операций можно исследовать напрямую. Главная сложность состояла в том, что квантовое состояние разрушается при измерении, а для прямого определения суперпозиции необходимо было внедрить измерение в траекторию фотона. Чтобы избежать разрушения состояния авторы добились в эксперименте уничтожения информации о том, какой конкретно путь был выбран до попадания фотона в детектор.
Схема экспериментальной установки
Giulia Rubino et al. / Science Advances, 2017
Установка для исследования суперпозиции порядка квантовых операций устроена следующем образом. На первом этапе оптоволокно, по которому путешествуют одиночные фотоны, направляет свет на светоделитель. Отраженный свет попадает сначала на модуль B (Боб), где происходит поворот плоскости поляризации фотона, затем направляется в модуль A (Алиса), где происходит еще одна серия поворотов плоскости поляризации. Затем, в том же модуле A, свет попадает на поляризующий светоделитель — фотоны с вертикальной поляризацией отправляются на одну пару детекторов, с горизонтальной — пройдя через еще одну серию поворотов плоскости поляризации — на другую пару детекторов. Перед детекторами располагается светоделитель, стирающий информацию о том, по какому пути пришел фотон.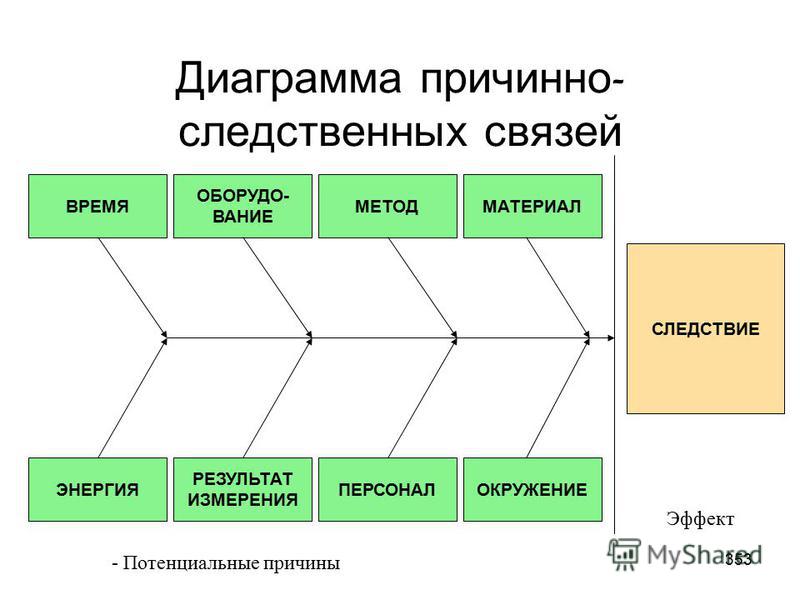 Преломленный луч попадает сначала в модуль А, затем в B и в детектор.
Преломленный луч попадает сначала в модуль А, затем в B и в детектор.
Таким образом, в эксперименте возникают сразу два «типа» суперпозиций. Первый — суперпозиция поляризаций одиночного фотона, второй — суперпозиция путей, по которым путешествовал фотон. Физики измеряют лишь поляризацию фотона после того, как он пролетел через установку и составляют «томограмму» — зависимость конечного состояния фотона от начального. Математическое описание, как и в случае со «свидетелем запутанности» позволяет ученым построить функцию, отличающую разделимые траектории от не разделимых (суперпозиции). Собрав статистику физики показали, что внутри установки действительно реализуется суперпозиция порядков операций над фотоном — статистическая значимость этого результата достигает семи сигма (стандартных отклонений).
Интересно, что эксперимент решает довольно простую задачу — как и в более ранних работах, он позволяет определить, есть ли разница между последовательностями операций A, затем B и B, затем A. Причем, любой классический алгоритм потребовал бы двух обращений к каждой из операций (A и B). Алгоритм, предложенный авторами, требует лишь одного обращения к каждой операции. По словам ученых, в ситуации когда операций больше, чем две, подобные суперпозиции порядков вычислений дадут еще больший прирост в скорости решения задачи.
Этот результат можно сравнить с тем, как квантовые компьютеры оказались эффективнее классических в некоторых задачах. Квантовые алгоритмы, например, алгоритм Шора разложения чисел на простые множители, используют то, что квантовые биты находятся в суперпозиции состояний «нуля» и «единицы». Здесь же возникает новая, дополнительная суперпозиция — порядка элементарных операций в алгоритме.
Владимир Королёв
Выяснение причинно-следственной связи между нарушением ПДД и смертью потерпевшего — Адвокат в Самаре и Москве
В отечественной правоприменительной практике бесспорным признано положение, согласно которому в случаях, если преступление по своей природе влечет наступление определенных последствий, они должны быть непосредственно связаны с самим деянием. Состав таких преступлений называется материальным, то есть преступление имеет свое объективное выражение – последствия. Важен не только факт наступления этих последствий, но и причинно-следственная связь между деянием и наступившими последствиями.
Состав таких преступлений называется материальным, то есть преступление имеет свое объективное выражение – последствия. Важен не только факт наступления этих последствий, но и причинно-следственная связь между деянием и наступившими последствиями.
Что касается причинения вреда здоровью в результате ДТП (ст.264 УК РФ), то уголовно-наказуемым это деяние становится только при наступлении смерти или тяжкого вреда, то есть имелась угроза жизни потерпевшему.
В качестве деяния в данном случае выступают различные нарушения ПДД. Причем это могут быть как конкретные предписания, регулирующие поведение лица в конкретной ситуации, так и общие положения о поведении лица при движении.
К конкретным предписаниям можно отнести запрет на движение на красный сигнал светофора (Приговор Советского районного суда г. Махачкалы от 26.02.2019 по делу № 1-772/2018).
Но чаще суды в обоснование незаконности поведения лица приводят общие положения ПДД, касающиеся видов скоростного режима, расположения автомобиля на дороге. Так, в мотивировочной части приговора может указываться п.1.3 ПДД, согласно которому участники дорожного движения обязаны знать и соблюдать ПДД (апелляционное постановление Псковского областного суда от 21.04.2017 по делу № 22–262).
Возможны и случаи, когда лицо совершает нарушение нескольких пунктов ПДД. Тогда суд должен обосновать, какие из нарушений привели к ПДД и причинению тяжкого вреда здоровью или смерти потерпевшему (приговор Пыталовского районного суда от 07.04.2015 по делу № 1–20/2015)
Причинно-следственная связь между деянием и наступившими последствиями должна быть, во-первых, закономерной – вытекать из совершенного деяния при нормальном, логичном течении событий (при нанесении удара появился синяк), и, во-вторых, необходимой – при нормальном течении событий иные последствия не могут возникнуть.
Как отмечал Пленум Верховного суда в Постановлении от 09.12.2008 № 25 «О судебной практике по делам о преступлениях, связанных с нарушением правил дорожного движения и эксплуатации транспортных средств, а также с их неправомерным завладением без цели хищения», ответственность по ст. 264 УК РФ наступает только тогда, когда доказана прямая причинно-следственная связь между действиями виновного и наступившими последствиями. Отдельно отмечено, что при постановлении приговора суд должен указать, какое конкретно нарушение было допущено.
264 УК РФ наступает только тогда, когда доказана прямая причинно-следственная связь между действиями виновного и наступившими последствиями. Отдельно отмечено, что при постановлении приговора суд должен указать, какое конкретно нарушение было допущено.
Так, если при расследовании дела было установлено и виновное деяние водителя, и смерть потерпевшего в результате травм, приговор суда может быть отменен, если между этими двумя событиями не исследована причинно-следственная связь (апелляционное постановление Псковского областного суда от 06.03.2014 по делу № 22–170).
Необходимо также установить, что при причинении подобного рода травм должны наступить тяжкие последствия для здоровья или смерть. В качестве критерия должного выступает реакция организма здорового человека. Поэтому, если на наступление смерти повлияли на только травмы, но и существовавшие на момента ДТП болезни лица, причинно-следственная связь не считается доказанной (приговор Опочецкого районного суда от 19.03.2015 по делу № 1–16/2015).
Безусловно, оценка характера и степени вреда здоровью, а также наличие причинно-следственной связи требует специальных знаний в области медицины, и в таких случаях в силу положений ст.196 УПК РФ назначение судебно-медицинской экспертизы обязательно.
Однако это не означает, что суд при оценке этих факторов должен всецело доверять мнению эксперта. Его заключение является лишь одним из доказательств и не имеет заранее установленного преимущества перед другими. Следовательно, заключение эксперта также должно оцениваться судом на предмет допустимости и обоснованности.
АНАЛИЗ ХАРАКТЕРА ПРИЧИННО-СЛЕДСТВЕННОЙ СВЯЗИ МЕЖДУ ИНФЛЯЦИЕЙ И ЗАРАБОТНОЙ ПЛАТОЙ В РОССИИ
Иванова Мария Анатольевна
Additional contact information
Иванова Мария Анатольевна: Научно-исследовательский финансовый институт
Studies on Russian Economic Development Проблемы прогнозирования, 2016, issue 5 (158), 119-132
Abstract:
В статье анализируется характер причинно-следственной связи между инфляцией и заработной платой в России в 2003-2014 гг. Автор решает задачу определения достоверности теории инфляции издержек и теории инфляции спроса, используя российские данные с помощью эконометрических методов (теста на причинность по Гренджеру и модели векторной коррекции ошибок). Стабильность результатов моделирования (с целью исключения структурных сдвигов в условиях изменения принципов денежно-кредитной политики Банка России при переходе к инфляционному таргетированию) проверяется с помощью процедуры Грегори-Хансена. Приводится сравнение полученных результатов с аналогичными исследованиями, проведенными для развитых стран и стран с развивающимися рынками.
Автор решает задачу определения достоверности теории инфляции издержек и теории инфляции спроса, используя российские данные с помощью эконометрических методов (теста на причинность по Гренджеру и модели векторной коррекции ошибок). Стабильность результатов моделирования (с целью исключения структурных сдвигов в условиях изменения принципов денежно-кредитной политики Банка России при переходе к инфляционному таргетированию) проверяется с помощью процедуры Грегори-Хансена. Приводится сравнение полученных результатов с аналогичными исследованиями, проведенными для развитых стран и стран с развивающимися рынками.
Date: 2016
References: Add references at CitEc
Citations: Track citations by RSS feed
Downloads: (external link)
http://cyberleninka.ru/article/n/analiz-haraktera- … tnoy-platoy-v-rossii
Related works:
This item may be available elsewhere in EconPapers: Search for items with the same title.
Export reference: BibTeX RIS (EndNote, ProCite, RefMan) HTML/Text
Persistent link: https://EconPapers.repec.org/RePEc:scn:009162:17023083
Access Statistics for this article
More articles in Studies on Russian Economic Development Проблемы прогнозирования from CyberLeninka, Федеральное государственное бюджетное учреждение науки Институт народнохозяйственного прогнозирования Российской академии наук
Bibliographic data for series maintained by CyberLeninka ().
причинно-следственных связей — Викисловарь
Английский [править]
Этимология [править]
Заимствовано из позднего латинского causalis , из латинского causa («причина»); см. причину .
Произношение [править]
Прилагательное [править]
причинный ( сравнительный более причинный , превосходный наиболее причинный )
- , относящиеся к чему-либо или являющиеся причиной чего-либо; вызывая
Нет причинно-следственной связи между поеданием моркови и видением в темноте.

- 2021 24 февраля, Грег Морс, «Великий черт: трагическая цепочка событий», в RAIL , номер 925, стр. 44:
Время меняет отношения, и пока действия Харта за рулем когда они были не в состоянии сделать это, безусловно, были в цепочке , вызвавшей происшествие в аварии Great Heck, сколько других водителей были за рулем, когда были слишком утомлены, чтобы сделать это?
Примечания по использованию [править]
Связанные термины [править]
Переводы [править]
, относящиеся к чему-либо или являющиеся их причиной
Существительное [править]
причинно-следственная связь ( множественное число причинно-следственная связь )
- (грамматика) слово (например, потому что), которое выражает причину или причину
Дополнительная литература [править]
Анаграммы [править]
Каталонский [править]
Этимология [править]
Заимствовано из позднего латинского causālis , из латинского causa .
Прилагательное [править]
причинный ( мужской и женский род множественного числа причинно-следственных связей )
- причинно-следственная связь
Связанные термины [править]
Этимология [править]
Заимствовано из позднего латинского causālis , из латинского causa .
Произношение [править]
Прилагательное [править]
причинный ( женский род единственного числа causale , мужской род множественного числа causaux , женский род множественного числа causales )
- причинно-следственная
Дополнительная литература [править]
Португальский [править]
Этимология [править]
Заимствовано из позднего латинского causālis , из латинского causa .
Прилагательное [править]
причинно-следственная m или f ( множественное число причинно-следственная связь , сопоставимая )
- причинно-следственная связь (относящаяся к чему-либо или являющаяся причиной чего-либо)
Связанные термины [править]
Испанский [править]
Этимология [править]
Заимствовано из позднего латинского causālis , из латинского causa .
Произношение [править]
Прилагательное [править]
причинный ( множественное число причинно )
- причинно-следственная связь
Связанные термины [править]
определение причинности по The Free Dictionary
Начало — это то, что само по себе ничему не следует из причинной необходимости, но после чего что-то естественно существует или возникает.Можно понять, что у Наполеона была власть, и поэтому события произошли; с некоторым усилием можно даже представить, что Наполеон вместе с другими влияниями был причиной события; но то, как книга Le Contrat social заставила французов начать топить друг друга, не может быть понято без объяснения причинной связи этой новой силы с событием. причинных законов, один из которых принадлежит физике, а другой — психологии.Гений изучает причинную мысль и еще в глубине материи видит лучи, расходящиеся от одного шара, которые расходятся, прежде чем упасть, на бесконечные диаметры. Он созерцает идеи и высказывает необходимое и причинное. Ибо сейчас мы говорим не о людях поэтических талантов или трудолюбивых и умелых людей, но об истинном поэте. Используя некоторые недавние аргументы, сделанные в методологии экономики и философии физики, подчеркивается, во-первых, что причинно-следственные связи понимание и свойства сущностей тесно связаны, и, во-вторых, плохая описательная работа не влечет отказа от характеристик сущностей, важных с точки зрения причинного понимания. Однако для количественной оценки производимого причинно-следственного вывода обычно используются статистические методы, которые сравнивают взаимосвязь между интересующими переменными, а не именно причинно-следственный эффект., По оценке Уэйд, доктор философии из Бристольского университета в Соединенном Королевстве, и его коллеги. причинно-следственное влияние ИМТ на общий уровень и детальное состояние сердечно-сосудистой системы у здоровых участников из Продольного исследования Avon родителей и детей в возрасте 17 лет (от 1420 до 3108 участников для разных исходов) и независимой выборки из той же когорты (для напоминания by-Genotype [RbG]) в возрасте 21 года (от 386 до 418 участников).Таким образом, хорошая стратегия зависит от эффективного выявления причинно-следственных связей и манипулирования ими. Окружной суд округа Хеннепин признал школы ответственными за мошенничество с потребителями и мошенническую торговую практику, и был издан судебный приказ о реституции, который предоставил учащимся уголовного правосудия опровержимую презумпцию причинения вреда. 4 июня Апелляционный суд постановил, что только 15 учащихся, давших показания, имели право на помощь, было ошибкой предполагать наличие причинно-следственной связи.Это, очевидно, оставляет остальных учащихся этой программы на протяжении многих лет без средств правовой защиты, поскольку Апелляционный суд обнаружил отсутствие доказательств причинно-следственной связи между мошенническим поведением школы и нанесением вреда учащимся. для анализа конкретных добродетелей, как показывает вводный пример книги о главной добродетели воздержания.
Однако для количественной оценки производимого причинно-следственного вывода обычно используются статистические методы, которые сравнивают взаимосвязь между интересующими переменными, а не именно причинно-следственный эффект., По оценке Уэйд, доктор философии из Бристольского университета в Соединенном Королевстве, и его коллеги. причинно-следственное влияние ИМТ на общий уровень и детальное состояние сердечно-сосудистой системы у здоровых участников из Продольного исследования Avon родителей и детей в возрасте 17 лет (от 1420 до 3108 участников для разных исходов) и независимой выборки из той же когорты (для напоминания by-Genotype [RbG]) в возрасте 21 года (от 386 до 418 участников).Таким образом, хорошая стратегия зависит от эффективного выявления причинно-следственных связей и манипулирования ими. Окружной суд округа Хеннепин признал школы ответственными за мошенничество с потребителями и мошенническую торговую практику, и был издан судебный приказ о реституции, который предоставил учащимся уголовного правосудия опровержимую презумпцию причинения вреда. 4 июня Апелляционный суд постановил, что только 15 учащихся, давших показания, имели право на помощь, было ошибкой предполагать наличие причинно-следственной связи.Это, очевидно, оставляет остальных учащихся этой программы на протяжении многих лет без средств правовой защиты, поскольку Апелляционный суд обнаружил отсутствие доказательств причинно-следственной связи между мошенническим поведением школы и нанесением вреда учащимся. для анализа конкретных добродетелей, как показывает вводный пример книги о главной добродетели воздержания.Обнаружение и количественная оценка причинно-следственных связей в больших наборах данных нелинейных временных рядов
ВВЕДЕНИЕ
Как основные климатические режимы, такие как Южное колебание Эль-Ниньо (ENSO), влияют на удаленные регионы через глобальные телесвязи? Как связаны физиологические процессы в организме человека? Кроме того, через какие пути взаимодействуют различные области мозга? Выявление причинно-следственных ассоциаций множества переменных и количественная оценка причинной силы являются ключевыми проблемами при анализе сложных динамических систем, особенно потому, что здесь интервенционные реальные эксперименты, золотой стандарт научных открытий, часто неэтичны или практически невозможны. В исследованиях климата моделирование может помочь проверить причинные механизмы, но это очень дорого, требует много времени и представляет собой лишь приближение реальных физических процессов ( 1 ). Здесь мы представляем подход, который изучает сети причинно-следственных связей непосредственно из данных временных рядов. Эти подходы, основанные на данных, становятся все более привлекательными, поскольку в последние десятилетия произошел взрывной рост доступности данных, полученных в результате моделирования и реальных наблюдений, например, в науках о Земле ( 2 ).Поэтому мы определяем острую необходимость в разработке новых методов обнаружения причин, которые могли бы использовать преимущества этого недавнего всплеска больших данных, которые, как мы показываем здесь, могут способствовать прогрессу во многих областях науки.
В исследованиях климата моделирование может помочь проверить причинные механизмы, но это очень дорого, требует много времени и представляет собой лишь приближение реальных физических процессов ( 1 ). Здесь мы представляем подход, который изучает сети причинно-следственных связей непосредственно из данных временных рядов. Эти подходы, основанные на данных, становятся все более привлекательными, поскольку в последние десятилетия произошел взрывной рост доступности данных, полученных в результате моделирования и реальных наблюдений, например, в науках о Земле ( 2 ).Поэтому мы определяем острую необходимость в разработке новых методов обнаружения причин, которые могли бы использовать преимущества этого недавнего всплеска больших данных, которые, как мы показываем здесь, могут способствовать прогрессу во многих областях науки.
В типичном сценарии анализа наблюдений, например, в науке о климате, исследователь выдвигает гипотезу о причинном влиянии между двумя процессами с учетом наблюдаемых данных временных рядов. Данные могут состоять из различных климатологических переменных (например,g., температура и давление) в одном месте или временные ряды, которые представляют региональные средние климатологические переменные, например, общепринятые климатические индексы. Например, ее может заинтересовать влияние регионального индекса ЭНСО на индекс, характеризующий изменчивость температуры на определенных участках суши Северной Америки. Предположим, временной ряд показывает четкую корреляцию, предполагающую связь между двумя процессами. Чтобы исключить другие возможные гипотезы, которые могут объяснить такую корреляцию, она затем включит другие соответствующие переменные.В сильно взаимосвязанных системах, как правило, есть много возможных драйверов, которые она может протестировать, что быстро приводит к многомерным проблемам обнаружения причин.
Целью обнаружения причинных связей временных рядов из сложных динамических систем является статистически достоверная оценка причинно-следственных связей, включая их временные запаздывания. Например, климатические телесвязи могут длиться от нескольких дней до месяцев. Двумя ключевыми проблемами являются обычно высокая размерность этих проблем обнаружения причин и часто сильная взаимозависимость.Например, в системе, содержащей от десятков до сотен переменных (например, различных региональных климатических индексов), корреляции будут возникать не только из-за прямых причинных эффектов, но также из-за эффектов автокорреляции внутри каждого временного ряда, косвенных связей или общих факторов (рис. . 1). В идеале метод обнаружения причин обнаруживает как можно больше истинных причинно-следственных связей (высокая степень обнаружения) и контролирует количество ложных срабатываний (обнаружение неверных ссылок). Обнаружение причинно-следственной связи может помочь лучше понять физические механизмы, построить более экономные модели прогнозирования и более надежно оценить силу причинных эффектов, что может быть выполнено в различных рамках, например, потенциальный результат ( 3 ) или графическая модель. каркасы ( 4 , 5 ).Проще говоря, причинное открытие будет полезно в ситуациях, когда исследователи хотят изучать сложные динамические системы способом, выходящим за рамки простого корреляционного анализа. Конечно, любая причинная интерпретация будет основываться на ряде предположений ( 4 , 5 ), о чем мы подробнее поговорим ниже.
Например, климатические телесвязи могут длиться от нескольких дней до месяцев. Двумя ключевыми проблемами являются обычно высокая размерность этих проблем обнаружения причин и часто сильная взаимозависимость.Например, в системе, содержащей от десятков до сотен переменных (например, различных региональных климатических индексов), корреляции будут возникать не только из-за прямых причинных эффектов, но также из-за эффектов автокорреляции внутри каждого временного ряда, косвенных связей или общих факторов (рис. . 1). В идеале метод обнаружения причин обнаруживает как можно больше истинных причинно-следственных связей (высокая степень обнаружения) и контролирует количество ложных срабатываний (обнаружение неверных ссылок). Обнаружение причинно-следственной связи может помочь лучше понять физические механизмы, построить более экономные модели прогнозирования и более надежно оценить силу причинных эффектов, что может быть выполнено в различных рамках, например, потенциальный результат ( 3 ) или графическая модель. каркасы ( 4 , 5 ).Проще говоря, причинное открытие будет полезно в ситуациях, когда исследователи хотят изучать сложные динамические системы способом, выходящим за рамки простого корреляционного анализа. Конечно, любая причинная интерпретация будет основываться на ряде предположений ( 4 , 5 ), о чем мы подробнее поговорим ниже.
Рассмотрим крупномасштабный набор данных временных рядов ( A ) из сложной системы, такой как система Земля, для которой мы пытаемся оценить лежащие в основе причинные зависимости ( B ), учитывая линейные и нелинейные зависимости и включая их временные запаздывания. (ярлыки ссылок).Парные корреляции приводят к ложным зависимостям из-за общих драйверов (например, X 1 ← X 2 → X 3 ) или транзитивных непрямых путей (например, X 2 → X 3 → X 4 ). Обнаружение причинно-следственных связей направлено на выявление таких ложных зависимостей, приводящих к расчетным причинным сетям, которые, следовательно, намного реже, чем сети корреляции.
Обнаружение причинно-следственных связей направлено на выявление таких ложных зависимостей, приводящих к расчетным причинным сетям, которые, следовательно, намного реже, чем сети корреляции.
Основным современным подходом не только к анализу данных о Земле ( 6 — 9 ), но и к нейробиологии ( 10 , 11 ), является оценка причинно-следственных связей с запаздыванием во времени с использованием авторегрессионных моделей в рамках Грейнджера. причинность ( 12 , 13 ).Если реализовано с использованием стандартных методов регрессии, то высокая размерность типичных наборов данных приводит к очень низкой способности обнаружения («проклятие размерности»), поскольку размеры выборки часто составляют всего несколько сотен (например, для ежемесячного разрешения по времени с 30 лет спутниковых данных). Этот недостаток приводит к дилемме, которая ограничивает применение причинности Грейнджера в основном для двумерного анализа, который, однако, не может учесть косвенные связи или общие факторы. В дополнение к линейной причинно-следственной связи Грейнджера методы пространства состояний ( 14 , 15 ) лучше решают нелинейные зависящие от состояния связи, но их также трудно распространить на сценарии большой размерности.
Существуют методы, которые могут справиться с высокой размерностью, такие как методы регуляризованной регрессии ( 16 — 18 ), но в основном в контексте прогнозирования, а не выявления причин, где оценка значимости причинных связей более важна. Исключением является регрессия Лассо ( 17 ), которая также позволяет обнаруживать активные переменные. Другой подход с некоторыми недавними приложениями в науках о Земле ( 19 — 24 ) — это алгоритмы, специально нацеленные на обнаружение причин ( 4 , 5 , 25 ), которые используют итеративную независимость и проверку условной независимости.Однако как регуляризованная регрессия ( 26 ), так и недавние реализации алгоритмов обнаружения причин не справляются с сильными взаимозависимостями из-за пространственно-временной природы переменных, как мы показываем здесь. В частности, для этих методов сложно контролировать ложные срабатывания на желаемом уровне, а для нелинейных оценщиков — еще больше. Таким образом, эти проблемы приводят к хрупким оценкам причинно-следственных связей и причинно-следственных связей, и требуется более надежная методология.В ( 2 ) авторы представляют обзор современного состояния методов причинного вывода и обсуждают связанные с этим проблемы, уделяя особое внимание наукам о Земле.
В частности, для этих методов сложно контролировать ложные срабатывания на желаемом уровне, а для нелинейных оценщиков — еще больше. Таким образом, эти проблемы приводят к хрупким оценкам причинно-следственных связей и причинно-следственных связей, и требуется более надежная методология.В ( 2 ) авторы представляют обзор современного состояния методов причинного вывода и обсуждают связанные с этим проблемы, уделяя особое внимание наукам о Земле.
Мы представляем метод обнаружения причинно-следственной сети на основе графической причинно-следственной модели ( 5 ), который хорошо масштабируется с большими наборами данных временных рядов с линейными и нелинейными зависимостями с задержкой по времени. Посредством аналитических результатов, реальных приложений и обширных численных экспериментов мы демонстрируем, что предлагаемый метод имеет существенные преимущества по сравнению с нынешним уровнем техники в работе с наборами данных взаимозависимых временных рядов от десятков до сотен переменных для размеров выборки несколько сотен или более, что дает надежный ложноположительный контроль и более высокую мощность обнаружения.Мы также обнаружили, что более надежные оценки причинно-следственной сети дают более точные оценки причинных эффектов, объединяя обнаружение причинно-следственных связей с системами вывода причинных эффектов, такими как структура потенциальных результатов. Наш подход позволяет проводить каузальный анализ большего числа переменных, открывая новые возможности для более достоверной оценки причинно-следственных связей и причинных эффектов из временных рядов в науке о земных системах, физиологии, нейробиологии и других областях.
ПРИЧИННОЕ ОБНАРУЖЕНИЕ
Мотивирующий пример из науки о климате
Далее мы проиллюстрируем проблему обнаружения причин в хорошо известной системе связи на большие расстояния.Мы выделяем два основных фактора, которые приводят к тому, что общий подход к каузальному моделированию авторегрессии по Грейнджеру имеет низкую способность обнаружения: уменьшенный размер эффекта из-за обусловливания нерелевантных переменных и высокая размерность.
Учитывая выборку конечного временного ряда, каждый метод обнаружения причин должен балансировать между слишком большим количеством ложных срабатываний (неправильное обнаружение ссылок) и слишком небольшим количеством истинных срабатываний (правильное обнаружение ссылок). Метод причинно-следственной связи идеально контролирует ложные срабатывания на заранее определенном уровне значимости (например,g., 5%) и максимизирует мощность обнаружения. Мощность метода обнаружения причинно-следственной связи зависит от доступного размера выборки, уровня значимости, размерности проблемы (например, количества коэффициентов в модели авторегрессии) и размера эффекта, который в данном случае является величиной величина эффекта, измеренная статистикой теста (например, частным коэффициентом корреляции). Поскольку размер выборки и уровень значимости обычно фиксированы в данном контексте, мощность метода может быть улучшена только за счет уменьшения размерности или увеличения размера эффекта (или того и другого).
Рассмотрим типичный сценарий открытия причин в исследованиях климата (рис. 2). Мы хотим проверить, подтверждают ли данные наблюдений гипотезу о том, что температура поверхности тропической части Тихого океана, представленная ежемесячным индексом Нино 3.4 (далее Нино; см. Карту и регион на рис. S2) ( 27 ), оказала причинное воздействие вне тропических районов. температуры воздуха на суше ( 28 ) над Британской Колумбией (BCT) за 1979–2017 гг. ( T = 468 месяцев). Мы выбрали этот пример, поскольку хорошо установлено и физически понятно, что цуги атмосферных волн, вызванные повышением температуры поверхности моря над тропической частью Тихого океана, могут влиять на температуру в Северной Америке, но не наоборот ( 9 , 29 — 31 ) .Таким образом, основная истина здесь — Nino → BCT во (внутри) сезонном временном масштабе, что позволяет нам проверять методы причинности.
Рис. 2 Пример мотивационного климата.
Корреляция, частичная корреляция FullCI и частичная корреляция PCMCI между месячным климатическим индексом Нино (область 3,4) ( 27 ) и температурой воздуха на суше над Британской Колумбией ( 28 ) ( A ) за 1979–2017 гг. ( T = 468 месяцев), а также искусственные переменные [ Z и W i в ( B и C )].Цвета узлов отображают силу автокорреляции, цвета краев — размер частичного эффекта корреляции, а ширину краев — частоту обнаружения, оцененную на основе 500 реализаций искусственных переменных Z и W i с уровнем значимости 5%. Максимальное запаздывание составляет τ max = 6. Корреляция не допускает причинной интерпретации, что приводит к ложным корреляциям (серые края) (A). FullCI определяет правильное направление Nino → BCT, но теряет мощность из-за меньшего размера эффекта (B) и большей размерности (C), если добавлено больше переменных.PCMCI избегает обусловливания нерелевантных переменных, что приводит к большему размеру эффекта, меньшей размерности и, следовательно, более высокой способности обнаружения. См. Рис. S2 для более подробной информации.
Мы начинаем с анализа корреляции с запаздыванием по времени и обнаруживаем, что две переменные коррелированы в обоих направлениях, то есть как для положительного, так и для отрицательного запаздывания (рис. 2A и см. Рис. S2 для функций запаздывания), что также предполагает влияние от БСТ по Нино. Корреляция Nino → BCT имеет величину эффекта ≈ 0,3 ( P <10 −4 ) с задержкой в 2 месяца.В сетях на рис. 2 цвета ссылок обозначают размеры эффекта (серые ссылки являются ложными), а цвета узлов обозначают силу автокорреляции.
Корреляция с запаздыванием не может использоваться для вывода причинной направленности и даже правильного запаздывания связи ( 20 ). Следовательно, мы переходим к причинным методам. Чтобы проверить Nino → BCT, наиболее простой подход состоит в том, чтобы подогнать линейную авторегрессионную модель BCT к прошлым лагам самого себя и Nino и проверить, действительно ли прошлые коэффициенты Nino значительно отличаются от нуля.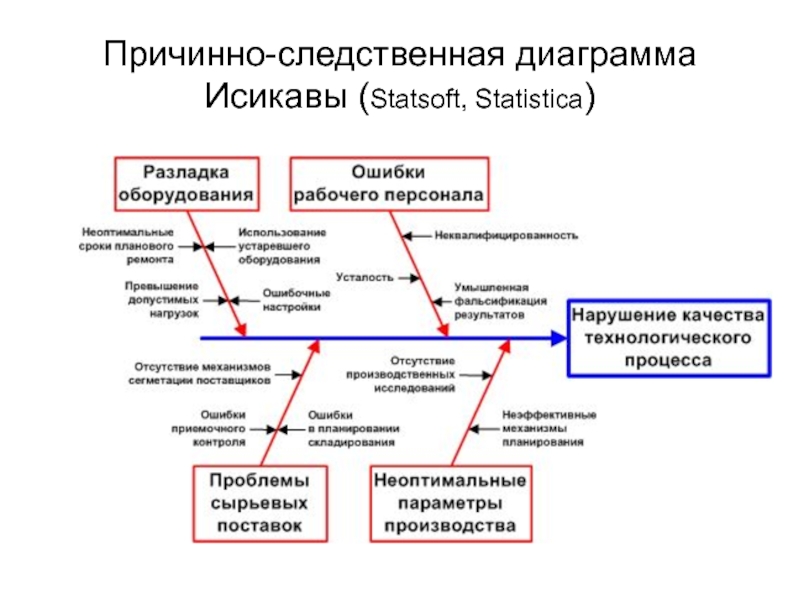 Это эквивалентно зависящей от лага версии причинности по Грейнджеру, но эту проблему можно также в более общем виде сформулировать как проверку условной независимости между Nino t −τ и BCT t при условии (или с учетом) общее прошлое Xt — = (Ninot − 1, BCTt − 1,…), обозначенное Ninot − τ⫫BCTt∣Xt — ∖ {Ninot − τ}. Для оценки условных зависимостей (см. Ниже) временной индекс t проходит через выборки до длины временного ряда T .На практике Xt− усекается при максимальном временном лаге τ max , который зависит от приложения и может быть выбран в соответствии с максимальным причинным временным лагом, ожидаемым в сложной системе, или на основе самого большого запаздывания со значительной корреляцией. Мы называем этот общий подход полным тестированием условной независимости (FullCI; см. Таблицу S3 для обзора методов, рассмотренных в этой статье) и проиллюстрируем его в реализации линейной частичной корреляции для этого примера, то есть мы проверяем ρ (Ninot − τ, BCTt ∣Xt — ∖ {Ninot − τ}) ≠ 0 для различных задержек τ, что является величиной эффекта для FullCI.
Это эквивалентно зависящей от лага версии причинности по Грейнджеру, но эту проблему можно также в более общем виде сформулировать как проверку условной независимости между Nino t −τ и BCT t при условии (или с учетом) общее прошлое Xt — = (Ninot − 1, BCTt − 1,…), обозначенное Ninot − τ⫫BCTt∣Xt — ∖ {Ninot − τ}. Для оценки условных зависимостей (см. Ниже) временной индекс t проходит через выборки до длины временного ряда T .На практике Xt− усекается при максимальном временном лаге τ max , который зависит от приложения и может быть выбран в соответствии с максимальным причинным временным лагом, ожидаемым в сложной системе, или на основе самого большого запаздывания со значительной корреляцией. Мы называем этот общий подход полным тестированием условной независимости (FullCI; см. Таблицу S3 для обзора методов, рассмотренных в этой статье) и проиллюстрируем его в реализации линейной частичной корреляции для этого примера, то есть мы проверяем ρ (Ninot − τ, BCTt ∣Xt — ∖ {Ninot − τ}) ≠ 0 для различных задержек τ, что является величиной эффекта для FullCI.
Используя максимальный временной лаг τ max = 6 месяцев, мы находим значимую частичную корреляцию FullCI для Nino → BCT при лаге 2, равном 0,1 ( P = 0,037) (рис. 2A), и отсутствие значительной зависимости в другом направление. То есть размер эффекта FullCI сильно уменьшается по сравнению с корреляцией (≈ 0,3) при учете прошлого. Однако, как упоминалось ранее, такой двумерный анализ обычно нельзя интерпретировать причинно, потому что другие процессы могут объяснить взаимосвязь.Чтобы дополнительно проверить нашу гипотезу, мы включаем другую переменную Z , которая может объяснить зависимость между Nino и BCT (рис. 2B). Здесь мы генерируем Z искусственно для целей иллюстрации и определяем Zt = 2 · Ninot − 1 + ηtZ для независимого стандартного нормального шума ηtZ. Таким образом, Nino управляет Z с задержкой 1, но Z не имеет причинного воздействия на BCT, которое мы предполагаем априори неизвестным.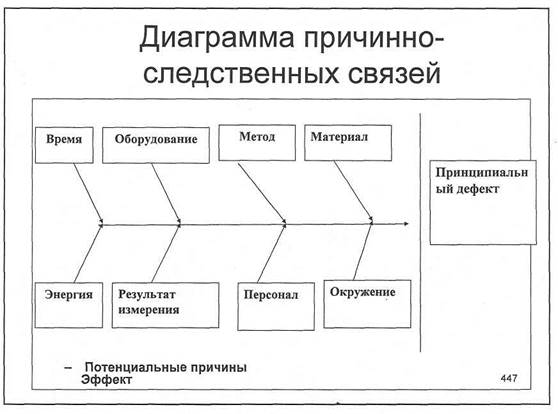 Здесь мы смоделировали различные реализации Z для измерения мощности обнаружения и количества ложных срабатываний.Мы обнаружили, что корреляция будет еще больше вводить в заблуждение причинно-следственную интерпретацию, поскольку мы наблюдаем ложные связи между всеми переменными (рис. 2B). Частичная корреляция FullCI, где Xt− включает прошлое всех трех процессов, а не только BCT и Nino, теперь имеет размер эффекта 0,09 для Nino t −2 → BCT t по сравнению с 0,1 в двумерный случай. На уровне значимости 5% эта связь обнаруживается только в 53% реализаций (истинно-положительная частота, ширина стрелки на рис.2).
Здесь мы смоделировали различные реализации Z для измерения мощности обнаружения и количества ложных срабатываний.Мы обнаружили, что корреляция будет еще больше вводить в заблуждение причинно-следственную интерпретацию, поскольку мы наблюдаем ложные связи между всеми переменными (рис. 2B). Частичная корреляция FullCI, где Xt− включает прошлое всех трех процессов, а не только BCT и Nino, теперь имеет размер эффекта 0,09 для Nino t −2 → BCT t по сравнению с 0,1 в двумерный случай. На уровне значимости 5% эта связь обнаруживается только в 53% реализаций (истинно-положительная частота, ширина стрелки на рис.2).
Что здесь произошло? Как упоминалось выше, мощность обнаружения зависит от размерности и размера эффекта. Условие на прошлое переменной Z немного увеличивает размерность теста условной независимости, но это лишь частично объясняет низкую способность обнаружения. Если Z сконструирован таким образом, что он не зависит от Nino, тогда частичная корреляция FullCI снова будет 0,1, как в двумерном случае, и истинно-положительный коэффициент составляет 85%. Более важным фактором является то, что, поскольку Нино управляет Z , Z содержит информацию о Нино, и поскольку Z является частью набора условий Xt−, теперь он «объясняет» некоторую часть частичной корреляции ρ ( Ninot − 2, BCTt∣Xt — ∖ {Ninot − 2}), что приводит к величине эффекта, равной нулю.01 меньше, что уже сильно снижает скорость обнаружения.
Предположим, мы получили одну из реализаций Z , для которой связь Nino t −2 → BCT t все еще значима. Чтобы дополнительно проиллюстрировать влияние высокой размерности на мощность обнаружения, мы теперь включаем еще шесть переменных W i ( i = 1,…, 6), которые все не зависят от Nino, BCT и Z , но соединены между собой следующим образом (рис.2C): Wti = aiWt − 1i + cWt − 2i − 1 + ηti для i = 2, 4, 6 и Wti = aiWt − 1i + ηti для i = 1, 3, 5, все с той же связью коэффициент c = 0,15 и a 1,2 = 0,1, a 3,4 = 0,5 и a 5,6 = 0,9. Теперь размер эффекта FullCI для Nino t −2 → BCT t все еще равен 0,09, но мощность обнаружения даже ниже, чем раньше, и уменьшается с 53% до всего 40% из-за более высокой размерности.Таким образом, истинная причинно-следственная связь Нино t −2 → BCT t , вероятно, будет упущена из виду.
Теперь размер эффекта FullCI для Nino t −2 → BCT t все еще равен 0,09, но мощность обнаружения даже ниже, чем раньше, и уменьшается с 53% до всего 40% из-за более высокой размерности.Таким образом, истинная причинно-следственная связь Нино t −2 → BCT t , вероятно, будет упущена из виду.
На величину эффекта также влияют эффекты автокорреляции включенных переменных: пары связанных переменных Wt − 2i − 1 → Wti ( i = 2, 4, 6) различаются своей автокорреляцией (как видно по цвету их узлов на рис. 2C), и хотя коэффициент связи c одинаков для каждой пары, их частичные корреляции FullCI равны 0,15, 0,13 и 0.11 (от нижней к высокой автокорреляции). Подобно вышеприведенному случаю, кондиционирование прошлых задержек, здесь Wt-1i ( i = 1, 3, 5), объясняет удаленную информацию, приводя к меньшему размеру эффекта и меньшей мощности, чем выше их автокорреляция. И наоборот, здесь мы наблюдаем больше ложных корреляций для более высоких автокорреляций (рис. 2C, слева).
Этот пример иллюстрирует повсеместную дилемму причинно-следственного обнаружения во многих областях: чтобы повысить надежность причинных интерпретаций, нам нужно включить больше переменных, которые могли бы объяснить ложные отношения, но они приводят к меньшей мощности для обнаружения истинных причинно-следственных связей из-за более высоких размерность и, возможно, меньшая величина эффекта.Низкая способность обнаружения также означает, что оценки причинно-следственных связей становятся менее надежными, как мы показываем в разделе «Результаты». В идеале мы хотим ограничиться только несколькими релевантными переменными, которые действительно объясняют отношения.
Обнаружение причинно-следственной сети с помощью PCMCI
Предыдущий пример продемонстрировал необходимость в автоматизированной процедуре, которая лучше идентифицирует обычно несколько релевантных переменных, на которые можно положиться.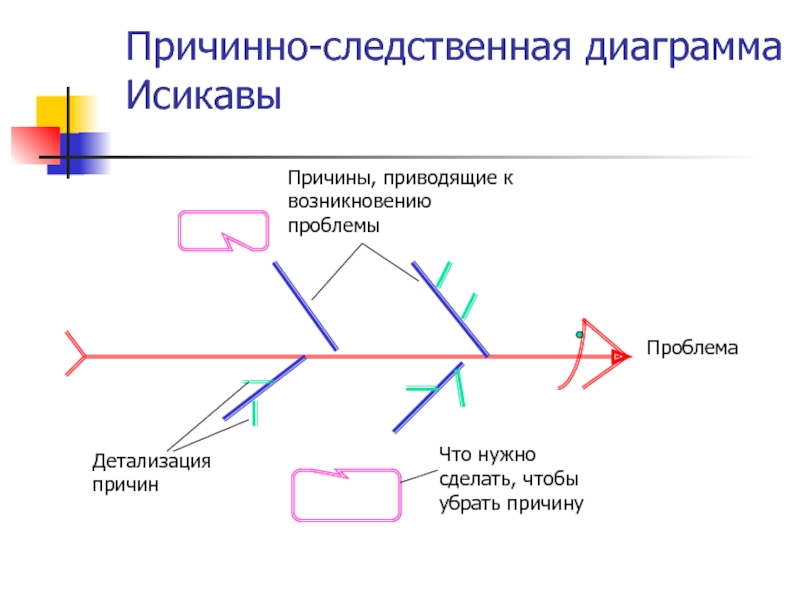 Теперь мы представляем такой метод обнаружения причин, который помогает преодолеть указанную выше дилемму и более надежно оценивает причинные сети на основе данных временных рядов.
Теперь мы представляем такой метод обнаружения причин, который помогает преодолеть указанную выше дилемму и более надежно оценивает причинные сети на основе данных временных рядов.
Графические модели ( 4 , 5 ) — удобный способ представить причинно-следственные связи системы. Хотя сети, изображенные на рис. 1В и 2, легче визуализировать, они не полностью представляют структуру пространственно-временной зависимости, лежащую в основе сложных динамических систем. Графики временных рядов ( 32 — 34 ) обеспечивают более полное представление (см. Рис. 3 и раздел S1 для более подробной информации). Рассмотрим основную зависящую от времени систему Xt = (Xt1,…, XtN) с Xtj = fj (P (Xtj), ηtj) (1), где f j — некоторая потенциально нелинейная функциональная зависимость, а ηtj представляет собой взаимно независимый динамический шум. .Узлы в графе временных рядов представляют переменные Xtj в разное время запаздывания, а P (Xtj) ⊂Xt — = (Xt − 1, Xt − 2,…) обозначает причинных родителей переменной Xtj (рис. 3B, узлы с черные стрелки) среди прошедших всех N переменных. Причинная связь Xt − τi → Xtj существует, если Xt − τi∈P (Xtj). Другой способ определения связей состоит в том, что Xt − τi не является условно независимым от Xtj с учетом прошлого всех переменных, определенных как Xt − τi⫫Xtj∣Xt — ∖ {Xt − τi}, где ⫫ означает отсутствие (условного) независимость ( 34 ).Таким образом, цель обнаружения причин — оценить причинных родителей на основе данных временных рядов. FullCI непосредственно проверяет определяющую связь условную независимость, но помните, что на рис. 3A высокая размерность включения условий N τ max -1, с одной стороны, и уменьшенная величина эффекта из-за кондиционирования на Xt − 11 и Xt-12 (аналогично примеру на фиг. 2), с другой стороны, приводит к потенциально радикально уменьшенной мощности обнаружения FullCI.
Инжир.3 Предлагаемый метод обнаружения причин.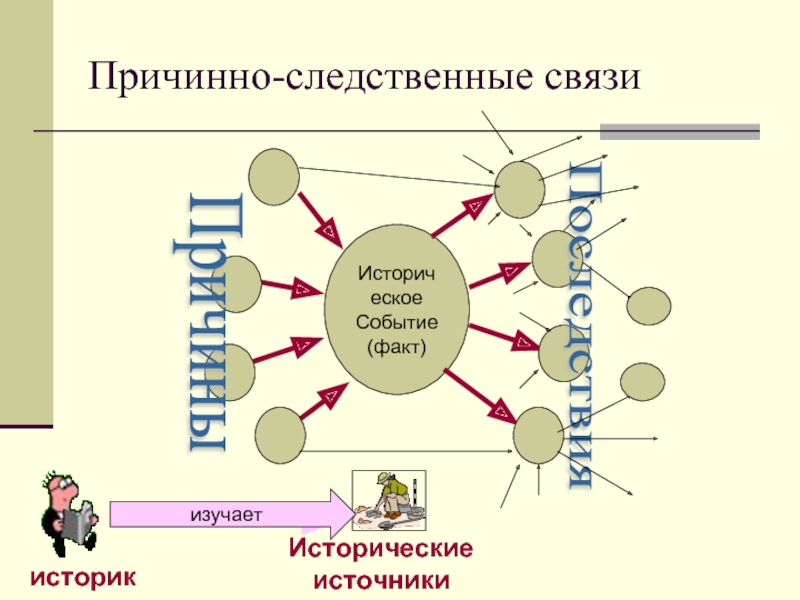
( A ) График временных рядов ( 32 — 34 ), представляющий структуру причинно-следственных зависимостей с запаздыванием по времени, лежащую в основе данных. FullCI проверяет наличие причинной связи с помощью Xt − τi⫫Xtj∣Xt — ∖ {Xt − τi}, где ⫫ обозначает (условную) независимость, а Xt — ∖ {Xt − τi} прошлое всех N переменных вплоть до максимальное запаздывание τ max без учета Xt − τi (серые прямоугольники). ( B ) Иллюстрация ПК 1 алгоритм выбора условий для переменных X 1 (вверху) и X 3 (внизу): алгоритм начинается с инициализации предварительных родителей Pˆ (Xtj) = Xt−.На первой итерации ( p = 0) переменные даже без безусловной зависимости (например, некоррелированные) удаляются из Pˆ (Xtj) (самый светлый оттенок красного и синего соответственно). Во второй итерации ( p = 1) удаляются переменные, которые становятся независимыми, обусловленными драйвером в Pˆ (Xtj) с наибольшей зависимостью в предыдущей итерации. На третьей итерации ( p = 2) удаляются переменные, которые условно независимы от двух самых сильных драйверов, и так далее до тех пор, пока не останется больше условий для проверки в Pˆ (Xtj).Таким образом, PC 1 адаптивно сходится, как правило, только к нескольким релевантным условиям (темно-красный / синий), которые включают причинных родителей P с высокой вероятностью и потенциально некоторые ложные срабатывания (отмечены звездочкой). ( C ) Эти низкоразмерные условия затем используются в тесте условной независимости MCI: для проверки Xt − 21 → Xt3 условия Pˆ (Xt3) (синие прямоугольники) достаточны для установления условной независимости, в то время как дополнительные условия на родители Pˆ (Xt − 21) (красные квадраты) учитывают автокорреляцию и делают MCI оценкой причинной силы.( D ) И PC 1 , и этап MCI можно гибко комбинировать с линейными (ParCorr) или нелинейными (GPDC и CMI) тестами независимости (см. Раздел S4 и таблицу S1). ParCorr предполагает линейные аддитивные модели шума, а GPDC — только аддитивность. Серые точечные графики иллюстрируют регрессии X , Y на Z , а черные точечные графики отображают остатки. Красные кубики в CMI иллюстрируют тест ближайшего соседа k без адаптивной модели к данным ( 44 ), который не требует аддитивности.
Раздел S4 и таблицу S1). ParCorr предполагает линейные аддитивные модели шума, а GPDC — только аддитивность. Серые точечные графики иллюстрируют регрессии X , Y на Z , а черные точечные графики отображают остатки. Красные кубики в CMI иллюстрируют тест ближайшего соседа k без адаптивной модели к данным ( 44 ), который не требует аддитивности.
Теория причинного открытия ( 4 , 5 ) говорит нам, что родители P (Xtj) переменной Xtj являются достаточным набором условий, который позволяет установить условную независимость [каузальное марковское свойство ( 5 )]. Таким образом, в отличие от кондиционирования всего прошлого всех процессов, как в FullCI, для выявления ложных связей достаточно только кондиционирования набора, который, по крайней мере, включает в себя родительские элементы переменной Xtj. Алгоритмы обнаружения Маркова ( 5 , 35 ), такие как алгоритм ПК (названный в честь его изобретателей) ( 25 ), позволяют нам обнаруживать этих родителей и могут быть гибко реализованы с помощью различных видов тестов условной независимости, которые могут учитывать нелинейные функциональные зависимости и переменные, которые являются дискретными или непрерывными.Эти свойства обеспечивают большую гибкость, чем попытки напрямую подогнать, возможно, очень сложные функциональные зависимости в формуле. 1. Однако, как показали наши численные эксперименты, алгоритм ПК не следует напрямую использовать для случая временных рядов.
Предлагаемый нами подход также основан на структуре условной независимости ( 5 ) и адаптирует ее к случаю сильной взаимозависимости временных рядов. Метод, который мы называем PCMCI, состоит из двух этапов: (i) выбор условия PC 1 (рис.3B и алгоритм S1) для определения соответствующих условий Pˆ (Xtj) для всех переменных временного ряда Xtj∈ {Xt1,…, XtN} и (ii) тест на моментальную условную независимость (MCI) (рис. 3C и алгоритм S2) для проверки того, действительно ли Xt − τi → Xtj с MCI: Xt − τi⫫Xtj∣Pˆ (Xtj) ∖ {Xt − τi}, Pˆ (Xt − τi) (2)
Таким образом, условия MCI для обоих родителей Xtj и сдвинутого во времени родители Xt − τi. Два этапа (i) и (ii) служат следующим целям: PC 1 — это алгоритм обнаружения марковского множества, основанный на алгоритме, устойчивом к ПК ( 36 ), который удаляет нерелевантные условия для каждой из переменных N путем итеративное тестирование независимости (показано оттенками красного и синего на рис.3Б). Либеральный уровень значимости α PC в тестах позволяет PC 1 адаптивно сходиться обычно только к нескольким релевантным условиям (темно-красный / синий), которые включают причинных родителей P в уравнении. 1 с высокой вероятностью, но может также включать некоторые ложные срабатывания (отмечены звездочкой на рис. 3B). Затем тест MCI (рис. 3C) обращается к ложноположительному контролю для случая сильно взаимозависимых временных рядов.
Два этапа (i) и (ii) служат следующим целям: PC 1 — это алгоритм обнаружения марковского множества, основанный на алгоритме, устойчивом к ПК ( 36 ), который удаляет нерелевантные условия для каждой из переменных N путем итеративное тестирование независимости (показано оттенками красного и синего на рис.3Б). Либеральный уровень значимости α PC в тестах позволяет PC 1 адаптивно сходиться обычно только к нескольким релевантным условиям (темно-красный / синий), которые включают причинных родителей P в уравнении. 1 с высокой вероятностью, но может также включать некоторые ложные срабатывания (отмечены звездочкой на рис. 3B). Затем тест MCI (рис. 3C) обращается к ложноположительному контролю для случая сильно взаимозависимых временных рядов.
Точнее, в алгоритме PC 1 мы начинаем для каждой переменной Xtj с инициализации предварительных родителей Pˆ (Xtj) = (Xt − 1, Xt − 2,…, Xt − τmax).На первой итерации ( p = 0) мы проводим тесты безусловной независимости и удаляем Xt − τi из Pˆ (Xtj), если нулевая гипотеза Xt − τi⫫Xtj не может быть отклонена на уровне значимости α PC . На рис. 3B для родителей Xt1 это, вероятно, будет иметь место для запаздывающих переменных Xt-τ4 (светлые оттенки красного). На каждой следующей итерации ( p → p + 1) мы сначала сортируем предварительных родителей по их (абсолютному) значению тестовой статистики, а затем проводим тесты условной независимости Xt − τi⫫Xtj∣S, где S — самые сильные p родителей в Pˆ (Xtj) ∖ {Xt − τi}.После каждой итерации независимые родительские элементы удаляются из Pˆ (Xtj), и алгоритм сходится, если больше нельзя проверить условия (см. Подробности в разделе «Материалы и методы»). На рис. 3B для Xt3 (синие оттенки) алгоритм сходится уже после того, как p = 1-мерные условия были протестированы. Поскольку все эти тесты очень низкоразмерны по сравнению с FullCI (или причинно-следственной связью по Грейнджеру), они имеют более высокую способность обнаружения.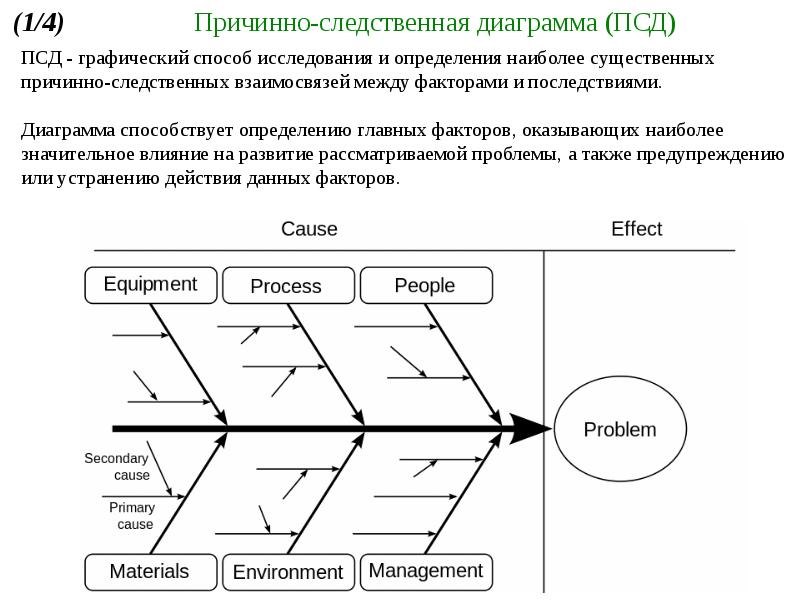
На втором этапе теста MCI (рис. 3C) используются следующие оценочные условия.Для тестирования Xt − 21 → Xt3 условий Pˆ (Xt3) (синие прямоугольники на рис. 3C) достаточно, чтобы установить условную независимость (свойство Маркова), то есть идентифицировать косвенные и общие связи. Дополнительное условие для отстающих родителей Pˆ (Xt − 21) (красные прямоугольники) учитывает автокорреляцию, приводящую к правильно контролируемым ложным срабатываниям на ожидаемом уровне, что дополнительно обсуждается ниже в наших теоретических результатах. Значимость каждой ссылки можно оценить на основе значений P теста MCI.Впоследствии они также могут быть отрегулированы в соответствии с такими процедурами, как контроль частоты ложных обнаружений ( 37 ). Основным свободным параметром PCMCI является уровень значимости α PC в PC 1 , который следует рассматривать как гиперпараметр и выбирать на основе критериев выбора модели, таких как информационный критерий Акаике (AIC) или перекрестный критерий. Проверка. Дополнительные технические подробности можно найти в разделе «Материалы и методы».
Наш метод решает проблему обнаружения топологической структуры причинно-следственных сетей, то есть наличия или отсутствия связей (с разными временными лагами).Следующим вопросом является количественная оценка причинных эффектов, то есть силы причинно-следственных связей, что можно сделать не только в рамках графических причинно-следственных моделей ( 4 , 5 , 38 , 39 ) но также с использованием других структур, таких как структурно-причинное моделирование ( 4 ) или потенциальных результатов ( 3 , 40 ). Три модели эквивалентны ( 41 ), но различаются обозначениями и формулировкой допущений. В разделе «Оценка причинно-следственных связей» мы продемонстрируем, как наш метод обнаружения причинно-следственных связей может быть использован для более надежной оценки причинных эффектов в условиях большой размерности.
Линейные и нелинейные реализации
Как PC 1 , так и этап MCI можно гибко комбинировать с любым видом теста условной независимости. Здесь мы представляем результаты для линейной частичной корреляции (ParCorr) и двух типов нелинейных (GPDC и CMI) тестов независимости (рис. 3D). GPDC основан на гауссовской регрессии процесса ( 42 ) и тесте корреляции расстояний ( 43 ) на остатках, который подходит для большого класса нелинейных зависимостей с аддитивным шумом.CMI — это полностью непараметрический тест, основанный на оценке ближайшего соседа k условной взаимной информации, который учитывает практически любой тип зависимости ( 44 ). Однако недостатком большей универсальности для GPDC или CMI является более низкая мощность для линейных соотношений при наличии малых размеров выборки. Эти тесты условной независимости более подробно рассматриваются в разделе S4 и таблице S1.
Допущения о причинном открытии на основе данных наблюдений
Наш метод и обозначения соответствуют структуре графической причинной модели ( 4 , 5 ).Для причинной интерпретации, основанной исключительно на данных наблюдений, эта структура опирается на стандартные допущения ( 5 ) о причинной достаточности (или необоснованности), подразумевая, что все общие факторы относятся к наблюдаемым переменным, причинно-марковскому условию, подразумевающему, что Xtj равно независимо от Xt− ∖ P (Xtj) с учетом его родителей P (Xtj) и допущения верности, которое требует, чтобы все наблюдаемые условные зависимости возникали из причинной графической структуры. Для данного случая временных рядов мы предполагаем отсутствие одновременных причинных эффектов и, поскольку обычно доступна только одна реализация, мы также предполагаем стационарность.Другой вариант — использовать независимые ансамбли реализаций отстающих процессов. Мы подробно остановимся на этих предположениях в разделе «Обсуждение». См. ( 2 , 34 ) для обзора причинного открытия временных рядов.
РЕЗУЛЬТАТЫ
Теоретические свойства PCMCI
Здесь мы кратко обсуждаем несколько полезных свойств PCMCI, в частности, его вычислительную сложность, согласованность, обычно больший размер эффекта, чем FullCI, и интерпретируемость как причинную силу, как более подробно объясняется в разделе S5.
На этапе выбора условия PCMCI эффективно использует разреженность в причинной сети и имеет сложность в количестве переменных N и максимальном временном лаге τ max , который является полиномиальным. В численных экспериментах мы показываем, что время работы сравнимо или быстрее, чем у современных методов. Согласованность подразумевает, что PCMCI доказуемо оценивает истинный причинный граф в пределе бесконечного размера выборки при стандартных предположениях о причинном обнаружении ( 5 , 34 ), а также в нелинейном случае при условии, что правильный класс критериев условной независимости использовал.В разделе S5.3 мы также подробно разъясняем, почему MCI эмпирически хорошо контролирует ложные срабатывания даже для сильно автокоррелированных переменных, что связано с обусловливанием родителей Pˆ (Xt − τi) запаздывающей переменной. Теоретические результаты для конечных выборок потребуют сильных предположений ( 45 , 46 ) или в большинстве случаев невозможны, особенно для нелинейных ассоциаций. Из-за стадии выбора условий MCI обычно имеет гораздо более низкую размерность кондиционирования, чем FullCI.Кроме того, можно показать, что избегание обусловливания нерелевантных переменных всегда дает больший (или равный) эффект, чем FullCI. Нерелевантные переменные не объясняют причинно-следственные связи, а также могут привести к меньшим размерам эффекта, если они вызваны рассматриваемой переменной-драйвером. Оба этих фактора обычно приводят к гораздо более высокой способности обнаружения, чем FullCI (или причинно-следственная связь по Грейнджеру) для малого и большого количества переменных, как более подробно обсуждается в разделе S5.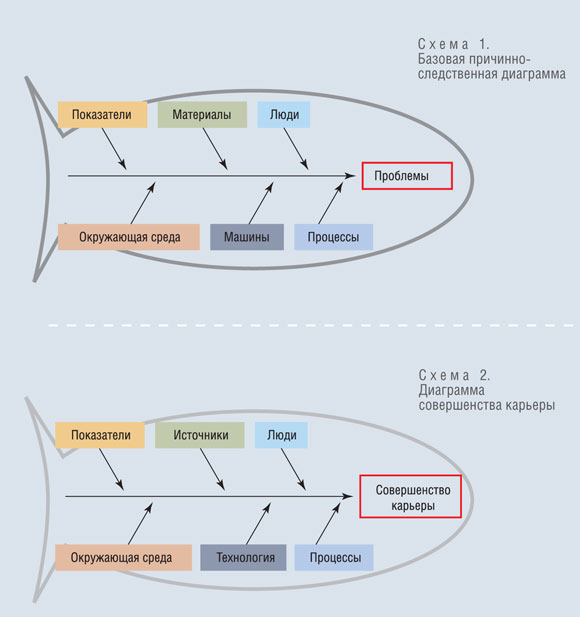 4. Наконец, хотя обнаружение структуры причинно-следственной сети является основной целью PCMCI, статистика теста MCI также дает хорошо интерпретируемое понятие нормализованной причинной силы, что более подробно обсуждается в разделе S5.5 и ( 38 , 39 ). Таким образом, значение статистики MCI (например, частичная корреляция или CMI) позволяет нам значимым образом ранжировать причинные связи в крупномасштабных исследованиях.
4. Наконец, хотя обнаружение структуры причинно-следственной сети является основной целью PCMCI, статистика теста MCI также дает хорошо интерпретируемое понятие нормализованной причинной силы, что более подробно обсуждается в разделе S5.5 и ( 38 , 39 ). Таким образом, значение статистики MCI (например, частичная корреляция или CMI) позволяет нам значимым образом ранжировать причинные связи в крупномасштабных исследованиях.
Реальные приложения
Для проверки методов обнаружения причинно-следственных связей в идеале мы должны иметь наборы данных реального мира с известной базовой истинностью причинных зависимостей. Такие наборы данных редки, особенно из-за причинной взаимозависимости большого числа переменных. Здесь мы анализируем мелкомасштабные климатические и сердечно-сосудистые примеры, в которых лежащие в основе физические механизмы хорошо изучены.В следующем разделе мы также проверяем метод на крупномасштабных синтетических наборах данных, которые имитируют свойства реальных данных. В ( 2 ) представлена платформа тестирования причинно-следственных связей www.causeme.net, которая упрощает оценку методов на растущем массиве синтетических и реальных наборов данных.
Возвращаясь к мотивирующему примеру климата, включающему синтетические переменные (рис. 2, справа), PCMCI эффективно оценивает истинные причинно-следственные связи с высокой степенью мощности во всех трех случаях, в отличие от FullCI.Алгоритм выбора условий PC 1 идентифицирует только релевантные условия и, в частности, обнаруживает, что Z не является родительским элементом BCT. Тогда тест условной независимости MCI для звена Nino t −2 → BCT t имеет такой же размер частичного эффекта корреляции ≈0,10 ( P = 0,036 в случае A) во всех трех случаях (рис. 2, от А до В). Мощность обнаружения составляет> 80% даже для случая большой размерности на рис. 2С. Кроме того, PCMCI правильно оценивает силу причинного эффекта ≈ 0.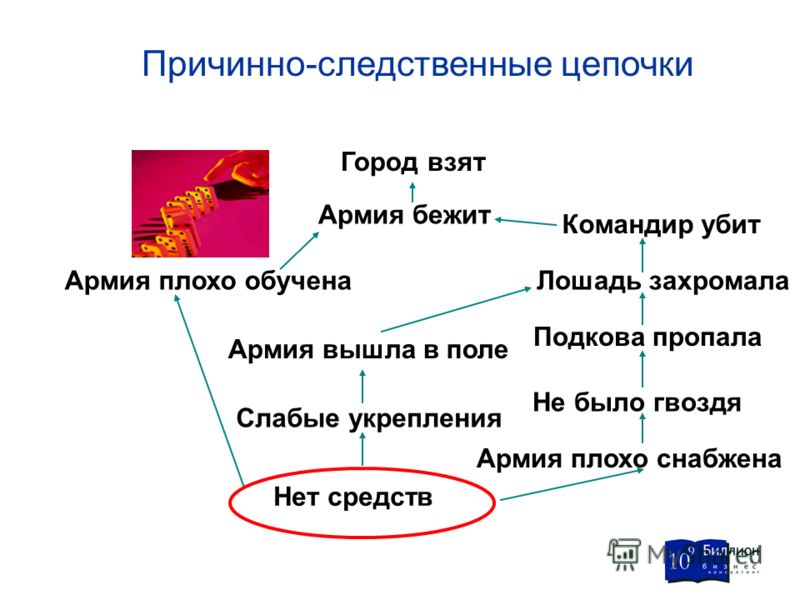 14 среди звеньев Wt-2i-1 → Wti ( i = 2, 4, 6), что приводит к одинаковой мощности обнаружения независимо от различных автокорреляций в разных временных рядах W i .
14 среди звеньев Wt-2i-1 → Wti ( i = 2, 4, 6), что приводит к одинаковой мощности обнаружения независимо от различных автокорреляций в разных временных рядах W i .
На рис. 4A мы показываем, что PCMCI может реконструировать циркуляцию Уокера ( 47 ) в тропической части Тихого океана, включая связь с Атлантикой, где лежащий в основе физический механизм теоретически хорошо изучен и подтвержден с помощью подробных экспериментов по физическому моделированию. ( 48 ): аномалии теплой приземной температуры воздуха в восточной части Тихого океана (EPAC) переносятся пассатами на запад через центральную часть Тихого океана (CPAC).Затем влажный воздух поднимается над западной частью Тихого океана (WPAC), и циркуляция закрывается прохладным и сухим воздухом, опускающимся на восток через всю тропическую часть Тихого океана. Кроме того, регион CPAC связывает температурные аномалии с тропической Атлантикой (ATL) через атмосферный мост ( 49 ). Чистый лаговый корреляционный анализ приводит к полностью связанному графику со значительными корреляциями почти во всех временных лагах (см. Функции лагов на рис. S3), в то время как PCMCI с линейным тестом условной независимости ParCorr лучше идентифицирует циркуляцию Уокера и атлантическую телесвязь.В частности, связь от EPAC к WPAC правильно определяется как косвенно опосредованная через CPAC.
Рис. 4 Реальные приложения. ( A ) Тропический климат. Пример зависимостей между месячными аномалиями приземного давления за 1948–2012 гг. ( T = 780 месяцев) в западной части Тихого океана (WPAC; регионы обозначены заштрихованными прямоугольниками под узлами), а также температурой приземного воздуха. аномалии в Центральной (CPAC) и восточной части Тихого океана (EPAC), а также в тропической Атлантике (ATL) ( 65 ).Левая панель показывает корреляцию (Corr), а правая панель показывает PCMCI в реализации ParCorr с τ max = 7 месяцев, чтобы также фиксировать большие временные задержки. Значимость оценивалась на строгом уровне 1%. ( B ) Сердечно-сосудистый пример связи между частотой сердечных сокращений (B) и диастолическим (D) и систолическим (S) артериальным давлением ( T = 600) 13 здоровых беременных женщин. Левая панель показывает MI, а правая панель показывает PCMCI в реализации CMI с τ max = 5 сердечных сокращений и параметрами по умолчанию k CMI = 60 и k perm = 5 (см. Таблицу S1) .Графики получены путем анализа PCMCI отдельно для 13 наборов данных и отображения только ссылок, значимых на уровне 1%, по крайней мере, для 80% субъектов. На всех панелях цвета узлов отображают силу самозависимости, а цвета краев — силу поперечных связей с запаздыванием с максимальным абсолютным значением. См. Функции задержки на рис. S3 и Материалы и методы для получения более подробной информации о наборах данных. Обратите внимание на разные шкалы цветовых полос.
Значимость оценивалась на строгом уровне 1%. ( B ) Сердечно-сосудистый пример связи между частотой сердечных сокращений (B) и диастолическим (D) и систолическим (S) артериальным давлением ( T = 600) 13 здоровых беременных женщин. Левая панель показывает MI, а правая панель показывает PCMCI в реализации CMI с τ max = 5 сердечных сокращений и параметрами по умолчанию k CMI = 60 и k perm = 5 (см. Таблицу S1) .Графики получены путем анализа PCMCI отдельно для 13 наборов данных и отображения только ссылок, значимых на уровне 1%, по крайней мере, для 80% субъектов. На всех панелях цвета узлов отображают силу самозависимости, а цвета краев — силу поперечных связей с запаздыванием с максимальным абсолютным значением. См. Функции задержки на рис. S3 и Материалы и методы для получения более подробной информации о наборах данных. Обратите внимание на разные шкалы цветовых полос.
От системы Земля обратимся к человеческому сердцу на рис.4Б. Мы исследуем временные ряды частоты сердечных сокращений (B), а также диастолического (D) и систолического (S) артериального давления у беременных здоровых женщин ( 50 , 51 ). Хорошо известно, что частота сердечных сокращений влияет на ударный объем сердца, который, в свою очередь, влияет на диастолическое артериальное давление (закон Старлинга). Кроме того, механизм, посредством которого диастолическое кровяное давление управляет систолическим кровяным давлением, является эффектом ударного объема, соответствующего пульсового давления и общего периферического сопротивления ( 52 ).Здесь мы не можем предполагать линейные взаимозависимости и, таким образом, использовать теоретико-информационную реализацию CMI PCMCI. Используя взаимную информацию (MI), мы получаем только полносвязный граф, в то время как физиологически вероятная причинная цепочка B → D → S правильно реконструируется с помощью PCMCI.
Эти примеры для относительно небольшого количества переменных показывают, как обнаружение причин с помощью PCMCI помогает идентифицировать физические механизмы из временных рядов. Как подробно описано в Обсуждении, поскольку этот анализ обычно не может предполагать, что не существует каких-либо ненаблюдаемых общих драйверов, следует проявлять осторожность с причинной интерпретацией прямых связей.С другой стороны, отсутствие прямых связей действительно может быть интерпретировано как отсутствие прямых причинно-следственных связей при более слабых предположениях, например, в случае таковых от EPAC к WPAC и от частоты сердечных сокращений к систолическому артериальному давлению.
Настройка модели для экспериментов с многомерными синтетическими данными
Следуя нашим иллюстративным примерам, мы более систематически оцениваем и сравниваем производительность PCMCI вместе с другими распространенными причинными методами в численных экспериментах, которые имитируют свойства реальных данных.Здесь мы моделируем шесть основных проблем временных рядов для сложных систем: высокая размерность, причинно-следственные зависимости с запаздыванием по времени, автокорреляция, сильная нелинейность, шум наблюдений и нестационарность ( 2 ). На рисунке 5A приведен пример модели для N = 10 переменных, где цвета краев обозначают (положительный или отрицательный) коэффициент, соответствующий причинно-следственным связям, а цвет узла отображает силу автокорреляции. На рисунке 5B показана реализация временного ряда, иллюстрирующая некоторые сильно автокоррелированные переменные.Мы создаем ряд моделей с различными случайными топологиями сети с переменными временного ряда N , причем каждая сеть имеет L = N линейных или нелинейных причинно-следственных зависимостей (за исключением двумерного случая N = 2 с L = 1). На основе каждой из этих моделей мы генерируем 100 наборов данных временных рядов (каждый длиной T ) для оценки истинных и ложноположительных результатов отдельных причинно-следственных связей в модели с использованием различных причинных методов. Как показано на рис.5A, прямоугольные диаграммы на следующих рисунках показывают распределение этих индивидуальных коэффициентов ложноположительных и истинно положительных ссылок по большому количеству случайных сетей, для каждого размера сети N , дифференцированных между слабо и сильно автокоррелированными парами переменных слева и правые прямоугольные диаграммы, соответственно (определяемые средней автокорреляцией обеих переменных меньше или больше 0,7). Здесь мы отображаем результаты только для перекрестных ссылок, а не для автоматических ссылок внутри переменной.Полная настройка модели подробно описана в разделе S6, в таблице S2 перечислены экспериментальные настройки, а в разделе S2 и таблице S3 приведены подробные сведения о сравниваемых методах.
Как показано на рис.5A, прямоугольные диаграммы на следующих рисунках показывают распределение этих индивидуальных коэффициентов ложноположительных и истинно положительных ссылок по большому количеству случайных сетей, для каждого размера сети N , дифференцированных между слабо и сильно автокоррелированными парами переменных слева и правые прямоугольные диаграммы, соответственно (определяемые средней автокорреляцией обеих переменных меньше или больше 0,7). Здесь мы отображаем результаты только для перекрестных ссылок, а не для автоматических ссылок внутри переменной.Полная настройка модели подробно описана в разделе S6, в таблице S2 перечислены экспериментальные настройки, а в разделе S2 и таблице S3 приведены подробные сведения о сравниваемых методах.
( A ) Полная настройка модели описана в разделе S6 и таблице S2. Всего случайным образом было создано 20 топологий связи для каждого размера сети N , где все коэффициенты перекрестной связи фиксированы, а переменные имеют разные автокорреляции.Показан пример сети для N = 10 с цветами узлов, обозначающими силу автокорреляции, а цвета стрелок обозначают силу коэффициента (положительную или отрицательную). Ширина стрелки показывает степень обнаружения конкретного метода. Как указано здесь, прямоугольные диаграммы на рисунках ниже показывают распределение уровней обнаружения по отдельным ссылкам, причем левый (правый) прямоугольный график изображает связи между парами слабо (сильно) автокоррелированных переменных, определяемых средней автокорреляцией обеих переменных, которая меньше или больше, чем 0.7. ( B ) Пример реализации временного ряда модели, изображающей частично сильно автокоррелированные переменные. Эффективность каждого метода оценивалась на 100 таких реализациях для каждой случайной сетевой модели. ( C ) Производительность различных методов для моделей с линейными отношениями с длиной временного ряда T = 150. В таблице S3 представлены детали реализации. В нижнем ряду показаны пары диаграмм (для слабо и сильно автокоррелированных переменных) распределений ложных срабатываний, а в верхнем ряду показаны распределения истинных срабатываний для различных размеров сети N вдоль оси x на каждом графике.Среднее время выполнения и его стандартное отклонение указаны сверху. ( D ) Численные эксперименты для реализации нелинейного GPDC с T = 250, где dCor обозначает корреляцию расстояний. ( E ) Результаты для реализации CMI с T = 500, где MI обозначает взаимную информацию. На обеих панелях мы различаем линейные и два типа нелинейных связей (верхние три строки). См. Таблицу S2 для настройки модели и раздел S4 и таблицу S1 для описания нелинейных тестов условной независимости.
В таблице S3 представлены детали реализации. В нижнем ряду показаны пары диаграмм (для слабо и сильно автокоррелированных переменных) распределений ложных срабатываний, а в верхнем ряду показаны распределения истинных срабатываний для различных размеров сети N вдоль оси x на каждом графике.Среднее время выполнения и его стандартное отклонение указаны сверху. ( D ) Численные эксперименты для реализации нелинейного GPDC с T = 250, где dCor обозначает корреляцию расстояний. ( E ) Результаты для реализации CMI с T = 500, где MI обозначает взаимную информацию. На обеих панелях мы различаем линейные и два типа нелинейных связей (верхние три строки). См. Таблицу S2 для настройки модели и раздел S4 и таблицу S1 для описания нелинейных тестов условной независимости.
Высокая размерность с линейными отношениями
На рис. 5C мы сначала исследуем эффективность линейных методов обнаружения причин в численных экспериментах с линейными причинными связями; нелинейные модели показаны на рис. 5 (D и E). Установка имеет длину выборки T = 150 наблюдений и N = 2,…, 100 переменных. Все поперечные связи имеют одинаковое абсолютное значение коэффициента связи (но с разными знаками) и, следовательно, одинаковую причинную силу. Наряду с корреляцией (Corr) и FullCI (аналогично причинно-следственной связи Грейнджера, здесь реализованной с помощью эффективной векторно-авторегрессионной модели оценки) мы сравниваем PCMCI с исходным алгоритмом ПК в качестве автономного метода и регрессии Лассо (псевдокод, указанный в алгоритме S3). как наиболее широко используемый представитель регуляризованных методов многомерной регрессии, которые можно использовать для выбора причинных переменных.Таблица S3 дает обзор сравниваемых методов, а детали реализации альтернативных методов приведены в разделе S2. Максимальное запаздывание составляет τ max = 5, а уровень значимости составляет 5% для всех методов.
Корреляция явно недостаточна для обнаружения причин с очень высокой частотой ложноположительных результатов (первый столбец на рис. 5C). Тем не менее, даже уровни обнаружения для истинных ссылок сильно различаются: некоторые ссылки имеют менее 20% истинных положительных результатов, несмотря на одинаковую силу коэффициентов для всех причинно-следственных связей.Этот противоречивый результат дополнительно исследуется на рис. 6. Напротив, все каузальные методы контролируют ложные срабатывания в пределах или ниже выбранного уровня значимости 5% с помощью Лассо и алгоритма ПК, избыточного контроля с более низкими, чем ожидалось, уровнями. Исключением здесь являются некоторые сильно автокоррелированные ссылки, которые неправильно контролируются алгоритмом ПК (усы, увеличивающиеся до 25% ложных срабатываний на рис. 5C), поскольку он не имеет надлежащего отношения к случаю временных рядов.
Инжир.6 Численные эксперименты по оценке причинно-следственных связей.Показана мощность обнаружения (верхняя строка) и размер причинного эффекта (нижняя строка), заданные одномерной линейной регрессией (CE-Corr), многомерной регрессией для всего прошлого многомерного процесса (CE-Full) и многомерной регрессией только для родители, полученные с помощью PCMCI (CE-PCMCI) для различных сил коэффициента связи c вдоль оси x на каждом участке. Последний столбец обозначает регрессию истинных родителей (CE-True).В нижнем ряду оранжевые оттенки показывают квантили 1, 25, 75 и 99% и медианное значение соответствующих причинных эффектов всех ссылок (в среднем более 100 реализаций для каждой ссылки), а черная линия обозначает истинный причинный эффект. сила | c |, который одинаков для всех ссылок в модели.
В то время как FullCI имеет мощность обнаружения около 80% для N = 5, эта скорость падает до 40% для N = 20, и FullCI больше не может применяться для больших N , когда размерность больше, чем размерность размер выборки ( N τ max > T = 150). Однако для N = 5 также некоторые связи между сильно автокоррелированными переменными имеют уровень обнаружения всего 60%. Лассо в среднем имеет более высокую мощность обнаружения, чем FullCI, и может применяться также к высокоразмерному корпусу N τ max > T . Алгоритм ПК не показывает большой разницы в мощности обнаружения между N = 5 и N = 100, но скорости ниже, чем в среднем для лассо, и более высокая автокорреляция здесь также имеет пагубный эффект.Обратите внимание, что здесь сложно сравнивать уровни мощности, поскольку лассо и ПК не могут быть легко откалиброваны для получения ожидаемого уровня значимости.
Однако для N = 5 также некоторые связи между сильно автокоррелированными переменными имеют уровень обнаружения всего 60%. Лассо в среднем имеет более высокую мощность обнаружения, чем FullCI, и может применяться также к высокоразмерному корпусу N τ max > T . Алгоритм ПК не показывает большой разницы в мощности обнаружения между N = 5 и N = 100, но скорости ниже, чем в среднем для лассо, и более высокая автокорреляция здесь также имеет пагубный эффект.Обратите внимание, что здесь сложно сравнивать уровни мощности, поскольку лассо и ПК не могут быть легко откалиброваны для получения ожидаемого уровня значимости.
PCMCI устойчиво демонстрирует высокую мощность обнаружения даже для сетей с размерами, превышающими размер выборки, и отображает почти одинаковую мощность для каналов с одинаковым причинным эффектом, независимо от того, являются ли автокорреляции слабыми или сильными, до N = 20.
Ковариационный анализ (ANCOVA) был проведен для более количественного исследования зависимости мощности обнаружения и ложных срабатываний от количества переменных N и размера выборки T (см. Раздел S6, рис.S17 и таблицы с S9 по S12). Это показывает, что FullCI действительно имеет самое сильное снижение, а PCMCI и Lasso имеют одинаковое снижение способности обнаружения для большего числа переменных N , при этом PCMCI немного превосходит Lasso для меньшего N . Точно так же PCMCI выигрывает немного больше, чем Lasso, от более крупных размеров выборки. Эффекты взаимодействия ANCOVA, касающиеся скоростей обнаружения между различными уровнями N, и T , присутствуют как для FullCI, так и для PCMCI, где мощность уменьшается менее сильно с N для больших размеров выборки.Лассо и алгоритм ПК не влияют на эффективность обнаружения. Для ложноположительных результатов мы не наблюдали соответствующей зависимости FullCI и PCMCI ни от N , ни от T , в то время как PC и Lasso имеют понижающиеся уровни для больших N , как отмечалось выше, и не сильно меняются для разных T .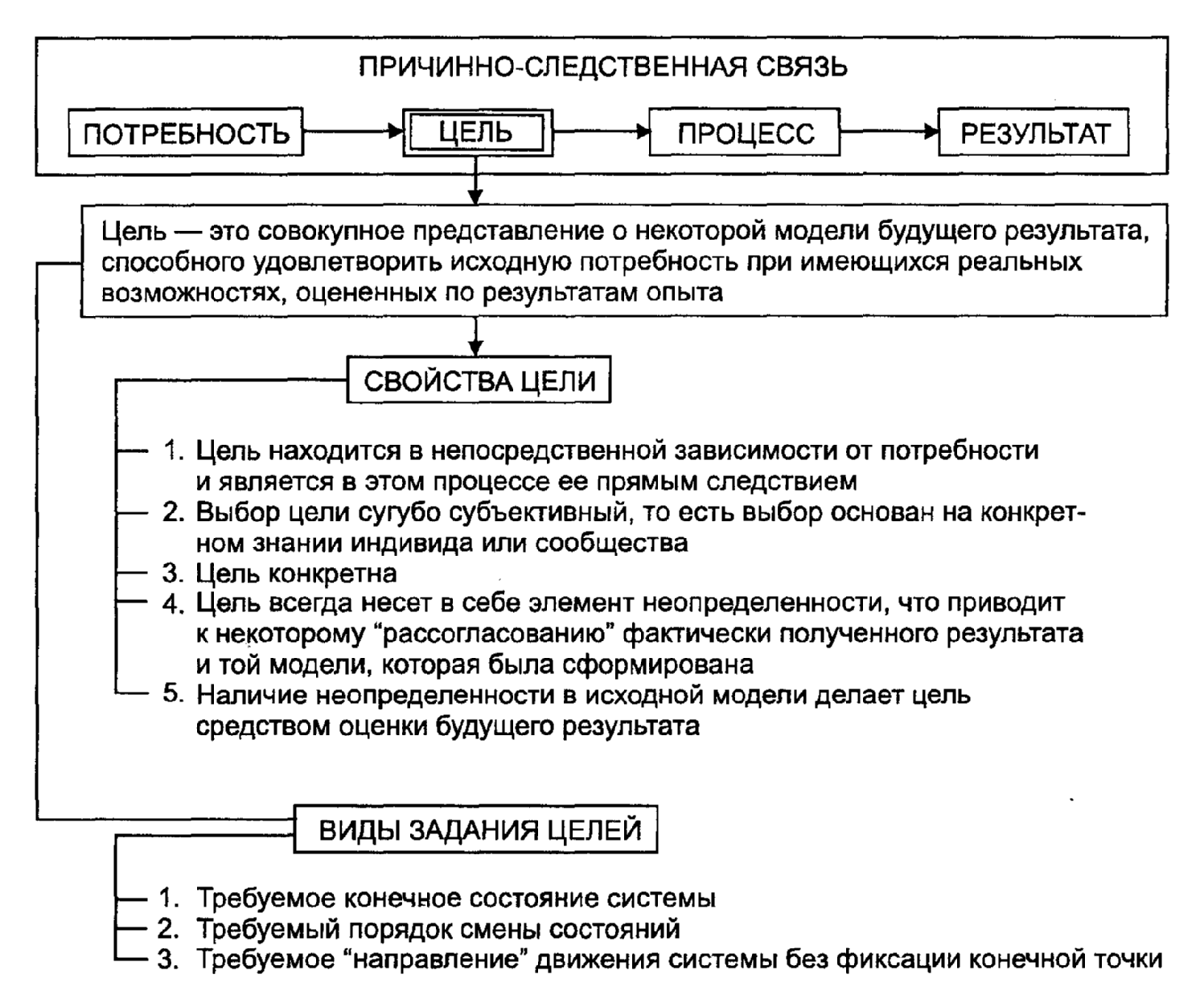
Время выполнения зависит от деталей реализации, но все методы имеют один и тот же порядок величины, за исключением FullCI, который был оценен с помощью эффективного решателя в этом линейном случае.Для нелинейных реализаций он может быть намного медленнее, чем PCMCI или ПК (см. Следующий раздел). PCMCI эффективно использует разреженность. Наши численные эксперименты показывают, что для небольших сетей PCMCI быстрее, чем Lasso, и наоборот для более крупных сетей, но обе имеют одинаковое время работы для более крупных T (рис. S16 и таблицы S4 — S7). Большая часть времени PCMCI тратится на этап выбора условий, в основном из-за оптимизации гиперпараметров α PC через AIC в показанной реализации.Исправление α PC происходит намного быстрее и по-прежнему дает хорошие результаты (рис. S4 и S16), но также может не контролировать ложные срабатывания. Время выполнения алгоритма автономного ПК сильно зависит от количества протестированных наборов условий. Теоретически тестируются все комбинации комплектов кондиционирования, что приводит, наряду с низким энергопотреблением, к медленному и сильно изменяющемуся времени выполнения, особенно для нелинейных реализаций (рис. S16), но здесь мы ограничили количество комбинаций (см. Раздел S2). . В этих линейных численных экспериментах PC по-прежнему работает быстрее, чем PCMCI, поскольку оптимизация гиперпараметров не проводилась, в то время как для нелинейных реализаций он часто медленнее (см. Следующий раздел).
Таким образом, наш ключевой результат заключается в том, что PCMCI имеет высокую мощность даже для размеров сетей, размерность которых равна N τ max , что превышает размер выборки. Средние уровни мощности (отмечены «x» на рис. 5C) выше, чем у FullCI (или причинности по Грейнджеру) и ПК для всех рассматриваемых размеров сети. PCMCI имеет аналогичные или более высокие уровни средней мощности по сравнению с Lasso, но важным отличием является производительность в худшем случае: даже для небольших сетей ( N = 10) значительная часть каналов постоянно игнорируется с помощью Lasso, в то время как для PCMCI , 99% ссылок имеют мощность обнаружения более 70%.
Высокая размерность с нелинейными связями
На рис. 5 (D и E) показаны результаты для нелинейных моделей, где мы различаем линейные и два типа нелинейных связей [верхние три строки, T = 250 (D) и T = 500 (E)]. По сути, здесь мы обнаруживаем, что способность PCMCI избегать высокой размерности даже более критична не только для мощности обнаружения, но и для правильного контроля ложных срабатываний.
На рис. 5D, FullCI, PC и PCMCI реализованы с помощью теста условной независимости GPDC, а dCor обозначает корреляцию расстояния как нелинейный аналог корреляции (см. Раздел S4 и таблицу S1).Одна только корреляция расстояния обнаруживает нелинейные связи, но не учитывает косвенные или общие эффекты драйверов, что приводит к большому количеству ложных срабатываний, особенно для сильной автокорреляции. FullCI здесь хорошо работает только до N = 5, но больше не может контролировать ложные срабатывания для N ≥ 10, поскольку тест GPDC не работает хорошо в этих высоких измерениях [см. Также анализ дисперсии (ANOVA) в таблицах S6 и S7]. ПК снова чрезмерно контролирует ложные срабатывания (за исключением сильной автокорреляции) и имеет самые низкие уровни мощности среди всех методов.PCMCI имеет самые высокие уровни мощности, которые лишь немного снижаются для больших сетей. Здесь мы обнаруживаем, что для нелинейных зависимостей слабые и сильно автокоррелированные связи также приводят к разным уровням мощности, в отличие от линейных связей (см. Раздел S5.5). Ложные срабатывания в основном контролируются правильно, но существует небольшое увеличение количества ложных срабатываний для более крупных сетей, опять же, потому что даже при выборе условий размерность увеличивается для более крупных сетей, а GPDC плохо работает в больших размерностях.Для GPDC время выполнения для ПК и PCMCI больше, чем для FullCI.
На рисунке 5E показаны результаты для полностью непараметрической реализации с CMI. Кроме того, у FullCI самое медленное время работы и почти нет энергии, особенно для нелинейных каналов, в то время как PCMCI правильно контролирует ложные срабатывания и в среднем имеет более высокую мощность, чем ПК. Тем не менее, сильные нелинейности трудно обнаружить для рассмотренных здесь случаев относительно большой размерности и с T = 500 выборок.
Тем не менее, сильные нелинейности трудно обнаружить для рассмотренных здесь случаев относительно большой размерности и с T = 500 выборок.
Дальнейшие эксперименты
В дополнительных материалах мы исследуем некоторые дополнительные методологические варианты (см. Разделы S2 и S3) и показываем, что наши результаты устойчивы также для больших размеров выборки (рис.S4, S5, S9, S11 и S13 и таблицы S4, S6 и S7) и более высокие плотности сетевого взаимодействия (рис. S6 и S7, а также таблица S5). Далее, мы исследуем влияние нарушений основных теоретических предположений, в частности, наблюдаемого шума, нестационарности и неверных процессов, последние представлены сильно нелинейными, чисто детерминированными зависимостями.
Все методы демонстрируют аналогичную чувствительность к шуму наблюдений, при этом PCMCI и Lasso подвержены немного большему влиянию, чем FullCI, согласно анализу ANOVA (рис.S14 и таблица S8) с уровнями до 25% динамического шума SD, оказывающего лишь незначительное влияние. Для уровней того же порядка, что и динамический шум, мы наблюдаем более сильную деградацию, а также неправильное управление ложными срабатываниями, за исключением FullCI, поскольку общие драйверы больше не обнаруживаются должным образом. См. ( 34 ) обсуждение шума наблюдений.
На рис. S15 и таблица S8, мы исследуем влияние нестационарного тренда, здесь моделируемого добавленным синусоидальным сигналом с разными амплитудами.Лассо особенно чувствителен здесь и имеет как более низкую мощность обнаружения, так и завышенную частоту ложных срабатываний, в то время как PCMCI устойчив даже для высоких амплитуд трендов.
Последняя, на рис. S18, мы изучаем влияние сильных общих драйверов для низкоразмерных детерминированных хаотических систем. Чисто детерминированные системы могут нарушать достоверность, поскольку они могут отображать переменные, связанные истинной причинно-следственной связью, как независимые по условию от другой переменной, которая полностью определяет любую из них. Метод, основанный на нелинейной динамике ( 15 , 53 ), адаптированный к этим системам, — это конвергентное перекрестное отображение (CCM; см. Раздел S2.4) ( 14 ), который мы здесь сравниваем с PCMCI в реализации CMI. Мы обнаружили, что для чисто детерминированных зависимостей (рис. S18, A и C) CCM имеет более высокие уровни обнаружения, которые ухудшаются только при очень сильной силе связи. PCMCI не очень подходит для систем с высокой степенью детерминированности, поскольку он сильно зависит от прошлого системы драйверов и, следовательно, удаляет большую часть информации, которая может быть измерена в системе отклика. Если мы исследуем ту же систему, управляемую динамическим шумом, то частота обнаружения PCMCI сильно возрастет и превзойдет CCM (рис.S18, B и D). Преимущество PCMCI в том, что он лучше контролирует ложные срабатывания, чем CCM, который может иметь очень высокие и неконтролируемые уровни ложных срабатываний. Обратите внимание, что для проверки причинно-следственной связи X → Y CCM использует только временные ряды X и Y с исходным предположением, что динамика общего драйвера может быть восстановлена с использованием встраивания задержки. См. ( 34 ) для более глубокого изучения.
Оценка причинных эффектов
В этом разделе мы покажем, как предлагаемый нами метод может быть использован для более точной количественной оценки причинных эффектов, предполагая наличие линейных зависимостей.В разделе «Обсуждение» мы рассматриваем различные способы более общей количественной оценки причинной силы. Но сначала мы кратко обсудим различные, но эквивалентные ( 41 ) теоретические основы вывода причинно-следственных связей. В рамках графической причинно-следственной модели ( 4 ) причинный эффект связи Xt − τi → Xtj основан на интервенционном распределении P (Xtj∣do (Xt − τi = x)), которое является распределением вероятностей Xtj в момент времени t , если Xt − τi был вынужден экзогенно иметь значение x .Причинно-следственные эффекты также могут быть изучены с использованием структуры потенциальных результатов ( 3 ), которая в основном ориентирована на социальные науки и медицину. В этой схеме причинно-следственные эффекты могут быть определены как разница между двумя потенциальными исходами: один, когда субъект и получил лечение, обозначается Y и ( X = 1), и второй, когда лечение не проводилось. дано, обозначено Y u ( X = 0). При наблюдении причинно-следственных связей, Y u ( X = 1) и Y u ( X = 0) никогда не измеряются одновременно (один объект нельзя лечить и не лечить одновременно), требуется предположение, называемое сильным игнорированием, для определения причинных эффектов.В нашем случае можно было бы записать Xtj как Xtj (Xt−), где время t заменяет единицу u и где нас интересует проверка, появляется ли запись Xt − τi в Xt− в функции обработки, определяющей причинное влияние из прошлого.
Как в структуре причинно-следственных связей Перла, так и в структуре потенциальных результатов ( 3 ), обычно предполагается, что структура причинной взаимозависимости известна качественно (наличие и отсутствие связей), и интерес больше заключается в количественной оценке причинных эффектов.В случае линейных непрерывных переменных средний причинный эффект и, что эквивалентно, потенциальный результат для Xt − τi → Xtj можно оценить на основе данных наблюдений с помощью линейной регрессии с использованием подходящего набора регрессоров для корректировки. Далее мы предполагаем причинную достаточность и сравниваем три подхода для оценки линейного причинного эффекта, когда истинная структура причинной взаимозависимости неизвестна. CE-Corr — это просто одномерная линейная регрессия Xtj на Xt − τi, CE-Full — это многомерная регрессия Xtj на всем прошлом многомерного процесса Xt− до максимального временного запаздывания τ max = 5 и, наконец, , CE-PCMCI — это многомерная регрессия Xtj только для родителей P (Xtj), полученных с помощью PCMCI.
На рис. 6 мы исследуем эти подходы численно. В отличие от предыдущей настройки модели, мы теперь фиксируем размер сети N = 20 переменных временного ряда ( T = 150) и рассматриваем модели с разными коэффициентами связи c (ось x на рис. 6). На нижних панелях показано распределение причинно-следственных связей. Абсолютное значение истинного причинного эффекта составляет c ∣ (черные линии). На верхних панелях показано распределение истинно-положительных показателей (по всем ссылкам в модели) для теста F при нулевой гипотезе о том, что эффект равен нулю при уровне значимости 5%.На крайних правых панелях показаны результаты регрессии по истинным родителям (CE-True).
Значения CE-Corr для линий с одинаковым причинным эффектом охватывают весь диапазон от нуля до значений сильного воздействия, указывая на то, что CE-Corr не имеет отношения к силе причинного эффекта. Некоторые значения CE-Corr намного меньше и даже стремятся к нулю, что свидетельствует о наблюдении на рис.5, что способность обнаружения корреляции (или других безусловных показателей dCor и MI) может, как ни странно, даже быть ниже, чем у FullCI или PCMCI.Распределение значений CE-Full сосредоточено вокруг истинного причинного эффекта, как и ожидалось, поскольку Xt− включает истинных родителей в качестве достаточного набора корректировок. Однако высокая размерность этого набора корректировок приводит к большой дисперсии оценки, что, в частности, означает, что причинные эффекты оцениваются менее надежно, о чем свидетельствуют низкие показатели истинно-положительных результатов в верхней панели. Наконец, CE-PCMCI лучше оценивает причинные эффекты и даже приближается к уровню обнаружения CE-True на основе истинных родителей.Хотя родители являются достаточным набором корректировок для оценки причинно-следственных связей, другие наборы корректировок могут дать даже более точные оценки, но в любом случае знание структуры зависимостей, оцененной с помощью PCMCI, является полезным ( 54 ).
ОБСУЖДЕНИЕ И ЗАКЛЮЧЕНИЕ
Причинное открытие в крупномасштабных наборах данных временных рядов сталкивается с дилеммой: включение большего количества переменных делает анализ более достоверным в отношении причинной интерпретации, но если добавленные переменные не имеют значения, то есть не объясняют причинно-следственные связи отношения, они не только увеличивают размерность, но также могут привести к меньшим размерам эффекта, в частности, если они вызваны рассматриваемой переменной драйвера.Оба эти фактора приводят к снижению мощности и повышают риск того, что важные истинные причинно-следственные связи будут упущены. Более того, некоторые нелинейные тесты больше не контролируют даже ложные срабатывания в больших измерениях.
Наш метод решает эту проблему за счет этапа выбора условий для удаления нерелевантных переменных и проверки условной независимости, разработанной для сильно взаимозависимых временных рядов. Первый улучшает уровни мощности для крупномасштабного анализа причинно-следственных связей, в то время как последний также дает больше возможностей, чем классические методы при анализе с участием всего лишь нескольких переменных, что подразумевает улучшенное «причинное отношение сигнал / шум».В то же время тест MCI демонстрирует правильно контролируемую частоту ложных срабатываний даже для сильно автокоррелированных данных временных рядов. Наши численные эксперименты показывают, что PCMCI имеет значительно более высокую способность обнаружения, чем известные методы, такие как лассо, алгоритм ПК или причинно-следственная связь по Грейнджеру и ее нелинейные расширения для наборов данных временных рядов от десятков до сотен переменных. Дальнейшие эксперименты показывают, что PCMCI устойчив к нестационарным тенденциям, и все методы имеют одинаковую чувствительность к шуму наблюдений.PCMCI не очень подходит для систем с высокой степенью детерминированности, где на каждом временном шаге генерируется не так много новой информации. В этих случаях метод пространства состояний давал более высокую мощность обнаружения; однако мы также обнаружили, что он плохо контролирует ложные срабатывания. PCMCI позволяет использовать большое количество тестов условной независимости, адаптированных к различным типам данных (см. Раздел S4), например, дискретным или непрерывным временным рядам.
Наш анализ причинно-следственных связей показал, что более надежное знание причинно-следственной сети также способствует более точной оценке силы причинно-следственных связей.Существуют разные подходы к количественной оценке причинной силы: от теоретико-информационного ( 39 , 55 — 58 ) до основанных на модели показателей, таких как коэффициенты линейной регрессии ( 21 , 38 ), как показано в причинно-следственный анализ. Сама статистика теста MCI может быть интерпретирована как мера причинной силы ( 39 , 55 ), что позволяет нам напрямую ранжировать причинные связи в поисковых исследованиях PCMCI на больших наборах данных с множеством временных рядов значимым образом.Эти рейтинги могут помочь определить наиболее сильные предполагаемые причинно-следственные связи, которые могут представлять основной интерес в контексте некоторых доменов. Наряду с оценкой причинно-следственной связи отдельных звеньев оценочная причинно-следственная сеть также может использоваться для определения причинно-следственных связей и оценки совокупных показателей причинного влияния отдельных переменных ( 38 , 39 , 58 ).
В настоящее время наш метод фокусируется на зависимостях с запаздыванием по времени и предполагает стационарные данные, а причинная интерпретация основывается, что наиболее важно, на предположении о причинной достаточности.Это имеет несколько важных последствий для практического использования PCMCI: Для зависимостей с запаздыванием во времени нет двусмысленности в терминах направленности причинно-следственных связей, то есть ориентации причинных границ. В последнее время появляется все больше литературы, посвященной выводу причинности без опоры на временные лагы ( 59 , 60 ), что может помочь определить причинную направленность одновременных связей.
Допущение о стационарности может быть нарушено в реальных временных рядах, например, из-за очевидных факторов, вызывающих затруднения, таких как сезонный цикл или различные динамические режимы, лежащие в основе временных рядов климата.На практике временные ряды часто можно сделать стационарными, удалив или отфильтровав эти влияния или ограничив анализ той частью временного ряда, где можно предположить стационарность. По сути, эти два подхода используют некоторые базовые знания о причине нестационарности. Если, однако, причинная зависимость от общей нестационарности неизвестна, результирующие причинные сети могут содержать ложные связи ( 34 ). Наши численные результаты показывают, что PCMCI более устойчив к нестационарности, чем Lasso и PC.
Что касается любого метода обнаружения причинно-следственных связей на основе данных наблюдений ( 4 , 5 ), причинная достаточность, вероятно, является самым сильным предположением. Невключенные или ненаблюдаемые переменные все же могут быть причиной связи в любом неэкспериментальном анализе, который необходимо принимать во внимание для любых научных выводов. Потенциальные причинно-следственные связи, выведенные из имеющихся данных наблюдений, могут дать новые гипотезы, которые будут отвергнуты или подтверждены дальнейшим анализом данных с участием большего количества переменных (как показано в нашем климатическом примере) или помогут при разработке численных и реальных экспериментов.Однако обнаружение беспричинности, то есть отсутствия причинно-следственной связи, основывается на более слабых предположениях ( 34 ): при условии, что наблюдаемые данные достоверно представляют основной процесс и что зависимости достаточно хорошо фиксируются статистикой теста, Отсутствие доказательств статистической взаимосвязи делает маловероятным, что физический механизм связи действительно существует. Эти выводы о беспричинности в этом смысле более надежны.
Растущая доступность данных обещает беспрецедентную возможность для нового понимания через причинно-следственные связи во многих научных дисциплинах — если основополагающие допущения будут тщательно приняты во внимание и будут решены методологические проблемы ( 2 ).PCMCI решает проблемы крупномасштабных многомерных, автокоррелированных, линейных и нелинейных наборов данных временных рядов, открывая новые возможности для более достоверного обнаружения причинно-следственных связей и оценки причинных эффектов во многих областях науки.
МАТЕРИАЛЫ И МЕТОДЫ
В этом разделе мы более подробно объясняем предлагаемый метод обнаружения причин и даем описание реальных данных. Дополнительные материалы содержат детали реализации альтернативных методов, используемых в этой работе, подробности о тестах условной независимости, дальнейшие теоретические обсуждения, описание установки численных экспериментов и псевдокоды алгоритмов, таблицы и другие рисунки.
PCMCI реализован в пакете программного обеспечения с открытым исходным кодом Tigramite для Python, доступном по адресу https://github.com/jakobarage/tigramite. Tigramite содержит классы для PCMCI и различных тестов условной независимости, а также модуль, который содержит несколько функций построения графиков для создания высококачественных графиков временных рядов, функций запаздывания и причинных графиков, как показано на рис. 4. Tigramite также содержит модули для оценки причинно-следственных связей и анализа путей посредничества ( 38 ), а также для выбора оптимальных предикторов ( 61 ).Документацию можно найти на сайте репозитория.
Подробное описание PCMCI
В нашей структуре структура зависимостей набора переменных временного ряда представлена в графической модели ( 62 ). Хотя граф процесса, изображенный на рис. 1B, легче визуализировать, он не полностью представляет структуру пространственно-временной зависимости, лежащую в основе сложных динамических систем. Графики временных рядов ( 32 — 34 ) обеспечивают более полное представление, как показано на рис.3. Если, например, графические модели оцениваются без учета запаздывающих переменных, то ассоциации легко могут быть искажены влиянием общих факторов в прошлом. Для формального определения графиков временных рядов см. Раздел S1.
Наша методика обнаружения причин для оценки графика временных рядов Gˆ основана на двухэтапной процедуре:
1. Выбор условий через ПК 1 : получить оценку Pˆ (Xtj) (надмножества) родителей P (Xtj) для всех переменных Xtj∈Xt = (Xt1, Xt2,…, XtN) с алгоритмом S1.
2. Используйте эти родительские элементы в качестве условий на этапе обнаружения причин MCI (алгоритм S2), который проверяет все пары переменных (Xt − τi, Xtj) с i , j ∈ {1,…, N } и задерживает τ ∈ {1,…, τ max } и устанавливает связь, то есть Xt − τi → Xtj∈Gˆ, тогда и только тогда, когда MCI: Xt − τi⫫Xtj∣ Pˆ (Xtj) ∖ {Xt− τi}, PˆpX (Xt − τi) (3) где PˆpX (Xt − τi) ⊆Pˆ (Xt − τi) обозначает p X самых сильных родителей согласно сортировке в алгоритме S1. Этот параметр является необязательным.Можно также ограничить максимальное количество родителей, используемых для Pˆ (Xtj), но здесь мы не налагаем никаких ограничений. При τ = 0 можно также рассматривать неориентированные одновременные связи ( 39 ).
Оба этапа, выбор условий и MCI, состоят из тестов условной независимости. Эти тесты могут быть реализованы с различной тестовой статистикой. Здесь мы использовали тесты ParCorr, GPDC и CMI, как подробно описано в разделе S4 и таблице S1.
PC 1 на первом этапе представляет собой вариант части алгоритма обнаружения скелета ( 25 ) в его более надежной модификации, называемой PC-стабильной ( 36 ) и адаптированной к временным рядам.Алгоритм кратко обсуждается в основном тексте, более формально (псевдокод в алгоритме S1): для каждой переменной Xtj∈Xt сначала предварительные родители Pˆ (Xtj) = (Xt − 1, Xt − 2,…, Xt −τmax) инициализируются. Начиная с p = 0, итеративно p → p + 1 увеличивается во внешнем цикле, а во внутреннем цикле проверяется для всех переменных Xt − τi из Pˆ (Xtj), является ли нулевая гипотеза PC: Xt − τi⫫Xtj∣S для любого S с ∣S∣ = p (4) может быть отклонено при пороге значимости α PC .Для реализованного здесь алгоритма ПК S выполняет итерацию по различным комбинациям подмножеств Pˆ (Xtj) ∖ {Xt − τi} с мощностью p , вплоть до максимального количества комбинаций q max . Наш быстрый вариант PC 1 получается путем тестирования только родителей p с самой сильной зависимостью, то есть ограничивая максимальное количество комбинаций q max на итерацию до q max = 1. В первая итерация ( p = 0), S пуста и, таким образом, проверяются безусловные зависимости.В каждой следующей итерации мощность увеличивается p → p + 1, и уравнение. 4 снова проверяется. Если нулевая гипотеза не может быть отклонена, тогда связь удаляется из Pˆ (Xtj) в конце каждой итерации p . Алгоритм сходится для связи Xt − τi → Xtj после того, как S = Pˆ (Xtj) ∖ {Xt − τi}, и нулевая гипотеза Xt − τi⫫Xtj∣ Pˆ (Xtj) ∖ {Xt − τi} отклоняется (если нулевая гипотеза не может быть отклонена, тогда ссылка удаляется). Pˆ (Xtj) сортируется после каждой итерации в соответствии с абсолютным значением статистики теста (ParCorr, GPDC или CMI), а S выбирается в лексикографическом порядке (актуально только для q max > 1).Другие алгоритмы выбора причинных переменных используют аналогичные эвристики ( 35 , 63 ). Этап MCI основан на передаче моментальной информации теоретико-информационных мер, представленной в различных вариантах в ( 55 , 64 ).
Свободными параметрами PCMCI (в дополнение к свободным параметрам статистики критерия условной независимости) являются максимальная временная задержка τ max , порог значимости α PC и максимальное количество p X условий переменной драйвера в формуле.3. Мы сокращаем выбор различных параметров как PC1α + MCI p X , если это не ясно из контекста.
Выбор из τ макс . Максимальная временная задержка зависит от приложения и должна выбираться в соответствии с максимальной физической задержкой, ожидаемой в сложной системе. Если соответствующий временной лаг, который может объяснить зависимость между двумя другими переменными, не включен, то предположение о причинной достаточности будет нарушено.На практике мы рекомендуем довольно большой выбор, например, последнее запаздывание со значительной безусловной зависимостью, потому что слишком большой выбор τ max просто приводит к увеличению времени работы PCMCI, но не столько к увеличению размера оценки, сколько для FullCI.
Выбор из α PC . α PC не следует рассматривать как уровень проверки значимости в PC 1 , поскольку итерационные проверки гипотез не позволяют точно оценить неопределенности на этом этапе.α PC здесь скорее играет роль параметра регуляризации, как в методах выбора модели. Наборы кондиционирования Pˆ, оцененные с помощью PC 1 , должны включать истинных родителей и, в то же время, быть небольшими по мощности, чтобы уменьшить размерность оценки теста MCI и повысить его мощность. Однако первое требование обычно более важно (см. Раздел S5.3). На рис. На этапе S8 мы исследовали производительность PCMCI, реализованного с помощью ParCorr, GPDC и CMI, для различных α PC .Слишком малые значения α PC приводят к тому, что многие истинные ссылки не включаются в условия, установленные для тестов MCI, и, следовательно, увеличивают количество ложных срабатываний. Слишком высокие уровни α PC приводят к большой размерности набора условий, что снижает мощность обнаружения и увеличивает время выполнения. Обратите внимание, что для порога α PC = 1 в PC 1 родительские элементы не удаляются, и все переменные N τ max будут выбраны в качестве условий. Затем тест MCI становится тестом FullCI.Как и в любом методе выбора переменных ( 35 ), α PC можно оптимизировать с помощью перекрестной проверки или на основе оценок, таких как байесовский информационный критерий (BIC) или AIC. Для всех экспериментов ParCorr (за исключением тех, которые помечены как PC1α + MCI p X ), мы оптимизировали α PC с AIC в качестве критерия выбора. Точнее, для каждого Xtj мы запускали PC 1 отдельно для каждого α PC ∈ {0,1, 0,2, 0,3, 0,4}, получая различные наборы условий Pˆα (Xtj).Затем мы подбираем линейную модель для каждого α PC Xtj = Pˆα (Xtj) β (5), что дает остаточную сумму квадратов (RSS), и выбираем α PC в соответствии с AIC (по модулю констант) αPC * = argminαPCnlog (RSSα) + 2∣Pˆα (Xtj) ∣ (6) где n — это размер выборки (обычно длина временного ряда T минус отсечка из-за τ max ), а ∣ · ∣ обозначает количество элементов. Для GPDC можно аналогичным образом выбрать α PC на основе логарифмической предельной вероятности подобранного гауссовского процесса, в то время как для CMI можно использовать перекрестную проверку на основе прогнозов ближайшего соседа для различных Pˆα (Xtj).Но поскольку GPDC и CMI уже достаточно требовательны к вычислениям, мы выбрали α PC = 0,2 во всех экспериментах, основываясь на наших выводах на рис. S8. На нижних панелях фиг. S4 — S7, мы проанализировали α PC = 0,2 также для ParCorr для всех численных экспериментов и обнаружили, что этот вариант также дает хорошие результаты для разреженных сетей и работает даже быстрее, чем Lasso. Однако существует потенциально более высокий риск завышенных ложных срабатываний. К сожалению, у нас нет результатов конечной согласованности выборки для выбора α PC .
Выбор p X . В то время как родителей Pˆ (Xtj) достаточно для оценки условной независимости, дополнительные условия PˆpX (Xt − τi) ⊆Pˆ (Xt − τi) используются для учета автокорреляции и делают статистику теста MCI мерой причинной силы, как анализируется в раздел S5.5. Чтобы ограничить высокую размерность, можно сильно ограничить количество условий PˆpX (Xt − τi) свободным параметром p X . Чтобы избежать наличия еще одного свободного параметра, мы оставили p X неограниченным в большинстве экспериментов.В некоторых экспериментах (см. Рис. S4, S5, S6, S7, S10 и S12) мы обнаружили, что небольшого значения p X = 3 уже достаточно, чтобы уменьшить завышенные ложные срабатывания из-за сильной автокорреляции и оценить причинную силу. . Причина в том, что, как правило, самой большой движущей силой является самозависимость, и обусловливание ее влияния уже уменьшает эффект сильных автокорреляций. Теоретически слишком маленький p X должен привести к менее хорошо откалиброванному тесту (см. Раздел S5.3), но на практике это кажется разумным компромиссом. В разделе S3 мы описываем вариант PCMCI для p X = 0 и двумерный вариант, который не зависит от внешних переменных. Оба они не могут гарантировать согласованных оценок графов причинно-следственных связей и, вероятно, содержат завышенные ложные срабатывания, особенно для сильной автокорреляции.
Контроль ложной скорости обнаружения . PCMCI также можно комбинировать с контролем частоты ложных открытий, например, используя подход Хохберга-Бенджамини ( 37 ).Этот подход позволяет контролировать ожидаемое количество ложных открытий путем корректировки значений P , полученных на этапе MCI для всего графика временных рядов. Точнее, мы получаем значения q asq = min (Pmr, 1) (7), где P — исходное значение P , r — ранг исходного значения P , когда P значения отсортированы в порядке возрастания, и м — это общее количество вычисленных значений P , то есть м = N 2 τ max для настройки только направленных каналов для τ> 0 и соответственно, если учесть одновременные связи при τ = 0.В наших численных экспериментах мы не контролировали частоту ложных открытий, поскольку нас интересовали характеристики отдельных каналов.
Реальные приложения
Климатические временные ряды представляют собой средние региональные значения (см. Вставки на рис. 4) по результатам повторного анализа ( 65 ) за период 1948–2012 годов с 780 месяцами. WPAC обозначает месячные аномалии приземного давления в западной части Тихого океана, аномалии приземной температуры воздуха CPAC и EPAC в центральной и восточной частях Тихого океана, соответственно, и аномалии приземной температуры воздуха ATL в тропической Атлантике.Аномалии берутся за весь период. Данные находятся в свободном доступе на сайте www.esrl.noaa.gov.
Сердечно-сосудистый анализ основан на ансамбле из 13 наборов данных о здоровых беременных женщинах, как это было изучено в ( 50 ), где данные подробно описаны. Исследование было одобрено местным комитетом по этике и получило информированное согласие всех субъектов. Временные ряды содержат 600 отсчетов (отсечение переходного процесса 300) и отсчитываются при сердечных сокращениях. B обозначает временной ряд интервалов между последовательными ударами сердца, а D — диастолическое, а S — систолическое артериальное давление.
Дополнительная информация в дополнительных материалах
Более подробное определение графиков временных рядов дается в разделе S1. В разделе S2 подробно описаны альтернативные методы: FullCI, Lasso, алгоритм ПК, CCM, а также безусловная корреляция, дистанционная корреляция и MI. В разделе S3 обсуждаются дополнительные варианты PCMCI, один из вариантов, исключающий условие для родительских переменных драйвера, т.е.е., p X = 0, и другой вариант, исключающий обусловливание внешних переменных. Используемые здесь тесты условной независимости (ParCorr, GPDC и CMI), которые составляют основу PCMCI, алгоритма ПК и FullCI, подробно описаны в разделе S4. Теоретические свойства PCMCI обсуждаются в разделе S5. В частности, полиномиальная вычислительная сложность выводится в разделе S5.1, согласованность доказывается в разделе S5.2, а в разделе S5.3 подробно рассматривается правильный контроль ложных срабатываний на заданном уровне значимости, также при наличии сильной автокорреляции. .Раздел S5.4 доказывает, что MCI больше или равен FullCI, и объясняет, как кондиционирование нерелевантных переменных уменьшает размер эффекта для FullCI. Интерпретация MCI как понятия причинной силы дается в разделе S5.5. Подробная настройка численных экспериментов представлена в разделе S6, включая анализ AN (C) OVA и показатели производительности. Оставшаяся часть дополнительных материалов содержит псевдокоды алгоритмов и таблиц, а также другие рисунки, на которые есть ссылки в основном тексте.
ДОПОЛНИТЕЛЬНЫЕ МАТЕРИАЛЫ
Дополнительные материалы к этой статье доступны по адресу http://advances.sciencemag.org/cgi/content/full/5/11/eaau4996/DC1
Раздел S1. Графики временных рядов
Раздел S2. Альтернативные методы
Раздел S3. Другие варианты PCMCI
Раздел S4. Тесты условной независимости
Раздел S5. Теоретические свойства PCMCI
Раздел S6. Численные эксперименты
Алгоритм S1. Псевдокод для алгоритма выбора условия.
Алгоритм S2. Псевдокод для стадии обнаружения причин MCI.
Алгоритм S3. Псевдокод для адаптивной регрессии Лассо.
Таблица S1. Обзор тестов условной независимости.
Таблица S2. Конфигурации модели для разных экспериментов.
Таблица S3. Обзор методов, сравниваемых в численных экспериментах.
Таблица S4. Обобщенные результаты дисперсионного анализа для многомерных экспериментов ParCorr.
Таблица S5. Обобщенные результаты ANOVA для экспериментов с высокой плотностью ParCorr.
Таблица S6. Обобщенные результаты дисперсионного анализа для многомерных экспериментов GPDC и CMI.
Таблица S7. Обобщенные результаты ANOVA для экспериментов с размером выборки.
Таблица S8. Обобщенные результаты дисперсионного анализа для экспериментов по шуму и нестационарности.
Таблица S9. Результаты ANCOVA для FullCI.
Таблица S10. Результаты ANCOVA для Лассо.
Таблица S11. Результаты ANCOVA для ПК.
Таблица S12. Результаты ANCOVA для FullCI.
Рис. S1. Иллюстрация обозначений.
Рис. S2. Пример мотивационного климата.
Рис. S3. Реальные климатические и сердечно-сосудистые приложения.
Рис. S4. Эксперименты для линейных моделей с короткими временными рядами.
Рис. S5. Эксперименты для линейных моделей с большей длиной временного ряда.
Рис. S6. Эксперименты для плотных линейных моделей с короткими временными рядами.
Рис. S7. Эксперименты для плотных линейных моделей с большей длиной временного ряда.
Рис. S8. Эксперименты для разных параметров метода.
Рис. S9. Эксперименты для линейных методов с разными объемами выборки.
Фиг. S10. Эксперименты на нелинейных моделях (часть 1).
Рис. S11. Эксперименты для нелинейных моделей с разными объемами выборки (часть 1).
Фиг. S12. Эксперименты на нелинейных моделях (часть 2).
Рис. S13. Эксперименты для нелинейных моделей с разными объемами выборки (часть 2).
Фиг. S14. Эксперименты для наблюдательных моделей шума.
Фиг. S15. Эксперименты для нестационарных моделей.
Фиг. S16. Время выполнения численных экспериментов.
Фиг. S17. Графики взаимодействия ANCOVA.
Фиг. S18. Сравнение PCMCI и CCM на логистических картах.
Ссылки ( 66 — 80 )
Благодарности: Мы благодарим Г. Баласиса, Д. Куму, Дж. Донгеса, Ф. Фрёлиха, К. Глимора, Дж. Хейга, Дж. Хайцига, Б. Хоскинса , J. Kurths, M. Mengel, M. Reichstein, C.-F. Schleussner, E. van Sebille, K. Zhang и J. Zscheischler за полезные обсуждения и комментарии.Мы благодарим К. Линстеда за помощь с высокопроизводительными вычислениями. Мы благодарим N. Wessel за помощь с примером приложения для сердечно-сосудистой системы и H. Stepan за предоставленные данные. J.R. особенно благодарит Э. Гиллиса за переписывание и улучшение больших частей Tigramite. Финансирование: J.R. получил финансирование за счет постдокторской премии Фонда Джеймса С. Макдоннелла. D.S. был частично поддержан Институтом Алана Тьюринга в рамках гранта EPSRC EP / N510129 / 1. П.Н. поддерживается через исследовательскую стипендию Имперского колледжа.Эта работа была поддержана Европейским фондом регионального развития (ERDF), Федеральным министерством образования и исследований Германии и Землей Бранденбург путем предоставления ресурсов на высокопроизводительную компьютерную систему в Потсдамском институте исследований воздействия на климат. М.К. был поддержан Федеральным министерством образования и исследований Германии (грант № 01LN1304A). Вклад авторов: J.R. разработал и внедрил метод, проанализировал данные, создал все рисунки и подготовил рукопись.Д.С. способствовал математической формулировке. П.Н. и М.К. внесла свой вклад в примеры климата. J.R., P.N., M.K., S.F. и D.S. обсудили результаты и внесли свой вклад в редактирование рукописи. Конкурирующие интересы: Авторы заявляют, что у них нет конкурирующих интересов. Доступность данных и материалов: Все данные, необходимые для оценки выводов в статье, представлены в документе и / или дополнительных материалах. Дополнительные данные, относящиеся к этой статье, могут быть запрошены у авторов.Платформа тестирования причинно-следственных связей www.causeme.net, разработанная одним из авторов, облегчает оценку методов на растущем массиве синтетических и реальных наборов данных.Причинное влияние — обзор
- а.
Примените метод Чоу к распределению Упражнения 3.3 , нарисуйте остовное дерево максимального веса и представьте P t в виде продукта.
- б.
Повторить задачу ( a ) в распределении, описанном в упражнении 4.3 .
- г.
Проблема повторения ( a ) в распределении, лежащем в основе рисунка 4.37.
Учитывая ковариационную матрицу Σ многомерного нормального распределения f ( x ), разработайте процедуру проверки для определения того, может ли f ( x ) быть представлено деревом, и, если это возможно, разработайте процедура нахождения структуры дерева из Σ (см. Демпстер [1972]).
Примените алгоритм восстановления многодерева к распределениям, описанным в упражнении 4.3 и рис. 4.37. Убедитесь, что направление стрелок совпадает с направлением исходной модели. Объяснять.
Приведите пример распределения вероятностей P для каждого из этих условий:
- a.
P имеет уникальное представление многодерева.
- б.
P имеет несколько представлений многодерева, которые имеют уникальный скелет.
- г.
P имеет ровно два представления многодерева с разными скелетами.
Распределение зависит от 3-дерева , если это поле Маркова относительно 3-дерева . 3-дерево — это дерево клик размера 3, такое, что никакие две клики не имеют более одного общего узла.
Изучить возможность поиска наилучшего зависящего от трех деревьев приближения к заданному распределению P , i.е., обобщить метод остовных деревьев максимального веса Чоу от стандартных деревьев до 3-деревьев.
Повторите упражнение 8.2 для многодеревьев.
Разработайте алгоритм для уникального восстановления двусторонних групп DAG (т. Е. Групп DAG глубины 2, таких как показанный на рис. 4.37).
Докажите, что коэффициент корреляции между любыми двумя переменными в дереве равен произведению коэффициентов корреляции на связях, соединяющих две переменные.
Семь двоичных переменных распределены древовидным распределением. Их коэффициенты корреляции приведены в таблице ниже.
1234567110.810.810.40320.40320.34560.3456210.810.40320.40320.34560.3456310.40320.40320.34560.3456410.490.188160.18816510.188160.18816610.3671
Разделите дерево коэффициентов и топологию его топологии на основе всех ветвей корреляции.
Покажите, что, исключая функциональные зависимости, семантика причинной связи минимальной модели (1) санкционирует следующий критерий всякий раз, когда доступна временная информация:
« X оказывает причинное влияние на Y , если существует третья переменная Z , предшествующая X , так что Z и Y являются зависимыми, а Z и Y являются независимыми при X ».
Другими словами, покажите, что обнаружение такого Z гарантирует, что должна существовать зависимость между X и Y , которая не связана со скрытыми переменными, действующими как общие причины для обоих.
Разработайте критерий для проверки ложной причинной связи, то есть зависимости между переменной X и более поздней переменной Y , которая объясняется исключительно влиянием других причинных факторов, общих для обеих.
Обобщите критерий из упражнения 8.10 на случаи отсутствия временной информации, показывая, что существует непереходный триплет { X, Z, Z ′}, удовлетворяющий I ( Z, S, Z ′), ¬ I ( Z, S, X ) и ¬ I ( Z ′, S, X ) могут быть заменены временным соотношением « Z предшествует X .”
Журнал причинно-следственных связей
Редакторы
Косуке Имаи , Гарвардский университет, США
Джудея Перл , Калифорнийский университет, Лос-Анджелес, США
Майя Петерсен , Калифорнийский университет, Школа общественного здравоохранения Беркли, США
Марк ван дер Лаан , Калифорнийский университет, Школа общественного здравоохранения Беркли, США
Редакционная коллегия
Альберто Абади , Гарвардский университет, США
Яап Х.Abbring , Тилбургский университет, Нидерланды
Питер Аронов , Йельский университет, США
Лаура Б. Бальцер , Массачусетский университет — Амхерст, США
Элиас Барейнбойм , Колумбийский университет, США
07 Дэвид Бенке Университет Эмори, США
Кеннет Боллен , Университет Северной Каролины, США
Марко Кароне , Вашингтонский университет, США
Матиас Д. Каттанео , Принстонский университет, США
Антуан Шамбаз , Университет Уэст-Нантер, Франция
Филип Давид , Кембриджский университет, Великобритания
Peng Ding, Калифорнийский университет, Беркли, США
Феликс Эльверт , Университет Висконсин-Мэдисон, США
Avi University Feller, Калифорния, Беркли, США
Дональд Грин , Колумбийский университет, США
Сандер Гринлан d , University of California, Los Angeles, USA
Jens Hainmueller , Stanford University, USA
Joseph Halpern , Cornell University, USA
James Heckman , University of Chicago, USA
Jennifer Hill , Нью-Йоркский университет, США
Кристофер Хичкок , Калифорнийский технологический институт, США
Пол Хюнермунд , Школа бизнеса и экономики Маастрихтского университета, Нидерланды
Маршалл Иоффе , Университет Пенсильвании, США
Cheng Ju, University of California, Berkeley, USA
Luke Keele , Penn State University, USA
Manabu Kuroki , Институт статистической математики, Токио, Япония
Edward Miguel , University of Калифорния, Беркли, США
Картика Мохан , Калифорнийский университет, Беркли, США 91 650 Romain Neugebauer , Kaiser Permanente
Michael Oakes , Школа общественного здравоохранения Университета Миннесоты, США
Sam Pimentel, University of California, Berkeley, USA
Ed Rigdon , Университет штата Джорджия, США
Джеймс Робинс , Гарвардская школа общественного здравоохранения, США
Майкл Розенблюм , Школа общественного здравоохранения Блумберга Джонса Хопкинса, США
Андреа Ротницки , Гарвардская школа общественного здравоохранения, США
Илья Шпицер , Саутгемптонский университет, Великобритания
Дилан Смолл , Школа Уортона, Пенсильванский университет, США
Майкл Собел , Колумбийский университет, США
Питер Спрайтс , Университет Карнеги-Меллона, США
Элизабет Стюарт , Университет Джона Хопкинса, США
Эрик Тчетген Тчетген , Гарвардская школа Общественное здравоохранение, США
Джин Тиан , Университет штата Айова, США
Тайлер Вандервил , Гарвардская школа общественного здравоохранения, США
Stijn Vansteelandt , Гентский университет, Бельгия, и Лондонская школа общественного здравоохранения, Великобритания
Эд Витлацил , Йельский университет, США
Стивен Вест , Государственный университет Аризоны, США
Кристофер Виншип , Гарвардский университет, США
Теппеи Ямамото , Массачусетский технологический институт, США 13
Simons Institute for theory of theory of Computing
Эта программа направлена на интеграцию достижений и методов теоретической информатики в методы причинного вывода и открытия.
Хотя попытки охарактеризовать причинно-следственные связи можно найти в некоторых из старейших письменных источников, история использования причинных понятий в научных дискуссиях за последние 100 лет была непростой, начиная с прямого отрицания какой-либо роли причинности в зрелом мире. научные теории к неискреннему использованию двусмысленных терминов, которые затемняют роль причины и следствия (например, «связь», «связь» и т. д.).
Существенное развитие новых формальных подходов к причинности в 1970-х и 1980-х годах ускорило изменение отношения к научному исследованию причинных вопросов.Изменения были вызваны развитием двух в значительной степени взаимопереводимых математических структур: схемы потенциальных результатов и схемы причинно-следственных графических моделей. Эти структуры объединили три концепции, центральные в понятии причинности: (1) связь между лежащими в основе причинными отношениями и наблюдаемыми данными, (2) различие, которое вмешательства могут внести в причинную систему, и (3) контрфактические утверждения о системе. Все эти аспекты причинности играют центральную роль в научном тестировании и объяснении, часто составляя цель самого научного исследования.
Математизация вопросов причинности привела к развитию методов вывода и методов обучения для вывода причинно-следственных связей из данных. Эти формальные подходы теперь начинают распространяться в прикладных науках, где практически в любой области исследований наблюдается возобновление и явный интерес к решению проблемы причинности.
Широкое применение этих теоретических основ в научных областях требует не только концептуальной ясности и «принципиальных» методов, но и детального понимания того, как методы ведут себя на практике, как масштабировать и приближать идеально желаемые вычисления и как оптимизировать методы для конкретные ограничения, присутствующие в домене.
Эта программа объединит теоретических и прикладных исследователей из самых разных областей с целью понимания сложности, оптимизации и возможных режимов аппроксимации, необходимых для превращения методов причинного вывода в широко применимый научный инструментарий.
sympa [at] lists.simons.berkeley.edu (body: subscribe% 20causalityannouncements2022% 40lists.simons.berkeley.edu) (Щелкните здесь, чтобы подписаться на нашу рассылку с объявлениями об этой программе).
Организаторы: Фредерик Эберхардт (Калифорнийский технологический институт; председатель), Константинос Даскалакис (Массачусетский технологический институт), Марлоис Маасуис (ETH), Томас Ричардсон (Вашингтонский университет), Леонард Шульман (Калифорнийский технологический институт), Василис Сиргканис (Microsoft), Кэролайн Улер (Массачусетский технологический институт)
uber / causalml: моделирование роста и причинный вывод с помощью алгоритмов машинного обучения
Этот проект стабилен и инкубируется для долгосрочной поддержки. Он может содержать новый экспериментальный код, API которого могут быть изменены.
Causal ML — это пакет Python, который предоставляет набор методов моделирования роста и причинно-следственных связей с использованием алгоритмов машинного обучения на основе последних
исследовать. Он предоставляет стандартный интерфейс, который позволяет пользователю оценить условный средний эффект лечения (CATE) или индивидуальное лечение.
Эффект (ITE) из экспериментальных или наблюдательных данных. По сути, он оценивает причинно-следственное влияние вмешательства T на результат Y для пользователей
с наблюдаемыми особенностями X , без строгих предположений о форме модели.Типичные варианты использования включают
Оптимизация таргетинга кампании : Важным рычагом увеличения рентабельности инвестиций в рекламной кампании является нацеливание рекламы на группу клиентов, которые получат положительный ответ по заданному KPI, например, по вовлечению или продажам. CATE идентифицирует этих клиентов, оценивая эффект KPI от показа рекламы на индивидуальном уровне на основе эксперимента A / B или исторических данных наблюдений.
Персонализированное взаимодействие : Компания имеет несколько вариантов взаимодействия со своими клиентами, например, различные варианты продуктов при дополнительных продажах или каналы обмена сообщениями для связи.CATE можно использовать для оценки неоднородного эффекта лечения для каждого клиента и комбинации вариантов лечения для создания оптимальной персонализированной системы рекомендаций.
В настоящее время пакет поддерживает следующие методы
- Древовидные алгоритмы
- Восходящее дерево / случайные леса на расхождении KL, евклидовом расстоянии и хи-квадрат
- Поднятые деревья / случайные леса при выборе контекстной обработки
- Алгоритмы метаобучения
- S-ученик
- Ти-ученик
- X-ученик
- R-обучающийся
- Алгоритмы инструментальных переменных
- 2-этапный метод наименьших квадратов (2SLS)
Предварительные требования
Установить зависимости:
$ pip install -r требования.текст
Установить из pip:
$ pip install causalml
Установить из исходников:
$ git clone https://github.com/uber/causalml.git
$ cd causalml
$ python setup.py build_ext --inplace
$ python setup.py установить
Оценка среднего эффекта лечения с учащимися S, T, X и R
из causalml.inference.meta import LRSRegressor
из causalml.inference.meta import XGBTRegressor, MLPTRegressor
из причинно-следственной связи.inference.meta импорт BaseXRegressor
from causalml.inference.meta import BaseRRegressor
из xgboost импортировать XGBRegressor
из causalml.dataset импортировать синтетические_данные
y, X, обращение, _, _, e = синтетические_данные (режим = 1, n = 1000, p = 5, сигма = 1.0)
lr = LRSRegressor ()
te, lb, ub = lr.estimate_ate (X, обращение, y)
print ('Средний эффект лечения (линейная регрессия): {: .2f} ({: .2f}, {: .2f})'. format (te [0], lb [0], ub [0]))
xg = XGBTRegressor (random_state = 42)
te, lb, ub = xg.estimate_ate (X, обработка, y)
print ('Средний эффект лечения (XGBoost): {:.2f} ({: .2f}, {: .2f}) '. Format (te [0], lb [0], ub [0]))
nn = MLPTRegressor (hidden_layer_sizes = (10, 10),
learning_rate_init = .1,
Early_stopping = Верно,
random_state = 42)
te, lb, ub = nn.estimate_ate (X, обработка, y)
print ('Средний эффект обработки (нейронная сеть (MLP)): {: .2f} ({: .2f}, {: .2f})'. format (te [0], lb [0], ub [0] ))
xl = BaseXRegressor (учащийся = XGBRegressor (random_state = 42))
te, lb, ub = xl.estimate_ate (X, e, treatment, y)
print ('Средний эффект лечения (BaseXRegressor с использованием XGBoost): {:.2f} ({: .2f}, {: .2f}) '. Format (te [0], lb [0], ub [0]))
rl = BaseRRegressor (обучающийся = XGBRegressor (random_state = 42))
te, lb, ub = rl.estimate_ate (X = X, p = e, treatment = treatment, y = y)
print ('Средний эффект лечения (BaseRRegressor с использованием XGBoost): {: .2f} ({: .2f}, {: .2f})'. format (te [0], lb [0], ub [0])) Подробнее см. В блокноте с примерами мета-учащихся.
Интерпретируемая причинно-следственная связь ML
Causal ML предоставляет методы интерпретации моделей эффекта лечения, обученных следующим образом:
Важность функций мета-обучающихся
из causalml.inference.meta импорт BaseSRegressor, BaseTRegressor, BaseXRegressor, BaseRRegressor
from causalml.dataset.regression импортировать синтетические_данные
# Загрузить синтетические данные
y, X, обработка, тау, b, e = синтетические_данные (режим = 1, n = 10000, p = 25, сигма = 0,5)
w_multi = np.array (['treatment_A' if x == 1 else 'control' для x in treatment]) # настроить названия процедур / элементов управления
slearner = BaseSRegressor (LGBMRegressor (), control_name = 'элемент управления')
slearner.estimate_ate (X, w_multi, y)
slearner_tau = slearner.fit_predict (X, w_multi, y)
model_tau_feature = RandomForestRegressor () # указать модель для model_tau_feature
слёрнер.get_importance (X = X, tau = slearner_tau, model_tau_feature = model_tau_feature,
normalize = True, method = 'auto', features = feature_names)
# Использование метода feature_importances_ в базовом учащемся (LGBMRegressor () в этом примере)
slearner.plot_importance (X = X, tau = slearner_tau, normalize = True, method = 'auto')
# Использование PermutationImportance в eli5
slearner.plot_importance (X = X, tau = slearner_tau, normalize = True, method = 'permutation')
# Использование SHAP
shap_slearner = slearner.get_shap_values (X = X, тау = slearner_tau)
# Построение значений shap без указания shap_dict
слёрнер.plot_shap_values (X = X, tau = slearner_tau)
# Построение значений shap с указанием shap_dict
slearner.plot_shap_values (X = X, shap_dict = shap_slearner)
# Interaction_idx установлено на 'auto' (поиск функции с наибольшим приблизительным взаимодействием)
slearner.plot_shap_dependence (treatment_group = 'treatment_A',
feature_idx = 1,
Х = Х,
тау = slearner_tau,
Interaction_idx = 'auto') Подробнее см. В блокноте с примером интерпретации функций.
Визуализация дерева подъема
из IPython.display import Image
from causalml.inference.tree import UpliftTreeClassifier, UpliftRandomForestClassifier
из causalml.inference.tree import uplift_tree_string, uplift_tree_plot
uplift_model = UpliftTreeClassifier (max_depth = 5, min_samples_leaf = 200, min_samples_treatment = 50,
n_reg = 100, evalFunction = 'KL', control_name = 'control')
uplift_model.fit (df [features] .values,
treatment = df ['ключ_группы_обработки'].значения,
y = df ['преобразование']. значения)
graph = uplift_tree_plot (uplift_model.fitted_uplift_tree, функции)
Изображение (graph.create_png ()) Подробнее см. В блокноте с примером визуализации «Дерево подъема».
Мы приветствуем участников сообщества, участвующих в проекте. Прежде чем начать, пожалуйста, прочтите наш кодекс поведения и сначала ознакомьтесь с правилами участия.
Авторы
Мы документируем версии и изменения в нашем журнале изменений.
Этот проект находится под лицензией Apache 2.0 Лицензия — подробности см. В файле ЛИЦЕНЗИИ.
Документация
Цитата
Чтобы цитировать CausalML в публикациях, вы можете обратиться к следующим источникам:
Белая книга: CausalML: пакет Python для каузального машинного обучения
Бибтекс:
@misc {chen2020causalml, title = {CausalML: пакет Python для каузального машинного обучения}, author = {Хуиган Чен, Тотте Харинен, Чон-Юн Ли, Майк Юнг и Чжэнью Чжао}, год = {2020}, eprint = {2002.11631}, archivePrefix = {arXiv}, primaryClass = {cs.CY} }
Документы
- Николас Дж. Рэдклифф и Патрик Д. Сарри. Моделирование подъемов в реальном мире с деревьями подъемов на основе значимости. Официальный документ TR-2011-1, Стохастические решения, 2011 г.
- Ян Чжао, Сяо Фан и Давид Симчи-Леви. Моделирование поднятия с использованием нескольких методов лечения и общих типов реакции. Труды 2017 г. Международная конференция SIAM по интеллектуальному анализу данных, SIAM, 2017.
- Сорен Р. Кюнцель, Ясджит С.Сехон, Питер Дж. Бикель и Бин Ю. Metalearners для оценки неоднородных эффектов лечения с помощью машинного обучения. Известия Национальной академии наук, 2019.
- Синкун Не и Стефан Вейджер. Квази-оракульная оценка неоднородных лечебных эффектов. Конференция по Атлантическому выводу причин, 2018.
Связанные проекты
- uplift: модели uplift в R
- grf: обобщенные случайные леса, которые включают оценку эффекта неоднородной обработки в рандов.
