Регрессия что это: Недопустимое название — Викисловарь — inakhan.ru

Содержание

Скучно, просто и ограниченно — все это изотоническая регрессия / Хабр

Вкратце о маленьком пакете cir.

Минутка теории

Изотоническая регрессия — это крайне специфический вид регрессии, который применяется при жестком требовании неубывания значения зависимой переменной при возрастании значения независимой переменной

Есть два основных применения данного вида регрессии в реальных задачах:

В фармакологических задачах, где нужно найти взаимосвязь типа «отклик — доза» (например, «концентрация препарата — доля умерших»)
При моделировании распределений, когда в качестве зависимой переменной выступает квантиль функции распределения

Классический алгоритм расчетов дает в результате кусочно-постоянную неубывающую функцию (Pool-Adjacent-Violators Algorithm, его схема представлена ниже):

Цитируется по: Assaf P. Oron, Nancy Flournoy. Centered Isotonic Regression: Point and Interval Estimation for Dose-Response Studies / Statistics in Biopharmaceutical Research.

№ 3 (9) DOI:10.1080/19466315.2017.1286256

Недавно алгоритм был модифицирован. Две работы позволили немного модифицировать алгоритм:

Oron A. P., Flournoy N. Centered Isotonic Regression: Point and Interval Estimation for Dose-Response Studies / Statistics in Biopharmaceutical Research. 2017. № 3 (9) DOI:10.1080/19466315.2017.1286256 — был представлен новый, сглаживающий алгоритм
Oron A. P., Flournoy N. Bias induced by adaptive dose-finding designs // Journal of Applied Statistics. 2019. DOI: 10.1080/02664763.2019.1649375 — была представлена методика расчета доверительных интервалов при предсказании значений зависимых переменных

Новый алгоритм основан на сглаживании кусочно-постоянной регрессии:

Цитируется по: Assaf P. Oron, Nancy Flournoy. Centered Isotonic Regression: Point and Interval Estimation for Dose-Response Studies / Statistics in Biopharmaceutical Research. № 3 (9) DOI:10.1080/19466315.2017.1286256

Собственно, на всем этом и основан пакет CIR, с которым мы будем знакомиться

Методология

Основа для данной статьи — база данных из исследования (что-то связано с инфекциями в человеческой популяции), которая отдельно доступна по ссылке.

В качестве независимой переменной выступает логарифм дозы носителей инфекции, в качестве зависимой переменной — вероятность заболеть.

База данных и все сопутствующие материалы есть на GitHub.

Расчеты

Data <- read_csv(".../Dataforfigure8.csv", 
                           col_names = FALSE)
nam<-t(Data[,1])
Base<-as.data.frame(t(Data[,2:24]))
colnames(Base)<-nam
ggplot(data=Base, aes(x=Base$log_dose, y=Base$Probability_of_infection_1)) +
  geom_point() + xlab("Логарифм дозы") + ylab("Вероятность инфицирования")

Если посмотреть на точечный график, то это будет что-то типа

Очень похоже на логистическую регрессию

В пакете представлены три алгоритма регрессии — их реализуют функции cirPAVA() — это новый алгоритм, oldPAVA — старый алгоритм и iterCIR() — итеративная версия нового алгоритма. Но мы воспользуемся другой функцией для построения регрессии и доверительных интервалов

x1<-Base[,2]
names(x1)<-c()
x2<-Base[,1]
names(x2)<-c()
dat<-doseResponse(y=x1,x=x2) 
quick1<-quickIsotone(dat)  # Быстрая регрессия - получение доверительных интервалов для значений у
ggplot(data=quick1, aes(x=x, y=y)) +
  geom_point() + xlab("Логарифм дозы") + ylab("Вероятность инфицирования") + 
  geom_line(data=quick1,aes(x=x, y=lower90conf))+
  geom_line(data=quick1,aes(x=x, y=upper90conf))

Вот и доверительные интервалы

При этом расчет доверительных интервалов может осуществляться тремя способами, выбрать которые можно при использовании функции isotInterval.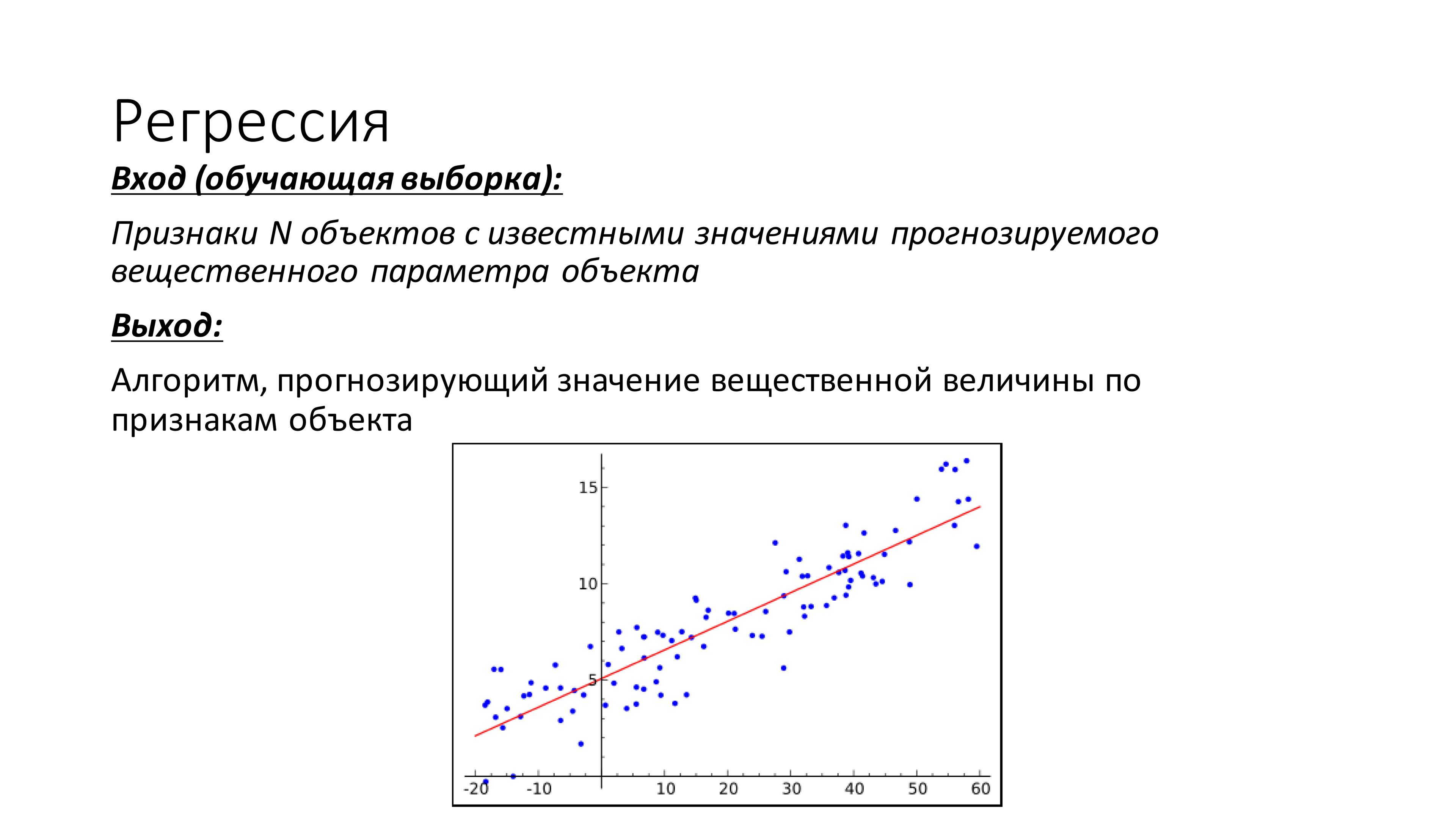 Все вместе будет выглядеть так:

slow1<-cirPAVA(dat,full=TRUE) # Построение регрессии по алгоритму CIR
slow1$output # Предсказанные значения
slow1$input # Исходные данные
slow1$shrinkage # Сокращенные данные для построения графика зависимости
int1_0<-isotInterval(slow1,narrower=FALSE) # Расчет доверительных интервалов по готовой модели
int1_0
ggplot(data=quick1, aes(x=x, y=y)) +
  geom_point() + xlab("Логарифм дозы") + ylab("Вероятность инфицирования") +
  geom_line(data=slow1$shrinkage,aes(x=x, y=y), color = "green") +
  geom_line(data=int1_0,aes(x=quick1$x, y=ciLow))+
  geom_line(data=int1_0,aes(x=quick1$x, y=ciHigh))

Доверительные интервалы чуть-чуть, но другие

Функция quickIsotone() может также осуществлять и прогнозирование. Для этого есть параметр outx

quickIsotone(dat, outx = c(2.15,7.75)) # Предсказание с доверительными интервалами для значения

Результат предсказания

Основы регрессионного анализа—ArcGIS Pro | Документация

Набор инструментов Пространственная статистика предоставляет эффективные инструменты количественного анализа пространственных структурных закономерностей. Инструмент Анализ горячих точек, например, поможет найти ответы на следующие вопросы:

Есть ли в США места, где постоянно наблюдается высокая смертность среди молодежи?
Где находятся «горячие точки» по местам преступлений, вызовов 911 (см. рисунок ниже) или пожаров?
Где находятся места, в которых количество дорожных происшествий превышает обычный городской уровень?

Анализ данных звонков в службу 911, показывающий горячие точки (красным), холодные точки (синим) и локализацию пожарных/полиции, ответственных за реагирование (зеленые круги)

Каждый из вопросов спрашивает «где»? Следующий логический вопрос для такого типа анализа – «почему»?

Почему в некоторых местах США наблюдается повышенная смертность молодежи? Какова причина этого?
Можем ли мы промоделировать характеристики мест, на которые приходится больше всего преступлений, звонков в 911, или пожаров, чтобы помочь сократить эти случаи?
От каких факторов зависит повышенное число дорожных происшествий? Имеются ли какие-либо возможности для снижения числа дорожных происшествий в городе вообще, и в особо неблагополучных районах в частности?

Инструменты в наборе инструментов Моделирование пространственных отношений помогут вам ответить на вторую серию вопросов «почему». К этим инструментам относятся Метод наименьших квадратов и Географически взвешенная регрессия.

Пространственные отношения

Регрессионный анализ позволяет вам моделировать, проверять и исследовать пространственные отношения и помогает вам объяснить факторы, стоящие за наблюдаемыми пространственными структурными закономерностями. Вы также можете захотеть понять, почему люди постоянно умирают молодыми в некоторых регионах страны, и какие факторы особенно влияют на особенно высокий уровень диабета. При моделирование пространственных отношений, однако, регрессионный анализ также может быть пригоден для прогнозирования. Моделирование факторов, которые влияют на долю выпускников колледжей, на пример, позволяют вам сделать прогноз о потенциальной рабочей силе и их навыках. Вы также можете использовать регрессионный анализ для прогнозирования осадков или качества воздуха в случаях, где интерполяция невозможна из-за малого количества станций наблюдения (к примеру, часто отсутствую измерительные приборы вдоль горных хребтов и в долинах).

МНК – наиболее известный метод регрессионного анализа. Это также подходящая отправная точка для всех способов пространственного регрессионного анализа. Данный метод позволяет построить глобальную модель переменной или процесса, которые вы хотите изучить или спрогнозировать (уровень смертности/осадки). Он создает уравнение регрессии, отражающее происходящий процесс. Географически взвешенная регрессия (ГВР) — один из нескольких методов пространственного регрессионного анализа, все чаще использующегося в географии и других дисциплинах. Метод ГВР (географически взвешенная регрессия) создает локальную модель переменной или процесса, которые вы прогнозируете или изучаете, применяя уравнение регрессии к каждому пространственному объекту в наборе данных. При подходящем использовании, эти методы являются мощным и надежным статистическим средством для проверки и оценки линейных взаимосвязей.

Линейные взаимосвязи могут быть положительными или отрицательными. Если вы обнаружили, что количество поисково-спасательных операций увеличивается при возрастании среднесуточной температуры, такое отношение является положительным; имеется положительная корреляция. Другой способ описать эту положительную взаимосвязь — сказать, что количество поисково-спасательных операций уменьшается при уменьшении среднесуточной температуры. Соответственно, если вы установили, что число преступлений уменьшается при увеличении числа полицейских патрулей, данное отношение является отрицательным. Также, можно выразить это отрицательное отношение, сказав, что количество преступлений увеличивается при уменьшении количества патрулей. На рисунке ниже показаны положительные и отрицательные отношения, а также случаи, когда две переменные не связаны отношениями:

Диаграммы рассеяния: положительная связь, отрицательная связь и пример с 2 не связанными переменными.

Корреляционные анализы, и связанные с ними графики, отображенные выше, показывают силу взаимосвязи между двумя переменными. С другой стороны, регрессионные анализы дают больше информации: они пытаются продемонстрировать степень, с которой 1 или более переменных потенциально вызывают положительные или негативные изменения в другой переменной.

Применения регрессионного анализа

Регрессионный анализ может использоваться в большом количестве приложений:

Моделирование числа поступивших в среднюю школу для лучшего понимания факторов, удерживающих детей в том же учебном заведении.
Моделирование дорожных аварий как функции скорости, дорожных условий, погоды и т.д., чтобы проинформировать полицию и снизить несчастные случаи.
Моделирование потерь от пожаров как функции от таких переменных как степень вовлеченности пожарных департаментов, время обработки вызова, или цена собственности. Если вы обнаружили, что время реагирования на вызов является ключевым фактором, возможно, существует необходимость создания новых пожарных станций. Если вы обнаружили, что вовлеченность – главный фактор, возможно, вам нужно увеличить оборудование и количество пожарных, отправляемых на пожар.

Существует три первостепенных причины, по которым обычно используют регрессионный анализ:

Смоделировать некоторые явления, чтобы лучше понять их и, возможно, использовать это понимание для оказания влияния на политику и принятие решений о наиболее подходящих действиях. Основная цель — измерить экстент, который при изменениях в одной или более переменных связанно вызывает изменения и в другой. Пример. Требуется понять ключевые характеристики ареала обитания некоторых видов птиц (например, осадки, ресурсы питания, растительность, хищники) для разработки законодательства, направленного на защиту этих видов.
Смоделировать некоторые явления, чтобы предсказать значения в других местах или в другое время. Основная цель — построить прогнозную модель, которая является как устойчивой, так и точной. Пример: Даны прогнозы населения и типичные погодные условия. Каким будет объем потребляемой электроэнергии в следующем году?
Вы также можете использовать регрессионный анализ для исследования гипотез. Предположим, что вы моделируете бытовые преступления для их лучшего понимания и возможно, вам удается внедрить политические меры, чтобы остановить их. Как только вы начинаете ваш анализ, вы, возможно, имеете вопросы или гипотезы, которые вы хотите проверить:
- «Теория разбитого окна» указывает на то, что испорченная общественная собственность (граффити, разрушенные объекты и т. д.) притягивает иные преступления. Имеется ли положительное отношение между вандализмом и взломами в квартиры?
- Имеется ли связь между нелегальным использованием наркотических средств и взломами в квартиры (могут ли наркоманы воровать, чтобы поддерживать свое существование)?
- Совершаются ли взломы с целью ограбления? Возможно ли, что будет больше случаев в домохозяйствах с большей долей пожилых людей и женщин?
- Люди больше подвержены риску ограбления, если они живут в богатой или бедной местности?
Вы можете использовать регрессионный анализ, чтобы исследовать эти взаимосвязи и ответить на ваши вопросы.

Термины и концепции регрессионного анализа

Невозможно обсуждать регрессионный анализ без предварительного знакомства с основными терминами и концепциями, характерными для регрессионной статистики:

Уравнение регрессии. Это математическая формула, применяемая к независимым переменным, чтобы лучше спрогнозировать зависимую переменную, которую необходимо смоделировать. К сожалению, для тех ученых, кто думает, что х и у это только координаты, независимая переменная в регрессионном анализе всегда обозначается как y, а зависимая – всегда X. Каждая независимая переменная связана с коэффициентами регрессии, описывающими силу и знак взаимосвязи между этими двумя переменными. Уравнение регрессии может выглядеть следующим образом (у – зависимая переменная, Х – независимые переменные, β – коэффициенты регрессии), ниже приводится описание каждого из этих компонентов уравнения регрессии):

Элементы Уравнения регрессии по методу наименьших квадратов

Зависимая переменная (y) – это переменная, описывающая процесс, который вы пытаетесь предсказать или понять (бытовые кражи, осадки). В уравнении регрессии эта переменная всегда находится слева от знака равенства. В то время, как вы можете использовать регрессию для предсказания зависимой величины, вы всегда начинаете с набора хорошо известных у-значений и используете их для калибровки регрессионной модели. Известные у-значения часто называют наблюдаемыми величинами.
Независимые переменные (X) это переменные, используемые для моделирования или прогнозирования значений зависимых переменных. В уравнении регрессии они располагаются справа от знака равенства и часто называются независимыми переменными. Зависимая переменная – это функция независимых переменных. Если вас интересует прогнозирование годового оборота определенного магазина, вы можете включить в модель независимые переменные, отражающие, например, число потенциальных покупателей, расстояние до конкурирующих магазинов, заметность магазина и структуру спроса местных жителей.
Коэффициенты регрессии (β) – это коэффициенты, которые рассчитываются в результате выполнения регрессионного анализа. Вычисляются величины для каждой независимой переменной, которые представляют силу и тип взаимосвязи независимой переменной по отношению к зависимой. Предположим, что вы моделируете частоту пожаров как функцию от солнечной радиации, растительного покрова, осадков и экспозиции склона. Вы можете ожидать положительную взаимосвязь между частотой пожаров и солнечной радиацией (другими словами, чем больше солнца, тем чаще встречаются пожары). Если отношение положительно, знак связанного коэффициента также положителен. Вы можете ожидать негативную связь между частотой пожаров и осадками (другими словами, для мест с большим количеством осадков характерно меньше лесных пожаров). Коэффициенты отрицательных отношений имеют знак минуса. Когда взаимосвязь сильная, значения коэффициентов достаточно большие (относительно единиц независимой переменной, с которой они связаны). Слабая взаимосвязь описывается коэффициентами с величинами около 0; β₀ – это отрезок, отсекаемый линией регрессии.Он представляет ожидаемое значение зависимой величины, если все независимые переменные равны 0.

P-значения. Большинство регрессионных методов выполняют статистический тест для расчета вероятности, называемой р-значением, для коэффициентов, связанной с каждой независимой переменной. Нулевая гипотеза данного статистического теста предполагает, что коэффициент незначительно отличается от нуля (другими словами, для всех целей и задач, коэффициент равен нулю, и связанная независимая переменная не может объяснить вашу модель). Маленькие величины р-значений отражают маленькие вероятности и предполагают, что коэффициент действительно важен для вашей модели со значением, существенно отличающимся от 0 (другими словами, маленькие величины р-значений свидетельствуют о том, что коэффициент не равен 0). Вы бы сказали, что коэффициент с р-значением, равным 0,01, например, статистически значимый для 99 % доверительного интервала; связанные переменные являются эффективным предсказателем. Переменные с коэффициентами около 0 не помогают предсказать или смоделировать зависимые величины; они практически всегда удаляются из регрессионного уравнения, если только нет веских причин сохранить их.

R²/R-квадрат: Статистические показатели составной R-квадрат и скорректированный R-квадрат вычисляются из регрессионного уравнения, чтобы качественно оценить модель. Значение R-квадрат лежит в пределах от 0 до 100 процентов. Если ваша модель описывает наблюдаемые зависимые переменные идеально, R-квадрат равен 1.0 (и вы, несомненно, сделали ошибку; возможно, вы использовали модификацию величины у для предсказания у). Вероятнее всего, вы увидите значения R-квадрат в районе 0,49, например, вы можете интерпретировать подобный результат как «Это модель объясняет 49 % вариации зависимой величины». Чтобы понять, как работает R-квадрат, постройте график, отражающий наблюдаемые и оцениваемые значения у, отсортированные по оцениваемым величинам. Обратите внимание на количество совпадений. Этот график визуально отображает, насколько хорошо вычисленные значения модели объясняют изменения наблюдаемых значений зависимых переменных. Просмотрите иллюстрацию. Скорректированный R-квадрат всегда немного меньше, чем множественный R-квадрат, т.к. он отражает всю сложность модели (количество переменных) и связан с набором исходных данных. Следовательно, скорректированный R-квадрат является более точной мерой для оценки результатов работы модели.

Невязки: Существует необъяснимое количество зависимых величин, представленных в уравнении регрессии как случайные ошибки ε. См. рисунок. Известные значения зависимой переменной используются для построения и настройки модели регрессии. Используя известные величины зависимой переменной (Y) и известные значений для всех независимых переменных (Хs), регрессионный инструмент создаст уравнение, которое предскажет те известные у-значения как можно лучше. Однако предсказанные значения редко точно совпадают с наблюдаемыми величинами. Разница между наблюдаемыми и предсказываемыми значениями у называется невязка или отклонение. Величина отклонений регрессионного уравнения — одно из измерений качества работы модели. Большие отклонения говорят о ненадлежащем качестве модели.

Создание регрессионной модели представляет собой итерационный процесс, направленный на поиск эффективных независимых переменных, чтобы объяснить зависимые переменные, которые вы пытаетесь смоделировать или понять, запуская инструмент регрессии, чтобы определить, какие величины являются эффективными предсказателями. Затем пошаговое удаление и/или добавление переменных до тех пор, пока вы не найдете наилучшим образом подходящую регрессионную модель. Т.к. процесс создания модели часто исследовательский, он никогда не должен становиться простым «подгоном» данных. Он должен учитывать теоретические аспекты, мнение экспертов в этой области и здравый смысл. Вы должным быть способны определить ожидаемую взаимосвязь между каждой потенциальной независимой переменной и зависимой величиной до непосредственного анализа, и должны задать себе дополнительные вопросы, когда эти связи не совпадают.

Особенности регрессионного анализа

Регрессия МНК – это простой метод анализа с хорошо проработанной теорией, предоставляющий эффективные возможности диагностики, которые помогут вам интерпретировать результаты и устранять неполадки. Однако, МНК надежен и эффективен, если ваши данные и регрессионная модель удовлетворяют всем предположениям, требуемым для этого метода (смотри таблицу внизу). Пространственные данные часто нарушают предположения и требования МНК, поэтому важно использовать инструменты регрессии в союзе с подходящими инструментами диагностики, которые позволяют оценить, является ли регрессия подходящим методом для вашего анализа, а приведенная структура данных и модель может быть применена.

Как регрессионная модель может не работать

Серьезной преградой для многих регрессионных моделей является ошибка спецификации. Модель ошибки спецификации — это такая неполная модель, в которой отсутствуют важные независимые переменные, поэтому она неадекватно представляет то, что мы пытаемся моделировать или предсказывать (зависимую величину, у). Другими словами, регрессионная модель не рассказывает вам всю историю. Ошибка спецификации становится очевидной, когда в отклонениях вашей регрессионной модели наблюдается статистически значимая пространственная автокорреляция, или другими словами, когда отклонения вашей модели кластеризуются в пространстве (недооценки – в одной области изучаемой территории, а переоценки – в другой). Благодаря картографированию отклонений регрессии или коэффициентов, связанных с географически взвешенной регрессией, вы сможете обратить ваше внимание на какие-то нюансы, которые вы упустили ранее. Запуск Анализа горячих точек по отклонениям регрессии также может раскрыть разные пространственные режимы, которые можно моделировать при помощи метода наименьших квадратов с региональными показателями или исправлять с использованием географически взвешенной регрессии. Предположим, когда вы картографируете отклонения вашей регрессионной модели, вы видите, что модель всегда заново предсказывает значения в горах, и, наоборот, в долинах, что может значить, что отсутствуют данные о рельефе. Однако может случиться так, что отсутствующие переменные слишком сложны для моделирования или их невозможно подсчитать или слишком трудно измерить. В этих случаях, вы можете воспользоваться ГВР (географически взвешенной регрессией) или другой пространственной регрессией, чтобы получить хорошую модель.

В следующей таблице перечислены типичные проблемы с регрессионными моделями и инструменты в ArcGIS:

Типичные проблемы с регрессией, последствия и решения

Типичные проблемы с регрессией и их решения
Ошибки спецификации относительно независимых переменных.	Когда ключевые независимые переменные отсутствуют в регрессионном анализе, коэффициентам и связанным с ними р-значениям нельзя доверять.	Создайте карту и проверьте невязки МНК и коэффициенты ГВР или запустите Анализ горячих точек по регрессионным невязкам МНК, чтобы увидеть, насколько это позволяет судить о возможных отсутствующих переменных.
Нелинейные взаимосвязи. Просмотрите иллюстрацию.	МНК и ГВР – линейные методы. Если взаимосвязи между любыми независимыми величинами и зависимыми – нелинейны, результирующая модель будет работать плохо.	Создайте диаграмму рассеяния, чтобы выявить взаимосвязи между показателями в модели.Уделите особое внимание взаимосвязям, включающим зависимые переменные. Обычно криволинейность может быть устранена трансформированием величин. Просмотрите иллюстрацию. Альтернативно, используйте нелинейный метод регрессии.
Выбросы данных. Просмотрите иллюстрацию.	Существенные выбросы могут увести результаты взаимоотношений регрессионной модели далеко от реальности, внося ошибку в коэффициенты регрессии.	Создайте диаграмму рассеяния и другие графики (гистограммы), чтобы проверить экстремальные значения данных. Скорректировать или удалить выбросы, если они представляют ошибки. Когда выбросы соответствуют действительности, они не могут быть удалены. Запустить регрессию с и без выбросов, чтобы оценить, как это влияет на результат.
Нестационарность. Вы можете обнаружить, что входящая переменная, может иметь сильную зависимость в регионе А, и в то время быть незначительной или даже поменять знак в регионе B (см. рисунок).	Если взаимосвязь между вашими зависимыми и независимыми величинами противоречит в пределах вашей области изучения, рассчитанные стандартные ошибки будут искусственно раздуты.	Инструмент МНК в ArcGIS автоматически тестирует проблемы, связанные с нестационарностью (региональными вариациями) и вычисляет устойчивые стандартные значения ошибок. Просмотрите иллюстрацию. Когда вероятности, связанные с тестом Koenker, малы (например, < 0,05), у вас есть статистически значимая региональная вариация и вам необходимо учитывать устойчивые вероятности, чтобы определить, является ли независимая переменная статистически значимой или нет. Как правило, результаты моделирования можно улучшить с помощью инструмента Географически взвешенная регрессия.
Мультиколлинеарность. Одна или несколько независимых переменных излишни. Просмотрите иллюстрацию.	Мультиколлинеарность ведет к переоценке и нестабильной/ненадежной модели.	Инструмент МНК в ArcGIS автоматически проверяет избыточность. Каждой независимой переменной присваивается рассчитанная величина фактора, увеличивающего дисперсию. Когда это значение велико (например, > 7,5), избыток является проблемой и излишние показатели должны быть удалены из модели или модифицированы путем создания взаимосвязанных величин или увеличением размера выборки. Просмотрите иллюстрацию.
Противоречивая вариация в отклонениях. Может произойти, что модель хорошо работает для маленьких величин, но становится ненадежна для больших значений. Просмотрите иллюстрацию.	Когда модель плохо предсказывает некоторые группы значений, результаты будут носить ошибочный характер.	Инструмент МНК в ArcGIS автоматически выполняет тест на несистемность вариаций в отклонениях (называемая гетероскедастичность или неоднородность дисперсии) и вычисляет стандартные ошибки, которые устойчивы к этой проблеме. Когда вероятности, связанные с тестом Koenker, малы (например, 0,05), необходимо учитывать устойчивые вероятности, чтобы определить, является ли независимая переменная статистически значимой или нет. Просмотрите иллюстрацию.
Пространственно автокоррелированные отклонения. Просмотрите иллюстрацию.	Когда наблюдается пространственная кластеризация в отклонениях, полученных в результате работы модели, это означает, что имеется переоценённый тип систематических отклонений, модель работает ненадежно.	Запустите инструмент Пространственная автокорреляция (Spatial Autocorrelation) по отклонениям, чтобы убедиться, что в них не наблюдается статистически значимой пространственной автокорреляции. Статистически значимая пространственная автокорреляция практически всегда является симптомом ошибки спецификации (отсутствует ключевой показатель в модели). Просмотрите иллюстрацию.
Нормальное распределение систематической ошибки. Просмотрите иллюстрацию.	Когда невязки регрессионной модели распределены ненормально со средним, близким к 0, р-значения, связанные с коэффициентами, ненадежны.	Инструмент МНК в ArcGIS автоматически выполняет тест на нормальность распределения отклонений. Когда статистический показатель Жака-Бера является значимым (например, 0,05), скорее всего в вашей модели отсутствует ключевой показатель (ошибка спецификации) или некоторые отношения, которые вы моделируете, являются нелинейными. Проверьте карту отклонений и возможно карту с коэффициентами ГВР, чтобы определить, какие ключевые показатели отсутствуют. Просмотр диаграмм рассеяния и поиск нелинейных отношений.

Важно протестировать модель на каждую из проблем, перечисленных выше. Результаты могут быть на 100 % неправильны, если игнорируются проблемы, упомянутые выше.

Пространственная регрессия

Для пространственных данных характерно 2 свойства, которые затрудняют (не делают невозможным) применение традиционных (непространственных) методов, таких как МНК:

Географические объекты довольно часто пространственно автокоррелированы. Это означает, что объекты, расположенные ближе друг к другу более похожи между собой, чем удаленные объекты. Это создает переоцененный тип систематических ошибок для традиционных моделей регрессии.
География важна, и часто наиболее важные процессы нестационарны. Эти процессы протекают по-разному в разных частях области изучения. Эта характеристика пространственных данных может относиться как к региональным вариациям, так и к нестационарности.

Настоящие методы пространственной регрессии были разработаны, чтобы устойчиво справляться с этими двумя характеристиками пространственных данных и даже использовать эти свойства пространственных данных, чтобы улучшать моделирование взаимосвязей. Некоторые методы пространственной регрессии эффективно имеют дело с 1 характеристикой (пространственная автокорреляция), другие – со второй (нестационарность). В настоящее время, нет методов пространственной регрессии, которые эффективны с обеими характеристиками. Для правильно настроенной модели ГВР пространственная автокорреляция обычно не является проблемой.

Пространственная автокорреляция

Существует большая разница в том, как традиционные и пространственные статистические методы смотрят на пространственную автокорреляцию. Традиционные статистические методы видят ее как плохую вещь, которая должна быть устранена, т.к. пространственная автокорреляция ухудшает предположения многих традиционных статистических методов. Для географа или ГИС-аналитика, однако, пространственная автокорреляция является доказательством важности пространственных процессов; это интегральная компонента данных. Удаляя пространство, мы удаляем пространственный контекст данных; это как только половина истории. Пространственные процессы и доказательство пространственных взаимосвязей в данных представляют собой особый интерес, и поэтому пользователи ГИС с радостью используют инструменты пространственного анализа данных. Однако, чтобы избежать переоцененный тип систематических ошибок в вашей модели, вы должны определить полный набор независимых переменных, которые эффективно опишут структуру ваших данных. Если вы не можете определить все эти переменные, скорее всего, вы увидите существенную пространственную автокорреляцию среди отклонений модели. К сожалению, вы не можете доверять результатам регрессии, пока все не устранено. Используйте инструмент Пространственная автокорреляция, чтобы выполнить тест на статистически значимую пространственную автокорреляцию для отклонений в вашей регрессии.

Как минимум существует 3 направления, как поступать с пространственной автокорреляцией в невязках регрессионных моделей.

Изменять размер выборки до тех пор, пока не удастся устранить статистически значимую пространственную автокорреляцию. Это не гарантирует, что в анализе будет полностью устранена проблема пространственной автокорреляции, но она значительно меньше, когда пространственная автокорреляция удалена из зависимых и независимых переменных. Это традиционный статистический подход к устранению пространственной автокорреляции и только подходит, если пространственная автокорреляция является результатом избыточности данных.
Изолируйте пространственные и непространственные компоненты каждой входящей величины, используя методы фильтрации в пространственной регрессии. Пространство удалено из каждой величины, но затем его возвращают обратно в регрессионную модель в качестве новой переменной, отвечающей за пространственные эффекты/пространственную структуру. ArcGIS в настоящее время не предоставляет возможности проведения подобного рода анализа.
Внедрите пространственную автокорреляцию в регрессионную модель, используя пространственные эконометрические регрессионные модели. Пространственные эконометрические регрессионные модели будут добавлены в ArcGIS в следующем релизе.

Региональные вариации

Глобальные модели, подобные МНК, создают уравнения, наилучшим образом описывающие общие связи в данных в пределах изучаемой территории. Когда те взаимосвязи противоречивы в пределах территории изучения, МНК хорошо моделирует эти взаимосвязи. Когда те взаимосвязи ведут себя по-разному в разных частях области изучения, регрессионное уравнение представляет средние результаты, и в случае, когда те взаимосвязи представляют 2 экстремальных значения, глобальное среднее не моделирует хорошо эти значения. Когда ваши независимые переменные испытывают нестационарность (региональные вариации), глобальные модели не подходят, а необходимо использовать устойчивые методы регрессионного анализа. Идеально, вы сможете определить полный набор независимых переменных, чтобы справиться с региональными вариациями в ваших зависимых переменных. Если вы не сможете определить все пространственные переменные, вы снова заметите статистически значимую пространственную автокорреляцию в ваших отклонениях и/или более низкие, чем ожидалось, значения R-квадрат. К сожалению, вы не можете доверять результатам регрессии, пока все не устранено.

Существует как минимум 4 способа работы с региональными вариациями в МНК регрессионных моделях:

Включить переменную в модель, которая объяснит региональные вариации. Если вы видите, что ваша модель всегда «перепредсказывает» на севере и «недопредсказывает» на юге, добавьте набор региональных значений:1 для северных объектов, и 0 для южных объектов.
Используйте методы, которые включают региональные вариации в регрессионную модель, такие как Географически взвешенная регрессия.
Примите во внимание устойчивые стандартные отклонения регрессии и вероятности, чтобы определить, являются ли коэффициенты статистически значимыми. ГВР рекомендуется
Изменить/сократить размер области изучения так, чтобы процессы в пределах новой области изучения были стационарными (не испытывали региональные вариации).

Дополнительные ресурсы

Для большей информации по использованию регрессионных инструментов, см. :

Связанные разделы

Отзыв по этому разделу?

Что такое регрессия программного обеспечения?

Программная регрессия — это ошибка в программном программировании, которая приводит к эффективной регрессии программного обеспечения в одной или нескольких областях. Существует два основных типа программного регресса: функциональный и нефункциональный. Функциональный означает, что программа работает с правильной скоростью, но одна или несколько функций не работают, в то время как нефункциональный означает, что все функции работают, но скорость резко снижается. Событие, такое как обновление, обычно является причиной регрессии. Регрессионное тестирование проверяет программное обеспечение, чтобы убедиться в отсутствии регрессии.

Функциональная программная регрессия — это один из способов проявления программной регрессии. Когда это произойдет, программа продолжит работу на полной скорости, поэтому пользователь может сначала не заметить регресс.

В этом проявлении есть определенные функции, которые больше не работают. Например, если программа может искать файлы, эта функция может больше не работать. Это может повлиять на вспомогательные функции — те, которые обычно не используются — или на основную функцию программы.

Нефункциональная программная регрессия более опасна и ее легче заметить, хотя все функции все еще работают. В этом случае регрессия замедляет выполнение программы, иначе вывод программы будет значительно меньше. Недостаток скорости означает, что программа также может стать уязвимой для злонамеренного кодирования и атак, в результате чего как программа, так и компьютер, на котором она запущена, подвергаются риску взлома. Скорость может стать настолько низкой, что использование программы может оказаться невозможным.

Чтобы произошла регрессия программного обеспечения, должно произойти так называемое событие. Это событие меняет код программного обеспечения и вводит эти ошибки, преднамеренно — что редко — или непреднамеренно. Разработчик может пытаться исправить ошибку или обновить версию, но неправильно вводит некоторый код, который ограничивает программу. Наиболее типичным событием является обновление, поскольку это напрямую влияет на кодирование программы. Другие события включают изменения версии или конфигурации.

Чтобы снизить вероятность регрессии программного обеспечения, обычно используется регрессионное тестирование. Этот тип тестирования смотрит на новую программу и сравнивает ее со всеми старыми версиями программы. Затем он запускает программирование через тест, чтобы увидеть, есть ли какие-либо признаки регрессии, и убедиться, что все кодирование функционирует. Любые признаки регрессивного или неработающего кода будут возвращены разработчику или пользователю и сообщат о том, что регрессировало или где регрессия обнаружена.

ДРУГИЕ ЯЗЫКИ

РЕГРЕССИЯ. Словарь по психоанализу

РЕГРЕССИЯ

Нем.: Regression. – Франц.: rйgression. – Англ.: regression. – Исп.: regresiфn. – Итал.: regressione. – Португ.: tegressвo.

• Если представить психический процесс как движение или развитие, то рецессией называется возврат от уже достигнутой точки к одной из предыдущих.

С точки зрения топики, по Фрейду, регрессия осуществляется в ходе смены психических систем, через которые обычно возбуждение движется в определенном направлении.

С точки зрения времени, регрессия предполагает определенную генетическую последовательность и обозначает возврат субъекта к уже пройденным этапам развития (либидинальные стадии, объектные отношения, (само)отождествления и пр.).

С точки зрения формальной, это переход к менее сложным, менее структурно упорядоченным и менее расчлененным способам выражения и поведения.

• Регрессия – это понятие, которое часто используется в психоанализе и современной психологии; обычно оно означает возврат к предыдущим формам развития мысли, объектных отношений, структуры поведения.

Поначалу Фрейд не интересовался возникновением регрессии. Впрочем, «регрессировать» – значит идти вспять, возвращаться назад, что можно себе представить как в логическом и пространственном, так и во временном смысле.

В «Толковании сновидений» (Die Traumdeutung, 1900) Фрейд ввел понятие регрессии для объяснения сущности сна: сновидные мысли предстают прежде всего в форме чувственных образов, которые преследуют субъекта почти как галлюцинация. Для объяснения этого феномена требуется подойти к нему с точки зрения топики*, чтобы психический аппарат имел вид ориентированной последовательности систем. В состоянии бодрствования возбуждения проходят сквозь эти системы, двигаясь вперед (т. е. от восприятия к движениям), тогда как во время сна мысли не способны разряжаться в движении и устремляются вспять, к системе восприятия (la). Таким образом, вводя понятие «регрессия», Фрейд понимал его прежде всего как понятие

топики (а).

Временное значение регрессии, поначалу неявное, стало усиливаться в концепции Фрейда одновременно с выявлением новых моментов в психосексуальном развитии индивида.

В «Трех очерках по теории сексуальности» (Drei Abhandlungen zur Sexualtheorie, 1905) термин «регрессия» не встречается, однако здесь мы уже видим указания на возможность возврата либидо на обходные пути удовлетворения (2а) и к прежним его объектам (2b). Заметим в этой связи, что те места текста, где речь идет о регрессии, были добавлены лишь в 1915 г. По сути, и сам Фрейд признавал, что мысль о регрессии либидо к предыдущему способу организации возникла лишь в более поздний период (За). В самом деле, для выработки понятия временной регрессии потребовалось (в 1910–1912 г.) прояснить последовательность стадий детского психосексуального развития. В «Предрасположенности к. неврозу навязчивости» (Die Disposition zur Zwangsneurose, 1913), например, Фрейд противопоставлял те случаи, когда «…сексуальная организация, предрасположенная к неврозу навязчивости, раз возникнув, сохраняется до конца», и те случаи, когда «она поначалу замещается организацией более высокого уровня, а затем приходит в регрессивное движение – вниз от этой стадии» (4).

Таким образом, судя по отрывку, добавленному к «Толкованию сновидений» в 1914 г., Фрейду пришлось провести в понятии регрессии внутренние разграничения: «Мы различаем регрессию трех видов: а) топическую, обусловленную функционированием психического аппарата; б) временную, при которой вновь вступают в действие прежние способы психической организации; в) формальную, заменяющую обычные способы выражения и образного представления более примитивными. Эти три формы регрессии в основе своей едины, поскольку более давнее во времени оказывается одновременно и более простым по форме, располагаясь в психической топике вблизи восприятия» (1b).

Топическая регрессия особенно ярко проявляет себя в сновидениях, где она осуществляется до конца. Однако ее можно обнаружить и в патологических процессах, где она распространяется не столь широко (галлюцинация), или в нормальных процессах, где она идет не столь далеко (память).

Понятие формальной регрессии реже использовалось Фрейдом, хотя оно охватывает многие явления, при которых происходит возврат от вторичных процессов к первичным (переход от тождества мысли* к функционированию сообразно с принципом тождества восприятия*). Здесь напрашивается сравнение того, что Фрейд называл формальной регрессией, с нейрофизиологическим «разложением» (поведения, сознания и т. д.) джексоновского типа. Предполагаемый при этом порядок связан не с последовательностью этапов развития индивида, но скорее с иерархией функций и структур.

В рамках временной регрессии Фрейд различает несколько линий: регрессию по отношению к объекту, регрессию по отношению к либидинальной стадии и регрессию по отношению к эволюции Я (Зb).

Все эти различия связаны не только с заботой о строгости классификации. Дело в том, что в некоторых нормальных или патологических структурах различные типы регрессии не совпадают друг с другом; Фрейд отмечал, например, что «…при истерии систематически наблюдается регрессия либидо к первичным сексуальным объектам инцестуозного типа, хотя регрессии к предыдущим стадиям сексуальной организации при этом не происходит» (Зс).

Фрейд настаивал на том, что прошлое ребенка – индивида, а тем самым и всего человечества – навсегда остается в нас: «Первичные состояния всегда могут возникнуть вновь. Первичная психика в собственном смысле слова неуничтожима» (5). Фрейд повторяет эту мысль о возврате к прошлому применительно к самым различным областям – психопатологии, сновидениям, истории культуры, биологии и пр. На обновление прошлого в настоящем указывает также и понятие навязчивого повторения. Для выражения этой мысли Фрейд использует не только термин Regression, но и смежные по смыслу термины – Rьckbildung, Rьckwendung, Rьckgreifen и т. д.

Понятие регрессии прежде всего описательное, как считал и сам Фрейд. И потому его недостаточно для понимания того, каким именно образом субъект осуществляет возврат к прошлому. Некоторые разительные психопатологические состояния подталкивают нас к реалистическому пониманию регрессии: иногда говорят, что шизофреник становится грудным младенцем, кататоник возвращается в зародышевое состояние и т. д. Однако, когда применительно к человеку, страдающему неврозом навязчивости, говорят о регрессии к анальной стадии, это понимается не так, как в предыдущих примерах. В еще более ограниченном смысле можно говорить о регрессии при трансфере, когда речь идет о поведении субъекта в целом.

Хотя все эти фрейдовские разграничения и не позволяют дать понятию регрессии строгое теоретическое обоснование, они по крайней мере запрещают нам мыслить ее как нечто всеобъемлющее. В результате мы видим, что понятие регрессии связано с понятием фиксации, вовсе не сводимым к закреплению поведенческих схем. Если понимать фиксацию как «запись» (см.: Фиксация; Представление как репрезентатор влечения), регрессия может быть истолкована как повторный ввод в действие того, что уже было «записано». Тогда, скажем, «оральную регрессию» (в особенности при прохождении психоанализа) стоило бы понимать так: в своих высказываниях и установках субъект заново открывает то. что Фрейд некогда называл «языком орального влечения» (6).

Линейная регрессия — понимание теории

Дата публикации Nov 26, 2018

Введение в теорию линейной регрессии.

фотоКелли ТунгайнаUnsplash

Я решил перейти от веб-разработки к науке о данных. Для этого я решил изучать науку о данных скучно; читать книги, делать заметки и заниматься самостоятельно. Как я уже сказал, это не самый сексуальный способ узнать что-то новое, но он усиливает вашу дисциплину, и вы создаете хорошую методологию работы, которая является ключом к тому, чтобы быть хорошим специалистом по данным.

В этом посте вы узнаете, что такое линейная регрессия и почему ее полезно знать. Я покажу математику и как оценить точность модели в разных случаях. Наконец, я кратко коснусь множественной линейной регрессии, как добавить эффект взаимодействия.

Предполагая, что вы не боитесь уравнений, и вы уже немного знакомы с наукой о данных, давайте приступим к этому!

Линейная регрессия, вероятно, является самым простым подходом для статистического обучения. Это хорошая отправная точка для более продвинутых подходов, и фактически многие причудливые статистические методы обучения можно рассматривать как расширение линейной регрессии. Следовательно, понимание этой простой модели создаст хорошую базу, прежде чем перейти к более сложным подходам.

Линейная регрессия очень хороша, чтобы ответить на следующие вопросы:

Есть ли связь между 2 переменными?
Насколько прочны отношения?
Какая переменная вносит наибольший вклад?
Насколько точно мы можем оценить влияние каждой переменной?
Насколько точно мы можем предсказать цель?
Являются ли отношения линейными? (Дух)
Есть ли эффект взаимодействия?

Оценка коэффициентов

Предположим, у нас есть только одна переменная и одна цель. Тогда линейная регрессия выражается как:

Уравнение для линейной модели с 1 переменной и 1 целью

В приведенном выше уравнениибетыявляются коэффициентами. Эти коэффициенты — то, что нам нужно, чтобы делать прогнозы с нашей моделью.

Итак, как мы можем найти эти параметры?

Чтобы найти параметры, нам нужно минимизироватьнаименьших квадратовилисумма квадратов ошибок, Конечно, линейная модель не идеальна, и она не будет точно предсказывать все данные, а это означает, что существует разница между фактическим значением и прогнозом. Ошибка легко вычисляется с помощью:

Вычтите прогноз из истинного значения

Но почему ошибки возводятся в квадрат?

Мы возводим в квадрат ошибку, потому что прогноз может быть выше или ниже истинного значения, что приводит к отрицательной или положительной разнице соответственно. Если бы мы не возводили в квадрат ошибки, сумма ошибок могла бы уменьшиться из-за отрицательных различий, а не потому, что модель хорошо подходит. Кроме того, возведение в квадрат ошибок учитывает большие различия, поэтому минимизация квадратов ошибок «гарантирует» лучшую модель. Давайте посмотрим на график, чтобы лучше понять.

Линейная подгонка к набору данных

На приведенном выше графике красные точки — это истинные данные, а синяя линия — линейная модель. Серые линии иллюстрируют ошибки между предсказанными и истинными значениями. Таким образом, синяя линия — это та, которая минимизирует сумму квадратов длины серых линий.

После некоторой математики, которая является слишком тяжелой для поста в блоге, вы можете наконец оценить коэффициенты с помощью следующих уравнений:

гдех бара такжеу барпредставляют собой среднее.

Ницца!

Оцените актуальность коэффициентов

Теперь, когда у вас есть коэффициенты, как вы можете определить, актуальны ли они для прогнозирования вашей цели?

Лучший способ — найтир-значение.р-значениеиспользуется для количественной оценки статистической значимости; это позволяет определить, следует ли отклонить нулевую гипотезу или нет.

Нулевая гипотеза?

Для любой задачи моделирования гипотеза состоит в том, чтоесть некоторая корреляциямежду функциями и целью. Таким образом, нулевая гипотеза противоположна:нет корреляциимежду функциями и целью.

Итак, нахождениер-значениедля каждого коэффициента будет указано, является ли переменная статистически значимой для прогнозирования цели. Как правило, еслир-значениеявляетсяменее чем 0,05: между переменной и целью существует тесная связь.

Оцените точность модели

Вы обнаружили, что ваша переменная была статистически значимой, найдя еер-значение, Большой!

Теперь, как узнать, хороша ли ваша линейная модель?

Чтобы оценить это, мы обычно используем RSE (остаточная стандартная ошибка) и статистику R².

Формула RSE Формула R²

Первая метрика ошибки проста для понимания: чем меньше остаточных ошибок, тем лучше модель соответствует данным (в этом случае, чем ближе данные к линейной зависимости).

Что касается метрики R², он измеряетдоля изменчивости в цели, которая может быть объяснена с помощью функции X Следовательно, при условии линейного отношения, если признак X может объяснить (предсказать) цель, тогда пропорция высока, и значение R² будет близко к 1. Если противоположное верно, значение R² будет тогда ближе к 0.

В реальных жизненных ситуациях никогда не будет единственной функции, чтобы предсказать цель. Итак, выполняем ли мы линейную регрессию по одному объекту за раз? Конечно нет. Мы просто выполняем множественную линейную регрессию.

Уравнение очень похоже на простую линейную регрессию; просто добавьте количество предикторов и соответствующие им коэффициенты:

Уравнение множественной линейной регрессии.пэто количество предикторов

Оцените актуальность предиктора

Ранее в простой линейной регрессии мы оценивали релевантность функции, находя еер-значение,

В случае множественной линейной регрессии мы используем другую метрику: F-статистику.

Формула F-статистики.Nколичество точек данных ипэто количество предикторов

Здесь F-статистика рассчитывается для всей модели, тогда какр-значениеспецифичен для каждого предиктора. Если существует сильная связь, то F будет намного больше 1. В противном случае она будет приблизительно равна 1.

Какбольшечем 1достаточно большой?

Это сложно ответить. Обычно, если имеется большое количество точек данных, F может быть немного больше 1 и предполагать тесную связь. Для небольших наборов данных значение F должно быть намного больше 1, чтобы предполагать тесную связь.

Почему мы не можем использоватьр-значениев этом случае?

Поскольку мы подгоняем много предикторов, нам нужно рассмотреть случай, когда есть много функций (пбольшой). При очень большом количестве предикторов всегда будет около 5%, у которых, случайнор-значениечетноехотя они не являются статистически значимыми.Поэтому мы используем F-статистику, чтобы не рассматривать неважные предикторы как значимые предикторы.

Оцените точность модели

Как и в простой линейной регрессии, R² может использоваться для множественной линейной регрессии. Однако знайте, что добавление большего количества предикторов всегда будет увеличивать значение R², потому что модель обязательно будет лучше соответствовать обучающим данным.

Тем не менее, это не означает, что он будет хорошо работать с тестовыми данными (делая прогнозы для неизвестных точек данных).

Добавление взаимодействия

Наличие нескольких предикторов в линейной модели означает, что некоторые предикторы могут влиять на другие предикторы.

Например, вы хотите предсказать зарплату человека, зная его возраст и количество лет, проведенных в школе. Конечно, чем старше человек, тем больше времени он мог бы проводить в школе. Итак, как мы моделируем этот эффект взаимодействия?

Рассмотрим этот очень простой пример с двумя предикторами:

Эффект взаимодействия при множественной линейной регрессии
Как видите, мы просто умножаем оба предиктора вместе и связываем новый коэффициент. Упрощая формулу, мы теперь видим, что на коэффициент влияет значение другого признака.
Как правило, если мы включаем модель взаимодействия, мы должны включать индивидуальный эффект объекта, даже если егор-значениенезначительный. Это известно какиерархический принцип, Это объясняется тем, что если два предиктора взаимодействуют, то включение их индивидуального вклада окажет небольшое влияние на модель.
Вот и все для теории линейной регрессии! В следующем посте я покажу, как применить то, что мы узнали здесь, для создания линейной модели для подгонки некоторых данных, оценки ее точности и определенияр-значениеи F-статистика.
Дайте мне знать в комментариях о любых вопросах или как я могу улучшить!
Оригинальная статья
Что такое регрессия и как ее строить (для стратегий парного трейдинга)
Многие трейдеры при торговле раночно-нейтральными стратегиями задаются вопросом, а как совершать сделки покупки продажи спреда, на основании чего принимать решение о входе и выходе в позицию.
Сегодня мы рассмотрим вариант входа в сделку основываясь на регрессии акций.
Если откинуть все умные фразы и дать определение регрессии на простом языке, то получается следующее:
Регрессия — это зависимость переменной 1 (в нашем случае акции Газпрома) от независимой переменной 2 (акции ЛУКОЙЛа). Данное выражение будет иметь статическую значимость.
Формула регрессии:
Yt=A+BX(t)+E(t)
Давайте с вами рассчитаем регрессию для акций Газпрома и Лукойла.
Алгоритм построения:
1. Скачиваем исторические дневные данные с финама. www.finam.ru/profile/moex-akcii/gazprom/export/
2. Вставляем все скаченные данные в эксель
3.Выбираем полностью столбцы C и D и строим точечную диаграмму. Это и есть наш график регрессии, который показывает при какой цене на акцию Газпрома, сколько стоит акция ЛУКОЙЛа. Далее добавим линию трейнда на график (линейный)
4. Следующим шагом нам необходимо построить график остатков E(t). На графике корреляции он выглядит следующим образом, теперь нам необходимо преобразовать это все в отдельную диаграмму. Это делается с помощью экселе (см. след. шаг)

5. Заходим в раздел данные Data Analysis и выбираем Regression
6.В появившемся окне Input Y Range заполняем ряд данных акций Газпрома, в окне Input X Range заполняем ряд данных акций ЛУКОЙЛа и обязательно выделяем галочкой пункт Residuals (это и есть график остатков)
7. Далее система вычисляет регрессию и выводит график остатков. Из всего того что эксель нам выдал, для нас будет интересны только две графы 18B(это коэффициент Бетта) и С 24 это данные остатков ( остатки это и есть то значение отклонения от средней линии тренда). Это отклонение говорит нам о том на сколько сильна разница между текущими ценами одной бумаги и другой. При большом отклонении графика остатков от нуля вверх система говорит что спред перекуплен и нам надо продать одну бумагу и купить другую.
8. Строим график остатков

9. Основываясь на данном графике остатков можно формировать позиции на вход и выход по паре Газпром/ЛУКОЙЛ. При сильном отклонении вверх продавать Газпром, покупать Лукойл. У средней закрывать позицию. Аналогично при сильном отклонении графика остатков в низ.
Если будут вопросы, пишите в комментариях.
Кто изобрел понятие о статистической регрессии?
Легендарный математик Карл Фридрих Гаусс (Carl Friedrich Gauss), изобретший метод статистической регрессии, недооценивал свое открытие. Он полагал, что не первый использует его, и был убежден в очевидности подхода. Гаусс публично заявил о своей находке лишь много лет спустя, когда его современник Адриен Мари Лежандр (Andrien-Marie Legendre) независимо от него открыл и опубликовал аналогичный метод.
Заявление Гаусса о том, что он обнаружил статистическую регрессию до Лежандра, спровоцировало один из самых известных споров в истории науки. Не без борьбы, но все же Гауссу удалось доказать свое право считаться первооткрывателем. Сегодня когда-то казавшееся своему автору незначительным открытие лежит в основе современной статистики и науки о данных.
Что такое статистическая регрессия?
Выражаясь простым языком, регрессия — это инструмент, предназначенный для исследования взаимосвязи между переменными. Он часто используется для прогнозирования будущего, и понимания, какие факторы влияют на результат.
Например, если вы хотите выяснить, какую роль играет образование с точки зрения зарплаты, предположить, кто победит на следующих выборах, или спрогнозировать эффект нового препарата, у вас есть отличная возможность — применить регрессию в действии.
Историк статистики Стефан М. Стиглер (Stephen M. Stigler) называет регрессию «автомобилем» статистического анализа: «Несмотря на ограничения, случайные происшествия и несущественные погрешности, данный метод и его многочисленные вариации составляют основу статистического анализа, и в настоящее время известны и оценены почти все из них».
Однако почему когда-то столь очевидная для Гаусса регрессия приобретает определяющее значение в современной науке?
На рубеже XVIII и XIX веков совершенствование способов навигации в океане было, пожалуй, важнейшей научно-практической проблемой. Эпоха Великих географических открытий привела к значительному обогащению и прибыльной торговле, но морские путешествия по-прежнему оставались опасными и ненадежными. Совершенствование технологий в этой области требовало значительных денежных вложений. С более точной навигацией суда и грузы, которые они перевозят, достигали бы целей более эффективно.
Учитывая огромные экономические выгоды, связанные с улучшением навигации и геодезии, в моде были исследования по измерению земли. В это время ключевым инструментом геодезистов стало использование движений других планет и комет по отношению к Земле, как способа понять форму и свойства планеты. Благодаря этим исследованиям, поддерживаемым монархами и аристократами, были улучшены карты и знания о местности, что в свою очередь позволило найти первый быстрый и безопасный путь из Португалии в Индию.
В таком историческом контексте математики Карл Фридрих Гаусс и Адриен Мари Лежандр независимо друг от друга и открыли метод наименьших квадратов (least squares) — важнейший инструмент статистической регрессии.
Наименьшие квадраты — это способ использования данных для количественных прогнозов. Эти прогнозы оптимизированы таким образом, что для любой точки в наборе данных возможность умножения ошибки модели на саму себя (получение квадрата) сводится к минимуму. И Гаусс, и Лежандр использовали метод наименьших квадратов для изучения орбит комет на основе неточных измерений их предыдущего местоположения:
Набор данных, который использовал математик Андриен Мари Лежандр для демонстрации статистической регрессии, впервые опубликованной им в начале XIX века
Благодаря открытию Карла Фридриха Гаусса стало возможным прогнозирование будущего и понимание взаимосвязи вещей

Твитнуть цитату
Проблемы, которыми занимались Гаусс и Лежандр, довольно сложны для понимания, однако сам метод можно объяснить на относительно простом примере. Представьте, что вам предстоит вести урок у пятиклассников. Вам известны пол, рост и вес всех учеников. Вдруг вам таинственно сообщают, что один из учеников сегодня отсутствует, но незнакомец знает только пол и рост школьника, но не его вес. Как вычислить вес ученика?
Существуют различные виды критериев оптимизации (или признаков, по которым судят об оптимальности решения задачи), на которые вы могли бы опереться. Например, критерий, минимизирующий абсолютную погрешность вашей догадки, или тот, который имеет наименьший шанс отличаться больше, чем на 10 фунтов (приблизительно 4,5 кг). Метод наименьших квадратов хорош тем, что минимизирует квадратичную ошибку.
Но что такого особенного в этой квадратичной ошибке? Почему и Гаусс, и Лежандр независимо друг от друга обратили на нее внимание?
Есть две основные причины, по которым квадратичная ошибка была практически сразу принята математическим сообществом. Во-первых, в то время ее было сравнительно легко вычислить (сегодня в меньшей степени). Хотя существует простая формула, с помощью которой можно получить наилучшее предположение для минимизации квадратичной ошибки, вычислить лучшее предположение для любого другого критерия оптимизации, в том числе абсолютную погрешность — серьезное испытание.
Во-вторых, оценка на основе наименьших квадратов имеет некоторые отличные статистические свойства. При определенных условиях вы можете сделать предположение, что ваша ошибка нормально распределяется, что довольно удобно для понимания того, насколько вы можете быть уверены в своей догадке:
Надпись на картинке: слева — нормальное распределение, справа — паранормальное распределение. Автор шутки: Роберт Буксбаум (Robert Buxbaum)
Лежандр первым опубликовал метод наименьших квадратов. В своей работе под названием «Новый метод определения орбит комет» (1805 г.) ученый продемонстрировал оригинальную точку зрения и пример использования наименьшего квадрата регрессии. Лежандр был уверен, что является первооткрывателем метода:
«Из всех принципов, которые могут быть предложены для оценки образца, мы полагаем, что нет более подходящего, более точного и простого, чем метод, который мы использовали… суть метода — в минимизации суммы квадратов отклонений».
К сожалению для Лежандра, один из блестящих умов в истории науки уже работал над той же проблемой.
В чем заслуга Гаусса?
Карл Фредрих Гаусс был одним из величайших математиков в истории и своего рода двигателем науки — его изображение можно было встретить даже на немецких марках
Из-за удивительного вклада в развитие математики Карла Фредриха Гаусса иногда называют «королем математиков». И хотя Лежандр признавал гений Гаусса, не исключено, что в узком кругу он называл Гаусса менее добрыми именами. По академическим меркам Гаусс совершил непристойный поступок, украв заслугу открытия наименьшего квадрата регрессии прямо из-под носа у Лежандра.
В трактате Гаусса «Теория движения небесных тел, обращающихся вокруг Солнца по коническим сечениям» математику удалось решить, казалось бы, неразрешимую проблему расчета планетарных орбит. Главной особенностью теории Гаусса была ее способность предсказать, в какой точке ночного неба появится астероид Церера, чего не мог сделать ни один другой ученый того времени. Большое количество сложных математических и геометрических проблем удалось решить при помощи метода наименьших квадратов.
«Наш принцип, который мы используем с 1795 года, был недавно опубликован Лежандром…» — пишет Гаусс, — «который объясняет несколько иные свойства этого метода». Как и другие математики того времени, Гаусс употребляет королевское «мы».
Лежандр был потрясен. Решение Гаусса претендовать на открытие, опубликованное им ранее, конечно, выглядело сомнительно. Известный историк статистики Стивен Стиглер говорит, что решение Гаусса было «лишено сочувствия». Лежандр отправил Гауссу письмо, чтобы выразить свое разочарование:
«Не без удовольствия я обнаружил, что в своих исследованиях вы использовали тот же метод, который я назвал методом наименьших квадратов в своих наблюдениях за кометами… Признаюсь вам, что я придаю некоторое значение этому маленькому открытию. Поэтому я не буду скрывать от вас, сэр: я испытал некоторое сожаление, что вы, ссылаясь на мою работу, говорите, что обнаружили метод в 1795 году. Не существует открытия, которое нельзя было бы приписать себе, сказав, что те же вещи были найдены на несколько лет раньше; но если не дано этим словам доказательства, состоящего в указании места, где они опубликованы, то это утверждение становится беспредметным и представляет собой только обиду для истинного автора открытия».
Лежандр заканчивает письмо весьма неуважительно:
«У вас хватает собственных богатств и нет необходимости завидовать кому-то. Я совершенно уверен в своем открытии. Кроме того, у меня есть основания оспаривать ваше высказывание».
Гаусс никогда не отступал от своего заявления о том, что он открыл метод первым. Хотя это высказывание выглядело не вполне убедительно, все же преобладающее количество доказательств говорит в пользу Гаусса. Его коллеги подтвердили, что он объяснял им метод наименьших квадратов, и были соответствующие записи расчетов, которые, безусловно, не могли быть сделаны иным методом.
Гаусс не опубликовал свое открытие сразу, потому что предпочитал полностью развить свою идею, прежде чем обнародовать ее. Он руководствовался девизом: «Лучше меньше да лучше». Историк математики Эрик Темпл Белл (Eric Temple Bell) считает, что если бы все теории Гаусса были опубликованы тогда, когда они пришли к нему, в математике произошел бы скачок более, чем на 50 лет вперед.
Сегодня Гаусс считается изобретателем метода наименьших квадратов и регрессии, потому что он предложил более точное описание, чем Лежандр. Стиглер объясняет: «Когда Гаусс опубликовал метод наименьших квадратов, стало очевидно, что в своих исследованиях он продвинулся намного дальше Лежандра как в концептуальном, так и в техническом плане, связав метод вероятности и представив алгоритмы для расчета оценок».
При этом Гаусс не придавал особого значения методу наименьших квадратов, не считая его величайшим открытием. Однажды Фредрих написал коллеге, как он был удивлен, что никто из его предшественников не открыл этот метод ранее. И добавил, что не будет публиковать его, не желая minxit in patrios cineres, что в переводе с латинского означает «осквернять прах своих предков».
Тем не менее, Гаусса всю жизнь беспокоили сомнения людей в том, что именно он открыл регрессию. Р. Л. Плакетт (R.L. Plackett) писал о Гауссе: «Искренное принятие принципа приоритетнее, чем его публикация».
По мнению Стиглера, такого рода приоритетные разногласия характерны для истории научных открытий. И поясняет: «Спор о приоритете свидетельствует о том, что происходит нечто важное»
Хорошо, но причем здесь регрессия?
Будучи первооткрывателями основного свойства регрессии, ни Гаусс, ни Лежандр не употребляли слово «регрессия» относительно своего метода.
Термин был впервые применен к статистике энциклопедистом Фрэнсисом Гальтоном (Francis Galton). Гальтон внес существенный вклад в развитие статистики и генетики. К сожалению, его исследования наследственности также привели к изобретению термина «евгеника» и утверждению права на селекцию лучшего общества.
Гальтон использовал термин «регрессия», чтобы объяснять явления природы. В 1870 году он собрал данные о высоте потомков экстремально высоких и экстремально низких деревьев. Он хотел выяснить, как связаны деревья со своими предками. Ученый опубликовал результаты исследования в 1886 году под названием «Регрессия к среднему в наследственности».
«Из моих наблюдений следует, что потомство не стремится походить на родителей по размеру, но всегда получается более средним — ниже, чем предки, если предки были высокими, и выше, чем предки, если предки были низкими».
В наше время явление, обнаруженное Гальтоном, так и называется — регрессией к среднему. Так, если сегодня чрезвычайно жаркий день, можно ожидать, что завтра тоже будет жарко, но уже не так жарко, как сегодня. Если игрок в бейсбол только что завершил свой лучший сезон в карьере, скорее всего, в следующем году вы будете разочарованы его игрой. За экстремальными событиями следуют более нормальные.
Регрессия к среднему: если сегодня чрезвычайно жаркий день, то завтра будет жарко, но уже не так жарко, как сегодня

Твитнуть цитату
Регрессия стала ассоциироваться с методом наименьших квадратов приблизительно в конце XVIII века. Карл Пирсон (Carl Pearson), один из основателей математической статистики и коллега Гальтона, заметил, что если отметить рост родителей на оси x и их детей на оси y — линия, наилучшим образом соединяющая данные в соответствии с методом, имеет наклон меньше единицы (y < x), что фактически является математическим представлением «регрессии к среднему». Пирсон называет этот наклон на графике «линией регрессии». Таким образом, метод наименьших квадратов и понятие регрессии стали своего рода синонимами:
В 1901 году статистик Карл Пирсон использовал метод “линии регрессии” для расчета наименьших квадратов
Регрессионный анализ, каким мы его знаем сегодня, впервые был озвучен в работе одного из самых известных статистов XX века Р.А. Фишера. Ученый объединил труды Гаусса и Пирсона, чтобы разработать совершенную теорию оценки свойств наименьших квадратов. Благодаря работе Фишера, регрессионный анализ используется не только для прогнозирования и понимания корреляции, но и для того, чтобы сделать вывод (иногда неверный) о взаимосвязи между фактором и результатом. После Фишера появилось много важных расширений метода, в том числе логистическая регрессия, непараметрическая регрессия, регрессия Байеса и регрессия, включающая регуляризацию.
Развитие вычислительной техники сделало регрессию популярным методом. В 20-е годы XX века IBM создала автоматизированные табуляторы с перфокартами, которые можно было использовать для проведения сложных вычислений статистического анализа, таких как регрессия. До этого все расчеты делались вручную — регрессию можно было рассчитать для очень небольших наборов данных или тех, для которых приходилось производить в уме ряд вычислительных операций.
Вплоть до 1970-х годов вычисления для получения регрессии занимали несколько дней, и технология была доступна ограниченному числу исследователей. Только с появлением персонального компьютера использование регрессионного анализа стало массовым. Сегодня любой человек, имеющий персональный компьютер, может рассчитать регрессию для небольшого объема данных меньше, чем за секунду.
Гаусс и Лежандр удивились бы, узнав, что метод наименьших квадратов так популярен сегодня. Регрессионный анализ часто используется учеными, политическими аналитиками, журналистами и даже спортивными командам, чтобы предсказать будущее и понять прошлое. С развитием более сложных алгоритмов прогнозирования и формулирования выводов, старый добрый метод наименьших квадратов не утратил своей актуальности и по-прежнему остается жемчужиной статистического анализа.
Высоких вам конверсий!
По материалам: priceonomics.com, image source thcastor
16-12-2015
Регрессионный анализ — формулы, объяснения, примеры и определения
Что такое регрессионный анализ?
Регрессионный анализ — это набор статистических методов, используемых для оценки взаимосвязей между зависимой переменной и одной или несколькими независимыми переменными. (результат). Его можно использовать для оценки силы взаимосвязи между переменными и для моделирования будущей взаимосвязи между ними.
Регрессионный анализ включает несколько вариантов, таких как линейный, множественный линейный и нелинейный. Самые распространенные модели — простые линейные и множественные линейные. Нелинейный регрессионный анализ обычно используется для более сложных наборов данных, в которых зависимые и независимые переменные показывают нелинейную взаимосвязь.
Регрессионный анализ предлагает множество приложений в различных дисциплинах, включая финансы.
Регрессионный анализ — предположения линейной модели
Линейный регрессионный анализ основан на шести фундаментальных предположениях:
Зависимые и независимые переменные показывают линейную зависимость между наклоном и точкой пересечения.
Независимая переменная не случайна.
Значение невязки (ошибки) равно нулю.
Значение невязки (ошибки) постоянно для всех наблюдений.
Значение невязки (ошибки) не коррелировано по всем наблюдениям.
Остаточные (ошибочные) значения соответствуют нормальному распределению.
Регрессионный анализ — Простая линейная регрессия
Простая линейная регрессия — это модель, которая оценивает взаимосвязь между зависимой переменной и независимой переменной.Простая линейная модель выражается с помощью следующего уравнения:
Y = a + bX + ϵ
Где:
Y — Зависимая переменная
X — Независимая (пояснительная) переменная
a — Пересечение
b — Наклон
ϵ — Остаточный (ошибка)
Регрессионный анализ — Множественная линейная регрессия
Множественный линейный регрессионный анализ по существу аналогичен простой линейной модели, за исключением того, что в модели используются несколько независимых переменных.Математическое представление множественной линейной регрессии:
Y = a + b
X ₁ + c X ₂ + d X ₃ + ϵ
Где:
Y — Зависимая переменная
X ₁, X ₂, X ₃ — Независимые (объясняющие) переменные
a — Пересечение
b, c, d — Наклоны
ϵ — Невязка (ошибка)
Множественная линейная регрессия следует тем же условиям, что и простая линейная модель.Однако, поскольку в множественном линейном анализе есть несколько независимых переменных, существует еще одно обязательное условие для модели:
Неколлинеарность: Независимые переменные должны показывать минимальную корреляцию друг с другом. Если независимые переменные сильно коррелированы друг с другом, будет трудно оценить истинные отношения между зависимыми и независимыми переменными.
Регрессионный анализ в финансах
Регрессионный анализ имеет несколько приложений в финансах.Например, статистический метод является фундаментальным для модели ценообразования капитальных активов (CAPM). Модель ценообразования капитальных активов (CAPM). Модель ценообразования капитальных активов (CAPM) — это модель, которая описывает взаимосвязь между ожидаемой доходностью и риском ценной бумаги. Формула CAPM показывает, что доходность ценной бумаги равна безрисковой доходности плюс премия за риск на основе бета-версии этой ценной бумаги. По сути, уравнение CAPM — это модель, которая определяет взаимосвязь между ожидаемой доходностью актива и премией за рыночный риск.
Анализ также используется для прогнозирования доходности ценных бумаг на основе различных факторов или для прогнозирования эффективности бизнеса. Узнайте больше о методах прогнозирования в курсе CFI по бюджетированию и прогнозированию!
1. Бета и CAPM
В финансах для расчета бета-бета используется регрессионный анализ. Бета (β) инвестиционной ценной бумаги (т. Е. Акции) является мерой ее волатильности доходности относительно всего рынка. Он используется в качестве меры риска и является неотъемлемой частью модели ценообразования капитальных активов (CAPM).Компания с более высокой бета-версией имеет больший риск, а также большую ожидаемую доходность. (волатильность доходности по отношению к рынку в целом) для акции. Это можно сделать в Excel с помощью функции наклона Функция наклона Функция наклона относится к категории статистических функций Excel. Он вернет наклон линии линейной регрессии через точки данных в известных_y и известных_x. В финансовом анализе SLOPE может быть полезен при расчете бета-версии акции. Формула = LOPE (известные_y, известные_x) Функция использует расширение.
Скачать бесплатный бета-калькулятор CFI Калькулятор бета-версииЭтот бета-калькулятор позволяет измерить волатильность доходности отдельной акции относительно всего рынка. Бета (β) инвестиционной ценной бумаги (т. Е. Акции) является мерой волатильности ее доходности относительно всего рынка. Он используется как мера риска и является неотъемлемой частью Cap!
2. Прогнозирование доходов и расходов
При прогнозировании финансовой отчетности Финансовое прогнозирование Финансовое прогнозирование — это процесс оценки или прогнозирования того, как бизнес будет работать в будущем.В этом руководстве о том, как построить финансовый прогноз для компании, может быть полезно провести множественный регрессионный анализ, чтобы определить, как изменения в определенных допущениях или драйверах бизнеса повлияют на доходы или расходы в будущем. Например, может быть очень высокая корреляция между количеством продавцов, нанятых компанией, количеством магазинов, которыми они управляют, и доходом, который приносит бизнес.
В приведенном выше примере показано, как использовать функцию прогнозирования Функция прогнозирования Функция прогнозирования относится к категории статистических функций Excel.Он рассчитает или спрогнозирует для нас будущую стоимость с использованием существующих значений. В финансовом моделировании функция прогноза может быть полезна при вычислении статистической ценности сделанного прогноза. Например, если мы знаем прошлые доходы и в Excel, чтобы рассчитать доход компании на основе количества показанных объявлений.
Узнайте больше о методах прогнозирования в курсе CFI по бюджетированию и прогнозированию!
Инструменты регрессии
Excel остается популярным инструментом для проведения базового регрессионного анализа в финансах, однако есть еще много более сложных статистических инструментов, которые можно использовать.
Python и R — мощные языки программирования, ставшие популярными для всех типов финансового моделирования, включая регрессию. Эти методы составляют основную часть науки о данных и машинного обучения, где модели обучаются обнаруживать эти отношения в данных.
Узнайте больше о регрессионном анализе, Python и машинном обучении в сертификации CFI Business Intelligence & Data Analysis.
Дополнительные ресурсы
Чтобы узнать больше о связанных темах, ознакомьтесь со следующими бесплатными ресурсами CFI:
Анализ поведения затрат
Навыки финансового моделирования организации Навыки финансового моделирования Изучите 10 наиболее важных навыков финансового моделирования и то, что необходимо для хорошего финансового моделирования в Excel.Важнейшие навыки: бухгалтерский учет
Методы прогнозированияМетоды прогнозированияЛучшие методы прогнозирования. В этой статье мы объясним четыре типа методов прогнозирования доходов, которые финансовые аналитики используют для прогнозирования будущих доходов.
Метод «высокая-низкая» Метод «высокая-низкая» В учете затрат метод «высокая-низкая» — это метод, используемый для разделения смешанных затрат на переменные и постоянные. Хотя метод high-low
Что такое линейная регрессия? — Статистические решения
Линейная регрессия — это основной и часто используемый тип прогнозного анализа.Общая идея регрессии состоит в том, чтобы исследовать две вещи: (1) хорошо ли помогает набор переменных-предикторов предсказывать переменную результата (зависимую)? (2) Какие переменные, в частности, являются значимыми предикторами переменной результата и каким образом они — на что указывает величина и знак бета-оценок — влияют на переменную результата? Эти оценки регрессии используются для объяснения взаимосвязи между одной зависимой переменной и одной или несколькими независимыми переменными. Простейшая форма уравнения регрессии с одной зависимой и одной независимой переменной определяется формулой y = c + b * x, где y = оценочная оценка зависимой переменной, c = константа, b = коэффициент регрессии и x = оценка по независимая переменная.
Именование переменных. Есть много имен зависимой переменной регрессии. Ее можно назвать выходной переменной, критериальной переменной, эндогенной переменной или регрессионным выражением. Независимые переменные можно назвать экзогенными переменными, переменными-предикторами или регрессорами.
Три основных применения регрессионного анализа: (1) определение силы предикторов, (2) прогнозирование эффекта и (3) прогнозирование тенденций.
Узнайте, как мы помогаем редактировать главы вашей диссертации
Согласование теоретической основы, сбор статей, обобщение пробелов, формулирование четкой методологии и плана данных, а также описание теоретических и практических последствий вашего исследования — это часть наших комплексных услуг по редактированию диссертаций.
Своевременно вносить экспертизу по редактированию диссертаций на главы 1-5.
Отслеживайте все изменения, а затем работайте с вами, чтобы писать научные статьи.
Постоянная поддержка по обратной связи с комитетом, сокращение количества исправлений.
Во-первых, регрессия может использоваться для определения силы воздействия, которое независимая (ые) переменная (ы) оказывает на зависимую переменную. Типичные вопросы: какова сила взаимосвязи между дозой и эффектом, расходами на продажи и маркетинг или возрастом и доходом.
Во-вторых, его можно использовать для прогнозирования эффектов или воздействия изменений. То есть регрессионный анализ помогает нам понять, насколько изменяется зависимая переменная при изменении одной или нескольких независимых переменных. Типичный вопрос: «Какой дополнительный доход от продаж я получу за каждую дополнительную 1000 долларов, потраченных на маркетинг?»
В-третьих, регрессионный анализ предсказывает тенденции и будущие значения. Для получения точечных оценок можно использовать регрессионный анализ. Типичный вопрос: «Какой будет цена на золото через 6 месяцев?»
Типы линейной регрессии
Простая линейная регрессия
1 зависимая переменная (интервал или отношение), 1 независимая переменная (интервал, отношение или дихотомия)
Множественная линейная регрессия
1 зависимая переменная (интервал или отношение), 2+ независимых переменных (интервал, отношение или дихотомия)
Логистическая регрессия
1 зависимая переменная (дихотомическая), 2+ независимая (ые) переменная (ы) (интервальная, или пропорциональная, или дихотомическая)
Порядковая регрессия
1 зависимая переменная (порядковая), 1+ независимых переменных (номинальных или дихотомических)
Мультиномиальная регрессия
1 зависимая переменная (номинальная), 1+ независимая (ые) переменная (ы) (интервал, соотношение или дихотомия)
Дискриминантный анализ
1 зависимая переменная (номинальная), 1+ независимая переменная (и) (интервал или соотношение)
При выборе модели для анализа важным моментом является подгонка модели.Добавление независимых переменных в модель линейной регрессии всегда будет увеличивать объясненную дисперсию модели (обычно выражаемую как R²). Однако переобучение может произойти из-за добавления в модель слишком большого количества переменных, что снижает возможность обобщения модели. Бритва Оккама очень хорошо описывает проблему — простая модель обычно предпочтительнее более сложной. Статистически, если модель включает большое количество переменных, некоторые из них будут статистически значимыми только благодаря случайности.
Для ссылки на эту страницу: Статистические решения. (2013). Что такое линейная регрессия. Получено отсюда.
Связанные страницы:
Предположения линейной регрессии
Statistics Solutions может помочь с количественным анализом, помогая разработать методологию и главы с результатами. Услуги, которые мы предлагаем, включают:
План анализа данных
Измените свои исследовательские вопросы и нулевые / альтернативные гипотезы
Напишите свой план анализа данных; указать конкретную статистику для ответа на вопросы исследования, допущения статистики и обосновать, почему они являются подходящей статистикой; предоставить ссылки
Обоснуйте размер вашей выборки / анализ мощности, предоставьте ссылки
Объясните вам свой план анализа данных, чтобы вы чувствовали себя комфортно и уверенно
Два часа дополнительной поддержки у вашего статистика
Раздел количественных результатов (Описательная статистика, двумерный и многомерный анализ, моделирование структурных уравнений, анализ траектории, HLM, кластерный анализ)
Чистый и кодовый набор данных
Проведение описательной статистики (т.е., среднее значение, стандартное отклонение, частота и процент, в зависимости от случая)
Проведите анализ для изучения каждого из вопросов вашего исследования
Результаты повторной записи
Предоставьте APA 6 ^{-е издание}, таблицы и рисунки
Объяснение выводов по главе 4
Постоянная поддержка всей статистики по главам результатов
Пожалуйста, позвоните 727-442-4290, чтобы запросить расценки на основе специфики вашего исследования, расписания с использованием календаря на этой странице или по электронной почте [адрес электронной почты защищен]
Когда мне следует использовать регрессионный анализ?
Используйте регрессионный анализ для описания отношений между набором независимых переменных и зависимой переменной.Регрессионный анализ создает уравнение регрессии, в котором коэффициенты представляют отношения между каждой независимой переменной и зависимой переменной. Вы также можете использовать уравнение для прогнозов.
Как статистик, я, вероятно, должен сказать вам, что люблю все статистические анализы одинаково — как родителей со своими детьми. Но, шшш, у меня есть секрет! Мне больше всего нравится регрессионный анализ, потому что он обеспечивает огромную гибкость, что делает его полезным во многих различных обстоятельствах.Фактически, я описал регрессионный анализ как вывод корреляции на новый уровень!
В этом сообщении в блоге я объясняю возможности регрессионного анализа, типы взаимосвязей, которые он может оценивать, как он контролирует переменные и в целом, почему мне это нравится! Вы узнаете, когда следует рассмотреть возможность использования регрессионного анализа.
Связанное сообщение : Что такое независимые и зависимые переменные?
Использование регрессии для анализа различных взаимосвязей
Регрессионный анализ может справиться со многими вещами.Например, вы можете использовать регрессионный анализ, чтобы сделать следующее:
Все эти способности классные, но они не включают почти магические способности. Регрессионный анализ может решить очень сложные проблемы, в которых переменные запутаны, как спагетти. Например, представьте, что вы исследователь, изучающий любое из следующего:
Влияют ли социально-экономический статус и раса на успеваемость?
Влияют ли образование и IQ на заработок?
Влияют ли физические упражнения и диета на вес?
Связаны ли употребление кофе и курение сигарет с риском смертности?
Влияет ли конкретное упражнение на плотность костной ткани в отличие от других физических нагрузок?
Подробнее о двух последних примерах позже!
Все эти исследовательские вопросы связаны между собой независимыми переменными, которые могут влиять на зависимые переменные.Как распутать паутину связанных переменных? Какие переменные статистически значимы и какую роль играет каждая из них? На помощь приходит регрессия, потому что вы можете использовать ее для всех этих сценариев!
Использование регрессионного анализа для управления независимыми переменными
Как я уже упоминал, регрессионный анализ описывает, как изменения каждой независимой переменной связаны с изменениями в зависимой переменной. Важно отметить, что регрессия также статистически контролирует каждую переменную в вашей модели.
Что означает контроль переменной?
При выполнении регрессионного анализа необходимо выделить роль каждой переменной. Например, я участвовал в исследовании интервенционных упражнений, где нашей целью было определить, повысило ли вмешательство минеральную плотность костей у испытуемых. Нам нужно было отделить роль упражнений от всего остального, что может повлиять на минеральную плотность костей, которая варьируется от диеты до другой физической активности.
Для достижения этой цели необходимо минимизировать влияние смешивающих переменных.Регрессионный анализ делает это, оценивая влияние, которое изменение одной независимой переменной оказывает на зависимую переменную, при этом все остальные независимые переменные остаются постоянными. Этот процесс позволяет вам узнать роль каждой независимой переменной, не беспокоясь о других переменных в модели. Опять же, вы хотите изолировать влияние каждой переменной.
Как вы контролируете другие переменные в регрессии?
Прекрасный аспект регрессионного анализа состоит в том, что вы поддерживаете другие независимые переменные постоянными, просто включая их в свою модель! Давайте посмотрим на это в действии на примере.
Недавнее исследование проанализировало влияние потребления кофе на смертность. Первые результаты показали, что более высокое потребление кофе связано с более высоким риском смерти. Однако любители кофе часто курят, и исследователи не включили курение в свою первоначальную модель. После того, как они включили курение в модель, результаты регрессии показали, что потребление кофе снижает риск смертности, в то время как курение увеличивает его. Эта модель изолирует роль каждой переменной, сохраняя при этом постоянную другую переменную.Вы можете оценить эффект от употребления кофе, контролируя курение. Удобно, что вы также контролируете потребление кофе, глядя на эффект курения.
Обратите внимание, что исследование также показывает, как исключение релевантной переменной может привести к ошибочным результатам. Отсутствие важной переменной приводит к тому, что она становится неконтролируемой, и может искажать результаты для переменных, которые вы действительно включаете в модель. Это предупреждение особенно применимо для наблюдательных исследований, где влияние пропущенных переменных может быть несбалансированным.С другой стороны, процесс рандомизации в реальном эксперименте имеет тенденцию равномерно распределять эффекты этих переменных, что уменьшает смещение по пропущенным переменным.
Связанное сообщение : Смешивающие переменные и смещение опущенных переменных
Как интерпретировать результат регрессии
Чтобы ответить на вопросы с помощью регрессионного анализа, вам сначала нужно подобрать и убедиться, что у вас хорошая модель. Затем вы просматриваете коэффициенты регрессии и p-значения. Когда у вас низкое значение p (обычно <0.05) независимая переменная статистически значима. Коэффициенты представляют собой среднее изменение зависимой переменной при изменении независимой переменной (IV) на одну единицу при управлении другими IV.
Например, если вашей зависимой переменной является доход, а ваши IV включают IQ и образование (среди других релевантных переменных), вы можете увидеть следующий результат:
Низкие значения p указывают на статистическую значимость как образования, так и IQ.Коэффициент для IQ показывает, что каждый дополнительный балл IQ увеличивает ваш доход в среднем примерно на 4,80 доллара при одновременном контроле всего остального в модели. Кроме того, дополнительная единица образования увеличивает средний заработок на 24,22 доллара, при этом остальные переменные остаются неизменными.
Регрессионный анализ — это форма логической статистики. P-значения помогают определить, существуют ли отношения, которые вы наблюдаете в своей выборке, в большей совокупности. Я написал целую запись в блоге о том, как интерпретировать коэффициенты регрессии и их p-значения, и настоятельно рекомендую.
Получение достоверных результатов регрессии
Огромные возможности использования регрессии влекут за собой большую ответственность. Извините, но так должно быть. Чтобы получить результаты регрессии, которым можно доверять, вам необходимо сделать следующее:
Использование регрессионного анализа дает вам возможность разделить эффекты сложных исследовательских вопросов. Вы можете распутать спагетти-лапшу, моделируя и контролируя все соответствующие переменные, а затем оценивая роль, которую играет каждая из них.
Существует множество различных процедур регрессионного анализа. Прочтите мой пост, чтобы определить, какой тип регрессии подходит для ваших данных.
Если вы изучаете регрессию и вам нравится подход, который я использую в своем блоге, посмотрите мою электронную книгу!
Связанные
Регрессионный анализ | Раскройте весь потенциал ваших данных
Регрессионный анализ — это невероятно мощный инструмент машинного обучения, используемый для анализа данных.Здесь мы рассмотрим, как это работает, каковы основные типы и что он может сделать для вашего бизнеса.
Что такое регресс в машинном обучении?
Регрессионный анализ — это способ прогнозирования будущих событий между зависимой (целевой) и одной или несколькими независимыми переменными (также известными как предиктор). Например, его можно использовать для прогнозирования взаимосвязи между безрассудным вождением и общим количеством дорожно-транспортных происшествий, вызванных водителем, или, используя бизнес-пример, влияния на продажи и трату определенной суммы денег на рекламу.
Регрессия — одна из наиболее распространенных моделей машинного обучения. Он отличается от моделей классификации, поскольку он оценивает числовое значение, тогда как модели классификации определяют, к какой категории принадлежит наблюдение.
Основное применение регрессионного анализа — это прогнозирование, моделирование временных рядов и поиск причинно-следственных связей между переменными.
Почему это важно?
Regression имеет широкий спектр реальных приложений.Это важно для любой задачи машинного обучения, связанной с непрерывными числами — сюда входит, помимо прочего, множество примеров, в том числе:
·  Финансовое прогнозирование (например, оценка цен на жилье или цены акций)
·  Прогноз продаж и рекламных акций
·  Испытание автомобилей
·  Анализ и прогноз погоды
·  Прогнозирование временных рядов
Регрессионный анализ не только сообщает вам, существует ли значимая взаимосвязь между двумя или более переменными, но и дает конкретные сведения об этой взаимосвязи.В частности, он может оценить силу воздействия, которое несколько переменных окажут на зависимую переменную. Если вы измените значение одной переменной (например, цены), регрессионный анализ должен сказать вам, какое влияние это окажет на зависимую переменную (продажи).
Компании могут использовать регрессионный анализ для проверки влияния переменных, измеренных в различных масштабах. Имея его в своем наборе инструментов, вы можете оценить лучший набор переменных для использования при построении прогнозных моделей, что значительно повысит точность вашего прогнозирования.
Наконец, регрессионный анализ — лучший способ решения задач регрессии в машинном обучении с использованием моделирования данных. Нанося точки данных на диаграмму и пропуская через них наиболее подходящую линию, вы можете предсказать вероятность ошибки каждой точки данных: чем дальше от линии, на которой они расположены, тем выше их ошибка предсказания (эта линия наилучшего соответствия также известна как линия регрессии).
Какие существуют типы регрессии?
1. Линейная регрессия
Один из самых основных типов регрессии в машинном обучении, линейная регрессия, состоит из переменной-предиктора и зависимой переменной, связанных друг с другом линейным образом. Линейная регрессия предполагает использование наиболее подходящей линии, как описано выше.
Вы должны использовать линейную регрессию, когда ваши переменные связаны линейно. Например, если вы прогнозируете влияние увеличения рекламных расходов на продажи. Однако этот анализ подвержен выбросам, поэтому его не следует использовать для анализа наборов больших данных.
2. Логистическая регрессия
Имеет ли ваша зависимая переменная дискретное значение? Другими словами, может ли он иметь только одно из двух значений (0 или 1, истина или ложь, черный или белый, спам или не спам и т. Д.)? В этом случае вы можете использовать логистическую регрессию для анализа ваших данных.
Логистическая регрессия использует сигмовидную кривую, чтобы показать взаимосвязь между целевой и независимыми переменными. Однако следует проявлять осторожность: логистическая регрессия лучше всего работает с большими наборами данных, которые имеют почти равное количество значений в целевых переменных.Набор данных не должен содержать высокой корреляции между независимыми переменными (явление, известное как мультиколлинеарность), поскольку это создаст проблему при ранжировании переменных.
3. Регрессия хребта
Если, однако, у вас есть высокая корреляция между независимыми переменными, гребневая регрессия является более подходящим инструментом. Он известен как метод регуляризации и используется для уменьшения сложности модели. Он вводит небольшое смещение (известное как «штраф за гребневую регрессию»), которое, используя матрицу смещения, делает модель менее подверженной переобучению.
4. Регрессия лассо
Подобно гребневой регрессии, лассо-регрессия — это еще один метод регуляризации, который снижает сложность модели. Это достигается путем запрета абсолютного размера коэффициента регрессии. Это приводит к тому, что значение коэффициента становится ближе к нулю, чего не происходит при регрессии гребня.
Преимущество? Он может использовать выбор объектов, что позволяет выбрать набор объектов из набора данных для построения модели. Используя только необходимые функции и устанавливая остальные как ноль, регрессия лассо позволяет избежать переобучения.
5. Полиномиальная регрессия
Полиномиальная регрессия моделирует нелинейный набор данных с использованием линейной модели. Это то же самое, что вставить квадратный штифт в круглое отверстие. Он работает аналогично множественной линейной регрессии (которая является просто линейной регрессией, но с несколькими независимыми переменными), но использует нелинейную кривую. Он используется, когда точки данных присутствуют нелинейным образом.
Модель преобразует эти точки данных в полиномиальные элементы заданной степени и моделирует их с помощью линейной модели.Это предполагает их наилучшую подгонку с использованием полиномиальной линии, которая изогнута, а не прямой линии, наблюдаемой в линейной регрессии. Однако эта модель может быть подвержена переобучению, поэтому рекомендуется проанализировать кривую ближе к концу, чтобы избежать странных результатов.
Существует больше типов регрессионного анализа, чем перечисленных здесь, но эти пять, вероятно, используются чаще всего. Убедитесь, что вы выбрали правильный вариант, и он может раскрыть весь потенциал ваших данных, направив вас на путь к более глубокому пониманию.
* Хотите узнать больше о том, как с помощью машинного обучения превратить ваши данные в полезные идеи? Свяжитесь с нашей командой сегодня для эксклюзивной консультации.
Простая регрессия
Простая регрессия
PPA 696 МЕТОДЫ ИССЛЕДОВАНИЯ
ПРОСТАЯ РЕГРЕССИЯ
Регрессия
Элементы уравнения регрессии
Оценка уравнения регрессии
шагов в линейной регрессии
Предположения линейной регрессии
Время Регрессия серий
РЕГРЕССИЯ
Наиболее часто используемая форма регрессии является линейной регрессией, и наиболее распространенным типом линейной регрессии является называется обычной регрессией наименьших квадратов.
Линейная регрессия использует значения из существующий набор данных, состоящий из измерений значений двух переменных, X и Y, чтобы разработать модель, которая полезна для прогнозирования значения зависимая переменная Y для заданных значений X.

ЭЛЕМЕНТЫ УРАВНЕНИЕ РЕГРЕССИИ
Уравнение регрессии записывается как Y = а + bX + е
Y — значение зависимой переменной (Y), что предсказывается или объясняется
а или Альфа, постоянная; равно значению Y, когда значение X = 0
b или Beta, коэффициент X; склон линии регрессии; насколько Y изменяется для каждого изменения на одну единицу в ИКС.
X — значение независимой переменной. (X), что предсказывает или объясняет значение Y
e — член ошибки; ошибка в предсказании значения Y, учитывая значение X (не отображается в большинстве регрессионных уравнения).
Например, мы знаем, что среднее скорость машин на автостраде, когда у нас есть 2 патруля на шоссе (средняя скорость = 75 миль / ч) или 10 патрулей на шоссе (средняя скорость = 35 миль / ч).Но какова будет средняя скорость машин на автостраде, когда мы развернуть 5 дорожных патрулей?
Средняя скорость на автостраде (Y) Количество развернутых патрульных машин (X)
75 2
35 10
По нашим известным данным мы можем использовать регрессию формула (вычисления не показаны) для вычисления значений и и получения следующее уравнение: Y = 85 + (-5) X, где
Y — средняя скорость автомобилей на автостраде.
a = 85, или средняя скорость при X = 0
b = (- 5), влияние на Y каждого дополнительного патруля машина развернута
X — количество развернутых патрульных машин
То есть средняя скорость машин на автострада, когда не работают патрули (X = 0) будет 85 миль / ч) на это, или называется Y-hat. Это относится к предсказанному значению Y. Y относится к наблюдаемым значениям Y в наборе данных, используемых для расчета уравнение регрессии.
Вы можете увидеть символы альфа (а) и бета (б) написаны греческими буквами, или вы можете увидеть их написанными на английском языке. письма. Коэффициент независимой переменной может иметь нижний индекс, как и термин для X, например, b ₁ X ₁ (это обычное явление при множественной регрессии).

ОЦЕНКА УРАВНЕНИЕ РЕГРЕССИИ
Теперь у нас есть уравнение регрессии. Но как хорошо уравнение при прогнозировании значений Y для заданных значений X? Для этого оценки, мы обращаемся к мерам ассоциации и мерам статистической значения, которые используются с уравнениями регрессии.
r ²
r ² — мера ассоциации; он представляет собой процент отклонения значений Y, который может быть объясняется знанием значения X.r ² варьируется от минимума 0,0 (ни одна из вариаций не объяснена) до максимального значения +1,0 (все объяснена дисперсия).
у.е.b
s.e.b — стандартная ошибка вычисленного значение b. T-критерий статистической значимости коэффициента: проводится делением значения b на стандартную ошибку. По правилу thumb, t-значение больше 2,0 обычно является статистически значимым но вы должны сверяться с t-таблицей, чтобы быть уверенным.Если t-значение указывает, что коэффициент b статистически значим, это означает, что независимая переменная или X (количество развернутых патрульных машин) следует сохранить в уравнении регрессии, поскольку оно имеет статистически значимая связь с зависимой переменной или Y (средняя скорость в миль / ч). Если бы отношений не было статистически значимо, значение коэффициента b будет (статистически говоря) неотличимы от нуля.
Факс
F — тест на статистическую значимость уравнения регрессии в целом.Он получается делением объясненного отклонение необъяснимым отклонением. По практическому правилу, значение F больше чем 4.0 обычно статистически значимо, но вы должны обращаться к F-таблице быть уверенным. Если F значимо, то уравнение регрессии нам помогает. чтобы понять взаимосвязь между X и Y.
Для нашего примера выше, скажем, мы получили следующие значения:
r ² = 0,9
Зная значение X (количество патрульных машин), мы можем объяснить 90% дисперсии Y (средняя скорость автомобилистов на автостраде).
у.е.b = 1,5
Разделив b на s.e.b, получим значение t = -5 / 1,5 = -3,3. Просматривая t-таблицу, мы находим, что коэффициент равен статистически значимый. Это означает, что независимая переменная X (число числа развернутых патрульных машин) следует сохранить в уравнении регрессии, поскольку имеет статистически значимую связь с зависимой переменной Y (средняя скорость в милях в час).
F = 8.4
Из F-таблицы мы видим, что регрессия уравнение в целом статистически значимо. Это означает, что уравнение регрессии помогает нам понять отношения между X и Y.

ЭТАПЫ ЛИНЕЙНОЙ РЕГРЕССИИ
1. Сформулируйте гипотезу.
2. Сформулируйте нулевую гипотезу.
3. Соберите данные.
4. Вычислите уравнение регрессии.
5. Изучите тесты статистически значимых и меры ассоциации
6.Свяжите статистические данные с гипотезой. Примите или отклоните нулевую гипотезу.
7. Отклоните, примите или пересмотрите исходную гипотезу. Вносите предложения по дизайну исследования и аспектам управления проблемой.
Пример: автопарк хочет знать, стоит ли это больше для обслуживания автомобилей, которыми ездят чаще.
Гипотеза: затраты на техническое обслуживание зависят от пробег машины
Нулевая гипотеза: нет связи между пробег и расходы на обслуживание
Зависимая переменная: Y — стоимость в долларах ежегодное обслуживание автомобиля
Независимая переменная: X — годовой пробег. на одном автомобиле
Данные собираются по каждому автомобилю в автопарке, относительно количества миль, пройденных за год, и затрат на техническое обслуживание на тот год.Вот образец собранных данных.
Автомобильный номер пройденных миль (X) Затраты на ремонт (г)
1 80 000 $ 1,200
2 29 000 $ 150
3 53 000 $ 650
4 13 000 $ 200
5 45 000 $ 325
Уравнение регрессии вычисляется как (вычисления не показано): Y = 50 +.03 X
Например, если X = 50 000, тогда Y = 50 + 0,03 (50 000) = 1550 долларов США
a = 50 или стоимость обслуживания при X = 0; если на машине нет пробега, то годовая стоимость обслуживания = 50 долларов США
b = 0,03 значение, которое Y увеличивается для каждой единицы увеличение X; за каждую дополнительную милю (X) стоимость годового обслуживания увеличивается на 0,03 доллара США
у.е.b = .0005; значение b разделенное пользователя s.e.b = 60,0; t-таблица показывает, что коэффициент b для X статистически значительный (связан с Y)
r ² = 0,90 мы можем объяснить 90% разницы в стоимости ремонта для разных автомобилей если мы знаем пробег для каждой машины
Заключение: отклонить нулевую гипотезу об отсутствии связи и принять гипотезу исследования о том, что пробег влияет на стоимость ремонта.

ДОПУЩЕНИЯ ЛИНЕЙНОЙ РЕГРЕССИИ
Теоретически есть несколько важных предположений. это должно быть выполнено, если будет использоваться линейная регрессия.Это:
1. Как независимые (X), так и зависимые (Y) переменные измеряются на уровне интервала или отношения.
2. Отношения между независимыми (X) и зависимые (Y) переменные линейны.
3. Ошибки в предсказании значения Y распределяются способом, приближающимся к нормальной кривой.
4.Ошибки в предсказании значения Y все независимы друг от друга.
5. Распределение ошибок прогноза. значения Y постоянно, независимо от значения X.
Существует ряд расширенных статистических тесты, которые могут быть использованы для проверки того, являются ли эти предположения правильными. верно для любого данного уравнения регрессии. Однако это выходит за рамки этого обсуждения.

ВРЕМЯ СЕРИЯ РЕГРЕССИЯ
Линейная регрессия полезна для изучения взаимосвязи независимой переменной, которая отмечает переход времени к зависимой переменной при линейной зависимости; то есть, когда есть очевидная тенденция к снижению или повышению данных со временем.
Однако, если тренд зависимой переменной с течением времени не является линейным, то линейная регрессия не захватит отношения.Линейная регрессия не учитывает сезонные, циклические и контрциклические тенденции в данных временных рядов. Также не делает линейная регрессия фиксирует эффекты изменения направления временного ряда данные, ни изменения в скорости изменения с течением времени. Для регрессии временных рядов важно получить график данных с течением времени и проверить его на наличие возможные нелинейные тренды.
Там тоже проблема если значения в одной точке временного ряда определены или строго под влиянием ценностей в предыдущий раз.Это называется автокорреляцией. Это происходит, когда значения зависимой переменной с течением времени не изменяются. распределены случайным образом.
Линейная регрессия может использоваться с планами исследования прерванных временных рядов. Например, скажите реализуется политика по снижению количества несчастных случаев среди подростков драйверы.
1. Данные собираются не менее чем за 20 или 30 периоды времени (месяцы или кварталы) до реализации политики, и затем еще 20 или 30 периодов времени после реализации политики.
2. Одна линейная регрессия выполняется для данные по частоте несчастных случаев за периоды, предшествующие полису.
3. Выполняется еще одна линейная регрессия. для данных по аварийности за период после полиса.
4. Должны быть различия в ценностях. постоянной, коэффициента b, s.e.b и r ² для двух уравнений.
Если есть разница между двумя уравнениями, то политика возымела действие. Если все точки данных (как до, так и после) были включены в уравнение регрессии, Объясненная величина отклонения (r ²) будет довольно низкой. Этот потому что, если есть изменение после введения политики, тренд больше не линейный. Вместо этого есть два разных линейных тренда: один до того, как была введена политика, и еще одна, другая, после того, как она была введен.
При настройке данных для регрессии временных рядов исследователь должен не забыть пронумеровать лет (или другие периоды времени) последовательно от 1 до n. Эти значения для независимой (X) переменной. Значение зависимой переменной — аварийность. Например,
Независимая переменная (X) — год Зависимая переменная (Y) — частота несчастных случаев
1 50 000
2 51 000
3 52 000
4 53 000
Регрессионный анализ: обзор
Регрессионный анализ: обзор
Интерпретация регрессионного анализа
Что такое регрессионный анализ?
Регрессионный анализ — это статистический метод изучения линейных отношений.^[1] Это начинается с предположения общей формы для взаимосвязь, известная как модель регрессии :
Y = α + β ₁ X ₁ + … + β _к X _к + ε.
Пример: В случае с автомобильной компанией руководитель моторпол считает модель
Стоимость = α + β ₁ Пробег + β ₂ Возраст + β ₃ Марка + ε.
Y — зависимая переменная , представляющая количество, которое варьируется от человека к индивид во всем населении, и является основным предметом интереса.Х ₁, …, X _k — это объясняющие переменные (так называемые «независимые переменные»). переменные »), которые также различаются от одного человека к другому и считаются связанными к Y. Наконец, ε — это остаточный член , который представляет собой совокупный эффект всех другие типы индивидуальных различий, явно не идентифицированные в модели. ^[2]
Помимо модели, другим входом в регрессионный анализ являются некоторые релевантные выборочные данные, состоящий из наблюдаемых значений зависимых и объясняющих переменных для выборки члены населения.
Первичный результат регрессионного анализа — это набор оценок регрессии . коэффициенты α, β ₁, …, β _k. Эти оценки сделаны нахождение значений для коэффициентов, которые делают среднюю невязку 0, и стандартное отклонение остаточный срок как можно меньше. Результат обобщен в прогнозе . уравнение :
Y _pred = a + b ₁ X ₁ + … + б _к х _к.
Пример: Подбирая модель, указанную выше, к данным автомобильной компании, получаем:
Стоимость _пред = 107,34 + 29,65 Пробег + 73,96 Возраст + 47,43 Марка.
(Погрузитесь для дальнейшего обсуждения предположений лежащий в основе регрессионный анализ или изучить книгу который иллюстрирует некоторые из лежащих в основе вычислений.)
Зачем нужен регрессионный анализ?
Обычно регрессионный анализ выполняется для одной из двух целей: чтобы предсказать значение зависимой переменной для лиц, для которых некоторая информация, касающаяся объяснительной переменных, или чтобы оценить влияние некоторой объясняющей переменной на зависимая переменная.
Создание индивидуальных прогнозов
Если мы знаем значение нескольких независимых переменных для отдельного человека, но не знаем значение зависимой переменной этого человека, мы можем использовать уравнение прогноза (на основе модель с использованием известных переменных в качестве независимых переменных) для оценки значения зависимая переменная для этого человека.
Чтобы увидеть, насколько нашему прогнозу можно доверять, мы используем стандартную ошибку прогноз ^[3] для построения уверенности интервалы для прогноза.(Изучите книгу, в которой подробное обсуждение стандартной ошибки предсказания.)
Пример: Чтобы спрогнозировать техническое обслуживание и ремонт в следующие двенадцать месяцев расходы на конкретный годовалый Ford, который в настоящее время работает в автомобильной корпорации, мы сначала проведем регрессионный анализ с использованием возраста и make в качестве независимых переменных:
Стоимость _пред = 705,66 + 8,53 Возраст — 54,27 Марка.
Тогда наш прогноз будет 714 долларов.19, а предел погрешности (на уровне уверенности 95%) для прогноз 2,1788 × 124,0141 = 270,20 $.
Если наша цель не сделать прогноз для отдельного человека, а скорее оценить среднее значение зависимой переменной в большом пуле схожих лиц, мы используем стандартную ошибку оценочного среднего вместо этого при вычислении доверительных интервалов.
Пример: Наша оценка средней стоимости содержания годовалых Фордов в рабочем состоянии составляет 714 долларов.19, с погрешностью 2,1788 × 41,573 = 90,58 доллара.
Оценка влияния объясняющей переменной на зависимую переменную
Чтобы оценить «чистый» эффект некоторой объясняющей переменной на зависимую переменной, мы хотим контролировать как можно больше других эффектов. То есть мы хотели бы видеть как наш прогноз изменился бы для человека, если бы эта объясняющая переменная была другой, в то время как все остальные аспекты личности остались прежними.Для этого мы должны всегда используйте наиболее полную доступную модель, т. е. мы должны включать все другие соответствующие факторы как дополнительные независимые переменные. (Погрузитесь для дальнейшего обсуждения.)
Наша оценка воздействия единичной разницы в целевой объясняющей переменной — это ее коэффициент в уравнении прогноза. Степень доверия к нашей оценке измеряется на стандартную ошибку коэффициента .
Пример: Используя модель полной регрессии, мы оцениваем, что средний маржинальный расходы на техническое обслуживание и ремонт, связанные с вождением одного из автомобилей в моторном отсеке, дополнительно 1000 миль — 29 долларов.65, с погрешностью оценки 2.2010 × 3,915 = 8,62 доллара. К лучше понять, почему мы используем наиболее полную доступную модель, обратите внимание, что любой «один из автомобили »имеют определенный возраст и марку, и мы хотим сохранить их неизменными, учитывая дополнительный эффект от вождения еще на 1000 миль.
Определение наличия свидетельства того, что независимая переменная принадлежит к регрессии модель
Учитывая конкретную модель, можно задаться вопросом, может ли конкретная одна из независимых переменных действительно «принадлежит» модели; эквивалентно, можно спросить, имеет ли эта переменная истинное значение коэффициент регрессии отличается от 0 (и, следовательно, может повлиять на прогнозы).
Мы используем стандартный подход проверки классических гипотез: чтобы увидеть, есть ли доказательства, подтверждающие включение переменной в модель, мы начинаем с предположения, что она не принадлежит , т.е. что его истинный коэффициент регрессии равен 0.
Разделив оцененный коэффициент на стандартную ошибку коэффициента, получим t-отношение переменной, которое просто показывает, сколько стандартных отклонений составляет выборка. должна была произойти ошибка, чтобы получить оценочный коэффициент, столь отличный от гипотетическое истинное значение 0.Затем мы спрашиваем, насколько вероятно, что у него было столько выборок. ошибка: это дает уровень значимости выборочных данных по отношению к нулевой гипотезе. что 0 — истинное значение коэффициента. Чем ближе этот уровень значимости к 0%, тем тем сильнее свидетельство против нулевой гипотезы, и, следовательно, тем сильнее свидетельствует о том, что истинный коэффициент действительно отличается от 0, т. е. что переменная принадлежат модели.
Пример: В полной модели уровень значимости t-отношения пробега равен 0.0011%. У нас есть неопровержимые доказательства того, что пробег имеет действительно ненулевой эффект на модель. С другой стороны, уровень значимости t-ratio of make составляет всего 12,998%. У нас есть здесь лишь небольшое свидетельство того, что истинная разница между Фордами и Хондами ненулевая. (Если мы действительно хотим предъявить иск против Hondas, мы потребуем, чтобы предполагаемая разница сохраняются по мере увеличения размера выборки, т. е. по мере сбора большего количества доказательств.)
Измерение объясняющей способности модели
Почему зависимая переменная принимает разные значения для разных членов совокупности? Есть два возможных ответа: «Потому что объясняющие переменные различаются.” «Потому что вещи, которые все еще сидят в остаточном члене, различаются». Полная вариация, наблюдаемая в зависимая переменная может быть разбита на эти два компонента, а коэффициент определение ^[4] — доля от общего вариация, которая объясняется моделью, то есть доля, объясняемая вариацией в объясняющие переменные. Вычитание коэффициента детерминации из 100% указывает на то, что доля вариации зависимой переменной, которую модель не может объяснить.
Пример: Если посмотреть только на пробег, можно объяснить 56% наблюдаемых межмашинных перевозок. изменение годовых затрат на техническое обслуживание. Глядя только на возраст, он не может многое объяснить что-нибудь. Но различия в пробеге и возрасте вместе могут объяснить более 78% различий в расходы. Причина, по которой они могут объяснить больше вместе, чем сумма того, что они могут объяснить по отдельности заключается в том, что пробег маскирует влияние возраста в наших данных. Когда оба включены в регрессию модели влияние пробега отделено от эффекта возраста, и последний эффект затем может быть видимый.
Естественным продолжением будет вопрос относительно важности вариации в объясняющие переменные предназначены для объяснения наблюдаемых вариаций зависимой переменной. Модель бета-веса ^[5] независимых переменных можно сравнить, чтобы ответить на этот вопрос. (Погрузитесь, чтобы обсудить различие между t-отношениями и бета-весами.)
Пример: В полной модели бета-вес пробега примерно в два раза больше, чем у возраст, который, в свою очередь, более чем в два раза больше, чем у производителя.Если спросить: «Почему годовой стоимость обслуживания варьируется от машины к машине? » можно было бы ответить: «В первую очередь потому, что автомобили варьируются в зависимости от того, как далеко они зашли. Второстепенное объяснительное значение имеет то, что они различаются по возрасту. И то, и другое — это тот факт, что одни из них — это Форды, а другие — Хонды, т. Е. Марки варьируются в зависимости от модели. флот ».
Сводка
Шесть «шагов» для интерпретации результата регрессионного анализа:
Посмотрите на уравнение прогнозирования, чтобы увидеть оценку взаимосвязи.
Обратитесь к стандартной ошибке прогноза (в соответствующей модели) при выполнении прогнозы для отдельных лиц и стандартная ошибка оценочного среднего при оценке среднее значение зависимой переменной для большого пула схожих лиц.
Обратитесь к стандартным ошибкам коэффициентов (в наиболее полной модели), чтобы узнать, насколько вы можете доверять оценкам влияния независимых переменных.
Посмотрите на уровни значимости t-соотношений, чтобы увидеть, насколько сильны доказательства в поддержку включая каждую из объясняющих переменных в модели.
Используйте коэффициент детерминации «прилагательное» для измерения потенциала объяснительная сила модели.
Сравните бета-веса независимых переменных, чтобы расположить их в порядке возрастания. объяснительное значение.
[1] Почему важно уметь распутывать линейные отношения? Некоторые интересные отношения — линейные, по сути все управленческие. отношения, по крайней мере, локально линейны, и несколько уловок моделирования помогают преобразовать больше всего часто встречающиеся нелинейные отношения в линейные отношения.
[2] Зависимые и объясняющие переменные, а также остаточный член, можно рассматривать как случайные величины, полученные в результате случайного выбора один член населения, то есть как количества, которые варьируются от одного человека к другому.
[3] Стандартная ошибка прогноза учитывает как наша подверженность ошибкам при использовании значения 0 для индивидуальной остаточной суммы при создании предсказание (измеренное стандартной ошибкой регрессии ) и наше воздействие на ошибка выборки при оценке коэффициентов регрессии (измеряется стандартной ошибкой расчетное среднее ).
[4] Коэффициент детерминации иногда называют «R-квадрат» модели. Некоторые компьютерные пакеты предлагают два коэффициента определение, одно с прилагательным — «скорректировано», «исправлено» или «Беспристрастный» — впереди. Если у вас есть выбор, используйте слово с прилагательным. Если это несколько меньше нуля, читается как 0%.
[5] Бета-вес независимой переменной имеет то же самое знак как оценочный коэффициент этой переменной. Это величина, т.е.е., абсолютное значение, из бета-вес, который имеет значение.
Что такое модель регрессии? — Определение | Значение
Определение: Регрессионная модель используется для исследования взаимосвязи между двумя или более переменными и оценки одной переменной на основе других.
Что означает модель регрессии?
Что такое определение регрессионной модели? В регрессионном анализе переменные могут быть независимыми, которые используются в качестве предикторов или причинно-следственных связей, и зависимыми, которые используются в качестве переменных отклика.В экспериментальных исследованиях независимая переменная X — это переменная, которой можно управлять, а переменная Y — это переменная, которая отражает изменения в независимой переменной X. Например, уровень рекламных расходов в компании зависит от спроса на конкретный продукт. . В выборочных тестах различие между независимыми и зависимыми переменными не так ясно, потому что все переменные случайны. Следовательно, в выборочных тестах причинно-следственная связь отсутствует.
Давайте посмотрим на пример.
Пример
Электроэнергия, потребляемая семьей в течение двух месяцев, и сумма, которую она платит за это потребление, связаны детерминированной зависимостью. Если семья потребляет больше электроэнергии в течение двух месяцев, чем обычно, сумма к оплате будет выше, чем обычно. Это детерминистская причинно-следственная связь.
Однако линейная зависимость не может описывать линейную стохастическую зависимость переменных X и Y, потому что если, например, переменная X является стоимостью продукта, а переменная Y — спросом на этот продукт, соответствующие значения Y будут разные в разных итерациях.

Средняя скорость на автостраде (Y)	Количество развернутых патрульных машин (X)
75	2
35	10

Автомобильный номер	пройденных миль (X)	Затраты на ремонт (г)
1	80 000	$ 1,200
2	29 000	$ 150
3	53 000	$ 650
4	13 000	$ 200
5	45 000	$ 325

Независимая переменная (X) — год	Зависимая переменная (Y) — частота несчастных случаев
1	50 000
2	51 000
3	52 000
4	53 000

Скучно, просто и ограниченно — все это изотоническая регрессия / Хабр

Минутка теории

Методология

Расчеты

Основы регрессионного анализа—ArcGIS Pro | Документация

Пространственные отношения

Применения регрессионного анализа

Термины и концепции регрессионного анализа

Особенности регрессионного анализа

Как регрессионная модель может не работать

Типичные проблемы с регрессией, последствия и решения

Пространственная регрессия

Пространственная автокорреляция

Региональные вариации

Дополнительные ресурсы

Связанные разделы

Что такое регрессия программного обеспечения?

ДРУГИЕ ЯЗЫКИ

РЕГРЕССИЯ. Словарь по психоанализу

Линейная регрессия — понимание теории

Оценка коэффициентов

Оцените актуальность коэффициентов

Оцените точность модели

Оцените актуальность предиктора

Оцените точность модели

Добавление взаимодействия

Что такое регрессия и как ее строить (для стратегий парного трейдинга)

Кто изобрел понятие о статистической регрессии?

Регрессионный анализ — формулы, объяснения, примеры и определения

Что такое регрессионный анализ?

Регрессионный анализ — предположения линейной модели

Регрессионный анализ — Простая линейная регрессия

Y = a + bX + ϵ

Регрессионный анализ — Множественная линейная регрессия

Y = a + b

Регрессионный анализ в финансах

1. Бета и CAPM

2. Прогнозирование доходов и расходов

Инструменты регрессии

Дополнительные ресурсы

Что такое линейная регрессия? — Статистические решения

Узнайте, как мы помогаем редактировать главы вашей диссертации

Типы линейной регрессии

Когда мне следует использовать регрессионный анализ?

Использование регрессии для анализа различных взаимосвязей

Использование регрессионного анализа для управления независимыми переменными

Что означает контроль переменной?

Как вы контролируете другие переменные в регрессии?

Как интерпретировать результат регрессии

Получение достоверных результатов регрессии

Регрессионный анализ | Раскройте весь потенциал ваших данных

Простая регрессия

PPA 696 МЕТОДЫ ИССЛЕДОВАНИЯ

ПРОСТАЯ РЕГРЕССИЯ

РЕГРЕССИЯ

ЭЛЕМЕНТЫ УРАВНЕНИЕ РЕГРЕССИИ

ОЦЕНКА УРАВНЕНИЕ РЕГРЕССИИ

ЭТАПЫ ЛИНЕЙНОЙ РЕГРЕССИИ

ДОПУЩЕНИЯ ЛИНЕЙНОЙ РЕГРЕССИИ

ВРЕМЯ СЕРИЯ РЕГРЕССИЯ

Регрессионный анализ: обзор

Интерпретация регрессионного анализа

Что такое регрессионный анализ?

Зачем нужен регрессионный анализ?

Создание индивидуальных прогнозов

Оценка влияния объясняющей переменной на зависимую переменную

Определение наличия свидетельства того, что независимая переменная принадлежит к регрессии модель

Измерение объясняющей способности модели

Сводка

Что такое модель регрессии? — Определение | Значение

Что означает модель регрессии?

Пример

Добавить комментарий Отменить ответ