Регрессия статистика: Недопустимое название | Наука | Fandom

Автор: | 21.04.2021
Нет комментариев

Содержание

Парная линейная регрессия. Задачи регрессионного анализа

Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.

Линейная регрессия — выраженная в виде прямой зависимость среднего значения какой-либо величины от некоторой другой величины. В отличие от функциональной зависимости y = f(x), когда каждому значению независимой переменной x соответствует одно определённое значение величины y, при линейной регрессии одному и тому же значению x могут соответствовать в зависимости от случая различные значения величины y.

Если в результате наблюдения установлено, что при каждом определённом значении x существует сколько-то (n) значений переменной y, то зависимость средних арифметических значений y от x и является регрессией в статистическом понимании.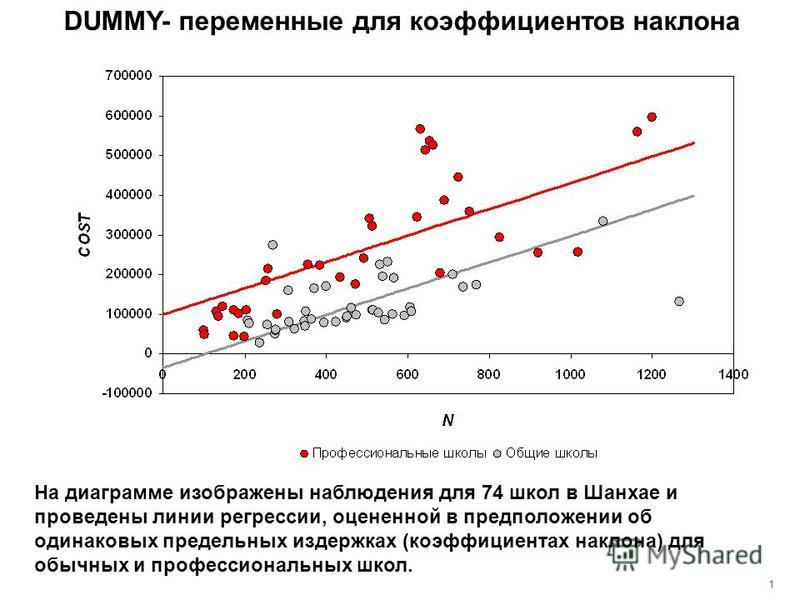

Если установленная зависимость может быть записана в виде уравнения прямой

y = ax + b,

то эта регрессионная зависимость называется линейной регрессией.

О парной линейной регрессии говорят, когда установлена зависимость между двумя переменными величинами (x и y). Парная линейная регрессия называется также однофакторной линейной регрессией, так как один фактор (независимая переменная x) влияет на результирующую переменную (зависимую переменную

y).

В уроке о корреляционной зависимости были разобраны примеры того, как цена на квартиры зависит от общей площади квартиры и от площади кухни (две различные независимые переменные) и о том, что результаты наблюдений расположены в некотором приближении к прямой, хотя и не на самой прямой. Если точки корреляционной диаграммы соединить ломанной линией, то будет получена линия эмпирической регрессии. А если эта линия будет выровнена в прямую, то полученная прямая будет прямой теоретической регрессии

. На рисунке ниже она красного цвета (для увеличения рисунка щёлкнуть по нему левой кнопкой мыши).

По этой прямой теоретической регрессии может быть сделан прогноз или восстановление неизвестных значений зависимой переменной по заданным значениям независимой переменной.

В случае парной линейной регрессии для данных генеральной совокупности связь между независимой переменной (факториальным признаком) X и зависимой переменной (результативным признаком) Y описывает модель

,

где

— свободный член прямой парной линейной регрессии,

— коэффициент направления прямой парной линейной регрессии,

— случайная погрешность,

N — число элементов генеральной совокупности.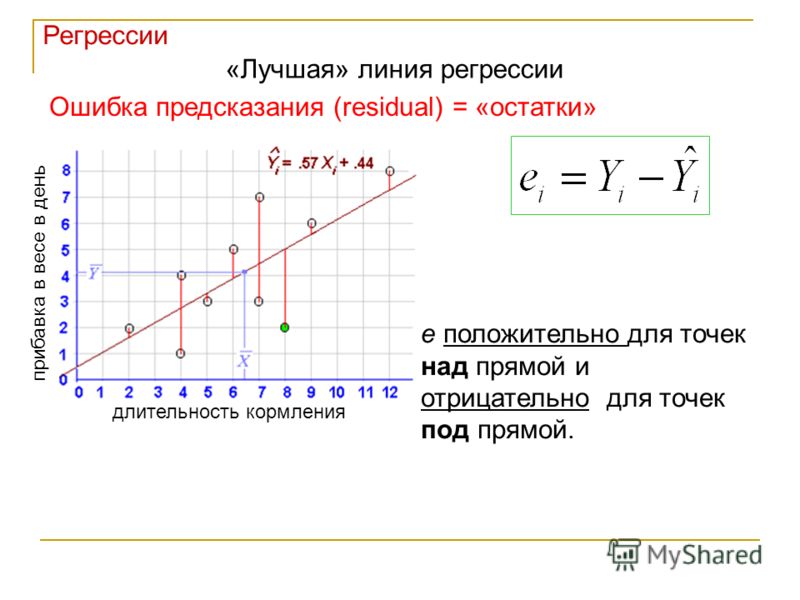

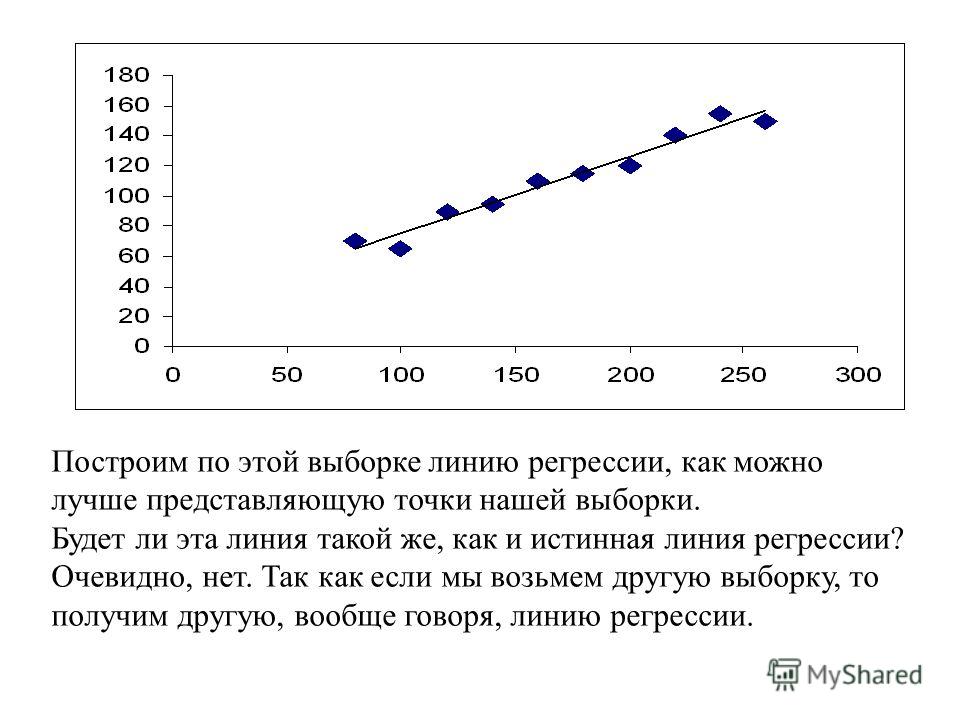
Уравнение парной линейной регрессии для генеральной совокупности можно построить, если доступны данные обо всех элементах генеральной совокупности. На практике данные всей генеральной совокупности недоступны, но доступны данные об элементах некоторой выборки.

Поэтому параметры генеральной совокупности оценивают при помощи соответствующих параметров соответствующей выборки: свободный член прямой парной линейной регрессии генеральной совокупности заменяют на свободный член прямой парной линейной регрессии выборки , а коэффициент направления прямой парной линейной регрессии генеральной совокупности — на коэффициент направления прямой парной линейной регрессии выборки .

В результате получаем уравнение парной линейной регрессии выборки

или

где

— оценка полученной с помощью модели линейной регрессии зависимой переменной Y

,

— погрешность,

n — размер выборки.

Чтобы уравнение парной линейной регрессии было более похоже на привычное уравнение прямой, его часто также записывают в виде

.

Определение коэффициентов уравнения парной линейной регрессии

Если заранее известно, что зависимость между факториальным признаком x и результативным признаком y должна быть линейной, выражающейся в виде уравнения типа  , задача сводится к нахождению по некоторой группе точек наилучшей прямой, называемой прямой парной линейной регрессии. Следует найти такие значения коэффициентов

a и b , чтобы сумма квадратов отклонений была наименьшей:

.

Если через и обозначить средние значения признаков X  и Y,то полученная с помощью метода наименьших квадратов функция регрессии удовлетворяет следующим условиям:

Условие метода наименьших квадратов выполняется, если значения коэффициентов равны:

,

.

Пример 1. Найти уравнение парной линейной регрессии зависимости между валовым внутренним продуктом (ВВП) и частным потреблением на основе данных примера урока о

корреляционной зависимости (эта ссылка, которая откроется в новом окне, потребуется и при разборе следующих примеров).

Решение. Используем рассчитанные в решении названного выше примера суммы:

Используя эти суммы, вычислим коэффициенты:

Таким образом получили уравнение прямой парной линейной регрессии:

Составить уравнение парной линейной регрессии самостоятельно, а затем посмотреть решение

Пример 2. Найти уравнение парной линейной регрессии для выборки из 6 наблюдений, если уже вычислены следующие промежуточные результаты:

;

;

;

;

Правильное решение и ответ.

Метод наименьших квадратов имеет по меньшей мере один существенный недостаток: с его помощью можно найти уравнение линейной регрессии и в тех случаях, когда данные наблюдений значительно рассеяны вокруг прямой регрессии, то есть находятся на значительном расстоянии от этой прямой. В таких случаях за точность прогноза значений зависимой переменной ручаться нельзя. Существуют показатели, которые позволяют оценить качество уравнения линейной регрессии прежде чем использовать модели линейной регрессии для практических целей. Разберём важнейшие из этих показателей.

Коэффициент детерминации

Коэффициент детерминации принимает значения от 0 до 1 и в случае качественной модели линейной регрессии стремится к единице. Коэффициент детерминации показывает, какую часть общего рассеяния зависимой переменной объясняет независимая переменная:

,

где

— сумма квадратов отклонений, объясняемых моделью линейной регрессии, которая характеризует рассеяние точек прямой регрессии относительно арифметического среднего,

— общая сумма квадратов отклонений, которая характеризует рассеяние зависимой переменной Y относительно арифметического среднего,

— сумма квадратов отклонений ошибки (не объясняемых моделью линейной регрессии), которая характеризует рассеяние зависимой переменной Y относительно прямой регресии.

Пример 3. Даны сумма квадратов отклонений, объясняемых моделью линейной регрессии (3500), общая сумма квадратов отклонений (5000) и сумма квадратов отклонений ошибки (1500). Найти коэффициент детерминации двумя способами.

Правильное решение и ответ.

F-статистика (статистика Фишера) для проверки качества модели линейной регрессии

Минимальное возможное значение F-статистики — 0. Чем выше значение статистики Фишера, тем качественнее модель линейной регрессии. Этот показатель представляет собой отношение объясненной суммы квадратов (в расчете на одну независимую переменную) к остаточной сумме квадратов (в расчете на одну степень свободы):

где m — число объясняющих переменных.

Сумма квадратов остатков

Сумма квадратов остатков (RSS) измеряет необъясненную часть дисперсии зависимой переменной:

где

—

остатки — разности между реальными значениями зависимой переменной и значениями, оценёнными уравнением линейной регрессии.

В случае качественной модели линейной регрессии сумма квадратов остатков стремится к нулю.

Стандартная ошибка регрессии

Стандартная ошибка регрессии (SEE) измеряет величину квадрата ошибки, приходящейся на одну степень свободы модели:

Чем меньше значение SEE, тем качественнее модель.

Пример 4. Рассчитать коэффициент детерминации для данных из примера 1.

Решение. На основании данных таблицы (она была приведена в примере урока о корреляционной зависимости) получаем, что SST = 63 770,593, SSE = 10 459,587, SSR = 53 311,007.

Можем убедиться, что выполняется закономерность SSR = SST — SSE:

63770,593-10459,587=53311,007.

Получаем коэффициент детерминации:

.

Таким образом, 83,6% изменений частного потребления можно объяснить моделью линейной регресии.

Итак, уравнение парной линейной регрессии:

.

В этом уравнении a — свободный член, b — коэффициент при независимой переменной.

Интерпретация свободного члена: a показывает, на сколько единиц график регрессии смещён вверх при x=0, то есть значение переменной y при нулевом значении переменной x.

Интерпретация коэффициента при независимой переменной: b показывает, на сколько единиц изменится значение зависимой переменной y при изменении x на одну единицу.

Пример 5. Зависимость частного потребления граждан от ВВП (истолкуем это просто: от дохода) описывается уравнением парной линейной регрессии .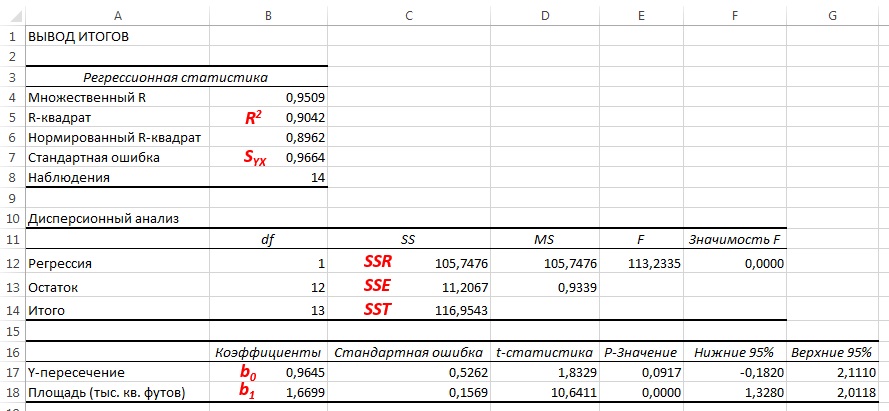 Сделать прогноз потребления при доходе в 20 000 у.е. Выяснить, на сколько увеливается потребление при увеличении дохода на 5000 у.е. Меняется ли потребление, если доход не меняется?

Решение. Подставляем в уравнение парной линейной регрессии xi = 20000 и получаем прогноз потребления при доходе в 20 000 у.е. yi = 17036,4662.

Подставляем в уравнение парной линейной регрессии xi = 5000 и получаем прогноз увеличения потребления при увеличении дохода на 5000 у.е. yi = 4161,9662.

Если доход не меняется, то xi = 0 и получаем, что потребление уменьшается на 129,5338 у.е.

Регрессионный анализ — раздел математической статистики, объединяющий практические методы исследования регрессионной зависимости между величинами по статистическим данным.

Наиболее частые задачи регрессионного анализа:

  • установление факта наличия или отсутствия статистических зависимостей между переменными величинами;
  • выявление причинных связей между переменными величинами;
  • прогноз или восстановление неизвестных значений зависимых переменных по заданным значениям независимых переменных.

Также делаются проверки статистических гипотез о регрессии. Кроме того, при изучении связи между двумя величинами по результатам наблюдений в соответствии с теорией регрессии предполагается, что зависимая переменная имеет некоторое распределение вероятностей при фиксированном значении независимой переменной.

В исследованиях поведения человека, чтобы они претендовали на объективность, важно не только установить зависимость между факторами, но и получить все необходимые статистические показатели для результата проверки соответствующей гипотезы.

Одна из важнейших гипотез в регрессионном анализе — гипотеза о том, что коэффициент направления прямой регрессии генеральной совокупности равен нулю.

Если это предположение верно, то изменения независимой переменной X не влияют на изменения зависимой переменной Y: переменные X и Y не коррелированы, то есть линейной зависимости Y от X нет.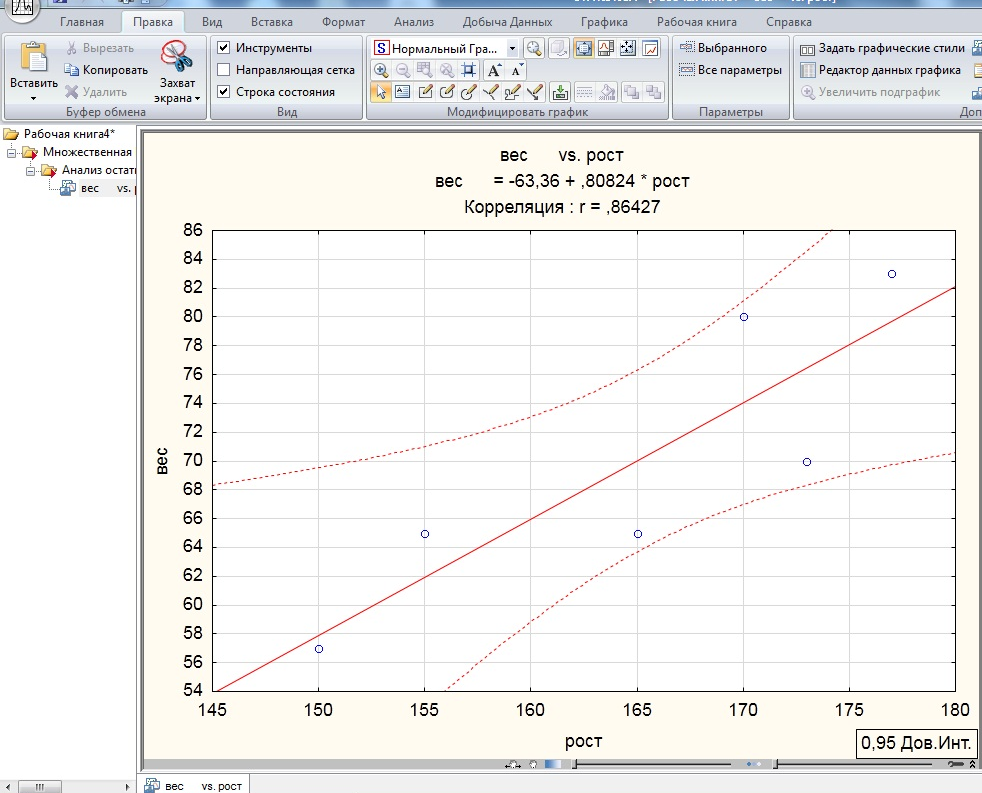

Нулевую гипотезу

рассматривают во взаимосвязи с альтернативной гипотезой

.

Статистика коэффициента направления

соответствует распределению Стьюдента с числом степеней свободы v = n — 2,

где — стандартная погрешность коэффициента направления прямой линейной регресии b1.

Доверительный интервал коэффициента направления прямой линейной регрессии:

.

Критическая область, в которой с вероятностью P = 1 — α отвергают нулевую гипотезу и принимают альтернативную гипотезу:

Пример 6. На основе данных из предыдущих примеров (о ВВП и частном потреблении) определить доверительный интервал коэффициента направления прямой линейной регресии 95% и проверить гипотезу о равенстве нулю коэффициента направления прямой парной линейной регрессии.

Можем рассчитать, что , а стандартная погрешность регрессии .

Таким образом, стандартная погрешность коэффициента направления прямой линейной регресии b1:

.

Так как и (находим по таблице в приложениях к учебникам по статистике), то доверительный интервал 95% коэффициента направления прямой парной линейной регрессии:

.

Так как гипотетическое значение коэффициента — нуль — не принадлежит доверительному интервалу, с вероятностью 95% можем отвергнуть основную гипотезу и принять альтернативную гипотезу, то есть считать, что зависимая переменная Y линейно зависит от независимой переменной X.

Всё по теме «Математическая статистика»

Методы статистики

Критерии и методы


Парная линейная регрессия подробно изучается в медицинских вузах и вполне может считаться рутинным методом. Она определяет значение одного количественного показателя (например, систолическое артериальное давление), исходя из известного значения другого показателя (например, возраста).

Уравнение парной линейной регрессии выглядит как:

y = a·x + b,

где y — зависимый показатель (в приведенном выше примере — систолическое артериальное давление), x — независимый показатель (в примере — возраст), a — коэффициент регрессии, показывающий на сколько вырастет y при увеличении x на 1, b — константа, соответствующая предполагаемому значению y при x=0.

Графиком данной функции является прямая линия, поэтому данный метод называется линейной регрессией.

Однако во многих ситуациях связь между показателями x и y — нелинейна, и ее следует описывать другими математическими функциями. Какие виды нелинейной регрессии наиболее известны?


  1. Полиномиальная регрессия — предполагает возведение x в разные степени (обычно, не выше 3). В зависимости от этого может иметь разные порядки:

    Например, регрессия второго порядка описывается уравнением квадратичной функции:

    y = a·x2 + b·x + c

    Описывает процессы, когда при увеличении x вначале происходит плавное снижение скорости изменения признака y, он достигает своего максимума или минимума («плато»), затем начинает изменяться в противоположном направлении.

    Примеры:

    Зависимость уровня общего тестостерона от содержания 25(OH)D в крови Зависимость доли зубов, пораженных кариесом, от возраста

  2. Гиперболическая (обратная) регрессия — описывает зависимость y от x в форме обыкновенной дроби, где x находится в знаменателе:

    y = 1/(a·x + b) + c

    При a>0 показывает обратную связь между признаками (увеличение одного из них сопровождается снижением другого).

    Примеры:

    Зависимость инфляции от безработицы (кривая Филлипса) Зависимость рейтинга государств по уровню заболеваемости раком молочной железы в зависимости от вклада углеводов в общую калорийность пищи

  3. Показательная регрессия — описывает изменения y в геометрической прогрессии. Здесь x — показатель степени:

    y = a·bx + c

    Если b = е (математическая постоянная, основание натурального логарифма, число Эйлера = 2,718…), такая функция называется экспоненциальной.

    Характеризует изменения с нарастающей скоростью. Вначале прогресс незначительный, но в дальнейшем он стремительно увеличивается.

    Примеры:

    Рост численности населения

  4. Логарифмическая регрессия — описывает зависимость y от логарифма значения х по основанию b:

    y = a·logbx + c

    Характеризует изменения показателя y со снижающейся скоростью. Вначале прогресс — значительный, но постепенно замедляется.

    Примеры:

    Зависимость точности работы нейронной сети от объема обучающей выборки
️

Как выбрать оптимальный вид регрессии? Обычно приходится использовать метод перебора, строя несколько разных функций. Качество приближения модели оценивается по коэффициенту детерминации R2. Зависимость y от x описывается лучше всего тем уравнением, которому соответствует наивысший коэффициент детерминации.

⠀

Статистика — Линейная регрессия — CoderLessons.com

После того, как степень взаимосвязи между переменными была установлена ​​с использованием анализа взаимосвязи, естественно, углубиться в природу взаимосвязи. Регрессионный анализ помогает определить причинно-следственную связь между переменными. Можно предсказать значение других переменных (называемых зависимой переменной), если значения независимых переменных можно предсказать с помощью графического метода или алгебраического метода.

Графический метод

Он включает в себя построение диаграммы рассеяния с независимой переменной на оси X и зависимой переменной на оси Y. После этого линия рисуется таким образом, что она проходит через большую часть распределения, а оставшиеся точки распределены почти равномерно по обе стороны от линии.

Линия регрессии известна как линия наилучшего соответствия, которая суммирует общее движение данных. Он показывает наилучшие средние значения одной переменной, соответствующие средним значениям другой. Линия регрессии основана на критериях того, что это прямая линия, которая минимизирует сумму квадратов отклонений между прогнозируемыми и наблюдаемыми значениями зависимой переменной.

Алгебраический метод

Алгебраический метод строит два уравнения регрессии X на Y и Y на X.

Уравнение регрессии Y на X

Y=a+bX

Где —

  • Y = Зависимая переменная

  • X = Независимая переменная

  • a = Константа, показывающая Y-перехват

  • b = Константа, показывающая наклон линии

Y = Зависимая переменная

X = Независимая переменная

a = Константа, показывающая Y-перехват

b = Константа, показывающая наклон линии

Значения a и b получают с помощью следующих нормальных уравнений:

 sumY=Na+b sumX[7pt] sumXY=a sumX+b sumX2

 sumY=Na+b sumX[7pt] sumXY=a sumX+b sumX2

Где —

N = Количество наблюдений

Уравнение регрессии X на Y

X=a+bY

Где —

  • X = Зависимая переменная

  • Y = Независимая переменная

  • a = Константа, показывающая Y-перехват

  • b = Константа, показывающая наклон линии

X = Зависимая переменная

Y = Независимая переменная

a = Константа, показывающая Y-перехват

b = Константа, показывающая наклон линии

Значения a и b получают с помощью следующих нормальных уравнений:

 sumX=Na+b sumY[7pt] sumXY=a sumY+b sumY2

 sumX=Na+b sumY[7pt] sumXY=a sumY+b sumY2

Где —

N = Количество наблюдений

пример

Постановка задачи:

Исследователь обнаружил, что существует взаимосвязь между весовыми тенденциями отца и сына. В настоящее время он заинтересован в разработке уравнения регрессии по двум переменным по приведенным данным:

Вес отца (в кг) 69 63 66 64 67 64 70 66 68 67 65 71
Вес сына (в кг) 70 65 68 65 69 66 68 65 71 67 64 72

развивать

  1. Уравнение регрессии Y на X.

  2. Уравнение регрессии по Y.

Уравнение регрессии Y на X.

Уравнение регрессии по Y.

Решение:

X X2 Y Y2 XY
69 4761 70 4900 4830
63 3969 65 4225 4095
66 4356 68 4624 4488
64 4096 65 4225 4160
67 4489 69 4761 4623
64 4096 66 4356 4224
70 4900 68 4624 4760
66 4356 65 4225 4290
68 4624 71 5041 4828
67 4489 67 4489 4489
65 4225 64 4096 4160
71 5041 72 5184 5112
 sumX=800  sumX2=53,402  sumY=810  sumY2=54750  sumXY=54,059

Уравнение регрессии Y на X

Y = a + bX

Где a и b получены нормальными уравнениями

 sumY=Na+b sumX[7pt] sumXY=a sumX+b sumX2[7pt]Где  sumY=810, sumX=800, sumX2=53,402[7pt], sumXY=54,049,N=12

 Rightarrow 810 = 12a + 800b … (i)

 Rightarrow 54049 = 800a + 53402 b … (ii)

 Rightarrow 810 = 12a + 800b … (i)

 Rightarrow 54049 = 800a + 53402 b … (ii)

Умножив уравнение (i) на 800 и уравнение (ii) на 12, получим:

96000 a + 640000 b = 648000 … (iii)

96000 + 640824 b = 648588 … (iv)

96000 a + 640000 b = 648000 … (iii)

96000 + 640824 b = 648588 … (iv)

Вычитая уравнение (iv) из (iii)

-824 b = -588

 Rightarrow b = -.0713

-824 b = -588

 Rightarrow b = -.0713

Подставляя значение b в уравнение (я)

810 = 12a + 800 (-0,713)

810 = 12а + 570,4

12а = 239,6

 Rightarrow a = 19,96

810 = 12a + 800 (-0,713)

810 = 12а + 570,4

12а = 239,6

 Rightarrow a = 19,96

Следовательно, уравнение Y на X можно записать в виде

Y=19,96−0,713X

Уравнение регрессии Y на X

X = a + bY

Где a и b получены нормальными уравнениями

 sumX=Na+b sumY[7pt] sumXY=a sumY+b sumY2[7pt]Где  sumY=810, sumY2=54750[7pt], sumXY=54,049,N=12

 Rightarrow 800 = 12a + 810a + 810b … (V)

 Rightarrow 54 049 = 810a + 54 750 … (vi)

 Rightarrow 800 = 12a + 810a + 810b … (V)

 Rightarrow 54 049 = 810a + 54 750 … (vi)

Умножив eq (v) на 810 и eq (vi) на 12, получим

9720 a + 656100 b = 648000 … (vii)

9720 + 65700 b = 648588 … (viii)

9720 a + 656100 b = 648000 … (vii)

9720 + 65700 b = 648588 … (viii)

Вычитание из формулы из уравнения

900b = -588

 Rightarrow b = 0,653

900b = -588

 Rightarrow b = 0,653

Подставляя значение b в уравнение (v)

800 = 12а + 810 (0,653)

12а = 271,07

 Rightarrow a = 22,58

800 = 12а + 810 (0,653)

12а = 271,07

 Rightarrow a = 22,58

Следовательно, уравнение регрессии X и Y

5 видов регрессии и их свойства. При помощи построения регрессионных… | by Margarita M | NOP::Nuances of Programming

Линейная и логистическая регрессии обычно являются первыми видами регрессии, которые изучают в таких областях, как машинное обучение и наука о данных. Оба метода считаются эффективными, так как их легко понять и использовать. Однако, такая простота также имеет несколько недостатков, и во многих случаях лучше выбирать другую регрессионную модель. Существует множество видов регрессии, каждый из которых имеет свои достоинства и недостатки.

Мы познакомимся с 7 наиболее распространенными алгоритмами регрессии и опишем их свойства. Также мы узнаем, в каких ситуация и с какими видами данных лучше использовать тот или иной алгоритм. В конце мы расскажем о некоторых инструментах для построения регрессии и поможем лучше разобраться в регрессионных моделях в целом!

Линейная регрессия

Регрессия — это метод, используемый для моделирования и анализа отношений между переменными, а также для того, чтобы увидеть, как эти переменные вместе влияют на получение определенного результата. Линейная регрессия относится к такому виду регрессионной модели, который состоит из взаимосвязанных переменных. Начнем с простого. Парная (простая) линейная регрессия — это модель, позволяющая моделировать взаимосвязь между значениями одной входной независимой и одной выходной зависимой переменными с помощью линейной модели, например, прямой.

Более распространенной моделью является множественная линейная регрессия, которая предполагает установление линейной зависимости между множеством входных независимых и одной выходной зависимой переменных. Такая модель остается линейной по той причине, что выход является линейной комбинацией входных переменных. Мы можем построить модель множественной линейной регрессии следующим образом:

Y = a_1*X_1 + a_2*X_2 + a_3*X_3 ……. a_n*X_n + b

Где a_n — это коэффициенты, X_n — переменные и b — смещение. Как видим, данная функция не содержит нелинейных коэффициентов и, таким образом, подходит только для моделирования линейных сепарабельных данных. Все очень просто: мы взвешиваем значение каждой переменной X_n с помощью весового коэффициента a_n. Данные весовые коэффициенты a_n, а также смещение b вычисляются с применением стохастического градиентного спуска. Посмотрите на график ниже в качестве иллюстрации!

Иллюстрация поиска оптимальных параметром для линейной регрессии с помощью градиентного спуска

Несколько важных пунктов о линейной регрессии:

  • Она легко моделируется и является особенно полезной при создании не очень сложной зависимости, а также при небольшом количестве данных.
  • Обозначения интуитивно-понятны.
  • Чувствительна к выбросам.

Полиномиальная регрессия

Для создания такой модели, которая подойдет для нелинейно разделяемых данных, можно использовать полиномиальную регрессию. В данном методе проводится кривая линия, зависимая от точек плоскости. В полиномиальной регрессии степень некоторых независимых переменных превышает 1. Например, получится что-то подобное:

Y = a_1*X_1 + (a_2)²*X_2 + (a_3)⁴*X_3 ……. a_n*X_n + b

У некоторых переменных есть степень, у других — нет. Также можно выбрать определенную степень для каждой переменной, но для этого необходимы определенные знания о том, как входные данные связаны с выходными. Сравните линейную и полиномиальную регрессии ниже.

Линейная и полиномиальная регрессии с нелинейно разделенными данными

Несколько важных пунктов о полиномиальной регрессии:

  • Моделирует нелинейно разделенные данные (чего не может линейная регрессия). Она более гибкая и может моделировать сложные взаимосвязи.
  • Полный контроль над моделированием переменных объекта (выбор степени).
  • Необходимо внимательно создавать модель. Необходимо обладать некоторыми знаниями о данных, для выбора наиболее подходящей степени.
  • При неправильном выборе степени, данная модель может быть перенасыщена.

Гребневая (ридж) регрессия

В случае высокой коллинеарности переменных стандартная линейная и полиномиальная регрессии становятся неэффективными. Коллинеарность — это отношение независимых переменных, близкое к линейному. Наличие высокой коллинеарности можно определить несколькими путями:

  • Коэффициент регрессии не важен, несмотря на то, что, теоретически, переменная должна иметь высокую корреляцию с Y.
  • При добавлении или удалении переменной из матрицы X, коэффициент регрессии сильно изменяется.
  • Переменные матрицы X имеют высокие попарные корреляции (посмотрите корреляционную матрицу).

Сначала можно посмотреть на функцию оптимизации стандартной линейной регрессии для лучшего понимания того, как может помочь гребневая регрессия:

min || Xw — y ||²

Где X — это матрица переменных, w — веса, y — достоверные данные. Гребневая регрессия — это корректирующая мера для снижения коллинеарности среди предикторных переменных в регрессионной модели. Коллинеарность — это явление, в котором одна переменная во множественной регрессионной модели может быть предсказано линейно, исходя из остальных свойств со значительной степенью точности. Таким образом, из-за высокой корреляции переменных, конечная регрессионная модель сведена к минимальным пределам приближенного значения, то есть она обладает высокой дисперсией.

Гребневая регрессия добавляет небольшой фактор квадратичного смещения для уменьшения дисперсии:

min || Xw — y ||² + z|| w ||²

Такой фактор смещения выводит коэффициенты переменных из строгих ограничений, вводя в модель небольшое смещение, но при этом значительно снижая дисперсию.

Несколько важных пунктов о гребневой регрессии:

  • Допущения данной регрессии такие же, как и в методе наименьших квадратов, кроме того факта, что нормальное распределение в гребневой регрессии не предполагается.
  • Это уменьшает значение коэффициентов, оставляя их ненулевыми, что предполагает отсутствие отбора признаков.

Регрессия по методу «лассо»

В регрессии лассо, как и в гребневой, мы добавляем условие смещения в функцию оптимизации для того, чтобы уменьшить коллинеарность и, следовательно, дисперсию модели. Но вместо квадратичного смещения, мы используем смещение абсолютного значения:

min || Xw — y ||² + z|| w ||

Существует несколько различий между гребневой регрессией и лассо, которые восстанавливают различия в свойствах регуляризаций L2 и L1:

  • Встроенный отбор признаков — считается полезным свойством, которое есть в норме L1, но отсутствует в норме L2. Отбор признаков является результатом нормы L1, которая производит разреженные коэффициенты. Например, предположим, что модель имеет 100 коэффициентов, но лишь 10 из них имеют коэффициенты отличные от нуля. Соответственно, «остальные 90 предикторов являются бесполезными в прогнозировании искомого значения». Норма L2 производит неразряженные коэффициенты и не может производить отбор признаков. Таким образом, можно сказать, что регрессия лассо производит «выбор параметров», так как не выбранные переменные будут иметь общий вес, равный 0.
  • Разряженность означает, что незначительное количество входных данных в матрице (или векторе) имеют значение, отличное от нуля. Норма L1 производит большое количество коэффициентов с нулевым значением или очень малые значения с некоторыми большими коэффициентами. Это связано с предыдущим пунктом, в котором указано, что лассо исполняет выбор свойств.
  • Вычислительная эффективность: норма L1 не имеет аналитического решения в отличие от нормы L2. Это позволяет эффективно вычислять решения нормы L2. Однако, решения нормы L1 не обладают свойствами разряженности, что позволяет использовать их с разряженными алгоритмами для более эффективных вычислений.

Регрессия «эластичная сеть»

Эластичная сеть — это гибрид методов регрессии лассо и гребневой регрессии. Она использует как L1, так и L2 регуляризации, учитывая эффективность обоих методов.

min || Xw — y ||² + z_1|| w || + z_2|| w ||²

Практическим преимуществом использования регрессии лассо и гребневой регрессии является то, что это позволяет эластичной сети наследовать некоторую стабильность гребневой регрессии при вращении.

Несколько важных пунктов о регрессии эластичной сети:

  • Она создает условия для группового эффекта при высокой корреляции переменных, а не обнуляет некоторые из них, как метод лассо.
  • Нет ограничений по количеству выбранных переменных.

Вывод

Вот и все! 5 распространенных видов регрессии и их свойства. Все данные методы регуляризации регрессии (лассо, гребневая и эластичной сети) хорошо функционирует при высокой размерности и мультиколлинеарности среди переменных в наборе данных.

Перевод статьи George Seif: 5 Types of Regression and their properties

Процедура «Регрессия» пакета «Анализ данных»

Процедура «Регрессия» пакета «Анализ данных»

Процедура решает простейшую задачу парной линейной регрессии:

  – по заданным значениям  , i =1, 2, …, n  строит методом наименьших квадратов линейную функцию регрессии ;

– вычисляет некоторые статистики для анализа качества аппроксимации.

Исходные данные для функции

— выборочные значения , i =1, 2, …, n  

Содержание отчёта о вычислениях, которые выполняются процедурой, определяется пользователем.

Основные численные результаты представлены в трёх таблицах под общим заголовком

 

ВЫВОД ИТОГОВ

 

Регрессионная статистика

Множественный R

 

R-квадрат

 

Нормированный R-квадрат

 

Стандартная ошибка

 

Наблюдения

 

 

 

Здесь:

 

R-квадрат – коэффициент детерминации:   ;

Стандартная ошибка  — стандартная ошибка регрессии:  ,     ;

Наблюдения —  количество наблюдений n.

 

 

Дисперсионный анализ

 

 

 

 

df

SS

MS

F

Значимость F

Регрессия

 

 

 

 

 

Остаток

 

 

 

 

 

Итого

 

 

 

 

 

 

 

 

 

 

 

 

В двух строках таблицы отображаются статистики, относящиеся соответственно к регрессии и к остаткам регрессии:

df — число степеней свободы: ;

SS — сумма квадратов регрессии: ;

MS — среднее суммы квадратов регрессии, сумма квадратов, делённая на число переменных m, в данном случае m = 1.

F — значение критерия Фишера: ;

Значимость F —  вычисленное по выборке значение плотности вероятности распределения Фишера с (1, n-2) степенями свободы;

Следующая таблица — основная таблица, описывающая линию регрессии.

 

 

Коэффициенты

Стандартная

ошибка

t-статистика

P-Значение

Y-пересечение

 

 

 

 

Переменная X 1

 

 

 

 

 

Нижние 95%

Верхние 95%

Нижние

p%

Верхние

p%

 

 

 

 

 

 

 

 

 

В двух строках таблицы отображаются статистики, относящиеся соответственно к константе b (Y-пересечение) и к коэффициенту a  (Переменная X 1) в уравнении линии регрессии y = ax + b:

Коэффициенты — значения коэффициентов соответственно b  и a  в уравнении линии регрессии y = ax + b;

 Стандартная ошибка— стандартная ошибка регрессии:  , ;

t-статистика — вычисленное по выборке значение критерия Стьюдента для проверки значимости коэффициентов (нулевая гипотеза – коэффициент равен нулю): точечная оценка коэффициента, делённая на его стандартную ошибку: ;

P-Значение значение плотности вероятности распределения Стьюдента  с (n-2) степенями свободы (малые значения вероятности свидетельствуют в пользу значимости коэффициентов).

Нижние 95%, Верхние 95%, Нижние 90.0%, Верхние 90.0% — соответственно нижние и верхние границы доверительных интервалов для коэффициентов b  и a (границы вычисляются с 95% доверительной вероятностью вычисляются по умолчанию,  и с p%, заданной пользователем).

На приведенном ниже рисунке можно видеть решение задачи для различных типов аппроксимирующих функций.

Мультиноминальная логистическая регрессия

16.5. Мультиномиальная логистическая регрессия

Этот метод является вариантом логистической регрессии, при которой зависимая переменная не является дихотомической, как при бинарной логистической регрессии, а имеет больше двух категорий. В то время как, при бинарной логистической регрессии независимая переменная может иметь интервальную шкалу, то мультиномиальная логистическая регрессия пригодна только для категориальных независимых переменных, причём имеет значение, относятся ли они к шкале наименований или к порядковой шкале. Конечно же, не исключается возможность задания в качестве ковариат переменных, имеющих интервальную шкалу.

Для независимых переменных, относящихся к порядковой шкале предусмотрен метод порядковой регрессии, который в данном случае является предпочтительным.

Для представления метода мультиномиальной логистической регрессии был сначала взят простой пример с одной независимой переменной. Данные для этого примера были взяты из ALLBUS (общий социологический опрос населения) 1998 года.

  • Откройте файл polein.sav, и при помощи выбора меню Analyze (Анализ) ► Descriptive Statistics (Дескриптивные статистики) ► Frequencies… (Частоты)

Частотные таблицы для четырёх переменных, находящихся в этом файле, выглядят так:

Alter (Возраст)

Frequency (Частота)Percent (Процент)Valid Percent (Действительный процент)Cumulative Percent (Совокупный процент)
Valid (Действительное значение)Bis 45 Jahre
(До 45 лет)		130650,150,150,1
Über 45 Jahre
(Свыше 45 лет)		130149,949,9100,0
Total (Сумма)2607100,0100,0

Politische Links-Rechts-Einschaetzung (Политическая принадлежность к левым или правым)

Frequency (Частота)Percent (Процент)Valid Percent (Действительный процент)Cumulative Percent (Совокупный процент)
Valid (Действительное значение)Eher links
(Скорее левый)		74028,428,428,4
Mitte
(Центрист)		121246,546,574,9
eher rechts
(Скорее правый)		65525,125,1100,0
Total (Сумма)2607100,0100,0

Schicht (Прослойка)

Frequency (Частота)Percent (Процент)Valid Percent (Действительный процент)Cumulative Percent (Совокупный процент)
Valid (Действительное значение)Unterschicht
(Нижняя прослойка)		87933,733,733,7
Mittelschicht
(Средняя прослойка)		147756,756,790,4
Oberschicht
(Верхняя прослойка)		2519,69,6100,0
Total (Сумма)2607100,0100,0

Schulbildung (Школьное образование)

Frequency (Частота)Percent (Процент)Valid Percent (Действительный процент)Cumulative Percent (Совокупный процент)
Valid (Действительное значение)Hauptschule (Неполное среднее)149957,557,557,5
Mittlere Reife (Среднее)61023,423,480,9
Abitur (Атестат зрелости)49819,119,1100,0
Total (Сумма)2607100,0100,0

Мы хотим рассмотреть переменную polire (Политическая принадлежность к левым или правым) как зависимую переменную, а три остальные — как независимые переменные (факторы). В первом примере в качестве независимой переменной мы возьмем только переменную Alter (Возраст). Прежде всего построим таблицу сопряженности для этих двух переменных.

Переменной alter присвойте статус строчной переменной (Row(s)), a polire — столбцовой переменной (Column(s)), и через выключатель Cells… (Ячейки) активируйте вывод процентных показателей для ячеек.

Alter * Politische Links-Rechts-Einschfltzung Crosstabulation

(Возраст * Политическая принадлежность к левым или правым — таблица сопряженности)

Politische Links-Rechts-Einschfltzung
(Политическая принадлежность)		Total (Сумма)
Eher links
(Скорее левый)		Mitte
(Центрист)		Eher rechts
(Скорее правый)
Alter (Возраст)Bis 45 Jahre
(До 45 лет)		Count
(Количество)		4466152451306
% within Alter
(% от возраста)		34,2%47,1%18,8%100,0%
Über 45 Jahre
(Свыше 45 лет)		Count % of Total
(Количество)		2945974101301
% within Alter
(% от возраста)		22,6%45,9%31,5%100,0%
Total
(Сумма)		Count
(Количество)		74012126552607
% within Alter
(% от возраста)		28,4%46,5%25,1%100,0%

Для младшей возрастной категории политическое самоопределение имеет тенденцию склонения симпатий к левым партиям, а для старшей — скорее к правым. Рассмотрим простую мультиномиальную логистическую модель, которая отражает взаимосвязь между политическим самоопределением и возрастом.

Так как политическое самоопределение, как зависимая переменная, включает три категории, то для определения вероятностей отнесения респондентов к этим трем категориям можно сформировать два недублированных логита, причём последняя категория «eher rechts» (скорее правый) будет использоваться как эталонная:

Нахождение коэффициентов b10, b11, b20 и b21 (называемых параметрическими оценками) и является основной задачей мультиномиальной логистической регрессии. Первая цифра индекса указывает на номер логита, а вторая на порядковый номер коэффициента в данном логите, причём цифра 0 на второй позиции индекса означает константу, за которой далее следует ровно столько коэффициентов, сколько независимых переменных (факторов) взято в рассмотрение. Коэффициентам последней (эталонной) категории присваивается значение 0.

Переменная Alter (Возраст), как единственная независимая переменная, имеет две категории, одна из которых рассматривается как эталонная, ее коэффициенты принимаются равными 0.

  • Выберите в меню Analyze (Анализ) ► Regression …(Регрессия) ► Multinomial Logistic… (Мультиномиальная логистическая). Откроется диалоговое окно Multinomial Logistic Regression (Мультиномиальная логистическая регрессия).

    • Рис. 16.17: Диалоговое окно Multinomial Logistic Regression (Множественная логистическая регрессия)

  • Переменную polire поместите в поле для зависимых переменных, а переменную alter (возраст) в поле для факторов.

  • Нажмите выключатель Statistics (Статистики). Откроется диалоговое окно Multinomial Logistic Regression: Statistics (Мультиномиальная логистическая регрессия: Статистики)

    • Рис. 16.18: Диалоговое окно Multinomial Logistic Regression: Statistics (Множественная логистическая регрессия: Статистики)

  • Оставьте активированным вывод параметрических оценок с доверительным интервалом соответствующим 95 % и покиньте это диалоговое окно нажатием Далее и ОК.

Содержание таблицы результатов расчёта, выглядит следующим образом. Для не дублирующих категорий она содержит параметрические оценки, стандартную ошибку, проверку значимости при помощи статистики Вальда, значение экспоненциальной функции от параметрической оценки и его доверительный интервал.

Parameter Estimates (Оценки параметров)

Politische Links-Rechts-Einschaetzung (Политическая принадлежность к левым или правым)ВStd. Error (Стандартная ошибка)Wald (Вальд)df (Степень свободы)Sig. (Значимость)Ехр(В)95% Confidence Interval for Ехр(В) (95% доверительный интервал для Ехр(В))
Lower Bound (Нижний предел)Upper Bound (Верхний предел)
eher links (Скорее левый)Intercept (Постоянное слагаемое)-,333,07618,9381,000
[alter = 1,00],932,11071,3531,0002,5392,0453,151
[alter = 2,00]0b..0....
Mitte (Центрист)Intercept (Постоянное слагаемое),376,06434,3201,000
[alter = 1,00],545,09930,1981,0001,7241,4202,094
[alter = 2,00]0b.......

a. This parameter is set to zero because it is redundant (Данный параметр обнуляется, т.к. он является дублирующим)

Из таблицы можно взять следующие значения для b-коэффициентов:
b10 = -0,333
b11 (до 45 лет) = 0,932
b20 = 0,376
b21 (до 45 лет) = 0,545

Таким образом, для возрастной группы до 45 лет получим:
g1 = -0,333 + 0,932 = 0,599
g2 = -0,376 + 0,545 = 0,921

и следовательно

Для дублирующего логита по правилам вычисления логарифма справедливо

К примеру, в возрастной категории до 45 лет вероятность быть более склонным к левым течениям в 1,820 раз выше вероятности склонности к правым течениям. Такой же расчёт можно произвести и для другой возрастной категории; в данном случае будут отсутствовать коэффициенты b11 и b21, т.к. они приравниваются к нулю.

Следует отметить, что прямое определение вероятности для трёх категорий политической самооценки, интересней, чем соотношение этих вероятностей между собой. Для каждой i-ой категории зависимых переменных эта вероятность может быть вычислена по следующей формуле:

Здесь для большей удобочитаемости экспоненциальная функция обозначена как ехр. n указывает на число категорий (здесь n=3).

Для возрастной группы до 45 лет для трёх категорий политической самооценки получатся следующие вероятности:

Стало быть, для отдельного человека, принадлежащего к возрастной группе до 45 лет вероятность склонения политической самооценки в сторону левых составляет, 0,341 или 34,1%, в сторону центристов 47,1% и в сторону правых 18,8%. Эти числа соответствуют процентным показателям таблицы сопряженности для возраста и политической самооценки. Таким образом, в случае наличия лишь одной независимой переменной легко удостовериться в правдоподобности расчётов, производимых при мультиномиальной логистической регрессии.

Для возрастной группы свыше 45 лет расчёты будут выглядеть следующим образом:
g1 = -0,333 + 0 = -0,333
g2 = 0,376 + 0 = 0,376
g3= 0
ехр (g1) = ехр (-0,333) = 0,717
ехр (g2) = ехр (0,376) = 1,456
ехр (g3) = ехр (0) = 1

Если выразить полученные показатели в процентах, то и здесь так же наблюдается полное согласование с соответствующими процентными показателями таблицы сопряженности.

Следует отметить, что только в случае наличия лишь одной независимой переменной, как в приведённом примере, проведение расчёта с применением столь громоздкого метода, как многозначная логистическая регрессия, является достаточно бессмысленным — все соотношения могут быть выяснены проще, при помощи таблиц сопряженности. Поэтому мы введем в рассмотрение ещё одну дополнительную переменную — переменную schule (образование).

  • В диалоговом окне Multinomial Logistic Regression (Мультиномиальная логистическая регрессия) поместите переменную schule вместе с переменной alter в поле факторов.

  • В диалоговом окне Multinomial Logistic Regression: Statistics (Мультиномиальная логистическая регрессия: Статистики) активируйте дополнительные опции Cell probabilities (Вероятность по ячейкам) и Likelihood ratio test (Тест отношения правдоподобия) и начните расчёт вновь.

Таблица теста коэффициентов правдоподобия содержит изменения функции правдоподобия для случая, когда исключается соответствующий главный действующий фактор; эти изменения выражаются через соответствующие значения теста X2 (хи-квадрат). Выдаваемый уровень значимости р < 0,001 указывает на то, что оба фактора (возраст и школьное образование) оказывают очень значимое влияние на зависимую переменную (политическая самооценка).

Model Fitting Information (Информация о приближении, обеспечиваемой моделью)

Model (Модель)-2 Log likelihood
(-2 логарифмическое правдоподобие)		Chi-square (Хи-квадрат)df (степень свободы)Sig. (Значимость)
Intercept Only (Только постоянное слагаемое)252,208
Final (Окончательно)93,429158,7796,000

Likelihood Ratio Tests (Тест отношения правдоподобия)

(Результат)-2 Log Likelihood of Reduced Model
(-2 логарифмическое правдоподобие для сокращённой модели)		Chi-square (Хи-квадрат)df
(Степень свободы)		Sig. (Значимость)
Intercept
(Постоянное слагаемое)		93,429,0000
ALTER (Возраст)171,49678,0672,000
SCHULE (Образование)178,48985,0604,000

The chi-square statistic is the difference in -2 log-likelihoods between the final model and a reduced model. The reduced model is formed by omitting an effect from the final model. The null hypothesis is that all parameters of that effect are 0 (Статистика хи-квадрат отображает различие -2 логарифмического правдоподобия между окончательной моделью и усеченной моделью. Суть расчёта усеченной модели сводится к тому, что из окончательной модели исключается один фактор влияния.

Нулевая гипотеза соответствует обнулению всех параметров параметрических оценок данного фактора влияния).

Таблица (b — коэффициентов) выглядит следующим образом.

Parameter Estimates (Оценки параметров)

Politische Links-Rechts-Einschaetzung (Политическая принадлежность к левым пли правым)ВStd. Error (Стандартная ошибка)Wald (Вальд)df (Степень свободы)Sig. (Значимость)Exp (В)95% Confidence Interval for Exp(B) (95% доверительный интервал для Ехр(В))
Lower Bound (Нижний предел)Upper Bound (Верхний предел)
eher links (Скорее левый)(Постоянное слагаемое)-,129,137,8901,345
[alter = 1,00],952,11766,6001,0002,5912,0613,256
[alter = 2,00]0a0,0,,,,
[schule = 1,00]-,179,142,5921,207,836,6321,104
[schule = 2,00]-,480,1589,2491,002,619,454,843
[schule = 3,00]0b0,0,,,,
Mine (Центрист)(Постоянное слагаемое)-,236,1372,9821,084
[alter = 1,00],766,10652,1741,0002,1521,7482,939
[alter = 2,00]Ob0,0,,,,
[schule = 1,00],802,14132,5391,0002,2311,6932,939
[schule = 2,00],149,155,9221,3371,161,8561,574
[schule = 3,00]Ob0,0,,,,

a. This parameter is set to zero because it is redundant (Данный параметр обнуляется, так как он является дублирующим)

В качестве примера определим вероятности для политической самооценки отдельного человека, принадлежащего к возрастной группе свыше 45 лет с неполным средним образованием. Для этого по аналогии с предыдущим примером произведём следующие вычисления:

g1 = -0,129 + 0 — 0,179 = -0,308
g2 = -0,236 + 0 + 0,802 = 0,566
g3 = 0
exp (g1) = 0,735
exp (g2) = 1,761
exp (g3) = 1

Если перевести данные результаты в процентные показатели, то они будут означать, что среди граждан в возрасте свыше 45 лет с неполным средним образованием 21,0% симпатизируют левым политическим течениям, 28,6% правым, а 50,4% остаются по центру.

Нет необходимости вычислять процентные показатели вероятностей самостоятельно. Вы можете взять их из следующей таблицы, отображающей наблюдаемые и прогнозируемые частоты:

Observed and Predicted Frequencies (Наблюдаемые и прогнозируемые частоты)

Schulbildung (Образование)Alter (Возраст)Politische Links-Rechts-Einschfltzung (Политическая принадлежность)Frequency (Частота)Percentage (Процент)
Observed (Наблюдаемая)Predicted (Прогнозируемая)Pearson Residual (Остаток Пирсона)Observed (Наблюдаемый)Predicted (Прогнозируемый)
Hauptschule (Неполное среднее)bis 45 Jahre (До 45 лет)eher links (Скорее левый)143157,488-1,36525,8%28,4%
Mitte (Центрист)312313,760-,15156,3%56,6%
eher rechts (Скорее правый)9982,7521,93717,9%14,9%
über 45 Jahre (Свыше 45 лет)eher links (Скорее левый)213198,5121,15722,5%21,0%
Mitte (Центрист)478476,240,11550,6%50,4%
eher rechts (Скорее правый)254270,248-1,17026,9%28,6%
Mifflere Reife (Среднее)bis 45 Jahre (до 45 лет)eher links (Скорее левый)129131,561-,27131,5%32,2%
Mitte (Центрист)192184,113,78446,9%45,0%
eher rechts (Скорее правый)8899,326-,62821,5%22.8%
über 45 Jahre(Свыше 45 лет)eher links (Скорее левый)4744,439,43523,4%22.1%
Mitte (Центрист)6774,887-1,15133,3%37,3%
eher rechts (Скорее правый)8781,674,76543,3%40,6%
Abitur (Аттестат зрелости)bis 45 Jahre (до 45 лет)eher links (Скорее левый)174156,9521,84850,7%45,8%
Mitte (Центрист)111117,127-,69832,4%34,1%
eher rechts (Скорее правый)5868,922-1,47216,9%20,1%
über 45 Jahre (Свыше 45 лет)eher links (Скорее левый)3451,048-2,91421,9%32,9%
Mitte (Центрист)5245,8731,07833,5%29,6%
eher rechts (Скорее правый)6958,0781,81244,5%37,5%

The percentages are based on total observed frequencies in each subpopulation (Процентные показатели основываются на наблюдаемых суммарных частотах для каждой частичной совокупности).

Теперь вы можете видеть, что наблюдаемые и прогнозированные значения оказались рассогласованными. Это произошло потому, что теперь в модель входят только главные факторы влияния, а не взаимодействия.

  • Чтобы это изменить, в диалоговом окне Multinomial Logistic Regression (Мультиномиальная логистическая регрессия) задействуйте выключатель Model (Модель).

Откроется диалоговое окно Multinomial Logistic Regression: Model (Мультиномиальная логистическая регрессия: Модель).

Вы можете включить в расчёт все главные факторы влияния и взаимодействия, если вместо предварительно установленной по умолчанию опции Main effects (Основные эффекты) активируете опцию Full factorial (Полнофакторная модель). При помощи опции Custom (Пользовательский режим), Вы можете отобрать включаемые в расчёт факторы влияния.

В таблице оценки параметра теперь находятся и взаимодействия. Если Вы обратите внимание на наблюдаемые и ожидаемые частоты, то заметите, что теперь они совпадают.

Рис. 16.19: Диалоговое окно Multinomial Logistic Regression: Model (Множественная логистическая регрессия: Модель)


Линейная регрессия, что говорит нам статистика F, квадрат R и остаточная стандартная ошибка?

Лучший способ понять эти термины — выполнить регрессионный расчет вручную. Я написал два тесно связанных ответа ( здесь и здесь ), однако они могут не полностью помочь вам понять ваш конкретный случай. Но все же прочитайте их. Возможно, они также помогут вам лучше понять эти термины.

р2р2р2р2R SЕрSЕ

  1. SSт о т лSSTоTaL
  2. SSт е с я ду лSSреsяdUaL
  3. SSм о дэ лSSмоdеL

Каждый из них оценивает, насколько хорошо модель описывает данные и является суммой квадратов расстояний от точек данных до подобранной модели (показаны на графике ниже красными линиями).

SSт о т лSSTоTaLcars

SSт е с я ду лSSреsяdUaL

SSм о дэ лSSмоdеLSSт о т лSSTоTaLSSт е с я ду лSSреsяdUaL

Чтобы ответить на ваши вопросы, давайте сначала вычислим те термины, которые вы хотите понять, начиная с модели и выводя в качестве справки:

# The model and output as reference
m1 <- lm(dist ~ speed, data = cars)
summary(m1)
summary.2)
ss.residual
ss.model <- ss.total-ss.residual
ss.model

Средние квадраты — это суммы квадратов, усредненные по степеням свободы:

# Calculate degrees of freedom (total, residual and model)
n <- length(cars$speed)
k <- length(m1$coef) # k = model parameter: b0, b1
df.total <- n-1
df.residual <- n-k
df.model <- k-1

# Calculate mean squares (note that these are just variances)
ms.residual <- ss.residual/df.residual
ms.residual
ms.model<- ss.model/df.model
ms.model

Мои ответы на ваши вопросы:

Q1:

  1. Таким образом, это фактически среднее расстояние наблюдаемых значений от линии lm?

R SЕрSЕMSт е с я ду лMSреsяdUaL

# Calculate residual standard error
res.se <- sqrt(ms.residual)
res.se

SSт е с я ду лSSреsяdUaLMSт е с я ду лMSреsяdUaL SSт е с я ду лSSреsяdUaLR SЕрSЕпредставляет среднее расстояние наблюдаемых данных от модели. Интуитивно понятно, что это также имеет смысл, потому что, если расстояние меньше, ваша модель будет лучше.

Q2:

  1. Теперь я в замешательстве, потому что, если RSE говорит нам, как далеко наши наблюдаемые точки отклоняются от линии регрессии, низкий RSE фактически говорит нам, что «ваша модель хорошо согласуется на основе наблюдаемых точек данных» -> таким образом, насколько хорошо наши модели соответствуют Так в чем же разница между R в квадрате и RSE?

р2р2SSм о дэ лSSмоdеLSSт о т лSSTоTaL

# R squared
r.sq <- ss.model/ss.total
r.sq

р2р2SSт о т лSSTоTaLSSм о дэ лSSмоdеL

R SЕрSЕр2р2R SЕрSЕ

р2р2

Q3:

  1. Верно ли, что мы можем иметь значение F, указывающее на сильные отношения, которые НЕ являются ЛИНЕЙНЫМИ, так что наш RSE высокий, а наш квадрат R низкий

FFMSм о дэ лMSмоdеLMSт е с я ду лMSреsяdUaL

# Calculate F-value
F <- ms.model/ms.residual
F
# Calculate P-value
p.F <- 1-pf(F, df.model, df.residual)
p.F

FF

Ваш третий вопрос немного сложен для понимания, но я согласен с приведенной вами цитатой.

Коэффициент детерминации

(R в квадрате): определение, расчет

Содержание :

Коэффициент детерминации (R в квадрате)

Коэффициент детерминации, 2 рэндов, используется для анализа того, как различия в одной переменной могут быть объяснены разницей во второй переменной. Например, , когда человек забеременеет, имеет прямое отношение к тому, когда он рожает.

Более конкретно, R-квадрат дает вам процентное изменение y, объясняемое переменными x.Диапазон составляет от 0 до 1 (т.е. от 0% до 100% вариации y можно объяснить переменными x).

Коэффициент детерминации, R 2 , аналогичен коэффициенту корреляции , R. Формула коэффициента корреляции покажет вам, насколько сильна линейная связь между двумя переменными. R в квадрате — это квадрат коэффициента корреляции, r (отсюда и термин r в квадрате). Посмотрите это видео, чтобы узнать о кратком определении r в квадрате и о том, как его найти:

Нахождение R в квадрате / Коэффициент детерминации

Нужна помощь с домашним заданием? Посетите нашу страницу обучения!
Шаг 1: Найдите коэффициент корреляции r (он может быть указан вам в вопросе). Пример, r = 0,543 .

Шаг 2: Возвести в квадрат коэффициент корреляции.
0,543 2 = ,295

Шаг 3: Преобразуйте коэффициент корреляции в проценты .
,295 = 29,5%

Вот и все!

Значение коэффициента детерминации

Коэффициент детерминации можно представить как процент. Это дает вам представление о том, сколько точек данных попадает в результаты линии, образованной уравнением регрессии.Чем выше коэффициент, тем больший процент точек проходит линия при построении точек данных и линии. Если коэффициент равен 0,80, то 80% точек должны попадать в линию регрессии. Значения 1 или 0 будут означать, что линия регрессии представляет все или никакие данные соответственно. Более высокий коэффициент является показателем лучшего соответствия наблюдениям.

CoD может быть отрицательным , хотя обычно это означает, что ваша модель плохо подходит для ваших данных.Он также может стать отрицательным, если вы не установили перехват.

Полезность R

2

Полезность R 2 заключается в его способности находить вероятность будущих событий, попадающих в пределы прогнозируемых результатов. Идея состоит в том, что если добавить больше выборок, коэффициент будет показывать вероятность падения новой точки на линии.
Даже если между двумя переменными существует сильная связь, определение не доказывает причинно-следственную связь. Например, исследование дней рождения может показать, что большое количество дней рождения происходит в течение одного или двух месяцев.Это не означает, что беременность наступает по прошествии времени или смене времен года.


Синтаксис

Коэффициент детерминации обычно записывается как R 2 _p. «P» указывает количество столбцов данных, что полезно при сравнении R 2 различных наборов данных.

В начало

Что такое скорректированный коэффициент детерминации?


Скорректированный коэффициент детерминации (скорректированный R-квадрат) — это поправка для коэффициента детерминации, которая учитывает числа переменных в наборе данных. Он также наказывает вас за очки, не соответствующие модели.

Возможно, вы знаете, что небольшое количество значений в наборе данных (слишком маленький размер выборки) может привести к вводящей в заблуждение статистике, но вы можете не знать, что слишком много точек данных также может привести к проблемам. Каждый раз, когда вы добавляете точку данных в регрессионный анализ, 2 рэндов будет увеличиваться. R 2 никогда не уменьшается. Следовательно, чем больше очков вы добавите, тем лучше будет казаться, что регрессия «соответствует» вашим данным.Если ваши данные не совсем умещаются в строке, может возникнуть соблазн продолжить добавление данных, пока вы не найдете более подходящего.

Некоторые из добавленных вами баллов будут значительными (соответствовать модели), а другие — нет. R 2 не заботится о мелочах. Чем больше вы добавите, тем выше коэффициент детерминации .

Скорректированный R 2 может быть использован для включения более подходящего числа переменных, что избавит вас от соблазна продолжать добавлять переменные к вашему набору данных.Скорректированный R 2 увеличится только в том случае, если новая точка данных улучшит регрессию в большей степени, чем вы могли бы ожидать случайно. R 2 не включает все точки данных, всегда меньше, чем R 2 и может быть отрицательным (хотя обычно положительным). Отрицательные значения вероятны, если R 2 близок к нулю — после настройки значение немного опустится ниже нуля.

Подробнее см .: Скорректированный R-квадрат.

Посетите мой канал на Youtube, чтобы получить больше советов по статистике и помощи!


Список литературы

Гоник, Л.(1993). Мультяшный справочник по статистике. HarperPerennial.
Kotz, S .; и др., ред. (2006), Энциклопедия статистических наук, Wiley.
Vogt, W.P. (2005). Словарь статистики и методологии: нетехническое руководство для социальных наук. МУДРЕЦ.

————————————————— —————————-

Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области.Ваши первые 30 минут с репетитором Chegg бесплатны!

Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице в Facebook .

11. Корреляция и регрессия

Слово корреляция используется в повседневной жизни для обозначения некоторой формы ассоциации. Можно сказать, что мы заметили корреляцию между туманными днями и приступами хрипов. Однако в статистических терминах мы используем корреляцию для обозначения связи между двумя количественными переменными.Мы также предполагаем, что связь является линейной, что одна переменная увеличивает или уменьшает фиксированную величину для увеличения или уменьшения единицы другой. Другой метод, который часто используется в этих обстоятельствах, — это регрессия, которая включает в себя оценку наилучшей прямой линии для резюмирования ассоциации.

Коэффициент корреляции

Степень ассоциации измеряется коэффициентом корреляции, обозначаемым r. Иногда его называют коэффициентом корреляции Пирсона по имени автора, и он является мерой линейной связи.Если для выражения взаимосвязи необходима изогнутая линия, необходимо использовать другие, более сложные меры корреляции.

Коэффициент корреляции измеряется по шкале от + 1 до 0 до — 1. Полная корреляция между двумя переменными выражается либо + 1, либо -1. Когда одна переменная увеличивается, а другая увеличивается, корреляция положительная; когда одно уменьшается, а другое увеличивается, оно отрицательно. Полное отсутствие корреляции обозначается цифрой 0. Рисунок 11.1 дает графическое представление корреляции.

Рисунок 11.1 Иллюстрированная корреляция.

Просмотр данных: диаграммы рассеяния

Когда исследователь собрал две серии наблюдений и хочет увидеть, существует ли между ними связь, он или она должны сначала построить диаграмму рассеяния. Вертикальная шкала представляет один набор измерений, а горизонтальная шкала — другой. Если один набор наблюдений состоит из экспериментальных результатов, а другой — из временной шкалы или какой-либо наблюдаемой классификации, обычно результаты экспериментов наносят на вертикальную ось.Они представляют собой то, что называется «зависимой переменной». «Независимая переменная», такая как время или высота или какая-либо другая наблюдаемая классификация, измеряется по горизонтальной оси или базовой линии.

Слова «независимый» и «зависимый» могут озадачить новичка, потому что иногда непонятно, что от чего зависит. Эта путаница — триумф здравого смысла над вводящей в заблуждение терминологией, потому что часто каждая переменная зависит от какой-то третьей переменной, которая может или не может быть упомянута.Разумно, например, полагать, что рост детей зависит от возраста, а не наоборот, но учитывать положительную корреляцию между средним выходом смол и выходом никотина для определенных марок сигарет. «Высвобожденный никотин вряд ли имеет свое происхождение. в смоле: оба эти фактора изменяются параллельно с некоторыми другими факторами или факторами в составе сигарет. Урожайность одного не кажется «зависимым» от другого в том смысле, что в среднем рост ребенка зависит от его возраста.В таких случаях часто не имеет значения, какой масштаб на какой оси диаграммы разброса. Однако, если намерение состоит в том, чтобы сделать выводы об одной переменной из другой, наблюдения, из которых должны быть сделаны выводы, обычно помещаются в базовую линию. В качестве еще одного примера, график ежемесячной смертности от сердечных заболеваний по сравнению с ежемесячными продажами мороженого покажет отрицательную связь. Однако вряд ли поедание мороженого защитит от сердечных заболеваний! Просто уровень смертности от сердечных заболеваний обратно пропорционален, а потребление мороженого положительно связано с третьим фактором, а именно температурой окружающей среды.

Расчет коэффициента корреляции

Педиатрический регистратор измерил анатомическое мертвое пространство легких (в мл) и рост (в см) 15 детей. Данные приведены в таблице 11.1 и диаграмме рассеяния, показанной на рисунке 11.2. Каждая точка представляет одного ребенка и помещается в точку, соответствующую измерению высоты (горизонтальная ось) и мертвого пространства (вертикальная ось). Регистратор теперь проверяет узор, чтобы определить, кажется ли вероятным, что область, покрытая точками, центрируется на прямой линии или нужна изогнутая линия.В этом случае педиатр решает, что прямая линия может адекватно описать общую тенденцию точек. Поэтому его следующим шагом будет вычисление коэффициента корреляции.

При построении диаграммы рассеяния (рисунок 11.2), чтобы показать рост и анатомические мертвые зоны легких у 15 детей, педиатр указал цифры, как в столбцах (1), (2) и (3) таблицы 11.1. Полезно расположить наблюдения в последовательном порядке независимой переменной, когда одна из двух переменных четко идентифицируется как независимая.Соответствующие цифры для зависимой переменной затем могут быть исследованы в отношении возрастающего ряда для независимой переменной. Таким образом мы получаем ту же картину, но в числовой форме, как показано на диаграмме разброса.

Рис. 11.2 Диаграмма разброса зависимости между ростом и анатомическим мертвым пространством легких у 15 детей.

Расчет коэффициента корреляции осуществляется следующим образом, где x представляет значения независимой переменной (в данном случае высота), а y представляет значения зависимой переменной (в данном случае анатомическое мертвое пространство).Используемая формула:

, которая может быть представлена ​​как:

Процедура калькулятора

Найдите среднее значение и стандартное отклонение x, как описано в разделе Найдите среднее и стандартное отклонение y:

Вычтите 1 из n и умножьте на SD (x) и SD (y), (n — 1) SD (x) SD (y)

Это дает нам знаменатель формулы. (Не забудьте выйти из режима «Stat».)

Для числителя умножьте каждое значение x на соответствующее значение y, сложите эти значения и сохраните их.

110 x 44 = Min

116 x 31 = M +

и т. Д.

Сохраняется в памяти. Вычтите

MR — 15 x 144,6 x 66,93 (5426,6)

Наконец, разделите числитель на знаменатель.

r = 5426,6 / 6412,0609 = 0,846.

Коэффициент корреляции 0,846 указывает на сильную положительную корреляцию между размером легочного анатомического мертвого пространства и ростом ребенка. Но при интерпретации корреляции важно помнить, что корреляция не является причинно-следственной связью.Причинная связь между двумя коррелированными переменными может быть, а может и не быть. Причем, если есть связь, она может быть косвенной.

Часть вариации одной из переменных (измеряемая по ее дисперсии) может рассматриваться как обусловленная ее взаимосвязью с другой переменной, а другая часть — как следствие неопределенных (часто «случайных») причин. Часть, обусловленная зависимостью одной переменной от другой, измеряется Ро. Для этих данных Rho = 0,716, поэтому мы можем сказать, что 72% различий между детьми в размере анатомического мертвого пространства объясняется ростом ребенка.Если мы хотим обозначить силу связи, для абсолютных значений r 0-0,19 считается очень слабым, 0,2-0,39 — слабым, 0,40-0,59 — умеренным, 0,6-0,79 — сильным и 0,8-1 — очень сильным. корреляция, но это довольно произвольные пределы, и следует учитывать контекст результатов.

Тест значимости

Чтобы проверить, очевидна ли связь и могла ли она возникнуть случайно, используйте тест t в следующем расчете:

вводится при n — 2 степенях свободы.

Например, коэффициент корреляции для этих данных составил 0,846.

Число пар наблюдений составляло 15. Применяя уравнение 11.1, мы имеем:

Вводя таблицу B при 15-2 = 13 степенях свободы, мы находим, что при t = 5,72, P <0,001, поэтому коэффициент корреляции можно рассматривать. как очень значительный. Таким образом (как сразу видно из диаграммы рассеяния) мы имеем очень сильную корреляцию между мертвым пространством и высотой, которая вряд ли возникла случайно.

Предположения, управляющие этим тестом:

  1. Что обе переменные правдоподобно Нормально распределены.
  2. Что между ними существует линейная зависимость.
  3. Нулевая гипотеза состоит в том, что между ними нет связи.

Тест не следует использовать для сравнения двух методов измерения одной и той же величины, например, двух методов измерения пиковой скорости выдоха. Его использование таким образом кажется распространенной ошибкой, при этом значительный результат интерпретируется как означающий, что один метод эквивалентен другому.Причины широко обсуждались (2), но стоит вспомнить, что значительный результат мало что говорит нам о прочности отношений. Из формулы должно быть ясно, что даже при очень слабой связи (скажем, r = 0,1) мы получим значительный результат с достаточно большой выборкой (скажем, n больше 1000).

Ранговая корреляция Спирмена

График данных может выявить отдаленные точки далеко от основной части данных, что может ненадлежащим образом повлиять на расчет коэффициента корреляции.В качестве альтернативы переменные могут быть количественными дискретными, такими как количество родинок, или упорядоченными категориальными, такими как оценка боли. Непараметрическая процедура по Спирмену заключается в замене наблюдений их рангами при вычислении коэффициента корреляции.

Это приводит к простой формуле для ранговой корреляции Спирмена, Rho.

где d — разница в рангах двух переменных для данного человека. Таким образом, мы можем вывести таблицу 11.2 из данных в таблице 11.1.

Отсюда получаем, что

В этом случае значение очень близко к значению коэффициента корреляции Пирсона. Для n> 10 коэффициент ранговой корреляции Спирмена можно проверить на значимость с помощью t-критерия, приведенного ранее.

Уравнение регрессии

Корреляция описывает силу связи между двумя переменными и является полностью симметричной, корреляция между A и B такая же, как корреляция между B и A. Однако, если две переменные связаны, это означает что когда один изменяется на определенную величину, другой изменяется в среднем на определенную величину.Например, у детей, описанных ранее, больший рост в среднем связан с большим анатомическим мертвым пространством. Если y представляет зависимую переменную, а x — независимую переменную, эта связь описывается как регрессия y по x.

Взаимосвязь может быть представлена ​​простым уравнением, называемым уравнением регрессии. В этом контексте «регрессия» (термин — историческая аномалия) просто означает, что среднее значение y является «функцией» от x, то есть изменяется вместе с x.

Уравнение регрессии, показывающее, насколько изменяется y при любом заданном изменении x, можно использовать для построения линии регрессии на диаграмме рассеяния, и в простейшем случае предполагается, что это прямая линия. Направление наклона линии зависит от того, положительная или отрицательная корреляция. Когда два набора наблюдений увеличиваются или уменьшаются вместе (положительно), линия наклоняется вверх слева направо; когда один набор уменьшается, а другой увеличивается, линия наклоняется вниз слева направо.Поскольку линия должна быть прямой, она, вероятно, пройдет через несколько точек, если вообще пройдет. Учитывая, что ассоциация хорошо описывается прямой линией, мы должны определить две особенности линии, если мы хотим правильно разместить ее на диаграмме. Первый из них — это расстояние от базовой линии; второй — его наклон. Они выражаются в следующем уравнении регрессии :

С помощью этого уравнения мы можем найти ряд значений переменной, которые соответствуют каждому из ряда значений x, независимой переменной.Параметры α и β необходимо оценить по данным. Параметр обозначает расстояние над базовой линией, на котором линия регрессии пересекает вертикальную ось (y); то есть, когда y = 0. Параметр β (коэффициент регрессии ) означает величину, на которую необходимо умножить изменение x, чтобы получить соответствующее среднее изменение y, или величину y, изменяющуюся на единицу увеличения x. Таким образом, он представляет степень уклона линии вверх или вниз.

и

можно показать, что

полезно, потому что мы вычислили все компоненты уравнения (11.2) при расчете коэффициента корреляции.

Расчет коэффициента корреляции по данным в таблице 11.2 дал следующее:

Применяя эти цифры к формулам для коэффициентов регрессии, мы имеем:

Следовательно, в этом случае уравнение регрессии y на x становится

Это означает, что в среднем на каждое увеличение высоты на 1 см увеличение анатомического мертвого пространства составляет 1,033 мл в диапазоне измерений, сделанных .

Линия, представляющая уравнение, наложена на диаграмму разброса данных на рисунке 11.2. Чтобы нарисовать линию, нужно взять три значения x, одно в левой части диаграммы рассеяния, одно в середине и одно справа, и подставить их в уравнение следующим образом:

Если x = 110 , y = (1,033 x 110) — 82,4 = 31,2

Если x = 140, y = (1,033 x 140) — 82,4 = 62,2

Если x = 170, y = (1,033 x 170) — 82,4 = 93,2

Хотя двух точек достаточно, чтобы обозначить линию, три лучше для проверки.Поместив их на диаграмму разброса, мы просто проводим через них линию.

Рис. 11.3 Линия регрессии, проведенная на диаграмме рассеяния, связывающая рост и анатомическое мертвое пространство легких у 15 детей

Стандартная ошибка наклона SE (b) определяется как:

, где — остаточное стандартное отклонение, определяемое как:

Это может будет показано, что алгебраически оно равно

Мы уже должны передать все члены в этом выражении. Таким образом получается квадратный корень из. Знаменатель (11.3) составляет 72,4680. Таким образом, SE (b) = 13,08445 / 72,4680 = 0,18055.

Мы можем проверить, существенно ли отличается наклон от нуля:

t = b / SE (b) = 1,033 / 0,18055 = 5,72.

Опять же, это n — 2 = 15 — 2 = 13 степеней свободы. Предположения, управляющие этим тестом:

  1. Что ошибки предсказания приблизительно нормально распределены. Обратите внимание, это не означает, что переменные x или y должны быть нормально распределены.
  2. Что связь между двумя переменными линейна.
  3. То, что разброс точек вокруг линии приблизительно постоянен — ​​мы не хотели бы, чтобы изменчивость зависимой переменной увеличивалась по мере увеличения независимой переменной. В этом случае попробуйте логарифмировать переменные x и y.

Обратите внимание, что критерий значимости для наклона дает точно такое же значение P, что и критерий значимости для коэффициента корреляции. Хотя эти два теста производятся по-разному, они алгебраически эквивалентны, что имеет интуитивный смысл.

Мы можем получить 95% доверительный интервал для b из

, где tstatistic from имеет 13 степеней свободы и равно 2,160.

Таким образом, 95% доверительный интервал составляет

от 1,033 — 2,160 x 0,18055 до 1,033 + 2,160 x 0,18055 = от 0,643 до 1,422.

Линии регрессии дают нам полезную информацию о данных, из которых они собираются. Они показывают, как одна переменная в среднем изменяется с другой, и их можно использовать, чтобы узнать, какой может быть одна переменная, если мы знаем другую — при условии, что мы зададим этот вопрос в рамках диаграммы разброса.Спроектировать линию на любом конце — для экстраполяции — всегда рискованно, потому что отношения между x и y могут измениться или может существовать какая-то точка отсечения. Например, можно провести линию регрессии, связывающую хронологический возраст некоторых детей с их костным возрастом, и это может быть прямая линия, скажем, между возрастом от 5 до 10 лет, но спроецировать ее на возраст 30 лет. явно приведет к ошибке. Компьютерные пакеты часто производят перехват из уравнения регрессии без предупреждения, что это может быть совершенно бессмысленным.Рассмотрим регресс артериального давления по сравнению с возрастом у мужчин среднего возраста. Коэффициент регрессии часто бывает положительным, что свидетельствует о повышении артериального давления с возрастом. Перехват часто близок к нулю, но было бы неправильно делать вывод, что это надежная оценка артериального давления у новорожденных мальчиков мужского пола!

Более сложные методы

Возможно использование нескольких независимых переменных — в этом случае метод известен как множественная регрессия. (3,4) Это наиболее универсальный из статистических методов, который может использоваться во многих ситуациях.Примеры включают: чтобы учесть более одного предиктора, возраст, а также рост в приведенном выше примере; чтобы учесть ковариаты — в клиническом исследовании зависимой переменной может быть результат после лечения, первая независимая переменная может быть бинарной, 0 для плацебо и 1 для активного лечения, а вторая независимая переменная может быть исходной переменной, измеренной до лечения, но может повлиять на результат.

Общие вопросы

Если две переменные взаимосвязаны, связаны ли они причинно?

Часто путают корреляцию и причинно-следственную связь.Все, что показывает корреляция, — это то, что две переменные связаны. Может быть третья переменная, смешивающая переменная, связанная с ними обоими. Например, ежемесячные смерти от утопления и ежемесячные продажи мороженого положительно коррелируют, но никто не скажет, что эта связь была причинной!

Как проверить предположения, лежащие в основе линейной регрессии?

Ссылки

  1. Russell MAH, Cole PY, Idle MS, Adams L. Выходы окиси углерода в сигаретах и ​​их связь с выходом никотина и типом фильтра.BMJ 1975; 3: 713.
  2. Бланд Дж. М., Альтман Д. Г.. Статистические методы оценки соответствия между двумя методами клинических измерений. Lancet 1986; я: 307-10.
  3. Браун Р.А., Свансон-Бек Дж. Медицинская статистика на персональных компьютерах, 2-е изд. Лондон: Издательская группа BMJ, 1993.
  4. Армитаж П., Берри Г. В: Статистические методы в медицинских исследованиях, 3-е изд. Оксфорд: Научные публикации Блэквелла, 1994: 312-41.

Упражнения

11.1 Было проведено исследование посещаемости больницы людей в 16 различных географических районах за фиксированный период времени.Расстояние центра от больницы каждого района измерялось в милях. Результаты были следующими:

(1) 21%, 6,8; (2) 12%, 10,3; (3) 30%, 1,7; (4) 8%, 14,2; (5) 10%, 8,8; (6) 26%, 5,8; (7) 42%, 2,1; (8) 31%, 3,3; (9) 21%, 4,3; (10) 15%, 9,0; (11) 19%, 3,2; (12) 6%, 12,7; (13) 18%, 8,2; (14) 12%, 7,0; (15) 23%, 5,1; (16) 34%, 4,1.

Каков коэффициент корреляции между посещаемостью и средней удаленностью географической области?

11.2 Найдите ранговую корреляцию Спирмена для данных, приведенных в 11.1.

11.3 Если значения x из данных в 11.1 представляют среднее расстояние области от больницы, а значения y представляют уровень посещаемости, каково уравнение для регрессии y на x? Что это значит?

11.4 Найдите стандартную ошибку и 95% доверительный интервал для наклона

Определение регрессии

Что такое регресс?

Регрессия — это статистический метод, используемый в финансах, инвестициях и других дисциплинах, который пытается определить силу и характер связи между одной зависимой переменной (обычно обозначаемой Y) и рядом других переменных (известных как независимые переменные).

Регрессия помогает инвестиционным и финансовым менеджерам оценивать активы и понимать взаимосвязь между переменными, такими как цены на сырьевые товары и акции предприятий, торгующих этими товарами.

Объяснение регрессии

Два основных типа регрессии — это простая линейная регрессия и множественная линейная регрессия, хотя существуют методы нелинейной регрессии для более сложных данных и анализа. Простая линейная регрессия использует одну независимую переменную для объяснения или предсказания результата зависимой переменной Y, тогда как множественная линейная регрессия использует две или более независимых переменных для предсказания результата.

Регрессия может помочь профессионалам в области финансов и инвестиций, а также специалистам в других сферах бизнеса. Регрессия также может помочь спрогнозировать продажи компании на основе погоды, предыдущих продаж, роста ВВП или других типов условий. Модель ценообразования капитальных активов (CAPM) — это часто используемая регрессионная модель в финансах для определения стоимости активов и определения стоимости капитала.

Общая форма каждого типа регрессии:

  • Простая линейная регрессия: Y = a + bX + u
  • Множественная линейная регрессия: Y = a + b 1 X 1 + b 2 X 2 + b 3 X 3 +… + b t X t + u

Где:

  • Y = переменная, которую вы пытаетесь предсказать (зависимая переменная).
  • X = переменная, которую вы используете для прогнозирования Y (независимая переменная).
  • a = перехват.
  • b = наклон.
  • u = остаток регрессии.

Существует два основных типа регрессии: простая линейная регрессия и множественная линейная регрессия.

Регрессия берет группу случайных величин, которые, как считается, предсказывают Y, и пытается найти математическую связь между ними.Эта взаимосвязь обычно имеет форму прямой линии (линейная регрессия), которая наилучшим образом аппроксимирует все отдельные точки данных. При множественной регрессии отдельные переменные различаются с помощью индексов.

Ключевые выводы

  • Регрессия помогает инвестиционным и финансовым менеджерам оценивать активы и понимать взаимосвязи между переменными
  • Regression может помочь специалистам в области финансов и инвестиций, а также специалистам в других сферах бизнеса.

Реальный пример использования регрессионного анализа

Регрессия часто используется для определения того, сколько конкретных факторов, таких как цена товара, процентные ставки, конкретные отрасли или секторы, влияют на движение цены актива. Вышеупомянутый CAPM основан на регрессии и используется для прогнозирования ожидаемой доходности акций и для определения стоимости капитала. Доходность акции сравнивается с доходностью более широкого индекса, такого как S&P 500, для создания бета-версии для конкретной акции.

Бета — это риск акции по отношению к рынку или индексу и отражается как наклон в модели CAPM. Доходность рассматриваемой акции будет зависимой переменной Y, а независимая переменная X — премией за рыночный риск.

Дополнительные переменные, такие как рыночная капитализация акций, коэффициенты оценки и недавняя доходность, могут быть добавлены в модель CAPM, чтобы получить более точные оценки доходности. Эти дополнительные факторы известны как факторы Фама-Френча, названные в честь профессоров, которые разработали модель множественной линейной регрессии для лучшего объяснения доходности активов.Взаимодействие с другими людьми

Что такое линейная регрессия? — Статистические решения

Линейная регрессия — это основной и часто используемый тип прогнозного анализа. Общая идея регрессии состоит в том, чтобы исследовать две вещи: (1) хорошо ли помогает набор переменных-предикторов предсказывать переменную результата (зависимую)? (2) Какие переменные, в частности, являются значимыми предикторами переменной результата и каким образом они — на что указывает величина и знак бета-оценок — влияют на переменную результата? Эти оценки регрессии используются для объяснения взаимосвязи между одной зависимой переменной и одной или несколькими независимыми переменными.Простейшая форма уравнения регрессии с одной зависимой и одной независимой переменной определяется формулой y = c + b * x, где y = оценочная оценка зависимой переменной, c = константа, b = коэффициент регрессии и x = оценка по независимая переменная.

Именование переменных. Есть много имен зависимой переменной регрессии. Ее можно назвать выходной переменной, критериальной переменной, эндогенной переменной или регрессионным выражением. Независимые переменные можно назвать экзогенными переменными, переменными-предикторами или регрессорами.

Три основных применения регрессионного анализа: (1) определение силы предикторов, (2) прогнозирование эффекта и (3) прогнозирование тенденций.

Во-первых, регрессия может использоваться для определения силы воздействия, которое независимая (ые) переменная (ы) оказывает на зависимую переменную. Типичные вопросы: какова сила взаимосвязи между дозой и эффектом, расходами на продажи и маркетинг или возрастом и доходом.

Во-вторых, его можно использовать для прогнозирования эффектов или воздействия изменений.То есть регрессионный анализ помогает нам понять, насколько изменяется зависимая переменная при изменении одной или нескольких независимых переменных. Типичный вопрос: «Какой дополнительный доход от продаж я получу за каждую дополнительную 1000 долларов, потраченных на маркетинг?»

В-третьих, регрессионный анализ предсказывает тенденции и будущие значения. Для получения точечных оценок можно использовать регрессионный анализ. Типичный вопрос: «Какой будет цена на золото через 6 месяцев?»

Регрессионный анализ — формулы, объяснения, примеры и определения

Что такое регрессионный анализ?

Регрессионный анализ — это набор статистических методов, используемых для оценки взаимосвязей между зависимой переменной и одной или несколькими независимыми переменными Независимая переменная Независимая переменная — это входные данные, предположения или драйверы, которые изменяются для оценки их влияния на зависимую переменную. (исход).. Его можно использовать для оценки силы взаимосвязи между переменными и для моделирования будущей взаимосвязи между ними.

Регрессионный анализ включает несколько вариантов, таких как линейный, множественный линейный и нелинейный. Наиболее распространены простые линейные и множественные линейные модели. Нелинейный регрессионный анализ обычно используется для более сложных наборов данных, в которых зависимые и независимые переменные показывают нелинейную взаимосвязь.

Регрессионный анализ предлагает множество приложений в различных дисциплинах, включая финансы.

Регрессионный анализ — предположения линейной модели

Линейный регрессионный анализ основан на шести фундаментальных предположениях:

  1. Зависимые и независимые переменные показывают линейную зависимость между наклоном и точкой пересечения.
  2. Независимая переменная не случайна.
  3. Значение невязки (ошибки) равно нулю.
  4. Значение невязки (ошибки) постоянно для всех наблюдений.
  5. Значение невязки (ошибки) не коррелировано по всем наблюдениям.
  6. Остаточные (ошибочные) значения подчиняются нормальному распределению.

Регрессионный анализ — Простая линейная регрессия

Простая линейная регрессия — это модель, которая оценивает взаимосвязь между зависимой переменной и независимой переменной. Простая линейная модель выражается с помощью следующего уравнения:

Y = a + bX + ϵ

Где:

  • Y — Зависимая переменная
  • X — Независимая (объяснительная) переменная
  • a — Перехват
  • b — Наклон
  • ϵ — Остаточный (ошибка)

Регрессионный анализ — Множественная линейная регрессия

Множественный линейный регрессионный анализ по существу аналогичен простой линейной модели, за исключением того, что в модели используются несколько независимых переменных.Математическое представление множественной линейной регрессии:

Y = a + b
X 1 + c X 2 + d X 3 + ϵ

Где:

  • Y — Зависимая переменная
  • X 1 , X 2 , X 3 — Независимые (объяснительные) переменные
  • a — Пересечение
  • b, c, d — Наклоны
  • ϵ — Невязка (ошибка)

Множественная линейная регрессия подчиняется тем же условиям, что и простая линейная модель.Однако, поскольку в множественном линейном анализе есть несколько независимых переменных, существует еще одно обязательное условие для модели:

  • Неколлинеарность: Независимые переменные должны показывать минимум корреляции друг с другом. Если независимые переменные сильно коррелированы друг с другом, будет трудно оценить истинные отношения между зависимыми и независимыми переменными.

Регрессионный анализ в финансах

Регрессионный анализ имеет несколько применений в финансах.Например, статистический метод является фундаментальным для модели ценообразования капитальных активов (CAPM). Модель ценообразования капитальных активов (CAPM). Модель ценообразования капитальных активов (CAPM) — это модель, которая описывает взаимосвязь между ожидаемой доходностью и риском ценной бумаги. Формула CAPM показывает, что доходность ценной бумаги равна безрисковой доходности плюс премия за риск на основе бета-версии этой ценной бумаги. По сути, уравнение CAPM — это модель, которая определяет взаимосвязь между ожидаемой доходностью актива и премией за рыночный риск.

Анализ также используется для прогнозирования доходности ценных бумаг на основе различных факторов или для прогнозирования эффективности бизнеса. Узнайте больше о методах прогнозирования в курсе CFI по бюджетированию и прогнозированию!

1. Бета и CAPM

В финансах для расчета бета-бета используется регрессионный анализ. Бета (β) инвестиционной ценной бумаги (т. Е. Акции) является мерой ее волатильности доходности относительно всего рынка. Он используется в качестве меры риска и является неотъемлемой частью модели ценообразования капитальных активов (CAPM).Компания с более высокой бета-версией имеет больший риск, а также большую ожидаемую доходность. (волатильность доходности по отношению к рынку в целом) для акции. Это можно сделать в Excel с помощью функции наклона Функция наклона Функция наклона относится к категории статистических функций Excel. Он вернет наклон линии линейной регрессии через точки данных в известных_y и известных_x. В финансовом анализе SLOPE может быть полезен при расчете бета-версии акции. Формула = LOPE (известные_y, известные_x) Функция использует расширение.

Скачать бесплатный бета-калькулятор CFI Калькулятор бета-версии Этот бета-калькулятор позволяет измерить волатильность доходности отдельной акции относительно всего рынка. Бета (β) инвестиционной ценной бумаги (т. Е. Акции) является мерой волатильности ее доходности относительно всего рынка. Он используется как мера риска и является неотъемлемой частью Cap!

2. Прогнозирование доходов и расходов

При прогнозировании финансовой отчетности Финансовое прогнозирование Финансовое прогнозирование — это процесс оценки или прогнозирования того, как бизнес будет работать в будущем.В этом руководстве о том, как построить финансовый прогноз для компании, может быть полезно провести множественный регрессионный анализ, чтобы определить, как изменения в определенных допущениях или драйверах бизнеса повлияют на доходы или расходы в будущем. Например, может быть очень высокая корреляция между количеством продавцов, нанятых компанией, количеством магазинов, которыми они управляют, и доходом, который приносит бизнес.

В приведенном выше примере показано, как использовать функцию прогноза Функция прогнозирования Функция прогнозирования относится к категории статистических функций Excel.Он рассчитает или спрогнозирует для нас будущую стоимость с использованием существующих значений. В финансовом моделировании функция прогноза может быть полезна при вычислении статистической ценности сделанного прогноза. Например, если мы знаем прошлые доходы и в Excel, чтобы рассчитать доход компании на основе количества показанных объявлений.

Узнайте больше о методах прогнозирования в курсе CFI по бюджетированию и прогнозированию!

Дополнительные ресурсы

Мы надеемся, что вам понравилось читать объяснение регрессионного анализа CFI.CFI предлагает сертификационную программу FMVA® для специалистов по финансовому моделированию и оценке (FMVA) ™. Присоединяйтесь к 350 600+ студентам, которые работают в таких компаниях, как Amazon, J.P. Morgan и Ferrari, для тех, кто хочет вывести свою карьеру на новый уровень. Чтобы узнать больше о связанных темах, ознакомьтесь со следующими бесплатными ресурсами CFI:

  • Анализ поведения затрат 10 самых важных навыков финансового моделирования и то, что необходимо для хорошего финансового моделирования в Excel.Важнейшие навыки: бухгалтерский учет
  • Методы прогнозированияМетоды прогнозированияЛучшие методы прогнозирования. В этой статье мы объясним четыре типа методов прогнозирования доходов, которые финансовые аналитики используют для прогнозирования будущих доходов.
  • Метод High-Low Метод High-Low В учете затрат метод high-low — это метод, используемый для разделения смешанных затрат на переменные и постоянные. Хотя метод высокого-низкого

Регрессионный анализ — обзор

Введение

Регрессионный анализ — это хорошо известный метод статистического обучения, полезный для вывода взаимосвязи между зависимой переменной Y и независимыми переменными p X = [ X 1 | … | X p ] .Зависимая переменная Y также известна как переменная ответа или результат , а переменные X k ( k = 1,…, p ) как предикторы , независимые переменные, или ковариаты . Точнее, регрессионный анализ направлен на оценку математического отношения f () для объяснения Y в терминах X as, Y = f ( X ), используя наблюдения ( x i , Y i ), i = 1,…, n, собраны на n наблюдаются статистических единиц .Если Y описывает одномерную случайную величину, регрессия называется одномерной регрессией , в противном случае она называется многомерной регрессией . Если Y зависит только от одной переменной x (т.е. ., P = 1 ), регрессия называется простой, в противном случае (т.е. p > 1), регрессия называется Кратное , см (Абрамович, Ритов, 2013; Casella, Berger, 2001; Faraway, 2004; Fahrmeir et al ., 2013; Джобсон, 1991; Рао, 2002; Сен и Шривастава, 1990).

Для краткости в этой главе мы ограничиваем внимание одномерной регрессии (простой и множественной), так что Y = ( Y 1 , Y 2 … Y n ) T представляет вектор наблюдаемых результатов, а X = (x1T… .xnT) представляет матрицу плана наблюдаемых ковариат, где x i = ( x i 1 ,…, x ip ) T (или x i = (1, x i 1 ,…, x i p ) T ).В этой настройке X = [ X 1 | … | X p ] — это размерная переменная p ( p≥1 ).

Методы регрессионного анализа можно разделить на две основные категории: непараметрические и параметрические. Первая категория содержит те методы, которые не принимают особую форму для f () ; , в то время как вторая категория включает эти методы, основанные на предположении о знании отношения f () до фиксированного числа параметров β , которые необходимо оценить на основе наблюдаемых данных.Когда связь между независимыми переменными X, и параметрами β является линейной, модель известна как модель линейной регрессии .

Модель линейной регрессии — одна из старейших и наиболее изученных тем в статистике и тип регрессии, наиболее часто используемый в приложениях. Например, регрессионный анализ можно использовать для изучения того, как определенный фенотип (например, артериальное давление) зависит от ряда клинических параметров (например,g., уровень холестерина, возраст, диета и др.) или как экспрессия генов зависит от набора факторов транскрипции, которые могут повышать / понижать уровень транскрипции и т. д. Несмотря на то, что линейные модели просты и легко обрабатываются математически, они часто обеспечивают адекватную и интерпретируемую оценку взаимосвязи между X и Y . Технически говоря, модель линейной регрессии предполагает, что отклик Y является непрерывной переменной, определенной в реальном масштабе, и все наблюдаемые данные моделируются как

Yi = β0 + β1xi1 +… + βpxip + εi = xiTβ + εii = 1 ,…, N

, где β = ( β 0 , β 1 ,…, β p ) T — вектор неизвестные параметры, называемые коэффициентами регрессии , и ε представляют собой ошибки или шумовой член , который учитывает случайность измеренных данных или остаточную изменчивость, не объясненную X .(и, следовательно, количественная оценка силы взаимосвязи между Y и каждой из объясняющих переменных p , когда оставшиеся p-1 фиксированы), но также выбор тех переменных, которые не связаны с Y (когда оставшиеся фиксированы), а также определение того, какие подмножества объясняющих переменных необходимо учитывать, чтобы достаточно хорошо объяснить ответ Y . Эти задачи могут быть выполнены путем тестирования значимости каждого отдельного коэффициента регрессии, когда другие фиксированы, путем удаления коэффициентов, которые не являются значимыми, и повторной подгонки линейной модели и / или с использованием подходов к выбору модели., соответствующее любому новому значению x0, и оценить неопределенность такого прогноза. Неопределенность зависит от типа прогноза, который нужно сделать. Фактически, можно вычислить два типа доверительных интервалов: один для ожидания предсказанного значения в данной точке x0 и один для будущего общего наблюдения в данной точке x0.

По мере увеличения числа независимых переменных p метод наименьших квадратов страдает от ряда проблем, таких как недостаточная точность предсказания и сложность интерпретации .Для решения этих проблем желательно иметь модель только с небольшим количеством «важных» переменных, которая способна дать хорошее объяснение результата и хорошее обобщение ценой принесения в жертву некоторых деталей. Выбор модели состоит в том, чтобы определить, какие подмножества объясняющих переменных должны быть «выбраны», чтобы в достаточной мере объяснить ответ Y , делая компромисс, называемый компромиссом смещения и отклонения . Это эквивалентно выбору между конкурирующими моделями линейной регрессии (т.е., с разными комбинациями переменных). С одной стороны, необходимо учитывать, что включение слишком небольшого числа переменных приводит к так называемому « не соответствует » данных, характеризующимся плохой производительностью прогнозирования с высоким смещением и низкой дисперсией. С другой стороны, выбор многих переменных приводит к так называемому « overfit » данных, характеризующемуся плохой производительностью прогнозирования с низким смещением и высокой дисперсией. Пошаговая линейная регрессия — это попытка решить эту проблему (Miller et al ., 2002; Sen and Srivastava, 1990), составляющие конкретный пример регрессионного анализа подмножеств. Хотя выбор модели можно использовать в контексте классической регрессии, это один из наиболее эффективных инструментов анализа данных большой размерности.

Классическая регрессия имеет дело со случаем n≥p , где n обозначает количество независимых наблюдений (т. Е. Размер выборки), а p — количество переменных. В настоящее время во многих приложениях, особенно в биомедицине, высокопроизводительные анализы способны измерять от тысяч до сотен тысяч переменных на одной статистической единице.Поэтому часто приходится иметь дело с корпусом p >> n . В таком случае нельзя применять обычные методы наименьших квадратов и другие типы подходов (например, включая использование функции штрафов), такие как регрессия Риджа, лассо или эластичная чистая регрессия (Hastie et al ., 2009; James et al., ., 2013; Tibshirani, 1996, 2011) должны использоваться для оценки коэффициентов регрессии. В частности, Лассо очень эффективен, поскольку он также выполняет выбор переменных и открыл новую структуру многомерной регрессии (Bühlmann and van de Geer, 2011; Hastie et al ., 2015). Выбор модели и анализ данных большой размерности тесно связаны, и им также могут быть полезны методы уменьшения размерности, такие как анализ главных компонентов или выбор функций.

В классической структуре Y рассматривается как случайная величина, тогда как X считаются фиксированными, следовательно, в зависимости от распределения Y могут быть определены различные типы регрессионных моделей. . При фиксированном X предположения о распределении Y выводятся через распределение члена ошибки ε = (ε1,…, εn) T.Как упоминалось выше, классическая линейная регрессия требует, чтобы член ошибки удовлетворял условиям Гаусса-Маркова и имел нормальное распределение. Однако, когда член ошибки не имеет нормального распределения, линейная регрессия может не подходить. Обобщенные линейные модели (GLM) представляют собой обобщение классической линейной регрессии, которое позволяет переменной отклика Y иметь распределение ошибок, отличное от нормального (McCullagh and Nelder, 1989). Таким образом, GLM обобщает линейную регрессию, позволяя связать линейную модель с переменной отклика через функцию связи и позволяя величине дисперсии каждого измерения быть функцией его предсказанного значения.Таким образом, GLM представляет собой широкую структуру, которая включает линейную регрессию, логистическую регрессию, регрессию Пуассона, полиномиальную регрессию и т. Д. В этой структуре коэффициенты регрессии могут быть оценены с использованием подхода максимального правдоподобия , часто решаемого с помощью алгоритмов наименьших квадратов с повторным взвешиванием.

Далее мы кратко суммируем ключевые концепции и определения, относящиеся к линейной регрессии, переходя от простой линейной модели к множественной линейной модели.В частности, обсуждаются условия Гаусса-Маркова и свойства оценки наименьших квадратов. Мы обсуждаем концепции выбора модели, а также даем предложения о том, как обрабатывать выбросы и отклонения от стандартных предположений. Затем мы обсудим современные формы регрессии, такие как регрессия гребня, лассо и эластичная сеть, которые основаны на терминах штрафов и особенно полезны, когда размерность пространства переменных, p , увеличивается. В заключение мы расширили концепции линейной регрессии до обобщенных линейных моделей (GLM).

Видя теория — регрессионный анализ

Дисперсионный анализ

Дисперсионный анализ (ANOVA) — это статистический метод проверки того, имеют ли группы данных одно и то же среднее значение. ANOVA обобщает t-критерий для двух или более групп, сравнивая сумму квадратичных ошибок внутри и между группами.

Выберите один из следующих наборов данных для исследования.

— выберите набор данных — квартет Anscombe’s Quartet, XQuartet, Y Iris Flower Dataset Species, Sepal LengthSpecies, Sepal WidthSpecies, Petal LengthSpecies, Petal Width Rat Feed Experiment Diet, WeightAmount, Weight

Перетащите точки данных, чтобы изучить, как это влияет на результат теста ANOVA.

Щелкните столбец таблицы ANOVA, чтобы узнать больше об этом параметре.

\ (\ Displaystyle {SSE} \) \ (\ Displaystyle {df} \) \ (\ Displaystyle {MS} \) \ (\ Displaystyle {F} \) \ (\ Displaystyle {p} \)
Лечение
Ошибка
Всего

\ (SSE \) — это сокращение от суммы квадратов ошибок, которая является суммой квадратных остатков.{2} $$

\ (df \) — это сокращение для степеней свободы, которое связано с количеством точек данных. Математически он определяется следующим образом:

$$ df = n — 1 $$

\ (MSE \) — это сокращение от среднеквадратичной ошибки, которая представляет собой частное от суммы квадратичных ошибок и степеней свободы. Математически он определяется следующим образом:

$$ MSE = \ dfrac {SSE} {df} $$

\ (F \) — это тестовая статистика, которая определяется следующим образом:

$$ F = \ dfrac {SST / (k-1)} {SSE / (n-k)} \ sim f_ {k-1, n-k} $$

\ (p \) — значение p, которое определяется из статистики F.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *