Релаксация физика: Релаксация (Физика) — это… Что такое Релаксация (Физика)? – Релаксация (физика) — это… Что такое Релаксация (физика)? — inakhan.ru

Содержание

Релаксация (Физика) — это… Что такое Релаксация (Физика)?

Релаксация (от лат. relaxatio — ослабление, уменьшение) — процесс установления термодинамического, а следовательно, и статистического равновесия в физической системе, состоящей из большого числа частиц.

Свойства и виды

Релаксация — многоступенчатый процесс, так как не все физические параметры системы (распределение частиц по координатам и импульсам, температура, давление, концентрация в малых объёмах и во всей системе и другие) стремятся к равновесию с одинаковой скоростью. Обычно сначала устанавливается равновесие по какому-либо параметру (частичное равновесие), что также называется релаксацией. Все процессы релаксации являются неравновесными процессами, при которых в системе происходит диссипация энергии, то есть производится энтропия (в замкнутой системе энтропия возрастает). В различных системах релаксация имеет свои особенности, зависящие от характера взаимодействия между частицами системы; поэтому процессы релаксации

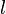весьма многообразны. Время установления равновесия (частичного или полного) в системе называется временем релаксации. Процесс установления равновесия в газах определяется длиной свободного пробега частиц $\,l$ и временем свободного пробега 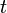$\,t$ (среднее расстояние и среднее время между двумя последовательными столкновениями молекул). Отношение 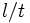$\,l/t$ имеет порядок величины скорости частиц. Величины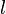 $\,l$

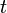и $\,t$ очень малы по сравнению с макроскопическими масштабами длины и времени. С другой стороны, для газов время свободного пробега значительно больше времени столкновения 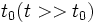$\,t_0 (t &gt;&gt; t_0)$ . Только при этом условии релаксация определяется лишь парными столкновениями молекул.

Описание процесса релаксации

Для одноатомных газов

В одноатомных газах (без внутренних степеней свободы, то есть обладающих только поступательными степенями свободы)

релаксация происходит в два этапа.

На первом этапе за короткий промежуток времени, порядка времени столкновения молекул то, начальное, даже сильно неравновесное, состояние хаотизируется таким образом, что становятся несущественными детали начального состояния и оказывается возможным так называемое «сокращённое описание» неравновесного состояния системы, когда не требуется знания вероятности распределения всех частиц системы по координатам и импульсам, а достаточно знать распределение одной частицы по координатам и импульсам в зависимости от времени, то есть одночастичную функцию распределения молекул. (Все остальные функции распределения более высокого порядка, описывающие распределения по состояниям двух, трёх и т. д. частиц, зависят от времени лишь через одночастичную функцию). Одночастичная функция удовлетворяет кинетическому уравнению Больцмана, которое описывает процесс

релаксации. Этот этап называется кинетическим и является очень быстрым процессом релаксации.

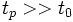релаксации медленно стремятся к равновесным, а состояние системы обычно мало отличается от равновесного. Время релаксации для локального равновесия $\,t_p &gt;&gt; t_0$ . После установления локального равновесия для описания релаксации неравновесного состояния системы служат уравнения гидродинамики (уравнения Навье — Стокса, уравнения теплопроводности, диффузии и т. п.). При этом предполагается, что термодинамические параметры системы (плотность, температура и т. д.) и массовая скорость (средняя скорость переноса массы) мало меняются за время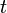 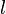$\,t$ и на расстоянии $\,l$ . Этот этап релаксации называется гидродинамическим. Дальнейшая релаксация системы к состоянию полного статистического равновесия, при котором выравниваются средние скорости частиц, средняя температура, средняя концентрация и т. д., происходит медленно в результате очень большого числа столкновений.

Такие процессы (вязкость, теплопроводность, диффузия, электропроводность и т. п.) называются медленными. Соответствующее время релаксации 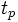$\,t_p$ зависит от размеров 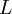$\,L$ системы и велико по сравнению с $\,t$ : $\,t0 \approx t(L/l)2 &gt;&gt; t$

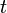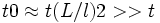
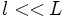, что имеет место при $\,l &lt;&lt; L$ , то есть для не сильно разреженных газов.

Для многоатомных газов

В многоатомных газах (с внутренними степенями свободы) может быть замедлен обмен энергией между поступательными и внутренними степенями свободы, и возникает процесс релаксации, связанный с этим явлением. Быстрее всего — за время порядка времени между столкновениями — устанавливается равновесие по поступательным степеням свободы; такое равновесное состояние можно охарактеризовать соответствующей температурой. Равновесие между поступательными и вращательными степенями свободы устанавливается значительно медленнее. Возбуждение колебательных степеней свободы может происходить лишь при высоких температурах. Поэтому в многоатомных газах возможны многоступенчатые процессы

релаксации энергии колебательных и вращательных степеней свободы.

Для смесей газов

В смесях газов с сильно различающимися массами молекул замедлен обмен энергией между компонентами, вследствие чего возможно возникновение состояния с различными температурами компонент и процессы релаксации их температур. Например, в плазме сильно различаются массы ионов и электронов. Быстрее всего устанавливается равновесие электронной компоненты, затем приходит в равновесие ионная компонента, и значительно большее время требуется для установления равновесия между электронами и ионами; поэтому в плазме могут длительное время существовать состояния, в которых ионные и электронные температуры различны а, следовательно, происходят процессы

релаксации температур компонент.

Для жидкостей

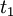— время и длина корреляции динамических переменных, описывающих потоки энергии или импульса; t₁ и l₁ характеризуют затухание во времени и в пространстве взаимного влияния молекул, то есть корреляции. При этом полностью остаётся в силе понятие гидродинамического этапа релаксации и 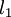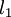локально-равновесного состояния. В макроскопически малых объёмах жидкости, но ещё достаточно больших по сравнению с длиной корреляции $\,l_1$ , локально-равновесное распределение устанавливается за время порядка времени корреляции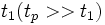 $\,t_1(t_p &gt;&gt; t_1)$

в результате интенсивного взаимодействия между молекулами (а не парных столкновений, как в газе), но эти объёмы по-прежнему можно считать приближённо изолированными. На гидродинамическом этапе релаксация в жидкости термодинамические параметры и массовая скорость удовлетворяют таким же уравнениям гидродинамики, как и для газов (при условии малости изменения термодинамических параметров и массовой скорости за время $\,t_1$ и на расстоянии $\,l_1$ ). 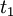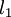Время релаксации к полному термодинамическому равновесию 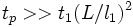$\,t_p &gt;&gt; t_1(L/l_1)^2$ (так же, как в газе и твёрдом теле) можно оценить с помощью кинетических коэффициентов. 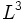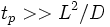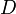Например, время релаксации концентрации в бинарной смеси в объёме $\,L^3$ порядка $\,t_p &gt;&gt; L^2/D$ , где $\,D$ — коэффициент диффузии, время релаксации температуры 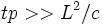$\,tp &gt;&gt; L^2/c$ , где $\,c$ — коэффициент температуропроводности, и т. д. Для жидкости с внутренними степенями свободы молекул возможно сочетание гидродинамического описания поступательных степеней свободы с дополнительными уравнениями для описания релаксации внутренних степеней свободы (релаксационная гидродинамика).

Для твёрдых тел и квантовых жидкостей

В твёрдых телах, как и в квантовых жидкостях, релаксацию можно описывать как релаксацию в газе квазичастиц. В этом случае можно ввести время и длину свободного пробега соответствующих квазичастиц (при условии малости возбуждения системы). Например, в кристаллической решётке при низких температурах упругие колебания можно трактовать как газ фононов. Взаимодействие между фононами приводит к квантовым переходам, то есть к столкновениям между ними. Релаксация энергии в кристаллической решётке описывается кинетическим уравнением для фононов. В системе спиновых магнитных моментов ферромагнетика квазичастицами являются магноны; Релаксацию (например, намагниченности) можно описывать кинетическим уравнением для магнонов. Релаксация магнитного момента в ферромагнетике происходит в два этапа: на первом этапе за счёт относительно сильного обменного взаимодействия устанавливается равновесное значение абсолютной величины магнитного момента.

На втором этапе за счёт слабого спин-орбитального взаимодействия магнитный момент медленно ориентируется вдоль оси лёгкого намагничивания; этот этап аналогичен гидродинамическому этапу релаксации в газах.

См. также

Литература

Лит.: Уленбек Д., форд Дж., Лекции по статистической механике, пер. с англ., М., 1965.

Ссылки

Wikimedia Foundation. 2010.

Релаксация (физика) — это… Что такое Релаксация (физика)?

Свойства и виды

Процесс установления равновесия в газах определяется длиной свободного пробега частиц и временем свободного пробега (среднее расстояние и среднее время между двумя последовательными столкновениями молекул). Отношение имеет порядок величины скорости частиц. Величины и очень малы по сравнению с макроскопическими масштабами длины и времени. С другой стороны, для газов время свободного пробега значительно больше времени столкновения . Только при этом условии релаксация определяется лишь парными столкновениями молекул.

Описание процесса релаксации

Для одноатомных газов

В одноатомных газах (без внутренних степеней свободы, то есть обладающих только поступательными степенями свободы) релаксация происходит в два этапа.

Одночастичная функция удовлетворяет кинетическому уравнению Больцмана, которое описывает процесс релаксации. Этот этап называется кинетическим и является очень быстрым процессом релаксации.

На втором этапе за время порядка времени свободного пробега молекул и в результате всего нескольких столкновений в макроскопически малых объёмах системы устанавливается локальное равновесие; ему соответствует локально-равновесное, или квазиравновесное, распределение, которое характеризуется такими же параметрами, как и при полном равновесии системы, но зависящими от пространственных координат и времени. Эти малые объёмы содержат ещё очень много молекул, а поскольку они взаимодействуют с окружением лишь на своей поверхности, их можно считать приближённо изолированными. Параметры локально-равновесного распределения в процессе релаксации медленно стремятся к равновесным, а состояние системы обычно мало отличается от равновесного. Время релаксации для локального равновесия . После установления локального равновесия для описания релаксации неравновесного состояния системы служат уравнения гидродинамики (уравнения Навье — Стокса, уравнения теплопроводности, диффузии и т. п.). При этом предполагается, что термодинамические параметры системы (плотность, температура и т. д.) и массовая скорость (средняя скорость переноса массы) мало меняются за время и на расстоянии . Этот этап релаксации называется гидродинамическим. Дальнейшая релаксация системы к состоянию полного статистического равновесия, при котором выравниваются средние скорости частиц, средняя температура, средняя концентрация и т. д., происходит медленно в результате очень большого числа столкновений.

Такие процессы (вязкость, теплопроводность, диффузия, электропроводность и т. п.) называются медленными. Соответствующее время релаксации зависит от размеров системы и велико по сравнению с : , что имеет место при , то есть для не сильно разреженных газов.

Для многоатомных газов

Для смесей газов

Для жидкостей

В жидкостях теряет смысл понятие времени и длины свободного пробега частиц (а следовательно, и кинетического уравнения для одночастичной функции распределения). Аналогичную роль для жидкости играют величины и — время и длина корреляции динамических переменных, описывающих потоки энергии или импульса; и характеризуют затухание во времени и в пространстве взаимного влияния молекул, то есть корреляции. При этом полностью остаётся в силе понятие гидродинамического этапа релаксации и локально-равновесного состояния. В макроскопически малых объёмах жидкости, но ещё достаточно больших по сравнению с длиной корреляции , локально-равновесное распределение устанавливается за время порядка времени корреляции в результате интенсивного взаимодействия между молекулами (а не парных столкновений, как в газе), но эти объёмы по-прежнему можно считать приближённо изолированными. На гидродинамическом этапе релаксация в жидкости термодинамические параметры и массовая скорость удовлетворяют таким же уравнениям гидродинамики, как и для газов (при условии малости изменения термодинамических параметров и массовой скорости за время и на расстоянии ). Время релаксации к полному термодинамическому равновесию (так же, как в газе и твёрдом теле) можно оценить с помощью кинетических коэффициентов. Например, время релаксации концентрации в бинарной смеси в объёме порядка , где — коэффициент диффузии, время релаксации температуры , где — коэффициент температуропроводности, и т. д. Для жидкости с внутренними степенями свободы молекул возможно сочетание гидродинамического описания поступательных степеней свободы с дополнительными уравнениями для описания релаксации внутренних степеней свободы (релаксационная гидродинамика).

Для твёрдых тел и квантовых жидкостей

Например, в кристаллической решётке при низких температурах упругие колебания можно трактовать как газ фононов. Взаимодействие между фононами приводит к квантовым переходам, то есть к столкновениям между ними. Релаксация энергии в кристаллической решётке описывается кинетическим уравнением для фононов. В системе спиновых магнитных моментов ферромагнетика квазичастицами являются магноны. Релаксацию (например, намагниченности) можно описывать кинетическим уравнением для магнонов. Релаксация магнитного момента в ферромагнетике происходит в два этапа: на первом этапе за счёт относительно сильного обменного взаимодействия устанавливается равновесное значение абсолютной величины магнитного момента.

Литература

Уленбек Д., Форд Дж. Лекции по статистической механике. — Пер. с англ. — М.: Мир, 1965.
Бондаревский С. И., Аблесимов Н. Е. Релаксационные эффекты в неравновесных конденсированных системах. Самооблучение в результате радиоактивного распада. — Владивосток: Дальнаука, 2002. — 232 с.
Аблесимов Н. Е., Земцов А. Н. Релаксационные эффекты в неравновесных конденсированных системах. Базальты: от извержения до волокна. — М.: ИТиГ ДВО РАН, 2010. — 400 с.
Осипов А. И. Термодинамика вчера, сегодня, завтра. Часть 1. Равновесная термодинамика // СОЖ. — 1999. — № 4. — с. 79-85.

См. также

РЕЛАКСАЦИЯ • Большая российская энциклопедия

РЕЛАКСА́ЦИЯ в физике, процесс установления термодинамич. равновесия в физич. системе, состоящей из большого числа частиц. Р. – многоступенчатый процесс, т. к. не все физич. параметры системы стремятся к равновесию с одинаковой скоростью. Обычно сначала устанавливается равновесие по к.-л. параметру (частичное равновесие). Все процессы Р. являются неравновесными и необратимыми процессами, при которых в системе происходит диссипация энергии. Исследование этих процессов составляет предмет кинетики физической.

Время τ установления частичного или полного равновесия в системе называется временем релаксации. Когда отклонение от равновесия невелико, Р. параметра $x$ со временем $t$ обычно происходит по закону $x=x_0\exp(–t/τ)$, где $x_0$ – начальное значение параметра $x$.

В газах Р. обусловлена обменом энергией и импульсом при парных столкновениях частиц, а время Р. определяется временем свободного пробега частиц и эффективностью обмена энергией между всеми степенями свободы сталкивающихся частиц. В одноатомных газах выделяют этап быстрой Р. (т. н. кинетич. стадия), когда за короткий период времени, порядка времени столкновения частиц, начальное (сильно неравновесное) состояние хаотизируется настолько, что для его описания достаточно знать, как изменяется во времени распределение по координатам и импульсам всего одной частицы (т. н. одночастичная функция распределения). На втором этапе Р. (т. н. гидродинамич. стадия) за время порядка времени свободного пробега в результате всего нескольких столкновений в макроскопически малых объёмах устанавливается локальное термодинамич. равновесие. Оно характеризуется параметрами состояния (темп-рой, химич. потенциалом и др.), которые зависят от пространственных координат и времени и медленно стремятся к равновесным значениям в результате большого числа столкновений (процессы теплопроводности, диффузии, вязкости и др.). Время Р. зависит от размера системы и велико по сравнению со ср. временем свободного пробега.

В многоатомных газах может быть замедлен обмен энергией между поступат. и внутр. степенями свободы частиц. Быстрее всего (за время порядка времени между столкновениями) устанавливается равновесие по поступат. степеням свободы. Равновесие между поступат. и вращат. степенями свободы устанавливается значительно медленнее.

В смесях газов с сильно различающимися массами частиц замедлен обмен энергией между компонентами, вследствие чего возможны появление состояния с разл. темп-рами компонент и процессы Р. их темп-р. Напр., в плазме быстрее всего устанавливается равновесие электронной компоненты, затем приходит в равновесие ионная компонента, и значительно большее время требуется для установления равновесия между электронами и ионами.

В жидкости Р. описывают с помощью пространственно-временны́х корреляционных функций, характеризующих затухание во времени и пространстве взаимного влияния молекул (корреляций). Эти корреляции являются причиной необратимых процессов – теплопроводности и вязкости.

В твёрдых телах Р. описывают как Р. в газе квазичастиц. Напр., в кристаллич. решётке при низких темп-pax упругие колебания трактуют как газ фононов. Р. внутр. энергии в кристаллич. решётке описывается кинетич. уравнением для фононов. В системе спиновых магнитных моментов ферромагнетика квазичастицами являются магноны (см. Релаксация магнитная). Р., обусловленная распространением звуковых волн в веществе, с которой связано поглощение звука, называется релаксацией акустической.

Лит. см. при ст. Кинетика физическая.

Релаксация (физика) — Википедия. Что такое Релаксация (физика)

Релаксация (от лат. relaxatio — ослабление, уменьшение) — процесс установления термодинамического, а следовательно, и статистического равновесия в физической системе, состоящей из большого числа частиц.

Релаксация — многоступенчатый процесс, так как не все физические параметры системы (распределение частиц по координатам и импульсам, температура, давление, концентрация в малых объёмах и во всей системе и другие) стремятся к равновесию с одинаковой скоростью. Обычно сначала устанавливается равновесие по какому-либо параметру (частичное равновесие), что также называется релаксацией. Все процессы релаксации являются неравновесными процессами, при которых в системе происходит диссипация энергии, то есть производится энтропия (в замкнутой системе энтропия не убывает). В различных системах релаксация имеет свои особенности, зависящие от характера взаимодействия между частицами системы; поэтому процессы релаксации весьма многообразны. Время установления равновесия (частичного или полного) в системе называется временем релаксации.

Процесс установления равновесия в газах определяется длиной свободного пробега частиц l{\displaystyle l} и временем свободного пробега t{\displaystyle t} (среднее расстояние и среднее время между двумя последовательными столкновениями молекул). Отношение l/t{\displaystyle l/t} имеет порядок величины скорости частиц. Величины l{\displaystyle l} и t{\displaystyle t} очень малы по сравнению с макроскопическими масштабами длины и времени. С другой стороны, для газов время свободного пробега значительно больше времени столкновения t0{\displaystyle t_{0}} (t≫t0){\displaystyle (t\gg t_{0})}. Только при этом условии релаксация определяется лишь парными столкновениями молекул.

Описание процесса релаксации

Для одноатомных газов

На втором этапе за время порядка времени свободного пробега молекул и в результате всего нескольких столкновений в макроскопически малых объёмах системы устанавливается локальное равновесие; ему соответствует локально-равновесное, или квазиравновесное, распределение, которое характеризуется такими же параметрами, как и при полном равновесии системы, но зависящими от пространственных координат и времени. Эти малые объёмы содержат ещё очень много молекул, а поскольку они взаимодействуют с окружением лишь на своей поверхности, их можно считать приближённо изолированными. Параметры локально-равновесного распределения в процессе релаксации медленно стремятся к равновесным, а состояние системы обычно мало отличается от равновесного. Время релаксации для локального равновесия tp≫t0{\displaystyle t_{p}\gg t_{0}}. После установления локального равновесия для описания релаксации неравновесного состояния системы служат уравнения гидродинамики (уравнения Навье — Стокса, уравнения теплопроводности, диффузии и т. п.). При этом предполагается, что термодинамические параметры системы (плотность, температура и т. д.) и массовая скорость (средняя скорость переноса массы) мало меняются за время t{\displaystyle t} и на расстоянии l{\displaystyle l}. Этот этап релаксации называется гидродинамическим. Дальнейшая релаксация системы к состоянию полного статистического равновесия, при котором выравниваются средние скорости частиц, средняя температура, средняя концентрация и т. д., происходит медленно в результате очень большого числа столкновений.

Такие процессы (вязкость, теплопроводность, диффузия, электропроводность и т. п.) называются медленными. Соответствующее время релаксации tp{\displaystyle t_{p}} зависит от размеров L{\displaystyle L} системы и велико по сравнению с t{\displaystyle t}: t0≈t(L/l)2≫t{\displaystyle t_{0}\approx t(L/l)2\gg t}, что имеет место при l≪L{\displaystyle l\ll L}, то есть для не сильно разреженных газов.

Для многоатомных газов

Для смесей газов

Для жидкостей

В жидкостях теряет смысл понятие времени и длины свободного пробега частиц (а следовательно, и кинетического уравнения для одночастичной функции распределения). Аналогичную роль для жидкости играют величины t1{\displaystyle t_{1}} и l1{\displaystyle l_{1}} — время и длина корреляции динамических переменных, описывающих потоки энергии или импульса; t1{\displaystyle t_{1}} и l1{\displaystyle l_{1}} характеризуют затухание во времени и в пространстве взаимного влияния молекул, то есть корреляции. При этом полностью остаётся в силе понятие гидродинамического этапа релаксации и локально-равновесного состояния. В макроскопически малых объёмах жидкости, но ещё достаточно больших по сравнению с длиной корреляции l1{\displaystyle l_{1}}, локально-равновесное распределение устанавливается за время порядка времени корреляции t1{\displaystyle t_{1}} (tp≫t1){\displaystyle (t_{p}\gg t_{1})} в результате интенсивного взаимодействия между молекулами (а не парных столкновений, как в газе), но эти объёмы по-прежнему можно считать приближённо изолированными. На гидродинамическом этапе релаксация в жидкости термодинамические параметры и массовая скорость удовлетворяют таким же уравнениям гидродинамики, как и для газов (при условии малости изменения термодинамических параметров и массовой скорости за время t1{\displaystyle t_{1}} и на расстоянии l1{\displaystyle l_{1}}). Время релаксации к полному термодинамическому равновесию tp≫t1(L/l1)2{\displaystyle t_{p}\gg t_{1}(L/l_{1})^{2}} (так же, как в газе и твёрдом теле) можно оценить с помощью кинетических коэффициентов. Например, время релаксации концентрации в бинарной смеси в объёме L3{\displaystyle L^{3}} порядка tp≫L2/D{\displaystyle t_{p}\gg L^{2}/D}, где D{\displaystyle D} — коэффициент диффузии, время релаксации температуры tp≫L2/c{\displaystyle t_{p}\gg L^{2}/c}, где c{\displaystyle c} — коэффициент температуропроводности, и т. д. Для жидкости с внутренними степенями свободы молекул возможно сочетание гидродинамического описания поступательных степеней свободы с дополнительными уравнениями для описания релаксации внутренних степеней свободы (релаксационная гидродинамика).

Для твёрдых тел и квантовых жидкостей

Литература

Уленбек Д., Форд Дж. Лекции по статистической механике. — Пер. с англ. — М.: Мир, 1965.
Бондаревский С. И., Аблесимов Н. Е. Релаксационные эффекты в неравновесных конденсированных системах. Самооблучение в результате радиоактивного распада. — Владивосток: Дальнаука, 2002. — 232 с.
Аблесимов Н. Е., Земцов А. Н. Релаксационные эффекты в неравновесных конденсированных системах. Базальты: от извержения до волокна. — М.: ИТиГ ДВО РАН, 2010. — 400 с.
Осипов А. И. Термодинамика вчера, сегодня, завтра. Часть 1. Равновесная термодинамика // СОЖ. — 1999. — № 4. — с. 79-85.

См. также

Релаксация (физика) — Википедия

Релакса́ция (от лат. relaxatio «ослабление, уменьшение») — процесс установления термодинамического, а следовательно, и статистического равновесия в физической системе, состоящей из большого числа частиц.

Релаксация — многоступенчатый процесс, так как не все физические параметры системы (распределение частиц по координатам и импульсам, температура, давление, концентрация в малых объёмах и во всей системе и другие) стремятся к равновесию с одинаковой скоростью. Обычно сначала устанавливается равновесие по какому-либо параметру (частичное равновесие), что также называется релаксацией. Все процессы релаксации являются неравновесными процессами, при которых в системе происходит диссипация энергии, то есть производится энтропия (в замкнутой системе энтропия не убывает). В различных системах релаксация имеет свои особенности, зависящие от характера взаимодействия между частицами системы; поэтому процессы релаксации весьма многообразны. Время установления равновесия (частичного или полного) в системе называется временем релаксации.

Описание процесса релаксации

Для одноатомных газов

На втором этапе за время порядка времени свободного пробега молекул и в результате всего нескольких столкновений в макроскопически малых объёмах системы устанавливается локальное равновесие; ему соответствует локально-равновесное, или квазиравновесное, распределение, которое характеризуется такими же параметрами, как и при полном равновесии системы, но зависящими от пространственных координат и времени. Эти малые объёмы содержат ещё очень много молекул, а поскольку они взаимодействуют с окружением лишь на своей поверхности, их можно считать приближённо изолированными. Параметры локально-равновесного распределения в процессе релаксации медленно стремятся к равновесным, а состояние системы обычно мало отличается от равновесного. Время релаксации для локального равновесия tp≫t0{\displaystyle t_{p}\gg t_{0}}. После установления локального равновесия для описания релаксации неравновесного состояния системы служат уравнения гидродинамики (уравнения Навье — Стокса, уравнения теплопроводности, диффузии и т. п.). При этом предполагается, что термодинамические параметры системы (плотность, температура и т. д.) и массовая скорость (средняя скорость переноса массы) мало меняются за время t{\displaystyle t} и на расстоянии l{\displaystyle l}. Этот этап релаксации называется гидродинамическим. Дальнейшая релаксация системы к состоянию полного статистического равновесия, при котором выравниваются средние скорости частиц, средняя температура, средняя концентрация и т. д., происходит медленно в результате очень большого числа столкновений.

Для многоатомных газов

Для смесей газов

Для жидкостей

В жидкостях теряет смысл понятие времени и длины свободного пробега частиц (а следовательно, и кинетического уравнения для одночастичной функции распределения). Аналогичную роль для жидкости играют величины t1{\displaystyle t_{1}} и l1{\displaystyle l_{1}} — время и длина корреляции динамических переменных, описывающих потоки энергии или импульса; t1{\displaystyle t_{1}} и l1{\displaystyle l_{1}} характеризуют затухание во времени и в пространстве взаимного влияния молекул, то есть корреляции. При этом полностью остаётся в силе понятие гидродинамического этапа релаксации и локально-равновесного состояния. В макроскопически малых объёмах жидкости, но ещё достаточно больших по сравнению с длиной корреляции l1{\displaystyle l_{1}}, локально-равновесное распределение устанавливается за время порядка времени корреляции t1{\displaystyle t_{1}} (tp≫t1){\displaystyle (t_{p}\gg t_{1})} в результате интенсивного взаимодействия между молекулами (а не парных столкновений, как в газе), но эти объёмы по-прежнему можно считать приближённо изолированными. На гидродинамическом этапе релаксация в жидкости термодинамические параметры и массовая скорость удовлетворяют таким же уравнениям гидродинамики, как и для газов (при условии малости изменения термодинамических параметров и массовой скорости за время t1{\displaystyle t_{1}} и на расстоянии l1{\displaystyle l_{1}}). Время релаксации к полному термодинамическому равновесию tp≫t1(L/l1)2{\displaystyle t_{p}\gg t_{1}(L/l_{1})^{2}} (так же, как в газе и твёрдом теле) можно оценить с помощью кинетических коэффициентов. Например, время релаксации концентрации в бинарной смеси в объёме L3{\displaystyle L^{3}} порядка tp≫L2/D{\displaystyle t_{p}\gg L^{2}/D}, где D{\displaystyle D} — коэффициент диффузии, время релаксации температуры tp≫L2/c{\displaystyle t_{p}\gg L^{2}/c}, где c{\displaystyle c} — коэффициент температуропроводности, и т. д. Для жидкости с внутренними степенями свободы молекул возможно сочетание гидродинамического описания поступательных степеней свободы с дополнительными уравнениями для описания релаксации внутренних степеней свободы (релаксационная гидродинамика).

Для твёрдых тел и квантовых жидкостей

См. также

Примечание

Литература

Уленбек Д., Форд Дж. Лекции по статистической механике. — Пер. с англ. — М.: Мир, 1965.
Бондаревский С. И., Аблесимов Н. Е. Релаксационные эффекты в неравновесных конденсированных системах. Самооблучение в результате радиоактивного распада. — Владивосток: Дальнаука, 2002. — 232 с.
Аблесимов Н. Е., Земцов А. Н. Релаксационные эффекты в неравновесных конденсированных системах. Базальты: от извержения до волокна. — М.: ИТиГ ДВО РАН, 2010. — 400 с.
Осипов А. И. Термодинамика вчера, сегодня, завтра. Часть 1. Равновесная термодинамика (недоступная ссылка) // СОЖ. — 1999. — № 4. — с. 79-85.

Время релаксации — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 июня 2016; проверки требуют 4 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 июня 2016; проверки требуют 4 правки.

Время релаксации — период времени, за который амплитудное значение возмущения в выведенной из равновесия физической системе уменьшается в e раз (e — основание натурального логарифма), в основном обозначается греческой буквой τ.

Согласно принципу Ле Шателье — Брауна, при отклонении физической системы от состояния устойчивого равновесия возникают силы, которые пытаются вернуть систему к равновесному состоянию. Если в состоянии равновесия некоторая физическая величина f имеет значение f0{\displaystyle f_{0}}, причём отклонение от равновесия |f−f0|≪f0{\displaystyle |f-f_{0}|\ll f_{0}}, то в первом приближении можно считать, что эти силы пропорциональны отклонению. Кинетическое уравнение для величины f запишется в виде

dfdt=−λ(f−f0){\displaystyle {\frac {df}{dt}}=-\lambda (f-f_{0})},

где λ — некоторый параметр, а знак минус указывает на то, что реакция системы на возмущение приводит к возвращению к равновесному состоянию.

Время релаксации

τ=1β{\displaystyle \tau ={\frac {1}{\beta }}}

В таком случае величина f будет изменяться по закону:

f(t)=f0+Δf0e−t/τ{\displaystyle f(t)=f_{0}+\Delta f_{0}e^{-t/\tau }},

где Δf0=f(0)−f0{\displaystyle \Delta f_{0}=f(0)-f_{0}} — начальное возмущение.

Приближение времени релаксации широко используется при описании кинетических процессов в физике, когда речь идет о кинетике установления равновесного состояния. Переход от неравновесного состояния к равновесию сопровождается диссипацией энергии и является необратимым процессом. Установление равновесия часто проходит в несколько этапов, которые характеризуются своими отдельными временами релаксации. Так, при возбуждении молекул светом установление теплового равновесия происходит за время порядка 10−12{\displaystyle 10^{-12}} с, а вот люминесценция — излучение света возбуждёнными состояниями, может иметь характерные времена порядка наносекунд и даже микросекунд.

При описании многих физических процессов время релаксации берётся как феноменологический параметр, однако в отдельных случаях его можно определить через параметры микроскопических процессов, таких как вероятность квантовомеханического перехода или сечение рассеяния.

Релаксация (физика) — Википедия

Релаксация — многоступенчатый процесс, так как не все физические параметры системы (распределение частиц по координатам и импульсам, температура, давление, концентрация в малых объёмах и во всей системе и другие) стремятся к равновесию с одинаковой скоростью. Обычно сначала устанавливается равновесие по какому-либо параметру (частичное равновесие), что также называется релаксацией. Все процессы релаксации являются неравновесными процессами, при которых в системе происходит диссипация энергии, то есть производится энтропия (в замкнутой системе энтропия не убывает). В различных системах релаксация имеет свои особенности, зависящие от характера взаимодействия между частицами системы; поэтому процессы релаксации весьма многообразны. Время установления равновесия (частичного или полного) в системе называется временем релаксации.

Описание процесса релаксации

Для одноатомных газов

На втором этапе за время порядка времени свободного пробега молекул и в результате всего нескольких столкновений в макроскопически малых объёмах системы устанавливается локальное равновесие; ему соответствует локально-равновесное, или квазиравновесное, распределение, которое характеризуется такими же параметрами, как и при полном равновесии системы, но зависящими от пространственных координат и времени. Эти малые объёмы содержат ещё очень много молекул, а поскольку они взаимодействуют с окружением лишь на своей поверхности, их можно считать приближённо изолированными. Параметры локально-равновесного распределения в процессе релаксации медленно стремятся к равновесным, а состояние системы обычно мало отличается от равновесного. Время релаксации для локального равновесия tp≫t0{\displaystyle t_{p}\gg t_{0}}. После установления локального равновесия для описания релаксации неравновесного состояния системы служат уравнения гидродинамики (уравнения Навье — Стокса, уравнения теплопроводности, диффузии и т. п.). При этом предполагается, что термодинамические параметры системы (плотность, температура и т. д.) и массовая скорость (средняя скорость переноса массы) мало меняются за время t{\displaystyle t} и на расстоянии l{\displaystyle l}. Этот этап релаксации называется гидродинамическим. Дальнейшая релаксация системы к состоянию полного статистического равновесия, при котором выравниваются средние скорости частиц, средняя температура, средняя концентрация и т. д., происходит медленно в результате очень большого числа столкновений.

Для многоатомных газов

Для смесей газов

Для жидкостей

В жидкостях теряет смысл понятие времени и длины свободного пробега частиц (а следовательно, и кинетического уравнения для одночастичной функции распределения). Аналогичную роль для жидкости играют величины t1{\displaystyle t_{1}} и l1{\displaystyle l_{1}} — время и длина корреляции динамических переменных, описывающих потоки энергии или импульса; t1{\displaystyle t_{1}} и l1{\displaystyle l_{1}} характеризуют затухание во времени и в пространстве взаимного влияния молекул, то есть корреляции. При этом полностью остаётся в силе понятие гидродинамического этапа релаксации и локально-равновесного состояния. В макроскопически малых объёмах жидкости, но ещё достаточно больших по сравнению с длиной корреляции l1{\displaystyle l_{1}}, локально-равновесное распределение устанавливается за время порядка времени корреляции t1{\displaystyle t_{1}} (tp≫t1){\displaystyle (t_{p}\gg t_{1})} в результате интенсивного взаимодействия между молекулами (а не парных столкновений, как в газе), но эти объёмы по-прежнему можно считать приближённо изолированными. На гидродинамическом этапе релаксация в жидкости термодинамические параметры и массовая скорость удовлетворяют таким же уравнениям гидродинамики, как и для газов (при условии малости изменения термодинамических параметров и массовой скорости за время t1{\displaystyle t_{1}} и на расстоянии l1{\displaystyle l_{1}}). Время релаксации к полному термодинамическому равновесию tp≫t1(L/l1)2{\displaystyle t_{p}\gg t_{1}(L/l_{1})^{2}} (так же, как в газе и твёрдом теле) можно оценить с помощью кинетических коэффициентов. Например, время релаксации концентрации в бинарной смеси в объёме L3{\displaystyle L^{3}} порядка tp≫L2/D{\displaystyle t_{p}\gg L^{2}/D}, где D{\displaystyle D} — коэффициент диффузии, время релаксации температуры tp≫L2/c{\displaystyle t_{p}\gg L^{2}/c}, где c{\displaystyle c} — коэффициент температуропроводности, и т. д. Для жидкости с внутренними степенями свободы молекул возможно сочетание гидродинамического описания поступательных степеней свободы с дополнительными уравнениями для описания релаксации внутренних степеней свободы (релаксационная гидродинамика).

Для твёрдых тел и квантовых жидкостей

См. также

Примечание

Литература

Уленбек Д., Форд Дж. Лекции по статистической механике. — Пер. с англ. — М.: Мир, 1965.
Бондаревский С. И., Аблесимов Н. Е. Релаксационные эффекты в неравновесных конденсированных системах. Самооблучение в результате радиоактивного распада. — Владивосток: Дальнаука, 2002. — 232 с.
Аблесимов Н. Е., Земцов А. Н. Релаксационные эффекты в неравновесных конденсированных системах. Базальты: от извержения до волокна. — М.: ИТиГ ДВО РАН, 2010. — 400 с.
Осипов А. И. Термодинамика вчера, сегодня, завтра. Часть 1. Равновесная термодинамика (недоступная ссылка) // СОЖ. — 1999. — № 4. — с. 79-85.

Релаксация (Физика) — это… Что такое Релаксация (Физика)?

Свойства и виды

Описание процесса релаксации

Для одноатомных газов

Для многоатомных газов

Для смесей газов

Для жидкостей

Для твёрдых тел и квантовых жидкостей

См. также

Литература

Ссылки

Релаксация (физика) — это… Что такое Релаксация (физика)?

Свойства и виды

Описание процесса релаксации

Для одноатомных газов

Для многоатомных газов

Для смесей газов

Для жидкостей

Для твёрдых тел и квантовых жидкостей

Литература

См. также

РЕЛАКСАЦИЯ • Большая российская энциклопедия

Релаксация (физика) — Википедия. Что такое Релаксация (физика)

Описание процесса релаксации

Для одноатомных газов

Для многоатомных газов

Для смесей газов

Для жидкостей

Для твёрдых тел и квантовых жидкостей

Литература

См. также

Релаксация (физика) — Википедия

Описание процесса релаксации

Для одноатомных газов

Для многоатомных газов

Для смесей газов

Для жидкостей

Для твёрдых тел и квантовых жидкостей

См. также

Примечание

Литература

Время релаксации — Википедия

Релаксация (физика) — Википедия

Описание процесса релаксации

Для одноатомных газов

Для многоатомных газов

Для смесей газов

Для жидкостей

Для твёрдых тел и квантовых жидкостей

См. также

Примечание

Литература

Добавить комментарий Отменить ответ