Тавтологии примеры: Тавтология и плеоназм — что это такое на примерах

Автор: | 26.07.1982
Нет комментариев

Содержание

Тавтология и плеоназм — что это такое на примерах

Обновлено 24 июля 2021 Просмотров: 100 530 Автор: Дмитрий Петров
  1. Что такое тавтология и плеоназм?
  2. Примеры
  3. Прижившиеся плеоназмы и тавтологии

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Хочу продолжить серию маленьких публикаций (заметок на полях), посвященных теме трактования довольно часто используемых на просторах рунета оборотов и «словечек». Чуть ранее мы заострили внимание на харизме, аннотации и дайждесте.

Сегодня хочу буквально пару слов сказать за тавтологию и плеоназм (вариант написания «тафтология» считается неправильным, хотя многие именно так это слово и произносят, делая его созвучным с «туфталогия», что в общем-то недалеко от истины).

Что же это такое? Какая крылатая фраза стала по сути синонимом тавтологии и почему чаще всего за это «ругают», а не «хвалят»? Чем плеоназм отличается от тавтологии? Или это одно и тоже? Все это, естественно, на примерах, ибо куда же без них.

Что такое тавтология и плеоназм?

Итак, сами по себе эти слова имеют однозначно греческие корни (точнее древне-греческие, когда эта страна была колыбелью философской мысли). Многих раздражает (и раздражало раньше), когда в речи собеседника присутствует множество «слов-паразитов» не несущих смысловой нагрузки, но сильно затягивающих и размывающих основную мысль (краткость, как известно, сестра таланта).

Так вот, ярким примером таких паразитических аномалий в нашей речи является плеоназм и одна из его вариаций — тавтология.

В переводе с древне-греческого слово плеоназм — это излишество (употребление ненужных для понимания слов или фраз), а тавтология — это повторение одного и того же (мысли, причины, описания) в одном предложении (по сути, это частный случай плеоназма).

Это то, что можно охарактеризовать термином — речевые излишества (ошибки). Они очень часто режут слух и засоряют нашу речь.

Подчеркну, что плеоназм представляет более емкое определение, ибо избыточность (излишество) в предложении может создаваться ведь не только употреблением похожих по смыслу слов, но и путем фраз, которые смело можно опустить. Примером такого плеоназма, который нельзя назвать тавтологией, могут служить такие вот фразы-пустышки:

  1. По направлению к дому ехала телега (можно убрать фразу «по направлению» и ничего по смыслу не изменится и не потеряется)
  2. Он рассказал мне о том, что… (фразу «о том» можно опустить без утери сути и лаконичости)
  3. Полезный навык (слово «полезный» тут лишние, ибо навык сам по себе подразумевает «полезное умение»)

Вроде бы пустяки, но это мусор, который засоряет наш мозг.

Но все же, под плеоназмами чаще всего подразумевают именно дублирование смыслов, т.е. чистой воды тавтологию. К тому же такие примеры намного ярче и производят больше впечатление, чем то, что уже было приведено выше.

Примеры тавтологии и плеоназма

Чаще всего такое безобразие происходит, когда употребляют однокоренные слова стоящие рядом. Это можно назвать «детской болезнью», ибо присуще чаще всего именно тем, кто только учится правильно и, что важно, четко формировать свои мысли.

Наверное, вы уже сталкивались с тем, что кто-то кому-то говорит, что это дескать «масло масляное». По сути, данная фраза уже стала сейчас синонимом слова «тавтология» и ее гораздо чаще употребляют, когда хотят указать человеку на выявленный в его речи очевидный недостаток, связанный с речевыми излишествами. «Ну, это же масло масляное!» — говорят в таких случаях.

Примерами «однокоренной» тавтологии могут служить фразы:

  1. старый старик
  2. заплатить плату
  3. высокая высота
  4. гость в гостях
  5. спросить вопрос
  6. белые белила
  7. проливной ливень
  8. писатель описывает
  9. рассказчик рассказал
  10. улыбнулся широкой улыбкой
  11. заработанная зарплата
  12. звенящий звонок
  13. закончить до конца
  14. добродушный добряк
  15. дымом дымится
  16. маленькие мелочи
  17. болел болезнью
  18. открытия открывать

Но есть примеры плеоназма (тавтологического толка, т. е. излишество за счет дублирования смыслов, а не за счет пустых фраз), когда используют не однокоренные слова, но очень близкие по смыслу:

  1. отрицательный недостаток
  2. горячий кипяток
  3. более лучшее
  4. очень прекрасно
  5. впервые познакомиться
  6. бесплатный подарок
  7. светловолосая блондинка
  8. мертвый труп

Ну, и еще примеры плеоназма без тавтологии (просто одно из слов лишнее, ибо по-другому просто быть не может и уточнять будет излишне):

  1. январь месяц
  2. минута времени
  3. затылок головы
  4. перспективы на будущее
  5. главный фаворит
  6. ностальгия по родине (что это такое?)
  7. промышленная индустрия
  8. моргать глазами

Примеры не раздражающей тавтологии п плеоназмов

Однако, есть примеры, когда явная тавтология совсем не раздражает:

  1. варить варенье
  2. начать сначала
  3. застегивать застежку
  4. угощать гостя
  5. закрыть крышкой
  6. облокотиться на локоть
  7. белое белье
  8. черные чернила
  9. приснилось во сне
  10. несоразмерность размера
  11. цветы расцветают
  12. отслужить службу
  13. битком набита
  14. сегодняшний день
  15. высочайшие вершины
  16. остановите на остановке
  17. делать дело
  18. шутки шутить
  19. петь песни
  20. тренировать у тренера
  21. работу работать
  22. красная краска (оба слова фразы имеют в своей основе корень «красивый»)

Так же можно много привести примеров, когда явные плеоназмы таковыми уже особо и не смотрятся из-за их частого и повседневного употребления:

  1. мимика лица
  2. спускаться вниз
  3. подниматься вверх
  4. другая альтернатива
  5. неприятный инцидент
  6. толпа людей
  7. сжатый кулак
  8. упал вниз
  9. идти пешком
  10. в конечном итоге
  11. лично я
  12. реальная действительность
  13. моя автобиография
  14. молодой парень
  15. полезный навык (навык — это само по себе «полезное умение»)

Объясняется последнее, скорее всего, просто силой привычки. Если вы эти фразы слышите с детства, употребляете их сами и все ваши окружающие, то замечания по поводу того, что это тавтология будут выглядеть просто напросто неуместными. Эти фразы уже не режут слух, как те, что употребляют по недоразумению.

Часто «тафто-фразы» приходят в нашу речь из пословиц и поговорок:

  1. сказка сказывается
  2. сидеть сиднем
  3. горе горькое
  4. ходить ходуном
  5. жизнь прожить
  6. есть поедом
  7. без вины виноватый
  8. вольному воля
  9. пропадать пропадом
  10. видать виды

Очень часто к устоявшимся (не разражающим) тавтологиям (плеоназмам) приводят употребления в одной фразе слов заимствованных из разных языков, но означающих почти одно и то же:

  1. выставочный экспонат (экспонат — это по определению «выставляемый предмет»)
  2. народная демократия (демократия — это и есть по определению «власть народа»)
  3. мемориальный памятник (мемориал — это и есть памятник по определению данного слова)
  4. впервые дебютировать
  5. свободная вакансия
  6. внутренний интерьер
  7. прейскурант цен
  8. госпитализировать в стационар
  9. памятные сувениры
  10. период времени
  11. полный аншлаг
  12. импортировать из-за рубежа
  13. первая премьера (первый дебют)
  14. народный фольклор

Кроме силы привычки, тавтология может использоваться для усиления эффекта. Об этом можно судить по большей части приведенных выше примеров. К ним еще можно добавить, например:

  1. крепко накрепко
  2. целиком и полностью
  3. истинная правда
  4. горе горькое
  5. яснее ясного
  6. суета сует
  7. полным полна
  8. всякая всячина
  9. нелепый абсурд

Как не допускать тавтологии и плеоназмов в своей речи? Побольше читать (или писать, как это делаю я 🙂 ). Тем самым вы неизбежно будете повышать свой словарный запас и формировать культуру речи. Все банально, но, к сожалению, в текущем 21 веке интернета не так то уж просто и осуществимо, ибо мы регулярно читаем лишь заголовки новостей и сообщения в соцсетях таких же как мы сами «книгочеев».

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Тавтология в русском языке. Что это такое? Примеры.

Тавтология – слово греческого происхождения обозначает буквально «то же самое слово».

Тавтология – это повторение в ряду слова, которое имеет одно и то же лексическое значение. Такой повтор считается необоснованным, так как не информативен. Тавтология – это почти всегда речевая ошибка и от неё следует избавляться и как можно реже употреблять её в речи.

Тавтология как термин встречается в логике и обозначает верное понятие, которое остается таковым, вне зависимости от того, о каком предмете, объекте или области идет речь. Это логически порочный круг, когда одно из понятий пытаются объяснять через это же самое понятие («Два плюс два равно или не равно нулю» или «Дом есть дом»).

Очень грубой ошибкой считается использование одного и того же слова. Встречается такая ошибка в наши дни, увы, довольно часто. Пример: «у оператора мобильной связи Билайн постоянно сложно дозвониться до живого оператора» или «выходя из дома, не забудь дома ключи».

Тавтология в художественной речи.

Исключением являются лишь художественные поэтические и прозаические тексты, когда тавтология призвана усилить речевую выразительность, это, так называемая риторическая тавтология:

  • старенький старичок,
  • падать вниз,
  • карабкаться вверх,
  • минута времени.

В литературе часто используется тавтология, примеры её встречаются не только в прозе, но и в стихах.

Пример тавтологии:

«Сквайр Трелони, доктор Ливси и другие джентльмены попросили меня написать все, что я знаю об «Острове сокровищ». Им хочется, чтобы я рассказал

всю историю, с самого начала до конца». (Д. Стивенсон)

Тавтологию как прием весьма часто используется в устном народном творчестве, которому присущи любовь к деталям и лексическим повторам, как для привлечения внимания слушателей и читателей, так и для придания особой напевности народного слога и его музыкальности. Нередко этот прием встречается в таких жанрах как

  • заклинания,
  • молитвы,
  • заговоры,

где повтор своего рода – гарант результата.

Примеры авторской тавтологии.

Многие авторы для создания народного колорита широко используют этот прием. Часто встречается в произведениях А. С. Пушкина («Вот на берег вышли гости, Царь Салтан зовёт их в гости»), в стихотворениях М. Ю. Лермонтова («За все, за все тебя благодарю я»).

Часто для предания внутреннего состояния романтического героя, его эмоций авторы используют тавтологию. Так, например, у Бальмонта:

«Я мечтою ловил уходящие тени,
«Уходящие тени погасавшего дня.
«Я на башню всходил, и дрожали ступени,

«И дрожали ступени под ногой у меня».

Похожие статьи

Лингвисты нашли новые причины употребления тавтологии в речи

«Знания, к которым обращается говорящий, делятся на шесть разновидностей: энциклопедические и метаязыковые, нормативные и описательные, локальные и общие. Раньше лингвисты считали, что языковые повторы употребляются только в ситуациях, когда все участники общения владеют информацией. Мы решили опровергнуть эту точку зрения и показать, что тавтология может быть также использована говорящим для того, чтобы избежать прямого ответа на вопрос, чтобы не давать собеседнику интересующие его сведения», — рассказывает руководитель проекта по гранту РНФ

Елена Вилинбахова, кандидат филологических наук, доцент кафедры общего языкознания имени Л. А. Вербицкой Санкт-Петербургского государственного университета.

Конструкции с лексическими повторами активно используются людьми в речи, хотя в буквальном смысле они не передают никакой новой информации. С помощью тавтологии говорящий может сделать отсылку к общему фонду знаний и представлений, стоящих за словом, не тратя времени на подробные объяснения слушателю. Этот прием встречается и в массовой культуре, например в высказывании «Dura lex, sed lex (закон есть закон)», во многих русских пословицах и поговорках.

В Испании тождественные лексические повторы часто употребляет политик Мариано Рахой — ему принадлежит фраза «Стакан — это стакан, а тарелка — это тарелка».

Ученые были заинтересованы в анализе большого количества разнообразных тавтологий, поэтому в качестве объекта исследования им служили 600 фрагментов, отобранные из Корпуса современного американского английского языка (COCA), составленного из статей журнала Time, выходивших с 1923 по 2006 год, и примерами из интернет-источников.

В статье авторы привели десятки примеров, в которых говорящий употребляет тавтологические высказывания, допускающие различные интерпретации. Например, лексический повтор «война — это война» можно интерпретировать как фразу об энциклопедическом определении войны как вооруженного конфликта, либо как прижившееся в обществе мнение о том, что война — это бессмысленное кровопролитие. В первом случае используется тавтология-ограничитель, отсылающая слушателя к точному определению, а во втором случае — тавтология-распространитель, отсылающая к стереотипу о войне.

Также ученые отметили еще одну причину использования тавтологии: по их мнению, такие повторы используются в разговоре, когда говорящий не может или не хочет содержательно ответить на вопрос на собеседника.

На данный момент изучению языковых повторов уделяется много внимания по всему миру. Работа ученых дополнит знания, полученные иностранными лингвистами при изучении лексических повторов. В будущем информация, появившаяся у ученых во время этого исследования, поможет в развитии систем машинного перевода. Одна из главных задач проекта по гранту РНФ состоит в создании базы данных, в которой будут содержаться вся информация, полученная исследователями.

Суть тавтологии с примерами | The Words // Всё о словах

В русском языке есть речевые явления, способные испортить текст. Одним из таких неграмотных феноменов является тавтология. Это специфический языковый тезис, широко используемый как в научной лингвистике, так и в повседневной жизни.

Что такое тавтология?
По-гречески слово «тавтология» означает «повторение одинаковых слов». В конструктивном понятии, это информационно бессмысленная языковая ошибка, усложняющая диалект.

Однокоренное дублирование нельзя путать с лексическим повтором речи. Это выразительная фигура слога, акцентированная повтором для вербального усиления, которая осознанно используется в СМИ или в литературных произведениях.

Значение термина простыми словами
Тавтология – повторение того, что уже было сказано. В разговоре или при письме используется как стилистический прием передачи однотипной информации. На слух воспринимается как показатель безграмотности или недостаточности словарного запаса у собеседника.

История образования термина
Термин заимствован из разговорного сленга древних греков. В античное время так именовали ситуацию, когда приходилось говорить одинаковые по значению или лексическому сложению слова. Использование однотипных фраз считалось неоправданным, так как эти словосочетания усложняли понимание диалога.

Однако повтор не всегда казался лишним. Литературное применение тавтологии помогало создавать экспрессивное выражение произведений. Стиль вносил яркие краски и эмоциональность в разговорную речь, давая зрителю возможность понять именно то, что имел в виду автор.


Где применяется тавтология?
В риторике тавтологией является словосочетание из двух однокоренных слов. Например, привычные в быту фразы «варить варенье», «остановить на остановке» и «загадать загадку». К скрытой форме однотипного суждения относятся косвенные выражения – «впервые дебютировать», «моя автобиография», «интерьер внутри», «январь месяц». В приведенных словосочетаниях первое слово дублирует смысл второго, а значит, является элементом речевого избытка. Риторически предложение с аналогичным повтором выглядит некорректным.

Существует отдельный вид тавтологических слов, получивших статус общепринятых разговорных вариантов. Эти выражения востребованы в фольклорном жанре, сказках или художественных произведениях. Авторы используют словосочетания как звучные афоризмы с уклоном на поэтическую эмоциональность. Получается забавный словесный каламбур, с усиленным позитивным оттенком за счет диалектического повторения. Например, «один одинешенек», «горькое горе», «дивное диво», «истинная правда», «старый старичок», «слыхом не слыхивал», «сделать дело».

В деловом стиле употребление тавтологических высказываний создает неприятный юмористический эффект, что недопустимо для такого рода общения.

Точные науки рассматривают тавтологию как истинное утверждение, включающее предпосыльную и заключительную часть. Независимо от отдельных его частей, выражение является правдивым. То есть одно понятие можно объяснить тем же словом.

Примеры употребления
В сущности, тавтология – это необоснованное наслоение речи, лишенное смысла, которое широко используется в разном языковом контексте.

Например, в разговорном жанре – «больной заболел», «белить белилами», «ливень проливной», «он поет песни», «звонить в звонок», «масляное масло», «кипяток горячий».

В логике – «проблемное обучение – это обучение через специально моделированную ситуацию, которую необходимо решить».

В деловом стиле – «акции падают вниз», «вип-персона».

В художественных произведениях – « давным-давно», «сказка сказывается».

Тавтологические словоформы популярны в молитвах и заговорах – стиль повторения усиливает образную визуализацию, придавая эффект рассеивания.

Тавтология в русском языке — Сочинение

Тавтология – это неоправданное повторение одно­коренных слов. Сущность тавтологии традиционно иллю­стрируют словосочетанием масло масляное, и мы не будем отказываться от этой традиции. Соединение двух слов, ка­залось бы, должно нести какой-то смысл, ведь минимальное суждение состоит из двух компонентов, субъекта и предика­та, или данного (того, о чем идет речь) и нового (того, о чем сообщается). В этом отношении предложение Волга – это река информативно, даже несмотря на то, что мы давно это знаем. А вот выражение масло масляное никакой информа­ции не несет.

С тавтологией часто смешивают повтор, который возни­кает в том случае, когда мы используем два однокоренных слова, которые существенно различаются по смыслу.

Возьмем, к примеру, словосочетание современное вре­мя. Оно вполне осмысленно. С одной стороны, есть слово время, которое мы можем использовать как синоним для слов период, эпоха, дни. С другой стороны, есть слово со­временный, которое также может быть употреблено умест­но. Ведь современный – это относящийся к той эпохе, к которой принадлежит говорящий; имеющий место сейчас, а не в прошлом или будущем. Времена бывают разные, и некоторые из них действительно современные, а некоторые нет. Все вроде бы правильно, но беда в том, что повтор кор­ней – современное время – звучит плохо, затрудняет вос­приятие мысли, стоящей за словами. Поэтому от одного из слов необходимо отказаться.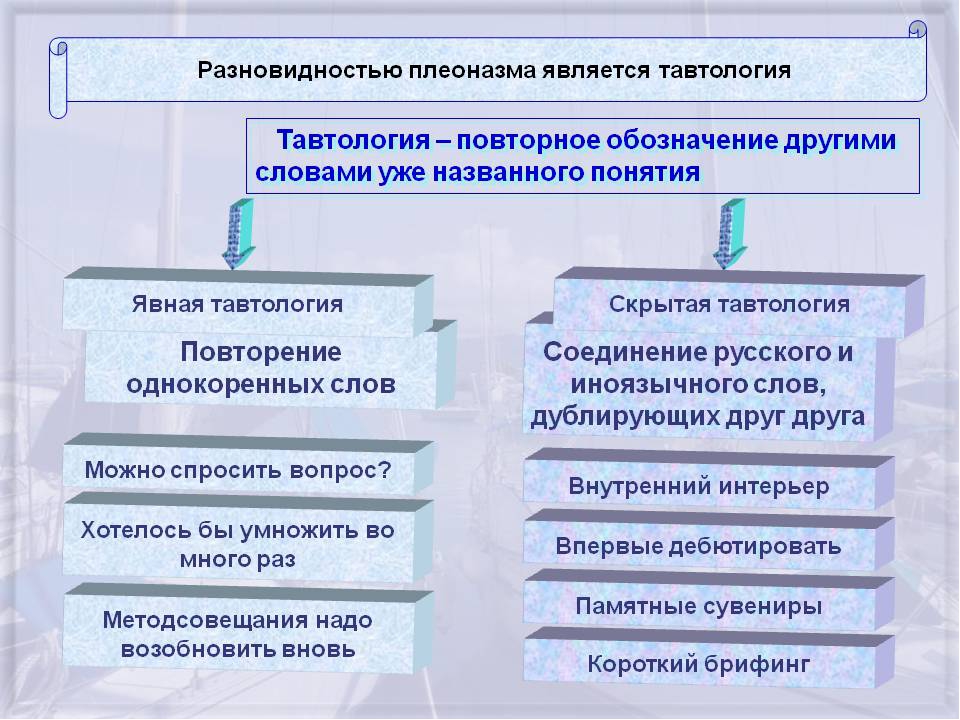 Мы либо заменяем слово время (современная эпоха), либо заменяем слово современное (наше время).

Повтор может быть важным средством выразительности, а потому иногда уместен в художественной литературе или публицистике: «Писатель пописывает. Читатель почитыва ет», – как писал (или пописывал?) когда-то М.Е. Салтыков- Щедрин. Не правда ли, звучит хорошо? А к тому же иро­нично… Но в официально-деловом и научном стилях такие повторы следует исключить, потому что это противоречит специфике этих стилей.

В некоторых случаях тавтология неиз­бежна, а потому считается допустимой. На­пример, мы вряд ли можем исправить такие словосочетания, как рисовать рисунок или варить варенье. Замена на синонимы здесь вряд ли поможет, потому что полноценных наименований- синонимов для соответствующих явлений нет. Рисунок – это не обязательно набросок, а тем более картина-, и варе­нье – это не то же самое, что джем или повидло.

ЛОГИЧЕСКИЕ ТАВТОЛОГИИ. По законам логики

ЛОГИЧЕСКИЕ ТАВТОЛОГИИ

В обычном языке слово «тавтология» означает повторение того, что уже было сказано; «Жизнь есть жизнь» или «Не повезет так не повезет».

Тавтологии бессодержательны и пусты, они не несут никакой информации. От них стремятся избавиться как от ненужного балласта, загромождающего речь и затрудняющего общение.

Иногда, правда, случается, что тавтология наполняется вдруг каким-то чужим содержанием. Попадая в определенный контекст, она как бы принимается светить отраженным светом.

Французский капитан Ла Паллис пал в битве при Павии в 1525 году. В его честь солдаты сложили дошедшую до наших дней песню «За четверть часа до смерти он был еще живой…». Понятая буквально, эта строка песни, ставшая ее названием, является тавтологией. Как таковая она совершенно пуста. Всякий человек до самой своей смерти жив. Сказать о ком-то, что он был жив за день до своей смерти или за четверть часа до нее, значит, ровным счетом ничего о нем не сказать.

И тем не менее какая-то мысль, какое-то содержание за этой строкой стоит. Оно каким-то образом напоминает о бренности человеческой жизни и особенно жизни солдата, о случайности и, так сказать, неожидаемости момента смерти и о чем-то еще другом.

Один писатель сказал о своем герое: он дожил до самой смерти, а потом умер. Козьме Пруткову принадлежит афоризм: «Не будь цветов, все ходили бы в одноцветных одеяниях». Буквально говоря, это тавтологии и пустота. Но на самом деле смысл здесь все-таки есть, хотя это и не собственный смысл данных фраз, а отражаемый или навеваемый ими смысл.

С легкой руки Л. Витгенштейна слово «тавтология» стало широко использоваться для характеристики законов логики.

Став логическим термином, оно получило строгие определения применительно к отдельным разделам логики. В общем случае логическая тавтология — это выражение, остающееся истинным независимо от того, о какой области объектов идет речь, или «всегда истинное выражение».

Все законы логики являются логическими тавтологиями. Если в формуле, представляющей закон, заменить переменные любыми постоянными выражениями соответствующей категории, эта формула превратится в истинное высказывание.

Например, в формулу «А или не-А», представляющую закон исключенного третьего, вместо переменной А должны подставляться высказывания, то есть выражения языка, являющиеся истинными или ложными.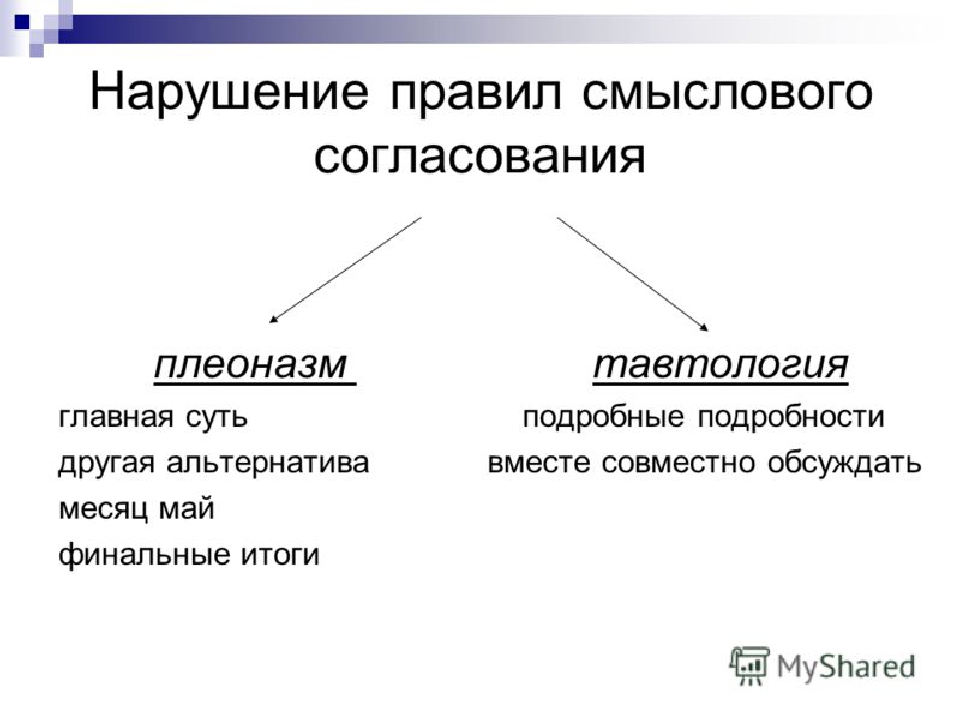 Результаты таких подстановок: «Дождь идет или не идет», «Два плюс два равно нулю или не равно нулю», «Бог существует или его нет» и тому подобное. Каждое из этих сложных высказываний является истинным. И какие бы дальнейшие высказывания ни подставлялись вместо А — как истинные, так и ложные, — результат будет тем же — полученное высказывание будет истинным.

Аналогично в случае формул, представляющих закон противоречия, закон тождества, закон двойного отрицания и т. д. «Неверно, что бог существует и не существует; что дождь идет и не идет; что я иду быстро и не иду быстро» — все это высказывания, полученные из формулы: «Неверно, что А и не-А», и все они являются истинными. «Если бога нет, то его нет; если я иду быстро, то я иду быстро; если два равно нулю, то два равно нулю» — это результаты подстановок в формулу «Если А, то А» и опять-таки истинные высказывания.

Тавтологический характер законов логики послужил отправным пунктом для многих спекуляций по их поводу.

Из тавтологии «Дождь идет или не идет» мы ничего не можем узнать о погоде. Тавтология «Неверно, что бог есть и его нет» ровным счетом ничего не говорит о существовании бога. Ни одна тавтология не несет содержательной информации о мире.

Тавтология не описывает никакого реального положения вещей. Она совместима с любым таким положением. Немыслима ситуация, сопоставлением с которой можно было бы тавтологию опровергнуть.

Эти специфические особенности тавтологий были истолкованы как несомненное доказательство отсутствия какой-либо связи законов логики с действительностью.

Такое «исключительное положение» законов логики среди всех предложений подразумевает прежде всего, что законы логики представляют собой априорные, известные до всякого опыта истины. Они не являются бессмысленными, но вместе с тем не имеют и содержательного смысла. Их невозможно ни подтвердить, ни опровергнуть ссылкой на опыт.

Действительно ли законы логики не несут никакой информации?

Если бы это было так, они по самой своей природе решительно отличались бы от законов других наук, описывающих действительность и что-то говорящих о ней.

Мысль об информационной пустоте логических законов является, конечно, ошибочной. В основе ее лежит крайне узкое истолкование опыта, способного подтверждать научные утверждения и законы. Этот опыт сводится к фрагментарным, изолированным ситуациям или фактам. Они достаточны для проверки истинности элементарных описательных утверждений типа «Идет дождь» или «Я иду быстро». Но явно недостаточны для суждения об истинности абстрактных теоретических обобщений, опирающихся не на отдельные, разрозненные факты, а на совокупный, систематический опыт. Даже законы опытных наук, подобных биологии или физике, нельзя обосновать простой ссылкой на факты и конкретику. Тем более это невозможно сделать в случае самых абстрактных из всех законов — законов логики. Они должны черпать свое обоснование из предельно широкого опыта мыслительной, теоретической деятельности. За законами логики стоит, конечно, опыт, и в этом они сходны со всеми иными научными законами. Но опыт не в форме каких-то изолированных, доступных наблюдению ситуаций, а конденсированный опыт всей истории человеческого познания.

Тавтологии обычного языка нередко наполняются содержанием, пришедшим со стороны, и светят отраженным светом. Так же обстоит дело и с логическими тавтологиями.

Изолированная от других тавтологий, оторванная от языка и от истории познания, логическая тавтология блекнет и создает впечатление отсутствия всякого содержания.

Это еще раз подтверждает мысль, что рассуждения о смысле и значении отдельных выражений языка, изъятых из среды своего существования, допустимы и справедливы только в ограниченных пределах. Нужно постоянно иметь в виду, что язык — это единый, целостный организм, части которого взаимосвязаны, взаимообусловлены и не способны действовать вне его.

Кроме того, сам язык не является некой самодостаточной системой. Он погружен в более широкую среду — среду познания и социальной жизни, когда-то создавшей его и с тех пор постоянно его воссоздающей.

Данный текст является ознакомительным фрагментом.

Продолжение на ЛитРес

Речевые ошибки, тавтология

Речевые ошибки: тавтология и плеоназм

В статье нет видимых ошибок, а заказчик остался недоволен, не пожелал оставить отзыв, не сказал пару тёплых слов. Виной всему речевая избыточность, коей грешат не только новички, но и зрелые авторы. Часто копирайтер долго, нудно, пространно рассуждает о том, что читателям «с младых ногтей» известно. Люди сразу утрачивают интерес и покидают сайт.

Разумеется, подобные статьи не нравятся заказчикам. Часто они в ТЗ пишут предупреждения, подобные этим:

Тавтология и плеоназм

Речевая избыточность появляется от неумения копирайтера подобрать точные слова для выражения различных понятий. Писатели и хорошие авторы перебирают несколько вариантов, пока не остановятся на наиболее удачном термине, позволяющем точно, ёмко, лаконично выразить мысль.

Многие копирайтеры не занимаются подбором точных слов и их шлифовкой, поэтому пускаются в долгие объяснения. Им требуется намного больше слов и предложений, чтобы донести идеи/мысли до читателя. Так появляется речевая избыточность. Две её главные разновидности — плеоназм и тавтология.

Классный пример в картинках попался на глаза. Захотелось сплагиатить, чтобы показать райтерам, как не следует повторяться. Избыточность легко увидеть самостоятельно!

Плеоназм

Плеоназм переводится с греческого как излишество. Термином обозначают употребление близких по смыслу слов, отсюда и проистекает избыточность. Самый распространённый плеоназм: так, например. Или фольклорные сочетания: на море-океане; путь-дорожка.

Иногда автор использует осознанно «мнимый плеоназм» (Не вернётся вспять время), чтобы усилить выразительность речи. Но не все читатели и заказчики это понимают. Хотя нарочитое несоответствие используется намеренно для привлечения внимания в надежде усилить эффект подобным выразительным приёмом.

Тавтология

Разновидность или частный случай плеоназма, когда повторяются однокоренные слова: «На остановке остановите, пожалуйста», «Я сейчас загадаю загадку». Дословный перевод термина тавтология — «то же самое слово».

Тавтологические ошибки проявляются, когда автор применяет слова, не зная их точного значения. Поэтому вычитка текста не поможет выявить и исправить допущенные неточности.

Не всегда повторы нужно устранять. Иногда исключение однокоренного слова и его замена синонимом придаст тексту ещё большую нелепость, исказит смысл. Например, как иначе можно описать деятельность «варить варенье».

Слово «варенье» заменить на «джем» или «конфитюр»? Это искажение, а не полезная замена.

Стилистически оправдано употребление однокоренных слов, находящихся в близком контексте, и применение терминологических выражений, если к ним невозможно подобрать синонимы: словарь словообразования русского языка.

Борьба с тавтологией

К речевой избыточности относят частые повторения слов. Чаще всего их тоже называют тавтологией, хотя в копирайтинге для них есть собственный термин — тошнотность.

Недопустимо в одном предложении (и даже в рядом стоящих) использовать:

  • повтор одного и тоже слова,
  • однокоренных слов.

Борьба с тавтологией уместна, если чрезмерное употребление одиночного или однокоренных слов легко вызовет у читателя неприязнь и тошноту.

Хотя иногда повтор воспринимается необычно и забавно — в поэзии, юмористических текстах:

Я оглянулся посмотреть,

Не оглянулась ли она,

Чтоб посмотреть,

Не оглянулся ли я.

Проверка тавтологии: онлайн сервисы
https://glvrd.ru/

Сервис «Главред» помимо тавтологии поможет выявить ещё массу клише и ненужных слов, особенно в продающих текстах.

http://yourtext.ru/ustranit-tavtologiyu-onlajn.html

Удобный сервис с примерами, поясняющий опасность тавтологии для копирайтера. Почему-то проигнорировал частые повторы слова «работа» и не заметил в последнем предложении в третий раз повторяющееся слово «специалисты».

http://quittance.ru/tautology.php#effectus

Результат после проверки «Свежего взгляда» (именно так называется услуга) такой же, как вердикт предыдущего сервиса.

Проверка тавтологии на трёх веб-сайтах показала не совсем удовлетворительный результат. Трижды повторяющееся в двух предложениях слово «работа» осталось за порогом внимания.

Вывод: надеяться больше на себя, но не забывать использовать программы. Иногда они помогут увидеть то, что копирайтер упустил из-за невнимательности или усталости.

А если тавтология, по мнению автора, применена, чтобы усилить экспрессию, а заказчик этого не понял, можно ему пояснить, для чего использован «запрещённый» приём.

«Работа копирайтером» приглашает к прочтению других статей:

таблиц истинности, тавтологий и логических эквивалентностей

таблиц истинности, тавтологий и логических эквивалентностей

Математики обычно используют двузначное число . логика : Каждый оператор либо Истина , либо Неверно . Это называется . Закон Исключенного Среднего .

Утверждение в логике предложений строится из простых утверждений с использованием логические связки,,, и. Правда или ложь утверждения, построенного с помощью этих связок, зависит от истины или ложность его составляющих.

Например, составной оператор строится с использованием логических связок, и. Правда или ложь зависит от правды или ложность P, Q и R.

Таблица истинности показывает, как правда или ложь составного утверждения зависит от истинности или ложности простого утверждения, из которых он построен. Итак, мы начнем с рассмотрения таблицы истинности для пяти логических связок.

Вот таблица для отрицания:

Эта таблица проста для понимания.Если P равно , истинно , его отрицание ложь . Если P ложно , то истинно .

должно быть истинно , когда и P, и Q равны истинно и ложно иначе:

равно истинно , если либо P равно истинно , либо Q равно правда (или оба — помните, что мы используем «или» в инклюзивном смысле). Только ложно , если и P, и Q равны ложь .

Вот таблица для логического вывода:

Чтобы понять, почему эта таблица такая, как она есть, рассмотрим следующие пример:

«Если вы получите пятерку, то я дам вам доллар».

Утверждение будет истинным , если я сдержу свое обещание и ложно , если я этого не сделаю.

Предположим, что истинно , что вы получили пятерку, и это истинно что я даю вам доллар.Поскольку я сдержал свое обещание, подразумевается правда . Это соответствует первой строке в таблице.

Предположим, что истинно , что вы получили пятерку, но это ложно что я даю вам доллар. Поскольку я не сдержал свое обещание , подразумевается ложное . Это соответствует второму строка в таблице.

Что, если вы получите пятерку неверно? Независимо от того, даю ли я вам доллар, я не нарушил свое обещание.Таким образом, значение не может быть false, поэтому (поскольку это двузначная логика) оно должно быть истинным. Этот объясняет последние две строки таблицы.

означает, что P и Q равны эквивалент . Таким образом, двойное значение истинно , если P и Q оба истинны или если P и Q оба ложны ; в противном случае двойная импликация ложна.

Вы должны помнить — или уметь составлять — таблицы истинности для логических связок.Вы будете использовать эти таблицы для построения таблицы для более сложных предложений. Проще продемонстрировать что делать, чем описывать словами, чтобы вы увидели порядок действий отработано в примерах.

Замечание. (а) Когда вы конструируете истину таблице, вы должны рассмотреть все возможные назначения True (T) и Ложь (F) для операторов компонента. Например, предположим, что операторы компонентов — это P, Q и R. Каждый из этих операторов может быть либо верно, либо неверно, значит, есть возможности.

Когда вы перечисляете возможности, вы должны присваивать значения истинности к операторам компонентов систематическим образом, чтобы избежать дублирования или упущение. Самый простой подход — использовать лексикографическая упорядоченность . Таким образом, для составного оператора с три компонента P, Q и R, я бы перечислил возможности этого способ:

(б) Существуют разные способы составления таблиц истинности. Вы можете для например, запишите значения истинности «под» логическим связки составного высказывания, постепенно наращивая столбец для «первичной» связки.

Я напишу подробности, построив столбцы для каждого «кусок» составного высказывания и постепенно наращивая к составному оператору. Любой стиль хорош, пока ты показываешь достаточно работы, чтобы оправдать ваши результаты.

Пример. Постройте таблицу истинности для формула.

Сначала я перечисляю все альтернативы для P и Q.

Затем в третьем столбце я перечисляю значения, основанные на значениях P.Я использую таблицу истинности для отрицание: когда P истинно, ложно, а когда P ложно, правда.

В четвертом столбце я перечисляю значения для. Убедитесь сами, что это только ложь («F»), если P истинно («T») и Q ложно («F»).

В пятом столбце приведены значения для моего составного выражения. Это «и» (третий столбец) и (четвертый столбец). «И» верно, только если обе части «и» верны; в противном случае это ложь. Итак, я смотрю на третья и четвертая колонки; если оба верны («T»), я ставлю T в пятом столбце, иначе я поставил F.

тавтология — это формула, которая «всегда истина «— то есть верно для каждого присвоения истины ценности к его простым компонентам. Вы можете думать о тавтологии как о правило логики .

Противоположность тавтологии — . противоречие , формула, которая «всегда ложна». В другими словами, противоречие ложно для каждого приписывания истины ценности к его простым компонентам.

Пример. Показать, что это тавтология.

Я составляю таблицу истинности и показываю, что формула всегда верна.

Последний столбец содержит только буквы T. Следовательно, формула представляет собой тавтология.

Пример. Постройте таблицу истинности для.

Вы можете видеть, что построение таблиц истинности для утверждений с множеством связок или множества простых утверждений довольно утомительно и подвержен ошибкам.Хотя могут быть некоторые применения этого (например, для цифровых схем), в какой-то момент лучше всего было бы написать программа для построения таблиц истинности (и это наверняка было сделано).

Дело здесь в том, чтобы понять, как истинное значение сложного утверждение зависит от истинности его простых утверждений и его логические связки. В большинстве работ математики обычно не используйте операторы, которые очень сложны с логической точки зрения Посмотреть.

Пример. (a) Предположим, что P ложно и истинно. Скажите, является ли Q истинным, ложным или его истинным значение не может быть определено.

(b) Предположим, что это неверно. Рассказывать истинно ли Q, ложно или его истинное значение не может быть определено.

(a) Поскольку истинно, либо P истинно, либо истинно. Поскольку P ложно, должно быть верно. Следовательно, Q должно быть ложным.

(b) Утверждение «если-то» неверно, когда часть «если» истина, а часть «тогда» — ложь.Поскольку ложно, верно. Утверждение «и» верно только когда обе части верны. В частности, должно быть истинным, поэтому Q ложно.

Пример. Предположим

» » правда.

«» ложно.

«У Кэлвина Баттерболла фиолетовые носки» — правда.

Определите истинность утверждения

Для простоты пусть

P = «».

Q = «».

R = «У Кэлвина Баттерболла фиолетовые носки».

Я хочу определить истинное значение. Поскольку мне были даны конкретные значения истинности для P, Q, и R, я установил таблицу истинности с единственной строкой, используя данную значения для P, Q и R:

Следовательно, утверждение верно .

Пример. Определите истинное значение утверждение

Утверждение «» ложно. Ты не можешь сказать есть ли в заявлении «Икабод Ксеркс шоколад» кексы «верно или неверно, но это не имеет значения.Если «если» часть утверждения «если-то» ложна, тогда утверждение «если-то» верно. (Проверить правду стол на случай, если вы не уверены в этом!) данное утверждение должно быть верным.

Два оператора X и Y логически равны . эквивалент , если это тавтология. Другой способ сказать это: Для каждого присвоения значений истинности простому операторы , составляющие X и Y, операторы X и Y имеют идентичные значения истинности.

С практической точки зрения вы можете заменить выражение в доказательство любым логически эквивалентным утверждением.

Чтобы проверить, являются ли X и Y логически эквивалентными, вы можете настроить таблица истинности, чтобы проверить, является ли тавтология — это есть ли «все ли Т в его столбце». Однако проще создать таблицу, содержащую X и Y, а затем проверьте, совпадают ли столбцы для X и Y.

Пример. Покажите, что и логически эквивалентны.

Поскольку столбцы для и идентичны, два оператора логически эквивалент.Эта тавтология называется условной . Дизъюнкция . Вы можете использовать эту эквивалентность для замены условно дизъюнкцией.

Существует бесконечное количество тавтологий и логических эквивалентностей; Я перечислил несколько ниже; более обширный список приведен в конце эта секция.

Когда тавтология имеет форму двоякого условия, два утверждения составляющие двусмысленность, логически эквивалентны. Следовательно, вы может заменить одну сторону на другую, не меняя логического имея в виду.

Вам часто нужно будет отрицать математическое утверждение. К посмотрим, как это сделать, мы начнем с того, что покажем, как отрицать символическое заявления.

Пример. Запишите отрицание следующие утверждения, упрощающие так, чтобы только простые утверждения отрицается.

(а)

(б)

(а) Я отвергаю данное утверждение, а затем упрощаю, используя логические эквивалентности. Я привел названия логических эквивалентов на правильно, чтобы вы могли видеть, какие из них я использовал.

(б)

Я показал это и логически эквивалентен в предыдущем примере.

В следующих примерах мы будем отрицать утверждения, написанные словами. Это более типично для того, что вам нужно делать по математике. В идея состоит в том, чтобы преобразовать слово-утверждение в символическое утверждение, тогда используйте логические эквивалентности, как в предыдущем примере.

Пример. Используйте закон ДеМоргана, чтобы написать отрицание следующего утверждения, упрощая так, чтобы отрицаются только простые утверждения:

«Кальвина нет дома, или Бонзо в кино.»

Пусть C будет утверждением «Кальвин дома» и пусть B будет заявление «Бонзо в движении». Данное заявление . Я должен опровергнуть это утверждение, затем упростите:

Результат: «Кальвин дома, а Бонзо нет в доме». фильмы ».

Пример. Используйте закон ДеМоргана, чтобы написать отрицание следующего утверждения, упрощая так, чтобы отрицаются только простые утверждения:

«Если Фиби покупает пиццу, то Кэлвин покупает попкорн. »

Пусть P будет утверждением «Фиби покупает пиццу» и пусть C будет заявление «Кэлвин покупает попкорн». Данное заявление . Чтобы упростить отрицание, я буду использовать тавтологию Conditional Disjunction , которая говорит

То есть я могу заменить на (или наоборот).

Итак, вот отрицание и упрощение:

Результат: «Фиби покупает пиццу, а Кэлвин не покупает. Попкорн».

Далее мы применим нашу работу с таблицами истинности и отрицательными утверждениями к задачи, связанные с построением обратного, обратного и противоположность утверждению «если-то».

Пример. Заменить следующую инструкцию на его противоположность:

«Если х и у рациональны, значит рационально».

В силу контрапозитивной эквивалентности это утверждение совпадает с утверждением «Если нерационально, значит, это не так. что и x, и y рациональны «.

Это правильный ответ в его нынешнем виде, но мы можем выразить его в немного лучший способ, который удаляет некоторые явные отрицания. Большинству людей легче понять положительное утверждение, чем отрицательное заявление.

По определению действительное число иррациональное , если это не рационально. Так что я мог бы заменить часть «если» в противоположно слову «иррационально».

«Тогда» часть контрапозитива — это отрицание «и» заявление.Вы можете повторить это так: «Это не случай, когда и x рационально, и y рационально «. (Слово «оба» гарантирует, что отрицание применимо ко всему «И», а не только «х рационально».)

По закону ДеМоргана это эквивалентно: «x нерационально или y не рационально «. В качестве альтернативы я мог бы сказать:» x есть иррационально или y иррационально ».

Объединив все вместе, я мог бы выразить контрапозитив как: «Если иррационально, то либо x иррационально или y иррационально «.

(Как обычно, я добавил слово «либо», чтобы было ясно, что часть «затем» — это целое «или».)

Пример. Покажите, что обратное и обратные от условного оператора логически эквивалентны.

Позвольте быть условным. Обратное. Обратное.

Я мог бы показать, что обратное и обратное эквивалентны построение таблицы истинности для. Вместо этого я воспользуюсь некоторыми известными тавтологиями.

Начнем с:

Помните, что я могу заменить выражение логическим эквивалент.Например, на последнем шаге я заменил на Q, потому что два оператора эквивалентны Двойное отрицание.

Пример. Предположим, что x — действительное число. Рассмотреть возможность заявление

«Если, то.»

Постройте обратное, обратное и противоположное. Определите истинность или ложность четырех утверждений — исходное утверждение, обратное, обратное и противоположное — используя свои знания алгебры.

Обратное — «Если, то».

Обратное — «Если, то».

Контрапозитив — «Если, то».

Исходное утверждение неверно:, но. Поскольку исходное утверждение эквивалентно контрапозитивный, контрапозитивный тоже должен быть ложным.

Верно и обратное. Обратное логически эквивалентно обратное, значит, верно и обратное.

\новая страница

\ centerline {\ bigssbold Список тавтологий}

Контактная информация

Домашняя страница Брюса Икенаги

Авторские права 2019 Брюс Икенага

Define Tautology — Cuemath

Если я скажу: «Я дам вам 5 долларов или не дам 5 долларов».Что вы подумаете об этом комментарии?
Я всегда буду правдой, независимо от того, даю я вам немного денег или нет.

Знаменитая фраза Джорджа Вашингтона «Я не могу солгать» также является еще одним примером таких заявлений.

Такие утверждения хорошо объяснены и подпадают под тавтологию.

Итак, приступим к изучению примеров тавтологии, определения тавтологии в математике и таблицы истинности тавтологии.

План урока

Что такое тавтология в математике?

Определение

Логическая комбинация предложений, которая всегда истинна, независимо от истинности или ложности составляющих предложений, известна как «тавтология».«

— Руди Ракер

Тавтология — это составное утверждение, которое всегда истинно, независимо от того, ложны ли отдельные утверждения или истинны.

Слово тавтология происходит от греческого слова, где «тауто» означает «тот же», а «логия» означает «логика».

Чтобы узнать, является ли данное утверждение тавтологией, нам нужно построить таблицу истинности и посмотреть на значение истинности в последнем столбце.

Если все значения верны, то это тавтология.

Вот несколько простых примеров тавтологии:

  • Либо прыгнешь, либо не прыгнешь.
  • Генри худощавый или Генри не стройный.
  • Эмануэль будет танцевать или Эмануэль не будет танцевать.

Все эти утверждения верны, несмотря ни на что.

Логические символы в математике

Поскольку математика является логическим предметом, она использует логические утверждения для определения ответов.

Чтобы узнать, является ли данное утверждение тавтологическим или нет, логика тавтологии должна быть истинной.

В тавтологии для представления составных утверждений используются разные логические символы.

Вот логические символы, которые используются в тавтологическом высказывании:

Операторы Символы Представительство
И \ (\ земля \) A \ (\ земля \) B
Или \ (\ lor \) A \ (\ lor \) B
Отрицание \ (\ lnot \) \ (\ lnot \) А
Нет \ (\ sim \) \ (\ sim \) А
Если и только если \ (\ iff \) А \ (\ iff \) В
Подразумевается или если-то \ (\ longrightarrow \) A \ (\ longrightarrow \) B
Эквивалент = А = В

Аналитический центр

Каково отрицание этих утверждений?

  • Если экзамен сложный, то сдашь, если учишься.
  • Если я стану врачом, то открою больницу.

Таблица истинности

Таблица истинности тавтологических утверждений приведена ниже:

Для этого:

X Y \ (\ sim \) X X \ (\ земля \) Y X \ (\ lor \) Y X \ (\ longrightarrow \) Y X \ (\ iff \) Y
Т Т F Т Т Т Т
Т F F F Т F F
Ф Т Т F Т Т F
Ф F Т F F Т Т

Важные примечания

Примеры тавтологии и математики

Пример 1. Проверить, является ли P \ (\ longrightarrow \) (P \ (\ land \) Q) тавтологическим.

п. Q (П \ (\ земля \) Q) P \ (\ longrightarrow \) (P \ (\ land \) Q)
Т Т Т Т
Т F F F
Ф Т F Т
Ф F F Т

Это не тавтологическое утверждение, потому что все значения в последнем столбце не истинны (T).

Пример 2. Проверьте, является ли \ (\ sim \) X \ (\ lor \) Y тавтологическим или нет.

X \ (\ сим \) Х Y \ (\ sim \) X \ (\ lor \) Y
Т F F F
Т F F F
Ф Т Т Т
Ф Т Т Т

Это не тавтологическое утверждение, потому что все значения в последнем столбце не истинны (T).

Разница между тавтологией и противоречием?

Тавтология — это составное утверждение, которое всегда истинно, независимо от того, ложны ли отдельные утверждения или истинны.

Тогда как противоречие противоположно тавтологии или просто отрицание тавтологии есть противоречие.

Противоречие также известно как заблуждение.

Противоречие — это составное утверждение, которое всегда ложно, независимо от того, являются ли отдельные утверждения ложными или истинными.

п. В (П \ (\ lor \) V) П \ (\ longrightarrow \) (П \ (\ lor \) V) \ (\ sim \) (P \ (\ longrightarrow \) (P \ (\ lor \) V))
Т Т Т Т F
Т F Т Т F
Ф Т Т Т F
Ф F F Т F

Глядя на таблицу истинности, P \ (\ longrightarrow \) (P \ (\ lor \) V) является тавтологией, тогда как \ (\ sim \) (P \ (\ longrightarrow \) (P \ ( \ lor \) V)) противоречивое утверждение.

Решенные примеры

Эшли было поручено построить таблицу истинности для {A \ (\ iff \) B} \ (\ lor \) {B \ (\ iff \) A}. Можете ли вы помочь ей сделать то же самое?

Раствор

А B (А \ (\ iff \) B) (В \ (\ iff \) А) {A \ (\ iff \) B} \ (\ lor \) {B \ (\ iff \) A}
Т Т Т Т Т
Т F F F F
Ф Т F F F
Ф F Т Т Т

Ян не понимает, является ли N \ (\ lor \) {\ (\ sim \) N} тавтологическим утверждением или нет. Вы можете помочь ему в этом разобраться?

Раствор

N \ (\ sim \) N N \ (\ lor \) {\ (\ sim \) N}
Т F Т
Ф Т Т

Это тавтологическое утверждение, поскольку все значения в последнем столбце верны.

Можете ли вы помочь Полу построить таблицу истинности для {Y \ (\ land \) Z} \ (\ longrightarrow \) Z?

Раствор

Таблица истинности {Y \ (\ land \) Z} \ (\ longrightarrow \) Z может быть составлена ​​следующим образом:

Y Z Y \ (\ land \) Z {Y \ (\ land \) Z} \ (\ longrightarrow \) Z
Т Т Т Т
Т F F Т
Ф Т F Т
Ф F F Т

Интерактивные вопросы

Вот несколько занятий для вас. Выберите / введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.

Подведем итоги!

Мини-урок был посвящен увлекательной концепции тавтологии, примеру тавтологии, как определять тавтологию в математике и таблице истинности тавтологии. Математическое путешествие по тавтологии начинается с того, что ученик уже знает, и продолжается творческим развитием новой концепции в молодых умах.Сделано таким образом, чтобы не только было понятно и легко понять, но и навсегда осталось с ними. В этом заключается магия Куэмат.

О компании Cuemath

В Cuemath наша команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов!

Благодаря интерактивному и увлекательному подходу «обучение-обучение-обучение» учителя исследуют тему со всех сторон.

Будь то рабочие листы, онлайн-классы, сеансы сомнений или любые другие формы отношений, мы в Cuemath верим в логическое мышление и интеллектуальный подход к обучению.

Часто задаваемые вопросы (FAQ)

1. Как вы определяете тавтологию?

Если вы хотите знать, что данное утверждение является тавтологией, тогда все, что вам нужно сделать, это построить таблицу истинности и посмотреть на значение истинности в последнем столбце.

Если все значения верны, это тавтология.

2. Что означают P и Q?

Утверждение от P до Q означает, что если P истинно, то Q также должно быть истинным.

3. Является ли тавтология заблуждением?

Тавтология — это составное утверждение, которое всегда истинно, независимо от того, истинны ли отдельные утверждения или нет.

А противоречие — противоположность тавтологии. Другими словами, отрицание тавтологии есть противоречие.

Противоречие также известно как заблуждение. Следовательно, тавтология — это не заблуждение.

Определение тавтологии и пример литературного приема — EnglishLiterature.Net

Определение

Тавтология

Тавтология — это повторяющееся использование фраз или слов, имеющих схожие значения. Проще говоря, это выражение одной и той же вещи, идеи или высказывания два или более раз. Слово тавтология происходит от греческого слова tauto , означающего «то же самое», и logos , что означает «слово или идея». Грамматическая тавтология относится к идее, повторяемой во фразе, абзаце или предложении, чтобы создать впечатление, что автор предоставляет дополнительную информацию.

Тавтологии очень распространены в английском языке из-за большого разнообразия слов, заимствованных из других языков.Учитывая тот факт, что в процессе своего развития английский язык находился под сильным влиянием нескольких других языков, включая германский и латинский, нередко можно найти несколько экзотических тавтологий. Так часто встречаются тавтологии в английской поэзии и прозе.

Типы

Тавтология

Существует несколько типов тавтологии, которые обычно используются в повседневной жизни, в поэзии, прозе, в песнях и в дискуссиях, в зависимости от требований ситуации. Некоторые из общих категорий включают:

  • Повторяющиеся слова из-за несоответствий в языке
  • Преднамеренная двусмысленность
  • Насмешка
  • Поэтическое устройство
  • Психологическое значение
  • Выступление неумелого оратора или рассказчика

Примеры

тавтологии в литературе

Тавтологию часто путают с повторением. Некоторые авторитеты говорят, что при повторении используются одни и те же слова, в то время как тавтология использует слова с похожим значением.Эта тавтология есть повторение не слов, а идей. Другие говорят, что между ними нет четкого различия, что тавтология включает в себя повторение слов. Чтобы лучше понять это, прочтите следующие примеры тавтологии.

Пример # 1:

«Ваша игра полностью лишена эмоций».

Devoid определяется как «полностью пустой». Таким образом, совершенно лишен пример тавтологии.

Пример № 2:

« Повторите еще раз , » и « повторите еще раз . “

Повторить или повторить что-то — значит повторить или повторить.

Пример № 3:

Кричите громко! (Поцелуй)

«Кричите, кричите, кричите вслух !»

Когда человек кричит, это всегда громко.

, пример №4: (Йоги Берра)

«Это как снова дежавю » (Йоги Берра)

Термин déjà vu означает ощущение того, что вы уже что-то делали или переживали, или делать это снова и снова.« Déjà vu снова и снова» — это пример тавтологии.

Пример № 5:

Пустошь (Т. С. Элиот)

Эмфатическая функция тавтологии раскрывается в следующем примере:

«Тогда я пришел в Карфаген.
Горящий горящий горящий горящий ».

Томас Стерн Элиот показывает выразительную функцию тавтологии, многократно используя слово «сжигание» в одной и той же строке.

Пример # 6:

Гамлет (Уильям Шекспир)

В некоторых отрывках тавтология используется намеренно, что подразумевает присущее ей насмешку.

Polonious: «Что вы читаете, милорд?»
Гамлет: « слов, , слов, , слов, ».

Здесь Гамлет использовал слова, чтобы показать, что он запутался в словах, которыми славится Полоний.

Пример # 7:

Колокола (Эдгар Аллен По)

«Сохранение времени, времени, времени ,
В своего рода рунической рифме…
Из колоколов, колокольчиков, колоколов, колоколов ».

Пример # 8:

Пустошь (Автор Т.С. Элиот)

“ Twit twit twit / Кувшин кувшин кувшин кувшин кувшин кувшин “

Пример № 9:

Пустые люди (Т. С. Элиот)

«Так кончается мир
Так кончается мир
Так кончается мир
Не с треском, а с хныканьем».

Здесь различные типы тавтологий использовались в техническом способе повторения, который преобладает над другими, такими как фигуры речи, имитация и орнамент.Все вышеперечисленные примеры могут появиться в повседневном использовании языка, а также как поэтические приемы.

Пример № 10:

Библия (Разные авторы)

В отличие от художественного вдохновения, присущего предыдущим типам избыточности, вот пара примеров тавтологии с психологическим подтекстом. Ораторы демонстрируют принятие своей судьбы в таких повторениях:

«Если я погибну , я погибну ».
(Есфирь 4:15)

«Если я потеряю детей, (моих детей), то я потеряю детей, человек.»
(Бытие 43:14)

Функция

Тавтология

Нельзя отрицать важность тавтологии в современном литературном творчестве. Однако сегодня писатели стараются избегать использования тавтологических слов и фраз, чтобы избежать однообразия и повторения. Практически стало нормой использовать короткие и по существу слова вместо повторяющихся и повторяющихся фраз.

Несмотря на то, что это считается серьезной стилевой ошибкой, некоторые писатели обычно используют тавтологию как мощный инструмент, чтобы подчеркнуть определенную идею или привлечь внимание читателей к определенному аспекту жизни.Но это не всегда считается признаком плохой грамматики; скорее, это было воспринято как особый риторический прием.

1.1.10: Классификация предложений — Engineering LibreTexts

Определенные типы предложений будут играть особую роль в нашей дальнейшей работе с логикой. В частности, мы определяем тавтологии, противоречия и случайности следующим образом:

Определение 2.4.

Составное суждение называется тавтологией тогда и только тогда, когда оно истинно для всех возможных комбинаций значений истинности пропозициональных переменных, которые оно содержит.Сложное предложение называется противоречием тогда и только тогда, когда оно ложно для всех возможных комбинаций значений истинности пропозициональных переменных, которые оно содержит. Сложное суждение называется случайностью тогда и только тогда, когда оно не является ни тавтологией, ни противоречием.

Например, предложение (( p ∨ q ) ∧ ¬ q ) → p является тавтологией. Это можно проверить 2 с помощью таблицы истинности:

Тот факт, что все записи в последнем столбце верны, говорит нам, что это выражение является тавтологией.Обратите внимание, что для любого составного предложения P , P является тавтологией тогда и только тогда, когда ¬ P является противоречием. (Здесь и в будущем я использую прописные буквы для обозначения сложных предложений. P обозначает любую формулу, состоящую из простых предложений, пропозициональных переменных и логических операторов.)

Логическая эквивалентность может быть определена с помощью тавтологии:

Определение 2.5.

Два составных предложения, P и Q , считаются логически эквивалентными тогда и только тогда, когда предложение P ↔ Q является тавтологией.

Утверждение, что P логически эквивалентно Q , будет символически выражено как « P ≡ Q ». Например, ( p → q ) ≡ (¬ p ∨ q ) и p ⊕ q ≡ ( p ∨ q ) ∧ ¬ ( p ∧ 9000 q ).

Что делать, если P → Q и P ложны? Из ложной посылки мы можем сделать любой вывод (проверьте таблицу истинности →).Таким образом, если k означает «Я король Нидерландов», то k → Q верно для любого составного предложения Q . Вы можете заменить Q чем угодно, и импликация k → Q останется в силе. Например, логически верный вывод: «Если я король Нидерландов, значит, единороги существуют». Продолжая это, из противоречия можно сделать любой вывод. Это называется Принцип взрыва .

Упражнения

1. Приведите три таблицы истинности, определяющие логические операторы ∧, ∨ и ¬.

2. Некоторые из следующих сложных суждений являются тавтологиями, некоторые — противоречиями, а некоторые — ни тем, ни другим (т. Е. Случайностями). В каждом случае используйте таблицу истинности, чтобы решить, к какой из этих категорий относится предложение:

a) ( p ∧ ( p → q )) → q b) (( p → q ) ∧ ( q → r )) → ( p → г )

c) p ∧ ¬ p d) ( p ∨ q ) → ( p ∧ q )
e) p ∨ ¬ p f) ( p q ) → ( p ∨ q )

3.Используйте таблицы истинности, чтобы показать, что каждое из следующих утверждений логически эквивалентно p ↔ q .

a) ( p → q ) ∧ ( q → p ) b) ¬ p ↔ ¬ q
c) ( p → q ) ∧ (¬ p → ¬ q ) d) ¬ ( p ⊕ q )

4. Является ли → ассоциативная операция? Это ( p → q ) → r логически эквивалентно p → ( q → r )? Является ли↔ ассоциативным?

  1. Пусть p представляет предложение «Вы уходите», а пусть q представляет предложение «Я ухожу».Выразите следующие предложения как составные предложения, используя p и q , и покажите, что они логически эквивалентны:

    а) Либо ты уйдешь, либо я уйду. (Или оба!) Б) Если ты не уйдешь, я уйду.

  2. Предположим, что м представляет утверждение «Земля движется», c представляет «Земля является центром вселенной», а g представляет «Галилей был ложно обвинен». Переведите на английский каждое из следующих составных предложений:

а) ¬ г ∧ в б) м ¬ в

c) м ↔ ¬ c d) ( м → г ) ∧ ( c → ¬ г )

7. Дайте обратное и противоположное для каждого из следующих английских предложений:

а) Если у вас все хорошо, Синтерклаас принесет вам игрушки.

б) Если посылка весит более одного килограмма, то вам потребуется дополнительная оплата.
в) Если есть выбор, то кабачки не ем.

8. В обычной колоде из пятидесяти двух игральных карт, для скольких карт верно а) что «Эта карта — десятка, а эта карта — сердце»?

б) что «Эта карта — десятка или эта карта — сердце»?
c) что «Если эта карта — десятка, то эта карта — сердце»?

d) что «Эта карта — десятка тогда и только тогда, когда эта карта — сердце»?

9.Определите логический оператор ↓ так, чтобы p ↓ q было логически эквивалентно ¬ ( p ∨ q ). (Этот оператор обычно называют «ни», сокращенно от «не или».) Покажите, что каждое из предложений ¬ p , p ∧ q , p ∨ q , p → q , p ↔ q и p ⊕ q можно переписать как логически эквивалентное утверждение, в котором ↓ используется в качестве единственного оператора.

10. Для нашего доказательства функциональной полноты {¬, ∨} нам нужно показать, что все формулы в пропозициональной логике могут быть выражены в эквивалентной форме, используя только {¬, ∧, ∨, →, ↔}.

а) Сколько существует уникальных таблиц истинности для формул, содержащих два атома?

б) Создайте функцию для каждой из возможных таблиц истинности, которая использует только 5 перечисленных операторов.

выше.

c) Приведите (неформальный) аргумент, почему это означает, что все формулы в логике высказываний могут быть

выражается с использованием только этих пяти операторов.

[M10] Пустое содержимое

Пустая инструкция — это любая инструкция который предназначен для предоставления информации, но на самом деле он не предоставляет информация вообще в соответствующем разговорном контексте.

В обычных ситуациях все тавтологий или тавтологические утверждения пусты. Тавтология — это утверждение, которое истинно в силу значения логических связок, присутствующих в утверждении. Эти связки являются связками типа «не», «и», «или», «если»… то … »,« есть »,« каждый »,« нет »и тому подобное.

Например, предположим, что Хелен спрашивает, придет ли Франсин на вечеринку, и Франсина отвечает: «Если я приду, то приду». Это тавтология, поскольку это обязательно верно, учитывая значение слова «если, то». Но в заявлении не содержится информации о том, примет ли Франсин участие в вечеринке. Так что это действительно пустое заявление.

Точно так же утверждение, что «либо завтра будет дождь, либо его не будет», тоже тавтология.Очевидно, что если мы хотим передавать информацию, нам следует избегать с использованием тавтологий, поскольку они не дают полезной информации о мире. Нельзя сказать, что они совершенно бесполезны. Тавтологии могут быть полезны в логике и иногда они служат напоминанием о доступных вариантах действий (например, «Либо мы поженимся, либо нет»).

Тавтология — это частный случай того, что мы могли бы назвать аналитическими утверждениями. Это утверждения, которые верны исключительно в силу их смысла.Вот некоторые Примеры:

  • Холостяк — неженатый мужчина.
  • Все, что большое, не мало.
  • Ничего из того, что работает, не останавливается.

Если утверждение является аналитическим, то его истинность зависит исключительно от его значения, а не от его значения. по любому другому эмпирическому факту. Обратите внимание, что все тавтологии являются аналитическими истинами, но не наоборот. Тавтологическое предложение — это предложение, которое истинно в силу значения логических слов в предложении.Аналитическое предложение — это предложение, которое истинно в силу значения слов в предложении. Три приведенных выше примера являются аналитическими истинами, но не тавтологиями. Почему? Возьмем первый пример, это правда, потому что «холостяк» имеет то же значение, что и «неженатый мужчина», но слово «холостяк» не логичное слово. В отличие от таких слов, как «и», «или», «если, то», «не», он не описывает никаких логических связей.

Если грамотный говорящий по-английски спрашивает, является ли Том холостяком, а вы отвечаете: «Холостяк — это неженатый мужчина», то ваше утверждение можно рассматривать как пустое утверждение.Хотя ваше утверждение обязательно верно, оно не содержит информации, относящейся к запросу. С другой стороны, если студент изучает английский язык и задается вопросом, что такое бакалавр, то ваш ответ содержит некоторую полезную информацию, поэтому в таком случае мы не должны говорить, что ответ пустой.

Если мы хотим четко и точно передавать информацию, то, конечно, нам следует избегать пустых заявлений. С другой стороны, может быть случаи, когда мы хотим быть уклончивыми и уклончивыми.В таких ситуациях пустые операторы действительно могут быть очень полезны.

тавтологий | Определение и факты

тавтология , в логике, утверждение, сформулированное так, что его нельзя отрицать без противоречия. Таким образом, выражение «Все люди — млекопитающие» должно утверждать в отношении чего бы то ни было, что это либо не человек, либо млекопитающее. Но эта универсальная «истина» следует не из каких-либо фактов о реальных людях, а только из фактического использования человека и млекопитающего и, таким образом, является чисто вопросом определения.

В исчислении высказываний — логика, в которой все предложения связаны такими связками, как ⊃ («если… то»), · («и»), ∼ («не») и ∨ («или»), даже сложные выражения, такие как [( A ⊃ B ) · ( C ⊃ ∼ B )] ⊃ ( C ⊃ ∼ A ), могут быть показаны как тавтологии путем отображения в таблице истинности каждая возможная комбинация истинностных значений — T (истина) и F (ложь) — ее аргументов A, B, C и после вычисления с помощью механического процесса истинностного значения всей формулы, отмечая что для каждой такой комбинации формула составляет T .Тест эффективен, потому что в любом конкретном случае общее количество различных присвоений истинностных значений переменным конечно, и вычисление истинностного значения всей формулы может выполняться отдельно для каждого присвоения истинности. ценности.

Подробнее по этой теме

Эпистемология: тавтологические и значимые суждения

Предложение называется тавтологическим, если составляющие его члены повторяются или если они могут быть сведены к терминам, которые повторяются, так что…

Понятие тавтологии в исчислении высказываний было впервые разработано в начале 20 века американским философом Чарльзом Сандерсом Пирсом, основателем школы прагматизма и крупным логиком. Сам термин, однако, был введен британским философом австрийского происхождения Людвигом Витгенштейном, который утверждал в Logisch-Philosophische Abhandlung (1921; Tractatus Logico-Philosophicus , 1922), что все необходимые предложения являются тавтологиями и что они существуют. следовательно, в смысле, в котором все необходимые предложения говорят одно и то же, а именно, вообще ничего.

Использование Витгенштейном термина требует его расширения от исчисления высказываний до исчисления предикатов первого порядка (с функциями), которое может распространяться на классы, множества и отношения, а также на отдельные переменные (переменные, которые могут обозначать индивидов) . Это расширенное понятие тавтологии, далее объясненное английским логиком Фрэнком П. Рэмси в 1926 году, на самом деле является менее точным предшественником того, что сейчас обычно называют валидностью.

Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту.Подпишитесь сейчас

Позже некоторые логические позитивисты, особенно Рудольф Карнап, внесли поправки в доктрину Витгенштейна в свете того различия, что существует эффективный тест на тавтологию в исчислении высказываний, но нет такой проверки достоверности даже в низшем исчислении предикатов. Логические позитивисты считали, что в общем вся необходимая истина (и, следовательно, всякая тавтология) выводится из некоторого правила языка; его единственная необходимость — это быть предписанным правилом определенной системы.Однако, поскольку такие выводы трудно выполнить на обычном языке — как в случае с утверждением «Все, что имеет начало во времени, должно иметь причину» — предпринимались попытки, как в книге Карнапа Der logische Aufbau der Welt (1928; The Logical Structure of the World: Pseudoproblems in Philosophy , 1967), чтобы построить искусственный язык, на котором можно было бы продемонстрировать все необходимые утверждения, обращаясь к формулам.

Тавтология | Примеры тавтологии

Определение и примеры тавтологии

Тавтология (происходит от греч. tauto, «то же самое» и logos, «высказывание») — риторический прием, состоящий в утомительном и ненужном повторении одной и той же идеи разными словами; как, когда Свифт говорит: «В Аттическом государстве было привилегий и первородства каждого гражданина, и поэта, — вслух, и публично. ”

Примеры и наблюдения

Следующее предложение Тиллотсона содержит множество тавтологий:

  • «В частности, в делах этого мира честность имеет много преимуществ перед всеми изящными и искусственными способами притворства и обмана ; это намного проще и проще, намного безопаснее и безопаснее способ взаимодействия с миром; в нем меньше проблем, и , из запутанностей, и затруднений, из опасностей и опасности в нем.Искусство обмана , и хитрость , постоянно ослабевают, и менее действенных, и годных, тем, кто их использует ».

Так же и в Аддисоне:

  • «Заря пасмурная; утро опускается,
    И сильно в облаках приносит день ».
    • [Эти три статьи отражают один и тот же факт.]

Постоянно стремясь к сбалансированной структуре предложения, Джонсон иногда подходит к этому недостатку.Говоря о стиле Pryor, он говорит:

  • «Он часто вкладывал в это много знаний и много мыслей; часто полировал до элегантности, часто возвышал до великолепия, и иногда повышал до величия; и не обнаружил, что ему нужна сила , привлекающая внимание, и , манящая любопытство ».

Использование синонимичных слов и словосочетаний является значительным только при следующих обстоятельствах

Когда одно слово не выражает полного смысла:

Нет двух слов, которые были бы синонимами для всех целей; у одного есть оттенок, который хочет другой; и может потребоваться и то, и другое, чтобы передать весь смысл.Следовательно, мы привыкли к таким фразам, как «пути и средства», «преходящее и преходящее», «предмет». В юридических документах синонимичные слова объединяются или для полной полноты. Когда Вордсворт соединяет «видение и божественную способность», он намеревается, что две фразы, которые почти одинаковы, должны раскрывать между собой большее количество смысла, чем любая из них.

Для того, чтобы выделить основные моменты экспозиции:

Хорошее изложение требует, чтобы главный предмет отличался от второстепенных.На это влияет, среди прочего, длительное пребывание на нем; и иногда можно прибегать к повторению посредством эквивалентных фраз. «Головка и передняя его обид:» « конец и дизайн. ”

Из вышеизложенного принципа подразумевается, что следует особенно избегать многословности в придаточных предложениях и утверждениях.

Часто лучше, чтобы придаточное предложение было слабым или неясным, чем поднимать его с места путем усиления.Гиббон, говоря об обожествлении римских императоров, говорит: «Эта законная и, казалось бы, необоснованная профанация, столь противная нашим более строгим принципам, была воспринята с очень слабым ропотом в году. Легкая природа политеизма. окно