Разновидности жесткости воды – смягчение воды | О воде
Жесткость воды можно определить как содержание растворенных в ней солей магния, кальция, а также ряда других элементов из периодической таблицы Д. И. Менделеева. К примеру, это могут быть соли железа и марганца, однако, содержание последних в воде, как правило, на порядок ниже в сравнении с содержанием солей кальция и магния, поэтому, говоря об общей жесткости воды, подразумевают именно содержание в воде растворенных солей кальция и магния. Общая жесткость включает в себя временную и постоянную жесткость, которые также иногда называют карбонатной и некарбонатной, соответственно.
Временная (карбонатная жесткость): Имеет обозначение KH. Она напрямую зависит содержания в воде гидрокарбонатов и карбонатов магния и кальция. Карбонатная жесткость называется временной, поскольку она может быть устранена путем кипячения воды. При кипячении данные соли выпадают в осадок и образуют накипь. Карбонатная жесткость определяет буферные свойства воды, в связи с чем, препятствует резким колебаниям уровня pH воды. Этот тип жесткости определяет ее пригодность для использования в быту, поскольку образование накипи на сантехнике и водонагревательных элементах бытовых приборов может легко вывести их из строя.
Этот тип жесткости определяет ее пригодность для использования в быту, поскольку образование накипи на сантехнике и водонагревательных элементах бытовых приборов может легко вывести их из строя.
Постоянная жесткость (некарбонатная жесткость): Имеет обозначение GH. Она обусловлена количественным содержанием в воде хлоридов, сульфатов и ряда других солей магния и кальция. При кипячении воды, такие соли в осадок выпадать не будут. Именно эта разновидность жесткости определяет степень пригодности воды для целей питья и приготовления пищи, т.к. ввиду невозможности ее удаления посредством кипячения, все соли кальция и магния, определяющие данные тип жесткости, попадут в организм человека. Кальций и магний – важнейшие макроэлементы, необходимые для нормального функционирования человеческого организма, однако, все хорошо в меру, и потребление воды с избыточным содержанием солей кальция и магния на протяжении длительного периода времени может привести к развитию мочекаменной болезни. Данный показатель может быть снижен путем применения технологии – смягчение.
Данный показатель может быть снижен путем применения технологии – смягчение.
Успешно справиться с избыточной жесткостью поможет фильтр, в котором реализована технология смягчения воды, которая позволит привести качество воды по данному показателю к приемлемому уровню.
Рейтинг лучших матрасов средней жесткости — ТОП из 10 моделей от МногоСна
Средняя жесткость — это своеобразная «золотая середина», потому что они наиболее универсальны, так как подходят подходят практически всем и обладают сбалансированными характеристиками. Матрасы с такой жесткостью одновременно удобны для мягких тканей и обеспечивают надежную упругую опору телу, которая важна для здорового сна. Изделия средней жесткости подходят детям подросткового возраста и взрослым с обычным телосложением.
В интернет-магазине МногоСна представлено свыше тысячи моделей средней жесткости с разными свойствами и материалами. Среди них каждый найдет себе что-нибудь по душе.
Чтобы упростить выбор, мы собрали самые практичные модели средней жесткости разных производителей. В приведенном ниже списке есть бюджетные матрасы и модели среднего ценового сегмента.
В приведенном ниже списке есть бюджетные матрасы и модели среднего ценового сегмента.
- Dimax Оптима Премиум Хард
- Son-tek Roll Memo 16
- MaterLux Simone
- BeautySon Промо 5 S600
- DreamRoll Contour Mix
- Alitte Meloni TFK M-19-N
- Lonax Fusion Mini
- BeautySon Hit Comfort S1200
- Mr.Mattress BioCrystal Sandwich L
- DreamLine Mix Massage
- Итог
- Каталог
Бюджетный Dimax Оптима Премиум Хард
Недорогой матрас средней высоты на блоке пружин ТФК — одна из самых популярных моделей на сайте. И не зря, ведь кроме доступной цены (всего 8 523 ₽ за 80×200 см), эта конструкция отличается рядом других преимуществ. У Dimax Оптима Премиум 2:
- Натуральная койра кокоса в составе. Это воздухопроницаемый гигиеничный материал. Расположенный поверх блока пружин он улучшает его ортопедические характеристики, лучше распределяя вес на упругие металлические элементы.

- Достойная высота — 21 см. Такой матрас будет удачно смотреться на любой кровати: с высокими или низкими бортами.
- Пена «Balance Foam» в качестве настилочного слоя. Материал мягче натурального латекса. Он повторяет контуры тела, мгновенно реагирует на смену положения во время отдыха, адаптируясь к смене позы. Что это дает? Повышенный уровень комфорта отдыха. Вам вряд ли захочется вставать с такого удобного матраса по утрам.
- Подарок при покупке. Приобретая матрас любого размера, все покупатели получают подарок — подушку Dimax Молли. Это ортопедическая модель, которая состоит из измельченного натурального и искусственного латекса. Роскошный подарок!
Пружинный |
1 жесткость |
Недорогой |
До 110 кг |
21 см |
Son-tek Roll Memo 16 — матрас 2 в 1
Основа модели — плита искусственного латекса.
Преимущество модели — возможность менять уровень комфорта, просто переворачивая матрас. Одна из сторон дополнена плитой материала с эффектом памяти. Она лучше подстраивается под контуры тела, на ней проще расслабиться и уснуть. Более мягкую сторону можно использовать при проблемах с засыпанием или если вам хочется как следует расслабиться после долгого дня.
Рельефный чехол сделан из двойного хлопкового жаккарда. Он достаточно прочный и роскошно выглядит.
Беспружинный |
2-в-1 |
Недорогой |
До 120 кг |
16 см |
Итальянский комфорт с MaterLux Simone
МатерЛюкс — итальянский бренд матрасов. Благородное происхождение модели Simone видно во всем: от белоснежного пышного чехла до высочайшего уровня комфорта. Матрас высотой 20 см сделан из монолитного блока искусственной гипоаллергенной пены. Она комфортная и упругая. Наполнитель хорошо пропускает воздух, а чтобы усилить это преимущество производитель оснастил чехол аэраторами для улучшенной циркуляции воздуха. Это станет гарантией того, что в модели не будет скапливаться пыль и влага, а значит микроклимат постели останется благоприятным для отдыха.
Матрас высотой 20 см сделан из монолитного блока искусственной гипоаллергенной пены. Она комфортная и упругая. Наполнитель хорошо пропускает воздух, а чтобы усилить это преимущество производитель оснастил чехол аэраторами для улучшенной циркуляции воздуха. Это станет гарантией того, что в модели не будет скапливаться пыль и влага, а значит микроклимат постели останется благоприятным для отдыха.
Модель доставляется в компактном рулоне. Небольшой рулон проще забрать самовывозом и самостоятельно доставить до дома.
Больше недорогих моделей МатерЛюкс смотрите в коллекции Light Soft. Есть одна модель даже за 7 400 ₽ за 80×200 см.
Беспружинный |
1 жесткость |
Средняя цена |
До 90 кг |
20 см |
BeautySon Промо 5 S600 с продуманной конструкцией
Пружинный матрас Промо 5 S600 от БьютиСон — пружинная модель, сделанная без клея.
Плюсы бесклеевой конструкции:
- Исключена аллергия на какой-либо из компонентов клея — его тут попросту нет.
- Улучшенная циркуляция воздуха. Сухой клей не будет препятствовать прохождению воздуха через внутренние слои.
- Нет характерного запаха нового изделия. Матрас не требует длительного проветривания после снятия заводской пленки. Подходит людям с чувствительным обонянием.
Это модель двусторонней жесткости. Сторона средней жесткости образована слоем искусственной пены. Сторона с жесткостью выше среднего — слоем пены и бикокоса. Этот материал сделан из смеси натурального кокоса с полиэфирными волокнами. На ней можно спать, когда спине требуется более выраженная поддержка. Например, после занятий спортом.
Например, после занятий спортом.
Пружинный |
2-в-1 |
Недорогой |
До 110 кг |
19 см |
Без клея |
Зональная поддержка тела в DreamRoll Contour Mix
Самая оригинальная модель в нашем рейтинге! И не только из-за внешнего вида наполнителя, но и из-за его свойств. Поверхность DreamRoll Contour Mix поделена на семь зон с разным уровнем жесткости. Зачем это нужно? Дело в том, что вес в человеческом теле распределен неравномерно — какие-то области легче, а какие-то — тяжелее. Они давят на матрас с разной силой. «ДримРолл Контур Микс» от ДримЛайн учитывает это — он более жесткий в зонах, где на матрас приходится увеличенная нагрузка. Это гарантирует улучшенную ортопедическую поддержку тела. Более тяжелые области не будут сильнее продавливать под собой матрас, а значит тело будет находится в правильном положении, без перекоса позвоночного столба.
Матрас сделан из плиты искусственного латекса. Нижняя сторона более жесткая, она формирует более выраженную ортопедическую поддержку, полезную для спины. На этой стороне можно спать на спине.
Беспружинный |
2-в-1 |
Средняя цена |
До 120 кг |
19 см |
Alitte Meloni TFK M-19-N из натуральных материалов
Практичный матрас из натуральных материалов. Несмотря на высокие слои натурального латекса и кокоса поверх пружин, он стоит заметно дешевле конкурентов. Секрет кроется в его конструкции — материалы расположены только на верхней стороне. Спать на нижней стороне нельзя, там расположен только изолирующий слой поверх пружин.
Существенный плюс матраса — довольно высокий слой натурального латекса. 3 см хватает, чтобы этот премиальный материал раскрыл все свои качества. Он мягкий, эластичный и приятен даже на ощупь. А когда вы ляжете на него, вам не захочется вставать с матраса до самого утра. Под латексом находится плита кокосового волокна, которая служит опорой позвоночнику и лучше распределяет вес на пружины с зональной структурой. Все это обеспечивает выраженный ортопедический эффект вкупе с высочайшим уровнем комфорта.
Он мягкий, эластичный и приятен даже на ощупь. А когда вы ляжете на него, вам не захочется вставать с матраса до самого утра. Под латексом находится плита кокосового волокна, которая служит опорой позвоночнику и лучше распределяет вес на пружины с зональной структурой. Все это обеспечивает выраженный ортопедический эффект вкупе с высочайшим уровнем комфорта.
Наличие только одной стороны существенно не повлияет на срок службы, потому что тут используются только натуральные наполнители. Кококс и латекс — одни из самых долговечных материалов, которые применяют при производстве матрасов. Так как эту модель нельзя переворачивать, периодически меняйте стороны голова-ноги, чтобы снизить износ наполнителей. Так матрас прослужит еще дольше.
Пружинный |
1 рабочая сторона |
Средняя цена |
До 135 кг |
19 см |
Lonax Fusion Mini из премиальных материалов
Эта беспружинная модель состоит только из латекса и кокоса — материалов премиального уровня. Они свободно пропускают воздух, не вызывают аллергию и хорошо переносят нагрузку.
Они свободно пропускают воздух, не вызывают аллергию и хорошо переносят нагрузку.
Данная модель подойдет и взрослым, и подросткам. Он поможет сохранить осанку безупречной. И все благодаря природным свойствам материалов! Они достаточно упругие, чтобы поддерживать тело в корректном положении. Сторона средней жесткости сформирована плитой натурального латекса высотой 3 см, а сторона высокой жесткости — таким же по высоте кокосом. Этого хватает для выраженной поддержки спины. Меняйте уровень комфорта, просто переворачивая матрас.
Чтобы помочь вам сохранить матрас в первозданном виде, при покупке мы дарим наматрасник Lonax Light. Его удобно снимать и надевать на матрас, он переносит даже частые стирки. Он станет надежным барьером от всех загрязнений.
Беспружинный |
2-в-1 |
Средняя цена |
До 90 кг |
13 см |
BeautySon Hit Comfort S1200 — идеален для пар
Матрас Hit Comfort S1200 от «БьютиСон» станет настоящим украшением спальни супругов.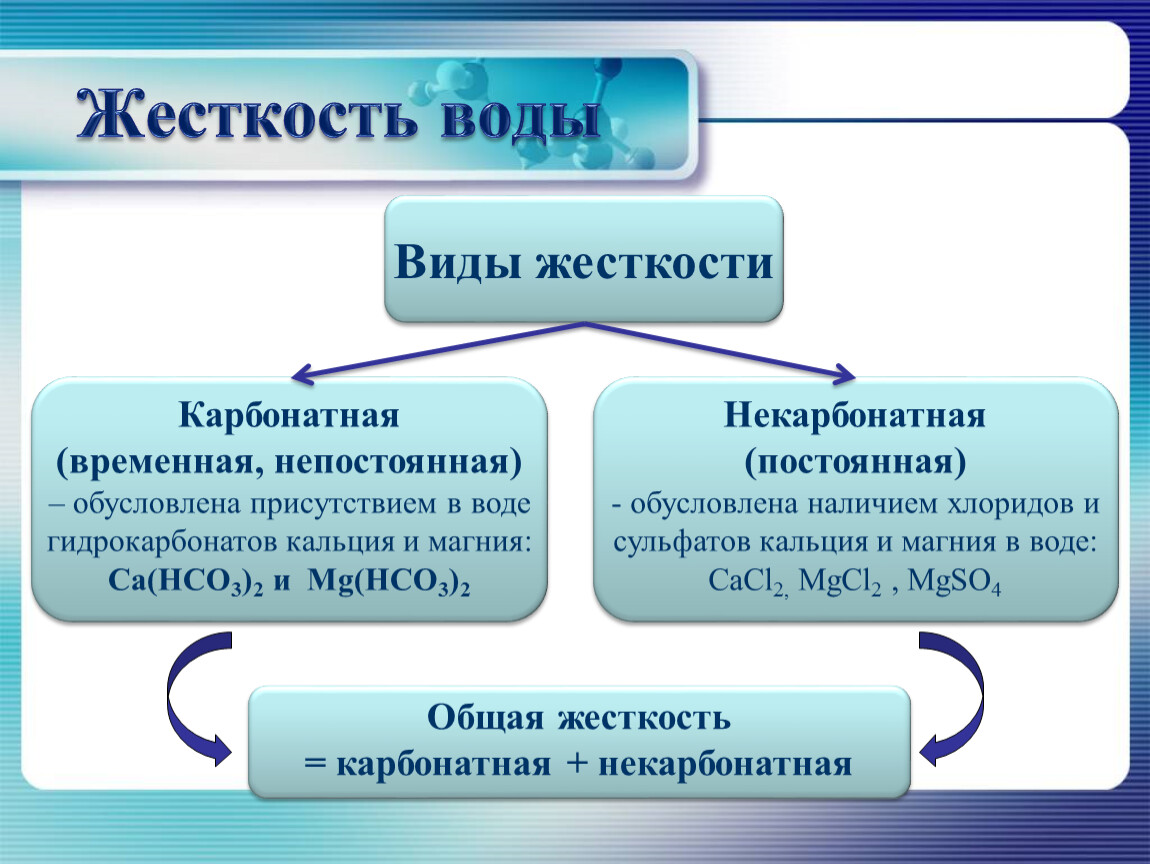 Его конструкция продумана до мельчайших деталей, чтобы сделать сон пары спокойным и крепким. В его основе — зональный блок пружин S1200, упруго поддерживающий тело. Он износостойкий и выдерживает большие нагрузки. Матрас не передает колебания на соседнее спальное место, а значит, сколько бы спящий рядом человек не ворочался, соседний не почувствует никаких колебаний. Это поможет сохранить гармонию в отношениях. Матрас в односпальном варианте идеально подойдет и для одного человека. В базовую комплектацию уже включены Z-пружины. Они усиливают конструкцию с боков, предохраняя систему пружин S1200 от повышенной нагрузки, когда пользователь садится на матрас. Так конструкция прослужит дольше.
Его конструкция продумана до мельчайших деталей, чтобы сделать сон пары спокойным и крепким. В его основе — зональный блок пружин S1200, упруго поддерживающий тело. Он износостойкий и выдерживает большие нагрузки. Матрас не передает колебания на соседнее спальное место, а значит, сколько бы спящий рядом человек не ворочался, соседний не почувствует никаких колебаний. Это поможет сохранить гармонию в отношениях. Матрас в односпальном варианте идеально подойдет и для одного человека. В базовую комплектацию уже включены Z-пружины. Они усиливают конструкцию с боков, предохраняя систему пружин S1200 от повышенной нагрузки, когда пользователь садится на матрас. Так конструкция прослужит дольше.
Стороны матраса различаются по ощущениям. Сторона с натуральным латексом и кокосовым волокном гарантирует средний уровень жесткости, а если спине нужна более ощутимая ортопедическая поддержка, матрас можно перевернуть на сторону пожестче — только с кокосом. Чтобы вам было удобнее переворачивать матрас, он оснащен крепкими ручками.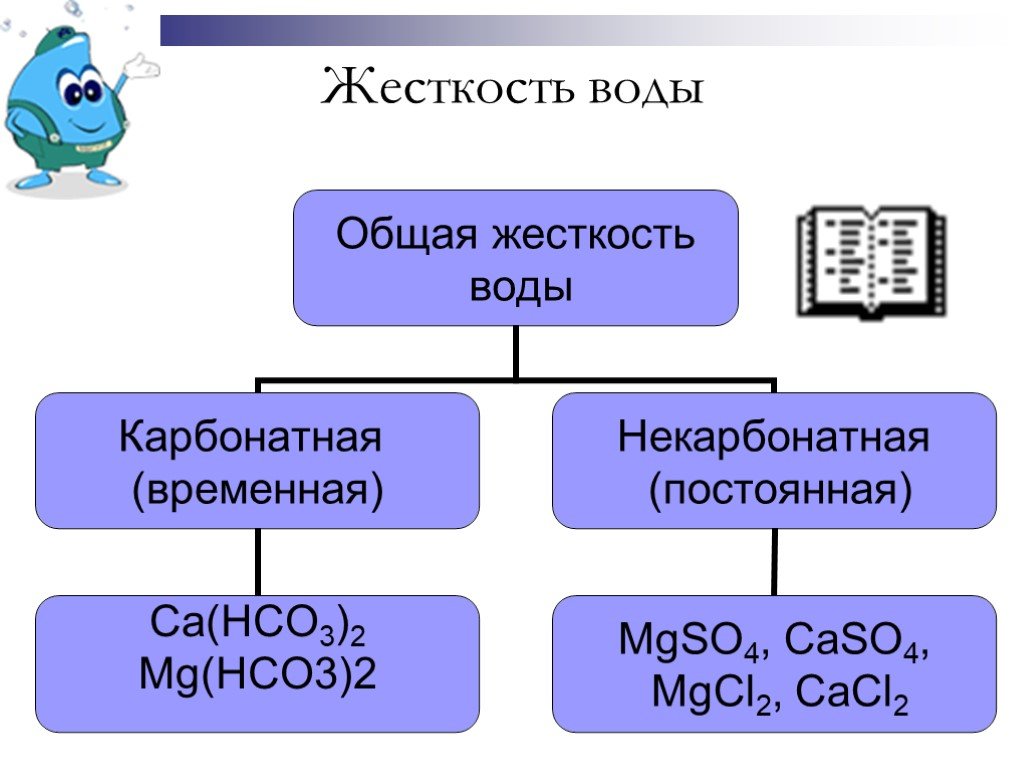
Отдельных слоев заслуживает чехол модели. Он очень пышный и мягкий из-за стежки на синтепоне и упругой искусственной пене. Ткань — двойной жаккард, прочный и стойкий к истиранию. По бокам вшиты аэраторы, которые улучшают вентиляцию модели.
Пружинный |
2-в-1 |
Средняя цена |
До 120 кг |
18 см |
Без клея |
Mr.Mattress BioCrystal Sandwich L с биокристаллами
Многослойная конструкция от «Мистер Матрас», которая состоит из поочередно расположенных плит из кокосового волокна и плотного пенополиуретана. Модели такого типа отличаются повышенной прочностью и выносливостью.
Главной «фишкой» матраса, которая отличает его от других, можно назвать особую кристаллическую изоляцию BioCrystal, созданную по хорватской технологии. Это смесь из 16 природных кристаллов (включая золото и серебро), которая благотворно сказывается на общем состоянии организма. Биокристаллы благотворно влияют на нервную систему, состояние кожи, нормализуют сердцебиение и способствуют более качественному отдыху. Вкупе с выраженной ортопедической поддержкой, которую обеспечивает упругая беспружинная конструкция, это сделает сон максимально эффективным и полезным, чтобы повысить вашу продуктивность в течение дня.
Биокристаллы благотворно влияют на нервную систему, состояние кожи, нормализуют сердцебиение и способствуют более качественному отдыху. Вкупе с выраженной ортопедической поддержкой, которую обеспечивает упругая беспружинная конструкция, это сделает сон максимально эффективным и полезным, чтобы повысить вашу продуктивность в течение дня.
Еще одна отличительная особенность матраса — роскошный пышный чехол, простеганный на мягкой пене, с красивым рельефным рисунком. Ткань изготовлена из 100% хлопка, она приятная на ощупь и достаточно плотная. Она не протрется со временем. Чехол оснащен молнией, поэтому, если он испачкается, его можно снять целиком и отдать в химчистку.
Беспружинный |
2-в-1 |
Средняя цена |
До 110 кг |
19 см |
Хлопковый чехол |
Зональный DreamLine Mix Massage
Достаточно один раз взглянуть на DreamLine Mix Massage, чтобы понять, что это премиальная модель. Она состоит только из натурального латекса и бикокоса. В качестве настилочных слоев используется особый латекс с зональной поверхностью. Благодаря рельефной структуре он более жесткий в тех местах, где на него приходится повышенная нагрузка. Это обеспечивает и улучшенную ортопедическую поддержку, и повышенный уровень комфорта из-за расслабляющего микромассажного эффекта. Один раз полежав на матрасе из натурального латекса, вам больше не захочется с него вставать — настолько он удобен и приятен для тела.
Она состоит только из натурального латекса и бикокоса. В качестве настилочных слоев используется особый латекс с зональной поверхностью. Благодаря рельефной структуре он более жесткий в тех местах, где на него приходится повышенная нагрузка. Это обеспечивает и улучшенную ортопедическую поддержку, и повышенный уровень комфорта из-за расслабляющего микромассажного эффекта. Один раз полежав на матрасе из натурального латекса, вам больше не захочется с него вставать — настолько он удобен и приятен для тела.
Чехол выполнен из велюровой ткани на основе хлопка и простеган на искусственном волокне. Приятная ворсистая поверхность мягкая и хорошо удерживает на себе простыни. За небольшую доплату чехол оснастят молнией. Его можно снять и почистить в любой момент. Обратите внимание, что допускается только сухая чистка!
Покупателям доступна внушительная гарантия — целых 10 лет. Такая уверенность производителя в своем продукте лучше всего говорит о долговечности матраса. Учитывая то, что он состоит из натуральных материалов, считающимися самыми прочными, нет никаких сомнений, что он прослужит много лет.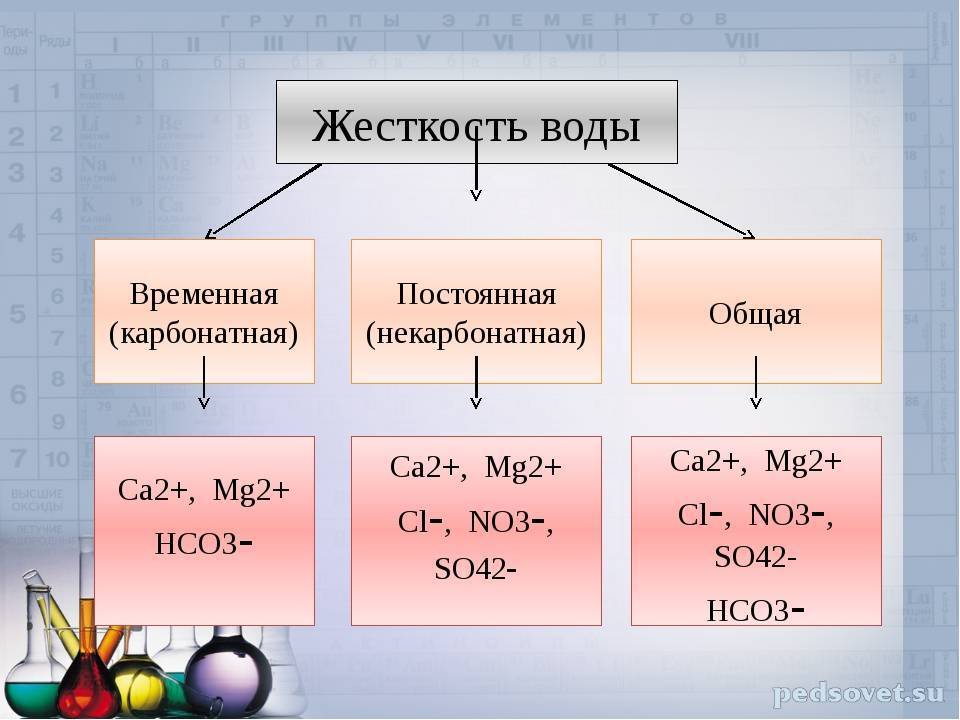
Беспружинный |
1 жесткость |
Средняя цена |
До 120 кг |
22 см |
Микромассаж |
Выводы
Изделие средней жесткости — хороший выбор, если вы ищите матрас для здорового сна. К таким моделям не нужно привыкать, как к жестким матрасам. Несмотря на это, они имеют отличные ортопедические качества, а значит, сон будет полезным, восстанавливающим силы. Они прекрасно подойдут людям с обычным телосложением и без ортопедических заболеваний.
Сегмент средне жестких моделей самый широкий, в нем представлены модели с разными типами конструкции.
Если вы все еще не можете определиться с выбором, обратитесь к нашим менеджерам. Они помогут подобрать высоту, размеры и другие параметры. Позвоните или напишите в чат.Что такое жесткость горных лыж?
lazyload/pixel.php» data-src=»https://www.youtube.com/embed/Xdx76yav6ks» frameborder=»0″ allowfullscreen=»»/>
Жесткость горных лыж.
Тема данного видео — жесткость горных лыж. Что это и зачем она нужна.
Так что же даёт жесткость лыжи, в чём её плюсы и минусы? В физике жёсткость — это способность конструктивных элементов сопротивляться деформации при внешнем воздействии.
Дело в том, что для того чтобы лыжи начали работать (прогибаться), на них нужно приложить определённое усилие. Усилие это складывается из веса лыжника и его скорости в повороте.
Исходя из вышеизложенного можно сделать вывод о том, что чем больше вес лыжника и его скорость, тем больше нагрузка на лыжи. Соответственно, лыжи должны быть жестче, чтобы эту нагрузку отрабатывать. Жесткость важна как продольная (по длине лыжи), так и торсионная (на скручивание лыжи). И напротив, слишком жесткие лыжи не будут должным образом прогибаться и работать при недостаточной на них нагрузке.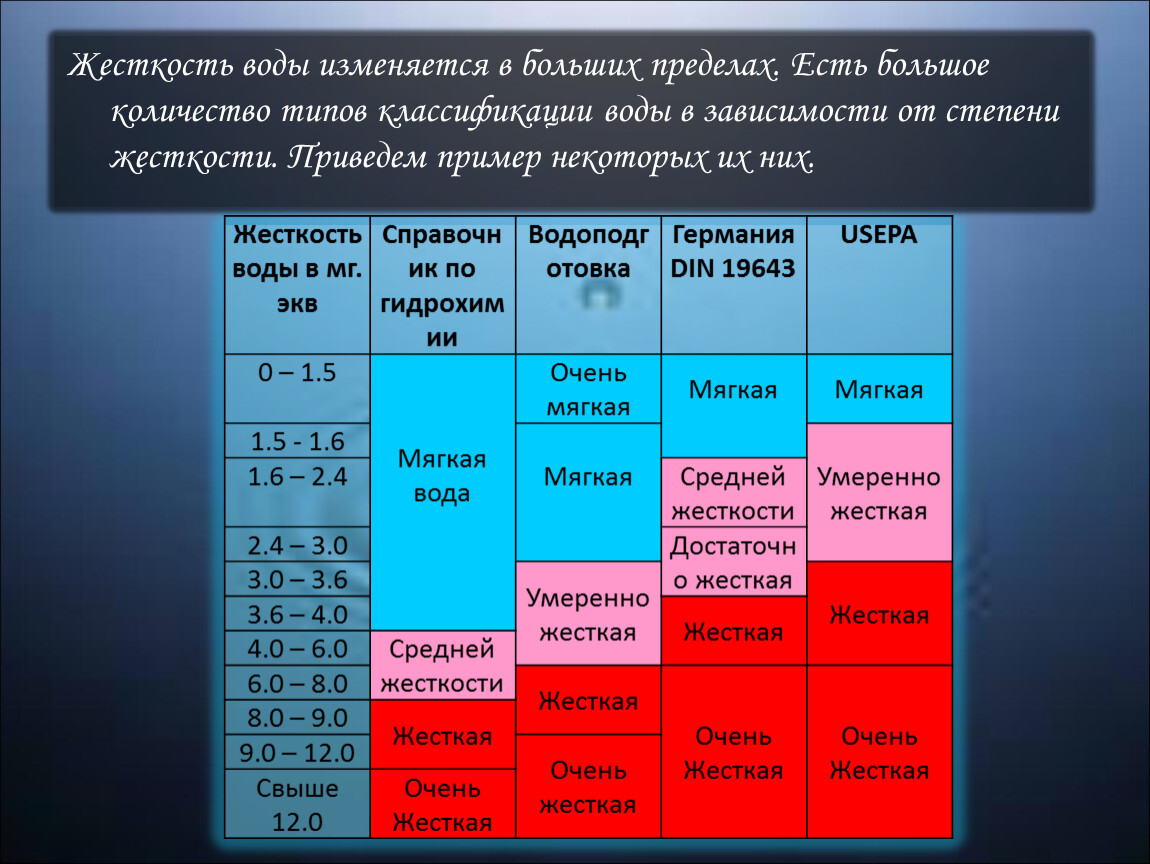
В целом в очень далёком приближении можно сказать, что скорость лыжника напрямую зависит от его опыта катания. Конечно же, есть определённые оговорки, но в общем это так.
Рассмотрим это на нескольких конкретных примерах.
Ситуация первая. Предположим лыжник, с хорошей техникой и достаточно высокой скоростью едет на мягких лыжах для новичков. Нагрузка в этом случае на лыжи очень большая, лыжи сильно скручиваются и прогибаются, вибрируют и перестают держать склон. Контроль над лыжами пропадает. Таким образом, катание на большой скорости в данном случае не возможно, нужно ехать медленнее. А техника-то позволяет быстрее! Меняем лыжи на более жесткие!
Ситуация вторая. Предположим, новичок едет на достаточно жестких лыжах для экспертов. Скорость его не велика, хотя вес может быть такой же, как у лыжника из первой ситуации. В этом случае нагрузка на лыжи недостаточна. Лыжи не работают должным образом и не поворачивают по дуге. Лыжнику приходится или сбрасывать пятки лыж или падать. В данном случае нужно менять лыжи на более мягкие.
В данном случае нужно менять лыжи на более мягкие.
Ситуация третья. Здесь всё хорошо. Лыжи по жесткости соответствуют уровню подготовки и технике лыжника. Будем считать, что уровень чуть выше среднего, ближе к экспертному. В данном случае, если лыжника всё устраивает, он не планирует менять условий катания или достигать новых высот в технике, то лыжи, конечно же, менять нет никакой необходимости. Но если условия катания будут меняться, появится желания ездить быстрее, развивать технику, или же просто наш лыжник солидно прибавит в весе (кг этак 10-15) то, конечно, здесь уже ему понадобятся другие, более жесткие лыжи.
Резюмируя вышесказанное, можно дать следующие рекомендации. Начинающим лыжникам с небольшим весом (до 75 кг) для быстрого прогресса в катании я рекомендую брать мягкие лыжи начального уровня. Если Ваш вес от 75 до 95 кг, то лучше брать лыжи пожёстче (среднего или экспертного уровня), модели с теми же параметрами я рекомендую и более легковесным лыжникам с уровнем подготовки средний и выше. Ну и, наконец, экспертам и спортсменам советую выбирать жесткие модели лыж, но на самом деле лыжники этой категории, как правило, сами прекрасно знают, какие лыжи им нужны.
Ну и, наконец, экспертам и спортсменам советую выбирать жесткие модели лыж, но на самом деле лыжники этой категории, как правило, сами прекрасно знают, какие лыжи им нужны.
Ссылки на наш каталог:
Комментарии В Контакте
Комментарии в Facebook
Как узнать жесткость воды: определение в домашних условиях
Воду добывают из земли. Это значит, что она постоянно контактирует с различными пластами почвы, веществами и минералами. Они оказывают прямое влияние на цвет, вкус, химические и физические свойства воды. Сюда же относится и жесткость, которая является одним из наиболее важных показателей качества. Если говорить научным языком, это положительно заряженные ионы кальция и магния. Именно поэтому многие хотят узнать больше про жесткость воды, как определить в домашних условиях этот параметр, и как смягчить воду.
Зачем узнавать показатели жесткости воды
Многие считают, что очищать воду нужно только в частных домах, где устроены скважина или колодец, но и в квартирах зачастую качество оставляет желать лучшего. В городских коммуникациях изначально применяют некоторые способы очистки. Но их хватает далеко не всегда. Самое безобидное, что может произойти, – это ухудшение вкуса и цвета жидкости. Но более серьезных проблем гораздо больше. Даже грамотная настройка посудомоечной машины и подбор стирального порошка зависят от подобных показателей. Жесткая вода влияет на все, с чем соприкасается, и среди основных отрицательных последствий:
В городских коммуникациях изначально применяют некоторые способы очистки. Но их хватает далеко не всегда. Самое безобидное, что может произойти, – это ухудшение вкуса и цвета жидкости. Но более серьезных проблем гораздо больше. Даже грамотная настройка посудомоечной машины и подбор стирального порошка зависят от подобных показателей. Жесткая вода влияет на все, с чем соприкасается, и среди основных отрицательных последствий:
- следы налета на сантехнике;
- плохое качество белья после стирки;
- поломка водонагревательного оборудования;
- засорение коммуникаций;
- потеря вкусовых качеств блюд и напитков, приготовленных на этой воде;
- ухудшение состояния кожи и волос после купания;
- нарушение работы сердца, пищеварительного тракта и другие негативные воздействия на организм человека.
Разные виды жесткости воды
Чем выше концентрация солей кальция и магния, тем более жесткая вода. Эти элементы встречаются в различных природных процессах, поэтому нет ничего удивительного, что они присутствуют в скважине, водопроводе или водоеме. Существуют 4 вида жесткости:
Существуют 4 вида жесткости:
- мягкая;
- средняя;
- жесткая;
- сверхжесткая.
Последний вид встречается крайне редко и, как правило, только в природе. Пить такую воду категорически запрещено.
В чем измеряют жесткость
Международная система единиц считает стандартом моль/м³. Но это очень неудобная система измерений. Иногда применяют еще одну условную единицу – Ppm (пропромилле). В каждой стране свои системы, поэтому и отталкиваться нужно от тех стандартов, под которые рассчитан тот или иной прибор измерений. В России для этих целей используют собственный показатель – градус жесткости. Например, средней жесткости считается вода, у которой от 2 до 10 °Ж. Хотя накипь обычно появляется уже при 4–5 °Ж.
Как измерить жесткость воды в домашних условиях
Чтобы правильно бороться с известковыми отложениями, сначала нужно узнать степень жесткости. Можно набрать воду и отнести ее в СЭС или узнать средние показания по городу и области, которые находятся в открытом доступе. Но они могут отличаться даже у стоящих рядом зданий, поэтому полностью полагаться на такую информацию не стоит. Чтобы не терять время и не стоять в очередях, лучше провести тест самостоятельно. Это легко, быстро и доступно, а использовать можно несколько способов.
Но они могут отличаться даже у стоящих рядом зданий, поэтому полностью полагаться на такую информацию не стоит. Чтобы не терять время и не стоять в очередях, лучше провести тест самостоятельно. Это легко, быстро и доступно, а использовать можно несколько способов.
Простое кипячение. Самый легкий, но и наименее точный способ. Достаточно заглянуть внутрь чайника. Когда вода жесткая, там образуется налет. Если его не убирать, постепенно он преобразуется в рыхлые камни. Чем выше жесткость, тем быстрее развивается этот процесс. Помимо этого, можно попробовать воду на вкус. Для этого нужно кипятить ее в течение 3–5 минут. Сладкий вкус покажет, что в воде много гипса. Терпкий свидетельствует о большом количестве железа. А горький вкус указывает на изобилие магния. Но надо учитывать, что это довольно субъективный метод.
Листовой чай. Лучше даже взять крупнолистовой, но, если такого нет, подойдет и обычный, только не гранулированный. Заваривать чай нужно так же, как и всегда. При повышенной жесткости он станет мутным и темным, и завариваться будет почти в 2 раза дольше. Если подождать некоторое время, то на поверхности появится своеобразная пленка. При этом чай будет иметь неприятный привкус. Кстати, если после чая на стенках бокала остается коричневый налет, это тоже свидетельствует о высокой жесткости.
При повышенной жесткости он станет мутным и темным, и завариваться будет почти в 2 раза дольше. Если подождать некоторое время, то на поверхности появится своеобразная пленка. При этом чай будет иметь неприятный привкус. Кстати, если после чая на стенках бокала остается коричневый налет, это тоже свидетельствует о высокой жесткости.
Зеркало или стекло. Достаточно капнуть водой на ровную стеклянную поверхность. Простейший способ, но придется дождаться полного высыхания. Для чистоты эксперимента лучше использовать и сырую, и кипяченую воду. Когда капли полностью высохнут, останется осадок. По нему и можно определить, насколько жесткая вода. Конечно, ни о каких точных показателях здесь речь не идет. Зато наглядно можно увидеть загрязнения. Если никаких следов на стекле не осталось, соответственно, вода мягкая.
Проверка с помощью мыла. Этот способ используют люди каждый день, хотя далеко не все обращают на него внимание. Достаточно просто помыть руки с мылом. Если оно хорошо пенится, но плохо смывается – вода мягкая. При повышенной жесткости намылить пену не так уж просто. Она в любом случае появится, но для этого потребуется время. Если есть вода с известной жесткостью, можно в нее покрошить мыло и перемешать. И одновременно сделать то же самое с тестируемым образцом. Останется только сравнить высоту пены. Где она больше, там вода мягче.
Если оно хорошо пенится, но плохо смывается – вода мягкая. При повышенной жесткости намылить пену не так уж просто. Она в любом случае появится, но для этого потребуется время. Если есть вода с известной жесткостью, можно в нее покрошить мыло и перемешать. И одновременно сделать то же самое с тестируемым образцом. Останется только сравнить высоту пены. Где она больше, там вода мягче.
Еще вариант с хозяйственным мылом. Такой способ уже более точный, хоть и не быстрый. Он тоже дает небольшую погрешность, но зато можно измерить реальный показатель в виде градусов жесткости. Мыло лучше взять с концентрацией 72 %, хотя подойдет и 60 %. Помимо этого, потребуются дистиллированная вода, литровая банка и стакан с диаметром 6 см. Чтобы было удобнее, лучше наклеить на него линейку снизу вверх. Сначала наливают дистиллированную воду примерно на 2 см от низа стакана. Затем следует отрезать от мыла 1 г и раскрошить его. Это примерно треть чайной ложки. Чтобы мыло лучше растворилось, дистиллированную воду немного подогревают. Перемешивать нужно аккуратно, чтобы пены было как можно меньше. Когда мыло полностью растворится, следует долить еще воды. Количество зависит от концентрации мыла. Если она 72 %, доливают до отметки 7,2 см. Если же она 60 %, достаточно будет 6 см. После этого нужно взять воду, которую планируется тестировать, в объеме 0,5 л. Ее наливают в литровую банку, а затем туда же аккуратно и по частям добавляют мыльный раствор. Все это нужно активно перемешивать до тех пор, пока пена не перестанет быстро оседать. То есть станет устойчивой. Мягкая вода образует больше пены. Каждый сантиметр мыльного раствора составляет 2 °Ж. Например, если пришлось вылить 4 см раствора, чтобы появилась пена, значит, жесткость воды составляет 8 °Ж.
Перемешивать нужно аккуратно, чтобы пены было как можно меньше. Когда мыло полностью растворится, следует долить еще воды. Количество зависит от концентрации мыла. Если она 72 %, доливают до отметки 7,2 см. Если же она 60 %, достаточно будет 6 см. После этого нужно взять воду, которую планируется тестировать, в объеме 0,5 л. Ее наливают в литровую банку, а затем туда же аккуратно и по частям добавляют мыльный раствор. Все это нужно активно перемешивать до тех пор, пока пена не перестанет быстро оседать. То есть станет устойчивой. Мягкая вода образует больше пены. Каждый сантиметр мыльного раствора составляет 2 °Ж. Например, если пришлось вылить 4 см раствора, чтобы появилась пена, значит, жесткость воды составляет 8 °Ж.
Тестовые полоски. Когда требуется более точный результат, можно приобрести специальные тесты для определения жесткости. Стоят они копейки, зато очень удобны. У них тоже есть погрешность, но обычно она составляет 1 °Ж. Для самостоятельного тестирования этого вполне достаточно. Полоску опускают в воду, а она меняет цвет в зависимости от количества солей. На упаковке или в инструкции находится специальная таблица, с помощью которой сравнивают результат.
Полоску опускают в воду, а она меняет цвет в зависимости от количества солей. На упаковке или в инструкции находится специальная таблица, с помощью которой сравнивают результат.
Тесты для аквариума. Большинству рыб не нужна слишком мягкая вода. Именно поэтому придумали специальные тесты, которые легко определяют жесткость. Обычно они представляют собой реагент, который вступает в реакцию при соединении с солями. Нужно добавлять его по капле в мерный стаканчик, пока не появится нужный цвет. Конечно, тесты бывают разными. Некоторые используют русские стандарты, другие – немецкие, третьи – вообще международные. Но в любом случае это один из самых быстрых, точных и легких способов определения жесткости.
TDS-метр. Если есть потребность контролировать жесткость воды на постоянной основе, а проводить эксперименты с мылом нет времени, можно задуматься о приобретении TDS-метра. Этот прибор определяет количество растворенных твердых веществ в жидкости. Почти все TDS-метры измеряют показания в Ppm, которые легко можно перевести в градусы жесткости: 50 Ppm = 1 °Ж. Перед началом работы прибор нужно откалибровать. Для этого в комплекте обычно идут специальные жидкости. Чтобы начать пользоваться прибором, нужно просто включить его и опустить электроды в воду. Устройство почти сразу покажет Ppm в виде цифр. Моделей такого оборудования достаточно много, но многофункциональные TDS-метры в быту почти не встречаются. Если требуется проверить фильтрованную воду из ионообменной системы, TDS-метр может показать неправильные результаты. Ведь он учитывает общую минерализацию, а она при замене ионов остается прежней.
Почти все TDS-метры измеряют показания в Ppm, которые легко можно перевести в градусы жесткости: 50 Ppm = 1 °Ж. Перед началом работы прибор нужно откалибровать. Для этого в комплекте обычно идут специальные жидкости. Чтобы начать пользоваться прибором, нужно просто включить его и опустить электроды в воду. Устройство почти сразу покажет Ppm в виде цифр. Моделей такого оборудования достаточно много, но многофункциональные TDS-метры в быту почти не встречаются. Если требуется проверить фильтрованную воду из ионообменной системы, TDS-метр может показать неправильные результаты. Ведь он учитывает общую минерализацию, а она при замене ионов остается прежней.
Важно учитывать, что точный результат проверки получить самостоятельно крайне сложно, но возможно понять – жесткая вода или нет. Для точных измерений лучше обращаться к специалистам.
Пенумбра и эффективная жесткость
При переходе от дипольного поля к реальному геомагнитному полю исчезает
аксиальная симметрия, поэтому, строго говоря, теория Штермера не применима. где G(Rc)
= 1 для разрешенных интервалов
жесткостей, G(Rc)
= 0 – для запрещенных
интервалов прихода. Reff = Rmin + (Rmax − Rmin)·n/N, где Reff —
эффективная жесткость обрезания, Rmin −
минимальная жесткость обрезания, определенная при численном интегрировании, Rmax максимальная
жесткость обрезания, n –
число погибших частиц в интервале (Rmin,
Rmax), N –
полное число частиц в этом интервале.
Численные расчеты показывают, что ширина пенумбры зависит от геомагнитной
широты: она практически равна нулю на высоких широтах, максимальна на средних
широтах и уменьшается к экватору почти до нуля. На рисунке представлены
результаты траекторных расчетов вертикальной жесткости обрезания для московского
меридиана в зависимости от географической широты. Нижняя граница зеленой области
соответствует минимальной жесткости частицы, достигающей границы магнитосферы,
верхняя граница зеленой области – максимальной жесткости частицы, гибнущей в
атмосфере. Выше зеленой области все траектории являются разрешенными, ниже этой
области все траектории – запрещенные. Красная линия соответствует эффективной
жесткости обрезания, внутри зеленой области она рассчитана по процедуре,
описанной выше. Планетарное распределение эффективной жесткости
Выше было показано, что жесткость геомагнитного обрезания зависит от
направления. В физике космических лучей широко используется вертикальная
жесткость, т.е. жесткость частицы, приходящей из вертикального направления.
Исторически это связано с тем, что в начальную эпоху исследования космических
лучей детекторы размещались либо на поверхности Земли, либо на высотных
аэростатах. Поэтому поток КЛ заведомо приходил из верхней полусферы. Расчеты
показывают, что вертикальная жесткость является хорошей оценкой глобальной
жесткости, усредненной по всем направлениям. Приведенное на рисунке планетарное
распределение вертикальной жесткости геомагнитного обрезания на высоте 450 км
(примерная высота полета международной космической станции), рассчитанное в
[14], в первом приближении соответствует наклоненному и смещенному диполю – в
западном полушарии в приэкваториальных областях жесткость меньше, чем в
восточном полушарии.
|
Жесткость воды. Соли жесткости — Инжиниринговый центр Техносистемы в Смоленске
Жесткость воды — это совокупность химических и физических свойств воды, связанных с содержанием в ней растворенных солей щелочноземельных металлов, главным образом, кальция и магния (так называемых «солей жесткости»).
Соли жесткости имеют разные свойства. Так, при нагреве воды, некоторые из них выпадают в осадок в виде накипи, а некоторые — не выпадают. По этому признаку их и начали разделять.
Соли, выпадающие в осадок, стали называть солями временной (или устранимой) жесткости, а соли, которые не выпадают в осадок при нагреве воды, солями постоянной жесткости.
Сульфаты, хлориды и нитраты магния и кальция, растворенные в воде, образуют постоянную (или некарбонатную) жесткость. Они выпадают в осадок исключительно при полном испарении воды.
Временная жесткость характеризуется присутствием в воде наряду с катионами Ca2+, Mg2+ и Fe2+ гидрокарбонатных, или бикарбонатных анионов (HCO3-).
При кипячении воды гидрокарбонаты разлагаются, образуя очень плохо растворимый карбонат кальция, углекислый газ и воду:
Ca2+ + 2HCO3- = CaCO3↓ + h3O + CO2↑
Общая жесткость складывается из постоянной и временной.
В данной таблице приведены основные катионы металлов, вызывающие жесткость, и главные анионы, с которыми они ассоциируются.
|
Катионы |
Анионы |
|
Кальций (Ca2+) |
Гидрокарбонат (HCO3-) |
|
Магний (Mg2+) |
Сульфат (SO42-) |
|
Стронций (Sr2+) |
Хлорид (Cl-) |
|
Железо (Fe2+) |
Нитрат (NO3-) |
|
Марганец (Mn2+) |
Силикат (SiO32-) |
На практике стронций, железо и марганец оказывают на жесткость столь небольшое влияние, что ими, как правило, пренебрегают. Алюминий (Al3+) и трехвалентное железо (Fe3+) также влияют на жесткость, но при уровнях рН, встречающихся в природных водах, их растворимость и, соответственно, «вклад» в жесткость ничтожно малы. Аналогично, не учитывается и незначительное влияние бария (Ва2+).
Алюминий (Al3+) и трехвалентное железо (Fe3+) также влияют на жесткость, но при уровнях рН, встречающихся в природных водах, их растворимость и, соответственно, «вклад» в жесткость ничтожно малы. Аналогично, не учитывается и незначительное влияние бария (Ва2+).
Жёсткость воды — происхождение
Ионы кальция (Ca2+) и магния (Mg2+), а также других щелочноземельных металлов, обуславливающих жесткость, присутствуют во всех минерализованных водах. Их источником являются природные залежи известняков, гипса и доломитов. Ионы кальция и магния поступают в воду в результате взаимодействия растворенного диоксида углерода с минералами и при других процессах растворения и химического выветривания горных пород. Источником этих ионов могут служить также микробиологические процессы, протекающие в почвах на площади водосбора, в донных отложениях, а также сточные воды различных предприятий.
Обычно в маломинерализованных водах преобладает (до 70%-80%) жесткость, обусловленная ионами кальция (хотя в отдельных редких случаях магниевая жесткость может достигать 50-60%). С увеличением степени минерализации воды содержание ионов кальция (Са2+) быстро падает и редко превышает 1 г/л. Содержание же ионов магния (Mg2+) в высокоминерализованных водах может достигать нескольких граммов, а в соленых озерах — десятков граммов на один литр воды.
С увеличением степени минерализации воды содержание ионов кальция (Са2+) быстро падает и редко превышает 1 г/л. Содержание же ионов магния (Mg2+) в высокоминерализованных водах может достигать нескольких граммов, а в соленых озерах — десятков граммов на один литр воды.
В целом, жесткость поверхностных вод, как правило, меньше жесткости вод подземных. Жесткость поверхностных вод подвержена заметным сезонным колебаниям, достигая обычно наибольшего значения в конце зимы и наименьшего в период половодья, когда обильно разбавляется мягкой дождевой и талой водой. Морская и океанская вода имеют очень высокую жесткость (десятки и сотни мг-экв/дм3).
Жесткость воды — единицы измерения
С 1 января 2014 года в России введен межгосударственный стандарт ГОСТ 31865-2012 «Вода. Единица жесткости». По новому ГОСТу жесткость выражается в градусах жесткости (°Ж).
1 °Ж соответствует концентрации щелочноземельного элемента, численно равной 1/2 его миллимоля на литр (1 °Ж = 1 мг-экв/л). В разных странах использовались (иногда используются до сих пор) различные внесистемные единицы — градусы жёсткости.
В разных странах использовались (иногда используются до сих пор) различные внесистемные единицы — градусы жёсткости.
За рубежом приняты другие единицы измерения жесткости воды, соотношение этих единиц представлено в таблице:
|
Страна |
Единицы измерения |
Россия |
Германия |
Великобритания |
Франция |
США |
|
Россия |
°Ж |
1 |
2,80 |
3,51 |
5,00 |
50,04 |
|
Германия |
°DH |
0,357 |
1 |
1,25 |
1,78 |
17,84 |
|
Великобритания |
°Clark |
0,285 |
0,80 |
1 |
1,43 |
14,3 |
|
Франция |
°F |
0,20 |
0,56 |
0,70 |
1 |
10 |
|
США |
ppm |
0,02 |
0,056 |
0,070 |
0,10 |
1 |
1°Ж = 20,04 мг Ca2+ или 12,15 Mg2+ в 1 дм3 воды;
1°DH = 10 мг CaO в 1 дм3 воды;
1°Clark = 10 мг CaCO3 в 0,7 дм3 воды;
1°F = 10 мг CaCO3 в 1 дм3 воды;
1 ppm = 1 мг CaCO3 в 1 дм3 воды.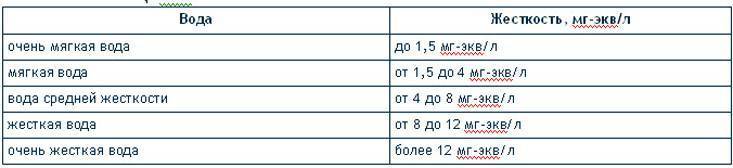
Численные значения жесткости измеренные в мг-экв/л, моль/м3, и °Ж, несмотря на различия в обозначении, равны между собой.
По значению общей жесткости природные воды делят на группы:
- очень мягкая вода (0–1,5 мг-экв/л)
- мягкая вода (1,5–4 мг-экв/л)
- вода средней жесткости (4–8 мг-экв/л)
- жесткая вода (8–12 мг-экв/л)
- очень жесткая вода (более 12 мг-экв/л).
Нормативные требования и рекомендации
Рекомендации всемирной организации здравоохранения (ВОЗ) для питьевой воды:
кальций – 20-80 мг/л; магний – 10-30 мг/л. Для жесткости какой-либо рекомендуемой величины не предлагается.
Российские нормативные документы (СанПиН 2.1.4.1074-01 и ГН 2.1.5.1315-03) для питьевой воды регламентируют:
кальций – норматив не установлен; магний – не более 50 мг/л; жесткость — не более 7°Ж.
Норматив физиологической полноценности бутилированной воды (СанПиН 2.1.4.1116-02):
кальций – 25-130 мг/л; магний – 5-65 мг/л; жесткость – 1,5-7°Ж.
По содержанию кальция и магния бутилированная вода высшей категории ничем не лучше воды из-под крана!
Как жесткость воды влияет на ее качество
Жесткость воды — это показатель, который зависит от содержания ионов кальция и магния. Он существенно влияет на эксплуатационные свойства воды, делая ее более или менее приемлемой для питья, приготовления пищи, использования в бытовых целях.
Параметр жесткости настолько важен, то регламентируется действующим ГОСТ Р, который регламентирует качества подаваемой водопроводной воды. Для его измерения введена отдельная единица — градусы жесткости. Жесткость должна находиться в заданном диапазоне, так как слишком мягкая вода также не подходит для потребления из-за повышенной коррозийной активности.
В централизованном водопроводе и из скважин обычно подается вода с высокой жесткостью. Поэтому в домашних условиях рекомендуется использовать умягчители. Это специальные фильтры, которые нормализуют показатель жесткости с помощью ионообменной смолы, где происходит замещение кальция и магния на натрий.
Откуда появляется жесткостьУченые под термином «жесткость» понимают свойства воды, которые зависят от концентрации солей магния и кальция. Если их много, вода становится жесткой, когда мало — мягкой. Показатель общей жесткости формируется из двух составляющих:
1. Постоянная. Она получается благодаря веществам, которые под действием высокой температуры остаются стабильными и не переходят из растворенной формы в нерастворенную. Уменьшить постоянную жесткость путем кипячения невозможно.
2. Переменная. Она зависит от карбонатов, которые при нагревании до высокой температуры переходят в твердую форму и оседают на поверхностях нагревательных приборов. Кроме того, эти частицы в виде тончайшей пленки остаются на поверхности горячего напитка и налипают на стенки чашки, оставляя след.
В лабораторных условиях при определении жесткости исследуют оба показателя и в протоколе указывают общий.
Жесткость воды из централизованного водопровода и скважины зависит от следующих факторов:
Состава пород на водоносном горизонте. Если вода перед попаданием в скважину протекает через известняк, она вымывает часть вещества и растворяет его. Следовательно, повышается содержание ионов кальция и увеличивается жесткость.
Время года. Летом из-за высокой температуры вода с поверхности водоемов испаряется и концентрируется в виде облаков. Следовательно, увеличивается процентное содержание минеральных веществ в реках и озерах. Как следствие, вода становится более жесткой.
Технологии очистки. Если на станциях централизованной очистки установлены системы смягчения воды, потребитель получает мягкую воду. Но, как правило, это оборудование ставят только индивидуально в квартирах, частных домах, коттеджах.
Свойства жесткой водыВ Российской Федерации потребители чаще всего сталкиваются с жесткой водой, за исключением жителей нескольких регионов. В некоторых населенных пунктах показатель жесткости настолько высок, что без умягчения она приобретает характерный горьковатый привкус.
Визуально определить жесткость воды невозможно. Косвенными признаками высокого содержания ионов кальция и магния являются:
- Плохое вспенивание мыла и других моющих веществ;
- Образование белого налета на стенках кастрюли или в чайнике при кипячении;
- Появление минерального налета на стенках сантехнических приборов;
- Сухость кожных покровов после принятия ванны или душа;
- Появление пленки на поверхности кофе или чая после заваривания.
Постоянное использование жесткой воды приводит к большому количеству негативных последствий:
- Поломки нагревательного оборудования. Чаще всего от жесткой воды ломаются котлы. Вода обычно используется в качестве теплоносителя и при нагревании из нее выпадает осадок и накапливается в теплообменнике отопительного устройства. По мере эксплуатации кальция будет откладываться все больше, что нарушит теплообмен и приведет к поломке. Чтобы избежать постоянной промывки труб необходимо использовать в качестве теплоносителя мягкую воду.
- Поломки посудомоечных и стиральных машин. Как и в случае котлов причиной неисправности будет минеральный налет на электрических нагревателях. Кроме того, из-за накопления осадка датчики начинают работать неправильно, что приводит к нарушению режимов стирки или мытья посуды.
- Камни в печени и почках. При постоянном употреблении жесткой воды минеральные отложения появляются во внутренних органах. Для их удаления может понадобиться хирургическое вмешательство.
Нельзя использовать и слишком мягкую воду. Это приводит к двум негативным последствиям:
- Недостаток в минералах и микроэлементах, которые нужны для нормального функционирования организма;
- Сильное коррозийное воздействие на металлические детали трубопроводов, что приводит к их выходу из строя.
Хотите понизить жесткость воды, сделать ее комфортной для использования в быту? Обращайтесь за помощью в нашу компанию. Мы подберем для вас индивидуальный фильтр-умягчитель с нужной производительностью и окажем помощь в его подключении к водопроводу. Для оформления заявки позвоните менеджерам отдела продаж или заполните форму обратной связи.
Читайте также:
Жесткость — Physiopedia
Ригидность, которую многие авторы часто используют как синоним гипертонии, является распространенным нарушением мышечного тонуса, при котором возникает сопротивление пассивному движению независимо от позы и скорости. Это одна из основных черт болезни Паркинсона, которая обычно присутствует при экстрапирамидных расстройствах. В равной степени действует как на агонисты, так и на антагонисты.
Его можно увидеть на —
Ригидность — это гипертоническое состояние, характеризующееся постоянным сопротивлением во всем диапазоне движений, которое не зависит от скорости движения.Это результат чрезмерного супраспинального возбуждения (облегчение верхних мотонейронов), действующего на альфа-мотонейроны; механизмы спинномозгового рефлекса обычно в норме. [1] При паркинсонической ригидности судороги в сухожилиях обычно нормальны [2]
«Ригидность» определяется как гипертонус, при котором выполняются все следующие условия [3] :
- Сопротивление внешнему движению сустава присутствует при очень низких скоростях движения, не зависит от заданной скорости и не имеет пороговых значений скорости или угла.
- Может происходить одновременное сокращение агонистов и антагонистов, что отражается в немедленном сопротивлении изменению направления движения вокруг сустава
- Конечность не стремится вернуться к определенной фиксированной позе или крайнему углу сустава
- Произвольная активность в отдаленных группах мышц не приводит к непроизвольным движениям вокруг жестких суставов, хотя ригидность может ухудшиться.
«Базальные ганглии» относятся к группе подкорковых ядер, отвечающих в первую очередь за моторный контроль, а также за другие роли, такие как моторное обучение, управляющие функции и поведение, а также эмоции. Классическая модель базальных ганглиев показывает, как информация течет через базальные ганглии обратно в кору по двум путям с противоположными эффектами для правильного выполнения движения.
Ригидность является результатом чрезмерного супраспинального возбуждения (облегчение верхних мотонейронов), действующего на альфа мотонейроны; механизмы спинномозгового рефлекса обычно в норме. [1] Нарушение нормального реципрокного торможения [4] . Когда баланс торможения и возбуждения в базальных ганглиях и моторной коре нарушается, появляются симптомы и признаки ригидности и непроизвольных движений наряду с аномалиями позы и связанными с ними движениями [2] . Однако наше нынешнее понимание патофизиологии базальных ганглиев не обеспечивает адекватного объяснения двух других кардинальных особенностей болезни Паркинсона, а именно ригидности и тремора [5] .
Несколько факторов могут повлиять на жесткость, некоторые из которых включают:
- Неспособность пациента расслабиться и полностью устранить активность в мышцах
- Повышенная жесткость из-за изменения вязкоупругих свойств мышц
- Аномальная совместная активация групп мышц-агонистов-антагонистов
- Повышение рефлексов растяжения
- снижение уровня дофамина
Ригидность болезни Паркинсона может быть охарактеризована как «свинцовая труба» или «зубчатое колесо».”
- Ригидность зубчатого колеса — относится к гипертоническому состоянию с наложенным трещоточным подергиванием и обычно наблюдается при движениях верхних конечностей (например, сгибание и разгибание запястья или локтя). Тип жесткости зубчатого колеса представляет собой сочетание жесткости ведущей трубы с тремором.
- Жесткость ведущей трубы — относится к гипертоническому состоянию во всем диапазоне движений, то есть одновременному сокращению агонистов и антагонистов, и это отражается в немедленном сопротивлении изменению направления движения вокруг сустава.
Разница между спастичностью и ригидностью [править | править источник]
Спастичность обычно возникает только во время растяжения мышц (т. Е. Не в состоянии покоя) и обычно сопровождается повышенными рефлексами сухожилий и реакцией Бабинского. Обычно существует разница между сопротивлением в одном направлении движения по сравнению с сопротивлением в противоположном направлении, и у некоторых пациентов может наблюдаться феномен застежки-ножа (внезапное высвобождение в конце диапазона движения).
При ригидности мышечный тонус повышается даже в состоянии покоя и обычно проявляется во время пассивного диапазона движений во всех направлениях отдельных суставов.Подошвенный рефлекс и рефлексы сухожилий обычно в норме. Нет синергии.
[6]
Эксперт должен держать руку патента выше запястья одной рукой и удерживать ее неподвижно. Другой рукой он захватывает пальцы и ладонь, а затем медленно вращает вдоль длинной оси руки. Если есть жесткость, экзаменующий будет испытывать сопротивление во время движения. Если явление зубчатого колеса положительное, экзаменатор будет испытывать прерывание или повторный захват во время движения, и если он присутствует на протяжении всего движения без каких-либо прерываний или изменений относительно скорости, это будет жесткость ведущей трубы. [2] Обычно при идиопатической болезни Паркинсона наблюдается односторонняя ригидность, которую можно сравнить во время обследования с противоположной стороной.
Медицинский менеджмент [править | править источник]
Лечение болезни Паркинсона левадопой (L-допа) в этих различных комбинациях чрезвычайно полезно для уменьшения брадикинезии и ригидности.
Было продемонстрировано, что стимуляция глубокого мозга в стимуляции Globus pallidus и стимуляция субталамического ядра улучшает ригидность [7]
Управление физиотерапией [править | править источник]
Для большинства пациентов лечение проходит лучше, если ригидность снижается в начале сеанса лечения.Таким образом, вмешательства в лечебной физкультуре, по-видимому, имеют более продолжительный эффект, когда лечение проводится во время «активной» фазы цикла приема лекарств. [8]
Методы релаксации, по-видимому, эффективны для снижения ригидности, включая плавное медленное покачивание, вращение конечностей и туловища, а также использование йоги. У пациентов с болезнью Паркинсона расслабление может быть лучше достигнуто в положении сидя или стоя, поскольку в положении лежа на спине может увеличиваться ригидность. Поскольку проксимальные мышцы часто задействованы в большей степени, чем дистальные, расслабление может быть легче достигнуть путем прогрессирования от дистального к проксимальному [8]
Показано, что ритмические упражнения снижают жесткость [8] Например.Хлопать в ладоши, делать круги руками или ногами.
Ритмическое начало и ритмическое вращение (проприоцептивное нервно-мышечное облегчение)
- ↑ 1.0 1.1 О’Салливан С.Б., Шмитц Т.Дж., Фулк Г. Физическая реабилитация. Ф.А. Дэвис; 2019 25 января.
- ↑ 2,0 2,1 2,2 Эдвардс С., редактор. Неврологическая физиотерапия: подход к решению проблем. Elsevier Health Sciences; 2002 г.
- ↑ Сэнгер Т.Д., Дельгадо М.Р., Геблер-Спира Д., Халлетт М., Норк Дж. У.Классификация и определение нарушений, вызывающих гипертонию в детском возрасте. Педиатрия. 1 января 2003 г .; 111 (1): e89-97.
- ↑ Электронная книга по физиотерапии Портера С. Тиди. Elsevier Health Sciences; 2013 17 января.
- ↑ Lanciego JL, Luquin N, Obeso JA. Функциональная нейроанатомия базальных ганглиев. Перспективы Колд-Спринг-Харбор в медицине. 2012 декабрь 1; 2 (12): a009621.
- ↑ Доктор Раджу. С. Кумар. Моделирование жесткости застежки ножа и зубчатого колеса. Доступно по адресу: https://www.youtube.com/watch?v=8xxe2WWWoYI [последний доступ 31.12.2020]
- ↑ Shapiro MB, Vaillancourt DE, Sturman MM, Metman LV, Bakay RA, Corcos DM.Влияние STN DBS на ригидность при болезни Паркинсона. IEEE Transactions по нейронным системам и реабилитационной инженерии. 18 июня 2007 г .; 15 (2): 173-81.
- ↑ 8,0 8,1 8,2 Umphred DA, Lazaro RT. Неврологическая реабилитация. Elsevier Health Sciences; 2012 14 августа.
Жесткость — Physiopedia
Ригидность, которую многие авторы часто используют как синоним гипертонии, является распространенным нарушением мышечного тонуса, при котором возникает сопротивление пассивному движению независимо от позы и скорости.Это одна из основных черт болезни Паркинсона, которая обычно присутствует при экстрапирамидных расстройствах. В равной степени действует как на агонисты, так и на антагонисты.
Его можно увидеть на —
Ригидность — это гипертоническое состояние, характеризующееся постоянным сопротивлением во всем диапазоне движений, которое не зависит от скорости движения. Это результат чрезмерного супраспинального возбуждения (облегчение верхних мотонейронов), действующего на альфа-мотонейроны; механизмы спинномозгового рефлекса обычно в норме. [1] При паркинсонической ригидности судороги в сухожилиях обычно нормальны [2]
«Ригидность» определяется как гипертонус, при котором выполняются все следующие условия [3] :
- Сопротивление внешнему движению сустава присутствует при очень низких скоростях движения, не зависит от заданной скорости и не имеет пороговых значений скорости или угла.
- Может происходить одновременное сокращение агонистов и антагонистов, что отражается в немедленном сопротивлении изменению направления движения вокруг сустава
- Конечность не стремится вернуться к определенной фиксированной позе или крайнему углу сустава
- Произвольная активность в отдаленных группах мышц не приводит к непроизвольным движениям вокруг жестких суставов, хотя ригидность может ухудшиться.
«Базальные ганглии» относятся к группе подкорковых ядер, отвечающих в первую очередь за моторный контроль, а также за другие роли, такие как моторное обучение, управляющие функции и поведение, а также эмоции. Классическая модель базальных ганглиев показывает, как информация течет через базальные ганглии обратно в кору по двум путям с противоположными эффектами для правильного выполнения движения.
Ригидность является результатом чрезмерного супраспинального возбуждения (облегчение верхних мотонейронов), действующего на альфа мотонейроны; механизмы спинномозгового рефлекса обычно в норме. [1] Нарушение нормального реципрокного торможения [4] . Когда баланс торможения и возбуждения в базальных ганглиях и моторной коре нарушается, появляются симптомы и признаки ригидности и непроизвольных движений наряду с аномалиями позы и связанными с ними движениями [2] . Однако наше нынешнее понимание патофизиологии базальных ганглиев не обеспечивает адекватного объяснения двух других кардинальных особенностей болезни Паркинсона, а именно ригидности и тремора [5] .
Несколько факторов могут повлиять на жесткость, некоторые из которых включают:
- Неспособность пациента расслабиться и полностью устранить активность в мышцах
- Повышенная жесткость из-за изменения вязкоупругих свойств мышц
- Аномальная совместная активация групп мышц-агонистов-антагонистов
- Повышение рефлексов растяжения
- снижение уровня дофамина
Ригидность болезни Паркинсона может быть охарактеризована как «свинцовая труба» или «зубчатое колесо».”
- Ригидность зубчатого колеса — относится к гипертоническому состоянию с наложенным трещоточным подергиванием и обычно наблюдается при движениях верхних конечностей (например, сгибание и разгибание запястья или локтя). Тип жесткости зубчатого колеса представляет собой сочетание жесткости ведущей трубы с тремором.
- Жесткость ведущей трубы — относится к гипертоническому состоянию во всем диапазоне движений, то есть одновременному сокращению агонистов и антагонистов, и это отражается в немедленном сопротивлении изменению направления движения вокруг сустава.
Разница между спастичностью и ригидностью [править | править источник]
Спастичность обычно возникает только во время растяжения мышц (т. Е. Не в состоянии покоя) и обычно сопровождается повышенными рефлексами сухожилий и реакцией Бабинского. Обычно существует разница между сопротивлением в одном направлении движения по сравнению с сопротивлением в противоположном направлении, и у некоторых пациентов может наблюдаться феномен застежки-ножа (внезапное высвобождение в конце диапазона движения).
При ригидности мышечный тонус повышается даже в состоянии покоя и обычно проявляется во время пассивного диапазона движений во всех направлениях отдельных суставов.Подошвенный рефлекс и рефлексы сухожилий обычно в норме. Нет синергии.
[6]
Эксперт должен держать руку патента выше запястья одной рукой и удерживать ее неподвижно. Другой рукой он захватывает пальцы и ладонь, а затем медленно вращает вдоль длинной оси руки. Если есть жесткость, экзаменующий будет испытывать сопротивление во время движения. Если явление зубчатого колеса положительное, экзаменатор будет испытывать прерывание или повторный захват во время движения, и если он присутствует на протяжении всего движения без каких-либо прерываний или изменений относительно скорости, это будет жесткость ведущей трубы. [2] Обычно при идиопатической болезни Паркинсона наблюдается односторонняя ригидность, которую можно сравнить во время обследования с противоположной стороной.
Медицинский менеджмент [править | править источник]
Лечение болезни Паркинсона левадопой (L-допа) в этих различных комбинациях чрезвычайно полезно для уменьшения брадикинезии и ригидности.
Было продемонстрировано, что стимуляция глубокого мозга в стимуляции Globus pallidus и стимуляция субталамического ядра улучшает ригидность [7]
Управление физиотерапией [править | править источник]
Для большинства пациентов лечение проходит лучше, если ригидность снижается в начале сеанса лечения.Таким образом, вмешательства в лечебной физкультуре, по-видимому, имеют более продолжительный эффект, когда лечение проводится во время «активной» фазы цикла приема лекарств. [8]
Методы релаксации, по-видимому, эффективны для снижения ригидности, включая плавное медленное покачивание, вращение конечностей и туловища, а также использование йоги. У пациентов с болезнью Паркинсона расслабление может быть лучше достигнуто в положении сидя или стоя, поскольку в положении лежа на спине может увеличиваться ригидность. Поскольку проксимальные мышцы часто задействованы в большей степени, чем дистальные, расслабление может быть легче достигнуть путем прогрессирования от дистального к проксимальному [8]
Показано, что ритмические упражнения снижают жесткость [8] Например.Хлопать в ладоши, делать круги руками или ногами.
Ритмическое начало и ритмическое вращение (проприоцептивное нервно-мышечное облегчение)
- ↑ 1.0 1.1 О’Салливан С.Б., Шмитц Т.Дж., Фулк Г. Физическая реабилитация. Ф.А. Дэвис; 2019 25 января.
- ↑ 2,0 2,1 2,2 Эдвардс С., редактор. Неврологическая физиотерапия: подход к решению проблем. Elsevier Health Sciences; 2002 г.
- ↑ Сэнгер Т.Д., Дельгадо М.Р., Геблер-Спира Д., Халлетт М., Норк Дж. У.Классификация и определение нарушений, вызывающих гипертонию в детском возрасте. Педиатрия. 1 января 2003 г .; 111 (1): e89-97.
- ↑ Электронная книга по физиотерапии Портера С. Тиди. Elsevier Health Sciences; 2013 17 января.
- ↑ Lanciego JL, Luquin N, Obeso JA. Функциональная нейроанатомия базальных ганглиев. Перспективы Колд-Спринг-Харбор в медицине. 2012 декабрь 1; 2 (12): a009621.
- ↑ Доктор Раджу. С. Кумар. Моделирование жесткости застежки ножа и зубчатого колеса. Доступно по адресу: https://www.youtube.com/watch?v=8xxe2WWWoYI [последний доступ 31.12.2020]
- ↑ Shapiro MB, Vaillancourt DE, Sturman MM, Metman LV, Bakay RA, Corcos DM.Влияние STN DBS на ригидность при болезни Паркинсона. IEEE Transactions по нейронным системам и реабилитационной инженерии. 18 июня 2007 г .; 15 (2): 173-81.
- ↑ 8,0 8,1 8,2 Umphred DA, Lazaro RT. Неврологическая реабилитация. Elsevier Health Sciences; 2012 14 августа.
Жесткость — Physiopedia
Ригидность, которую многие авторы часто используют как синоним гипертонии, является распространенным нарушением мышечного тонуса, при котором возникает сопротивление пассивному движению независимо от позы и скорости.Это одна из основных черт болезни Паркинсона, которая обычно присутствует при экстрапирамидных расстройствах. В равной степени действует как на агонисты, так и на антагонисты.
Его можно увидеть на —
Ригидность — это гипертоническое состояние, характеризующееся постоянным сопротивлением во всем диапазоне движений, которое не зависит от скорости движения. Это результат чрезмерного супраспинального возбуждения (облегчение верхних мотонейронов), действующего на альфа-мотонейроны; механизмы спинномозгового рефлекса обычно в норме. [1] При паркинсонической ригидности судороги в сухожилиях обычно нормальны [2]
«Ригидность» определяется как гипертонус, при котором выполняются все следующие условия [3] :
- Сопротивление внешнему движению сустава присутствует при очень низких скоростях движения, не зависит от заданной скорости и не имеет пороговых значений скорости или угла.
- Может происходить одновременное сокращение агонистов и антагонистов, что отражается в немедленном сопротивлении изменению направления движения вокруг сустава
- Конечность не стремится вернуться к определенной фиксированной позе или крайнему углу сустава
- Произвольная активность в отдаленных группах мышц не приводит к непроизвольным движениям вокруг жестких суставов, хотя ригидность может ухудшиться.
«Базальные ганглии» относятся к группе подкорковых ядер, отвечающих в первую очередь за моторный контроль, а также за другие роли, такие как моторное обучение, управляющие функции и поведение, а также эмоции. Классическая модель базальных ганглиев показывает, как информация течет через базальные ганглии обратно в кору по двум путям с противоположными эффектами для правильного выполнения движения.
Ригидность является результатом чрезмерного супраспинального возбуждения (облегчение верхних мотонейронов), действующего на альфа мотонейроны; механизмы спинномозгового рефлекса обычно в норме. [1] Нарушение нормального реципрокного торможения [4] . Когда баланс торможения и возбуждения в базальных ганглиях и моторной коре нарушается, появляются симптомы и признаки ригидности и непроизвольных движений наряду с аномалиями позы и связанными с ними движениями [2] . Однако наше нынешнее понимание патофизиологии базальных ганглиев не обеспечивает адекватного объяснения двух других кардинальных особенностей болезни Паркинсона, а именно ригидности и тремора [5] .
Несколько факторов могут повлиять на жесткость, некоторые из которых включают:
- Неспособность пациента расслабиться и полностью устранить активность в мышцах
- Повышенная жесткость из-за изменения вязкоупругих свойств мышц
- Аномальная совместная активация групп мышц-агонистов-антагонистов
- Повышение рефлексов растяжения
- снижение уровня дофамина
Ригидность болезни Паркинсона может быть охарактеризована как «свинцовая труба» или «зубчатое колесо».”
- Ригидность зубчатого колеса — относится к гипертоническому состоянию с наложенным трещоточным подергиванием и обычно наблюдается при движениях верхних конечностей (например, сгибание и разгибание запястья или локтя). Тип жесткости зубчатого колеса представляет собой сочетание жесткости ведущей трубы с тремором.
- Жесткость ведущей трубы — относится к гипертоническому состоянию во всем диапазоне движений, то есть одновременному сокращению агонистов и антагонистов, и это отражается в немедленном сопротивлении изменению направления движения вокруг сустава.
Разница между спастичностью и ригидностью [править | править источник]
Спастичность обычно возникает только во время растяжения мышц (т. Е. Не в состоянии покоя) и обычно сопровождается повышенными рефлексами сухожилий и реакцией Бабинского. Обычно существует разница между сопротивлением в одном направлении движения по сравнению с сопротивлением в противоположном направлении, и у некоторых пациентов может наблюдаться феномен застежки-ножа (внезапное высвобождение в конце диапазона движения).
При ригидности мышечный тонус повышается даже в состоянии покоя и обычно проявляется во время пассивного диапазона движений во всех направлениях отдельных суставов.Подошвенный рефлекс и рефлексы сухожилий обычно в норме. Нет синергии.
[6]
Эксперт должен держать руку патента выше запястья одной рукой и удерживать ее неподвижно. Другой рукой он захватывает пальцы и ладонь, а затем медленно вращает вдоль длинной оси руки. Если есть жесткость, экзаменующий будет испытывать сопротивление во время движения. Если явление зубчатого колеса положительное, экзаменатор будет испытывать прерывание или повторный захват во время движения, и если он присутствует на протяжении всего движения без каких-либо прерываний или изменений относительно скорости, это будет жесткость ведущей трубы. [2] Обычно при идиопатической болезни Паркинсона наблюдается односторонняя ригидность, которую можно сравнить во время обследования с противоположной стороной.
Медицинский менеджмент [править | править источник]
Лечение болезни Паркинсона левадопой (L-допа) в этих различных комбинациях чрезвычайно полезно для уменьшения брадикинезии и ригидности.
Было продемонстрировано, что стимуляция глубокого мозга в стимуляции Globus pallidus и стимуляция субталамического ядра улучшает ригидность [7]
Управление физиотерапией [править | править источник]
Для большинства пациентов лечение проходит лучше, если ригидность снижается в начале сеанса лечения.Таким образом, вмешательства в лечебной физкультуре, по-видимому, имеют более продолжительный эффект, когда лечение проводится во время «активной» фазы цикла приема лекарств. [8]
Методы релаксации, по-видимому, эффективны для снижения ригидности, включая плавное медленное покачивание, вращение конечностей и туловища, а также использование йоги. У пациентов с болезнью Паркинсона расслабление может быть лучше достигнуто в положении сидя или стоя, поскольку в положении лежа на спине может увеличиваться ригидность. Поскольку проксимальные мышцы часто задействованы в большей степени, чем дистальные, расслабление может быть легче достигнуть путем прогрессирования от дистального к проксимальному [8]
Показано, что ритмические упражнения снижают жесткость [8] Например.Хлопать в ладоши, делать круги руками или ногами.
Ритмическое начало и ритмическое вращение (проприоцептивное нервно-мышечное облегчение)
- ↑ 1.0 1.1 О’Салливан С.Б., Шмитц Т.Дж., Фулк Г. Физическая реабилитация. Ф.А. Дэвис; 2019 25 января.
- ↑ 2,0 2,1 2,2 Эдвардс С., редактор. Неврологическая физиотерапия: подход к решению проблем. Elsevier Health Sciences; 2002 г.
- ↑ Сэнгер Т.Д., Дельгадо М.Р., Геблер-Спира Д., Халлетт М., Норк Дж. У.Классификация и определение нарушений, вызывающих гипертонию в детском возрасте. Педиатрия. 1 января 2003 г .; 111 (1): e89-97.
- ↑ Электронная книга по физиотерапии Портера С. Тиди. Elsevier Health Sciences; 2013 17 января.
- ↑ Lanciego JL, Luquin N, Obeso JA. Функциональная нейроанатомия базальных ганглиев. Перспективы Колд-Спринг-Харбор в медицине. 2012 декабрь 1; 2 (12): a009621.
- ↑ Доктор Раджу. С. Кумар. Моделирование жесткости застежки ножа и зубчатого колеса. Доступно по адресу: https://www.youtube.com/watch?v=8xxe2WWWoYI [последний доступ 31.12.2020]
- ↑ Shapiro MB, Vaillancourt DE, Sturman MM, Metman LV, Bakay RA, Corcos DM.Влияние STN DBS на ригидность при болезни Паркинсона. IEEE Transactions по нейронным системам и реабилитационной инженерии. 18 июня 2007 г .; 15 (2): 173-81.
- ↑ 8,0 8,1 8,2 Umphred DA, Lazaro RT. Неврологическая реабилитация. Elsevier Health Sciences; 2012 14 августа.
Жесткость — Physiopedia
Ригидность, которую многие авторы часто используют как синоним гипертонии, является распространенным нарушением мышечного тонуса, при котором возникает сопротивление пассивному движению независимо от позы и скорости.Это одна из основных черт болезни Паркинсона, которая обычно присутствует при экстрапирамидных расстройствах. В равной степени действует как на агонисты, так и на антагонисты.
Его можно увидеть на —
Ригидность — это гипертоническое состояние, характеризующееся постоянным сопротивлением во всем диапазоне движений, которое не зависит от скорости движения. Это результат чрезмерного супраспинального возбуждения (облегчение верхних мотонейронов), действующего на альфа-мотонейроны; механизмы спинномозгового рефлекса обычно в норме. [1] При паркинсонической ригидности судороги в сухожилиях обычно нормальны [2]
«Ригидность» определяется как гипертонус, при котором выполняются все следующие условия [3] :
- Сопротивление внешнему движению сустава присутствует при очень низких скоростях движения, не зависит от заданной скорости и не имеет пороговых значений скорости или угла.
- Может происходить одновременное сокращение агонистов и антагонистов, что отражается в немедленном сопротивлении изменению направления движения вокруг сустава
- Конечность не стремится вернуться к определенной фиксированной позе или крайнему углу сустава
- Произвольная активность в отдаленных группах мышц не приводит к непроизвольным движениям вокруг жестких суставов, хотя ригидность может ухудшиться.
«Базальные ганглии» относятся к группе подкорковых ядер, отвечающих в первую очередь за моторный контроль, а также за другие роли, такие как моторное обучение, управляющие функции и поведение, а также эмоции. Классическая модель базальных ганглиев показывает, как информация течет через базальные ганглии обратно в кору по двум путям с противоположными эффектами для правильного выполнения движения.
Ригидность является результатом чрезмерного супраспинального возбуждения (облегчение верхних мотонейронов), действующего на альфа мотонейроны; механизмы спинномозгового рефлекса обычно в норме. [1] Нарушение нормального реципрокного торможения [4] . Когда баланс торможения и возбуждения в базальных ганглиях и моторной коре нарушается, появляются симптомы и признаки ригидности и непроизвольных движений наряду с аномалиями позы и связанными с ними движениями [2] . Однако наше нынешнее понимание патофизиологии базальных ганглиев не обеспечивает адекватного объяснения двух других кардинальных особенностей болезни Паркинсона, а именно ригидности и тремора [5] .
Несколько факторов могут повлиять на жесткость, некоторые из которых включают:
- Неспособность пациента расслабиться и полностью устранить активность в мышцах
- Повышенная жесткость из-за изменения вязкоупругих свойств мышц
- Аномальная совместная активация групп мышц-агонистов-антагонистов
- Повышение рефлексов растяжения
- снижение уровня дофамина
Ригидность болезни Паркинсона может быть охарактеризована как «свинцовая труба» или «зубчатое колесо».”
- Ригидность зубчатого колеса — относится к гипертоническому состоянию с наложенным трещоточным подергиванием и обычно наблюдается при движениях верхних конечностей (например, сгибание и разгибание запястья или локтя). Тип жесткости зубчатого колеса представляет собой сочетание жесткости ведущей трубы с тремором.
- Жесткость ведущей трубы — относится к гипертоническому состоянию во всем диапазоне движений, то есть одновременному сокращению агонистов и антагонистов, и это отражается в немедленном сопротивлении изменению направления движения вокруг сустава.
Разница между спастичностью и ригидностью [править | править источник]
Спастичность обычно возникает только во время растяжения мышц (т. Е. Не в состоянии покоя) и обычно сопровождается повышенными рефлексами сухожилий и реакцией Бабинского. Обычно существует разница между сопротивлением в одном направлении движения по сравнению с сопротивлением в противоположном направлении, и у некоторых пациентов может наблюдаться феномен застежки-ножа (внезапное высвобождение в конце диапазона движения).
При ригидности мышечный тонус повышается даже в состоянии покоя и обычно проявляется во время пассивного диапазона движений во всех направлениях отдельных суставов.Подошвенный рефлекс и рефлексы сухожилий обычно в норме. Нет синергии.
[6]
Эксперт должен держать руку патента выше запястья одной рукой и удерживать ее неподвижно. Другой рукой он захватывает пальцы и ладонь, а затем медленно вращает вдоль длинной оси руки. Если есть жесткость, экзаменующий будет испытывать сопротивление во время движения. Если явление зубчатого колеса положительное, экзаменатор будет испытывать прерывание или повторный захват во время движения, и если он присутствует на протяжении всего движения без каких-либо прерываний или изменений относительно скорости, это будет жесткость ведущей трубы. [2] Обычно при идиопатической болезни Паркинсона наблюдается односторонняя ригидность, которую можно сравнить во время обследования с противоположной стороной.
Медицинский менеджмент [править | править источник]
Лечение болезни Паркинсона левадопой (L-допа) в этих различных комбинациях чрезвычайно полезно для уменьшения брадикинезии и ригидности.
Было продемонстрировано, что стимуляция глубокого мозга в стимуляции Globus pallidus и стимуляция субталамического ядра улучшает ригидность [7]
Управление физиотерапией [править | править источник]
Для большинства пациентов лечение проходит лучше, если ригидность снижается в начале сеанса лечения.Таким образом, вмешательства в лечебной физкультуре, по-видимому, имеют более продолжительный эффект, когда лечение проводится во время «активной» фазы цикла приема лекарств. [8]
Методы релаксации, по-видимому, эффективны для снижения ригидности, включая плавное медленное покачивание, вращение конечностей и туловища, а также использование йоги. У пациентов с болезнью Паркинсона расслабление может быть лучше достигнуто в положении сидя или стоя, поскольку в положении лежа на спине может увеличиваться ригидность. Поскольку проксимальные мышцы часто задействованы в большей степени, чем дистальные, расслабление может быть легче достигнуть путем прогрессирования от дистального к проксимальному [8]
Показано, что ритмические упражнения снижают жесткость [8] Например.Хлопать в ладоши, делать круги руками или ногами.
Ритмическое начало и ритмическое вращение (проприоцептивное нервно-мышечное облегчение)
- ↑ 1.0 1.1 О’Салливан С.Б., Шмитц Т.Дж., Фулк Г. Физическая реабилитация. Ф.А. Дэвис; 2019 25 января.
- ↑ 2,0 2,1 2,2 Эдвардс С., редактор. Неврологическая физиотерапия: подход к решению проблем. Elsevier Health Sciences; 2002 г.
- ↑ Сэнгер Т.Д., Дельгадо М.Р., Геблер-Спира Д., Халлетт М., Норк Дж. У.Классификация и определение нарушений, вызывающих гипертонию в детском возрасте. Педиатрия. 1 января 2003 г .; 111 (1): e89-97.
- ↑ Электронная книга по физиотерапии Портера С. Тиди. Elsevier Health Sciences; 2013 17 января.
- ↑ Lanciego JL, Luquin N, Obeso JA. Функциональная нейроанатомия базальных ганглиев. Перспективы Колд-Спринг-Харбор в медицине. 2012 декабрь 1; 2 (12): a009621.
- ↑ Доктор Раджу. С. Кумар. Моделирование жесткости застежки ножа и зубчатого колеса. Доступно по адресу: https://www.youtube.com/watch?v=8xxe2WWWoYI [последний доступ 31.12.2020]
- ↑ Shapiro MB, Vaillancourt DE, Sturman MM, Metman LV, Bakay RA, Corcos DM.Влияние STN DBS на ригидность при болезни Паркинсона. IEEE Transactions по нейронным системам и реабилитационной инженерии. 18 июня 2007 г .; 15 (2): 173-81.
- ↑ 8,0 8,1 8,2 Umphred DA, Lazaro RT. Неврологическая реабилитация. Elsevier Health Sciences; 2012 14 августа.
Ригидность и болезнь Паркинсона: виды, лечение и многое другое
Болезнь Паркинсона — это заболевание центральной нервной системы, которое со временем ухудшается и не поддается лечению.Поскольку он воздействует на нервную систему, он затрудняет движение.
Ригидность — один из основных симптомов болезни Паркинсона, характеризующийся ригидностью мышц. Хотя степень тяжести варьируется, существуют варианты лечения, которые могут снизить интенсивность и замедлить прогрессирование ригидности.
О болезни Паркинсона
Симптомы болезни Паркинсона. Симптомы могут различаться у разных людей и могут оставаться незамеченными на ранних этапах развития.Они обычно начинаются и усиливаются на одной стороне тела. Обе стороны в конечном итоге страдают болезнью Паркинсона.
Общие симптомы болезни Паркинсона включают:
- Тремор и дрожь
- Брадикинезия или замедленное движение
- Жесткость мышц
- Потеря равновесия и координации
- Дистония или мышечные спазмы и судороги
- Сгорбленная осанка
As симптомы ухудшаются, развиваются вторичные симптомы из-за потери моторного контроля.Некоторые из симптомов включают:
- Утрата мимики
- Изменения голоса
- Изменения почерка
- Беспокойство и депрессия
- Проблемы с жеванием, глотанием и приемом пищи
- Затруднение при мочеиспускании
- Нарушения сна, такие как беспокойная нога синдром
Причины болезни Паркинсона. Болезнь Паркинсона вызывает разрушение определенных нервных клеток в головном мозге. Потеря нервных клеток или нейронов приводит к нерегулярной мозговой деятельности и нарушению двигательной функции.
Неизвестно, что именно вызывает болезнь Паркинсона. Хотя определенные генетические вариации могут привести к болезни Паркинсона, они встречаются редко. Нет конкретного способа предотвратить развитие болезни Паркинсона.
Взрослые мужчины в возрасте 60 лет и старше более подвержены риску развития болезни Паркинсона. Если у вас много членов семьи с болезнью Паркинсона, вы можете подвергаться более высокому риску.
Диагностика болезни Паркинсона . Болезнь Паркинсона сложно диагностировать.Нет тестов, которые это обнаруживают. Ваш врач или невролог поставит диагноз на основании ваших симптомов и истории болезни.
Лечение болезни Паркинсона. Нет лекарства. Для лечения симптомов используются лекарства, изменение образа жизни и физиотерапия.
Ригидность мышц: ригидность ведущей трубы и зубчатого колеса
Ригидность мышц из-за болезни Паркинсона можно ошибочно принять за артрит или общую стесненность в результате старения. Жесткость может повлиять на ваши ноги, руки, туловище и лицо.
Какая жесткость ощущается. Ваши мышцы могут ощущаться напряженными и вам трудно двигаться. Они также могут непроизвольно напрягаться, как мышечный спазм. Эта жесткость также может вызывать боль в суставах и мышцах.
Жесткость и повседневная жизнь. Этот тип жесткости может начать влиять на ваши нормальные функции. Простые задачи, такие как уборка, упражнения и выполнение хобби, могут стать трудными из-за жесткости. Вы также можете испытывать:
- Скованность в лицевых мышцах, которая затрудняет самовыражение
- Скованность во время сна, из-за которой трудно уснуть и хорошо уснуть
- Постоянное напряжение в мышцах, которое приводит к мышечной усталости и недостатку энергии
- Затруднения с определенными двигательными навыками, такими как письмо или одевание
- Скованность в руках, затрудняющая удержание равновесия при ходьбе
Жесткость свинцовой трубы. Этот тип скованности характеризуется ощущением замороженных мышц. Кажется, что мышцы застряли и не могут двигаться.
Попытки пошевелить конечностями наталкиваются на сопротивление на протяжении всего движения. Они длительное время кажутся жесткими и тяжелыми, как «свинцовая труба».
Жесткость зубчатого колеса. Этот тип жесткости похож на мышечные спазмы. Конечности, испытывающие скованность, могут двигаться небольшими рывками, как храповик. Вы можете даже почувствовать небольшие щелчки при движении руки.
Подергивание может происходить независимо от того, насколько медленно или быстро вы двигаетесь. Жесткость зубчатого колеса может сделать перемещение рискованным. Например, попытка приготовить пищу или работать с оборудованием в условиях жесткости зубчатого колеса может привести к опасным неудачам.
Управление и лечение ригидности
Ваш врач диагностирует ригидность, демонстрируя вам различные двигательные функции, такие как разгибание суставов и сгибание мышц.
Варианты лечения болезни Паркинсона помогают снизить ригидность.Но если вы рано заметили ригидность и хотите избежать дискомфорта в будущем, есть варианты лечения.
Упражнение. В частности, упражнения, направленные на гибкость и растяжку мышц. Рекомендуется выполнять растяжку хотя бы раз в день. Вы можете сделать это, выполняя упражнения на растяжку или используя такие программы, как йога.
Может быть трудно начать тренировку, когда мышцы напряжены. Это может усугубить и ухудшить ваше самочувствие из-за того, что вы не занимаетесь спортом.Разорвите этот круговорот, сделайте первый шаг и работайте над своим общим здоровьем.
Замачивает. Теплые ванны с английской солью помогают расслабить мышцы. Это может обеспечить мгновенное облегчение жесткости мышц и продлить их эффективность.
Физиотерапия. Физическая терапия может помочь снизить ригидность и уменьшить скованность. Это также может помочь вам найти распорядок дня и упражнения, которые вам подходят. Речевую терапию можно использовать для лечения ригидности мышц лица.
Лекарства .Ваш врач может порекомендовать лекарства, которые помогут уменьшить жесткость мышц. Многие лекарства можно использовать для лечения болезни Паркинсона. Ваш врач вместе с вами разработает план лечения.
Как проверить ригидность и спастичность?
Mov Disord Clin Pract. 2015 июн; 2 (2): 204.
, МБ MRCPI, 1 , МБ, 1 и, МБ FRCPI 1Конор Фирон
1 Дублинский неврологический институт при университетской больнице Mater Misericordiae, Дублин, Ирландия,
Лаура Доэрти
1 Дублинский неврологический институт при университетской больнице Mater Misericordiae, Дублин, Ирландия,
Тим Линч
1 Дублинский неврологический институт при университетской больнице Mater Misericordiae, Дублин, Ирландия,
1 Дублинский неврологический институт при университетской больнице Mater Misericordiae, Дублин, Ирландия,
Автор, ответственный за переписку. * Для корреспонденции: Доктору Конору Фирону, Дублинский неврологический институт, 57 Eccles Street, Dublin 7, Ирландия; Электронная почта: [email protected]Получено 8 декабря 2014 г .; Принято 15 декабря 2014 г.
Copyright © 2015 International Parkinson and Movement Disorder Society- Дополнительные материалы
Видео, сопровождающее эту статью, доступно во вспомогательной информации здесь.
Видео. В этом видео описывается подход к обследованию пациентов с ригидностью и спастичностью.
GUID: A8021413-016B-43AA-84EB-32646C43E74C
Abstract
Исследование тона (повышенное сопротивление пассивному движению сустава) является клинически полезной и иногда игнорируемой частью неврологического обследования. Ригидность и спастичность — это два разных типа гипертонуса, которые возникают из-за разных анатомических путей. Таким образом, способность различать эти две сущности дает важную информацию о локализации.В то время как спастичность возникает в результате повреждения кортикоретикулоспинальных (пирамидных) трактов, ригидность вызвана дисфункцией экстрапирамидных путей, чаще всего базальных ганглиев, но также в результате поражения среднего и спинного мозга. Спастичность характеризуется аномально высоким мышечным тонусом, который часто асимметрично влияет на антагонистические группы мышц. Он зависит как от амплитуды, так и от скорости, и поэтому лучше всего оценивается с помощью быстрых движений соответствующего сустава, чтобы вызвать резкое растяжение задействованной группы мышц.Когда достигается пороговая скорость, угол или амплитуда, резкое усиление тона может быть обнаружено как характерный «улов». Ригидность отличается от спастичности тем, что повышенный тонус остается постоянным во всем диапазоне движений сустава. Он не зависит от скорости и должен быть обнаружен даже при очень медленных движениях. Он в равной степени присутствует в группах мышц-сгибателей и разгибателей, обеспечивая однородность во всех направлениях, часто описываемую как жесткость «свинцовой трубы». Учитывая, что ригидность часто возникает при заболеваниях базальных ганглиев, тремор может сосуществовать, вызывая прерывистый эффект «зубчатого колеса».Здесь мы описываем подход к обследованию пациентов с ригидностью и спастичностью.
Ключевые слова: Ригидность, спастичность
Роли авторов
(1) Исследовательский проект: A. Концепция, B. Организация, C. Выполнение; (2) Статистический анализ: A. Дизайн, B. Выполнение, C. Обзор и критика; (3) Рукопись: A. Написание первого варианта, B. Обзор и критика.
C.F .: 1A, 1B, 1C, 3A
L.D .: 1A, 1B, 1C, 3B
T.L .: 1A, 1B, 1C, 3B
Раскрытие информации
Источники финансирования и конфликт интересов: Авторы не сообщают об источниках финансирования и конфликте интересов.
Раскрытие финансовой информации за предыдущие 12 месяцев: Авторы заявляют, что они не раскрывают информацию, о которой нужно сообщить.
Вспомогательная информация
Видео, сопровождающее эту статью, доступно во вспомогательной информации здесь.
Видео. В этом видео описывается подход к обследованию пациентов с ригидностью и спастичностью.
Примечания
Соответствующая информация и конфликты интересов перечислены в конце этой статьи.
Подход минимальной длины объединяет жесткость в недостаточно жестких материалах
Значение
Что общего у гитарной струны и воздушного шара? Оба они гибкие, если не связаны геометрической несовместимостью. Такой же вид перехода жесткости в недостаточно ограниченных материалах недавно обсуждался в контексте неупорядоченных биополимерных сетей и моделей биологических тканей. Здесь мы предлагаем общий подход к количественному описанию таких переходов.На основе функции минимальной длины, которая линейно масштабируется с собственными колебаниями в системе и квадратично с деформацией сдвига, мы делаем конкретные прогнозы относительно упругого отклика этих материалов, которые мы проверяем численно и которые согласуются с предыдущими экспериментами. Наконец, наш подход может помочь разработать методы, связывающие макроскопические упругие свойства неупорядоченных материалов с их микроскопической структурой.
Abstract
Мы представляем подход к пониманию жесткости, вызванной геометрической несовместимостью, в недостаточно ограниченных материалах, включая субизостатические 2D пружинные сети и 2D и 3D модели вершин для плотных биологических тканей.Мы показываем, что во всех этих моделях геометрический критерий, представленный минимальной длиной ℓ¯min, определяет возникновение предварительных напряжений и жесткости. Это позволяет нам предсказать не только правильные масштабные значения для свойств упругого материала, но также и точные значения модуля объемной упругости и неоднородности модуля сдвига при переходе жесткости, а также величину эффекта Пойнтинга. Мы также предсказываем, исходя из первых принципов, что отношение избыточного модуля сдвига к напряжению сдвига должно быть обратно пропорционально критической деформации с предварительным коэффициентом 3.Мы предполагаем, что этот коэффициент 3 является общим признаком геометрически индуцированной жесткости в недостаточно ограниченных материалах и может использоваться, чтобы отличить этот эффект от нелинейной механики отдельных компонентов в экспериментах. Наконец, наши результаты могут заложить важную основу для способов оценки ℓ¯min из измерений локальной геометрической структуры и, таким образом, помочь в разработке методов для характеристики крупномасштабных механических свойств по данным изображений.
Жесткость материала напрямую зависит от его геометрии.В кристаллизующихся материалах жесткость возникает, когда составные части образуют решетку. Напротив, гранулированные системы могут затвердеть, оставаясь неупорядоченными, и аргументы, разработанные Максвеллом (1), точно предсказывают, что материал затвердевает в изостатической точке, где количество ограничений на движение частицы равно количеству степеней свободы.
Дальнейшая работа Калладина (2) подчеркнула важную роль состояний самонапряжения, продемонстрировав, что теорема об индексе связывает жесткость с общим количеством ограничений, степеней свободы и самонапряжений.Недавняя работа расширила эти идеи как для упорядоченных, так и для неупорядоченных систем, чтобы разработать материалы с геометрией, которая допускает топологически защищенные гибкие режимы (3-5).
Третий способ придания жесткости — геометрическая несовместимость, которую мы проиллюстрируем на гитарной струне. Перед тем, как натянуть струну, гибкая струна недостаточно натянута, с меньшим количеством ограничений, чем степеней свободы, и есть много способов деформировать струну без каких-либо энергетических затрат. Поскольку расстояние между двумя концами увеличивается по сравнению с остальной длиной струны, эта геометрическая несовместимость вместе с сопутствующим возникновением самонапряжения делает систему жесткой (3, 6).Любая деформация будет связана с энергетическими затратами, что приведет к конечным частотам колебаний. Было высказано предположение, что этот же механизм важен для эластичности каучуков и гелей (6), а также биологических клеток (7).
В частности, было показано, что он укрепляет недостаточно жесткие, неупорядоченные волоконно-оптические сети под действием приложенной деформации, с применением в биополимерных сетях (8⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓ – 22). Как и в случае с гитарной струной, жесткость возникает, когда размер и форма коробки вводят внешние ограничения, несовместимые с локальными сегментами сети, достигающими желаемой длины покоя.Например, при приложении внешнего сдвига волоконная сеть сильно затвердевает при некоторой критической деформации сдвига γ * (9, 14, 16, 18⇓ – 20, 22, 23), хотя остается спорным вопрос о том, является ли начало жесткости непрерывным (14, 15, 20, 24) или прерывистым (18) в пределе без жесткости волокна на изгиб. Точно так же волоконная сеть также может быть усилена изотропным растяжением (10), а взаимодействие между изотропной упругостью и упругостью сдвига в этих системах характеризуется аномальным отрицательным эффектом Пойнтинга (19, 21, 25–27), т.е.е. развитие нормального растягивающего напряжения в ответ на приложенный извне простой сдвиг. Однако до сих пор остается неясным, как все эти наблюдения и их критическое масштабное поведение (9, 16, 18, 20, 28) количественно связаны с основной геометрической структурой сети. Более того, хотя в предыдущих работах отмечалось, что некоторые особенности повышения жесткости в волоконных сетях на удивление не зависят от деталей модели (13), остается неясным, существуют ли общие механизмы, лежащие в основе.
Переходы жесткости обнаружены также в плотных биологических тканях (29⇓⇓⇓ – 33). В частности, вершинные модели или модели Вороного, которые описывают ткани как мозаику пространства в многоугольники или многогранники, демонстрируют переходы жесткости (34⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓ – 49), которые имеют общие черты с обоими, основанными на частицах. модели, в которых переход вызван изменениями в связности (48), и оптоволоконными (или пружинными) сетями, которые могут стать жесткими из-за деформации. Таким образом, остается открытым вопрос, как и связность, и деформация могут взаимодействовать для придания жесткости материалам (22).
Совсем недавно некоторые из нас показали, что трехмерная модель Вороного демонстрирует переход жесткости, обусловленный геометрической несовместимостью (46), аналогично волоконным сетям. Это также было продемонстрировано для 2D-вершинной модели с использованием подхода континуальной эластичности, основанного на локальной эталонной метрике (42). Для случая трехмерной модели Вороного мы обнаружили, что существует особая связь между свойствами геометрии сети и местом перехода жесткости, в значительной степени не зависящая от реализации беспорядка (46).
Здесь мы показываем, что такая взаимосвязь между жесткостью и геометрической структурой характерна для широкого класса недостаточно ограниченных материалов, включая пружинные сети и модели вершин / Вороного в различных измерениях (Таблица 1 и Рис. 1). Сначала мы продемонстрируем, что все эти модели демонстрируют одно и то же общее поведение в ответ на изотропное расширение. Понимание ключевых геометрических структурных свойств этих систем позволяет нам предсказать точные значения неоднородности модуля объемной упругости в точке перехода.Затем мы расширили наш подход, включив в него деформации сдвига, что позволяет аналитически прогнозировать скачок модуля сдвига в начале жесткости. Более того, мы можем сделать точные количественные прогнозы значений критической деформации сдвига γ *, масштабного поведения модуля сдвига за пределами γ *, эффекта Пойнтинга и нескольких связанных критических показателей. В каждом случае мы численно демонстрируем применимость нашего подхода для случая пружинных сетей.
Таблица 1.Модели, рассматриваемые в этой статье
Рис.1.Сравнение перехода жесткости в разных моделях. Изучаемые модели: ( A и B ) 2D пружинные сети (координационные числа z = 3,2,3,4,3,6,3,8,3,99), ( C и D ) 2D модель Вороного (с kA = 0) , и 2D-модель вершины (с kA = 0 в C и kA = 0,0.1,1,10 в D ), и ( E и F ) 3D-модель Вороного (с kV = 0 в E и kV = 0,1,10,100 в F ). Во всех моделях переход является прерывистым по модулю объемной упругости ( A , C и E ) и непрерывным по модулю сдвига ( B , D и F ).( B , Inset ) Для двухмерных пружинных сетей значение точки перехода ℓ0 * (определенное количественно с использованием протокола деления пополам, подробно описанного в SI Приложение , раздел IVB) увеличивается с координационным числом z. Эта зависимость приблизительно линейна в окрестности изостатической точки zcÀ4. Синие кружки — данные моделирования, а красная линия показывает линейную аппроксимацию с ℓ0 * = (1,506 ± 0,004) — (0,378 ± 0,009) Δz при Δz = zc − z. Ближе к точке перехода в C и E точки данных разбросаны между нулем и максимальным значением.Это рассеяние связано с недостаточной минимизацией энергии в этих случаях. В B , D и F заштрихованные области обозначают SEM.
Мы также сравниваем наши прогнозы с ранее опубликованными экспериментальными данными и выделяем дополнительные прогнозы, в том числе предварительный коэффициент 3, который мы ожидаем найти в целом в масштабном коллапсе модуля сдвига, напряжения сдвига и критической деформации.
Мы достигаем этих результатов, связывая макроскопические механические свойства сети с лежащими в основе геометрическими свойствами.В случае гитарной струны струна сначала натягивается, когда расстояние между двумя концами достигает критического значения ℓ0 *, равного внутренней длине струны, так что граничные условия для струны геометрически несовместимы с внутренней геометрией. строки. Когда струна растягивается, можно предсказать ее шаг (или, что эквивалентно, эффективный модуль упругости), определив фактическую длину струны ℓ относительно ее внутренней длины. Хотя это просто в одномерной геометрии струны, мы заинтересованы в понимании того, регулирует ли аналогичный геометрический принцип, основанный на средней длине пружины ¯, поведение вблизи начала жесткости в неупорядоченных сетях в 2D и 3D.
Здесь мы формулируем критерий геометрической совместимости в терминах ограниченной минимизации средней длины пружины ℓ¯min в неупорядоченной сети. Как и для гитарной струны, эта длина ℓ¯min достигает критического значения ℓ0 * в начале жесткости. Поскольку система деформирована за пределами перехода жесткости, мы демонстрируем аналитически и численно, что геометрия ограничивает ℓ¯min простым изменением с двумя наблюдаемыми: колебаниями длины пружины σℓ и деформацией сдвига γ.Поскольку ¯min минимизируется по всей сети, это коллективное геометрическое свойство сети.
Так же, как и в случае гитарной струны, описание геометрии, заданное параметром ℓ¯min, позволяет нам вычислить многие характеристики упругого отклика, включая объемные модули и модули сдвига. Это, в свою очередь, обеспечивает общую основу для аналитического понимания реакции жесткости недоограниченных материалов как на изотропную, так и на анизотропную деформацию в рамках общей структуры.Несмотря на то, что ℓ¯min описывает коллективные геометрические эффекты, наша работа может также обеспечить важную основу для понимания макроскопических механических свойств из локальной геометрической структуры.
Модели
Здесь мы сосредоточимся на четырех классах моделей, которые включают двумерные субизостатические случайные пружинные сети без жесткости на изгиб (9, 50⇓⇓⇓ – 54) и три модели для биологических тканей: двумерную вершинную модель (34, 37) , 2D-модель Вороного (38, 44) и 3D-модель Вороного (46) (таблица 1).
Двумерные пружинные сети состоят из узлов, которые соединены в общей сложности N пружинами, где среднее количество пружин, подключенных к узлу, является координационным числом z.Мы создаем сети с определенным значением z, переводя заклинившие конфигурации двухдисперсных дисков в пружинные сети, а затем произвольно сокращая пружины до тех пор, пока не будет достигнуто желаемое координационное число z (9, 27). Мы используем гармонические пружины, так что полная механическая энергия системы равна es2D = ∑i (li − l0i) 2. [1] Здесь сумма ведется по всем пружинам i с длиной li и длиной покоя l0i, которые, как правило, различны для разные пружины. Для удобства мы повторно выражаем уравнение. 1 в терминах средней длины опоры пружины ℓ0 = [(∑il0i2) / N] 1/2, которую мы используем в качестве управляющего параметра, действующего как общий коэффициент масштабирования для всех длин опоры пружины.Это позволяет нам переписать энергию ases2D = ∑iwi (ℓi − ℓ0) 2 [2] с измененной длиной пружины ℓi = ℓ0li / l0i и весами wi = (l0i / ℓ0) 2, так что ∑i wi = N (подробнее , см. SI Приложение , раздел IA). В простых аргументах с подсчетом ограничений каждая пружина рассматривается как одно ограничение, и здесь нас интересуют субизостатические (т. Е. Недостаточно ограниченные, также называемые гипостатическими) сети с z Модели тканей описывают биологические ткани как полигональные (2D) или многогранные (3D) фрагменты пространства.Для моделей Вороного эти мозаики являются мозаиками Вороного, а степени свободы — центрами Вороного ячеек. Напротив, в 2D-модели вершин степенями свободы являются положения вершин (т. Е. Углов многоугольника). Силы между клетками описываются функционалом эффективной энергии. Для 2D-моделей (безразмерный) функционал энергии isec2D = ∑i (pi − p0) 2 + kA (ai − 1) 2. [3] Здесь сумма идет по всем N ячейкам i с периметром pi и площадью ai. В этой модели есть два параметра: предпочтительный периметр p0 и относительная упругость по площади kA.Для трехмерной модели Вороного энергия определяется аналогично: ec3D = ∑i (si − s0) 2 + kV (vi − 1) 2. [4] Сумма опять же по всем N ячейкам i конфигурации с поверхностью ячеек. площадь si и объем vi, а двумя параметрами модели являются предпочтительная площадь поверхности s0 и относительная объемная упругость kV. Все четыре из этих моделей имеют недостаточные ограничения на основе простого подсчета ограничений, как видно из соответствующих чисел степеней свободы и ограничений, перечисленных в таблице 1. Мы подчеркиваем, что вывод Калладина с подсчетом ограничений (2, 3) также применим ко многим -частичные, нецентрально-силовые взаимодействия. В этой статье мы часто обсуждаем сразу все четыре модели. Таким образом, когда мы обычно говорим об «элементах», мы имеем в виду пружины в пружинных сетях и клетки в моделях тканей. Точно так же, говоря о «длинах» (размерности d), мы имеем в виду длину пружин ℓ в пружинных сетях, периметры клеток p в 2D-моделях ткани и площади поверхности клеток s в 3D-модели ткани (Таблица 1). Наконец, когда мы говорим об «областях a» (размерности D), мы имеем в виду области клеток a в 2D-моделях ткани, а также объемы клеток v в 3D-модели ткани. Здесь мы исследуем поведение локальных минимумов энергии всех четырех моделей при периодических граничных условиях с фиксированным безразмерным размером системы N; т.е. модель обезразмерена так, что средняя площадь на элемент равна единице (41, 44, 46). В этих условиях переход жесткости существует во всех моделях даже без жесткости по площади. В частности, для двумерной вершинной и трехмерной моделей Вороного мы отдельно обсуждаем частный случай kA = 0 (таблица 1). Более того, атермическая 2D-модель Вороного не демонстрирует перехода жесткости при kA> 0 (44), поэтому мы обсуждаем только случай kA = 0 для этой модели. Мы начинаем со сравнения переходов жесткости в четырех различных моделях, используя рис. 1, где мы строим график зависимости дифференциального модуля объемной упругости B и дифференциального модуля сдвига G от предпочтительной длины ℓ0. В этой первой части мы используем для всех моделей предпочтительную длину ℓ0 в качестве управляющего параметра. Обратите внимание, что, поскольку ℓ0 обезразмеривается с использованием плотности числа элементов, изменение ℓ0 соответствует приложению изотропной деформации (т.е. изменение объема без сопутствующего изменения формы). Позже мы дополнительно включим деформацию сдвига γ в качестве управляющего параметра. Во всех моделях мы находим жесткий режим (B, G> 0) для предпочтительных длин ниже точки перехода ℓ0 * и гибкий режим (B = G = 0) над ней, причем переход является прерывистым по модулю объемной упругости. и непрерывна по модулю сдвига. Для пружинных сетей мы обнаруживаем, что точка перехода ℓ0 * зависит от координационного числа, где вблизи изостатической точки zc≡4 она линейно масштабируется с расстоянием Δz = zc − z до изостатичности (рис.1 B , Inset ), как ранее аналогичным образом обсуждалось в исх. 10. Нечто подобное также было описано для 2D вершинной модели (48). Для сотовых моделей мы находим, что точка перехода для случая без площадной жесткости, kA = 0, обычно меньше, чем в случае с площадной жесткостью, kA> 0 (рис. 1 D и F и Таблица 1). Более того, точка перехода нашей 2D-вершинной модели при kA> 0 несколько выше, чем сообщалось ранее (37). Здесь мы использовали другую реализацию вершинной модели, чем в исх.37 ( SI Приложение , раздел IVC), а расположение перехода в вершинных моделях в некоторой степени зависит от протокола минимизации энергии (44), что характерно для других моделей для неупорядоченных материалов (55). Кроме того, на рис. 1 D и F усредненный модуль сдвига всегда становится равным нулю при более высоком значении, чем соответствующая средняя точка перехода, указанная в таблице 1. Это связано с распределением точек перехода, имеющих конечную ширину (см. также конечная ширина областей ℓ0 как с нулевым, так и с ненулевым модулем объемного сжатия на рис.1 C и E ). Мы обнаружили, что во всех этих моделях механизм создания перехода один и тот же: жесткость создается геометрической несовместимостью, на которую указывает наличие предварительных напряжений. Мы уже показали это для 3D-модели Вороного (46) и 2D-модели Вороного с kA = 0 (44), в то время как другие показали это для упорядоченной 2D-вершинной модели (42). Кроме того, наши данные подтверждают, что это имеет место для двумерных пружинных сетей и случаев kA = 0 как (неупорядоченных) двумерных вершинных моделей, так и трехмерных моделей Вороного ( SI Приложение , раздел IIA). Нечто подобное мы находим для неупорядоченной 2D вершинной модели при kA> 0. Хотя есть особые случаи, когда предварительные напряжения появляются также в гибком режиме ( SI Приложение , раздел IIA), для упрощения нашего обсуждения здесь мы рассматриваем только конфигурации без таких обычно локализованных предварительных напряжений. Мы видим, что во всех этих моделях геометрический критерий, который мы описываем в терминах минимальной средней длины ℓ¯min, определяет возникновение предварительных напряжений. Например, мы можем точно преобразовать энергию пружинной сети Ур. 2 в ( SI Приложение , раздел IA) es2D = N (ℓ¯ − ℓ0) 2 + σℓ2. [5] Здесь ℓ¯ = (∑iwiℓi) / N и σℓ2 = (∑iwi (ℓi − ℓ ¯) 2) / N — средневзвешенные значения и SD измененных длин пружин. Это означает, что ℓ¯ и σℓ являются средними и SD фактических длин пружины li, каждая из которых измеряется относительно ее фактической длины покоя l0i. В частности, SD σℓ обращается в нуль, когда все пружины i имеют одинаковое значение доли li / l0i, даже если абсолютные длины li могут различаться для разных пружин. Более того, что важно, средняя длина покоя ℓ0 входит в определения ℓ¯ и σℓ, но только через отношения l0i / ℓ0, которые характеризуют распределение относительной длины пружины.Следовательно, «измененная» геометрическая информация, содержащаяся как в ℓ¯, так и в σℓ, представляет собой комбинацию фактических длин пружин и распределения относительной длины покоя, но не зависит от абсолютной средней длины покоя ℓ0. Согласно формуле. 5 , минимизация энергии соответствует одновременной минимизации по | ℓ¯ − ℓ0 | и σℓ: В режиме гибкого диска мы численно находим, что обе величины могут обращаться в нуль одновременно, и, таким образом, все длины достигают своих остаточных длин, i = ℓ0 ( SI Приложение , раздел IIA).Напротив, в жестком режиме | ℓ¯ − ℓ0 | и σℓ не могут одновременно обращаться в нуль, создавая напряжения 2 (ℓi − ℓ0), которых достаточно для придания жесткости сети. Точка перехода ℓ0 * соответствует наименьшей возможной предпочтительной длине пружины ℓ0, при которой система все еще может быть гибкой. Другими словами, это соответствует локальному минимуму в средней измененной длине пружины ℓ0 * = min ℓ¯ сети при ограничении отсутствия колебаний измененной длины, σℓ = 0. Поскольку эта минимизация относится ко всем позициям узлов и включает все пружины, она определяет распределение точек перехода ℓ0 * как коллективное свойство масштабированной геометрии 2D пружинных сетей. Для сотовых моделей с kA> 0 аналогично находим, что точка перехода задается минимальным периметром ячейки ℓ¯ (поверхность в 3D) при ограничении отсутствия периметра ячейки и флуктуаций площади σℓ = σa = 0, что теперь дополнительно появляются в уравнении энергии. 5 (46). Опять же, это геометрический критерий, который также объясняет, почему точка перехода ℓ0 * не зависит от kA при kA> 0 (рис. 1 D и F ). Более того, мы можем понять, почему точка перехода меньше при kA = 0: в этом случае энергия не ограничивает колебания площади, а точка перехода задается минимальным периметром при более слабом ограничении отсутствия флуктуаций периметра.Таким образом, точка перехода обычно будет меньше для случая kA = 0, чем для случая kA> 0. Далее мы исследуем масштабирование минимальной длины в жесткой окрестности перехода. В жестком режиме система должна искать компромисс между минимизацией | ℓ¯ − ℓ0 | и σℓ (и, если применимо, σa в клеточных моделях). Чтобы понять, как это сделать, мы должны учесть геометрические ограничения, которые мы выражаем в терминах того, как минимальная длина ℓ¯min = min ℓ¯ зависит от флуктуаций ℓ¯min = ℓ¯min (σℓ, σa).В жестком режиме наблюдаемая средняя длина всегда больше, чем предпочтительная длина, ℓ¯> ℓ0, и поэтому средняя длина вместо этого принимает свое локально минимальное возможное значение ℓ¯ = ℓ¯min (σℓ, σa). Следовательно, знание функциональной формы ¯min (σℓ, σa) позволит нам предсказать, как энергия системы e (и, следовательно, также объемный модуль и модули сдвига) зависят от управляющего параметра ℓ0 ( SI Приложение , разделы IC– IE). В SI Приложение , раздел IB, мы показываем аналитически, что при отсутствии предварительных напряжений в гибком режиме минимальная длина ℓ¯min линейно зависит от стандартных отклонений σℓ и σa.Это напрямую связано с состоянием самонапряжения, которое возникает в начале геометрической несовместимости при ℓ0 = ℓ0 * ≡ℓ¯min (0,0) (3). Чтобы проверить это предсказание, мы численно моделируем эти модели и действительно наблюдаем линейное масштабирование функций ¯min (σℓ) вблизи точки перехода (рис. 2). В частности, для двумерных пружинных сетей и случаев kA = 0 клеточных моделей мы находим ¯min (σℓ) = ℓ0 * −aℓσℓ [6] с масштабным коэффициентом aℓ. Мы перечисляем его значение в таблице 1 для различных моделей.Интересно, что мы обнаружили, что коэффициент aℓ в значительной степени не зависит от случайной реализации системы, в частности, для клеточных моделей с kA = 0. Проверка геометрической линейности вблизи точки перехода. Разница между средней длиной и точкой перехода, 0 * −ℓ¯, линейно масштабируется с SD длин σℓ и площадей σa. Здесь показаны ( A ) 2D пружинные сети, ( B ) 2D модели Вороного и вершинные модели и ( C ) 3D модель Вороного.Значения z, kA и kV соответствуют значениям на рис. 1. ( A, , , вставка ) Для 2D пружинных сетей коэффициент aℓ в формуле. 6 масштабируется с расстоянием до изостатичности приблизительно как aℓ∼Δz − 1/2. В A – C отклонения от линейности существуют для больших ℓ0 * −ℓ¯, поскольку уравнения 6 и 7 описывают поведение вблизи точки перехода, а отклонения для малых ℓ0 * −ℓ¯ обусловлены конечным отсечением модуля сдвига, используемым для получения значения точки перехода ℓ0 * ( SI Приложение , раздел IV). Для 2D пружинных сетей aℓ зависит от координационного числа z и приблизительно масштабируется как aℓ∼Δz − 1/2 (рис. 2 A , вставка ). Такое масштабное поведение aℓ можно рационализировать, используя аргумент масштабирования, основанный на плотности состояний ( SI Приложение , раздел IF). Для сотовых моделей, где площадь играет роль, уравнение. 6 расширен (рис. 2 B и C ): ℓ¯min (σℓ, σa) = ℓ0 * −aℓσℓ − aaσa. [7] Снова коэффициенты aℓ и aa перечислены в таблице 1 для 2D вершинные и 3D модели Вороного.Коэффициенты aℓ значительно различаются между случаями kA> 0 и kA = 0 одной и той же модели, что имеет смысл, поскольку уравнения 6 и 7 представляют собой линейные разложения функции ℓ¯min (σℓ, σa) в различных точках (σℓ, σa). Знание поведения функции минимальной длины ℓ¯min (σℓ, σa) в жесткой фазе вблизи точки перехода дает нам явное выражение для энергии через управляющий параметр ℓ0 ( SI Приложение , раздел IC), e (ℓ0) = NZ (ℓ0 * −ℓ0) 2 [8] с Z = 1 + aℓ2 + aa2 / kA, где для моделей без члена площади термин aa2 / kA опускается.Поскольку изменения ℓ0 соответствуют изменениям в размере системы, мы можем предсказать точное значение неоднородности объемного модуля упругости, ΔB, при переходе во всех моделях (Рис.1 A — C и SI Приложение , раздел IE ): ΔB = 2d2 (ℓ0 *) 2D2Z. [9] Это уравнение предназначено для модели с d-мерными «длинами», вложенными в D-мерное пространство (Таблица 1). Для частного случая гексагональной решетки в 2D вершинной модели этот результат согласуется с исх. 56. В более общем смысле, для неупорядоченных сетей геометрические коэффициенты aℓ и aa появляются в знаменателе, потому что они описывают неаффинности, которые возникают в ответ на глобальные изотропные деформации ( SI Приложение , раздел IE).Сравнение прогнозируемого ΔB с результатами моделирования показано на рис. 3. ( A — C ) Прогнозируемое и наблюдаемое поведение неоднородности объемного модуля упругости ΔB для ( A ) 2D пружинные сети для разных значений координационного числа z, ( B ) 2D вершинная модель для разных значений жесткости площади kA и ( C ) 3D модель Вороного для разных значений объемной жесткости kV. Синие кружки указывают на моделирование, а красные кривые указывают на прогнозы без подгоночных параметров, основанных на уравнении. 9 . В A черная пунктирная кривая вычисляется с использованием значений для точки перехода ℓ0 * и геометрического масштабного коэффициента aℓ, непосредственно измеренных для каждого значения z, в то время как для красной линии мы использовали масштабные соотношения из таблицы 1. Как было показано ранее (8⇓ – 10, 12, 14⇓ – 16, 18⇓⇓ – 21), недостаточно жесткие системы также могут быть усилены путем приложения конечной деформации сдвига. Теперь мы включаем деформацию сдвига γ в наш формализм и проверяем наши прогнозы на двумерных пружинных сетях.Однако мы ожидаем, что наши выводы в равной степени применимы к моделям на основе ячеек ( SI Приложение , разделы IC и ID). Мы также численно подтвердили, что наши аналитические прогнозы также применимы к 2D волоконным сетям без жесткости на изгиб ( SI Приложение , раздел IIC) (57). Чтобы расширить наш подход, мы принимаем во внимание, что функция минимальной длины ℓ¯min (σℓ) в принципе может также зависеть от деформации сдвига γ. Таким образом, мы разложим Тейлора по γ, ℓ¯min (σℓ, γ) = ℓ0 * −aℓσℓ + bγ2, [10] где линейный член в γ опускается из-за симметрии при расширении относительно изотропного состояния (на практике, для нашего конечного -размерных систем, мы опускаем линейный член в γ, определяя точку γ = 0 с помощью стабилизации сдвига; SI Приложение , разделы ID и IV).Хотя на данный момент у нас нет формального доказательства того, что ¯min является аналитическим, и окончательное обоснование уравнения. 10 получается в результате численной проверки (следующий абзац), мы предполагаем, что для большинства систем ℓ¯min будет аналитичным по γ, вплоть до случайно разбросанных точек γ, где возникают сингулярности в виде пластических перестроек. При фиксированном значении γ граница раздела между гибким диском и жестким режимом снова задается ¯min (σℓ = 0, γ), а соответствующая фазовая диаграмма с точки зрения обоих управляющих параметров γ и ℓ0 показана на Инжир.4 А . В самом деле, мы также численно находим квадратичный масштаб для линии перехода, ℓ0 − ℓ0 * = b (γ *) 2, до деформаций сдвига γ∼0,1 (рис. 4 C и SI Приложение , раздел IIB ). Находим, что для пружинных сетей коэффициент b зависит от Δz примерно как b∼Δz − 1 (рис. 4 C , вставка ), что можно понять из свойств плотности состояний ( SI Приложение , раздел ЕСЛИ). Для оптимизации точности значения b были извлечены из отношения G = 4b (ℓ¯ − ℓ0) на этом графике (см. Ниже и сравните с рис.4 F ). Нелинейное упругое поведение субизостатических пружинных сетей при сдвиге. ( A ) Схематическая фазовая диаграмма, иллюстрирующая параболическую границу между жестким (серое затенение) и гибким (без затенения) режимами, в зависимости от предпочтительной длины пружины ℓ0 и деформации сдвига γ. ( B ) Схема, показывающая зависимость модуля сдвига G от деформации сдвига γ для различных значений 0 (сравните с A ). Обратите внимание, что при 0> ℓ0 * (красная кривая) уравнение. 12 предсказывает неоднородность ΔG * модуля сдвига в начале жесткости. ( C ) Мы численно находим квадратичную зависимость между ℓ0 − ℓ0 * и критическим сдвигом γ *, при котором сеть становится жесткой при заданном ℓ0> ℓ0 *. Это согласуется с нашим разложением Тейлора в уравнении. 10 , а квадратичный режим распространяется на деформации сдвига до γ∼0,1. Отклонения для очень малых ℓ0 − ℓ0 * объясняются ограничением конечного модуля сдвига 10−10, используемым для зондирования границы раздела фаз ( SI Приложение , раздел IVB).( C , Вставка ) Префактор b, связанный с квадратичным соотношением в C , масштабируется приблизительно как b∼1 / Δz. ( D ) Масштабирование модуля сдвига за пределами неоднородности модуля сдвига, (G − ΔG *) / ΔG * по (γ − γ *) / γ * с ℓ0 − ℓ0 * = 10−4. Пунктирная черная линия указывает на прогноз по формуле. 12 без подгоночных параметров. ( D , Вставка ) Масштабирование неоднородности модуля сдвига ΔG * с ℓ0 − ℓ0 *. ( E и F ) Масштабирование модуля сдвига с γ и ℓ0 * -ℓ0, соответственно.В C – F координационное число z = 3,2. Знание функциональной формы ℓ¯min (σℓ, γ) вблизи линии перехода позволяет нам явно выразить энергию в жестком режиме через оба управляющих параметра ( SI Приложение , раздел IC): e (ℓ0 , γ) = N1 + aℓ2ℓ0 * −ℓ0 + bγ22. [11] Это позволяет нам явно вычислить модуль сдвига G = (d2e / dγ2) / N. Как для гибкого, так и для жесткого режима получаем G (ℓ0, γ) = Θℓ0 * −ℓ0 + bγ24b1 + aℓ2ℓ0 * −ℓ0 + 3bγ2, [12] где Θ — функция Хевисайда.Теперь обсудим некоторые следствия этого выражения для модуля сдвига (рис. 4 B ). При срезании системы, начиная с гибкого режима (т. Е. При 0> 0 *), уравнение. 12 предсказывает скачкообразное изменение модуля сдвига ΔG * = 8b (ℓ0 − ℓ0 *) / (1 + aℓ2) в начале жесткости при γ * = [(ℓ0 − ℓ0 *) / b] 1/2 . Мы проверяем линейное масштабирование ΔG * ∼ (ℓ0 − ℓ0 *) на Рис. 4 D , Вставка и значение масштабного коэффициента в SI Приложение , раздел IIB.Кроме того, уравнение. 12 также правильно предсказывает поведение за пределами γ *, как показано на фиг. 4 D . Ур. 12 также правильно предсказывает поведение модуля сдвига для ℓ0≤ℓ0 *. Для ℓ0 = ℓ0 * модуль сдвига масштабируется квадратично с γ (рис. 4 E ), в то время как для γ = 0 модуль сдвига изменяется линейно с (ℓ0 * −ℓ0)> 0 (рис. 4 F ; см. приложение SI , идентификатор раздела для сотовых моделей), как сообщалось ранее для многих сотовых моделей (37, 46, 56).В обоих случаях мы проверили, что соответствующие коэффициенты совпадают с их ожидаемыми значениями на основе значений aℓ и b. В частности, для γ = 0, поскольку (ℓ0 * −ℓ0) = (1 + aℓ2) (ℓ¯ − ℓ0), мы получаем простое соотношение G = 4b (ℓ¯ − ℓ0), которое объясняет коллапс в масштабирование модуля сдвига для различных кВ в трехмерной модели Вороного, о которой некоторые из нас сообщили ранее (46). Мы также получаем явные выражения для напряжения сдвига σ̃ = (de / dγ) / N и изотропного напряжения, то есть отрицательного давления −p ( SI Приложение , разделы ID и IE).Для последнего находим отрицательный эффект Пойнтинга с коэффициентом χ≡p / γ2 = −2dbℓ0 * / D (1 + aℓ2) при ℓ0 = ℓ0 *. Более того, мы находим следующие соотношения для модуля сдвига: G = ΔG * + 3γσ̃ G = ΔG * −6Dbdℓ0 * p. [13] Действительно, мы наблюдаем коллапс наших данных моделирования для 2D пружинных сетей в обоих случаях (рис. 5 и рис. 5, , вставка ), где мы используем значение, близкое к началу жесткости, γ≃γ *. Избыточный модуль сдвига G − ΔG * линейно масштабируется с напряжением сдвига σ̃ в 2D пружинных сетях.Мы обнаруживаем коллапс при изменении масштаба G − ΔG * на критическую деформацию сдвига γ *. Черная пунктирная линия соответствует предварительному коэффициенту 3, как предсказано уравнением. 13 . ( Вставка ) Избыточный модуль сдвига G − ΔG * линейно масштабируется с изотропным напряжением −p, и мы получаем обрушение при изменении масштаба на b / ℓ0 *. Черная пунктирная линия — прогноз согласно формуле. 13 . В этой статье мы предлагаем объединяющую точку зрения на материалы с недостаточными ограничениями, которые усилены геометрической несовместимостью.Это актуально для широкого класса материалов (6) и недавно обсуждалось в контексте биополимерных гелей (8, 12–14, 21) и биологических тканей (31, 37, 42, 46). Как и в случае с гитарной струной, мы можем предсказать многие особенности механической реакции этих систем путем количественной оценки геометрической несовместимости — мы разработали общее геометрическое правило ℓ¯min, определяющее, как обобщенные пружины в неупорядоченной сети отклоняются от своей длины покоя. Используя эту функцию минимальной средней длины ℓ¯min, мы затем выводим макроскопические упругие свойства очень широкого класса недонагруженных, предварительно напряженно-жестких материалов из первых принципов.Мы численно проверяем наши результаты, используя модели для биополимерных сетей (9, 14) и биологических тканей (34, 38, 46). Наша работа актуальна для экспериментаторов и может объяснить воспроизводимость ряда общих механических характеристик, обнаруженных, в частности, для биополимерных сетей (12, 17, 21, 25). Хотя здесь мы пренебрегаем жесткостью на изгиб волокна, которая присутствует во многих моделях биополимерных сетей (12⇓⇓ – 15, 21), будущая работа, которая будет включать такой термин, позволит дополнительно уточнить наши теоретические результаты (обсуждение ниже) и следующее сравнение с экспериментами. .Для деформаций сдвига с ℓ0, достаточно близким к ℓ0 * и близким к началу жесткости γ≃γ *, мы предсказываем линейное масштабирование дифференциального модуля сдвига G с помощью касательного напряжения σ̃, где (G − ΔG *) / σ̃∼1 / γ *, о чем сообщалось ранее для биополимерных сеток (12, 13, 21). Однако здесь мы дополнительно предсказываем из первых принципов, что значение префактора равно 3, что согласуется с предыдущими экспериментальными результатами (12, 21). Более того, наша работа убедительно свидетельствует о том, что соотношение (G − ΔG *) / σ̃ = 3 / γ является общим признаком жесткости, вызванной предварительным напряжением, в недостаточно жестких материалах.Таким образом, мы предлагаем его в качестве общего экспериментального критерия для проверки того, можно ли понять наблюдаемое деформационное усиление с точки зрения геометрически индуцированной жесткости. Если это применимо к биополимерным гелям, это может помочь определить, связано ли деформационное усиление геля с нелинейной механикой отдельных нитей или с геометрическими эффектами, обсуждаемыми здесь, что является давним вопросом в данной области (8, 58). Мы также можем применить эти прогнозы к типичной геометрии реометра ( SI Приложение , раздел IG).Мы прогнозируем, что нетипичное нормальное напряжение растяжения σzz развивается при простом сдвиге, что соответствует отрицательному эффекту Пойнтинга, и что σzz линейно масштабируется с напряжением сдвига и модулем сдвига: σzz∼σ̃∼ (G − ΔG *) (уравнение 13 ). и SI Приложение , раздел IG). Именно это было обнаружено для многих биополимерных гелей, таких как коллаген, фибрин или матригель (12, 21, 25, 26). Однако, в отличие от исх. 21 наша работа предполагает, что коэффициент масштабирования между σzz и (G − ΔG *) должен быть в значительной степени независимым от γ *.Хотя эти эффекты также можно объяснить нелинейностями (25, 58⇓ – 60) и уже обсуждались в контексте жесткости, вызванной предварительным напряжением (13, 19, 21), мы показываем здесь, что они представляют собой очень общую характеристику жесткости. в недостаточно стесненных материалах. Наша работа также подчеркивает важность изотропных деформаций при изучении жесткости, вызванной предварительным напряжением, что экспериментально продемонстрировано в справочнике. 17. В то время как предыдущие работы (8, 9, 12, 14, 15, 18, 20, 21) были сосредоточены почти (10) полностью на деформациях сдвига, мы дополнительно изучаем влияние изотропных деформаций, представленных управляющим параметром ℓ0.Во-первых, из-за неоднородности объемного модуля упругости наша работа предсказывает нулевое нормальное напряжение при сжатии и линейно увеличивающееся нормальное напряжение при расширении, что согласуется с экспериментальными данными по биополимерным сеткам (17) (предполагая, что в одноосной реакции преобладает изотропная часть тензора напряжений. ; SI Приложение , раздел IG). Во-вторых, мы также правильно предсказываем увеличение критической деформации сдвига γ * при сжатии, что соответствует увеличению ℓ0 (17) (ср. С рис.4 А ). Хотя мы также прогнозируем увеличение модуля сдвига G при растяжении, которое также наблюдалось (17), дополнительные эффекты, возникающие из-за суперпозиции чистого сдвига и простого сдвига, весьма вероятно, играют важную роль в этом случае. Хотя мы считаем, что это выходит за рамки данной статьи, будет несложно расширить нашу работу этим аспектом. Таким образом, мы разработали подход, позволяющий понять, сколько недостаточно ограниченных неупорядоченных материалов затвердевает аналогично гитарной струне.Хотя ясно, что 1D-струна становится жесткой именно тогда, когда она растягивается на оставшуюся длину, мы показываем, что в 2D- и 3D-моделях жесткость регулируется геометрической функцией минимальной длины ℓ¯min с общими характеристиками (например, линейным масштабированием с собственными флуктуациями, квадратичным масштабированием с деформацией сдвига). Это понимание позволяет нам делать точные прогнозы для многих функций масштабирования и предварительных факторов, которые описывают линейный отклик этих материалов. Кроме того, выполняя численные измерения геометрии в жесткой фазе для извлечения коэффициентов функции ℓ¯min, мы можем даже предсказать точные величины некоторых макроскопических механических свойств. Кроме того, эти прогнозы помогают объединить или прояснить несколько масштабных коллапсов, которые ранее были идентифицированы в литературе. Для двумерных пружинных сетей, полученных из застрявших насадок, мы изучили зависимость наших геометрических коэффициентов от координационного числа z и пришли к выводу, что приблизительно aℓ∼Δz − 1/2 и b∼Δz − 1. В сочетании с нашим выводом о том, что значение ℓ0 сразу после инициализации зависит линейно от z, так что (ℓ0 − ℓ0 *) ∼Δz ( SI Приложение , рис. S5 A , вставка ), мы получаем, что критический деформация сдвига γ * масштабируется как γ * ∼Δzβ с β = 1.Аналогичным образом находим соответствующий разрыв модуля сдвига ΔG * ∼Δzθ с θ = 1. Хотя оба показателя согласуются с более ранними выводами Wyart et al. (9) и связанный с недавней работой Cui и Zaccone (61), наш подход подчеркивает важность начального значения ℓ0 для упругих свойств при сдвиге. В другой работе регулярные сети с разбавленными связями давали разные показатели β и θ (16), что неудивительно, потому что показатели масштабирования aℓ и b с Δz, вероятно, зависят от способа создания сети.В более общем плане, хотя мы наблюдали, что значения ℓ0 *, aℓ, aa и b в некоторой степени зависят от протокола подготовки системы и минимизации энергии, они относительно воспроизводимы среди различных случайных реализаций данного протокола (55). Кроме того, мы аналитически прогнозируем и численно подтверждаем существование и точное значение неоднородности модуля сдвига ΔG * в отношении деформации сдвига, существование которой для волоконных сетей без жесткости на изгиб обсуждалось недавно (14, 15, 18, 20). , 24).Мы также предсказываем общий масштаб модуля сдвига за пределами этого разрыва: (G − ΔG *) ∼ (γ − γ *) f при f = 1. Меньшие значения f, о которых сообщалось ранее для различных типов пружинных и волоконных сетей (14, 15, 18, 20), вероятно, связаны с членами более высокого порядка в ¯min. Учитывая очень общий характер нашего подхода, мы ожидаем найти значение f = 1 и в этих системах, если зондирование будет достаточно близким к ℓ0 = ℓ0 *. Одним из основных препятствий при определении упругих свойств неупорядоченных материалов является появление неоднородностей, которые могут привести к срыву подходов, подобных теории эффективной среды, близкой к переходу (10).В нашем случае эффекты неоднородностей по построению полностью включаются в геометрические коэффициенты aℓ, aa и b. Однако, хотя меры неаффинности обсуждались ранее (9, 15, 20, 28, 62), они обычно сильно отличаются от наших коэффициентов aℓ, aa и b. Например, для пружинных сетей такие ранние определения обычно включают поворот пружины, в то время как наши коэффициенты представляют только изменения длины пружины. Следовательно, в то время как более ранние определения отражают большую часть фактического движения микроскопических элементов, наши коэффициенты сохраняют только ту часть, которая имеет непосредственное отношение к энергии системы и, следовательно, к механике.Другими словами, коэффициенты aℓ, aa, b (и ℓ0 *) можно рассматривать как минимальный набор параметров, необходимых для характеристики свойств упругой системы вблизи перехода. Есть несколько возможных будущих расширений этой работы. Во-первых, мы сосредоточились здесь на переходах, созданных минимальной длиной, где система гибкая для больших 0 и жесткая для малых 0. Однако в принципе существует также возможность перехода, создаваемого, например, максимальной длиной, что, например, имеет место при классическом заклинивании сфер.Хотя мы иногда видели что-то подобное в наших пружинных сетях, близких к изостатичности, мы обычно ожидаем, что это будет менее типичным для недостаточно ограниченных систем из-за потери устойчивости. Во-вторых, хотя мы изучали здесь окрестность одного локального минимума ¯min, зависящего, например, от γ, было бы интересно изучить поведение системы за его пределами, включив члены более высокого порядка в ¯min и за счет явного учета пластических событий (63). В случае биологических тканей пластические события обычно соответствуют так называемым T1 переходам (64), которые в нашем подходе будут соответствовать переходу на другую ℓ¯min “ветвь.” В-третьих, важно изучить, что определяет точные значения геометрических коэффициентов aℓ, aa и b; как они зависят от сетевой статистики; и почему они относительно воспроизводимы. Для клеточных моделей с термином площади предварительные результаты показывают, что отношение обоих коэффициентов «a» может быть оценено как aa / aℓ≈dℓ0 * / D, потому что самонапряжение, возникающее в начале жесткости, по-видимому, преобладает. за счет баланса сил между натяжением по периметру ячейки и давлением внутри каждой ячейки. В-четвертых, поскольку мы отделили геометрию от энергетики, в принципе возможно обобщить нашу работу на другие потенциалы взаимодействия, например, на правильное выражение для полугибких нитей (58, 60), и включить эффект активных напряжений (54, 65⇓ – 67). Обратите внимание, что наша работа напрямую обобщается на любой аналитический потенциал взаимодействия с локальным минимумом на конечной длине. Хотя в этом более общем случае уравнение. 5 будет включать в себя кумулянты более высокого порядка ℓi, эти члены более высокого порядка не будут иметь значения в гибком режиме, и мы ожидаем, что они будут незначительными в жесткой окрестности перехода, где мы делаем большинство наших прогнозов. В-пятых, эта работа может также предоставить основы для систематической связи макроскопических механических свойств материала с лежащей в основе локальной геометрической структурой. Например, для биополимерных сетей свойства локальной геометрической структуры могут быть извлечены с помощью рассеяния света, сканирующей электронной микроскопии или конфокальной отражательной микроскопии (21, 68, 69). В частности, наши симуляции показывают, что в моделях без члена площади функция ℓ¯min не сильно меняется при увеличении размера системы почти на порядок ( SI Приложение , раздел IID), что предполагает, что локальная геометрия действительно может быть достаточно, чтобы охарактеризовать крупномасштабные механические свойства таких систем.В число оставшихся проблем в будущем входит разработка простого способа вычисления наших геометрических коэффициентов на основе простых свойств, характеризующих локальную геометрическую структуру без необходимости моделирования, и поиск способов обнаружения возможных остаточных напряжений, которые могли быть встроены в гель во время полимеризации. Наконец, наш подход, вероятно, можно расширить, включив также изостатические и сверхограниченные материалы. Например, обычно предполагается, что в механике биополимерных сетей преобладает жесткость на растяжение волокон, которые образуют субизостатическую сеть, но что дополнительная жесткость на изгиб волокна превращает сеть в чрезмерно ограниченную систему (12–15, 21). , 22).Прогнозы, которые мы делаем здесь, сосредоточены на пределе с преобладанием растяжения, когда жесткостью волокна при изгибе можно пренебречь, что достигается за счет слабого модуля изгиба волокна и / или в более жестких частях фазового пространства. Обобщение нашего формализма на чрезмерно ограниченные системы позволит нам расширить наши прогнозы за пределы этого режима и, таким образом, уточнить наше сравнение с экспериментальными данными. 2D пружинные сети были инициализированы как случайно разрезанные сети, полученные из упаковки (9, 27).Чтобы повысить точность по сравнению с клеточными моделями, мы создали нашу собственную реализацию версии Полака – Рибьера метода минимизации сопряженного градиента (70), где для поиска линий мы используем саморазработанный метод Ньютона, основанный только на производных энергии. Все состояния были минимизированы до тех пор, пока средняя сила на степень свободы не стала меньше 10-12. Для развертки ℓ0 на рис. 1 A и B и для нахождения точки (γ, ℓ0) = (0, ℓ0 *) мы использовали стабилизацию сдвига. Подробности приведены в Приложении SI , раздел IVB. Для моделирования двумерных вершинных моделей мы всегда начинали с мозаики Вороного случайных точечных шаблонов, созданных с использованием библиотеки алгоритмов вычислительной геометрии (CGAL) (https://www.cgal.org/), и мы использовали реализацию BFGS2 Научная библиотека GNU (GSL) (https://gnu.org/software/gsl/) для минимизации энергии. Мы применили трехсторонние вершины, и отрезок длины для переходов T1 был установлен на 10−5, и есть максимально возможное количество переходов T1 на интерфейсе одна ячейка-ячейка, равное 104.Все изученные конфигурации вершинных 2D-моделей были стабилизированы сдвигом. Для моделирования 2D модели Вороного мы начали со случайных точечных шаблонов и минимизировали энергию системы с помощью подпрограммы BFGS2 GSL, каждый раз используя CGAL для вычисления мозаики Вороного. Из-за ограничений CGAL конфигурации не были стабилизированы на сдвиг. Для моделирования трехмерной модели Вороного мы использовали стабилизированные сдвигом состояния с минимизированной энергией, сгенерированные в исх. 46 с использованием подпрограммы многомерной минимизации BFGS2 GSL. Подробная информация о различных протоколах моделирования (0 разверток и деление пополам для получения точки перехода) подробно обсуждается в Приложении SI , раздел IV. Мы благодарим Дэниела М. Сассмана за плодотворные обсуждения. М.М. и М.Л.М. выражаем благодарность за финансирование от Фонда Саймонса в рамках гранта 446222, Фонда Альфреда П. Слоана, Фонда Гордона и Бетти Мур и Исследовательской корпорации по развитию науки в рамках программы Cottrell Scholars и вычислительной поддержки в рамках гранта NSF ACI-1541396.М.Л.М. также благодарит за поддержку со стороны Simons Foundation в рамках гранта 454947 и NSF-DMR-1352184 и NSF-PHY-1607416. К.Б. и B.P.T. выражаем благодарность за финансирование от Нидерландской организации научных исследований. Вклад авторов: M.M., B.P.T. и M.L.M. спланированное исследование; М.М. проведенное исследование; М.М. и К. проанализированные данные; и M.M., B.P.T. и M.L.M. написал газету. Авторы заявляют об отсутствии конфликта интересов. Эта статья представляет собой прямое представление PNAS. Эта статья содержит вспомогательную информацию на сайте www. Результаты
Жесткость обусловлена геометрической несовместимостью, соответствующей критерию минимальной длины.
Минимальная длина шкалы линейно с колебаниями.
Прогнозирование неоднородности модуля объемной упругости.
Nonlinear Elastic Behavior Под сдвигом.
Обсуждение
Материалы и методы
Благодарности
Сноски

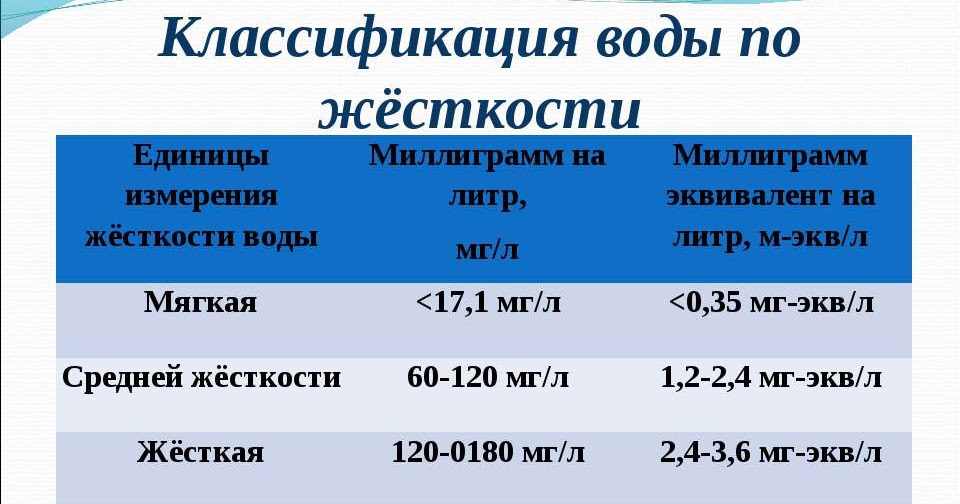 Однако отклонения от дипольного поля во многих случаях можно рассматривать как
малое возмущение. Вторым важным фактором становится пересечение некоторыми
траекториями поверхности Земли, точнее, верхней атмосферы. Очевидно, что частица
не может прийти по такой траектории. В результате между минимальным и
максимальным значением жесткости формируется область — так называемая пенумбра,
имеющая сложную структуру чередования разрешенных и запрещенных траекторий. На
рисунке приведено несколько рассчитанных примеров пенумбры. Черный цвет
соответствует запрещенным траекториям. Первая левая белая полоса соответствует
минимальной жесткости, край правого черного прямоугольника – максимальной.
Однако отклонения от дипольного поля во многих случаях можно рассматривать как
малое возмущение. Вторым важным фактором становится пересечение некоторыми
траекториями поверхности Земли, точнее, верхней атмосферы. Очевидно, что частица
не может прийти по такой траектории. В результате между минимальным и
максимальным значением жесткости формируется область — так называемая пенумбра,
имеющая сложную структуру чередования разрешенных и запрещенных траекторий. На
рисунке приведено несколько рассчитанных примеров пенумбры. Черный цвет
соответствует запрещенным траекториям. Первая левая белая полоса соответствует
минимальной жесткости, край правого черного прямоугольника – максимальной. Для однозначного определения жесткости обрезания вводится т.н. «эффективная»
жесткость (Rэф),
определяемая по формуле:
Для однозначного определения жесткости обрезания вводится т.н. «эффективная»
жесткость (Rэф),
определяемая по формуле:
 Отметим, что верхняя огибающая области пенумбры, как и кривая
жесткости в приэкваториальной области, изменяется практически регулярным образом
в соответствии с теорией Штермера.
Отметим, что верхняя огибающая области пенумбры, как и кривая
жесткости в приэкваториальной области, изменяется практически регулярным образом
в соответствии с теорией Штермера. При расчетах проведено усреднение по местному времени.
Рассчитанные данные могут быть проинтерполировнаы на произвольные значения
географических координат, а также на различные высоты, местные времена и
значения Kp-индекса [15].
При расчетах проведено усреднение по местному времени.
Рассчитанные данные могут быть проинтерполировнаы на произвольные значения
географических координат, а также на различные высоты, местные времена и
значения Kp-индекса [15].